Figures and data in Coevolution-based inference of amino acid interactions underlying protein function

Figures
Tables
Additional files

8 figures, 1 table and 2 additional files

Figures

Figure 1 with 2 supplements

Download asset Open asset

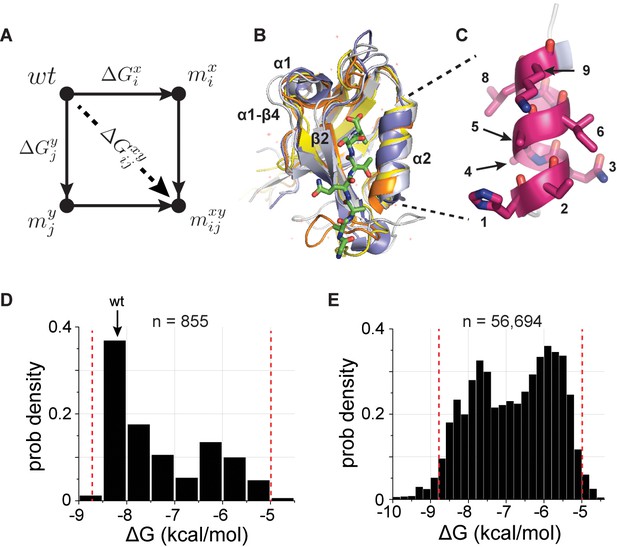
A deep coupling scan (DCS) for the PDZ binding pocket.

(A), The thermodynamic double mutant cycle (TDMC), a formalism for studying the energetic coupling of pairs of mutations in a protein. Given two mutations ( $x$ at postion $i$ and $y$ at position $j$ ), the coupling free energy between them is defined as the extent to which the effect of the double mutation ( $Δ G_{i j}^{x y}$ ) is different from the summed effect of the mutations taken individually ( ${Δ G}_{i}^{x} + {Δ G}_{j}^{y}$ ), a measure of the interaction (or epistasis) between the two mutations (see Equation 1, main text). (B), Structural overlay of the five PDZ homologs used in this study (PSD95^pdz3 (1BE9, white), PSD95^pdz2 (1QLC, orange), ZO1^pdz (2RRM, yellow), Shank3^pdz (5IZU, gray), and Syntrophin^pdz (1Z86, blue)), emphasizing the conserved αβ-fold architecture of these sequence-diverse proteins (33% average identity, Table 1).Structural elements discussed in this work are indicated. (C), The nine-amino acid α2-helix, which forms one wall of the ligand-binding site. (**D–E**), The distribution of experimentally determined binding free energies, $Δ G_{b i n d}$ , for all single mutations (D, 855/855) and nearly all double mutations (E, 56,694/64,980) in the α2-helix for the 5 PDZ homologs, with the affinity of wild-type PSD95pdz3 indicated (wt). The red lines indicate the independently validated range of the assay (Figure 1—figure supplement 1); essentially all measurements fall within this range. These data comprise the basis for a deep analysis of conserved thermodynamic coupling in the PDZ family.

https://doi.org/10.7554/eLife.34300.002

Figure 1—figure supplement 1

Download asset Open asset

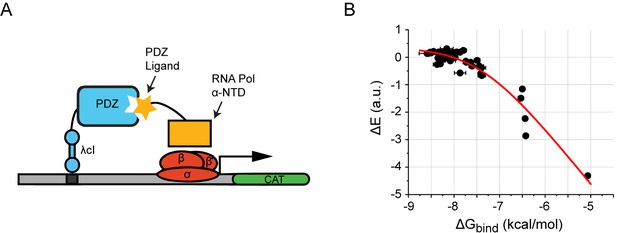
The bacterial two-hybrid assay for PDZ ligand binding.

(A) The bacterial two-hybrid system consists of three parts, (1) a PDZ domain fused to the C-terminus of a $λ$ -cI DNA binding domain, (2) a ligand peptide as a C-terminal fusion to the $α$ -subunit of RNA polymerase, and (3) a reporter plasmid encoding chloramphenicol acetyltransferase (*CAT*). Ligand binding induces transcription of the reporter gene, which enables growth in the presence of the antibiotic chloramphenicol. (B) Binding free energies for 45 PSD95^pdz3 single mutants plotted against the relative enrichment values $Δ E$ derived from deep sequencing before and after selection (see Supplementary Methods). Horizontal bars around each point represent the range of values from replicate binding experiments, and the red curve represents a fit to a model in which the relative enrichment is proportional to the log fraction bound of ligand ( $Δ E \propto \ln f_{B}$ , see Supplementary Methods). Parameters of the assay (inductions conditions, temperature, length of growth, promoter structure) are optimized such relative enrichment values quantitatively report the binding free energy (fit shows an adjusted $r^{2} = 0.91$ ).

https://doi.org/10.7554/eLife.34300.003

Figure 1—figure supplement 2

Download asset Open asset

Reproducibility and quality of the bacterial two-hybrid assay.

The panels show 2D histograms of all single and double mutant binding free energies for four independent experimental trials of the bacterial two-hybrid assay for PSD95^pdz3. The data show that the assay is remarkably reproducible, with >95% of values with a variance less than 0.31 kcal/mol. See Table 1 for counting statistics of all mutants and number of double mutant cycles estimated per PDZ homolog.

https://doi.org/10.7554/eLife.34300.004

Figure 2 with 5 supplements

Download asset Open asset

Distributions of pairwise thermodynamic couplings in a single PDZ homolog (PSD95^pdz3).

Each subplot shows the distribution of coupling free energies ( $Δ Δ G$ , see Equation 1, main text) for all measured mutants at one pair of positions in the α2-helix (numbering per Figure 1C) in PSD95^pdz3. The distributions are fit to single or double Gaussians, using the Bayes Information Criterion to justify choice of model, and the position of zero coupling is indicated by the solid line and circle above. Population-weighted mean values are represented by dashed lines. The data are remarkably well defined by the fitted models. Most position pairs have distributions centered close to zero, with only eight pairs comprising all pairwise couplings between positions 1, 4, 5, and 8, and 1-2, 1-9 showing deviations. For these pairs, distributions of mutational coupling follow either a single mode (1-2, 1-5) or two modes with one centered at zero (1-4, 1-8, 1-9, 4-5, 4-8, 5-8); population-weighted mean values for these pairs are indicated in red. Figure 2—figure supplement 1–4 show similar data for each of the other homologs taken individually.

https://doi.org/10.7554/eLife.34300.006

Figure 2—figure supplement 1

Download asset Open asset

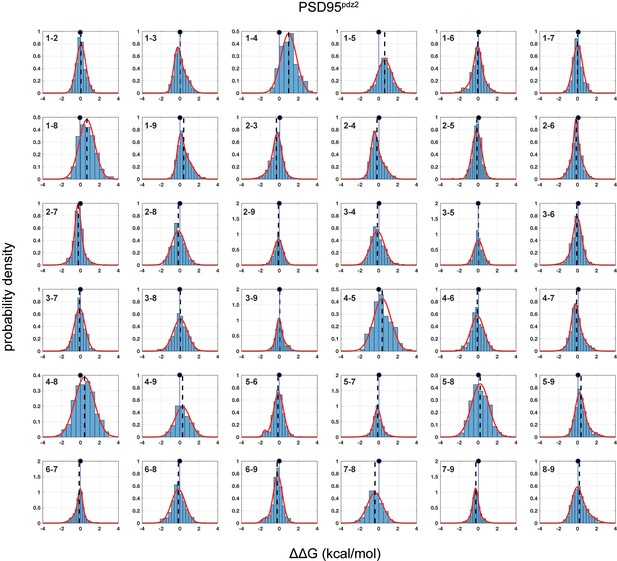
Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for PSD95^pdz2.

As in Figures 2–3, distributions are fit to single or double Gaussians, using the Bayes Information Criterion to choose the model. The position of zero coupling is indicated by the solid line and circle above, and the population weighted mean is represented in dashed lines.

https://doi.org/10.7554/eLife.34300.007

Figure 2—figure supplement 2

Download asset Open asset

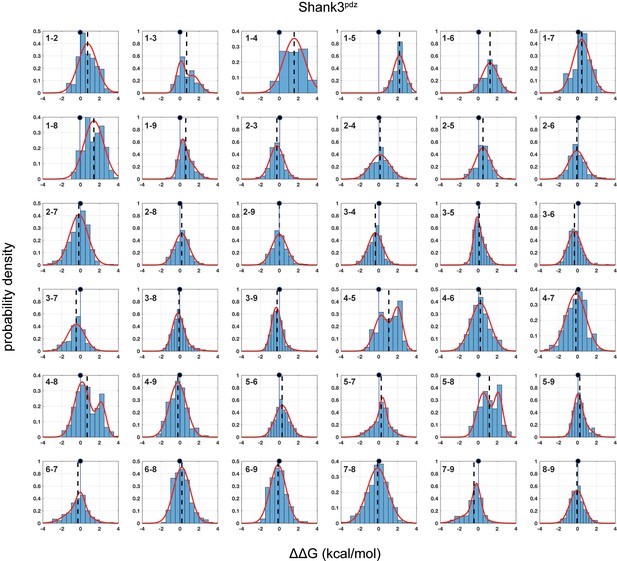
Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Shank3^pdz.

As in Figure 3. 2–3, distributions are fit to single or double Gaussians, using the Bayes Information Criterion to choose the model. The position of zero coupling is indicated by the solid line and circle above, and the population weighted mean is represented in dashed lines.

https://doi.org/10.7554/eLife.34300.008

Figure 2—figure supplement 3

Download asset Open asset

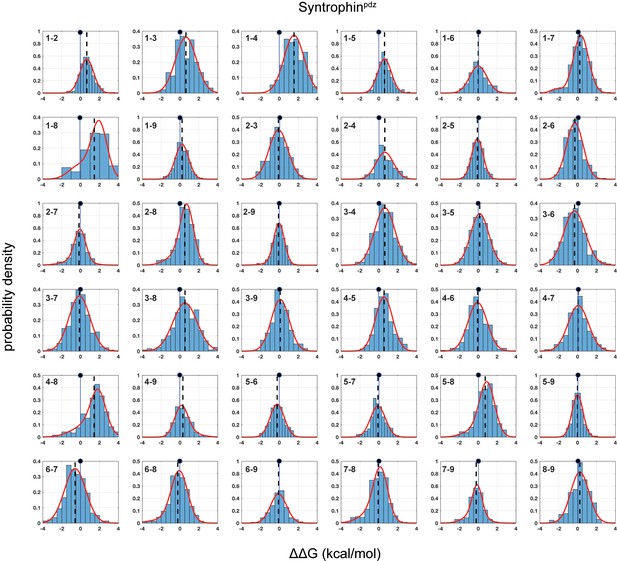
Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Syntrophin^pdz.

As in Figures 2–3, distributions are fit to single or double Gaussians, using the Bayes Information Criterion to choose the model. The position of zero coupling is indicated by the solid line and circle above, and the population weighted mean is represented in dashed lines.

https://doi.org/10.7554/eLife.34300.009

Figure 2—figure supplement 4

Download asset Open asset

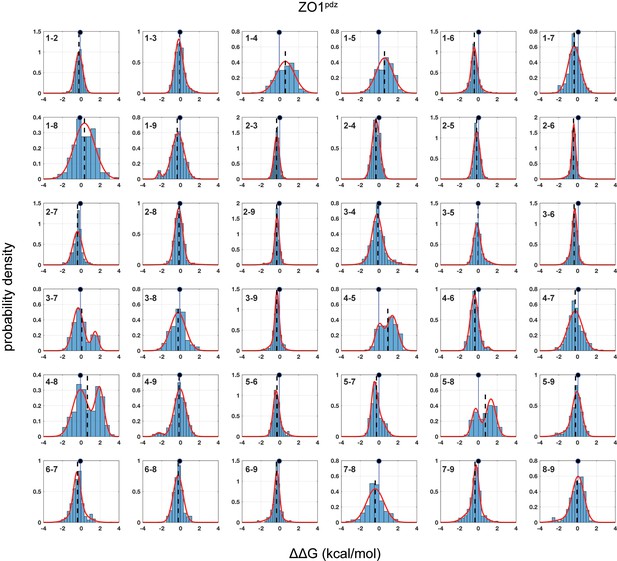
Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for ZO1^pdz.

As in Figures 2–3, distributions are fit to single or double Gaussians, using the Bayes Information Criterion to choose the model. The position of zero coupling is indicated by the solid line and circle above, and the population weighted mean is represented in dashed lines.

https://doi.org/10.7554/eLife.34300.010

Figure 2—figure supplement 5

Download asset Open asset

Distributions of coupling in relative enrichment ( $Δ Δ E$ ) for a sampling of position pairs in the GB1 domain of the immunoglobulin-binding protein G.

The data are from (Olson et al., 2014), and position numbering is as given in that work; note that coupling is calculated here directly from enrichment scores. As in Figures 1 and 2, distributions are fit to single or double Gaussians, using the Bayes Information Criterion to choose the model. The population weighted mean is represented in dashed lines, and values for each position pair are shown. Note that coupling energies are reported with the opposite sign due to the inverse relationship between $∆ E$ in Olsen et al. and $Δ G$ in this work.

https://doi.org/10.7554/eLife.34300.011

Figure 3 with 1 supplement

Download asset Open asset

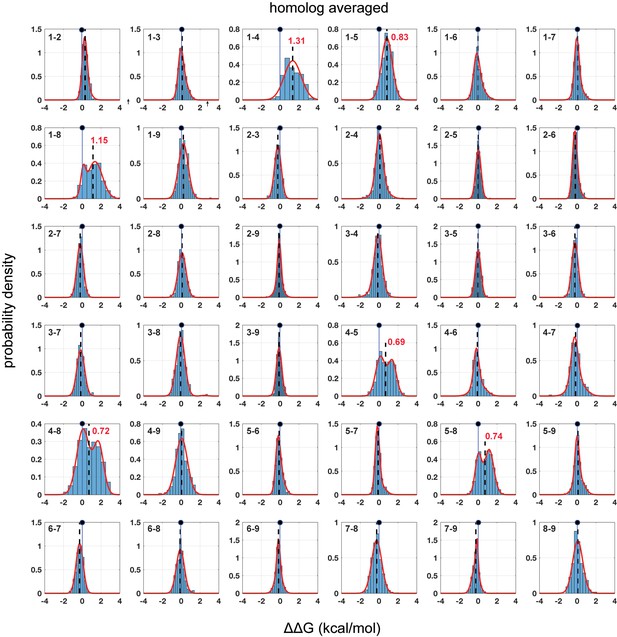
Homolog-averaged pairwise thermodynamic couplings in the PDZ domain.

Each subplot shows the distribution of coupling free energies ( $Δ Δ G$ , see Equation 1, main text) for all measured mutants at one pair of positions in the α2-helix, but here averaged over the five homologs. As in Figure 2, the distributions are fit to single or double Gaussians, using the Bayes Information Criterion to justify choice of model. The position of zero coupling is indicated by the solid line and circle above and population-weighted mean values are represented by dashed lines. Averaging over homologs reveals the conserved pattern of couplings; now, only six pairs comprising all pairwise couplings between positions 1, 4, 5, and 8 show deviations from zero. For these pairs, distributions of mutational coupling follow either a single mode (1-4, 1-5) or two modes with one centered at zero (1-8, 4-5, 4-8, 5-8); population-weighted mean values for these pairs are indicated in red.

https://doi.org/10.7554/eLife.34300.012

Figure 3—figure supplement 1

Download asset Open asset

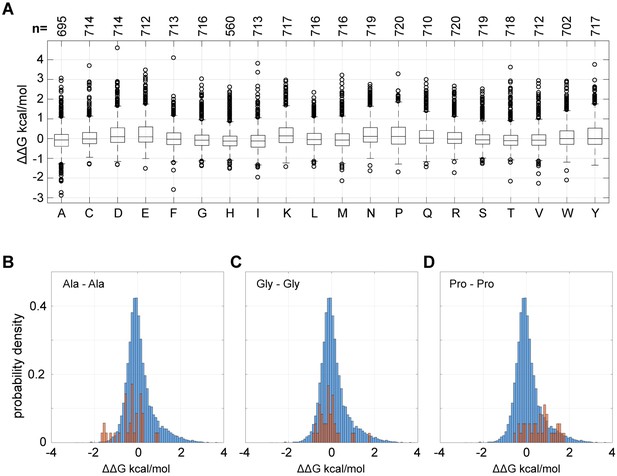
Amino acid contributions to distributions of double mutant cycle coupling energies for the PDZ α2 helix.

(A), Boxplots showing the couplings for each amino acid substitution with every other amino acid substitution in the homolog-averaged dataset. The data show that every amino acid substitution is involved in essentially the full range of observed couplings, and mean couplings for each mutation is near zero. These findings indicate that the magnitude of couplings is not a simple property of the average chemical properties of different amino acids, and that mutations on average are subtle perturbations to protein function. (**B–D**), Each graph shows the distribution of pairwise thermodynamic couplings for all pairs of positions in the homolog-averaged dataset (blue), with couplings for Ala – Ala (B), Gly – Gly (C), and Pro – Pro (D) mutations highlighted in red. The data suggest a broad range of couplings for all these substitutions, arguing that the magnitude of coupling energies is not obviously defined by intuitive classifications of mutations expected to be subtle (Ala) and mutations expected to be disruptive for the α2 helix (Gly, Pro).

https://doi.org/10.7554/eLife.34300.013

Figure 4

Download asset Open asset

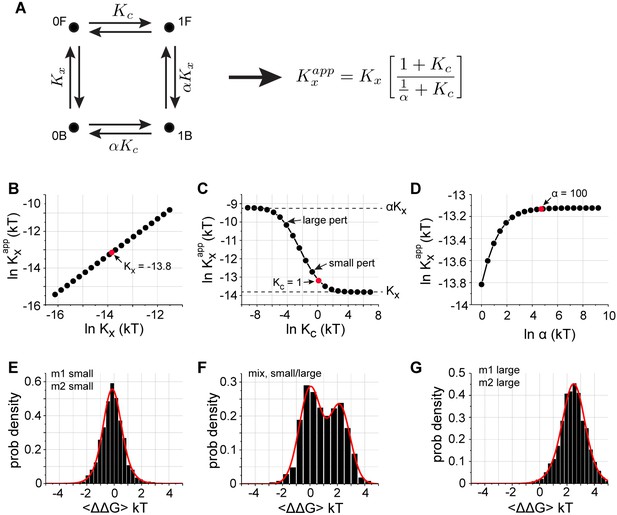
A basic model for observed distributions of double mutant cycle coupling energies.

(A), A schematic representation of two coupled equilibria in a protein molecule – a reaction with equilibrium constant $K_{x}$ corresponding to function (here, binding), an internal two-state conformational equilibrium defined by $K_{c}$ , and a coupling parameter $α$ linking the two. The equation at right shows the general analytic solution for how the apparent equilibrium constant $K_{x}^{a p p}$ depends on these three parameters, and panels (**B–D**) show graphs of these relationships over a relevant range of values. Note that $K_{x}$ (and ${α K}_{x}$ ) are defined as dissociation constants, and $K_{c} \equiv [0 F] / [1 F]$ and ${α K}_{c} \equiv [0 B] / [1 B]$ . (**B–D**), $K_{x}^{a p p}$ shows a linear dependence on $K_{x}$ , a saturating relationship with $α$ , and a sigmoidal relationship with $K_{c}$ . For a range of $K_{c}$ , $K_{x}^{a p p}$ ranges between $K_{x}$ and $α K_{x}$ , the two extreme limits set by the reaction diagram in panel (A). (**E–G**), distributions of coupling energies for simulations in which we choose a set of 'wild-type' values of $K_{x}$ , $K_{c}$ , and $α$ (red dots, panels **B–D**) and consider mutations that cause random Gaussian perturbations of $K_{x}$ and $α$ , but either small or large perturbations of $K_{c}$ (indicated in panel C). If all mutations cause small effects in $K_{c}$ , we obtain unimodal distributions centered at zero coupling energy (E), and if all mutations cause large effects in $K_{c}$ , we obtain unimodal distributions centered at a non-zero coupling energy (G). However, if mutations cause a mix of small and large effects on $K_{c}$ , we obtain bimodal distributions with one mode centered at zero (F). These three types recapitulate all the observed distributions for all PDZ homologs (main Figure 2 and Figure 1—figure supplement 1–4), for the GB1 protein (Figure 1—figure supplement 5), and for the average over homologs (Figure 3). Note that higher order cooperativity between amino acids specifying $K_{c}$ (a plausible scenario), would further steepen the relationship shown in panel (C) and would cause the all-or-nothing character of mutations with regard to $K_{c}$ with even less distinction between large and small perturbations. This model is not intended as a proof of mechanism for the observed distributions, but instead provides a logical scheme that explains the observations in light of known two-state allosteric equilibria is some PDZ domains (Mishra et al., 2007; Raman et al., 2016).

https://doi.org/10.7554/eLife.34300.014

Figure 5

Download asset Open asset

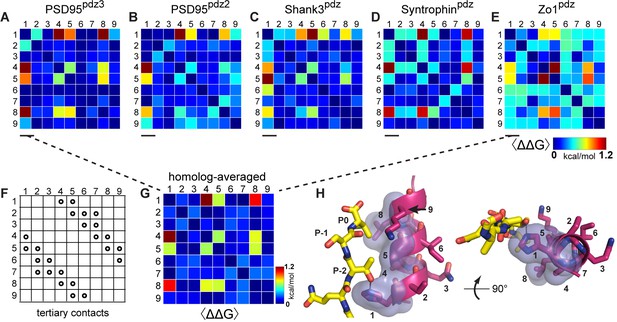
Conservation and idiosyncrasy in the pattern of energetic couplings over PDZ homologs.

(**A–E**), Matrices of mutation averaged pairwise thermodynamic couplings for the α2-helix in each PDZ homolog. The color scale is chosen to represent the full range of measured energetic couplings. The data show that some couplings are specific to individual homologs or shared by a subset of homologs, but that couplings between positions 1, 4, 5, and 8 are conserved over homologs. (F), the pattern of direct tertiary contacts between amino acid positions in the PDZ α2 helix. By convention (Morcos et al., 2011), trivial contacts between residues with sequence distance less than three are not shown. (G), The homolog and mutation averaged couplings (corresponding to Figure 3), displaying the conserved interactions between amino acids in the PDZ α2-helix. (H), Two views of the α2-helix, with the four interacting positions in the homolog-averaged dataset shown in transparent surface representation, and ligand in yellow stick bonds. These include three positions in direct contact with ligand (1, 5, 8) and one allosteric position buried in the core of the protein (4).

https://doi.org/10.7554/eLife.34300.015

Figure 6 with 2 supplements

Download asset Open asset

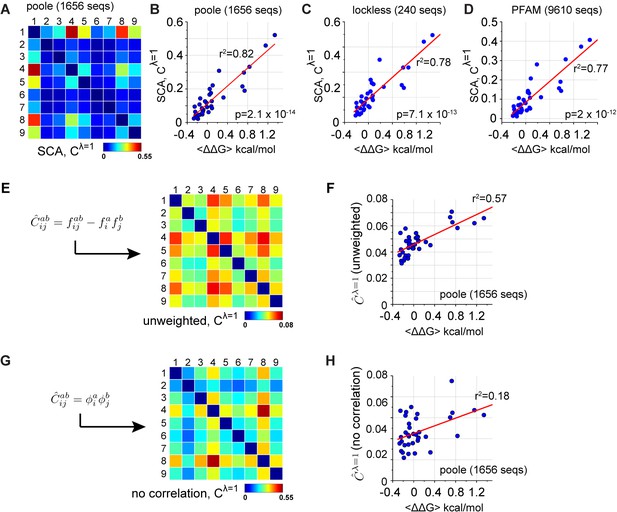
Coevolution-based inference of energetic couplings - SCA.

(A), Coevolution of sequence positions corresponding to the top eigenmode of the SCA matrix, derived from an alignment of 1656 eukaryotic PDZ domains (the 'Poole' alignment). The data show that a subset of positions coevolve within the PDZ α2-helix. (**B–D**), The relationship between experimental homology-averaged energetic couplings ( $⟨Δ Δ G⟩$ ) and SCA-based coevolution computed for three different alignments that differ in size and method of construction. The p-values give the significance of the coefficient of determination ( $r^{2}$ ) by the F-test. (**E–H**), The basic calculation in SCA is to compute a conservation-weighted correlation matrix ${\tilde{C}}_{i j}^{a b} = ϕ_{i}^{a} ϕ_{j}^{b} [f_{i j}^{a b} - f_{i}^{a} f_{j}^{b}]$ , where $f_{I}^{a}$ and $f_{i j}^{a b}$ represent the frequency and joint frequencies of amino acids $a$ and $b$ at positions $i$ and $j$ , respectively, in a multiple sequence alignment. The term $f_{i j}^{a b} - f_{i}^{a} f_{j}^{b}$ gives the correlation of amino acids at each pair of positions, and $ϕ$ represents a weighting function for each amino acid at each position that is related to its conservation (Halabi et al., 2009; Rivoire et al., 2016). We compared the relationship of the experimental energetic couplings ( $⟨Δ Δ G⟩$ ) with measures of coevolution that leave out the conservation weights (**E–F**), or that leave out the correlations (**G–H**). The analysis shows that both terms contribute to predicting native energetic couplings between amino acids.

https://doi.org/10.7554/eLife.34300.016

Figure 6—figure supplement 1

Download asset Open asset

Robustness of the SCA to alignment size.

(**A–F**) The graphs show scatterplots of homolog-averaged experimental couplings in the α2 helix against the first eigenmode of the SCA coevolution matrix for six independent trials of randomly sub-sampling the Poole PDZ alignment (1656 seqs) to retain half the sequences. SCA focuses on conserved correlations and is expectedly robust to alignment size.

https://doi.org/10.7554/eLife.34300.017

Figure 6—figure supplement 2

Download asset Open asset

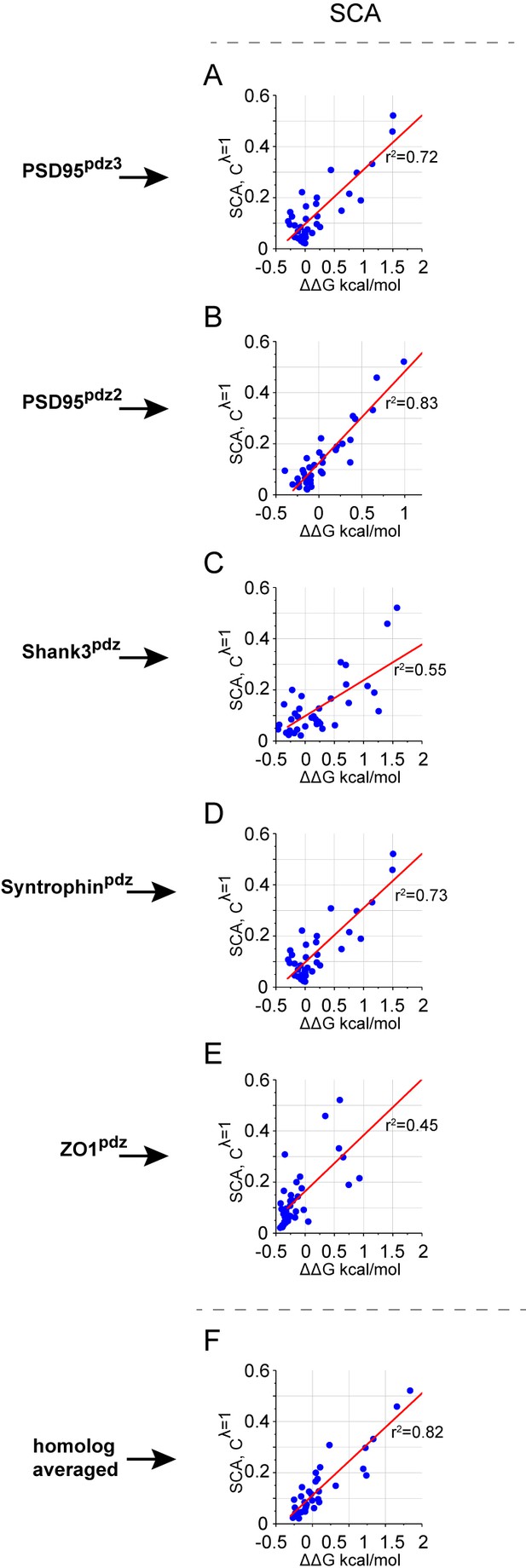
The relationship between mutation-averaged couplings and predictions from SCA for individual domains.

(**A–E**), Scatterplots of experimental couplings in the α2 helix of each individual PDZ homolog against the first eigenmode of the SCA coevolution matrix. Linear fits are shown in red lines with adjusted Pearson correlation coefficients indicated. (F), For comparison, the relationship of SCA with the homolog averaged data (same as Figure 6B).

https://doi.org/10.7554/eLife.34300.018

Figure 7

Download asset Open asset

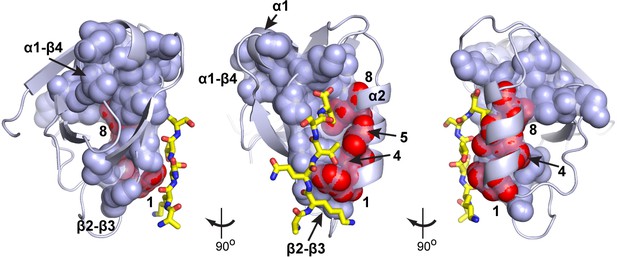
Homolog-averaged thermodynamic couplings and protein sectors.

Analysis of the top eigenmodes of the SCA coevolution matrix exposes groups of coevolving amino acids that empirically are found to form physically contiguous networks in the tertiary structure, often connecting the main functional site to remote allosteric sites (Halabi et al., 2009; Lockless and Ranganathan, 1999; Rivoire et al., 2016; Süel et al., 2003). In the PDZ family, the protein sector (shown as CPK spheres and transparent surface on three rotations of a representative structure, PDB 1BE9) connects the ligand binding pocket to two known allosteric sites, one in the α1-β4 loop (Peterson et al., 2004) and the other in the β2-β3 loop (Raman et al., 2016); the ligand is shown in yellow stick bonds. The homolog-averaged thermodynamic couplings in the α2 helix (positions 1, 4, 5, and 8) precisely correspond to the portion of the PDZ sector contributed by the secondary structure element. The selective cooperative action of these residues is consistent with the idea that the sector represents a global collective mode in the PDZ structure associated with function, embedded within a more independent environment.

https://doi.org/10.7554/eLife.34300.019

Figure 8 with 2 supplements

Download asset Open asset

Coevolution-based inference of energetic couplings - DCA.

(A), The matrix of direct couplings ( $J_{i j}$ ) from the DCA method, with tertiary contacts in the PDZ structure (1BE9) indicated by white or black circles. By convention (Morcos et al., 2011), trivial contacts between residues with sequence distance less than three are not shown. The data show that all top direct couplings identified by DCA are indeed tertiary structural contacts. (B), The DCA method involves the inference of a statistical energy function $E (σ)$ that for each sequence $σ$ , is parameterized by a set of intrinsic constraints on amino acids ( $h_{i}$ ) and pairwise interactions between amino acids ( $J_{i j}$ ). These parameters are optimized to reproduce the observed alignment frequencies and pairwise correlations. Using the model, the matrix shows mutation- and homolog-averaged energetic couplings, computed precisely as for the experimental data; see Materials and methods for details. (**C–E**), The relationship between experimental ( $⟨Δ Δ G⟩$ ) and DCA-inferred ( $⟨Δ Δ E⟩$ ) couplings in the PDZ α2-helix, for three PDZ alignments that differ in size and method of construction. The p-values give the significance of the coefficient of determination ( $r^{2}$ ) by the F-test. (F), The relationship between experimental and DCA-inferred couplings from $J_{i j}$ in which top couplings defining contacts are preserved and all non-contact couplings are randomly scrambled. The DCA model used for this analysis is from the Poole alignment, as in panel D. The data show that pairwise couplings in the DCA model between non-contacting positions contribute significantly to prediction of protein function.

https://doi.org/10.7554/eLife.34300.020

Figure 8—figure supplement 1

Download asset Open asset

Robustness of DCA to alignment size.

(**A–F**), The graphs show scatterplots of homolog-averaged experimental couplings in the α2 helix against computed DCA model coupling energies for six independent trials of randomly sub-sampling the Poole PDZ alignment (1656 seqs) to retain half the sequences. DCA expectedly shows more sensitivity to alignment size. The Poole alignment provides the best correspondence between experimental data and DCA and is therefore chosen for this analysis.

https://doi.org/10.7554/eLife.34300.021

Figure 8—figure supplement 2

Download asset Open asset

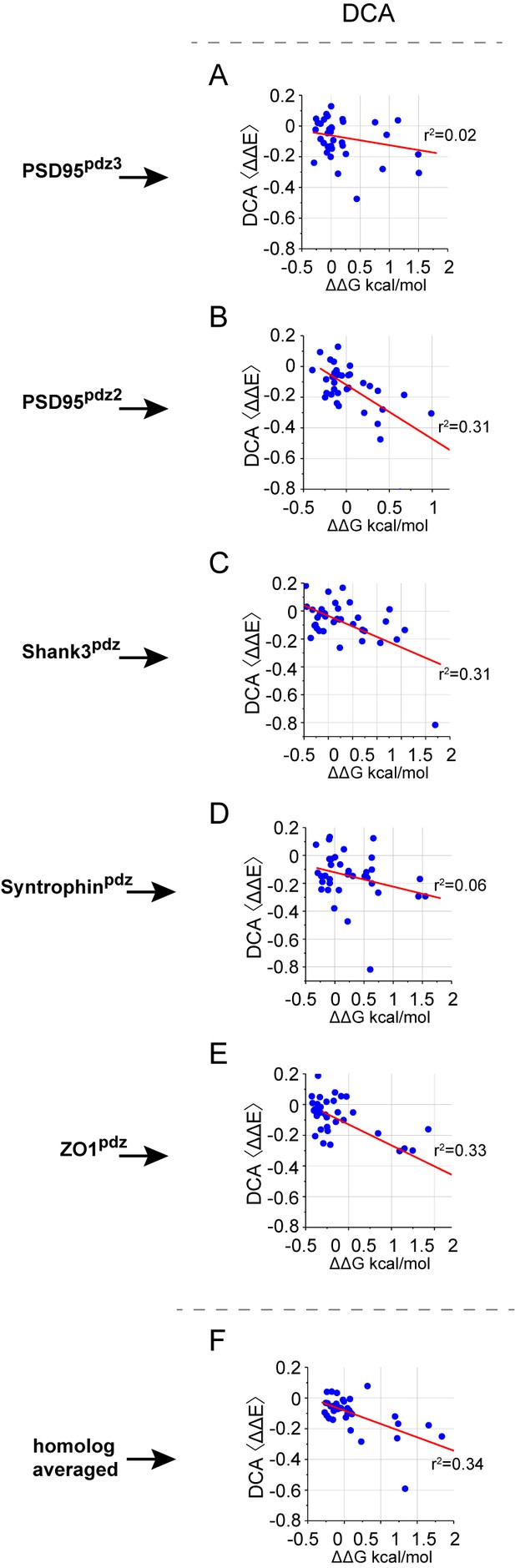
The relationship between mutation-averaged couplings and predictions from DCA for individual domains.

(**A–E**), scatterplots of experimental couplings for individual PDZ homologs against the coupling values computed from the DCA model. Linear fits are shown in red lines with adjusted Pearson correlation coefficients indicated. (F), For comparison, the relationship of DCA predictions with the homolog averaged data (same as Figure 8C).

https://doi.org/10.7554/eLife.34300.022

Tables

Table 1

Summary of data collection.

For each PDZ homolog, we indicate the target ligand, the wild-type affinity, the top-hit sequence identity within the ensemble of homologs, and the assay/sequencing statistics.

https://doi.org/10.7554/eLife.34300.005

PDZ homolog	Ligand	Ligand sequence	Affinity	Top ID% (PDZ)	No. of single mutants (out of 171)	No. of double mutants (out of 12,996)	Mean cycles/position pair (out of 361)	Sequence readsunsel/sel
PSD95^pdz3	CRIPT	TKNYKQTSV	0.8 μM (McLaughlin et al., 2012)	41.0 (Syntrophin^pdz)	171	11,531	320	12,190,079/14,358,962
PSD95^pdz2	NMDAR2A	KMPSIESDV	3.6 μM (Stiffler et al., 2006)	40.5 (PSD95^pdz3)	171	12,072	335	9,402,209/14,965,473
Shank3^pdz	Dlgap1/2/3	YIPEAQTRL	0.2 μM (Stiffler et al., 2006)	25.0 (PSD95^pdz2)	171	10,454	290	17,232,329/6,429,999
Syntrophin^pdz	Scn5a (Nav1.5)	PDRDRESIV	1.6 μM (Stiffler et al., 2006)	41.0 (PSD95^pdz3)	171	10,757	298	8,227,200/15,248,680
ZO-1^pdz	Claudin8	SIYSKSQYV	4.6 μM (Zhang et al., 2006)	37.5 (PSD95^pdz3)	171	11880	330	5,365,041/11,523,044

Additional files

Supplementary file 1 Salinas_Ranganathan_data.: https://doi.org/10.7554/eLife.34300.023
Download elife-34300-supp1-v3.mat
Transparent reporting form: https://doi.org/10.7554/eLife.34300.024
Download elife-34300-transrepform-v3.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Victor H Salinas
Rama Ranganathan

(2018)

Coevolution-based inference of amino acid interactions underlying protein function

eLife 7:e34300.

https://doi.org/10.7554/eLife.34300

Share this article

Cite this article

A deep coupling scan (DCS) for the PDZ binding pocket.

The bacterial two-hybrid assay for PDZ ligand binding.

Reproducibility and quality of the bacterial two-hybrid assay.

Distributions of pairwise thermodynamic couplings in a single PDZ homolog (PSD95pdz3).

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for PSD95pdz2.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Shank3pdz.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Syntrophinpdz.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for ZO1pdz.

Distributions of coupling in relative enrichment (ΔΔE) for a sampling of position pairs in the GB1 domain of the immunoglobulin-binding protein G.

Homolog-averaged pairwise thermodynamic couplings in the PDZ domain.

Amino acid contributions to distributions of double mutant cycle coupling energies for the PDZ α2 helix.

A basic model for observed distributions of double mutant cycle coupling energies.

Conservation and idiosyncrasy in the pattern of energetic couplings over PDZ homologs.

Coevolution-based inference of energetic couplings - SCA.

Robustness of the SCA to alignment size.

The relationship between mutation-averaged couplings and predictions from SCA for individual domains.

Homolog-averaged thermodynamic couplings and protein sectors.

Coevolution-based inference of energetic couplings - DCA.

Robustness of DCA to alignment size.

The relationship between mutation-averaged couplings and predictions from DCA for individual domains.

Summary of data collection.

Supplementary file 1

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Distributions of pairwise thermodynamic couplings in a single PDZ homolog (PSD95^pdz3).

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for PSD95^pdz2.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Shank3^pdz.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for Syntrophin^pdz.

Distributions of double mutant cycles for each α2 helix position pair (numbering as in Figure 1C) for ZO1^pdz.

Distributions of coupling in relative enrichment ( $Δ Δ E$ ) for a sampling of position pairs in the GB1 domain of the immunoglobulin-binding protein G.