Figures and data in The Ca2+ transient as a feedback sensor controlling cardiomyocyte ionic conductances in mouse populations

Figures
Tables
Additional files

7 figures, 6 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

Schematic representation of the sarcolemmal currents and intracellular Ca²⁺ cycling proteins of the mouse ventricular myocyte model.
https://doi.org/10.7554/eLife.36717.002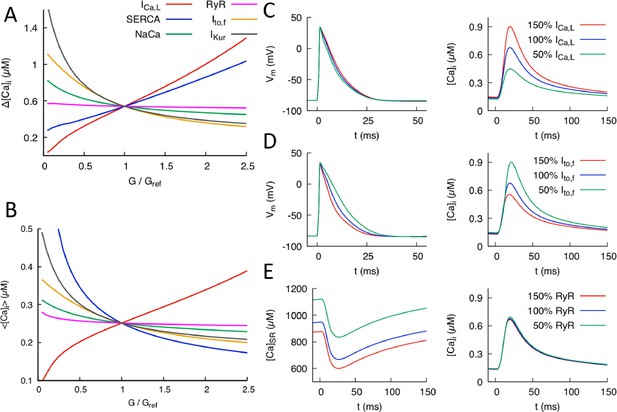

Figure 2

Download asset Open asset

Effects of individual conductances on the Ca²⁺ transient (CaT).

(A) CaT amplitude defined as the difference $Δ {[Ca]}_{i}$ between the peak and diastolic values of the cytosolic Ca²⁺ concentration ${[Ca]}_{i}$ versus G/G_ref where G is the individual conductance value and G_ref some fixed reference value. (B) Time-averaged ${[C a]}_{i}$ over one pacing period ( $⟨ {[Ca]}_{i} ⟩$ ) versus G/G_ref. Illustration of the effect of varying $I_{Ca, L}$ conductance (C) and $I_{to, f}$ conductance (D) on AP and CaT profiles, where 50%, 100%, and 150% correspond to G_ref=0.5, 1.0, and 1.5, respectively. (E) Effect of varying RyR conductance on SR Ca²⁺concentration ${[C a]}_{S R}$ and CaT. Different time windows are plotted for the CaT and SR load (0 to 150 ms) and AP waveforms (0 to 50 ms) in (**C-–E**).

https://doi.org/10.7554/eLife.36717.003

Figure 3 with 3 supplements

Download asset Open asset

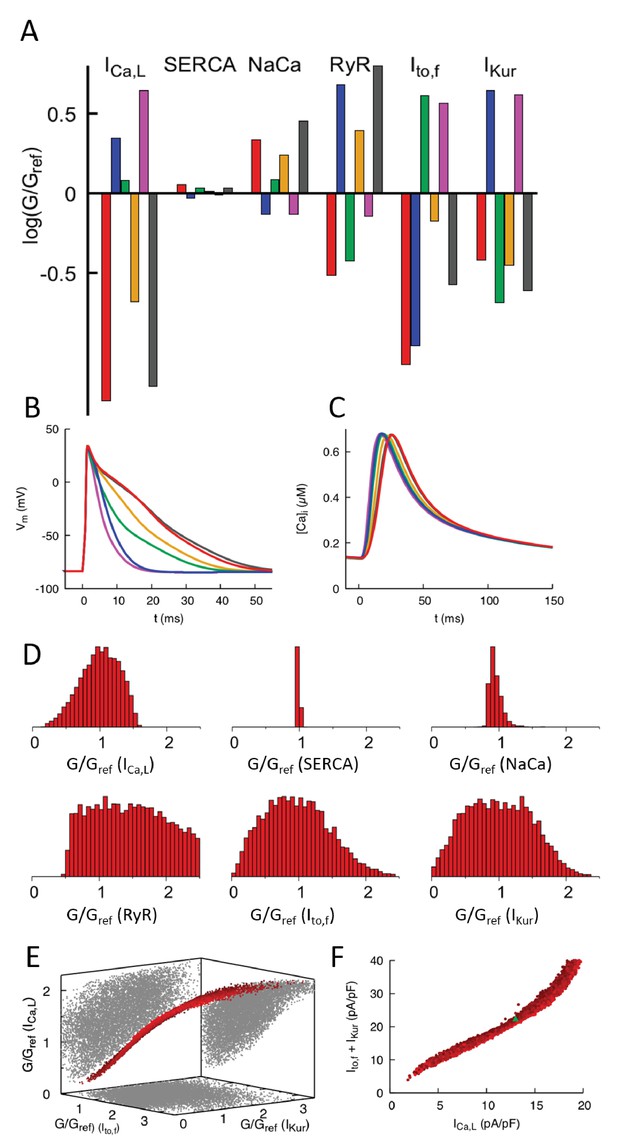
Computationally determined good enough solutions (GES) with calcium sensing.

(A) Examples of GES representing combinations of 6 conductances that produce a normal CaT and intracellular Na⁺ concentration. Each color represents a different GES and the corresponding AP and CaT profiles are shown in B) and C), respectively. (D) Histograms of individual normalized conductances G/G_ref for a collection of 7263 GES showing that some conductances are highly variable while others are highly constrained. (E) Three-dimensional (3D) plot revealing a three-way compensation between conductances of $I_{Ca, L}$ , $I_{to, f}$ , and $I_{Kur}$ . Each GES is represented by a red dot. All GES lie close to a 2D surface in this 3D plot. Pairwise projections (grey shadows) do not show evidence of two-way compensation between pairs of conductances. (F) Alternate representation of three-way compensation obtained by plotting $I_{Ca, L}$ versus the sum of $I_{to, f}$ and $I_{Kur}$ . Peak values of those currents after a voltage step from −50 to 0 mV are used to make this plot that can be readily compared to experiment. Different time windows are plotted for the AP waveforms and CaT in B and C, respectively.

https://doi.org/10.7554/eLife.36717.004

Figure 3—figure supplement 1

Download asset Open asset

Histograms of individual ion channel conductances in 8320 GESs found by a GES search constrained only by Ca²⁺ transient amplitude and average, but not constrained by intracellular sodium concentration ${[N a]}_{i}$ .
https://doi.org/10.7554/eLife.36717.005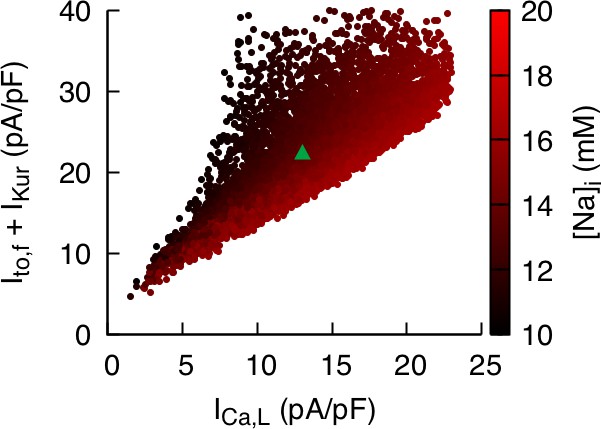

Figure 3—figure supplement 2

Download asset Open asset

Correlation between $I_{Ca, L}$ and the sum of $I_{to, f}$ and $I_{Kur}$ is weaker but still significant when intracellular sodium concentration is not constrained.
https://doi.org/10.7554/eLife.36717.006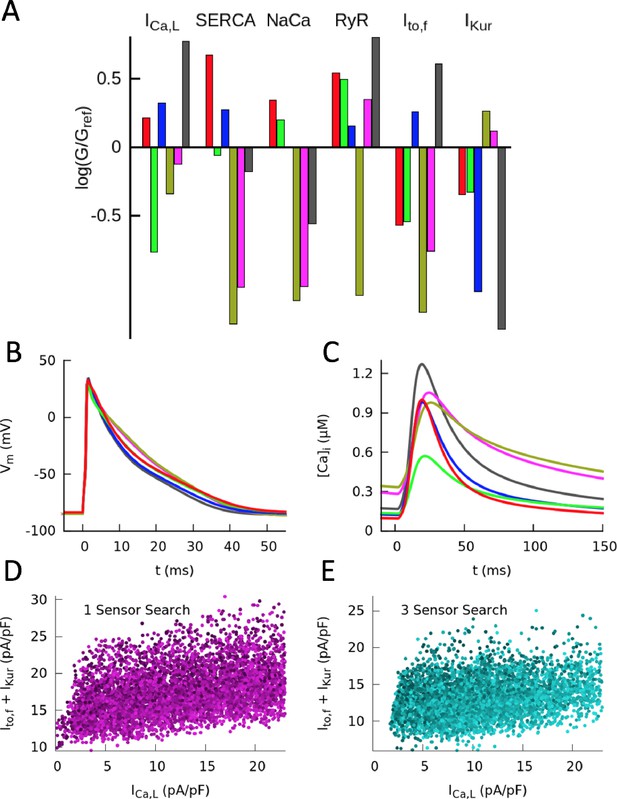

Figure 3—figure supplement 3

Download asset Open asset

Computationally determined GES with voltage sensing.

(A) Examples of GES representing combinations of 6 conductances that produce a normal AP with predominantly voltage sensing. Sensors are $S_{1}$ = ${A P D}_{90}$ , $S_{2}$ = ${A P D}_{30}$ and $S_{3}$ = ${[N a]}_{i}$ with $ϵ = 0.05$ . Each color represents a different GES and the corresponding AP and CaT profiles are shown in (B) and (C), respectively. Correlation between $I_{Ca, L}$ and the sum of $I_{to, f}$ and $I_{Kur}$ is not present among models constrained by ${A P D}_{90}$ (D) or by ${A P D}_{90}$ , ${A P D}_{30}$ and ${[N a]}_{i}$ (E).

https://doi.org/10.7554/eLife.36717.007

Figure 4 with 1 supplement

Download asset Open asset

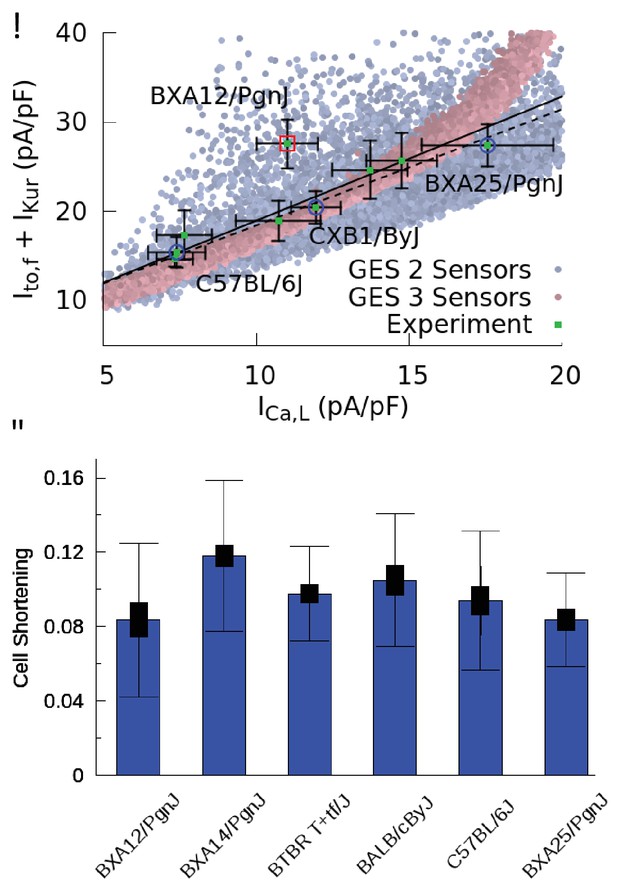
Good enough solutions in the Hybrid Mouse Diversity Panel (HMDP).

(A) Central result of this paper showing quantitative agreement between theoretically predicted and experimentally measured compensation of inward Ca²⁺ and outward K⁺ currents. Equivalent plot of Figure 3F showing the sum of $I_{to, f}$ and $I_{Kur}$ versus $I_{Ca, L}$ for nine different mouse strains using peak values of those currents (proportional to conductances) after a voltage step from −50 to 0 mV. Mean current values (green filled squares) are shown together with standard errors of the mean (thin bars) for each strain. The number of cells used for each strain is given in Table 1 of the Materials and methods section. Computationally determined GES are superimposed and shown as faded red points using all three sensors (CaT amplitude, average ${[C a]}_{i}$ , and diastolic ${[N a]}_{i}$ ) and faded blue points for two sensors (CaT amplitude and average ${[C a]}_{i}$ ). Lines represent linear regression fits using the method of Chi-squared minimization with errors in both coordinates including (solid line, p=0.0144) and excluding (dashed line, p=0.0007) the outlier strain BXA12/PgnJ marked by a red box. The small p values of those fit validate the computationally predicted three-way compensation of Ca²⁺ and K⁺ currents. The three strains selected for the organ scale study (C57BL/6J, CXB1/ByJ, and BXA25/PgnJ) with low, medium, and high $I_{Ca, L}$ conductance, respectively, are highlighted by blue circles. (B) Cell shortening, measured as the fraction of resting cell length at 4 Hz pacing frequency in different HMPD strains where thick and thin bars correspond to standard error of the mean and standard deviation, respectively. A standard ANOVA test shows no significant differences in cell shortening between strains (p=0.4136) supporting the hypothesis that different combinations of conductances produce a similar CaT and contractile activity.

https://doi.org/10.7554/eLife.36717.008

Figure 4—figure supplement 1

Download asset Open asset

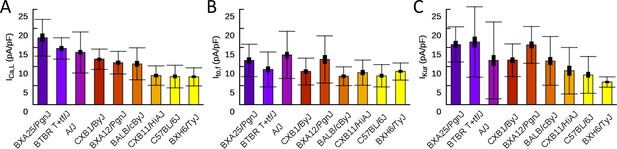
Patch clamp measurements of mean $I_{Ca, L}$ (A), $I_{to, f}$ (B), and $I_{Kur}$ (C) functional current density averaged over multiple cells for nine HMDP mouse strains with standard errors (thick bars) and standard deviations (thin bars).
https://doi.org/10.7554/eLife.36717.009

Figure 5 with 2 supplements

Download asset Open asset

Organ scale compensation.

(A) Mean $I_{Ca, L}$ conductance in three different HMDP strains where thick and thin bars denote standard error and standard deviation, respectively. (B) Sets of conductances generated to be representative of individual cells within ventricular tissue of the three strains by assigning normally distributed random values to the $I_{Ca, L}$ , $I_{to, f}$ and $I_{Kur}$ conductances using experimentally determined means and standard deviations. The blue, green, and red points correspond to the three HMDP strains with low (C57BL/6J), medium (CXB1/ByJ), and high (BXA25/PgnJ) $I_{Ca, L}$ conductance, respectively, and the grey points are the results of the three-sensor GES search (same as Figure 3F). (C) Variable AP waveforms in uncoupled myocytes with conductances randomly chosen from the distribution shown in B for C57BL/6J and D) AP waveforms for coupled myocytes in tissue for C57BL/6J and the two other strains. AP waveforms of uncoupled cells vary significantly from cell to cell as observed experimentally (Fig. Figure 5—figure supplement 1) but are uniform in electrotonically coupled cells, as expected. (E) Histograms of Ca²⁺ transient (CaT) amplitude ( $Δ$ Ca) and action potential duration (APD) for C57BL/6J in electrotonically uncoupled and coupled cells. Importantly, in coupled cells, the more uniform APD translates into a much more uniform CaT amplitude, reflecting the strong effect of the cell’s APD on its CaT amplitude. (F) Distribution of CaT amplitudes within electrotonically coupled cells in tissue scale simulations using the parameter distributions from B. The three strains have the same mean CaT amplitude averaged over all cells marked by a thick vertical gray line, thereby demonstrating that compensation of Ca²⁺ and K⁺ currents remains operative at a tissue scale. (G) Distribution of CaT amplitudes obtained by varying only $I_{Ca, L}$ conductance and with $I_{to, f}$ and $I_{K u r}$ conductances fixed to their reference values. Lack of compensation between Ca²⁺ and K⁺ currents in this case yields different mean CaT amplitude.

https://doi.org/10.7554/eLife.36717.011

Figure 5—figure supplement 1

Download asset Open asset

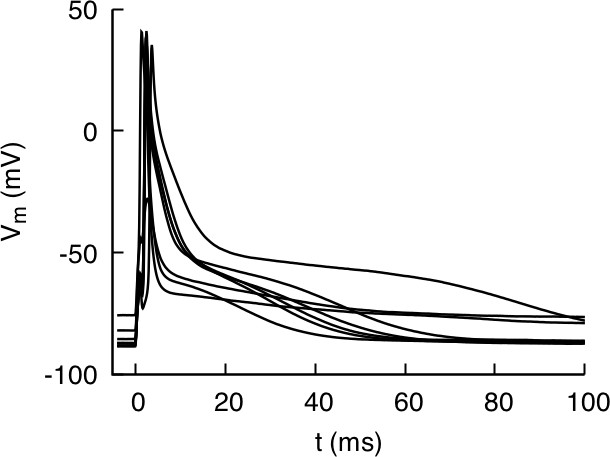
Action potential recordings from isolated myocytes for mouse strain C57BL/6J paced at 4 Hz under current clamp.

The recordings illustrate the typical degree of cell-to-cell variability of AP morphology observed in all strains.

https://doi.org/10.7554/eLife.36717.012

Figure 5—figure supplement 2

Download asset Open asset

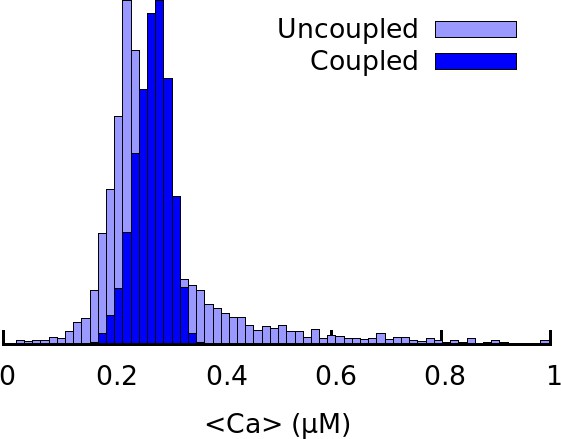
Histogram of average Ca²⁺ concentration corresponding to Figure 5E for C57BL/6J in electrotonically uncoupled and coupled cells.
https://doi.org/10.7554/eLife.36717.013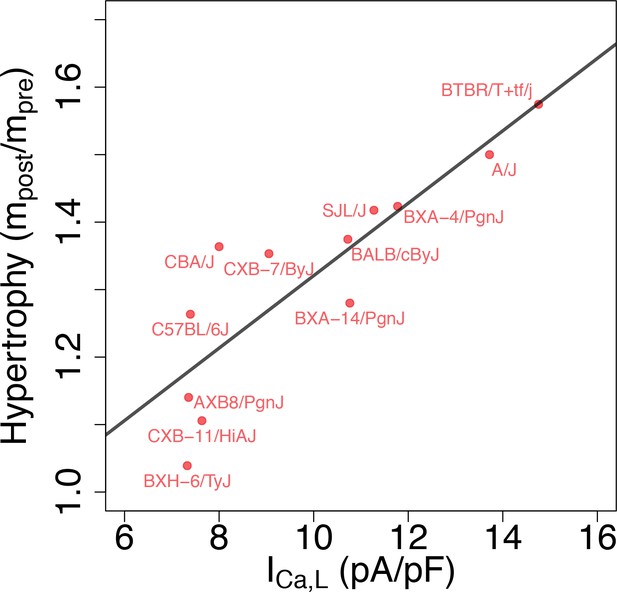

Figure 6

Download asset Open asset

Correlation between L-type Ca²⁺ current conductance and cardiac hypertrophic response to a stressor for different HMDP strains.

The Pearson correlation is r = 0.86 (p=3e-4).

https://doi.org/10.7554/eLife.36717.014

Figure 7

Download asset Open asset

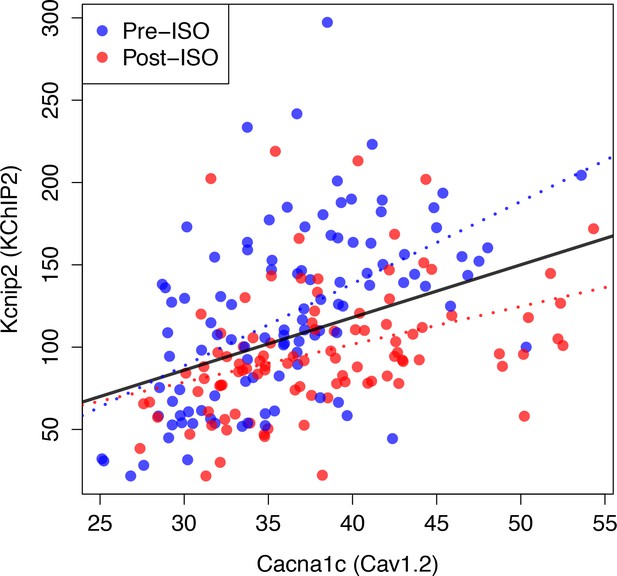
Compensation and gene expression.

Plot showing the existence of a statistically very significant correlation (Pearson correlation coefficient $r = 0.47$ and p-value, $p = 8.1 10^{- 13}$ ) between the expression level of Kcnip2, encoding the KChIP2 accessory $β$ subunits that interact with Kv4.2 channels ( $I_{to, f}$ ) and of Cacna1c, a gene encoding the $α$ 1C subunit of the Cav1.2 L-type calcium channels ( $I_{Ca, L}$ ) across 206 mice. Cardiac gene expression was measured in $106$ control (Pre-ISO) strains and 21 days after injection of isoproterenol (post-ISO) in 100 HMDP strains (a smaller number due to higher mortality of certain strains). Note that the significant correlation holds when considering separately pre-ISO (blue points, $r = 0.59$ , $p = 2 10^{- 11}$ ) and post-ISO (red points, $r = 0.42$ , $p = 1.5 10^{- 5}$ ) data. Lines show best fits of a linear model for pre-ISO (blue), post-ISO (red), and pre- and post-ISO combined (black). Expression data is taken from Santolini et al. (2018) and is averaged over all microarray probes for each gene.

https://doi.org/10.7554/eLife.36717.016

Tables

Table 1

Patch clamp measurements of $I_{Ca, L}$ , $I_{to, f}$ , and $I_{Kur}$ functional current density.

Mean current density averaged over $n$ cells isolated from multiple hearts for each strain is given together with the standard error.

https://doi.org/10.7554/eLife.36717.010

Strain	$I_{Ca, L}$ (pA/pF)	n	$I_{Kur}$ (pA/pF)	n	$I_{to, f}$ (pA/pF)	n	$I_{Kss}$ (pA/pF)	n
A/J	13.71947 $\pm$ 1.23085	19	11.61804 $\pm$ 2.79089	13	13.03735 $\pm$ 1.64818	14	5.23445 $\pm$ 0.48377	13
BALB/cByJ	10.72278 $\pm$ 1.3951	9	11.496 $\pm$ 2.03274	10	7.46938 $\pm$ 0.82615	9	8.197 $\pm$ 0.62438	10
BTBR T+tf/J	14.75667 $\pm$ 1.14159	6	16.42364 $\pm$ 2.78295	11	9.271 $\pm$ 1.43985	10	6.093 $\pm$ 0.39553	9
BXA12/PgnJ	11.01333 $\pm$ 0.98995	9	15.66429 $\pm$ 1.70548	8	11.89875 $\pm$ 2.18027	8	8.34556 $\pm$ 1.30065	9
BXA25/PgnJ	17.57 $\pm$ 4.81376	5	15.8049 $\pm$ 1.74509	7	11.62704 $\pm$ 1.59613	7	7.11986 $\pm$ 1.31554	6
BXH6/TyJ	7.32625 $\pm$ 0.59327	16	5.954 $\pm$ 0.43731	10	8.73172 $\pm$ 0.67617	11	7.98545 $\pm$ 0.87545	11
C57BL/6J	7.3925 $\pm$ 0.93181	10	7.82727 $\pm$ 1.45134	11	7.594 $\pm$ 0.92097	10	9.16273 $\pm$ 1.62148	11
CXB1/ByJ	11.93909 $\pm$ 0.81022	11	11.69556 $\pm$ 1.42095	9	8.73883 $\pm$ 1.11087	10	6.089 $\pm$ 0.5724	10
CXB11/HiAJ	7.63625 $\pm$ 0.89344	8	8.90316 $\pm$ 2.49755	6	8.42537 $\pm$ 1.24635	7	6.8481 $\pm$ 1.3638	7
AXB8/PgnJ	7.355 $\pm$ 1.09612	6	-		-		-
BXA14/PgnJ	11.28091 $\pm$ 1.00796	15	-		-		-
BXA4/PgnJ	11.77615 $\pm$ 1.19476	13	-		-		-
BXD34/TyJ	11.12556 $\pm$ 1.13741	9	-		-		-
CBA/J	7.956 $\pm$ 0.81269	10	-		-		-
CXB7/ByJ	9.05386 $\pm$ 0.6087	16	-		-		-
SJL/J	11.2745 $\pm$ 0.99708	20	-		-		-

Table 3

Heart mass before and 3 weeks after Isoproterenol (ISO) injection.

https://doi.org/10.7554/eLife.36717.015

Strain	Heart mass pre-ISO, $m_{pre}$ (g)	Heart mass post-ISO, $m_{post}$ (g)
A/J	0.088666667	0.133
AXB8/PgnJ	0.087	0.0992
BALB/cByJ	0.10105	0.1389
BTBR T+tf/J	0.14162	0.223
BXA-12/PgnJ	0.064	NA
BXA-14/PgnJ	0.0975	0.1248
BXA-4/PgnJ	0.1031	0.14675
BXD-34/TyJ	0.1215	NA
BXH-6/TyJ	0.0845	0.0878
C57BL/6J	0.096716667	0.1222
CBA/J	0.095333333	0.13
CXB-11/HiAJ	0.1135	0.1255
CXB-7/ByJ	0.109	0.1475
SJL/J	0.087	0.123333333

Table 2

Cell Shortening at 4 Hz pacing.

https://doi.org/10.7554/eLife.36717.017

Strain	$Δ$ L/L (4 Hz)	n
BXA12/PgnJ	0.0835 $\pm$ 0.0184	5
BXA14/PgnJ	0.1182 $\pm$ 0.0108	14
BTBR T+tf/J	0.0978 $\pm$ 0.0095	7
BALB/cByJ	0.105 $\pm$ 0.0158	5
C57BL/6J	0.0989 $\pm$ 0.016	6
BXA25/PgnJ	0.0838 $\pm$ 0.0112	5

Table 4

Reference values of ionic current parameters varied in the GES search.

https://doi.org/10.7554/eLife.36717.018

Parameter	Definition	Reference value	Reference source
$g_{Ca}$	Ca²⁺ current flux	333.32 mmol/(Cm C)	Measured
$v_{up}$	Peak uptake rate	1.17 $μ$ M/ms	Chosen^*
$g_{NaCa}$	Peak NaCa rate	36.6 $μ$ M/s	Bondarenko et al., 2004
$g_{RyR}$	Release current strength	12.9 sparks ${c m}^{2}$ /mA	Mahajan et al. (2008)
$g_{to, f}$	$I_{to, f}$ peak conductance	0.16 A/F	Measured
$g_{Kur}$	$I_{Kur}$ peak conductance	0.144 A/F	Measured

^* $v_{up}$ was chosen such that the reference Ca²⁺ transient amplitude was normal.

Table 5

Mouse ventricular myocyte model parameters.

https://doi.org/10.7554/eLife.36717.019

Parameter	Definition	Value
Physical constants and ionic concentrations
$C_{m}$	Cell capacitance	3.1 $\times$ 10 $^{- 4}$ $μ$ F
$v_{i}$	Cell volume	2.58 $\times$ 10 $^{- 5}$ $μ$ l
$v_{s}$	Submembrane volume	0.02 $v_{i}$
F	Faraday Constant	96.485 C/mmol
R	Universal gas constant	8.314 J ${mol}^{- 1}$ $K^{- 1}$
T	Temperature	298 K
${[N a]}_{o}$	External Na⁺ concentration	140 mM
${[K]}_{i}$	Internal K⁺ concentration	143.5 mM
${[K]}_{o}$	External K⁺ concentration	5.4 mM
${[{C a}^{2 +}]}_{o}$	External Ca²⁺ concentration	1.8 mM
Cytosolic buffering parameters
$B_{T}$	Troponin C concentration	70 $μ$ mol/l cyt
$k_{on}^{T}$	on rate for Troponin C binding	0.0327 ( $μ$ M ms) $^{- 1}$
$k_{off}^{T}$	off rate for Troponin C binding	0.0196 (ms) $^{- 1}$
$B_{SR}$	SR binding site concentration	47 $μ$ mol/l cyt
$K_{SR}$	SR binding site disassociation constant	0.6 $μ$ M
$B_{Cd}$	Calmodulin binding site concentration	24 $μ$ mol/l cyt
$K_{Cd}$	Calmodulin binding site disassociation constant	7 $μ$ M
$B_{mem}$	Membrane binding site concentration	15 $μ$ mol/l cyt
$K_{mem}$	Membrane binding site disassociation constant	0.3 $μ$ M
$B_{sar}$	Sarcolemma binding site concentration	42 $μ$ mol/l cyt
$K_{sar}$	Sarcolemma binding site disassociation constant	13 $μ$ M
SR release parameters
$τ_{r}$	Spark lifetime	10 ms
$τ_{a}$	NSR-JSR diffusion time	20 ms
u	Release slope	4 ${m s}^{- 1}$
$c_{sr}$	Release slope threshold	90 $μ$ M / l cytosol
$τ_{d}$	$c_{p}$ - $c_{s}$ diffusion time	0.50 ms^*
$τ_{s}$	$c_{s}$ - $c_{i}$ diffusion time	0.75 ms
Exchanger, uptake, and SR leak parameters
$c_{up}$	Uptake threshold	0.5 $μ$ M
$k_{sat}$	NaCa saturation threshold	0.1
$ξ$	NaCa energy barrier position	0.35
$K_{m, N a i}$	Ion mobility constant	21 mM
$K_{m, N a o}$	Ion mobility constant	87.5 mM
$K_{m, C a o}$	Ion mobility constant	1380 $μ$ M
$g_{l}$	Leak current conductance	1.74 $\times$ 10 $^{- 5}$ ${m s}^{- 1}$
Ionic current parameters
$g_{N a}$	Na⁺ current conductance	13 mS/ $μ$ F
$g_{N a, b}$	Na⁺ background current conductance	0.0026 mS/ $μ$ F
$g_{Ca, b}$	Ca²⁺ background current conductance	0.000367 mS/ $μ$ F
${\bar{g}}_{C a}$	Strength of local LCC calcium flux	9000 mM/(cm C)
$g_{K 1}$	$I_{K 1}$ conductance	0.2938 mS/ $μ$ F
$g_{NaK}$	$I_{NaK}$ conductance	1.716 mS/ $μ$ F
$g_{Kss}$	$I_{Kss}$ conductance	0.025 mS/ $μ$ F
$g_{to, s}$	$I_{to, s}$ conductance	0 mS/ $μ$ F
$J_{PMCA, max}$	Maximal $J_{PMCA}$ flux	one pA/pF
$K_{PMCA}$	Saturation constant for Ca²⁺ current	0.5 $μ$ M
$P_{Ca}$	Constant	0.00054 cm/s
$P_{o, max}$	Constant	0.083

^*We have reduced this value from the original value of Mahajan et al. (2008) so that the Ca²⁺ transient increases when SERCA uptake rate is increased.

Table 6

Simulation outputs corresponding to physiological sensors

https://doi.org/10.7554/eLife.36717.020

Abbreviation	Description	Reference value
$⟨ {[C a]}_{i} ⟩$	Average cytostolic Ca²⁺ over one beat	0.24 $μ$ M
$Δ {[C a]}_{i}$	Ca²⁺ transient amplitude	0.5 $μ$ M
${[N a]}_{i}$	Diastolic Na⁺	14 mM

Additional files

Transparent reporting form: https://doi.org/10.7554/eLife.36717.021
Download elife-36717-transrepform-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Colin M Rees
Jun-Hai Yang
Marc Santolini
Aldons J Lusis
James N Weiss
Alain Karma

(2018)

The Ca²⁺ transient as a feedback sensor controlling cardiomyocyte ionic conductances in mouse populations

eLife 7:e36717.

https://doi.org/10.7554/eLife.36717

Share this article

Cite this article

Schematic representation of the sarcolemmal currents and intracellular Ca2+ cycling proteins of the mouse ventricular myocyte model.

Effects of individual conductances on the Ca2+ transient (CaT).

Computationally determined good enough solutions (GES) with calcium sensing.

Histograms of individual ion channel conductances in 8320 GESs found by a GES search constrained only by Ca2+ transient amplitude and average, but not constrained by intracellular sodium concentration [Na]i.

Correlation between ICa,L and the sum of Ito,f and IKur is weaker but still significant when intracellular sodium concentration is not constrained.

Computationally determined GES with voltage sensing.

Good enough solutions in the Hybrid Mouse Diversity Panel (HMDP).

Patch clamp measurements of mean ICa,L (A), Ito,f (B), and IKur (C) functional current density averaged over multiple cells for nine HMDP mouse strains with standard errors (thick bars) and standard deviations (thin bars).

Organ scale compensation.

Action potential recordings from isolated myocytes for mouse strain C57BL/6J paced at 4 Hz under current clamp.

Histogram of average Ca2+ concentration corresponding to Figure 5E for C57BL/6J in electrotonically uncoupled and coupled cells.

Correlation between L-type Ca2+ current conductance and cardiac hypertrophic response to a stressor for different HMDP strains.

Compensation and gene expression.

Patch clamp measurements of ICa,L, Ito,f, and IKur functional current density.

Heart mass before and 3 weeks after Isoproterenol (ISO) injection.

Cell Shortening at 4 Hz pacing.

Reference values of ionic current parameters varied in the GES search.

Mouse ventricular myocyte model parameters.

Simulation outputs corresponding to physiological sensors

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Schematic representation of the sarcolemmal currents and intracellular Ca²⁺ cycling proteins of the mouse ventricular myocyte model.

Effects of individual conductances on the Ca²⁺ transient (CaT).

Histograms of individual ion channel conductances in 8320 GESs found by a GES search constrained only by Ca²⁺ transient amplitude and average, but not constrained by intracellular sodium concentration ${[N a]}_{i}$ .

Correlation between $I_{Ca, L}$ and the sum of $I_{to, f}$ and $I_{Kur}$ is weaker but still significant when intracellular sodium concentration is not constrained.

Patch clamp measurements of mean $I_{Ca, L}$ (A), $I_{to, f}$ (B), and $I_{Kur}$ (C) functional current density averaged over multiple cells for nine HMDP mouse strains with standard errors (thick bars) and standard deviations (thin bars).

Histogram of average Ca²⁺ concentration corresponding to Figure 5E for C57BL/6J in electrotonically uncoupled and coupled cells.

Correlation between L-type Ca²⁺ current conductance and cardiac hypertrophic response to a stressor for different HMDP strains.

Patch clamp measurements of $I_{Ca, L}$ , $I_{to, f}$ , and $I_{Kur}$ functional current density.