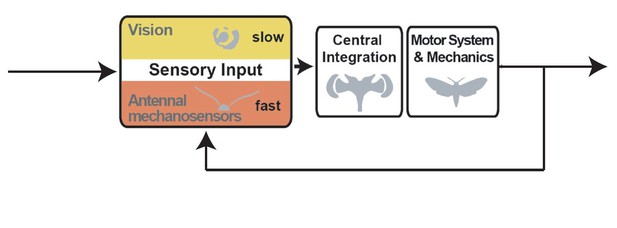
The roles of vision and antennal mechanoreception in hawkmoth flight control
- Lund University, Sweden
- Tata Institute of Fundamental Research, India
Figures
Figure 1 with 1 supplement
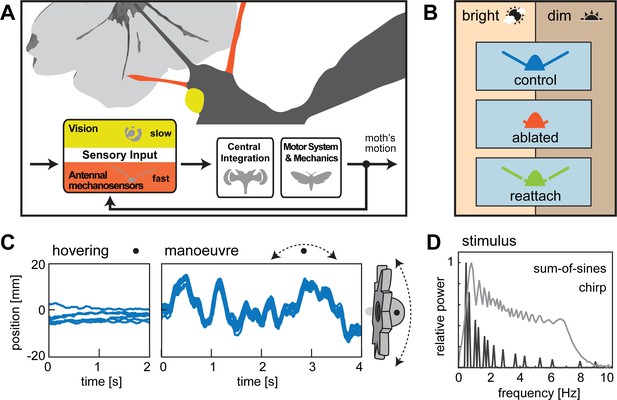
Flight control in hawkmoths requires vision and mechanosensation.
(A) Flight control in insects requires sensory feedback on perturbations of body position. The visual system supplies such feedback, but with comparably long response latencies. In addition, insects use mechanosensory systems to control their position in the air, which provide rapid feedback and thus are crucial for fast flight manoeuvres. Here, we investigated the role of antennal mechanosensation and vision on flight control in the hummingbird hawkmoth Macroglossum stellatarum. (B) In order to quantify the effects of antennal mechanosensation in free flight, we subjected each hawkmoth to three treatments: intact antennae (control, blue), ablated flagella (ablated, red) and re-attached flagella (reattach, green). To quantify the role of vision, we tested these three antennal treatments in two different light intensities (bright: 3000 lux, corresponding to partially overcast daylight and dim: 30 lux, corresponding to sunset intensities). (C) All conditions were tested in free hovering flight at artificial flowers, which were either stationary (hovering) or moved at different temporal frequencies (manœuvre). (D) We used a stimulus composed of a sum-of-sines to sample distinct frequencies with similar velocities (amplitude adjusted accordingly), as well as a stimulus ramping up in frequency, while retaining similar amplitude (chirp).
Figure 1—figure supplement 1
Antennal surgery.
To obtain flagella ablated animals, the flagella were cut between the 5th and 10th annulus (red arrows in middle panel). The flagella were preserved and re-attached to the same individual with a small amount of super glue (green arrows, right panel).
Figure 2 with 2 supplements
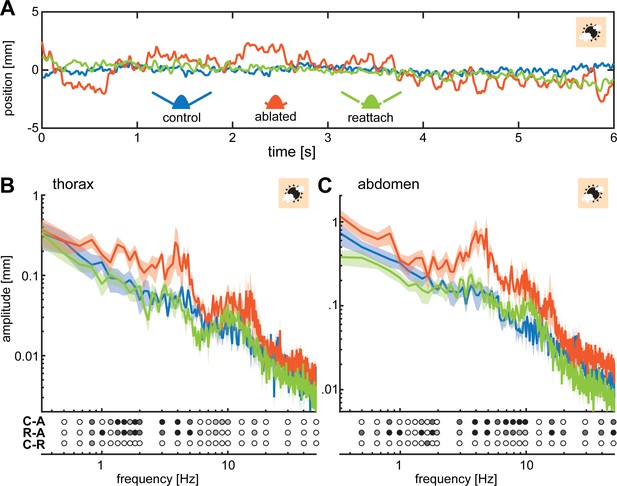
Flagella ablated hawkmoths showed greater thorax and abdomen movements during hovering flight at a stationary flower.
(A) When hawkmoths hovered in front of a stationary flower at 3000 lux, it was notable that flagella ablated moths jittered around their target position with larger amplitudes than moths of the other two antennal conditions, as quantified by the position of their thorax. The nectary is centered at 0 mm in this graph. (B) The thorax of moths with ablated flagella jittered with significantly higher amplitudes than the other two antennal conditions at frequencies between 1 and 5 Hz. There was no significant difference between control and re-attached moths. (C) The position of the abdomen in the three antennal treatments showed a similar trend to the thorax: the flagella ablated moths exhibited significantly larger abdomen jitter in the frequency range between 0.5 and 10 Hz than the other two treatments. (B, C) Lines show average, and shaded areas ± SEM. Statistical significance is indicated below the plots as: black p < 0.001, dark grey: p < 0.01, grey p < 0.05, white p > 0.05. Post-hoc tests were performed as part of a general linear model including antennal treatment and frequency (binned to the logarithmic scale) as factors, see Supplementary file 2 and Supplementary file 3.
-
Figure 2—source data 1
Contains the source data for the frequency spectra shown in Figure 2 and Figure 2—figure supplement 2.
- https://doi.org/10.7554/eLife.37606.008
Figure 2—figure supplement 1
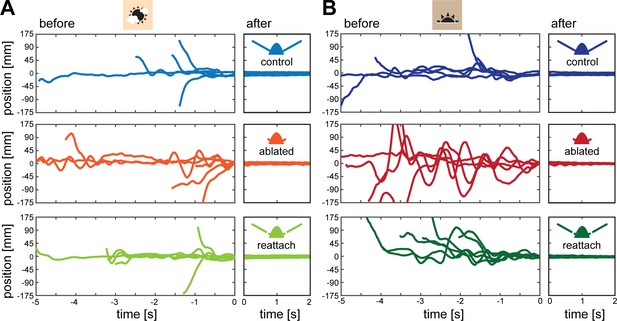
Hawkmoth flower approach.
Flight tracks of hawkmoths approaching a stationary flower in bright (A, 3000 lux) and dim (B, 30 lux) light. Before refers to time intervals before their proboscis made contact with the nectary of the flower, after to the period after contact was initiated.
Figure 2—figure supplement 2
Flagella ablated hawkmoths performed less stable hovering at a stationary flower at 30 lux.
Thorax (A) and abdomen (B) position of hawkmoths hovering in front of a stationary flower at 30 lux. Post-hoc tests were performed as part of a general linear model including antennal treatment and frequency (binned to the logarithmic scale) as factors. Lines show average, and shaded areas ± SEM. Statistical significance is indicated below the plots as: black p < 0.001, dark grey: p < 0.01, grey p < 0.05, white p > 0.05, see Supplementary files 9,10.
Figure 3 with 4 supplements
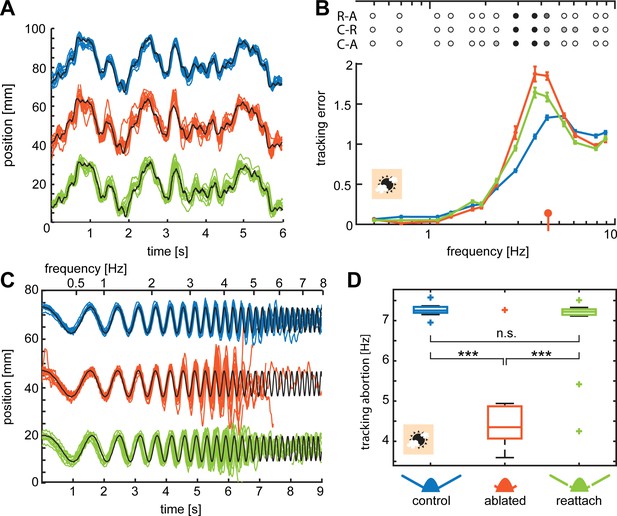
Flagella ablated hawkmoths showed reduced tracking performance of flowers moving at high frequencies.
(A, C) Trajectories of hawkmoths tracking moving flowers with the sum-of-sines (A) and the chirp (C) stimulus. Trajectories of the different antennal conditions are stacked for comparability. When tracking a moving robotic flower at 3000 lux, hawkmoths with ablated flagella often overshot the movements of the flower, specifically at higher frequencies. With increasing frequencies, moths also increasingly lagged behind the phase of flower movements more strongly. While the amplitude in the sum-of-sines stimulus was adjusted such that moths of all conditions could track the entirety of the stimulus, the chirp stimulus forced moths with too large overshoots and phase-lags to loose contact with the flower, and abort tracking (see red tracks in C). (B) Together, overshooting and phase-lags resulted in an increased tracking error of flagella ablated moths with the sum-of-sines stimulus at frequencies between 2 and 6 Hz, compared to both the control and re-attached condition. Linear mixed-effects models were used to compare the tracking error of the different antennal treatments with respect to frequency. Colours indicate significance (black p < 0.001, dark grey: p < 0.01, grey p < 0.05, white p > 0.05, Supplementary file 4). The red indicator on the x-axis gives the median frequency at which flagella ablated moths aborted tracking the chirp-stimulus (D). Curves show the mean and 95% confidence intervals of the mean, calculated in the complex plane. (D) For the chirp stimulus, we compared the movement frequency of the flower, at which the moths aborted tracking across antennal treatments, showing that flagella ablated moths lost contact with the flower at significantly lower frequencies than the control and re-attached condition. A Friedman test was used to compare between the treatments (***p<0.001, **: p<0.01, *p<0.05, Supplementary file 5).
-
Figure 3—source data 1
Contains the source data for the original traces of flower and moth for all moving flower experiments shown in Figure 3, and further analyzed in Figure 4A,B and Figure 3—figure supplements 1,3,4.
- https://doi.org/10.7554/eLife.37606.014
-
Figure 3—source data 2
Contains the source data complex valued responses of moths tracking the sum-of-sines stimulus shown in Figure 3 and Figure 3—figure supplement 1.
- https://doi.org/10.7554/eLife.37606.015
Figure 3—figure supplement 1
Hawkmoth tracking performance with the sum-of-sines stimulus in bright and dim light.
Tracking error (A–C), gain (D–F) and phase (G–I) of hawkmoths tracking a moving robotic flower which moved as a sum-of-sines (see Materials and methods) at 3000 and 30 lux. Curves show the mean and 95% confidence intervals of the mean, calculated in the complex plane. For statistical analysis of flower tracking performance see Supplementary files 4,11.
Figure 3—figure supplement 2
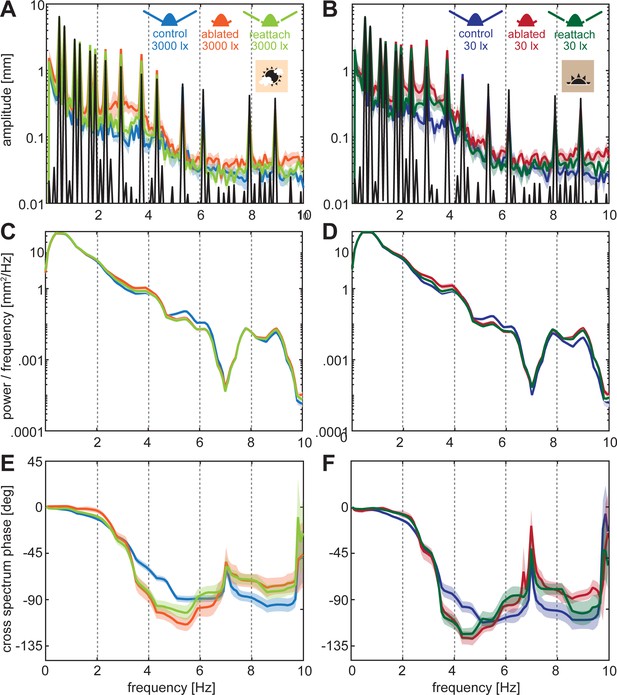
Frequency analysis of sum-of-sines stimulus tracking performance.
(A, C) Amplitude spectrum of the flight tracks (colours) while following the sum-of-sines stimulus (black). (B,C) Cross power spectral density of the moth tracks and the stimulus. (E,F) Cross spectral phase of the moth tracks relative to the sum-of-sines stimulus. (A,C,E) at 3000 lux and (B,D,F) at 30 lux. Curves show the mean and shaded areas show the standard error of the mean (SEM).
Figure 3—figure supplement 3
Frequency analysis of chirp stimulus tracking performance.
(A, C) Amplitude spectrum of the flight tracks (colours) while following the chirp stimulus (black). (B,C) Cross power spectral density of the moth tracks and the chirp stimulus. (E,F) Cross spectral phase of the moth tracks relative to the chirp stimulus. (A,C,E) at 3000 lux and (B,D,F) at 30 lux. Curves show the mean and shaded areas show the standard error of the mean (SEM).
Figure 3—figure supplement 4
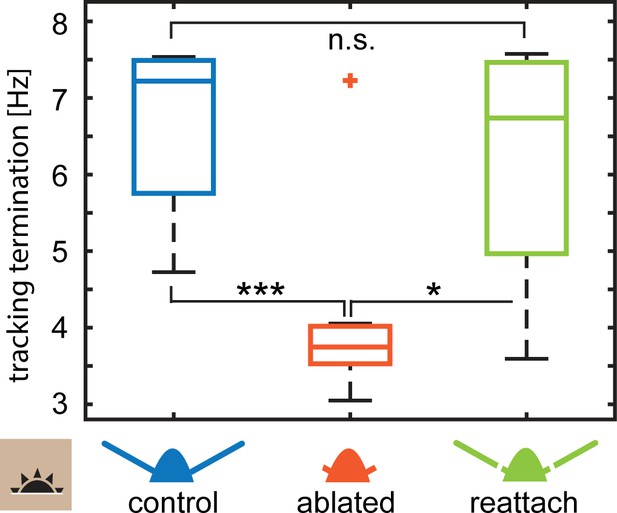
Flower tracking performance with chirp stimuli in dim light.
Comparison of the temporal frequency of the flower at which the moths aborted tracking across antennal treatments at 30 lux. A Friedman test was used to compare between the treatments (***p<0.001, **: p<0.01, *p<0.05, Supplementary file 12).
Figure 4
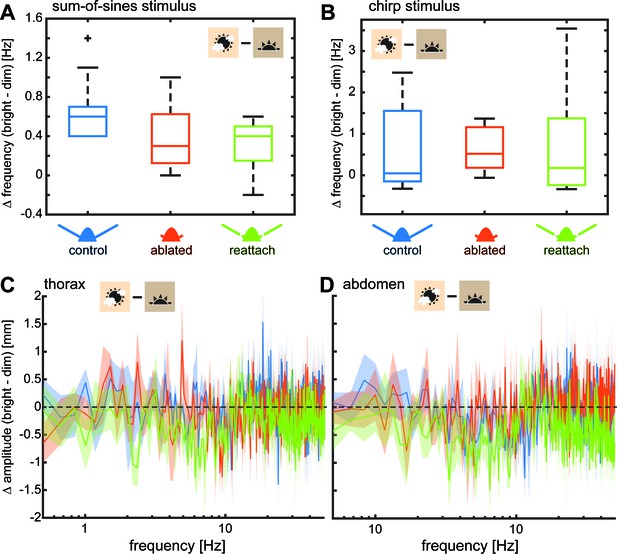
Light intensity had the same effect on all antennal treatments.
To test the effect of visual feedback and its possible interaction with antennal mechanosensory feedback on flower tracking, we performed all experiments both in bright (3000 lux) and dim (30 lux) light intensities. Hawkmoths showed reduced tracking performance of artificial flowers moving at higher frequencies in dim light, due to the slowing of their visual system (Figure 2—figure supplement 2, Figure 3—figure supplements 1,4). Here, we compare tracking performance between bright and dim light across antennal treatments. (A) We quantified the difference in frequency between light intensities at which moths reached a tracking error of 1 with the sum-of-sines stimulus. There was no significant difference (Supplementary file 8) between antennal conditions, suggesting that vision reduced tracking performance in dim light irrespective of the presence or absence of mechano-sensory feedback. (B) Similarly, there was no significant difference between the tracking performance in dim and bright light for the chirp stimulus (quantified as the difference of tracking abortion frequency at the two light conditions) (Supplementary file 6). (C–D) We determined the difference between the log-transformed magnitude spectra for thorax (C) and abdomen (D) jitter in bright and dim light. No significant effect of antennal condition was found using Friedman comparisons of the average difference in thorax or abdomen movements (Supplementary files 7 and 13). Lines show average, and shaded areas ± SEM.
Author response image 1
Author response image 2
Tables
Table 1
Proportion of hawkmoths performing specific behaviours across antennal conditions and light intensities.
Proportion of trials in which animals performed the following behaviours: no flight, flight (but no tracking of the flower), tracking. This dataset is based on the animals participating in the moving flower experiments. Of the total number of animals, 27 control, 22 flagella ablated, and 14 re-attached moths were tested in both light intensities. Some were tested multiple times to collect the necessary tracking data, and thus have contributed multiple trials to this dataset. Statistical comparisons were performed using multinomial regression including individual identity as a random factor, to model the rates of one of the three behaviours as a function of antennal condition and light intensity (without interaction terms). Statistical significance is indicated by: *p < 0.05, **p < 0.01, ***p < 0.001. For statistical details, see Supplementary file 1.
| Control | Ablated | Reattach | ||
|---|---|---|---|---|
| bright | No flight | 0.03 | 0.11 | 0.05 |
| Flight | 0.15 | 0.29 | 0.1 | |
| Tracking | 0.82 | 0.60 *** | 0.85 | |
| Total | 38 | 42 | 20 | |
| dim *** | No flight | 0.03 | 0.34 | 0.08 |
| Flight | 0.09 | 0.30 | 0.08 | |
| Tracking | 0.88 | 0.36 *** | 0.84 | |
| Total | 35 | 66 | 25 |
Additional files
-
Source data 1
Contains the ‘sum-of-sines’ and ‘chirp’ stimulus used in this study as MATLAB arrays, as well as MATLAB scripts to generate the stimuli.
- https://doi.org/10.7554/eLife.37606.017
-
Supplementary file 1
Results of the statistical models assessing the effect of antennal treatment and light intensity on the proportion of different behaviours in the flight cages.
The behaviour of each animal was classified into the following categories: no flight, flight (but no tracking of the flower), and tracking. Some moths were tested multiple times to collect the necessary tracking data, and thus have contributed multiple trials to this dataset. Statistical comparisons were performed using multinomial regression including the identity of individual moths as a random factor, to model the rates of one of the three behaviours as a function of antennal condition and lighting. As no significant interaction between antennal condition and light intensity was found, the fixed effects of the fitted model took the form: behavioural category (no flight, flight, tracking)~antennal condition+light intensity. All statistical results are expressed in relation to the probability of observing the no flight behaviour in the control condition in bright light.
- https://doi.org/10.7554/eLife.37606.018
-
Supplementary file 2
Results of the statistical models assessing the effect of antennal treatment on thorax jitter in the stationary experiment in bright light (Figure 2B).
A general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.019
-
Supplementary file 3
Results of the statistical models assessing the effect of antennal treatment on abdomen jitter in the stationary experiment in bright light (Figure 2C).
A general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.020
-
Supplementary file 4
Results of the statistical model assessing the effect of antennal treatment on flower tracking performance with the sum-of-sines stimulus in bright light (Figure 3B): a general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.023
-
Supplementary file 5
Results of the statistical model assessing the effect of antennal treatment on flower tracking performance with the chirp stimulus in bright light (Figure 3D): a Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.024
-
Supplementary file 6
Results of the statistical model assessing the effect of antennal condition on the difference in flower tracking error between light conditions with the chirp stimulus (Figure 4B).
A Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.028
-
Supplementary file 7
Results of the statistical model assessing the effect of antennal condition on the difference in thorax stability during hovering between light conditions (Figure 4C).
A Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.029
-
Supplementary file 8
Results of the statistical model assessing the effect of antennal condition on the difference in flower tracking error between light conditions with the sum-of-sines stimulus (Figure 4A).
A Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.027
-
Supplementary file 9
Results of the statistical models assessing the effect of antennal treatment on thorax jitter in the stationary experiment in dim light (Figure 2—figure supplement 2A).
A general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.021
-
Supplementary file 10
Results of the statistical models assessing the effect of antennal treatment on abdomen jitter in the stationary experiment in dim light (Figure 2—figure supplement 2B).
A general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.022
-
Supplementary file 11
Results of the statistical model assessing the effect of antennal treatment on flower tracking performance with the sum-of-sines stimulus in dim light (Figure 3—figure supplement 1): a general linear model was constructed with antennal treatment and frequency (binned to the logarithmic scale) as factors: log(response)~antennal condition * frequency +1|individual.
- https://doi.org/10.7554/eLife.37606.025
-
Supplementary file 12
Results of the statistical model assessing the effect of antennal treatment on flower tracking performance with the chirp stimulus in dim light (Figure 3—figure supplement 4): a Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.026
-
Supplementary file 13
Results of the statistical model assessing the effect of antennal condition on the difference in abdomen stability during hovering between light conditions (Figure 4D).
A Friedman test was performed, with a Tukey-Kramer post-hoc comparison correction for multiple comparisons.
- https://doi.org/10.7554/eLife.37606.030
-
Transparent reporting form
- https://doi.org/10.7554/eLife.37606.031
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The roles of vision and antennal mechanoreception in hawkmoth flight control
eLife 7:e37606.
https://doi.org/10.7554/eLife.37606
