Neuronal morphologies built for reliable physiology in a rhythmic motor circuit
- Brandeis University, United States
- Marine Biological Laboratories, United States
Figures
Figure 1 with 2 supplements
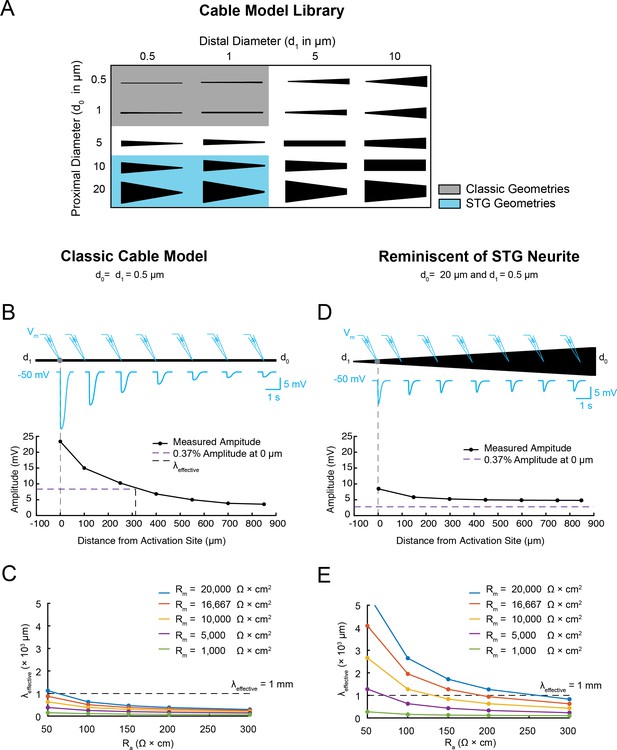
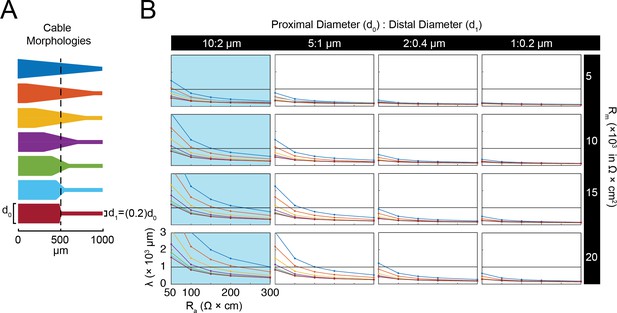
Electrotonus in cable models with diverse passive properties and geometries.
(A) Illustration of the complete matrix of cable model geometries assessed in the computational simulation. Proximal diameters (d0) ranged between 0.5–20 µm and distal diameters (d1) ranged between …
Figure 1—figure supplement 1
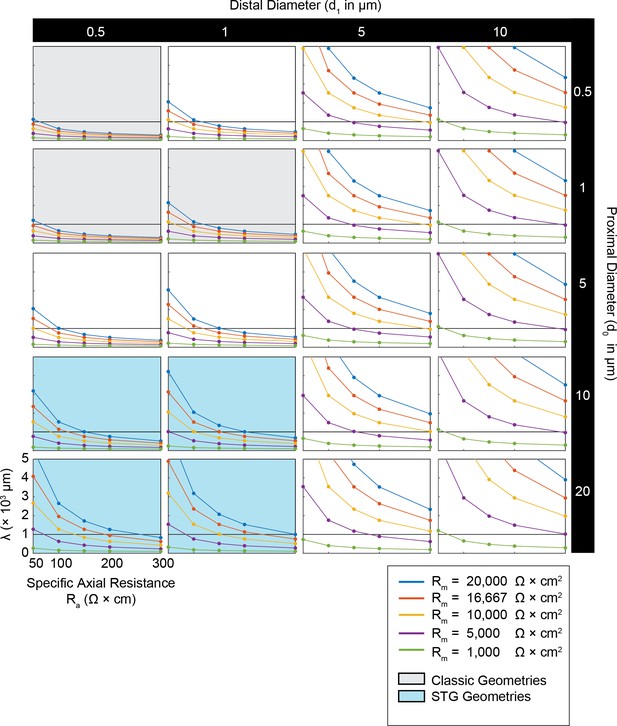
Simulated measurement of electrotonus in neurites with diverse passive properties and geometries.
Measurement of λeffective was simulated in NEURON as shown in Figure 1A,D and plotted for all cable morphologies as a function of passive properties as shown in Figure 1B,E. This array of plots …
Figure 1—figure supplement 2
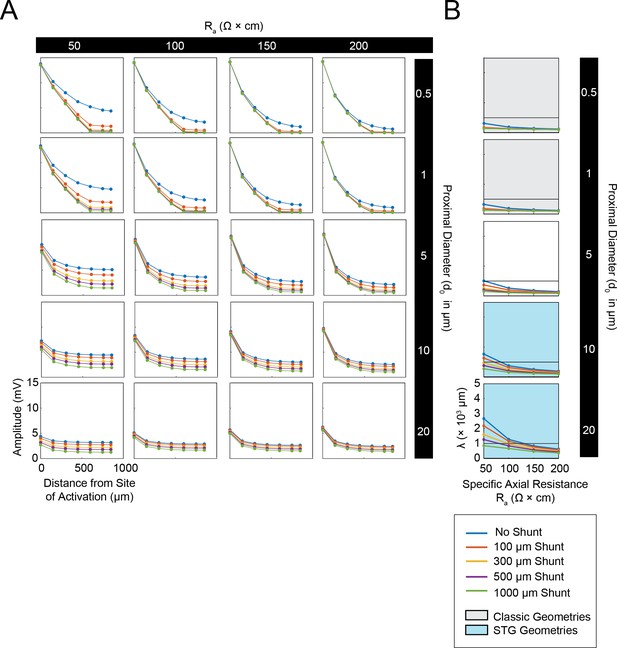
Simulated measurement of electrotonus in neurites in cables with unsealed proximal ends.
Measurement of λeffective was simulated in NEURON as shown in Figure 1A,D and plotted for a representative subspace of the cable model library with a specific membrane resistance (Rm) of 10,000 Ω*cm2…
Figure 2 with 3 supplements
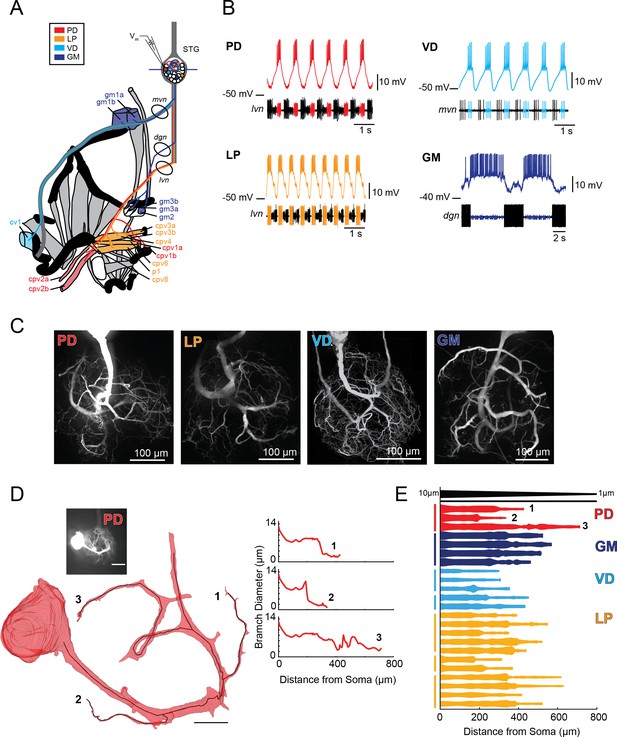
Characteristics of four identified STG neuron types.
(A) Bilateral innervation patterns of each neuron type, depicted on one side of the dissected foregut. Axons from the four neuron types project from the STG (top) and project to specific muscle …
Figure 2—figure supplement 1
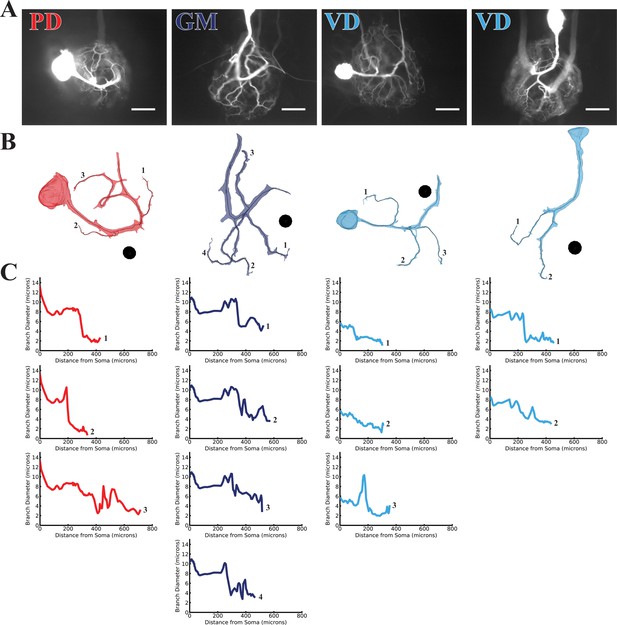
Branch diameter on uncaged branches as a function of path distance from soma.
(A) Low magnification (20x objective) images of four dye-filled neurons used in uncaging experiments. The PD, GM, and both VD preparations were imaged after a post-photo-uncaging dye-fill with …
Figure 2—figure supplement 2
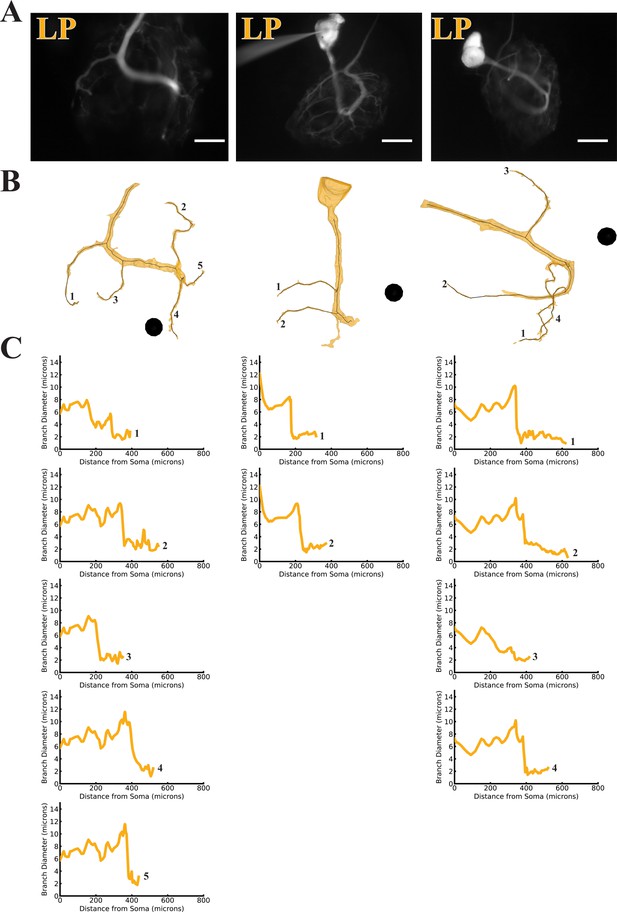
Branch diameter on uncaged branches as a function of path distance from soma.
(A) Low magnification (20x objective) images of three dye-filled neurons used in uncaging experiments. The three LP preparations were imaged with an Alexa Fluor 488 fills prior to the Lucifer Yellow …
Figure 2—figure supplement 3
Simulated measurement of electrotonus in neurites with varying degrees of taper.
Measurement of λeffective was simulated in NEURON as shown in Figure 1A,D. (A) seven cable geometries with varying degrees of taper: from a gradual linear taper (blue, top) to abrupt step-reduction …
Figure 3 with 4 supplements
Variable response amplitudes and invariant apparent reversal potentials (Erevs) across STG neuronal structures.
(A and B) Glutamate photo-uncaging and measurement of apparent Erevs in a representative PD neurite. (A) Fluorescence images of an Alexa Fluor 488 dye-fill showing the neurite tree at 20x …
Figure 3—figure supplement 1
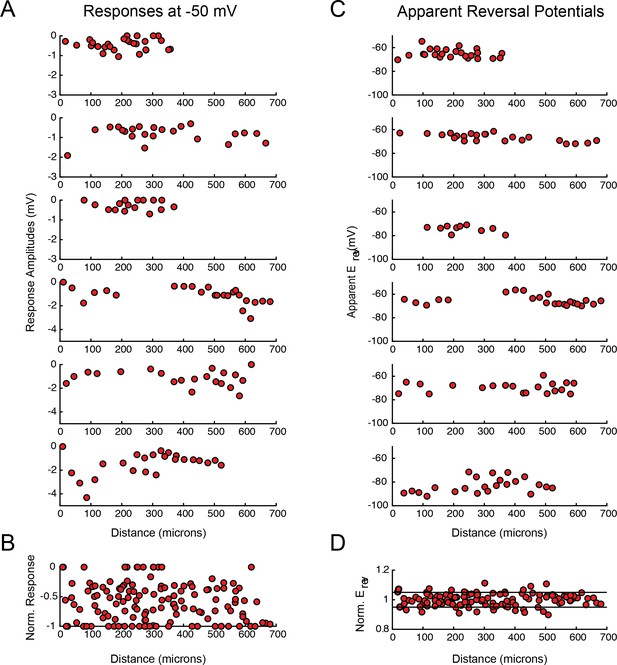
PD response magnitudes and apparent reversal potentials (Erevs) as a function of distance from the somatic recording site.
(A) Maximum response amplitudes were measured at −50 mV for individual sites. Each plot shows response amplitudes for many sites in one neuron. (B) Apparent Erevs measured for each site. Each plot …
Figure 3—figure supplement 2
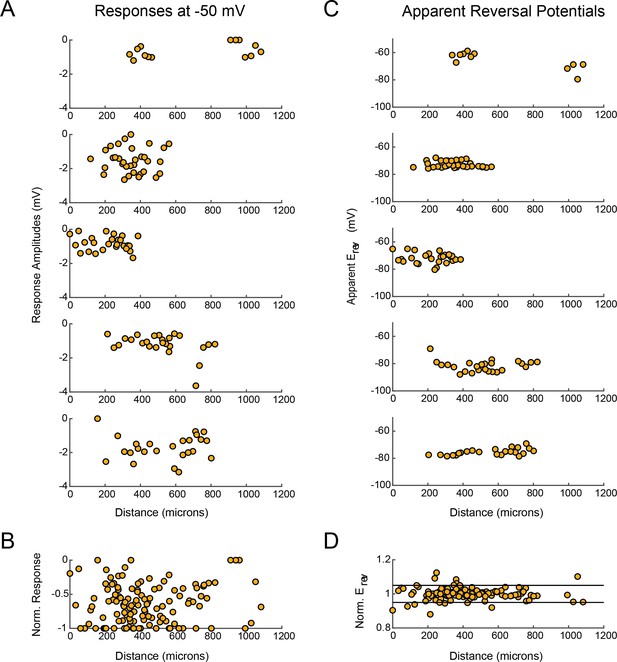
LP response magnitudes and apparent reversal potentials (Erevs) as a function of distance from the somatic recording site.
(A) Maximum response amplitudes were measured at −50 mV for individual sites. Each plot shows response amplitudes for many sites in one neuron. (B) Apparent Erevs measured for each site. Each plot …
Figure 3—figure supplement 3
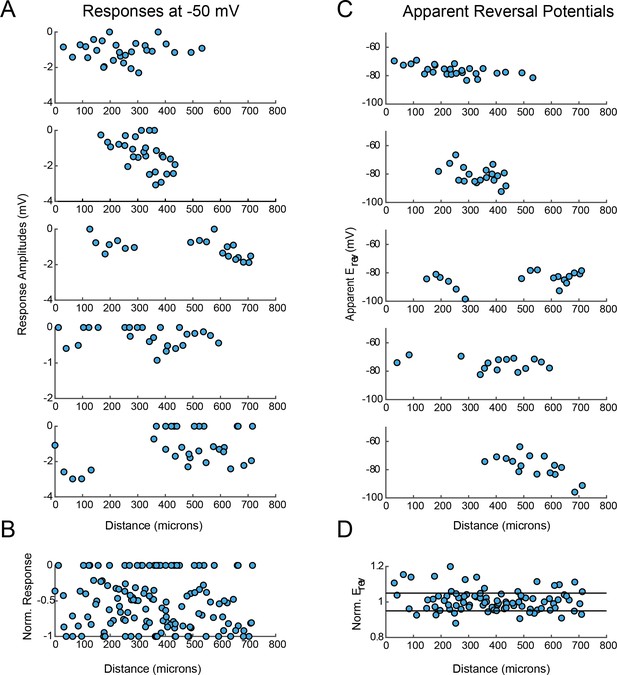
VD response magnitudes and apparent reversal potentials (Erevs) as a function of distance from the somatic recording site.
(A) Maximum response amplitudes were measured at −50 mV for individual sites. Each plot shows response amplitudes for many sites in one neuron. (B) Apparent Erevs measured for each site. Each plot …
Figure 3—figure supplement 4
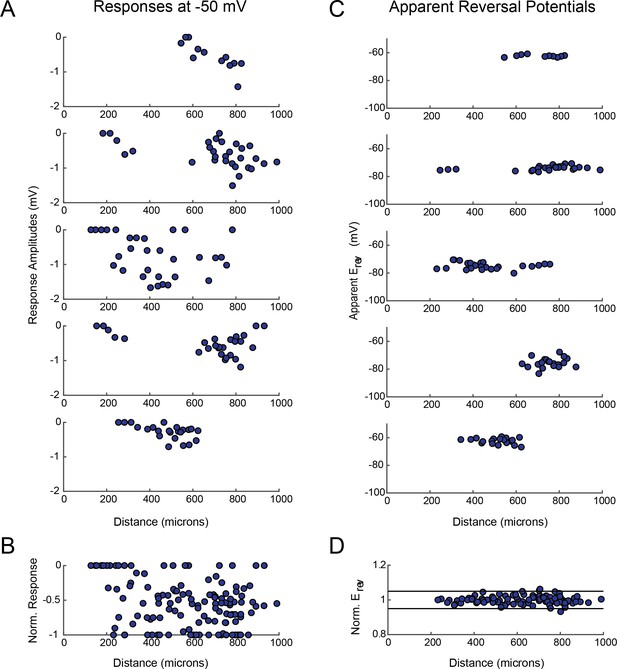
GM response magnitudes and apparent reversal potentials (Erevs) as a function of distance from the somatic recording site.
(A) Maximum response amplitudes were measured at −50 mV for individual sites. Each plot shows response amplitudes for many sites in one neuron. (B) Apparent Erevs measured for each site. Each plot …
Figure 4 with 2 supplements
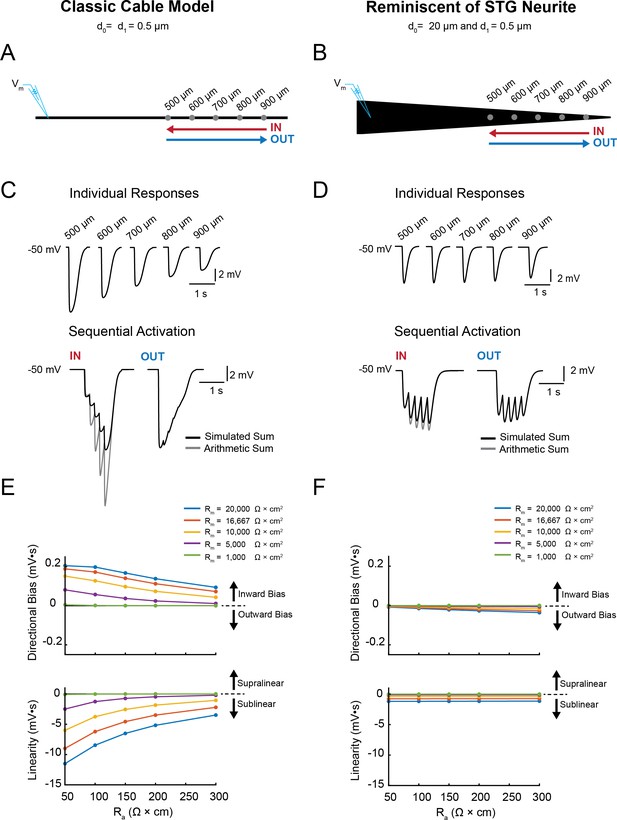
Simulating voltage summation in neurites with diverse passive properties and geometries.
Voltage summation experiments were simulated in NEURON. Inhibitory potentials were evoked at five sites (500, 600, 700, 800, and 900 µm away from the recording electrode) individually or in sequence …
Figure 4—figure supplement 1
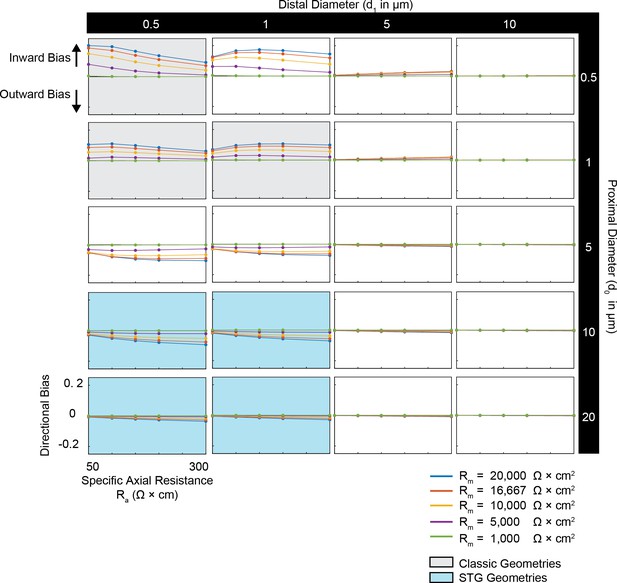
Simulated measurement of directional bias of voltage summation in neurites with diverse passive properties and geometries.
Voltage summation experiments were simulated in NEURON as shown in Figure 4A,B. This array of plots shows directional bias, calculated as the integral of the inward voltage sum minus the outward …
Figure 4—figure supplement 2
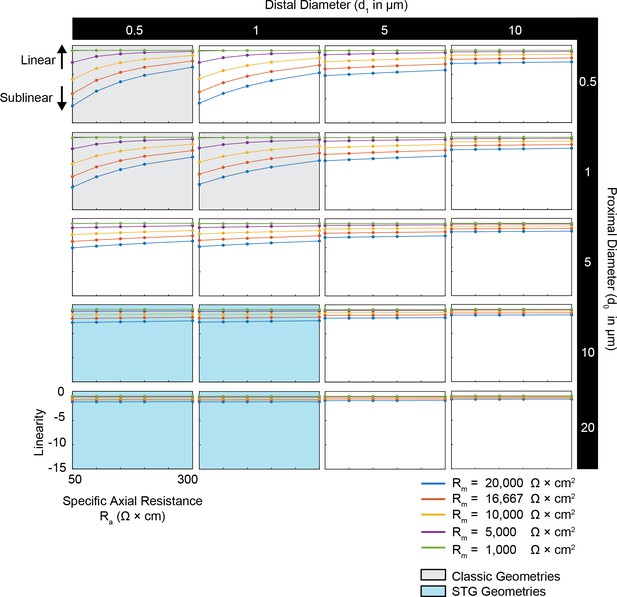
Simulated measurement of voltage summation arithmetic in neurites with diverse passive properties and geometries.
Voltage summation experiments were simulated in NEURON as shown in Figure 4A,B. This array of plots shows the linearity of voltage summation, calculated as the integral of the inward voltage sum …
Figure 5 with 4 supplements
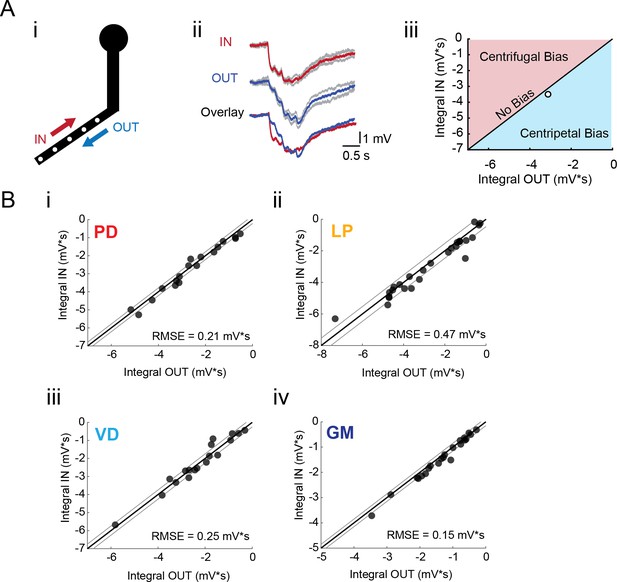
Directional sensitivity of voltage propagation in four STG neuron types.
(A) (i) 4–6 sites on single secondary neurites were sequentially photo-activated at 5 Hz in the inward (IN) or outward (OUT) directions. The integrals (ii) of these inhibitory summation responses …
Figure 5—figure supplement 1
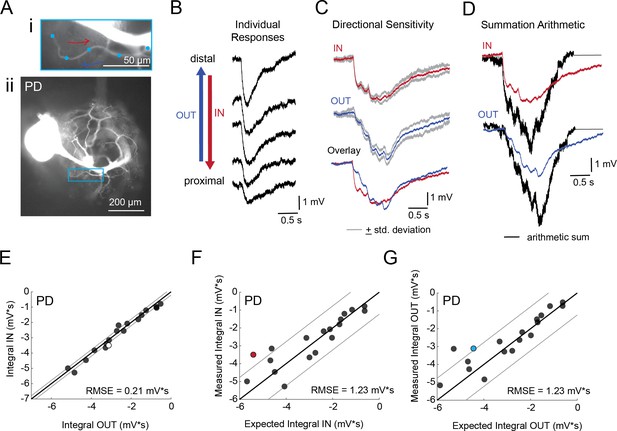
Directional sensitivity and arithmetic of voltage propagation in PD neurons.
(A) Representative images depicting one secondary neurite branch (i) at 40x magnification and (ii) in context of the entire dye-filled structure at 20x magnification. Arrows indicate inward (IN; …
Figure 5—figure supplement 2
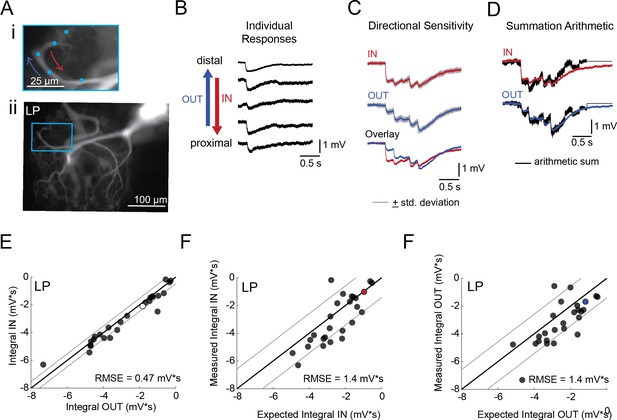
Directional sensitivity and arithmetic of voltage propagation in LP neurons.
(A) Representative images depicting one secondary neurite branch (i) at 40x magnification and (ii) in context of the entire dye-filled structure at 20x magnification. Arrows indicate inward (IN; …
Figure 5—figure supplement 3
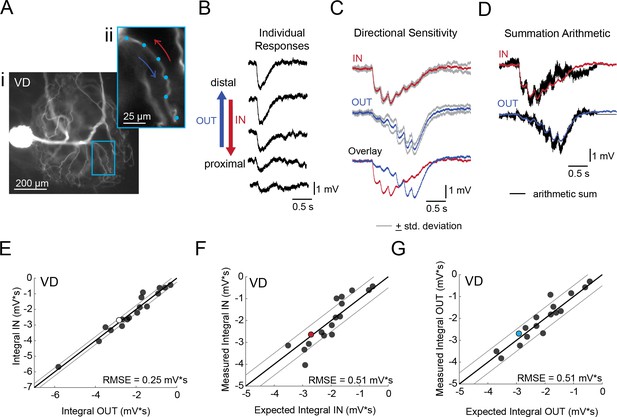
Directional sensitivity and arithmetic of voltage propagation in VD neurons.
(A) Representative images depicting one secondary neurite branch (i) at 40x magnification and (ii) in context of the entire dye-filled structure at 20x magnification. Arrows indicate inward (IN; …
Figure 5—figure supplement 4
Directional sensitivity and arithmetic of voltage propagation in GM neurons.
(A) Representative images depicting one secondary neurite branch (i) at 40x magnification and (ii) in context of the entire dye-filled structure at 20x magnification. Arrows indicate inward (IN; …
Figure 6
Arithmetic of voltage propagation in four neuron types.
(A) (i) 4–6 sites spaced 50–100 µm apart on the same secondary neurite were sequentially photo-activated at 5 Hz in the inward (IN) direction. (ii) Raw responses at individual sites from most distal …
Tables
Table 1
Linear regression analyses for response amplitudes and apparent reversal potentials (Erevs) as a function of distance from the somatic recording site for sites in individual neurons or pooled by cell type.
The data contributing to these analyses are shown graphically in Figure 3C and D and Figure 3—figure supplement 1–4 to Figure 3.
| Amplitude vs. Distance | Apparent Erev vs. Distance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Neuron | Sites | MSE | R | p | Slope (mV/µm | MSE | R | p | Slope (mV/µm) |
| PD | 30 | 0.08 | 0.05 | 7.98E-01 | 1.67E-04 | 13.61 | 0.17 | 4.22E-01 | -7.23E-03 |
| PD | 23 | 0.15 | -0.05 | 8.38E-01 | -1.03E-04 | 4.66 | -0.73 | 8.43E-05 | -1.35E-02 |
| PD | 10 | 0.05 | -0.06 | 8.28E-01 | -1.77E-04 | 6.65 | -0.42 | 2.26E-01 | -1.60E-02 |
| PD | 23 | 0.37 | -0.47 | 2.05E-02 | -1.56E-03 | 15.13 | -0.19 | 3.88E-01 | -3.87E-03 |
| PD | 20 | 0.40 | -0.18 | 4.26E-01 | -6.35E-04 | 17.96 | 0.05 | 8.50E-01 | 1.05E-03 |
| PD | 23 | 0.77 | 0.40 | 5.18E-02 | 2.62E-03 | 32.09 | 0.37 | 8.55E-02 | 1.62E-02 |
| PDMEAN | 21.5 | 0.30 | -0.05 | 4.94E-01 | 5.18E-05 | 11.60 | -0.29 | 3.77E-01 | -7.91E-03 |
| PDSD | 6.5 | 0.27 | 0.29 | 3.86E-01 | 1.40E-03 | 9.79 | 0.38 | 3.04E-01 | 1.16E-02 |
| LP | 11 | 0.14 | 0.43 | 1.23E-01 | 5.87E-04 | 12.09 | -0.81 | 2.67E-03 | -1.54E-02 |
| LP | 26 | 0.50 | -0.02 | 9.25E-01 | -1.15E-04 | 5.07 | -0.19 | 3.08E-01 | -4.00E-03 |
| LP | 25 | 0.17 | -0.15 | 4.75E-01 | -5.56E-04 | 14.18 | -0.17 | 4.16E-01 | -5.79E-03 |
| LP | 25 | 0.34 | -0.40 | 4.70E-02 | -1.56E-03 | 5.75 | -0.09 | 6.75E-01 | -2.15E-03 |
| LP | 24 | 0.51 | 0.02 | 9.30E-01 | 7.01E-05 | 0.70 | 0.55 | 5.00E-03 | 7.26E-03 |
| LPMEAN | 22.2 | 0.33 | -0.02 | 5.00E-01 | -3.15E-04 | 10.16 | -0.14 | 2.81E-01 | -4.02E-03 |
| LPSD | 6.3 | 0.18 | 0.30 | 4.22E-01 | 8.08E-04 | 5.45 | 0.48 | 2.86E-01 | 8.12E-03 |
| VD | 27 | 0.31 | 0.05 | 7.95E-01 | 2.32E-04 | 193.71 | -0.35 | 7.64E-02 | -4.17E-02 |
| VD | 19 | 0.54 | -0.53 | 3.49E-03 | -6.51E-03 | 28.63 | -0.45 | 5.57E-02 | -3.85E-02 |
| VD | 24 | 0.28 | -0.14 | 5.06E-01 | -2.46E-04 | 41.44 | 0.22 | 3.16E-01 | 5.07E-03 |
| VD | 15 | 0.07 | -0.20 | 3.36E-01 | -3.28E-04 | 15.74 | -0.29 | 2.97E-01 | -7.76E-03 |
| VD | 15 | 0.87 | 0.35 | 4.73E-02 | 1.81E-03 | 33.58 | -0.69 | 3.29E-03 | -5.59E-02 |
| VDMEAN | 20.0 | 0.42 | -0.09 | 3.38E-01 | -1.01E-03 | 62.62 | -0.31 | 1.50E-01 | -2.78E-02 |
| VDSD | 5.4 | 0.31 | 0.33 | 3.29E-01 | 3.19E-03 | 73.87 | 0.33 | 1.46E-01 | 2.54E-02 |
| GM | 10 | 0.04 | -0.84 | 6.83E-04 | -3.23E-03 | 0.56 | -0.14 | 6.93E-01 | -1.17E-03 |
| GM | 28 | 0.09 | -0.53 | 2.02E-03 | -8.74E-04 | 2.09 | 0.31 | 1.13E-01 | 2.49E-03 |
| GM | 25 | 0.64 | -0.24 | 1.78E-01 | -1.12E-03 | 5.56 | -0.13 | 5.28E-01 | -2.23E-03 |
| GM | 20 | 0.09 | -0.41 | 3.50E-02 | -5.76E-04 | 11.76 | 0.17 | 4.76E-01 | 9.37E-03 |
| GM | 19 | 0.03 | -0.57 | 4.56E-03 | -1.14E-03 | 4.03 | -0.24 | 3.26E-01 | -6.53E-03 |
| GMMEAN | 20.4 | 0.18 | -0.52 | 4.41E-02 | -1.39E-03 | 4.80 | -0.01 | 4.27E-01 | 3.85E-04 |
| GMSD | 6.9 | 0.26 | 0.22 | 7.62E-02 | 1.06E-03 | 4.33 | 0.23 | 2.19E-01 | 5.97E-03 |
Table 2
Apparent Mean Erevs, standard deviations (SD) and coefficients of variance (CV) for individual neurons and within neuron type.
https://doi.org/10.7554/eLife.41728.015| Neuron | Sites | Branches | Mean Erev (mV) | SD (mV) | CV |
|---|---|---|---|---|---|
| PD | 30 | 6 | -64.70 | 3.80 | 0.06 |
| PD | 23 | 4 | -66.30 | 3.20 | 0.05 |
| PD | 10 | 3 | -74.30 | 3.00 | 0.04 |
| PD | 23 | 4 | -64.18 | 4.05 | 0.06 |
| PD | 20 | 4 | -69.56 | 4.35 | 0.06 |
| PD | 23 | 4 | -83.00 | 6.22 | 0.08 |
| PDMEAN | 21.5 | 4.2 | -70.34 | 4.10 | 0.06 |
| LP | 11 | 2 | -65.72 | 6.18 | 0.09 |
| LP | 26 | 5 | -72.82 | 2.33 | 0.03 |
| LP | 25 | 5 | -71.87 | 3.89 | 0.05 |
| LP | 25 | 5 | -81.67 | 4.07 | 0.05 |
| LP | 24 | 5 | -71.87 | 3.89 | 0.05 |
| LPMEAN | 22.2 | 4.4 | -72.79 | 4.07 | 0.05 |
| VD | 27 | 4 | -76.22 | 3.75 | 0.05 |
| VD | 19 | 4 | -80.83 | 6.14 | 0.08 |
| VD | 24 | 4 | -83.86 | 6.75 | 0.08 |
| VD | 15 | 4 | -74.81 | 4.29 | 0.06 |
| VD | 15 | 5 | -77.84 | 8.23 | 0.11 |
| VDMEAN | 20 | 4.2 | -78.71 | 5.83 | 0.08 |
| GM | 10 | 2 | -62.33 | 0.80 | 0.01 |
| GM | 28 | 5 | -74.00 | 1.55 | 0.02 |
| GM | 25 | 6 | -74.78 | 2.43 | 0.03 |
| GM | 20 | 5 | -75.42 | 3.57 | 0.05 |
| GM | 19 | 4 | -65.66 | 7.05 | 0.11 |
| GMMEAN | 20.4 | 4.4 | -70.44 | 3.08 | 0.04 |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.41728.025
