Leave-One-Trial-Out, LOTO, a general approach to link single-trial parameters of cognitive models to neural data
Figures

Fisher information and performance of LOTO for the binomial distribution.
(A) Fisher information (left panel), average correlation between and LOTO’s estimate (middle panel), and example correlation for values of θt in the range [.4,.6] (right panel) for the Bernoulli distribution. (B) The same as in panel A but generalized to the binomial distribution, that is, assuming that θ is stable over m trials, for different levels of m (the example correlation in the right panel uses m = 20).
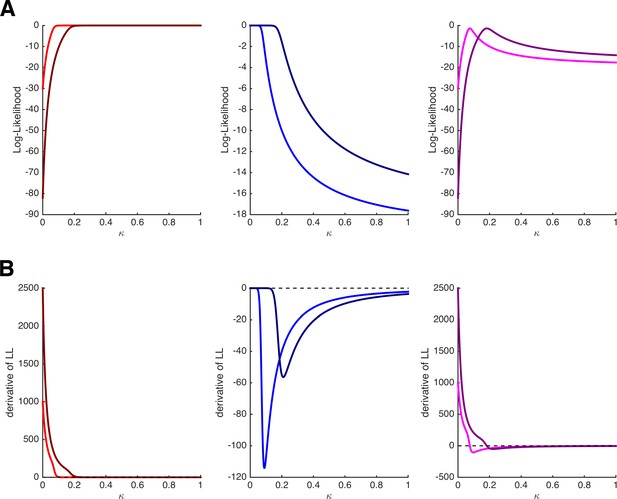
Log-likelihoods and derivatives for the hyperbolic discounting model.
(A) Log-likelihoods for choosing the immediate option (left panel), choosing the delayed option (middle panel), and choosing the immediate option once and the delayed option once (right panel) as a function of parameter κ. The bright and dark colors refer to two different trials with different amounts and delays. (B) First derivatives of the log-likelihoods shown in panel A. Note that the estimation of κ will depend on the features of the task only when both options are chosen at least once.
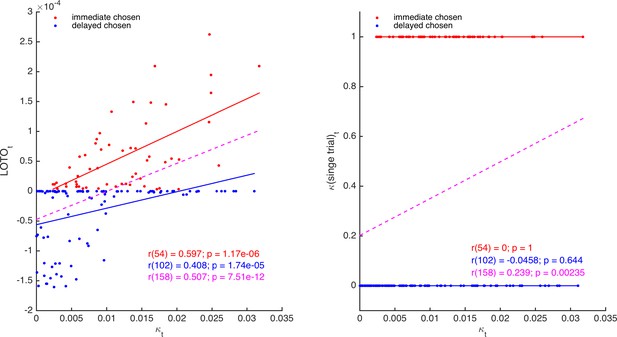
Comparison of LOTO and single-trial fitting.
The left panel shows the correlation of the trial-specific parameter κt of the HD model with LOTO’s estimates, separately for choosing the immediate (red) and for choosing the delayed (blue) option. The dashed line (magenta) shows the regression slope when collapsing over all trials. The right panel shows the same for the single-trial-fitting approach.
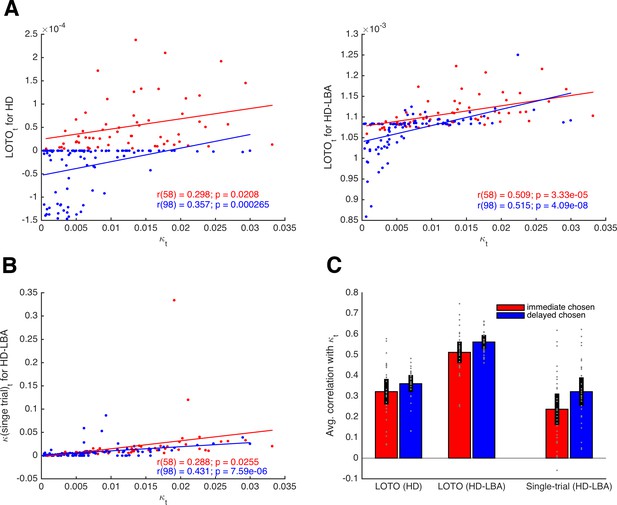
Comparison of LOTO for the HD and the HD-LBA models.
(A) Correlation of the trial-specific parameter κt with LOTO’s estimates for an example participant. The left panel shows the results when using the HD model, the right panel when using the HD-LBA model. (B) Same as panel (A) but for the single-trial fitting method when using the HD-LBA model. (C) Average correlation for all 30 simulated participants. Individual values (gray dots) are shown together with the 95% confidence intervals of the mean (black error bars).

A test for the presence of parameter variability.
(A) Improvement of the HD model’s deviance (in the n–1 trials included per LOTO step) from the ‘all-trials’ fit to the LOTO fit when variability in κ is absent (histogram) and when variability in κ of increasing amount is present (blue to red vertical lines). The black dashed line indicates the 5% of simulations under the null hypothesis with the largest improvement and serves as the statistical threshold. (B) Same as in panel A but with variability in β instead of κ.
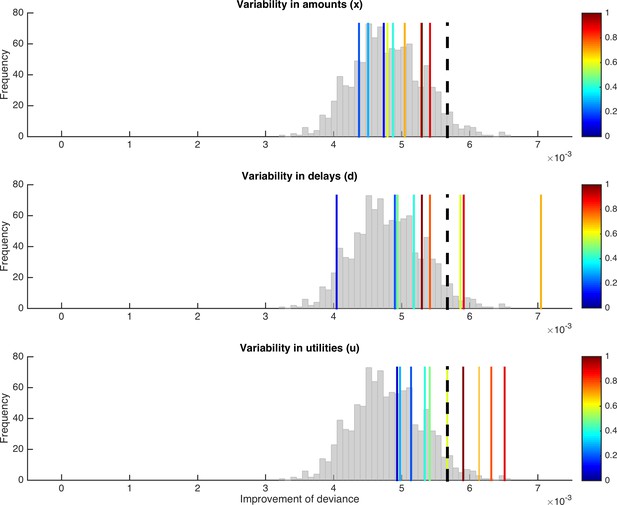
Testing for misattribution of variability in input and output variables to variability in a parameter.
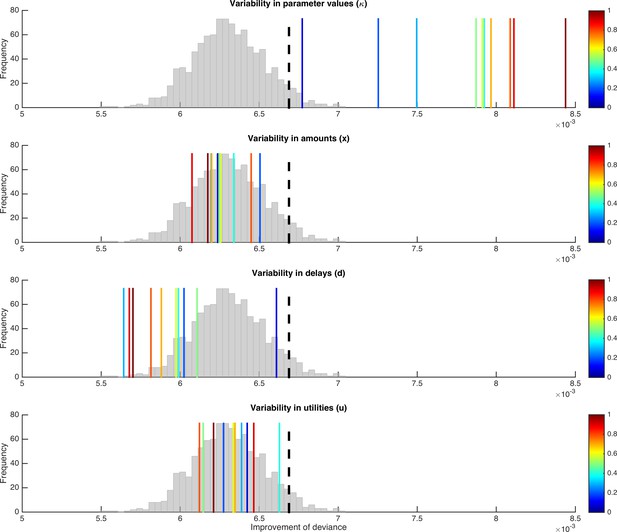
Depicted are tests for systematic trial-by-trial variability of κ, but with true variability in input variables (amounts or delays; upper and middle panel) or output variables (utilities; lower panel). As in Figure 5, the histogram represents the distribution of improvement in model fit under the null hypothesis, the dashed black line indicates the significance criterion, and the colors of the vertical lines indicate the degree of variability induced in the respective variables.
Testing for the presence of parameter variability and for misattributions in an adapted task.
In the intertemporal choice task with three choice options, true variability in discount factor κ still leads to improvements in model fit that exceed the improvement under the null hypothesis (first panel). At the same time, variability in input or output variables is not misattributed to κ anymore (lower panels). As in Figure 5, the histogram represents the distribution of improvement in model fit under the null hypothesis, the dashed black line indicates the significance criterion, and the colors of the vertical lines indicate the degree of variability induced in the respective variables.
Capturing trial-by-trial variability in two parameters.
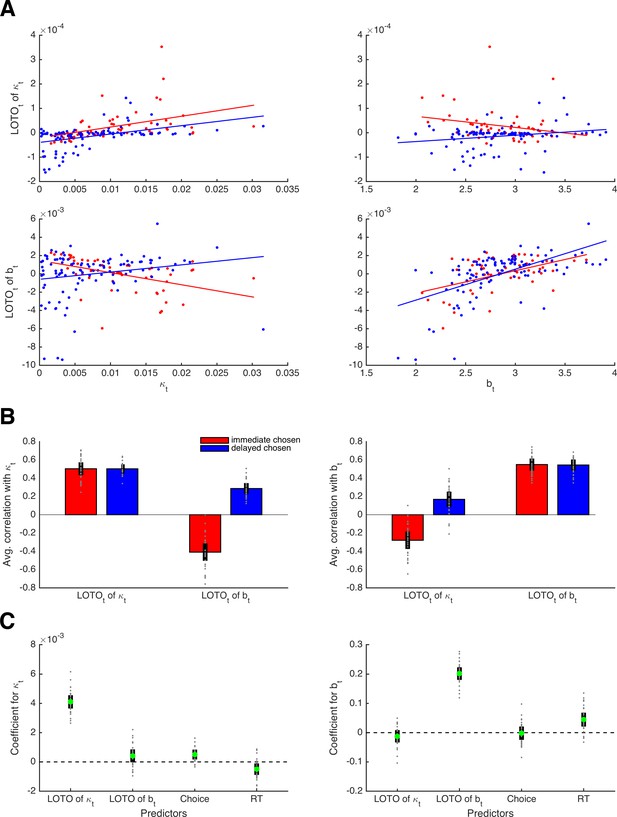
(A) Correlations of true parameter values κt and bt with their LOTO estimates for an example participant; the on-diagonal elements show the ‘correct’ inferences, the off-diagonal elements show the ‘wrong’ inferences. (B) Average correlations for all simulated participants (left panel: correlation with κt; right panel: correlation with bt). (C) Average standardized regression coefficients of LOTO estimates, choices, and RT when explaining variance in κt (left panel) and bt (right panel). Individual values (gray dots) are shown together with 95% confidence intervals of the mean (black error bars).
Relationship between the performance of LOTO and the number of trials.
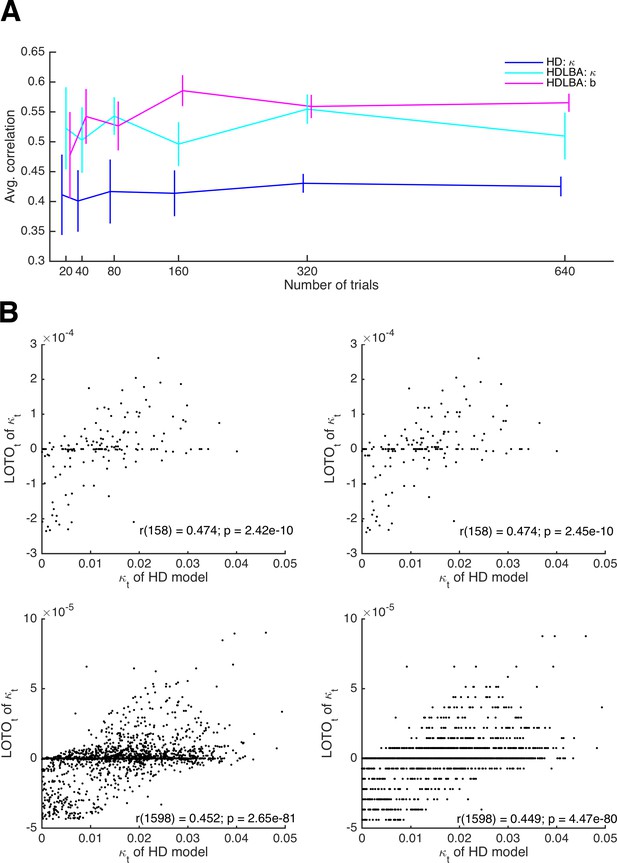
(A) Average correlations between true parameter values and LOTO estimates for parameters of the HD and the HD-LBA models as a function of the number of trials per simulated participant. (B) Example correlations between true values and LOTO estimates for 160 trials (upper panels) and for 1,600 trials (lower panels), separately for a strict tolerance criterion for convergence of the minimization algorithm (left panels) and for a more lenient, default tolerance criterion (right panels). Error bars indicate 95% confidence intervals of the mean.
Invariance of LOTO with respect to the underlying parameter distribution.
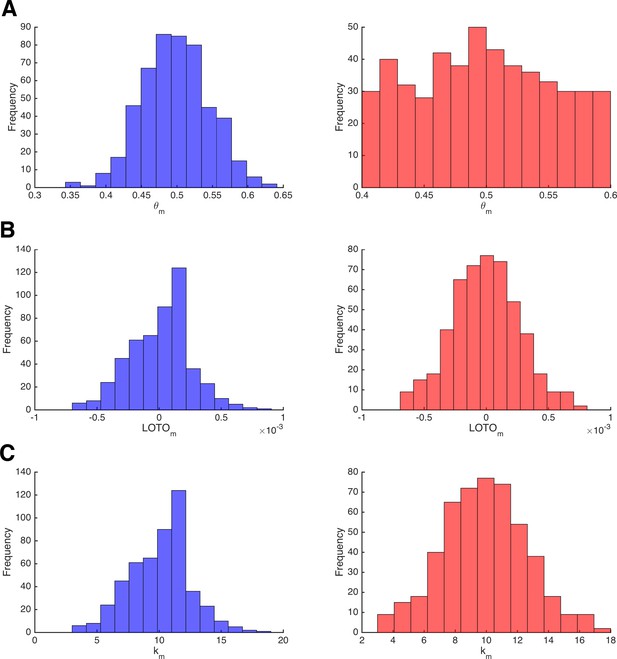
(A) Distribution of the data-generating parameter values θm for two simulations that sample from a normal distribution (left, blue) or from a uniform distribution (right, red). (B) The corresponding distributions of LOTO estimates. (C) The corresponding distributions of observations km.
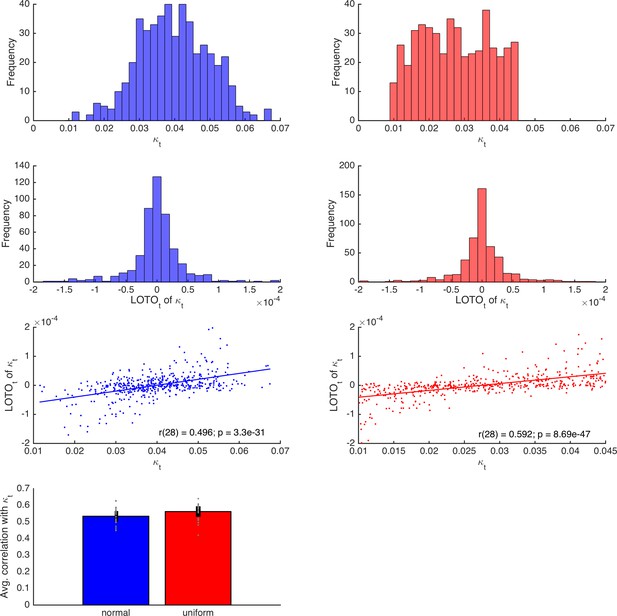
Comparison of LOTO distributions for parameter κ of the HD-LBA model.
The first and second rows depict the distributions of true parameters and LOTO estimates, respectively, for thenormally (left, blue) and uniformly (right, red) distributed true parameters. The third row depicts correlations between true parameters and LOTO estimates for an example participant. The lowest panel depicts the average correlations for all 30 participants for the normally and uniformly distributed true parameters.
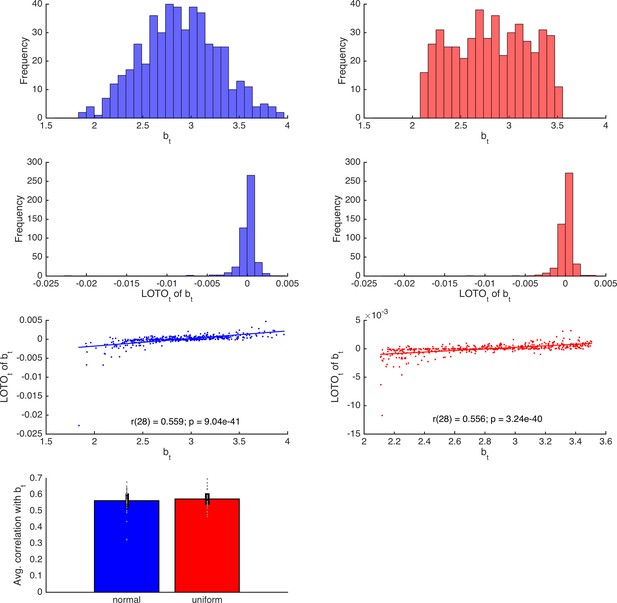
Comparison of LOTO distributions for parameter b of the HD-LBA model.
The first and second rows depict the distributions of true parameters and LOTO estimates, respectively, fornormally (left, blue) and uniformly (right, red) distributed true parameters. The third row depicts correlations between true parameters and LOTO estimates for an example participant. The lowest panel depicts average correlations for all 30 participants for the normally and uniformly distributed true parameters.
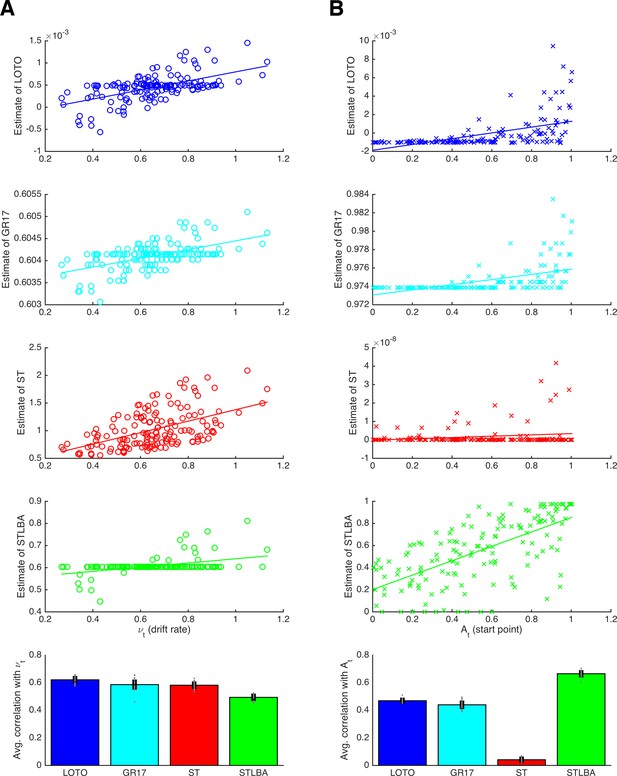
Comparison of methods for capturing trial-wise parameter values.
(A) Results for the LBA drift rate parameter. The first four panels show correlations for an example participant for the methods LOTO (blue), GR17 (cyan), single-trial fitting (ST; red), and STLBA (green). The lowest panel shows correlations averaged over all simulations. (B) Same as panel A but for the LBA start point parameter. Individual values (gray dots) are shown together with 95% confidence intervals of the mean (black error bars).
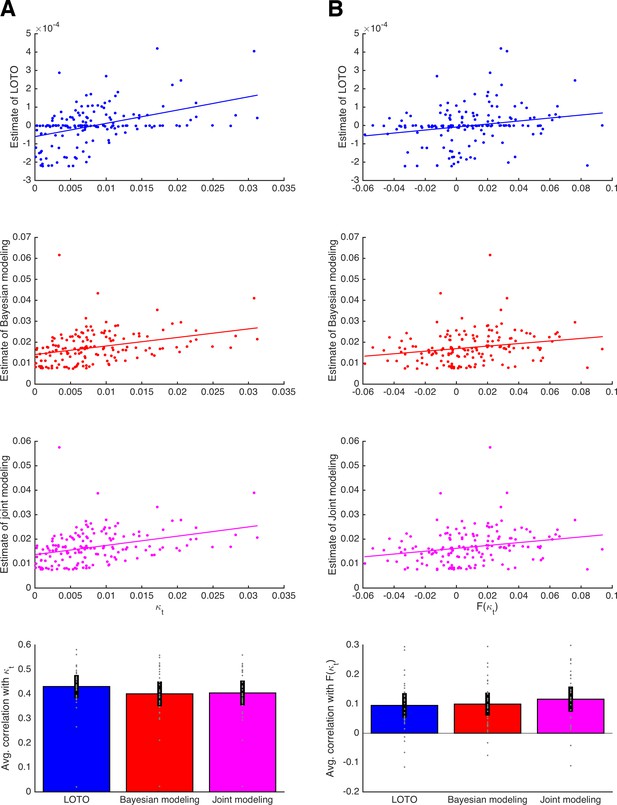
Comparison of LOTO with Bayesian modeling and joint modeling.
(A) Results for the HD model with respect to capturing variability in the discount factor κ. The three upper panels show correlations of an example participant for LOTO (blue), Bayesian modeling (red), and joint modeling (magenta). The lowest panel shows correlations averaged over all 30 simulated participants. (B) Same as panel A but with respect to capturing the variability in a (correlated) neural signal F(κ)t. Individual values (gray dots) are shown together with 95% confidence intervals of the mean (black error bars).
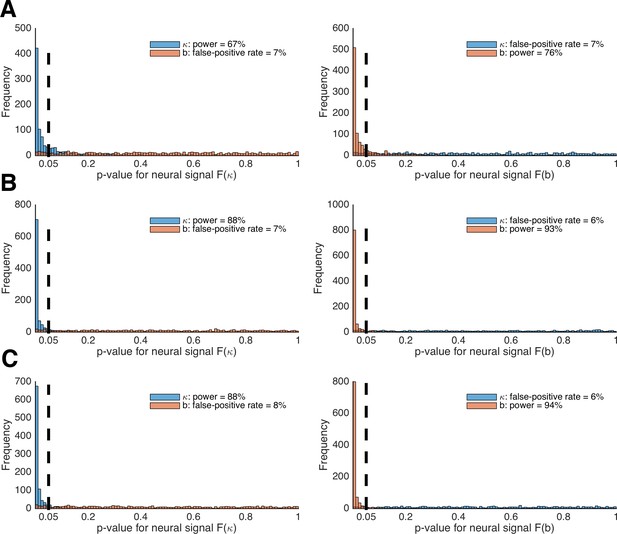
Power analysis of LOTO for detecting brain–parameter correlations.
(A) Histogram of the p-values from tests of the significant relationships between κ and b and brain signals F(κ) (left panel) and F(b) (right panel). (B) The same as in panel A but for 50 instead of 30 participants per simulated experiment. (C) The same as in panel A but for 267 instead of 160 trials per participant.
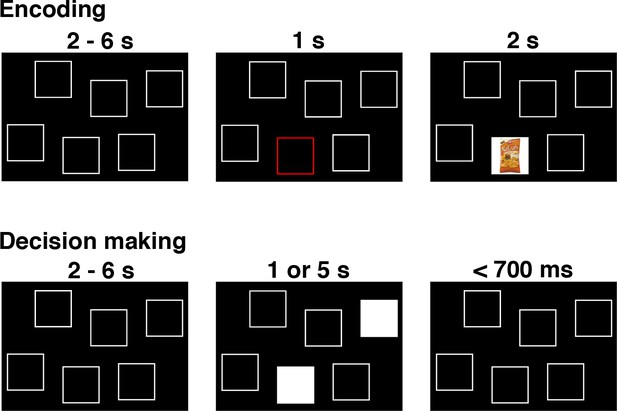
The remember-and-decide task (Gluth et al., 2015).
This figure shows one example trial from the encoding and decision-making phases of the task. During an encoding trial, participants learned the association between one out of six different snacks with a specific screen position. During a decision-making trial, two screen positions were highlighted, and participants had to retrieve the two associated snacks from memory in order to choose their preferred option. Here, we apply LOTO to a decision-making model in order to infer memory-related activity during encoding. For a more detailed illustration of the study design, see Figure 1 in Gluth et al. (2015).

Results of the example LOTO application.
(A) Average standardized regression coefficients for predicting memory performance in cued recall (1x/2x refers to how often an item was encoded). (B) Testing for systematic variability in memory; the green line shows the average trial-wise improvement of fit for the real dataset. The vertical dashed line represents the significance threshold based on the simulated data under the null hypothesis of no variability (gray histogram). (C) fMRI signals linked to the LOTO-based estimate of item-specific memory; the red outline depicts the anatomical mask of the hippocampus. (D) ROI analysis with anatomical masks of left and right hippocampus (HC) and average fMRI signals in these ROIs (the analyses in panels C and D are analogous to those in Figure 5 of Gluth et al., 2015). Individual values (gray dots) are shown together with 95% confidence intervals of the mean (black error bars).
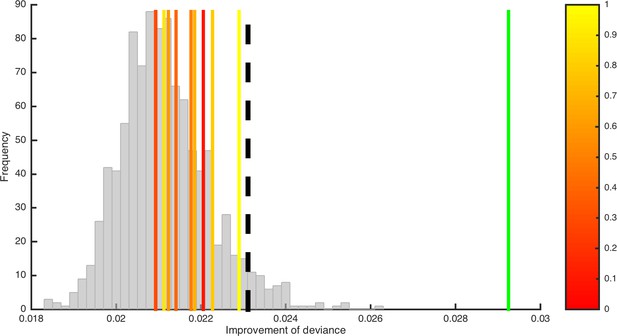
Testing for potential misattribution of variability in ‘decision noise’ parameter σ.
The analysis shown in Figure 12B was repeated for simulated data with true trial-by-trial variability in parameter σ (vertical lines in red to yellow colors). In contrast to the real data (green vertical line), the improvements of deviance for these simulations did not exceed those generated under the null hypothesis of no variability (gray histogram), suggesting that any potential variability in parameter σ is unlikely to be misattributed to the memory-related parameters.
Tables
| Reagent type (species) or resource | Designation | Source or reference | Identifiers |
|---|---|---|---|
| Software | MATLAB | MathWorks | RRID:SCR_001622 |
| Software | R Project for Statistical Computing | https://cran.r-project.org/ | RRID:SCR_001905 |
| Software | Just Another Gibbs Sampler (JAGS) | http://mcmc-jags.sourceforge.net/ | - |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.42607.020





