Modularity, criticality, and evolvability of a developmental gene regulatory network
Figures
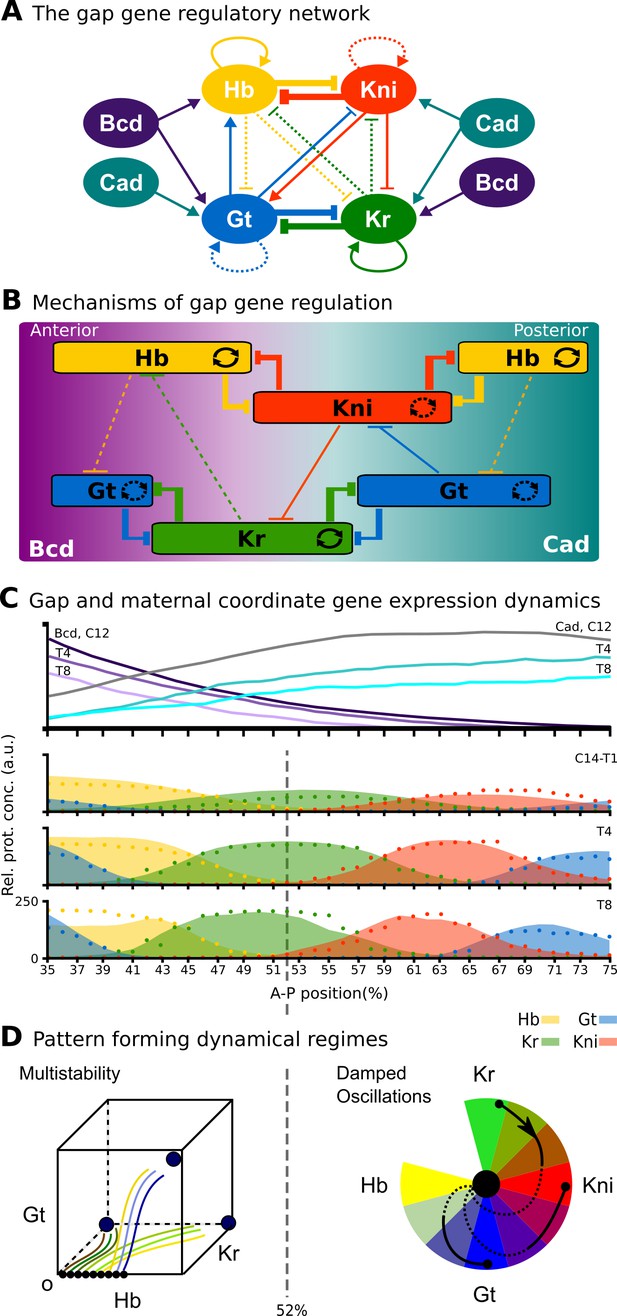
The gap gene system: structure, regulation, and expression.
(A) The regulatory structure of the gap gene network. Nodes represent transcription factors encoded by maternal coordinate genes bicoid (bcd, purple) and caudal (cad, cyan), as well as trunk gap genes hunchback (hb, yellow), Krüppel (Kr, green), knirps (kni, red) and giant (gt, blue). Activating interactions are indicated by arrows, repressive interactions by T-bars. Circular arrows indicate auto-activation. Dashed lines represent weak, solid lines stronger regulatory interactions. (B) Spatial representation of gap gene regulation: boxes indicate relative positions of gap domains along the antero-posterior (A–P) axis of the embryo. Anterior is to left, posterior to the right. Background colour indicates predominant activating inputs by maternal gradients. T-bars indicate gap gene cross-repression. Circular arrows represent gap gene auto-activation. (C) Gene expression dynamics of maternal coordinate genes bcd (purple) and cad (cyan), as well as trunk gap genes hb (yellow), Kr (green), kni (red) and gt (blue). Quantified expression patterns are shown as lines (maternal coordinate) and coloured areas (gap genes). Output of the fitted full model is shown as dots. Y-axes represent relative protein concentration in arbitrary units (a.u.); X-axes represent A–P position in %, where 0% is the anterior pole. C12 and C14 refer to cleavage cycle 12 and 14A, respectively. C14A is subdivided into eight time classes T1–8 of equal length. Only the trunk region of the embryo from 35 to 75% is shown. (D) Dynamical regimes driven by the gap gene system. Multistable (switch-like) behaviour in the anterior is indicated by a phase space with trajectories converging to multiple point attractors (represented by circles). Damped oscillations leading to dynamic anterior shifts of gap domains in the posterior are indicated by a colour wheel with trajectories cycling through successions of different gap genes. The bifurcation boundary between the two regimes at 52% A–P position is indicated by a dashed line. See text for details. Figure adapted from Verd et al. (2017); Verd et al. (2018).
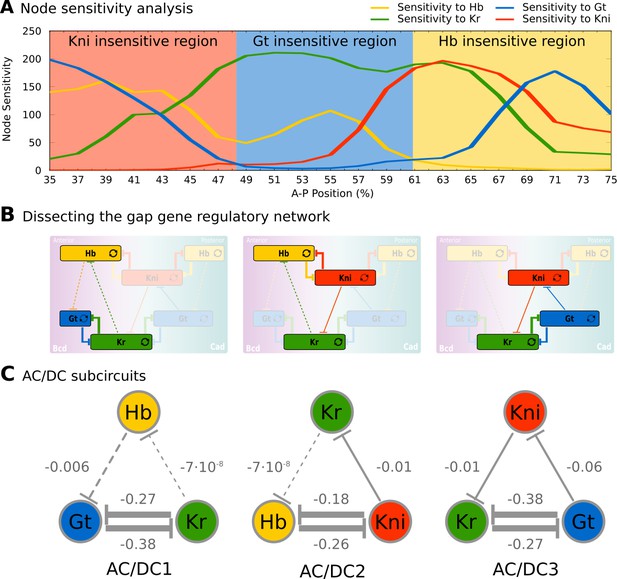
Identification of dynamical modules in the gap gene system.
(A) Node sensitivity analysis. The plot shows sensitivity of model output to the removal of hb (yellow), Kr (green), kni (red) and gt (blue). Y-axis represents node sensitivity as defined in ‘Materials and methods,’ Equation (4); X-axis represents A–P position in %, where 0% is the anterior pole. Regions insensitive to the absence of specific gap genes are indicated by background colour. (B) Dissecting the gap gene network into dynamical modules. Network schemata as in Figure 1B. Subcircuits active in each region identified in (A) are highlighted. (C) AC/DC subcircuits. All subcircuits identified in (A) and (B) share the same regulatory structure, indicated by T-bar connectors. Numbers indicate strength of interactions (in arbitrary units). Maternal inputs and auto-activation are omitted for clarify. Note that there is a fourth AC/DC subcircuit posterior of the region included in the present analysis (not shown, see ‘Materials and methods’). See text for details.
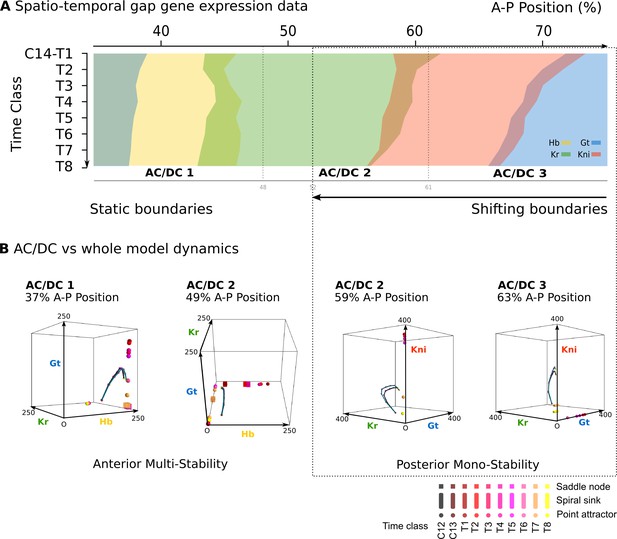
AC/DC subcircuits faithfully reproduce the dynamics of the full model.
(A) Spatio-temporal dynamics of gap gene expression in the trunk region of the embryo. Coloured areas show the position of gap domains for hb (yellow), Kr (green), kni (red), and gt (blue). Y-axis represents time (flowing downwards) during cleavage cycle C14A. Time classes T1–eight as defined in Figure 1. X-axis represents % A–P position, where 0% is the anterior pole. Regions of influence for each AC/DC subcircuit is indicated by grey lines. Black dotted line indicates the bifucation at 52% position separating static from shifting gap domain boundaries. (B) Comparative dynamical analysis of AC/DC subcircuits and the full model. Instantaneous phase portraits of AC/DC1 (nucleus at 37%), AC/DC2 (nuclei at 49 and 59%), and AC/DC3 (nucleus at 63% A–P position) are shown. Point attractors are shown as spheres, spiral sinks as cylinders, saddles as cubes. Colour code indicates time class, from T1 (dark red) to T8 (yellow). Trajectories from simulations of AC/DC subcircuits are shown in turquoise, trajectories from simulations of the full model in black. Axes represent concentrations of gap proteins (in arbitrary units) as indicated. See ‘Materials and methods’ for model definition and details on phase space analysis.
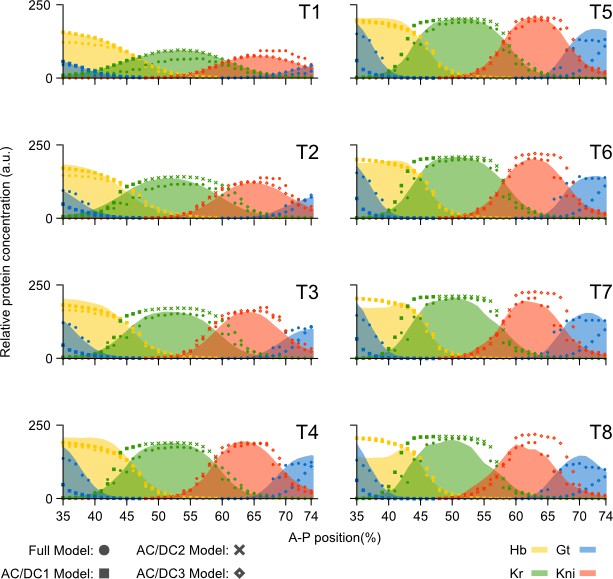
Comparison of AC/DC subcircuits and the full model.
Model output (represented by dots for the full model, and symbols for the AC/DC subcircuits) is shown compared to quantitative spatio-temporal gene expression data (coloured areas) for each time class T1–T8 during cleavage cycle 14 (C14). Subcircuits AC/DC1 (squares), AC/DC2 (crosses), and AC/DC3 (diamonds) were simulated in their respective regions of influence (35-47% for AC/DC1, 49-59% for AC/DC2, and 61-75% for AC/DC3). hb shown in yellow, Kr in green, kni in red, and gt in blue. Y-axes represent relative protein concentration in arbitrary units (a.u.); X-axes represent A–P position in %, where 0% is the anterior pole. Only the trunk region of the embryo from 35 to 75% is shown.
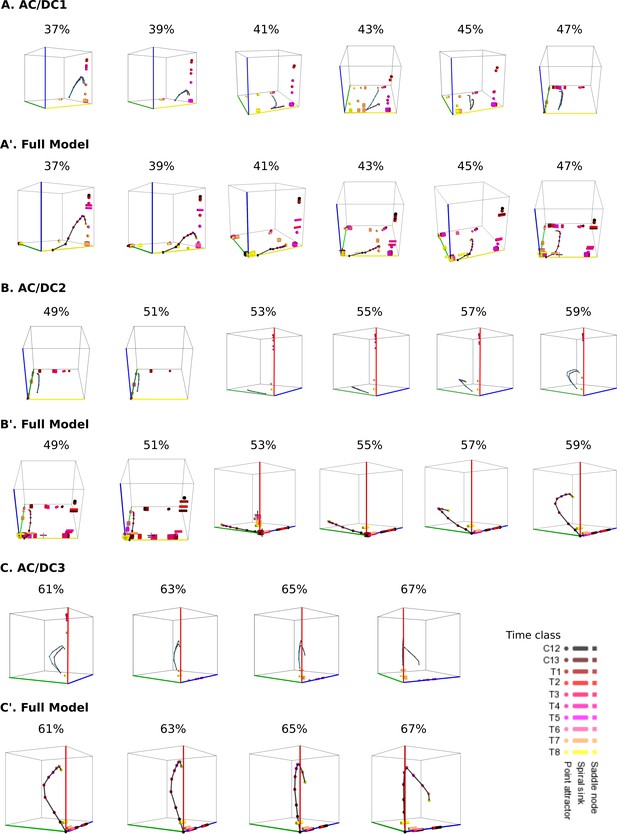
Comparative dynamical analysis of AC/DC subcircuits and the full model.
In all phase portraits point attractors are shown as spheres, spiral sinks as cylinders, saddles as cubes. Colour code indicates time class, from C12 (black) to T8 (yellow). Trajectories simulated from AC/DC subcircuits are shown in turquoise and trajectories from simulations of the full model in black. (A) Instantaneous phase portraits of AC/DC1 (A) and the full model (A’) in nuclei between 37 and 47% A–P position. (B) Instantaneous phase portraits of AC/DC2 (B) and the full model (B’) in nuclei between 49 and 59% A–P position. (C) Instantaneous phase portraits of AC/DC3 (C) and the full model (C’) in nuclei between 61 and 67% A–P position. (A, B, C) show trajectories of both AC/DC1 (turquoise) and the full model (black) from C14A-T1 to T8; (A’, B’, C’) show trajectories of the full model from C12 to C14A-T8 (black). Point attractors are shown as spheres, spiral sinks as cylinders, saddles as cubes. Colour code indicates time class, from C12 (black) to T1(dark red) to T8 (yellow). Axes represent concentrations of gap proteins (in arbitrary units) as indicated. See ‘Materials and methods’ for model definition and details on phase space analysis.
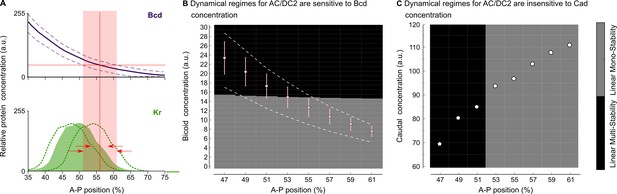
Intra-species robustness of gap gene patterning to perturbations in levels of maternal gradients.
(A) The position of gap gene expression features is relatively robust towards changes in maternal gradient concentrations. This sketch—modified from Figure 1 of Manu et al. (2009b)—shows concentration variation in the maternal Bcd gradient (above) and the zygotic expression domain of Kr (below). Solid line and coloured area indicate averaged expression patterns, dashed lines indicate expression variation. Red arrows show the difference between the range of positional variation in Bcd (red background) and Kr. (B) Phase diagram for AC/DC2 in response to variation in Bcd concentration. Pink dots and error bars show average Bcd concentration with standard deviation between 47 and 61% A–P position. Dashed lines show the maximum range of Bcd profiles in the data. AC/DC2 subcircuits for nuclei indicated by the X-axis, where simulated with Cad concentration fixed to its value at T1, and Bcd concentration fixed to the values given by the Y-axis. Background colour indicates the resulting dynamical regime: the multistable anterior regime is shown in black, the monostable posterior regime in grey. (C) Phase diagram for AC/DC2 in response to variation in Cad concentration. White dots indicate Cad concentrations between 47 and 61% A–P position. AC/DC2 subcircuits for nuclei indicated by the X-axis, where simulated with Bcd concentration fixed to its value at T1, and Cad concentration fixed to the values given by the Y-axis. Background indicates dynamical regime as in (B). See text for details.
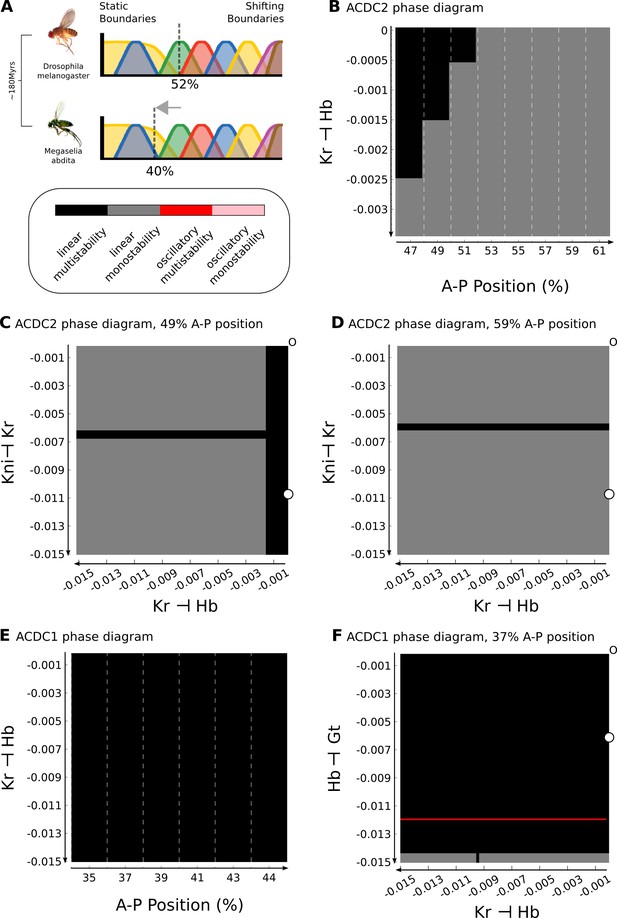
Inter-species lability of the bifurcation boundary depends on altered gap-gap interactions.
(A) The position of the bifurcation boundary separating static and shifting gap gene expression domains differs between D. melanogaster (upper panel, 52%) and M. abdita (lower panel, 40% A–P position). The difference between species is highlighted by a grey arrow. Phylogenetic distance between the two species is indicated to the left in ‘million years ago’ (mya). (B) Phase diagram for AC/DC2 in response to altering the strength of hb repression by Kr (plotted against A–P position). (C, D) Phase diagram for AC/DC2 in response to altering both hb repression by Kr (X-axis) and Kr repression by Kni (Y-axis) shown for subcircuits in nuclei at 49 (C) and 59% (D) A–P position. (E) Phase diagram for AC/DC1 in response to altering the strength of hb repression by Kr (plotted against A–P position). (F) Phase diagram for AC/DC1 in response to altering both hb repression by Kr (X-axis) and gt repression by Hb (Y-axis) shown for the subcircuit in the nucleus at 37% A–P position. (A–F) Background indicates dynamical regimes as in Figure 4: the multistable anterior regime is shown in black, the monostable posterior regime in grey. In addition, there is a narrow strip of a multistable oscillatory regime in (F) (shown in red). All Phase diagrams were calculated with maternal gradient concentrations fixed to their values at T1. See text for details.
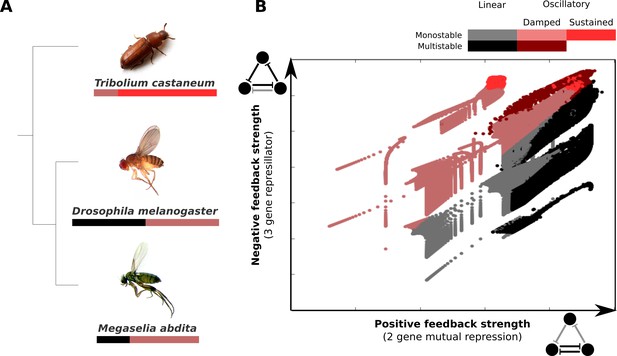
AC/DC subcircuits and their possible role in the evolution of long-germband from short-germband segment determination.
(A) Phylogenetic relationships between the intermediate-germband insect T. castaneum and the two long-germband dipteran species analysed in this paper. Coloured bars indicate which dynamical regimes are active in which relative region along the A–P axis of the embryo (see key). (B) Visualisation of the dynamical regimes of an AC/DC circuit. We combine equation parameters into two composite control parameters which correspond to the and parameters in Equations (28) and (29) of Appendix 1 and represent the strength of the positive feedback between two of the genes in the circuit (X-axis) and the strength of the negative feedback involving all three genes (Y-axis) respectively. We used simplified connectionist models (see ‘Materials and methods’)—with all degradation rates set to equal values, time-constant basal activation terms, and no auto-activation—to evaluate the dynamical regimes for varying values of these two control parameters. The results are colour-coded as indicated in the key. Possible dynamical regimes are: monostability and multistability without (grey), and with damped oscillations (light/dark red), as well as sustained limit-cycle oscillations (bright red) (see Appendix 1 for details).
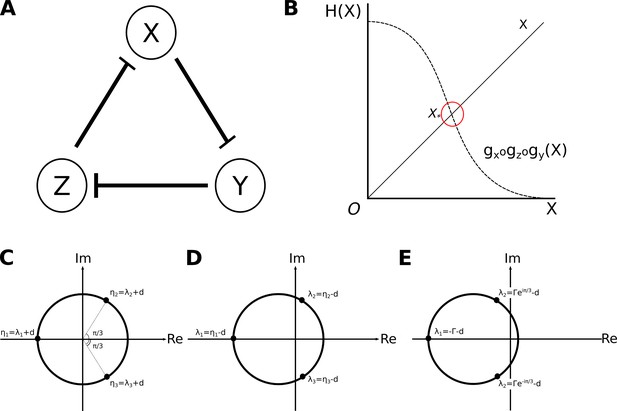
Analysis of the repressilator circuit.
(A) Structure of the repressilator circuit: the nodes of the network represent genes and their products X, Y, and Z (circles). Repressive interactions among these nodes are indicated by T-bars. We assume constitutive activation of all three nodes. (B) Uniqueness of solutions: solutions of Equation (7) are defined by intersections of the curves given by and . In this particular case, the shape of both curves results in them intersecting at only one value of , , and therefore there is only one solution. (C) Complex roots of is a real negative number, therefore it has one real negative, and two complex roots: , and . (D, E) Two different sets of possible eigenvalues: (D) Eigenvalues of a saddle point. One of the eigenvalues associated with the steady state has a negative real part, while the other two have positive real parts. In this case, the steady state is a saddle point. The uniqueness of the steady state, and the nature of the regulation-expression functions we’ve chosen, allows us to infer the presence of a limit cycle driving stable oscillations. (E) Eigenvalues of a stable spiral sink. All eigenvalues associated with the steady state have negative real parts and two of them are complex. In this case, the steady state is a stable spiral sink, which drives damped oscillations.

Analysis of the AC/DC circuit.
(A) Structure of the AC/DC circuit: the nodes of the network represent genes and their products X, Y, and Z (circles). T-bars represent the repressive interactions between the genes, where A,B,C and D denote the strengths of those respressions. Repressive interactions among these nodes are indicated by T-bars. We assume constitutive activation of all three nodes. (B) General shape of the function given by . (C–E) Effect of increasing the back reaction on the number of steady states. Functions as defined in the text. (C) No back reaction: there is only one intersection point. (D) Weak back reaction: still, there is only one intersection point. (E) Strong back reaction: now there are three intersection points. (F) The simplified characteristic Equation (27) defines a depressed cubic. Its dependence on parameter values is shown. (G,H) Roots of the depressed cubic given by Equation (27). (G) Option 1: one real negative root, and two complex roots with positive real part. (H) Option 2: real roots, where one has negative real part and two have positive real parts. (I–M) Combinations of eigenvalues for steady states in the AC/DC circuit. (I) Unstable spiral sink: a steady state with one real negative eigenvalue and two complex eigenvalues with positive real parts. (J) Stable spiral sink: a steady state with one real negative eigenvalue and two complex eigenvalues with negative real parts. (K) Point attractor: a steady state with real negative eigenvalues. (L) Saddle1,2: a steady state with real eigenvalues where one is positive and two are negative. (M) Saddle2,1: a steady state with real eigenvalues where two are positive and one is negative.
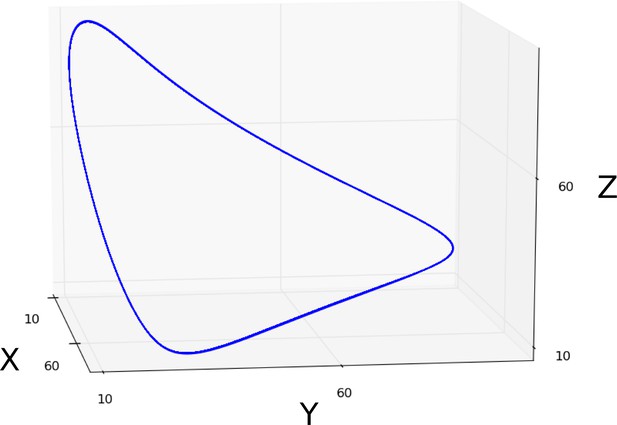
Sustained limit-cycle oscillations: simulation showing a limit cycle (blue curve) driving sustained oscillations in the phase portrait of an AC/DC circuit.
This circuit was simulated using the connectionist formulation given by Equation 33, and the parameter values shown in Appendix 1—table 1.

Damped oscillations: simulation of the damped oscillatory dynamical regime.
Two spiralling trajectories (blue and green curves) are shown converging towards a stable spiral sink. This circuit was simulated using the connectionist formulation given by Equation 33, and the parameter values shown in Appendix 1—table 2.

Bistability: simulation of the bistable dynamical regime.
Trajectories with varying initial conditions (coloured curves) are shown to converge towards the two point attractors. This circuit was simulated using the connectionist formulation given by Equation 33, and the parameter values shown in Appendix 1—table 3.
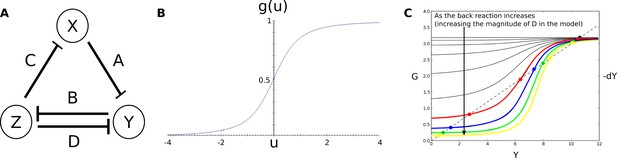
Connectionist AC/DC circuit.
(A) Regulatory structure and parameters of the simulated AD/DC circuit. Nodes represent genes and their transcription-factor products. T-bars represent repressive regulatory interactions. All genes are constitutively activated. (B) Sigmoidal regulation-expression function used for the simulations (Equation 31). (C) The number of steady states in the connectionist AD/DC circuit, can be one (black curves), or three (coloured curves) depending on the strength of the back reaction.
Tables
Parameter values used to simulate the limit cycle shown in Appendix 1—figure 3.
See Equation 33 for parameter definitions.
| Dynamical regime | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| H | A | B | C | D | ||||
| Sustained Oscillations | ||||||||
Parameter values used to simulate the damped oscillations shown in Appendix 1—figure 4.
See Equation 33 for parameter definitions.
| Dynamical regime | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| H | A | B | C | D | ||||
| Damped Oscillations | ||||||||
Parameter values used to simulate the bistable regime shown in Appendix 1—figure 4.
See Equation 33 for parameter definitions.
| Dynamical regime | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| H | A | B | C | D | ||||
| Bi-stability | ||||||||
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.42832.010





