Coupling adaptive molecular evolution to phylodynamics using fitness-dependent birth-death models
- North Carolina State University, United States
- ETH Zürich, Switzerland
- Swiss Institute of Bioinformatics, Switzerland
Figures
Figure 1
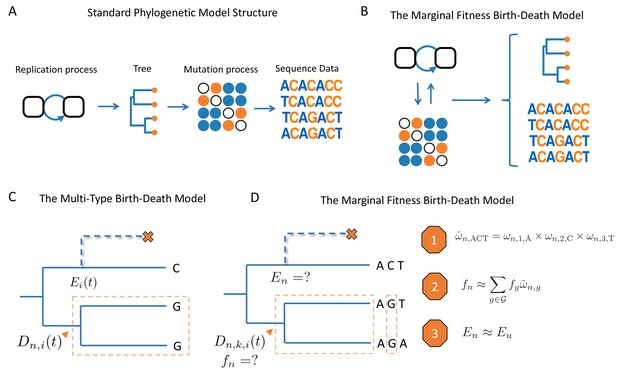
Schematic overview of birth-death models.
(A) Standard phylogenetic models assume that there is an underlying process by which individuals replicate and give rise to a phylogeny. Mutations occur along the lineages of the tree, generating the sequence data observed at the tips. The mutation process is assumed to be independent of tree generating process, such that mutations do not impact the branching structure of the tree. (B) The MFBD allows us to relax this assumption, such that mutations at multiple sites feedback and shape both the tree and sequence data. (C) Under the original multi-type birth-death model we track , the probability density that a lineage at time in state produces the subtree descending from and the observed tip states. We also track , the probability that a lineage produces no sampled descendants and is therefore unobserved. (D) In the MFBD model we instead track , the probability that a lineage in state at site produces the subtree and the observed tip states at site . Because the fitness of a lineage will depend on its genotype at all sites, we use the marginal site probabilities to compute the probability that a lineage has a certain genotype, such as ACT (Approximation 1). We can then marginalize over the fitness of each genotype weighted by its approximate genotype probability to compute the fitness of a lineage (Approximation 2). Finally, we need to know the probability that a lineage left no other sampled descendants, which we approximate using the probability that a lineage with same expected fitness leaves no sampled descendants (Approximation 3). The schematic in A was reproduced from the original figure by Louis du Plessis (https://github.com/Taming-the-BEAST/TechnicalLectureSources/tree/master/BeastIntro2018) with permission under a Creative Commons license.
Figure 2
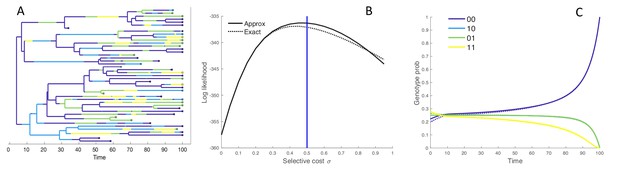
Performance of the MFBD approximation under the four genotype model.
(A) Simulated phylogeny showing the genotype of each lineage through time. (B) Joint likelihood of the phylogeny and tip genotypes under different values of using the the approximate MFBD (solid line) or the exact MTBD model (dotted line). The vertical blue line marks the true parameter value. (C) The normalized probability of a single hypothetical lineage being in each genotype back through time based on the MFBD approximation (solid line) versus the exact MTBD model (dotted line) with . Note that the probabilities for genotypes 10 and 01 are identical. All parameters besides were fixed at , , . The mutation rate was symmetric between forward and backwards mutations and fixed at 0.05.
Figure 3
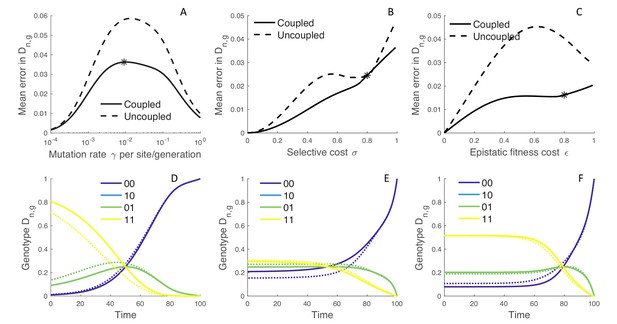
The error introduced by approximating genotype probabilities under the MFBD model.
(A–C) The error introduced by approximating the genotype probability densities based on the marginal sites probabilities under the MFBD model for different mutation rates (A), strengths of selection (B), and epistatic fitness effects (C). The solid line represents the MFBD approximation with fitness effects coupled across sites whereas the dashed line represents a more naive approximation that ignores the fitness effects of other sites entirely. The mean error represents the time-integrated average over all genotypes. (D–F) Normalized probabilities for a single hypothetical lineage being in each genotype back through time based on the MFBD approximation (solid line) versus the exact MTBD model (dotted line). Each plot shows the dynamics of for the parameter values marked by asterisks in the plots immediately above. Other parameters are fixed at , , .
Figure 4
The error introduced by approximating the probability of no sampled descendants.
(A–C) The error introduced by approximating in a discretized fitness space under the MFBD model for different mutation rates (A), strengths of selection (B), and epistatic fitness effects (C). The solid line represents the approximation where lineages are allowed to transition between fitness classes whereas the dashed line represents the assumption that fitness does not change along unobserved lineages. To obtain a single value comparable across both models, we summed over all genotypes weighted by the exact probability of the lineage being in each genotype and then took the time-integrated average to compute the mean error. (D–F) The dynamics of for a single hypothetical lineage back through time based on the MFBD approximation (solid line) versus the exact MTBD model (dotted line). Each plot shows the dynamics of for the parameter values marked by asterisks in the plots immediately above.
Figure 5
Estimating site-specific fitness effects.
(A) A phylogeny simulated under a model with five evolving sites each with a random fitness effect. The lineages are colored according to the number of mutations they carry (blue = 0; yellow = 5). The distribution of fitness effects was assumed to be LogNormal with a mean of 0.85 and a standard deviation of 0.32. (B) Site-specific fitness effects estimated using the marginal fitness BD model. Red lines indicate the posterior median and 95% credible intervals. Blue lines mark the true fitness effect at each site.
Figure 6
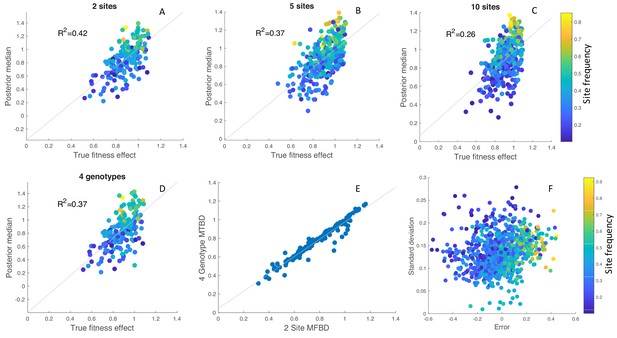
Inference of site-specific fitness effects from simulated phylogenies.
(A–C) Correlation between the true and estimated posterior median fitness effects for phylogenies simulated with 2, 5 or 10 evolving sites. Results are aggregated over 100 simulated phylogenies, with each point representing an estimate for a single site and phylogeny. The points are colored according to the frequency of the mutant allele among sampled individuals in the phylogeny. (D) Fitness effects estimated under the exact MTBD model tracking all four possible genotypes for the same two site simulations as in A. (E) Correlation between the site-specific fitness effects estimated under the approximate MFBD and exact MTBD for the two site simulations. (F) Error and uncertainty in estimated site-specific fitness effects across all 2, 5, and 10 site simulations. Error was calculated as the posterior median estimate minus the true fitness effect. Uncertainty was calculated as the standard deviation of the posterior values sampled via MCMC. In all simulations, sites where the Effective Sample Size of the MCMC samples was below 100 (less than 5% of all sites across simulations) were discarded. The death rate was fixed at but the birth, mutation and sampling rates were randomly drawn for each simulation from a prior distribution: Uniform(0.1,0.2); Exponential(0.01); Uniform(0,1). Only the birth rate was jointly inferred with the site-specific fitness effects.
Figure 7
Relative fitness of Ebola virus genotypes circulating during the 2013–16 epidemic in Western Africa.
Ancestral fitness values were reconstructed by first finding the probability of a lineage being in each possible genotype based on the marginal site probabilities computed using (Equation 20). Ancestral fitness values were then computed by averaging the posterior median fitness of each genotype, weighted by the probability that the lineage was in each genotype. Fitness values are given relative to the Makona genotype isolated at the start of the epidemic. Clades are labeled according to their most probable genotype.
Figure 8
Influenza H3N2 mutational fitness effects.
(A) The fitness effects of mutations estimated in vitro using deep mutational scanning versus their estimated population-level effects. In vitro fitness effects were quantified as the relative preference for the mutant versus the consensus amino acid residue in the deep mutational scanning experiments, given on a log2 scale. Population-level fitness effects were estimated using the MFBD model assuming multiplicative effects across sites. Error bars show the 95% credible intervals on the estimated population-level fitness effects. (B) Coancestry matrix showing the fraction of ancestry shared between each pair of mutations in the H3N2 phylogeny. The coancestry value represents the fraction of branches in the phylogeny that share both mutations based on a maximum parsimony reconstruction. The diagonal gives the fraction of all branches in the phylogeny with each individual mutation.
Figure 9
Relative fitness of influenza H3N2 lineages circulating in the United States between 2009 and 2012.
Fitness values were reconstructed based on a fitness model that maps mutational fitness effects predicted based on deep mutational scanning experiments to population level fitness. The inset shows this fitness mapping for the model parameters with the highest posterior probability: and . Uncertainty in ancestral amino acid sequences was taken into account by first computing the marginal site probability at each site. Ancestral fitness values were then reconstructed by marginalizing over all possible ancestral sequences using the marginal site probabilities.
Tables
Table 1
Estimated posterior median fitness and 95% CI for the Ebola GP mutants relative to the Makona genotype
https://doi.org/10.7554/eLife.45562.008| Genotype | Sample freq | Base model | Model + geo effects | Effect in cell culture |
|---|---|---|---|---|
| Makona | 0.036 | 1.00 | 1.00 | Reference genotype |
| A82V | 0.720 | 1.05 (1.04–1.07) | 1.26 (1.19–1.35) | Increases infectivity 2X |
| P330S | 0.002 | 0.98 (0.82–1.14) | 1.11 (0.96–1.24) | Decreases infectivity |
| P330S+N107D+G480D | 0.037 | 1.04 (0.98–1.12) | 1.27 (1.16–1.39) | Increases infectivity > 2X |
| A82V+R410S | 0.044 | 1.09 (1.00–1.18) | 1.31 (1.17–1.45) | No or small effect |
| A82V+R410S+K439E | 0.035 | 1.14 (1.01–1.26) | 1.36 (1.20–1.54) | Increases infectivity 2-3X |
| A82V+R29K | 0.019 | 1.06 (0.93–1.19) | 1.27 (1.10–1.45) | Increases infectivity 2-3X |
| A82V+T230A | 0.026 | 1.03 (0.93–1.11) | 1.23 (1.10–1.37) | Increases infectivity 2-3X |
| A82V+I371V | 0.067 | 1.03 (0.98–1.09) | 1.24 (1.14–1.35) | Increases infectivity 2-3X |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Coupling adaptive molecular evolution to phylodynamics using fitness-dependent birth-death models
eLife 8:e45562.
https://doi.org/10.7554/eLife.45562
