A geometric attractor mechanism for self-organization of entorhinal grid modules
- University of Pennsylvania, United States
- University of California, Berkeley, United States
Figures
Figure 1
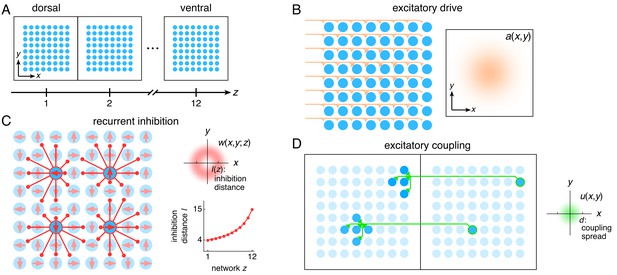
The entorhinal grid system as coupled 2D continuous attractor networks (Materials and methods).
(A) Each network z corresponds to a region along the dorso-ventral MEC axis and contains a 2D sheet of neurons with positions (x,y). (B) Neurons receive excitatory drive a(x,y) that is greatest at the network center and decays toward the edges. (C) Neurons inhibit neighbors within the same network with a weight w(x,y;z) that peaks at a distance of l(z) neurons, which increases as a function of z. Each neuron has its inhibitory outputs shifted slightly in one of four preferred network directions and receives slightly more drive when the animal moves along its preferred spatial direction. (D) Each neuron at position (x,y) in network z excites neurons located within a spread d of (x,y) in network z – 1.
Figure 2
Uncoupled and coupled systems produce grid cells with a range of scales.
(A–D) A representative simulation without coupling. (A) Network activities at the end of the simulation. (B) Activity overlays between adjacent networks depicted in A. In each panel, the network with smaller (larger) z is depicted in magenta (green), so white indicates activity in both networks. (C) Spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. (D) Spatial autocorrelations of the rate maps depicted in C. (E–H) Same as A–D but for a representative simulation with coupling. Standard parameter values provided in Table 1. White scale bars, 50 neurons. Black scale bars, 50 cm.
Figure 3
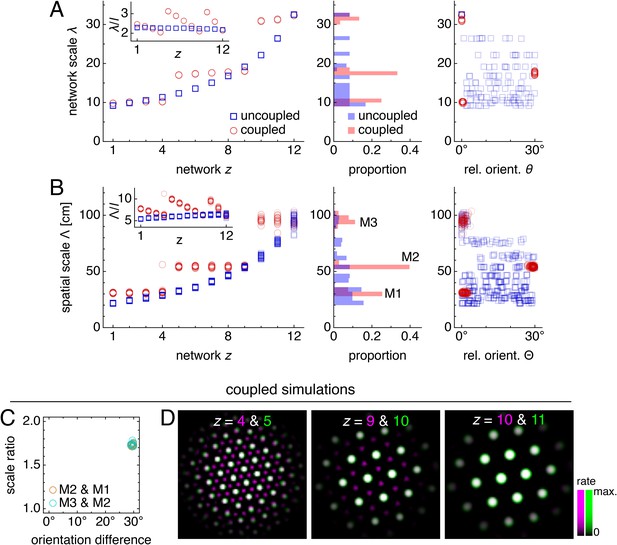
Coupling can induce modularity with fixed scale ratios and orientation differences.
(A–C) Data from 10 replicate uncoupled and coupled simulations. (A) Left: network grid scales λ(z). For each network, there are 10 closely spaced red circles and 10 closely spaced blue squares corresponding to replicate simulations. Inset: λ(z) divided by the inhibition distance l(z). Middle: histogram for λ collected across all networks. Right: network grid orientations θ relative to the network in the same simulation with largest scale. (B) Left: spatial grid scales Λ(z). For each z, there are up to 30 red circles and 30 blue squares corresponding to three neurons recorded during each simulation. Inset: Λ(z) divided by the inhibition distance l(z). Middle: histogram for Λ collected across all networks. In the coupled model, grid cells are clustered into three modules. Right: spatial grid orientations Θ relative to the grid cell in the same simulation with largest scale. (C) Spatial scale ratios and orientation differences between adjacent modules for the coupled model. (D) Activity overlays enlarged from Figure 2F to emphasize lattice relationships. In each panel, the network with smaller (larger) z is depicted in magenta (green), so white indicates activity in both networks. Standard parameter values provided in Table 1.
Figure 4 with 3 supplements
Modules produced by commensurate lattices maintain the same scale ratios and orientation differences across various perturbations, architectures, and sources of noise.
Data from 10 replicate simulations in each subfigure, which shows spatial grid scales Λ(z) and scale ratios and orientation differences between modules. (A) Left: less concave inhibition distance profile l(z) (dark) compared to Figure 1C (light). (B) Same as A, but for a more concave l(z). (C) Dorsal-to-ventral coupling from each network z to network z + 1. (D) Bidirectional coupling from each network z to networks z – 1 and z + 1. (E) Left: coupling spread d(z) set to l(z) (dark) instead of a constant d (light). (F) Grid system with fewer networks h = 6 of smaller size n × n = 76 × 76. (G) Independent noise added to each neuron’s firing rate at each timestep. (H) Coupling outputs randomly shifted for each neuron by one neuron in both x- and y-directions. (I) Spiking simulations with spikes generated by an independent Poisson process. Detailed methods for each system provided in Appendix 1.
Figure 4—figure supplement 1
Representative network activities and single neuron rate maps corresponding to Figure 4A–C.
Top row of each subfigure: network activities at the end of the simulation. Second row: activity overlays between adjacent networks depicted in the top row. In each panel, the network at smaller (larger) z is depicted in magenta (green), so white indicates regions of activity in both networks. Third row: spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. Bottom row: spatial autocorrelations of the rate maps depicted in the third row. (A) Corresponding to Figure 4A. (B) Corresponding to Figure 4B. (C) Corresponding to Figure 4C. White scale bars, 50 neurons. Black scale bars, 50 cm.
Figure 4—figure supplement 2
Representative network activities and single neuron rate maps corresponding to Figure 4D–F.
Panels same as in Figure 4–Figure supplement 1. (A) Corresponding to Figure 4D. (B) Corresponding to Figure 4E. (C) Corresponding to Figure 4F. White scale bars, 50 neurons. Black scale bars, 50 cm.
Figure 4—figure supplement 3
Representative network activities and single neuron rate maps corresponding to Figure 4G–I.
Panels same as in Figure 4–Figure supplement 1. (A) Corresponding to Figure 4G. (B) Corresponding to Figure 4H. (C) Corresponding to Figure 4I. White scale bars, 50 neurons. Black scale bars, 50 cm.
Figure 5 with 3 supplements
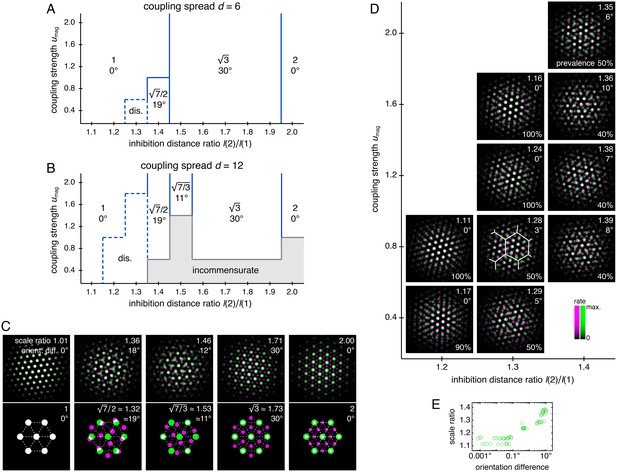
Diverse lattice relationships emerge over wide ranges in simulation parameters.
In models with only two networks z = 1 and 2, we vary the coupling strength umag and the ratio of inhibition distances l(2)/l(1) for two different coupling spreads d. (A, B) Approximate phase diagrams based on 10 replicate simulations for each set of parameters, with the mean of l(1) and l(2) fixed to be 9. The most frequently occurring scale ratio and orientation difference are indicated for each region; coexistence between multiple lattice relationships may exist at drawn boundaries. (A) Phase diagram for small coupling spread d = 6. Solid lines separate four regions with different commensurate lattice relationships labeled by scale ratio and orientation difference, and dotted lines mark one region of discommensurate lattice relationships. (B) Phase diagram for large coupling spread d = 12. There are five different commensurate regions, a discommensurate region, as well as a region containing incommensurate lattices (gray). (C) Network activity overlays for representative observed (left) and idealized (right) commensurate relationships. Numbers at the top right of each image indicate network scale ratios λ(2)/λ(1) and orientation differences θ(2) − θ(1). Networks z = 1 and 2 in magenta and green, respectively, so white indicates activity in both networks. (D) Expanded region of B displaying discommensurate lattice statistics. For each set of parameters, a representative overlay for the most prevalent discommensurate lattice relationship is shown. The number in the lower right indicates the proportion of replicate simulations with scale ratio within 0.02 and orientation difference within 3° of the values shown at top right. In one overlay, discommensurations are outlined by white lines. (E) The discommensurate relationships described in D demonstrate positive correlation between scale ratio and the logarithm of orientation difference (Pearson’s ρ = 0.91, p ∼ 10–26 ; Spearman’s ρ = 0.92, p ∼ 10–27 ). Simulation details provided in Appendix 1.
Figure 5—figure supplement 1
Raw scale ratio and orientation difference data used to produce Figure 5A.
Two-network model with coupling spread d = 6. (A) Network scale ratios λ(2)/λ(1). (B) Network orientation differences θ(2) − θ(1). For each l(2)/l(1) and umag, 10 replicate simulations subject are represented by circles with colors corresponding across the two subfigures. Small horizontal offsets are introduced for clarity, and each set of replicate simulations is ordered by θ(2) − θ(1). Gray lines track mean values as a function of l(2)/l(1).
Figure 5—figure supplement 2
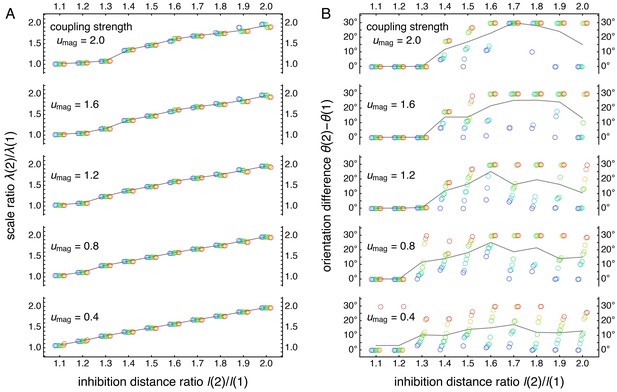
Raw scale ratio and orientation difference data used to produce Figure 5B.
Panels same as in Figure 5—figure supplement 1, but for coupling spread d = 12.
Figure 5—figure supplement 3
Commensurate and discommensurate relationships are robust against activity noise and coupling noise.
Two-network model with no noise, activity noise as in Figure 4G, and coupling noise as in Figure 4H. (A, B) Network parameters that, in accordance with Figure 5, produce a predominance of the commensurate relationship. (A) Representative activity overlays. Networks z = 1 and 2 in magenta and green, respectively, so white indicates activity in both networks. Prevalence is the proportion of replicate simulations with scale ratio within 0.02 and orientation difference within 3° of the values shown at top right. (B) Network scale ratios and orientation differences for 10 replicate simulations per noise condition. (C, D) Same as A, B, but for parameters that produce a predominance of the commensurate relationship. (E, F) Same as A, B, but for parameters that produce a predominance of discommensurate relationships with scale ratio ≈1.24 and orientation difference ≈0°. Note that for each set of parameters, the predominant lattice relationship is maintained in the presence of noise. Data for the no noise condition taken from Figure 5—figure supplement 1 and Figure 5—figure supplement 2.
Figure 6 with 2 supplements
Discommensurate lattice relationships can produce realistic modules.
(A) We use a shallower inhibition distance profile l(z) (dark) compared to Figure 1C (light). (B) Large activity overlays from a representative simulation that emphasize discommensurate lattice relationships. (C) All activity overlays from the representative simulation in B between adjacent networks z in magenta and green, so white indicates activity in both networks. Scale bar, 50 neurons. (D–F) Data from 10 replicate simulations. (D) Left: spatial grid scales Λ(z). For each network, there are up to 30 red circles corresponding to three neurons recorded during each simulation. Middle: histogram for Λ collected across all networks. Right: spatial orientations Θ relative to the grid cell in the same simulation with largest scale. (E) Clustering of spatial scales and orientations for three representative simulations. Due to sixfold lattice symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules. (F) Spatial scale ratios and orientation differences between adjacent modules. (G) Representative activity overlay demonstrating defect with low activity overlap. Maximum inhibition distance lmax = 10, coupling spread d = 12. We use larger network size n × n = 230 × 230 to allow for discommensurate relationships whose periodicities span longer distances on the neural sheets. Other parameter values are in Table 1.
Figure 6—figure supplement 1
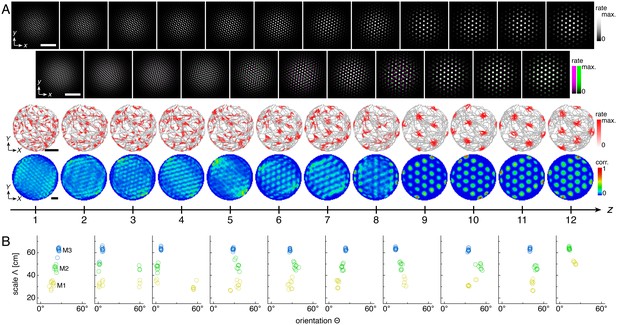
Representative network activities and single neuron rate maps; module clustering for all replicate simulations.
(A) Representative network activities and single neuron rate maps for the discommensurate system. Top row: network activities at the end of the simulation. Second row: activity overlays between adjacent networks depicted in the top row. In each panel, the network at smaller (larger) z is depicted in magenta (green), so white indicates regions of activity in both networks. Third row: spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. Bottom row: spatial autocorrelations of the rate maps depicted in the third row. White scale bars, 50 neurons. Black scale bars, 50 cm. (B) Clustering of spatial scales and orientations for all replicate simulations. Due to sixfold lattice symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules.
Figure 6—figure supplement 2
Sample comparison of field-to-field firing rate variability between an experimental recording and our model.
(A) Sample experimentally recorded single neuron rate map adapted from Figure 1a of Dunn et al. (2017). (B) Sample single neuron rate map from a simulation with the same parameters as in Figure 6 that exhibits discommensurate lattice relationships. Note that firing rate decreases across fields from the bottom left to the top right of both A and B; the presence of firing rate modulation over long distances has been considered by Stemmler and Herz (2017). In B, the fields at the top right correspond to a discommensuration on the neural sheet and the fields at the bottom left correspond to a region in between discommensurations that exhibits activity overlap. A comprehensive test requires analysis with experiments using circular enclosures to eliminate confounding boundary effects (see Discussion).
Figure 7 with 2 supplements
Simulations spanning different parameters contain diversity in lattice relationships, but average scale ratios are still constant between module pairs.
Data from five replicate simulations for each set of parameters, encompassing 51 total module pairs. (A) Clustering of spatial scales and orientations for one representative simulation (left) and lattice relationship distribution across all pairs of adjacent modules (right) for each set of parameters. (B) Spatial scale ratios and orientation differences between adjacent modules with respective histograms to the right and above. Scale ratios and orientation differences exhibit positive rank correlation (Spearman’s ρ = 0.44, p = 0.001). (C) Spatial scale ratios. Means indicated by lines. Medians compared through the Mann-Whitney U test with reported p-value. (D) Spatial scale differences normalized by the scale of the first module (M1) in each simulation. Same interpretation of lines and p-value as in C. The umag = 2.6 and lmax = 10 data are taken from simulations in Figure 5. Some simulations produced only two modules M1 and M2; one simulation produced four modules, and M4 was excluded from further analysis. Coupling spread d = 12 and network size n × n = 230 × 230. Other parameter values are in Table 1.
Figure 7—figure supplement 1
Module clustering for all simulations.
Clustering of scales and orientations for all replicate simulations spanning a range of parameters. Due to 6-fold lattice symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules. Simulations use network size n × n = 230 × 230 and coupling spread d = 12.
Figure 7—figure supplement 2
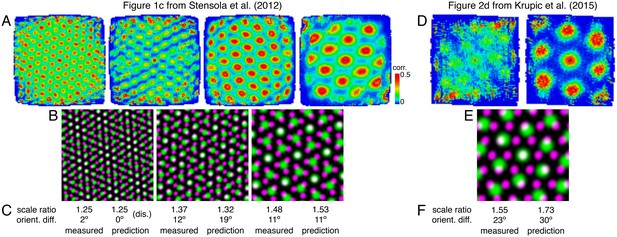
Lattice relationships that may underlie scale ratios and orientation differences for sample experimental recordings.
(A) Sample single neuron autocorrelation maps of grid cells belonging to four modules from Figure 1c of Stensola et al. (2012). (B) Overlays between sheared triangular lattices extracted from the maps in A (see Appendix 1 for details). In each panel, the lattice with smaller (larger) scale is depicted in magenta (green), so white indicates activity in both lattices. (C) Measured scale ratios and orientation differences, which involves averaging over lattice vectors because the triangular lattices are sheared, and comparable lattice relationships by our model with predicted values. For the left panel, a discommensurate relationship is assigned by visual identification of discommensurations in the left panel of B. Because discommensurate lattices allow for a range of scale ratios with corresponding orientation differences, we performed linear regression on Figure 5E to obtain the predicted orientation difference that corresponds to the measured scale ratio. For the middle and right panels, commensurate lattice relationships are assigned by identifying the lattice points in the middle and right panels of B closest to, but not including, the center that exhibit significant overlap and comparing with the idealized relationships in Figure 5C. Note that our predicted values do not account for the shearing observed in the experimental grids, which will change scale ratios and orientation differences from their unsheared values even for idealized lattice relationships. Shearing may result from tethering of grids to environmental boundaries, perhaps through interactions with border cells (Keinath et al., 2018; Krupic et al., 2015; Stensola et al., 2015). (D–F) Same as A–C, but for two modules from Figure 2d of Krupic et al. (2015). A comprehensive test requires analysis of experiments using circular enclosures to eliminate confounding boundary effects (see Discussion).
Figure 8 with 3 supplements
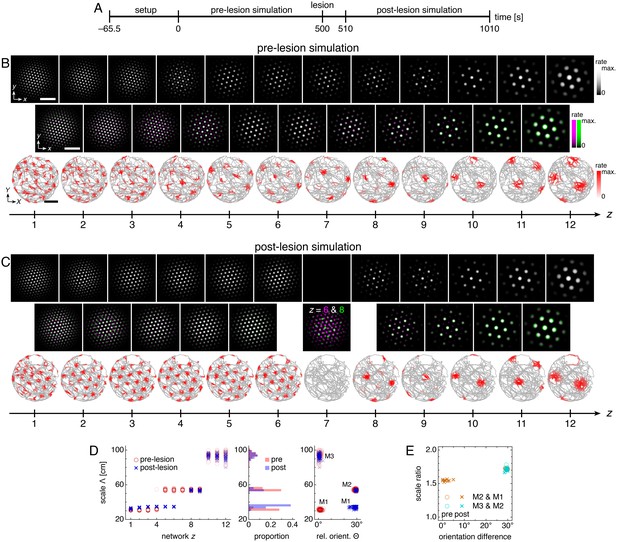
Lesioning a network changes grid scales and orientations of more dorsal networks.
(A) Lesion protocol. The lesion inactivates network z = 7. (B) A representative simulation before the lesion. Top row: network activities at the end of the pre-lesion simulation. Second row: activity overlays between adjacent networks depicted in the top row. In each panel, the network with smaller (larger) z is depicted in magenta (green), so white indicates activity in both networks. Third row: spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. White scale bars, 50 neurons. Black scale bars, 50 cm. (C) Same as B but after the lesion. Spatial rate maps are recorded from the same neurons as in B. (D, E) Data from 10 replicate simulations. (D) Left: spatial grid scales Λ(z) before and after the lesion. Middle: histogram for Λ collected across all networks. Right: spatial orientations Θ relative to the grid cell in the same simulation with largest scale. (E) Spatial scale ratios and orientation differences between adjacent modules. Standard parameter values provided in Table 1.
Figure 8—figure supplement 1
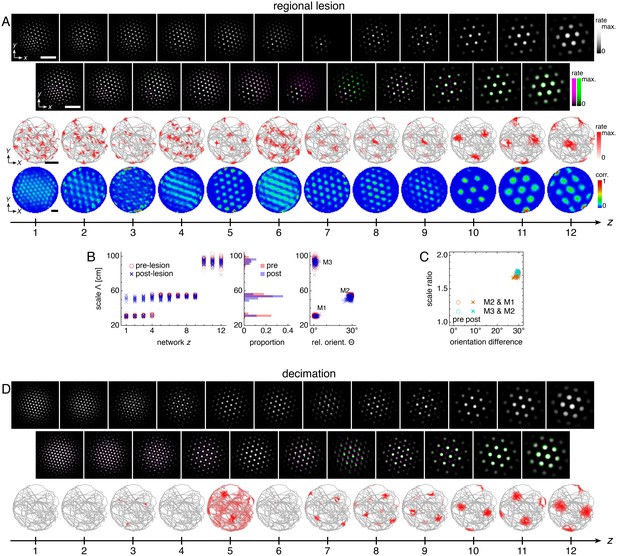
The effects of incomplete lesions on grid cells in more dorsal networks.
(A–C) A regional lesion of network z = 7 that spares the lower left quadrant. (A) A representative post-lesion simulation. Top row: network activities at the end of the post-lesion simulation. Second row: activity overlays between adjacent networks depicted in the top row. In each panel, the network with smaller (larger) z is depicted in magenta (green), so white indicates activity in both networks. Third row: spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. Bottom row: spatial autocorrelations of the rate maps depicted in the third row. White scale bars, 50 neurons. Black scale bars, 50 cm. (B) Left: spatial grid scales Λ(z) before and after the lesion. Middle: histogram for Λ collected across all networks. Right: spatial orientations Θ relative to the grid cell in the same simulation with largest scale. For each z, two neurons are selected from the lower left quadrant and two neurons are selected from elsewhere. (C) Spatial scale ratios and orientation differences between adjacent modules. (D) A representative post-lesion simulation of a decimation of network n = 7 that spares the top left neuron in every 3 × 3 block. Rows same as the top three rows of A.
Figure 8—video 1
Last 100 s of the simulation displayed in Figure 8—figure supplement 1A.
Top left: accumulated rat trajectory (gray curve) with current rat position (blue dot). Top right, bottom left, and bottom right: activity overlays between adjacent networks with the network at smaller (larger) z depicted in magenta (green), so white indicates regions of activity in both networks. White scale bar, 50 neurons. Black scale bar, 50 cm.
Figure 8—video 2
Last 100 s of the simulation displayed in Figure 8—figure supplement 1D.
Panels same as in Figure 8—video 1.
Appendix 2—figure 1
Simulations with a varying velocity gain α(z) and constant inhibition distance l produce modules that do not exhibit preferred relationships.
(A) Representative simulation. Top rows: activity overlays between adjacent networks with the network at smaller (larger) z depicted in magenta (green). Bottom rows: spatial autocorrelations of spatial rate maps. (B) Velocity gain profile α(z). (C–E) Data from 10 replicate simulations. (C) Left: spatial grid scales Λ(z). For each network, there are up to 30 red circles corresponding to three neurons recorded during each simulation. Inset: Λ(z) multiplied by the velocity gain α(z). Middle: histogram for Λ(z) collected across all networks. Right: spatial grid orientations Θ relative to the grid cell in the same simulation with largest scale. (D) Distributions of spatial grid scales and orientations for each replicate simulation. Due to hexagonal symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules. The ninth panel corresponds to the overlays in A. (E) Spatial grid scale ratios and orientation differences between adjacent modules. Maximum velocity gain αmax = 0.40 s/m, minimum velocity gain αmin = 0.12 s/m, and scaling exponent αexp = 0. Network size n × n = 174 × 174, coupling spread d = 12, coupling strength umag = 0.6, and inhibition distance l = 6. Other parameter values are in Table 1. White scale bars, 50 neurons. Black scale bars, 50 cm.
Appendix 2—figure 2
Activities of additional replicate simulations with a varying velocity gain contributing to Appendix 2—figure 1.
Top rows: activity overlays between adjacent networks with the network at smaller (larger) z depicted in magenta (green). Bottom rows: autocorrelations of spatial rate maps. White scale bars, 50 neurons. Black scale bars, 50 cm.
Appendix 3—figure 1
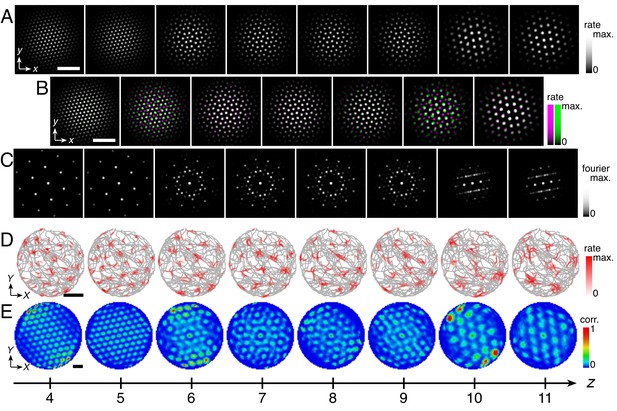
Quasicrystal approximant grids in a simulation with dorsal-to-ventral coupling.
Networks z = 4 to 11 shown out of 12 total. (A) Network activities at the end of the simulation. (B) Activity overlays between adjacent networks depicted in the top row. In each panel, the network at smaller (larger) z is depicted in magenta (green), so white indicates regions of activity in both networks. (C) Fourier power spectra for network activities with the origin at the center of each image and the edges cropped. (D) Spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. (E) Spatial autocorrelations of the rate maps depicted in D. Network size n × n = 230 × 230, coupling spread d = 2, coupling strength umag = 0.6, maximum inhibition distance αexp = 0, and velocity gain α = 0.12 s/m. Other parameter values are in Table 1. White scale bars, 50 neurons. Black scale bars, 50 cm.
Videos
Appendix 2—video 1
Last 100 s of the simulation displayed in Appendix 2—figure 1A.
Top left: accumulated rat trajectory (gray curve) with current rat position (blue dot). Top right, bottom left, and bottom right: activity overlays between adjacent networks with the network at smaller (larger) z depicted in magenta (green), so white indicates regions of activity in both networks. White scale bar, 50 neurons. Black scale bar, 50 cm.
Tables
Table 1
Main model parameters and their values unless otherwise noted.
https://doi.org/10.7554/eLife.46687.006| Parameter | Variable | Value |
|---|---|---|
| Number of networks | 12 | |
| Number of neurons per network | 160 × 160 | |
| Neurons recorded per network | 3 | |
| Animal speed | 0–1 m/s | |
| Diameter of enclosure | 180 cm | |
| Simulation time | 500 s | |
| Simulation timestep | 1 ms | |
| Neural relaxation time | 10 ms | |
| Broad input strength | 1 | |
| Broad input falloff | 4 | |
| Inhibition distance minimum | 4 | |
| Inhibition distance maximum | 15 | |
| Inhibition distance exponent | –1 | |
| Inhibition strength | 2.4 | |
| Subpopulation shift | 1 | |
| Coupling spread | 8 | |
| Coupling strength | 2.6 | |
| Velocity gain | 0.3 s/m |
Additional files
-
Source code 1
Source code for the main simulations written in C.
- https://doi.org/10.7554/eLife.46687.025
-
Transparent reporting form
- https://doi.org/10.7554/eLife.46687.026
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A geometric attractor mechanism for self-organization of entorhinal grid modules
eLife 8:e46687.
https://doi.org/10.7554/eLife.46687
