Figures and data in Bridging the gap between single-cell migration and collective dynamics

Figures
Tables
Additional files

10 figures, 1 table and 2 additional files

Figures

Figure 1

Download asset Open asset

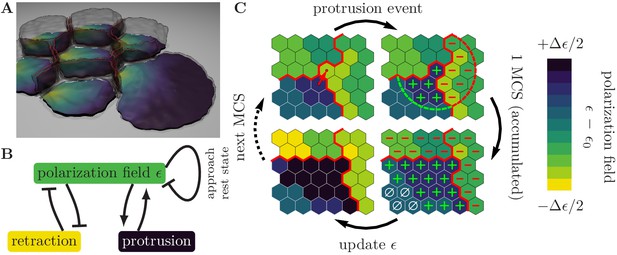
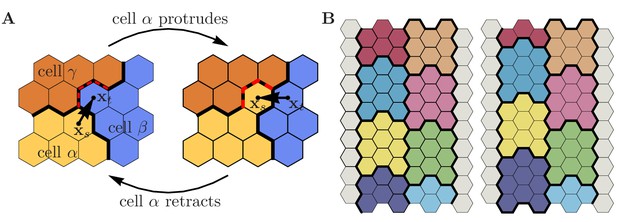
Illustration of the computational model with the pertinent simulation steps.

(A) Illustration of a small cell cohort that adheres to a surface ( $(x, y)$ -plane). The polarization field, $ϵ$ , is defined on the contact surface with the adhesion plane. The magnitude of the polarization field, which is indicated by the colorbar in Figure (C), encodes the local strength of cell-substrate adhesions and emulates the local mass of force-generating (pushing) cytoskeletal structures. Cell-cell adhesions are indicated in red. (B) Cytoskeletal structures respond to external mechanical stimuli through reaction networks involving different feedback loops. We greatly simplify these complex processes into two prototypic feedback loops, which break detailed balance and drive cell migration, as follows. The polarization field induces membrane protrusions and inhibits retractions. In turn, protrusions increase the polarization field (positive feedback) and therefore the likelihood of further protrusive activity, while retractions decrease the polarization field (negative feedback). In the absence of mechanochemical signals, the polarization field approaches its rest state. (C) Zoom-in to a common boundary shared between the substrate contact areas of three cells (bounded by the red lines), each represented by a contiguous set of occupied grid sites (hexagons). *Top left:* The upper right corner of the lower left cell (source cell) initiates a protrusion event against a neighboring element in the cell to its right (target cell), as indicated by the arrow, in an attempt to displace it. The success of each such attempted elementary event depends on the balance between contractile forces, cytoskeletal forces, and cell adhesion. *Top right:* If the protrusion event is successful, then the levels of regulatory factors are increased (decreased) in integer steps, at all lattice sites inside the source (target) cell that lie within a radius $R$ of the accepted protrusion event (as indicated by the plus and minus signs). *Bottom right:* During the course of one MCS, different levels of regulatory factors accumulate locally within each cell, with positive levels of regulatory factors (green plus signs) promoting a build-up of cytoskeletal structures, negative levels of regulatory factors (red minus signs) causing degradation of cytoskeletal structures, and neutral levels of regulatory factors (white zero signs) causing relaxation towards a resting state, as indicated in the *lower left image*. The color code indicates local levels of cytoskeletal structures, $ϵ$ .

Figure 2 with 2 supplements

Download asset Open asset

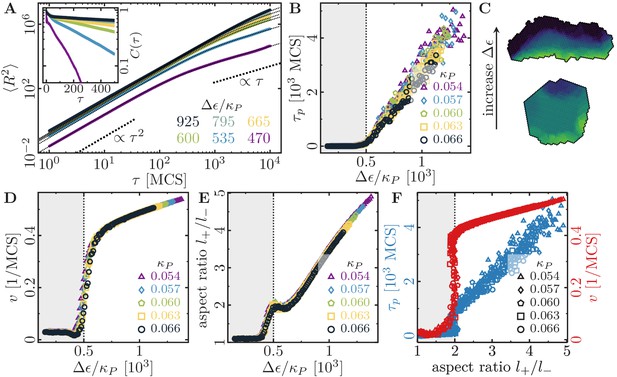
Cell shape and persistence of migration as a function of cell polarizability.

(A) Mean-squared displacement (MSD) for single-cell movements at different maximum cell polarity $Δ ϵ$ (stiffness parameters $κ_{P} = 0.060$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; signaling radius $R = 5$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ; cytoskeletal update rate $μ = 0.1$ ; $100$ independent simulations for each set of parameters). Single cells perform a persistent random walk, i.e. they move ballistically ( $MSD \propto τ^{2}$ ) for $τ ≪ τ_{p}$ , and diffusively ( $MSD \propto τ$ ) for $τ ≫ τ_{p}$ . *Inset:* Normalized velocity auto-correlation function for the same parameters as in the main figure. (B) Persistence time of directed cell migration plotted as a function of maximum cell polarity $Δ ϵ$ , and perimeter stiffness $κ_{P}$ (area stiffness $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; signaling radius $R = 5$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ; cytoskeletal update rate $μ = 0.1$ ; $100$ independent simulations for each set of parameters). The persistence time of the random walk increases with increasing cytoskeletal polarity and decreasing perimeter elasticity. (C) Cytoskeletal polarity also controls cell shapes, with crescent cell shapes (long persistence times) being observed at large cytoskeletal polartities, and round cell shapes (short persistence times) at small cytoskeletal polarities. Color code: cell polarization; cf. color bar in Figure 1C. (D) Single cell speed plotted as a function of maximum cell polarity $Δ ϵ$ , and perimeter stiffness $κ_{P}$ . (E) Single cell aspect ratio plotted as a function of maximum cell polarity $Δ ϵ$ , and perimeter stiffness $κ_{P}$ . (F) Speed and persistence time of single cells are correlated with the cell aspect ratio.

Figure 2—figure supplement 1

Download asset Open asset

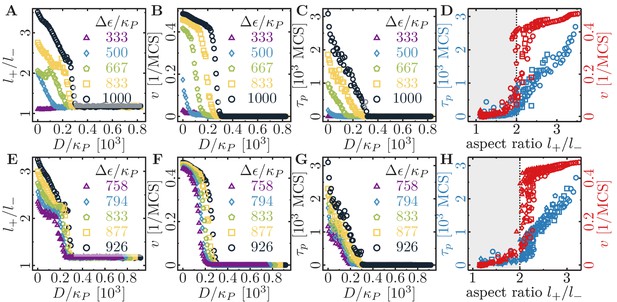
Role of substrate dissipation for cell shape and motility.

(**A–D**) Role of substrate dissipation for cells of varying maximum cell polarity $Δ ϵ$ . The aspect ratio $l_{+} / l_{-}$ (A), the speed $v$ (B), and the persistence time $τ_{p}$ (C) as a function of substrate dissipation $D$ for a series of values for $Δ ϵ / κ_{P}$ indicated in the graphs. (D) Cell persistence and cell speed are correlated with the aspect ratio of the cell. Only cells with an aspect ratio larger than 2 are motile. In the simulations, the substrate dissipation was varied in the interval $D \in [0, 50]$ , and the maximum cell polarity $Δ ϵ \in {20, 30, 40, 50, 60}$ . Fixed parameters: average polarization field $ϵ_{0} = 225$ ; area elasticity $κ_{A} = 0.18$ ; membrane elasticity $κ_{P} = 0.060$ ; cytoskeletal update rate $μ = 0.1$ ; cell-substrate adhesion penalty $φ = 0$ ; $100$ independent simulations for each set of parameters. (**E–F**) Role of substrate dissipation for cells of varying membrane stiffness $κ_{P}$ . The aspect ratio $l_{+} / l_{-}$ (E), the speed $v$ (F), and the persistence time $τ_{p}$ (G) as a function of substrate dissipation $D$ for a series of values for $Δ ϵ / κ_{P}$ indicated in the graphs. (H) Cell persistence and cell speed are correlated with the aspect ratio of the cell. Only cells with an aspect ratio larger than 2 are motile. In the simulations, the substrate dissipation was varied in the interval $D \in [0, 50]$ , and the membrane elasticity $κ_{P} \in {0.054, 0.057, 0.060, 0.063, 0.066}$ . Fixed parameters: average polarization field $ϵ_{0} = 225$ ; area elasticity $κ_{A} = 0.18$ ; maximum cell polarity $Δ ϵ = 50$ ; cytoskeletal update rate $μ = 0.1$ ; cell-substrate adhesion penalty $φ = 0$ ; $100$ independent simulations for each set of parameters.

Figure 2—video 1

Download asset

posterframe for video — Single cell motility and shape for different maximum cell polarities ( $κ_{P} = 0.060$ , $R = 5$ ).

Figure 3 with 1 supplement

Download asset Open asset

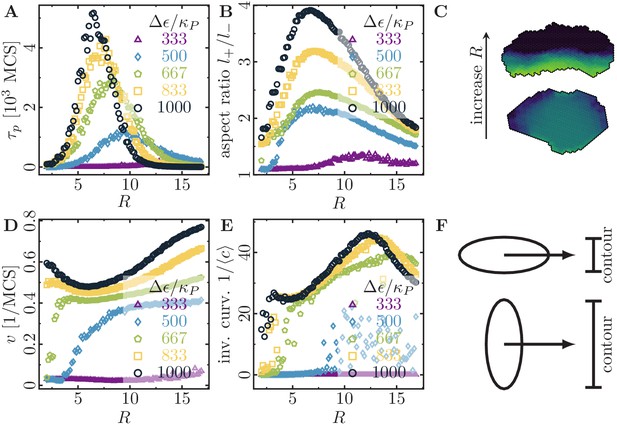
Migratory behavior of single cells as a function of the cell’s signaling radius $R$ at different values for the maximal cytoskeletal polarity $Δ ϵ$ .

(Stiffness parameters $κ_{P} = 0.060$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ; cytoskeletal update rate $μ = 0.1$ ; $100$ independent simulations for each set of parameters). (A) The persistence times of directed migration of single cells exhibit a pronounced maximum at an optimal signaling radius, which depends on cell polarizability. (B) The shapes of single cells exhibit a pronounced maximal elongation at an optimal signaling radius, which depends on cell polarizability. (C) The signaling radius critically determines the synchronicity of internal cytoskeletal remodeling processes. Small signaling radii frequently lead to transient formation of mutually independent lamellipodia at different positions around the cell perimeter, thereby interrupting persistent motion (reducing persistence times of directed migration). Large signaling radii lead to structurally stable front-rear polarization profiles across the entire cell body (long persistence times of directed migration). Color code: cell polarization; cf. color bar in Figure 1C. (D) The speed of single cells does not drop to zero even when their persistence time of directed migration vanishes. This indicates single cell rotations. (E) The inverse curvature of the cell trajectories as a function of the signaling radius. (F) Depending on whether a cell migrates along its long axis (top) or short axis (bottom), it has to move a different projected contour length. If each protrusion takes roughly the same amount of time, then migration along the long axis (top; cell has to move a smaller projected contour length) allows for greater cell speeds than migration along the short axis (bottom; cell has to move a larger projected contour length).

Figure 3—video 1

Download asset

Figure 4 with 6 supplements

Download asset Open asset

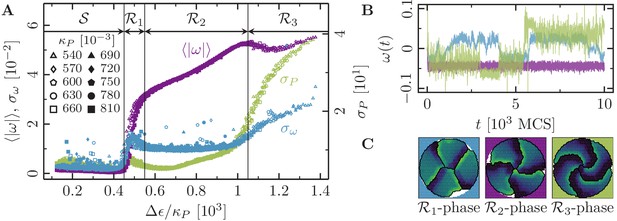
Phases of collective motion.

( $4$ -cell systems; confinement radius $r_{0} = 30.6$ ; area stiffness $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 0$ ; cell-cell dissipation $Δ B = 12$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ( $r < r_{0}$ ), $φ \to - \infty$ ( $r > r_{0}$ ); 100 independent simulations for each set of parameters). (A) Characteristic observables of collective cell rotation at different values of the cell perimeter stiffness parameter $κ_{P}$ : mean ( $⟨ | ω | ⟩$ ) and standard deviation ( $σ_{ω}$ ) of the magnitude of the cell cluster's angular velocity, and the standard deviation of the cell perimeter ( $σ_{P}$ ). The statistics of collective cell motion depends only on the ratio of maximum cell polarity, $Δ ϵ$ , to cell contractility, $κ_{P}$ (specific polarizability). (B) Representative angular trajectories and (C) cell shapes (color code represents cell polarization; cf. Figure 1C) for the different parameter regimes as described in the main text. The cellular dynamics in the different parameter regimes are shown in Figure 4—video 1, Figure 4—video 2 and Figure 4—video 3.

Figure 4—figure supplement 1

Download asset Open asset

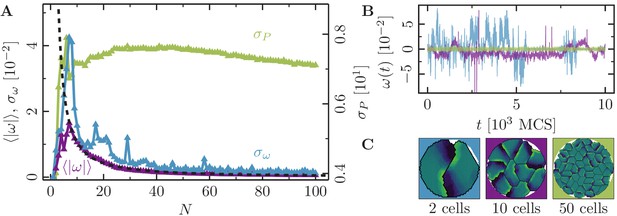
Collective motion for varying number of cells at low polarizability.

( $N$ -cell systems; confinement radius $r_{0} = \sqrt{234 N}$ ; stiffness parameters $κ_{P} = 0.060$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; maximum cell polarity $Δ ϵ = 28$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 0$ ; cell-cell dissipation $Δ B = 12$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ( $r < r_{0}$ ), $φ \to - \infty$ ( $r > r_{0}$ ); $100$ independent simulations for each set of parameters). For this choice of parameters $4$ -cell populations rotate in the $ℛ_{1}$ -phase. We observe a similar behavior here: the cell clusters rotate slowly and reorient frequently. (A) Characteristic observables of collective cell rotation at different values of the cell perimeter stiffness parameter $κ_{P}$ : mean ( $⟨ | ω | ⟩$ ) and standard deviation ( $σ_{ω}$ ) of the angular velocity magnitude of cell motion, and the standard deviation of the cell perimeter ( $σ_{P}$ ). The black line corresponds to a power-law fit of the form $⟨ | ω | ⟩ \propto N^{- k / 2} \propto r_{0}^{- k}$ with the fitted exponent $k \approx 8 / 3$ . (B) Representative angular trajectories and (C) cell shapes (color code represents cell polarization; cf. Figure 1) for the different parameter regimes as described in the main text. .

Figure 4—figure supplement 2

Download asset Open asset

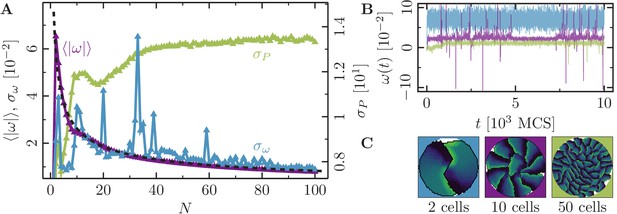
Collective motion for varying number of cells at intermediate polarizability.

( $N$ -cell systems; confinement radius $r_{0} = \sqrt{234 N}$ ; stiffness parameters $κ_{P} = 0.060$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; maximum cell polarity $Δ ϵ = 50$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 0$ ; cell-cell dissipation $Δ B = 12$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ( $r < r_{0}$ ), $φ \to - \infty$ ( $r > r_{0}$ ); $100$ independent simulations for each set of parameters). For this choice of parameters $4$ -cell populations rotate in the $ℛ_{2}$ -phase. We observe a similar behavior here: highly correlated rotations with no changes in rotational direction. (A) Characteristic observables of collective cell rotation at different values of the cell perimeter stiffness parameter $κ_{P}$ : mean ( $⟨ | ω | ⟩$ ) and standard deviation ( $σ_{ω}$ ) of the angular velocity magnitude of cell motion, and the standard deviation of the cell perimeter ( $σ_{P}$ ). The black line corresponds to a power-law fit of the form $⟨ | ω | ⟩ \propto N^{- 1 / 2} \propto r_{0}^{- 1}$ . (B) Representative angular trajectories and (C) cell shapes (color code represents cell polarization; cf. Figure 1) for the different parameter regimes as described in the main text. .

Figure 4—figure supplement 3

Download asset Open asset

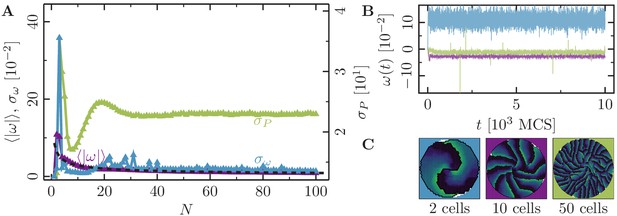
Collective motion for varying number of cells at high polarizability.

( $N$ -cell systems; confinement radius $r_{0} = \sqrt{234 N}$ ; stiffness parameters $κ_{P} = 0.060$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 225$ ; maximum cell polarity $Δ ϵ = 70$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 0$ ; cell-cell dissipation $Δ B = 12$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ( $r < r_{0}$ ), $φ \to - \infty$ ( $r > r_{0}$ ); $100$ independent simulations for each set of parameters). For this choice of parameters $4$ -cell populations rotate in the $ℛ_{3}$ -phase. We observe a similar behavior here: highly correlated rotations. (A) Characteristic observables of collective cell rotation at different values of the cell perimeter stiffness parameter $κ_{P}$ : mean ( $⟨ | ω | ⟩$ ) and standard deviation ( $σ_{ω}$ ) of the angular velocity magnitude of cell motion, and the standard deviation of the cell perimeter ( $σ_{P}$ ). The black line corresponds to a power-law fit of the form $⟨ | ω | ⟩ \propto N^{- 1 / 2} \propto r_{0}^{- 1}$ . (B) Representative angular trajectories and (C) cell shapes (color code represents cell polarization; cf. Figure 1) for the different parameter regimes as described in the main text.

Figure 4—video 1

Download asset

Figure 4—video 2

Download asset

Figure 4—video 3

Download asset

Figure 5 with 3 supplements

Download asset Open asset

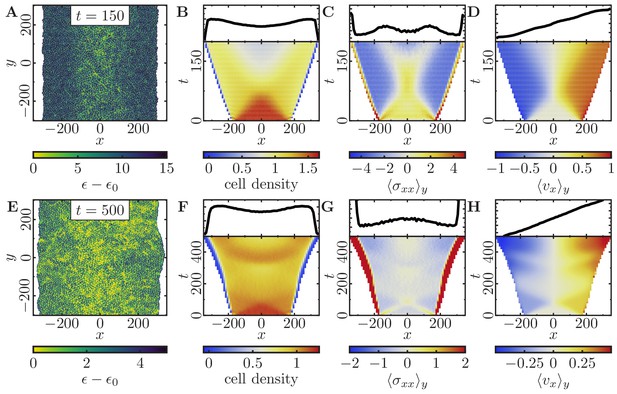
Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings.

(Stiffness parameters $κ_{P} = 0.12$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 35$ ; signaling radius $R = 2$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 12$ ; cell-cell dissipation $Δ B = 0$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ; $100$ independent simulations for each set of parameters). (**A–D**) Tissue expansion for a migration-dominated setup without explicit cell growth and mitosis. ( $3300$ -cell system; maximum cell polarity $Δ ϵ = 30$ ). (**E–H**) Tissue expansion at low density and cell polarizability for a cell sheet comprised of dividing cells. (Initially a $2500$ -cell system; maximum cell polarity $Δ ϵ = 10$ ; growth time $T_{g} = 180$ ; division time $T_{d} = 20$ ; size threshold for cell growth $A_{T} = 1 A_{ref}$ , where $A_{ref}$ is the size of a solitary cell in equilibrium). (**A, E**) Snapshots of the polarization field $ϵ$ ; cf. Figure 5—video 1 and Figure 5—video 2. (**B, F**) Kymographs showing the cell density averaged over the $y$ -direction and (*top*) final snapshots of the cell density profiles. (**C, G**) Kymographs showing the component $σ_{x x}$ of the stress tensor averaged over the $y$ -direction and (*top*) final snapshots of the stress profiles. (**D, H**) Kymographs showing the component $v_{x}$ of the cell velocities averaged over the $y$ -direction and (*top*) final snapshot of the velocity profiles.

Figure 5—figure supplement 1

Download asset Open asset

Monolayer expansion depends on dissipation and cell polarizability.

Cell monolayer expansion depends on the cell-cell dissipation, cell-substrate dissipation, and maximum cell polarity. (Initially a $2500$ -cell system; stiffness parameters $κ_{P} = 0.12$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 35$ ; maximum cell polarity $Δ ϵ = 10$ ; signalling radius $R = 2$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 12$ ; cell-substrate adhesion penalty $φ = 0$ ; growth time $T_{g} = 180$ ; division time $T_{d} = 20$ ; size threshold for cell growth $A_{T} = 1 A_{ref}$ , where $A_{ref}$ is the size of a solitary cell in equilibrium; $100$ independent simulations for each set of parameters). (**A,B**) Cell monolayer expansion depends on the cell-cell dissipation $Δ B$ (maximum cell polarity $Δ ϵ = 10$ ; cell-substrate dissipation $D = 0$ ). (A) Maximal monolayer extension and roughness (we exclude an initial time interval of 200 MCS because it takes at least that long for first daughter cells to appear). *Inset*: Relative roughness of the spreading monolayer relative to its size. (B) Time traces for selected values of $Δ B$ . (**C,D**) Cell monolayer expansion depends on the cell-substrate dissipation $D$ (maximum cell polarity $Δ ϵ = 10$ ; cell-cell dissipation $Δ B = 0$ ). (C) Maximal monolayer extension and roughness (we exclude an initial time interval of 200 MCS because it takes at least that long for first daughter cells to appear). (D) Time traces for selected values of $D$ . (**E,F**) Cell monolayer expansion depends on the maximum cell polarity $Δ ϵ$ (cell-cell dissipation $Δ B = 0$ ; cell-substrate dissipation $D = 0$ ). (E) Maximal monolayer extension and roughness (we exclude an initial time interval of 200 MCS because it takes at least that long for first daughter cells to appear). (F) Time traces for selected values of $Δ ϵ / κ_{P}$ . .

Figure 5—video 1

Download asset

Figure 5—video 2

Download asset

Figure 6 with 2 supplements

Download asset Open asset

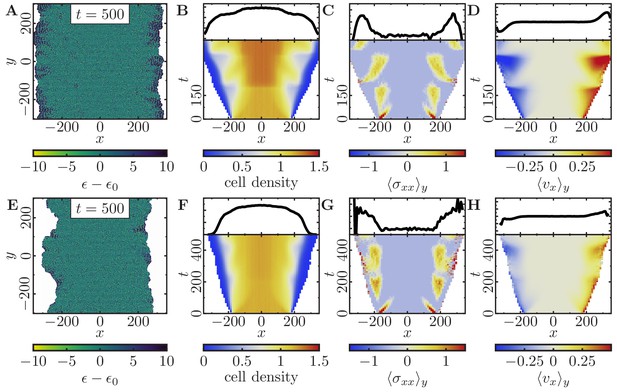
Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings that produce rough tissue fronts.

(Initially a $2500$ -cell system; stiffness parameters $κ_{P} = 0.10$ , $κ_{A} = 0.18$ ; average polarization field $ϵ_{0} = 35$ ; maximum cell polarity $Δ ϵ = 20$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-cell adhesion $B = 5$ ; cell-cell dissipation $Δ B = 10$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ ; growth time $T_{g} = 180$ ; division time $T_{d} = 20$ ; $100$ independent simulations for each set of parameters). (**A–D**) Tissue expansion at low density and cell polarizability for a cell sheet comprised of quickly dividing cells. (Size threshold for cell growth $A_{T} = 1.05 A_{ref}$ , where $A_{ref}$ is the size of a solitary cell in equilibrium). (**E–H**) Tissue expansion at low density and cell polarizability for a cell sheet comprised of slowly dividing cells. (Size threshold for cell growth $A_{T} = 1.10 A_{ref}$ , where $A_{ref}$ is the size of a solitary cell in equilibrium). (**A, E**) Snapshots of the polarization field $ϵ$ ; cf. Figure 6—video 1 and Figure 6—video 2. (**B, F**) Kymographs showing the cell density averaged over the $y$ -direction and (*top*) final snapshots of the cell density profiles. (**C, G**) Kymographs showing the component $σ_{x x}$ of the stress tensor averaged over the $y$ -direction and (*top*) final snapshots of the stress profiles. (**D, H**) Kymographs showing the component $v_{x}$ of the cell velocities averaged over the $y$ -direction and (*top*) final snapshot of the velocity profiles.

Figure 6—video 1

Download asset

Figure 6—video 2

Download asset

Appendix 1—figure 1

Download asset Open asset

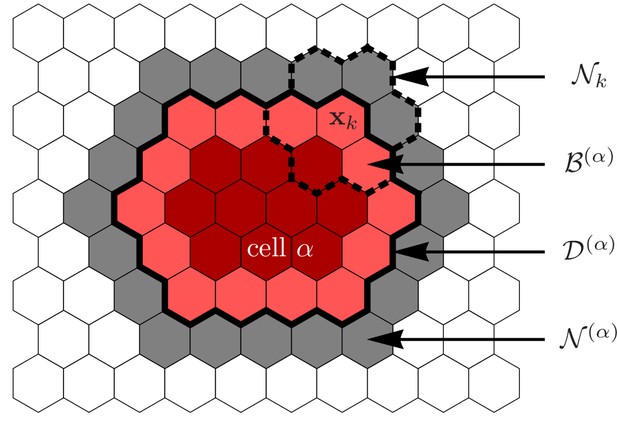
Illustration of the various sets defining a cell and its environment.

Grid sites occupied by cell $α$ , i.e. its domain $𝒟^{(α)}$ , are indicated in red colors. The cell’s membrane sites, $ℬ^{(α)}$ , are indicated by the lighter red color, the cell’s immediate neighborhood, $𝒩^{(α)}$ , is indicated in gray. Elementary events involving cell $α$ always involve one grid site in $ℬ^{(α)}$ and one grid site in $𝒩^{(α)}$ . For the hexagonal lattices used in this work, each grid site $𝐱_{k}$ is surrounded by $6$ nearest neighbors which we collectively denote by $𝒩_{k}$ .

Appendix 1—figure 2

Download asset Open asset

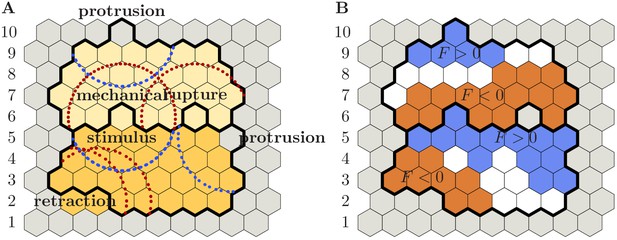
Distribution of regulatory factors on the basis of accepted elementary events.

For ease of reference, grid rows have been numbered from $1$ to $10$ . *Left* (A): Solid black lines indicate cells’ membrane positions *after* acceptance of the respective elementary event; colors indicate cellular domains *before* the respective elementary event has been accepted (gray: substrate; shades of yellow: cells). Blue and red circular arcs (of radius $R$ ) delineate areas of local increase or decrease in the level of regulatory factors, respectively. The following elementary events are depicted: (i) lower cell retracts (two grid sites in row $2$ ); (ii) lower cell protrudes (row $5$ ); (iii) upper cell protrudes (row $10$ ). In addition, the following elementary events occur across the cell-cell boundary: (iv) retraction of upper cell leads to rupture of cell-cell contacts (row $6$ , right event); (v) either the lower cell protrudes and pushes the upper cell or the upper cell retracts and pulls on the lower cell (row $6$ , left event). Specifically, event (v) entails mechanical signaling between the upper and lower cell and, therefore, affects the distribution of regulatory factors in both cells. *Right* (B): Identical copy of the left image (A). Colors indicate local levels of regulatory factors $F$ (blue: $F$ is positive; white: $F$ is zero; red: $F$ is negative; gray: substrate site). Note, in particular, that a substrate grid site has been inserted where cell rupture occurred (row $6$ , right grid site). The following cases can be distinguished: (i) Grid site $x_{k}$ lies in the zone of influence of only positive (blue circles) or negative (red circles) chemical feedback, in which case the level of regulatory factors is positive or negative, respectively (e.g. red grid sites in row $2$ , or blue grid sites in row $5$ ). (ii) Grid site $x_{k}$ lies outside of any zone of influence, in which case the level regulatory factors is zero (e.g. white grid sites in row $2$ ). (iii) Grid site $x_{k}$ lies in the zone of influence of equally many positive and negative feedbacks, in which case the level of regulatory factors remains zero (e.g. fourth grid site in row $4$ ). (iv) Grid site $x_{k}$ lies in a zone of predominantly positive or negative feedback, in which case the level of regulatory factors is positive or negative, respectively (e.g. third grid site in row $4$ ). Recall that only the sign of $F$ is of significance to update the cells’ polarization field; cf. Equation S13.

Appendix 1—figure 3

Download asset Open asset

Cell-cell adhesion.

(A) Adhesive energy contribution in a cyclic process, where a protrusion of source cell $α$ against target cell $β$ is followed by the inverse retraction event. Both events involve a third party cell $γ$ , leading to net energy dissipation after the cyclic process has been completed. *Protrusion*: (i) Three pre-existing cell-cell contacts between $β$ and $γ$ are torn apart (red dashed contacts); (ii) three new contacts between $α$ and $γ$ are formed; (iii) the contact length between source cell $α$ and target cell $β$ increases by one unit of length. This implies $Δ ℋ_{adh} (𝒯_{pro}) = ℓ (3 B_{β, γ}^{'} - 3 B_{α, γ} - B_{α, β})$ . *Retraction*: (i) Three pre-existing cell-cell contacts between $α$ and $γ$ are torn apart (red dashed contacts); (ii) three new contacts between $β$ and $γ$ are formed; (iii) the contact length between source cell $α$ and target cell $β$ decreases by one unit of length. This implies $Δ ℋ_{adh} (𝒯_{ret}) = ℓ (3 B_{α, γ}^{'} - 3 B_{β, γ} + B_{α, β})$ . Altogether, this leads to $Δ ℋ_{adh}^{(cycl)} = Δ ℋ_{adh} (𝒯_{pro}) + Δ ℋ_{adh} (𝒯_{ret}) = ℓ (3 (Δ B)_{α, γ} + 3 (Δ B)_{β, γ}) \geq 0$ , i.e. a (non-negative) dissipative contribution, whose magnitude depends on the dissipation matrix $(Δ B)_{α, β} = B_{α, β}^{'} - B_{α, β} \geq 0$ . (B) Shear viscosity due to cell-cell adhesion. Consider two rows of adhesive cells sliding past each other as indicated in the figure (left row of cells moves up by one grid site; colors indicate different cells). The associated adhesion energy change (per cell) reads $Δ ℋ_{adh} / n_{c} = 2 (B^{'} - B) \geq 0$ , where $n_{c}$ denotes the number of cells sliding past each other, and where we assumed cells of like type, i.e. $B_{α, β} \equiv B$ and $B_{α, β}^{'} \equiv B^{'}$ ( $α \neq β$ ). The condition $B^{'} > B$ , Equation S15e, thus implies positive friction associated with cellular shear flows, whose magnitude is proportional to the number of cells sliding past each other. Note that this shear viscosity vanishes for $B^{'} = B$ , i.e. for zero dissipation matrix.

Appendix 2—figure 1

Download asset Open asset

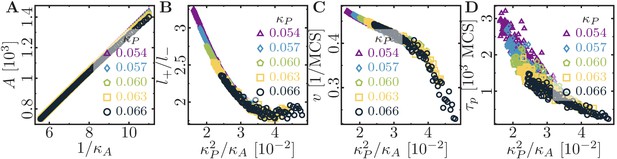
Role of area stiffness $κ_{A}$ for cell size and motility.

(A) The cell area increases linearly with $1 / κ_{A}$ . The aspect ratio (B), speed (C) and persistence (D) of the cell decrease with increasing cell size. In the simulations, the area elasticity was varied in the interval $κ_{A} \in [0.09, 0.18]$ , and the membrane elasticity was chosen from $κ_{P} \in {0.054, 0.057, 0.060, 0.063, 0.066}$ . Fixed parameters: average cell polarization field $ϵ_{0} = 225$ ; maximum cell polarity $Δ ϵ = 50$ ; signaling radius $R = 5$ ; cytoskeletal update rate $μ = 0.1$ ; cell-substrate dissipation $D = 0$ ; cell-substrate adhesion penalty $φ = 0$ .

Tables

Table 1

Source and parameter files used for each figure.

All source and parameter files are found in Source data 1.

Figure	Simulation code	Processing code	Parameters
Figure 2	CPM_NoDivision	TrajectoryAnalysisSingle	single_Q
Figure 2—figure supplement 1 (A-D)	CPM_NoDivision	TrajectoryAnalysisSingle	single_DQ
Figure 2—figure supplement 1 (E-H)	CPM_NoDivision	TrajectoryAnalysisSingle	single_DM
Figure 3	CPM_NoDivision	TrajectoryAnalysisSingle	single_R
Figure 4	CPM_NoDivision	TrajectoryAnalysisCircularPattern	rotation_Q
Figure 4—figure supplement 1	CPM_NoDivision	TrajectoryAnalysisCircularPattern	rotation_N_R1
Figure 4—figure supplement 2	CPM_NoDivision	TrajectoryAnalysisCircularPattern	rotation_N_R2
Figure 4—figure supplement 3	CPM_NoDivision	TrajectoryAnalysisCircularPattern	rotation_N_R3
Figure 5 (A-D)	CPM_Division		wound_nodiv
Figure 5 (E-H)	CPM_Division		wound_div
Figure 5—figure supplement 1 (A-B)	CPM_Division_Supplement	FrontAnalysis	wound_div_A
Figure 5—figure supplement 1 (C-D)	CPM_Division_Supplement	FrontAnalysis	wound_div_D
Figure 5—figure supplement 1 (E, F)	CPM_Division_Supplement	FrontAnalysis	wound_div_Q
Figure 6 (A-D)	CPM_Division		wound_div_fing_1.0
Figure 6 (E-H)	CPM_Division		wound_div_fing_1.1
Appendix 2—figure 1	CPM_NoDivision	TrajectoryAnalysisSingle	single_A

Additional files

Source code 1 Simulation code, processing code and parameter files.: https://cdn.elifesciences.org/articles/46842/elife-46842-code1-v2.tar
Download elife-46842-code1-v2.tar
Transparent reporting form: https://cdn.elifesciences.org/articles/46842/elife-46842-transrepform-v2.pdf
Download elife-46842-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Florian Thüroff
Andriy Goychuk
Matthias Reiter
Erwin Frey

(2019)

Bridging the gap between single-cell migration and collective dynamics

eLife 8:e46842.

https://doi.org/10.7554/eLife.46842

Figures

Illustration of the computational model with the pertinent simulation steps.

Cell shape and persistence of migration as a function of cell polarizability.

Role of substrate dissipation for cell shape and motility.

Single cell motility and shape for different maximum cell polarities ( $κ_{P} = 0.060$ , $R = 5$ ).

Migratory behavior of single cells as a function of the cell’s signaling radius $R$ at different values for the maximal cytoskeletal polarity $Δ ϵ$ .

Single cell motility and shape for different signaling radii ( $Δ ϵ = 60$ , $κ_{P} = 0.060$ ).

Phases of collective motion.

Collective motion for varying number of cells at low polarizability.

Collective motion for varying number of cells at intermediate polarizability.

Collective motion for varying number of cells at high polarizability.

Collective rotations of $4$ cells in the $ℛ_{1}$ -phase ( $Δ ϵ = 28$ ; $Δ ϵ / κ_{P} = 467$ ).

Collective rotations of $4$ cells in the $ℛ_{2}$ -phase ( $Δ ϵ = 50$ ; $Δ ϵ / κ_{P} = 833$ ).

Collective rotations of $4$ cells in the $ℛ_{3}$ -phase ( $Δ ϵ = 70$ ; $Δ ϵ / κ_{P} = 1167$ ).

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings.

Monolayer expansion depends on dissipation and cell polarizability.

Motility-dominated tissue dynamics.

Proliferation-dominated tissue dynamics.

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings that produce rough tissue fronts.

Weak monolayer roughening (fingering) in motility-dominated tissue with quick proliferation.

Strong monolayer roughening in motility-dominated tissue with slow proliferation.

Illustration of the various sets defining a cell and its environment.

Distribution of regulatory factors on the basis of accepted elementary events.

Cell-cell adhesion.

Role of area stiffness $κ_{A}$ for cell size and motility.

Tables

Source and parameter files used for each figure.

Additional files

Source code 1

Transparent reporting form

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Illustration of the computational model with the pertinent simulation steps.

Cell shape and persistence of migration as a function of cell polarizability.

Role of substrate dissipation for cell shape and motility.

Single cell motility and shape for different maximum cell polarities (κP=0.060, R=5).

Migratory behavior of single cells as a function of the cell’s signaling radius R at different values for the maximal cytoskeletal polarity Δ⁢ϵ.

Single cell motility and shape for different signaling radii (Δ⁢ϵ=60, κP=0.060).

Phases of collective motion.

Collective motion for varying number of cells at low polarizability.

Collective motion for varying number of cells at intermediate polarizability.

Collective motion for varying number of cells at high polarizability.

Collective rotations of 4 cells in the ℛ1-phase (Δϵ=28; Δϵ/κP=467).

Collective rotations of 4 cells in the ℛ2-phase (Δϵ=50; Δϵ/κP=833).

Collective rotations of 4 cells in the ℛ3-phase (Δϵ=70; Δϵ/κP=1167).

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at x=±175 for two different parameter settings.

Monolayer expansion depends on dissipation and cell polarizability.

Motility-dominated tissue dynamics.

Proliferation-dominated tissue dynamics.

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at x=±175 for two different parameter settings that produce rough tissue fronts.

Weak monolayer roughening (fingering) in motility-dominated tissue with quick proliferation.

Strong monolayer roughening in motility-dominated tissue with slow proliferation.

Illustration of the various sets defining a cell and its environment.

Distribution of regulatory factors on the basis of accepted elementary events.

Cell-cell adhesion.

Role of area stiffness κA for cell size and motility.

Source and parameter files used for each figure.

Source code 1

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Single cell motility and shape for different maximum cell polarities ( $κ_{P} = 0.060$ , $R = 5$ ).

Migratory behavior of single cells as a function of the cell’s signaling radius $R$ at different values for the maximal cytoskeletal polarity $Δ ϵ$ .

Single cell motility and shape for different signaling radii ( $Δ ϵ = 60$ , $κ_{P} = 0.060$ ).

Collective rotations of $4$ cells in the $ℛ_{1}$ -phase ( $Δ ϵ = 28$ ; $Δ ϵ / κ_{P} = 467$ ).

Collective rotations of $4$ cells in the $ℛ_{2}$ -phase ( $Δ ϵ = 50$ ; $Δ ϵ / κ_{P} = 833$ ).

Collective rotations of $4$ cells in the $ℛ_{3}$ -phase ( $Δ ϵ = 70$ ; $Δ ϵ / κ_{P} = 1167$ ).

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings.

Expansion of a confluent epithelial cell sheet after removal of boundaries positioned at $x = \pm 175$ for two different parameter settings that produce rough tissue fronts.

Role of area stiffness $κ_{A}$ for cell size and motility.