Molecular mechanisms of human P2X3 receptor channel activation and modulation by divalent cation bound ATP

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

P2X3 receptor channels expressed in sensory neurons are activated by extracellular ATP and serve important roles in nociception and sensory hypersensitization, making them attractive therapeutic targets. Although several P2X3 structures are known, it is unclear how physiologically abundant Ca²⁺-ATP and Mg²⁺-ATP activate the receptor, or how divalent cations regulate channel function. We used structural, computational and functional approaches to show that a crucial acidic chamber near the nucleotide-binding pocket in human P2X3 receptors accommodates divalent ions in two distinct modes in the absence and presence of nucleotide. The unusual engagement between the receptor, divalent ion and the γ-phosphate of ATP enables channel activation by ATP-divalent complex, cooperatively stabilizes the nucleotide on the receptor to slow ATP unbinding and recovery from desensitization, a key mechanism for limiting channel activity. These findings reveal how P2X3 receptors recognize and are activated by divalent-bound ATP, aiding future physiological investigations and drug development.

https://doi.org/10.7554/eLife.47060.001

Introduction

P2X3 receptors are a family of trimeric cation channels that are activated by extracellular ATP. They play particularly important roles in sensory neurons where their activation is critical for gustatory and nociceptive responses (Barclay et al., 2002; Chen et al., 1995; Cook et al., 1997; Finger et al., 2005; Huang et al., 2011; North, 2003; North, 2004; Vandenbeuch et al., 2015), visceral reflexes and sensory hypersensitization (Cockayne et al., 2000; Deiteren et al., 2015; Ford et al., 2015; Souslova et al., 2000). Accordingly, P2X3 knock-out or knock-down in rodents reduces nociception and visceral reflexes (Barclay et al., 2002; Cockayne et al., 2000; Souslova et al., 2000; Vlaskovska et al., 2001), and the P2X3 receptor antagonist A-317491 reduces inflammatory and neuropathic pain (Hansen et al., 2012; Jarvis et al., 2002). Clinical studies in humans have shown that high-affinity P2X3 antagonist AF-219 is well tolerated and can significantly reduce cough frequency in patients with refractory chronic cough (Abdulqawi et al., 2015; Ford and Undem, 2013; Wang et al., 2018). P2X3 receptor antagonists are also being developed for migraine, itch and cancer pain (Ginnetti et al., 2018; North, 2003).

P2X3 homomeric receptors activate and desensitize on the millisecond timescale upon binding ATP but unbind ATP and recover from desensitization on the timescale of minutes (Cook and McCleskey, 1997; Giniatullin and Nistri, 2013; Sokolova et al., 2006). This unusually long recovery time limits channel activation frequency, which may be an important protective mechanism for preventing sensory hypersensitivity. The molecular mechanisms underlying these unique gating processes remain to be fully established. X-ray structures of human P2X3 (hP2X3) receptor channels have recently been solved in the absence of ATP, as well as bound to free-ATP (i.e. ATP not complexed with a divalent ion) or to antagonists (Mansoor et al., 2016). These structures elegantly reveal how free-ATP binds to the large extracellular domain to open the transmembrane pore, and to subsequently close during the process of desensitization. Specifically, the nucleotide adopts a bent pose with the adenosine ring positioned above an aromatic residue (F174), the α−phosphate group interacting with S275, and the β− and γ−phosphates intimately engaging with K63, K65, K299, R281 and N279 (Figure 1D) (Hattori and Gouaux, 2012; Mansoor et al., 2016).

Figure 1 with 1 supplement see all

Download asset Open asset

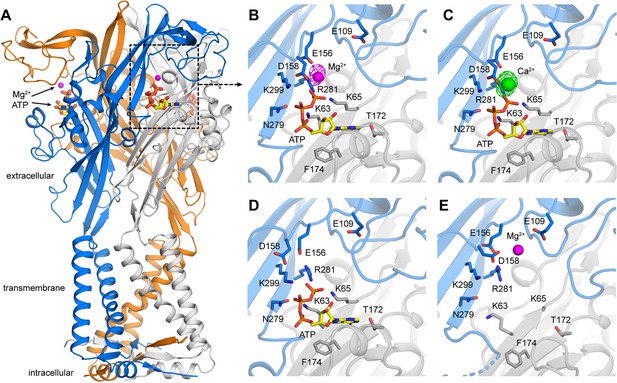
X-ray structures of hP2X3 receptors with divalent ions bound..

(A) Overall structure of hP2X3 MFC_slow with ATP and Mg²⁺ bound (PDB ID 6AH5). Agonist binding pockets are formed at each of the three interfaces between adjacent subunits (blue, orange, gray). (B) Close-up view of the binding site for Mg²⁺-ATP in hP2X3 MFC_slow, highlighting key interactions between the receptor and both ligands. In this ‘lower mode’, Mg²⁺ interacts directly with the γ phosphate of ATP and acidic residues in the receptor. The omit Fo-Fc density map for Mg²⁺ is overlaid (magenta mesh), contoured at 3.5σ. (C) Same as B), for the structure of hP2X3 MFC_slow with ATP and Ca²⁺ bound (PDB ID 6AH4). The omit Fo-Fc density map for Ca²⁺ (green) is contoured at 5σ. (D) Same view of the agonist-binding pocket in an existing structure of hP2X3 MFC_slow bound to ATP only (PDB ID 5SVK). Note the mode of ATP binding is nearly identical to that in B) and C), except for the acidic sidechains near Mg²⁺ or Ca²⁺. (E) Same view of the agonist-binding pocket in an existing structure of hP2X3 MFC_slow bound to Mg²⁺ only (PDB ID: 5SVJ). In this ‘upper mode’, Mg²⁺ shifts upwards and is stabilized by a cluster of acidic sidechains. .

https://doi.org/10.7554/eLife.47060.002

Although free-ATP is an agonist in laboratory conditions, P2X3 receptors are activated primarily by Ca²⁺-ATP and Mg²⁺-ATP under physiological conditions because ATP released from cells at micromolar concentrations would largely be in complex with Ca²⁺ and Mg²⁺, both of which are present in millimolar concentrations in extracellular physiological solutions (Lazarowski et al., 2003; Li et al., 2013). From the available structure of hP2X3 bound by free-ATP, it is unclear how the receptor might accommodate a divalent-bound nucleotide. When ATP is in solution, the divalent ion preferably interacts with the β− and γ−phosphate groups simultaneously, or alternatively, with all three phosphate groups (Branduardi et al., 2016; Cohn and Hughes, 1962). Whether these interactions are compatible with those observed between free ATP and the receptor in the ATP-bound structure is unclear; even if they are, the presence of divalent ions would effectively weaken the interaction between agonist and receptor, which would be physiologically counterintuitive. It would seem reasonable to anticipate that when bound to the receptor, Mg²⁺ and ATP interact differently than when in solution. Intriguingly, a Mg²⁺ binding site was identified in previous structures of hP2X3 in the absence of ATP (apo), or in the presence of antagonists (Figure 1E) (Mansoor et al., 2016; Wang et al., 2018). However, from the comparison of free-ATP bound and Mg²⁺ bound apo structures, this site would be too far from the nucleotide-binding pocket to directly interact with ATP (Figure 1D,E), making its functional significance unclear. To add to the complexity of P2X3 receptor activation in the presence of divalent cations, Mg²⁺ has been reported to inhibit P2X3 receptors and Ca²⁺ to stimulate the activity of the channel (Cook et al., 1998; Giniatullin et al., 2003; Li et al., 2013). To elucidate the mechanisms of these physiologically and therapeutically important ion channels, it is essential to determine the sites and mechanisms of divalent ion action. We therefore set out to elucidate the mechanism by which Ca²⁺-ATP and Mg²⁺-ATP activate P2X3 receptors, and to explore how divalent cations regulate the receptor.

Results

Structures of hP2X3 receptor reveal Mg²⁺-ATP and Ca²⁺-ATP bind in a unique mode

We began by crystalizing the hP2X3 MFC_slow construct (Mansoor et al., 2016) in solutions containing ATP with either Mg²⁺ or Ca²⁺. This construct shows minimal desensitization (Hausmann et al., 2014; Mansoor et al., 2016), and was previously used to obtain an open state structure of hP2X3 with free-ATPbound. We solved X-ray structures of the receptor with Mg²⁺-ATP or Ca²⁺-ATP bound at resolutions of 3.8 Å and 3.3 Å, respectively (Supplementary file 1). The pores appear to be in an open-like conformation in both structures, similar to that observed in the structure of hP2X3 bound to free-ATP (Figure 1—figure supplement 1). Importantly, we observed strong residual electron densities around the ATP binding site in these structures (Figure 1B,C). Considering that the crystallization conditions included either 50 mM Mg-acetate or 50 mM Ca-acetate with no other divalent cations, and that the electron densities are surrounded by acidic residues, we interpreted the densities as Mg²⁺ and Ca²⁺ ions, respectively. In both structures, the divalent ions are detected at the edge of the ATP binding pocket, simultaneously interacting with D158 on the receptor and with the γ-phosphate of ATP; E156 is also positioned nearby and appears to be involved in coordinating the ion. Because the similar binding sites we observed for Ca²⁺ and Mg²⁺ imply a common mechanism for activation by Ca²⁺-ATP and Mg²⁺-ATP, we largely focused our efforts on Mg²⁺-ATP so we could take advantage of the more extensive data on this form of divalent-bound ATP.

A survey of the Protein Data Bank (PDB) reveals that the geometry of the Mg²⁺-ATP and Ca²⁺-ATP complexes observed in our structures is highly unusual (Figure 2A). Among non-redundant structures determined at 2.5 Å resolution or better with Mg²⁺-ATP (or Ca²⁺-ATP) bound (see Materials and methods), only 4% (or none) feature a complex in which Mg²⁺ is coordinated solely by the γ-phosphate (and 2% for the AMP-PNP analog). The prevalent geometries are instead those in which Mg²⁺ is coordinated by both the β- and γ-phosphates or by all three phosphate groups concurrently. These two interaction modes are also the most energetically favorable when Mg²⁺-ATP is in solution (Branduardi et al., 2016). That the Mg²⁺-ATP complex observed in our structures adopts a rare configuration suggests that interactions between the receptor and divalent ions have a dominant effect in determining the structure and stability of the complex.

Figure 2 with 3 supplements see all

Download asset Open asset

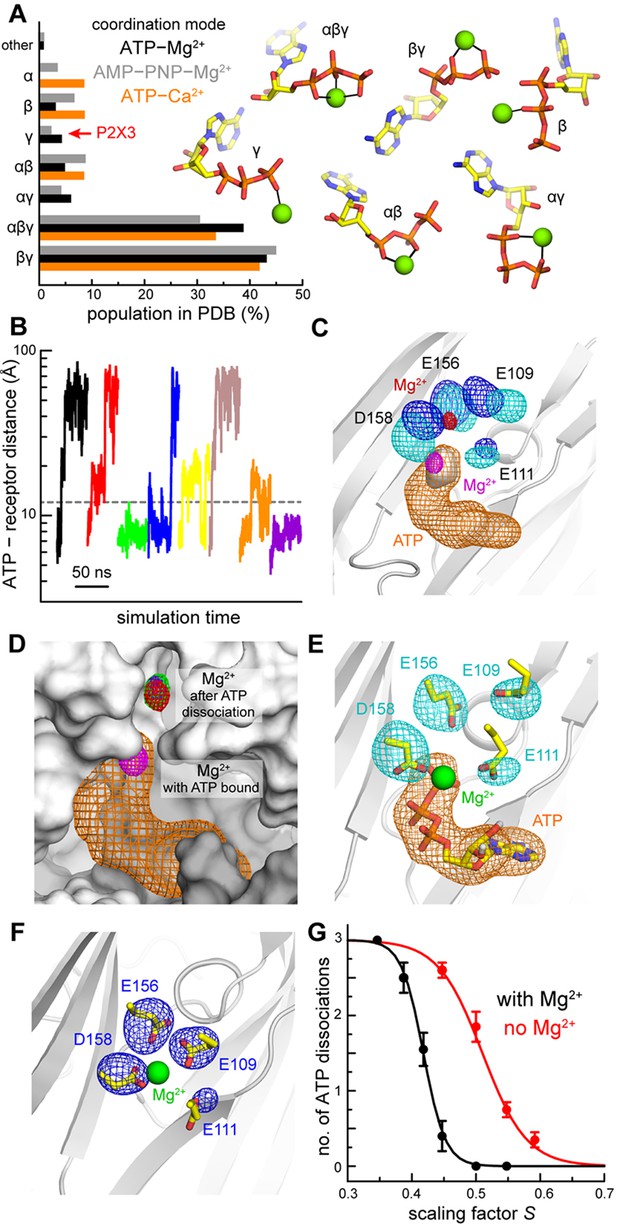
Computational study of the mode of ATP and Mg²⁺ recognition by P2X3.

(A) Occurrence of different modes of Mg²⁺-ATP and Ca²⁺-ATP interaction in non-redundant high-resolution crystal structures available in the Protein Data Bank. Each mode is indicated by the phosphate groups in ATP that coordinate the cation. Analogous data is shown for complexes of Mg²⁺ with the non-hydrolyzable analog AMP-PNP. (B) A sample of the simulated trajectories of the P2X3-ATP-Mg²⁺ complex produced with the solute-tempering protocol (S = 0.39). Trajectories showing spontaneous ATP dissociation from P2X3 (and Mg²⁺) are those in which the distance between the center of ATP and the center of the binding site in the receptor exceed 12 Å. Additional trajectories are depicted in Figure 2—figure supplement 1. (C) Comparison of P2X3-ATP-Mg²⁺ and P2X3-Mg²⁺ following ATP dissociation. For P2X3-ATP-Mg²⁺, 3D density maps calculated from the simulation data (see Materials and methods) are shown for ATP (orange), the γ-phosphate (gray surface), Mg²⁺ (magenta) and the surrounding carboxyl groups of acidic residues (cyan). Analogous maps are shown for ion and sidechains (red and blue, respectively), following ATP dissociation. The maps shown are averages of the data for the three protein subunits. The contour levels used for Mg²⁺ are the same in both cases; likewise for the sidechains. The protein conformation (gray cartoons) is a snapshot of the ATP-bound state. (D) Same as panel C, for Mg²⁺ and ATP in the ATP-bound state. For the ATP-free state, individual Mg²⁺ density maps are shown for each binding site in the trimer (red, green, purple), to demonstrate the observed displacement is reproducible. The protein snapshot is that in panel C, now represented as a surface, with adjacent protein subunits in light and dark gray. (E) Same as panel C, for the ATP-bound state, now showing a randomly selected configuration of Mg²⁺, ATP and the four acidic sidechains that represents the density. Non-polar hydrogen atoms and other components of the simulation system are omitted for clarity. (F) Same as panel E, for the ATP-dissociated state, in a slightly different view, for clarity. (G) Impact of Mg²⁺ on the nature of the interaction between ATP and P2X3. The plot quantifies the number of ATP dissociation events expected to occur in a 50-ns time-window, deduced from our simulation data, for each value of the scaling factor S, and in the presence or absence of Mg²⁺. Note that one ATP molecule is bound to each of the three protein subunits, and hence the maximum number of dissociation events is also 3. Each data point is an average of N = 20 independent simulations. Error bars denote the S.E.M. The data was fitted to a sigmoidal function f = 3/(1 + exp [m (*S - n*)]. The resulting parameters (C.C. > 99%) are: with Mg²⁺, m = 58.6, n = 0.42; without Mg²⁺, m = 29.1, n = 0.51.

https://doi.org/10.7554/eLife.47060.004

The ion binding mode we observe with ATP bound, which we designate as the ‘lower’ mode, is distinct from that observed previously in structures without ATP. In those previous structures, Mg²⁺ was proposed to be coordinated by the side chains of E109 and D158, and the carbonyl oxygen of E156, which we designate as the ‘upper’ mode (Figure 1E) (Mansoor et al., 2016). Although Mg²⁺ in the upper mode is near the ATP binding pocket, it is too far to interact directly with the bound nucleotide. Conversely, in our ATP-bound structure, with Mg²⁺ directly coordinated by the ATP γ-phosphate and D158, the ion is ~9 Å away from the side chain of E109. The key residue involved in both binding modes is D158, whose side chain points towards E109 for the upper mode or towards the γ-phosphate of ATP for the lower mode (Figure 1B–E). Therefore, these structures not only reveal the mode of recognition of ATP in its physiologically predominant forms with Ca²⁺ or Mg²⁺ bound, but also demonstrate how the acidic chamber near the nucleotide binding pocket enables the receptor to accommodate Mg²⁺ in two distinct configurations.

Simulations reveal Mg²⁺ displacement to upper mode results from ATP dissociation

Our crystal structures suggest a correlation between the mode of Mg²⁺ binding to P2X3, that is lower or upper mode, and the presence or absence of ATP. To evaluate whether there is a causal relationship between these two observations, we devised a molecular-simulation protocol to induce the spontaneous dissociation of ATP from the receptor and evaluated how Mg²⁺ responds to this event (see Materials and methods). In this protocol, based on the solute-tempering method (Liu et al., 2005), a scaling factor is used to weaken the interactions of a ligand (i.e. ATP) with both the surrounding solvent and receptor (i.e. P2X3 with bound Mg²⁺). As a result, the free-energy barriers and minima that underlie ligand binding and unbinding become shallower, accelerating the kinetics of these processes exponentially. Dissociation trajectories can be therefore observed within a relatively short simulation time, without imposing a specific direction of movement or time course.

Following this strategy, we produced tens of ATP-dissociation trajectories with varying scaling factors (Figure 2B, Figure 2—figure supplement 1). We then analyzed our simulation data to determine the most populated configuration of Mg²⁺ once ATP dissociates, and how it differs from that preferred in the ATP-bound state. In the presence of ATP and Mg²⁺, the simulation data (obtained with a conventional algorithm) is highly consistent with our crystal structures, showing stable close-range interactions between Mg²⁺ and both the ATP γ-phosphate and D158 (Figure 2C, Figure 2—figure supplement 2). The ion retains part of its first hydration shell, and water molecules mediate additional interactions with E156, E111 and E109 (Figure 2—figure supplement 2, Video 1). The γ- and β-phosphates are also tightly coordinated by multiple basic sidechains in the receptor, some of which concurrently form salt-bridges with the acidic sidechains coordinating Mg²⁺, that is K299-D158 and R281-E156 (Figure 2—figure supplement 2, Video 1). Altogether, this network of electrostatic interactions appears to mediate a highly stable complex with a well-defined geometry. Following ATP dissociation, this mode of Mg²⁺ binding changes noticeably and reproducibly. We detect a clear upward shift in the preferred location of Mg²⁺ (Figure 2C), consistent for all three protein subunits (Figure 2D), despite the fact that ATP dissociation from each site occurs at different time points in the simulations. This displacement is seemingly driven by a re-optimization of ion-protein interactions upon ATP release. Specifically, D158, E109 and E111 reorient (Figure 2E,F) to interact with the ion at a closer distance, whether directly or via water molecules, while E156 is approximately unchanged (so are the K299-D158, R281-E156 salt-bridges) (Figure 2—figure supplement 2, Video 2). Altogether, these results suggest the existence of a pathway whereby Mg²⁺ bound to P2X3 receptors exchanges dynamically between the two distinct modes.

Video 1

Download asset

posterframe for video — Close-up of the binding site for ATP-Mg²⁺ in P2X3, in the ATP-bound state, in a representative simulation snapshot (same as Figure 2E and Figure 2—figure supplement 2E).

Residue numbers are indicated in Figure 2—figure supplement 3.

https://doi.org/10.7554/eLife.47060.008

Video 2

Download asset

Divalent cations stabilize ATP on hP2X3 receptor channels

Dissociation of ATP plays a key role in the function of P2X3 receptors as this process is required for recovery from desensitization. The observation that divalent ions mediate additional interactions between ATP and P2X3 suggests that the ions might slow ATP dissociation. We examined this possibility computationally by inducing ATP-dissociation trajectories from a receptor lacking a divalent ion bound, following the same protocol outlined above. Using this data and that obtained for Mg²⁺-ATP bound P2X3, we derived the apparent ATP dissociation probability as a function of the interaction-scaling factor, in the absence or presence of Mg²⁺. As anticipated, the simulation results show that the ATP dissociation probability increases as the value of the scaling factor decreases, whether Mg²⁺ is present or not, with sigmoidal-like dependence (Figure 2G). Crucially, though, the presence of Mg²⁺ produces a clear left-shift in this trend, indicating that Mg²⁺ strengthens the effective ATP-receptor interaction. Moreover, the sigmoidal slope becomes steeper (by about a factor of 2), indicating Mg²⁺ and receptor act cooperatively. Indeed, in many simulated trajectories we observe Mg²⁺ holding on to a partially unbound nucleotide, fostering re-binding (Figure 2—figure supplement 1, Figure 2—figure supplement 3). Altogether these results substantiate the hypothesis that the presence of Mg²⁺ in our ATP-bound P2X3 structures is not incidental; rather, the ion appears to be a dominant contributing factor to the lifetime and geometry of the ligand-receptor complex.

To experimentally test this hypothesis, we used electrophysiological measurements. Characterizing the dissociation of ATP using functional approaches is not possible for wild-type hP2X3 because the receptor desensitizes much faster than ATP unbinds (Cook and McCleskey, 1997; Giniatullin and Nistri, 2013; Sokolova et al., 2006). Instead we used whole-cell patch clamp recordings of a slowly desensitizing mutant, and measured the time required for channel closure (deactivation) after removing external ATP, both in the absence and presence of divalent cations. ATP unbinding is the rate-limiting step for closure or deactivation of the slowly desensitizing P2X receptor channels (Rettinger and Schmalzing, 2004), and we therefore used the kinetics of channel deactivation in hP2X3 slow as a measure of the kinetics of ATP unbinding. The hP2X3 slow construct used for these experiments was generated by mutating three residues in the N-terminus (T13P/S15V/V16I) to greatly slow desensitization (Figure 3A), as previously described (Hausmann et al., 2014; Mansoor et al., 2016). In the absence of divalent cations, the hP2X3 slow construct deactivates with a time constant of 2.1 ± 0.3 s following removal of external ATP (Figure 3B,C). By contrast, the presence of 1 mM Mg²⁺ slowed deactivation by ~8-fold, while 1 mM Ca²⁺ slowed deactivation by ~ 4 fold (Figure 3B,C), suggesting that both ions slow ATP dissociation. In addition to these results obtained at pH 7.3, we also tested the effect of Mg²⁺ at pH 5.0, the acidic condition used for crystallization, and observed that 1 mM Mg²⁺ increased the deactivation time constant from 0.7 ± 0.1 s to 6.6 ± 0.6 s (Figure 3C, Figure 3—figure supplement 1). The deactivation time constants were faster at pH 5.0, in agreement with previous reports that P2X3 receptors have a lower affinity for ATP under acidic conditions (Gerevich et al., 2007; Wildman et al., 1999). Although both Mg²⁺ and Ca²⁺ ions slow hP2X3 slow deactivation, the effect of Ca²⁺ is more modest when compared to Mg²⁺, suggesting that Ca²⁺ might compete with Mg²⁺ to hasten unbinding under physiological conditions. We estimated divalent cation affinity by measuring the deactivation time constant in the presence of different concentrations of Mg²⁺ or Ca²⁺, and obtained an EC₅₀ of 102 µM for Mg²⁺ and 39 µM for Ca²⁺ (Figure 3D,E), revealing that all receptors are regulated by divalent ions under physiological conditions and that Ca²⁺ might play a more prominent role. When we tested a physiological solution containing 1 mM Mg²⁺ and 2 mM Ca²⁺, we measured a deactivation time constant of 10.2 ± 1.8 s, close to that with 1 mM Ca²⁺ (Figure 3B,C), even though the concentrations of Ca²⁺-ATP and Mg²⁺-ATP would be similar in this solution because the stability constant for Ca²⁺ binding to ATP is weaker than for Mg²⁺. In addition to prolonging deactivation, stabilizing ATP on the receptor would be expected to increase the apparent affinity for ATP activation of the receptor. We therefore constructed concentration-response relations for ATP activation of hP2X3 slow in the absence and presence of Mg²⁺. We found that 0.5 mM Mg²⁺ shifts the EC₅₀ from 40 nM to 18 nM, demonstrating that Mg²⁺ increases the apparent ATP affinity for the receptor (Figure 3—figure supplement 2).

Figure 3 with 3 supplements see all

Download asset Open asset

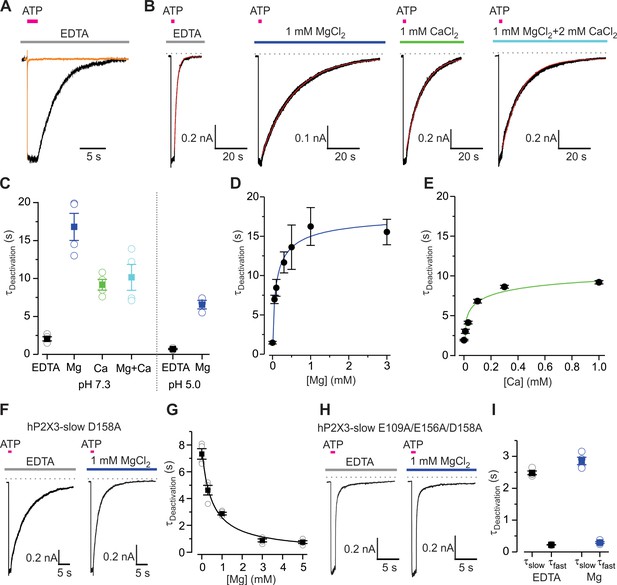
Mg²⁺ and Ca²⁺ slow deactivation of hP2X3 receptors.

(A) Superimposed fast-desensitizing hP2X3 wt (orange) and slow-desensitizing hP2X3 slow (black) macroscopic receptor channel currents activated by extracellular application of a saturating concentration of free ATP (10 µM) in the presence of EDTA (10 mM). (B) hP2X3 slow receptor channel currents activated by ATP (10 μM) were recorded in different extracellular divalent cation concentrations at pH 7.3 and shown on the same time scale. A single exponential function was fit to current deactivation and fits are shown in red, superimposed with the currents in black. (C) Summary of deactivation time constants in the absence and presence of different divalent cations at neutral or acidic pH, with individual cells shown in open symbols and filled symbols representing the mean and error bars S.E.M. (n = 4 for each). (**D and E**) Concentration-response relations for divalent cation slowing hP2X3 slow channel deactivation at pH 7.3. Each data point is the mean ± S.E.M. with n = 3. The Hill equation was fit to the data in D (Mg²⁺) with EC₅₀ = 102 ± 56 μM and n_H = 0.7 ± 0.3, and to the data in E (Ca²⁺) with EC₅₀ = 39 ± 6 μM and n_H = 0.5 ± 0.4. (F) 100 μM ATP activated macroscopic currents for D158A hP2X3 slow were recorded in the absence or presence of MgCl₂. (G) Deactivation time constants obtained from single exponential fits to current decay recorded after removing ATP in the absence and presence of Mg²⁺ at different concentrations. Filled symbols are the mean ± S.E.M. with n = 4, individual measurements are shown as open symbols. The Hill equation was fit to the data (EC₅₀ = 482 ± 106 μM, n_H = 0.9). (H) 300 μM ATP activated macroscopic currents for the E109A/E156A/D158A hP2X3 slow triple mutant were recorded in the absence or presence of MgCl₂. (I) Deactivation time constants obtained from double exponential fits to current deactivation. Filled symbols are the mean ± S.E.M. with n = 4, individual measurements are shown as open symbols.

https://doi.org/10.7554/eLife.47060.010

The lower mode of Mg²⁺ binding is essential for stabilizing ATP on the receptor

The structures of Mg²⁺-ATP and Ca²⁺-ATP bound P2X3 receptors suggest that D158 is a critical residue for the lower mode of divalent cation coordination. When D158 is mutated to Ala in hP2X3 slow, we observed considerably slower deactivation in the absence of divalent ions (τ = 7.3 ± 0.4 s) compared to the control construct, demonstrating that mutations near the ATP binding site can influence dissociation of ATP. Remarkably, instead of slowing deactivation, Mg²⁺ actually accelerated deactivation of the D158A mutant, with an affinity somewhat weaker than observed for Mg²⁺ slowing of deactivation for the control receptor (Figure 3F,G). We also studied the E156A mutation in hP2X3 slow and found that the mutation did not appreciably alter deactivation in the absence of divalent ions (Figure 3—figure supplement 3A), but Mg²⁺ accelerated channel deactivation, with an affinity that is also lower than the control receptor (Figure 3—figure supplement 3B), suggesting that Mg²⁺ can still bind to hP2X3 with lower affinity when either E156 or D158 is mutated, and that both E156 and D158 are required for Mg²⁺ to stabilize ATP on the receptor. In contrast, when the crucial residue E109 involved in the upper mode of coordination is mutated to Ala, Mg²⁺ slowed deactivation as in the control receptor (Figure 3—figure supplement 3C,D), suggesting that this residue is not involved in stabilizing ATP. When all three residues E109-E156-D158 are mutated to Ala in hP2X3 slow, Mg²⁺ has no discernable effect on channel deactivation (Figure 3H,I), revealing that acidic residues contributing to the lower mode of divalent binding are essential for the ions to interact with and stabilize ATP.

Divalent cations slow hP2X3 recovery from desensitization

The wild-type hP2X3 receptor desensitizes much more rapidly than ATP unbinds, leading to a very slow recovery from desensitization. Since Mg²⁺ binding to the lower mode slows ATP dissociation, we hypothesized that the reported inhibitory effects of Mg²⁺ (Giniatullin et al., 2003; Li et al., 2013) might result from the ion stabilizing a desensitized state (Figure 4—figure supplement 1A). Moreover, we suspected the reported facilitation of P2X3 receptor by Ca²⁺ observed in solutions containing Mg²⁺ (Cook et al., 1998) might be related to our observation that Ca²⁺ slows unbinding of ATP less dramatically than Mg²⁺ and that the influence of Ca²⁺ prevails when both divalent ions are present at physiological concentrations (Figure 3B–E). To investigate how divalent cations influence gating of the wild-type hP2X3 receptor, we used a rapid piezo-controlled solution exchange system to apply saturating concentration of ATP for 500 ms to activate channels in the absence or presence of either Mg²⁺ or Ca²⁺ and examined the resulting current kinetics. In all cases, hP2X3 receptor channels activate rapidly and currents reach a maximum value within 1 ms (Figure 4A), a value that is close to the limit of our solution exchange. Once activated, channels rapidly desensitize in the continuous presence of ATP, with the kinetics of current decay being well fit by a double exponential function, with time constants (τ) that were not discernably different in the absence or presence of either Mg²⁺, Ca²⁺ or a physiological concentration of the two ions (Figure 4A,B). We then investigated the kinetics of recovery from desensitization by reapplying ATP at different time points after the initial ATP application that activates and desensitizes the receptors. The time constant for recovery from desensitization in the absence of divalent cations was 63 ± 8 s (Figure 4C), significantly faster than previous results obtained using physiological concentrations of divalent ions (Cook and McCleskey, 1997; Cook et al., 1998). In contrast, recovery from desensitization was slowed by almost 4-fold (τ = 248 ± 71 s) in the presence of Mg²⁺ (1 mM) and to a lesser extent by external Ca²⁺ (τ = 115 ± 42 s at 1 mM) (Figure 4C). We also examined the kinetics of recovery from desensitization in the presence of physiological concentrations of Mg²⁺ and Ca²⁺ and obtained a time constant of 140 ± 44 s, close to that observed with 1 mM Ca²⁺ (Figure 4C). These results demonstrate that Mg²⁺ (and to a lesser extent Ca²⁺) stabilizes a desensitized state of the hP2X3 receptor, most likely by increasing stability of the receptor-ATP complex.

Figure 4 with 1 supplement see all

Download asset Open asset

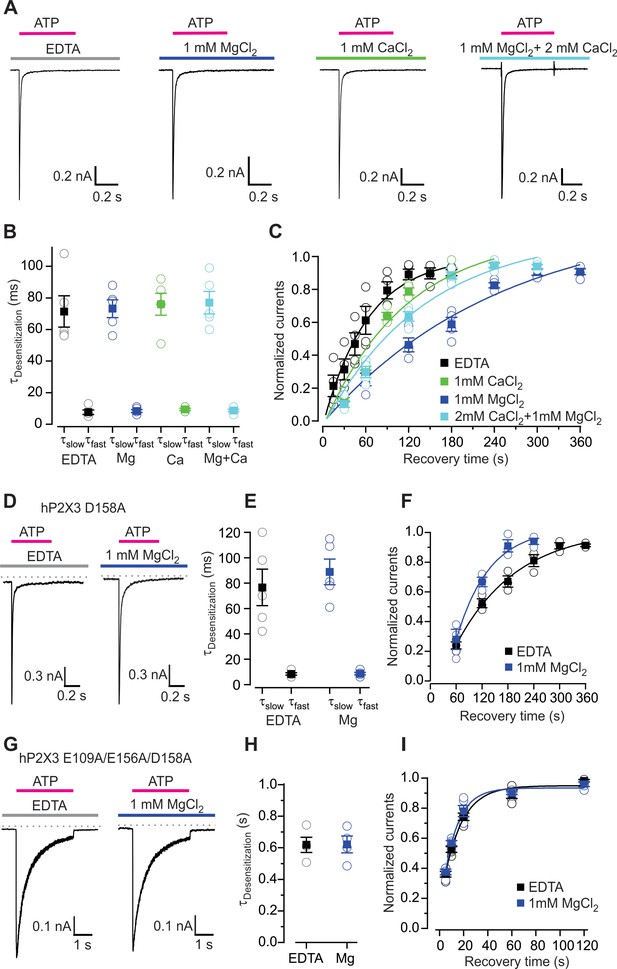
Influence of Mg²⁺ and Ca²⁺ on desensitization of hP2X3 receptor channels.

(A) Macroscopic wt hP2X3 receptor channel currents activated by a saturating concentration of ATP (300 μM) under different conditions. (B) Summary of desensitization time constants obtained by double exponential fits of desensitizing currents in the absence and presence of Mg²⁺ or Ca²⁺, with individual cells shown in open symbols and mean values in filled symbols, with error bars representing S.E.M. (n = 5 for each). (C) Time courses for recovery from desensitization of hP2X3 receptor channels in the absence and presence of divalent cations. Responses were normalized to the amplitude of current activated by the first application of a saturating concentration of ATP (300 µM) for 500 ms (n = 4). Smooth lines are single exponential fits to the time courses with τ = 63 ± 8 s for EDTA, τ = 248 ± 71 s for Mg²⁺, τ = 115 ± 42 s for Ca²⁺ and τ = 140 ± 44 s for Mg²⁺ plus Ca²⁺. (D) 300 μM ATP activated macroscopic currents for D158A were recorded in the absence or presence of MgCl₂. (E) Desensitization time constants obtained by fitting a double exponential function to the current decay during ATP (100 µM) application with individual cells shown in open symbols and mean values in filled symbols, with error bars representing S.E.M. (n = 5 for each). (F) Time courses for recovery from desensitization obtained as in panel C (n = 3). Smooth lines are single exponential fits to the time courses with τ = 140 ± 21 s for EDTA and τ = 76 ± 25 s for Mg²⁺. (G) ATP activated macroscopic currents recorded for the E109A/E156A/D158A triple mutant were recorded in response to 1 mM ATP in the absence or presence of MgCl₂. (H) Desensitization time constants obtained by single exponential fits to the current decay during ATP (1 mM) application with individual cells shown in open symbols and mean values in filled symbols, with error bars representing S.E.M. (n = 4 for each). (I) Time courses for recovery from desensitization obtained as in panel C (n = 5). Smooth lines are single exponential fits to the time courses with τ = 15 ± 3 s for EDTA and τ = 12 ± 2 s for Mg²⁺.

https://doi.org/10.7554/eLife.47060.014

To further link the effects of divalent ions on ATP dissociation and recovery from desensitization, we examined the effects of the D158A mutant. Interestingly, although the onset of desensitization for D158A is similar to wild-type (Figure 4D,E), the mutant slowed recovery from desensitization in the absence of divalent ions, consistent with slower deactivation of D158A mutant in hP2X3 slow (Figure 4F) (τ = 140 s for D158A compared to τ = 63 s for wild-type). Mg²⁺ hastened recovery from desensitization in D158A, an effect that is similar to the acceleration of ATP dissociation by Mg²⁺ in hP2X3 slow D158A (Figure 4F). We also examined the D109A/D156A/D158A triple mutant, and observed that the mutant exhibited slower desensitization, faster recovery from desensitization and that Mg²⁺ had no discernable effect on either of these measures (Figure 4G–I). From these results we conclude that Mg²⁺ binding to the lower mode observed in our structures stabilizes ATP on the receptor and slows recovery from desensitization. Stabilization of a desensitized state by Mg²⁺ can explain why this ion inhibits the activity of P2X3 receptor channels when the nucleotide is applied at a frequency that is sufficient for recovery from desensitization in the absence of the divalent, but not in its presence (Giniatullin et al., 2003; Li et al., 2013) (Figure 4—figure supplement 1A,B).

The divalent cation binding chamber is crucial for activation by Mg²⁺-ATP

We next explored the role of the two modes of divalent binding for activation of hP2X3 receptor channels by Mg²⁺-ATP using a protocol where ATP is applied along with enough Mg²⁺ for Mg²⁺-ATP to be the major form of the nucleotide present in solution (Figure 5). Using this protocol, the wild type hP2X3 as well as hP2X3 slow receptors can be robustly activated by a solution containing a low concentration of free ATP and a high concentration of Mg²⁺-ATP (Li et al., 2013) (Figure 5A–C, Figure 5—figure supplement 1). For the D158A and E156A mutants that contribute to the lower mode of divalent binding, although the extent of activation by Mg²⁺-ATP was somewhat less than for the wild-type receptor, we still observed robust activation by Mg²⁺-ATP (Figure 5A–C). For the E109A and E111A mutants within the upper mode of divalent binding, activation by Mg²⁺-ATP was indistinguishable from the wild type receptor (Figure 5—figure supplement 2A–C). In contrast, when both E156A and D158A mutants were combined, we observed considerably weakened activation by Mg²⁺-ATP (Figure 5A–C), indicating that the lower mode is important for Mg²⁺-ATP activation. We also observed a ‘resurgent’ current upon removal of Mg²⁺-ATP from the external solution in the E156A/D158A double mutant (Figure 5B). A similar resurgent current was previously observed for the P2X2 receptor following removal of Mg²⁺-ATP solutions, where we established that the receptor can bind both free ATP and Mg²⁺-ATP, but that only free ATP can robustly promote channel opening (Li et al., 2013). In the case of P2X2 receptors, the resurgent current appears following removal of Mg²⁺-ATP because Mg²⁺ unbinds more rapidly than free ATP, giving rise to the transient activation by free ATP remaining on the receptor (Figure 5—figure supplement 3B,C). Interestingly, when either the D158A or E156A mutants in the lower mode were combined with either the E109A or E111A mutants within the upper mode, we also observed greatly reduced activation by Mg²⁺-ATP and a resurgent current upon removal of Mg²⁺-ATP (Figure 5—figure supplement 2A–C). For the triple mutant (E09A/E156A/D158A) involving both lower and upper modes of divalent ion binding, we saw no discernable activation by Mg²⁺-ATP in either hP2X3 or hP2X3 slow, but Mg²⁺-ATP concentration dependent resurgent current (Figure 5—figure supplement 1, Figure 5—figure supplement 2, Figure 5—figure supplement 3A–C). From these findings we conclude that the lower mode of divalent binding to P2X3 receptors is essential for activation by divalent bound ATP and that the upper mode also plays a detectable role.

Figure 5 with 3 supplements see all

Download asset Open asset

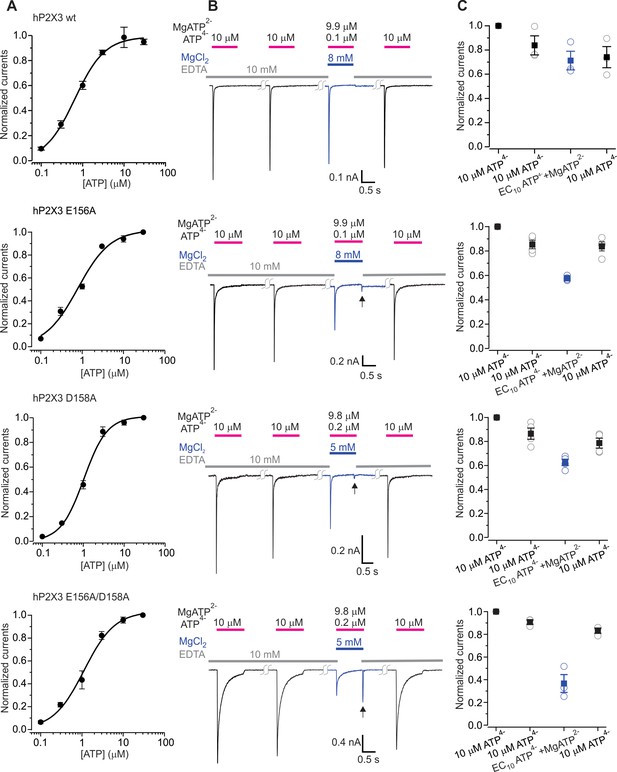
The divalent cation binding chamber is critical for Mg²⁺-ATP activation.

(A) Concentration-response relations for ATP activation of wt hP2X3, E156A, D158A and the E156A/D158A double mutant in divalent-free solution. Each data point is the mean of four measurements (± S.E.M.). Smooth lines are fits of the Hill equation to the data where EC₅₀ and n_H are 0.7 ± 0.1 μM and 1.2 ± 0.1 for wt hP2X3, 0.8 ± 0.1 μM and 1.1 ± 0.2 for E156A, 1.0 ± 0.1 μM and 1.5 ± 0.2 for D158A and 1.1 ± 0.2 μM and 1.2 ± 0.2 for E156A/D158A. (B) Macroscopic currents activated with solutions containing either a saturating concentration of free ATP or one containing mostly Mg²⁺-ATP plus an EC₁₀ quantity of free ATP for wt hP2X3, E156A, D158A or the E156A/D158 double mutant. The first applications of free ATP at 2 min intervals were used to estimate the extent of rundown between consecutive applications of ATP. Note the resurgent current (black arrows) for E156A, D158A and the E156A/D158A double mutant upon removal of Mg²⁺-ATP solution. (C) Summary of currents in response to each ATP application, normalized to the amplitude of the first. Open symbols are individual cells and fill symbols are the mean, with error bars representing S.E.M. (n = 3 for wt and the double mutant and n = 4 for all others).

https://doi.org/10.7554/eLife.47060.016

Discussion

The goal of the present study was to understand how P2X3 receptors are activated by ATP in the presence of physiological concentrations of Ca²⁺ and Mg²⁺ where most of the nucleotide is divalent-bound. Collectively, our results show how the receptor uses an acidic chamber to accommodate those ions in two distinct modes; either bound in the lower mode where the ion interacts with the γ-phosphate of ATP, or in the upper mode in the absence of the nucleotide. The interaction between divalent ions and the ATP γ-phosphate seen in our crystal structures is distinct from that in most other structures in the PDB and also from that typical of ATP in solution; in both cases, the divalent ions preferentially interact with both β-and γ-phosphates of the nucleotide. Our computational and functional results collectively show that binding of Mg²⁺ stabilizes ATP on the receptor, slowing unbinding and recovery from desensitization, and increasing the apparent affinity for ATP, with similar results for Ca²⁺ in functional experiments. Our mutagenesis results show that the acidic chamber is required for activation of the receptor when divalent-bound forms of ATP predominate in solution. Although the lower mode of divalent binding is critical for activation by divalent-bound ATP, the upper mode also seems to play a role because combining mutations in the two modes diminishes activation when divalent-bound forms of the nucleotide predominate.

Our results suggest that the following sequence of events occur as divalent-bound ATP binds to activate P2X3 receptors (Figure 6). We know that Mg²⁺ can bind to the upper mode seen in the X-ray structure of apo hP2X3 when present in mM concentrations (Mansoor et al., 2016), so we assume that the upper mode would be occupied by Mg²⁺ (and likely Ca²⁺) under physiological conditions prior to the recognition of divalent-bound ATP. In one scenario, initial engagement of divalent-bound ATP with the receptor would weaken the interaction of the ion bound to the β- and γ-phosphates of ATP; in addition, dissociation of the ion would be fostered by the ion occupying the upper mode in the acidic chamber, as this ion shifts to the lower mode to interact with the γ-phosphate of ATP, while still engaged to E156 and D158. In our simulations, both ATP and Mg²⁺ (in the lower mode) remain stably associated with the receptor, and when ATP dissociation is accelerated the ion spontaneously moves from the lower mode to the upper mode, demonstrating the existence of a pathway for the movement of divalent ions between the two modes and reinforcing the idea that ion binding within the upper mode is favored in the absence of the nucleotide. An alternate scenario would be that when divalent-bound ATP is recognized by the receptor, it is the divalent ion originally occupying the upper mode that dissociates, allowing the ion bound to β− and γ−phosphates of ATP to reposition to the lower mode seen in our X-ray structures. Our simulations do not permit us to discriminate between these two scenarios, as they probe the dissociation of ATP only. Nevertheless, two arguments can be put forward in favor of the first scenario. From a structural standpoint, dissociation of the ion occupying the upper mode appears less likely because it would be sterically hindered not only by the surrounding receptor but also ATP itself; by contrast, the ion bound to ATP would be completely exposed to the solvent. In addition, a mechanism whereby the ion bound to ATP must dissociate to permit complete agonist recognition and channel activation would be applicable to P2X2 receptors and P2X3 E109A/E156A/D158A mutants, which as noted above, can bind divalent-bound ATP even though the complex does not promote robust activation of the receptor.

Figure 6

Download asset Open asset

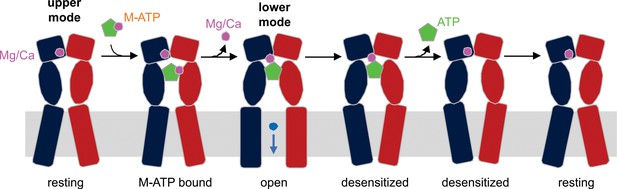
Schematic illustration of the mechanism of Mg²⁺-ATP/Ca²⁺-ATP activation of P2X3 receptor channels.

Mg²⁺ or Ca²⁺ binds to hP2X3 receptors in the upper mode under physiological conditions. When ATP divalent cation complex (M-ATP) enters the nucleotide binding pocket, a divalent cation will rapidly dissociate, leaving one to be coordinated by the γ-phosphate of ATP and residues E156 and D158. The divalent cation sandwiched between ATP and receptor strengthens the effective ATP-receptor interaction, and also fosters re-binding of ATP molecules that become transiently dislodged from the nucleotide-binding pocket, rendering a very slow recovery from desensitization for hP2X3 receptors. Only two of three subunits of a hP2X3 receptor are shown for clarity.

https://doi.org/10.7554/eLife.47060.020

In both of these scenarios, the P2X3 receptor uses the acidic chamber to enable activation and to stabilize ATP on the receptor in the presence of divalent ions. Following receptor activation and desensitization, dissociation of ATP would be much slower in the presence of divalent ions, in no small part due to the divalent ion anchoring the nucleotide to D158. Not only does this ion (at this position) strengthen the effective ATP-receptor interaction; it also fosters re-binding of ATP molecules that become transiently dislodged from the nucleotide-binding pocket, that is the dissociation (and recognition) process becomes cooperative. When the wild-type P2X3 receptor is not occupied by Ca²⁺ or Mg²⁺, and ATP is recognized in its free form under divalent-free laboratory conditions, binding is likely suboptimal because D158 is electrostatically repulsive with the γ-phosphate of ATP. Consistent with this hypothesis, when D158 is mutated to Ala, receptors actually hold on to ATP more strongly than the wild-type in the absence of divalent ions, as reflected in slower ATP dissociation and recovery from desensitization (Figure 3C,G; Figure 4C,F). In contrast, for the D158A mutant, when the agonist is an ATP-divalent complex, the incoming ion bound to the nucleotide would be less likely to move away from β− and γ−phosphates of ATP, and ATP would thus spend more time in a conformation that is in part incompatible with the intricate network of receptor-ligand-solvent interactions observed in the wild-type receptor, resulting in accelerated ATP dissociation and recovery from desensitization (Figure 3G; Figure 4F). Consistent with this model, a priori disruption of this network, for example in the E109A/E156A/D158A mutant, results in minimal Mg²⁺ effects, but ATP binding is markedly weakened, with dramatically accelerated dissociation and recovery from desensitization (Figure 3I; Figure 4I).

In conclusion, we have uncovered a previously unrecognized structural element in P2X3 receptors that is essential for channel activation under physiological conditions where divalent-bound forms of ATP predominate. Our results also reveal that divalent ions play a fundamental role in tuning the gating properties of P2X3 receptors. By hampering ATP dissociation, acting cooperatively with the protein, divalent ions slow down the receptor recovery from desensitization, thereby reducing the frequency with which the channel is available for activation by extracellular ATP. Interestingly, the influence of Ca²⁺ on stabilizing ATP on the receptor and slowing recovery from desensitization is less pronounced than for Mg²⁺, which could explain why Ca²⁺ can facilitate activation of P2X3 receptors in physiological solutions containing Mg²⁺ in response to repeated applications of ATP (Cook and McCleskey, 1997; Cook et al., 1998). Appreciating the pronounced influence of divalent ions on the gating properties of P2X3 receptors will be essential for understanding how these receptors are involved in sensory processes in the nervous system.

Materials and methods

Purification, crystallization and structure determination

Request a detailed protocol

The crystallization construct of human P2X3 ΔN5ΔC33-T13P/S15V/V16I (hP2X3 MFC_slow) were expressed and purified as described previously (Wang et al., 2018). For the crystallization of hP2X3 MFC_slow with ATP and Mg²⁺, 1 μl of hP2X3 MFC_slow at 2–3 mg/ml and 1 mM ATP were mixed with 1 μl of the reservoir solution (0.05 M Mg-acetate, 0.05 M Na-acetate pH 5.0 and 21.2–25.8% PEG400). For the crystallization with ATP and Ca²⁺, 1 μl of hP2X3 MFC_slow at 2–3 mg/ml and 1 mM ATP were mixed with 1 μl of the reservoir solution (0.2 M NaCl, 0.05 M Ca-acetate pH 5.0 and 21.2–25.8% PEG 400). Both crystals with Mg²⁺ and Ca²⁺ ions grew using the vapor diffusion method over the reservoir resolutions after 3 weeks, and were harvested with the respective cryoprotectant solutions for the crystals with Mg²⁺ (0.05 M Mg-acetate, 0.05 M Na-acetate pH 5.0, 40% PEG400 and 1 mM ATP) and for the crystals with Ca²⁺ (0.2 M NaCl, 0.05 M Ca-acetate pH 5.0, 40% PEG 400 and 1 mM ATP) before cryo-cooling. All X-ray diffraction data sets were collected at the SPring-8 beamline BL41XU. The data sets were processed using XDS2 (Kabsch, 2010). Both ATP and Mg²⁺-bound and ATP and Ca²⁺-bound hP2X3 structures were solved by molecular replacement with Phaser, using the ATP-bound, open state structure of hP2X3 (PDB ID: 5SVK) as a template. The models were further improved by iterative cycles of manual modeling with COOT3 (Emsley and Cowtan, 2004). and refined using PHENIX4 (Adams et al., 2010). Data collection and refinement statistics are shown in Supplementary file 1.

Survey of ATP-Mg²⁺ complexes in the Protein Data Bank

Request a detailed protocol

The statistical analysis described in Figure 2A comprises entries in the PDB obtained through X-ray crystallography at a resolution higher than or equal to 2.5 Å and containing at least one ATP bound to one Mg²⁺ (or Ca²⁺) ion. Redundant structures with more that 70% of sequence identity were eliminated from this set. Structures in which ATP is bound concurrently to Mg²⁺(or Ca²⁺) and other cations were also eliminated. The resulting sets includes 171 entries (12 entries for Ca²⁺). An analogous set of 152 entries was obtained for Mg²⁺ complexes with the non-hydrolysable ATP analog AMP-PNP. Both sets were divided into classes according the proximity of Mg²⁺ and each of the phosphate groups in the ATP tri-phosphate moiety. For example in the configuration referred as ‘βγ’, Mg²⁺ is directly and concurrently coordinated only by oxygen atoms in the β- and γ-phosphate groups. To carry out this classification in practice, we defined and calculated the following ‘ion-coordination number’ for each of the phosphate groups and each of the PDB entries:

N^{s} = \frac{R}{l o g \sum_{i} e x p [R / d (O_{i}^{s}, M g^{2 +})]}

where d (O, Mg²⁺) denotes an oxygen-Mg²⁺ distance, s denotes either the α-, β- or γ-phosphates, and i denotes each of the oxygen atoms in each phosphate not forming the ATP backbone (i.e. three atoms in γ, and two atoms in α and β). For R = 1,000 Å, a value of N^s smaller than 3.2 Å reflects direct coordination by the s-phosphate; for example in the αβγ geometry N^α, N^β and N^γ are concurrently smaller than this threshold.

Molecular dynamics simulations

Request a detailed protocol

All MD simulations were carried out with NAMD version 2.13 (Phillips et al., 2005), using the CHARMM36 force field (Best et al., 2012), at constant temperature (298 K) and pressure (1 atm). The integration time-step was 2 fs. Electrostatic interactions were calculated using the PME method with a real-space cut-off of 12 Å; van-der-Waals interactions were also cut-off at 12 Å, with a switching function turned on at 10 Å. Periodic boundary conditions were used. The simulations of ATP-bound P2X3 in the absence of Mg²⁺ were based on PDB entry 5SVK (Mansoor et al., 2016). Those of P2X3 bound to ATP and Mg²⁺ were based on PDB entry 5SVL (Mansoor et al., 2016). In the latter, a density signal near the ATP γ-phosphate designated as Na⁺ in the PDB entry was reassigned as Mg²⁺; this assignment is confirmed by the crystal structures reported here. Each of the simulation systems is a cubic box of side approximately equal to 100 Å. The systems comprise the extracellular domain of P2X3 (residues 47 to 317), immersed in a 100 mM KCl solution (plus counterions neutralizing the total charge). Disulfide bonds were assumed between residues 107 and 153, 116 and 137, 122 and 147, 203 and 213, and 247 and 256, in all three protomers. Following a PROPKA evaluation (Bas et al., 2008), all ionizable residues were set to be in their default state at pH 7, with the exception of Glu109 in the Mg²⁺-free ATP-bound structure. Three types of simulations were carried out for each system, in three consecutive stages. The first stage, or equilibration, comprised a sequence of simulations during which the dynamics of the protein-ligand complex is limited, primarily through internal-coordinate restraints (RMSD, distance restraints), to a degree that is gradually diminished over a period of 85 ns. In the second stage, a simulation of 50 ns was carried whereby the structural dynamics of the complex was for the most part unrestricted; however, to preclude large deviations resulting from the deletion of the transmembrane domain, a weak restraint was applied to approximately maintain the relative arrangement of the secondary-structure elements of the protein as in the experimental structure of the full-length complex. Specifically, this restraint is a harmonic function of the RMSD of the backbone, relative to the X-ray structure, with force constant k = 1 kcal/mol/Å². On average, the RMSD values of the resulting ensembles of protein configurations are 1.5 ± 0.2 Å for the secondary-structure core and 2.3 ± 0.3 Å for all backbone; that is this weak restraint is such that the variability of the configurations explored by the protein is not unlike what could be expected for a simulation of the full-length protein. A third set of MD simulations were carried out subsequently for both the P2X3-ATP and P2X3-ATP-Mg²⁺ complex, whereby the dissociation of ATP was induced using the so-called solute-tempering method (Jo and Jiang, 2015; Liu et al., 2005). That is, the energy function was modified so as to scale down the non-bonded interactions of ATP with all other components in the simulation system by a factor $S = \sqrt{λ}$ ; non-bonded interactions within ATP were also scaled, down, by a factor λ. After a series of initial tests, a total of 80 independent simulations of 50 ns each were carried out for the P2X3-ATP complex, for λ values equal to 0.20, 0.25, 0.30 and 0.35 (20 trajectories for each value of λ). An Analogously for the P2X3-ATP-Mg²⁺ complex, 120 simulations were carried out with λ values equal to 0.12, 0.15, 0.175, 0.20, 0.25 and 0.30. The dissociation of ATP from each of the 3 protein subunits was monitored over time by evaluating (1) the distance between the centers-of-mass of ATP and the residues defining its binding site (Thr172, Lys63, Lys65, Arg281, Arg299; hydrogen atoms excluded), or D₁, and (2) the distance between the ATP γ-phosphorus atom and the Mg²⁺ ion, or D₂. In our simulation of the P2X3-ATP-Mg²⁺ complex with unperturbed intramolecular interactions, the characteristic values of D₁ and D₂ are 5.9 ± 0.3 and 3.2 ± 0.1 Å, respectively. The density maps, snapshots and distributions shown in Figure 2C-D, 2E, Figure 2—figure supplement 1A-C, E and Video 1 derive from this simulation. To evaluate the ATP-dissociated state, from the solute-tempering trajectories, we first considered all snapshots for which D₁ > 12 Å and concurrently D₂ > 5 Å (each binding site in the protein trimer was analyzed separately). The distributions shown in Figure 2A-D describe these configurations, combining the data obtained for all λ values and all binding sites. (Note that the solute-tempering scheme does not perturb the inter- or intra-molecular interactions for the receptor, Mg²⁺ and solvent, so once ATP dissociates, the dynamics of the P2X3-Mg²⁺ complex is represented with the standard energy function.) These distributions are however not stationary, as they reflect an evolving configuration of the P2X3-Mg²⁺ complex. For clarity, therefore, the density maps and snapshots shown in Figure 2C-D, 2F, Figure 2—figure supplement 2F and Video 2 reflect the subset of this data that appears representative of the emerging most-populated configuration, namely all snapshots of the P2X3-Mg²⁺ complex (with ATP dissociated) in which the distance between Mg²⁺ and the carboxyl groups of D158, E156, E111 and E109 is equal or smaller than 6 Å.

Cell culture and transfection for electrophysiology

Request a detailed protocol

Human embryonic kidney 293 (HEK-293) cells were purchased from ATCC (ATCC CRL-1573), cultured in Dulbecco's Modified Eagle's Medium (DMEM) supplemented with 10% fetal bovine serum and 10 mg/L gentamicin. Following an initial passage, cells were frozen in liquid nitrogen using Freezing Media (Life Technologies) and these aliquots used to generate subsequent cultures. To minimize cell variability, cells were used with fewer than 15 passages (<2 months). All cell culture reagents were obtained from Life Technologies. Trypsin treated HEK293 cells were seeded onto glass coverslips in 35 mm dish or 6-well plates the day of transfection and placed in a 37°C incubator with 95% air and 5% CO₂. Transfections were performed using FuGENE6 Transfection Reagent (Promega). hP2X3 receptors were co-transfected with a green fluorescent protein (GFP) cDNA construct pcDNA3-Clover (addgene) at a ratio of 2:1. Cells were used for whole-cell recording 18–30 hr after transfection. hP2X3 in pCMV6-XL4 was purchased from OriGENE and then cloned into pcDNA3. All the mutations were introduced into hP2X3 using QuikChange II site-directed mutagenesis kit and verified by DNA sequencing.

Whole-cell patch clamp recording

Request a detailed protocol

Whole-cell patch clamp recordings were used to record P2X receptor channel currents from transiently transfected HEK-293 cells. Membrane currents were recorded under voltage-clamp using an Axopatch 200B patch clamp amplifier (Axon Instruments, Inc) and digitized on-line using a Digidata 1322A interface board and pCLAMP 9.2 software (Axon Instruments, Inc). Currents were filtered at 2 kHz using 8-pole Bessel filters, and digitized at 5 or 10 kHz. The pipette solution for standard whole-cell recording on HEK cells contained (mM): 140 NaCl, 10 EGTA and 10 HEPES, adjusted to pH 7.0 with NaOH. The divalent-free extracellular solution contained (mM): 140 NaCl, 10 EDTA, and 10 HEPES, adjusted to pH 7.3 or 5.0 with NaOH. Assuming that divalent ion contaminations from reagents and water is less than 1 μM, any possible free divalent cations in the 10 mM EDTA solution would be less than 0.5 nM. The extracellular solutions with different concentrations of Mg²⁺ or Ca²⁺ contained (mM): 140 NaCl, 10 HEPES, and desired concentration of MgCl₂ or CaCl₂, adjusted to pH 7.3 or 5.0. Na₂ATP (referred to as ATP) was used in all the experiments. The stability constants of ATP binding to cations present in our solutions are: Mg²⁺ 10^4.10, Ca²⁺ 10^3.76, Na⁺ 10^0.83, and K⁺ 10^1.17 (NIST Critically Selected Stability Constants of Metal Complexes). Max Chelator (http://maxchelator.stanford.edu) was used to calculate concentrations of Mg²⁺, MgATP^2- and ATP^4- in solutions with different concentrations of MgCl₂ and ATP. Recording solutions were adjusted to the correct pH after adding MgCl₂ and ATP. Solution exchange was achieved using either the Rapid Solution Changer RSC-200 (BioLogic), which can change solution within ~ 50 ms and has the capacity of switching between nine solutions to construct dose-response relationships, or a Piezo driven system (AutoMate Scientific), which can change between two solutions within 1 ms to resolve rapidly desensitizing currents. To generate concentration-response relationships, a reference concentration of ATP was applied before each test concentration was applied, as previously described (Li et al., 2008). The Hill equation was fit to the data according to: I/I_max= [ATP]ⁿ^H / ([ATP]ⁿ^H + EC₅₀ⁿ^H), where I is the normalized current at a given concentration of ATP, I_max is the maximum normalized current, EC₅₀ is the concentration of ATP ([ATP]) producing half-maximal currents and n_H is the slope factor.

Data availability

All data needed to evaluate the conclusions in this paper are available in the main text and supplementary materials. Refined atomic models have been deposited with the Protein Data Bank (entry codes 6AH4 and 6AH5).

The following data sets were generated

1. Hattori M
(2019) Protein Data Bank
ID 6AH4. Structure of an ion channel in state I.

http://www.rcsb.org/structure/6AH4
1. Hattori M
(2019) Protein Data Bank
ID 6AH5. Structure of an ion channel in state II.

http://www.rcsb.org/structure/6AH5

References

1. Abdulqawi R
2. Dockry R
3. Holt K
4. Layton G
5. McCarthy BG
6. Ford AP
7. Smith JA
(2015) P2X3 receptor antagonist (AF-219) in refractory chronic cough: a randomised, double-blind, placebo-controlled phase 2 study
The Lancet 385:1198–1205.

https://doi.org/10.1016/S0140-6736(14)61255-1
- Google Scholar
1. Adams PD
2. Afonine PV
3. Bunkóczi G
4. Chen VB
5. Davis IW
6. Echols N
7. Headd JJ
8. Hung LW
9. Kapral GJ
10. Grosse-Kunstleve RW
11. McCoy AJ
12. Moriarty NW
13. Oeffner R
14. Read RJ
15. Richardson DC
16. Richardson JS
17. Terwilliger TC
18. Zwart PH
(2010) PHENIX: a comprehensive Python-based system for macromolecular structure solution
Acta Crystallographica Section D Biological Crystallography 66:213–221.

https://doi.org/10.1107/S0907444909052925
- PubMed
- Google Scholar
1. Barclay J
2. Patel S
3. Dorn G
4. Wotherspoon G
5. Moffatt S
6. Eunson L
7. Abdel'al S
8. Natt F
9. Hall J
10. Winter J
11. Bevan S
12. Wishart W
13. Fox A
14. Ganju P
(2002) Functional downregulation of P2X3 receptor subunit in rat sensory neurons reveals a significant role in chronic neuropathic and inflammatory pain
The Journal of Neuroscience 22:8139–8147.

https://doi.org/10.1523/JNEUROSCI.22-18-08139.2002
- PubMed
- Google Scholar
(2008) Very fast prediction and rationalization of pKa values for protein-ligand complexes
Proteins: Structure, Function, and Bioinformatics 73:765–783.

https://doi.org/10.1002/prot.22102
- PubMed
- Google Scholar
1. Best RB
2. Zhu X
3. Shim J
4. Lopes PE
5. Mittal J
6. Feig M
7. Mackerell AD
(2012) Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles
Journal of Chemical Theory and Computation 8:3257–3273.

https://doi.org/10.1021/ct300400x
- PubMed
- Google Scholar
(2016) Atomic-resolution dissection of the energetics and mechanism of isomerization of hydrated ATP-Mg²⁺ through the SOMA string method
Journal of Computational Chemistry 37:575–586.

https://doi.org/10.1002/jcc.23991
- PubMed
- Google Scholar
(1995) A P2X purinoceptor expressed by a subset of sensory neurons
Nature 377:428–431.

https://doi.org/10.1038/377428a0
- PubMed
- Google Scholar
1. Cockayne DA
2. Hamilton SG
3. Zhu QM
4. Dunn PM
5. Zhong Y
6. Novakovic S
7. Malmberg AB
8. Cain G
9. Berson A
10. Kassotakis L
11. Hedley L
12. Lachnit WG
13. Burnstock G
14. McMahon SB
15. Ford AP
(2000) Urinary bladder hyporeflexia and reduced pain-related behaviour in P2X3-deficient mice
Nature 407:1011–1015.

https://doi.org/10.1038/35039519
- PubMed
- Google Scholar
1. Cohn M
2. Hughes TR
(1962)
Nuclear magnetic resonance spectra of Adenosine di- and triphosphate. II. effect of complexing with divalent metal ions

The Journal of Biological Chemistry 237:176–181.
- PubMed
- Google Scholar
(1997) Distinct ATP receptors on pain-sensing and stretch-sensing neurons
Nature 387:505–508.

https://doi.org/10.1038/387505a0
- PubMed
- Google Scholar
(1998) A memory for extracellular Ca2+ by speeding recovery of P2X receptors from desensitization
The Journal of Neuroscience 18:9238–9244.

https://doi.org/10.1523/jneurosci.18-22-09238.1998
- PubMed
- Google Scholar
1. Cook SP
2. McCleskey EW
(1997) Desensitization, recovery and ca(2+)-dependent modulation of ATP-gated P2X receptors in nociceptors
Neuropharmacology 36:1303–1308.

https://doi.org/10.1016/S0028-3908(97)00132-9
- PubMed
- Google Scholar
(2015) P2X3 receptors mediate visceral hypersensitivity during acute chemically-induced colitis and in the post-inflammatory phase via different mechanisms of sensitization
PLOS ONE 10:e0123810.

https://doi.org/10.1371/journal.pone.0123810
- PubMed
- Google Scholar
1. Emsley P
2. Cowtan K
(2004) Coot: model-building tools for molecular graphics
Acta Crystallographica. Section D, Biological Crystallography 60:2126–2132.

https://doi.org/10.1107/S0907444904019158
- PubMed
- Google Scholar
1. Finger TE
2. Danilova V
3. Barrows J
4. Bartel DL
5. Vigers AJ
6. Stone L
7. Hellekant G
8. Kinnamon SC
(2005) ATP signaling is crucial for communication from taste buds to gustatory nerves
Science 310:1495–1499.

https://doi.org/10.1126/science.1118435
- PubMed
- Google Scholar
1. Ford AP
2. Undem BJ
3. Birder LA
4. Grundy D
5. Pijacka W
6. Paton JF
(2015) P2X3 receptors and sensitization of autonomic reflexes
Autonomic Neuroscience 191:16–24.

https://doi.org/10.1016/j.autneu.2015.04.005
- PubMed
- Google Scholar
1. Ford AP
2. Undem BJ
(2013) The therapeutic promise of ATP antagonism at P2X3 receptors in respiratory and urological disorders
Frontiers in Cellular Neuroscience 7:267.

https://doi.org/10.3389/fncel.2013.00267
- PubMed
- Google Scholar
1. Gerevich Z
2. Zadori ZS
3. Köles L
4. Kopp L
5. Milius D
6. Wirkner K
7. Gyires K
8. Illes P
(2007) Dual effect of acid pH on purinergic P2X3 receptors depends on the histidine 206 residue
Journal of Biological Chemistry 282:33949–33957.

https://doi.org/10.1074/jbc.M705840200
- PubMed
- Google Scholar
(2003) Modulation of P2X3 receptors by Mg2+ on rat DRG neurons in culture
Neuropharmacology 44:132–140.

https://doi.org/10.1016/S0028-3908(02)00338-6
- PubMed
- Google Scholar
1. Giniatullin R
2. Nistri A
(2013) Desensitization properties of P2X3 receptors shaping pain signaling
Frontiers in Cellular Neuroscience 7:245.

https://doi.org/10.3389/fncel.2013.00245
- PubMed
- Google Scholar
1. Ginnetti AT
2. Paone DV
3. Stauffer SR
4. Potteiger CM
5. Shaw AW
6. Deng J
7. Mulhearn JJ
8. Nguyen DN
9. Segerdell C
10. Anquandah J
11. Calamari A
12. Cheng G
13. Leitl MD
14. Liang A
15. Moore E
16. Panigel J
17. Urban M
18. Wang J
19. Fillgrove K
20. Tang C
21. Cook S
22. Kane S
23. Salvatore CA
24. Graham SL
25. Burgey CS
(2018) Identification of second-generation P2X3 antagonists for treatment of pain
Bioorganic & Medicinal Chemistry Letters 28:1392–1396.

https://doi.org/10.1016/j.bmcl.2018.02.039
- PubMed
- Google Scholar
1. Hansen RR
2. Nasser A
3. Falk S
4. Baldvinsson SB
5. Ohlsson PH
6. Bahl JM
7. Jarvis MF
8. Ding M
9. Heegaard AM
(2012) Chronic administration of the selective P2X3, P2X2/3 receptor antagonist, A-317491, transiently attenuates cancer-induced bone pain in mice
European Journal of Pharmacology 688:27–34.

https://doi.org/10.1016/j.ejphar.2012.05.008
- PubMed
- Google Scholar
1. Hattori M
2. Gouaux E
(2012) Molecular mechanism of ATP binding and ion channel activation in P2X receptors
Nature 485:207–212.

https://doi.org/10.1038/nature11010
- PubMed
- Google Scholar
(2014) A hydrophobic residue in position 15 of the rP2X3 receptor slows desensitization and reveals properties beneficial for pharmacological analysis and high-throughput screening
Neuropharmacology 79:603–615.

https://doi.org/10.1016/j.neuropharm.2014.01.010
- PubMed
- Google Scholar
1. Huang YA
2. Stone LM
3. Pereira E
4. Yang R
5. Kinnamon JC
6. Dvoryanchikov G
7. Chaudhari N
8. Finger TE
9. Kinnamon SC
10. Roper SD
(2011) Knocking out P2X receptors reduces transmitter secretion in taste buds
Journal of Neuroscience 31:13654–13661.

https://doi.org/10.1523/JNEUROSCI.3356-11.2011
- PubMed
- Google Scholar
1. Jarvis MF
2. Burgard EC
3. McGaraughty S
4. Honore P
5. Lynch K
6. Brennan TJ
7. Subieta A
8. Van Biesen T
9. Cartmell J
10. Bianchi B
11. Niforatos W
12. Kage K
13. Yu H
14. Mikusa J
15. Wismer CT
16. Zhu CZ
17. Chu K
18. Lee CH
19. Stewart AO
20. Polakowski J
21. Cox BF
22. Kowaluk E
23. Williams M
24. Sullivan J
25. Faltynek C
(2002) A-317491, a novel potent and selective non-nucleotide antagonist of P2X3 and P2X2/3 receptors, reduces chronic inflammatory and neuropathic pain in the rat
PNAS 99:17179–17184.

https://doi.org/10.1073/pnas.252537299
- PubMed
- Google Scholar
1. Jo S
2. Jiang W
(2015) A generic implementation of replica exchange with solute tempering (REST2) algorithm in NAMD for complex biophysical simulations
Computer Physics Communications 197:304–311.

https://doi.org/10.1016/j.cpc.2015.08.030
- Google Scholar
1. Kabsch W
(2010) XDS
Acta Crystallographica. Section D, Biological Crystallography 66:125–132.

https://doi.org/10.1107/S0907444909047337
- PubMed
- Google Scholar
(2003) Mechanisms of release of nucleotides and integration of their action as P2X- and P2Y-receptor activating molecules
Molecular Pharmacology 64:785–795.

https://doi.org/10.1124/mol.64.4.785
- PubMed
- Google Scholar
1. Li M
2. Chang TH
3. Silberberg SD
4. Swartz KJ
(2008) Gating the pore of P2X receptor channels
Nature Neuroscience 11:883–887.

https://doi.org/10.1038/nn.2151
- PubMed
- Google Scholar
(2013) Subtype-specific control of P2X receptor channel signaling by ATP and ^Mg2+
PNAS 110:E3455–E3463.

https://doi.org/10.1073/pnas.1308088110
- PubMed
- Google Scholar
1. Liu P
2. Kim B
3. Friesner RA
4. Berne BJ
(2005) Replica exchange with solute tempering: a method for sampling biological systems in explicit water
PNAS 102:13749–13754.

https://doi.org/10.1073/pnas.0506346102
- PubMed
- Google Scholar
(2016) X-ray structures define human P2X(3) receptor gating cycle and antagonist action
Nature 538:66–71.

https://doi.org/10.1038/nature19367
- PubMed
- Google Scholar
1. North RA
(2003)
The P2X3 subunit: a molecular target in pain therapeutics

Current Opinion in Investigational Drugs 4:833–840.
- PubMed
- Google Scholar
1. North RA
(2004) P2X3 receptors and peripheral pain mechanisms
The Journal of Physiology 554:301–308.

https://doi.org/10.1113/jphysiol.2003.048587
- PubMed
- Google Scholar
1. Phillips JC
2. Braun R
3. Wang W
4. Gumbart J
5. Tajkhorshid E
6. Villa E
7. Chipot C
8. Skeel RD
9. Kalé L
10. Schulten K
(2005) Scalable molecular dynamics with NAMD
Journal of Computational Chemistry 26:1781–1802.

https://doi.org/10.1002/jcc.20289
- Google Scholar
1. Rettinger J
2. Schmalzing G
(2004) Desensitization masks nanomolar potency of ATP for the P2X1 receptor
The Journal of Biological Chemistry 279:6426–6433.

https://doi.org/10.1074/jbc.M306987200
- PubMed
- Google Scholar
(2006) Experimental and modeling studies of desensitization of P2X3 receptors
Molecular Pharmacology 70:373–382.

https://doi.org/10.1124/mol.106.023564
- PubMed
- Google Scholar
1. Souslova V
2. Cesare P
3. Ding Y
4. Akopian AN
5. Stanfa L
6. Suzuki R
7. Carpenter K
8. Dickenson A
9. Boyce S
10. Hill R
11. Nebenuis-Oosthuizen D
12. Smith AJ
13. Kidd EJ
14. Wood JN
(2000) Warm-coding deficits and aberrant inflammatory pain in mice lacking P2X3 receptors
Nature 407:1015–1017.

https://doi.org/10.1038/35039526
- PubMed
- Google Scholar
1. Vandenbeuch A
2. Larson ED
3. Anderson CB
4. Smith SA
5. Ford AP
6. Finger TE
7. Kinnamon SC
(2015) Postsynaptic P2X3-containing receptors in gustatory nerve fibres mediate responses to all taste qualities in mice
The Journal of Physiology 593:1113–1125.

https://doi.org/10.1113/jphysiol.2014.281014
- PubMed
- Google Scholar
1. Vlaskovska M
2. Kasakov L
3. Rong W
4. Bodin P
5. Bardini M
6. Cockayne DA
7. Ford AP
8. Burnstock G
(2001) P2X3 knock-out mice reveal a major sensory role for urothelially released ATP
The Journal of Neuroscience 21:5670–5677.

https://doi.org/10.1523/jneurosci.21-15-05670.2001
- PubMed
- Google Scholar
1. Wang J
2. Wang Y
3. Cui WW
4. Huang Y
5. Yang Y
6. Liu Y
7. Zhao WS
8. Cheng XY
9. Sun WS
10. Cao P
11. Zhu MX
12. Wang R
13. Hattori M
14. Yu Y
(2018) Druggable negative allosteric site of P2X3 receptors
PNAS 115:4939–4944.

https://doi.org/10.1073/pnas.1800907115
- PubMed
- Google Scholar
(1999) Modulatory activity of extracellular H+ and Zn2+ on ATP-responses at rP2X1 and rP2X3 receptors
British Journal of Pharmacology 128:486–492.

https://doi.org/10.1038/sj.bjp.0702802
- PubMed
- Google Scholar

Article and author information

Author details

Mufeng Li

Molecular Physiology and Biophysics Section, Porter Neuroscience Research Center, National Institute of Neurological Disorders and Stroke, National Institutes of Health, Bethesda, United States

Contribution
Conceptualization, Data curation, Formal analysis, Validation, Investigation, Visualization, Writing—original draft

Competing interests
No competing interests declared
Yao Wang

State Key Laboratory of Genetic Engineering, Collaborative Innovation Center of Genetics and Development, Multiscale Research Institute for Complex Systems, Department of Physiology and Biophysics, School of Life Sciences, Fudan University, Shanghai, China

Contribution
Data curation, Formal analysis, Validation, Investigation

Competing interests
No competing interests declared
Rahul Banerjee

Theoretical Molecular Biophysics Laboratory, National Heart, Lung and Blood Institute, National Institutes of Health, Bethesda, United States

Contribution
Data curation, Formal analysis, Validation, Investigation

Competing interests
No competing interests declared
Fabrizio Marinelli

Theoretical Molecular Biophysics Laboratory, National Heart, Lung and Blood Institute, National Institutes of Health, Bethesda, United States

Contribution
Data curation, Formal analysis, Validation, Investigation

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0044-6718
Shai Silberberg

Molecular Physiology and Biophysics Section, Porter Neuroscience Research Center, National Institute of Neurological Disorders and Stroke, National Institutes of Health, Bethesda, United States

Contribution
Conceptualization, Investigation

Competing interests
No competing interests declared
José D Faraldo-Gómez

Theoretical Molecular Biophysics Laboratory, National Heart, Lung and Blood Institute, National Institutes of Health, Bethesda, United States

Contribution
Conceptualization, Formal Analysis, Investigation, Visualization, Supervision, Funding acquisition, Writing—original draft, Writing—review and editing

For correspondence
jose.faraldo@nih.gov

Competing interests
Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0001-7224-7676
Motoyuki Hattori

State Key Laboratory of Genetic Engineering, Collaborative Innovation Center of Genetics and Development, Multiscale Research Institute for Complex Systems, Department of Physiology and Biophysics, School of Life Sciences, Fudan University, Shanghai, China

Contribution
Conceptualization, Data curation, Formal analysis, Supervision, Funding acquisition, Validation, Investigation, Visualization, Writing—original draft, Writing—review and editing

For correspondence
hattorim@fudan.edu.cn

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-5327-5337
Kenton Jon Swartz

Molecular Physiology and Biophysics Section, Porter Neuroscience Research Center, National Institute of Neurological Disorders and Stroke, National Institutes of Health, Bethesda, United States

Contribution
Conceptualization, Supervision, Funding acquisition, Investigation, Writing—original draft, Project administration, Writing—review and editing

For correspondence
swartzk@ninds.nih.gov

Competing interests
Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0003-3419-0765

Funding

National Institute of Neurological Disorders and Stroke

Kenton Jon Swartz

National Heart, Lung, and Blood Institute

José D Faraldo-Gómez

Key Technologies Research and Development Program

Motoyuki Hattori

National Natural Science Foundation of China

Motoyuki Hattori

State Key Laboratory of Genetic Engineering

Motoyuki Hattori

Office of Global Experts Recruitment in China

Motoyuki Hattori

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Mark Mayer, Miguel Holmgren and members of the Swartz, Faraldo-Gómez and Hattori laboratories for helpful discussions. We also thank Giacomo Fiorin for assistance with simulation and data analysis tools. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov). We thank the staff from BL41XU beamline at SPring-8 (Proposal Nos. 2017B2523 and 2018A2507), from BL19U1 beamline of National Facility for Protein Science Shanghai (NFPS) at Shanghai Synchrotron Radiation Facility (SSRF) (Proposal Nos. 2016-NFPS-PT-001047 and 2017-NFPS-PT-001191), and from BL17U1 at SSRF (Proposal Nos. 15ssrf02687 and 2016-SSRF-PT-005911), for assistance during data collection.

Copyright

This is an open-access article, free of all copyright, and may be freely reproduced, distributed, transmitted, modified, built upon, or otherwise used by anyone for any lawful purpose. The work is made available under the Creative Commons CC0 public domain dedication.