Evolution of asymmetric gamete signaling and suppressed recombination at the mating type locus

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: August 29, 2019 (This version)
Accepted: July 25, 2019
Received: May 7, 2019

1. Of interest
Task-dependent optimal representations for cerebellar learning

Marjorie Xie, Samuel P Muscinelli ... Ashok Litwin-Kumar

Research Article Sep 29, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The two partners required for sexual reproduction are rarely the same. This pattern extends to species which lack sexual dimorphism yet possess self-incompatible gametes determined at mating-type regions of suppressed recombination, likely precursors of sex chromosomes. Here we investigate the role of cellular signaling in the evolution of mating-types. We develop a model of ligand-receptor dynamics, and identify factors that determine the capacity of cells to send and receive signals. The model specifies conditions favoring the evolution of gametes producing ligand and receptor asymmetrically and shows how these are affected by recombination. When the recombination rate evolves, the conditions favoring asymmetric signaling also favor tight linkage of ligand and receptor loci in distinct linkage groups. These results suggest that selection for asymmetric gamete signaling could be the first step in the evolution of non-recombinant mating-type loci, paving the road for the evolution of anisogamy and sexes.

https://doi.org/10.7554/eLife.48239.001

eLife digest

Sexual reproduction, from birds to bees, relies on distinct classes of sex cells, known as gametes, fusing together. Most single cell organisms, rather than producing eggs and sperm, have similar sized gametes that fall into distinct ‘mating types’. However, only sex cells belonging to different mating types can fuse together and sexually reproduce.

At first glance, it seems illogical that cells from the same mating type cannot reproduce with each other, as this restricts eligible partners within a population and makes finding a mate more difficult. Yet the typical pattern amongst single cell organisms is still two distinct classes of sex cells, just as in birds and bees. How did the obsession with mating between two different types become favored during evolution?

One possibility is that cells with different mating types can recognize and communicate with each other more easily. Cells communicate by releasing proteins known as ligands, which bind to specific receptors found on the cell’s surface. Using mathematical modelling, Hadjivasiliou and Pomiankowski showed that natural selection typically favors ‘asymmetric’ signaling, whereby cells evolve to either produce receptor A with ligand B, or have the reverse pattern and produce receptor B with ligand A. These asymmetric mutants are favored because they avoid producing ligands that clog or activate the receptors on their own surface. As a result, different types of cells are better at recognizing each other and mating more quickly.

When cells sexually reproduce they exchange genetic material with each other to produce offspring with a combination of genes that differ to their own. However, if the genes coding for ligand and receptor pairs were constantly being ‘swapped’, this could lead to new combinations, and a loss of asymmetric signaling. Hadjivasiliou and Pomiankowski showed that for asymmetric signaling to evolve, natural selection favors the genes encoding these non-compatible ligand and receptor pairs to be closely linked within the genome. This ensures that the mis-matching ligand and receptor are inherited together, preventing cells from producing pairs which can bind to themselves.

This study provides an original way to address an evolutionary question which has long puzzled biologists. These findings raise further questions about how gametes evolved to become the sperm and egg, and how factors such as signaling between cells can determine the sex of more complex organisms, such as ourselves.

https://doi.org/10.7554/eLife.48239.002

Introduction

Sex requires the fusion of two cells. With few exceptions, the sexual process is asymmetric with partnering cells exhibiting genetic, physiological or behavioral differences. The origins of sexual asymmetry in eukaryotes trace back to unicellular organisms with isogametes lacking any size or mobility difference in the fusing cells (Parker et al., 1972; Bell, 1978; Charlesworth, 1978; Hoekstra, 1987; Randerson and Hurst, 2001; Lehtonen et al., 2016). Isogamous organisms are divided into genetically distinct mating types, determined by several mating type specific genes that reside in regions of suppressed recombination (Fraser et al., 2004; Ahmed et al., 2014; Branco et al., 2017; Branco et al., 2018). The morphologically identical gametes mate disassortatively, scarcely ever with members of the same mating type. It follows that only individuals of a different mating type are eligible mating partners. This arrangement poses a paradox as it restricts the pool of potential partners to those of a different mating type, introducing a major cost (Hoekstra, 1987).

Several hypotheses have been proposed to explain the evolution of isogamous mating types (Billiard et al., 2011; Billiard et al., 2012; Perrin, 2012). Mating types could serve as a restrictive mechanism preventing matings between related individuals thereby avoiding the deleterious consequences of inbreeding (Charlesworth and Charlesworth, 1979; Uyenoyama, 1988; Czárán and Hoekstra, 2004). Another idea is that mating types facilitate uniparental inheritance of mitochondria, which leads to improved contribution of the mitochondrial genome to cell fitness (Hastings, 1992; Hurst and Hamilton, 1992; Hutson and Law, 1993; Hurst, 1996; Hadjivasiliou et al., 2012; Hadjivasiliou et al., 2013; Christie et al., 2015; Christie and Beekman, 2017a). Both hypotheses have been studied extensively and offer compelling arguments. Nevertheless, the existence of several species where inbreeding (Billiard et al., 2011; Perrin, 2012) or biparental inheritance of mitochondria (Billiard et al., 2011; Wilson and Xu, 2012) are the rule but nonetheless maintain mating types, indicates that these ideas may not alone explain the evolution of mating types.

An alternative hypothesis is that mating types are determined by the molecular system regulating gamete interactions (Hoekstra, 1987; Hadjivasiliou et al., 2015; Hadjivasiliou and Pomiankowski, 2016). Such interactions dictate the success of mating by guiding partner attraction and recognition and the process of cell fusion, and have been shown to be more efficient when operating in an asymmetric manner (Hadjivasiliou et al., 2015). For example, diffusible molecules are often employed as signals that guide synchronous entry to gametogenesis or as chemoattractants (Tsubo, 1961; Maier, 1993; Kuhlmann et al., 1997; Merlini et al., 2013). Secreting and sensing the same diffusible molecule impedes the ability of cells to accurately detect external signals and makes partner finding many-fold slower (Hadjivasiliou et al., 2015). In addition, secreting and detecting the same molecule in cell colonies can prevent individuals responding to signals from others (Youk and Lim, 2014). Our previous review revealed that sexual signaling and communication in isogamous species are universally asymmetric (Hadjivasiliou and Pomiankowski, 2016). This applies throughout the sexual process from signals that lead to gametic differentiation, to attraction via diffusible pheromones and interactions via surface bound molecules during cell fusion (Hadjivasiliou and Pomiankowski, 2016).

In this work we take this analysis further by explicitly considering ligand-receptor interactions between and within cells. We directly follow the dynamics of ligand and receptor molecules that are surface bound and determine the conditions under which the formation of within cell ligand-receptor pairs impedes between cell communication. We use this framework to explore the evolution of gametic interactions and show that asymmetric signaling roles and tight linkage between receptor and ligand loci both evolve due to selection for intercellular communication and quick mating. Our findings demonstrate that the evolution of mating type loci with suppressed recombination can be traced back to the fundamental selection for asymmetric signaling during sex.

Theoretical set-up

Consider a population where cells encounter one another at random and can mate when in physical contact. Interactions between cells leading to successful mating are dictated by a ligand-receptor pair. Population wide effects may emerge if the ligand is highly diffusible (Youk and Lim, 2014; Hadjivasiliou et al., 2015). The employment of membrane bound ligands during sexual signaling is universal, whereas diffusible signals are not (Hadjivasiliou and Pomiankowski, 2016). In this work we therefore assume that the ligand-receptor interactions only operate locally. Receptors remain bound to the cell surface and ligands only undergo localized diffusion (Figure 1) as is the case in several yeast and other unicellular eukaryotes (Cappellaro et al., 1991; Wilson et al., 1999; Phadke and Zufall, 2009; Merlini et al., 2013). The following equations describe the concentration of free ligand $L$ , free receptor $R$ and bound ligand $L R$ within a single cell,

\frac{d [L]}{d t} = ν_{L} - k^{+} [R] [L] + k^{-} [L R] - γ_{L} [L],

\frac{d [R]}{d t} = ν_{R} - k^{+} [R] [L] + k^{-} [L R] - γ_{R} [R],

\frac{d [L R]}{d t} = k^{+} [R] [L] - k^{-} [L R] - γ_{L R} [L R] .

$ν_{L}$ and $ν_{R}$ describe the rate of production of the ligand and receptor respectively. $γ_{L}$ , $γ_{R}$ , and $γ_{L R}$ , are the degradation rate of the ligand, receptor and bound complex respectively. The terms $k^{+}$ and $k^{-}$ are the binding and unbinding rates that determine the affinity of the ligand to its receptor within a single cell. We can solve Equations (1-3) by setting the dynamics to zero to obtain the amount of free ligand, free receptor ( ${[L]}^{*}$ , ${[R]}^{*}$ ) and bound complex at steady state ( ${[L R]}^{*}$ ),

{[L]}^{*} = \frac{k^{+} γ_{L R} (ν_{L} - ν_{R}) - k^{-} γ_{L} γ_{R} - γ_{L} γ_{R} γ_{L R} + Δ}{2 k^{+} γ_{L} γ_{L R}}

{[R]}^{*} = \frac{k^{+} γ_{L R} (ν_{R} - ν_{L}) - k^{-} γ_{L} γ_{R} - γ_{L} γ_{R} γ_{L R} + Δ}{2 k^{+} γ_{R} γ_{L R}},

{[L R]}^{*} = \frac{k^{+} γ_{L R} (ν_{R} + ν_{L}) + k^{-} γ_{L} γ_{R} + γ_{L} γ_{R} γ_{L R} - Δ}{2 k^{+} γ_{L R}^{2}},

Where $Δ$ is given by,

Δ = \sqrt{{(k^{-} γ_{L} γ_{R} + γ_{L R} (γ_{L} γ_{R} + k^{+} γ_{L R} (ν_{R} + ν_{L})))}^{2} + 4 k^{+} γ_{L} γ_{R} γ_{L R} (k^{-} + γ_{L R}) ν_{R}} .

Figure 1

Download asset Open asset

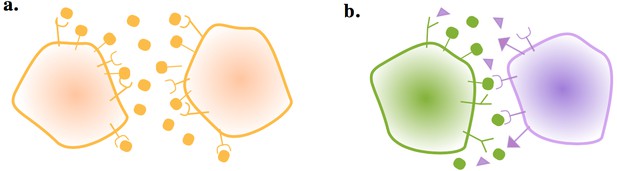
Gametes communicate through ligand and receptor molecules.

The ligand can be either membrane bound or released in the local environment. (a) When the interacting cells produce ligand and receptor symmetrically, the ligand will bind to receptors on its own membrane as well as those on the other cell. This may impair intercellular signaling. (b) Producing the ligand and receptor in an asymmetric manner resolves this issue.

https://doi.org/10.7554/eLife.48239.003

We assume that the rates of ligand and receptor production and degradation are associated to timescales that are much shorter than the timescale of interactions between cells. Hence the concentrations of $[L]$ , $[R]$ and $[L R]$ in individual cells will be at steady state when two cells meet. The likelihood of a successful mating between two cells depends not just on partner signaling levels but also on how accurately the cells can compute the signal produced by their partner. Binding of ligand and receptor originating from the same cell can obstruct this interaction. To capture this, we define the strength of the incoming signal for cell₁ when it interacts with cell₂ as,

W_{12} = k_{b} {[L_{2}]}^{*} {[R_{1}]}^{*} {(1 - \frac{{[L R_{1}]}^{*}}{{[L R_{1}]}^{*} + k_{b} {[L_{2}]}^{*} {[R_{1}]}^{*}})}^{n},

where subscripts denote concentrations in cell₁ and cell₂, and the parameter $k_{b}$ determines the affinity of the ligand and receptor between cells. If $k_{b}$ is the same as the affinity of receptor and ligand within cells, then $k_{b} = \frac{k^{+}}{k^{-}}$ . We also consider cases where $k_{b} \neq \frac{k^{+}}{k^{-}}$ , for example, when ligand interacts differently with receptors on the same as opposed to a different cell (LeBon et al., 2014; Hadjivasiliou et al., 2016a).

The cost of self-signaling is determined by $n$ . When $n = 0$ , $W_{12}$ reduces to $k_{b} {[R_{1}]}^{*} {[L_{2}]}^{*}$ with the incoming signal dependent on the concentration of ligand produced by cell₂ and receptor produced by cell₁. This corresponds to a case where self-binding does not lead to activation but only causes an indirect cost through the depletion of available ligand and receptor molecules. When $n \geq 1$ , binding within a cell leads to some form of activation that interferes with between cell signaling, imposing a cost in evaluating the incoming signal. Higher values for $n$ correspond to more severe costs due to self-binding.

The likelihood that two cells successfully mate ( $P$ ) depends on the quality of their interaction given by,

P = \frac{W_{12} W_{21}}{K + W_{12} W_{21}} .

Equation (9) transforms the signaling interaction into a mating probability. For the analysis that follows, we choose large values of $K$ so that $P$ is far from saturation and depends almost linearly on the product $W_{12} W_{21}$ . In summary, the probability that two cells mate is defined by the production and degradation rates of the ligand and receptor molecules, and the binding affinities between and within cells.

Evolutionary model

To explore the evolution of signaling roles, we simplify the model by assuming that the degradation rates $γ_{L,} γ_{R,} γ_{L R}$ are constant and equal to $γ$ , and investigate mutations that quantitatively modify the ligand and receptor production rates. We consider a finite population of $N$ haploid cells and set $N = 1000$ throughout the analysis unless otherwise stated. Ligand and receptor production are controlled by independent loci with infinite alleles (Tajima, 1996). The ligand and receptor production rates of cell_i is denoted by $(ν_{L_{i}}, ν_{R_{i}})$ . We also consider different versions of the ligand and its receptor. Cells have two ligand-receptor pairs, $(L, R)$ and $(l, r)$ which are mutually incompatible, so the binding affinity is zero between $l$ and $R$ , and between $L$ and $r$ . Each cell has a $(L, R)$ and $(l, r)$ state, which are subject to mutational and evolutionary pressure as described below. $W_{12}$ is re-defined as the summation of the interactions of these two ligand-receptor pairs,

W_{12} = k_{b} {[L_{2}]}^{*} {[R_{1}]}^{*} {(1 - \frac{{[L R_{1}]}^{*}}{{[L R_{1}]}^{*} + k_{b} {[L_{2}]}^{*} {[R_{1}]}^{*}})}^{n} + k_{b} {[l_{2}]}^{*} {[r_{1}]}^{*} {(1 - \frac{{[l r_{1}]}^{*}}{{[l r_{1}]}^{*} + k_{b} {[l_{2}]}^{*} {[r_{1}]}^{*}})}^{n} .

Again for the sake of simplicity, the ligand-receptor affinities are set to be the same between and within cells for each ligand-receptor pair (i.e. $k^{+}$ , $k^{-}$ and $k_{b}$ are the same for $L - R$ and $l - r$ interactions). A cell undergoes recurrent mutation that changes the production rate for the ligand $L$ so that $ν_{L_{i}}^{^{'}} = ν_{L_{i}} + ϵ$ with $ϵ \sim N (0, σ)$ with probability μ. The same mutational process occurs for all ligand and receptor production rates. We assume that mutation occurs independently at different loci and that there is a maximum capacity for ligand and receptor production, so that $ν_{L} + ν_{l} < 1$ and $ν_{R} + ν_{r} < 1$ . It follows that the production rates of the two ligand genes are not independent of one another and similarly for the two receptor genes.

We also consider cases where $ν_{L} + ν_{l} < α$ and $ν_{R} + ν_{r} < α$ for $α \neq 1$ to reflect the relative synergy ( $α > 1$ ) or relative competition ( $α < 1$ ) between the production of the two ligands (or receptors). For example, synergy between two ligands (or receptors) could reflect reduced energy expenditure for the cell if the same machinery is used to produce the two molecules. Competition on the other hand could reflect additional costs due to the production of two different ligands (or receptors).

Selection on ligand-receptor production rates is governed by the likelihood that cells pair and produce offspring. We assume that cells enter the sexual phase of their life cycle in synchrony, as is the case in the majority of unicellular eukaryotes (Hadjivasiliou and Pomiankowski, 2016). Pairs of cells are randomly sampled (to reflect random encounters) and mate with probability $P$ defined in Equation (9). Cells failing to mate are returned to the pool of unmated individuals. The process is repeated until $M$ cells have mated, giving rise to $M / 2$ mated pairs (we set $M < N$ , so only some cells mate). Each mated pair produces 2 haploid offspring so the population size shrinks from $N$ to $M$ . The population size is restored back to $N$ by sampling with replacement. It follows that Equations (9) and (10) together provide a proxy for fitness according to the ligand and receptor production rates of individual cells. Initially, recombination is not allowed between the genes controlling ligand and receptor production but then is considered in a later section.

Results

Dependence of gamete interactions on physical parameters

The strength of an incoming signal $W_{12}$ depends on the concentration of free receptor in cell₁ and free ligand in cell₂, and the cost of self-binding ( $n$ ) (Equation (10)). The steady state concentration of $[L]$ , $[R]$ and $[L R]$ are governed by different production rates (Figure 2—figure supplement 1; details of the derivation can be found in the Materials and methods section). For low degradation rates ( $γ$ small), the removal of available molecules is dominated by self-binding ( $k^{+}$ ) (Equations (1) and (2) and Figure 2a,b). At the same time, a lower degradation rate leads to higher levels of ligand and receptor (Figure 2a) even if the relative drop of free ligand and receptor is steeper as $k^{+}$ increases (Figure 2b). As a consequence, the ability of a cell to generate a strong signal and read incoming signals can change drastically when the pair of interacting cells produce the ligand and receptor in a symmetric manner (e.g. $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ for both cells) rather than in an asymmetric manner (e.g. $(ν_{L_{1}}, ν_{R_{1}}, ν_{l_{1}}, ν_{r_{1}}) = (1, 0, 0, 1)$ and $(ν_{L_{2}}, ν_{R_{2}}, ν_{l_{2}}, ν_{r_{2}}) = (0, 1, 1, 0)$ ). The fold-increase in $W_{12}$ is large even when self-binding confers no cost $(n = 0)$ , while larger values for $n$ ramp up the costs (Figure 2c). If cells produce the ligand and receptor asymmetrically, self-binding ceases to be a problem in receiving incoming signals.

Figure 2 with 1 supplement see all

Download asset Open asset

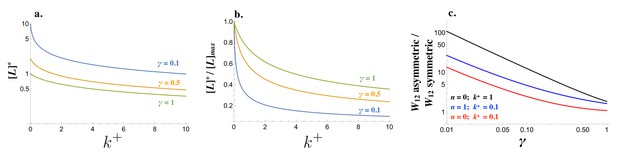
Signaling interactions between mating cells can be severely impaired due to ligand-receptor interactions in the same cell.

(a) The amount of free ligand in individual cells at steady state ${[L]}^{*}$ and (b) normalized amount of free ligand at steady state ${[L]}^{*} / {[L]}_{m a x}$ varies with the intracellular binding rate $k^{+}$ and degradation rate $γ$ . (c) The relative amount of incoming signal $W_{12}$ for a cell that produces ligand and receptor asymmetrically versus symmetrically decreases with the degradation rate $γ$ and values of intracellular binding $k^{+}$ . Other parameters used: $n = 1, k^{-} = 1, k_{b} = 1$ .

https://doi.org/10.7554/eLife.48239.004

Although the strength of the signaling interaction between two cells ( $W_{12} W_{21}$ ) may improve when the interacting cells produce the ligand and receptor asymmetrically, this need not be the case. Consider the interaction of a resident cell with production rates ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1, 1, 0, 0)$ with itself and a mutant cell with production rates given by ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (1 - d x, 1 - d y, d x, d y)$ . For all values of $d x$ and $d y$ , ${[W_{12} W_{21}]}_{r e s + m u t} - {[W_{12} W_{21}]}_{r e s + r e s}$ < 0 (Figure 3a). It follows that $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ cannot be invaded by any single mutant.

Figure 3

Download asset Open asset

Fitness advantage of rare mutations conferring signaling asymmetry.

The fitness of a rare mutant is plotted relative to the resident ${[W_{12} W_{21}]}_{r e s + m u t} - {[W_{12} W_{21}]}_{r e s + r e s}$ . The production rate of the mutant cell is $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) {}_{m u t}= (1 - d x, 1 - d y, d x, d y)$ , where $d x$ and $d y$ are plotted on the $x$ and $y$ axes respectively. The resident production rate $(ν_{L}, ν_{R}, ν_{l}, ν_{r})_{r e s}$ is shown as a red dot and varies (a) ${(1, 1, 0, 0)}_{r e s}$ , (b) ${(1, 0.9, 0, 0.1)}_{r e s}$ , (c) ${(0.5, 0.5, 0.5, 0.5)}_{r e s}$ and (d) ${(1, 0, 0, 1)}_{r e s}$ . The mutant ( $d x, d y$ ) with maximum fitness is shown as a black dot. The contour where ${[W_{12} W_{21}]}_{r e s + m u t} = {[W_{12} W_{21}]}_{r e s + r e s}$ is marked by a black dashed line (**b and c**). The fitness difference is always negative in (a) and always positive in (d). Other parameters used: $n = 1, γ = 0.5, k^{+} = 1, k^{-} = 1, k_{b} = 1$ .

https://doi.org/10.7554/eLife.48239.006

However, if the resident is already slightly asymmetric, for example ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1, 0.9, 0, 0.1)$ , then a mutant conferring an asymmetry in the opposite direction can be better at interacting with the resident (Figure 3b). When the resident produces both ligand and receptor equally (e.g. ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (0.5, 0.5, 0.5, 0.5)$ ; Figure 3c), then most mutants conferring an asymmetry in either ligand or receptor production are favored. The strongest interaction occurs with mutants that produce the ligand or receptor fully asymmetrically (i.e. ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (1, 0, 0, 1)$ or $(0, 1, 1, 0)$ ; (Figure 3c)). Finally, when the resident production rates are already strongly asymmetric given by ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1, 0, 0, 1)$ , a mutant with an asymmetry in the opposite direction is most strongly favored (Figure 3d). Note that a population composed only of cells with production rates at ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1, 0, 0, 1)$ is not viable since the probability that two such cells mate is zero. However, this analysis provides insight about how asymmetry in signaling evolves.

Evolution of mating types with asymmetric signaling roles

To explore the evolution of signaling asymmetry, we follow mutations that alter the relative production of two mutually incompatible types of ligand and receptor ( $L, R$ ) and ( $l, r$ ). To ease understanding, the population symmetry $s$ in the production of ligand and receptor is measured,

s = 1 - \frac{1}{2 N} \sum_{i = 1}^{N} (| ν_{L_{i}} - ν_{R_{i}} | + | ν_{l_{i}} - ν_{r_{i}} |) .

The population is symmetric ( $s = 1$ ) if cells produce ligand and receptor equally, for both types (i.e. $(ν_{R}, ν_{L}, ν_{r}, ν_{l}) = (a, a, 1 - a, 1 - a)$ , for constant $a$ ), and fully asymmetric ( $s = 0$ ) when cells adopt polarized roles (i.e. $(ν_{L}, ν_{R}, ν_{l}, ν_{r})$ = $(1, 0, 0, 1)$ and $(0, 1, 1, 0)$ ).

Starting from a population where all cells are symmetric producers of only one ligand and receptor, $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ , the population evolves to one of two equilibria (Figure 4a). $E_{1}$ where $s^{*} \approx 1$ and all cells produce the ligand and receptor symmetrically $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) \approx (1, 1, 0, 0)$ or $E_{2}$ where $s^{*} \approx 0$ and the population is divided into ligand and receptor producing cells, with equal frequencies of $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) \approx (1, 0, 0, 1)$ and $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) \approx (0, 1, 1, 0)$ (Figure 4b,c). Equilibria with intermediate values of $s^{*}$ are not found. The exact production rates at $E_{1}$ and $E_{2}$ exhibit some degree of noise due to mutation and finite population size (Figure 4b,c). At $E_{2}$ , individual cells with high $ν_{R}$ (and low $ν_{r}$ ) have low $ν_{L}$ (and high $ν_{l}$ ), confirming that $s^{*} \approx 0$ captures a fully asymmetric steady state (Figure 4b,c).

Figure 4 with 2 supplements see all

Download asset Open asset

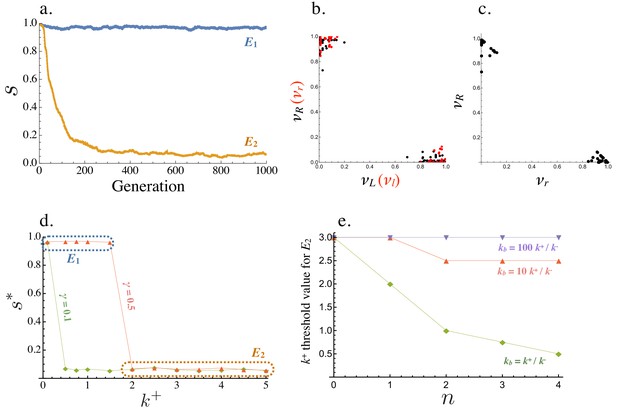
Evolution of asymmetric signaling.

(a) An example of evolution to the two signaling equilibria, $E_{1}$ ( $s = 1$ full symmetry when $k^{+} = 1$ ) and $E_{2} (s = 0$ full asymmetry when $k^{+} = 5$ ). (b) Production rates of individual cells in the population for the receptor-ligand pairs $L - R$ (black) and $l - r$ (red) at $E_{2}$ . (c) Production rates of individual cells for the two receptor types $R$ and $r$ at $E_{2}$ . (d) Steady state signaling symmetry $s^{*}$ against the intracellular binding rate ( $k^{+}$ ) for different degradation rates ( $γ$ ). (e) Threshold value of $k^{+}$ , beyond which $E_{2}$ evolves from $E_{1}$ , plotted versus the cost of self-binding ( $n$ ). The relationship is shown for different values of strength of between cell signaling ( $k_{b}$ ) relative to strength of within cell signaling ( $k^{+} / k^{-}$ ). Other parameters used in numerical simulations are given in the Supplemental Material.

https://doi.org/10.7554/eLife.48239.007

Whether $E_{2}$ is reached from $E_{1}$ depends on key parameters that determine the strength of self-binding and signaling interactions between cells. $E_{1}$ persists and no asymmetry evolves when $k^{+}$ (the intracellular ligand-receptor binding coefficient) is small (Figure 4d). In this case, the concentration of self-bound ligand-receptor complex is small (Equation (6)) and there is little cost of self-signaling (Equation (8)), so there is weak selection in favor of asymmetry. When the population is at $E_{1}$ , asymmetric mutants are slightly deleterious on their own (Figure 3a). They are therefore more likely to be lost when $k^{+}$ is small and selection for asymmetric signaling is weak (Figure 4d). The opposite is true for larger values of $k^{+}$ , as self-binding now dominates and restricts between cell signaling, promoting the evolution of asymmetry (Figure 4d). The transition from $E_{1}$ to $E_{2}$ occurs at a smaller value of $k^{+}$ when the degradation rate ( $γ$ ) is decreased (Figure 4d), as the effective removal of free ligand and receptor depends more strongly on intercellular binding (Figure 2a,b). Furthermore, the mutation rate affects the value of $k^{+}$ at which the transition from $E_{1}$ to $E_{2}$ occurs. The transition from $E_{1}$ to $E_{2}$ when mutation rates are smaller occurs at larger $k^{+}$ (Figure 4—figure supplement 1). We further explore the role of the mutational process below.

Another important consideration is the relative strength of signaling within and between cells, given by $k^{+} / k^{-}$ and $k_{b}$ respectively. For example, the threshold value of the within cell binding rate beyond which symmetric signaling ( $E_{1}$ ) evolves to asymmetric signaling ( $E_{2}$ , Figure 4a) increases when $k_{b}$ becomes much larger than $k^{+} / k^{-}$ (Figure 4e). Furthermore, this threshold value is smaller for larger values of $n$ indicating that asymmetric signaling is more likely to evolve when the cost for self-signaling is higher (larger $n$ , Figure 4e). However, asymmetric signaling can evolve even when self-binding carries no cost $(n = 0)$ as high rates of self-binding can restrict the number of ligand and receptor molecules free for between cell interactions (Figure 4e).

We also wondered how the relative synergy or competition between the two ligands (or receptors) could affect our results. When the two ligands (or receptors) exhibit synergy so that $ν_{L} + ν_{l} < α$ and $ν_{R} + ν_{r} < α$ for $α > 1$ , a signaling asymmetry evolves more easily (for smaller values of $k^{+}$ , Figure 4—figure supplement 2). Now the second ligand (or receptor) begins to evolve without imposing a cost on the preexisting ligand (or receptor) and can therefore remain present in the population longer until an asymmetry in the opposite direction evolves in other cells. The reverse dynamics are observed when the two ligands (or receptors) compete with one another ( $ν_{L} + ν_{l} < α$ and $ν_{R} + ν_{r} < α$ for $α < 1$ ) (Figure 4—figure supplement 2).

The observations above suggest that both $E_{1}$ and $E_{2}$ are evolutionary stable states and the transition from $E_{1}$ to $E_{2}$ depends on the mutational process, drift and the parameters that determine signaling interactions. To explore this we investigated the stability of $E_{1}$ in response to rare mutations in the receptor and ligand production rates. We assume the population is initially at $E_{1}$ (i.e. $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ ), introduce mutations in the receptor and ligand loci $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1 - d x, 1, d x, 0)$ and $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1 - d y, 0, d y)$ at frequency $p$ , and calculate the population symmetry at steady state for different values of $d x$ and $d y$ (Figure 5). Single mutations never spread (i.e. if $d x = 0$ no value of $d y$ allows mutants to spread and vice versa). This is in agreement with the analytical predictions presented in the previous section (Figure 3a). When both $d x$ and $d y$ are nonzero the population may evolve to $E_{2}$ , where the two mutants reach equal frequencies at ~0.5 and replace the resident. The basin of attraction for $E_{2}$ (and so asymmetric signaling roles) is larger when $k^{+}$ and $p$ are high and $γ$ is small (Figure 5a–d), as predicted analytically (Figures 2 and 3) and in accordance with our findings when mutations were continuous (Figure 4).

Figure 5

Download asset Open asset

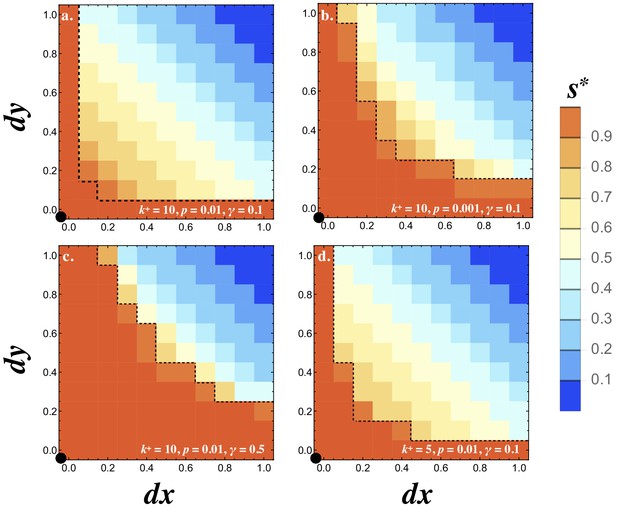
Invasion of $E_{1}$ .

Contour plots showing the steady state degree of symmetry ( $s^{*}$ ) in a population with resident $(ν_{R}, ν_{L}, ν_{r}, ν_{l}) = (1, 1, 0, 0)$ . Two mutations are introduced $(1 - d x, 1, d x, 0)$ and $(1, 1 - d y, 0, d y)$ at frequency $p$ and their fate is followed until they reach a stable frequency. No recurrent mutation is assumed. Orange contours inside the dotted line show the region where both mutants are eliminated and the resident persists ( $s^{*} = 1$ ). All other colors indicate that the two mutants spread to equal frequency $0.5$ displacing the resident ( $s^{*} < 1$ ). The degree of signaling symmetry at equilibrium is dictated by the magnitude of the mutations given by $d x$ and $d y$ . The different panels show (a) between cell signaling $k^{+} = 10$ , mutation frequency $p = 0.01$ and degradation rate $γ = 0.1$ , (b) lower mutation frequency $p = 0.001$ , (c) high degradation rate $γ = 0.5$ and (d) weaker between cell signaling $k^{+} = 5$ . The resident type is marked by a black dot at the origin. The frequency of the resident and two mutants at steady state was recorded and the heat maps show the average steady state value of $s^{*}$ for 20 independent repeats and the population size $N = 10000$ . Other parameters used and simulation details are given in the Supplementary Material.

https://doi.org/10.7554/eLife.48239.010

Note that the initial mutation frequency ( $p$ ) matters in our system. Single mutations are slightly deleterious on their own as predicted analytically (Figure 3a) and seen here when $d x = 0$ or $d y = 0$ (Figure 5). The two mutants, however, can be favored when they are asymmetric in opposite directions (i.e. $d x > 0$ and $d y > 0$ ; Figure 5). When mutants are introduced at a lower frequency (compare Figure 5a–b), the probability that they meet one another before they are lost by drift increases. This explains why smaller values of $p$ result in narrower basins of attraction for $E_{2}$ (Figure 5a–b).

We next investigated how mutations invade when the resident already signals asymmetrically (i.e. produces both ligands). The resident was set to ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1 - d x, 1, d x, 0)$ and a mutant able to produce both receptors ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (1, 1 - d y, 0, d y)$ was introduced. If $d x > 0$ , a mutant conveying a small asymmetry in receptor production (i.e. $d y > 0$ ) increases in frequency until the population reaches a polymorphic state with the resident and mutant at 50% (Figure 6a). If $d x > 0$ but the mutant only produces one receptor (i.e. $d y = 0$ ), the mutant invades, reaching a low frequency when $d x$ is small and replaces the resident when $d x$ is large. It follows that an asymmetry in both ligand and receptor production is necessary for the evolution of a signaling asymmetry as predicted analytically (Figure 3a).

Figure 6

Download asset Open asset

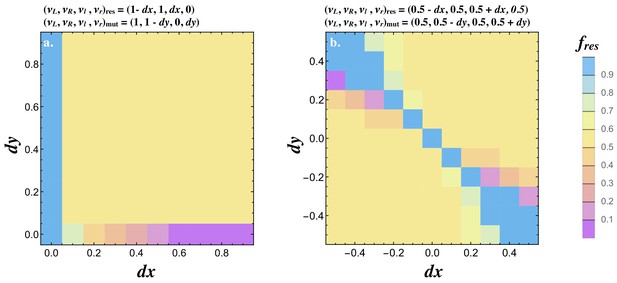
Joint evolution of receptor and ligand asymmetry.

Contour plots show the equilibrium frequency of the resident ( $f_{r e s}$ ) following the introduction of a mutatant when (a) $(ν_{L}, ν_{R}, ν_{l}, ν_{r})_{r e s} = (1 - d x, 1, d x, 0)$ and, ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (1, 1 - d y, 0, d y)$ , and (b) $(ν_{L}, ν_{R}, ν_{l}, ν_{r})_{r e s} = (0.5 - d x, 0.5, 0.5 + d x, 0.5)$ and $(ν_{L}, ν_{R}, ν_{l}, ν r)_{m u t} = (0.5, 0.5 - d y, 0.5, 0.5 + d y)$ . The mutant is introduced at a frequency $p = 0.01$ and no recurrent mutation is assumed. Other parameters used and simulation details are given in the Supplemental Material.

https://doi.org/10.7554/eLife.48239.011

We also consider a resident type that produces both ligands and both receptors with some degree of asymmetry in ligand production (i.e. ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (0.5 - d x, 0.5, 0.5 + d x, 0.5)$ ) and map the spread of a mutant with asymmetry is receptor production ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (0.5, 0.5 - d y, 0.5, 0.5 + d y)$ . The pairwise invasibility plots for values of $d x$ and $d y$ show that signaling asymmetries in opposite directions are favored. These evolve to a polymorphic state with equal frequencies of cells at $d x = d y = - 0.5$ and $d x = d y = 0.5$ (Figure 6b). These findings together illustrate how the asymmetric state $E_{2}$ evolves from the symmetric state $E_{1}$ .

Effects of recombination

The results above assume that the loci controlling ligand and receptor production are tightly linked which prevents the production of deleterious combinations following meiosis. Recombination is a minor problem at the $E_{1}$ equilibrium which is monomorphic (except for mutational variation). But it is likely to be a problem at the polymorphic $E_{2}$ equilibrium. For example, at $E_{2}$ mating between $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 0, 0, 1)$ and $(0, 1, 1, 0)$ cells generates non-asymmetric recombinant ligand-receptor combinations, either $(1, 1, 0, 0)$ or $(0, 0, 1, 1)$ . To implement recombination we assume that the two ligands are tightly linked in a single locus and are inherited as a pair (likewise the two receptors), and investigate the effects of recombination between the ligand locus and the receptor locus. Note that if we allow recombination between ligands (or receptors), this would be expected to generate combinations with a similar deleterious impact.

Consider the effect of recombination on a population at $E_{1}$ . As before, the population either stays at $E_{1}$ or evolves to $E_{2}$ dependent on parameter values (Figure 7a). When the population evolves to $E_{2}$ , $s^{*}$ becomes larger as the recombination rate, ( $ρ$ ), increases (Figure 7b). For low recombination rates ( $ρ \leq 0.1$ ), the population largely consists of equal frequencies of $(1, 0, 0, 1)$ and $(0, 1, 1, 0)$ cells, producing the ligand and receptor asymmetrically. A small percentage of recombinant cells produce conspecific pairs of ligand and receptor $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ and $(0, 0, 1, 1)$ (Figure 7b,c). Recombination in this case creates ‘macromutations’ where production rates that were 0 become 1 and vice versa. As the recombination rate rises ( $ρ \geq 0.2$ ), the two leading cell types diverge from $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 0, 0, 1)$ and $(0, 1, 1, 0)$ towards $(1 - ϵ_{1}, ϵ_{2}, ϵ_{3}, 1 - ϵ_{4})$ and $(ϵ_{5}, 1 - ϵ_{6}, 1 - ϵ_{7}, ϵ_{8})$ where the $ϵ_{i}$ are below $0.5$ but greater than zero Figure 7d). Higher recombination rates ( $ρ \geq 0.3$ ) push $s^{*} = 0.5$ at $E_{2}$ (Figure 7b). Ηere, there is a predominance of $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 0.5, 0, 0.5)$ and $(0, 0.5, 1, 0.5)$ cells at equal frequencies (or $(0.5, 1, 0.5, 0)$ and $(0.5, 0, 0.5, 1)$ by symmetry). This arrangement is robust to recombination since the receptor locus is fixed at $(ν_{R}, ν_{r}) = (0.5, 0.5)$ and the ligand locus is either at $(ν_{L}, ν_{l}) = (1, 0)$ or $(0, 1)$ (or $(ν_{L}, ν_{l}) = (0.5, 0.5)$ ) and the receptor is either at $(ν_{R}, ν_{r}) = (1, 0)$ or $(0, 1)$ ). So pairing between these two cell types results in $(1, 0.5, 0, 0.5)$ and $(0, 0.5, 1, 0.5)$ offspring, whether recombination occurs or not. Note that this arrangement maintains some degree of asymmetry even with free recombination ( $ρ = 0.5$ ). Even though both cell types produce both receptors, they produce the ligand asymmetrically (or vice versa). Cells on average are more likely to mate successfully between rather than within the two types of cells.

Figure 7

Download asset Open asset

The effect of recombination on $E_{2}$ .

(a) An example of evolution of the two signaling equilibria, $E_{1}$ (for $k^{+} = 1$ ) and $E_{2}$ (for $k^{+} = 5$ ) given a fixed recombination rate $ρ = 0.1$ . (b) Steady state $s^{*}$ varies with the recombination rate. (**c–d**) Production rates of individual cells in the population for receptor-ligand pairs $L - R$ (black) and $l - r$ (red) for recombination rates (c) $ρ = 0.1$ , (d) $ρ = 0.2$ and (e) $ρ = 0.4$ . (f) Contour plot showing the steady state degree of symmetry ( $s^{*}$ ) in a population with resident $(ν_{R}, ν_{L}, ν_{r}, ν_{l}) = (1, 1, 0, 0)$ , given a recombination rate $ρ = 0.2$ . Two mutations are introduced $(1 - d x, 1, d x, 0)$ and $(1, 1 - d y, 0, d y)$ at rate $p$ and their fate is followed until they reach a stable frequency. The population size $N = 1000$ for panels (a) - (e) and $N = 10000$ for panel (f). Other parameters used and simulation details are given in the Supplemental Material.

https://doi.org/10.7554/eLife.48239.012

Similar to the case of no recombination, the invasion of $E_{1}$ by $E_{2}$ depends on the mutational process and parameter values. Figure 7f shows the steady state symmetry measure in a population initially at $(ν_{L}, ν_{R}, ν_{l}, ν_{r})$ = $(1, 1, 0, 0)$ when two mutations $(1 - d x, 1, d x, 0)$ and $(1, 1 - d y, 0, d y)$ are introduced at low frequencies. Whether or not the mutants invade depends on the magnitude of the mutation in a similar way as in the case of no recombination (Figure 5d versus Figure 7f). However, the value of $s^{*}$ now diverges from zero reflecting the nonzero rate of recombination.

Evolution of linkage

In the analysis above, recombination between the ligand and receptor loci is fixed. However, the recombination rate itself can evolve. To investigate this, we let the recombination rate $ρ$ undergo recurrent mutation with probability $μ_{ρ}$ so that the mutant recombination rate becomes $ρ^{'} = ρ + ε_{ρ}$ with $ε_{ρ} \sim N (0, σ_{ρ})$ . In a diploid zygote, the rate of recombination is given by the average of the two recombination alleles, $ρ_{1}$ and $ρ_{2}$ , carried by the mating cells. In this way, the recombination rate evolves together with the ligand and receptor production rates. We start with maximal recombination rate $ρ = 0.5$ and $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ for all cells and allow the recombination rate to evolve by drift for 1000 generation before we introduce mutation in the ligand and receptor loci.

The recombination rate evolves to $ρ^{*} = 0$ whenever $E_{2}$ was reached from $E_{1}$ in the no recombination analysis. Under these conditions, tight linkage between receptor and ligand genes is favored (Figure 8a). Furthermore, asymmetric signaling roles coevolve together with the recombination rate. The evolved trajectories of $s$ and $ρ$ depend on the strength of selection for asymmetric signaling. For example, when $k^{+}$ is large ( $k^{+} = 10$ ), signal asymmetry rapidly evolves; $s$ moves away from one and this is followed by a sharp drop in the recombination rate (Figure 8b). Eventually the population evolves asymmetric signaling roles ( $s$ in orange, Figure 8b) and tight linkage ( $ρ$ in blue, Figure 8b). These dynamics are similar when $k^{+}$ is smaller ( $k^{+} = 3$ , Figure 8c) and selection for asymmetry is weaker. However, it now takes longer for the asymmetric types to co-evolve (Figure 8c). When selection for asymmetric signaling is even weaker ( $k^{+} = 1$ , Figure 8d), no asymmetry evolves ( $s$ remains at 1) and the recombination rate fluctuates randomly between its minimum and maximum value as one would expect in the case of a neutral allele.

Figure 8

Download asset Open asset

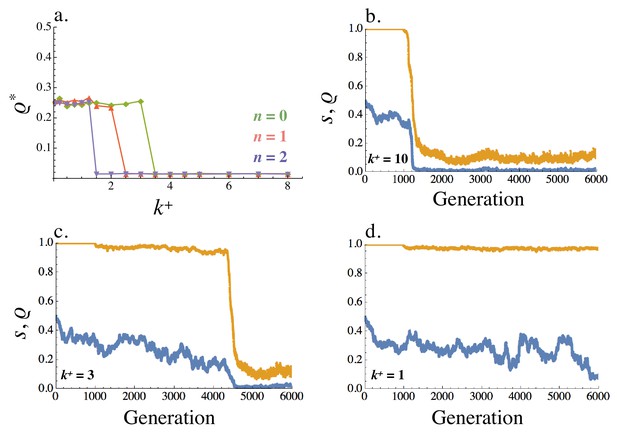
Equilibrium recombination rate $ρ^{*}$ .

(a) Averaged across the population, $ρ^{*}$ varies with $k^{+}$ (within cell binding rate) and $n = 0, 1, 2$ (cost of self-binding). (**b–d**) Evolution of the recombination rate $ρ$ (blue) and signaling symmetry levels $s$ (orange) for different within cell binding rates: (b) $k^{+} = 10$ , (c) $k^{+} = 3$ and (d) $k^{+} = 1$ . The recombination rate evolves under drift for the first 1000 generations, following which mutation at the ligand and receptor loci were introduced. When no asymmetry evolves the recombination rate fluctuates randomly between 0 and 0.5 (i.e. between its minimum and maximum value like a neutral allele). Other parameters used in simulations are given in the Supplemental Material.

https://doi.org/10.7554/eLife.48239.013

Discussion

Explaining the evolution of mating types in isogamous organisms constitutes a major milestone in understanding the evolution of anisogamy and sexes (Randerson and Hurst, 2001; Lehtonen et al., 2016). Mating type identity is determined by a number of genes that reside in regions of suppressed recombination and code for ligands and receptors that guide partner attraction and recognition, as well as genes that orchestrate cell fusion and postzygotic events (Billiard et al., 2011; Perrin, 2012; Hadjivasiliou and Pomiankowski, 2016; Branco et al., 2018). In this work we show that an asymmetry in ligand and receptor production evolves as a response to selection for swift gamete communication and mating. Furthermore, the same conditions favoring asymmetric signaling select for tight linkage between the receptor and ligand genes. Our findings indicate that selection for asymmetric signaling roles could have played an important role in the early evolution of gamete differentiation and identity.

We investigated the evolution of mating type roles by considering two types of ligand and receptor in individual cells. Gene duplication followed by mutation is a well established route to novelty evolution (Susumu, 1970; Zhang, 2003; Magadum et al., 2013) and could explain the co-existence of two pairs of ligand and receptor in our system. Alternatively, individual cells could produce multiple ligands and receptors which evolve independently, as is the case in some basidiomycete fungi (Fowler and Vaillancourt, 2007). The production rate of the two types of ligand (and receptor) in our system is subject to mutation using an assumption of infinite alleles (Tajima, 1996), so that the amount of expressed ligand (and receptor) of each kind is modulated quantitatively. In this way we were able to explicitly express the likelihood of mating as a function of the amount of free and bound molecules on the cell membrane and the ability of cells to accurately read their partner’s signal. This framework allowed us to follow the evolution of the quantitative production of ligand and receptor in mating cells for the first time.

We found that the ligand-receptor binding rate within a cell ( $k^{+}$ ) is key in the evolution of asymmetric signaling roles (Figures 3 and 4). $k^{+}$ holds an important role because it dictates the rate at which free ligand and receptor molecules are removed from the cell surface. In addition, $k^{+}$ determines the amount of intracellular signal that interferes with the ability of cells to interpret incoming signal. Although in theory cells could avoid self-binding (by reducing $k^{+}$ to zero), there is likely to be a strong association of the within-cell and between-cell binding affinities. So reductions in $k^{+}$ are likely to have knock-on costs in reducing $k_{b}$ as well. An extreme example is the case of locally diffusible signals (Figure 1), such as those used by ciliates and yeasts to stimulate and coordinate fusion (Sugiura et al., 2010; Merlini et al., 2013). Here binding affinities between and within cells are inevitably identical (since the ligand is not membrane bound). Work in yeast cells has shown that secreted ligands utilized for intercellular signaling during sex are poorly read by cells that both send and receive the same ligand (Youk and Lim, 2014). In the case of strictly membrane bound molecules avoiding self-binding could also be an issue as it requires a ligand and receptor pair that bind poorly within a cell without compromising intercellular binding. For example, choosy budding yeast gametes (which are better at discriminating between species) take longer to mate (Rogers et al., 2015). It would be interesting to further study these trade-offs experimentally.

We never observed the co-existence of a symmetric ‘pansexual’ type with asymmetric self-incompatible types. The two steady states consist of either a pansexual type alone or two mating types with asymmetric signaling roles. This could explain why the co-existence of mating types with pansexuals is rare in natural populations (Billiard et al., 2011; Billiard et al., 2012). This is in contrast to previous models where pansexual types were very hard to eliminate due to negative frequency dependent selection (Hoekstra, 1982; Czárán and Hoekstra, 2004; Hadjivasiliou et al., 2013). For example, in the case of the mitochondrial inheritance model, uniparental inheritance raises fitness not only in individuals that carry genes for uniparental inheritance but also for pansexual individuals (benefits ‘leak’ to biparental individuals) (Hadjivasiliou et al., 2013; Christie and Beekman, 2017b).

A similar pattern is seen with inbreeding avoidance because the spread of self-incompatibility reduces the population mutation load, and so reduces the need for inbreeding avoidance (Czárán and Hoekstra, 2004). These dynamics are reversed in the present model where there is positive frequency dependent selection. The spread of asymmetric signalers generates stronger selection for further asymmetry (Figures 3 and 4). This also occurs when there is recombination (Figures 7 and 8). Even though recombination between the two asymmetric types generates symmetric recombinant offspring, these are disfavored and eliminated by selection. These observations suggest that the mitochondrial inheritance and inbreeding avoidance models are unlikely to generate strong selection for suppressed recombination which is the hallmark of mating types. Finally, it would be interesting to explore how the reinstatement of recombination could be a route back to homothallism which is a state derived from species with mating types (Billiard et al., 2011).

Mating type identity in unicellular eukaryotes is determined by mating type loci that typically carry a number of genes (Billiard et al., 2012; Hadjivasiliou and Pomiankowski, 2016). Suppressed recombination at the mating type locus is a common feature across the evolutionary tree (Branco et al., 2018). Our work predicts the co-evolution of mating type specific signaling roles and suppressed recombination with selection favoring linkage between loci responsible for signaling and an asymmetry in signaling roles. This finding suggests that selection for asymmetric signaling could be the very first step in the evolution of tight linkage between genes that control mating type identity. In yeasts, the only genes in the mating type locus code for the production of ligand and receptor molecules (Merlini et al., 2013). These then trigger a cascade of other signals downstream that also operate asymmetrically. Evidence across species suggests that mating type loci with suppressed recombination are precursors to sex chromosomes (Menkis et al., 2008; Geng et al., 2014). In this way our work provides crucial insights about the origin of sex chromosomes.

The framework developed here could be used together with recent efforts to understand numerous features of mating type evolution. For example, opposite mating type gametes often utilize diffusible signals to attract partners (Luporini et al., 1995; Tsuchikane et al., 2005). The inclusion of long range signals such as those used in sexual chemotaxis will provide further benefits for asymmetric signaling roles and mating types (Hadjivasiliou et al., 2015). Furthermore the number of mating types varies greatly across species and is likely to depend on the frequency of sexual reproduction and mutation rates (Constable and Kokko, 2018). Signaling interactions between gametes could also play a role in determining the number of mating types and reducing their number to only two in many species (Hadjivasiliou et al., 2016b). It would be interesting to use the framework developed here to study the evolution of additional ligands and receptors and their role in reaching an optimal number of mating types. Other important features such as the mechanism of mating type determination (Billiard et al., 2011; Vuilleumier et al., 2013) and stochasticity in mating type identity (Hadjivasiliou et al., 2016b; Nieuwenhuis and Immler, 2016; Nieuwenhuis et al., 2018) could also be understood in light of this work.

Our analysis revealed that the evolution of asymmetric gamete signaling and mating types is contingent upon the mutation rate. Single mutants that exhibit an asymmetry are initially slightly disadvantageous. When further mutations emerge that are asymmetric in the opposite direction, a positive interaction between these mutants occurs that can lead to the evolution of distinct mating types. When the population size is small and mutation rates are low, there is a low probability that individuals carrying asymmetric mutations in opposite directions are segregating at the same time. Increasing the population size or the mutation rate would enhance the probability of co-segregation, making the evolution of asymmetric signaling more likely. In an infinite population the evolution of signaling asymmetry should be independent of the mutation rate. Finally, it is worth noting that unicellular eukaryotes undergo several rounds of asexual growth (tens to thousands) between each sexual reproduction (Hadjivasiliou et al., 2016b; Constable and Kokko, 2018). It follows that the effective mutation rate between sexual rounds will end up being orders of magnitude higher than the mutation rates at each vegetative step.

Taken together our findings suggest that selection for swift and robust signaling interactions between mating cells can lead to the evolution of self-incompatible mating types determined at non-recombinant mating type loci. We conclude that the fundamental selection for asymmetric signaling between mating cells could be the very first step in the evolution of sexual asymmetry, paving the way for the evolution of anisogamy, sex chromosomes and sexes.

Materials and methods

General model

Request a detailed protocol

We model $N$ cells so that each cell is individually characterized by a ligand locus $ℒ$ and a receptor locus $ℛ$ . Two ligand genes at the locus $ℒ$ determine the production rates for two ligand types $l$ and $L$ given by $ν_{l}$ and $ν_{L}$ . Similarly, two receptor genes at the locus $ℛ$ determine the production rates for the two receptor types $r$ and $R$ given by $ν_{r}$ and $ν_{L}$ . The two ligand and receptor genes in our model could could arise from duplication followed by mutation that leaves two closely linked genes that code for different molecules. In our computational set-up each cell is associated with production rates $ν_{l}$ , $ν_{L}$ , $ν_{r}$ and $ν_{R}$ where we assume a normalized upper bound so that $ν_{l} + ν_{L} < 1$ and $ν_{r} + ν_{R} < 1$ .

The steady state concentrations for $L, R$ , and $L R$ are computed by setting $\frac{d [L]}{d t} = \frac{d [R]}{d t} = \frac{d [L R]}{d t} = 0$ in Equations (1-3) and solving the resulting quadratic equations. This leads two solutions only one of which gives positive concentrations. It follows that there is a unique physical solution to our system, which is what we use to define the probability of mating in our numerical simulations.

The program is initiated with $ν_{L} = ν_{R} = 1$ and $ν_{l} = ν_{r} = 0$ for all cells (unless otherwise stated, see Section 5.4). We introduce mutation so that the ligand and receptor production rates of individual cells mutate independently with probability $μ$ . A mutation event at a production gene changes the production rate by an increment $ϵ$ where $ϵ \sim N (0, σ)$ . Mutation events at the different genes $l, L, r$ and $R$ are independent of one another. If $ν_{l} + ν_{L} > 1$ or $ν_{l} + ν_{L} > 1$ the production rates are renormalized so their sum is capped at 1. If a mutation leads to a production rate below 0 or above one it is ignored and the production rate does not change.

We implement mating by randomly sampling individual cells. The probability that two cells mate is determined by their ligand and receptor production rates as defined in Equation (9) in the main text. We assume that $K$ takes a large value relative to $W_{12} W_{21}$ so that $P$ is linear in $W_{12} W_{21}$ . Because the absolute value for $W_{12} W_{21}$ varies greatly between parameter sets, and what we are interested in is the relative change in $W_{12} W_{21}$ when signaling levels change, we chose $K$ to be equal to the maximum value $W_{12} W_{21}$ can take for a given choice of $γ$ , $k^{+}$ , $k^{-}$ and $k_{b}$ . Sampled cells that do not mate are returned to the pool of unmated cells. This process is repeated until $M = N / 2$ cells have successfully mated. This produces $N / 4$ pairs of cells each of which gives rise to two offspring. These are sampled with replacement until the population returns to size $N$ . We assume that a mutation-selection balance has been reached when the absolute change in $s$ , defined in Equation (10) in the main text, between time steps $t_{1}$ and $t_{2}$ is below $ϵ = 10^{- 5}$ across $t_{2} - t_{1} = 100$ . Certain parameter sets resulted in noisy steady states and were terminated following $10^{5}$ generations. The numerical code keeps track of all production rates for individual cells over time.

Adaptive dynamics

Request a detailed protocol

We model adaptive dynamics by initiating the entire population at state ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s}$ and introducing a mutant ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t}$ at low frequency $p$ . We allow the population to evolve according to the life cycle introduced in the main text and record the frequency of the resident and mutant type when a steady state is reached. For the purposes of Figure 5, the resident type is set to ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s}$ and two mutants ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t_{1}}$ and ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t_{2}}$ are introduced both at frequency $p$ . In this case we track the frequencies of the resident and both mutants until steady state is reached. We define steady state as the point where the average value of $s$ in the population between time steps $t_{1}$ and $t_{2}$ is below $ϵ = 10^{- 7}$ across $t_{2} - t_{1} = 100$ . The population always reached steady state.

Recombination

Request a detailed protocol

We implement recombination by considering a modifier $ℳ$ that lies between the ligand and receptor loci $ℒ$ and $ℛ$ . That is, we assume that the two ligand genes and two receptor genes are tightly linked on the ligand and receptor locus $ℒ$ and $ℛ$ respectively, and only model recombination between the two loci. For simplicity, we assume that $ℳ$ determines the physical distance between $ℒ$ and $ℛ$ so that the distances $ℒ - ℳ$ and $ℛ - ℳ$ are the same. The modifier $ℳ$ determines the rate of recombination between the ligand and receptor loci quantitatively by determining $ρ_{M}$ , the probability of a single recombination event following mating. Consider for example two individuals whose ligand and receptor production rates and recombination rates are determined by the triplets $R_{1} - M_{1} - L_{1}$ and $R_{2} - M_{2} - L_{2}$ , the possible offspring resulting from such a mating are given by,

$R_{1} - M_{1} - L_{1}$ and $R_{2} - M_{2} - L_{2}$ with probability ${(1 - ρ_{M_{1, 2}})}^{2}$ – equivalent to no recombination events
$R_{1} - M_{2} - L_{1}$ and $R_{2} - M_{1} - L_{2}$ with probability $ρ_{M_{1, 2}}^{2}$ – equivalent to two recombination events
$R_{1} - M_{2} - L_{2}$ and $R_{2} - M_{1} - L_{1}$ with probability $ρ_{M_{1, 2}} (1 - ρ_{M_{1, 2}})$ – equivalent to one recombination event
$R_{1} - M_{1} - L_{2}$ and $R_{2} - M_{2} - L_{1}$ with probability $ρ_{M_{1, 2}} (1 - ρ_{M_{1, 2}})$ – equivalent to one recombination event

where $ρ_{M_{1, 2}} = \frac{1}{2} (ρ_{M_{1}} + ρ_{M_{2}})$ is the joint recombination rate when cell₁ and cell₂ with recombination rates $ρ_{M_{1}}$ and $ρ_{M_{2}}$ respectively mate.

We allow mutation at the recombination locus at rate $μ_{ρ}$ independently of the ligand and receptor loci. A mutation event leads to a new recombination rate so that $ρ_{M}^{'} = ρ_{M} - ϵ$ for $ϵ \sim N (0, σ_{ρ})$ . We assume that the mutation-selection balance has been reached when the absolute change in $s$ , defined in Equation (10) in the main text, and the change in the average recombination rate between time steps $t_{1}$ and $t_{2}$ is below $ϵ = 10^{- 5}$ across $t_{2} - t_{1} = 100$ .

Methods and parameters used for simulated figures

Figure 4

Request a detailed protocol

(a): Individual simulations following the trajectory of $s$ over time. Population is initiated at $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ and $ρ = 0$ for all cells at time 0. $μ = 0.01$ for all ligand and receptor genes and $μ_{r} = 0$ , $γ = 0.1$ , $k^{-} = 1$ , $n = 1$ , $k_{b} = k^{+} / k^{-}$ and $k^{+} = 1$ for $E_{1}$ trajectory and 5.0 for $E_{2}$ trajectory. Population size $N = 1000$ and number of cells allowed to mate $M = N / 2$ .

(b-c): Parameters as for (a) with $k^{+} = 5.0$ . Each dot is represents an individual cell in the simulation.

(d): Parameters used as for (a) with varying $k^{+}$ and $γ$ as indicated in the Figure. Simulation was run until a steady state was reached and the value of $s^{*}$ was averaged over the last 1000 time steps to account for noise.

(e): Parameters used as for (a), varying $k_{b}$ and $n$ as indicated in the Figure. $k^{+}$ was also varied here and the value of $k^{+}$ beyond which $E_{2}$ evolved at the expense of $E_{1}$ was noted (the y-axis value).

Figure 5

Request a detailed protocol

Adaptive dynamics simulations following the frequency of two mutants $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1 - d x, 1, d x, 0)$ and $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1 - d y, 0, d y)$ introduced at frequency $p$ (indicated on Figure ) in a resident population with $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ . The frequency of the resident and two mutants at steady state was recorded and the heat maps show the average steady state value of $s^{*}$ for 20 independent repeats. Parameters used: $γ = 0.5$ , $k^{-} = 1$ , $n = 1$ , $k_{b} = k^{+} / k^{-}$ , $N = 10000$ , $M = N / 2$ .

Figure 6

Request a detailed protocol

Joint evolution of receptor and ligand asymmetry. Contour plots show the equilibrium frequency of the resident ( $f_{r e s}$ ) with production rates ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (1 - d x, 1, d x, 0)$ (a) ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{r e s} = (0.5 - d x, 0.5, 0.5 + d x, 0.5)$ (b), following a mutation ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (1, 1 - d y, 0, d y)$ (a) and ${(ν_{L}, ν_{R}, ν_{l}, ν_{r})}_{m u t} = (0.5, 0.5 - d y, 0.5, 0.5 + d y)$ (b). The mutant is introduced at a frequency $p = 0.001$ . Other parameters used and simulations details are given in the Supplemental Material.

Figure 7

Request a detailed protocol

(a): Individual simulations following the trajectory of $s$ over time. Population is initiated at $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ and $ρ = 0.1$ for all cells at time 0. $μ = 0.01$ for all ligand and receptor genes and $μ_{r} = 0$ . $σ = 0.1$ , $γ = 0.5$ , $k^{-} = 1$ , $n = 1$ , $k_{b} = k^{+} / k^{-}$ and $k^{+} = 1$ for $E_{1}$ trajectory and 5.0 for $E_{2}$ trajectory. Population size $N = 1000$ and number of cells allowed to mate $M = N / 2$ .

(b): Parameters as in (a) but varying $ρ$ as indicated in the Figure and using $k^{+} = 3.0$ . The $y$ axis shows the steady state value of $s$ averaged over 1000 steps after steady state has been reached.

(c-e): Parameters as for (a) with $k^{+} = 5.0$ and recombination rate $ρ$ as shown in each Figure . Each dot is represents an individual cell in the simulation.

(f): Parameters as for (a) with $k^{+} = 5$ , $μ_{b} = 0.01$ , $ρ = 0.2$ and $N = 10000$ . The heat maps show the value of $s^{*}$ at steady state averaged over 20 repeats. Heat map was obtained in the same way as Figure 5.

Figure 8

Request a detailed protocol

(a): Population is initiated at $(ν_{L}, ν_{R}, ν_{l}, ν_{r}) = (1, 1, 0, 0)$ and $ρ = 0.5$ for all cells at time 0. $μ = 0.01$ for all ligand and receptor genes and $μ_{ρ} = 0.01$ , $γ = 0.5$ , $k^{-} = 1$ , $k_{b} = k^{+} / k^{-}$ and $n$ vary as shown in the plot. The y axis shows the steady state value of $ρ$ averaged over 1000 steps after steady state has been reached. Population size $N = 1000$ and number of cells allowed to mate $M = N / 2$ .

(b-d): Parameters as in (a) with $k^{+}$ varied as shown in the individual plots.

Data availability

Code for simulations was written in C++ and the simulated data was analysed using Mathematica. C++ code and Mathematica notebooks are available on GitHub (https://github.com/zenah12/SignalingMatingTypes; copy archived at https://github.com/elifesciences-publications/SignalingMatingTypes).

References

1. Ahmed S
2. Cock JM
3. Pessia E
4. Luthringer R
5. Cormier A
6. Robuchon M
7. Sterck L
8. Peters AF
9. Dittami SM
10. Corre E
11. Valero M
12. Aury JM
13. Roze D
14. Van de Peer Y
15. Bothwell J
16. Marais GA
17. Coelho SM
(2014) A haploid system of sex determination in the brown alga Ectocarpus sp
Current Biology 24:1945–1957.
https://doi.org/10.1016/j.cub.2014.07.042
- PubMed
- Google Scholar
1. Bell G
(1978) The evolution of anisogamy
Journal of Theoretical Biology 73:247–270.
https://doi.org/10.1016/0022-5193(78)90189-3
- PubMed
- Google Scholar
(2011) Having sex, yes, but with whom? inferences from fungi on the evolution of anisogamy and mating types
Biological Reviews 86:421–442.
https://doi.org/10.1111/j.1469-185X.2010.00153.x
- PubMed
- Google Scholar
(2012) Sex, outcrossing and mating types: unsolved questions in fungi and beyond
Journal of Evolutionary Biology 25:1020–1038.
https://doi.org/10.1111/j.1420-9101.2012.02495.x
- PubMed
- Google Scholar
(2017) Evolutionary strata on young mating-type chromosomes despite the lack of sexual antagonism
PNAS 114:7067–7072.
https://doi.org/10.1073/pnas.1701658114
- PubMed
- Google Scholar
(2018) Multiple convergent supergene evolution events in mating-type chromosomes
Nature Communications 9:2000.
https://doi.org/10.1038/s41467-018-04380-9
- PubMed
- Google Scholar
1. Cappellaro C
2. Hauser K
3. Mrśa V
4. Watzele M
5. Watzele G
6. Gruber C
7. Tanner W
(1991) Saccharomyces cerevisiae a- and alpha-agglutinin: characterization of their molecular interaction
The EMBO Journal 10:4081–4088.
https://doi.org/10.1002/j.1460-2075.1991.tb04984.x
- PubMed
- Google Scholar
1. Charlesworth B
(1978) The population genetics of anisogamy
Journal of Theoretical Biology 73:347–357.
https://doi.org/10.1016/0022-5193(78)90195-9
- PubMed
- Google Scholar
1. Charlesworth D
2. Charlesworth B
(1979) The evolution and breakdown of S-allele systems
Heredity 43:41–55.
https://doi.org/10.1038/hdy.1979.58
- Google Scholar
(2015) Selection against Heteroplasmy explains the evolution of uniparental inheritance of mitochondria
PLOS Genetics 11:e1005112.
https://doi.org/10.1371/journal.pgen.1005112
- PubMed
- Google Scholar
1. Christie JR
2. Beekman M
(2017a) Uniparental inheritance promotes adaptive evolution in cytoplasmic genomes
Molecular Biology and Evolution 34:677–691.
https://doi.org/10.1093/molbev/msw266
- PubMed
- Google Scholar
1. Christie JR
2. Beekman M
(2017b) Selective sweeps of mitochondrial DNA can drive the evolution of uniparental inheritance
Evolution 71:2090–2099.
https://doi.org/10.1111/evo.13291
- Google Scholar
1. Constable GWA
2. Kokko H
(2018) The rate of facultative sex governs the number of expected mating types in isogamous species
Nature Ecology & Evolution 2:1168–1175.
https://doi.org/10.1038/s41559-018-0580-9
- PubMed
- Google Scholar
1. Czárán TL
2. Hoekstra RF
(2004) Evolution of sexual asymmetry
BMC Evolutionary Biology 4:34.
https://doi.org/10.1186/1471-2148-4-34
- PubMed
- Google Scholar
Book
1. Fowler TJ
2. Vaillancourt LJ
(2007)
Pheromones and pheromone receptors in Schizophyllum commune mate recognition: a retrospective of a half-century of progress, and a look ahead

In: Heitman J, Kronstad JT, Casselton LA, editors. Sex in Fungi: Molecular Determination and Evolutionary iImplications. Washington: American Society of Microbiology (ASM) Press. pp. 301–315.
- Google Scholar
1. Fraser JA
2. Diezmann S
3. Subaran RL
4. Allen A
5. Lengeler KB
6. Dietrich FS
7. Heitman J
(2004) Convergent evolution of chromosomal sex-determining regions in the animal and fungal kingdoms
PLOS Biology 2:e384.
https://doi.org/10.1371/journal.pbio.0020384
- PubMed
- Google Scholar
1. Geng S
2. De Hoff P
3. Umen JG
(2014) Evolution of sexes from an ancestral mating-type specification pathway
PLOS Biology 12:e1001904–e1001916.
https://doi.org/10.1371/journal.pbio.1001904
- PubMed
- Google Scholar
(2012) Selection for mitonuclear co-adaptation could favour the evolution of two sexes
Proceedings of the Royal Society B: Biological Sciences 279:1865–1872.
https://doi.org/10.1098/rspb.2011.1871
- Google Scholar
(2013) Dynamics of mitochondrial inheritance in the evolution of binary mating types and two sexes
Proceedings of the Royal Society B: Biological Sciences 280:20131920.
https://doi.org/10.1098/rspb.2013.1920
- Google Scholar
(2015) Cell–cell signalling in sexual chemotaxis: a basis for gametic differentiation, mating types and sexes
Journal of the Royal Society Interface 12:20150342.
https://doi.org/10.1098/rsif.2015.0342
- Google Scholar
(2016a) A new mechanism for spatial pattern formation via lateral and protrusion-mediated lateral signalling
Journal of the Royal Society Interface 13:20160484.
https://doi.org/10.1098/rsif.2016.0484
- Google Scholar
(2016b) The evolution of mating type switching
Evolution 70:1569–1581.
https://doi.org/10.1111/evo.12959
- Google Scholar
1. Hadjivasiliou Z
2. Pomiankowski A
(2016) Gamete signalling underlies the evolution of mating types and their number
Philosophical Transactions of the Royal Society B: Biological Sciences 371:20150531.
https://doi.org/10.1098/rstb.2015.0531
- Google Scholar
1. Hastings IM
(1992) Population genetic aspects of deleterious cytoplasmic genomes and their effect on the evolution of sexual reproduction
Genetical Research 59:215–225.
https://doi.org/10.1017/S0016672300030500
- PubMed
- Google Scholar
1. Hoekstra RF
(1982) On the asymmetry of sex: evolution of mating types in Isogamous populations
Journal of Theoretical Biology 98:427–451.
https://doi.org/10.1016/0022-5193(82)90129-1
- Google Scholar
Book
1. Hoekstra RF
(1987) The evolution of sexes
In: Stearns S. C, editors. The Evolution of Sex and Its Consequences, Pages. Basel: Birkhauser Verlag. pp. 59–91.
https://doi.org/10.1007/978-3-0348-6273-8_3
- Google Scholar
1. Hurst LD
(1996) Why are there only two sexes?
Proceedings of the Royal Society B: Biological Sciences 263:415–422.
https://doi.org/10.1098/rspb.1996.0063
- Google Scholar
1. Hurst LD
2. Hamilton WD
(1992) Cytoplasmic fusion and the nature of sexes
Proceedings of the Royal Society B: Biological Sciences 247:189–194.
https://doi.org/10.1098/rspb.1992.0027
- Google Scholar
1. Hutson V
2. Law R
(1993) Four steps to two sexes
Proceedings. Biological Sciences 253:43–51.
https://doi.org/10.1098/rspb.1993.0080
- PubMed
- Google Scholar
(1997) Pheromones of the ciliate Euplotes octocarinatus not only induce conjugation but also function as chemoattractants
The Journal of Experimental Zoology 277:38–48.
https://doi.org/10.1002/(SICI)1097-010X(19970101)277:1<38::AID-JEZ4>3.0.CO;2-C
- PubMed
- Google Scholar
(2014) Fringe proteins modulate Notch-ligand Cis and trans interactions to specify signaling states
eLife 3:e02950.
https://doi.org/10.7554/eLife.02950
- PubMed
- Google Scholar
(2016) What do isogamous organisms teach Us about sex and the two sexes?
Philosophical Transactions of the Royal Society B: Biological Sciences 371:20150532.
https://doi.org/10.1098/rstb.2015.0532
- Google Scholar
(1995) Chemical signaling in ciliates
The Journal of Eukaryotic Microbiology 42:208–212.
https://doi.org/10.1111/j.1550-7408.1995.tb01567.x
- PubMed
- Google Scholar
(2013) Gene duplication as a major force in evolution
Journal of Genetics 92:155–161.
https://doi.org/10.1007/s12041-013-0212-8
- PubMed
- Google Scholar
1. Maier I
(1993) Gamete orientation and induction of gametogenesis by pheromones in algae and plants
Plant, Cell and Environment 16:891–907.
https://doi.org/10.1111/j.1365-3040.1993.tb00513.x
- Google Scholar
(2008) The mating-type chromosome in the filamentous ascomycete Neurospora tetrasperma represents a model for early evolution of sex chromosomes
PLOS Genetics 4:e1000030.
https://doi.org/10.1371/journal.pgen.1000030
- PubMed
- Google Scholar
(2013) Mate and fuse: how yeast cells do it
Open Biology 3:130008.
https://doi.org/10.1098/rsob.130008
- PubMed
- Google Scholar
(2018) Repeated evolution of self-compatibility for reproductive assurance
Nature Communications 9:1639.
https://doi.org/10.1038/s41467-018-04054-6
- PubMed
- Google Scholar
1. Nieuwenhuis BP
2. Immler S
(2016) The evolution of mating-type switching for reproductive assurance
BioEssays 38:1141–1149.
https://doi.org/10.1002/bies.201600139
- PubMed
- Google Scholar
(1972) The origin and evolution of gamete dimorphism and the male-female phenomenon
Journal of Theoretical Biology 36:529–553.
https://doi.org/10.1016/0022-5193(72)90007-0
- PubMed
- Google Scholar
1. Perrin N
(2012) What uses are mating types? The "developmental switch" model
Evolution 66:947–956.
https://doi.org/10.1111/j.1558-5646.2011.01562.x
- Google Scholar
1. Phadke SS
2. Zufall RA
(2009) Rapid diversification of mating systems in ciliates
Biological Journal of the Linnean Society 98:187–197.
https://doi.org/10.1111/j.1095-8312.2009.01250.x
- Google Scholar
1. Randerson JP
2. Hurst LD
(2001) The uncertain evolution of the sexes
Trends in Ecology & Evolution 16:571–579.
https://doi.org/10.1016/S0169-5347(01)02270-4
- Google Scholar
(2015) Experimental evolution of species recognition
Current Biology 25:1753–1758.
https://doi.org/10.1016/j.cub.2015.05.023
- PubMed
- Google Scholar
(2010) Behavioural changes induced by the conjugation-inducing pheromones, gamone 1 and 2, in the ciliate Blepharisma japonicum
European Journal of Protistology 46:143–149.
https://doi.org/10.1016/j.ejop.2010.01.002
- PubMed
- Google Scholar
Book
1. Susumu O
(1970)
Evolution by Gene Duplication

New York: Springer Science.
- Google Scholar
1. Tajima F
(1996) Infinite-allele model and infinite-site model in population genetics
Journal of Genetics 75:27–31.
https://doi.org/10.1007/BF02931749
- Google Scholar
1. Tsubo Y
(1961) Chemotaxis and sexual behavior in Chlamydomonas *
The Journal of Protozoology 8:114–121.
https://doi.org/10.1111/j.1550-7408.1961.tb01191.x
- Google Scholar
1. Tsuchikane Y
2. Fujii T
3. Ito M
4. Sekimoto H
(2005) A sex pheromone, protoplast release-inducing protein (PR-IP) inducer, induces sexual cell division and production of PR-IP in Closterium
Plant and Cell Physiology 46:1472–1476.
https://doi.org/10.1093/pcp/pci158
- PubMed
- Google Scholar
1. Uyenoyama MK
(1988) On the evolution of genetic incompatibility systems. III. introduction of weak gametophytic self-incompatibility under partial inbreeding
Theoretical Population Biology 34:47–91.
https://doi.org/10.1016/0040-5809(88)90035-4
- PubMed
- Google Scholar
(2013) Transitions from reproductive systems governed by two self-incompatible loci to one in fungi
Evolution 67:501–516.
https://doi.org/10.1111/j.1558-5646.2012.01783.x
- Google Scholar
1. Wilson NF
2. O'Connell JS
3. Lu M
4. Snell WJ
(1999) Flagellar adhesion between mt(+) and mt(-) Chlamydomonas gametes regulates phosphorylation of the mt(+)-specific homeodomain protein GSP1
The Journal of Biological Chemistry 274:34383–34388.
https://doi.org/10.1074/jbc.274.48.34383
- PubMed
- Google Scholar
1. Wilson AJ
2. Xu J
(2012) Mitochondrial inheritance: diverse patterns and mechanisms with an emphasis on fungi
Mycology 3:158–166.
https://doi.org/10.1080/21501203.2012.684361
- Google Scholar
1. Youk H
2. Lim WA
(2014) Secreting and sensing the same molecule allows cells to achieve versatile social behaviors
Science 343:1242782.
https://doi.org/10.1126/science.1242782
- PubMed
- Google Scholar
1. Zhang J
(2003) Evolution by gene duplication: an update
Trends in Ecology & Evolution 18:292–298.
https://doi.org/10.1016/S0169-5347(03)00033-8
- Google Scholar

Decision letter

Michael Doebeli

Reviewing Editor; University of British Columbia, Canada
Detlef Weigel

Senior Editor; Max Planck Institute for Developmental Biology, Germany

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

[Editors’ note: a previous version of this study was rejected after peer review, but the authors submitted for reconsideration. The first decision letter after peer review is shown below.]

Thank you for submitting your work entitled "Evolution of the mating type locus with suppressed recombination" for consideration by eLife. Your article has been reviewed by a Senior Editor, a Reviewing Editor, and three reviewers. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that we have decided to reject your paper in its present form. However, we would be willing to consider a revised version of your manuscript that takes into account the extensive reviewer comments.

The most important point in such a revision would be to address the criticism that it is unclear in the present version of the manuscript what exactly leads to the evolution of the mating type equilibrium E2. In particular, it is unclear whether the analytical and the simulation results presented in the paper lead to the same conclusions, and how the evolution of the asymmetric state depends on the mutational process. The relationship between the analytical and the simulation results needs to be made much clearer, and both reviewers 1 and 3 suggest doing an invasion analysis to clarify this point, e.g. using adaptive dynamics and pairwise in viability plots.

Other points you may wish to consider are the evolution of more than two mating types, as well as the possible effects of population-wide ligand and receptor production.

Reviewer #1:

Here the authors ask if self-incompatible mating types evolve from a self-compatible ancestor lacking mating types as a result of selection to improve cross-cell signalling. The intuition is clear; by producing a signal different from that being received from potential partners there is less self-interference, and this selects for two different mating types (one sending A and receiving B, one sending B and receiving A). This intuition is demonstrated with a ligand-receptor (signal-receiver) model, in which an individual can produce two different pairs of ligands and receptors. These molecules interact to form bound complexes, these complexes break down, and all molecules and complexes decay (equations 1-3). From this the equilibrium concentrations of receptors, ligands, and complexes are calculated (equations 4-7) and used to determine the probability of mating given meeting (equation 9) as a function of the signal strengths between the two cells (equation 10). The population is updated, from one generation to the next, by randomly sampling pairs of cells, until M pairs have mated. The offspring of these pairs are sampled with replacement until a population size of N is recovered. Genetic variation arises by mutation, inducing a small random normal deviation, at each of the 4 genes controlling the production rates of the 2 ligands and 2 receptors, independently (with some renormalization to keep the total ligand and receptor production below a maximum). The authors first show how the signal strength (and as a result, fitness) depends on the trait value (ligand-receptor production rates) of both the focal individual and the potential mating partner (Figure 2). In particular, populations producing only one pair of ligand-receptor molecules are evolutionary stable, but as more individuals produce the other ligand or receptor (e.g., by drift) there can be selection for individuals producing the ligand or receptor that matches this, suggesting the evolution of mating types might be an alternative stable evolutionary state. The authors then perform simulations to investigate the characteristics of this mating type equilibrium and the factors allowing it (Figure 3), as well as how the rate of recombination between the ligand and receptor loci affect this equilibrium (Figure 4). Finally, the authors then allow the recombination rate itself to evolve, showing that there is strong selection for reduced recombination at the mating type equilibrium (Figure 5). Thus, the model describes a hypothesis for the evolution of mating types with non-recombining mating type loci from an ancestor without mating types.

I do not know the literature well enough to assess the novelty of this paper. I enjoyed reading it and thought it thought provoking. As far as I can tell the analysis is correct (I did not check the simulations).

Essential revisions:

I think a bit more could be done to demonstrate why the mating type equilibrium (E2) evolves from the monomorphic ancestor (E1), which I think is unclear in a few places (details below). One way to do this would be to take the approach of adaptive dynamics, and assume a monomorphic population (e.g., all individuals make only ligand 1 and receptor 1, v = (1,1,0,0)). You then calculate the fitness of a mutant with trait value v' = (x,y,1-x,1-y) in this population, take the derivatives with respect to x and y, and evaluate at the resident equilibrium (v' = v). A phase plane can then be shown, illustrating the direction of selection acting on small mutations around the resident. Immediately from this one sees that E1 is locally stable (as the current Figure 2D suggests), as are the other four corners of the phase space. Of particular interest are the basins of attraction for each equilibrium, the effect of parameter values on the size of these basins, and the effects of parameter values on the strength of selection keeping a population within each basin (the "depth" of the basin if you will). The authors have rightly stated that there are multiple basins of attraction (subsection “Evolution of mating types with asymmetric signaling roles”) but in other places claim that E2 evolves from E1 because of strong selection for asymmetry (subsection “Evolution of mating types with asymmetric signaling roles”), implying E1 is instead unstable (i.e., there is no basin of attraction for E1). This idea of instability is implicit in Figure 3D-E, where the idea is that there are threshold values of k⁺, γ, and n that make E1 unstable. I think that the phase plane demonstrates that E1 remains stable for k⁺ finite and γ positive (I've only looked at n=0). Instead of changing the local stability of E1 these parameters change the size of the basin of attraction and its depth, therefore affecting the rate of drift out of E1 (so that "threshold" values of k⁺, γ, and n are just the values that allow this rate to be high enough to see E1 lost by the maximum number of generations simulated). In particular, increasing k⁺ decreases E1's basin of attraction and also makes the basin shallower, greatly facilitating drift out. In contrast, decreasing γ shrinks E1's basin of attraction but makes it deeper, meaning the rate at which E1 transitions to E2 might be less sensitive to changes in γ. This selection surface approach brings a number of new insights (e.g., increasing the size of basin vs. increasing the depth of the basin, the possibility of calculating the amount of drift needed to leave E1), could be used to explain the quantitative patterns in Figure 3D-F (e.g., yellow in Figure 3F is the boundary of the basin of attraction of E1), and highlights that E1 is always a stable state (which is not always clear from the text; subsection “Evolution of mating types with asymmetric signaling roles”). Further investigations along these lines could help illustrate the location and properties of the branching point leading to E2 (e.g., is there are "garden of eden" branching point at v = (0.5, 0.5, 0.5, 0.5)?). Additionally, one might take a quantitative genetic approach and use, for example, diffusion equations to ask what the rate of drift out of E1 is (e.g., Barton and Rouhani, 1987).

Reviewer #2:

This paper investigates the early evolution of the architecture of mating type locus, where individuals are initially bearing two pairs of ligand-receptors genes. The authors show that asymmetry in ligand-receptors production rates and linkage between genes are expected under a wide variety of conditions. The fundamental underlying mechanisms are the propensity of individuals to successfully mate with other individuals, which depends on their propensity to bind others' ligands on their own receptors, i.e. properly receiving a good signal. This propensity is modeled following a system of equations derived from biochemical reaction systems.

The authors investigate in particular the evolution of a population where mutations affect production rates of receptors and ligands. The model is analysed with computer individual-based simulations in a finite population with a fixed size.

In my opinion, this paper is excellent, especially because the model presented is very simple, and yet, it explains a lot. This model explains (1) why individuals can have an advantage in providing asymmetrical receptor-ligand production, (2) under which biochemical conditions should asymmetry evolve, (3) to what extent linkage between genes can affect the evolution of asymmetry, and (4) that recombination between genes is expected to evolve to zero (tight linkage) as asymmetry evolves to maximum. Such a model can apply to many different taxa: ciliates, fungi, algae, where receptor-ligand asymmetry in a mating type locus without recombination is common. Because it is very simple, the model is certainly very general. These results provide a first principle for the evolution of asymmetry between two kinds of individuals in a single population, which could trigger further differentiation for instance anisogamy or sexual chromosomes.

My only criticism would be that there can be a contradiction between two hypotheses: diffusion of ligands is local, and the use of differential equations with products between molecular concentrations as the rate of contact. This precludes the possibility that ligands produced by the whole population might interact and disturb the signalling between cells. Considering interactions between only two close cells would need more precise modeling of spatialized and stochastic processes. I am not sure that it would change a lot of the results, but I can imagine that considering the whole population ligands production could affect a lot the evolutionary outcomes since it might affect a lot the importance of the self-binding parameter k⁺. It would have been interesting to compare whole population vs. two cells interactions.

Reviewer #3:

Summary:

The authors study the evolution of unicellular mating types, where mating types are defined in terms of their ligand-receptor signalling toolkit. Each cell can produce two different types of receptors and ligands. Cells reproduce faster more compatible cells, i.e. ligands and receptors, there are in the population. They find that when self-binding rate is not small, evolution favours "asymmetric signalling". That is, half of the cells in the population start producing only one receptor and ligand-type, which are of opposite type to avoid self-binding, while in the other half of the population it is the other way round. I find the paper very clearly written, the research interesting and worthy of publication. I do however have few concerns and comments that must be addressed before I can recommend this paper for publication.

Essential revisions:

1) How does the evolution towards asymmetry kick off?a) It seems that for either of the two initially non-utilized receptors "r" or ligands "l" to have a selective advantage, the other must already be present in the population. Is this true?

b) If true, is it that you can nevertheless get evolution towards asymmetry because the mutation rates are assumed high and so at the mutation-selection balance there are always some "l" and "r" in the population? Would you ever observe evolution towards E2 if mutation rates would be of several orders lower?

c) To gain more insight on the evolution towards asymmetry, can you perform some (analytical) invasion analysis e.g. check the stability of E1 and E2?

2) It could be helpful to include some simple phase-plane/stability analysis for the model (1-3), at least in the appendix. How do we know the concentration of L and R reach their steady state (4-6)? Also, is this the only steady state? Also, in (1-3) should it be dt instead of d[R]?

3) Subsection “Theoretical set-up: Should the timescale separation argument be the other way round? Because if cells encounter each other at high rate, they’re within cell concentration of L and R would not have enough time to reach their steady state. Why is this a reasonable assumption?

4) Is there a reason for not assuming trade-off in v_L vs. v_R? One could imagine that cell can't arbitrarily increase the production of both L and R. Also, wouldn't such a trade-off alleviate the conditions for the evolution of asymmetry?

5) If you would allow for three different receptors and ligands per cell, would three mating types evolve? Using the same logic, would you get an arbitrary number of mating types if the population would be sufficiently large and the mutation rates sufficiently high?

[Editors’ note: what now follows is the decision letter after the authors submitted for further consideration.]

Thank you for submitting your article "Evolution of asymmetric gamete signaling and suppressed recombination at the mating type locus" for consideration by eLife. Your article has been reviewed by Detlef Weigel as the Senior Editor, a Reviewing Editor, and two reviewers. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission. The consensus was that this is essentially ready to be accepted for publication, provided that the few points are addressed. The revised submission will not need to be sent out for review again.

Reviewer #1:

Thanks to the authors for carefully addressing my comments. I'm glad to see some of my ideas implemented, which I think add to the intuition gained here. I think there is still a bit of care needed in describing the stability of E1 and E2 (both comments in subsection “Evolution of mating types with asymmetric signaling roles”and Discussion section). I also think some care is needed in using "epistasis" to describe frequency dependent selection (subsection “Evolution of mating types with asymmetric signaling roles”), and analogies to fitness valley crossing might be useful.

Reviewer #3:

In my opinion the authors adequately addressed all the points raised by the reviewers. I recommend this paper for publication, provided the two points below will be taken into account.

1) It would be good to mention in the "main" text the population size that was used in the simulations. For example, in Figure 5 where you discuss the different mutation rates, in my opinion the population size should also be present. This leads me to a more general comment that it should be made clearer that the mutation rates used throughout the manuscript are unusually high (or at least I failed to find any mention on this caveat.). My guess is that if they would be decreased below the rates used in the paper, say to 10^-4 or 10^-6, the evolution to asymmetry would become extremely difficult, hinting that perhaps something else is going on in the evolution of gamete signalling in addition to what is already discussed in the model. At least a sentence or two to discuss this point would be good, e.g. in the Discussion section or somewhere else in the main text.

2) In subsection “Theoretical set-up” the timescale argument is now "correct", but, it would make more sense that the modeller assumes the rates (probability/unit of time) to be of different order from which it follows that the densities operate on different timescales (units of time).

https://doi.org/10.7554/eLife.48239.016

Author response

[Editors’ note: the author responses to the first round of peer review follow.]

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that we have decided to reject your paper in its present form. However, we would be willing to consider a revised version of your manuscript that takes into account the extensive reviewer comments.

The most important point in such a revision would be to address the criticism that it is unclear in the present version of the manuscript what exactly leads to the evolution of the mating type equilibrium E2. In particular, it is unclear whether the analytical and the simulation results presented in the paper lead to the same conclusions, and how the evolution of the asymmetric state depends on the mutational process. The relationship between the analytical and the simulation results needs to be made much clearer, and both reviewers 1 and 3 suggest doing an invasion analysis to clarify this point, e.g. using adaptive dynamics and pairwise in viability plots.

We have gone through the reviewer’s comments meticulously, have made several revisions and added further analyses to address these concerns. In particular, we have performed a detailed invasion analysis to demonstrate how and when the equilibrium state E2 evolves from E1. We have also computed pairwise invasibility plots and have made an effort throughout the Results section to better illustrate that our analytical and simulated results are in good agreement. Our detailed responses are attached to the reviewer comments below. We believe that the manuscript has greatly improved and appreciate the thorough review and feedback.

Other points you may wish to consider are the evolution of more than two mating types, as well as the possible effects of population-wide ligand and receptor production.

The evolution of the number of mating types is an interesting question. However, we believe that adding work in this direction would divert attention from the core messages of this paper (the evolution of a signaling asymmetry, mating types and suppressed recombination) and falls outside of this scope of the current work. We and others have addressed the evolution of the number of mating types in previous work (Hadjivasiliou and Pomiankowski, 2016 and Constable and Kokko, 2018), and the framework we have developed could be used in future work to investigate the role of ligand-receptor interactions in the evolution of the number of mating types. We discuss this in more detail in the revised manuscript (Discussion section).

The effects of population-wide ligand receptor signals also raise interesting questions. Such effects are to be expected when the ligand is highly diffusible so that its baseline concentration in the background environment is comparable to that produced by individual cells. In this sense our work does not apply to such signals, which are expected to be utilized for sexual chemotaxis. We chose to focus on membrane bound or only locally released (non-diffusible) molecules because this type of signaling is universal amongst isogamous eukaryotes with mating types, whereas diffusible signals are not (see Hadjivasiliou and Pomiankowski, 2016). We justify our choice in the revised manuscript (Introduction).

Reviewer #1:

[…]

Essential revisions:

I think a bit more could be done to demonstrate why the mating type equilibrium (E2) evolves from the monomorphic ancestor (E1), which I think is unclear in a few places (details below). One way to do this would be to take the approach of adaptive dynamics, and assume a monomorphic population (e.g., all individuals make only ligand 1 and receptor 1, v = (1,1,0,0)). You then calculate the fitness of a mutant with trait value v' = (x,y,1-x,1-y) in this population, take the derivatives with respect to x and y, and evaluate at the resident equilibrium (v' = v). A phase plane can then be shown, illustrating the direction of selection acting on small mutations around the resident. [I can send my Mathematica file that produces some examples if the authors wish.] Immediately from this one sees that E1 is locally stable (as the current Figure 2D suggests), as are the other four corners of the phase space. Of particular interest are the basins of attraction for each equilibrium, the effect of parameter values on the size of these basins, and the effects of parameter values on the strength of selection keeping a population within each basin (the "depth" of the basin if you will). The authors have rightly stated that there are multiple basins of attraction (subsection “Evolution of mating types with asymmetric signaling roles”) but in other places claim that E2 evolves from E1 because of strong selection for asymmetry (subsection “Evolution of mating types with asymmetric signaling roles”), implying E1 is instead unstable (i.e., there is no basin of attraction for E1). This idea of instability is implicit in Figure 3D-E, where the idea is that there are threshold values of k⁺, γ, and n that make E1 unstable. I think that the phase plane demonstrates that E1 remains stable for k⁺ finite and γ positive (I've only looked at n=0). Instead of changing the local stability of E1 these parameters change the size of the basin of attraction and its depth, therefore affecting the rate of drift out of E1 (so that "threshold" values of k⁺, γ, and n are just the values that allow this rate to be high enough to see E1 lost by the maximum number of generations simulated). In particular, increasing k⁺ decreases E1's basin of attraction and also makes the basin shallower, greatly facilitating drift out. In contrast, decreasing γ shrinks E1's basin of attraction but makes it deeper, meaning the rate at which E1 transitions to E2 might be less sensitive to changes in γ. This selection surface approach brings a number of new insights (e.g., increasing the size of basin vs. increasing the depth of the basin, the possibility of calculating the amount of drift needed to leave E1), could be used to explain the quantitative patterns in Figure 3D-F (e.g., yellow in Figure 3F is the boundary of the basin of attraction of E1), and highlights that E1 is always a stable state (which is not always clear from the text; subsection “Evolution of mating types with asymmetric signaling roles”). Further investigations along these lines could help illustrate the location and properties of the branching point leading to E2 (e.g., is there are "garden of eden" branching point at v = (0.5, 0.5, 0.5, 0.5)?). Additionally, one might take a quantitative genetic approach and use, for example, diffusion equations to ask what the rate of drift out of E1 is (e.g., Barton and Rouhani, 1987).

Thank you for such an in-depth review and detailed suggestions. We have used an adaptive dynamics approach to clarify the stability of E1. Reviewer 1 is correct in stating that E1 is stable to any single mutation. The population only evolves away from E1 when two mutations are present, conferring an asymmetry in ligand production and receptor production in opposite directions. No single mutation can confer an advantage on its own in a population where (v_L, v_R, v_l, v_r) = (1, 1, 0, 0) (Figure 3 and subsection “Dependence of gamete interactions on physical parameters” in revised manuscript). This effect can be thought of as a form of positive epistasis whereby the individual mutations are not favored but confer an advantage when they appear together.

This is discussed in more detail in the revised manuscript (subsection “Dependence of gamete interactions on physical parameters”).

We have made considerable effort to implement the reviewer’s suggestions. Note that this required an analysis considering two mutations and we opted to use a combination of analytical and numerical results to address this point. In particular:

1) We show the relative fitness of a mutant in different resident populations using our analytical results. This nicely illustrates that an asymmetry in both the ligand and receptor is required for mating types to evolve.

2) We investigate how the basin of attraction of E1 depends on key parameters (k⁺, γ and mutation rates) by considering the effect of small mutations in the ligand and receptor in a population initially at (v_L, v_R, v_l, v_r) = (1, 1, 0, 0) (Figure 5).

3) We also performed an invasion analysis and computed pairwise invasibility plots by investigating how a resident at (v_L, v_R, v_l, v_r)_res = (1-dx, 1, dx, 0) is invaded by a mutant at (v_L, v_R, v_l, v_r)_mut = (1, 1-dy, 0, dy) (Figure 6A). We find that the population reaches a polymorphic state with the mutant and resident at equal frequencies. We also use this approach to investigate how the population evolves from (v_L, v_R, v_l, v_r) = (0.5, 0.5, 0.5, 0.5) (Figure 6B). Our numerical results are in agreement with our analytical predictions (Figure 3 and Figure 5, Figure 6 are aligned). Note that the resident and mutant in our PIPs confer an asymmetry in opposite directions. This allowed us to produce two dimensional plots that illustrate how an asymmetry in ligand and receptor evolves.

We believe that these modifications and additions to our work have helped clarify our findings. We thank the reviewer for their detailed suggestions and hope that the revisions have adequately addressed the concerns raised above.

Reviewer #2:

[…]

My only criticism would be that there can be a contradiction between two hypotheses: diffusion of ligands is local, and the use of differential equations with products between molecular concentrations as the rate of contact. This precludes the possibility that ligands produced by the whole population might interact and disturb the signalling between cells. Considering interactions between only two close cells would need more precise modeling of spatialized and stochastic processes. I am not sure that it would change a lot the results, but I can imagine that considering the whole population ligands production could affect a lot of the evolutionary outcomes since it might affect a lot the importance of the self-binding parameter k⁺. It would have been interesting to compare whole population vs. two cells interactions.

We agree that the effects of population-wide ligand receptor signals raise interesting questions. Such effects are to be expected when the ligand is highly diffusible so that its baseline concentration in the background environment is comparable to that produced by individual cells. This is because diffusion gives rise to exponentially decaying profiles that would be unlikely to be comparable in magnitude to the concentration profiles in the vicinity of a single cell. This would not be true if the ligand was very highly diffusible but we restrict this work to consider either ligands that are released locally and effectively do not diffuse, or ligands that remain surface bound (Introduction). In this sense our work does not apply to diffusible signals, which are utilized for sexual chemotaxis or to synchronize entry into meiosis. We chose to focus on membrane bound or only locally released (non-diffusible) molecules because this type of signaling is universal amongst isogamous eukaryotes with mating types, whereas diffusible signals are not (Hadjivasiliou and Pomiankowski, 2016). It is therefore more pertinent to consider membrane bound signals when thinking about the early evolution of mating types. It would be interesting to explore how mating type interactions would be affected in situations where signals are diffusible, and cells have to communicate at a distance (e.g. to coordinate entry into meiosis). We touch on these interesting issues in the manuscript (Discussion section).

Reviewer #3:

[…]

Essential revisions:

1) How does the evolution towards asymmetry kick off?a) It seems that for either of the two initially non-utilized receptors "r" or ligands "l" to have a selective advantage, the other must already be present in the population. Is this true?

This is correct. No single mutation can confer an advantage on its own in a population where (v_L, v_R, v_l, v_r) = (1, 1, 0, 0) (Figure 3 and subsection “Dependence of gamete interactions on physical parameters” in revised manuscript). This effect can be thought of as a form of positive epistasis whereby the individual mutations are not favored but confer an advantage when they appear together. This is discussed in more detail in the revised manuscript (subsection “Evolution of mating types with asymmetric signaling roles”).

b) If true, is it that you can nevertheless get evolution towards asymmetry because the mutation rates are assumed high and so at the mutation-selection balance there are always some "l" and "r" in the population? Would you ever observe evolution towards E2 if mutation rates would be of several orders lower?

Indeed, the mutation rates in our analysis impact whether or not E2 evolves from E1 (Figure 5, Figure 4—figure supplement 1). E2 still evolves when the mutation rates are decreased by an order of magnitude but the basin of attraction for E2 shrinks (Figure 5). Reducing the mutation rate even further is likely to shrink the basin of attraction for E2 further. It follows that larger mutational steps would be required for E2 to evolve when mutation rates are low and populations are small. This is an interesting observation that goes back to the role of genetic drift. We made an effort to clarify these considerations in the revised manuscript (subsection “Evolution of mating types with asymmetric signaling roles”).

c) To gain more insight on the evolution towards asymmetry, can you perform some (analytical) invasion analysis e.g. check the stability of E1 and E2?

This is an important point and we have taken a few steps to further clarify how E2 evolves from E1 (please also see our response to reviewer 1). Because, as the reviewer points out above, more than one mutation is required for the evolution of E2 from E1 we had to use a combination of analytical and numerical methods to study and visualize how E2 evolves from E1. First, we have added a figure that shows the relative fitness of a mutant that appears in different resident populations (Figure 3) based on our analytical results. This was then verified by an invasion analysis using simulation (Figure 5). We show that E1 can be invaded by small mutations that confer signaling asymmetry in opposite directions (Figure 5). We explore how the basin of attraction for E2 changes based on different key parameters. We also used simulation to explore how resident populations with a varying degree of asymmetry are invaded by mutants conferring an asymmetry in the opposite direction to reach a polymorphic equilibrium (Figure 6). We think that these changes have helped clarify and solidify our previous findings and thank the reviewer for their suggestions.

2) It could be helpful to include some simple phase-plane/stability analysis for the model (1-3), at least in the appendix. How do we know the concentration of L and R reach their steady state (4-6)? Also, is this the only steady state?

Figure 2—figure supplement 1 shows the steady state concentration for L, R and [LR] for varying values of v_R and v_L. We assume that the rate of encounters and the duration of the mating process occur at time scales longer than those of the production and degradation rates of the ligand and receptor. This is a reasonable assumption as it takes many hours for cells to meet and mate whereas degradation rates (determining the timescale for reaching a steady state) are generally faster. There is a unique steady state solution with positive concentrations, this follows from solving the quadradic equations that emerge by setting d[L]/dt = d[R]/dt = d[LR]/dt = 0. We now clarify this in the Materials and methods section.

Also, in (1-3) should it be dt instead of d[R]?

Yes. Very silly typo, now corrected.

3) Subsection “Theoretical set-up”: Should the timescale separation argument be the other way round? Because if cells encounter each other at high rate, they’re within cell concentration of L and R would not have enough time to reach their steady state. Why is this a reasonable assumption?

Reviewer 3 is correct. This was an unfortunate mistake, apologies for the confusion. Now corrected.

4) Is there a reason for not assuming trade-off in v_L vs. v_R? One could imagine that cell can't arbitrarily increase the production of both L and R. Also, wouldn't such a trade-off alleviate the conditions for the evolution of asymmetry?

We assume that there is an upper limit in v_L and v_R (normalized at 1). We did consider imposing a trade-off between v_L and v_R. However, cells require both a ligand and a receptor to be able to mate and so imposing a trade-off between the production of the two seemed somewhat artificial. If we were to impose (v_L+v_l) + (v_R+v_r) < 1, we expect to simply shift the upper limit for v_L+v_l and v_R+v_r to 0.5 (rather than 1) which is why we have refrained from doing so.

5) If you would allow for three different receptors and ligands per cell, would three mating types evolve? Using the same logic, would you get an arbitrary number of mating types if the population would be sufficiently large and the mutation rates sufficiently high?

This is certainly possible. Given our own past work and that of others (e.g. Hadjivasiliou and Pomiankowski, 2016 and Constable and Kokko, 2018), we expect the strength of the interaction between the different receptors and ligands, the mutation rates at which new ligands/receptors appear, the population size and duration of asexual phase to together determine the optimal number of mating types. It would be interesting to explore this further using the current framework but we fear than doing so would divert from the core message of this manuscript. We discuss these ideas in the revised manuscript (Discussion section) and hope to explore these questions within the framework developed here in future work.

[Editors' note: the author responses to the re-review follow.]

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission. The consensus was that this is essentially ready to be accepted for publication, provided that the few points are addressed. The revised submission will not need to be sent out for review again.

Reviewer #1:

Thanks to the authors for carefully addressing my comments. I'm glad to see some of my ideas implemented, which I think add to the intuition gained here. My remaining comments are relatively minor. I think there is still a bit of care needed in describing the stability of E1 and E2 (both comments in subsection “Evolution of mating types with asymmetric signaling roles”and Discussion section). I also think some care is needed in using "epistasis" to describe frequency dependent selection (subsection “Evolution of mating types with asymmetric signaling roles”), and analogies to fitness valley crossing might be useful.

We have made several edits to address these concerns.

Reviewer #3:

In my opinion the authors adequately addressed all the points raised by the reviewers. I recommend this paper for publication, provided the two points below will be taken into account.

1) It would be good to mention in the "main" text the population size that was used in the simulations. For example, in Figure 5 where you discuss the different mutation rates, in my opinion the population size should also be present. This leads me to a more general comment that it should be made clearer that the mutation rates used throughout the manuscript are unusually high (or at least I failed to find any mention on this caveat.). My guess is that if they would be decreased below the rates used in the paper, say to 10^-4 or 10^-6, the evolution to asymmetry would become extremely difficult, hinting that perhaps something else is going on in the evolution of gamete signalling in addition to what is already discussed in the model. At least a sentence or two to discuss this point would be good, e.g. in the Discussion section or somewhere else in the main text.

This is an important point. In fact, the key reason mutation rates are so important is that the population sizes we consider are relatively small. This introduces drift that leads to the loss of mutants exhibiting an asymmetry before they increase in frequency. We predict that higher population sizes would lead to the evolution of asymmetric signaling for smaller mutation rates. In addition, when the population size is “infinite” the evolution of asymmetry should become independent of the mutation rate, μ (or frequency at which the mutant is introduced, p). These are interesting effects, but we refrain from studying drift in this work and instead place more emphasis on the relative impact of the physical parameters that dictate signaling interactions.

It is also worth pointing out that unicellular eukaryotes undergo several rounds of asexual growth between each sexual phase (this can vary from tens to thousands of vegetative steps, see Constable and Kokko, 2018 and Hadjivasiliou, Pomiankowski and Kuijper, 2016). The effective mutation rate introducing variation in the production of ligands and receptors between sexual rounds is therefore likely to be several orders of magnitude higher than the actual mutation rate at each vegetative step.

We now explicitly state the relevant population size used (Introduction and in figure legends where relevant) and have added a paragraph in the Discussion section addressing the issues raised above.

2) In subsection “Theoretical set-up” the timescale argument is now "correct", but, it would make more sense that the modeller assumes the rates (probability/unit of time) to be of different order from which it follows that the densities operate on different timescales (units of time).

We have slightly modified the text to reflect this.

https://doi.org/10.7554/eLife.48239.017

Article and author information

Author details

Zena Hadjivasiliou
1. Department of Biochemistry, University of Geneva, Geneva, Switzerland
2. Centre for Mathematics and Physics in the Life Sciences and Experimental Biology (CoMPLEX), University College London, London, United Kingdom
3. Department of Genetics, Evolution and Environment, University College London, London, United Kingdom
Contribution
Conceptualization, Data curation, Formal analysis, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing

For correspondence
zena.hadjivasiliou@unige.ch

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-1174-1421
Andrew Pomiankowski
1. Centre for Mathematics and Physics in the Life Sciences and Experimental Biology (CoMPLEX), University College London, London, United Kingdom
2. Department of Genetics, Evolution and Environment, University College London, London, United Kingdom
Contribution
Data curation, Formal analysis, Funding acquisition, Investigation, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-5171-8755

Funding

Human Frontier Science Program (Long Term Fellowship)

Zena Hadjivasiliou

Engineering and Physical Sciences Research Council (EP/L50488/)

Zena Hadjivasiliou

Engineering and Physical Sciences Research Council (EP/F500351/1)

Andrew Pomiankowski

Natural Environment Research Council (NE/R010579/1)

Andrew Pomiankowski

Engineering and Physical Sciences Research Council (EP/I017909/1)

Andrew Pomiankowski

Engineering and Physical Sciences Research Council (EP/K038656/1)

Andrew Pomiankowski

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This research was funded by an Engineering and Physical Sciences Research Council Fellowship (EP/L50488/) and HFSP Long Term Fellowship to ZH, and by grants from the Engineering and Physical Sciences Research Council (EP/F500351/1, EP/I017909/1, EP/K038656/1) and the Natural Environment Research Council (NE/R010579/1) to AP. The authors thank Michael Doebeli and three anonymous reviewers for comments that have helped improve this manuscript. ZH would like to thank Natalia Tokarova for her work on an earlier version of this project as a summer student at UCL, and Marcos Gonzalez-Gaitan for his support.

Senior Editor

Detlef Weigel, Max Planck Institute for Developmental Biology, Germany

Reviewing Editor

Michael Doebeli, University of British Columbia, Canada

Version history

Received: May 7, 2019
Accepted: July 25, 2019
Version of Record published: August 29, 2019 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

1,480

Page views
141

Downloads
2

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Zena Hadjivasiliou
Andrew Pomiankowski

(2019)

Evolution of asymmetric gamete signaling and suppressed recombination at the mating type locus

eLife 8:e48239.

https://doi.org/10.7554/eLife.48239

Share this article

Cite this article

Gametes communicate through ligand and receptor molecules.

Signaling interactions between mating cells can be severely impaired due to ligand-receptor interactions in the same cell.

Fitness advantage of rare mutations conferring signaling asymmetry.

Evolution of asymmetric signaling.

Invasion of E1.

Joint evolution of receptor and ligand asymmetry.

The effect of recombination on E2.

Equilibrium recombination rate ρ*.

Author details

Zena Hadjivasiliou

Contribution

For correspondence

Competing interests

Andrew Pomiankowski

Contribution

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading

Invasion of $E_{1}$ .

The effect of recombination on $E_{2}$ .

Equilibrium recombination rate $ρ^{*}$ .