Modeling the dynamics of Plasmodium falciparum gametocytes in humans during malaria infection
- University of Melbourne, Australia
- Radboud University Medical Center, Netherlands
- QIMR Berghofer Medical Research Institute, Australia
- Mahidol University, Thailand
- University of Oxford, United Kingdom
- Peter Doherty Institute for Infection and Immunity, Australia
Figures
Figure 1 with 15 supplements
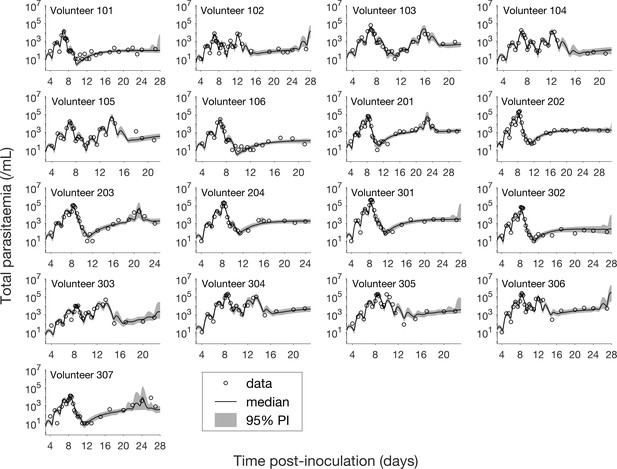
Results of model fitting for all 17 volunteers.
Data are presented by circles. The median of posterior predictions (solid line) and 95% prediction interval (PI, shaded area) are generated by 5000 model simulations based on 5000 samples from the …
Figure 1—figure supplement 1
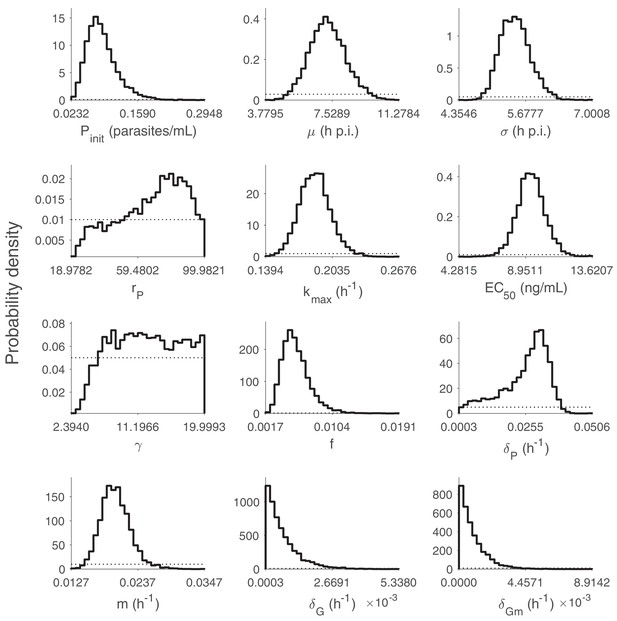
Marginal posterior distributions for the 12 population mean parameters (hyperparameters).
5000 samples are used to generate the distributions. The dashed curves indicate the uniform prior distributions. p.i.: post-inoculation. Note that the y-axis is probability density instead of number …
Figure 1—figure supplement 2
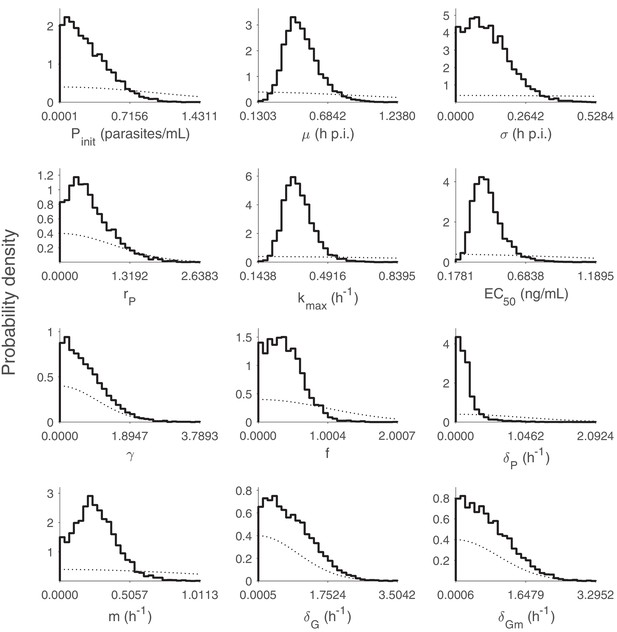
Marginal posterior distributions for the 12 population SD parameters (hyperparameters).
5000 samples are used to generate the distributions. The dashed curves indicate the half-normal prior distributions. p.i.: post-inoculation. Note that the y-axis is probability density instead of …
Figure 1—figure supplement 3
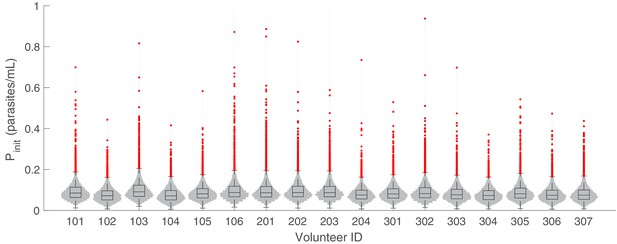
The marginal posterior distributions of the individual parameter of (inoculation size) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 4
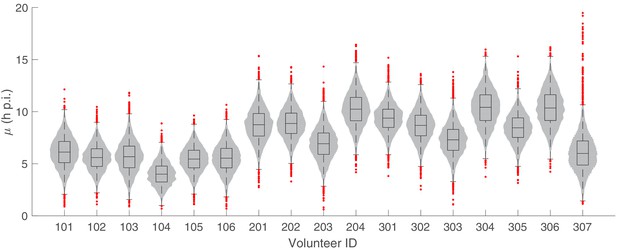
The marginal posterior distributions of the individual parameter of µ (mean of the initial parasite age distribution) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 5
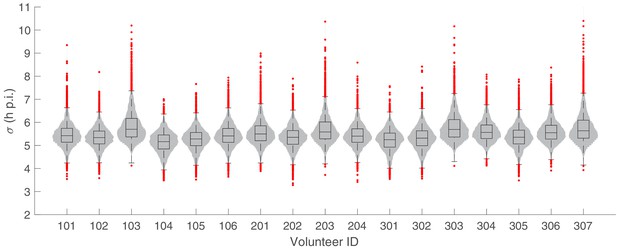
The marginal posterior distributions of the individual parameter of (Standard deviation of the initial parasite age distribution) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 6
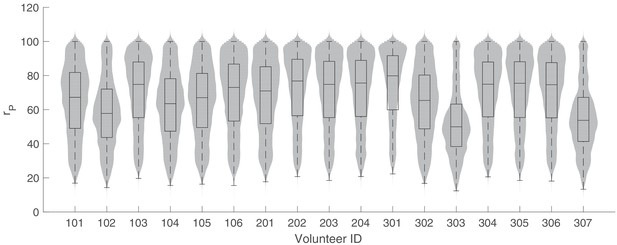
The marginal posterior distributions of the individual parameter of (parasite replication rate) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 7
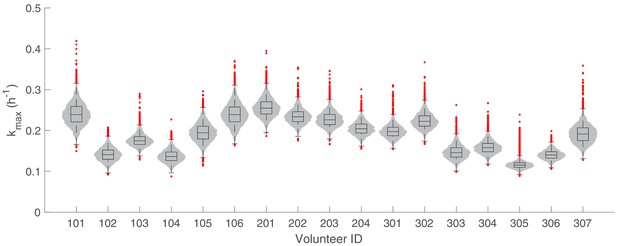
The marginal posterior distributions of the individual parameter of (maximum rate of parasite killing by PQP) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 8
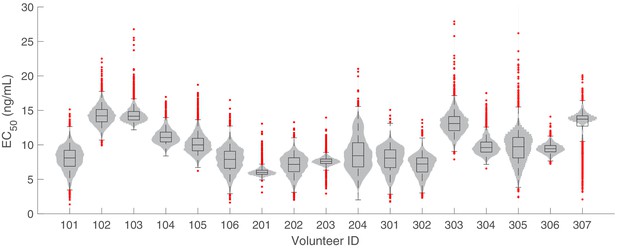
The marginal posterior distributions of the individual parameter of (half-maximum effective PQP concentration) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 9
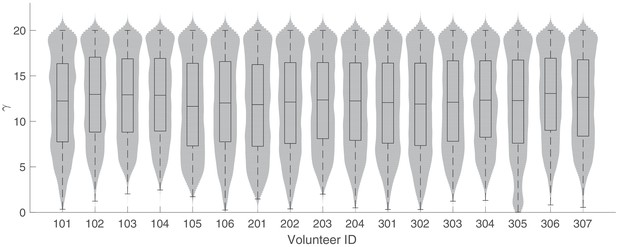
The marginal posterior distributions of the individual parameter of (Hill coefficient for PQP) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 10
The marginal posterior distributions of the individual parameter of (sexual commitment rate; not converted to percentage) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 11
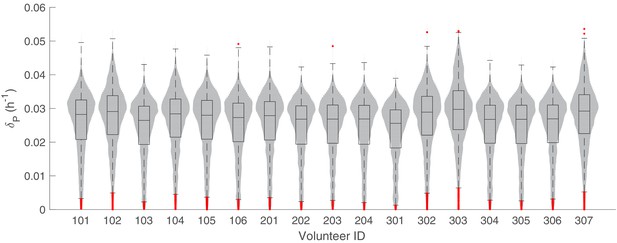
The marginal posterior distributions of the individual parameter of (death rate of asexual and sexual parasites) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 12
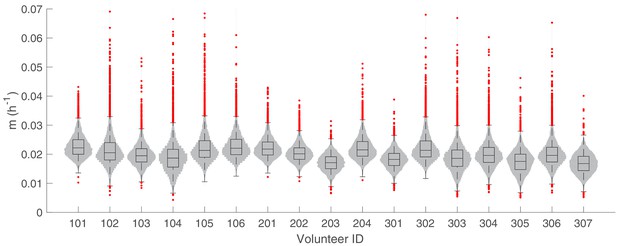
The marginal posterior distributions of the individual parameter of (maturation rate of gametocytes) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 13
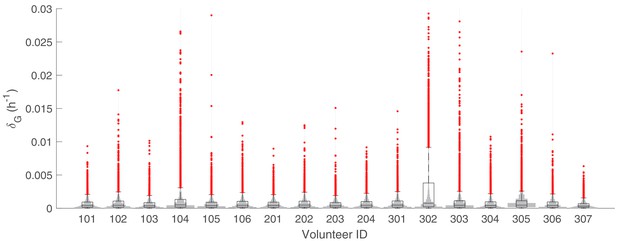
The marginal posterior distributions of the individual parameter of (death rate of sequestered gametocytes) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 14
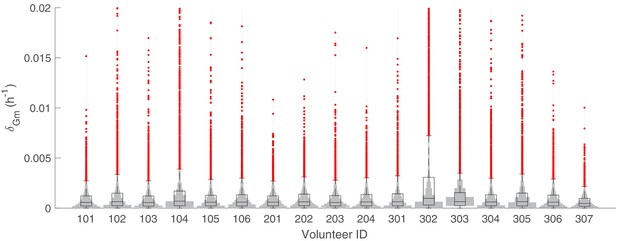
The marginal posterior distributions of the individual parameter of (death rate of circulating gametocytes) for all 17 volunteers.
The violin plots (gray area) show the distributions of 5000 posterior samples. Box plots show the 25%, 50% (median) and 75% quantiles with outliers indicated by red dots. Relevant details of the …
Figure 1—figure supplement 15
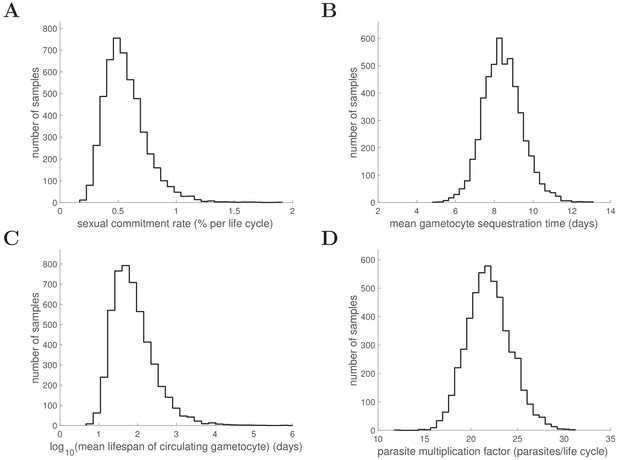
Marginal posterior distributions of some key biological parameters.
5000 samples from the posterior parameter distribution are used to generate the figures. Full details about the definitions and expressions of those biological parameters are provided in the …
Figure 2
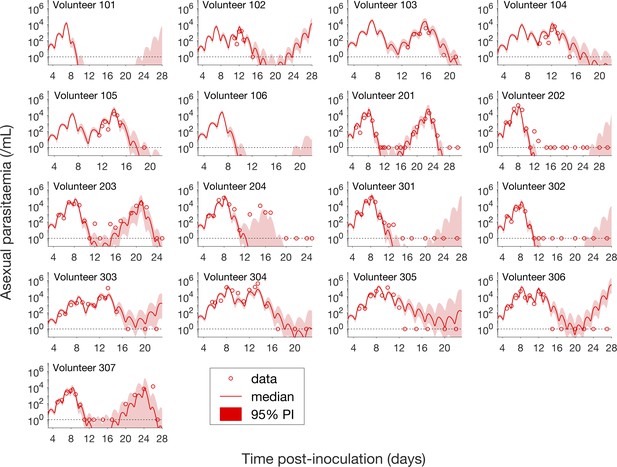
Comparison of model predictions and clinical data for the asexual parasitemia for all 17 volunteers.
Data are presented by circles. The median of posterior predictions (solid curve) and 95% PI (shaded area) are generated by 5000 model simulations based on 5000 samples from the posterior parameter …
Figure 3
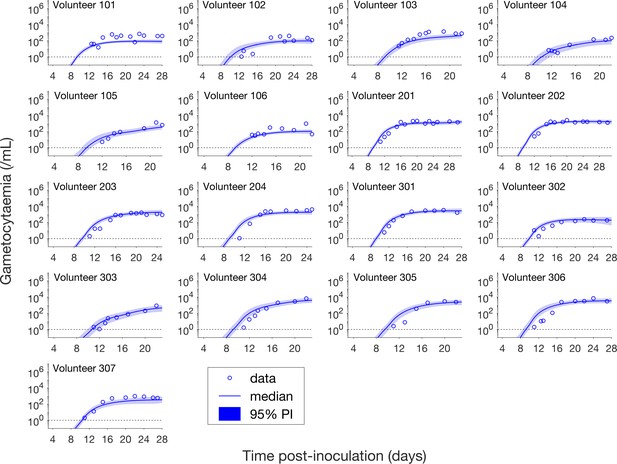
Comparison of model predictions and clinical data for the gametocytemia for all 17 volunteers.
Data are presented by circles. The median of posterior predictions (solid curve) and 95% PI (shaded area) are generated by 5000 model simulations based on 5000 samples from the posterior parameter …
Figure 4
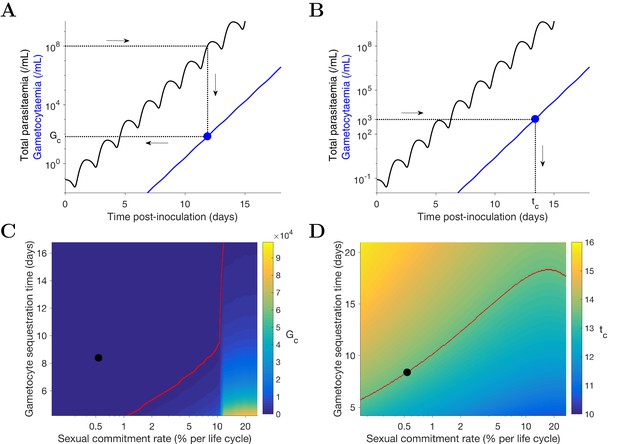
Simulation of two scenarios predicting the dependence of human-to-mosquito transmissibility on the sexual commitment rate and gametocyte sequestration time.
(A) illustration of the first scenario: predicting the critical gametocytemia level (indicated by Gc) at the time when the total parasitemia reaches 108 parasites/mL. (B) illustration of the second …
Figure 5
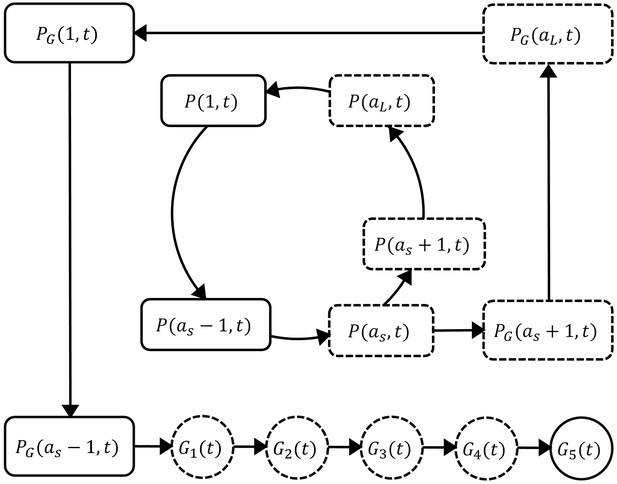
Schematic diagram showing the model compartments and transitions.
The model is comprised of three parts describing three populations of parasites: asexual parasites (), sexually committed parasites () and gametocytes (). P and PG are functions of asexual …
Figure 6 with 1 supplement
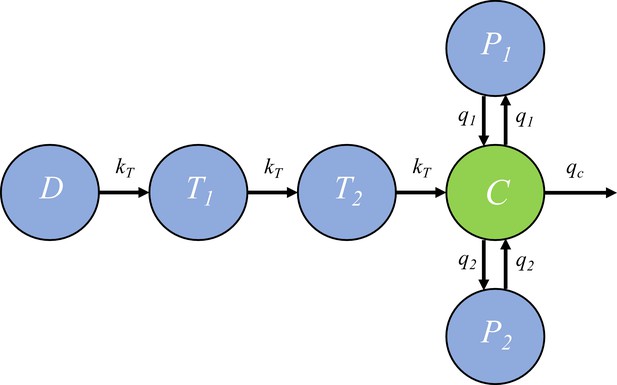
The pharmacokinetic model of piperaquine (PQP).
The model is a three-compartment disposition model with two transit compartments for absorption. State D represents the dose of PQP. T1 and T2 represent the two transit compartments. C is the …
Figure 6—figure supplement 1
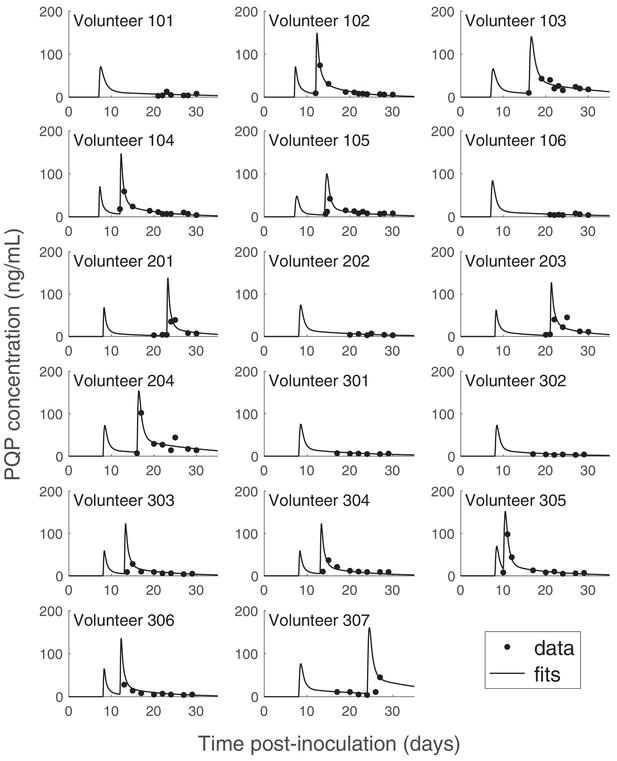
PK data and optimized PK curves (the ‘fits’) of piperaquine (PQP) concentration for all volunteers.
The details of the optimization approach are provided in the Materials and methods in the main text and Appendix 1. Some volunteers have two peaks of PQP concentrations because they had recrudescent …
Tables
Table 1
Estimates of some key biological parameters and comparison with the literature.
The estimates of the biological parameters (middle column) are shown as the median and 95% credible interval (CI) of the marginal posterior parameter distribution (Figure 1—figure supplement 15). …
| Biological parameters (unit) | Median estimate (95% CI) | Estimates in the literature |
|---|---|---|
| Sexual commitment rate (%/asexual replication cycle) | 0.54 (0.30–1.00) | 11 (6.2–15.8) (Filarsky et al., 2018) (in vitro) 0.64 [0.027–13.5] (Eichner et al., 2001) (in vivo) |
| Gametocyte sequestration time (days) | 8.39 (6.54–10.59) | 7.4 [4 – 12] (Eichner et al., 2001) (in vivo) |
| Circulating gametocyte lifespan (days) | 63.5 (12.7–1513.9) | 16–32 (Gebru et al., 2017) (in vitro) 6.4 [1.3–22.2] (Eichner et al., 2001) (in vivo) |
| Parasite multiplication factor (per asexual replication cycle) | 21.8 (17.6–26.9) | 10–33 (Wockner et al., 2017) (in vivo) 16.4 (15.1–17.8)a (in vivo) |
-
a JS McCarthy, personal communication, May 2019.
Table 2
Details of the gametocyte dynamics model parameters.
The table includes the unit, description and prior distribution for each model parameter. For the uniform prior distributions (U), the lower bounds are non-negative based on the definitions of the …
| Parameter | Unit | Description | Prior distribution |
|---|---|---|---|
| parasites/mL | inoculation size | U(0, 10) | |
| h | mean of the initial parasite age distribution | U(0, 35) | |
| h | SD of the initial parasite age distribution | U(0, 20) | |
| (unitless) | parasite replication rate | U(0, 100) | |
| h−1 | maximum rate of parasite killing by PQP | U(0, 1) | |
| ng/mL | half-maximum effective PQP concentration | U(1, 100) | |
| (unitless) | Hill coefficient for PQP | U(0, 20) | |
| (unitless) | the fraction of parasites entering sexual development per asexual replication cycle | U(0, 1) | |
| h−1 | death rate of asexual and sexual parasites | U(0, 0.2) | |
| h−1 | maturation rate of gametocytes | U(0, 0.1) | |
| h−1 | death rate of sequestered gametocytes | U(0, 0.1) | |
| h−1 | death rate of circulating gametocytes | U(0, 0.1) | |
| h | sequestration age of asexual parasites | fixed to be 25 | |
| h | length of life cycle of asexual parasites | fixed to be 42 |
-
SD: standard deviation; h: hour.
Appendix 1—table 1
Parameter values used to generate the optimized PK curves for all 17 volunteers.
The units of the model parameters are given in the parentheses. The optimized PK curves are shown in Figure 6—figure supplement 1.
| PK parameter (unit) | kT(h-1) | qc(L/h) | Vc(L) | q1(L/h) | V1(L) | q2(L/h) | v2(L) |
|---|---|---|---|---|---|---|---|
| Volunteer 101 | 1/2.43 | 53.7 | 831 | 2240 | 3958 | 118 | 17177 |
| Volunteer 102 | 1/2.32 | 123.4 | 582 | 849 | 3985 | 163 | 10355 |
| Volunteer 103 | 1/3.07 | 61.3 | 756 | 2686 | 3910 | 127 | 14346 |
| Volunteer 104 | 1/2.32 | 134.7 | 488 | 746 | 3986 | 190 | 15007 |
| Volunteer 105 | 1/3.25 | 160 | 1342 | 5034 | 3986 | 190 | 17546 |
| Volunteer 106 | 1/2.40 | 60.7 | 667 | 2992 | 3043 | 123 | 16374 |
| Volunteer 201 | 1/2.32 | 160 | 469 | 746 | 3986 | 190 | 15557 |
| Volunteer 202 | 1/2.79 | 71.4 | 804 | 2020 | 3010 | 149 | 13300 |
| Volunteer 203 | 1/2.32 | 141.9 | 1243 | 803 | 3973 | 190 | 11825 |
| Volunteer 204 | 1/2.32 | 63.3 | 895 | 2169 | 3327 | 165 | 16205 |
| Volunteer 301 | 1/2.79 | 61.4 | 804 | 2020 | 3010 | 149 | 13300 |
| Volunteer 302 | 1/2.79 | 81.4 | 804 | 2020 | 3010 | 149 | 13300 |
| Volunteer 303 | 1/2.45 | 159.4 | 1332 | 779 | 3970 | 190 | 17355 |
| Volunteer 304 | 1/2.48 | 158.9 | 1339 | 762 | 3981 | 190 | 17290 |
| Volunteer 305 | 1/2.53 | 120.9 | 1152 | 1905 | 2979 | 123 | 13896 |
| Volunteer 306 | 1/2.32 | 158.8 | 870 | 761 | 3983 | 190 | 17488 |
| Volunteer 307 | 1/2.79 | 51.4 | 804 | 2020 | 3010 | 149 | 13300 |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.49058.026
