Golgi compartments enable controlled biomolecular assembly using promiscuous enzymes
- Simons Centre for the Study of Living Machines, National Centre for Biological Sciences, Tata Institute of Fundamental Research, India
Figures
Figure 1
Glycan synthesis by promiscuous enzymes in Golgi compartments.
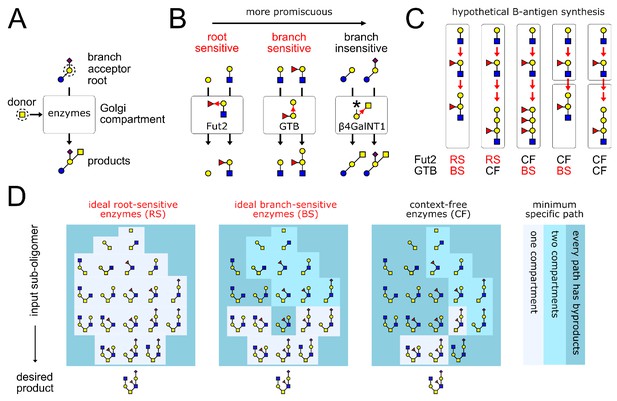
(A) A GTase enzyme catalyzes a glycosidic linkage between a specific donor monomer type (the ‘donor-substrate’) and a specific acceptor monomer type with specific branches or roots (the ‘acceptor-substrate’). We represent distinct monomer types in an oligomer by shapes/colors, and linkages between distinct monomer carbons by distinct bond angles (Varki et al., 2017). (B) GTase enzymes can show varying degrees of promiscuity, demonstrated here by three real examples of enzymes that act on galactose acceptors (Taniguchi and Honke, 2014, Chapter 39,44,47). We represent each GTase enzyme graphically, showing its acceptor-substrate and the specific monomer-addition reaction it catalyzes (red arrow from acceptor to donor at distinct angles for distinct acceptor carbons). The root-sensitive enzyme Fut2 requires the galactose acceptor to be linked to a GlcNAc root monomer. The branch-sensitive enzyme GTB requires its galactose acceptor to have a fucose branch. The branch-insensitive enzyme β4GalNT1 can act on branched or un-branched galactose monomers. (C) The localization of enzymes in successive Golgi compartments can sometimes mitigate the variability caused by enzyme promiscuity. This is demonstrated using the example of blood group B-antigen synthesis by the root-sensitive (RS) enzyme Fut2 and branch-sensitive (BS) enzyme GTB. We consider hypothetical scenarios in which these enzymes are context-free (CF). Increased enzyme promiscuity leads to tandem repeat byproducts. Placing the context-free Fut2 enzyme in a separate compartment from branch-sensitive GTB restores specific synthesis of the B-antigen. (D) Our main result is illustrated by this example (elaborated in Figure 4). We show the minimum number of compartments needed to specifically synthesize the same product oligomer from any of its sub-oligomers. We compare three broad classes of enzymes: ideal root-sensitive and branch-sensitive enzymes (ideal enzymes can read root chains or branches to arbitrary depth) or context-free enzymes. Ideal root-sensitive enzymes can distinguish the position of every acceptor monomer in an oligomer, so they can specifically synthesize any product in a single compartment. Branch-sensitive and context-free enzymes are more promiscuous; splitting such enzymes across multiple compartments increases the repertoire of oligomers they can specifically synthesize.
Figure 2
Observed patterns of glycan variability.
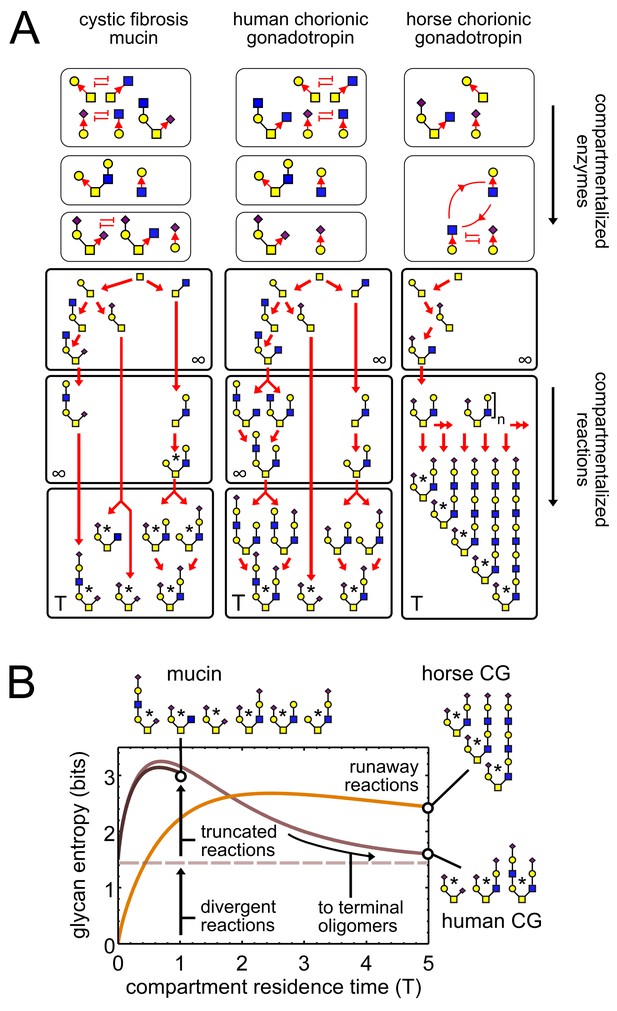
(A) We compare oligomer profiles from three datasets (Lo-Guidice et al., 1994; Hård et al., 1992; Hokke et al., 1994); observed oligomers are starred, only non-fucosylated oligomers are shown. For each profile, we show a hypothetical set of compartmentalized enzymes leading to its synthesis; cyclic arrows represent runaway reactions, blunt arrows represent the action of one enzyme blocking the action of another. Each enzyme set is associated with a reaction network; red arrows show single-monomer-addition reactions. All oligomers exit the compartment as outputs after some average residence time. The residence time of the last compartment in each series is ; the residence time of all other compartments is . (B) Effect of compartment residence time on glycan variability, quantified using Shannon entropy. The entropy of the compartment’s output distribution depends on that of its input distribution, on the structure of the compartment’s reaction network, and on its average residence time .
Figure 3
Enzymatic causes of glycan variability.
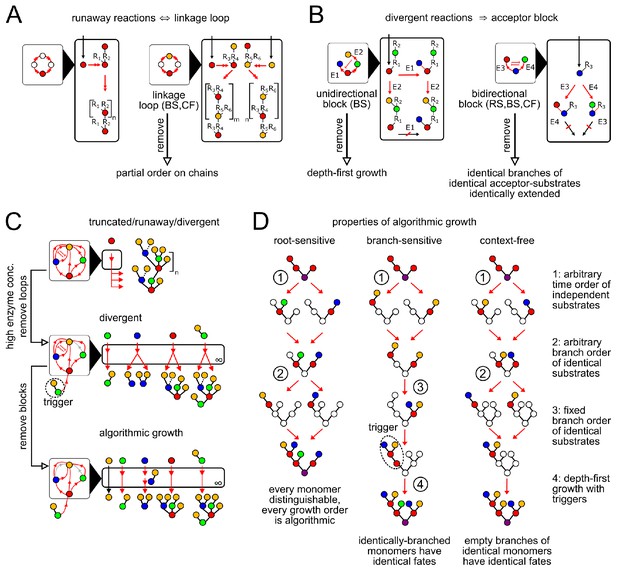
(A) Runaway reactions occur whenever certain steps of oligomer growth can be iterated to produce tandem repeats. Loops in the linkage network are necessary and sufficient for runaway reactions (Appendix 2, Lemma 1). An acyclic linkage network imposes a partial order on monomer types along any chain. represents an arbitrary oligomer. Boxes with black triangles represent the linkage network, showing all orders in which monomer types can be linked, with arrows from acceptor monomer types to donor monomer types (Appendix 2, Remark 2). Double arrows in linkage and reaction networks represent multiple reaction steps. (B) Divergent reactions occur whenever the reaction network has a fork that can never reconverge. This occurs when the action of one enzyme blocks the subsequent action of another, so the fate of the oligomer depends on the random order of enzyme action. Blunt red arrows in the linkage network represent the action of one enzyme blocking the action of another. Acceptor blocks are necessary (but not sufficient) for divergent reactions (Appendix 2, Lemma 2). Unidirectional acceptor block (only branch-sensitive enzymes): the acceptor-substrate of one enzyme is on some branch of the acceptor-substrate of another. Bidirectional acceptor block (all enzyme classes): two enzymes compete for the same acceptor-substrate. (C) We start with a compartment containing an arbitrary collection of enzymes. We can eliminate truncated reactions by ensuring high enzyme concentrations. We can eliminate runaway reactions by removing (or disabling with triggers, for branch-sensitive enzymes) at least one enzyme involved in each linkage loop. We can eliminate divergent reactions by removing all but one enzyme involved in each block. The result is an algorithmic compartment: for each possible input, it specifically synthesizes a corresponding unique output. (D) Properties of algorithmic growth, for different enzyme classes. See Appendix 3—figure 1 for a detailed example of branch-sensitive algorithmic growth.
Figure 4
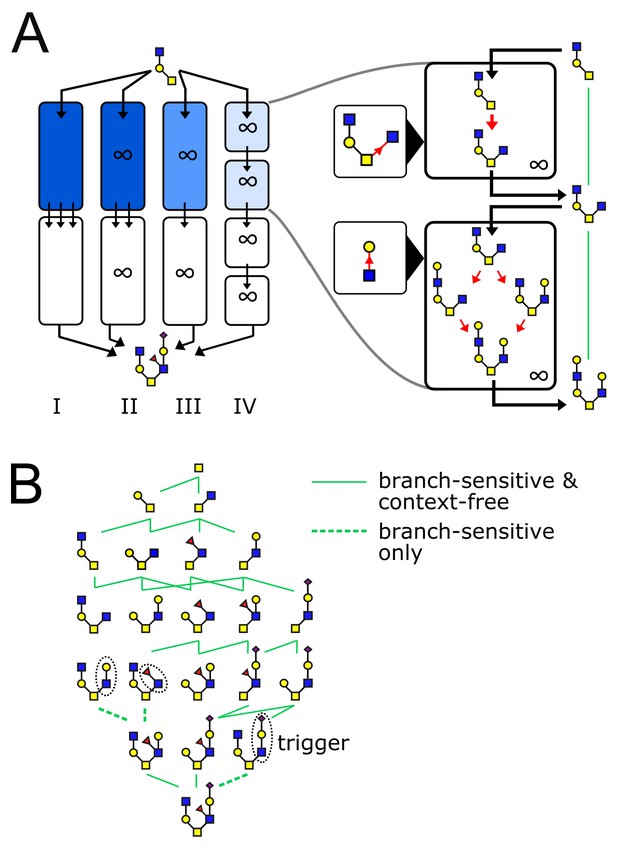
The glycan biosynthetic repertoire of multi-compartment systems.
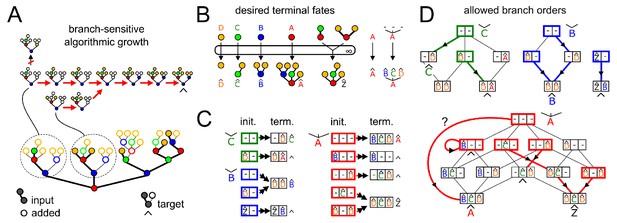
(A) Outline of Theorem 1 (Appendix 2). Suppose we are given a series of compartments that specifically synthesizes a desired target oligomer from a given input oligomer. We now proceed to modify the original compartments through several steps. Step I → II: Ensure enzyme concentrations are high, to eliminate intermediate oligomers. Step II → III: Remove all enzymes with acceptor blocks, to eliminate divergent reactions. Step III → IV: Replace each compartment with a series of infinite-residence-time compartments each containing a single enzyme. At each step, at least one of the original growth orders still remains, leading to the desired target oligomer. (B) We are given a target oligomer (bottom). We list all its sub-oligomers, and connect two oligomers by a green edge if some single-enzyme compartment can specifically synthesize the lower oligomer from the higher oligomer. All single-monomer additions can be achieved with ideal root-sensitive enzymes; only a subset of these can be achieved with branch-sensitive or context-free enzymes. To find the minimum number of compartments required to synthesize the target oligomer from any sub-oligomer, we decompose allowed paths into algorithmic growth stretches (Figure 1D).
Appendix 3—figure 1
Efficient search for a branch-sensitive algorithmic growth order from input to target.
Tables
Table 1
Variability caused by promiscuous, stochastic enzymes.
| Observed product pattern | Type of reaction variability | Enzymatic cause | ||
|---|---|---|---|---|
| intermediate oligomers | ⇔ | truncated reaction | ⇔ | low concentration |
| tandem repeats | ⇔ | runaway reaction | ⇔ | linkage loop |
| mutually exclusive fates | ⇔ | divergent reaction | ⇒ | acceptor block |
Additional files
-
Source code 1
MATLAB code to accompany Figure 2B.
- https://cdn.elifesciences.org/articles/49573/elife-49573-code1-v2.m.zip
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/49573/elife-49573-transrepform-v2.pdf
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Golgi compartments enable controlled biomolecular assembly using promiscuous enzymes
eLife 9:e49573.
https://doi.org/10.7554/eLife.49573
