Figures and data in Correcting for physical distortions in visual stimuli improves reproducibility in zebrafish neuroscience | eLife

Figures
Additional files

5 figures and 1 additional file

Figures

Figure 1

Download asset Open asset

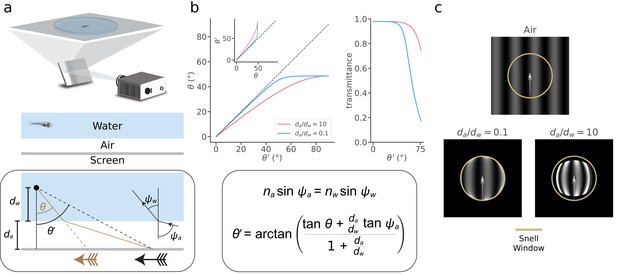
Snell's law describes visual stimulus distortions that occur via air-water interfaces encountered in a typical experiment.

(a) Top, In a typical zebrafish neuroscience experiment, an image is presented via projection onto a screen underneath an animal in a water-filled plastic dish. Middle, A small layer of air separates the screen from the dish and water. Bottom box, This configuration causes the image received at the eye (brown arrow) to be distorted and translated relative to the projected image (black arrow). We can describe this transformation as a relationship between the true position of a projected point ( $θ^{'}$ ) and its apparent position ( $θ$ ), depending on the ratio between the distance from the air-water interface to the screen ( $d_{a}$ ) and the distance from the eye to the air-water interface ( $d_{w}$ ). To solve the transformation, we use Snell’s law (illustrated in inset and panel b), which relates the angle at which a light ray leaves the air-water interface ( $ψ_{w}$ ) to the angle at which it hits the interface ( $ψ_{a}$ ), depending on the refractive indices of the media (air, $n_{a} = 1$ ; water, $n_{w} = 1.333$ ). Note that the effects of the plastic dish are typically minor (Appendix 1). (b) Top left, the apparent position of a point ( $θ$ ) as a function of its true position ( $θ^{'}$ ), and its inverse (inset), for $d_{a} / d_{w} = 10$ (pink) and $d_{a} / d_{w} = 0.1$ (blue). Top right, fraction of light transmitted into the water as a function of $θ^{'}$ for the same two values of $d_{a} / d_{w}$ . Bottom box, Using Snell’s law, we derived $θ^{'} (θ)$ (top left inset), whose inverse we take numerically to arrive at $θ (θ^{'})$ (top left). (c) Simulated distortion of a standard sinusoidal grating. Yellow circle denotes the extent of the Snell window (~97.2° visual angle). The virtual screen is modeled as a 4 × 4 cm square with 250 pixels/cm resolution, and we fixed the total distance between the fish and the virtual screen, $d_{a} + d_{w}$ , to be 1 cm. Note that only a fraction of the screen is apparent when $d_{a} / d_{w}$ is small (bottom left), but a distorted view of the full screen appears within the Snell window when $d_{a} / d_{w}$ becomes large (bottom right). Contrast axes are matched across panels and saturate to de-emphasize the ring of light at the Snell window, whose magnitude would be attenuated by unmodeled optics in the fish eye (Materials and methods).

Figure 2 with 1 supplement

Download asset Open asset

Snell's law corrections reduce discrepancies in the literature and predict effects on receptive field mapping.

(a) In the zebrafish literature, two configurations were used to probe the neural circuitry processing looming stimuli that expand over time. In one, fish were embedded off-center in a curved plastic dish and a screen presented stimuli in front of the animal through the curved interface of the dish (Temizer et al., 2015). In the other, fish were embedded (or swam freely) in a similar dish, but stimuli were presented on a screen below the dish (as in Figure 1a; Dunn et al., 2016a). (b) Plot detailing the changes to the looming expansion time courses after correcting for Snell’s law and converting to solid angle, which more accurately describes the irregular stimulus shapes produced by the optical distortion (Materials and methods). Curves corresponding to Dunn et al. and Temizer et al. are plotted in black and magenta, respectively. (c) Snell’s law corrections reduced the discrepancy between Dunn et al. and Temizer et al. Black: Snell’s law corrections decreased the absolute magnitude of the discrepancy (Dunn et al. critical solid angle minus Temizer et al. critical solid angle). We report discrepancies as fractions of the maximal solid angle (4π steradians) to aid intuition for stimulus sizes. Blue: Snell’s law corrections also decreased the relative magnitude of the discrepancy (Dunn et al. size divided by Temizer et al. size). (d) In a simple receptive field (RF) mapping experiment, dots appear at different positions on a screen (Top), and behavioral or neural responses (Bottom) are measured. In the latter case, a map of a single neuron’s RF is constructed by assigning the measured $Δ F / F$ signal to the point on the screen that evoked the $Δ F / F$ response. (e) Snell’s law predicts changes in RF peak positions (Top) and RF sizes (Bottom). The magnitude of these changes depends on the true RF position (x-axis), true RF size (line color), and $d_{a} / d_{w}$ (warm versus cool colors). True RF positions and sizes correspond to the means and standard deviations of Gaussian receptive fields. The black dots indicate the RFs in panel f, top, and the gray dots show the RFs in panel f, bottom. (f) Illustrations of two simulated "true" RFs and their corresponding measurement distortions predicted using Snell’s law. For simplicity, we show only one quadrant of the screen space, with the fish at the top left corner. The brown circle denotes the extent of the Snell window. As RFs are mapped directly to screen pixels, the axes are nonlinear in terms of angle relative to the fish (top left corner). Each blue "x" denotes the peak position of the RF displayed in each plot. The dashed blue border denotes the half-maximum value of each RF, and the size of the RF is the solid angle within one of these borders.

Figure 2—video 1

Download asset

posterframe for video — Optical refraction distorts the appearance of looming visual stimuli.

Left: Example looming stimulus that grows with a time course mimicking an approaching object. Here the looming stimulus is a dark circle, the time course of its diameter corresponds to the Dunn et al. (2016a) "stimulus angle" curve in Figure 2b, and the stimulus eventually fills the screen. This is an example of a visual stimulus that would be projected directly onto the screen by Dunn et al. Right: Illustration of what the example looming stimulus would look like inside the water. Because of the flat air-water interface that separates the fish from the screen, eccentric regions of the visual field are compressed into the Snell window. The visual stimulus is therefore irregularly shaped. Since the looming stimulus is presented off-center, it is initially compressed within a small region near the periphery of the Snell window. The stimulus grows to eventually fill the entire Snell window.

Appendix 1—figure 1

Download asset Open asset

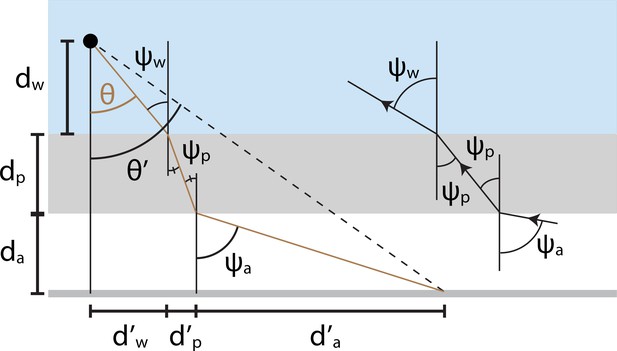
Illustration of mathematical variables used to analyze optical distortions in arena geometries where flat air-plastic and plastic-water interfaces separate the fish from the projection screen.

The brown line denotes the trajectory of a light ray traveling from the screen to the fish. We quantify the image transformation by relating the true angular position of each projected point ( $θ^{'}$ ) to its apparent position ( $θ$ ). The derivation involves several distances (e.g. $d_{w}$ ) that summarize the ray’s trajectory through air (white region), plastic (gray region), and water (blue region). Refraction angles ( $ψ_{a}, ψ_{p}, ψ_{w}$ ) describe the bending of light at each interface.

Appendix 2—figure 1

Download asset Open asset

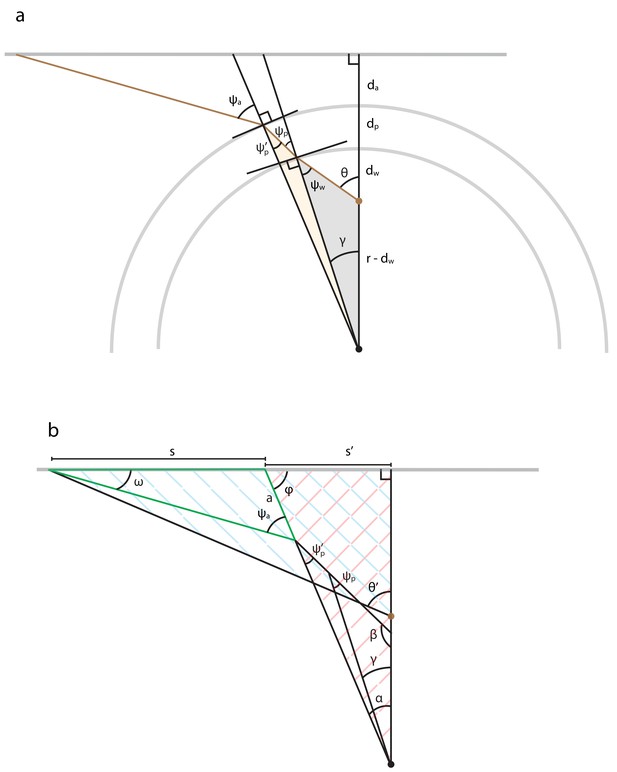
Illustration of mathematical variables used to analyze optical refraction at curved interfaces.

(a) We assume that the interfaces are circular, that the fish is mounted off-center (brown dot), and that the screen and fish are at the same elevation. We neglect distortions that could result from the flat vertical interface running parallel to the longitudinal axis of the cylindrical dish. We denote the radius of the arena’s water-filled compartment as $r$ . The derivation additionally involves several distances that summarize the placement of the fish in the dish ( $d_{w}$ ), the thickness of the plastic ( $d_{p}$ ), and the distance separating the dish from the screen ( $d_{a}$ ). Refraction angles ( $ψ_{a}, ψ_{p}^{'}, ψ_{p}, ψ_{w}$ ) of the light ray (brown line) are relative to each interface’s normal vector and describe the bending of light. Each shaded region highlights a triangle whose trigonometry is helpful for relating the refraction angles to the apparent angular position of a light source ( $θ$ ). (b) Illustration of mathematical variables used to trigonometrically relate the true angular position of each projected point ( $θ^{'}$ ) to its apparent position ( $θ$ ), assuming the same arena geometry as panel a. The derivation utilizes most triangles shown, several of which are cross-hatched or outlined to direct the reader’s eye.

Author response image 1

Download asset Open asset

Left: The image of a grayscale checkerboard that our tool suggests a user display in order to achieve an undistorted checkerboard from the point of view of the fish.

Center: Simulation of chromatic aberrations for the resulting transformed checkerboard when it consists of equal parts red and blue light. Right: Zoom of image at Center.

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/53684/elife-53684-transrepform-v2.docx
Download elife-53684-transrepform-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Timothy W Dunn
James E Fitzgerald

(2020)

Correcting for physical distortions in visual stimuli improves reproducibility in zebrafish neuroscience

eLife 9:e53684.

https://doi.org/10.7554/eLife.53684

Sign up for email alerts

Privacy notice