Research Article

Spatially compartmentalized phase regulation of a Ca²⁺-cAMP-PKA oscillatory circuit

Department of Biophysics and Biophysical Chemistry, The Johns Hopkins University School of Medicine, United States
Department of Pharmacology, University of California, San Diego, United States
Chemical Engineering Graduate Program, University of California, San Diego, United States
Department of Mechanical and Aerospace Engineering, University of California, San Diego, United States
Department of Chemistry and Biochemistry, University of California, San Diego, United States

Nov 17, 2020

https://doi.org/10.7554/eLife.55013

Open access
Copyright information

Figures
Tables
Additional files

9 figures, 14 tables and 1 additional file

Figures

Figure 1 with 2 supplements

Download asset Open asset

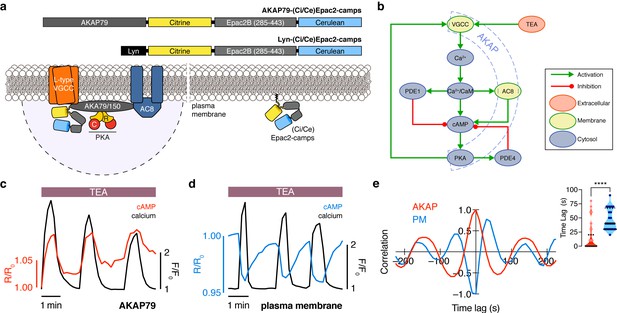
The phase of oscillating cAMP is shifted between the AKAP79/150 compartment and the general plasma membrane compartment, relative to Ca²⁺.

(a) Depiction of the AKAP79/150 and plasma membrane compartments, including the targeted cAMP biosensor (Ci/Ce)Epac2-camps to measure the compartment-specific cAMP signaling. Schematics of the lyn-(Ci/Ce)Epac2-camps and AKAP79-(Ci/Ce)Epac2-camps sensors are shown above. (b) Network diagram describing the key players in the β cell Ca²⁺-cAMP-PKA oscillatory circuit. (c) Representative single-cell trace of in-phase oscillating responses of AKAP79-(Ci/Ce)Epac2-camps and RCaMP, whole-cell fluorescence measured. Red trace is cAMP (cyan direct channel divided by CY-FRET channel) and black trace is Ca²⁺ (RFP). (d) Representative single-cell trace of out-of-phase oscillating responses of lyn-(Ci/Ce)Epac2-camps and RCaMP, whole-cell fluorescence measured. Blue trace is cAMP (cyan direct channel divided by CY-FRET channel) and black trace is Ca²⁺ (RFP). (e) Cross-correlation between the oscillatory Ca²⁺ and cAMP signals from the representative in-phase AKAP79 (red) and out-of-phase plasma membrane (PM, blue) responses from c, d. Time lag (sec) between the cAMP and Ca²⁺ signals for the two compartments (AKAP79/150, red, is 13 ± 3 sec n=60 and PM, blue, is 47 ± 4 s n=24). ****p<0.0001; unpaired two-tailed Student’s t-test.

Figure 1—figure supplement 1

Download asset Open asset

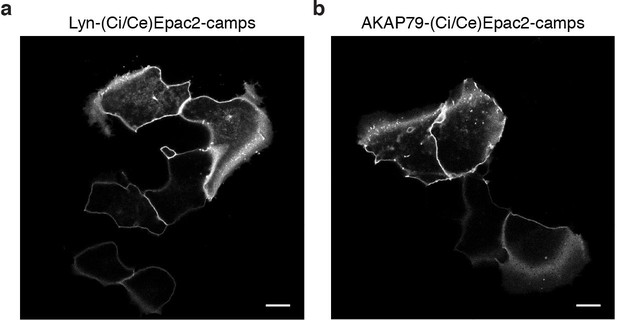
The AKAP79/150 and PM-targeted sensors are localized at the plasma membrane.

(a) Confocal image of lyn(Ci/Ce)Epac2camps showing efficient localization of the probe at the PM in MIN6 cells (YFP channel, scale 5 μm). (b) Confocal image of AKAP79-(Ci/Ce)Epac2camps also depicting localization of the scaffold-fused biosensor at the PM in MIN6 cells (YFP channel, scale 5 μm).

Figure 1—figure supplement 2

Download asset Open asset

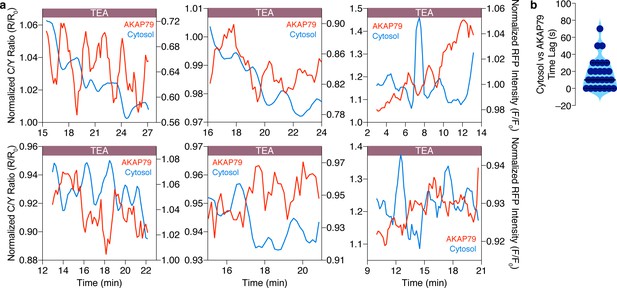
Cytosolic and AKAP79-specific cAMP oscillations are anti-correlated in the same cell.

(a) Representative single-cell traces showing that cytosolic cAMP (red, measured with R-FlincA sensor) oscillations are anti-correlated with cAMP oscillations at AKAP79 (blue, measured with AKAP79-(Ci/Ce)Epac2-camps) within individual MIN6 β cells ( n = 25 cells total). (b) Violin plot summarizing the time lag (sec) between the cytosolic and AKAP79-localized cAMP oscillations within all of the cells analyzed (n = 25).

Figure 2 with 3 supplements

Download asset Open asset

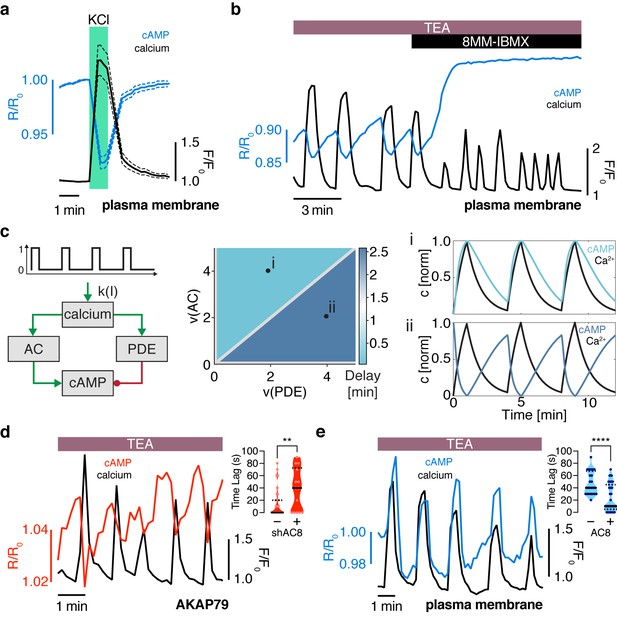
The oscillation phase is regulated by a balance between Ca²⁺-sensitive AC and PDE activity.

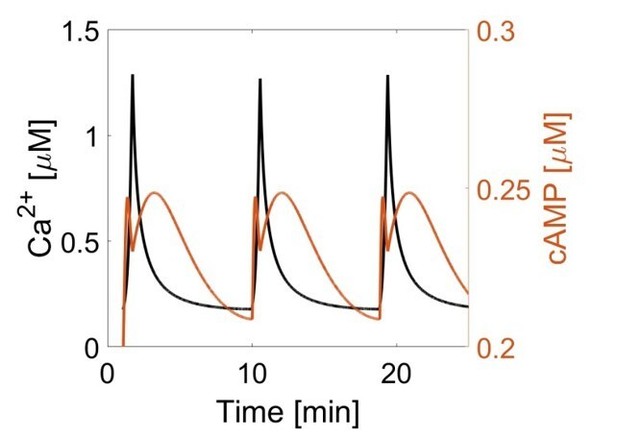
(a) Impulse response of plasma membrane cAMP (blue) to a spike in Ca²⁺ entry (black), triggered by KCl-mediated membrane depolarization (wash in/out). The transient decrease in PM-cAMP is coupled to the transient increase in intracellular Ca²⁺. (b) Acute inhibition of Ca²⁺-sensitive PDE1 decouples the out-of-phase PM-cAMP oscillations from Ca²⁺ oscillations, as observed in this representative cell trace (Ca²⁺ – black, PM-cAMP – blue). (c) The oscillatory phase of cAMP can be manipulated by tuning the relative activity of Ca²⁺-sensitive PDE and AC, as demonstrated by a simplified mathematical model. The schematic shows the network architecture. The relative activities of AC and PDE, denoted as v(AC) and v(PDE), control the delay between Ca²⁺ and cAMP. Point (i), with high AC activity and low PDE, shows in phase oscillations of Ca²⁺ and cAMP, whereas point (ii), with high PDE and low AC activity shows out of phase oscillations. These dynamics are shown in the line graphs. (d) Knocking down AC8 is correlated with an increase in the time lag for oscillatory cAMP at the AKAP79/150 microdomain (37 ± 9 s, n = 11), indicating more cells exhibiting out-of-phase cAMP oscillations (representative cell trace, Ca²⁺ – black, AKAP79/150-cAMP – red). (e) Over-expressing AC8 is sufficient to reverse the phase at the PM to in-phase (23 ± 2 s, n = 56) (representative cell trace, Ca²⁺ – black, PM cAMP – blue). **p=0.0014, ****p<0.0001; unpaired two-tailed Student’s t-test.

Figure 2—figure supplement 1

Download asset Open asset

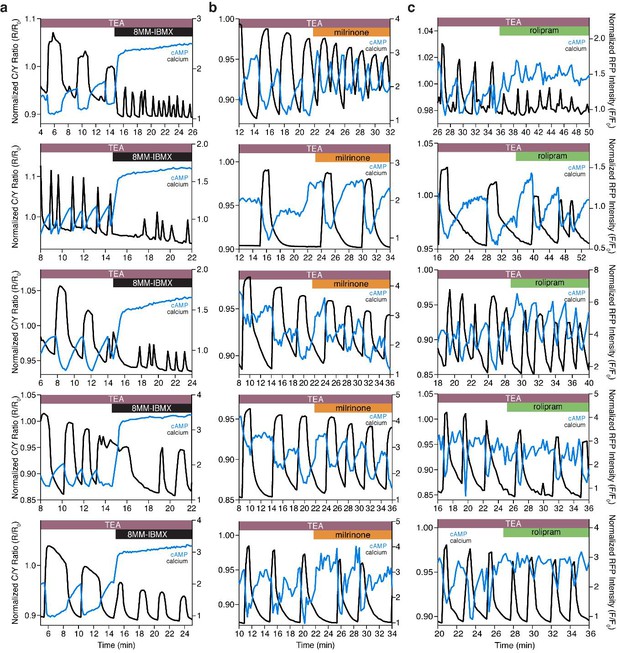
The Ca²⁺-dependent cAMP response is dependent on PDE1, but not PDE3 or PDE4.

(a) Representative single cell traces depicting the decoupling of oscillating cAMP at the PM (measured by lyn-(Ci/Ce)Epac2-camps, blue trace) from oscillating Ca²⁺ (black trace) upon inhibition of PDE1 with 8MM-IBMX. Representative single cell traces showing cAMP still oscillates at the PM (blue trace) together with Ca²⁺ (black trace) upon inhibition of PDE3 (milrinone) (b) and PDE4 (rolipram) (c), respectively.

Figure 2—figure supplement 2

Download asset Open asset

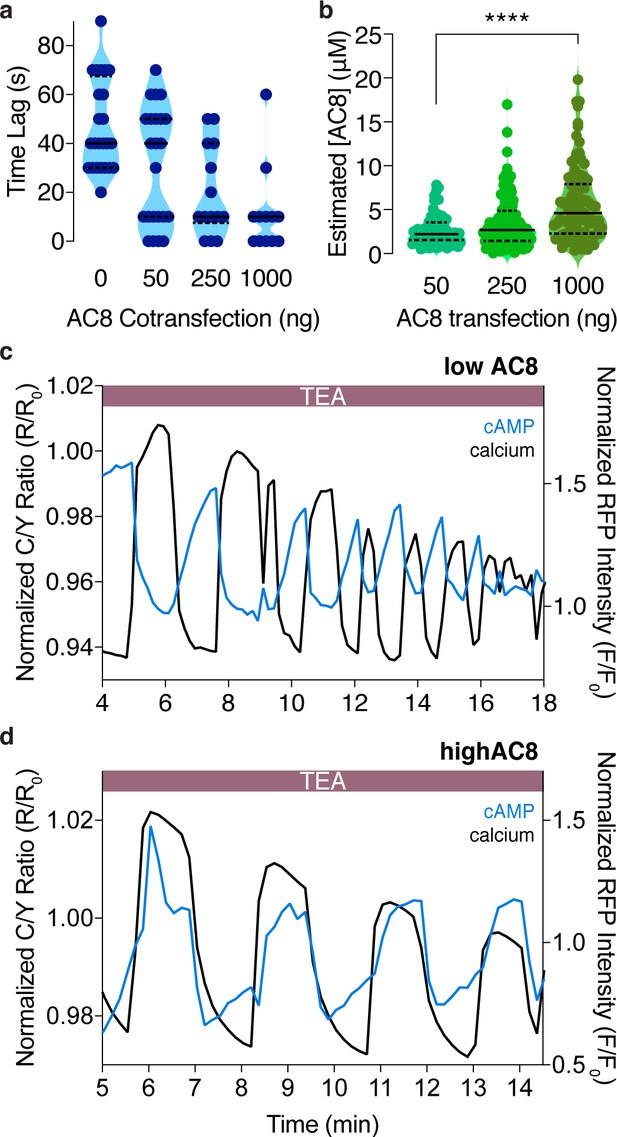
The cAMP-Ca²⁺ phase relationship at the PM can be tuned by expression of the Ca²⁺-dependent AC8.

(a) Plot depicting a dose-dependence between the time lag of cAMP at the PM and the amount of plasmid-encoded AC8 co-transfected (n = 56). (b) Violin plots depicting the relationship between estimated cellular AC8 expression levels and the amount of GFP-AC8 plasmid transfected into cells (50 ng: n = 68 cells, 250 ng: n = 116 cells, 1000 ng: n = 91 cells). p=0.00001, 50 ng vs 1000 ng; Kruskal-Wallis test followed by Dunn's multiple comparisons test. (c) Representative single cell trace of an oscillating β cell control with no AC8 co-expression, illustrating an out-of-phase cAMP-Ca²⁺ phase relationship. Blue trace is cAMP at PM and black trace is Ca²⁺. (d) Representative single cell trace of an oscillating β cell with 1 μg of an AC8 expression vector co-transfected, illustrating an in-phase cAMP-Ca²⁺ phase relationship. Blue trace is cAMP at PM and black trace is Ca²⁺.

Figure 2—figure supplement 3

Download asset Open asset

No difference in endogenous AC8 levels is observed between cells expressing AKAP79-(Ci/Ce)Epac2-camps and lyn-(Ci/Ce)Epac2-camps.

(a) Average intensity per AC8-stained MIN6 cell, expressing AKAP79-(Ci/Ce)Epac2-camps (AKAP79), lyn-(Ci/Ce)Epac2-camps (Lyn), or no sensor (control). AC8 intensity does not significantly differ between the three populations. ns, p=0.2525; ordinary one-way ANOVA. (b) Representative Western blot quantifying endogenous expression of AC8 and expression of transfected biosensor (AKAP79-(Ci/Ce)Epac2-camps (AKAP79), Lyn-(Ci/Ce)Epac2-camps (Lyn), or Cerulean (Cer) only) in MIN6 cells. A small increase in AC8 expression was observed between sensor-expressing populations compared to Cerulean alone (AKAP79 vs. Cer, *p=0.0134; Lyn vs. Cer, p=0.0979; ordinary one-way ANOVA followed by Tukey’s multiple comparisons test). However, no significant difference in AC8 expression was measured between the AKAP79- and Lyn-tagged sensor-expressing populations (AC8 band intensity normalized to β tubulin, n = 4 replicates, p=0.4373).

Figure 3 with 3 supplements

Download asset Open asset

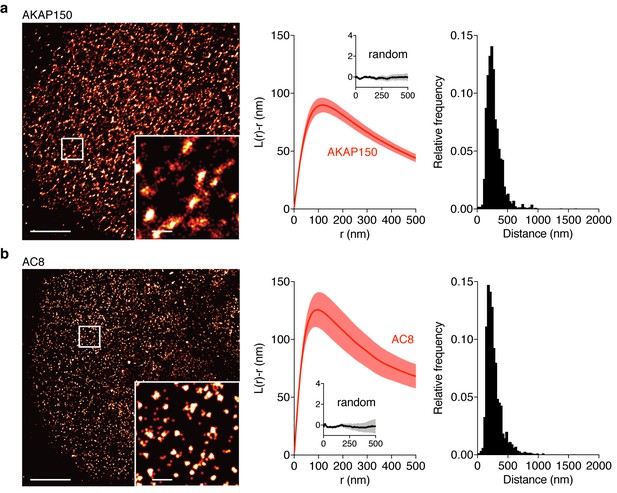
AKAP150 and AC8 both form nanoclusters at the surface of MIN6 β cells.

(a) Representative super-resolution STORM image of the AKAP150 scaffold (scale 5 μm, inset 500 nm). Ripley-K analysis measures the average radii of the nanoclusters and indicates that AKAP150 forms clusters of 127 ± 9 nm, n = 20 (uniform random distribution control in inset). The nearest-neighbor distance distribution describes the distance between nanoclusters (average distance for AKAP150 is 313 ± 20 nm). (b) Representative super-resolution STORM image of Ca²⁺-sensitive AC8 (scale 5 μm, inset 500 nm) depicts AC8 nanoclusters of average radius 88 ± 8 nm and average nearest-neighbor distance 292 ± 16 nm, n = 16.

Figure 3—figure supplement 1

Download asset Open asset

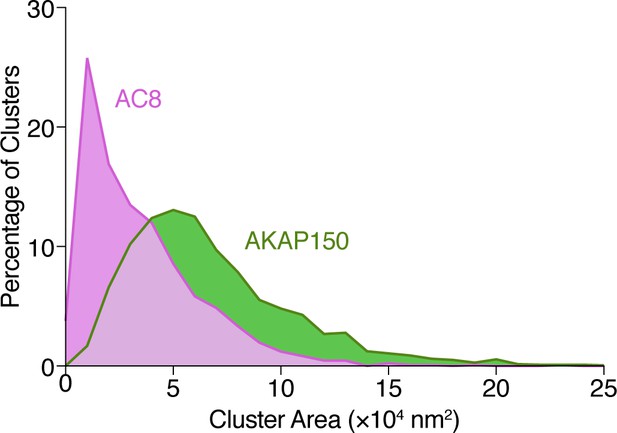
Analysis of AKAP150 and AC8 cluster area.

Histogram showing the size distribution (area, nm²) for AKAP150 (green) and AC8 (magenta) clusters derived from STORM imaging.

Figure 3—figure supplement 2

Download asset Open asset

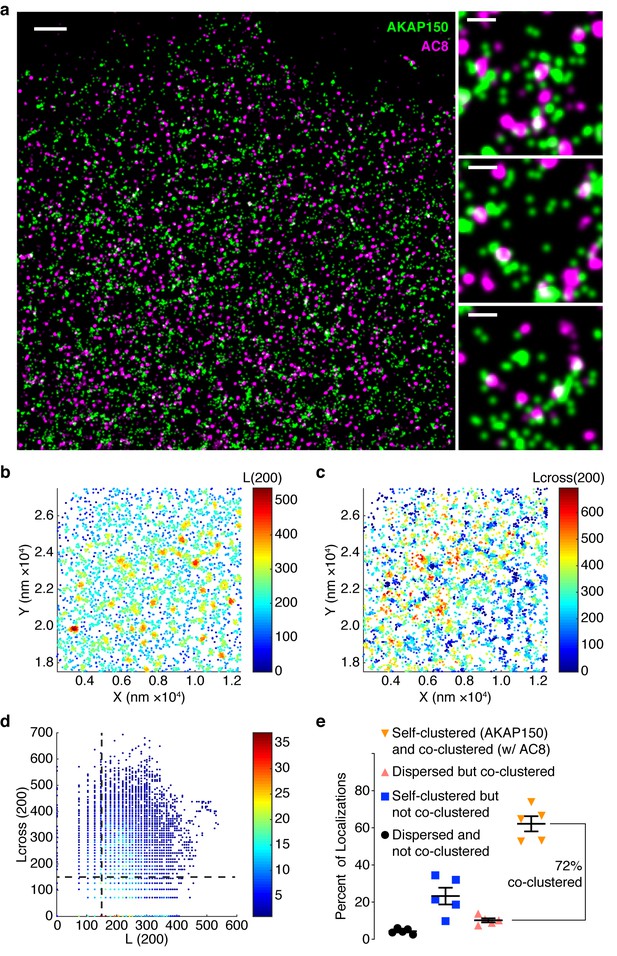
AKAP150 is co-clustered with AC8 at the plasma membrane in MIN6 cells.

(a) A representative two-color STORM image of AKAP150 (green) and AC8 (magenta) in a MIN6 cell with specific examples of AKAP150/AC8 co-clusters to the right (scale 1 μm, inset 200 nm). Representative 1 x 1 μm scatter plot showing molecular localizations for AKAP150, color-coded with the values of L(200) (b) or Lcross(200) (c), which reflect the number of localizations of its own species or of the AC8 species, respectively, within a 200 nm radius of each AKAP150 localization. (d) Scatter plot of Lcross(200) and L(200) is shown for the representative ROI. AKAP150 localizations with a Lcross(200) score above 150 were considered co-clustered with AC8. (e) Summary of Getis-Franklin co-clustering analyses of the two-color STORM images identifying populations with different AKAP150/AC8 cluster relationships. A majority of AKAP150 localizations (72%) are co-clustered with AC8 localizations (n = 5 cells).

Figure 3—figure supplement 3

Download asset Open asset

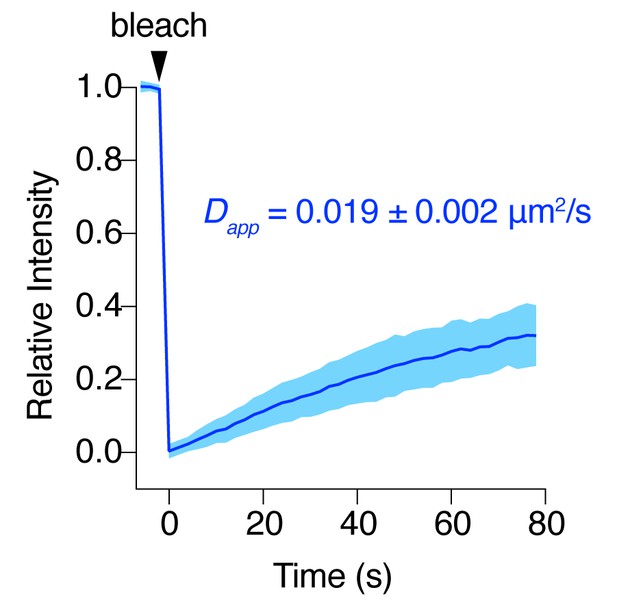
AC8 diffuses slowly at the plasma membrane.

FRAP curve for EGFP-tagged AC8 in MIN6 cells. AC8 diffuses slowly with an apparent diffusivity of 0.019 ± 0.002 μm²/s and an average immobile fraction of approx. 42.3% (n = 16, extrapolated).

Figure 4 with 1 supplement

Download asset Open asset

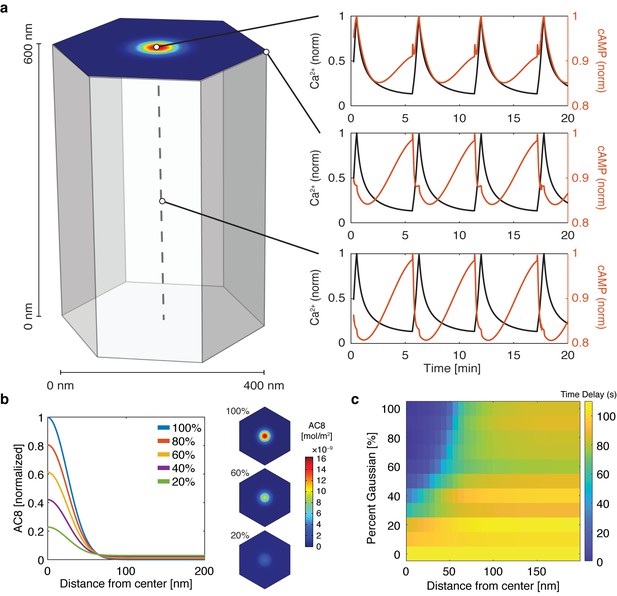
cAMP-Ca²⁺ phase relationship can be described by a 3D reaction-diffusion model involving clusters of AKAP79/150 and AC8.

(a) 3D reaction-diffusion model with a single AKAP79/150:AC8 co-cluster positioned at the PM in the β cell in a hexagonal prism volume. cAMP oscillates in-phase immediately within the AKAP79/150:AC8 nanocluster due to the high effective concentration of AC8, but out-of-phase at the PM or cytosol due to the presence of PDE1 (cAMP – red, Ca²⁺– blue). (b) Disruption of the AKAP79/150:AC8 interaction can redistribute AC8 from within the cluster to the PM, shown by the half-Gaussian cross-sections and representative AC8 concentration heatmaps at the PM. (c) Heatmap depicting the time lag (s) for AC8 distribution (% Gaussian) and spatial distance (nm) from cluster center along PM.

Figure 4—figure supplement 1

Download asset Open asset

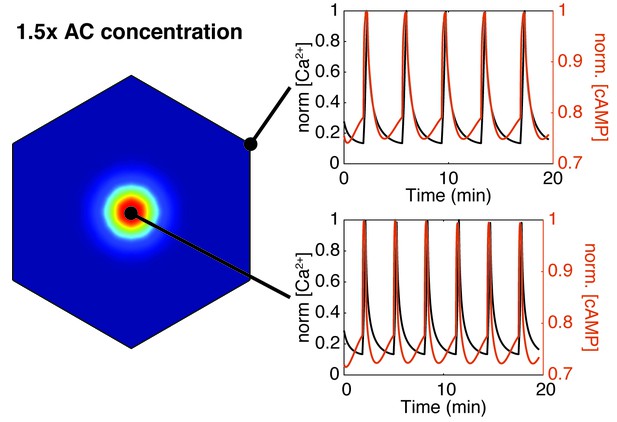
Increasing AC8 concentration within the cluster leads to loss of compartmentalized cAMP-calcium phase relationship.

Spatial simulations of cAMP (red) and calcium (black) when AC8 concentration is increased within the nanocluster. Entrainment of cAMP and calcium oscillations (in-phase) occurs globally at the plasma membrane (edge - top right, cluster center - bottom right).

Figure 5 with 1 supplement

Download asset Open asset

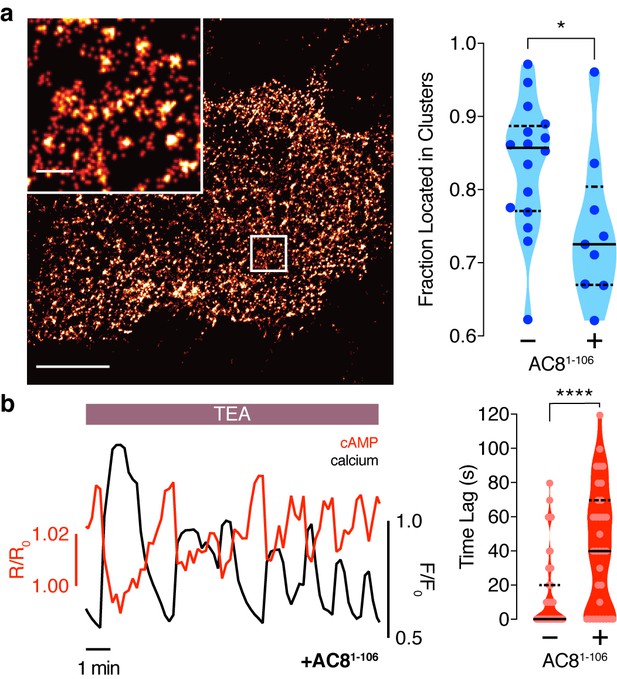
Disruption of the AKAP79/150:AC8 interaction is associated with a redistribution of AC8 at the PM and a phase shift of cAMP at the AKAP79/150 nanodomain.

(a) Over-expression of the N-terminus of AC8, which is necessary and sufficient for mediating the AKAP79/150:AC8 interaction, redistributes AC8 from within nanoclusters to the general PM, as seen in the STORM image (scale 5 μm, inset 500 nm) and measured by the percent of localizations that fall into nanoclusters. (b) Disruption of the AKAP79/150:AC8 interaction lengthens the time lag between the cAMP (red) and Ca²⁺ (black) signals at the AKAP79/150 compartment (avg. time lag in absence of disruptor is 13 ± 3 s, n = 60, and in presence of disruptor 43 ± 6 s, n = 33) due to more cells displaying out-of-phase cAMP oscillations. *p=0.0341, ****p<0.0001; unpaired two-tailed Students t-test.

Figure 5—figure supplement 1

Download asset Open asset

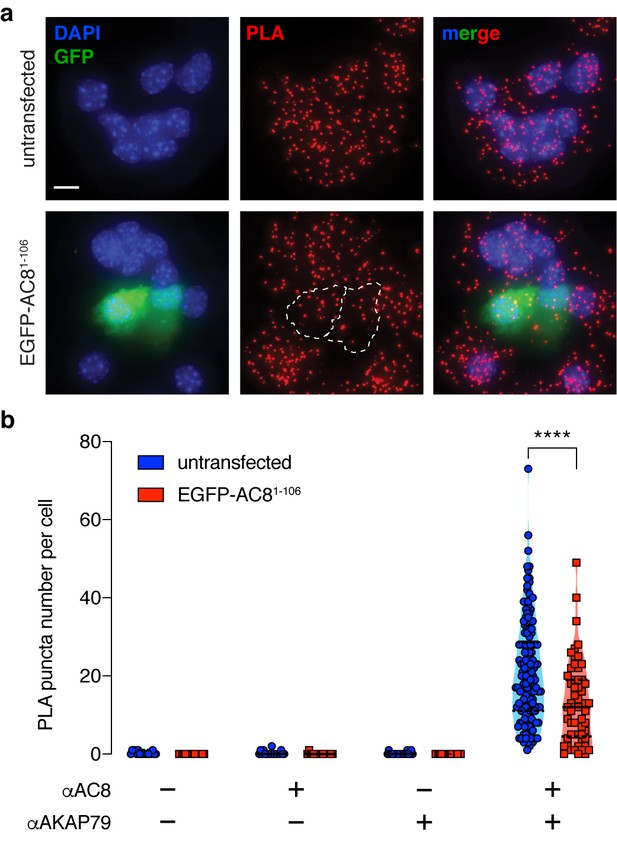
Expression of the N-terminus of AC8 perturbed the interaction between endogenous AKAP150 and AC8 in MIN6.

(a) Widefield maximum intensity projections of a proximity ligation assay to depict the extent of interactions between AC8 and AKAP150 in MIN6 β cells (scale 10 μm). Expression of EGFP-tagged AC8^1-106 results in less PLA puncta per cell. (b) Number of PLA puncta per AC8^1-106-expressing cell is significantly decreased compared to non-transfected control (n = 142 and 57 cells, respectively) (****p<0.0001; unpaired two-tailed Student’s t-test).

Figure 6 with 2 supplements

Download asset Open asset

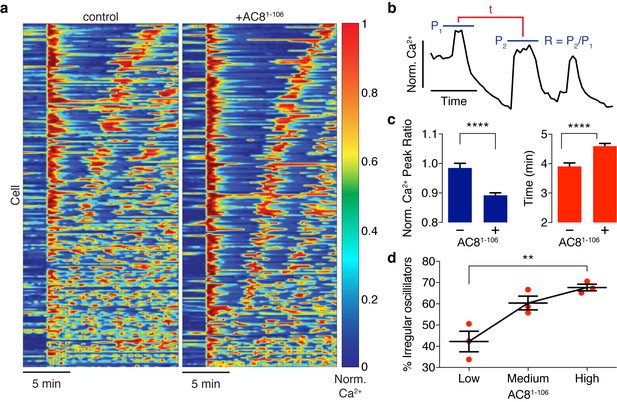
Ca²⁺ oscillatory dynamics are affected by expression of the disruptor peptide in β cells.

(a) Heatmaps depicting Ca²⁺ oscillations for 220 randomly selected cells co-expressing EGFP alone (control, left) or EGFP-tagged AC8^1-106 (AKAP79/150:AC8 disruptor, right), ordered by a mixed parameter describing the time lag between the first two Ca²⁺ peaks and the avg. timelag between all Ca²⁺ peaks. (b) Schematic describing two Ca²⁺ oscillatory parameters: the ratio between the first two Ca²⁺ peaks (R = P₂ / P₁) and the interpeak timing (t). (c) The peak ratio R is decreased in the presence of the AKAP79/150:AC8 disruptor (left), indicating less of a sustained Ca²⁺ oscillatory response. Over-expression of the disruptor also lengthens the timing between peaks (right). (d) The level of disruptor peptide expression is correlated with an increase in the percentage of cells exhibiting irregular oscillations (total n = 562). p=0.0054, ordinary one-way ANOVA.

Figure 6—figure supplement 1

Download asset Open asset

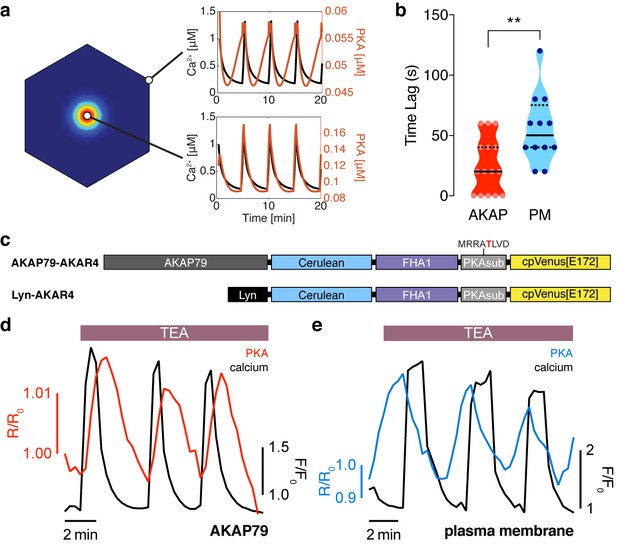
The phase of oscillating PKA activity, relative to Ca²⁺, is also spatially compartmentalized.

(a) PKA activity is predicted to oscillate near the center of the AKAP79/150:AC8 cluster with a short time delay and a longer delay outside of the cluster, relative to Ca²⁺. (b) Experimentally-measured time lag between PKA activity oscillations and Ca²⁺ for AKAP79 (orange) and the general PM (teal) compartments (n = 15 and 12, respectively). **p=0.0063, unpaired two-tailed Student’s t-test. (c) Representative single cell trace showing in-phase PKA activity within the AKAP79 compartment. Orange trace is PKA activity at AKAP79 (CY-FRET channel divided by cyan donor channel) and black trace is Ca²⁺ (RFP). (d) Representative single cell trace showing out-of-phase PKA activity within the general PM compartment. Teal trace is PKA activity at PM (CY-FRET channel divided by cyan donor channel) and black trace is Ca²⁺ (RFP).

Figure 6—figure supplement 2

Download asset Open asset

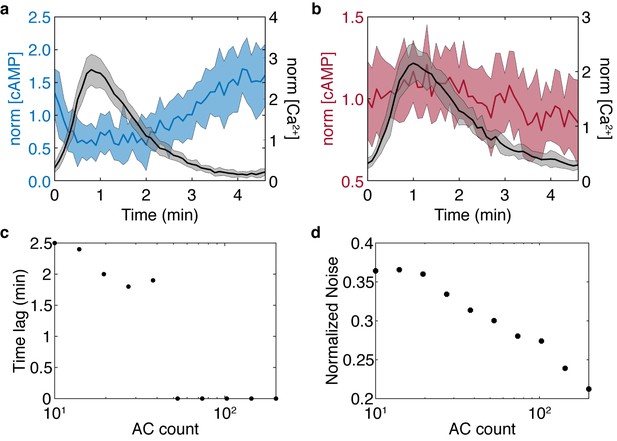
Stochastic model results for the simplified model show the cAMP-Ca²⁺ phase relationship is preserved and noise is reduced in higher flux conditions.

Stochastic simulations were performed for high and low AC8 counts of 200 (a) and 10 (b). (c) Reducing the AC8 count shifts the solution from in-phase to out-of-phase with respect to Ca²⁺, as predicted in the previous four component model. (d) Increasing the AC8 count suppresses cAMP noise within the system, relative to the mean.

Appendix 1—figure 1

Download asset Open asset

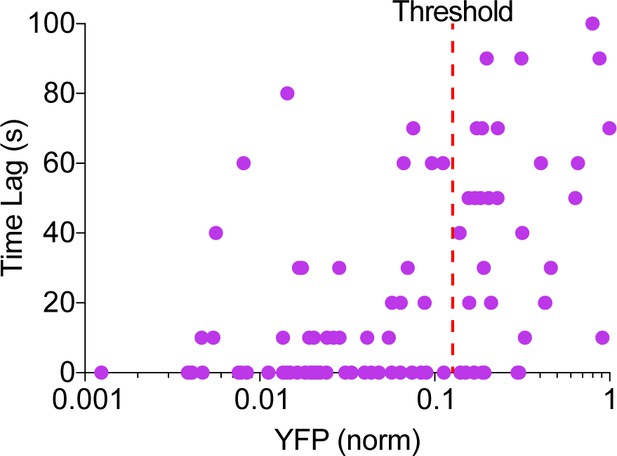
Phase of cAMP correlates with the expression level of the AKAP79-(Ci/Ce)Epac2-camps.

Scatter plot of the time lag (sec) and the YFP donor channel intensity (normalized to non-saturating maximum) for each cell expressing AKAP79-(Ci/Ce)Epac2-camps. Cells with higher expression of the probe correlated with a longer time lag, therefore a YFP intensity threshold was designated for analysis purposes.

Appendix 1—figure 2

Download asset Open asset

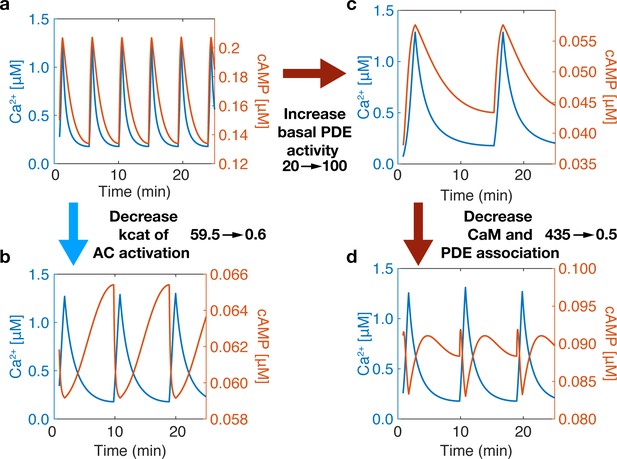
Phase is driven by activity variability within the Ca²⁺ oscillatory regime.

The phase of the system can be switched by tuning the association of CaM to sources (ACs) and sinks (PDEs). (a) At base system conditions, the system acts in an in-phase manner. (b) Decreasing the rate of Ca²⁺ association to the AC-CaM complex causes the phase to switch to out-of-phase. (c) Increasing basal PDE activity does not allow a phase switch only after decreasing PDE and CaM association rates will the system allow a phase switch (d). A phase switch is controlled by the variability in the activity of source or sink. If the sink dominates, then the system is out-of-phase. If the source dominates, the system is in-phase.

Author response image 1

Download asset Open asset

of CaM⁺²Ca, CaMAC⁺²Ca, and CaMPDE⁺²Ca, were represented as multi step reactions with rates in the table given below.

The system still exhibits in-phase and out-of-phase qualitative responses, with an additional 3 parameters. Since additional parameters did not affect outcome, we retained the Michaelis-Menten formulation.

Tables

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Cell line (Mus musculus)	MIN6	Dr. Jun-Ichi Miyazaki, Osaka University	RRID:CVCL_0431
Chemical compound, drug	Tetraethylammonium chloride (TEA)	Sigma	T2265	20 mM
Chemical compound, drug	8-Methoxymethyl-3-isobutyl- 1-methylzanthine (8MM-IBMX)	Sigma-Aldrich	M2547	100 μM
Chemical compound, drug	Milrinone	Alexis	Cat# ALX-270–083 M005	10 μM
Chemical compound, drug	Rolipram	Alexis	Cat# ALX-270–119	1 μM
Chemical compound, Drug	KCl	Sigma-Aldrich	P9541	15 mM
Commercial assay or kit	Lipofectamine-2000	Invitrogen	11668019
Recombinant DNA reagent	pCDNA3 AKAR4	PMID:20838685
Recombinant DNA reagent	(Ci/Ce)Epac2-camps	Dr. Dermot Cooper, University of Cambridge
Recombinant DNA reagent	AKAP79 (AKAP5, Homo sapiens)	Dr. John D. Scott, University of Washington
Recombinant DNA reagent	AC8 (Adcy8, Rattus norvegicus)	Dr. Dermot Cooper, University of Cambridge
Recombinant DNA reagent	ShAdcy8 Plasmid	Dr. Jochen Lang, University of Bordeaux	ShAdcy8 #2
Recombinant DNA reagent	RCaMP	Dr. Loren Looger, Janelia Farms
Recombinant DNA reagent	R-FlincA	Dr. Kazuki Horikawa, Tokushima University Graduate School
Commercial assay or kit	Duolink in situ red starter kit	Sigma	DUO92101
Commercial assay or kit	Duolink in situ Probemaker MINUS	Sigma	DUO92010
Commercial assay or kit	Duolink in situ Probemaker PLUS	Sigma	DUO92009
Antibody	Anti-AC8, rat polyclonal	Abcam	ab196686	1:2000
Antibody	Anti-AKAP150, rat polyclonal	Millipore Sigma	07–210	1:500
Antibody	Anti-AKAP79, mouse monoclonal	BD	610314	1:500
Antibody	Goat anti-rabbit AlexaFluor647	ThermoFisher Scientific	A21245	1:1000
Antibody	Goat anti-mouse AlexaFluor568	ThermoFisher Scientific	A11031	1:1000
Software, algorithm	FIJI	https://imagej.net/Fiji	RRID:SCR_014294
Software, algorithm	MetaFluor	https://www.moleculardevices.com/	RRID:SCR_002285
Software, algorithm	MATLAB	https://www.mathworks.com/	RRID:SCR_001622
Software, algorithm	GraphPad Prism	https://www.graphpad.com/ scientific-software/prism/	RRID:SCR_002798
Software, algorithm	COPASI	http://copasi.org/ Hoops et al., 2006	RRID:SCR_014260
Software, algorithm	Virtual Cell	https://vcell.org/ Cowan et al., 2012	RRID:SCR_007421

Appendix 1—table 1

Voltage gated channel reactions.

#	Species	Expression	Parameters	Ref.
1	Membrane Voltage	$\frac{d V}{d t} = \frac{- I_{C a} - I_{K} - I_{L} - I_{K C a}}{C_{m}}$	$C_{m}$ = 5.3 pF	Ni et al., 2011
2	Ca²⁺ current	$I_{C a} = g_{C a} m_{\infty} (V - E_{C a})$	$g_{C a}$ = 600 pS, $E_{C a}$ = 100 mV	Ni et al., 2011
3	Fraction of open VGCC (at steady state)	$m_{\infty} = \frac{1}{2} (1 + t a n h (\frac{V - v_{1}}{v_{2}}))$	$v_{1}$ = -20 mV, $v_{2}$ = 24 mV	Ni et al., 2011
4	K⁺ current	$I_{K} = g_{K} w (V - E_{K})$	$g_{K}$ = 240 pS, $E_{C a}$ = -75 mV	Ni et al., 2011
5	Fraction of open K⁺ channels (at steady state)	$\frac{d w}{d t} = \frac{Φ (w_{\infty - w})}{τ}$	ϕ = 35 $\frac{1}{s}$	Ni et al., 2011
6	Time constant for K⁺ channel open probability	$τ = \frac{1}{c o s h (\frac{V - v_{3}}{2 v_{4}})}$	$v_{3}$ = -16 mV $v_{4}$ = 11.2 mV	Ni et al., 2011
7	leak current	$I_{L} = g_{L} (V - E_{L})$	$g_{L}$ = 150 pS, $E_{L}$ = -75 mV	Zhang et al., 2005
8	Ca²⁺ gated K⁺ current	$I_{K C a} = g_{K C a} \frac{C a}{C a + K_{K C a}} (V - E_{K})$	$g_{K C a}$ = 2000 pS, $E_{C a}$ = -75 mV, $K_{K C a}$ = 5 $μ M$	Ni et al., 2011

Appendix 1—table 2

Ca²⁺flux and reactions.

#	Reaction	Reaction flux	Kinetic parameters	Ref.
9	→ Ca	$j_{C a_{v}} (1 + k_{P K A_{V}} [P K A]) + j_{C a_{l}}$	$k_{P K A V}$ = 3000 s⁻¹ · µM⁻¹	Ni et al., 2011
10	$j_{C a_{V}}$	$f_{i} (- α I_{C a} - v_{L P M} [C a])$	$f_{i}$ = 1 x 10⁻⁵ $α$ = 0.0045 $μ M$ · f^A−1 · s⁻¹ $v_{L P M}$ = 75 s⁻¹	Ni et al., 2011
11	$j_{C a_{I}}$	$\frac{C k_{I P 3 R} [P K A] A [C a]}{1 + A [C a] + [B] [C a]^{2}} ([C a_{s t o r e s}] - [C a]) - \frac{V_{s} [C a]^{2}}{K_{s}^{2} + [C a]^{2}}$	K_s = 10 µM, Ca_stores = 1.56 µM, V_s = 0.1 µM · s⁻¹, k_IP3R = 0.05, A = 0.2869µM⁻¹, B = 2.869µM⁻², C = 0.2133	Ni et al., 2011
12	2Ca + CaM ↔ Ca²CaM	$k_{f} [C a] [C a M] - k_{r} [C a^{2} C a M]$	$k_{f}$ = 3.6 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 8 $s^{- 1}$	Lai et al., 2015
13	Ca + Ca²CaM ↔ Ca³CaM	$k_{f} [C a] [C a^{2} C a M] - k_{r} [C a^{3} C a M]$	$k_{f}$ =11 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 195 $s^{- 1}$	Lai et al., 2015
14	Ca + Ca³CaM ↔ Ca⁴CaM	$k_{f} [C a] [C a^{3} C a M] - k_{r} [C a^{4} C a M]$	$k_{f}$ = 59 $s^{- 1}$ ⋅µM⁻¹, $k_{r}$ = 500 $s^{- 1}$	Lai et al., 2015
15	AC + Ca²CaMCaM ↔ CaM · AC	$k_{f} [A C] [C a^{2} C a M] - k_{r} [C a M \cdot A C]$	$k_{f}$ = 1.7 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 10 $s^{- 1}$	Masada et al., 2009; Masada et al., 2012
16	CaM · AC + 2Ca ↔ AC*	$K_{c a t} \frac{[C a] [C a M \cdot A C]}{C a + K_{m}} - k_{r} [A C *]$	$K_{c a t}$ = 59.5 $s^{- 1}$ , $K_{m}$ = 0.1 $μ M$ , $k_{r}$ = 10 $s^{- 1}$	Masada et al., 2009; Masada et al., 2012
17	PDE + Ca²CaM ↔ CaM · PDE	$k_{f} [P D E] [C a^{2} C a M] - k_{r} [C a M \cdot P D E]$	$k_{f}$ = 435 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 1 $s^{- 1}$	Ang and Antoni, 2002
18	CaM · PDE + 2Ca ↔ PDE*	$K_{c a t} \frac{[C a] [C a M \cdot P D E]}{C a + K_{m}} - k_{r} [P D E *]$	$K_{c a t}$ = 1.81 $s^{- 1}$ , $K_{m}$ = 0.18 $μ M$ , $k_{r}$ = 1 $s^{- 1}$	Ang and Antoni, 2002
19	PDE + Ca⁴CaM ↔ PDE*	$k_{f} [P D E] [C a^{4} C a M] - k_{r} [P D E *]$	$k_{f}$ = 435 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 1 $s^{- 1}$	Ang and Antoni, 2002

*denotes the activated form

Appendix 1—table 3

cAMP reactions.

#	Reaction	Reaction flux	Kinetic parameters	Ref.
20	→ cAMP	$k_{b a s e} ([C a M \cdot A C] + [A C] + [A C_{i n d}]) + k_{a c t} [A C *]$	$k_{b a s e}$ = 0.1 $s^{- 1}$ , $k_{a c t}$ = 0.785 $s^{- 1}$	Leonid E. Fridlyand & Philipson, 2016; Ni et al., 2011
21	cAMP→	$k_{b a s e} [c A M P] \frac{[C a M \cdot P D E] + [P D E]}{[c A M P] + K_{m}} + k_{a c t} \frac{[c A M P] [P D E *]}{[c A M P] + K_{m}}$	$k_{b a s e}$ = 0.2 $s^{- 1}$ , $K_{m}$ = 0.6 $μ M$ $k_{a c t}$ = 2.5 $s^{- 1}$	Ni et al., 2011; Fridlyand and Philipson, 2016
22	cAMP→	$V_{i n d} \frac{[c A M P]}{[c A M P] + K_{m}}$	$V_{i n d}$ = 2.5 $μ M$ ⋅ s⁻¹, $K_{m}$ = 1.4 $μ M$	Ni et al., 2011; Fridlyand and Philipson, 2016
23	cAMP + R2 → R2_b	$k_{f} [c A M P] [R 2] - k_{r} [R 2_{b}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.00033 $s^{- 1}$	Boras et al., 2014
24	cAMP + R2_b → R2_ba	$k_{f} [c A M P] [R 2_{b}] - k_{r} [R 2_{b a}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.00105 $s^{- 1}$	Boras et al., 2014
25	cAMP + R2_b → R2_bb	$k_{f} [c A M P] [R 2_{b}] - k_{r} [R 2_{b b}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.00132 $s^{- 1}$	Boras et al., 2014
26	cAMP + R2_ba → R2_bba	$k_{f} [c A M P] [R 2_{b a}] - k_{r} [R 2_{b b a}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.0013 $s^{- 1}$	Boras et al., 2014
27	cAMP + R2_bb → R2_bba	$k_{f} [c A M P] [R 2_{b b}] - k_{r} [R 2_{b b a}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.00103 $s^{- 1}$	Boras et al., 2014
28	cAMP + R2_bba → R2_bbaa	$k_{f} [c A M P] [R 2_{b b a}] - k_{r} [R 2_{b b a a}]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 0.0114 $s^{- 1}$	Boras et al., 2014
29	PKA + R2 → R2C	$k_{f} [P K A] [R 2] - k_{r} [R 2 C]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 1.26E-7 $s^{- 1}$	Boras et al., 2014
30	PKA + R2_b → R2_bcC	$k_{f} [P K A] [R 2_{b}] - k_{r} [R 2_{b} C]$	$k_{f}$ = 1 $s^{- 1}$ ⋅ µM⁻¹, $k_{r}$ = 2.52E-7 $s^{- 1}$	Boras et al., 2014

Appendix 1—table 4

cAMP reactions (cont.).

#	Reaction	Reaction flux	Kinetic parameters	Ref.
31	PKA + R2_ba → R2_ba C	$k_{f} [P K A] [R 2_{b a}] - k_{r} [R 2_{b a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ $k_{r}$ = 3.4E-6 $s^{- 1}$	Boras et al., 2014
32	PKA + R2_bba → R2_bba C	$k_{f} [P K A] [R 2_{b b a}] - k_{r} [R 2_{b b a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.000936 $s^{- 1}$	Boras et al., 2014
33	PKA + R2_bbaa → R2_bbaa C	$k_{f} [P K A] [R 2_{b b a a}] - k_{r} [R 2_{b b a a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.645 $s^{- 1}$	Boras et al., 2014
34	cAMP + R2C → R2_b C	$k_{f} [c A M P] [R 2 C] - k_{r} [R 2_{b} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ , $k_{r}$ = 0.000659 s^-1	Boras et al., 2014
35	cAMP + R2_b C → R2_ba C	$k_{f} [c A M P] [R 2_{b} C] - k_{r} [R 2_{b a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ , $k_{r}$ = 0.0142 s^-1	Boras et al., 2014
36	cAMP + R2_ba C → R2_bbc C	$k_{f} [c A M P] [R 2_{b a} C] - k_{r} [R 2_{b b a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.0142 s^-1	Boras et al., 2014
37	cAMP + R2_bba C → R2_bbaa C	$k_{f} [c A M P] [R 2_{b b a} C] - k_{r} [R 2_{b b a a} C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 7.84 s^-1	Boras et al., 2014
38	PKA + R2_b C → R2_b C₂	$k_{f} [P K A] [R 2_{b} C] - k_{r} [R 2_{b} C_{2}]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.00324 s^-1	Boras et al., 2014
39	PKA + R2C → R2C₂	$k_{f} [P K A] [R 2 C] - k_{r} [R 2 C_{2}]$	$k_{f}$ = 1 $s^{- 1}$ · µM⁻¹, $k_{r}$ = 2.81E-6 s^-1	Boras et al., 2014
40	PKA + R2_ba C → R2_ba C₂	$k_{f} [P K A] [R 2_{b a} C] - k_{r} [R 2_{b a} C_{2}]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.666 s^-1	Boras et al., 2014
41	cAMP + R2C₂→ R2_b C₂	$k_{f} [c A M P] [R 2 C_{2}] - k_{r} [R 2_{b} C_{2}]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 0.762 s^-1	Boras et al., 2014
42	cAMP + R2_b C₂→ R2_ba C₂	$k_{f} [c A M P] [R 2_{b} C_{2}] - k_{r} [R 2_{b a} C_{2}]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹, $k_{r}$ = 2.91 s^-1	Boras et al., 2014

Appendix 1—table 5

Initial conditions.

#	Species	Initial value
IC1	AC8	1 µM
IC2	AC_ind	1 µM
IC3	Ca²⁺	1 µM
IC4	CaM	10 µM
IC5	cAMP	0.1 µM
IC6	PDE1	1 µM
IC7	PDE4	0.4 µM
IC8	R2C2	0.4 µM
IC9	V	−60 mV

Appendix 1—table 6

Initial conditions for the stochastic model.

Species	Number of molecules in the system
Ca²⁺	10
PDE	45
PDE*	5
AC	10–200 (log scale)
s0	10000
s4	1000

Appendix 1—table 7

Compartment volumes for the stochastic model.

Compartment	Compartment size
Cytosol	0.083 μm³
Membrane	0.28 μm²
Oscillator	6563.0 μm²

Appendix 1—table 8

Lotka-Volterra model to initiate the membrane depolarization events.

#	Reaction	Parameters
1	s0 → 2s0	K_f = 1.7 s⁻¹
2	s0 + s4 → 2s4	K_f = 1 μm² ⋅ molecule^-1 ⋅ s^-1
3	s4 →	K_f = 1.7 s^-1

Appendix 1—table 9

simplified model reactions for the stochastic model.

#	Reaction	Parameters
4	s4 → > s4 + Ca²⁺	K_f = 150 s⁻¹
5	Ca²⁺→	K_f = 500 μm⁻² ⋅ molecule ⋅ s⁻¹ ⋅ μM⁻¹
6	AC + Ca²⁺ → AC*	K_f = 200 s⁻¹ ⋅ μM⁻¹ K_r = 300 s⁻¹
7	AC* → > cAMP + AC*	K_f = 300 s⁻¹
8	AC → cAMP + AC	K_f = 5 s⁻¹
9	PDE + Ca²⁺ → PDE*	K_f = 150 s⁻¹ ⋅ μM⁻¹ K_f = 100 s⁻¹
10	PDE + cAMP → PDE	K_f = 50 s⁻¹ ⋅ μM⁻¹
11	PDE* + cAMP → PDE*	K_f = 1000 s⁻¹ ⋅ μM⁻¹
12	→ cAMP	J = 9000 μm⁻² ⋅ molecule ⋅ s⁻¹
13	cAMP →	K_f = 50 s⁻¹

Appendix 1—table 10

Ca²⁺ Flux and reactions modified from Appendix 1—table 2.

#	Reaction	Reaction flux	Kinetic parameters	Ref.
S1	→ Ca²⁺	$j_{C a_{V}} (1 + k_{P K A_{V}} [P K A]) + J_{C a_{I}}$	$k_{P K A V}$ = 100 $μ M^{- 1}$	FRET constraint
S2	$j_{C a_{V}}$	$f_{i} (- α I_{C a} - v_{L P M} [C a])$	$f_{i}$ = 1 x 10⁻⁶, $α$ = 4.15 x 10⁵mol · m⁻² · A⁻² · s⁻¹,, $v_{L P M}$ = 7.5 x 10⁻⁴m · s⁻¹	Ni et al., 2011
S3	$j_{C a_{I}}$	$\frac{C k_{I P A R} [P K A] A [C a]}{1 + A [C a] + [B] [C a]^{2}} ([C a_{s t o r e s}] - [C a]) - \frac{V_{s} [C a]^{2}}{K_{s}^{2} + [C a]^{2}}$	$K_{s}$ = 10 $μ M$ , $C a_{s t o r e s}$ = 1.56 $μ M$ , $V_{s}$ = 0.1 µM · s⁻¹, $k_{I P 3 R}$ = 0.05 $μ M^{- 1} s^{- 1}$ , A = 0.2869 $μ M^{- 1}$ , B = 2.869 $μ M^{- 2}$ , C = 0.2133	Ni et al., 2011
S4	AC + Ca²CaM ↔ CaM · AC	$k_{f} [A C] [C a^{2} C a M] - k_{r} [C a M \cdot A C]$	$k_{f}$ = 10.8 $s^{- 1}$ · µM⁻¹, $k_{r}$ = 10 $s^{- 1}$	FRET constraint
S5	CaM · AC + 2Ca2+ ↔ AC*	$K_{c a t} \frac{[C a] [C a M \cdot A C]}{C a + K_{m}} - k_{r} [A C *]$	$K_{c a t}$ = 90 $s^{- 1}$ , $K_{m}$ = 1 $μ M$ , $k_{r}$ = 10 $s^{- 1}$	FRET constraint
S6	PDE + Ca²CaM ↔ CaM · PDE	$k_{f} [P D E] [C a^{2} C a M] - k_{r} [C a M \cdot P D E]$	$k_{f}$ = 0.25 $s^{- 1}$ · µM⁻¹, $k_{r}$ = 1 $s^{- 1}$	FRET constraint
S7	CaM · PDE + 2Ca2+ ↔ PDE*	$K_{c a t} \frac{[C a] [C a M \cdot P D E]}{C a + K_{m}} - k_{r} [P D E *]$	$K_{c a t}$ = 60 $s^{- 1}$ , $K_{m}$ = 1 $μ M$ , $k_{r}$ = 1 $s^{- 1}$	FRET constraint
S8	PDE + Ca⁴CaM ↔ PDE*	$k_{f} [P D E] [C a^{4} C a M] - k_{r} [P D E *]$	$k_{f}$ = 0.25 $s^{- 1}$ · µM⁻¹, $k_{r}$ = 1 $s^{- 1}$	FRET constraint

Appendix 1—table 11

cAMP reactions modified from Appendix 1—table 3.

#	Reaction	Reaction flux	Kinetic parameters	Ref.
S9	→ cAMP	$k_{b a s e} ([C a M \cdot A C] + [A C] + [A C_{i n d}]) + k_{a c t} [A C *]$	$k_{b a s e}$ = 0.2 $s^{- 1}$ , $k_{a c t}$ = 23.55 $s^{- 1}$ , ACind = 3 x 10⁻⁸	FRET constraint
S10	cAMP →	$\begin{array}{ll} k_{b a s e} [c A M P] \frac{[C a M \cdot P D E] + [P D E]}{[c A M P] + K_{m}} + \\ k_{a c t} \frac{[c A M P] [P D E *]}{[c A M P] + K_{m}} \end{array}$	$k_{b a s e}$ = 0.6 $s^{- 1}$ , $K_{m}$ = 0.6 µM $k_{a c t}$ = 720 $s^{- 1}$	FRET constraint
S11	cAMP →	$V_{i n d} \frac{[c A M P]}{[c A M P] + K_{m}}$	$V_{i n d}$ = 0.25 µM · s⁻¹, $K_{m}$ = 1.4 µM	FRET constraint
S12	2cAMP + R2C2 → R2C + PKA	$k_{f} {[c A M P]}^{2} [R 2 C 2] - k_{r} [R 2 C] [P K A]$	$k_{f}$ = 20 min⁻¹ · µM⁻², $k_{r}$ = 12 min⁻¹ · µM⁻¹
S13	2cAMP + R2C → R2 + PKA	$k_{f} {[c A M P]}^{2} [R 2 C] - k_{r} [R 2] [P K A]$	$k_{f}$ = 20 min⁻¹ · µM⁻², $k_{r}$ = 12 min⁻¹ · µM⁻¹

Appendix 1—table 12

Additional AKAP interactions for the spatial model.

#	Reaction	Reaction flux	Kinetic parameters	Ref
S14	AKAP + R2 → AKAP-R2	$k_{f} [R 2] [A K A P - R 2 C 2] - k_{r} [A K A P - R 2]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ $k_{f}$ = 0.1 $s^{- 1}$	Est.
S15	AKAP + R2C → AKAP-R2C	$k_{f} [R 2 C] [A K A P - R 2 C 2] - k_{r} [A K A P - R 2 C]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ $k_{f}$ = 0.1 $s^{- 1}$	Est.
S16	AKAP + R2C2 → AKAP-R2C2	$k_{f} [R 2 C 2] [A K A P - R 2 C 2] - k_{r} [A K A P - R 2 C 2]$	$k_{f}$ = 1 s⁻¹ · µM⁻¹ $k_{f}$ = 0.1 $s^{- 1}$	Est.
S17	2cAMP + AKAP-R2C2 → AKAP-R2C + PKA	$k_{f} {[c A M P]}^{2} [A K A P - R 2 C 2] - k_{r} [A K A P - R 2 C] [P K A]$	$k_{f}$ = 20 min⁻¹ · µM⁻², $k_{r}$ = 12 min⁻¹ · µM⁻²
S18	2cAMP + AKAP-R2C → AKAP-R2 + PKA	$k_{f} {[c A M P]}^{2} [A K A P - R 2 C] - k_{r} [A K A P - R 2] [P K A]$	$k_{f}$ = 20 min⁻¹ · µM⁻², $k_{r}$ = 12 min⁻¹ · µM⁻²

Appendix 1—table 13

Initial conditions and diffusion coefficients used in the model.

#	Species	Initial value	Diffusion	Ref.
SIC1	Ca²⁺	0.001 µM	100 $\frac{μ m^{2}}{s}$	(Donahue and Abercrombie, 1987), Est. from steady state
SIC2	CaM	2.9 µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC3	Ca₂CaM	0.1 µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC4	Ca₃CaM	4 x 10⁻³ µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC5	Ca₄CaM	1 x 10⁻² µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC6	R₂	0.04 µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC7	R₂C₂	0.2 µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC8	PKA	0.05 µM	0.01 $\frac{μ m^{2}}{s}$	Est. from steady state, diffusion fitted
SIC9	PDE1	0.9 µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC10	PDE1_act	1 x 10⁻³ µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC11	CaMPDE1	1 x 10⁻³ µM	10 $\frac{μ m^{2}}{s}$	Est. from steady state*
SIC12	AC	4 x 10⁻¹⁰ $\frac{m o l}{m^{2}}$	0	Est.
SIC13	CaMAC	0 $\frac{m o l}{m^{2}}$	0	Est.
SIC14	AC_act	0 $\frac{m o l}{m^{2}}$	0	Est.
SIC15	AC_ind	4 x 10⁻¹⁰ $\frac{m o l}{m^{2}}$	1 $\frac{μ m^{2}}{s}$	Est.^†
SIC16	V	−60 mV	1 $\frac{μ m^{2}}{s}$	Fridlyand et al., 2003; Ni et al., 2011^†
SIC17	cAMP	4 x 10⁻⁶ µM	60 $\frac{μ m^{2}}{s}$	Agarwal et al., 2016, Est. from steady state

*For all cytosolic species without well-constrained diffusions, we used 10 $\frac{μ m^{2}}{s}$

^†For all membrane species without well-constrained diffusions we used 1 $\frac{μ m^{2}}{s}$

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/55013/elife-55013-transrepform-v2.pdf
Download elife-55013-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Brian Tenner
Michael Getz
Brian Ross
Donya Ohadi
Christopher H Bohrer
Eric Greenwald
Sohum Mehta
Jie Xiao
Padmini Rangamani
Jin Zhang

(2020)

Spatially compartmentalized phase regulation of a Ca²⁺-cAMP-PKA oscillatory circuit

eLife 9:e55013.

https://doi.org/10.7554/eLife.55013

Share this article

Cite this article

The phase of oscillating cAMP is shifted between the AKAP79/150 compartment and the general plasma membrane compartment, relative to Ca2+.

The AKAP79/150 and PM-targeted sensors are localized at the plasma membrane.

Cytosolic and AKAP79-specific cAMP oscillations are anti-correlated in the same cell.

The oscillation phase is regulated by a balance between Ca2+-sensitive AC and PDE activity.

The Ca2+-dependent cAMP response is dependent on PDE1, but not PDE3 or PDE4.

The cAMP-Ca2+ phase relationship at the PM can be tuned by expression of the Ca2+-dependent AC8.

No difference in endogenous AC8 levels is observed between cells expressing AKAP79-(Ci/Ce)Epac2-camps and lyn-(Ci/Ce)Epac2-camps.

AKAP150 and AC8 both form nanoclusters at the surface of MIN6 β cells.

Analysis of AKAP150 and AC8 cluster area.

AKAP150 is co-clustered with AC8 at the plasma membrane in MIN6 cells.

AC8 diffuses slowly at the plasma membrane.

cAMP-Ca2+ phase relationship can be described by a 3D reaction-diffusion model involving clusters of AKAP79/150 and AC8.

Increasing AC8 concentration within the cluster leads to loss of compartmentalized cAMP-calcium phase relationship.

Disruption of the AKAP79/150:AC8 interaction is associated with a redistribution of AC8 at the PM and a phase shift of cAMP at the AKAP79/150 nanodomain.

Expression of the N-terminus of AC8 perturbed the interaction between endogenous AKAP150 and AC8 in MIN6.

Ca2+ oscillatory dynamics are affected by expression of the disruptor peptide in β cells.

The phase of oscillating PKA activity, relative to Ca2+, is also spatially compartmentalized.

Stochastic model results for the simplified model show the cAMP-Ca2+ phase relationship is preserved and noise is reduced in higher flux conditions.

Phase of cAMP correlates with the expression level of the AKAP79-(Ci/Ce)Epac2-camps.

Phase is driven by activity variability within the Ca2+ oscillatory regime.

of CaM+2Ca, CaMAC+2Ca, and CaMPDE+2Ca, were represented as multi step reactions with rates in the table given below.

Voltage gated channel reactions.

Ca2+flux and reactions.

cAMP reactions.

cAMP reactions (cont.).

Initial conditions.

Initial conditions for the stochastic model.

Compartment volumes for the stochastic model.

Lotka-Volterra model to initiate the membrane depolarization events.

simplified model reactions for the stochastic model.

Ca2+ Flux and reactions modified from Appendix 1—table 2.

cAMP reactions modified from Appendix 1—table 3.

Additional AKAP interactions for the spatial model.

Initial conditions and diffusion coefficients used in the model.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

The phase of oscillating cAMP is shifted between the AKAP79/150 compartment and the general plasma membrane compartment, relative to Ca²⁺.

The oscillation phase is regulated by a balance between Ca²⁺-sensitive AC and PDE activity.

The Ca²⁺-dependent cAMP response is dependent on PDE1, but not PDE3 or PDE4.

The cAMP-Ca²⁺ phase relationship at the PM can be tuned by expression of the Ca²⁺-dependent AC8.

cAMP-Ca²⁺ phase relationship can be described by a 3D reaction-diffusion model involving clusters of AKAP79/150 and AC8.

Ca²⁺ oscillatory dynamics are affected by expression of the disruptor peptide in β cells.

The phase of oscillating PKA activity, relative to Ca²⁺, is also spatially compartmentalized.

Stochastic model results for the simplified model show the cAMP-Ca²⁺ phase relationship is preserved and noise is reduced in higher flux conditions.

Phase is driven by activity variability within the Ca²⁺ oscillatory regime.

of CaM⁺²Ca, CaMAC⁺²Ca, and CaMPDE⁺²Ca, were represented as multi step reactions with rates in the table given below.

Ca²⁺flux and reactions.

Ca²⁺ Flux and reactions modified from Appendix 1—table 2.