Geometric models for robust encoding of dynamical information into embryonic patterns
- Department of Physics, McGill University, Canada
- Division of Developmental Biology, Department of Biology, Friedrich-Alexander-Universität Erlangen-Nürnberg, Germany
Figures
Figure 1 with 2 supplements
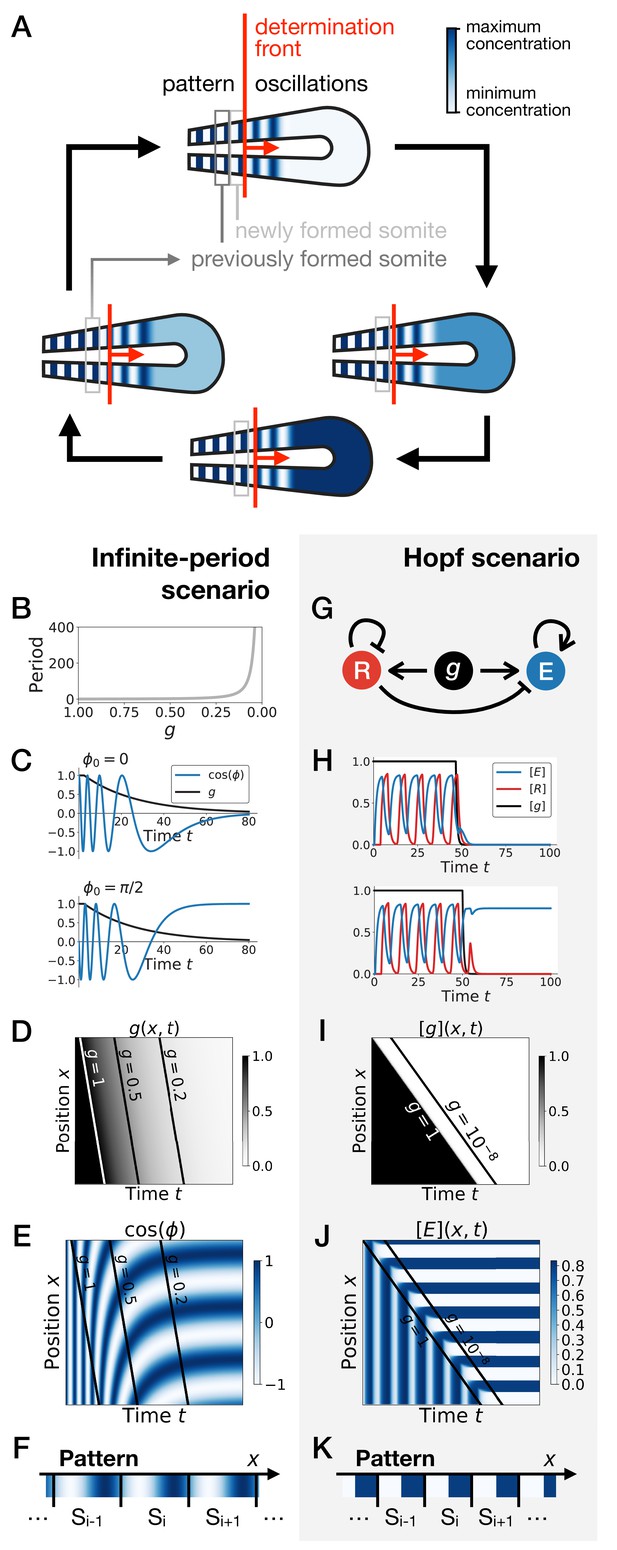
Scenarios for segment formation.
(A) General phenomenology of segment or somite formation. The white to blue gradient represents the oscillating system (e.g. some Notch signaling pathway gene). The determination front (red vertical line) sweeps the embryo in the posterior direction (red arrow) and translates the periodic expression of a genetic clock into a spatial pattern. (B–F) Pattern formation with the infinite-period scenario. (B) Period divergence is imposed as control parameter decreases from 1 to 0. (C) Two simulated cells with the same dynamics of end up with different final values of the phase. (D–E) Kymographs showing respectively the dynamics of parameter used in the simulated embryo and the dynamics of the genetic clock. (F) Schematic of the final pattern. (G–K) Pattern formation with the Hopf scenario. (G) Schematic of the gene regulatory network. (H) Depending on the dynamics of , simulated cells can end up with either a high or a low concentration of protein E. (I–J) Kymograph showing respectively the dynamics of parameter g used in the simulated embryo and the dynamics of protein E. (K) Schematic of the final pattern. The boundary between two segments (‘Si’) is set arbitrarily at the transition from high to low concentrations of protein E.
Figure 1—figure supplement 1
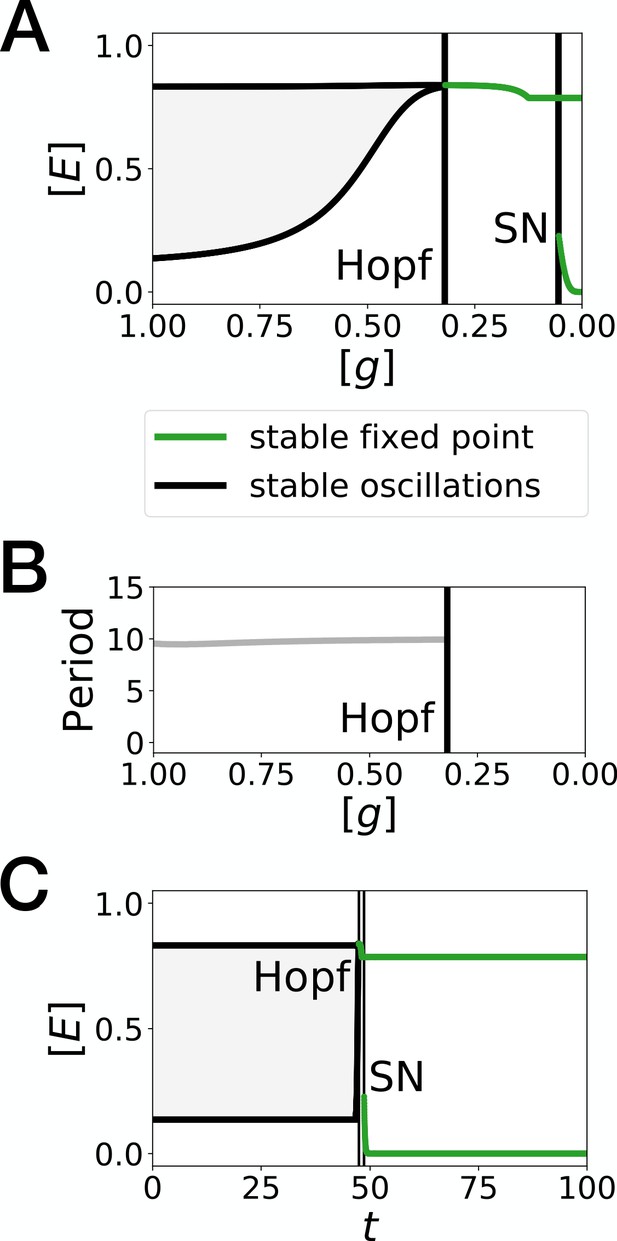
Bifurcation analysis of the Hopf scenario of Figure 1.
(A) Bifurcation diagram showing the types of dynamicsavailable to the system as a function of morphogen concentration. The maximum and minimum concentrations of gene on the stable limit cycle are shown in black. Stable fixed points are show in green. The main bifurcation events are identified with vertical lines. ‘SN’ stands for saddle-node bifurcation. (B) Period of the oscillations along the limit cycle. (C) Same bifurcation diagram as in A, but as a function of time instead. For any given time, the diagram shows the stable fixed points and the extrema of the stable limit cycles for the concentration of morphogen that is found in a given simulated cell at that time. The specific cell used in this diagram is the first cell of Figure 1H.
Figure 1—figure supplement 2
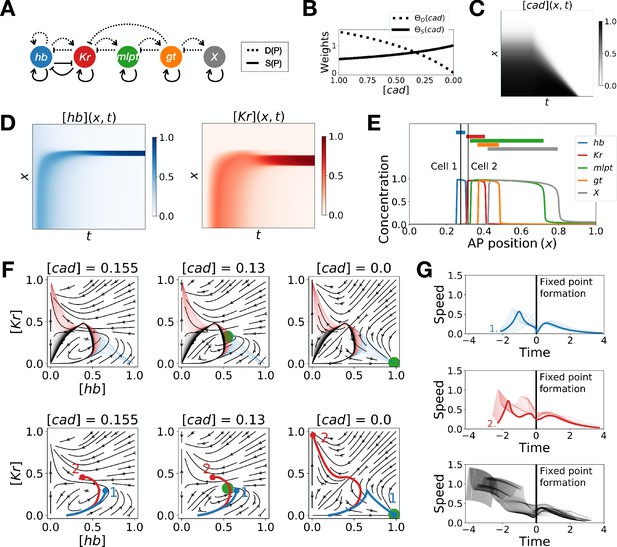
Two-enhancer model for Tribolium segmentation.
(A) Schematic of the gene regulatory networks encoded by the dynamic term (dotted line) and the static term (solid line). (B) Weights of the dynamic (dotted line) and static (solid line) enhancers. (C) Kymograph showing the dynamics of the concentration of morphogen caudal (cad) used in the simulated embryo. (D) Kymographs showing the dynamics of the concentration of proteins hunchback (hb) and Krüppel (Kr). (E) Final pattern of protein expression. The vertical lines identify the positions of the two cells whose trajectories are shown on the bottom subpanels of panel F. (F) Flow in the phase space defined by hb and Kr for different concentrations of morphogen cad. The green disk represents the stable fixed point corresponding to the fate with high concentration of hb. (Top subpanels) Projection of the trajectories of all cells in the hb-Kr phase space. The trajectories of cells that end up with high hb, Kr, and X concentrations are represented with transparent blue, red and black lines, respectively. (Bottom subpanels) Projection of the trajectories of the two cells identified on panel E. For a given cell, the part of the trajectory that is shown is from the initial time point until the time point when cad reaches the concentration used to compute the flow. (G) Speed in phase space of all cells as a function of the time since the formation of the fixed point. The top, middle, and bottom subpanels show the speed of the cells that end up with high hb, Kr, and X concentrations at the end of the simulation, respectively. The thick blue and red lines correspond to the speed of cells 1 and 2, respectively.
Figure 2 with 2 supplements
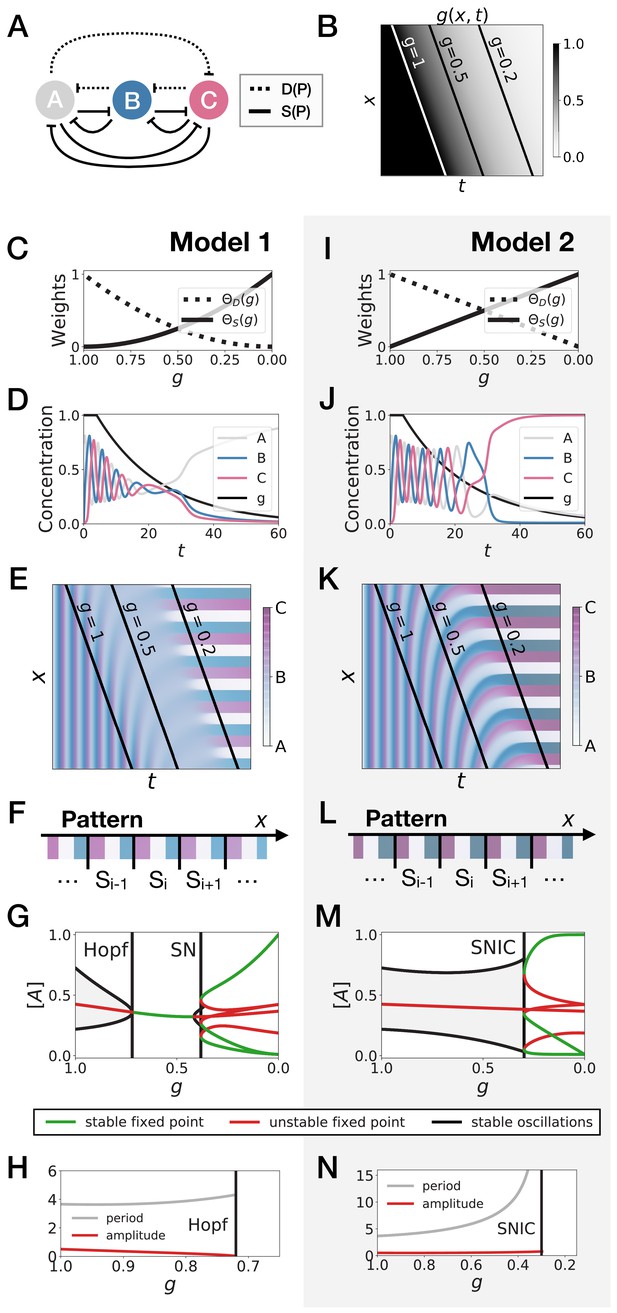
3-gene models for pattern formation.
(A) Schematic of the gene regulatory networks encoded by the dynamic term (dotted line) and the static term (solid line). (B) Kymograph showing the dynamics of parameter used in the simulated embryos for both Models 1 and 2. (C–H) Simulation results for Model 1. (C) Weights of the dynamic (dotted line) and static (solid line) modules as a function of parameter . (D) Gene concentration and value of parameter inside a representative simulated cell as a function of time. (E) Kymograph showing the dynamics of gene expression in the simulated embryo. Transparent colors are used to represent the concentration of the three genes, so that mixes of the three genes can be easily perceived. Genes A, B, and C are shown in transparent white, blue and purple, respectively. Simulated cells with intermediate concentrations of all genes appear grey. (F) Schematic of the final pattern. (G) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . The maximum and minimum concentrations of gene A on the stable limit cycles are shown in black. Stable and unstable fixed points are shown in green and red, respectively. ‘SN’ stands for saddle-node bifurcation. (H) Period (grey line) and amplitude (red line) of the oscillations along the stable limit cycle. (I–N) Simulation results for Model 2.
Figure 2—figure supplement 1
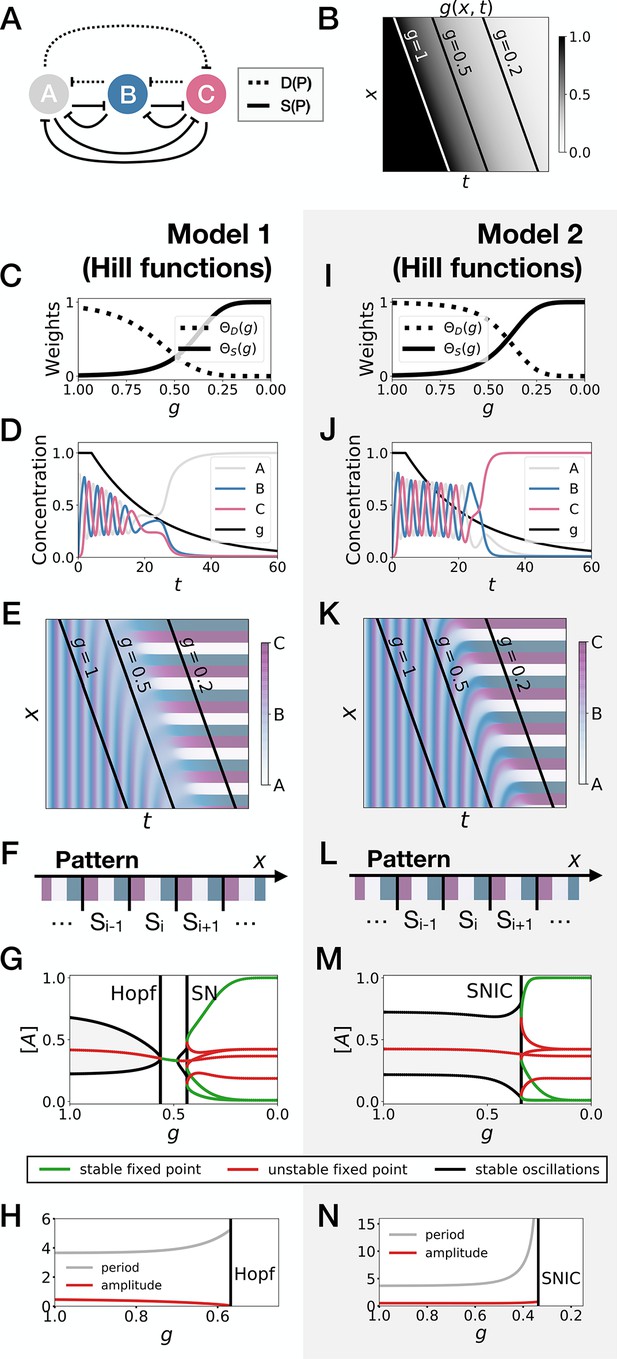
3-gene models for pattern formation with Hill functions for the weights.
(A) Schematic of the gene regulatory networks encoded by the dynamic term (dotted line) and the static term (solid line). (B) Kymograph showing the dynamics of parameter used in the simulated embryos for both Models 1 and 2. (C–H) Simulation results for Model 1. (C) Weights of the dynamic (dotted line) and static (solid line) enhancers as a function of parameter . (D) Gene concentration and value of parameter inside a representative simulated cell as a function of time. (E) Kymograph showing the dynamics of gene expression in the simulated embryo. (F) Schematic of the final pattern. (G) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . ‘SN’ stands for saddle-node bifurcation. (H) Period (grey line) and amplitude (red line) of the oscillations along the stable limit cycle. (I–N) Simulation results for Model 2.
Figure 2—figure supplement 2
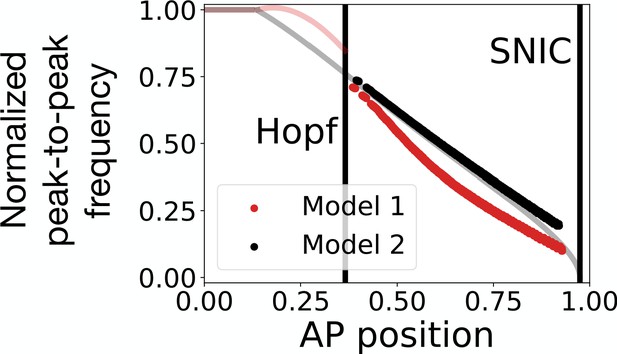
Peak-to-peak frequency in the 3-gene models.
The red and black dots represent the normalized peak-to-peak frequency as a function of the position along the antero-posterior (AP) axis for Models 1 and 2, respectively. These data points were computed numerically by using equation 2 of Giudicelli et al., 2007. The transparent red and black lines are the theoretical normalized frequencies of Models 1 and 2, respectively, obtained via bifurcation analysis. Note that after the Hopf bifurcation in Model 1, the system performs damped oscillations. It is therefore possible to extract a numerical peak-to-peak frequency even after the stable oscillations die during the Hopf bifurcation.
Figure 3 with 1 supplement
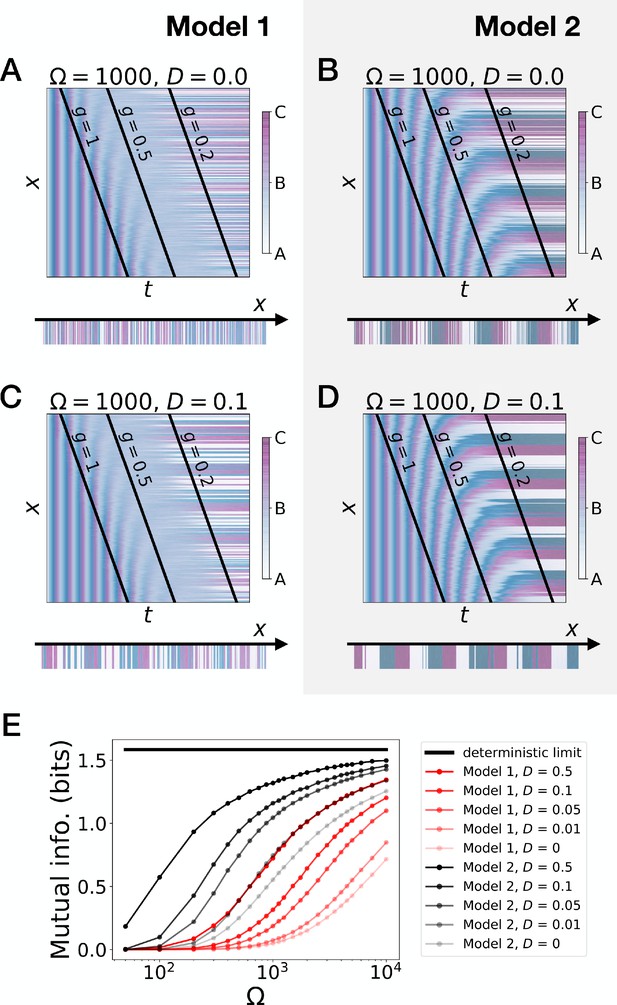
Stochastic simulations of the 3-gene models.
(A–D) Kymographs showing the stochastic dynamics of gene expression in simulated embryos. The specific values of the typical concentration Ω and of the diffusion constant D used to generate each kymograph are indicated on the panels. The concentration of the three genes at the last simulated time point is shown schematically in the lower part of each panel. (E) Mutual information as a function of typical concentration Ω for Model 1 (red lines) and Model 2 (black lines). Paler colors correspond to lower values of the diffusion constant D. The thick horizontal black line indicates the ideal mutual information for three mutually exclusive genes. Note that higher values of Ω correspond to lower noise levels.
Figure 3—figure supplement 1
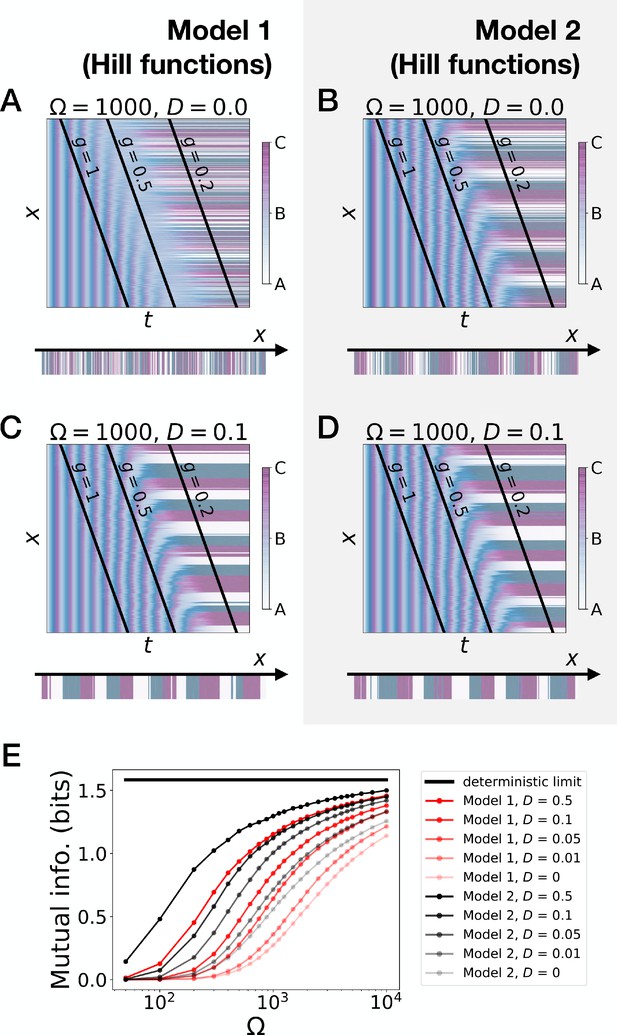
Stochastic simulations of the 3-gene models with Hill functions for the weights.
(A–D) Kymographs showing the stochastic dynamics of gene expression in simulated embryos. The concentration of the three genes at the last simulated time point is shown schematically in the lower part of each panel. (E) Mutual information as a function of typical concentration Ω for Model 1 (red lines) and Model 2 (black lines). Paler colors correspond to lower values of the diffusion constant D. The thick horizontal black line indicates the ideal mutual information for three mutually exclusive genes.
Figure 4 with 9 supplements
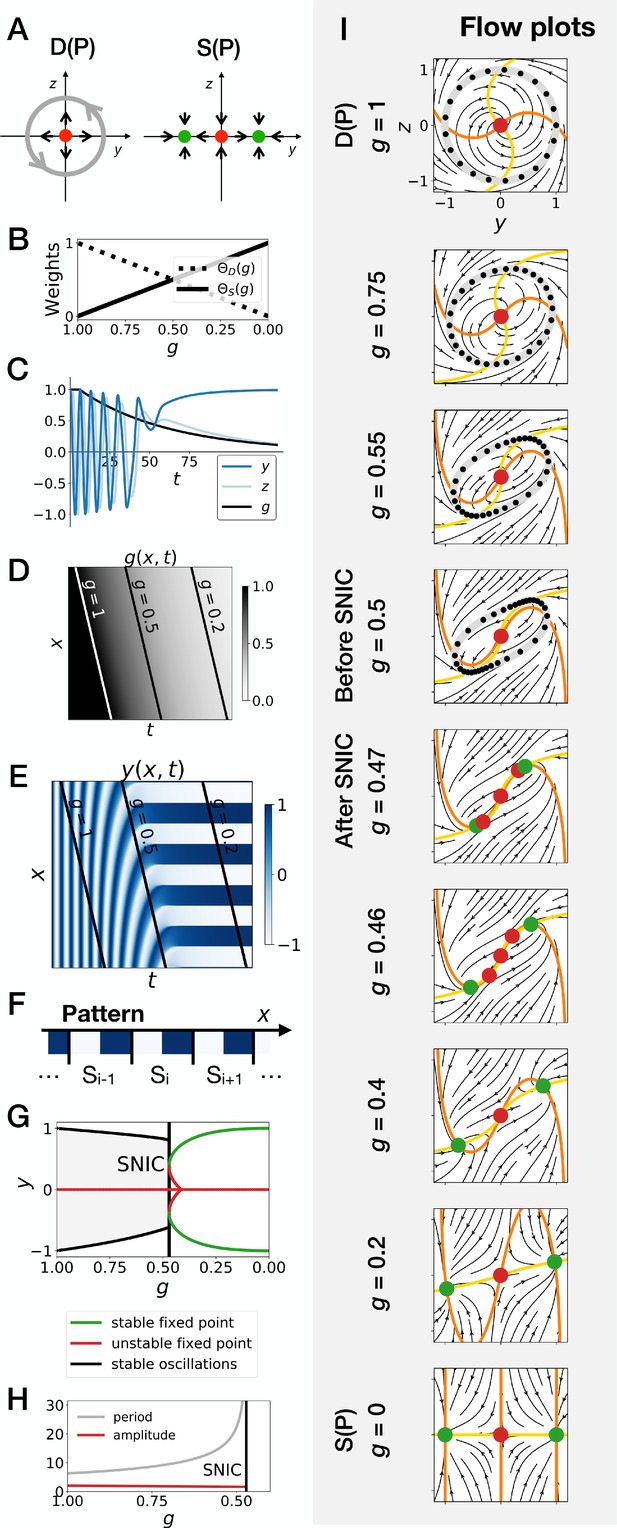
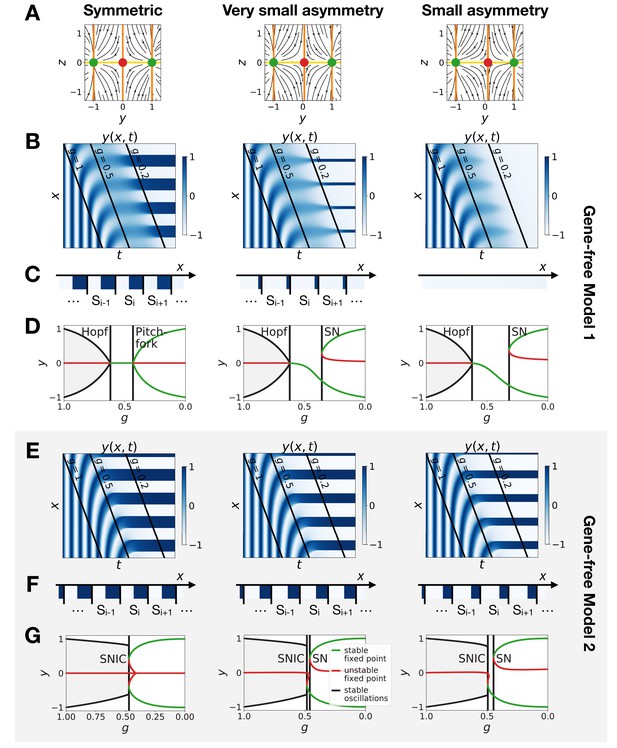
Gene-free geometric model for pattern formation (Model 2).
(A) Schematic of the flow encoded by the dynamic and static terms. The grey circle represents oscillations on the unit circle. Green and red dots represent unstable and stable fixed points, respectively. (B) Weights of the dynamic (dotted line) and static (solid line) modules as a function of parameter . (C) Values of geometric coordinates and and of parameter in a simulated cell as a function of time. (D–E) Kymographs showing respectively the dynamics of parameter used in the simulated embryo and the dynamics of coordinate . (F) Schematic of the final pattern. (G) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . The maximum and minimum values of coordinate on the stable limit cycles are shown in black. Stable and unstable fixed points are shown in green and red, respectively. (H) Period and amplitude of the oscillations. (I) Flow in phase space for different values of parameter . The same color scheme than panel A is used to represent the cycles and the fixed points. Positions along the limit cycle at time points separated by a fixed time interval are indicated with black dots, so that variations of the speed of the oscillations along the limit cycle can be visualized. The yellow and orange lines represent the and nullclines, respectively.
Figure 4—figure supplement 1
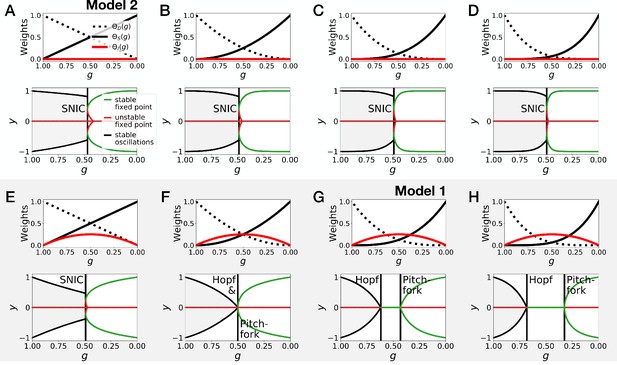
Gene-free models with different weights for the dynamic and static modules .
(A–D) Bifurcation analysis of gene-free models with linear weights (Model 2), quadratic weights, cubic weights and weights to the power 4. (E–H) Bifurcation analysis of gene-free models with linear weights, quadratic weights, cubic weights (Model 1) and weights to the power 4.
Figure 4—figure supplement 2
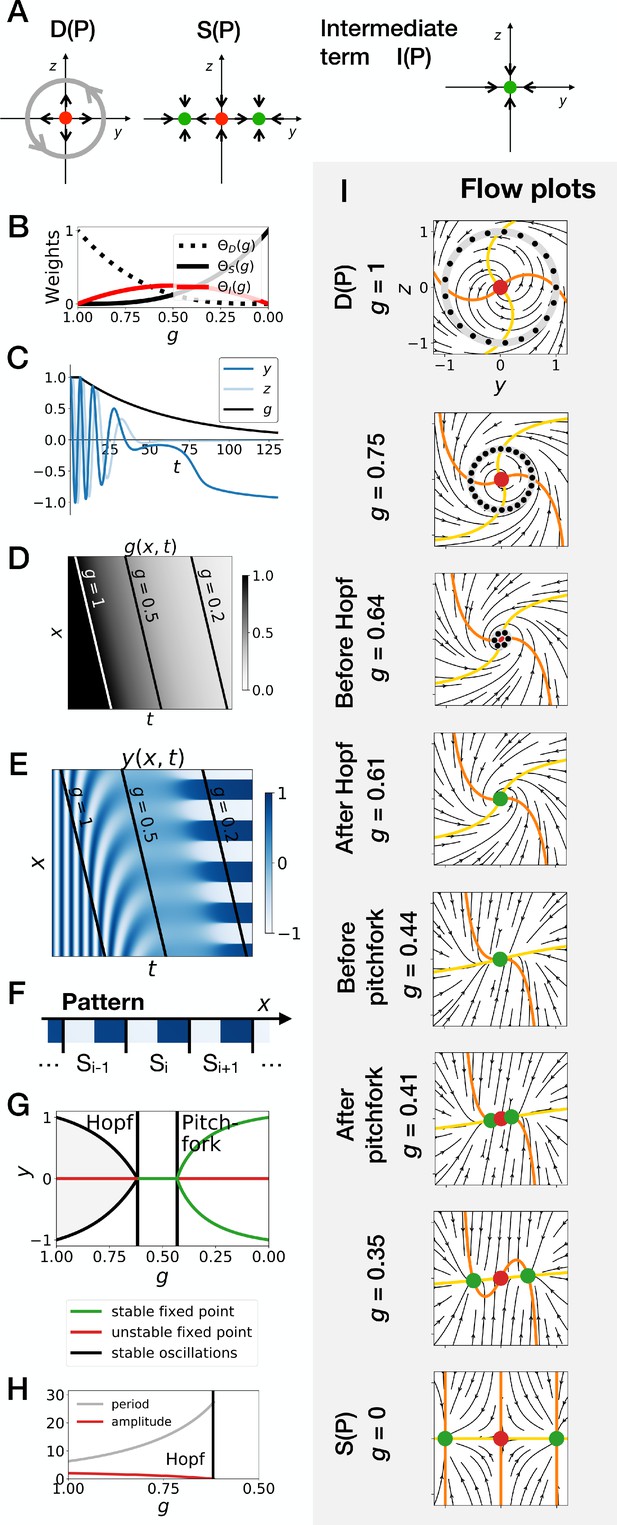
Supercritical Hopf scenario in the gene-free model (Model 1).
(A) Schematic of the flow encoded by the dynamic, static and intermediate terms. (B) Weights of the dynamic (dotted black line), static (solid black line) and intermediate (solid red line) enhancers as a function of parameter . (C) Values of geometric coordinates and , and of parameter in a simulated cell as a function of time. (D) Kymograph showing the dynamics of parameter used in the simulated embryo. (E) Kymograph showing the dynamics of geometric coordinate . (F) Schematic of the final pattern. (G) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . (H) Period (grey line) and amplitude (red line) of the oscillations. (I) Flow in phase space for different values of parameter . The limit cycles are represented by thick grey lines. Positions along the limit cycle at time points separated by a fixed time interval are indicated with black dots, such that the (absence of) variations of the speed along the limit cycles can be visualized. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively.
Figure 4—figure supplement 3
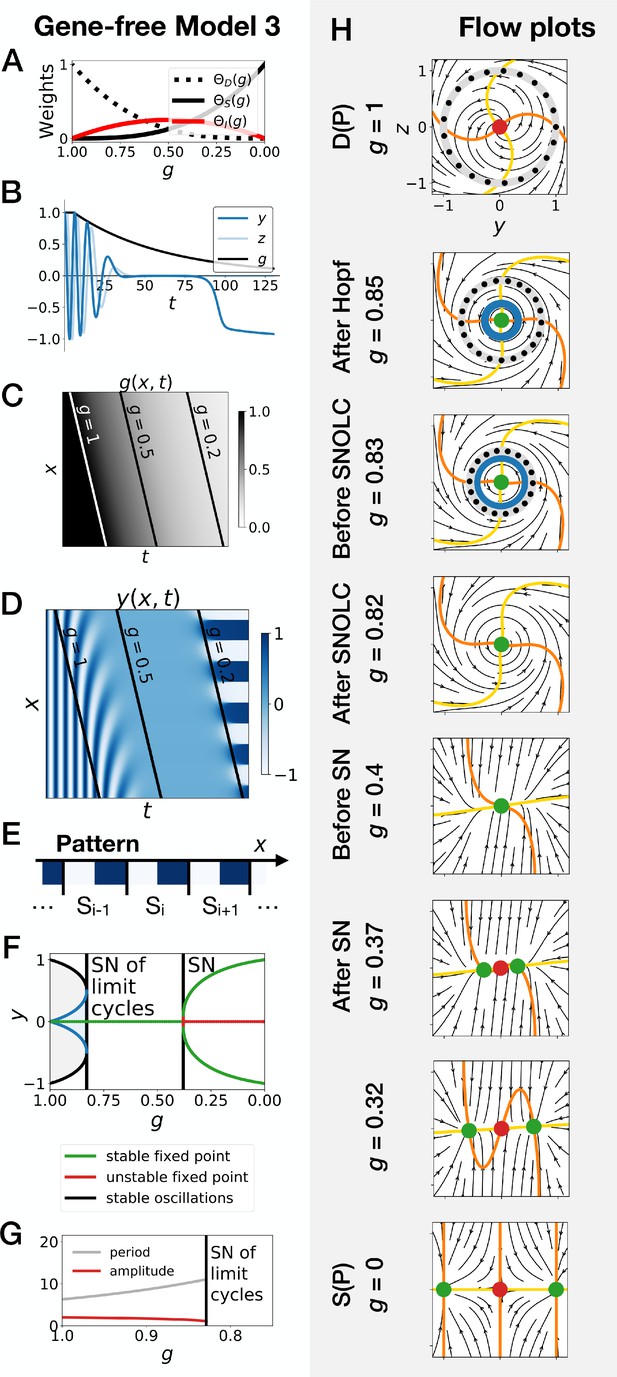
Subcritical Hopf scenario in the gene-free model (Model 3).
We can modify the dynamic module (making it more non linear) to obtain subcritical Hopf scenario (see equations in appendix). (A) Weights of the dynamic (dotted black line), static (solid black line) and intermediate (solid red line) enhancers as a function of parameter . (B) Values of geometric coordinates and , and of parameter in a simulated cell as a function of time. (C) Kymograph showing the dynamics of parameter used in the simulated embryo. (D) Kymograph showing the dynamics of geometric coordinate . (E) Schematic of the final pattern. (F) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . ‘SN’ stands for saddle-node bifurcation. (G) Period (grey line) and amplitude (red line) of the oscillations. (H) Flow in phase space for different values of parameter . The limit cycles are represented by thick grey lines. Positions along the limit cycle at time points separated by a fixed time interval are indicated with black dots, such that the variations of the speed along the limit cycles can be visualized. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively. ‘SNOLC’ stands for saddle-node of limit cycles bifurcation.
Figure 4—figure supplement 4
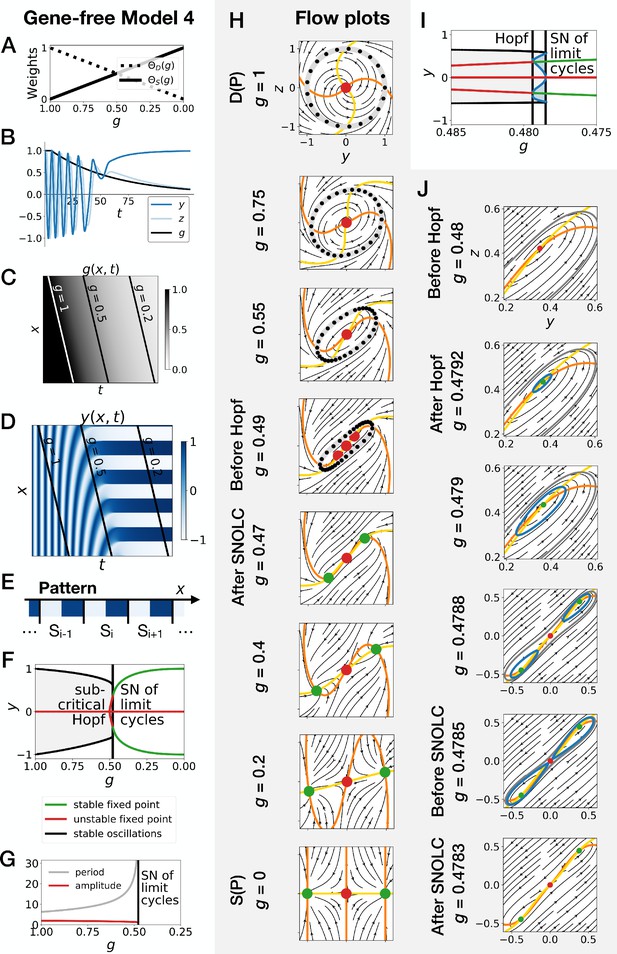
Gene-free model with two subcritical Hopf bifurcations (Model 4).
We can modify the dynamic module (making it more non linear) to obtain subcritical Hopf scenario (see equations in appendix). (A) Weights of the dynamic and static enhancers as a function of parameter . (B) Values of geometric coordinates and , and of parameter in a simulated cell as a function of time. (C) Kymograph showing the dynamics of parameter used in the simulated embryo. (D) Kymograph showing the dynamics of geometric coordinate . (E) Schematic of the final pattern. (F) Bifurcation diagram showing the types of dynamics available to the simulated embryo as a function of parameter . ‘SN’ stands for saddle-node bifurcation. (G) Period and amplitude of the oscillations. (H) Flow in phase space for different values of parameter . The limit cycles are represented by thick grey lines. Positions along the limit cycle at time points separated by a fixed time interval are indicated with black dots, such that the (absence of) variations of the speed along the limit cycles can be visualized. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively. (I–J) Bifurcation diagram and flow plots for values of close to the subcritical Hopf and saddle-node of limit cycles bifurcations. ‘SNOLC’ stands for saddle-node of limit cycles bifurcation.
Figure 4—figure supplement 5
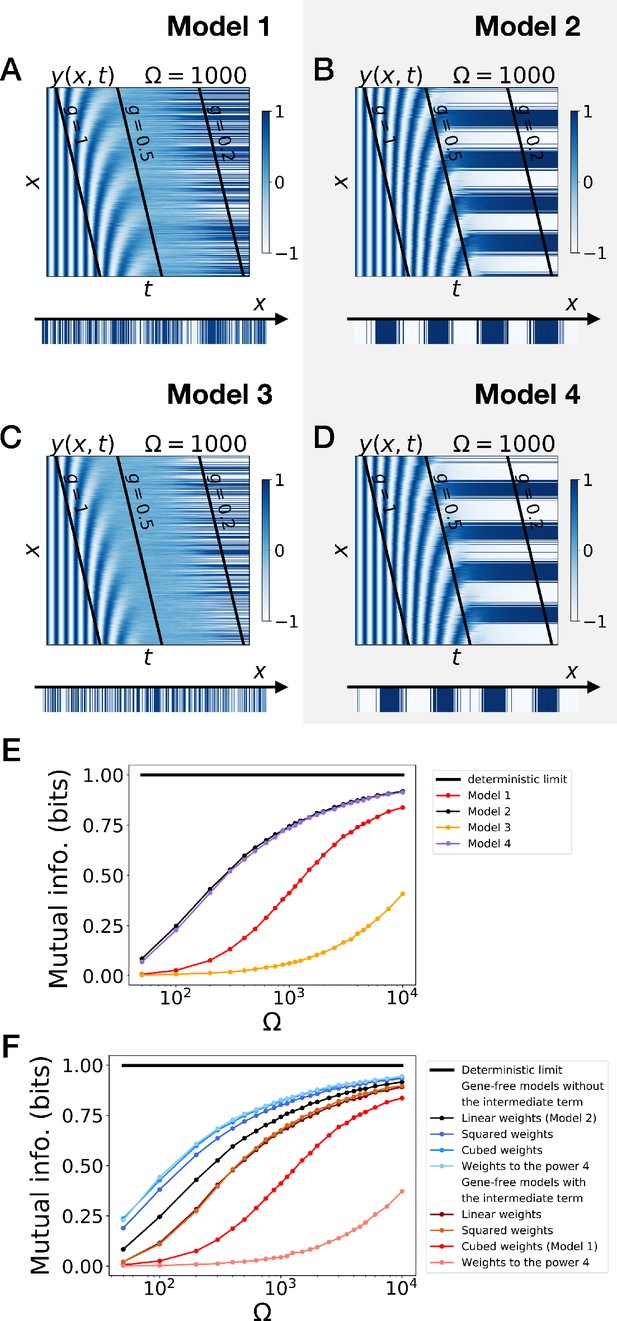
Stochastic simulations of the gene-free models.
(A–D) Kymographs showing the stochastic dynamics of variable in simulated embryos. The specific value of parameter Ω used to generate each kymograph is indicated on the panels. (E) Mutual information as a function of typical concentration Ω for Models 1, 2, 3 and 4. The thick horizontal black line indicates the ideal mutual information for a pattern with two symmetric regions. (F) Mutual information as a function of typical concentration Ω for the gene-free models of Figure 4—figure supplement 4.
Figure 4—video 1
Flow of the gene-free model with a SNIC bifurcation (Model 2).
Flow in phase space as parameter goes from 1 to 0. The stable limit cycles are represented by thick grey lines. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively.
Figure 4—video 2
Flow of the gene-free model with a supercritical Hopf bifurcation (Model 1).
Flow in phase space as parameter goes from 1 to 0. The stable limit cycles are represented by thick grey lines. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively.
Figure 4—video 3
Flow of the gene-free model with a subcritical Hopf bifurcation (Model 3).
Flow in phase space as parameter goes from 1 to 0. The stable and unstable limit cycles are represented by thick grey and blue lines, respectively. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively.
Figure 4—video 4
Flow of the gene-free model with two subcritical Hopf bifurcations (Model 4).
Flow in phase space as parameter goes from 1 to 0. The stable limit cycles are represented by thick grey lines. The yellow and orange lines represent the and nullclines, respectively. The green and red dots represent stable and unstable fixed points, respectively.
Figure 5 with 2 supplements
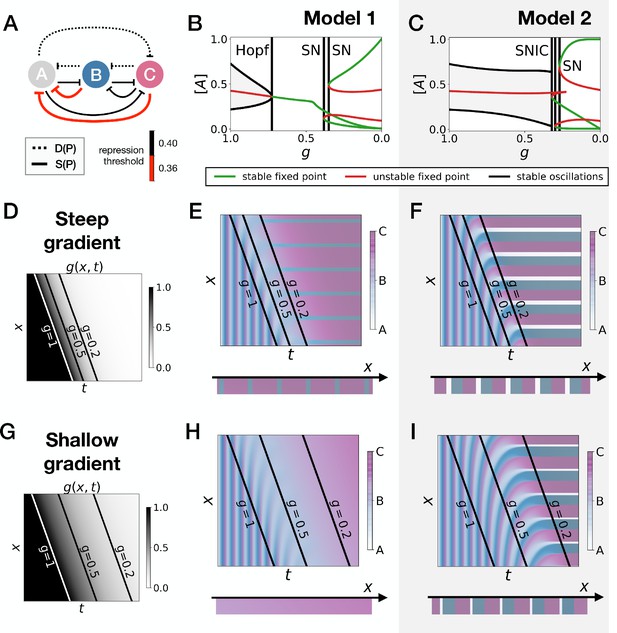
Perturbation of the morphogen gradient steepness in asymmetric 3-gene models.
(A) Schematic of the gene regulatory networks encoded by the dynamic term (dotted line) and the static term (solid line). The thick red lines indicate stronger repression than the black lines (see the parameters in the Appendix). (B–C) Bifurcation diagram showing the types of dynamics available in Models 1 and 2. The maximum and minimum concentrations of gene A on the stable limit cycles are shown in black. Stable and unstable fixed points are shown in green and red, respectively. The main bifurcations are identified with vertical lines. ‘SN’ stands for saddle-node bifurcation. (D–F) Simulation results for a steep gradient of parameter . (D) Kymograph showing the dynamics of parameter used in the simulated embryos for both Models 1 and 2. (E–F) Kymographs showing the dynamics of gene expression in the simulated embryos of Models 1 and 2. The concentration of the three genes at the last simulated time point is shown schematically in the lower part of the panels. (G–I) Simulation results for a shallow gradient of parameter .
Figure 5—figure supplement 1
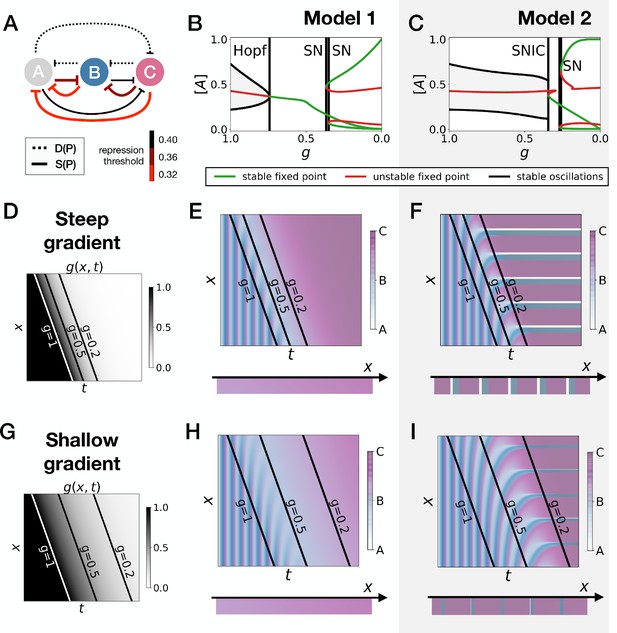
Perturbation of the morphogen gradient steepness in strongly asymmetric 3-gene models.
(A) Schematic of the gene regulatory networks encoded by the dynamic (dotted line) and static (solid line) terms. For each interaction, the color indicates the strength of the repression, with darker shades of red corresponding to weaker repression. (B–C) Bifurcation diagram showing the types of dynamics available in Models 1 and 2. ‘SN’ stands for saddle-node bifurcation. (D–F) Simulation results for a steep gradient of parameter . (D) Kymograph showing the dynamics of parameter used in the simulated embryos of both Models 1 and 2. (E) Kymograph showing the dynamics of gene expression in the simulated embryos of Model 1. The concentration of the three genes at the last simulated time point is shown schematically in the lower part of the panel. (F) Kymograph showing the dynamics of gene expression in the simulated embryos of Model 2. (G–I) Simulation results for a shallow gradient of parameter .
Figure 5—figure supplement 2
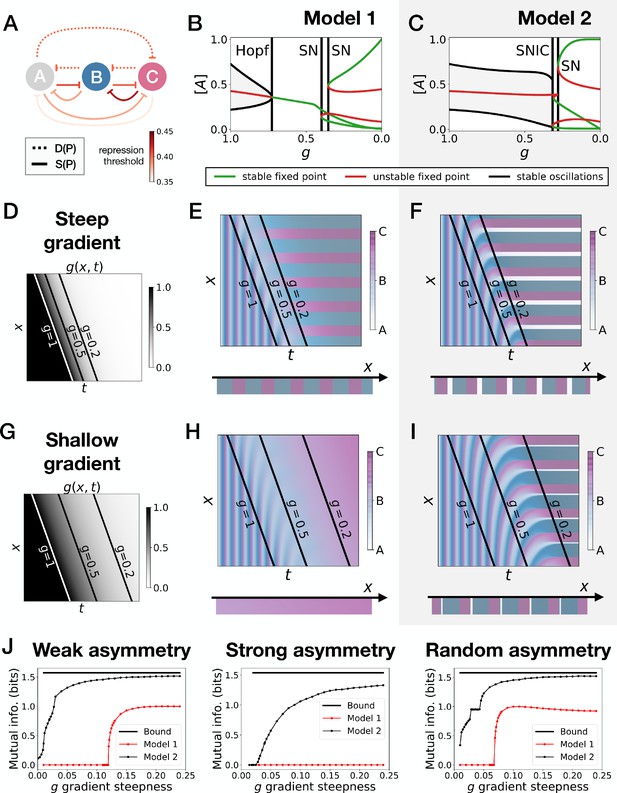
Perturbation of the morphogen gradient steepness in randomly asymmetric 3-gene models.
(A) Schematic of the gene regulatory networks encoded by the dynamic (dotted line) and static (solid line) terms. For each interaction, the color indicates the strength of the repression, with darker shades of red corresponding to weaker repression. (B–C) Bifurcation diagram showing the types of dynamics available in Models 1 and 2. ‘SN’ stands for saddle-node bifurcation. (D–F) Simulation results for a steep gradient of parameter . (D) Kymograph showing the dynamics of parameter used in the simulated embryos of both Models 1 and 2. (E) Kymograph showing the dynamics of gene expression in the simulated embryos of Model 1. The concentration of the three genes at the last simulated time point is shown schematically in the lower part of the panel. (F) Kymograph showing the dynamics of gene expression in the simulated embryos of Model 2. (G–I) Simulation results for a shallow gradient of parameter . (J) Mutual information as a function of the steepness of the gradient for Models 1 (red line) and 2 (black line). The thick horizontal black line indicates the theoretical upper bound. The left, center and right subpanels show respectively the mutual information for models with a weak asymmetry in the fixed points of the static term (Figure 5), with a strong asymmetry (Figure 5—figure supplement 1) and with a random asymmetry (this figure).
Figure 6 with 1 supplement
Perturbation of the morphogen gradient steepness in the gene-free geometric models.
(A) Flow plots showing the changes of geometry of the static module. (B–C) Corresponding kymographs and final patterns for Model 1. (D) Associated bifurcations diagrams. ‘SN’ stands for saddle-node bifurcation. (E–F) Corresponding kymographs and final patterns for Model 2. (G) Associated bifurcation diagrams.
Figure 6—figure supplement 1
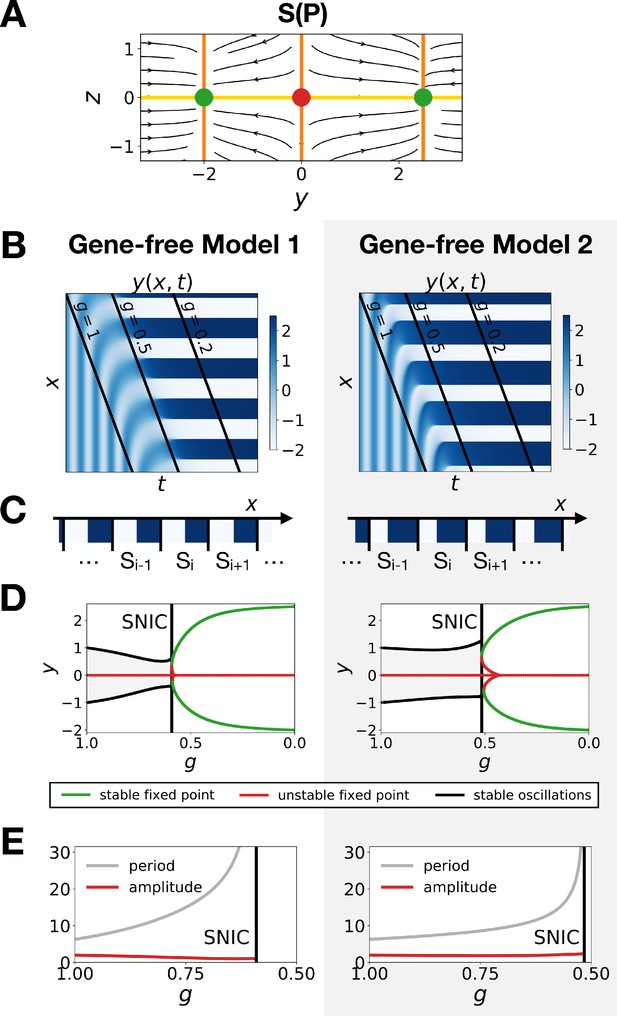
Model one becomes a SNIC when fixed points are outside the limit cycle.
(A) Flow plots showing the change of geometry of the static module. (B–C) Corresponding kymographs and final patterns for Models 1 and 2. (D–E) Associated bifurcations diagrams and plots of the period and amplitude of the oscillations as a function of parameter .
Figure 7 with 3 supplements
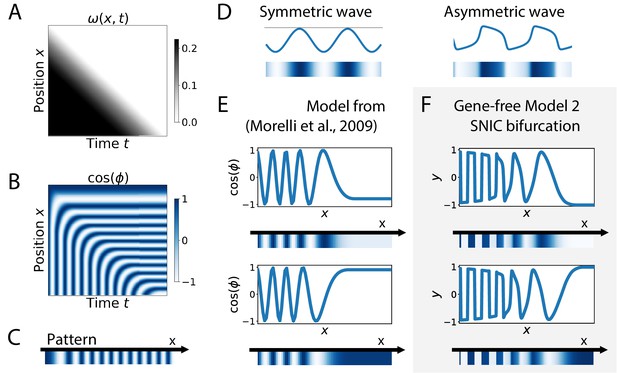
Wave pattern in different models for the infinite-period scenario.
(A) Frequency profile for the simulation of the model of coupled oscillators from Morelli et al., 2009. (B–C) Kymograph showing the dynamics of the phase of the oscillators and the corresponding final pattern. (D) Two schematic examples of possible wave patterns (symmetrical vs asymmetrical). The symmetric wave is obtained with a sine function. The asymmetric wave is retrieved from simulations of a Van der Pol oscillator. (E) Wave pattern for the model of Panels (A–C) for two different time points. (F) Wave pattern for Model 2 of Figure 4 for two different time points.
Figure 7—figure supplement 1
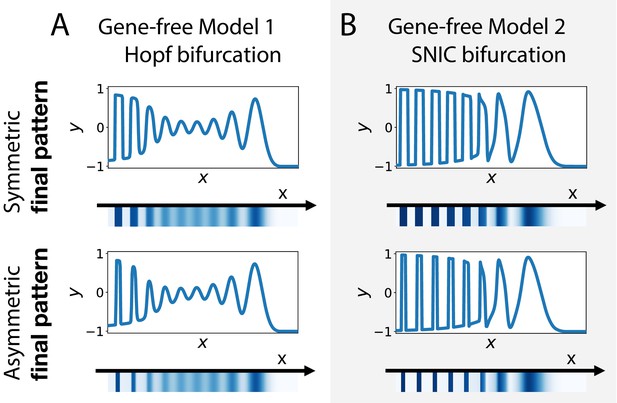
Wave pattern in different versions of the 2D gene-free model.
(A) Wave patterns of the gene-free Model one with a Hopf bifurcation. The top and bottom subpanels show the wave pattern for symmetric and asymmetric fixed points in the static term, respectively. (B) Wave patterns of the gene-free Model 2 with a SNIC bifurcation.
Figure 7—figure supplement 2
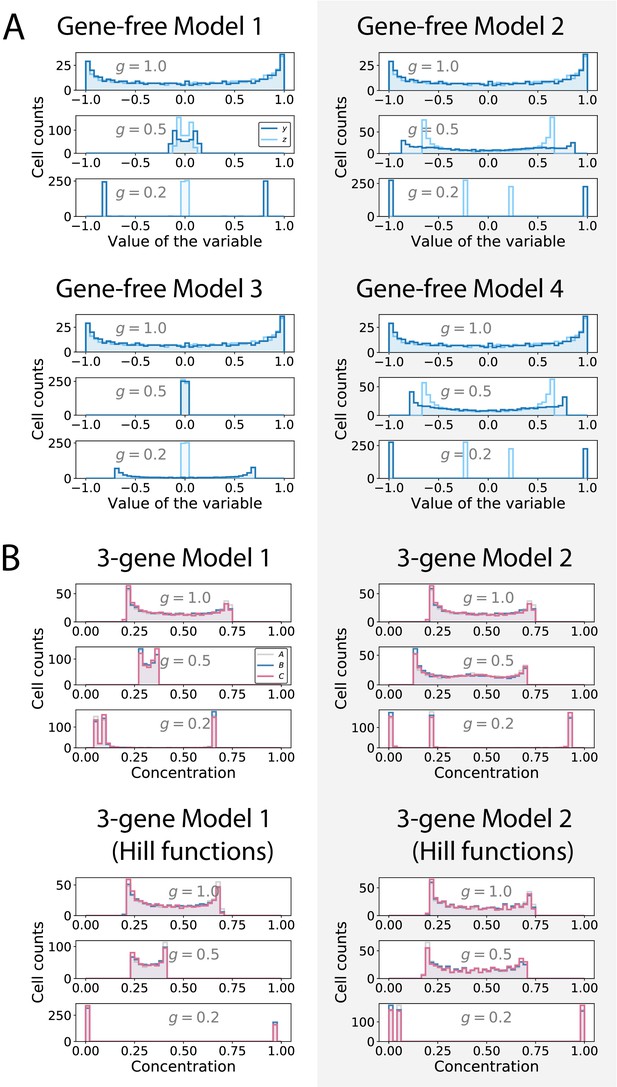
Distribution of the values of the geometric variables (gene-free models) and of the gene concentrations (3-gene models).
(A) Histograms showing the distributions of the values of the (dark blue) and (light blue) variables in gene-free Models 1, 2, 3 and 4 for different values of parameter . (B) Histograms showing the distributions of the concentrations of genes (grey), (blue) and (pink) in 3-gene Models 1 and 2 for different values of parameter .
Figure 7—video 1
Comparison of pattern formation dynamics in different models.
Dynamics of the spatial wave patterns in four models: a phase model with diverging period similar to the infinite-period scenario of Figure 1, the symmetric gene-free Model 1, the symmetric gene-free Model 2, and the asymmetric gene-free Model 2.
Tables
Appendix 1—table 1
Parameter values for the repression interactions of the 3-gene models.
| Model version | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Symmetric | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Weak asymmetry | 0.4 | 0.4 | 0.4 | 0.36 | 0.36 | 0.4 | 0.4 | 0.4 | 0.4 |
| Strong asymmetry | 0.4 | 0.4 | 0.4 | 0.32 | 0.32 | 0.36 | 0.36 | 0.4 | 0.4 |
| Randomized asymmetry | 0.4 | 0.4 | 0.4 | 0.3825 | 0.3560 | 0.4334 | 0.4102 | 0.3802 | 0.4038 |
Appendix 1—table 2
Weights of the dynamic and static terms of the 3-gene models.
| Weights | Model 1 | Model 2 | Model 1 with hill functions | Model 2 with hill functions |
|---|---|---|---|---|
| g | ||||
Appendix 1—table 3
Weights of the dynamic, static and intermediate terms of the gene-free models.
| Weights | Models 1 and 3 | Models 2 and 4 |
|---|---|---|
| g | ||
| 0 |
Appendix 1—table 4
Parameter values for the ODE of the phase oscillators in the infinite-period scenario of Figure 7.
| 0.07 | 1 | 0 | 0.3886 | 0.255 | 36 |
Appendix 1—table 5
Parameter values for the ODE of the effector protein in the Hopf scenario of Figure 1.
| 0.7176 | 0.4942 | 0.0678 | 0.3213 | 0.48 | 0.8538 | 3 | 4.3549 | 4.5321 |
Appendix 1—table 6
Parameter values for the ODE of the repressor protein in the Hopf scenario of Figure 1.
| 0.9422 | 0.1156 | 0.5047 | 3.92 | 0.9759 | 3.2136 | 4.522 |
Appendix 1—table 7
Parameter values for the spatio-temporal profile of input g.
| Model | S | V | |
|---|---|---|---|
| Infinite-period scenario of Figure 1 | 0.5 | 0.08 | 0.2 |
| Hopf scenario of Figure 1 | 0.5 | 3 | 0 |
| 3-gene models, shallow gradient | 1 | 0.05 | 0.2 |
| 3-gene models, steep gradient | 2.5 | 0.05 | 0.2 |
| Gene-free models (Figure 4, its supplements and Figure 7—figure supplement 2) | 0.5 | 0.035 | 0.2 |
| Gene-free models (Figure 6 and its supplement) | 1 | 0.036 | 0 |
| Gene-free models (Figure 7 and Figure 7—figure supplement 1) | 6 | 0.0042 | 0 |
| Gene-free models (Figure 7—video 1) | 0.9 | 0.04 | 0 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Geometric models for robust encoding of dynamical information into embryonic patterns
eLife 9:e55778.
https://doi.org/10.7554/eLife.55778
