Figures and data in Stochastic bond dynamics facilitates alignment of malaria parasite at erythrocyte membrane upon invasion

Figures
Videos
Tables
Additional files

9 figures, 3 videos, 2 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

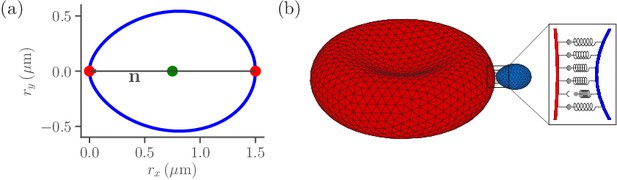
Sketch of parasite and RBC models.

(a) Two-dimensional sketch of a parasite with a directional vector $𝐧$ from the parasite’s back at $r_{x} = 1.5 μ m$ to its apex at $r_{x} = 0$ . (b) Three-dimensional triangulated surfaces of a RBC (red) and a parasite (blue). Bonds between the parasite and RBC can form within the contact zone which is illustrated by a magnified view, where discrete receptor-ligand interactions (or bonds) are sketched. A bond can form with a constant on-rate $k_{on}$ and break with a constant off-rate $k_{off}$ .

Figure 2

Download asset Open asset

Calibration of parasite adhesion parameters.

(a) A time instance of parasite motion at RBC membrane from an experimental video (Weiss et al., 2015) (top) and simulation (bottom), see also Video 1. To obtain the distribution of merozoite fixed-time displacements, the marked parasite (red circle) is tracked over the course of its interaction with the RBC membrane. (b) Comparison between experimental (20 samples) and simulated (100 samples) fixed-time displacements ( $Δ d$ ) of the parasite at RBC membrane, which is normalized by the effective RBC diameter $D_{0} = \sqrt{A_{0} / π}$ calculated from the membrane area $A_{0}$ . By adapting the interaction parameters, the displacement distribution in simulations is calibrated against the experimental distribution. The resulting reference parameters for our model can be found in Table 2. (c) Mean squared displacement (MSD) of a parasite from simulations as a function of time. The black solid line marks a diffusive regime with $MSD \sim t$ . Note the subdiffusive dynamics for short times, less than about $1 s$ .

Figure 2—source data 1 Source data for graphs shown in Figure 2(b,c).: https://cdn.elifesciences.org/articles/56500/elife-56500-fig2-data1-v2.zip
Download elife-56500-fig2-data1-v2.zip

Figure 3 with 1 supplement

Download asset Open asset

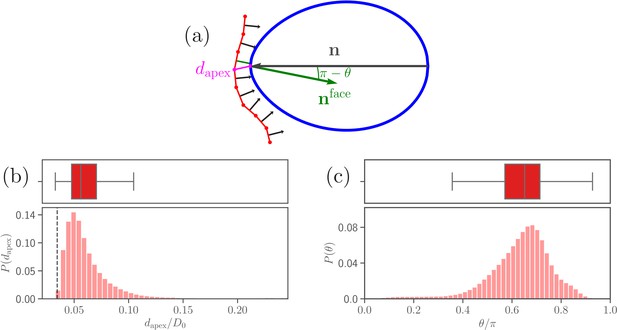
Parasite adhesion to a deformable RBC.

(a) Sketch of apex distance $d_{apex}$ and alignment angle $θ$ . The apex distance $d_{apex}$ is defined as a distance (magenta line) between the parasite’s apex and the closest vertex of RBC membrane. The alignment angle $θ$ corresponds to the angle between the parasite’s directional vector (black arrow) and the normal vector $𝐧^{face}$ (green arrow) of a triangular face whose center is closest to the apex. Note that the angle $π - θ$ is drawn in the plot. (b and c) Probability distributions of the apex distance $d_{apex} / D_{0}$ and the alignment angle $θ / π$ . Data are obtained for parameters shown in Table 2, and accumulated starting from an initial adhesion contact (i.e., formation of a few bonds). The dashed line in the apex distance distribution indicates the cutoff $2^{1 / 6} σ$ of repulsive LJ interactions. Note that a good parasite alignment requires small values of $d_{apex} / D_{0}$ and values of $θ / π$ close to unity.

Figure 3—source data 1 Source data for graphs shown in Figure 3b,c and Figure 3—figure supplement 1.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig3-data1-v2.zip
Download elife-56500-fig3-data1-v2.zip

Figure 3—figure supplement 1

Download asset Open asset

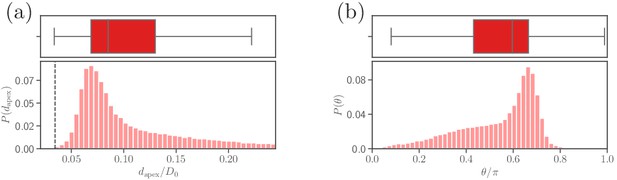
Parasite adhesion to a rigid RBC (see section ‘Effect of RBC rigidity’).

Probability distributions of (a) the apex distance $d_{apex} / D_{0}$ , and (b) the alignment angle $θ / π$ . The dashed line in the apex distance distribution indicates the cutoff $2^{1 / 6} σ$ of repulsive LJ interactions.

Figure 4

Download asset Open asset

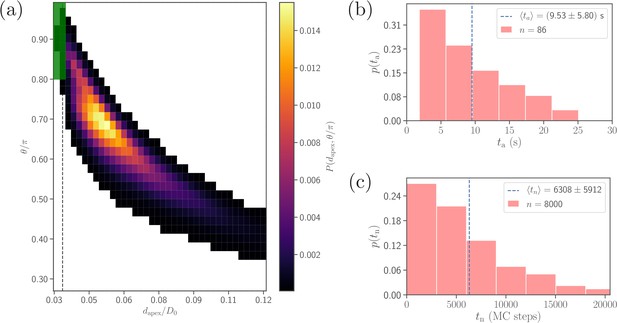
Comparison of alignment times obtained from direct DPD simulations and MC sampling.

(a) Two-dimensional probability map as a function of $d_{apex}$ and $θ$ . Each bin represents a single alignment state and the color corresponds to probability of that state. The dark green area ( $d_{apex} / D_{0} \leq 0.036$ and $θ / π \geq 0.8$ , compare with Equation 4) represents the criteria for a successful alignment. The black dashed line corresponds to the cutoff $2^{1 / 6} σ$ of repulsive LJ interactions. (b) Distribution of alignment times $t_{a}$ obtained from 86 statistically independent DPD simulations. $t_{a}$ is defined as a time interval starting from an initial adhesive contact (i.e., formation of a few bonds) to the instance when the alignment criteria for $d_{apex}$ and $θ$ in Equation 4 are met. The average alignment time is equal to $⟨ t_{a} ⟩ ≃ 9.53 s$ . (c) Alignment time distribution from MC sampling using the probability map in (a). The alignment time is defined as a number of MC steps needed to satisfy the alignment criteria, as the MC procedure does not have an inherit timescale. Note that the sample size in MC modeling (8000 trajectories) is much larger than that in (b).

Figure 4—source data 1 Source data for graphs shown in Figure 4a–c.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig4-data1-v2.zip
Download elife-56500-fig4-data1-v2.zip

Figure 5 with 2 supplements

Download asset Open asset

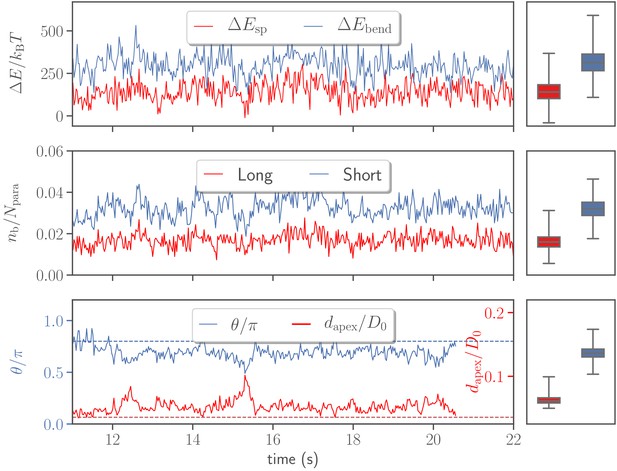
Variations in stretching $Δ E_{sp}$ and bending $Δ E_{bend}$ energies, the number of bonds $n_{b}$ , the head distance $d_{apex}$ , and the alignment angle $θ$ as a function of time for the default parameter set given in Table 2.

Temporal changes in the number of bonds are shown for both long and short bond types. The dashed lines in the bottom plot correspond to the alignment criteria in Equation 4. For all quantities, the corresponding averages and variances represented by box plots are depicted on the right.

Figure 5—source data 1 Source data for graphs shown in Figure 5 and Figure 5—figure supplements 1 and 2.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig5-data1-v2.zip
Download elife-56500-fig5-data1-v2.zip

Figure 5—figure supplement 1

Download asset Open asset

Dependence of parasite wrapping on the position at RBC membrane.

(a) Average total number of bonds between the merozoite and RBC as a function of the distance $d_{cm}$ between their centers of mass. (b) Illustration of parasite adhesion at the RBC rim (marked by I) and in the dimple (II). The parasite forms more bonds in the dimples (position II) than at the RBC rim (position I).

Figure 5—figure supplement 2

Download asset Open asset

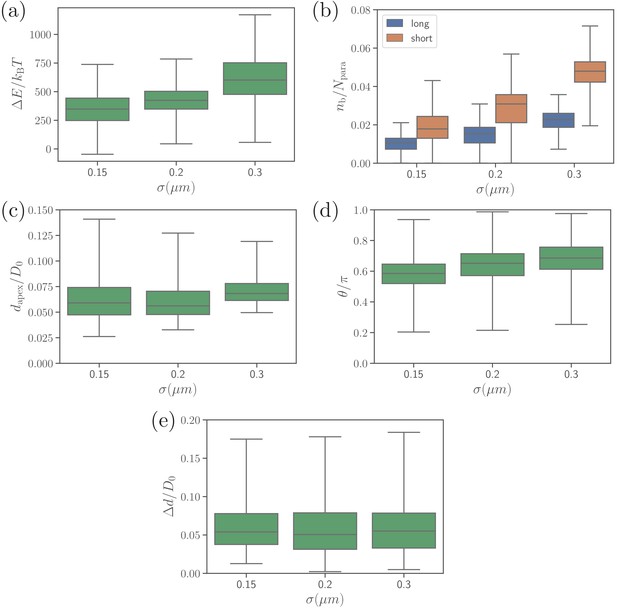
Different alignment characteristics, including (a) deformation energy, (b) number of bonds, (c) apex distance, (d) alignment angle, and (e) fixed-time displacement, for several values of parameter $σ$ which determines the effective membrane thickness.

Figure 6 with 1 supplement

Download asset Open asset

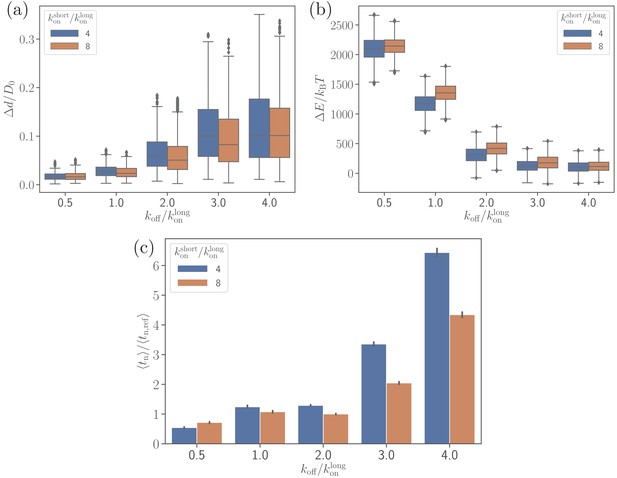
Effect of the off-rate $k_{off}$ on (a) the parasite’s fixed-time displacement, (b) RBC deformation energy, and (c) alignment time.

Since the off-rate controls the lifetime of bonds, a smaller off-rate results in a stronger adhesion, a lower parasite displacement, and a faster alignment time.

Figure 6—source data 1 Source data for graphs shown in Figure 6a–c and Figure 6—figure supplement 1.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig6-data1-v2.zip
Download elife-56500-fig6-data1-v2.zip

Figure 6—figure supplement 1

Download asset Open asset

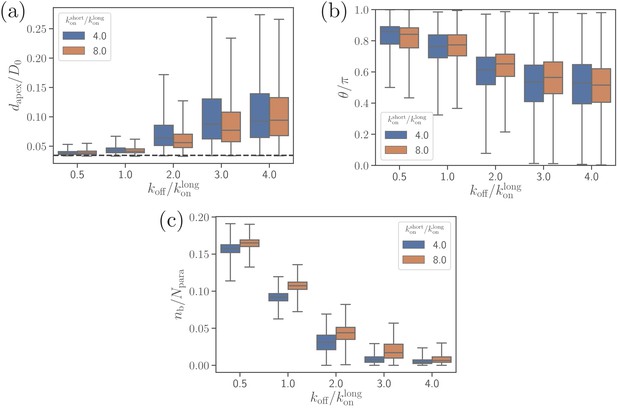
Effect of the off-rate $k_{off}$ on (a) the apex distance, (b) alignment angle, and (c) the number of bonds.

Figure 7 with 1 supplement

Download asset Open asset

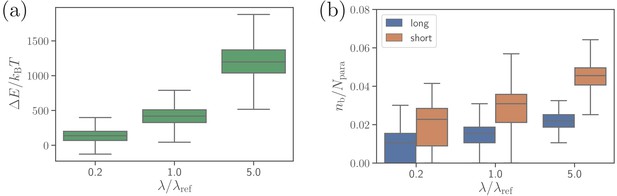
Effect of the extensional bond rigidities on parasite alignment.

(a) RBC deformation energy and (b) the number of short and long bonds as a function of $λ / λ_{r e f}$ . $λ_{r e f}$ corresponds to the reference case with parameters given in Table 2. Note that both $λ_{long}$ and $λ_{short}$ are changed by the same factor with respect to their $λ_{r e f}$ values. Here, the bond kinetic rates are $k_{on}^{short} = 290.3 τ^{- 1}$ , $k_{on}^{long} = 36.3 τ^{- 1}$ , and $k_{off} = 72.6 τ^{- 1}$ .

Figure 7—source data 1 Source data for graphs shown in Figure 7a,b and Figure 7—figure supplement 1.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig7-data1-v2.zip
Download elife-56500-fig7-data1-v2.zip

Figure 7—figure supplement 1

Download asset Open asset

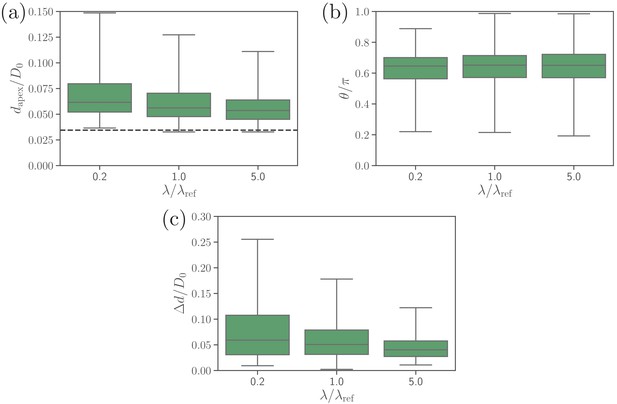
Effect of the extensional bond rigidities on (a) the apex distance, (b) alignment angle, and (c) fixed-time displacement of the parasite.

Figure 8 with 2 supplements

Download asset Open asset

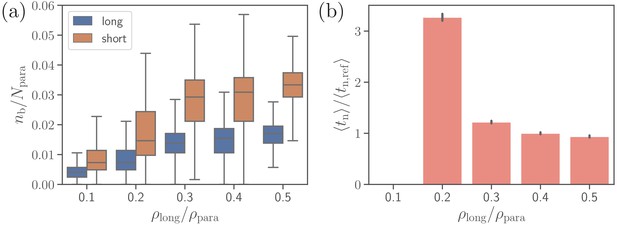
Effect of the density of long ligands $ρ_{long}$ on parasite alignment.

(a) Number of short and long bonds and (b) parasite alignment times as a function of $ρ_{long} / ρ_{para}$ . Note that $ρ_{long} + ρ_{short} = ρ_{para}$ remains constant in all simulations. Here, the bond kinetic rates are $k_{on}^{short} = 290.3 τ^{- 1}$ , $k_{on}^{long} = 36.3 τ^{- 1}$ , and $k_{off} = 72.6 τ^{- 1}$ . In case of $ρ_{long} / ρ_{para} = 0.1$ , parasite alignment time could not be computed through the MC sampling, since merozoite alignment has never occurred in direct simulations.

Figure 8—source data 1 Source data for graphs shown in Figure 8a,b and Figure 8—figure supplements 1 and 2.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig8-data1-v2.zip
Download elife-56500-fig8-data1-v2.zip

Figure 8—figure supplement 1

Download asset Open asset

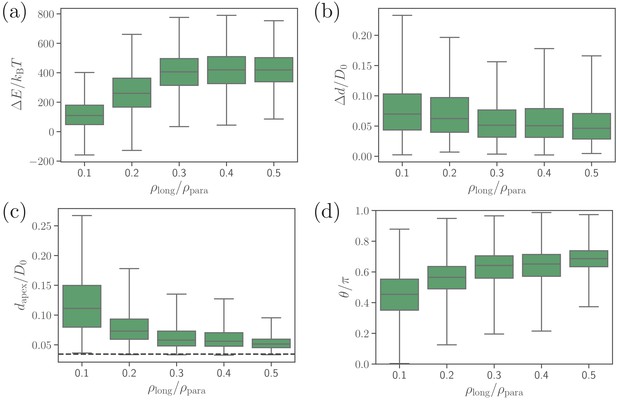
Effect of the density of long ligands $ρ_{long}$ on (a) deformation energy, (b) fixed-time displacement, (c) apex distance, and (d) alignment angle.

Figure 8—figure supplement 2

Download asset Open asset

Alignment results of simulations with only long ligands, i.e. for $ρ_{long} / ρ_{para} = 1$ .

(a) Deformation energy, (b) the number of bonds, (c) apex distance, (d) alignment angle, and (e) fixed-time displacement of the merozoite for the three cases: (1) $ρ_{long} / ρ_{para} = 1$ and $k_{off} / k_{on}^{long} = 2$ , (2) $ρ_{long} / ρ_{para} = 0.4$ and $k_{off} / k_{on}^{long} = 2$ (the reference case), (3) $ρ_{long} / ρ_{para} = 1$ and $k_{off} / k_{on}^{long} = 0.25$ .

Figure 9

Download asset Open asset

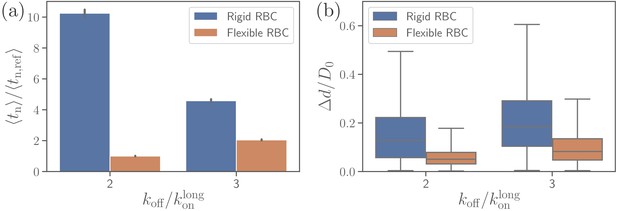
Effect of RBC membrane rigidity on (a) alignment time and (b) parasite fixed-time displacement for different off-rates $k_{off}$ .

Note that for a rigid RBC with $k_{off} / k_{on}^{long} = 1$ , parasite alignment time could not be computed through the MC sampling, as the alignment criteria have never been met in direct simulations.

Figure 9—source data 1 Source data for graphs shown in Figure 9a,b.: https://cdn.elifesciences.org/articles/56500/elife-56500-fig9-data1-v2.zip
Download elife-56500-fig9-data1-v2.zip

Videos

Video 1

Download asset

posterframe for video — Parasite motion at the membrane of a deformable RBC for the reference RBC-parasite interactions from Table 2.

$k_{off} / k_{on}^{long} = 2$ . See Figure 2a.

Video 2

Download asset

Video 3

Download asset

Tables

Table 1

Simulation parameters given in both model and physical units.

The effective RBC diameter $D_{0} = \sqrt{A_{0} / π}$ sets a basic length, the thermal energy $k_{B} T$ defines an energy scale, and RBC relaxation time $τ = η D_{0}^{3} / κ$ sets a time scale in the simulated system, where $A_{0}$ is the RBC surface area, $κ$ is the bending rigidity, and $η$ is the fluid dynamic viscosity. The values of bending rigidity $κ$ , 2D shear µ and Young’s $Y$ moduli are chosen such that they correspond to average properties of a healthy RBC. Parameters $σ$ and $ϵ$ correspond to RBC-parasite excluded-volume interactions represented by the purely repulsive LJ potential in Equation 11.

Parameter	Simulation value	Physical value
$A_{0}$	133.5	$133.5 μ m^{2}$
$D_{0}$	$\sqrt{A_{0} / π} = 6.5$	$6.5 μ m$
$k_{B} T$	0.01	$4.282 \times 10^{- 21} J$
$τ$	$η D_{0}^{3} / κ = 725.8$	0.92 s
$η$	1.85	$1 \times 10^{- 3} P a s$
$κ$	$70 k_{B} T$	$3.0 \times 10^{- 19} J$
µ	$4.6 \times 10^{4} k_{B} T / D_{0}^{2}$	$4.8 μ N / m$
$Y$	$1.82 \times 10^{5} k_{B} T / D_{0}^{2}$	$18.9 μ N / m$
$N_{para}$	1230
$N_{rbc}$	3000
$σ$	$0.031 D_{0}$	$0.2 μ m$
$ϵ$	$1000 k_{B} T$	$4.282 \times 10^{- 18} J$

Table 2

List of bond parameters that are used to calibrate displacement of the parasite at the RBC membrane in simulations (see Video 1) against available experimental data (Weiss et al., 2015), as shown in Figure 2b.

The parameter values in simulations are given in terms of the length scale $D_{0}$ , energy scale $k_{B} T$ , and timescale $τ = η D_{0}^{3} / κ$ . The densities of long and short ligands are given in terms of parasite vertex density $ρ_{p a r a} ≃ 270 μ m^{- 2}$ . Note that $ρ_{long} + ρ_{short} = ρ_{para}$ in all simulations.

Parameter	Simulation value	Physical value
$ℓ_{eff}^{long}$	$0.0154 D_{0}$	$100 nm$
$ℓ_{eff}^{short}$	$0.0031 D_{0}$	$20 nm$
$ρ_{long}$	0.4 $ρ_{para}$	$107 μ m^{- 2}$
$ρ_{short}$	0.6 $ρ_{para}$	$161 μ m^{- 2}$
$k_{on}^{long}$	$36.3 τ^{- 1}$	$39.6 s^{- 1}$
$k_{on}^{short}$	$290.3 τ^{- 1}$	$317.0 s^{- 1}$
$k_{off}$	$72.58 τ^{- 1}$	$79.2 s^{- 1}$
$λ_{long}$	$25.3 \times 10^{5} k_{B} T / D_{0}^{2}$	$0.264 pN / nm$
$λ_{short}$	$8.45 \times 10^{5} k_{B} T / D_{0}^{2}$	$0.0882 pN / nm$

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/56500/elife-56500-transrepform-v2.pdf
Download elife-56500-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Sebastian Hillringhaus
Anil K Dasanna
Gerhard Gompper
Dmitry A Fedosov

(2020)

Stochastic bond dynamics facilitates alignment of malaria parasite at erythrocyte membrane upon invasion

eLife 9:e56500.

https://doi.org/10.7554/eLife.56500

Figures

Sketch of parasite and RBC models.

Calibration of parasite adhesion parameters.

Figure 2—source data 1

Parasite adhesion to a deformable RBC.

Figure 3—source data 1

Parasite adhesion to a rigid RBC (see section ‘Effect of RBC rigidity’).

Comparison of alignment times obtained from direct DPD simulations and MC sampling.

Figure 4—source data 1

Variations in stretching $Δ E_{sp}$ and bending $Δ E_{bend}$ energies, the number of bonds $n_{b}$ , the head distance $d_{apex}$ , and the alignment angle $θ$ as a function of time for the default parameter set given in Table 2.

Figure 5—source data 1

Dependence of parasite wrapping on the position at RBC membrane.

Different alignment characteristics, including (a) deformation energy, (b) number of bonds, (c) apex distance, (d) alignment angle, and (e) fixed-time displacement, for several values of parameter $σ$ which determines the effective membrane thickness.

Effect of the off-rate $k_{off}$ on (a) the parasite’s fixed-time displacement, (b) RBC deformation energy, and (c) alignment time.

Figure 6—source data 1

Effect of the off-rate $k_{off}$ on (a) the apex distance, (b) alignment angle, and (c) the number of bonds.

Effect of the extensional bond rigidities on parasite alignment.

Figure 7—source data 1

Effect of the extensional bond rigidities on (a) the apex distance, (b) alignment angle, and (c) fixed-time displacement of the parasite.

Effect of the density of long ligands $ρ_{long}$ on parasite alignment.

Figure 8—source data 1

Effect of the density of long ligands $ρ_{long}$ on (a) deformation energy, (b) fixed-time displacement, (c) apex distance, and (d) alignment angle.

Alignment results of simulations with only long ligands, i.e. for $ρ_{long} / ρ_{para} = 1$ .

Effect of RBC membrane rigidity on (a) alignment time and (b) parasite fixed-time displacement for different off-rates $k_{off}$ .

Figure 9—source data 1

Videos

Parasite motion at the membrane of a deformable RBC for the reference RBC-parasite interactions from Table 2.

Parasite adhesion and dynamics on a deformable RBC for a reduced off-rate $k_{off}$ .

Parasite dynamics at the surface of a rigid RBC for the reference RBC-parasite interactions from Table 2.

Tables

Simulation parameters given in both model and physical units.

List of bond parameters that are used to calibrate displacement of the parasite at the RBC membrane in simulations (see Video 1) against available experimental data (Weiss et al., 2015), as shown in Figure 2b.

Additional files

Transparent reporting form

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Sketch of parasite and RBC models.

Calibration of parasite adhesion parameters.

Figure 2—source data 1

Parasite adhesion to a deformable RBC.

Figure 3—source data 1

Parasite adhesion to a rigid RBC (see section ‘Effect of RBC rigidity’).

Comparison of alignment times obtained from direct DPD simulations and MC sampling.

Figure 4—source data 1

Variations in stretching Δ⁢Esp and bending Δ⁢Ebend energies, the number of bonds nb, the head distance dapex, and the alignment angle θ as a function of time for the default parameter set given in Table 2.

Figure 5—source data 1

Dependence of parasite wrapping on the position at RBC membrane.

Different alignment characteristics, including (a) deformation energy, (b) number of bonds, (c) apex distance, (d) alignment angle, and (e) fixed-time displacement, for several values of parameter σ which determines the effective membrane thickness.

Effect of the off-rate koff on (a) the parasite’s fixed-time displacement, (b) RBC deformation energy, and (c) alignment time.

Figure 6—source data 1

Effect of the off-rate koff on (a) the apex distance, (b) alignment angle, and (c) the number of bonds.

Effect of the extensional bond rigidities on parasite alignment.

Figure 7—source data 1

Effect of the extensional bond rigidities on (a) the apex distance, (b) alignment angle, and (c) fixed-time displacement of the parasite.

Effect of the density of long ligands ρlong on parasite alignment.

Figure 8—source data 1

Effect of the density of long ligands ρlong on (a) deformation energy, (b) fixed-time displacement, (c) apex distance, and (d) alignment angle.

Alignment results of simulations with only long ligands, i.e. for ρlong/ρpara=1.

Effect of RBC membrane rigidity on (a) alignment time and (b) parasite fixed-time displacement for different off-rates koff.

Figure 9—source data 1

Parasite motion at the membrane of a deformable RBC for the reference RBC-parasite interactions from Table 2.

Parasite adhesion and dynamics on a deformable RBC for a reduced off-rate koff.

Parasite dynamics at the surface of a rigid RBC for the reference RBC-parasite interactions from Table 2.

Simulation parameters given in both model and physical units.

List of bond parameters that are used to calibrate displacement of the parasite at the RBC membrane in simulations (see Video 1) against available experimental data (Weiss et al., 2015), as shown in Figure 2b.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Variations in stretching $Δ E_{sp}$ and bending $Δ E_{bend}$ energies, the number of bonds $n_{b}$ , the head distance $d_{apex}$ , and the alignment angle $θ$ as a function of time for the default parameter set given in Table 2.

Different alignment characteristics, including (a) deformation energy, (b) number of bonds, (c) apex distance, (d) alignment angle, and (e) fixed-time displacement, for several values of parameter $σ$ which determines the effective membrane thickness.

Effect of the off-rate $k_{off}$ on (a) the parasite’s fixed-time displacement, (b) RBC deformation energy, and (c) alignment time.

Effect of the off-rate $k_{off}$ on (a) the apex distance, (b) alignment angle, and (c) the number of bonds.

Effect of the density of long ligands $ρ_{long}$ on parasite alignment.

Effect of the density of long ligands $ρ_{long}$ on (a) deformation energy, (b) fixed-time displacement, (c) apex distance, and (d) alignment angle.

Alignment results of simulations with only long ligands, i.e. for $ρ_{long} / ρ_{para} = 1$ .

Effect of RBC membrane rigidity on (a) alignment time and (b) parasite fixed-time displacement for different off-rates $k_{off}$ .

Parasite adhesion and dynamics on a deformable RBC for a reduced off-rate $k_{off}$ .