Learning excitatory-inhibitory neuronal assemblies in recurrent networks

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: April 26, 2021 (This version)
Accepted: March 3, 2021
Received: June 5, 2020

1. Of interest
ACC neural ensemble dynamics are structured by strategy prevalence

Mikhail Proskurin, Maxim Manakov, Alla Karpova

Research Article Dec 7, 2023
Further reading

Abstract
Introduction
Results
Discussion
Materials and methods
Appendix 1
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Understanding the connectivity observed in the brain and how it emerges from local plasticity rules is a grand challenge in modern neuroscience. In the primary visual cortex (V1) of mice, synapses between excitatory pyramidal neurons and inhibitory parvalbumin-expressing (PV) interneurons tend to be stronger for neurons that respond to similar stimulus features, although these neurons are not topographically arranged according to their stimulus preference. The presence of such excitatory-inhibitory (E/I) neuronal assemblies indicates a stimulus-specific form of feedback inhibition. Here, we show that activity-dependent synaptic plasticity on input and output synapses of PV interneurons generates a circuit structure that is consistent with mouse V1. Computational modeling reveals that both forms of plasticity must act in synergy to form the observed E/I assemblies. Once established, these assemblies produce a stimulus-specific competition between pyramidal neurons. Our model suggests that activity-dependent plasticity can refine inhibitory circuits to actively shape cortical computations.

Introduction

With the advent of modern optogenetics, the functional role of inhibitory interneurons has developed into one of the central topics of systems neuroscience (Fishell and Kepecs, 2020). Aside from the classical perspective that inhibition serves to stabilize recurrent excitatory feedback loops in neuronal circuits (van Vreeswijk and Sompolinsky, 1996; Brunel, 2000; Murphy and Miller, 2009; Sprekeler, 2017), it is increasingly recognised as an active player in cortical computation (Isaacson and Scanziani, 2011; Priebe and Ferster, 2008; Rubin et al., 2015; Pouille and Scanziani, 2001; Letzkus et al., 2011; Adesnik et al., 2012; Hennequin et al., 2014; Phillips et al., 2017; Barron et al., 2016; Barron et al., 2017; Tovote et al., 2015).

Within cortical neurons, excitatory and inhibitory currents are often highly correlated in their response to stimuli (Wehr and Zador, 2003; Froemke et al., 2007; Tan et al., 2011; Bhatia et al., 2019), in time (Okun and Lampl, 2008; Dipoppa et al., 2018) and across neurons (Xue et al., 2014). This co-tuning of excitatory and inhibitory currents has been attributed to different origins. In topographically organised sensory areas such as cat primary visual cortex (V1), the co-tuning with respect to sensory stimuli could be a natural consequence of local feedback inhibition and does not impose strong constraints on inhibitory circuitry (Harris and Mrsic-Flogel, 2013). In the case of feedforward inhibition, co-tuning of excitatory and inhibitory currents was suggested to arise from homeostatic synaptic plasticity in GABAergic synapses (Vogels et al., 2011; Clopath et al., 2016; Weber and Sprekeler, 2018; Hennequin et al., 2017).

In sensory areas with poor feature topography, such as V1 of rodents (Ohki et al., 2005), feedback inhibition has been hypothesised to be largely unspecific for stimulus features, a property inferred from the dense connectivity (Fino and Yuste, 2011; Packer and Yuste, 2011) and reliable presence of synapses connecting pyramidal (Pyr) neurons to inhibitory interneurons with dissimilar stimulus tuning (Harris and Mrsic-Flogel, 2013; Bock et al., 2011; Hofer et al., 2011). However, recent results cast doubt on this idea of a ‘blanket of inhibition’ (Fino and Yuste, 2011; Packer and Yuste, 2011).

In mouse V1, Znamenskiy et al., 2018 report that although the presence of synaptic connections between Pyr cells and parvalbumin-expressing (PV) interneurons is independent of their respective stimulus responses, the efficacy of those synapses is correlated with their response similarity, both in PV → Pyr and in Pyr → PV connections. These mutual preferences in synaptic organisation suggest that feedback inhibition may be more stimulus-specific than previously thought and that Pyr and PV neurons form specialised—albeit potentially overlapping—excitatory-inhibitory (E/I) assemblies (Chenkov et al., 2017; Yoshimura et al., 2005; Litwin-Kumar and Doiron, 2012; Litwin-Kumar and Doiron, 2014). While the presence of such E/I assemblies (Znamenskiy et al., 2018; Rupprecht and Friedrich, 2018) suggests the need for an activity-dependent mechanism for their formation and/or refinement (Khan et al., 2018; Najafi et al., 2020), the requirements such a mechanism must fulfil remain unresolved.

Here, we use a computational model to identify requirements for the development of stimulus-specific feedback inhibition. We find that the formation of E/I assemblies requires a synergistic action of plasticity on two synapse types: the excitatory synapses from Pyr neurons onto PV interneurons and the inhibitory synapses from those interneurons onto the Pyr cells. Using ‘knock-out experiments’, in which we block plasticity in either synapse type, we show that both must be plastic to account for the observed functional microcircuits in mouse V1. In addition, after the formation of E/I assemblies, perturbations of individual Pyr neurons lead to a feature-specific suppression of other Pyr neurons as recently found in mouse V1 (Chettih and Harvey, 2019). Thus, synergistic plasticity of the incoming and outgoing synapses of PV interneurons can drive the development of stimulus-specific feedback inhibition, resulting in a competition between Pyr neurons with similar stimulus preference.

Results

To understand which activity-dependent mechanisms can generate specific feedback inhibition in circuits without feature topography—such as mouse V1 (Figure 1a), we studied a rate-based network model consisting of $N^{E} = 512$ excitatory Pyr neurons and $N^{I} = 64$ inhibitory PV neurons. To endow the excitatory neurons with a stimulus tuning similar to Pyr cells in layer 2/3 of mouse V1 (Znamenskiy et al., 2018), each excitatory neuron receives external excitatory input that is tuned to orientation, temporal frequency and spatial frequency (Figure 1b). The preferred stimuli of the Pyr neurons cover the stimulus space evenly. Because we are interested under which conditions feedback inhibition can acquire a stimulus selectivity, inhibitory neurons receive external inputs without stimulus tuning, but are recurrently connected to Pyr neurons. While the network has no stimulus topography, Pyr neurons are preferentially connected to other Pyr neurons with similar stimulus tuning (Hofer et al., 2011; Cossell et al., 2015), and connection strength is proportional to the signal correlation of their external inputs. Note that the Pyr → Pyr connections only play a decisive role for the results in Figure 4 but are present in all simulations for consistency. Connection probability across the network is $p = 0.6$ , with the remaining network connectivity (Pyr → PV, PV → PV, PV → Pyr) initialised randomly according to a log-normal distribution (Song et al., 2005; Loewenstein et al., 2011), with a variability that is similar to that measured in the respective synapses (Znamenskiy et al., 2018).

Figure 1 with 5 supplements see all

Download asset Open asset

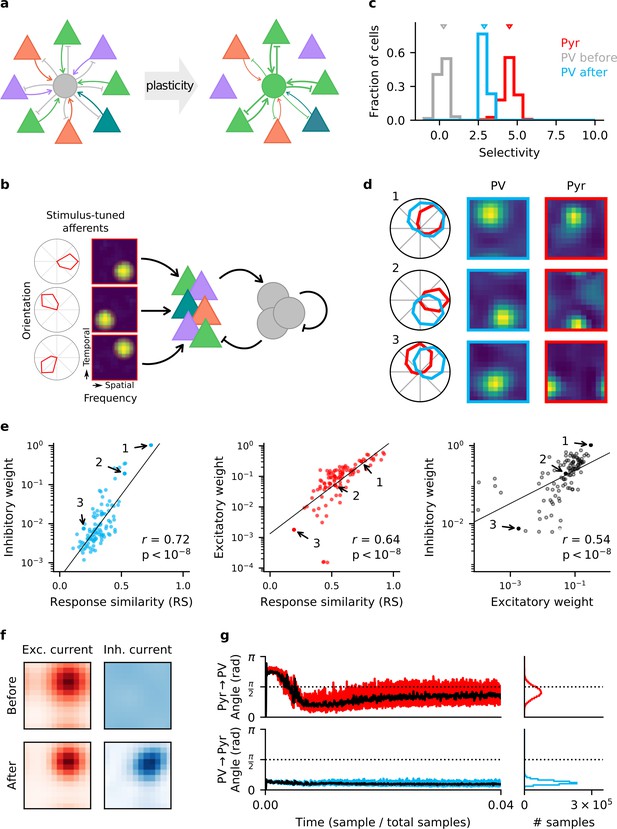
Homeostatic plasticity in input and output synapses of interneurons drives the formation of excitatory-inhibitory (E/I) assemblies.

(a) Emergence of E/I assemblies comprised of pyramidal (Pyr) neurons (triangles) and parvalbumin-expressing (PV) interneurons (circles) in circuits without feature topography. (b) Network architecture and stimulus tuning of external inputs to Pyr cells. (c) Stimulus selectivity of Pyr neurons and PV interneurons (before and after learning). Arrows indicate the median. (d) Example responses of reciprocally connected Pyr cells and PV interneurons. Examples chosen for large, intermediate, and low response similarity (RS). Numbers correspond to points marked in (e). (e) Relationship of synaptic efficacies of output (left) and input connections (centre) of PV interneurons with RS. Relationship of input and output efficacies (right). Black lines are obtained via linear regression. Reported r and associated p-value are Pearson’s correlation. (f) Stimulus tuning of excitatory and inhibitory currents onto an example Pyr cell, before and after learning. For simplicity, currents are shown for spatial and temporal frequency only, averaged across all orientations. (g) Angle between the weight update and the gradient rule while following the local approximation for input (top) and output (bottom) connections of PV interneurons. Time course for first 4% of simulation (left) and final distribution (right) shown. Black lines are low-pass filtered time courses.

E/I assemblies are formed by homeostatic plasticity rules in input and output connections of PV interneurons

In feedforward networks, a stimulus-specific balance of excitation and inhibition can arise from homeostatic inhibitory synaptic plasticity that aims to minimise the deviation of a neuron’s firing rate from a target for all stimuli of a given set (Vogels et al., 2011; Clopath et al., 2016; Weber and Sprekeler, 2018). We wondered whether a stimulus-specific form of homeostasis can also generate stimulus-specific feedback inhibition by forming E/I assemblies. To that end, we derive synaptic plasticity rules for excitatory input and inhibitory output connections of PV interneurons that are homeostatic for the excitatory population (see 'Materials and methods'). A stimulus-specific homeostatic control can be seen as a ‘trivial’ supervised learning task, in which the objective is that all Pyr neurons should learn to fire at a given target rate $ρ_{0}$ for all stimuli. Hence, a gradient-based optimisation would effectively require a backpropagation of error (Rumelhart et al., 1985) through time (BPTT; Werbos, 1990).

Because backpropagation rules rely on non-local information that might not be available to the respective synapses, their biological plausibility is currently debated (Lillicrap et al., 2020; Sacramento et al., 2018; Guerguiev et al., 2017; Whittington and Bogacz, 2019; Bellec et al., 2020). However, a local approximation of the full BPTT update can be obtained under the following assumptions: First, we assume that the sensory input to the network changes on a time scale that is slower than the intrinsic time scales in the network. This eliminates the necessity of backpropagating information through time, albeit still through the synapses in the network. This assumption results in what we call the ‘gradient-based’ rules (Equation 15 in Appendix 1), which are spatially non-local. Second, we assume that synaptic interactions in the network are sufficiently weak that higher-order synaptic interactions can be neglected. Third and finally, we assume that over the course of learning, the Pyr → PV connections and the PV → Pyr connections become positively correlated (Znamenskiy et al., 2018), such that we can replace PV → Pyr synapses by the reciprocal Pyr → PV synapse in the Pyr → PV learning rule, without rotating the update too far from the true gradient (see Appendix 1).

The resulting learning rule for the output connections of the interneurons is similar to a previously suggested form of homeostatic inhibitory plasticity (Figure 1—figure supplement 1a, left) (Vogels et al., 2011). Specifically, PV output synapses $W^{E \leftarrow I}$ undergo Hebbian changes in proportion to presynaptic interneuron activity $r_{j}^{I}$ and the signed deviation of total postsynaptic Pyr cell input $h_{i}^{E}$ from the homeostatic target:

Δ W_{i j}^{E \leftarrow I} \propto r_{j}^{I} (h_{i}^{E} - ρ_{0}) + w e i g h t d e c a y .

In contrast, the PV input synapses $W^{I \leftarrow E}$ are changed such that the total excitatory drive $I_{i}^{E,rec}$ from the Pyr population to each interneuron is close to some target value I₀ (Figure 1—figure supplement 1a, right):

Δ W_{i j}^{I \leftarrow E} \propto r_{j}^{E} (I_{i}^{E,rec} - I_{0}) + w e i g h t d e c a y .

Both synapse types are subject to a weak weight decay, to avoid the redundancy that a multiplicative rescaling of input synapses can be compensated by a rescaling of the output synapses.

While our main results are obtained using the local approximations, we also simulated the gradient-based rules to verify that the approximation does not qualitatively change the results (Figure 1—figure supplement 2).

When we endow the synapses of an initially randomly connected network of Pyr neurons and PV interneurons with plasticity in both the input and the output synapses of the interneurons, the network develops a synaptic weight structure and stimulus response that closely resemble that of mouse V1 (Znamenskiy et al., 2018). Before learning, interneurons show poor stimulus selectivity (Figure 1c), in line with the notion that in a random network, interneurons pool over many Pyr neurons with different stimulus tuning (Harris and Mrsic-Flogel, 2013). The network is then exposed to randomly interleaved stimuli. By the end of learning, interneurons have developed a pronounced stimulus tuning, albeit weaker than that of Pyr neurons (Figure 1c,d). Interneurons form strong bidirectional connections preferentially with Pyr neurons with a similar stimulus tuning, whereas connections between Pyr-PV pairs with dissimilar stimulus tuning are weaker (Figure 1d,e). To make our results comparable to Znamenskiy et al., 2018, we randomly sample an experimentally feasible number of synaptic connections from the network ( $n = 100$ ). Both the efficacy of PV input and output connections are highly correlated with the response similarity (RS) (see 'Materials and methods') of the associated Pyr neurons and interneurons (Figure 1e, left and centre). For bidirectionally connected cell pairs, the efficacies of the respective input and output connections are highly correlated (Figure 1e, right). The stimulus tuning of the inhibitory inputs onto the Pyr cells—initially flat—closely resembles that of the excitatory inputs after learning (Figure 1f, Figure 1—figure supplement 3; Tan et al., 2011), that is, the network develops a precise E/I balance (Hennequin et al., 2017).

Finally, the optimal gradient rules produce very similar results to the local approximations (Figure 1—figure supplement 2). Over the course of learning, the weight updates by the approximate rules align to the updates that would result from the gradient rules (Figure 1g, Figure 1—figure supplement 4), presumably by a mechanism akin to feedback alignment (Lillicrap et al., 2016; Akrout et al., 2019).

In summary, these results show that combined homeostatic plasticity in input and output synapses of interneurons can generate a similar synaptic structure as observed in mouse V1, including the formation of E/I assemblies.

PV → Pyr plasticity is required for the formation of E/I assemblies

Having shown that homeostatic plasticity acting on both input and output synapses of interneurons are sufficient to learn E/I assemblies, we now turn to the question of whether both are necessary. To this end, we perform ‘knock-out’ experiments, in which we selectively block synaptic plasticity in either of the synapses. The motivation for these experiments is the observation that the incoming PV synapses follow a long-tailed distribution (Znamenskiy et al., 2018). This could provide a sufficient stimulus selectivity in the PV population for PV → Pyr plasticity alone to achieve a satisfactory E/I balance. A similar reasoning holds for static, but long-tailed outgoing PV synapses. This intuition is supported by results from Litwin-Kumar et al., 2017, where for a population of neurons analogous to our interneurons, the dimensionality of responses in that population can be high for static input synapses, when those are log-normally distributed.

When we knock out output plasticity but keep input plasticity intact, the network fails to develop E/I assemblies and a stimulus-specific E/I balance. While there is highly significant change in the distribution of PV interneuron stimulus selectivity (Mann-Whitney U test, $U = 1207$ , $p < 10^{- 4}$ ), the effect is much stronger when output plasticity is also present (Figure 2a,b). Importantly, excitatory and inhibitory currents in Pyr neurons are poorly co-tuned (Figure 2c, Figure 1—figure supplement 3b). In particular, feedback inhibition remains largely untuned because output connections are still random, so that Pyr neurons pool inhibition from many interneurons with different stimulus tuning.

Figure 2

Download asset Open asset

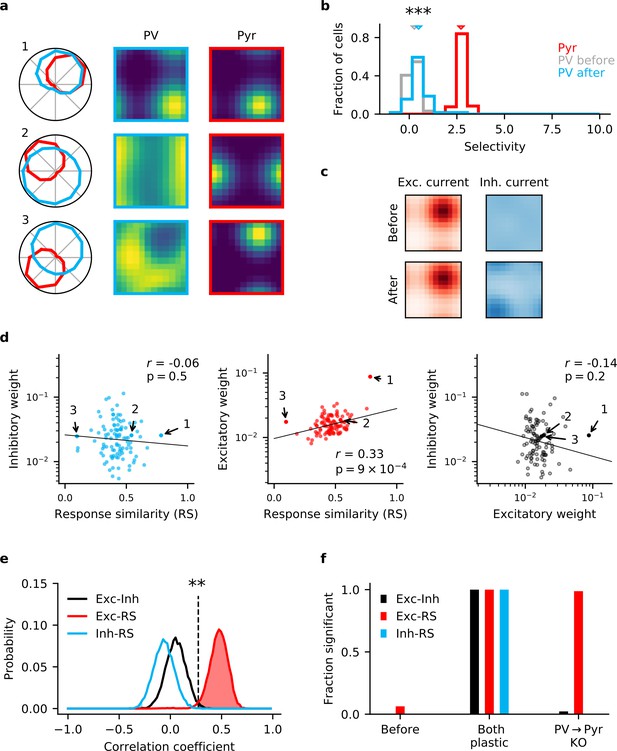
Knock-out (KO) of plasticity in parvalbumin-expressing (PV) interneuron output connections prevents inhibitory co-tuning.

(a) Example responses of reciprocally connected pyramidal (Pyr) cells and PV interneurons. Numbers correspond to points marked in (d). (b) Stimulus selectivity of Pyr cells and PV interneurons (before and after learning; Mann-Whitney U test, $p < 10^{- 4}$ ). Arrows indicate median. (c) Stimulus tuning of excitatory and inhibitory input currents in a Pyr cell before and after learning. For simplicity, currents are shown for spatial and temporal frequency only, averaged across all orientations. (d) Relationship of output (left) and input (centre) synaptic efficacies of PV interneurons with response similarity. Relationship of input and output efficacies (right). Plotted lines are obtained via linear regression. Reported r and associated p-value are the Pearson’s correlation. (e) Distribution of Pearson’s correlation coefficients for multiple samples as shown in (d). Dashed line marks threshold of high significance ( $p < 0.01$ ). (f) Fraction of samples with highly significant positive correlation before plasticity, after plasticity in both input and output connections, and for KO of plasticity in PV output connections (based on 10,000 random samples of 100 synaptic connections).

To investigate whether the model without output plasticity is consistent with the synaptic structure of mouse V1, we repeatedly sample an experimentally feasible number of synapses ( $n = 100$ , Figure 2d) and plot the distribution of the three pairwise Pearson’s correlation coefficients between the two classes of synaptic weights and RS (Figure 2e). When both forms of plasticity are present in the network, a highly significant positive correlation ( $p < 0.01$ ) is detected in all samples for all three correlation types (Figure 2f). When output plasticity is knocked out, we still find a highly significant positive correlation between input weights and RS in 99% of the samples (Figure 2d–f). In contrast, correlations between input and output synapses are weaker and cannot reliably be detected (2% of samples). Notably, we find a correlation between output weights and RS in <0.01% of samples (Figure 2f). Finally, for an experimentally realistic sample size of $n = 100$ , the probability of a correlation coefficient equal or higher than that observed by Znamenskiy et al., 2018 is <0.01% for the correlation between output weights and RS ( $r = 0.55$ ), and <0.01% for the correlation between input and output synapses ( $r = 0.52$ ).

The non-local gradient rule for the PV input synapses alone also does not permit the formation of E/I assemblies (Figure 1—figure supplement 2). While the selectivity of interneurons increases more than for the local approximation (Figure 1—figure supplement 2b), feedback inhibition still remains untuned in the absence of output plasticity (Figure 1—figure supplement 2c,d).

We therefore conclude that input plasticity alone is insufficient to generate the synaptic microstructure observed in mouse V1.

Pyr → PV plasticity is required for assembly formation

When we knock out input plasticity but keep output plasticity intact, we again observe no formation of E/I assemblies. This remains true even when using the gradient-based rule (Figure 1—figure supplement 2). The underlying reason is that input weights remain random. Interneurons collect excitation from many Pyr neurons with different preferences, and absent plasticity on their input synapses, they maintain their initial poor stimulus selectivity (Figure 3a–c). Because of the poor stimulus tuning of the interneurons, output plasticity cannot generate stimulus-specific inhibitory inputs to the Pyr neurons (Figure 3d). Instead, they essentially receive a tonic, unspecific background inhibition that is weakly modulated by the stimulus (Figure 1—figure supplement 3b). While this weak modulation is correlated with the excitatory inputs, the overall similarity between excitatory and inhibitory input remains low (Figure 1—figure supplement 3c).

Figure 3 with 2 supplements see all

Download asset Open asset

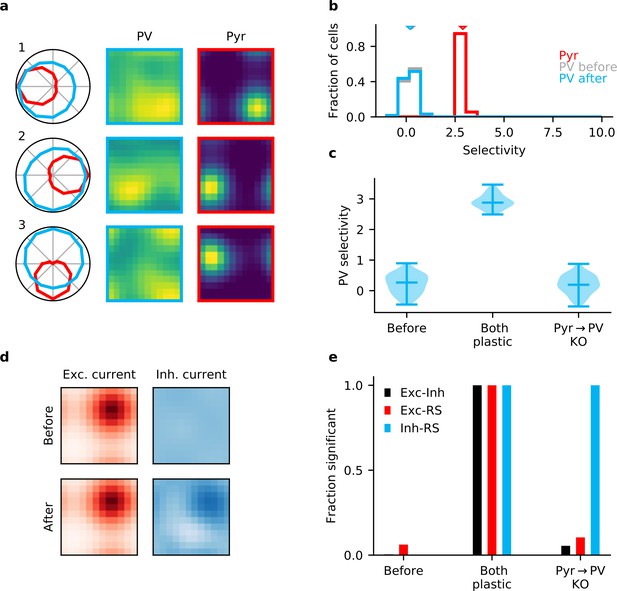
Plasticity of parvalbumin-expressing (PV) interneuron input connections is required for inhibitory stimulus selectivity and current co-tuning.

(a) Example responses of reciprocally connected pyramidal (Pyr) cells and PV interneurons. (b) Stimulus selectivity of Pyr cells and PV interneurons (before and after learning). Arrows indicate median. (c) Violin plots of inhibitory stimulus selectivity before plasticity, after learning with plasticity in both input and output connections of PV interneurons and for knock-out (KO) of plasticity in PV input connections. (d) Stimulus tuning of excitatory and inhibitory currents in a Pyr cell before and after learning. Dimensions correspond to spatial and temporal frequency of the stimuli averaged across all orientations. (e) Fraction of samples with highly significant ( $p < 0.01$ ) positive correlation before plasticity, after plasticity in both input and output connections, and for KO of plasticity in PV input connections (based on 10,000 random samples of 100 synaptic connections).

This modulation is made possible by the fact that interneurons still possess a weak, but consistent stimulus tuning arising from random variations in their input weights. A particularly strong input connection will cause the postsynaptic interneuron to prefer similar stimuli to the presynaptic Pyr. Because of the resulting correlated activity, the Hebbian nature of the output plasticity potentiates inhibitory weights for such cell pairs that are reciprocally connected. The tendency of strong input synapses to generate a strong corresponding output synapse is reflected in a positive correlation between output synapses and RS (Figure 3e, Figure 3—figure supplement 1), despite the fact that input synapses remain random.

This effect further increases when input synapses are drawn from a distribution with an even heavier tail, beyond what is observed in mouse V1 (Znamenskiy et al., 2018; Figure 3—figure supplement 2a). In this case, the stimulus tuning of the interneurons is dominated by a small number of very large synapses. The resulting higher selectivity of the interneurons (Figure 3—figure supplement 2b) allows a better co-tuning of excitation and inhibition in Pyr neurons (Figure 3—figure supplement 2c), in line with theoretical arguments for sparse connectivity (Litwin-Kumar et al., 2017). However, the dominance of a small number of large synapses also makes it unlikely that those synapses are observed in an experiment in which a finite number of synapses are sampled. As a result, a heavier tail does not yield the correlation of reciprocal input and output synapses observed by Znamenskiy et al., 2018 (Figure 3—figure supplement 2d,e), although it increases the probability of observing correlations between input synapses and RS when weak synapses are discarded. See Appendix 1 for a more extensive discussion.

Collectively, these results indicate that plasticity of both the inhibitory output and the excitatory input synapses of PV interneurons is required for the formation of E/I assemblies in cortical areas without feature topography, such as mouse V1.

Single-neuron perturbations

Our findings demonstrate that in networks without feature topography, only a synergy of excitatory and inhibitory plasticity can account for the emergence of E/I assemblies. But how does stimulus-specific feedback inhibition affect interactions between excitatory neurons? In layer 2/3 of V1, similarly tuned excitatory neurons tend to have stronger and more frequent excitatory connections (Ko et al., 2011). It has been hypothesised that this tuned excitatory connectivity supports reliable stimulus responses by amplifying the activity of similarly tuned neurons (Cossell et al., 2015). However, the presence of co-tuned feedback inhibition could also induce the opposite effect, such that similarly tuned excitatory neurons are in competition with each other (Chettih and Harvey, 2019; Moreno-Bote and Drugowitsch, 2015).

To investigate the effect of stimulus-specific inhibition in our network, we simulate the perturbation experiment of Chettih and Harvey, 2019: First, we again expose the network to the stimulus set, with PV input and output plasticity in place to learn E/I assemblies. Second, both before and after learning, we probe the network with randomly selected stimuli from the same stimulus set, while perturbing a single Pyr cell with additional excitatory input, and measure the resulting change in activity of other Pyr neurons in the network (Figure 4a).

Figure 4 with 1 supplement see all

Download asset Open asset

Single-neuron perturbations suppress responses of similarly tuned neurons.

(a) Perturbation of a single pyramidal (Pyr) neuron. Responses of other Pyr neurons are recorded for different stimuli, both with and without perturbation. (b) Perturbation-induced change in activity ( $Δ$ Act.) of a subset of Pyr cells, for a random subset of stimuli (with neuron 1 being perturbed). (c) Influence of perturbing a Pyr neuron on the other Pyr neurons, averaged across all stimuli, for a subset of Pyr neurons. (d) Dependence of influence among Pyr neurons on their receptive field correlation (Pearson’s r), across all neurons in the network (see 'Materials and methods'). Dotted lines indicate plasticity knock-out (KO) experiments; see Figure 4—figure supplement 1b for details. Error bars correspond to the standard error of the sample mean, but are not visible due to their small values. (e) Total strength of output synapses from a Pyr neuron predicts the average effect perturbing it has on other neurons. Dashed line is the result of a linear regression, while r and its associated p-value correspond to the Pearson’s correlation.

While the activity of the perturbed neuron increases, many of the other Pyr neurons are inhibited in response to the perturbation (Figure 4b). Although comparing the pairwise influence of Pyr neurons on each other does not reveal any apparent trend (Figure 4c), recent experiments report that the influence a single-cell perturbation has on other neurons depends on the similarity of their stimulus feature tuning (Chettih and Harvey, 2019). To test whether we observe the same feature-specific suppression, we compute the influence of perturbing a Pyr on the rest of the network as a function of the receptive field correlation of the perturbed cell and each measured cell. In line with recent perturbation studies (Chettih and Harvey, 2019; Sadeh and Clopath, 2020), we observe that—on average—neurons are more strongly inhibited if they have a similar tuning to the perturbed neuron (Figure 4d). The opposite holds before learning: the effect of single-neuron perturbations on the network is increasingly excitatory as receptive field correlation increases. Notably, the networks in which input or output plasticity was knocked out during learning (and therefore did not develop E/I assemblies) show the same excitatory effect (Figure 4d, Figure 4—figure supplement 1b). This confirms that a ‘blanket of inhibition’ does not account for feature-specific suppression between excitatory neurons (Sadeh and Clopath, 2020).

To better understand this behaviour, we use the Pyr-Pyr receptive field correlations to compute the coefficient of determination for all pairs ( $R^{2}$ , which quantifies how well the receptive field of one Pyr neuron predicts that of another). Learning changes the correlative structure in the network (Figure 4—figure supplement 1a) and thereby decreases the coefficient of determination on average, indicating a reduction in Pyr-Pyr correlations within the network ( $E [R^{2}] = 0.06$ before learning, 0.02 after). Thus, plasticity suppresses some of the strongest correlations, resulting in ‘feature competition’ which is believed to aid sensory processing (Lochmann et al., 2012; Moreno-Bote and Drugowitsch, 2015).

While on average the network exhibits feature competition, the influence of individual Pyr neurons on the rest of the network is highly variable. According to recent modelling work (Sadeh and Clopath, 2020), the strength of Pyr → PV synapses strongly influences whether a network will exhibit feature competition. In our network, the total outgoing weight of a Pyr cell onto the PV neurons indeed predicts the average influence that neuron will have on the rest of the network when perturbed (Figure 4e; $r = - 0.6$ ).

In summary, the stimulus-specific feedback inhibition that emerges in the model also captures the paradoxical suppression of similarly tuned excitatory neurons observed in single-cell perturbation experiments.

Discussion

The idea that feedback inhibition serves as a ‘blanket of inhibition’ (Packer and Yuste, 2011; Fino and Yuste, 2011) that can be selectively broken (Karnani et al., 2016) has been gradually relaxed over recent years and replaced by the notion that feedback inhibition can be rather selective (Rupprecht and Friedrich, 2018) and could thereby support specific neuronal computations (Vogels and Abbott, 2009; Hennequin et al., 2014; Denève and Machens, 2016; Najafi et al., 2020), even in networks without topographic organisation (Znamenskiy et al., 2018; Rupprecht and Friedrich, 2018). Here, we used a computational model to show that the development of E/I assemblies similar to those observed in mouse V1 (Znamenskiy et al., 2018) or zebrafish olfactory areas (Rupprecht and Friedrich, 2018) can be driven by a homeostatic form of plasticity of the incoming and outgoing synapses of inhibitory interneurons. Based on the results of virtual knock-out experiments, we suggest that, on their own, input or output plasticity of interneurons are insufficient to explain the Pyr-PV microcircuitry in mouse V1 and that input and output plasticity in interneurons must act in synergy for stimulus-specific feedback inhibition to develop. To investigate how the presence of E/I assemblies affects interactions between excitatory neurons, we mimicked a perturbation experiment and found that—as in mouse visual cortex—stimulating single excitatory cells paradoxically suppresses similarly tuned neurons (Chettih and Harvey, 2019). Our findings suggest that, by driving the development of tuned feedback inhibition, plasticity of interneurons can fundamentally shape cortical processing.

The learning rules for the input and output synapses of PV interneurons are based on a single homeostatic objective that aims to keep the net synaptic current onto Pyr neurons close to a given target for all stimuli. The two forms of plasticity fulfil different purposes, however. Plasticity of input synapses is required for interneurons to acquire a stimulus selectivity, whereas plasticity of output synapses can exploit interneuron selectivity to shape inhibitory currents onto excitatory cells. The output plasticity we derived for our recurrent network is very similar to a previously suggested form of inhibitory plasticity (Vogels et al., 2011; Sprekeler, 2017). Homeostatic plasticity rules for inhibitory synapses are now used regularly in computational studies to stabilise model circuits (Vogels et al., 2011; Hennequin et al., 2017; Landau et al., 2016). In contrast, a theoretically grounded approach for the plasticity of excitatory input synapses onto inhibitory neurons is missing.

Homeostatic changes in excitatory synapses onto interneurons in response to lesions or sensory deprivation have been reported (Keck et al., 2011; Takesian et al., 2013; Kuhlman et al., 2013), but the specific mechanisms and functions of this form of interneuron plasticity are not resolved. The plasticity rule we derived for the input synapses of interneurons effectively changes the selectivity of those neurons according to the demands of the Pyr cells, that is, such that the interneurons can best counteract deviations of Pyr activity from the target. By which mechanisms such a (nearly teleological) form of plasticity can be achieved is at its core a problem of credit assignment, whose biological implementation remains open (Lillicrap et al., 2016; Guerguiev et al., 2017; Sacramento et al., 2018).

Here, we used a local approximation of the gradient, backpropagation rules, which produces qualitatively similar results, and which we interpret as a recurrent variant of feedback alignment, applied to the specific task of a stimulus-specific E/I balance (Lillicrap et al., 2016; Akrout et al., 2019). The excitatory input connections onto the interneurons serve as a proxy for the transpose of the output connections. The intuition why this replacement is reasonable is the following: The task of balancing excitation by feedback inhibition favours symmetric connections, because excitatory cells that strongly drive a particular PV interneuron should receive a strong feedback connection in return. Therefore, E/I balance favours a positive correlation between the incoming and outgoing synapses of PV neurons and thus the two weight matrices will be aligned in a final balanced state (Lillicrap et al., 2016; Akrout et al., 2019). This weight replacement effectively replaces the ‘true’ feedback errors by a deviation of the total excitatory input to the PV neurons from a target (Hertäg and Sprekeler, 2020). The rule therefore has the structure of a homeostatic rule for the recurrent excitatory drive received by PV neurons.

A cellular implementation of such a plasticity rule would require the following ingredients: (i) a signal that reflects the cell-wide excitatory current and (ii) a mechanism that changes Pyr → PV synapses in response to variations in this signal. For the detection of excitatory inputs, postsynaptic sodium or calcium concentrations are natural candidates. Due to the lack of spines in PV dendrites, both are expected to diffuse more broadly in the dendritic arbor than in spiny neurons (Hu et al., 2014; Kullmann and Lamsa, 2007) and may thus provide a signal for overall dendritic excitatory currents. Depending on how excitatory inputs are distributed on PV interneuron dendrites (Larkum and Nevian, 2008; Jia et al., 2010; Grienberger et al., 2015), the integration of the excitatory currents may not need to be cell-wide—which could limit the temporal resolution of the plasticity—but could be local, for example, to a dendrite, if local excitatory input is a sufficient proxy for the global input. Notably, in PV interneurons, NMDA receptors are enriched in excitatory feedback relative to feedforward connections (Le Roux et al., 2013), suggesting those two sources of excitation are differentially treated on the postsynaptic side. As for many other excitatory synapses (Sjöström et al., 2008), postsynaptic calcium is likely a key factor also for the plasticity of excitatory input synapses onto interneurons. Blocking NMDA receptors interferes with Hebbian long-term plasticity in some of these synapses (Lamsa et al., 2007; Kullmann and Lamsa, 2007), as does a block of excitatory input (Le Roux et al., 2013). Furthermore, NMDAR-dependent plasticity in Pyr → PV synapses is expressed postsynaptically and seems to require presynaptic activation (Kullmann and Lamsa, 2007). In summary, we believe that there are no conceptual issues that would rule out an implementation of the suggested plasticity rule for excitatory inputs onto PV interneurons.

We also expect that the rules we suggest here are only one set of many that can establish E/I assemblies. Given that the role of the input plasticity in the interneurons is the formation of a stimulus specificity, it is tempting to assume that this could equally well be achieved by classical forms of plasticity like the Bienenstock-Cooper-Munro (BCM) rule (Bienenstock et al., 1982), which is commonly used in models of receptive field formation. However, in our hands, the combination of BCM plasticity in Pyr → PV synapses with homeostatic inhibitory plasticity in the PV → Pyr synapses showed complex dynamics, an analysis of which is beyond the scope of this article. In particular, this combination of rules often did not converge to a steady state, probably for the following reason. BCM rules tend to make the postsynaptic neuron as stimulus-selective as possible. Given the limited number of interneurons in our circuit, this can lead to a situation in which parts of stimulus space are not represented by any interneurons. As a result, Pyr neurons that respond to those stimuli cannot recruit inhibition and maintain a high firing rate far above the target. Other Pyr cells, which have access to interneurons with a similar stimulus tuning, can recruit inhibition to gradually reduce their firing rates towards the target rate. Because the BCM rule is Hebbian, it tends to strengthen input synapses from Pyr neurons with high activity. This shifts the stimulus tuning of the interneurons to those stimuli that were previously underrepresented. However, this in turn renders a different set of stimuli uncovered by inhibition and withdraws feedback inhibition from the corresponding set of Pyr cells, which can now fire at high rates.

We suspect that this instability can also arise for other Hebbian forms of plasticity in interneuron input synapses when they are combined with homeostatic inhibitory plasticity (Vogels et al., 2011) in their output synapses. The underlying reason is that for convergence, the two forms of plasticity need to work synergistically towards the same goal, that is, the same steady state. For two arbitrary synaptic plasticity rules acting in different sets of synapses, it is likely that they aim for two different overall network configurations. Such competition can easily result in latching dynamics with a continuing turn-over of transiently stable states, in which the form of plasticity that acts more quickly gets to reach its goal transiently, only to be undermined by the other one later.

Both Pyr → PV and PV→ Pyr plasticity have been studied in slice (for reviews, see, e.g., Kullmann and Lamsa, 2007; Vogels et al., 2013), but mostly in isolation. The idea that the two forms of plasticity should act in synergy suggests that it may be interesting to study both forms in the same system, for example, in reciprocally connected Pyr-PV pairs.

Like all computational models, the present one contains simplifying design choices. First, we did not include stimulus-specific feedforward inhibition, because the focus lay on the formation of stimulus-specific feedback inhibition. The model could be enriched by feedforward inhibition in different ways. In particular, we expect that the two forms of plasticity will establish E/I assemblies even in the presence of stimulus-selective external inputs to the interneurons, because stimulus-specific external excitation should always be more supportive of the homeostatic objective than unspecific inputs. It may be worth exploring whether adding feedforward inhibition leaves more room for replacing the PV input plasticity that we used by classical Hebbian rules, because the activity of the external inputs remains unaltered by the plasticity in the network (such that the complex instability described above may be mitigated). Given that the focus of this work was on feedback inhibition, an extensive evaluation of the different variants of feedforward inhibition is beyond the scope of the present article.

Second, we neglected much of the complexity of cortical interneuron circuits by including only one class of interneurons. We interpret these interneurons as PV interneurons, given that PV interneurons provide local feedback inhibition (Hu et al., 2014) and show a stimulus-selective circuitry akin to E/I assemblies (Znamenskiy et al., 2018). With their peri-somatic targets on Pyr cells, PV-expressing (basket) cells are also a prime candidate for the classical feedback model of E/I balance (van Vreeswijk and Sompolinsky, 1996). Note that our results do not hinge on any assumptions that are specific to PV neurons and may thus also hold for other interneuron classes that provide feedback inhibition (Tremblay et al., 2016). Given that the division of labour of the various cortical interneuron classes is far from understood, an extension to complex interneuron circuits (Litwin-Kumar et al., 2016; Hertäg and Sprekeler, 2019) is clearly beyond the present study.

Similarly tuned Pyr cells tend to be recurrently connected (Cossell et al., 2015; Harris and Mrsic-Flogel, 2013), in line with the notion that excitatory cells with similar tuning mutually excite each other. This notion is questioned by a recent perturbation experiment demonstrating feature-specific suppression between Pyr cells with similar tuning (Chettih and Harvey, 2019). It has been suggested that this apparently paradoxical effect requires strong and tuned connections between excitatory and inhibitory neurons (Sadeh and Clopath, 2020). The E/I assemblies that develop in our model provide sufficiently strong and specific inhibitory feedback to cause a suppression between similarly tuned Pyr neurons in response to perturbations. Hence, despite the presence of stimulus-specific excitatory recurrence, Pyr neurons with similar stimulus preference effectively compete. Computational arguments suggest that this feature competition may be beneficial for stimulus processing, for example, by generating a sparser and more efficient representation of the stimuli (Olshausen and Field, 2004; Denève and Machens, 2016).

In addition to predicting that knocking out plasticity of inhibitory input or output synapses should prevent the development of E/I assemblies, our model also predicts different outcomes for single-neuron perturbation experiments in juvenile and adult mice. Given that in rodents, stimulus tuning of inhibitory currents occurs later in development than that of excitation (Dorrn et al., 2010), we expect that in juvenile mice single-cell perturbations would not cause feature-specific suppression but amplification due to excitatory recurrence and unspecific feedback inhibition.

Materials and methods

Network and stimuli

Request a detailed protocol

We use custom software to simulate a rate-based recurrent network model containing $N^{E} = 512$ excitatory and $N^{I} = 64$ inhibitory neurons. The activation of the neurons follows Wilson-Cowan dynamics:

\begin{aligned} (1a) & τ_{E} \frac{d}{d t} h^{E} & = - h^{E} + W^{E \leftarrow E} r^{E} - W^{E \leftarrow I} r^{I} + I^{bg} + I (s) \\ (1b) & τ_{I} \frac{d}{d t} h^{I} & = - h^{I} + W^{I \leftarrow E} r^{E} - W^{I \leftarrow I} r^{I} + I^{bg} . \end{aligned}

Here, $r^{E} = [h^{E}]_{+}$ , $r^{I} = [h^{I}]_{+}$ denote the firing rates of the excitatory and inhibitory neurons, which are given by their rectified activation. $W^{Y \leftarrow X}$ denotes the matrix of synaptic efficacies from population $X$ to population $Y$ ( $X, Y \in {E, I}$ ). The external inputs $𝐈 (𝐬)$ to the excitatory neurons have a bell-shaped tuning in the three-dimensional stimulus space consisting of spatial frequency, temporal frequency, and orientation (Znamenskiy et al., 2018). To avoid edge effects, the stimulus space is periodic in all three dimensions, with stimuli ranging from - $π$ to $π$ . The stimulus tuning of the external inputs is modelled by a von Mises function with a maximum of 50 Hz and a tuning width $κ = 1$ . The preferred stimuli of the $N^{E} = 512$ excitatory cells cover the stimulus space evenly on a $12 \times 12 \times 12$ grid. All neurons receive a constant background input of $I^{bg} = 5$ Hz.

Recurrent connections $W^{E \leftarrow E}$ among excitatory neurons have synaptic weight between neurons i and j that grows linearly with the signal correlation of their external inputs:

W_{i j}^{E \leftarrow E} = {[c o r r (I_{i} (𝐬), I_{j} (𝐬)) - C]}_{+} .

The cropping threshold C is chosen such that the overall connection among the excitatory neurons probability is 0.6. The remaining synaptic connections (E→I, I→E, I→I) are initially random, with a connection probability $p = 0.6$ and log-normal weights. For parameters, please refer to Table 1.

Table 1

Model parameters.

$N^{E}$	512	$N^{I}$	64	Number of exc. and inh. neurons.
$τ_{E}$	50 ms	$τ_{I}$	25 ms	Rate dynamics time constants
$d t$	1 ms			Numerical integration time step
$p^{E \leftarrow X}$	0.6	$p^{I \leftarrow X}$	0.6	Connection probability to exc. and inh. neurons
$J_{i}^{E \leftarrow E}$	2	$J_{i}^{I \leftarrow E}$	5	Total of exc. weights onto neuron i: $\sum_{j} W_{i j}^{X \leftarrow E}$
$J_{i}^{E \leftarrow I}$	1	$J_{i}^{I \leftarrow I}$	1	Total of inh. weights onto neuron i: $\sum_{j} W_{i j}^{X \leftarrow I}$
$σ^{E \leftarrow X}$	0.65	$σ^{I \leftarrow X}$	0.65	Std. deviation of the logarithm of the weights
$θ^{E \leftarrow I}$	$10^{- 4}$	$θ^{I \leftarrow E}$	$10^{- 4}$	Experimental detection threshold for synapses
$I^{bg}$	5 Hz	$\max (𝐈 (𝐬))$	50 Hz	Background and maximum stimulus-specific input
$N^{S}$	$12 \times 12 \times 12$	$N^{trials}$	500	Number of stimuli and trials
$R^{S}$	$2 π \times 2 π \times 2 π$	$κ$	1	Range of stimuli and Pyr RF von Mises width
$Δ I$	10 Hz			Change of input for perturbation experiments
$η^{Approx.}$	$10^{- 5}$	$η^{Grad.}$	$10^{- 3}$	Learning rates (approximate and gradient rules)
$δ^{E \leftarrow I}$	0.1	$δ^{I \leftarrow E}$	0.1	Weight decay rates
$ρ_{0}$	1 Hz			Homeostatic plasticity target
$β_{1}$	0.9	$β_{2}$	0.999	Adam parameters for gradient rules
$ϵ$	$10^{- 9}$

During learning, we repeatedly draw all 12 × 12 × 12 preferred stimuli of the Pyr neurons, in random order. This procedure is repeated 500 times to ensure convergence of synaptic weights. To reduce simulation time, we present each stimulus long enough for all firing rates to reach steady state and only then update the synaptic weights.

Synaptic plasticity

Request a detailed protocol

The PV → Pyr and Pyr → PV synapses follow plasticity rules that aim to minimise the deviation of the excitatory activations from a target rate $ρ_{0}$ ( $ρ_{0} = 1$ Hz):

ℰ (h^{E}) = {⟨ \frac{1}{2} \sum_{j = 1}^{N^{E}} {(h_{j}^{E} - ρ_{0})}^{2} ⟩}_{s},

where ${⟨ \cdot ⟩}_{𝐬}$ denotes the average over all stimuli. When plastic, synaptic weights change according to

\begin{aligned} (4a) & Δ W_{j i}^{E \leftarrow I} & \propto (h_{j}^{E} - ρ_{0}) r_{i}^{I}, \\ (4b) & Δ W_{i j}^{I \leftarrow E} & \propto [\sum_{k = 1}^{N^{E}} W_{i k}^{I \leftarrow E} (h_{k}^{E} - ρ_{0})] r_{j}^{E} \\ \approx [\sum_{k = 1}^{N^{E}} W_{i k}^{I \leftarrow E} (r_{k}^{E} - ρ_{0})] r_{j}^{E} \\ (4c) & = (I_{i}^{E,rec} - I_{0}) r_{j}^{E} . \end{aligned}

After every update of the Pyr → PV matrix, the incoming weights for each PV interneuron are multiplicatively scaled such that their sum is $J^{I \leftarrow E}$ (Akrout et al., 2019). In that case, the rule in Equation 4b is approximately local in that it compares the excitatory input current $I_{i}^{E, rec}$ received by the postsynaptic PV neuron to a target value $I_{0} = J^{I \leftarrow E} ρ_{0}$ , and adjusts the incoming synapses in proportion to this error and to presynaptic activity (see Equation 4c).

Both plasticity rules are approximations of the gradient of the objective function Equation 3. Interested readers are referred to Appendix 1 for their mathematical derivation. For the results in Figure 1—figure supplement 2, we use the Adaptive Moment Estimation (Adam) algorithm (Kingma and Ba, 2014) to improve optimisation performance.

We used a standard reparameterisation method to ensure the sign constraints of an E/I network. Moreover, all weights are subject to a small weight-dependent decay term, which aids to keep the firing rates of the interneurons in a reasonable range. For details, please refer to Appendix 1 . The learning rule Equation 4a for the output synapses of the inhibitory neurons is similar to the rule proposed by Vogels et al., 2011, wherein each inhibitory synapse increases in strength if the deviation of the postsynaptic excitatory cell from the homeostatic target $ρ_{0}$ is positive (and decreases it when negative). In contrast, the learning rule Equation 4b increases activated input synapses for an interneuron if the weighted sum of deviations in its presynaptic excitatory population is positive (and decreases them if it is negative). Though it is local, when operating in conjunction with the plasticity of Equation 4a, this leads to feedback alignment in our simulations and effectively performs backpropagation without the need for weight transport (Akrout et al., 2019).

Note that the objective function Equation 3 can also be interpreted differently. The activation $h^{E}$ of a neuron is essentially the difference between its excitatory and inhibitory inputs. Therefore, the objective function Equation 3 is effectively the mean squared error between excitation and inhibition, aside from a small constant offset $ρ_{0}$ . The derived learning rules can therefore be seen as supervised learning of the inhibitory inputs, with excitation as the label. They hence aim to establish the best co-tuning of excitation and inhibition that is possible given the circuitry.

Perturbation experiments

Request a detailed protocol

The perturbation experiments in Figure 4 are performed in a network in which both forms of plasticity have converged. The network is then exposed to different stimuli, while the afferent drive to a single excitatory cell i is transiently increased by $Δ I = 10$ Hz. For each stimulus, we compute the steady-state firing rates r_j of all excitatory cells both with and without the perturbation. The influence of the perturbation of neuron i on neuron j is defined as the difference between these two firing rates, normalised by the pertubation magnitude (Sadeh and Clopath, 2020). This stimulation protocol is repeated for 90 randomly selected excitatory neurons. The dependence of the influence on the tuning similarity (Figure 4d) is obtained by binning the influence of the perturbed neuron i and the influenced neuron j according to their stimulus response correlation, and then averaging across all influences in the bin. During the perturbation experiments, synaptic plasticity was disabled.

Quantitative measures

Request a detailed protocol

The response similarity (RS) of the stimulus tuning of two neurons i and j is measured by the dot product of their steady-state firing rates in response to all stimuli, normalised by the product of their norms (Znamenskiy et al., 2018):

RS (r_{i}, r_{j}) = \frac{\sum_{𝐬} r_{i} (𝐬) r_{j} (𝐬)}{{(\sum_{𝐬} {(r_{i} (𝐬))}^{2} \sum_{𝐬} {(r_{j} (𝐬))}^{2})}^{1 / 2}} .

The same measure is used for the similarity of synaptic currents onto excitatory neurons in Figure 1—figure supplement 3c and Figure 1—figure supplement 2d.

There is no structural plasticity, that is, synapses are never added or pruned. However, when calculating Pearson’s correlation between synaptic weights and RS, we exclude synapses that are too weak to be detected using the experimental protocol employed by Znamenskiy et al., 2018. The threshold values $θ^{E \leftarrow I}$ and $θ^{I \leftarrow E}$ were chosen to be approximately four orders of magnitude weaker than the strongest synapses in the network. The rules that we investigate here tend to produce bimodal distributions of weights, with the lower mode well below this threshold (Figure 1—figure supplement 5).

The stimulus selectivity of the neurons is measured by the skewness of their response distribution across all stimuli:

γ_{i} = \frac{{⟨ {(r_{i} (𝐬) - {\bar{r}}_{i})}^{3} ⟩}_{𝐬}}{{⟨ {(r_{i} (𝐬) - {\bar{r}}_{i})}^{2} ⟩}_{𝐬}^{3 / 2}}

where ${\bar{r}}_{i} = {⟨ r_{i} (𝐬) ⟩}_{𝐬}$ . Both the RS Equation 5 and the stimulus selectivity Equation 6 are adapted from Znamenskiy et al., 2018.

Finally, the angle $θ$ between the gradient G from Equation 15 and its approximation A from Equation 4 is given by

θ = \arccos (\frac{\sum_{i j} G_{i j} A_{i j}}{{(\sum_{i j} G_{i j}^{2} \sum_{i j} A_{i j}^{2})}^{1 / 2}})

Appendix 1

Plasticity rules

The general framework we follow to derive homeostatic rules is to minimise the mean squared deviation of individual excitatory (Pyr) neuron activations from a target for all stimuli. More specifically, we perform gradient descent on the following objective function:

ℰ (h^{E}) = {⟨ \frac{1}{2} \sum_{j = 1}^{N^{E}} {(h_{j}^{E} - ρ_{0})}^{2} ⟩}_{s} .

Note that the activations $h^{E}$ are given by the difference between the excitatory and the inhibitory inputs to the excitatory neurons. Our approach can hence be interpreted as supervised learning of the inhibitory circuitry, with the goal of minimising the mean squared loss between the inhibitory and the excitatory inputs (plus the constant target $ρ_{0}$ ). In this sense, the derived gradient rules aim to generate the best possible E/I balance across stimuli that is possible with the circuitry at hand.

For reasons of readability, we will first simply state the derived rules. The details of their derivation can be found in the following section.

The sign constraints in excitatory-inhibitory networks require all synaptic weights to remain positive. To ensure this, we reparameterised all plastic weights of the network by a strictly positive soft-plus function $W = s^{+} (V) = α^{- 1} \ln (1 + \exp α V)$ and optimised the weight parameter V by gradient descent.

In summary, the derived learning rules for the synaptic weight parameters between excitatory neuron j and inhibitory interneuron i are given by

\begin{aligned} (8a) & Δ V_{j i}^{E \leftarrow I} & = η^{I} (h_{j}^{E} - ρ_{0}) \frac{\partial W_{j i}^{E \leftarrow I}}{\partial V_{j i}^{E \leftarrow I}} r_{i}^{I} - δ^{I} W_{j i}^{E \leftarrow I}, \\ (8b) & Δ V_{i j}^{I \leftarrow E} & = η^{E} [\sum_{k = 1}^{N^{E}} W_{i k}^{I \leftarrow E} (h_{k}^{E} - ρ_{0})] \frac{\partial r_{i}^{I}}{\partial h_{i}^{I}} \frac{\partial W_{i j}^{I \leftarrow E}}{\partial V_{i j}^{I \leftarrow E}} r_{j}^{E} - δ^{E} W_{i j}^{I \leftarrow E} . \end{aligned}

Please note that we added a small weight decay to both learning rules. The purpose of this decay term is to avoid an ambiguity in the solution. When the firing rates of the interneurons are increased, but their output weights are decreased accordingly, the firing rates of the excitatory population remain unchanged. Pure gradient-based rules can therefore generate extreme values for the synaptic weights, in which the interneurons have biologically unrealistic firing rates. The additional decay terms in the learning rules solve this issue.

Finally, we replaced the derivative $\frac{\partial r}{\partial h}$ (which should be a Heaviside function, because rates are the rectified activations) by the derivative of a soft-plus function with finite sharpness ( $α = 1$ ). This allows interneurons to recover from a silent state, in which all gradients vanish. Note that this replacement is done only in the learning rules. The firing rates are still the rectified activations. This method is similar to recent surrogate gradient approaches in spiking networks (Neftci et al., 2019).

Derivation of the homeostatic plasticity rules in recurrent networks

The challenging aspect of the derivation of the learning rules lies in the recurrence of the network. The effects of changes in individual synapses can percolate through the network and thereby change the firing rates of all neurons. Moreover, the temporal dynamics of the network would in principle require a backpropagation of the gradient through time. We circumvent this complication by assuming that the external stimuli to the network change slowly compared to the dynamical time scales of the network, and that the network adiabatically follows the fixed point in its dynamics as the stimulus changes. This assumption significantly simplifies the derivation of the gradient.

The goal is to minimise the total deviation of the excitatory activations $h^{E}$ from the homeostatic target value $ρ_{0}$ . To this end, we calculate the gradient of the objective function in Equation 3 with respect to a given synaptic weight parameter $v \in {V_{i j}^{I \leftarrow E}$ , $V_{j i}^{E \leftarrow I}}$ :

\frac{\partial}{\partial v} ℰ (h^{E}) = {⟨ {(h^{E} - ρ_{0})}^{⊺} \frac{\partial h^{E}}{\partial v} ⟩}_{s} .

We therefore need the gradient of the activations $h^{E}$ of excitatory cells with respect to a parameter $v$ . In the steady state, the activations are given by

h^{E} = W^{E \leftarrow E} r^{E} - W^{E \leftarrow I} r^{I} + I_{bg} + I (s) .

The gradient of the activations $h^{E}$ is therefore given by the following implicit condition:

\frac{\partial h^{E}}{\partial v} = W^{E \leftarrow E} D^{E} \frac{\partial h^{E}}{\partial v} - [\frac{\partial W^{E \leftarrow I}}{\partial v} r^{I} + W^{E \leftarrow I} D^{I} \frac{\partial h^{I}}{\partial v}],

where we introduced the diagonal matrices $D_{i j}^{E / I} := δ_{i j} \partial r_{i}^{E / I} / \partial h_{i}^{E / I}$ for notational convenience, $δ_{i j}$ being the Kronecker symbol. Derivatives of expressions that do not depend on any of the synaptic weights in question are excluded.

Equation 11 requires the gradient $\frac{\partial h^{I}}{\partial v}$ of the inhibitory activations with respect to the parameter $v$ , which can be calculated by a similar approach:

\begin{array}{ll} \frac{\partial h^{I}}{\partial v} & = \frac{\partial}{\partial v} (W^{I \leftarrow E} r^{E} - W^{I \leftarrow I} r^{I} + I_{bg}) \\ = (\frac{\partial W^{I \leftarrow E}}{\partial v} r^{E} + W^{I \leftarrow E} D^{E} \frac{\partial h^{E}}{\partial v}) - W^{I \leftarrow I} D^{I} \frac{\partial h^{I}}{\partial v} . \end{array}

Introducing the effective interaction matrix $ℳ := 𝕀 + W^{I \leftarrow I} D^{I}$ among the interneurons ( $𝕀$ being the identity matrix) allows to solve for the gradient of $h^{I}$ :

\frac{\partial h^{I}}{\partial v} = ℳ^{- 1} [W^{I \leftarrow E} D^{E} \frac{\partial h^{E}}{\partial v} + \frac{\partial W^{I \leftarrow E}}{\partial v} r^{E}]

Inserting this expression into Equation 11 yields

\frac{\partial h^{E}}{\partial v} = [W^{E \leftarrow E} D^{E} - W^{E \leftarrow I} D^{I} ℳ^{- 1} W^{I \leftarrow E} D^{E}] \frac{\partial h^{E}}{\partial v} - \frac{\partial W^{E \leftarrow I}}{\partial v} r^{I} - W^{E \leftarrow I} D^{I} ℳ^{- 1} \frac{\partial W^{I \leftarrow E}}{\partial v} r^{E} .

Introducing the effective interaction matrix $𝒲 = 𝕀 - W^{E \leftarrow E} D^{E} + W^{E \leftarrow I} D^{I} ℳ^{- 1} W^{I \leftarrow E} D^{E}$ among the excitatory neurons yields an explicit expression for the gradient of $h^{E}$ :

\frac{\partial h^{E}}{\partial v} = - 𝒲^{- 1} \frac{\partial W^{E \leftarrow I}}{\partial v} r^{I} - 𝒲^{- 1} W^{E \leftarrow I} D^{I} ℳ^{- 1} \frac{\partial W^{I \leftarrow E}}{\partial v} r^{E} .

To obtain gradients with respect to a particular network parameter, we simply substitute the chosen parameter into Equation 12. For the parameters $V_{i j}^{I \leftarrow E}$ of the input synapses to the interneurons, the gradient reduces to

\frac{\partial h^{E}}{\partial V^{I \leftarrow E}} = - 𝒲^{- 1} W^{E \leftarrow I} D^{I} ℳ^{- 1} \frac{\partial W^{I \leftarrow E}}{\partial V^{I \leftarrow E}} r^{E},

and for the parameters $V_{i j}^{E \leftarrow I}$ of the output synapses from the interneurons we get

\frac{\partial h^{E}}{\partial V^{I \leftarrow E}} = - 𝒲^{- 1} \frac{\partial W^{E \leftarrow I}}{\partial V^{E \leftarrow I}} r^{I} .

By inserting these expressions into Equation 9 and dropping the average, we obtain online learning rules for the input and output synapses of the interneurons:

\begin{aligned} (15a) & Δ V^{I \leftarrow E} \propto [(h^{E} - ρ_{0})^{⊺} 𝒲^{- 1} W^{E \leftarrow I} D^{I} ℳ^{- 1}] \frac{\partial W^{I \leftarrow E}}{\partial V^{I \leftarrow E}} r^{E} \\ (15b) & Δ V^{E \leftarrow I} \propto [(h^{E} - ρ_{0})^{⊺} 𝒲^{- 1}] \frac{\partial W^{E \leftarrow I}}{\partial V^{E \leftarrow I}} r^{I} . \end{aligned}

Note that the same approach also yields learning rules for the threshold and the gain of the transfer function of the inhibitory interneurons, if those are parameters of the system. Although we did not use such intrinsic plasticity rules, we include them here for the interested reader. We assumed a threshold linear transfer function of the interneurons: $r_{i}^{I} = g_{i} {[h_{i}^{I} - θ_{i}]}^{+}$ , where $g_{i}$ is the gain of the neuronal transfer function and $θ_{i}$ a firing threshold. While the firing threshold can become negative, gain is reparameterised via the strictly positive soft-plus $g_{i} = s^{+} (v_{i}^{g})$ . The gradient-based learning rule for the firing thresholds $θ_{i}$ of the interneurons is given by

Δ θ_{i} \propto - {[{(h^{E} - ρ_{0})}^{⊺} 𝒲^{- 1} W^{E \leftarrow I} ℳ^{- 1}]}_{i} \frac{\partial r_{i}^{I}}{\partial θ_{i}},

and the corresponding learning rule for the interneuron gain $g_{i}$ is

Δ v_{i}^{g} \propto - {[{(h^{E} - ρ_{0})}^{⊺} 𝒲^{- 1} W^{E \leftarrow I} ℳ^{- 1}]}_{i} \frac{\partial r_{i}^{I}}{\partial g_{i}} \frac{\partial g_{i}}{\partial v_{i}^{g}} .

Approximating the gradient rules

In the gradient-based rules derived in the previous section, the $𝒲^{- 1}$ and $ℳ^{- 1}$ terms account for the fact that a change in a given synaptic connections percolates through the network. As a result, the learning rules are highly non-local and hard to implement in a biologically plausible way. To resolve this challenge, we begin by noting that

𝒲^{- 1} = {(𝕀 - \hat{𝒲})}^{- 1} = \sum_{k = 0}^{\infty} {\hat{𝒲}}^{k},

which holds if $‖ \hat{𝒲} ‖ < 1$ . $\hat{𝒲}$ is a matrix that depends on the synaptic weights in the network. A similar relation holds for $ℳ^{- 1}$ . Since those matrices are contained in Equation 15a, we substitute the equivalent sums into the relevant sub-expression and truncate the geometric series after the zeroth order, as in

\begin{aligned} 𝒲^{- 1} W^{E \leftarrow I} D^{I} ℳ^{- 1} & = (\sum_{k = 0}^{\infty} {\hat{𝒲}}^{k}) W^{E \leftarrow I} D^{I} (\sum_{k = 0}^{\infty} {\hat{ℳ}}^{k}) \\ = W^{E \leftarrow I} D^{I} + \hat{𝒲} W^{E \leftarrow I} D^{I} + W^{E \leftarrow I} D^{I} \hat{ℳ} + (\sum_{k = 1}^{\infty} {\hat{𝒲}}^{k}) W^{E \leftarrow I} D^{I} (\sum_{k = 1}^{\infty} {\hat{ℳ}}^{k}) \\ \approx W^{E \leftarrow I} D^{I} . \end{aligned}

The truncation to zeroth order in the last line should yield an acceptable approximation if synapses are sufficiently weak. The effect of higher-order interactions in the network can then be ignored. This approximation can be substituted into Equation 15a and yields an equation that resembles a backpropagation rule in a feedforward network (E → I → E) with one hidden layer—the interneurons. The final, local approximation used for the simulations in the main text is then reached by replacing the output synapses of the interneurons by the transpose of their input synapses. While there is no mathematical argument why this replacement is valid, it turns out to be in the simulations, presumably because of a mechanism akin to feedback alignment (Lillicrap et al., 2016; see discussion in the main text). In feedback alignment, the matrix that backpropagates the errors is replaced by a random matrix $B$ . Here, we instead use the feedforward weights in the layer below. Similar to the extension to feedback alignment of Akrout et al., 2019, those weights are themselves plastic. However, we believe that the underlying mechanism of feedback alignment still holds. The representation in the hidden layer (the interneurons) changes as if the weights to the output layer (the Pyr neurons) were equal to the weight matrix they are replaced with (here, the input weights to the PV neurons). To exploit this representation, the weights to the output layer then align to the replacement weights, justifying the replacement post hoc (Figure 1G).

Note that the condition for feedback alignment to provide an update in the appropriate direction ( $e^{T} B^{T} W e > 0$ , where $e$ denotes the error, $W$ the weights in the second layer, and $B$ the random feedback matrix) reduces to the condition that $W^{E \leftarrow I} W^{I \leftarrow E}$ is positive definite (assuming the errors are full rank). One way of assuring this is a sufficiently positive diagonal of this matrix product, that is, a sufficiently high correlation between the incoming and outgoing synapses of the interneurons. A positive correlation of these weights is one of the observations of Znamenskiy et al., 2018 and also a result of learning in our model.

While such a positive correlation is not necessarily present for all learning tasks or network models, we speculate that it will be for the task of learning an E/I balance in networks that obey Dale’s law.

The same logic of using a zeroth order approximation of $𝒲^{- 1}$ that neglects higher-order interactions is employed to recover the inhibitory synaptic plasticity rule of Vogels et al., 2011 from Equation 15b.

Overall, the local approximation of the learning rule relies on three assumptions: slowly varying inputs, weak synaptic weights, and alignment of input and output synapses of the interneurons. These assumptions clearly limit the applicability of the learning rules for other learning tasks. In particular, the learning rules will not allow the network to learn temporal sequences.

The effect of static but heavy-tailed PV input weights

We investigated whether plasticity is required on both input and output synapses. The main argument why plasticity may not be required is that a static but heavy-tailed weight distribution for Pyr → PV synapses might provide sufficient stimulus selectivity in PV neurons, such that plasticity of output synapses alone can account for the experimental data of Znamenskiy et al., 2018. To test this, we sampled weights from a log-normal distribution (Loewenstein et al., 2011), with parameters that are in line with the data reported by Znamenskiy et al., 2018. Weights spanned approximately two orders of magnitude. For this setting, PV neurons do not have sufficient stimulus selectivity for output plasticity alone to co-tune inhibitory currents with excitatory currents, when Pyr → PV plasticity is knocked out. Moreover, if we sample PV input and output synapses, correlations between excitatory input synapse strength and RS are not reliably found, nor are correlations between input and output synapse strength (Figure 3).

Nevertheless, one could expect that a sufficiently heavy-tailed distribution of PV excitatory input weights could account for the experimentally observed correlations, even in the absence of Pyr → PV plasticity. We therefore repeated the simulations of Figure 3 with a weight distribution that spans almost five orders of magnitude (Figure 3—figure supplement 2). We also tested other distributions, but the results remain qualitatively unchanged.

With this heavy-tailed distribution of excitatory input weights, PV neurons indeed exhibit increased stimulus selectivity (Figure 3—figure supplement 2b, cf. Figure 3c). This increased selectivity enables greater stimulus-specific co-tuning of inhibitory and excitatory currents (Figure 3—figure supplement 2c, cf. Figure 1—figure supplement 2d). Despite this, repeated random sampling of excitatory input synaptic weights ( $n = 100$ drawn 10⁴ times) produces positive correlations with RS only about half the time, and for reciprocally connected Pyr-PV cell pairs, input synaptic weights are unlikely to be correlated with output weights (Figure 3—figure supplement 2d). Observing the correlations of Znamenskiy et al., 2018 is therefore unlikely in the absence of some kind of PV input plasticity.

Note that the setting in Figure 3—figure supplement 2 is conservative in that we chose parameters that made the observation of positive correlations likely. In particular, it is important to note that—similar to the results of Figure 3—we consider synapses below a chosen threshold as too weak to be detected during the sampling procedure. We set the threshold of detectability to be approximately two orders of magnitude below the strongest weights (dashed lines in Figure 3—figure supplement 2e). For lower thresholds, the fraction of significant Exc-RS and Exc-Inh correlations rapidly decreases, to essentially zero if we include all weights. This is due to the fact that the inhibitory stimulus tuning is determined by a small number of large weights, and if samples are drawn from all synapses, the probability of sampling one of these large weights is small.

In summary, randomly drawn input weights to PV neurons from the distribution observed by Znamenskiy et al., 2018 are not sufficiently sparse to ensure enough PV selectivity for the observed E/I assemblies, and sampling from even sparser distributions makes the observation of the few influential weights too unlikely. This suggests that the input weights to PV neurons are not random, but that these synaptic weights and the stimulus tuning of their inputs are correlated, consistent with the presence of synaptic plasticity.

Of course, the question whether random connectivity is sufficient for selectivity not only depends on the weight distribution, but also on the total number of synapses received by the PV neurons and the stimulus selectivity of the Pyr neurons they receive input from. Even when the weights are not sparsely distributed, a small number of inputs combined with sufficiently sparse inputs could generate substantial selectivity. We did not explore these additional parameters (in-degree of PV neurons, Pyr selectivity) in detail here, because we believe that our choices are already rather conservative. Due to the small size of the network, PV neurons receive only about 300 excitatory inputs, which is unlikely to be an overestimate, and the stimulus tuning of the Pyr neurons in the model is comparable to V1 (Znamenskiy et al., 2018, Figure 1), although the diversity of the Pyr neuron selectivity in the data is of course higher.

Data availability

Source code for the simulator that generated all data is available at https://github.com/owenmackwood/ei-assemblies (copy archived at https://archive.softwareheritage.org/swh:1:rev:e2f029a7e7285230cbbdbc7e817e25c8c5535fc1).

References

(2012) A neural circuit for spatial summation in visual cortex
Nature 490:226–231.
https://doi.org/10.1038/nature11526
- PubMed
- Google Scholar
Conference
(2019)
Deep learning without weight transport

Advances in Neural Information Processing Systems. pp. 976–984.
- Google Scholar
1. Barron HC
2. Vogels TP
3. Emir UE
4. Makin TR
5. O'Shea J
6. Clare S
7. Jbabdi S
8. Dolan RJ
9. Behrens TE
(2016) Unmasking latent inhibitory connections in human cortex to reveal dormant cortical memories
Neuron 90:191–203.
https://doi.org/10.1016/j.neuron.2016.02.031
- PubMed
- Google Scholar
(2017) Inhibitory engrams in perception and memory
PNAS 114:6666–6674.
https://doi.org/10.1073/pnas.1701812114
- PubMed
- Google Scholar
1. Bellec G
2. Scherr F
3. Subramoney A
4. Hajek E
5. Salaj D
6. Legenstein R
7. Maass W
(2020) A solution to the learning dilemma for recurrent networks of spiking neurons
Nature Communications 11:3625.
https://doi.org/10.1038/s41467-020-17236-y
- Google Scholar
(2019) Precise excitation-inhibition balance controls gain and timing in the Hippocampus
eLife 8:e43415.
https://doi.org/10.7554/eLife.43415
- PubMed
- Google Scholar
(1982) Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex
The Journal of Neuroscience 2:32–48.
https://doi.org/10.1523/JNEUROSCI.02-01-00032.1982
- PubMed
- Google Scholar
1. Bock DD
2. Lee WC
3. Kerlin AM
4. Andermann ML
5. Hood G
6. Wetzel AW
7. Yurgenson S
8. Soucy ER
9. Kim HS
10. Reid RC
(2011) Network anatomy and in vivo physiology of visual cortical neurons
Nature 471:177–182.
https://doi.org/10.1038/nature09802
- PubMed
- Google Scholar
1. Brunel N
(2000) Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons
Journal of Computational Neuroscience 8:183–208.
https://doi.org/10.1023/a:1008925309027
- PubMed
- Google Scholar
(2017) Memory replay in balanced recurrent networks
PLOS Computational Biology 13:e1005359.
https://doi.org/10.1371/journal.pcbi.1005359
- PubMed
- Google Scholar
1. Chettih SN
2. Harvey CD
(2019) Single-neuron perturbations reveal feature-specific competition in V1
Nature 567:334–340.
https://doi.org/10.1038/s41586-019-0997-6
- PubMed
- Google Scholar
Preprint
(2016) Receptive field formation by interacting excitatory and inhibitory synaptic plasticity
bioRxiv.
https://doi.org/10.1101/066589
- Google Scholar
1. Cossell L
2. Iacaruso MF
3. Muir DR
4. Houlton R
5. Sader EN
6. Ko H
7. Hofer SB
8. Mrsic-Flogel TD
(2015) Functional organization of excitatory synaptic strength in primary visual cortex
Nature 518:399–403.
https://doi.org/10.1038/nature14182
- PubMed
- Google Scholar
1. Denève S
2. Machens CK
(2016) Efficient codes and balanced networks
Nature Neuroscience 19:375–382.
https://doi.org/10.1038/nn.4243
- PubMed
- Google Scholar
(2018) Vision and locomotion shape the interactions between neuron types in mouse visual cortex
Neuron 98:602–615.
https://doi.org/10.1016/j.neuron.2018.03.037
- PubMed
- Google Scholar
1. Dorrn AL
2. Yuan K
3. Barker AJ
4. Schreiner CE
5. Froemke RC
(2010) Developmental sensory experience balances cortical excitation and inhibition
Nature 465:932–936.
https://doi.org/10.1038/nature09119
- PubMed
- Google Scholar
1. Fino E
2. Yuste R
(2011) Dense inhibitory connectivity in neocortex
Neuron 69:1188–1203.
https://doi.org/10.1016/j.neuron.2011.02.025
- PubMed
- Google Scholar
1. Fishell G
2. Kepecs A
(2020) Interneuron types as attractors and controllers
Annual Review of Neuroscience 43:1–30.
https://doi.org/10.1146/annurev-neuro-070918-050421
- PubMed
- Google Scholar
(2007) A synaptic memory trace for cortical receptive field plasticity
Nature 450:425–429.
https://doi.org/10.1038/nature06289
- PubMed
- Google Scholar
(2015) Dendritic function in vivo
Trends in Neurosciences 38:45–54.
https://doi.org/10.1016/j.tins.2014.11.002
- PubMed
- Google Scholar
(2017) Towards deep learning with segregated dendrites
eLife 6:e22901.
https://doi.org/10.7554/eLife.22901
- PubMed
- Google Scholar
1. Harris KD
2. Mrsic-Flogel TD
(2013) Cortical connectivity and sensory coding
Nature 503:51–58.
https://doi.org/10.1038/nature12654
- PubMed
- Google Scholar
(2014) Optimal control of transient dynamics in balanced networks supports generation of complex movements
Neuron 82:1394–1406.
https://doi.org/10.1016/j.neuron.2014.04.045
- PubMed
- Google Scholar
(2017) Inhibitory plasticity: balance, control, and codependence
Annual Review of Neuroscience 40:557–579.
https://doi.org/10.1146/annurev-neuro-072116-031005
- PubMed
- Google Scholar
1. Hertäg L
2. Sprekeler H
(2019) Amplifying the redistribution of somato-dendritic inhibition by the interplay of three interneuron types
PLOS Computational Biology 15:e1006999.
https://doi.org/10.1371/journal.pcbi.1006999
- PubMed
- Google Scholar
1. Hertäg L
2. Sprekeler H
(2020) Learning prediction error neurons in a canonical interneuron circuit
eLife 9:e57541.
https://doi.org/10.7554/eLife.57541
- PubMed
- Google Scholar
1. Hofer SB
2. Ko H
3. Pichler B
4. Vogelstein J
5. Ros H
6. Zeng H
7. Lein E
8. Lesica NA
9. Mrsic-Flogel TD
(2011) Differential connectivity and response dynamics of excitatory and inhibitory neurons in visual cortex
Nature Neuroscience 14:1045–1052.
https://doi.org/10.1038/nn.2876
- PubMed
- Google Scholar
1. Hu H
2. Gan J
3. Jonas P
(2014) Interneurons. Fast-spiking, parvalbumin⁺ GABAergic interneurons: from cellular design to microcircuit function
Science 345:1255263.
https://doi.org/10.1126/science.1255263
- PubMed
- Google Scholar
1. Isaacson JS
2. Scanziani M
(2011) How inhibition shapes cortical activity
Neuron 72:231–243.
https://doi.org/10.1016/j.neuron.2011.09.027
- PubMed
- Google Scholar
1. Jia H
2. Rochefort NL
3. Chen X
4. Konnerth A
(2010) Dendritic organization of sensory input to cortical neurons in vivo
Nature 464:1307–1312.
https://doi.org/10.1038/nature08947
- PubMed
- Google Scholar
(2016) Opening holes in the blanket of inhibition: localized lateral disinhibition by VIP interneurons
Journal of Neuroscience 36:3471–3480.
https://doi.org/10.1523/JNEUROSCI.3646-15.2016
- PubMed
- Google Scholar
1. Keck T
2. Scheuss V
3. Jacobsen RI
4. Wierenga CJ
5. Eysel UT
6. Bonhoeffer T
7. Hübener M
(2011) Loss of sensory input causes rapid structural changes of inhibitory neurons in adult mouse visual cortex
Neuron 71:869–882.
https://doi.org/10.1016/j.neuron.2011.06.034
- PubMed
- Google Scholar
1. Khan AG
2. Poort J
3. Chadwick A
4. Blot A
5. Sahani M
6. Mrsic-Flogel TD
7. Hofer SB
(2018) Distinct learning-induced changes in stimulus selectivity and interactions of GABAergic interneuron classes in visual cortex
Nature Neuroscience 21:851–859.
https://doi.org/10.1038/s41593-018-0143-z
- PubMed
- Google Scholar
Preprint
1. Kingma DP
2. Ba J
(2014) Adam: a method for stochastic optimization
arXiv.

https://arxiv.org/abs/1412.6980
- Google Scholar
(2011) Functional specificity of local synaptic connections in neocortical networks
Nature 473:87–91.
https://doi.org/10.1038/nature09880
- PubMed
- Google Scholar
1. Kuhlman SJ
2. Olivas ND
3. Tring E
4. Ikrar T
5. Xu X
6. Trachtenberg JT
(2013) A disinhibitory microcircuit initiates critical-period plasticity in the visual cortex
Nature 501:543–546.
https://doi.org/10.1038/nature12485
- PubMed
- Google Scholar
1. Kullmann DM
2. Lamsa KP
(2007) Long-term synaptic plasticity in hippocampal interneurons
Nature Reviews Neuroscience 8:687–699.
https://doi.org/10.1038/nrn2207
- PubMed
- Google Scholar
(2007) NMDA receptor-dependent long-term potentiation in mouse hippocampal interneurons shows a unique dependence on Ca(2+)/calmodulin-dependent kinases
The Journal of Physiology 584:885–894.
https://doi.org/10.1113/jphysiol.2007.137380
- PubMed
- Google Scholar
(2016) The impact of structural heterogeneity on excitation-inhibition balance in cortical networks
Neuron 92:1106–1121.
https://doi.org/10.1016/j.neuron.2016.10.027
- PubMed
- Google Scholar
1. Larkum ME
2. Nevian T
(2008) Synaptic clustering by dendritic signalling mechanisms
Current Opinion in Neurobiology 18:321–331.
https://doi.org/10.1016/j.conb.2008.08.013
- PubMed
- Google Scholar
(2013) Input-specific learning rules at excitatory synapses onto hippocampal parvalbumin-expressing interneurons
The Journal of Physiology 591:1809–1822.
https://doi.org/10.1113/jphysiol.2012.245852
- PubMed
- Google Scholar
1. Letzkus JJ
2. Wolff SB
3. Meyer EM
4. Tovote P
5. Courtin J
6. Herry C
7. Lüthi A
(2011) A disinhibitory microcircuit for associative fear learning in the auditory cortex
Nature 480:331–335.
https://doi.org/10.1038/nature10674
- PubMed
- Google Scholar
(2016) Random synaptic feedback weights support error backpropagation for deep learning
Nature Communications 7:13276.
https://doi.org/10.1038/ncomms13276
- PubMed
- Google Scholar
(2020) Backpropagation and the brain
Nature Reviews Neuroscience 21:1–12.
https://doi.org/10.1038/s41583-020-0277-3
- PubMed
- Google Scholar
(2016) Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes
Journal of Neurophysiology 115:1399–1409.
https://doi.org/10.1152/jn.00732.2015
- PubMed
- Google Scholar
(2017) Optimal degrees of synaptic connectivity
Neuron 93:1153–1164.
https://doi.org/10.1016/j.neuron.2017.01.030
- PubMed
- Google Scholar
1. Litwin-Kumar A
2. Doiron B
(2012) Slow dynamics and high variability in balanced cortical networks with clustered connections
Nature Neuroscience 15:1498–1505.
https://doi.org/10.1038/nn.3220
- PubMed
- Google Scholar
1. Litwin-Kumar A
2. Doiron B
(2014) Formation and maintenance of neuronal assemblies through synaptic plasticity
Nature Communications 5:5319.
https://doi.org/10.1038/ncomms6319
- PubMed
- Google Scholar
(2012) Perceptual inference predicts contextual modulations of sensory responses
Journal of Neuroscience 32:4179–4195.
https://doi.org/10.1523/JNEUROSCI.0817-11.2012
- PubMed
- Google Scholar
(2011) Multiplicative dynamics underlie the emergence of the log-normal distribution of spine sizes in the neocortex in vivo
Journal of Neuroscience 31:9481–9488.
https://doi.org/10.1523/JNEUROSCI.6130-10.2011
- PubMed
- Google Scholar
1. Moreno-Bote R
2. Drugowitsch J
(2015) Causal inference and explaining away in a spiking network
Scientific Reports 5:17531.
https://doi.org/10.1038/srep17531
- PubMed
- Google Scholar
1. Murphy BK
2. Miller KD
(2009) Balanced amplification: a new mechanism of selective amplification of neural activity patterns
Neuron 61:635–648.
https://doi.org/10.1016/j.neuron.2009.02.005
- PubMed
- Google Scholar
(2020) Excitatory and inhibitory subnetworks are equally selective during Decision-Making and emerge simultaneously during learning
Neuron 105:165–179.
https://doi.org/10.1016/j.neuron.2019.09.045
- PubMed
- Google Scholar
(2019) Surrogate gradient learning in spiking neural networks: bringing the power of Gradient-Based optimization to spiking neural networks
IEEE Signal Processing Magazine 36:51–63.
https://doi.org/10.1109/MSP.2019.2931595
- Google Scholar
1. Ohki K
2. Chung S
3. Ch'ng YH
4. Kara P
5. Reid RC
(2005) Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex
Nature 433:597–603.
https://doi.org/10.1038/nature03274
- PubMed
- Google Scholar
1. Okun M
2. Lampl I
(2008) Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities
Nature Neuroscience 11:535–537.
https://doi.org/10.1038/nn.2105
- PubMed
- Google Scholar
1. Olshausen BA
2. Field DJ
(2004) Sparse coding of sensory inputs
Current Opinion in Neurobiology 14:481–487.
https://doi.org/10.1016/j.conb.2004.07.007
- PubMed
- Google Scholar
1. Packer AM
2. Yuste R
(2011) Dense, unspecific connectivity of neocortical parvalbumin-positive interneurons: a canonical microcircuit for inhibition?
Journal of Neuroscience 31:13260–13271.
https://doi.org/10.1523/JNEUROSCI.3131-11.2011
- PubMed
- Google Scholar
(2017) Cortical interneurons differentially regulate the effects of acoustic context
Cell Reports 20:771–778.
https://doi.org/10.1016/j.celrep.2017.07.001
- PubMed
- Google Scholar
1. Pouille F
2. Scanziani M
(2001) Enforcement of temporal fidelity in pyramidal cells by somatic feed-forward inhibition
Science 293:1159–1163.
https://doi.org/10.1126/science.1060342
- PubMed
- Google Scholar
1. Priebe NJ
2. Ferster D
(2008) Inhibition, spike threshold, and stimulus selectivity in primary visual cortex
Neuron 57:482–497.
https://doi.org/10.1016/j.neuron.2008.02.005
- PubMed
- Google Scholar
(2015) The stabilized supralinear network: a unifying circuit motif underlying multi-input integration in sensory cortex
Neuron 85:402–417.
https://doi.org/10.1016/j.neuron.2014.12.026
- PubMed
- Google Scholar
Report
(1985)
Learning Internal Representations by Error Propagation

Technical report, California Univ San Diego La Jolla Inst for Cognitive Science.
- Google Scholar
1. Rupprecht P
2. Friedrich RW
(2018) Precise synaptic balance in the zebrafish homolog of olfactory cortex
Neuron 100:669–683.
https://doi.org/10.1016/j.neuron.2018.09.013
- PubMed
- Google Scholar
Conference
1. Sacramento J
2. Costa RP
3. Bengio Y
4. Senn W
(2018)
Dendritic cortical microcircuits approximate the backpropagation algorithm

Advances in Neural Information Processing Systems. pp. 8721–8732.
- Google Scholar
1. Sadeh S
2. Clopath C
(2020) Theory of neuronal perturbome: linking connectivity to coding via perturbations
PNAS 117:26966–26976.
https://doi.org/10.1073/pnas.2004568117
- Google Scholar
(2008) Dendritic excitability and synaptic plasticity
Physiological Reviews 88:769–840.
https://doi.org/10.1152/physrev.00016.2007
- PubMed
- Google Scholar
(2005) Highly nonrandom features of synaptic connectivity in local cortical circuits
PLOS Biology 3:e68.
https://doi.org/10.1371/journal.pbio.0030068
- PubMed
- Google Scholar
1. Sprekeler H
(2017) Functional consequences of inhibitory plasticity: homeostasis, the excitation-inhibition balance and beyond
Current Opinion in Neurobiology 43:198–203.
https://doi.org/10.1016/j.conb.2017.03.014
- PubMed
- Google Scholar
(2013) Hearing loss differentially affects thalamic drive to two cortical interneuron subtypes
Journal of Neurophysiology 110:999–1008.
https://doi.org/10.1152/jn.00182.2013
- PubMed
- Google Scholar
1. Tan AY
2. Brown BD
3. Scholl B
4. Mohanty D
5. Priebe NJ
(2011) Orientation selectivity of synaptic input to neurons in mouse and cat primary visual cortex
The Journal of Neuroscience 31:12339–12350.
https://doi.org/10.1523/JNEUROSCI.2039-11.2011
- PubMed
- Google Scholar
(2015) Neuronal circuits for fear and anxiety
Nature Reviews Neuroscience 16:317–331.
https://doi.org/10.1038/nrn3945
- PubMed
- Google Scholar
1. Tremblay R
2. Lee S
3. Rudy B
(2016) GABAergic interneurons in the neocortex: from cellular properties to circuits
Neuron 91:260–292.
https://doi.org/10.1016/j.neuron.2016.06.033
- PubMed
- Google Scholar
1. van Vreeswijk C
2. Sompolinsky H
(1996) Chaos in neuronal networks with balanced excitatory and inhibitory activity
Science 274:1724–1726.
https://doi.org/10.1126/science.274.5293.1724
- PubMed
- Google Scholar
(2011) Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks
Science 334:1569–1573.
https://doi.org/10.1126/science.1211095
- PubMed
- Google Scholar
1. Vogels TP
2. Froemke RC
3. Doyon N
4. Gilson M
5. Haas JS
6. Liu R
7. Maffei A
8. Miller P
9. Wierenga CJ
10. Woodin MA
11. Zenke F
12. Sprekeler H
(2013) Inhibitory synaptic plasticity: spike timing-dependence and putative network function
Frontiers in Neural Circuits 7:119.
https://doi.org/10.3389/fncir.2013.00119
- PubMed
- Google Scholar
1. Vogels TP
2. Abbott LF
(2009) Gating multiple signals through detailed balance of excitation and inhibition in spiking networks
Nature Neuroscience 12:483–491.
https://doi.org/10.1038/nn.2276
- PubMed
- Google Scholar
1. Weber SN
2. Sprekeler H
(2018) Learning place cells, grid cells and invariances with excitatory and inhibitory plasticity
eLife 7:e34560.
https://doi.org/10.7554/eLife.34560
- PubMed
- Google Scholar
1. Wehr M
2. Zador AM
(2003) Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex
Nature 426:442–446.
https://doi.org/10.1038/nature02116
- PubMed
- Google Scholar
Conference
1. Werbos PJ
(1990) Backpropagation through time: what it does and how to do it
Proceedings of the IEEE. pp. 1550–1560.
https://doi.org/10.1109/5.58337
- Google Scholar
1. Whittington JCR
2. Bogacz R
(2019) Theories of error Back-Propagation in the brain
Trends in Cognitive Sciences 23:235–250.
https://doi.org/10.1016/j.tics.2018.12.005
- PubMed
- Google Scholar
(2014) Equalizing excitation-inhibition ratios across visual cortical neurons
Nature 511:596–600.
https://doi.org/10.1038/nature13321
- PubMed
- Google Scholar
(2005) Excitatory cortical neurons form fine-scale functional networks
Nature 433:868–873.
https://doi.org/10.1038/nature03252
- PubMed
- Google Scholar
Preprint
(2018) Functional selectivity and specific connectivity of inhibitory neurons in primary visual cortex
bioRxiv.
https://doi.org/10.1101/294835
- Google Scholar

Decision letter

Stephanie E Palmer

Reviewing Editor; University of Chicago, United States
Richard B Ivry

Senior Editor; University of California, Berkeley, United States

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

Understanding the connectivity patterns observed in the brain and how these connectivity patterns emerge from local, cell-to-cell plasticity is a grand challenge in modern neuroscience. This manuscript describes conditions under which synaptic plasticity can organize excitatory/inhibitory networks in the brain into assemblies in which both kinds of neurons have structured connectivity, as observed in real networks. The work makes predictions about what kinds of plasticity can give rise to this and accounts for recent experimental findings about manipulating inhibitory neurons and, thereby, the stimulus-dependence of their connectivity. It will be of interest to both the experimental and theoretical neuroscience community, and asks and answers a deep question about how the brain self-organizes its detailed connectivity patterns.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "Learning excitatory-inhibitory neuronal assemblies in recurrent networks" for consideration by eLife. Your article has been reviewed by two peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by a Senior Editor. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.

The work detailed here explores model of recurrent cortical networks and shows that synaptic plasticity must be present in both excitatory to inhibitory neurons and vice versa to produce the known E/I assemblies found in cortex. There are some interesting findings about the consequences of assemblies formed in this way. A major claim in the manuscript (that argues for the broad impact of the work) is that this shows for the first time how a local approximation rule can instantiate feedback in a biologically plausible way.

While the reviewers found the work to be solid and interesting, they failed to find that the work was appropriate for eLife, specifically because of other recent papers that show that a biologically plausible alternative to backpropagation can be instantiated in recurrent neural nets, e.g. a paper published here last year by J. Murray, Local online learning in recurrent networks with random feedback. It's understood that the authors were focusing here on the E/I interactions, but in that case it seems that the novelty of the result needs to be somewhat reframed.

The reviewers were also concerned about the exposition in the introduction and some results that could have been added to a few figures, and had questions about why exactly a BCM rule did not work in this model. Those technical concerns along with doubts about the strong novelty claim led to this decision.

Reviewer #1:

The manuscript investigates the situations in which stimulus-specific assemblies can emerge in a recurrent network of excitatory (E) and inhibitory (I, presumed parvalbumin-positive) neurons. The authors combine (1) Hebbian plasticity of I->E synapses that is proportional to the difference between the E neuron's firing rate and a homeostatic target and (2) plasticity of E->I synapses that is proportional to the difference between the total excitatory input to the I neuron and a homeostatic target. These are sufficient to produce E/I assemblies in a network in which only the excitatory recurrence exhibits tuning at the initial condition. While the full implementation of the plasticity rules, derived from gradient descent on an objective function, would rely on nonlocal weight information, local approximations of the rules still lead to the desired results.

Overall the results make sense and represent a new unsupervised method for generating cell assemblies consisting of both excitatory and inhibitory neurons. My main concerns are that the proposed rule ends up predicting a rather nonstandard form of plasticity for certain synapses, and that the results could be fleshed out more.

1) The main text would benefit from greater exposition of the plasticity rule and the distinction between the full expression and the approximation. While the general idea of backpropagation may be familiar to a good number of readers, here it is being used in a nonstandard way (to implement homeostasis), and this should be described more fully, with a few key equations.

Additionally, the point that, for a recurrent network, the proposed rules are only related to gradient descent under the assumption that the network adiabatically follows the stimulus, seems important enough to state in the main text.

2) The paper has a clear and simple message, but not much exploration of that message or elaboration on the results. Figure 2 and Figure 3 do not convey much information, other than the fact that blocking either form of plasticity fails to produce the desired effects. This seems somewhat obvious -- almost by definition one can't have E/I assemblies if E->I or I->E connections are forced to remain random. I would think this point deserves at most one figure, or maybe even just a few panels.

3) The derived plasticity rule for E->I synapses, which requires modulation of I synapses based on a difference from a target value for the excitatory subcomponent of the input current, does not take a typical form for biologically plausible learning rules (which usually operate on firing rates or voltages, for example). The authors should explore and discuss in more depth this assumption. Is there experimental evidence for it? It seems like it might be a difficult quantity to signal to the synapse in order to guide plasticity. The authors note in the discussion that BCM-type rules fail here -- are there other approaches that would work? What about a more local form of plasticity that involves only the excitatory current local to a dendrite, for example?

4) Does the initial structure in excitatory recurrence play a role, or is it just there to match the data?

Reviewer #2:

In this work, the authors simulated a rate-based recurrent network with 512 excitatory and 64 inhibitory neurons. The authors use this model to investigate which forms of synaptic plasticity are needed to reproduce the stimulus-specific interactions observed between pyramidal neurons and parvalbumin-expressing (PV) interneurons in mouse V1. When there is homeostatic synaptic plasticity from both excitatory to inhibitory and reciprocally from inhibitory to excitatory neurons in the simulated networks, they showed that the emergent E/I assemblies are qualitatively similar to those observed in mouse V1, i.e., stronger synapses for neurons responding to similar stimuli. They also identified that synaptic plasticity must be present in both directions (from pyramidal neurons to PV neurons and vice versa) to produce such E/I assemblies. Furthermore, they identified that these E/I assemblies enable the excitatory population in their simulations to show feature-specific suppression. Therefore, the author claimed that they found evidence that these inhibitory circuits do not provide a "blanket of inhibition", but rather a specific, activity-dependent sculpting of the excitatory response. They also claim that the learning rule they developed in this model shows for the first time how a local approximation rule can instantiate feedback alignment in their network, which is a method for achieving an approximation to a backpropagation-like learning rule in realistic neural networks.

1) The authors claim that their synaptic plastic rule implements a recurrent variant of feedback alignment. Namely, "When we compare the weight updates the approximate rules perform to the updates that would occur using the gradient rule, the weight updates of the local approximations align to those of the gradient rules over learning". They also claim that this is the first time feedback alignment is demonstrated in a recurrent network. It seems that the weight replacement in this synaptic plastic rule is uniquely motivated by E/I balance, but the feedback alignment in [Lillicrap et al., 2016] is much more general. Thus, the precise connections between feedback alignment and this work remains a bit unclear.

It would be good if the following things about this major claim of the manuscript could be expanded and/or clarified:

i) In Figure 1—figure supplement 3 (upper, right vs. left), it is surprising that the Pyr->PV knock-out seems to produce a better alignment in PV->Pyr. Comparing the upper right of Figure 1—figure supplement 3 and the bottom figure of Figure 1G, it seems that the Pyr->PV knock-out performs equally well with a local approximation for the output connections of PV interneurons. Is this a special condition in this model that results in the emergence of the overall feedback alignment?

ii) In the feedback alignment paper [Lillicrap et al., 2016], they introduced a "Random Feedback Weights Support": this uses a random matrix B to replace the transpose of the backpropagation weight matrix. Here, the alignment seems to be based on the intuition that "The excitatory input connections onto the interneurons serve as a proxy for the transpose of the output connections," and "the task of balancing excitation by feedback inhibition favours symmetric connection." It seems synaptic plasticity here is mechanistically different; it is only similar to the feedback alignment [Lillicrap et al., 2016] because both reach a final balanced state. Please clarify how the results here are interpreted as an instantiation of feedback alignment – if it is simply that the end state is similar or if the mechanism is thought to be more deeply connected.

iii) The feedback alignment [Lillicrap et al., 2016] works when the weight matrix has its entries near zero (e^TWBe>0). Are there any analogous conditions for the synaptic plastic rule to succeed?

iv) In the Appendix, the local approximation rule is developed using a 0th-order truncation of Equations 15a and 15b. Is it noted that "If synapses are sufficiently weak.…, this approximation can be substituted into Equation 15a and yields an equation that resembles a backpropagation rule in a feedforward network (E -> I -> E) with one hidden layer -- the interneurons." It would be helpful if the authors can discuss how this learning rule works in a general recurrent network, or if it will work for any network with sufficiently weak synapses.

v) This synaptic plasticity rule seems to be closely related to another local approximation of backpropagation in recurrent neural network: e-prop in (Bellec et al., 2020, https://www.nature.com/articles/s41467-020-17236-y) and broadcast alignment (Nøkland, 2016, Samadi et al., 2017). These previous works do not consider E/I balance in their approximations, but is E/I balance necessary for successful local approximation to these rules?

2) In the Discussion, it reads as if the BCM rule cannot apply to this recurrent network because of the limited number of interneurons in the simulation ("parts of stimulus space are not represented by any interneurons"). Is this a limitation of the size of the model? Would scaling up the simulation change how applicable the BCM learning rule is? It would be helpful if the authors offer a more detailed discussion on why Hebbian forms of plasticity in interneurons fail to produce stimulus specificity.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Learning excitatory-inhibitory neuronal assemblies in recurrent networks" for consideration by eLife. Your article has been reviewed by two peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Richard Ivry as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

We would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). Specifically, we are asking editors to accept without delay manuscripts, like yours, that they judge can stand as eLife papers without additional data, even if they feel that they would make the manuscript stronger. Thus the revisions requested below only address clarity and presentation.

Summary:

The manuscript describes conditions under which synaptic plasticity can organize excitatory/inhibitory networks into assemblies in which both neurons have structured connectivity. The work makes predictions about what kinds of plasticity can give rise to this and accounts for recent experimental findings about manipulating inhibitory neurons and the stimulus-dependence of their connectivity.

While recurrent networks in which connections between excitatory (E) neurons are structured into neural "assemblies" are a classic model for the cortex (e.g. the Hopfield model), inhibitory (I) neurons are often assumed to be unstructured in computational models. This simplification is at odds with the observation of E/I connectivity that is organized with respect to stimulus preference and the results of experiments in which activity of I neurons are perturbed. In brain regions spatially organized according to stimulus preference this may be a consequence of local connectivity, but in regions like mouse V1 that lack an obvious topography, it may arise from experience-dependent synaptic plasticity.

The manuscript investigates the situations in which stimulus-specific assemblies can emerge through synaptic plasticity in a recurrent network of E and I (presumed parvalbumin-positive) neurons. The authors combine (1) Hebbian plasticity of I->E synapses that is proportional to the difference between the E neuron's firing rate and a homeostatic target and (2) plasticity of E->I synapses that is proportional to the difference between the total excitatory input to the I neuron and a homeostatic target. These are sufficient to produce E/I assemblies in a network in which only the excitatory recurrence exhibits tuning at the initial condition. While the full implementation of the plasticity rules, derived from gradient descent on an objective function, would rely on nonlocal weight information, local approximations of the rules still lead to the desired results.

The manuscript makes predictions about the results of blocking plasticity of E->I or I->E synapses as well as accounting for the results of experiments in which activating a pyramidal neuron suppresses similarly tuned neurons through recurrent inhibition.

An interesting prediction of the analysis, that is derived through the approximation to the gradient-based weight update, is that synaptic plasticity rules depend on the deviation of recurrent excitatory input current to a neuron from a target value. This quantity is different from those often used in computational models of synaptic plasticity, such as firing rates or voltages. Experiments targeting this quantity and its influence on the results of synaptic plasticity protocols would be an interesting direction for future study.

Essential revisions:

The modifications the authors have made have improved the manuscript. Addressing the following points will further enhance the clarity of the presentation, and will make the work suitable for publication in eLife.

1) Could the authors please expand on the negative result about developing selectivity in PV neurons through quenched random connections? Would it be possible to adjust the parameters of the model, such as the weight distribution or number of connections onto PV neurons, so that they would exhibit enough selectivity?

2) Relatedly, the text around Figure 3D says that, "Because of the poor stimulus tuning of the interneurons, output plasticity cannot generate stimulus-specific inhibitory inputs to the Pyr neurons (Figure 3D)." But it looks like there is a definite stimulus-specific inhibitory input that emerges. The authors should clarify what they mean.

3) It would be good if the Abstract could be revised to be accessible to a broader audience of readers.

https://doi.org/10.7554/eLife.59715.sa1

Author response

[Editors’ note: The authors appealed the original decision. What follows is the authors’ response to the first round of review.]

Reviewer #1:

The manuscript investigates the situations in which stimulus-specific assemblies can emerge in a recurrent network of excitatory (E) and inhibitory (I, presumed parvalbumin-positive) neurons. The authors combine (1) Hebbian plasticity of I->E synapses that is proportional to the difference between the E neuron's firing rate and a homeostatic target and (2) plasticity of E->I synapses that is proportional to the difference between the total excitatory input to the I neuron and a homeostatic target. These are sufficient to produce E/I assemblies in a network in which only the excitatory recurrence exhibits tuning at the initial condition. While the full implementation of the plasticity rules, derived from gradient descent on an objective function, would rely on nonlocal weight information, local approximations of the rules still lead to the desired results.

Overall the results make sense and represent a new unsupervised method for generating cell assemblies consisting of both excitatory and inhibitory neurons. My main concerns are that the proposed rule ends up predicting a rather nonstandard form of plasticity for certain synapses, and that the results could be fleshed out more.

1) The main text would benefit from greater exposition of the plasticity rule and the distinction between the full expression and the approximation. While the general idea of backpropagation may be familiar to a good number of readers, here it is being used in a nonstandard way (to implement homeostasis), and this should be described more fully, with a few key equations.

Additionally, the point that, for a recurrent network, the proposed rules are only related to gradient descent under the assumption that the network adiabatically follows the stimulus, seems important enough to state in the main text.

Thanks, that's a good point. We modified the relevant portion of the main text as follows:

“[…] To that end, we derive synaptic plasticity rules for excitatory input and inhibitory output connections of PV interneurons that are homeostatic for the excitatory population (see Materials and methods). A stimulus-specific homeostatic control can be seen as a "trivial" supervised learning task, in which the objective is that all pyramidal neurons should learn to fire at a given target rate ρ0 for all stimuli. Hence, a gradient-based optimisation would effectively require a backpropagation of error [Rumelhart et al., 1985] through time [BPTT; Werbos, 1990].

Because backpropagation rules rely on non-local information that might not be available to the respective synapses, their biological plausibility is currently debated [Lillicrap et al., 2020, Sacramento et al., 2018, Guerguiev et al., 2017, Whittington and Bogacz, 2019, Bellec et al., 2020]. However, a local approximation of the full BPTT update can be obtained under the following assumptions: First, we assume that the sensory input to the network changes on a time scale that is slower than the intrinsic time scales in the network. This eliminates the necessity of backpropagating information through time, albeit still through the synapses in the network. This assumption results in what we call the “gradient-based” rules (Equation 15 in the Appendix), which are spatially non-local. Second, we assume that synaptic interactions in the network are sufficiently weak that higher-order synaptic interactions can be neglected. Third and finally, we assume that over the course of learning, the Pyr→PV connections and the PV→Pyr connections become positively correlated [Znamenskiy et al., 2018], such that we can replace PV->Pyr synapses by the reciprocal Pyr->PV synapse in the Pyr->PV learning rule, without rotating the update too far from the true gradient (see Appendixs)."

We also added the learning rules to the main text.

2) The paper has a clear and simple message, but not much exploration of that message or elaboration on the results. Figure 2 and Figure 3 do not convey much information, other than the fact that blocking either form of plasticity fails to produce the desired effects. This seems somewhat obvious -- almost by definition one can't have E/I assemblies if E->I or I->E connections are forced to remain random. I would think this point deserves at most one figure, or maybe even just a few panels.

We appreciate that the result that both forms of plasticity are necessary may feel somewhat obvious. However, it may not be as obvious as it appears, because the incoming synapses onto INs follow a long-tailed distribution, like many other synapse types. Randomly sampling from such a distribution could in principle generate sufficient stimulus selectivity to render learning in the E->I connections superfluous (see Litwin-Kumar et al., 2017). That’s why we made sure to initialize the E->I weights such that they show a similar variability as in the data. We now comment on this aspect in the Results section:

"Having shown that homeostatic plasticity acting on both input and output synapses of interneurons are sufficient to learn E/I assemblies, we now turn to the question of whether both are necessary. To this end, we perform "knock-out" experiments, in which we selectively block synaptic plasticity in either of the synapses. The motivation for these experiments is the observation that the incoming PV synapses follow a long-tailed distribution (Znamenskiy et al., 2018). This could provide a sufficient stimulus selectivity in the PV population for PV->Pyr plasticity alone to achieve a satisfactory E/I balance. A similar reasoning holds for static, but long-tailed outgoing PV synapses. This intuition is supported by result of Litwin-Kumar et al., (2017) that in a population of neurons analogous to our interneurons, the dimensionality of responses in that population can be high for static input synapses, when those are log-normally distributed."

Secondly, we tried to write a manuscript for both fellow modelers (how to self-organize an E/I assembly?) and to our experimental colleagues (what conclusions can we draw from the Znamenskiy data?). In electrophysiological studies, the plasticity of incoming and outgoing synapses of INs both have been studied independently. The insight that those two forms of plasticity should act in synergy is something that we wanted to emphasize, because it could be studied in parallel in paired recordings. Hence the two figures. Looks like we got only modelers as reviewers. Along these lines, we added a short paragraph to the Discussion:

“Both Pyr->PV and PV->Pyr plasticity have been studied in slice (for reviews, see, Kullmann et al., 2007, Vogels et al., 2013), but mostly in isolation. The idea that the two forms of plasticity should act in synergy suggests that it may be interesting to study both forms in the same system, e.g., in reciprocally connected Pyr-PV pairs.”

3) The derived plasticity rule for E->I synapses, which requires modulation of I synapses based on a difference from a target value for the excitatory subcomponent of the input current, does not take a typical form for biologically plausible learning rules (which usually operate on firing rates or voltages, for example). The authors should explore and discuss in more depth this assumption. Is there experimental evidence for it? It seems like it might be a difficult quantity to signal to the synapse in order to guide plasticity. The authors note in the discussion that BCM-type rules fail here -- are there other approaches that would work? What about a more local form of plasticity that involves only the excitatory current local to a dendrite, for example?

We agree that the rule we propose for E->I synapses warrants a more extensive discussion regarding its potential biological implementation. We have added the following paragraph to the manuscript:

"A cellular implementation of such a plasticity rule would require the following ingredients: (i) a signal that reflects the cell-wide excitatory current (ii) a mechanism that changes Pyr->PV synapses in response to variations in this signal. For the detection of excitatory inputs, postsynaptic sodium or calcium concentrations are natural candidates. Due to the lack of spines in PV dendrites, both are expected to diffuse more broadly in the dendritic arbor than in spiny neurons [Hu et al., 2014, Kullmann and Lamsa, 2007], and may thus provide a signal for overall dendritic excitatory currents. Depending on how excitatory inputs are distributed on PV interneuron dendrites [Larkum and Nevian, 2008, Jia et al., 2010, Grienberger et al., 2015], the integration of the excitatory currents may not need to be cell-wide -- which could limit the temporal resolution of the plasticity --, but could be local, e.g. to a dendrite, if local excitatory input is a sufficient proxy for the global input. Notably, in PV interneurons, NMDA receptors are enriched in excitatory feedback relative to feedforward connections [LeRoux et al., 2013], suggesting those two sources of excitation are differentially treated on the postsynaptic side.

As for many other excitatory synapses [Sjöström et al., 2008], postsynaptic calcium is likely a key factor also for the plasticity of excitatory input synapses onto interneurons. Blocking NMDA receptors interferes with Hebbian long-term plasticity in some of these synapses [Kullmann and Lamsa, 2007], as does a block of excitatory input [LeRoux et al., 2013]. Furthermore, NMDAR-dependent plasticity in Pyr->PV synapses is expressed postsynaptically and seems to require presynaptic activation [Kullmann and Lamsa, 2007]. In summary, we believe that there are no conceptual issues that would rule out an implementation of the suggested plasticity rule for excitatory inputs onto PV interneurons.”

Concerning other potential types of plasticity, we certainly do not expect that the suggested pair of rules is the only one that will work. The above paragraph is now followed by:

“We also expect that the rules we suggest here are only one set of many that can establish E/I assemblies. Given that the role of the input plasticity in the interneurons is the formation of a stimulus specificity, it is tempting to assume that this could equally well be achieved by classical forms of plasticity like the Bienenstock-Cooper-Munro (BCM) rule [Bienenstock et al., 1982], which is commonly used in models of receptive field formation. However, in our hands, the combination of BCM plasticity in Pyr->PV synapses with homeostatic inhibitory plasticity in the \ItoE synapses showed complex dynamics, an analysis of which is beyond the scope of this article. In particular, this combination of rules often did not converge to a steady state, probably for the following reason. BCM rules tend to […].

We suspect that this instability can also arise for other Hebbian forms of plasticity in interneuron input synapses when they are combined with homeostatic inhibitory plasticity [Vogels et al., 2011] in their output synapses. The underlying reason is that for convergence, the two forms of plasticity need to work synergistically towards the same goal, i.e., the same steady state. For two arbitrary synaptic plasticity rules acting in different sets of synapses, it is likely that they aim for two different overall network configurations. Such competition can easily result in latching dynamics with a continuing turn-over of transiently stable states, in which the form of plasticity that acts more quickly gets to reach its goal transiently, only to be undermined by the other one later [Clopath et al., 2016].”

4) Does the initial structure in excitatory recurrence play a role, or is it just there to match the data?

For the results of Figure 4, the structure of excitatory recurrence is essential, because similarly tuned Pyr neurons should excite each other (absent the E-I assemblies). Without that structure in the Pyr->Pyr connections, the “paradoxical” inhibitory effect we report would not be paradoxical at all. For the results of Figure 1, Figure 2, Figure 3, we primarily included them for consistency, because it's known that this structure is present in V1, and because it's good to see that their presence doesn't change the results. It plays a role only insofar as it permits and reinforces stimulus selectivity in pyramidal neurons. If those synapses were unstructured (and strong), it could disrupt the Pyr selectivity, and there would be nothing to guide the formation of E/I assemblies. We have added the following sentence to the beginning of the Results section:

“[…] Note that the Pyr->Pyr connections only play a decisive role for the results in Figure 4, but are present in all simulations for consistency. […]”

Reviewer #2:

In this work, the authors simulated a rate-based recurrent network with 512 excitatory and 64 inhibitory neurons. The authors use this model to investigate which forms of synaptic plasticity are needed to reproduce the stimulus-specific interactions observed between pyramidal neurons and parvalbumin-expressing (PV) interneurons in mouse V1. When there is homeostatic synaptic plasticity from both excitatory to inhibitory and reciprocally from inhibitory to excitatory neurons in the simulated networks, they showed that the emergent E/I assemblies are qualitatively similar to those observed in mouse V1, i.e., stronger synapses for neurons responding to similar stimuli. They also identified that synaptic plasticity must be present in both directions (from pyramidal neurons to PV neurons and vice versa) to produce such E/I assemblies. Furthermore, they identified that these E/I assemblies enable the excitatory population in their simulations to show feature-specific suppression. Therefore, the author claimed that they found evidence that these inhibitory circuits do not provide a "blanket of inhibition", but rather a specific, activity-dependent sculpting of the excitatory response. They also claim that the learning rule they developed in this model shows for the first time how a local approximation rule can instantiate feedback alignment in their network, which is a method for achieving an approximation to a backpropagation-like learning rule in realistic neural networks.

We thank you for your thorough evaluation of the role of feedback alignment (FA) in our model. While we will attempt to address them point-by-point below, we feel that we may have misled this reviewer regarding the focus of the article.

For us, the core novelty of this work lies in elucidating potential mechanisms of experimentally observed E/I neuronal assemblies in mouse V1, and furthermore in proposing plasticity rules that can achieve such E/I assemblies. That they do so via a

mechanism akin to feedback alignment is mentioned relatively briefly in the manuscript, and is merely offered as a mechanistic explanation for how inhibitory currents are ultimately balanced with excitation. We are fully aware of the fact that the suggested rules are by no means a local approximation of the full BPTT problem in RNNs. We rephrased the paper and hope that the emphasis of the paper is now clearer.

1) The authors claim that their synaptic plastic rule implements a recurrent variant of feedback alignment. Namely, "When we compare the weight updates the approximate rules perform to the updates that would occur using the gradient rule, the weight updates of the local approximations align to those of the gradient rules over learning". They also claim that this is the first time feedback alignment is demonstrated in a recurrent network. It seems that the weight replacement in this synaptic plastic rule is uniquely motivated by E/I balance, but the feedback alignment in [Lillicrap et al., 2016] is much more general. Thus, the precise connections between feedback alignment and this work remains a bit unclear.

We had hoped that our claims in the manuscript were phrased sufficiently carefully, and regret that the reviewer was led to believe that our goal was to provide a general solution to biological backprop in recurrent networks. Of course, the problem we are tackling is not the full backprop problem, and we do not expect that the approximation holds for general tasks. It clearly won't, given that it effectively relies on a truncation after two time steps and makes a stationarity assumption. Still, we felt that it would have been a lost opportunity not to discuss the relation to feedback alignment, because any approximation warrants a justification, and for the replacement of I->E weights by E->I weights, feedback alignment readily provides one. We now discuss the assumptions underlying the local approximation more extensively in the main paper (see reply to reviewer 1, comment 1).

We also added a discussion to the section in the Appendix, where the local approximations are derived:

“Overall, the local approximation of the learning rule relies on three assumptions: Slowly varying inputs, weak synaptic weights and alignment of input and output synapses of the interneurons. These assumptions clearly limit the applicability of the learning rules for other learning tasks. In particular, the learning rules will not allow the network to learn temporal sequences.”

It would be good if the following things about this major claim of the manuscript could be expanded and/or clarified:

i) In Figure 1—figure supplement 3 (upper, right vs. left), it is surprising that the Pyr->PV knock-out seems to produce a better alignment in PV->Pyr. Comparing the upper right of Figure 1—figure supplement 3 and the bottom figure of Figure 1G, it seems that the Pyr->PV knock-out performs equally well with a local approximation for the output connections of PV interneurons. Is this a special condition in this model that results in the emergence of the overall feedback alignment?

The 0-th order approximation of PV->Pyr plasticity is, by itself, relatively good at following the full gradient for those synapses, because PV->Pyr synapses have virtually unmediated control over Pyr neuron activity. When Py->PV plasticity is also present, we believe that the higher variance in angle to the gradient (for PV->Pyr updates) may be due to perturbations introduced by the Pyr->PV updates. Each update to one weight matrix changes the gradient for the other, but this is ultimately what brings them into alignment with one another. Because this is a very technical point, we prefer not to discuss this at length in the manuscript. The more important point is conveyed in the two bottom figures, which demonstrate that the gradients on the Pyr->PV synapses only align within 90 degrees when both synapse types are plastic.

ii) In the feedback alignment paper [Lillicrap et al., 2016], they introduced a "Random Feedback Weights Support": this uses a random matrix B to replace the transpose of the backpropagation weight matrix. Here, the alignment seems to be based on the intuition that "The excitatory input connections onto the interneurons serve as a proxy for the transpose of the output connections," and "the task of balancing excitation by feedback inhibition favours symmetric connection." It seems synaptic plasticity here is mechanistically different; it is only similar to the feedback alignment [Lillicrap et al., 2016] because both reach a final balanced state. Please clarify how the results here are to interpreted as an instantiation of feedback alignment – if it is simply that the end state is similar or if the mechanism is thought to be more deeply connected.

We believe that the mechanisms are indeed more deeply connected, as supported by the fact that the gradients align early on during learning. We added an extended discussion to the Appendix:

“In feedback alignment, the matrix that backpropagates the errors is replaced by a random matrix B. Here, we instead use the feedforward weights in the layer below. Similar to the extension to feedback alignment of Akrout et al., [2019], those weights are themselves plastic. However, we believe that the underlying mechanism of feedback alignment still holds. The representation in the hidden layer (the interneurons) changes as if the weights to the output layer (the Pyr neurons) were equal to the weights they are replaced with (here, the input weights to the PV neurons). To exploit this representation, the weights to the output layer then align to the replacement weights, justifying the replacement post-hoc (Figure 1G).”

iii) The feedback alignment [Lillicrap et al., 2016] works when the weight matrix has its entries near zero (e^TWBe>0). Are there any analogous conditions for the synaptic plastic rule to succeed?

Yes, the condition is very similar. We have added a corresponding discussion to the Appendix:

“Note that the condition for feedback alignment to provide an update in the appropriate direction (e^T B^T W e>0, where e denotes the error, W the weights in the second layer, and B the random feedback matrix) reduces to the condition that Wei W_ie is positive definite (assuming the errors are full rank).

One way of assuring this is a sufficiently positive diagonal of this matrix product, i.e., a sufficiently high correlation between the incoming and outgoing synapses of the interneurons. A positive correlation of these weights is one of the observations of Znamenskiy et al., 2018 and also a result of learning in our model.

While such a positive correlation is not necessarily present for all learning tasks or network models, we speculate that it will be for the task of learning an E/I balance in a Dalean network.”

iv) In the Supplementary material, the local approximation rule is developed using a 0th-order truncation of Equations 15a and 15b. Is it noted that "If synapses are sufficiently weak.…, this approximation can be substituted into Equation 15a and yields an equation that resembles a backpropagation rule in a feedforward network (E -> I -> E) with one hidden layer -- the interneurons." It would be helpful if the authors can discuss how this learning rule works in a general recurrent network, or if it will work for any network with sufficiently weak synapses.

We now discuss the assumptions and their consequences more extensively, see reply to reviewer 1, comment 1.

v) This synaptic plasticity rule seems to be closely related to another local approximation of backpropagation in recurrent neural network: e-prop in (Bellec et al., 2020, https://www.nature.com/articles/s41467-020-17236-y) and broadcast alignment (Nøkland, 2016, Samadi et al., 2017). These previous works do not consider E/I balance in their approximations, but is E/I balance necessary for successful local approximation to these rules?

We are not sure if we fully understand the comment. We do not expect that E/I balance is necessary for other biologically plausible approximations of BPTT. We merely suggest that for the task of learning E/I balance, the presented local approximation is valid.

2) In the Discussion, it reads as if the BCM rule cannot apply to this recurrent network because of the limited number of interneurons in the simulation ("parts of stimulus space are not represented by any interneurons"). Is this a limitation of the size of the model? Would scaling up the simulation change how applicable the BCM learning rule is? It would be helpful if the authors offer a more detailed discussion on why Hebbian forms of plasticity in interneurons fail to produce stimulus specificity.

Increasing the size of the model would help only if it would increase the redundancy in the Pyr population response. Otherwise, the problem can only be solved by changing the E to I ratio.

We feel that an exhaustive discussion of the dynamics of BCM in our network is beyond the scope of the paper, particularly because BCM comes in a broad variety (weight normalisation, weight limits, exact form of the sliding threshold?) and the exact behavior depends on various parameter choices. Similarly, we preferred to limit the discussion of other Hebbian rules, because it would be somewhat arbitrary which rules to discuss. Instead we added the following more abstract arguments to the Discussion section:

“We expect that the rules we suggest here are only one set of many that can establish E/I assemblies. Given that the role of the input plasticity in the interneurons is the formation of a stimulus specificity, it is tempting to assume that this could equally well be achieved by classical forms of plasticity like the Bienenstock-Cooper-Munro (BCM) rule {Bienenstock82}, which is commonly used in models of receptive field formation. However, in our hands, the combination of BCM plasticity in Pyr->PV synapses with homeostatic inhibitory plasticity in the PV->Pyr synapses showed complex dynamics, an analysis of which is beyond the scope of this article. In particular, this combination of rules often did not converge to a steady state, probably for the following reason. […]

We suspect that this instability can also arise for other Hebbian forms of plasticity in interneuron input synapses when they are combined with homeostatic inhibitory plasticity (Vogels et al., 2011) in their output synapses. The underlying reason is that for convergence, the two forms of plasticity need to work synergistically towards the same goal, i.e., the same steady state. For two arbitrary synaptic plasticity rules acting in different sets of synapses, it is likely that they aim for two different overall network configurations. Such competition can easily result in dynamics with a continuing turn-over of transiently stable states, in which the form of plasticity that acts more quickly gets to reach its goal transiently, only to be undermined by the other one later.”

[Editors’ note: what follows is the authors’ response to the second round of review.]

Essential revisions:

The modifications the authors have made have improved the manuscript. Addressing the following points will further enhance the clarity of the presentation, and will make the work suitable for publication in eLife.

1) Could the authors please expand on the negative result about developing selectivity in PV neurons through quenched random connections? Would it be possible to adjust the parameters of the model, such as the weight distribution or number of connections onto PV neurons, so that they would exhibit enough selectivity?

The reviewers raised an interesting question, which motivated us to investigate if sampling PV input weights from a distribution with an even longer tail may affect these results. In brief, the broader distribution can indeed increase the selectivity in the PV interneurons, but it is not sufficient to account for the correlation structure in the synaptic weights observed by Znamenskiy et al. The underlying reason is that the selectivity of the interneurons is then controlled by a very small number of large excitatory input weights, which are unlikely to be sampled in an experiment. We have added a new figure supplement and corresponding text to the manuscript (see below).

We would like to emphasize that our original choice of the weight distribution is motivated by observations in the mouse cortex (Song et al., 2005, Loewenstein et al., 2011), covering about two orders of magnitude. Similarly, the connection probability of 60% we used is in line mouse V1 connectivity (Znamenskiy et al., 2018). We do not exclude the possibility that the parameters in our model could in principle be fine-tuned to produce a measurable correlation between PV input and output synapses. However the underlying network model would probably not be consistent with observations from mouse V1.

“[…] A particularly strong input connection will cause the postsynaptic interneuron to prefer similar stimuli to the presynaptic Pyr. Because of the resulting correlated activity, the Hebbian nature of the output plasticity potentiates inhibitory weights for such cell pairs that are reciprocally connected. This tendency of strong input synapses to generate a strong corresponding output synapse is reflected in a positive correlation between output synapses and response similarity (Figure 3E, Figure 3—figure supplement 1A), despite the fact that input synapses remain random.

This effect further increases when input synapses are drawn from a distribution with an even heavier tail, beyond what is observed in mouse V1 [Znamenskiy et al., 2018] (Figure 3—figure supplement 2A). In this case, the stimulus tuning of the interneurons is dominated by a small number of very large synapses. The resulting higher selectivity of the interneurons (Figure 3—figure supplement 2B) allows a better co-tuning of excitation and inhibition in Pyr neurons (Figure 3—figure supplement 2C), in line with theoretical arguments for sparse connectivity [Litwin-Kumar et al., 2017]. However, the dominance of a small number of large synapses also makes it unlikely that those synapses are observed in an experiment in which a finite number of synapses is sampled. As a result, a heavier tail does not yield the correlation of reciprocal in- and output synapses observed by Znamenskiy et al., [2018] (Figure 3—figure supplement 2D,E), although it increases the probability of observing correlations between input synapses and response similarity when weak synapses are discarded. See Appendix for a more extensive discussion.”

2) Relatedly, the text around Figure 3D says that, "Because of the poor stimulus tuning of the interneurons, output plasticity cannot generate stimulus-specific inhibitory inputs to the Pyr neurons (Figure 3D)." But it looks like there is a definite stimulus-specific inhibitory input that emerges. The authors should clarify what they mean.

Thank you for pointing this out. We agree that this was not clear in the text and have extended the paragraph:

“Because of the poor stimulus tuning of the interneurons, output plasticity cannot generate stimulus-specific inhibitory inputs to the Pyr neurons (Figure 3D). Instead, they essentially receive a tonic, unspecific background inhibition that is weakly modulated by the stimulus (Figure 1—figure supplement 2B). This weak modulation is indeed correlated with the excitatory inputs, but the overall similarity between excitation and inhibition remains low (Figure 1—figure supplement 2C).”

3) It would be good if the Abstract could be revised to be accessible to a broader audience of readers.

We appreciate the feedback on the current Abstract and agree that particularly the first few sentences needed to be refined. We have revised the Abstract to convey the problem setting and our main findings to a broader audience. You can find the revised Abstract below:

“In contrast to sensory circuits with feature topography, neurons in the mouse primary visual cortex (V1) are not arranged according to the stimulus features they respond to. Yet, synapses between excitatory pyramidal neurons and inhibitory parvalbumin-expressing (PV) interneurons tend to be stronger for neurons that respond to similar stimulus features. The presence of such excitatory-inhibitory (E/I) neuronal assemblies indicates a stimulus-specific form of feedback inhibition despite the absence of feature topography. Here, we show that activity-dependent synaptic plasticity on input and output synapses of PV interneurons generates a circuit structure that is consistent with mouse V1. Using a computational model, we show that both forms of plasticity must act in synergy to form the observed E/I assemblies. Once established, these assemblies produce a stimulus-specific competition between pyramidal neurons. Our model suggests that activity-dependent plasticity can refine inhibitory circuits to actively shape cortical computations.”

https://doi.org/10.7554/eLife.59715.sa2

Article and author information

Author details

Owen Mackwood
1. Bernstein Center for Computational Neuroscience Berlin, Berlin, Germany
2. Department for Electrical Engineering and Computer Science, Technische Universität Berlin, Berlin, Germany
Contribution
Conceptualization, Data curation, Software, Formal analysis, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-8569-6614
Laura B Naumann
1. Bernstein Center for Computational Neuroscience Berlin, Berlin, Germany
2. Department for Electrical Engineering and Computer Science, Technische Universität Berlin, Berlin, Germany
Contribution
Writing - original draft, Project administration, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-7919-7349
Henning Sprekeler
1. Bernstein Center for Computational Neuroscience Berlin, Berlin, Germany
2. Department for Electrical Engineering and Computer Science, Technische Universität Berlin, Berlin, Germany
Contribution
Conceptualization, Resources, Formal analysis, Supervision, Funding acquisition, Writing - original draft, Project administration, Writing - review and editing

For correspondence
h.sprekeler@tu-berlin.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-0690-3553

Funding

Bundesministerium für Bildung und Forschung (FKZ 01GQ1201)

Owen Mackwood
Henning Sprekeler

Deutsche Forschungsgemeinschaft (FOR 2143)

Owen Mackwood
Henning Sprekeler

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Joram Keijser for helpful discussions that inspired parts of this work. He, along with Denis Alevi, Loreen Hertäg and Robert T Lange also provided careful proof-reading of the manuscript. This project was funded by the German Federal Ministry for Science and Education through a Bernstein Award (BMBF, FKZ 01GQ1201) and by the German Research Foundation (DFG, collaborative research centre FOR 2143).

Senior Editor

Richard B Ivry, University of California, Berkeley, United States

Reviewing Editor

Stephanie E Palmer, University of Chicago, United States

Version history

Received: June 5, 2020
Accepted: March 3, 2021
Version of Record published: April 26, 2021 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

3,376

Page views
379

Downloads
11

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Owen Mackwood
Laura B Naumann
Henning Sprekeler

(2021)

Learning excitatory-inhibitory neuronal assemblies in recurrent networks

eLife 10:e59715.

https://doi.org/10.7554/eLife.59715

Share this article

Cite this article

Homeostatic plasticity in input and output synapses of interneurons drives the formation of excitatory-inhibitory (E/I) assemblies.

Knock-out (KO) of plasticity in parvalbumin-expressing (PV) interneuron output connections prevents inhibitory co-tuning.

Plasticity of parvalbumin-expressing (PV) interneuron input connections is required for inhibitory stimulus selectivity and current co-tuning.

Single-neuron perturbations suppress responses of similarly tuned neurons.

Model parameters.

Author details

Owen Mackwood

Contribution

Competing interests

Laura B Naumann

Contribution

Competing interests

Henning Sprekeler

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading