Figures and data in Proofreading through spatial gradients

Figures
Tables
Additional files

19 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

Error correction schemes that operate by delaying product formation.

(a) The traditional proofreading scheme with multiple biochemically distinct intermediates, transitions between which are typically accompanied by energy–consuming reactions. The T-cell activation mechanism with successive phosphorylation events is used for demonstration (McKeithan, 1995; Cui and Mehta, 2018). (b) The spatial proofreading scheme where the delay between binding and catalysis is created by constraining these events to distinct physical locations. The wavy arrows stand for the diffusive motion of the complex. Binding events primarily take place on the length scale $λ_{_{S}}$ of substrate localization.

Figure 2

Download asset Open asset

Dependence of fidelity on the diffusion time scale in the limit of very high substrate localization.

Individual curves were made for different choices of $k_{off}^{W}$ (varied in the $[10 - 100] k_{off}^{R}$ range). $τ_{off}^{R} = 1 / k_{off}^{R}$ is the unbinding time scale of right substrates, kept fixed in the study. Fidelity values corresponding to integer degrees of proofreading in a traditional sense ( $η / η_{eq} = η_{eq}^{n}$ , $n = 1, 2, 3, \dots$ ) are marked as circles. Dominant processes in the two limiting regimes are highlighted in red in the schematics shown as insets.

Figure 3

Download asset Open asset

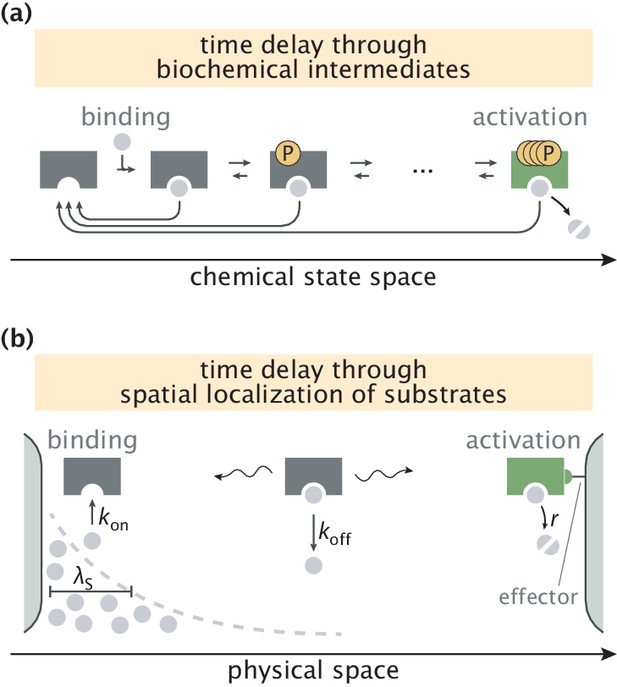
Speed–fidelity trade-off and consequences of having weak substrate gradients.

(a) Speed and fidelity evaluated for sampled values of the diffusion time scale ( $τ_{D}$ ) and substrate localization length scale ( $λ_{_{S}}$ ). Here, $v_{eq} \sim 1 / k_{off}^{R}$ is the speed in the equilibrium limit of a uniform substrate profile ( $λ_{_{S}} \to \infty$ ). The red line corresponds to the Pareto-optimal front and is reached in the high substrate localization limit. The example speed–fidelity trade-off illustrated through the black dotted curve is obtained for $τ_{D} \approx 20 τ_{off}^{R}$ . (b) Density profiles of wrong (EW) and right (ER) complexes in three qualitatively different performance regimes. The normalization factor $ρ_{_{ES}}^{eq}$ corresponds to the equilibrium complex densities. (c) Fidelity as a function of diffusion time scale for different choices of $λ_{_{S}}$ (varied in the $[0.04, 0.4] L$ range). The dashed line corresponds to the ideal substrate localization limit ( $λ_{_{S}} \to 0$ ). Inset: Fidelity as a function of $L / λ_{_{S}}$ for a fixed $τ_{D}$ . Shaded area indicates the range where the bulk of fidelity enhancement takes place. Equilibrium fidelity $η_{eq} = 10$ was used in generating all the panels.

Figure 4

Download asset Open asset

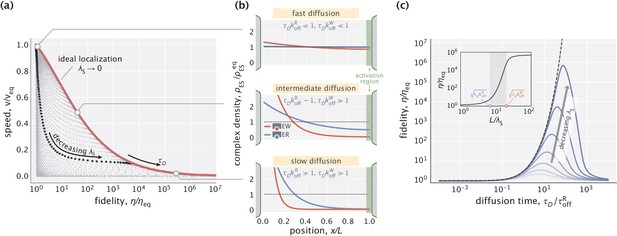
Power–fidelity relationship when tuning the effective driving force $Δ μ$ for different choices of the diffusion time scale $τ_{D}$ .

$J_{b i n d} = k_{o n} ρ_{E} \int ρ_{S} (x) d x$ is the integrated rate of substrate binding. The red line indicates the large dissipation limit of fidelity given by Equation 5. The circles indicate the $Δ μ$ range specified in Equation 11 for different $τ_{D}$ choices. For sufficiently large $τ_{D}$ values, the cost per binding event approaches $β \sqrt{η_{eq}}$ at the end of this range (see Appendix 2.1 for details). In making this plot, $η_{eq} = 10$ was used.

Figure 5

Download asset Open asset

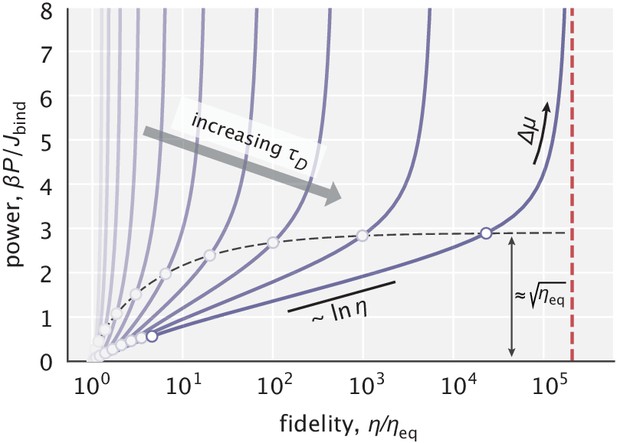
Proofreading based on substrate gradients formed by spatially separated kinases and phosphatases.

(a) The active form $S^{*}$ of many proteins exhibits gradients because kinases that phosphorylate $S$ are anchored to a membrane while phosphatases can diffuse in the cytoplasm (Kholodenko, 2006). An enzyme can exploit the resulting spatial gradient for proofreading. (b) At low enzyme activity (i.e. low $k_{on} ρ_{_{E}}$ ), the gradient of $S^{*}$ is successfully maintained, allowing for proofreading. The upper dashed line corresponds to the peak fidelity when the substrate profile is exponential. At high enzyme activity (large $k_{on} ρ_{_{E}}$ ), the dephosphorylation with rate $k_{p} = 5$ s^-1 is no longer sufficient to maintain the gradient and proofreading is lost. (c) Profiles of right substrates for different choices of enzyme activity. Numbers indicate $k_{on} ρ_{_{E}}$ in s^-1 units. The black line shows an exponential substrate profile with a length scale $λ_{_{S}} = \sqrt{D / k_{p}} \sim 0.5$ μm.

Appendix 1—figure 1

Download asset Open asset

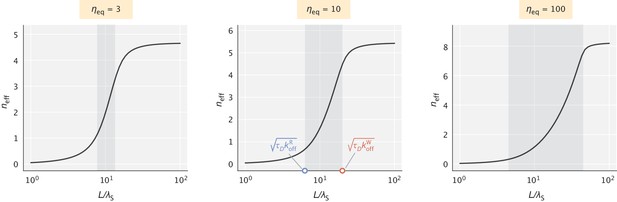
The effective number of proofreading realizations ( $n_{eff}$ ) as a function of $L / λ_{_{S}}$ .

The shaded region represents the range of $L / λ_{_{S}}$ values set by the key dimensionless numbers $\sqrt{τ_{D} k_{off}^{R}}$ and $\sqrt{τ_{D} k_{off}^{W}}$ . $τ_{D}$ values chosen for the demonstration were 60, 40, and 20 (in $1 / k_{off}^{R}$ units) for the three different choices of $η_{eq}$ , respectively.

Appendix 1—figure 2

Download asset Open asset

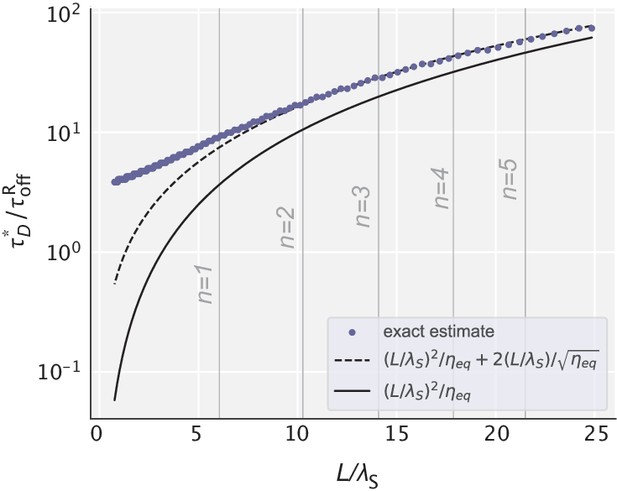
Optimal diffusion time scale for different choices of $λ_{_{S}}$ .

Blue dots represent the exact values obtained numerically for the data in Figure 3c. Dashed and solid lines represent the analytical estimates with and without the correction term. Vertical lines correspond to those values of $L / λ_{_{S}}$ that yield an integer number of effective proofreading realizations.

Appendix 2—figure 1

Download asset Open asset

Discrete-state representation of diffusive transport and substrate binding/unbinding events.

Transparent clusters of different numbers of substrates illustrate the spatial variation of substrate concentration.

Appendix 2—figure 2

Download asset Open asset

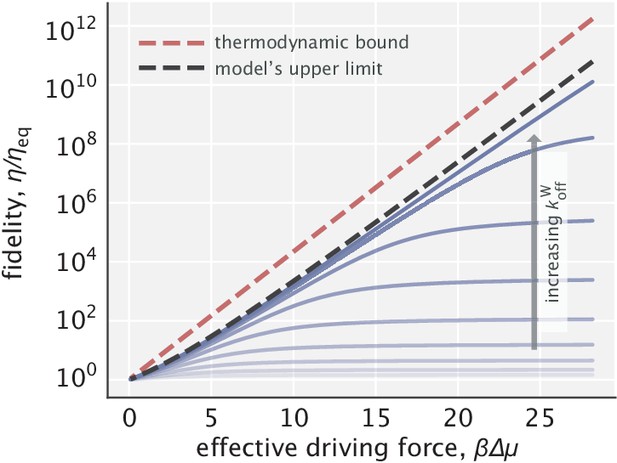
Fidelity enhancement as a function of the effective driving force for varying choices of $k_{off}^{W}$ .

The red dashed line indicates the thermodynamic bound given by $e^{β Δ μ}$ . The black dashed line corresponds to the model’s upper limit on fidelity enhancement given by Equation S40.

Appendix 3—figure 1

Download asset Open asset

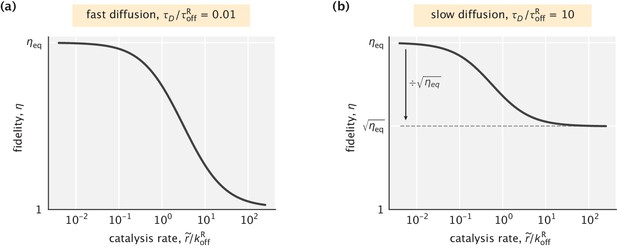
Dependence of fidelity on the catalysis rate in the case where the substrate profile is uniform.

(a) Fast diffusion setting ( $\sqrt{τ_{D} k_{off}^{R}} ≪ 1$ ). The highest fidelity reduction is a factor of $η_{eq}$ . (b) Slow diffusion setting ( $\sqrt{τ_{D} k_{off}^{R}} ≳ 1$ ). The highest fidelity reduction is a factor of $\sqrt{η_{eq}}$ . In both cases, $η_{e q} = 10$ was used.

Appendix 3—figure 2

Download asset Open asset

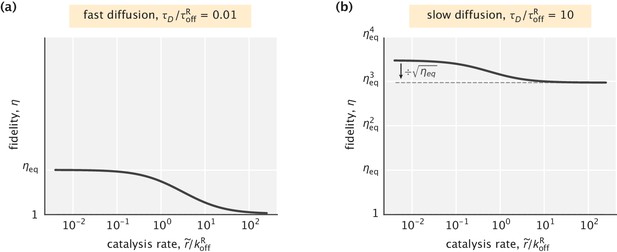
Fidelity as a function of the catalysis rate in an ideal substrate localization setting.

(a) Fast diffusion case, where the behavior of the system is identical to that in Appendix 3—figure 1a. (b) Slow diffusion case where efficient proofreading is achieved. Catalysis can reduce the fidelity by up to a factor of $\sqrt{η_{eq}}$ . In both cases, $η_{e q} = 10$ was used.

Appendix 3—figure 3

Download asset Open asset

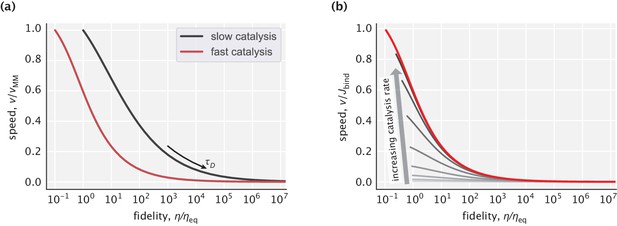
Pareto front of the speed–fidelity trade-off at different levels of catalytic activity.

(a) Cases of slow and fast catalysis limits, with the y-axis for speed normalized to the [0,1] interval. (b) Family of Pareto fronts for different choices of the catalysis rate. Speed on the y-axis is reported relative to the substrate binding flux $J_{bind}$ .

Appendix 3—figure 4

Download asset Open asset

Linear trade-off between speed and fidelity when tuning the rate of catalysis.

$η_{min}$ is the fidelity in the fast catalysis limit and is up to $η_{eq}$ lower than $η_{0}$ (based on the results of the previous section). Linear scale is used for both axes.

Appendix 4—figure 1

Download asset Open asset

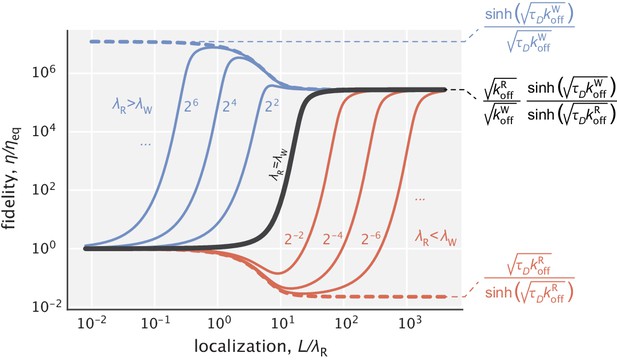
Fidelity as a function of $L / λ_{_{R}}$ for different choices of the ratio $λ_{_{R}} / λ_{_{W}}$ .

The solid black line corresponds to the earlier studied regime where substrates had identical localization length scales. The blue curves represent the cases where $λ_{_{R}} > λ_{_{W}}$ , while the red curves represent the cases where $λ_{_{R}} < λ_{_{W}}$ . Numbers next to the curves correspond to the $λ_{_{R}} / λ_{_{W}}$ ratios used for generating them. Expressions for the highest and lowest fidelity values, as well as the fidelity expression in the limit where both substrates are highly localized are shown on the right side of the figure. $τ_{D} = 40 τ_{off}^{R}$ and $η_{eq} = 10$ were used for demonstration.

Appendix 5—figure 1

Download asset Open asset

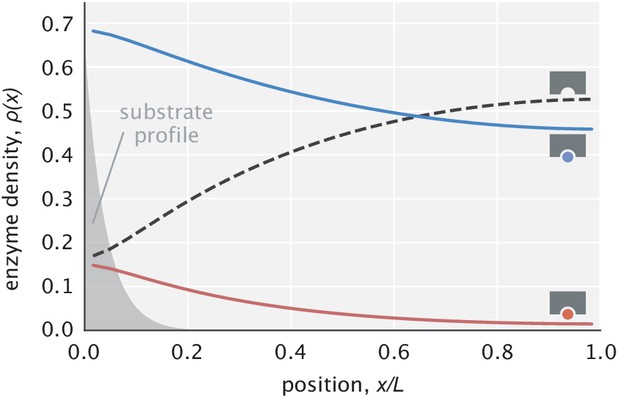
Example profiles of free and substrate-bound enzymes.

Enzyme profiles are normalized so that the sum of areas under the curves is unity. The substrate profile (rescaled on the y-axis) is shown in transparent gray.

Appendix 5—figure 2

Download asset Open asset

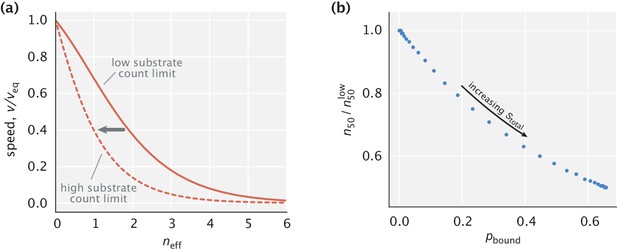
Consequences of relaxing the $ρ_{_{E}} (x) \approx constant$ assumption on the Pareto front.

(a) Pareto fronts in the low and high substrate concentration limits. (b) Reduction in the effective number of proofreading realizations at half-maximum speed as a function of the fraction of enzymes bound. $η_{eq} = 10$ was used in making the plots.

Appendix 5—figure 3

Download asset Open asset

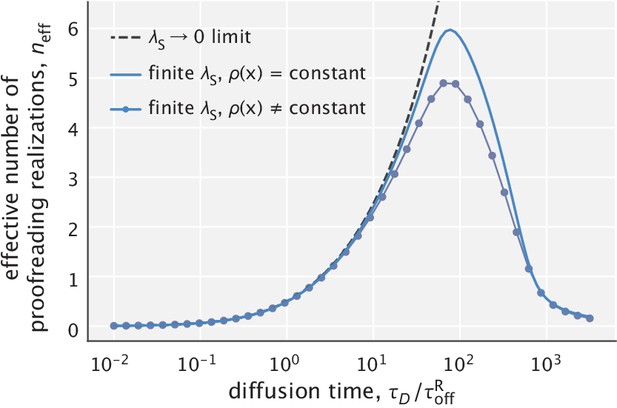
Fidelity as a function of diffusion time scale calculated with and without making the $ρ_{_{E}} (x) \approx constant$ approximation.

The total number of free substrates is chosen so that ${\bar{ρ}}_{_{S}} / K_{d}^{R} = 3$ . The substrate localization length scale used for generating the solid curves is $λ_{_{S}} / L = 0.04$ .

Appendix 5—figure 4

Download asset Open asset

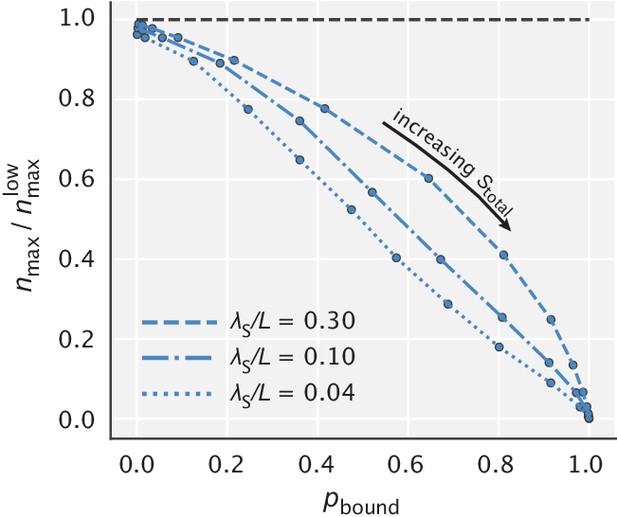
Reduction in the peak effective number of proofreading realizations as a function of $p_{bound}$ .

$n_{m a x}^{l o w}$ represents the peak value of $n_{eff}$ in the limit of low substrate concentration (the maximum of the solid blue curve in Appendix 5—figure 3).

Appendix 6—figure 1

Download asset Open asset

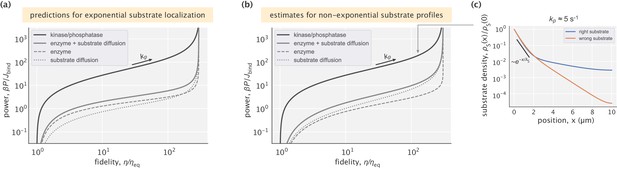
Energetic performance of the kinase/phosphatase–based mechanism.

(a) Total dissipation and calculated lower bounds under the assumption of exponential substrate localization. (b) Total dissipation and lower bounds estimated without assuming exponential substrate profiles. In both (a) and (b) $k_{b} = 1 s^{- 1}$ and $Δ ε_{kin} = Δ ε_{phosph} = 10 k_{B} T$ were used. (c) Example profiles of right and wrong substrates for the physiologically relevant dephosphorylation rate $k_{p} = 5 s^{- 1}$ . Exponential decay of the substrate profile with the predicted length scale $λ_{_{S}} = \sqrt{D_{_{S}} / k_{p}}$ holds in the first $\sim 2$ μm of the compartment.

Tables

Appendix 1—table 1

Fidelity of the scheme in different regimes of right and wrong complex densities.

The upper-right cell is empty because the two conditions on $λ_{_{S}}$ cannot be simultaneously met, since $λ_{_{ER}} > λ_{_{EW}}$ by construction (follows from $k_{off}^{R} < k_{off}^{W}$ ).

	$λ_{_{S}} ≪ λ_{_{ER}}$	$λ_{_{S}} ≫ λ_{_{ER}}$
$λ_{_{S}} ≪ λ_{_{EW}}$	$\frac{λ_{_{EW}}}{λ_{_{ER}}} e^{L (λ_{_{EW}}^{- 1} - λ_{_{ER}}^{- 1})}$	-
$λ_{_{S}} ≫ λ_{_{EW}}$	$\frac{2 λ_{_{S}}}{λ_{_{ER}}} e^{L (λ_{_{S}}^{- 1} - λ_{_{ER}}^{- 1})}$	$η_{eq}$

Additional files

Source code 1 Code files to reproduce the figures.: https://cdn.elifesciences.org/articles/60415/elife-60415-code1-v2.zip
Download elife-60415-code1-v2.zip

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Vahe Galstyan
Kabir Husain
Fangzhou Xiao
Arvind Murugan
Rob Phillips

(2020)

Proofreading through spatial gradients

eLife 9:e60415.

https://doi.org/10.7554/eLife.60415

Share this article

Cite this article

Error correction schemes that operate by delaying product formation.

Dependence of fidelity on the diffusion time scale in the limit of very high substrate localization.

Speed–fidelity trade-off and consequences of having weak substrate gradients.

Power–fidelity relationship when tuning the effective driving force Δ⁢μ for different choices of the diffusion time scale τD.

Proofreading based on substrate gradients formed by spatially separated kinases and phosphatases.

The effective number of proofreading realizations (neff) as a function of L/λS.

Optimal diffusion time scale for different choices of λS.

Discrete-state representation of diffusive transport and substrate binding/unbinding events.

Fidelity enhancement as a function of the effective driving force for varying choices of koffW.

Dependence of fidelity on the catalysis rate in the case where the substrate profile is uniform.

Fidelity as a function of the catalysis rate in an ideal substrate localization setting.

Pareto front of the speed–fidelity trade-off at different levels of catalytic activity.

Linear trade-off between speed and fidelity when tuning the rate of catalysis.

Fidelity as a function of L/λR for different choices of the ratio λR/λW.

Example profiles of free and substrate-bound enzymes.

Consequences of relaxing the ρE⁢(x)≈constant assumption on the Pareto front.

Fidelity as a function of diffusion time scale calculated with and without making the ρE⁢(x)≈constant approximation.

Reduction in the peak effective number of proofreading realizations as a function of pbound.

Energetic performance of the kinase/phosphatase–based mechanism.

Fidelity of the scheme in different regimes of right and wrong complex densities.

Source code 1

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Power–fidelity relationship when tuning the effective driving force $Δ μ$ for different choices of the diffusion time scale $τ_{D}$ .

The effective number of proofreading realizations ( $n_{eff}$ ) as a function of $L / λ_{_{S}}$ .

Optimal diffusion time scale for different choices of $λ_{_{S}}$ .

Fidelity enhancement as a function of the effective driving force for varying choices of $k_{off}^{W}$ .

Fidelity as a function of $L / λ_{_{R}}$ for different choices of the ratio $λ_{_{R}} / λ_{_{W}}$ .

Consequences of relaxing the $ρ_{_{E}} (x) \approx constant$ assumption on the Pareto front.

Fidelity as a function of diffusion time scale calculated with and without making the $ρ_{_{E}} (x) \approx constant$ approximation.

Reduction in the peak effective number of proofreading realizations as a function of $p_{bound}$ .