Constructing and optimizing 3D atlases from 2D data with application to the developing mouse brain
- Department of Psychiatry and Behavioral Sciences, UCSF Weill Institute for Neurosciences, University of California, San Francisco, United States
- Institute of Molecular and Cell Biology, Agency for Science, Technology and Research, Singapore
Figures
Figure 1
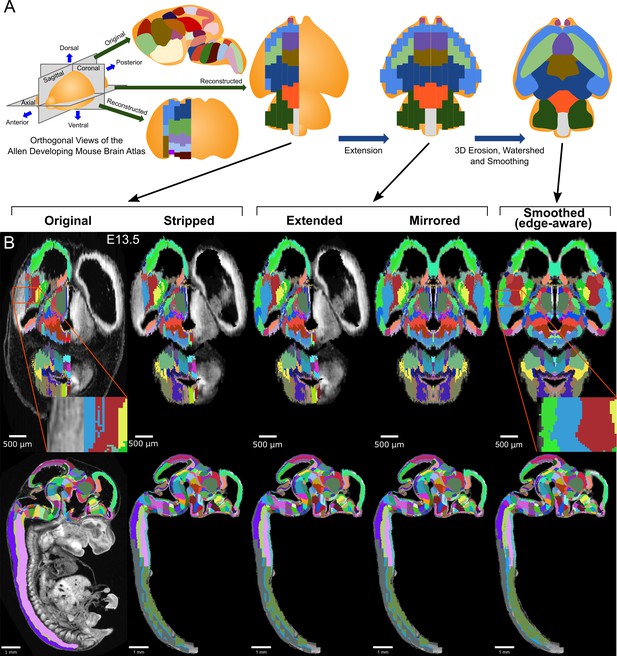
3D atlas refinement pipeline overview and full example in the E13.5 atlas.
(A) 2D-derived atlases, such as those in the Allen Developing Mouse Brain Atlas, are smooth and consistent in the sagittal plane in which they were annotated. However, in the 3D reconstructions of these 2D sagittal planes, the coronal and axial planes reveal missing sections and jagged edges. To improve their performance for annotating 3D data, the lateral edges are extended to complete the labeled hemisphere. A 3D rotation is applied to bring the brain parallel to the image borders, then both the completed hemisphere labels and underlying microscopy sections are mirrored across the sagittal midline to complete coverage in the opposite hemisphere. To improve anatomical registration, the labels are each eroded and re-grown through a 3D watershed, guided by the anatomical edge map. To smooth the final product, labels are iteratively filtered with a morphological opening operation, or a closing operation for small, disconnected labels that would otherwise be lost. (B) The pipeline illustrated in axial (top) and sagittal (bottom) views on the ADMBA E13.5 atlas, which requires the full pipeline shown in ‘A’, including an additional step to strip out non-CNS tissue from the original whole-embryo imaging. The nomenclature for pipeline steps shown here is used consistently throughout the manuscript. Insets of the ‘Original’ and ‘Smoothed (edge-aware)’ lateral regions highlight the label extension and smoothing. A spreadsheet mapping colors to label names and IDs in the Allen ontology for each atlas in this manuscript can be found in Supplementary file 1.
Figure 2 with 3 supplements
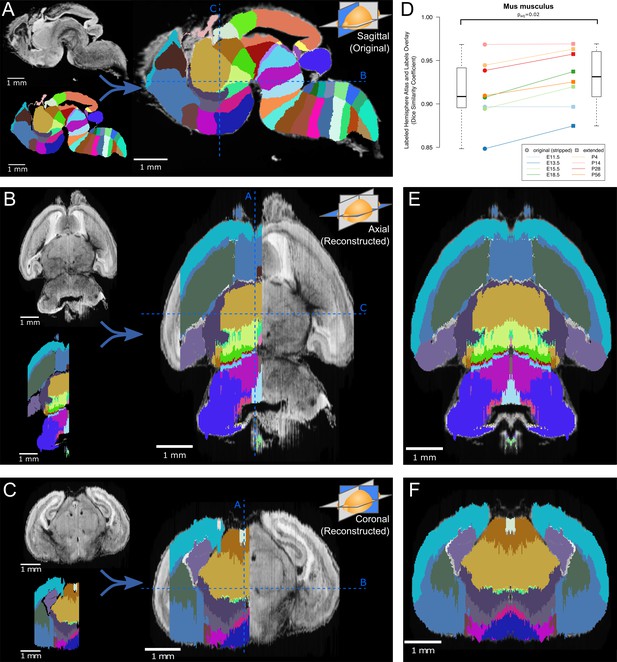
Atlas lateral extension and mirroring for complete brain annotation.
(A) The original E18.5 atlas labels (bottom left), viewed sagittally, demonstrate smooth borders and close correspondence with the underlying microscopy images (upper left; overlaid on right). The dashed blue lines show the sections viewed in ‘B’ and ‘C’. (B) When viewed axially, the most lateral sections lack labels, one hemisphere lacks labels entirely, and label borders are jagged. Slight rotation of the underlying microscopy images leads to asymmetry between its two hemispheres. (C) Similar findings are apparent in the coronal view. (D) The Dice Similarity Coefficient (DSC), a measure of the completeness of labeling compared to the thresholded atlases, for the labeled hemispheres increased for all brains in the ADMBA after lateral edge extension (original median = 0.91, extended median = 0.93; p=0.02, Wilcoxon signed-rank test (WSRT); ‘Mus musculus’ level −1, ID 15564 in the Allen ontology). (E) To fill in the lateral edges using existing labels, a representative lateral label plane was iteratively resized to fit the underlying microscopy images. The plane for each subsequent microscopy plane was thresholded, the bounding box extracted, and the labels resized to fit this bounding box, followed by conforming labels to the underlying gross anatomical boundaries (Figure 2—figure supplement 2). A stretch of compressed planes was expanded (Figure 2—figure supplement 3), and the completed hemisphere of labels mirrored to the other hemisphere after rotation for symmetry to complete the labeling. (F) Coronal view after the lateral edge extension.
Figure 2—figure supplement 1
Fraction of hemisphere that is unlabeled in each of the ADMBA atlases.
(A) The fraction of unlabeled planes in a given hemisphere is taken as the number of sagittal planes without any labels over the total number of sagittal planes in the hemisphere that should have labels. By definition the extended atlases have no detected unlabeled planes because any plane determined to require labeling was filled. (B) Unlabeled volume fractions are measured by taking label volume over the thresholded histology foreground in the hemisphere. Each hemisphere is taken as the predominantly labeled hemisphere of the given atlas.
Figure 2—figure supplement 2
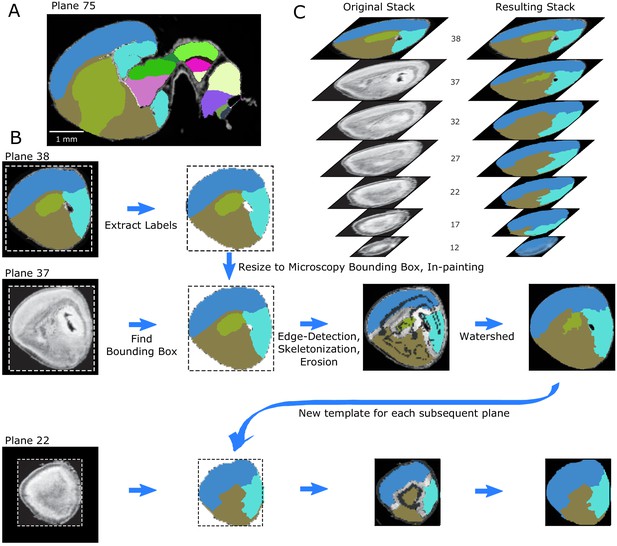
Lateral edge extension pipeline.
(A) Example labeled sagittal section toward the lateral edge in the ADMBA E18.5 atlas. (B) Overview of the extension algorithm. Plane 38 represents one of the farthest lateral labeled planes. For each discrete structure, the labels are extracted to serve as templates for the subsequent plane. In plane 37, the corresponding template is resized to the bounding box of the microscopy image in that plane. To further fit labels to the underlying anatomy, gross anatomical edges are found in 3D for the full volumetric microscopy images. Labels are eroded, skeletons are added back to avoid loss of thin sections, and labels are regrown by a compact watershed guided by the anatomical edges in the plane. This refined plane of labels thus becomes the template for the next plane. As the extension progresses, some labels disappear during the erosion step, preferentially central labels, modeling the tapering of labels laterally. (C) Every fifth label in a stack after the original template plane in (left) the original atlas and (right) after label extension.
Figure 2—figure supplement 3
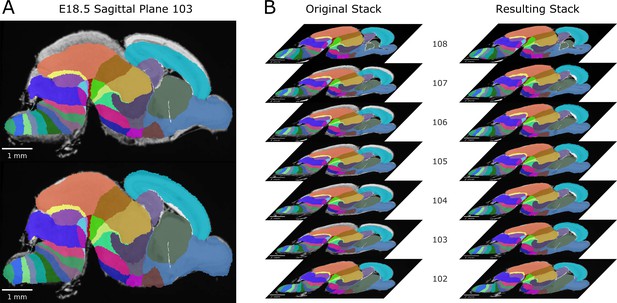
Expansion of compressed labels in a stretch of planes in the E18.5 atlas.
(A) Example plane from a stretch of sagittal planes in the original ADMBA E18.5 atlas where the labels are compressed dorsoventrally. The original labels (top) were re-expanded (bottom) to match the extent of the underlying histology section. (B) The stack of original (left) and re-expanded (right) planes from just before until just after this stretch of compressed label planes.
Figure 3 with 3 supplements
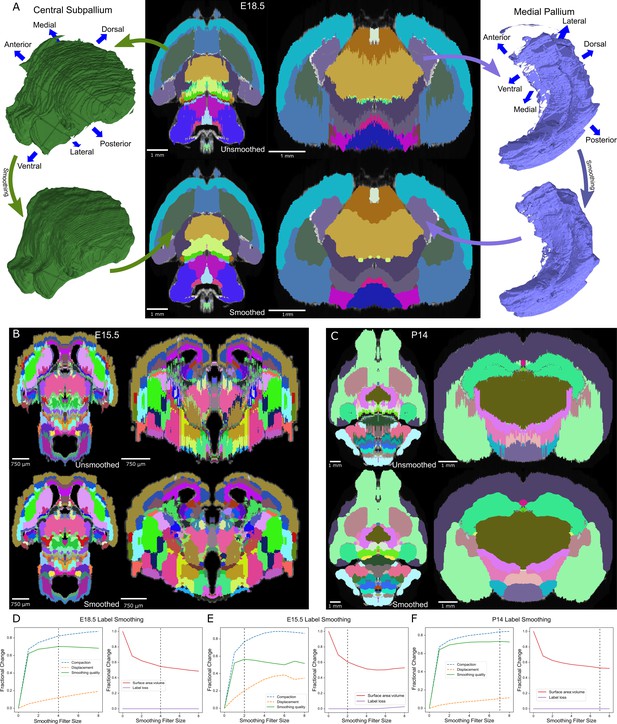
Atlas smoothing and optimization by adaptive morphological filtering.
(A) Irregularities at the label edges in the original (mirrored) E18.5 atlas (top) were smoothed by applying an adaptive morphological opening filter iteratively to each label, starting from the largest to the smallest labels (bottom). 3D renderings (outer columns) are depicted for two representative labels before (top) and after (bottom) smoothing in the axial (middle left) and coronal (middle right) views. (B, C) The view in ‘A’ is repeated for E15.5 and P14, respectively. (D) To identify the optimal filter structuring element size, we devised an ‘atlas-wide smoothing quality’ metric to incorporate the balance between smoothing (compaction) and changes in size and shape (displacement). While compaction continued to improve with increasing structuring element size, displacement eventually caught up, giving an optimal atlas-wide smoothing quality with a structuring element size of 4 for the E18.5 atlas (left). We also assessed the number of labels that were lost (none in this example) and the surface area to volume ratio, for which lower values reflect smoother shapes (right). Vertical dashed lines indicate the optimal filter structuring element size, based on ‘atlas-wide smoothing quality’. (E, F) This plot is repeated for E15.5 and P14, respectively.
Figure 3—figure supplement 1
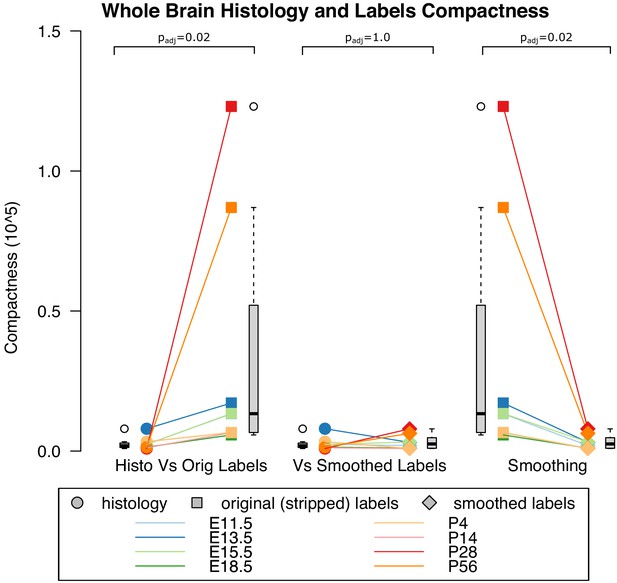
Compactness of whole brain histology and labels.
(A) Compactness of the whole brain histology can serve as a proxy for compactness of a biological structure since the whole brain is a well-defined structure whose boundaries are broadly accepted, unlike those of individual labels. After thresholding the microscopy images and taking their compactness, we found this compactness to be significantly lower (i.e. more compact) compared with that of the original (stripped) labels (p=0.02, WSRT, Bonferroni corrected across all three comparisons) but (B) similar to that of smoothed labels (p=1.0). (C) Original (stripped) were also significantly less compact (higher compactness) than smoothed labels were (p.=0.02).
Figure 3—figure supplement 2
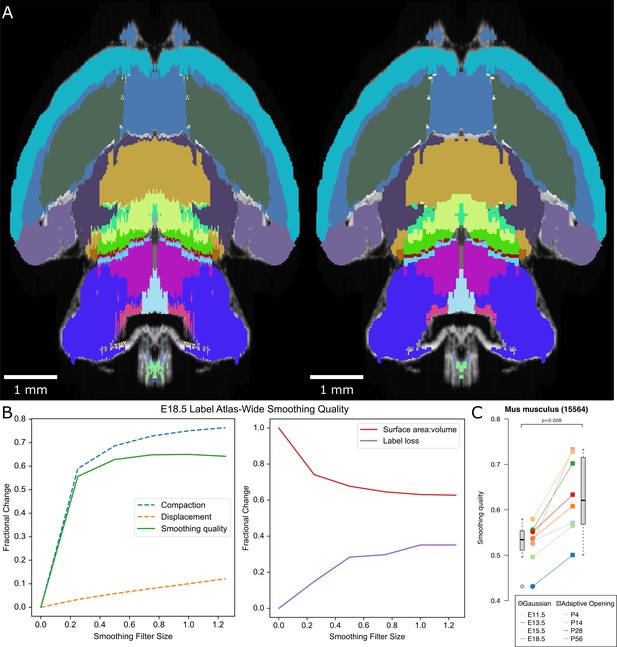
Smoothing labels by Gaussian blur.
(A) Example of the E18.5 atlas before (left) and after (right) smoothing by a Gaussian filter with a sigma of 0.25. (B) Smoothing quality metrics show increased compaction with a relatively slower increase in displacement with increasing filter sizes, leading to a peak smoothing quality at sigma of 1. This smoothing comes at a cost of label loss at all tested sigmas, including 15% at even the lowest tested sigma of 0.25. (C) Compared with Gaussian smoothing at this sigma across all ADMBA atlases, the adaptive opening filter approach showed a significant increase in atlas-wide smoothing quality (median 0.53 by Gaussian vs. 0.62 by adaptive opening filter; p=0.008, WSRT; mean 0.53 vs. 0.63).
Figure 3—figure supplement 3
Smoothing quality across filter sizes for all ADMBA atlases.
Smoothing quality metrics for each atlas in the ADMBA across filter structuring elements sizes, with size 0 corresponding to the original (mirrored) atlas. For each atlas, the top plot depicts the overall, brain-wide smoothing quality along with its separate compaction and displacement components, with peak smoothing quality lying between filter sizes 2–7. The bottom plot for each atlas shows the overall surface area to volume across labels as well as fraction of labels lost during smoothing, typically occurring at larger sizes, starting at four or higher.
Figure 4 with 6 supplements
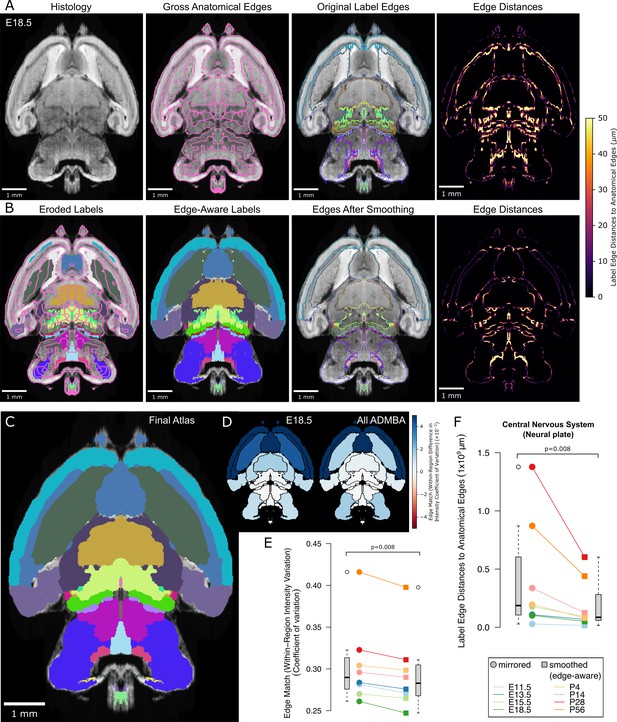
Edge-aware atlas reannotation based on underlying anatomical boundaries.
(A) Edge detection of the volumetric histology image delineated gross anatomical edges (left), shown here with the E18.5 atlas. To compare these histology-derived anatomical edges with the extended and mirrored but unsmoothed label edges (center left), we used a distance transform method to find the distance from each label edge pixel to the nearest anatomical edge (center right), shown here as a heat map of edge distances (right). (B) Eroded labels served as seeds (left) from which to grow edge-aware labels through a watershed algorithm (center left), guided by the gross anatomical edges. After smoothing, borders matched the anatomical edges more closely (center right), as shown in the edge distance heat map for the modified labels (right), using the same intensity scale. (C) The final E18.5 atlas after edge-aware reannotation and label smoothing to minimize edge artifacts. (D) To evaluate the level of edge match by label, we mapped differences in the intensity coefficient of variation weighted by relative volume for each label before and after label refinement onto each corresponding label for the E18.5 atlas (left) and across all ADMBA atlases (right). For both, the anatomical map depicts this metric as a color gradient across all of the sublevel labels present in a cross-section of the E18.5 atlas. Improvements of this metric with the refined atlas are colored in blue, minimal change is shown in white, while red represents better performance with the original atlas. (E) Applied across the full ADMBA, edge-aware reannotation and smoothing led to a significant improvement in the overall variation of intensities, taken as a weighted mean across all labels to incorporate parcellation changes while weighting by label volume (central nervous system, or ‘neural plate,’ level 0, ID 15565 in the Allen ontology; p=0.008, n = 8 atlases, WSRT). (F) Distances from labels to anatomical edges taken as the sum across all labels similarly showed a significant improvement across atlases (p=0.008, n = 8, WSRT).
Figure 4—figure supplement 1
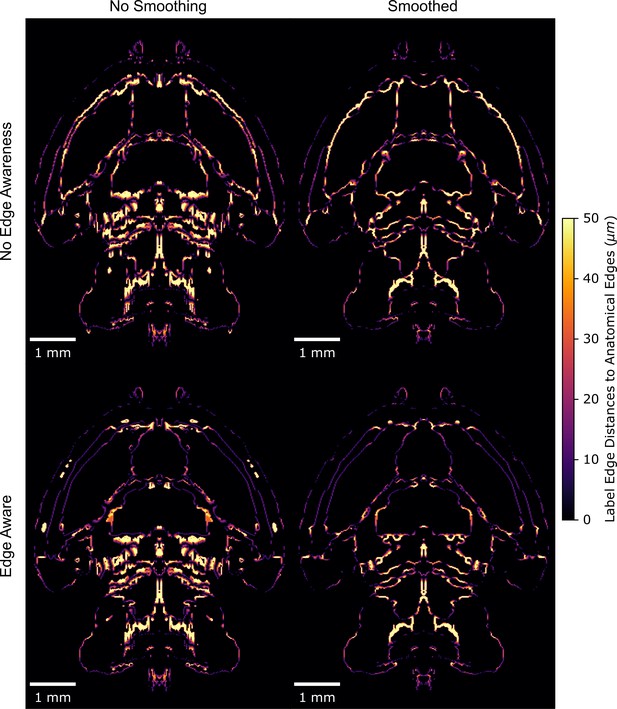
Edge distances with smoothing, edge-aware reannotation, or both.
Distances between labels and gross anatomical edges in the ADMBA E18.5 atlas show improvement from the original (top left) with either smoothing (top right) or edge-aware reannotation (bottom left) alone, but even more so when combining the two approaches through edge aware reannotation followed by label smoothing (bottom right).
Figure 4—figure supplement 2
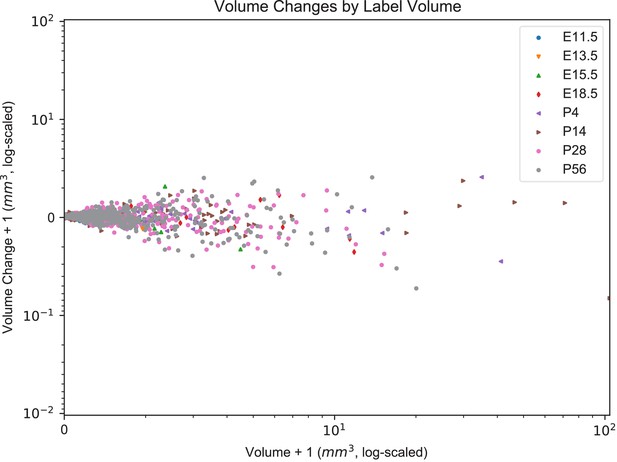
Volume changes by label from edge-aware smoothing across the ADMBA.
The change in volume from each mirrored to its smoothed (edge-aware) atlas is shown by total volume for each label. Scaling is log-modulus transformed to log-scale all values including non-positive volumes. 3132 labels are present where x < 0.2.
Figure 4—figure supplement 3
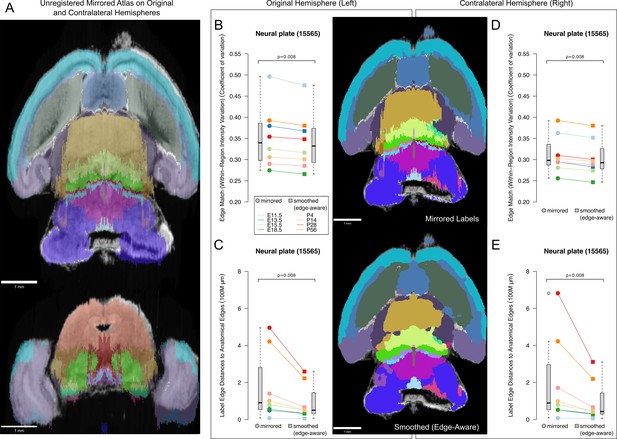
Internal control using the asymmetric, contralateral hemispheres from the original atlases.
(A) The asymmetry of the right hemisphere, contralateral to that of the left, originally annotated hemisphere, in the original atlas microscopy image is apparent when the mirrored labels are overlaid as illustrated here in the E18.5 atlas, notably in the olfactory bulb (top, axial view) and lateral cortex (bottom, coronal view). (B–E) Image registration of the mirrored (top, illustrated on the E18.5 atlas) or smoothed (edge-aware, bottom) atlases allows separate assessment of the original hemisphere (left) as an internal control for the contralateral (right) hemisphere within each atlas. In the original, left hemispheres, the (B) intensity coefficient of variation decreased from a median of 0.340 to 0.331 (p=0.008, WSRT) across the ADMBA, and (C) edge distances decreased from a median of 91 million to 50 million µm (p=0.008, WSRT), similarly to the full mirrored atlases. Findings were similar in the contralateral, right hemispheres, from which neither the original labels nor the 3D reconstruction were derived, where both (D) variation decreased from a median of 0.298 to 0.291 (p=0.008, WSRT) and (E) edge distances decreased from a median of 89 million to 41 million (µm, p=0.008, WSRT).
Figure 4—figure supplement 4
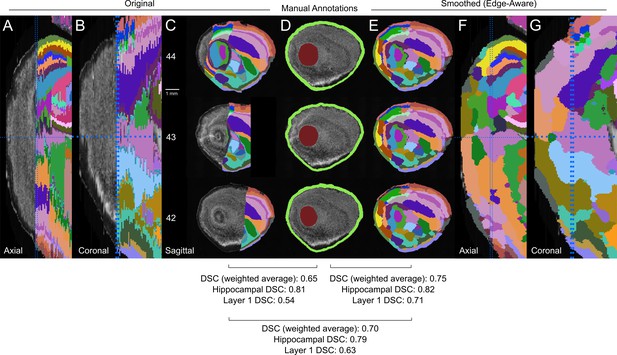
Lateral extension comparison with partial annotations and ground truth.
(A–C) The original P28 atlas contains partially labeled lateral planes that were not included in the 3D reconstruction as seen in the axial (A), coronal (B), and sagittal (C) views. (D) To measure the accuracy of the computationally generated labels with these partially labeled planes, we manually annotated the most clearly demarcated structures in these planes (center column; brown = hippocampus, green = cortical layer 1). (E–G) Computationally generated labels in the lateral planes of the smoothed (edge-aware) atlases as seen in the sagittal (E), axial (F), and coronal planes (G). The similarity between the composite set of labels corresponding to each manual annotation as measured by the Dice Similarity Coefficient (DSC) for the original and generated labels increased with the computationally generated labels, more prominently in layer 1 and the average weighted by volume. Manual annotations were cropped to the extent of all labels to only compare the partially labeled original planes where they were annotated.
Figure 4—figure supplement 5
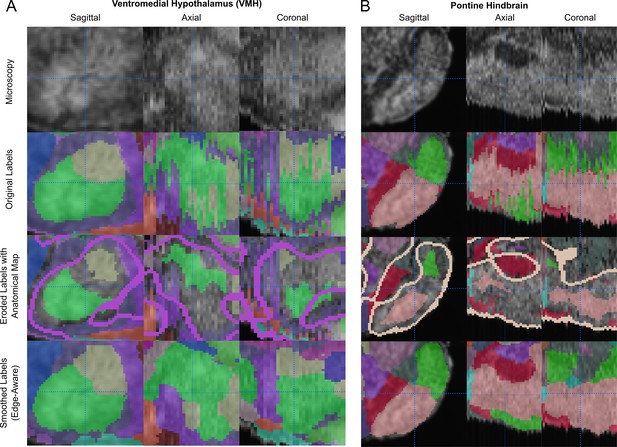
Edge-aware adjustment in delicate sub-regions with subtle contrast.
(A) The ventromedial hypothalamus (VMH) is a region with low contrast as shown here in the microscopy images (top row) in each orthogonal view of the P28 atlas along with its original labels (upper middle row; originally annotated, sagittal planes are shown in the left column alongside their orthogonal planes in the center and right columns). Erosion of each label (lower middle row) preserves the core of highest confidence annotation while removing artifacts that were particularly visible in the axial and coronal views. Eroded label edges near anatomical boundaries (light purple lines) take advantage of them during watershed-based regrowth (bottom row; see the green structure), while edges far from these boundaries meet in-between neighboring labels (green and tan structures). The relatively coarse anatomical edge map captures only clearly demarcated boundaries with strong contrast differential, limiting the number of artifactual boundaries around low-contrast regions, while the erosion and regrowth remove artifacts in the axial and coronal views. (B) Similar views in the pontine hindbrain.
Figure 4—figure supplement 6
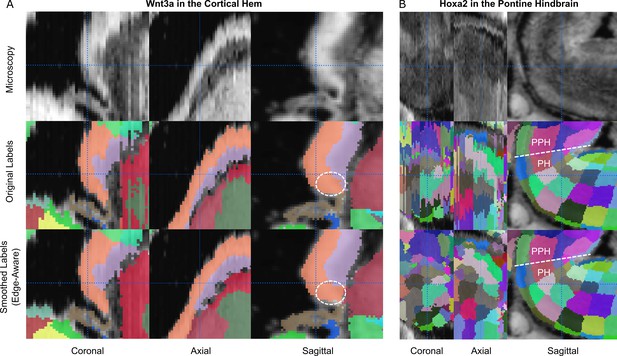
Preservation of regions demarcated by in-situ hybridization markers.
(A) Wnt3a is selectively expressed in the cortical hem at E13.5 (orange structure) and used by Thompson et al., 2014b to define its boundaries based on in-situ hybridization (ISH). The region corresponding to Wnt3a (dashed circle) remains contained within the cortical hem in the original (middle row) and 3D reconstructed (bottom row) atlases. (B) Similarly, the Hoxa2 ISH signal was used to demarcate the border between the pontine hindbrain (PH) and prepontine hindbrain (PPH) in the E15.5 atlas. This boundary remains well-demarcated before (lower middle row) and after (bottom row) 3D reconstruction.
Figure 5 with 17 supplements
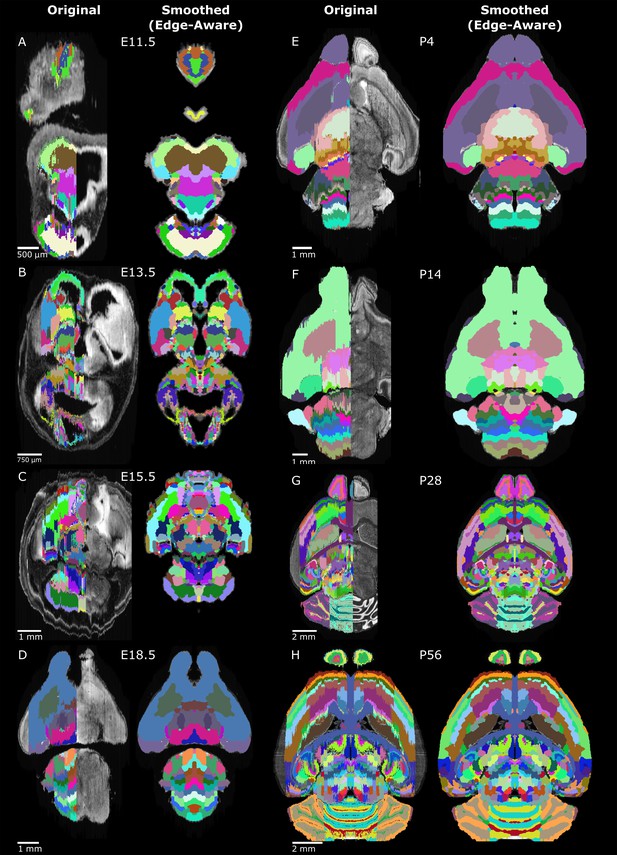
Original and 3D reconstructed atlas comparison across the ADMBA.
(A-H) Representative axial planes from all atlases. For each pair of images, a plane of the original (left) atlas is depicted next to the refined (right) atlas after undergoing the full refinement pipeline. Complete atlases before and after refinement are shown as movies in Figure 5—videos 1–16.
Figure 5—figure supplement 1
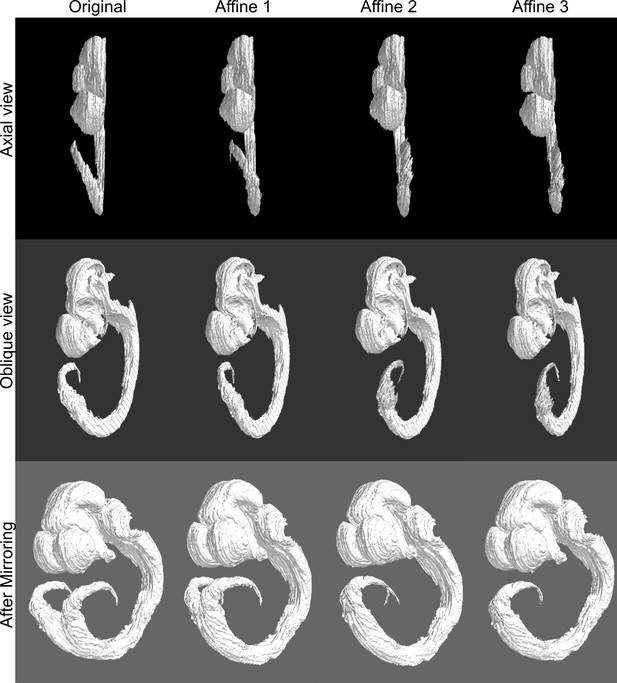
Piecewise 3D affine transformation of the spinal cord in the E11.5 atlas.
(column 1) The distal cord of the ADMBA E11.5 atlas specimen is skewed laterally as seen in the axial view (top), preventing mirroring without duplicating the distal cord (bottom). (columns 2–4) A series of three successive piecewise affine transformations straightened the cord to avoid duplication with mirroring.
Figure 5—video 1
Original ADMBA E11.5 Atlas.
Figure 5—video 2
3D reconstructed ADMBA E11.5 Atlas.
Figure 5—video 3
Original ADMBA E13.5 Atlas.
Figure 5—video 4
3D reconstructed ADMBA E13.5 Atlas.
Figure 5—video 5
Original ADMBA E15.5 Atlas.
Figure 5—video 6
3D reconstructed ADMBA E15.5 Atlas.
Figure 5—video 7
Original ADMBA E18.5 Atlas.
Figure 5—video 8
3D reconstructed ADMBA E18.5 Atlas.
Figure 5—video 9
Original ADMBA P4 Atlas.
Figure 5—video 10
3D reconstructed ADMBA P4 Atlas.
Figure 5—video 11
Original ADMBA P14 Atlas.
Figure 5—video 12
3D reconstructed ADMBA P14 Atlas.
Figure 5—video 13
Original ADMBA P28 Atlas.
Figure 5—video 14
3D reconstructed ADMBA P28 Atlas.
Figure 5—video 15
Original ADMBA P56 Atlas.
Figure 5—video 16
3D reconstructed ADMBA P56 Atlas.
Figure 6 with 3 supplements
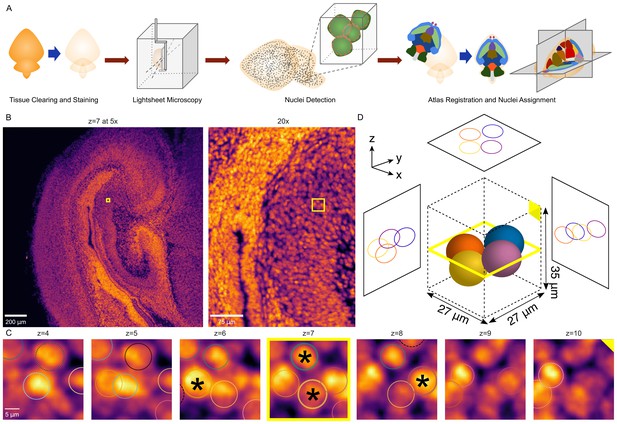
3D whole-brain nuclei detection pipeline.
(A) Overview of the nuclei detection and assignment pipeline. After tissue clearing by CUBIC and nuclear staining, we imaged intact whole P0 mouse brains by lightsheet microscopy (Figure 6—figure supplement 1). The E18.5 mouse brain atlas was registered to volumetric sample images. Nuclei were identified brain-wide with a 3D blob detector algorithm, and the nuclei coordinates were used to map to specific region labels, allowing quantification of nuclei counts and density for each label. (B) Axial view of the hippocampus of a P0 mouse brain at the original magnification of 5x (left) and zoomed to 20x (right), with the same region of interest (ROI) depicted by the yellow box in both. (C) Serial 2D planes along the ROI shown by the yellow box in part ‘B’ show the emergence and disappearance of nuclei while progressing vertically (z-axis) through the ROI. Each of four individual nuclei is assigned a unique colored circle. The most central image of the nuclei is indicated by a solid circle and asterisk, while images above or below have dashed circles. (D) 3D schematic of the four nuclei from part ‘C’ demonstrating their spatial orientation.
Figure 6—figure supplement 1
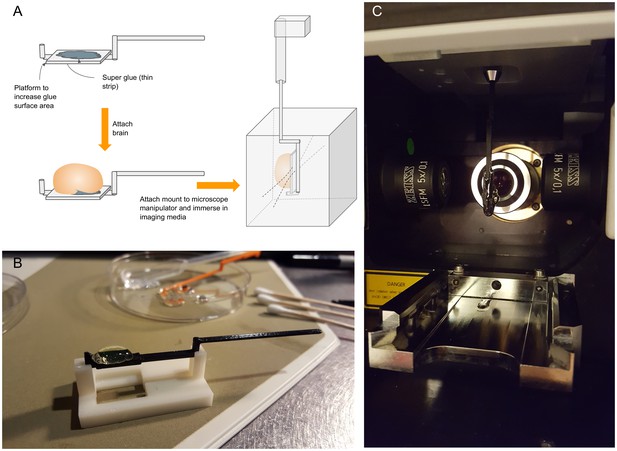
Custom 3D printed specimen mount for suspending samples in the Zeiss Lightsheeet Z.1 microscope.
(A) Mount schematic and orientation in the chamber. The lightsheet chamber requires the specimen to be suspended between the two illumination objectives producing a plane of light and detection objective perpendicular to this plane. To hold the brain in place while immersed in the refractive index matching solution, we devised a mount with a platform to maximize surface contact with the ventral surface of the brain, attached by super glue. To allow full latitude of the specimen within the chamber, we added a mount neck to center the specimen between the illumination objectives when the manipulator was approximately centered. (B) Photograph of mount and custom mount holder to facilitate gluing the specimen to the mount platform. Cotton buds were used to dry the ventral surface of the brain before attachment. We used the rod end of another mount to gently press the brain into the glue. (C) Photograph of specimen suspended and centered between the illumination objections, facing the detection objective.
Figure 6—figure supplement 2
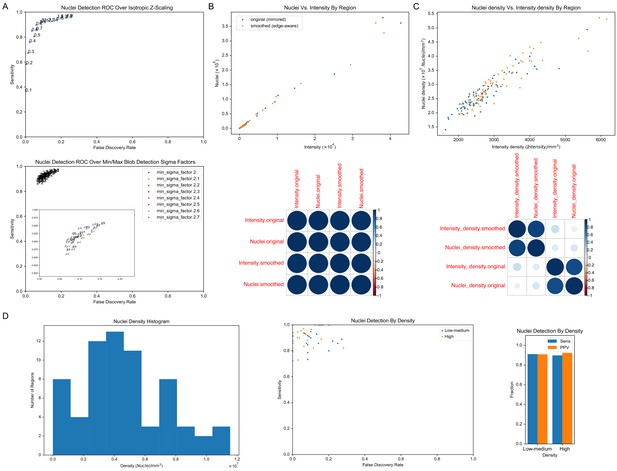
Nuclei detection optimization and comparison with intensity.
(A) Example receiver operating characteristic (ROC) curves. (top) Example ROC of nuclei detection across varying isotropic scaling factors along the z-axis. Scaling is shown as the fraction of isotropy along the z-axis, where 1 = isotropic. For example, 0.5 indicates that each ROI was resized so that the z-axis was half of the size it would need to be for full isotropy with the x- and y-axes. (bottom) Example ROC evaluating two hyperparameters, the minimum and maximum standard deviations for the Gaussian kernel used for multi-scale detection, to find the optimal size bounds for blob detection. Inset shows a zoomed view of the clustered points. (B) Total nuclei vs. intensity by label showed a linear relationship using labels defined by either the original (mirrored; r = 0.997, p≤1×10−16) or smoothed (edge-aware; r = 0.997, p≤1×10−16) atlases. In the correlation plot (bottom), the size of the circle indicates the size of the correlation coefficient (r). (C) Similarly, nuclei density vs. intensity density relationships were approximately linear in the original (mirrored; r = 0.894, p≤1×10−16) and smoothed (edge-aware; r = 0.929, p≤1×10−16) atlases. (D) Sensitivity and False Discovery Rate stratified by nuclei density in manually annotated truth sets as seen in the histogram (left) showed a similar distribution by region (middle) and overall metrics (right) by density group, with numerically lower recall and slightly higher precision in denser regions.
Figure 6—figure supplement 3
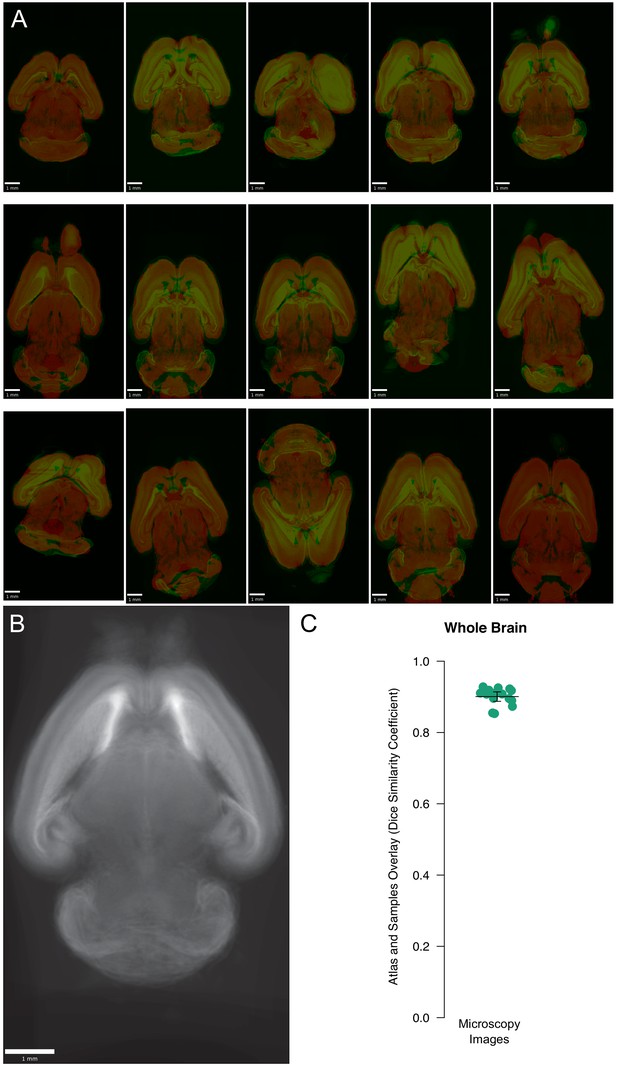
Registration of atlas to WT brains.
(A) Overlays of each registered atlas microscopy image on its corresponding downsampled wild-type brain. All examples are shown at the same plane. (B) Composite image of wild-type sample brains registered in reverse, using the same settings but registering the sample to the atlas to evaluate overall alignment of registered brains. (C) Overall registration quality as expressed by the DSC between the foreground of each sample and its registered atlas showed a median of 0.91 (mean 0.90).
Figure 7 with 4 supplements
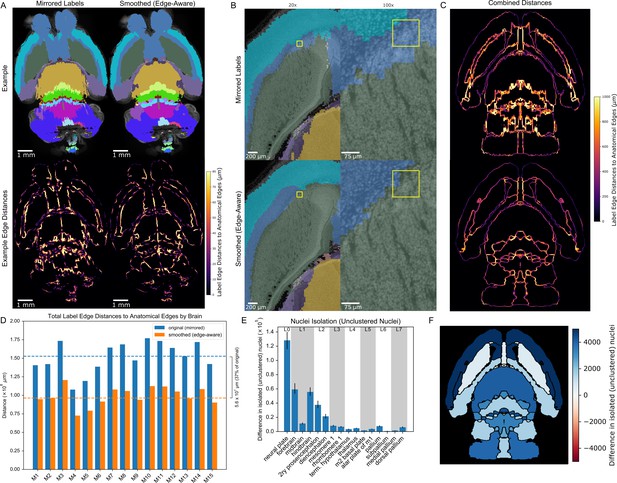
3D reconstructed atlas validation in wild-type mouse brains at cellular resolution.
(A) Example of the original (mirrored, left) and smoothed (edge-aware, right) E18.5 atlases registered to a representative cleared, optically-sectioned P0 wild-type mouse brain. Edge distances between the registered labels and the brain’s own anatomical edge map are reduced for this example brain, shown by the color gradient for each edge (bottom). (B) Label alignment at higher resolution. The top row depicts the registered original (mirrored) atlas at 20x and 100x around a region of interest highlighted by a yellow box. This same brain region is depicted in the bottom row, but overlaid with the refined atlas registered using identical transformations as in the original atlas. (C) Summation of the edge distances across all 15 wild-type brains with color gradient showing the edge distances with the original (top) and smoothed (bottom) labels. (D) Total edge distance at the whole-brain level before and after atlas refinement for each of these brains. (E) Density-based nuclei clustering within each label. Many of the isolated nuclei that could not be clustered in the original labels were clustered in the refined labels, with differences in unclustered nuclei shown from 16 regions selected across the hierarchy of labels from the grossest (neural plate, L0, left) to the finest (e.g. dorsal pallidum, L7, right). Error bars represent 95% confidence intervals. (F) The differences between the original and refined labels’ unclustered nuclei are depicted on an anatomical map showing this metric as a color gradient across all the sublevel labels present in a cross section. Improvements with the refined atlas are colored in blue, while red represents better performance with the original atlas. A complete list of differences for each metric in each label is provided in Supplementary file 2.
Figure 7—figure supplement 1
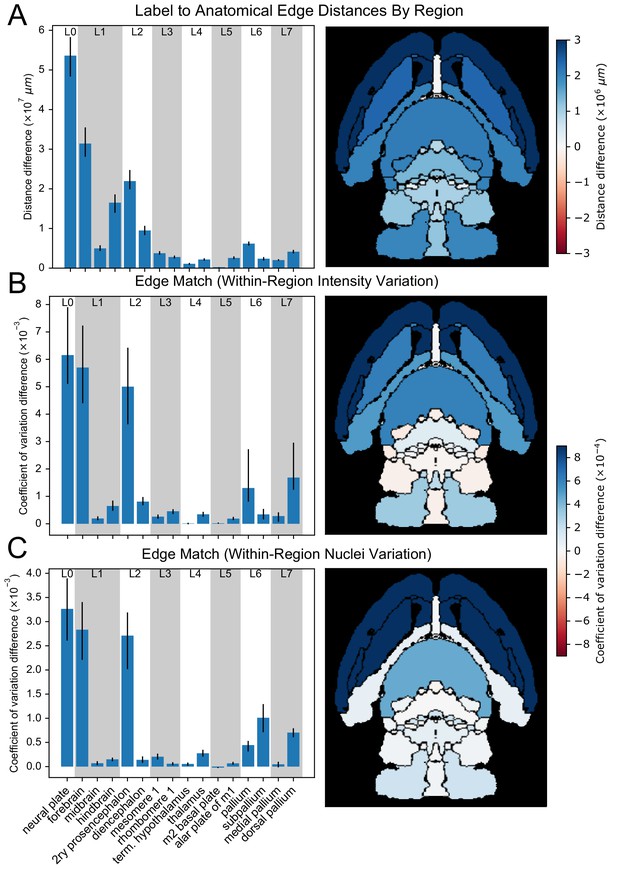
Region homogeneity in wild-type brains based on the original vs.refined atlases.
(A) The differences between the original (mirrored) and smoothed (edge-aware) labels’ edge distance sum and (B) intensity and (C) nuclei density coefficients of variation as reflections of region homogeneity are quantified with bar plots (left) for selected regions across the hierarchy of labels. Error bars represent 95% confidence intervals. Anatomical maps depict these metrics as a color gradient across all of the finest labels present in a cross section (right). Increases in a metric with the original atlas are colored in blue, while red represents increases with the refined atlas.
Figure 7—figure supplement 2
Changes in volumes, nuclei, and densities across wild-type brains based on atlas labels.
(A) The differences between the original (mirrored) and smoothed (edge-aware) labels’ volume, (B) nuclei, and (C) nuclei densities (bottom) are quantified with bar (right) and volcano (left) plots. Selected regions are shown across the hierarchy of labels from the grossest (neural plate, L0, left) to the finest (e.g. dorsal pallium, L7, right). Positive values indicate decreased size in the refined atlas. Error bars represent 95% confidence intervals. Volcano plots depict each label as a separate point with point size correlating with label size and colors corresponding to major parent structure (neural plate = light blue, forebrain = dark blue, midbrain = light green, hindbrain = dark green). Points higher and farther from 0 have stronger statistical significance and effect size, respectively. p-Values are calculated by the WSRT, Bonferroni corrected for all 120 labels within each measurement. Effect sizes are standardized based on the WSRT Z-statistic.
Figure 7—figure supplement 3
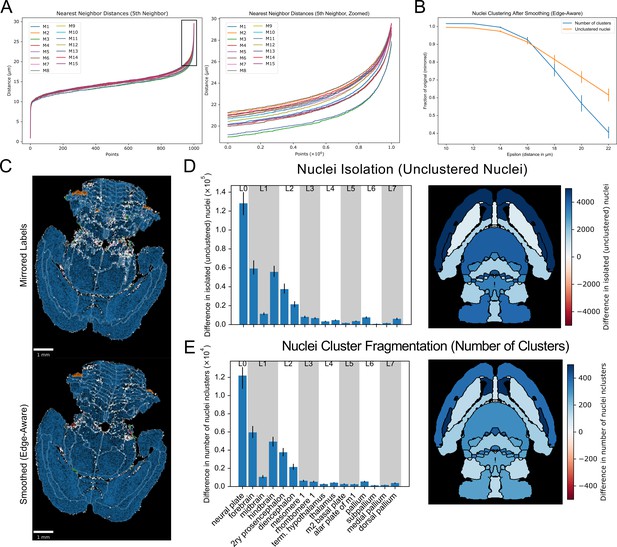
Nuclei clustering in the original vs. refined atlases.
(A-B) To determine the appropriate cluster neighborhood distance parameter, the fifth nearest neighbor distances for all nuclei in each wild-type brain are plotted in ascending order (right), following the convention in DBSCAN of taking the 2·ndim−1th neighbor (Schubert et al., 2017). (left) The zoomed view allows identification of the distance at the ‘elbow’ or ‘knee,’ or maximum curvature, typically at 20 µm or higher. (C) Nuclei clustering within each label in the smoothed (edge-aware) atlas as a fraction of that of the original (mirrored) atlas across a range of distance values. The number of isolated, unclustered nuclei and total clusters, indicative of nuclei isolation and cluster fragmentation, respectively, decreased in the smoothed atlas relative to the original atlas, starting even prior to the minimum distance based on the max curvature seen in part ‘B.’ (E) Example using a conservative neighbor distance of 20 µm for clustering in a brain before (top) and after (bottom) label refinement. Light gray lines show label boundaries. Unclustered nuclei are depicted as white points. All other points are clustered nuclei. Within each region, nuclei are colored by cluster size, where blue represents nuclei in the largest cluster, followed by orange, green, and red for the next successively smaller clusters. (D) Differences in unclustered nuclei and (E) number of clusters by region across all wild-type brains with this distance setting for selected regions across label hierarchies in bar plots (left) and as color gradients on an anatomical map (right).
Figure 7—figure supplement 4
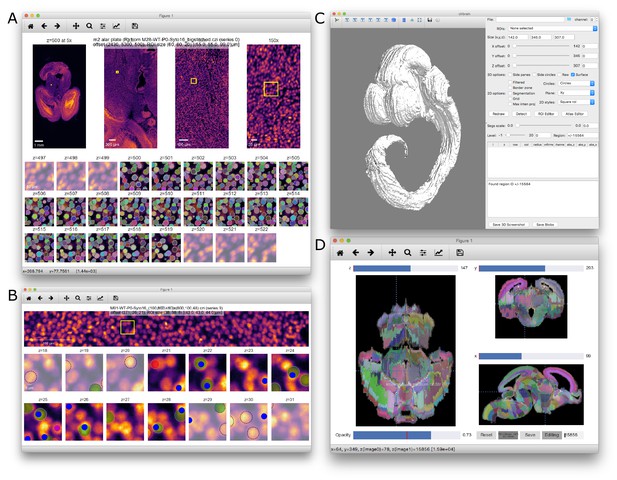
MagellanMapper software GUI screenshots.
(A) ROI serial 2D viewer and annotation editor GUI. The viewer provides overview images at increasing magnifications, zooming into the ROI outlined in yellow. Overview images are scrollable to show how the z-planes change through the ROI in place. Sequential z-planes of the ROI alone depict the original 2D images side-by-side through the entire 3D ROI, with a few additional opacified planes shown above and below the ROI for context. Overlaid labels show an example of automated nuclei segmentation. (B) Another example of the ROI viewer, here in nuclei annotation and verification mode. Automated nuclei centroid ‘blob detections’ are depicted as interactive circles corresponding to blob positions and radii. For building truth sets, circles provide drag-n-drop and copy-paste controls to reposition, add, or subtract these detections for accuracy. Green and red flags allow scoring for detection correctness. To compare with truth sets, blue and purple dots depict previously annotated nuclei positions pulled in from a database. Automated verification of current blob detections against the truth set shows blue dots as correctly detected truth blobs, purple as missed truth blobs, green circles as correct detections based on a matched truth blob, and red as incorrect detections (no remaining truth blob matches). (C) ROI selector and 3D visualization GUI. The right panel displays ROI offset and size controls, 2D and 3D display options, label controls including ontology depth, and an editable blob table. The left panel shows an example whole atlas 3D visualization using the ADMBA E11.5 atlas. (D) Atlas editor GUI. The GUI provides simultaneous orthogonal views in all three dimensions, with planes corresponding to the crosshairs. With ‘Editing’ selected, labels can be painted into adjacent labels as shown in the intermediate stratum of Str label in the left hemisphere of the z-plane. Editing a second, non-contiguous z-plane in the same label will enable the ‘Fill’ button to perform edge interpolation for this label through all intervening planes.
Author response image 1
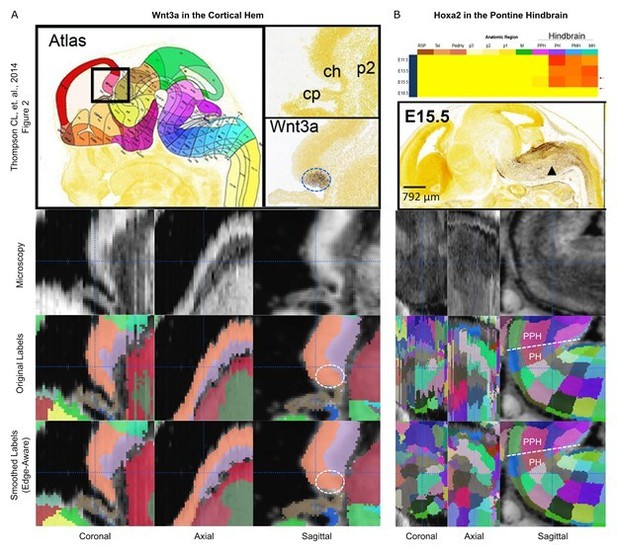
Preservation of regions demarcated by ISH markers.
(A) The Wnt3a ISH signal (dashed circle) shown in Thompson CL, et al. (2014, Figure 2; top row) is expressed selectively within the cortical hem in the original labels of the E13.5 atlas (lower middle row, orange structure) and remains contained in this region in the 3D reconstructed atlas (bottom row). (B) The Hoxa2 ISH signal demarcates the border between the pontine hindbrain and prepontine hindbrain in the E15.5 atlas (top row). This boundary remains well-demarcated before (lower middle row) and after (bottom row) 3D reconstruction.
Author response image 2
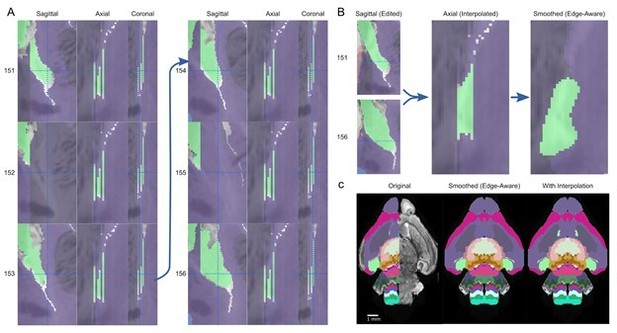
Interpolation to fill gaps in and recover a thin substructure.
(A) A thin extension in the medial pallium (green structure) in the P4 atlas is missing sagittal annotations in planes 152 and 155, visible as two gaps in the axial and coronal view, as well as gaps between the extension and the rest of the structure in planes 151, 154, and 155. (B) Reconnecting this extension (left) and interpolating between the edited planes fills the gaps as seen in the axial view (middle), recovering this thin substructure in the final smoothed atlas. (C) This substructure is apparent in the anterior section of the original atlas (left) but lost in the 3D reconstructed atlas (middle), although the rest of the medial pallium is present in other planes. After interpolation and 3D reconstruction, the substructure is recovered (right).
Author response image 3
Post-registration landmark distance for wild-type lightsheet images.
Mean distances between manually annotated atlas and wild-type brain image landmarks are plotted for each brain after registration.
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Genetic reagent (Mus. musculus) | C57BL/6J | Jackson Laboratory | Stock #: 000664 RRID:MGI_3028467 | |
| Commercial assay or kit | SYTO 16 | Thermo Fisher Scientific | Cat. #: S7578 | 1 µM |
| Software, algorithm | FIJI/ImageJ software | FIJI/ImageJ | RRID:SCR002285 | Version 1.52 |
| Software, algorithm | MagellanMapper software | This paper | ||
| Software, algorithm | Zeiss Zen software | Zeiss | RRID:SCR_018163 | Version 2014 |
Additional files
-
Supplementary file 1
Spreadsheet mapping colors to label names and IDs in the Allen ontology for each atlas in the ADMBA.
- https://cdn.elifesciences.org/articles/61408/elife-61408-supp1-v2.xlsx
-
Supplementary file 2
Spreadsheet of metric differences by label for WT brains before and after edge-aware atlas refinement.
- https://cdn.elifesciences.org/articles/61408/elife-61408-supp2-v2.xlsx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/61408/elife-61408-transrepform-v2.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Constructing and optimizing 3D atlases from 2D data with application to the developing mouse brain
eLife 10:e61408.
https://doi.org/10.7554/eLife.61408
