Computational modeling of threat learning reveals links with anxiety and neuroanatomy in humans
Figures
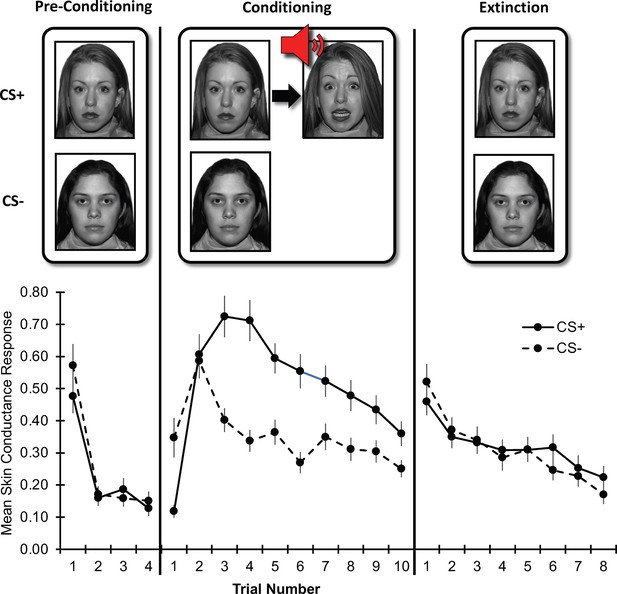
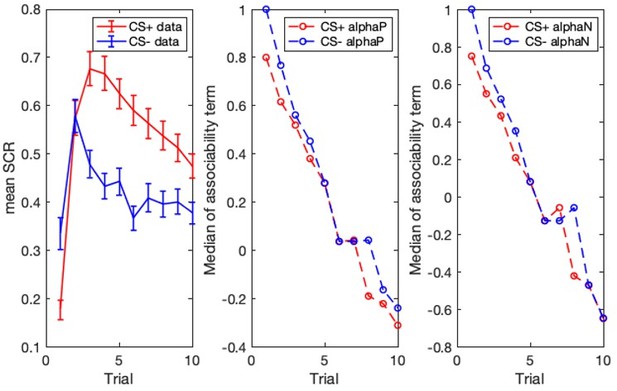
Threat learning task and physiological data.
Top: Schematic representation of the threat learning paradigm. During the pre-conditioning phase, the designated threat (CS+) and safety (CS-) stimuli were presented without reinforcement. During the conditioning phase, the CS + was paired with a fearful face co-terminating with a scream (UCS); the CS- was never reinforced. During the extinction phase, both CS + and CS- were not reinforced by the UCS. Bottom: Mean raw skin conductance response for the CS + and CS- by task phase and trial. Note: Trial number indicates the nth trial for that stimulus. However, the CS+ and CS- trials were presented in counterbalanced order throughout the task. CS = conditioned stimulus; UCS = unconditioned stimulus. Error bars indicate one standard error of the mean.
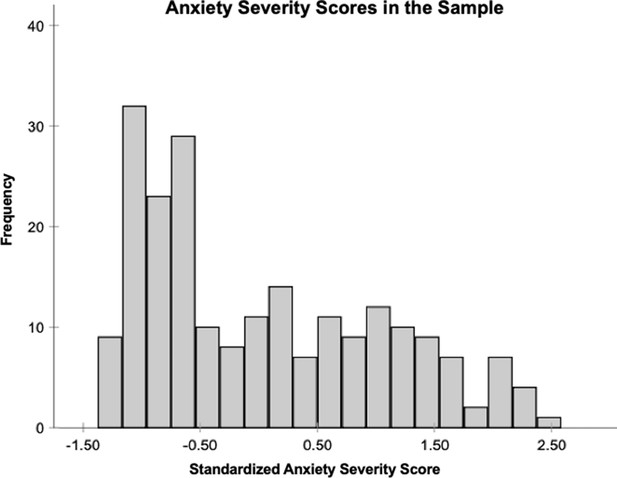
Histogram depicting the distribution of the standardized anxiety severity scores across the sample.
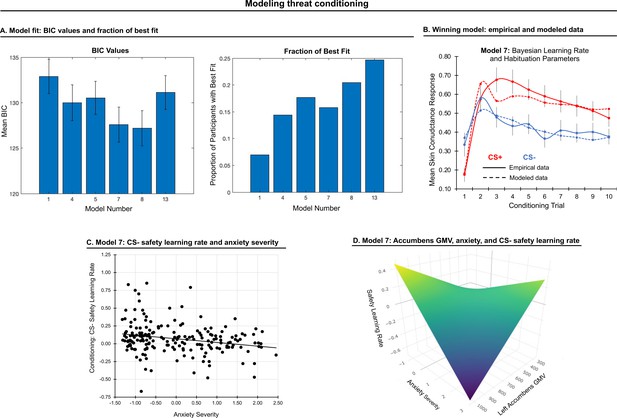
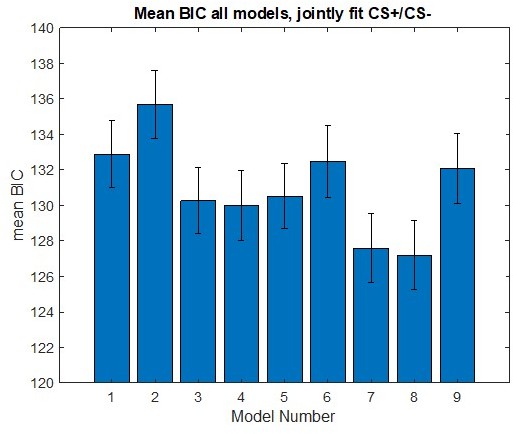
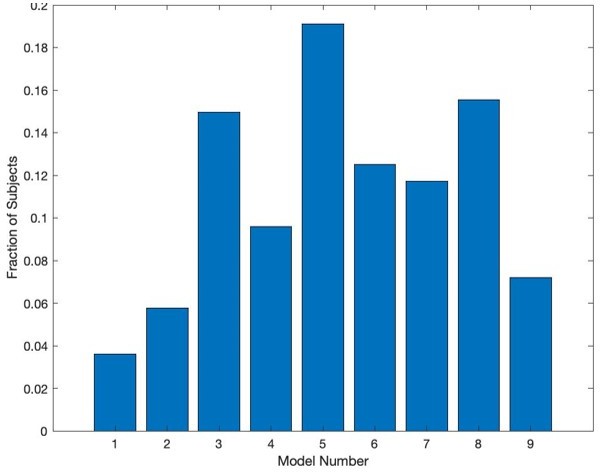
Modeling threat conditioning.
(A) Bars in left panel depict BIC values for each of the fourteen models fit to the CS- and CS + conditioning data. Error bars indicate one standard error of the mean. Bars in right panel depict the proportion of participants for whom each model provided the best fit. (B) Based on model fit indices, model 7 was chosen as the best-fitting model for conditioning data. Graphs depict empirical skin conductance data (full line) and fitted data (dashed line) for model 7 fitted to CS+ (red) and CS- (blue) conditioning data. Data are smoothed for display purposes only. (C) Association between model 7’s CS- learning rate parameter and anxiety severity. (D) The association between model 7’s CS- learning rate parameter and anxiety severity was moderated by left accumbens gray matter volume (GMV).
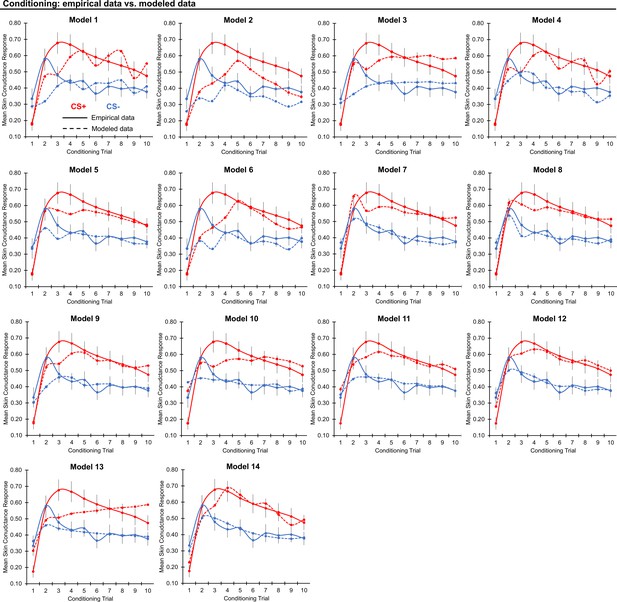
Threat conditioning model fits.
Graphs depict empirical skin conductance data (full line) and fitted data (dashed line) for each of the models fitted to CS+ (red) and CS- (blue) conditioning data. Data are smoothed for display purposes only.
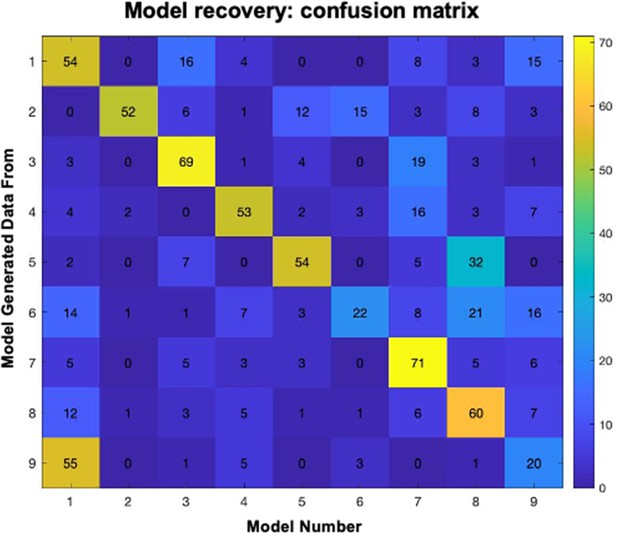
Conditioning model recovery.
Confusion matrix depicting distribution of selected models when data were simulated with each model. For each row (model), columns depict the number of simulated datasets that were identified as generated from that model.

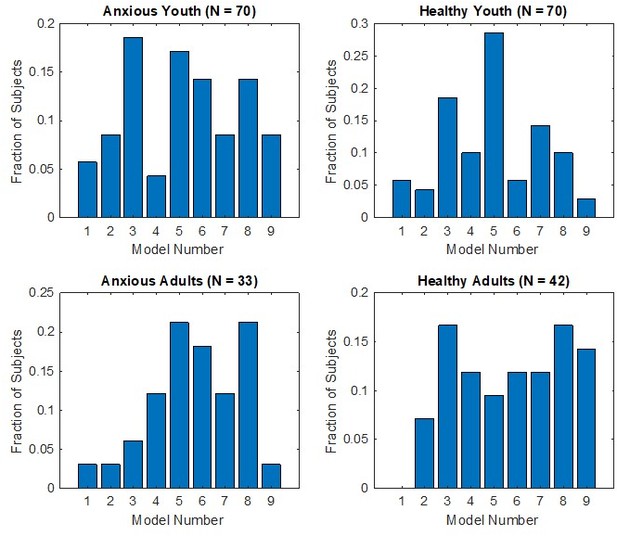
Proportions of participants for whom each model provided the best fit, when the sample is divided into anxiety (patients vs healthy comparisons) and age (youth vs adults) groups.
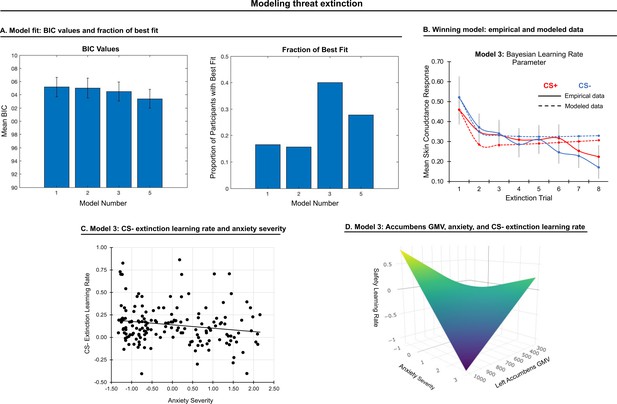
Modeling threat extinction.
(A) Bars in left panel depict BIC values for each of the twelve models fit to the CS- and CS+ extinction data. Error bars indicate one standard error of the mean. Bars in right panel depict the proportion of participants for whom each model provided the best fit. (B) Based on model fit indices, model 3 was chosen as the best-fitting model for extinction data. Graphs depict empirical skin conductance data (full line) and fitted data (dashed line) for model 3 fitted to CS+ (red) and CS- (blue) extinction data. Data are smoothed for display purposes only. (C) Association between model 3’s CS- extinction rate parameter and anxiety severity; this association is only trend-level significant. (D) The association between model 3’s CS- learning rate parameter and anxiety severity was moderated by left accumbens gray matter volume (GMV); this association is only trend-level significant.

Threat extinction model fit.
Graphs depict empirical skin conductance data (full line) and fitted data (dashed line) for each of the models fitted to CS+ (red) and CS- (blue) extinction data. Data are smoothed for display purposes only.
Tables
Specifications and estimated free parameters for each model fit to the CS- and CS+.
| Model | Model specification | Free parameters | Initialization values |
|---|---|---|---|
| 1.RW | , | where vi is the SCR value from the last habituation trial (acquisition) and SCR value from the first extinction trial (extinction) | |
| 2.RW with inertia | , whereby, , with m=number of recent trials | same as model 1 | |
| 3.RW with Bayesian learning-rate decay | , with | same as model 1 | |
| 4.RW with habituation | , with multiplied by after update | same as model 1 | |
| 5.RW with inertia and Bayesian learning-rate decay | , with , and , with m=number of recent trials | same as model 1 | |
| 6.RW with inertia and habituation | , whereby , with m=number of recent trials, and multiplied by after update | same as model 1 | |
| 7.RW with Bayesian learning-rate decay and habituation | , whereby and multiplied by after update | same as model 1 | |
| 8.RW with inertia and Bayesian learning-rate decay, and habituation | , whereby, and , with m=number of recent trials, and multiplied by after update | same as model 1 | |
| 9.RW-PH hybrid | , whereby | ||
| 10.Hybrid(V) Li et al., 2011 | (Changing Vn for ), where bUCS(n)=1 if a UCS was delivered and bUCS(n)=0 if no UCS was delivered (b indicates binary UCS). SCR was then predicted using a regression: The squared error: | where vi is the SCR value on the last habituation trial and SCR value from the first extinction trial (extinction) | |
| 11.Hybrid(α) Li et al., 2011 | Same as model 10 (changing Vn for ) except The squared error: | same as model 10 | |
| 12.Hybrid (V+α) Li et al., 2011 | Same as model 10 changing Vn for with additional regression such that: | same as model 10 | |
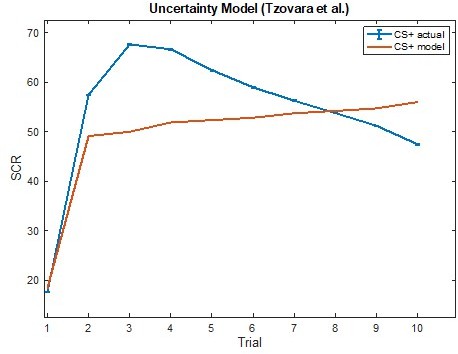
| 13.Mixed prior mean and uncertainty model Tzovara et al., 2018 | Where is a Beta function whose parameters are updated according to: Where if a US occurred and otherwise. are the regression parameters relating to SCR | ||
| 14.Mixed prior mean and uncertainty model (Model 13) Tzovara et al., 2018 with habituation | Same as model 13 with the addition: multiplied by after update for habituation | same as model 13 |
Demographics (sex, age, IQ) and anxiety severity (by diagnosis: anxious/healthy; by continuous anxiety scores on the Screen for Child Anxiety Related Emotional Disorders or ) for participants who were included or excluded from data analysis due to excessive missing data.
Differences between included and excluded participants were tested using chi-squared or independent-samples t-tests.
| Excluded | Included | Test Statistic | |
|---|---|---|---|
| N | 136 (94 F) | 215 (116 F) | |
| % Female | 69.11 | 53.95 | = 7.35, P=.006 |
| N Anxiety diagnosis | 55 | 104 | = 1.81, P=.18 |
| N Healthy | 85 | 111 | = 3.56, P=.06 |
| Mean (SD) age | 23.40 (9.16) | 18.76 (9.39) | t(302.29) = 4.62, P<.001 |
| Mean (SD) anxiety | –0.09 (0.89) | 0.05 (1.06) | t(288.66) = 1.27, P=.21 |
| Mean (SD) IQ | 114.68 (13.32) | 113.98 (11.90) | t(271) = .50, P=.61 |
Corelations between the actual parameters and recovered parameters for each of the 14 models for acquisition data.
Models in bold met the criteria for model comparison (all corelation values for all parameters >0.20). Note that the last row reflects an additional variant of the Tzovara et al. model with two additional habituation parameters (habituation for CS+ and CS- for 6 total parameters) that was examined for completeness (see Methods).
| Model | Parameter 1, CS+ learning Rate | Parameter 2, CS- learning Rate | Parameter 3, CS+ habituation | Parameter 4, CS- habituation | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.99 | 0.56 | |||||
| 2 (inertia) | 0.86 | 0.22 | |||||
| 3 (Bayesian) | 0.52 | 0.21 | |||||
| 4 | 0.76 | 0.99 | >0.99 | 0.99 | |||
| 5 (inertia +Bayesian) | 0.74 | 0.46 | |||||
| 6 (inertia) | 0.38 | 0.17 | 0.53 | >0.99 | |||
| 7 (Bayesian) | 0.59 | 0.42 | 0.98 | >0.99 | |||
| 8 (inertia +Bayesian) | 0.52 | 0.62 | 0.96 | >0.99 | |||
| Parameter 1, CS +learning Rate | Parameter 2, CS- learning Rate | Parameter 3, CS +learning rate update | Parameter 4, CS- learning rate update | Parameter 5, regression βo | Parameter 6 regression β1 | Parameter 7 regression β2 | |
| 9 | 0.53 | 0.13 | 0.52 | 0.02 | |||
| 10 | –0.09 | 0.04 | –0.37 | 0.46 | 0.35 | 0.21 | |
| 11 | 0.49 | 0.07 | –0.37 | 0.46 | 0.35 | 0.21 | |
| 12 | 0.34 | 0.04 | –0.39 | 0.66 | 0.002 | 0.02 | 0.99 |
| Parameter 1, βo | Parameter 2, β1 | Parameter 5, CS+ habituation | Parameter 4, CS- habituation | ||||
| 13 | 0.90 | 0.96 | |||||
| 14 | 0.81 | 0.90 | –0.03 | 0.33 |
Correlations between the actual parameters and recovered parameters for each model for extinction data.
Models in bold met the criteria for model comparison (all correlation values for all parameters > 0.20).
| Model | Parameter 1, CS+ learning rate | Parameter 2, CS- learning rate | Parameter 3, CS+ habituation | Parameter 4, CS- habituation | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.59 | 0.45 | |||||
| 2 (inertia) | 0.51 | 0.46 | |||||
| 3 (Bayesian) | 0.83 | 0.69 | |||||
| 4 | 0.28 | 0.07 | 0.46 | 0.93 | |||
| 5 (inertia + Bayesian) | 0.80 | 0.82 | |||||
| 6 (inertia) | 0.49 | 0.27 | 0.05 | -0.04 | |||
| 7 (Bayesian) | 0.32 | 0.40 | 0.05 | 0.40 | |||
| 8 (inertia + Bayesian) | 0.22 | 0.25 | -0.003 | 0.01 | |||
| Parameter 1, CS+ learning rate | Parameter 2, CS- learning rate | Parameter 3, CS+ learning rate update | Parameter 4, CS- learning rate update | Parameter 5, regression βo | Parameter 6, regression β1 | Parameter 7, regression β2 | |
| 9 | 0.47 | 0.33 | 0.11 | 0.01 | |||
| 10 | 0.28 | 0.01 | 0.01 | 0.03 | 0.82 | 0.19 | |
| 11 | 0.85 | 0.11 | 0.99 | 0.86 | –0.31 | –0.03 | |
| 12 | 0.99 | -0.002 | 0.99 | 0.93 | 0.90 | 0.90 | –0.01 |
Additional files
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/66169/elife-66169-transrepform1-v2.docx
-
Source code 1
Code for reinforcement learning models.
- https://cdn.elifesciences.org/articles/66169/elife-66169-code1-v2.zip
-
Source code 2
Code for imaging processing and analysis.
- https://cdn.elifesciences.org/articles/66169/elife-66169-code2-v2.zip