Random sub-diffusion and capture of genes by the nuclear pore reduces dynamics and coordinates inter-chromosomal movement
- Department of Molecular Biosciences, Northwestern University, United States
- Department of Physics, Harvard University, United States
Figures
Figure 1
Continuous and dynamic positioning at the nuclear periphery.
(A) Representative confocal micrographs of cells having the LacO array integrated at a locus of interest, expressing GFP-LacI and Pho88-mCherry (Robinett et al., 1996; Brickner and Walter, 2004; Brickner et al., 2019) and scored as either nucleoplasmic (left) or peripheral (right). (B) Peripheral localization (% of cells ± SEM) of URA3 and HIS4 in cells grown ± histidine. The hatched blue line, here and throughout: peripheral localization predicted by chance. (C, E–G) Kymographs of 10 cells with a LacO array integrated at HIS4 (C), URA3 (E), INO1 (F), or URA3:GRS1 (G) were grown in the indicated medium and scored for peripheral localization every 10 s for 5 min. Yellow: peripheral; purple: nucleoplasmic. (D) Peripheral localization (± SEM) of URA3, INO1, URA3:INO1, and URA3:GRS1 in cells grown ± inositol. (H–J) Summary plots from (C, E–G): (H) mean percentage of cells (± SD) in which the locus is peripheral at each time point (i.e., each dot represents a summary of a single column from kymographs); (I) mean percentage of time (± SD) each locus spent colocalized with the nuclear envelope (i.e., each dot represents a summary of a single row from kymographs); and (J) the distribution and median duration of periods of peripheral localization of each locus.
Figure 2 with 1 supplement
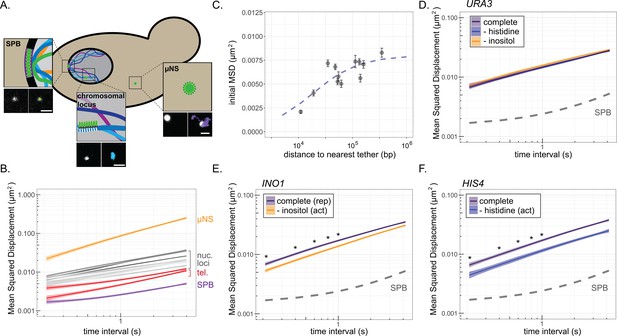
Mean-squared displacement (MSD) of chromatin sub-diffusion.
(A) Schematic of fluorescent foci within the yeast cell. Fluorescently tagged spindle pole body (SPB), cytoplasmic µNS, and chromosomal locus were tracked over 200 × 200 ms. Example micrographs of each particle (left) and overlaid path (right) are shown for each. Scale bar = 1 µm. (B) Average MSD for µNS (orange), SPB (purple), 10 nucleoplasmic loci (gray; listed in Supplementary file 1) and two telomeres (red) at different time intervals (τ). The ribbon around the mean represents standard error. (C) Mean MSD ± standard deviation for τ = 200 ms for each chromosomal locus in (B) vs log10 (base pairs) to the nearest tether point (centromere or telomere). The line is from the fit of the data to a non-linear model for a hyperbolic curve, as described in the text. (D–F) MSD plots of INO1 (D), URA3 (E), or HIS4 (F) in cells grown in the indicated media. In all plots, the dashed line represents the MSD of the SPB. *p<0.05 based on Kolmogorov–Smirnov test comparing MSDs at the indicated times.
-
Figure 2—source data 1
Comma-separated tables of tracking data used for Figure 2B, D, E, and F.
- https://cdn.elifesciences.org/articles/66238/elife-66238-fig2-data1-v2.zip
Figure 2—figure supplement 1
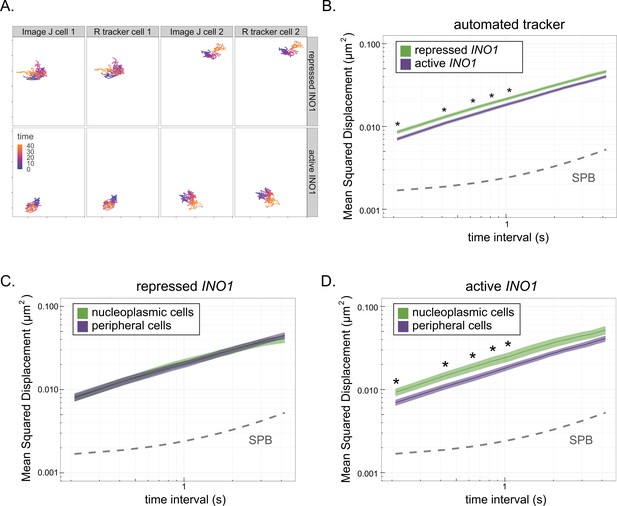
MSD of peripheral vs nucleoplasmic cells.
To monitor peripheral localization during particle tracking for MSD, we developed an automated tracking system in R that uses the imageR package to threshold, denoise, and detect both the nuclear periphery and the center of mass of fluorescent loci. Markdowns containing the functions used in this system are available through GitHub (https://github.com/MCnu/R_sim_scripts; Sumner, 2021a Sumner, 2021b); copy archived at swh:1:rev:6440995193e1245c44d2c9a9e0b21b161d98e788. (A) Comparison of the Image J tracking method (see Materials and methods) to the R tracker. Repressed or active INO1 were tracked in two representative cells over time with each method, and the resulting paths are shown. (B) MSD analysis of repressed and active INO1 using the R tracker. (C, D) MSD analysis of repressed INO1 (C) or active INO1 (D) from cells in which the locus was predominantly nucleoplasmic or predominantly peripheral. For repressed INO1, the nucleoplasmic population (n = 22) had >90% nucleoplasmic steps, and the peripheral population (n = 22) showed >40% peripheral steps over 40 s. For active INO1, the nucleoplasmic population (n = 20) showed >75% nucleoplasmic steps and the peripheral population (n = 20) showed >60% peripheral steps over 40 s.
Figure 3
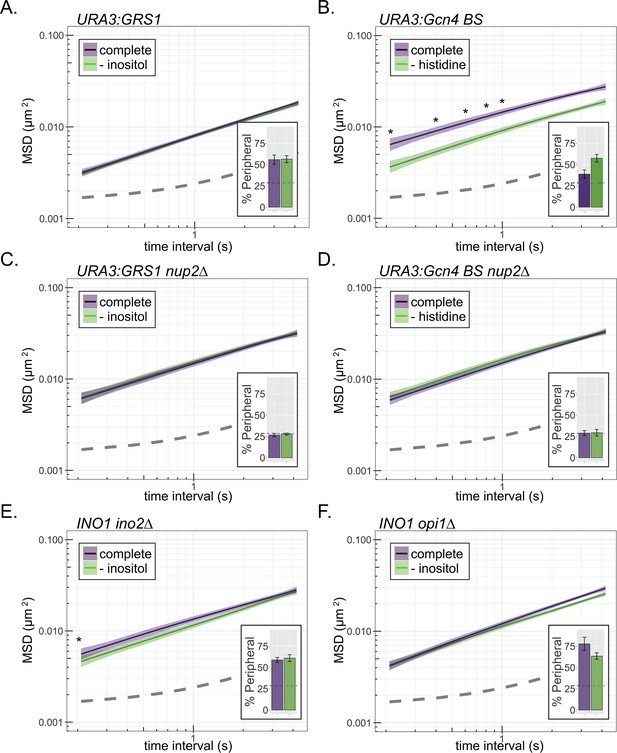
Interaction with the NPC reduces chromatin sub-diffusion.
(A–F) MSD of URA3 (A–D) and INO1 (E, F) in strains grown in the indicated media. Dark line indicates average MSD, ribbon = bootstrapped SEM. Insets: peripheral localization of each locus (mean % of cells ± SEM). The GRS1 zip code from the INO1 promoter (A, C) or the Gcn4 binding site (B, D) was integrated and integrated at URA3 in wild-type (A, B) or nup2∆ (C, D) strains. MSD of INO1 in ino2∆ (E) or opi1∆ (F) strains. *p<0.05 based on Kolmogorov–Smirnov test comparing MSD at the indicated time points.
-
Figure 3—source data 1
Comma-separated tables of tracking data used for Figure 3.
- https://cdn.elifesciences.org/articles/66238/elife-66238-fig3-data1-v2.zip
Figure 4 with 2 supplements
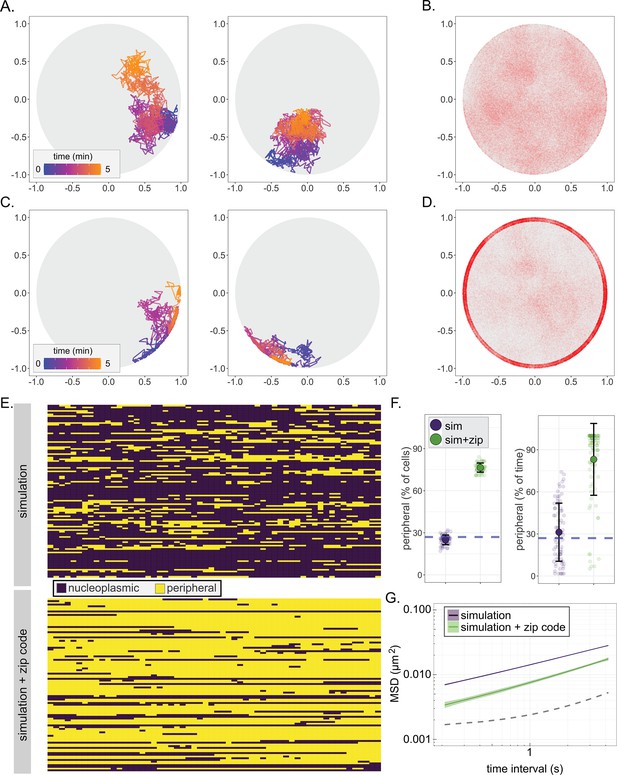
A fractional Brownian motion simulation of chromatin sub-diffusion.
(A, C) Randomly selected example paths over 5 min at 200 ms time resolution. Color scale represents time. Paths were simulated using parameters (diffusion coefficient and anomalous exponent) extracted from a non-linear regression fit to URA3 MSD (A; simulation) or by also allowing interaction at the nuclear envelope, slowing sub-diffusion to that of the SPB (C; simulation+zip code). (B, D) 150,000 positions visited in 100 simulated 5 min paths at 200 ms time resolution for the simulation (B) or the simulation+zip code (D). (E) Peripheral localization (i.e., positioned ≤150 nm from the edge of the nucleus) every 10 s over 10 min for 100 paths from the simulation (top) and simulation+zip code (bottom). (F) Summary plots for percent of cells in that scored as peripheral at each time (left) or the percent of time each cell scored as peripheral (right) in either the simulation or the simulation+zip code. (G) MSD of the paths from the simulation or the simulation+zip code. Dark line is the mean, and the colored band represents the bootstrapped standard error.
Figure 4—figure supplement 1
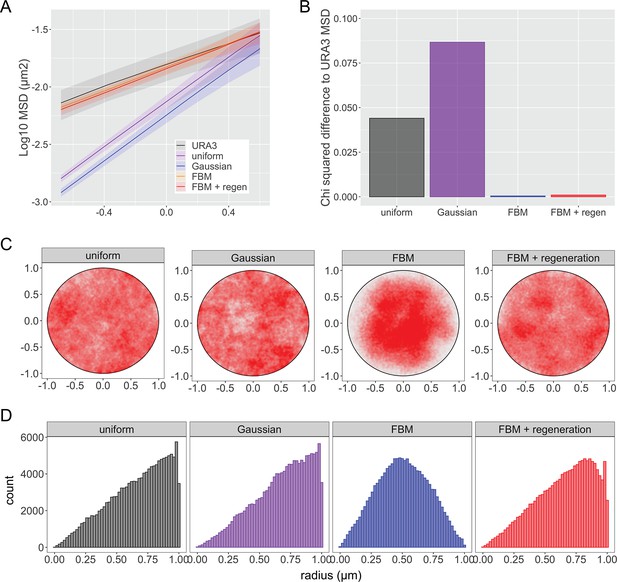
Comparison of simulations of sub-diffusion of nucleoplasmic chromatin.
Four different simulations of chromatin diffusion were compared with URA3 for MSD (A, B) or nuclear position (C, D). The uniform simulation generated uniformly distributed step sizes in the x and y dimensions with a mean step size of 0 ± 0.05 µm. The Gaussian simulation generated normally distributed step sizes in the x and y dimensions with a mean step size of 0 and a sigma of 0.025 µm. The fractional Brownian motion simulation (FBM) and a modified FBM with regeneration are detailed in Materials and methods (Γ = 0.015 μm2s−1, α = 0.52). Each simulation condition consists of 100 trajectories, each composed of 2000 steps at 210 ms step time intervals. (A) Plot of MSD for URA3 and the different simulations. (B) Χ2 sum of differences between mean MSD plots of URA3 and each simulation (t ≤ 4 s). (C) Positions generated over 5 min of 100 simulations for each type. (D) Histograms of radial positions.
Figure 4—figure supplement 2
Optimization of binding probability and retention probability by comparison with URA3:GRS1.
The probability of binding and the probability of retention were independently varied and compared with the behavior of URA3:GRS1. (A, B) Χ2 sum of differences between mean MSD plots of URA3:GRS1 and each simulation (τ ≤ 4 s). Each panel represents a set of simulated paths with the indicated probability of remaining bound (A) or the probability of binding (B). Within each panel, the probability of binding (A) or remaining bound (B) was varied. The hatched line is the C-squared difference between the simulation with both binding and retention probabilities equal to zero and MSD of URA3:GRS1, for comparison. (C, D) Percent of time per cell (C) and the percent of cells at each time (D), that loci occupied the periphery (outer 150 nm shell of 1 µm radius nucleus) for URA3, URA3:GRS1 (experimental observations from Figure 1) and each combination of binding and retention probabilities. (E) Kymographs as in Figure 1 (experimental data from Figure 1 shown in inset), for each simulated combination of binding and retention probabilities. For all panels, red boxes highlight simulations similar to URA3:GRS1 for the analyzed component.
Figure 5 with 1 supplement
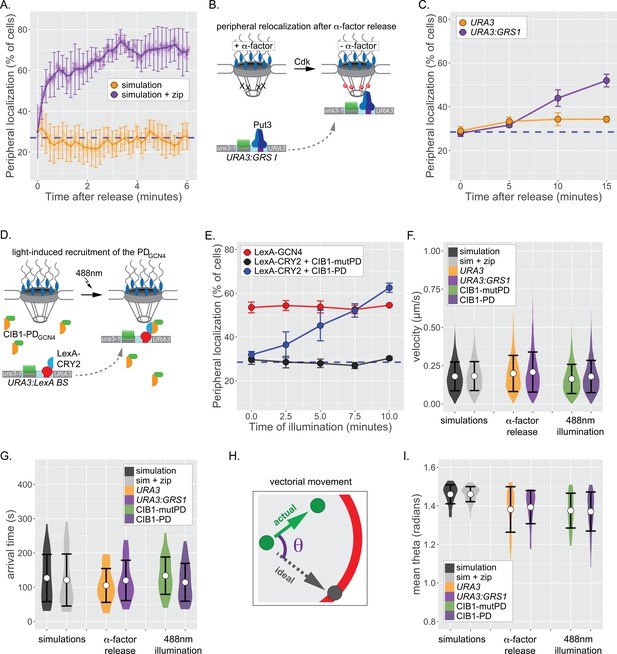
Repositioning from the nucleoplasm to the NPC.
(A) Simulated repositioning. Simulated paths, using either the fractional Brownian simulation or the simulation+zip code, were initiated at random positions within 2 µm diameter nucleus and followed for 20 min (200 ms resolution). Colocalization with the periphery (i.e., ≤150 nm from the edge) was scored for each simulation at each time and smoothed by averaging over 10 s windows. For each time point, three replicates of 33 paths were scored to generate an average (points) ± SEM (error bars). Blue, hatched line: peripheral localization expected for a random distribution. (B) Schematic for repositioning to the nuclear periphery upon release from α-factor arrest. (C) Peripheral localization (% of cells ± SEM) of URA3 or URA3:GRS1 over time after removing α-factor. (D) Schematic for optogenetic light-induced repositioning to the nuclear periphery. (E) Peripheral of URA3:LexABS in strains expressing either LexA-GCN4, LexA-CRY2+mutant PDGCN4-CIB1, or LexA-CRY2+wild-type PDGCN4 at the indicated times after illumination with 488 nm light. (F–I) Summary plots of velocity (F), arrival time (G), and angular deviation from an ideal path (I) from each cell before initial colocalization with nuclear periphery. White circles are the mean values, and error bars represent the standard deviation. For (F–I), simulated paths were initiated at random positions within a 1 µm diameter sphere in the center of the 2 µm diameter nucleus and followed for 5 min. Paths that did not make contact with the nuclear periphery were excluded.
-
Figure 5—source data 1
Comma-separated tables of simulated paths and tracking data used for Figure 5.
- https://cdn.elifesciences.org/articles/66238/elife-66238-fig5-data1-v2.zip
Figure 5—figure supplement 1
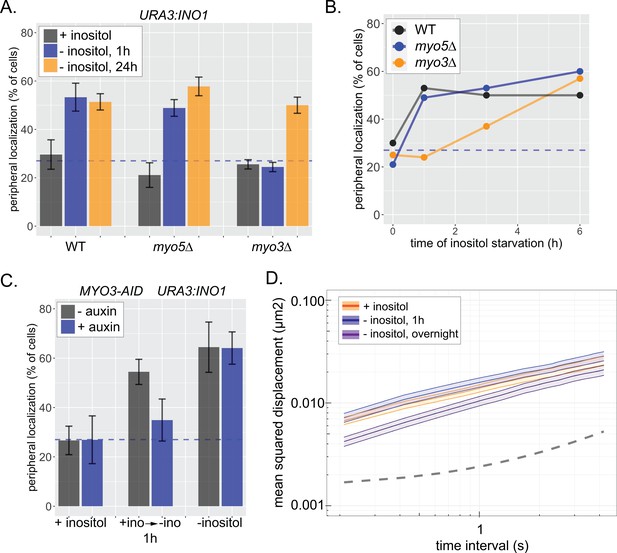
Loss of Myo3 delays GRS1-dependent repositioning to the nuclear periphery.
The URA3:INO1 locus (having GRS1 but not GRS2) tagged with the LacO array shows GRS1-dependent localization to the nuclear periphery upon activation (Ahmed et al., 2010). (A) Wild-type, myo5∆, and myo3∆ strains were scored for URA3:INO1 gene positioning under repressing (+inositol) and activating conditions (either 1 hr or 24 hr −inositol). (B) Localization of URA3:INO1 over time upon inositol starvation in wild-type, myo5∆, and myo3∆ strains. (C) URA3:INO1 localization in strains expressing Myo3 tagged with the auxin-inducible degron (AID) ±1 mM auxin for 1 hr under repressing conditions (+inositol) or under activating conditions (1 hr or 24 hr). In the case of the 1 hr −inositol condition, cells were pretreated with auxin for 1 hr before shifting into medium lacking inositol, with auxin. (D) MSD analysis of URA3:INO1 in myo3∆ cells under repressing conditions (+inositol) or under activating conditions (1 hr or 24 hr).
Figure 6
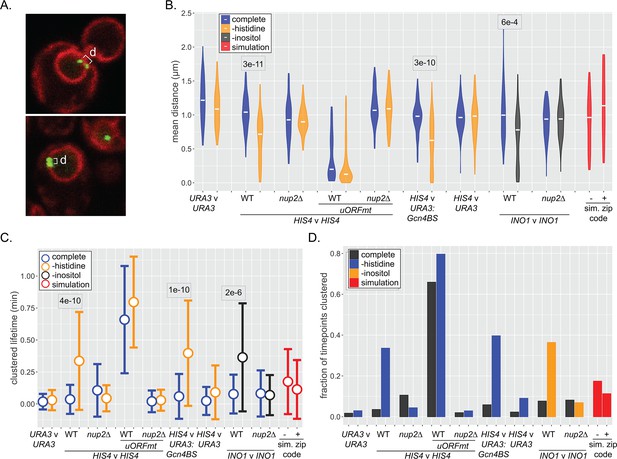
Dynamics of inter-chromosomal clustering.
(A) Confocal micrographs of diploid cells with two loci marked with LacO arrays, expressing LacI-GFP and Pho88-mCherry. Distance between LacO arrays was measured over 200 × 200 ms time points in 40–50 cells (B–D). (B) Distribution of mean distances between loci for each cell, with the median for each strain or condition indicated with a white dash. p-values<0.05 from the Kolmogorov–Smirnov test are shown. (C) Distribution of lifetimes during which d ≤ 0.55 µm. Dot = mean, error bars = SD. (D) The fraction of all time points that d ≤ 0.55 µm for each strain and media condition. For (B–D), mean distances, the lifetimes, and fraction of timepoints clustered were also determined for pairs of randomly selected simulated paths (with or without zip code; red).
-
Figure 6—source data 1
Comma-separated tables of simulated paths and tracking data used for Figures 6 and 7.
- https://cdn.elifesciences.org/articles/66238/elife-66238-fig6-data1-v2.zip
Figure 7 with 1 supplement
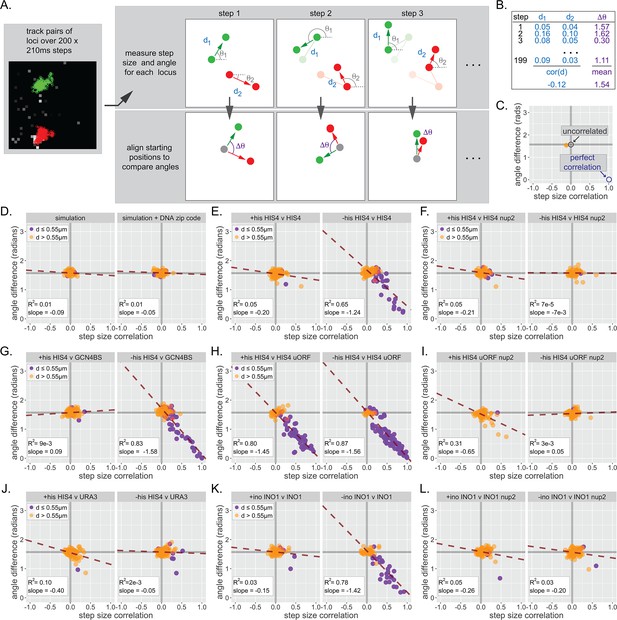
Inter-chromosomal clustering leads to coordinated movement.
(A) Workflow for tracking and analyzing movement of LacO array pairs. For each step from a time series, step distance and step angle are measured (top) and the difference in angles computed (bottom). (B) Each time series produces two values: a Pearson correlation coefficient (cor(d)) for all step sizes and a mean difference in angles (∆θ). (C) Each cell produces a single point on the summary plot (orange). Gray lines highlight cor(d) = 0 and ∆θ = π/2. Uncorrelated movement of two loci would be expected to cluster near cor(d) = 0 and ∆θ = π/2, while perfectly correlated movement would result in cor(d) = 1 and ∆θ = 0. (D–L) Summary plots for correlation analysis of the indicated pairs of loci in the indicated strains grown in the media described in the headers. Cells in which the mean distance between the loci was >0.55 µm appear in orange, while cells in which the mean distance between the loci was ≤0.55 µm appear in purple. For each plot, the slope and R2 for a linear relationship between cor(d) and ∆θ are indicated. Forty to 50 cells were analyzed per strain and condition. Simulations are the 50 pairs of paths generated for Figure 6.
Figure 7—figure supplement 1
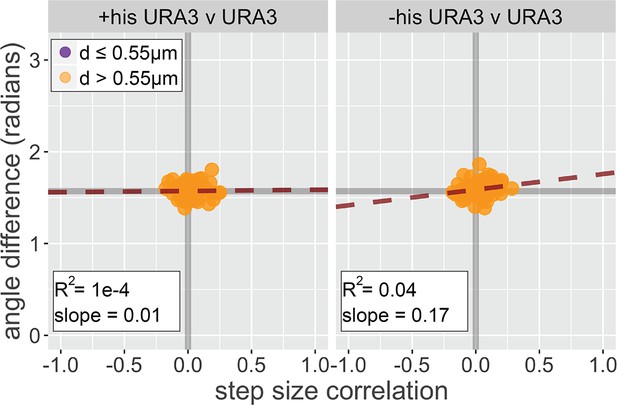
Dynamic coordination analysis of URA3.
Diploid strains having the LacO array integrated at both alleles of URA3 were grown in SDC ± histidine; the loci were tracked and analyzed for correlated step size and step angle as described for Figure 7. The slope and R2 for each plot are for a linear relationship between cor(d) and ∆θ.
Author response image 1
Additional files
-
Supplementary file 1
Mean squared displacement parameters.
- https://cdn.elifesciences.org/articles/66238/elife-66238-supp1-v2.docx
-
Supplementary file 2
Strains used in this study.
- https://cdn.elifesciences.org/articles/66238/elife-66238-supp2-v2.docx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/66238/elife-66238-transrepform-v2.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Random sub-diffusion and capture of genes by the nuclear pore reduces dynamics and coordinates inter-chromosomal movement
eLife 10:e66238.
https://doi.org/10.7554/eLife.66238
