A mechanism with severing near barbed ends and annealing explains structure and dynamics of dendritic actin networks
Figures
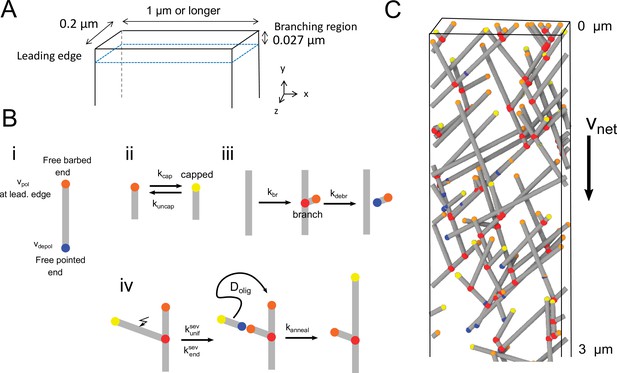
Three-dimensional model of the lamellipodial actin network.
(A) Diagram of the simulation box near the leading edge, which is positioned at (in the reference frame of the cell) with an open boundary at . The thickness of the lamellipodium in the z-direction is 0.2 µm. Periodic conditions are applied along the -direction. Filaments cannot elongate past other boundaries (representing the plasma membrane), where they either stop polymerizing or undergo kinking to elongate along the boundary. (B) Cartoons of the processes in the simulation in which filaments are represented as line segments. (i) Polymerization at free barbed and depolymerization at free pointed ends. The polymerization rate of free barbed ends away from the leading edge is assumed to occur at a lower rate. (ii) Capping and uncapping of barbed ends. (iii) Branching at 70° occurs along a filament segment within the branching region. (iv) Severing occurs with uniform rate or with a rate enhanced close to barbed ends. If severing results in a fragment of length smaller than , the oligomer fragment is assumed to undergo diffusion with diffusion coefficient (not simulated explicitly). The diffusing oligomer can anneal to a nearby free barbed, or pointed end if the oligomer is uncapped. (C) Snapshot of a simulation. Relative speed of the network with respect to leading edge is . Gray lines: actin filaments; red: Arp2/3 complex; yellow:free barbed ends; orange: capped barbed ends; blue: free pointed ends.
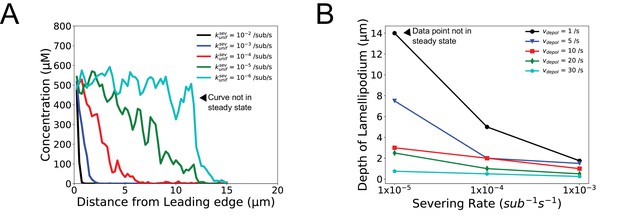
Simulated lamellipodium concentration and depth as a function of uniform severing rate and pointed end depolymerization rate .
(A) F-actin concentration profile as function of . (B) Lamellipodium depth as a function of and . The depth is the distance from the leading edge at which the concentration decreases by 50%. Both panels show the result of a single simulation at 300 s using XTC parameters listed in Table 1 (XTC parameters) but without annealing, enhanced end severing or uncapping, .

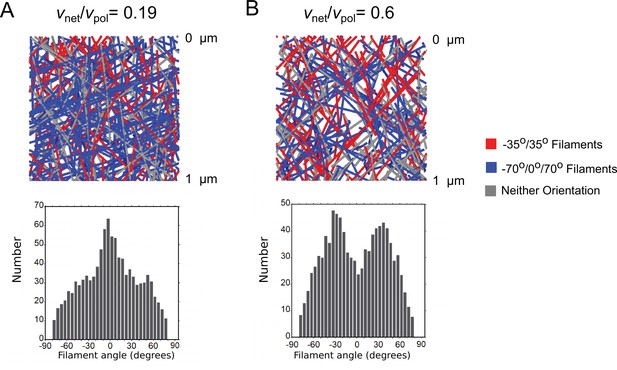
Steady-state filament orientation patterns in 2D and 3D and dependence on planar branching restriction.
(A) Orientation order parameter as a function of relative network growth speed, in a simulation where branching always occurs along the lamellipodium plane (within 1°). Numerical data with or without backward branching are compared to numerical results in 2D without backward branching from Figure S1A in Weichsel and Schwarz, 2010. For the plots, was constant and was varied. An orientation order parameter equal to 1 indicates a network with all filaments in the orientation, while –1 indicates the ±35° orientation. Vertical dashed lines indicate the critical for filaments at 70° and 35° along the lamellipodium plane. (B) Same as panel A but for a 3D simulation in which 70° branching occurs at random orientation or uniformly within 10° of the lamellipodium plane, without backward branching. The filament orientation is calculated from the filament projection along the lamellipodium plane. Uniform branching leads to a less ordered network, even when kinking of filaments hitting a boundary is implemented. (C) Top: 3D simulation snapshots, colored by orientation pattern, for (no kinking). Bottom: orientation distribution of filaments with a portion located within 1 µm of the leading edge, average of 5 simulations reaching steady state. Restricting branching along the lamellipodium plane sharpens the orientation pattern. (D) Same as panel C, for (no kinking), showing that restricting branching along the lamellipodium plane sharpens the ±35° orientation pattern. Parameters are as listed in Table 1 (keratocyte parameter set) with sub/s, but with no oligomer annealing or enhanced end severing: .
Addition of kinking does not effect the orientation pattern.
(A) Top: 3D simulation snapshots, colored by orientation pattern, for with kinking. Bottom: orientation distribution of filaments with a portion located within 1 µm of the leading edge, average of 5 simulations reaching steady state. Addition of kinking does not significantly alter the orientation distribution compared to the uniform 3D branching of Figure 2C. (B) Same as panel A, for with kinking, showing that kinking does not significantly change the orientation distribution compared to the uniform 3D branching of Figure 2D. Snapshots are taken from simulations with a branching rate of 75/sub/s and other parameters as in Table 1 (keratocyte parameters) with sub/s, and no annealing or enhanced end severing, .

The model without annealing cannot reproduce both the actin speckle lifetime and F-actin concentration profiles.
(A) Comparison of optimized parameters of model with uniform severing or model with enhanced barbed end severing to experiments in keratocytes. Left: Probability density of simulated actin speckle lifetimes and comparison to SiMS measurements in Yamashiro et al., 2014. Distributions were normalized between 2 and 60 s, to exclude short lifetimes beyond experimental resolution. Right: F-actin concentration profile for keratocyte parameters. Keratocyte parameters as in Table 1 with /sub/s; sub (black) and /sub/s; /sub/s; sub (red). Increasing the severing rate near the barbed end to better match the short speckle lifetime experimental peak leads to short lamellipodium. (B) Comparison of optimized parameters of model with uniform severing or model with enhanced barbed end severing to experiments XTC cells by Watanabe and Mitchison, 2002 (as they were corrected for photobleaching). Same as panel A, with probability density of speckle lifetimes normalized between 4 and 144 s. XTC parameters as in Table 1 with , and sub/s; sub (black) or /sub/s; /sub/s; sub (red). Concentration profiles are the average of 5 simulations in steady state. Speckle lifetimes measured for speckles within 12 µm of the leading edge over a 20 s interval in steady state for 5 simulations.
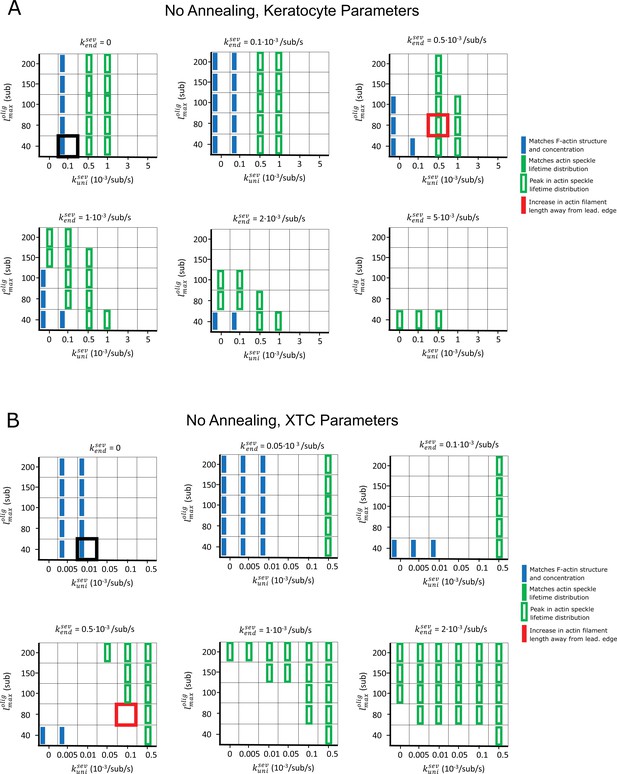
Parameter scan of uniform severing and enhanced end severing rates (, ) and maximum oligomer length () without annealing.
Parameters are listed in Table 1, without annealing or debranching: . Boxes highlighted with thick black and red frames correspond to the parameters used in the black and red curves of Figure 3. Blue rectangles indicate that F-actin, barbed end, and branch concentration profiles agree with experimental observations. Open green rectangles indicate that the simulated actin speckle lifetimes peaked at short times, but not within 2 s (keratocyte) or 4 s (XTC). No parameter combinations matched the SiMS speckle lifetime distribution and appearance or disappearance profiles (solid green) or provided a length increase away from the leading edge (red). (A) Keratocyte parameter scan. (B) Same as panel A, for XTC cells.
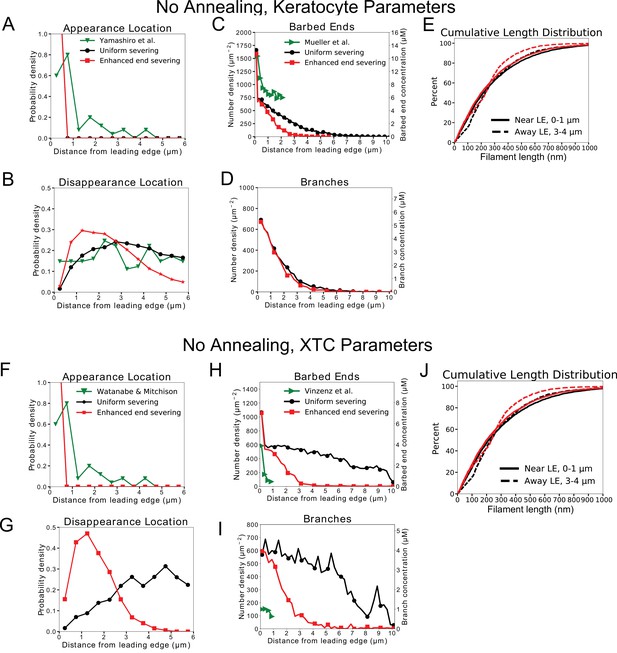
Quantification of model without annealing that did not reproduce the actin speckle lifetime and F-actin concentration profiles (continuation of Figure 3).
Results for models with uniform severing (black) or model with severing, enhanced near barbed end (red). (A–E) Keratocyte parameters as in Table 1 with /sub/s; sub (black) and /sub/s; /sub/s; sub (red). (A) Simulated actin speckle appearance location and comparison to Yamashiro et al., 2018. Distributions were normalized within the indicated range, considering speckles with lifetimes longer than 2 s. (B) Same as C, for disappearance location. (C) Distribution of barbed ends and comparison to measurements in Mueller et al., 2017. (D) Concentration of simulated Arp2/3 complex branches. (E) Cumulative filament length distributions near (, solid) and away from the leading edge (, dashed). (F–J) Same as A-E for XTC cells and comparing to experimental data by Watanabe and Mitchison, 2002 or Vinzenz et al., 2012. XTC parameters as in Table 1 with /sub/s; sub (black) or /sub/s; /sub/s; sub (red). (F,G) Distributions were normalized within the indicated range, considering speckles with lifetimes longer than 4 s. Data averaged over five independent simulations. Speckle data measured for speckles within 12 µm of the leading edge over a 20 s interval in steady state for each simulations.

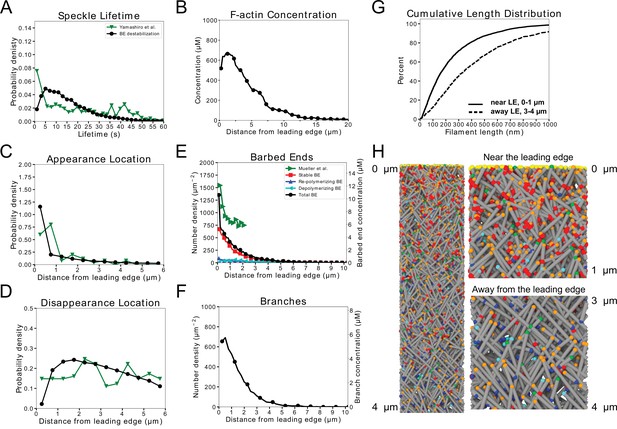
Model results for optimized parameters of model for keratocytes with uniform severing and annealing (black) or model with annealing and severing, enhanced near barbed end (red).
The latter case provides good agreement with SiMS data, actin network structure, and filament length increase away from the leading edge. (A) Probability density of simulated actin speckle lifetimes and comparison to SiMS measurements in Yamashiro et al., 2014. Distributions were normalized between 2 and 60 s, to exclude short lifetimes beyond experimental resolution. (B) F-actin concentration profile. The oligomeric actin concentration (within 0–10 µm) was less than 0.1% of F-actin in that region. (C) Simulated actin speckle appearance location and comparison to Yamashiro et al., 2014. Distributions were normalized within the indicated range, considering speckles with lifetimes longer than 2 s. (D) Same as C, for disappearance location. (E) Distribution of barbed ends and comparison to measurements in Mueller et al., 2017. The experimental data are plotted according to the left y-axis. The concentrations on the right -axis use the model’s assumed lamellipodial thickness. (F) Concentration of simulated Arp2/3 complex branches. (G) Cumulative filament length distributions near (, solid) and away from the leading edge (, dashed). (H) Snapshot of simulation with enhanced end severing (left). Zoomed in views close and away from the leading edge (right). Lamellipodium width is 1 µm. Gray lines: actin filaments; red: Arp2/3 complex. Parameters are listed in Table 1 (keratocyte parameters). The simulation with uniform severing used /sub/s; sub and with enhanced end severing /sub/s; sub/s; sub. Data averaged over 5 independent simulations. Speckle data measured for speckles within 12 µm of the leading edge over a 20 s interval in steady state for 5 simulations.
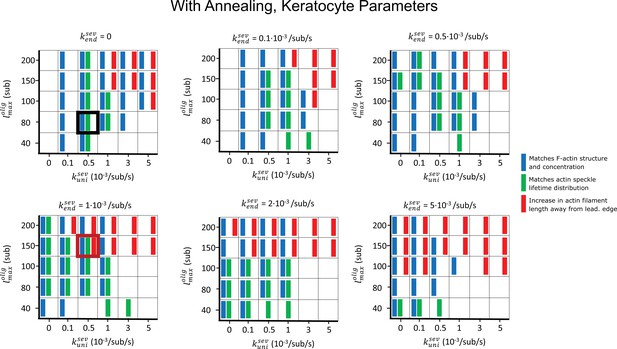
Parameter scan of uniform and enhanced end severing rates (, ) and maximum oligomer length (), with oligomer annealing but no debranching .
Other parameters are listed in Table 1. Boxes highlighted with thick black and red frames correspond to the parameters used in the black and red curves of Figure 4. Blue rectangles indicate that F-actin, barbed end, and branch concentration profiles agree with experimental observations. Green rectangles indicate that speckle lifetimes, appearance and disappearance locations agreed with the results of SiMS measurements. Red rectangles indicate an increase in length between the filament lengths measured in and .

Additional quantification of model results for keratocytes with annealing and uniform severing (top row), or annealing and severing enhanced near barbed ends (bottom row).
Parameters same as in Figure 4. (A,D) Profile of fraction of capped and uncapped barbed ends. Their ratio is approximately uniform in space and determined by . In our model, a significant number of barbed ends must be available for annealing, so any capping mechanism (through capping protein specifically or other protein) should be transient. The concentration profiles do show a significant fraction of uncapped ends, though the precise value of this ratio or the capping protein profile across the leading edge is not heavily constrained by our model. (B,E) Distribution of oligomer sizes. The distribution is approximately uniform between 0 and , as a result of our assumption of uniform severing within the enhanced severing region, with modifications due to oligomer creation through pointed-end disassembly, debranching, and from severing into two oligomers. (E,F) Concentration profile of F-actin depending on the origin of F-actin through polymerization as monomer or oligomer annealing. The calculation was performed by tracking the origin of simulated actin speckles. The two curves add up to the give the total concentration profile of Figure 4. All data is taken after the system has been in steady state for at least 50 s and averaged over 5 simulations.
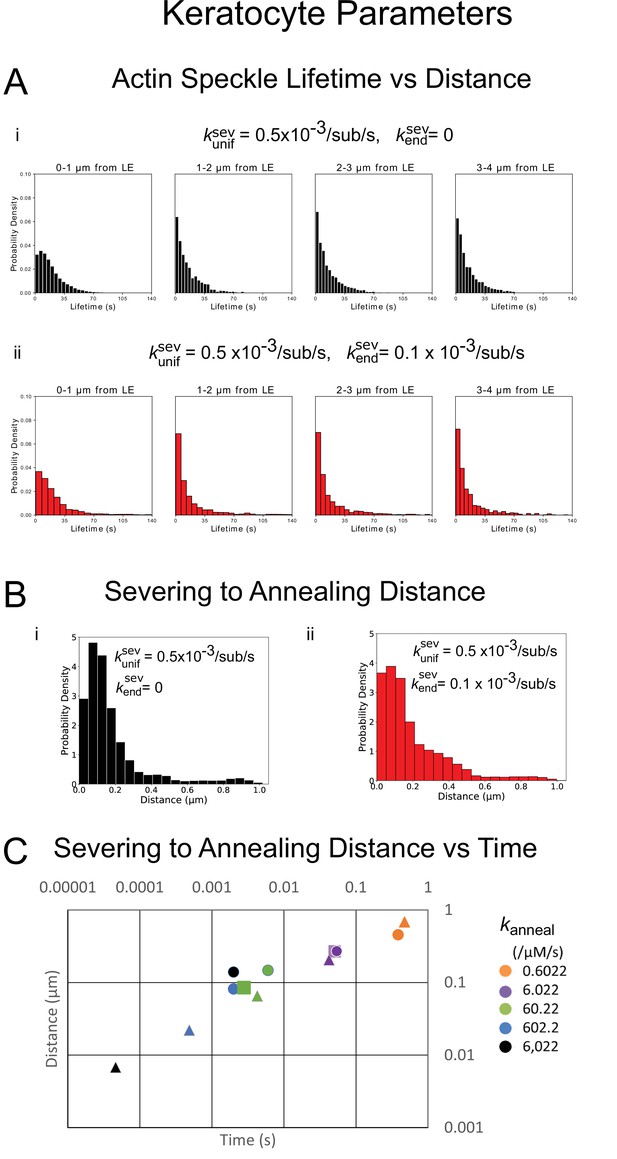
Quantification of actin turnover in simulations with severing and annealing of keratocyte parameters from 5 simulations in steady-state over 20 s each.
(A) Probability density of simulated actin speckle lifetimes separated into 1 µm regions based on their appearance location for parameters with annealing and uniform severing (i, black) or with enhanced end severing (ii, red). (B) Probability density of the distance between the location the oligomer was created (within 4 µm of the leading edge) and annealing position for parameters with annealing and uniform severing (i, black) or with enhanced end severing (ii, red). (C) Log-log plot of the median distance traveled by an oligomer in between severing and annealing versus the median time spent diffusing, for various annealing rate constants. This plot serves as a check of the effect smallness of simulation time step. Triangles are the expected values from with and is average concentration of free barbed ends. Circles are values from simulations with the standard time step, s. Squares show simulations with a smaller time step of s. The simulated lamellipodium width was 1 µm. For 602.2 µM-1s-1, the simulation results are limited by the chosen time step.
Results of alternate model for keratocytes with frequent barbed end depolymerization followed by rapid repolymerization (Video 5).
In this model uncapped barbed ends have a 50% chance of undergoing rapid depolymerization and 50% of chance of repolymerizing before recapping or completely depolymerizing. See Materials and methods for other parameters. (A–G) Same graphs as Figure 4 but for the alternate model. Panel E now shows the concentration profiles of all barbed end types. The model shows some agreement with SiMS data (panel A) but lacks a peak at short lifetimes (however we note that we cannot exclude better agreement with finer parameter tuning). The model also shows a broad F-actin concentration profile (panel B) and an increase in filament length with distance from the leading edge. (H) Simulation snapshot. Red: branches; yellow: barbed ends not yet capped; orange: capped barbed ends; cyan: rapidly depolymerizing barbed ends; green: repolymerizing barbed end; blue: pointed ends. Results are averaged over 5 simulations. Speckle data measured for speckles within 12 µm of the leading edge over a 20 s interval in steady state for each simulations.
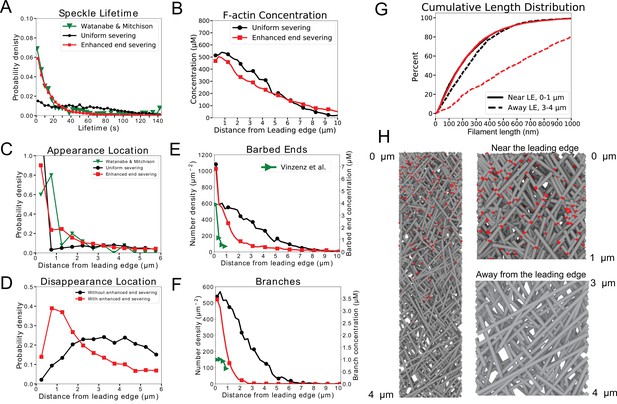
Model results for optimized parameters of model for XTC cells with uniform severing and annealing (black) or model with annealing and severing, enhanced near barbed end (red).
The latter case provides good agreement with SiMS data and actin network structure; it can also lead to filament length increase away from the leading edge. (A–H) Panels are the same as Figure 4 but comparing to SiMS data of Watanabe and Mitchison, 2002 (as they were corrected for photobleaching) on XTC cells and structural data from fibroblasts by Vinzenz et al., 2012. In panel A, the distributions were normalized between 4 and 144 s. The fraction of oligomers is less than 0.1%. In panels E,F, the experimental data are plotted according to the left -axes; the concentrations on the right y-axes use the model’s assumed lamellipodial thickness. The simulation with uniform severing used /sub/s; sub and with enhanced end severing /sub/s; /sub/s; sub. Other parameters listed in Table 1 (XTC parameters).
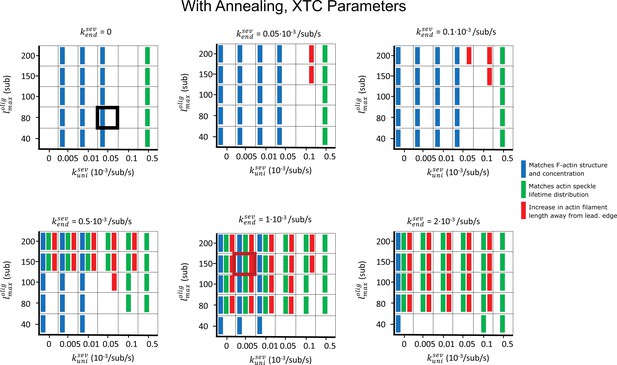
Parameter scan of uniform and enhanced end severing rates (, ) and maximum oligomer length (), with oligomer annealing but no debranching .
Other parameters are listed in Table 1. Boxes highlighted with thick black and red frames correspond to the parameters used in the black and red curves of Figure 5. Blue rectangles indicate that F-actin, barbed end, and branch concentration profiles agree with experimental observations. Green rectangles indicate that speckle lifetimes, appearance and disappearance locations agreed with the results of SiMS measurements. Red rectangles indicate an increase in length between the filament lengths measured in and .
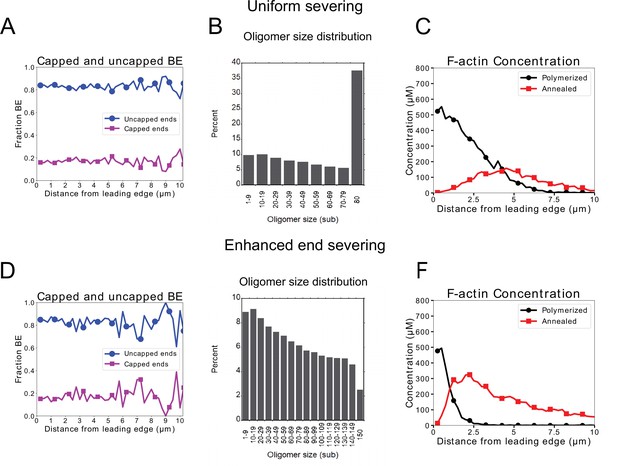
Additional quantification of model results for XTC cells with annealing and uniform severing (top row), or annealing and severing enhanced near barbed ends (bottom row).
Parameters same as in Figure 5. (A,D) Profile of fraction of capped and uncapped barbed ends. Their ratio is approximately uniform in space and determined by . In our model, a significant number of barbed ends must be available for annealing, so any capping mechanism (through capping protein specifically or other protein) should be transient. The concentration profiles do show a significant fraction of uncapped ends, though the precise value of this ratio or the capping protein profile across the leading edge is not heavily constrained by our model. (B,E) Distribution of oligomer sizes. The distribution is approximately uniform between 0 and , as a result of our assumption of uniform severing within the enhanced severing region, with modifications due to oligomer creation through pointed-end disassembly, debranching, and from severing into two oligomers. (E,F) Concentration profile of F-actin depending on the origin of F-actin through polymerization as monomer or oligomer annealing. The calculation was performed by tracking the origin of simulated actin speckles. The two curves add up to the total concentration profile of Figure 5. All data is taken after the system has been in steady state for at least 50 s and are averaged over 5 simulations.

Repeat of simulations of Figure 5 (XTC cells) with doubled branching rate .
(A–G) Repeat of simulations of Figure 5 (XTC cells) with doubled branching rate . Doubling the branching rate in the XTC parameter set results in concentrations closer to prior estimates for XTC cells but the barbed end and branch concentrations become larger than the measurements of Vinzenz et al. for fibroblasts. Black and red curves are the same data as in Figure 5 for uniform or enhanced end severing, respectively. Gray curves show the case of uniform severing as in the black curve, but with doubled . Magenta curves show the case of enhanced severing as in the red curve but with doubled . Gray and magenta results are from one simulation evolved to steady state. (H) Simulation snapshot for case of enhanced end severing and doubled as in magenta curves.

Comparison of enhanced end severing simulation of Figure 5 (XTC cells) where polymerizing ends cannot be severed to same parameter set where they can be severed.
(A–G) Same as Figure 5 panels. Red is for the simulation where end severing was excluded from barbed ends located within 0.1µm of the leading edge or polymerizing. This was implemented to allow the network to form under very high severing rates. Magenta curves are from a simulation where all barbed ends could sever. There is no significant difference between these two simulations. (H) Simulation snapshot for case of enhanced end severing where all barbed ends would sever (magenta curves). Results are averaged over 5 simulations. Speckle data measured for speckles within 12 µm of the leading edge over a 20 s interval in steady state for each simulations.
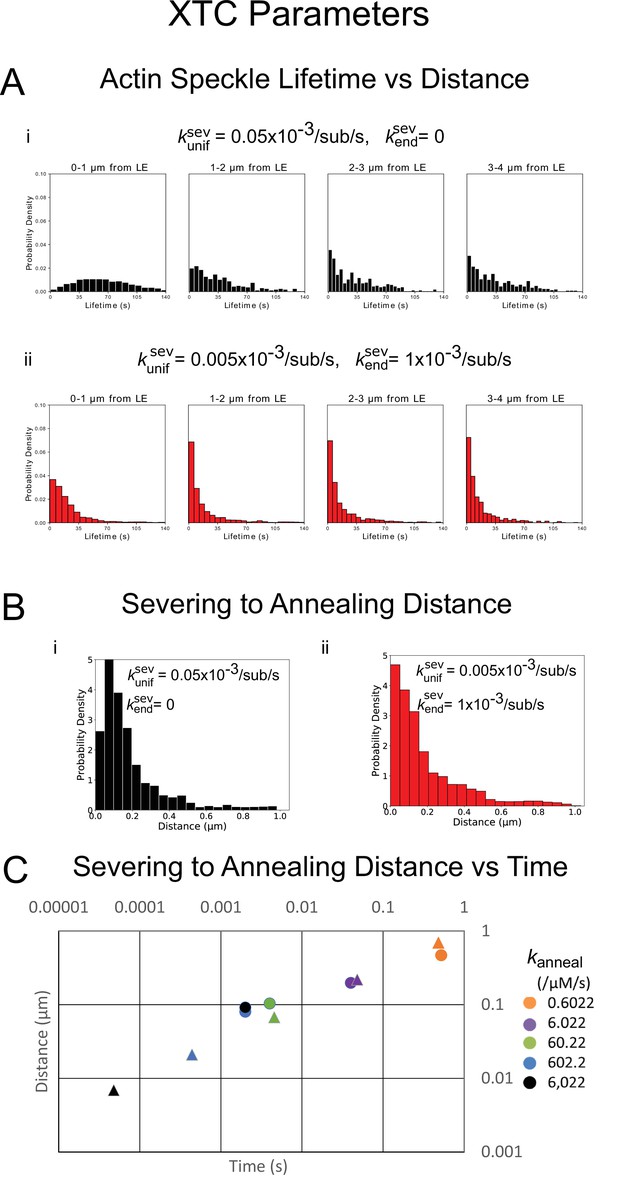
Quantification of actin turnover in simulations with severing and annealing of XTC parameters from 5 simulations in steady-state over 20 s each.
(A) Probability density of simulated actin speckle lifetimes separated into 1 µm regions based on their appearance location for parameters with annealing and uniform severing (i, black) or with enhanced end severing (ii, red). (B) Probability density of the distance between the location the oligomer was created (within 4 µm of the leading edge) and annealing position for parameters with annealing and uniform severing (i, black) or with enhanced end severing (ii, red). (C) Log-log plot of the median distance traveled by an oligomer in between severing and annealing versus the median time spent diffusing, for various annealing rate constants. This plot serves as a check of the effect smallness of simulation time step. Triangles are the expected values from with and is average concentration of free barbed ends. Circles are values from simulations with the standard time step, s. The simulated lamellipodium width was 1µm. For 602.2 µM-1s-1, the simulation results are limited by the chosen time step. Used a maximum oligomer length sub.
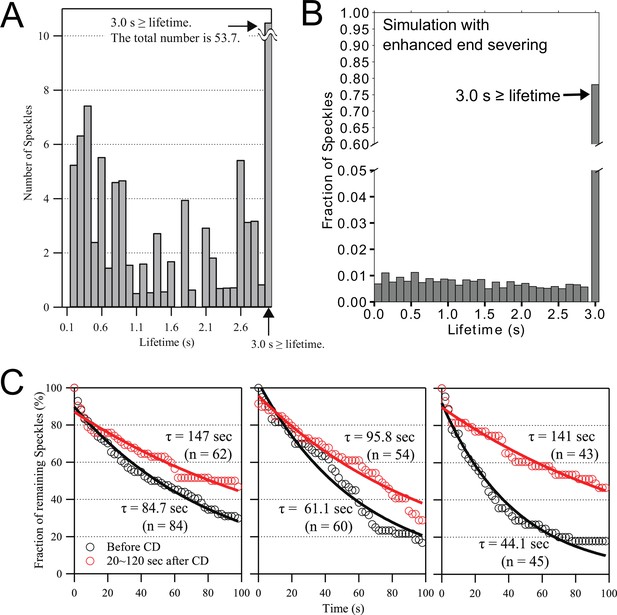
SiMS experiments support rapid disassembly of newly-assembled actin filaments near the leading edge, with disassembly inhibited by cytochalasin D.
(A) Lifetime distribution of Dylight 550 actin speckles that appeared within ~0.5 µm of the leading edge of XTC lamellipodia, imaged for 10 s at 0.1 s/frame (n=6 cells, total number of speckles = 124). Lifetimes of 0.1 s are omitted as being beyond the temporal resolution limit. Right end bar indicates the sum of lifetime at 3 s or more. (B) Simulated actin speckle lifetime distribution for the case of enhanced end severing and annealing of XTC parameters in Figure 5, except that end severing was allowed to occur on any barbed end, including polymerizing ones (which does not have any significant influence on the results of Figure 5, see Figure 5—figure supplement 4). The fraction of lifetimes longer than 3 s were 79% (the fraction becomes 90 % if we exclude end severing of polymerizing ends). Lifetimes were averaged over 5 independent simulations and over 20 s in steady state for speckles within 1 µm of the leading edge. (C) The disassembly rate of Dylight 550 actin SiMS in lamellipodia of XTC cells was decreased by the treatment of 5 µM cytochalasin D (CD). The number of single-molecule speckles in lamellipodia were determined in one reference frame, and the reduction in the number was followed over subsequent frames. Data are from three experiments. Black and red lines are single exponential fits with decay time . Mean of and the standard deviation are 63.3 ±16.6 s before treatment and 128 ±22.8 s for 20–120 s after treatment. The increase in is statistically significant (P=0.024; paired t-test).
-
Figure 6—source data 1
SiMS SpeckleTrackerJ output for panel A.
- https://cdn.elifesciences.org/articles/69031/elife-69031-fig6-data1-v3.xlsx
-
Figure 6—source data 2
SiMS SpeckleTrackerJ output for panel C.
- https://cdn.elifesciences.org/articles/69031/elife-69031-fig6-data2-v3.xlsx
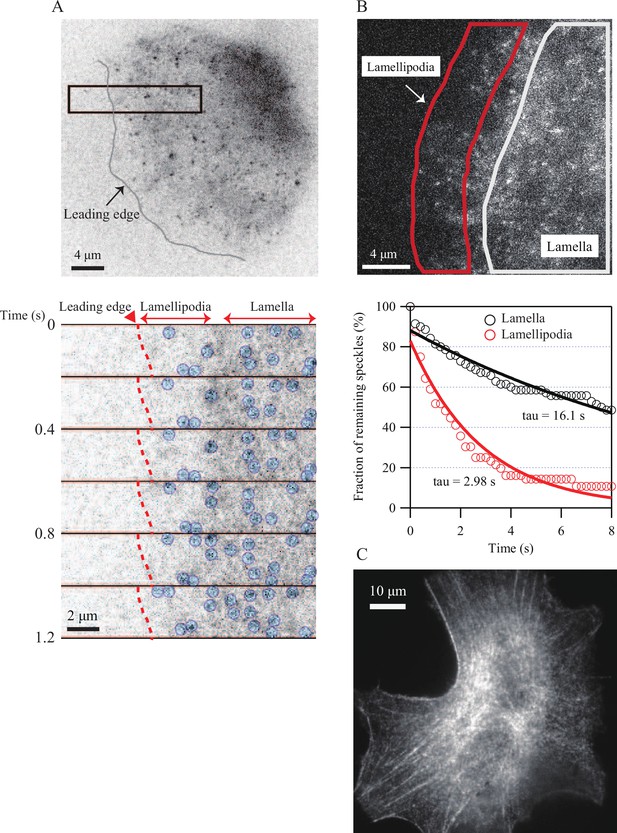
Tropomyosin imaging in XTC cells.
(A) Representative images of tropomyosin single-molecule speckles (SiMS) in a lamellipodium of XTC cells spreading on poly-L-lysine-coated glass coverslips for 30 min. Time-lapse images in the black square of the top image are paneled. The gray line indicates the leading edge. Red dashed lines and blue circles indicate the leading edge and tropomyosin SiMS, respectively. Note that tropomyosin SiMS are less abundant in lamellipodia than in lamella. (B) The dissociation rate of tropomyosin SiMS in lamellipodia and in lamella. The reduction in the numbers of tropomyosin SiMS identified in one frame was followed over subsequent frames. The decay time tau is shown after normalization for the photobleaching rate, 0.016 s-1. The data are from 56 speckles in lamellipodia and 70 speckles in lamella. (C) Association of tropomyosin-EGFP with actin stress fibers in an XTC cell after 24 hr in the presence of fetal calf serum.
-
Figure 6—figure supplement 1—source data 1
SiMS SpeckleTrackerJ output for panel B.
- https://cdn.elifesciences.org/articles/69031/elife-69031-fig6-figsupp1-data1-v3.xlsx
Videos
Simulated keratocyte lamellipodium.
Video of simulated keratocyte lamellipodium in the rest frame of the cell (0–4 µm with the leading edge located at the top) for the enhanced end severing parameter set (Figure 4). Oligomer fragments not shown. Fragments of filaments that appear correspond to annealing events and fragments that disappear to the creation of oligomers. End severing events are shown by disappearance of fragments near barbed ends. Uniform severing events can be identified by the appearance of pairs of pointed and barbed ends. Some filaments overlap one another as we do not have excluded volume interactions. Few filaments near the leading edge can be seen polymerizing after uncapping. These barbed ends were annealed to by a polymerizing oligomer created by uniform severing. The barbed end state of the oligomer was transferred to the filament resulting in a polymerizing filament away from the leading edge. Gray lines: actin filaments; red: Arp2/3 complex; yellow:free barbed ends; orange: capped barbed ends; blue: free pointed ends. Each frame is 0.1 s. Leading edge is 2 µm wide.
Simulated XTC lamellipodium.
Simulated keratocyte actin SiMS.
Simulated actin SiMS for the enhanced end severing keratocyte parameter set (Figure 4) with 0.01% of actin monomers tracked. Speckles are positioned based on the actin monomer location. Each frame is a collection of the appearance, disappearance, and motion within 1 s. Speckles that appeared within 1 s are colored in orange and located at their appearance location. Blue speckles remained associated to the network throughout the time range and are relocating with retrograde flow. Speckles that disappeared within this time frame are colored green and located at the disappearance location. Time stamp indicates the beginning of the 1 s interval.
Simulated XTC cell actin SiMS.
Simulated keratocyte lamellipodium with frequent barbed end rapid depolymerization.
Same as Video 1, using parameters for keratocyte cells but with no enhanced end severing, no annealing, and frequent barbed end rapid depolymerization and repolymerization. Gray lines: actin filaments; red: Arp2/3 complex; yellow:free barbed ends; orange: capped barbed ends; blue: free pointed ends not yet capped; cyan: rapidly depolymerizing barbed ends; green: repolymerizing barbed ends. Stationary green ends are barbed ends that do not polymerize because they have reached the top or bottom cell boundary (since filament kinking is turned off).
SiMS of TPM-EGFP in XTC cells.
The Video corresponds to Figure 6—figure supplement 1. Time shown in s.
Tables
Parameter table for simulations.
| Parameter | Name | Keratocyte Value | XTC Value | Reference/Justification |
|---|---|---|---|---|
| Polymerization rate at leading edge | 150 sub s-1 | 38 sub s-1 | Matches observed protrusion rate | |
| Pointed end depolymerization rate | 5 sub s-1 | 5 sub s-1 | Wioland et al., 2017; Johnston et al., 2015 | |
| Capping rate | 0.6 s-1 | 0.2 s-1 | Estimated (Materials and methods) | |
| Uncapping rate | 1.0 s-1 | 1.0 s-1 | Miyoshi et al., 2006 | |
| Branching rate | 150 s-1µm-1 | 30 s-1µm-1 | Estimated (Materials and methods) | |
| Debranching rate | 0.1 s-1 | 0* | Narrower distribution of Arp2/3 complex compared to F-actin (Lai et al., 2008, Miyoshi et al., 2006, Ryan et al., 2012) | |
| Network velocity with respect to leading edge | 0.2µm s-1 | 0.05µm s-1 | ||
| Uniform severing rate | Varied | Varied | ||
| Severing rate near barbed end | Varied | Varied | ||
| Annealing rate constant | 60µM-1s-1 | 60µM-1s-1 | Close to Popp et al., 2007 | |
| Maximum oligomer size | Varied | Varied | ||
| Oligomer diffusion coefficient | 0.25µm2 s-1 | 0.25µm2 s-1 | Estimated |
-
*Since severing and depolymerization contributed to debranching in XTC cells, we did not include a separate debranching rate constant.
Barbed end, branch and filament number for fibroblast cells in Vinzenz et al., 2012 and keratocyte cells from Mueller et al., 2017 for lamellipodia region of 1µm.
Since the leading edge is not well defined in the EM tomograms, we consider the leading edge to begin at the maximum barbed end value but we also include the number of barbed ends that would be considered outside the cell (with this definition) in the region of 0–0.212 µm.
| Quantity | Fibroblast | Fibroblast | Keratocyte | Keratocyte |
|---|---|---|---|---|
| Region (µm) | Value (µm-1) | Region (µm) | Value (µm-1) | |
| Barbed ends (first bin) | 0–0.25 | 145 | 0–0.212 | 309 |
| Barbed ends (second bin) | 0.25–0.5 | 42.5 | 0.212–0.424 | 238 |
| Branches (first bin) | 0–0.25 | 37.5 | N/A | N/A |
| Branches (second bin) | 0.25–0.5 | 37.5 | N/A | N/A |
| Pointed ends (first bin) | N/A | N/A | 0–0.212 | 91 |
| Pointed ends (second bin) | N/A | N/A | 0.212–0.424 | 231 |
| Filaments (first bin) | 0–0.25 | 150 | 0–0.106 | 200 |
| Filaments (second bin) | 0.25–0.5 | 130 | 0.106–0.212 | 256 |





