Figures and data in Cost-precision trade-off relation determines the optimal morphogen gradient for accurate biological pattern formation

Figures
Tables
Additional files

8 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

Positional information transfer by the morphogen gradient.

(Top) The specification of the anterior region of the fruit fly embryo. The uniformly distributed nuclei (gray circles) are subjected to different concentrations of the morphogen (red dots) in the local environment, which leads to the anterior expression of the target gene (blue shade). (Bottom) The red and blue lines respectively depict the morphogen profile, $ρ (x)$ , and the target gene expression, $g (x)$ , which together specify cell fate. The squared positional error at the boundary $x_{b}$ , $σ_{x}^{2} (x_{b})$ , is defined as the product between the variance of the morphogen concentration, $σ_{ρ}^{2} (x_{b})$ , and the squared inverse slope of the morphogen profile, ${(\partial_{x} ρ (x))}_{x = x_{b}}^{- 2}$ .

Figure 2 with 1 supplement

Download asset Open asset

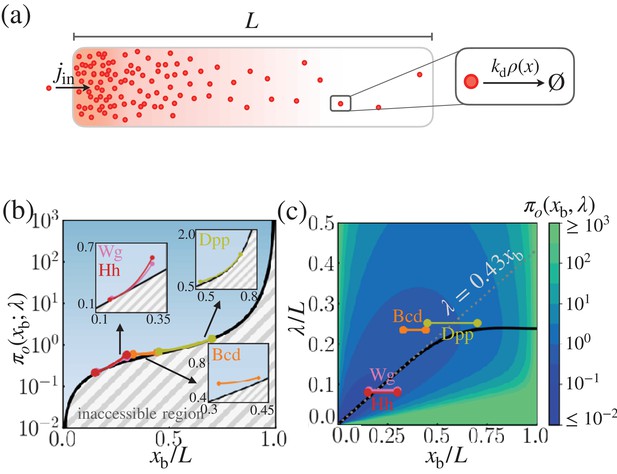
Cost-precision trade-off associated with the point measurement.

(a) Schematic of the model. (b) The position-dependent lower bound of the trade-off product $π_{o, \min} (x_{b})$ , obtained numerically. The gray hashed area represent the inaccessible regions. The trade-off product of the morphogen profiles of Bcd, Wg, Hh, and Dpp are shown in the respective insets. (c) The black line denotes the optimal characteristic decay length ( $λ_{\min}$ ) with respect to the position $x_{b} / L$ . The color scale indicates the trade-off product $π_{o} (x_{b})$ computed for each pair of $λ / L$ and $x_{b} / L$ values. The grea dotted line depicts the linear approximation of $λ_{\min}$ at large $L$ . In (b) and (c), the depicted trade-off product is normalized by $α_{o} L / l_{cell}$ . The parameters for the naturally occurring morphogen profiles are further described in Appendix 3, Length scales of Bcd, Wg, Hh, and Dpp, and Appendix 3—table 1.

Figure 2—figure supplement 1

Download asset Open asset

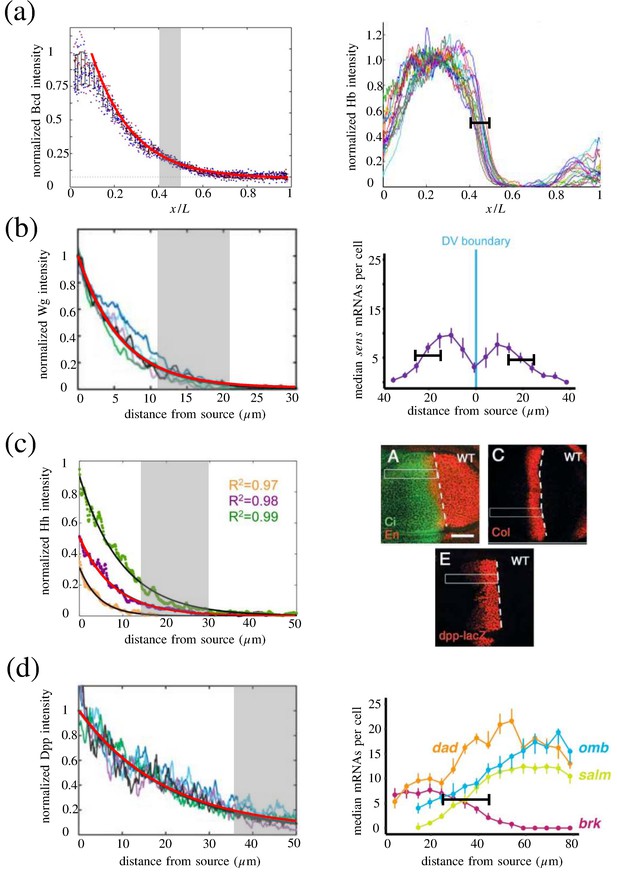
Length scales of naturally occurring morphogen profiles.

Length scales of naturally occurring morphogen profiles. The left column depicts the exponentially decaying morphogen profiles. The solid red lines denote the exponentially decaying profiles with the associated λ’s in Appendix 3—table 1. The gray shaded regions depict the respective range of target boundary positions. The right column depicts the target gene expression profiles from which the range of boundary positions are obtained. (a) (Left) Bcd morphogen profile. (Right) Bcd target Hb profile. (b) (Left) Wg morphogen profile. (Right) Wg target *sens* gene expression profile. (c) (Left) Hh morphogen profile. The colors green, purple, and orange correspond to different stages of development. The characteristic decay length corresponding to the purple profile, $λ \approx 8 μ m$ , was used in Figures 2 and 3 of the present work. (Right) Hh target Engrailed, Collier, and Dpp profiles. The white dotted line denotes the AP border, as specified by the staining of Ci. The length of the expression domains of the target genes were estimated from the 50 $μ m$ scale bar. (d) (Left) Dpp morphogen profile. (Right) Dpp target gene expression profiles. In the right column of (**a,b,d**), the black intervals denote the range of boundary positions, $x_{b}$ . (a) Panel 1 is reprinted from Figure 5 Cell, 130(1), Gregor, T., Tank, D. W., Wieschaus, E. F., and Bialek, W., Probing the Limits to Positional Information, 153–164, Copyright (2007), with permission from Elsevier. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (a) Panel 2 is reprinted from Figure 3 Current Biology, 22(23), Perry, M. W., Bothma, J. P., Luu, R. D., and Levine, M., Precision of hunchback expression in the *Drosophila* embryo, 2247–2252, Copyright (2012), with permission from Elsevier. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (b) Panel 1 is reproduced from Figure 3, Kicheva, A., Pantazis, P., Bollenbach, T., Yannis, K., Bittig, T., Frank, J., and González-Gaitán, M. (2007). Kinetics of Morphogen Gradient Formation. Science, 315 (5811):521–525. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (b) Panel 2 reproduced from Figure 1 (Bakker et al., 2020). (c) Panel 1 is reproduced from Figure S2, Wartlick, O., Mumcu, P., Kicheva, A., Bittig, T., Seum, C., Jülicher, F., and González-Gaitán, M. (2011). Dynamics of Dpp signaling and proliferation control. Science, 331 (6021):1154–1159. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (c) Panel 2 is reproduced from Figure 5, Torroja, C., Gorfinkiel, N., and Guerrero, I. (2004). Patched cotrols the Hedgehog gradient by encocytosis in a dynamin-dependent manner, but this internalization does not play a major role in signal transduction. Development, 131(10):2395–2408, https://doi.org/10.1242/dev.01102, with permission from The Company of Biologists. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (d) Panel 1 is reproduced from Figure 1, Kicheva, A., Pantazis, P., Bollenbach, T., Yannis, K., Bittig, T., Frank, J., and González-Gaitán, M. (2007). Kinetics of Morphogen Gradient Formation. Science, 315 (5811):521–525. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder. (d) Panel 2 reproduced from Figure 2 (Bakker et al., 2020).

© 2007, Elsevier. Figure 2—figure supplement 1A panel 1 is reprinted from Figure 5 Gregor et al., 2007, Copyright (2007), with permission from Elsevier. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2012, Elsevier. Figure 2—figure supplement 1A panel 2 is reprinted from Figure 3 Perry et al., 2012, Copyright (2007), with permission from Elsevier. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2007, The American Association for the Advancement of Science. Figure 2—figure supplement 1B panel 1 is reproduced from Figure 3, Kicheva et al., 2007. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2020, AAAS. Figure 2—figure supplement 1B panel 2 reproduced from Figure 1 Bakker et al., 2020. Reprinted with permission from AAAS Creative Commons Attribution 4.0 International Public License.

© 2011, The American Association for the Advancement of Science. Figure 2—figure supplement 1C panel 1 is reproduced from Figure S2, Wartlick et al., 2011. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder

© 2004, The Company of Biologists. Figure 2—figure supplement 1C panel 2 is reproduced from Figure 5, Torroja et al., 2004, with permission from The Company of Biologists. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2007, The American Association for the Advancement of Science. Figure 2—figure supplement 1D panel 1 is reproduced from Figure 1, Kicheva et al., 2007. Reprinted with permission from AAAS. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2020, AAAS. Figure 2—figure supplement 1C panel 2 reproduced from Figure 2 Bakker et al., 2020. Reprinted with permission from AAAS Creative Commons Attribution 4.0 International Public License.

Figure 3

Download asset Open asset

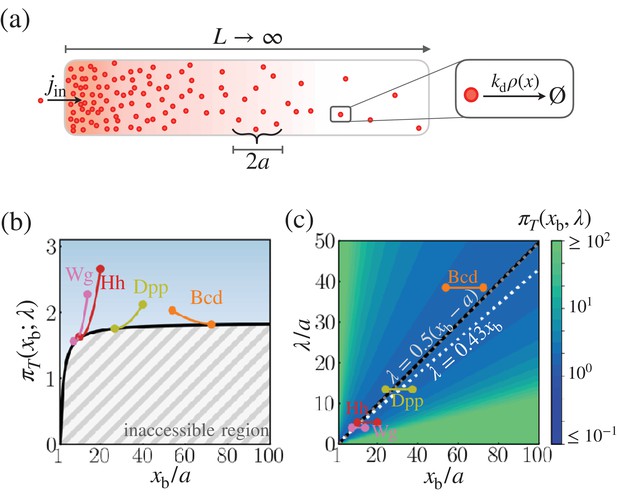
Cost-precision trade-off associated with the space-time-averaged measurement.

(a) Schematic of the model. (b) The optimal trade-off product $π_{T} (x_{b})$ obtained numerically with respect to the location of the target boundary position normalized by the sensor size ( $x_{b} / a$ ). The gray hashed area represent the inaccessible regions. Shown are the trade-off products of the morphogens profiles of Bcd, Wg, Hh, and Dpp. (c) The black line denotes the optimal characteristic decay length ( $λ_{\min}$ ) with respect to the position $x_{b} / a$ . The color scale indicates the trade-off product $π_{T} (x_{b})$ computed for each pair of $λ / a$ and $x_{b} / a$ values. The gray dotted line depicts the linear approximation of $λ_{\min}$ . The white dotted line depicts the linear approximation of $λ_{\min}$ for the point measurement model. In (b) and (c), the depicted trade-off product is normalized by $α_{o}$ . The parameters for the naturally occurring morphogen profiles are further described in the Appendix 3, Length scales of Bcd, Wg, Hh, and Dpp, and Appendix 3—table 1.

Figure 4

Download asset Open asset

Optimal concentration profile of morphogens.

(a) Three possible morphogen profiles (i) (red), (ii) (cyan), (iii) (brown) with different λ’s ( $λ^{(i)} < λ^{(i i)} < λ^{(i i i)}$ ), generated with different values of morphogen influxes $j_{i n}$ ( $j_{in}^{(i)} > j_{in}^{(ii)} > j_{in}^{(iii)}$ ). The morphogen concentration of the three profiles coincide at $x_{b}$ , giving rise to the same threshold value $ρ (x_{b})$ but different positional errors ( $ϵ^{2} (x_{b}; λ)$ ). (b) The precision of three possible morphogen profiles (i) (red), (ii) (cyan), (iii) (brown) with different λ’s ( $λ^{(i)} < λ^{(i i)} < λ^{(i i i)}$ ), generated with different values of morphogen influxes $j_{i n}$ ( $j_{in}^{(i)} > j_{in}^{(iii)} > j_{in}^{(ii)}$ ). The λ values are identical to those with matching colors in (a), but the red and brown curves are generated with different $j_{i n}$ values from those in (a). The cost associated with each morphogen profile are shown in units of $α_{o} L / l_{cell}$ . (c) The diagram of the trade-off product associated with the point measurement, $π_{o} (x; λ)$ , plotted with respect to $x$ and λ. The black line indicates the optimal decay length, $λ_{\min}$ at position $x$ . Shown on the diagram are the trade-off product $π_{o}$ ’s for the three cases shown in (a) and (b). (d) The value of $π_{o}$ as a function of λ at $x = x_{b}$ . The trade-off product is minimized to $π_{o} = π_{o}^{(ii)} \approx α_{o} (L / l_{cell}) 0.4$ with $π_{o}^{(ii)} < π_{o}^{(iii)} < π_{o}^{(i)}$ .

Appendix 1—figure 1

Download asset Open asset

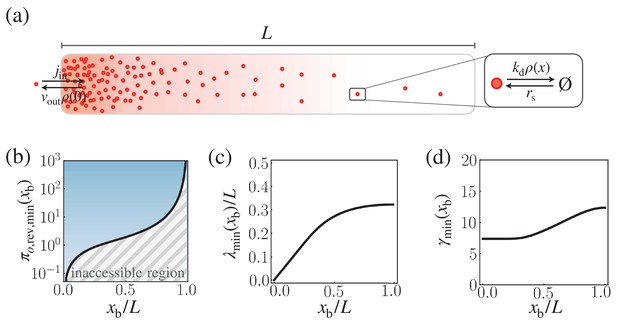
Speed-precision-cost trade-off for the reversible morphogen dynamics.

(a) Schematic of the reversible reaction-diffusion dynamics of morphogen profile formation. (b) The solid black line depicts the optimal trade-off product $π_{o, rev, \min} (x_{b})$ , obtained numerically by minimizing $π_{o, rev} (x_{b})$ with respect to λ and γ, with $β_{out} \to \infty$ . The trade-off product is normalized by $L / l_{cell}$ . (**c,d**) The optimal characteristic decay length $λ_{\min}$ (b) and $γ_{\min}$ (c) corresponding to $π_{o, rev, \min} (x_{b})$ .

Appendix 2—figure 1

Download asset Open asset

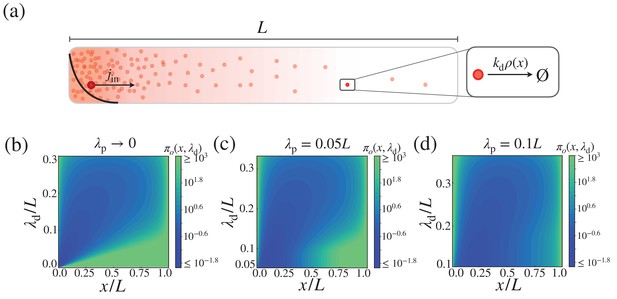
Cost-precision trade-off in the morphogen dynamics with distributed synthesis.

(a) Schematic of the distributed synthesis of the morphogen. The black solid line represents the morphogen synthesis rate which is roughly exponentially distributed with characteristic decay length $λ_{p}$ . (**b–d**) The trade-off product ( $π_{o} (x, λ_{d})$ ) for (b) $λ_{p} = 0$ , (c) $λ_{p} = 0.05 L$ , and (d) $λ_{p} = 0.1 L$ . The color scale indicates the trade-off product $π_{o}$ normalized by $α_{o} L / l_{cell}$ . The characteristic length scale $λ_{d}$ is defined as $λ_{d} \equiv \int_{0}^{L} 𝑑 x (ρ_{ss} (x) - ρ_{ss} (L)) / (ρ_{ss} (0) - ρ_{ss} (L))$ .

Appendix 2—figure 2

Download asset Open asset

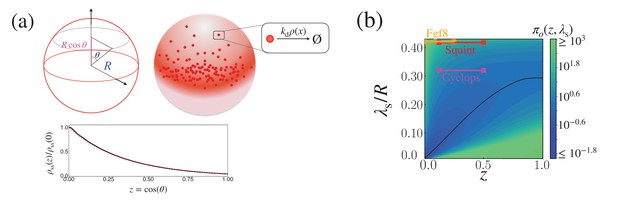
Cost-precision trade-off of the morphogen dynamics on a sphere.

(a) (Top) Schematic of the morphogen synthesized from the equator of the spherical shell (red region). (Bottom) The relative steady state concentration profile $ρ_{ss} (z)$ when $R^{2} / λ^{2} = 10$ . The solid black line was computed from evaluating $ρ_{ss} (z) = {lim}_{s \to 0} s \hat{ρ} (z, s)$ up to $l = 84$ (Equation 53). The dotted red line was obtained by numerically solving Equation 51. (b) The trade-off product ( $π_{o} (z, λ_{s})$ ) for pairs of target position $z$ and characteristic length scale $λ_{s}$ values, normalized by $α_{o} (2 π R / l_{cell})$ . The characteristic length scale $λ_{s}$ is defined as $λ_{s} \equiv \int_{0}^{1} 𝑑 z (ρ_{ss} (z) - ρ_{ss} (1)) / (ρ_{ss} (0) - ρ_{ss} (1))$ . The parameters for the naturally occurring morphogen profiles are further described in Appendix 3, Length scales of Cyclops, Squint, and Fgf8, and Appendix 3—table 1.

Appendix 2—figure 3

Download asset Open asset

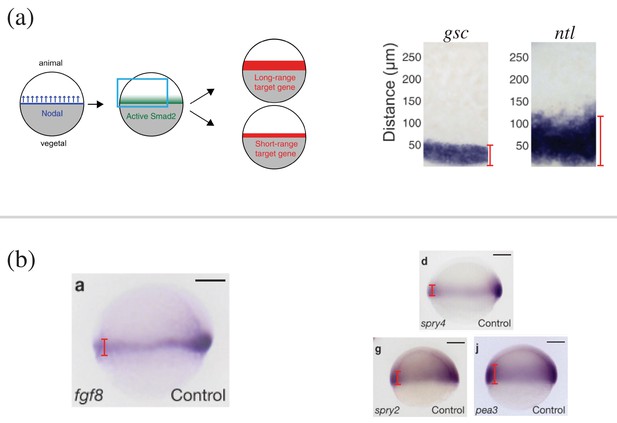
Length scales of naturally occurring morphogen profiles in the zebrafish embryo.

(a) (Left) Schematic of the Nodal ligands Cyclops and Squint patterning the vegetal-animal axis of the zebrafish embryo. The Nodal signals activate Smad2, which affects the expression of short-range and long-range target genes. (Right) The expression profile of Nodal target genes *gsc* and *ntl* obtained by in situ hybridization. The profiles are from the zebrafish embryos 5 hr post fertilization, when the embryo covers roughly 50% of the yolk. The red lines denote the width of the target gene expression domain away from the vegetal margin. (b) (Left) Expression of *fgf8* in 60% epiboly whole-mount embryos obtained by in situ hybridization. Animal side of the embryo is to the top, and dorsal is to the right. (Right) The expression profiles of the Fgf8 target genes *spry4*, *spry2*, and *pea3*. The red lines denote the width of the target gene expression domain away from the vegetal margin. Scale bars = 100 $μ m$ . (A) is reproduced from Figure 2 Dubrulle et al., 2015. (B) is reproduced from Figure 1 Nowak et al., 2011. Reprinted by permission from Springer Nature: Springer Nature, Nature Cell Biology, Interpretation of the FGF8 morphogen gradient is regulated by endocytic trafficking, Nowak, M., MacHate, A., Yu, S. R., Gupta, M., and Brand, M. 2011, Nat. Cell Biol., 13(2):153–158 Copyright 2011. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.

© 2015, Dubrulle et al. Appendix 2—figure 3A is reproduced from Figure 2 Dubrulle et al. 2015, with permission from The Company of Biologists Creative Commons Attribution 4.0 International Public License.

© 2011, Springer Nature. Appendix 2—figure 3B is reproduced from Figure 1 Nowak et al., 2011. Reprinted by permission from Springer Nature: Nowak et al., 2011 Copyright 2011. It is not covered by the CC-BY 4.0 licence and further reproduction of this panel would need permission from the copyright holder.Creative Commons Attribution 4.0 International Public License.

Tables

Appendix 3—table 1

Various length scales associated with the naturally occurring morphogen profiles found in the fruit fly (*) and zebrafish (†) embryos.

For each plot of the morphogen profile in Figure 2—figure supplement 1, the solid red line denotes the exponentially decaying profile with the associated characteristic length $λ$ . Further details on how each value was obtained from the associated reference are provided in the text of Appendix 3.

	$L^{*}$ or $R^{†}$ (µm)	$λ [\equiv \sqrt{D / k_{d}}]$ (µm)	Range of $x_{b}^{*}$ or $z_{b}^{†}$ (µm)	$a$ (µm)
Bcd*	425 Houchmandzadeh et al., 2002	100 Houchmandzadeh et al., 2002	140–188 Perry et al., 2012	2.6 Gregor et al., 2007
Wg*	70 Chaudhary et al., 2019	6 Kicheva et al., 2007	11–21 Bakker et al., 2020	2 Chaudhary et al., 2019
Hh*	100 Torroja et al., 2004	8 Wartlick et al., 2011	15–30 Torroja et al., 2004	2 Chaudhary et al., 2019
Dpp*	80 Bakker et al., 2020	20 Kicheva et al., 2007	36–54 Bakker et al., 2020	2 Chaudhary et al., 2019
Cyclops†	200 Nowak et al., 2011	76 Dubrulle et al., 2015	25–100 Dubrulle et al., 2015	10 Yu et al., 2009
Squint†	200 Nowak et al., 2011	178 Dubrulle et al., 2015	25–100 Dubrulle et al., 2015	10 Yu et al., 2009
Fgf8†	200 Nowak et al., 2011	197 Yu et al., 2009	0–50 Nowak et al., 2011	10 Yu et al., 2009