Calcium dependence of neurotransmitter release at a high fidelity synapse

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

The Ca²⁺-dependence of the priming, fusion, and replenishment of synaptic vesicles are fundamental parameters controlling neurotransmitter release and synaptic plasticity. Despite intense efforts, these important steps in the synaptic vesicles’ cycle remain poorly understood due to the technical challenge in disentangling vesicle priming, fusion, and replenishment. Here, we investigated the Ca²⁺-sensitivity of these steps at mossy fiber synapses in the rodent cerebellum, which are characterized by fast vesicle replenishment mediating high-frequency signaling. We found that the basal free Ca²⁺ concentration (<200 nM) critically controls action potential-evoked release, indicating a high-affinity Ca²⁺ sensor for vesicle priming. Ca²⁺ uncaging experiments revealed a surprisingly shallow and non-saturating relationship between release rate and intracellular Ca²⁺ concentration up to 50 μM. The rate of vesicle replenishment during sustained elevated intracellular Ca²⁺ concentration exhibited little Ca²⁺-dependence. Finally, quantitative mechanistic release schemes with five Ca²⁺ binding steps incorporating rapid vesicle replenishment via parallel or sequential vesicle pools could explain our data. We thus show that co-existing high- and low-affinity Ca²⁺ sensors mediate priming, fusion, and replenishment of synaptic vesicles at a high-fidelity synapse.

Introduction

Neurotransmitter release is mediated by the presynaptic vesicle cycle (Südhof, 2004) including (1) the priming of neurotransmitter-filled vesicles, (2) the fusion of primed vesicles, and (3) the replenishment of new vesicles after fusion. The Ca²⁺-sensitivity of these steps is difficult to determine due to the large spatial gradients of the Ca²⁺ concentration, which occur during Ca²⁺ influx through the Ca²⁺ channels. While the basal free intracellular Ca²⁺ concentration is ~50 nM, thousandfold higher local microdomains of Ca²⁺ build and decay very fast around the Ca²⁺ channels (Simon and Llinás, 1985; Yamada and Zucker, 1992). The small size and the rapid kinetics of the microdomain signals complicate the quantification of the local Ca²⁺ signals with the imaging techniques (Neher, 1998). Ca²⁺ uncaging circumvented this problem by allowing for the homogenous elevation of Ca²⁺ concentration throughout the whole presynaptic compartment via UV-photolysis of caged Ca²⁺ compounds (Kaplan and Ellis-Davies, 1988) and thus the direct measurement of the Ca²⁺-concentration immediately relevant for vesicle fusion (reviewed by Neher, 1998; Kochubey et al., 2011).

Among the steps of the presynaptic vesicle cycle, the Ca²⁺-sensitivity of vesicle fusion is best studied. First experiments with Ca²⁺ uncaging at retinal bipolar cells of goldfish found a very low sensitivity of the release sensors with a half saturation at ∼100 μM Ca²⁺ concentration and a fourth to fifth power relationship between Ca²⁺ concentration and neurotransmitter release (Heidelberger et al., 1994), similar to previous estimates at the squid giant synapse (Adler et al., 1991; Llinás et al., 1992). Subsequent work at other preparations showed different dose-response curves. For example, analysis of a central excitatory synapse, the calyx of Held (Forsythe, 1994) at a young pre-hearing age, found a much higher affinity with significant release below 5 µM intracellular Ca²⁺ concentration and a steep dose-response curve (Bollmann et al., 2000; Lou et al., 2005; Schneggenburger and Neher, 2000; Sun et al., 2007). Further analysis of the calyx of Held during neuronal development comparing the Ca²⁺-sensitivity of the release sensors at the age of P9 to P12-P15 (Kochubey et al., 2009) and P9 to P16-P19 (Wang et al., 2008) showed a developmental decrease in the Ca²⁺-sensitivity of vesicle fusion. Studies at two other central synapses, the hippocampal mossy fiber boutons of rats (P18–30; Fukaya et al., 2021) and the boutons of cerebellar basket cells of mice (P11-16; Sakaba, 2008), also described a high Ca²⁺-sensitivity of vesicle fusion with a steep dose-response curve. In contrast, the dose-response curve of sensory neurons of the rod photoreceptors was more shallow (Duncan et al., 2010; Thoreson et al., 2004) and vesicle fusion below 7 µM Ca²⁺ concentration was absent at the cochlear inner hair cells (Beutner et al., 2001).

The steps preceding the fusion of synaptic vesicles are in general still poorly understood (Südhof, 2013). We refer to vesicle priming as the molecular and positional preparation of vesicles for fusion near Ca²⁺ channels (Neher and Sakaba, 2008). Molecular priming has recently been shown to be the functional correlate of vesicle docking (Imig et al., 2014; Maus et al., 2020). Vesicle replenishment refers to the delivery of new vesicles during sustained activity. The effect of the residual Ca²⁺ on the strength of synapses particularly during synaptic facilitation has been studied for decades with a particular focus on the release probability of vesicles (see Discussion). Here, we investigate the Ca²⁺-dependence of priming and replenishment, which increases the number of release-ready vesicles. Previous work provided evidence that priming and replenishment are strongly Ca²⁺-dependent (reviewed by Silva et al., 2021, and Neher and Sakaba, 2008). The following findings demostrate the Ca²⁺-dependence of vesicle priming and replenishment. First, the size of the pool of fast-releasing vesicles linearly depends on the intracellular Ca²⁺ concentration at the calyx of Held synapse (Hosoi et al., 2007; see also Awatramani et al., 2005; Wang and Kaczmarek, 1998). Second, the sustained component of release, presumably reflecting vesicle replenishment, linearly depends on the intracellular Ca²⁺ concentration at cerebellar basket cell synapses (Sakaba, 2008). Third, the number of docked vesicles assessed by electron microscopic techniques is rapidly and reversibly regulated depending on the resting Ca²⁺ levels and neuronal activity at hippocampal neurons (Chang et al., 2018; Imig et al., 2020; Kusick et al., 2020; Vandael et al., 2020; Vevea et al., 2021). Fourth, the occupancy of the docking sites increases upon elevating extracellular Ca²⁺ levels at cerebellar synapses (Blanchard et al., 2020; Malagon et al., 2020). Finally, in several studies on chromaffin cells and synapses of vertebrates and invertebrates, the assumption of Ca²⁺-dependent priming was required to explain the experimental data (Doussau et al., 2017; Kobbersmed et al., 2020; Millar et al., 2005; Pan and Zucker, 2009; Voets, 2000; Walter et al., 2013). In contrast, previous studies at cerebellar mossy fiber synapses could explain release during trains of action potentials or prolonged depolarizations with Ca²⁺-independent vesicle priming and replenishment (Hallermann et al., 2010; Ritzau-Jost et al., 2014; Ritzau-Jost et al., 2018; Saviane and Silver, 2006).

The discrepant findings of the Ca²⁺-sensitivity of vesicle priming, fusion, and replenishment could be due to methodological errors. However, synapses show type-specific functional and structural differences (Atwood and Karunanithi, 2002; Nusser, 2018; Zhai and Bellen, 2004). The rate at which vesicles are replenished to empty release sites seems to be particularly different between types of synapses. The cerebellar mossy fiber bouton (cMFB) conveys high-frequency sensory information to the cerebellar cortex and relies on extremely fast vesicle replenishment (Miki et al., 2020; Ritzau-Jost et al., 2014; Saviane and Silver, 2006). The aim of this study was therefore to determine the Ca²⁺-sensitivity of vesicle priming, fusion, and replenishment at mature cMFBs synapses at physiological temperature, and to test whether and how the prominent fast vesicle replenishment affects the Ca²⁺-dependence of the vesicle priming, fusion, and replenishment at this synapse. To measure the Ca²⁺-dependence of vesicle priming, we first directly manipulated the free basal intracellular Ca²⁺ concentration and measured the amount of action potential-evoked release. To meaure the Ca²⁺-dependence of vesicle fusion, we focused the initial release kinetics of the fusion of the primed vesicles upon Ca²⁺ uncaging (with time constants mostly << 10 ms). To finally measure the Ca²⁺-dependence of vesicle replenishment, we focused on the sustained component of release occurring during 100 ms of flash-evoked Ca²⁺ increase.

Our data revealed a strong dependence of the number of release-ready vesicles on basal Ca²⁺ concentrations between 30 and 180 nM, a significant release below 5 µM, an apparent shallow dose-response curve in the studied Ca²⁺ concentration range of 1 to 50 µM, and little Ca²⁺-dependence of vesicle replenishment during sustained elevated intracellular Ca²⁺ concentrations. Computational simulations incorporating mechanistic release schemes with five Ca²⁺ binding steps and fast vesicle replenishment via sequential or parallel pools of vesicles could explain our data. Our results show the co-existence of Ca²⁺ sensors with high- and low-affinities that cover a large range of intracellular Ca²⁺ concentrations and mediate fast signaling at this synapse.

Results

Action potential-evoked synaptic release critically depends on basal intracellular Ca²⁺ concentration

To investigate the impact of the basal intracellular Ca²⁺ concentration on synaptic release, we performed simultaneous patch-clamp recordings from presynaptic cerebellar mossy fiber boutons (cMFB) and postsynaptic granule cells (GC) of 5- to 6-week-old mice at physiological temperatures (Figure 1A and B). We aimed at clamping the free Ca²⁺ concentration in the presynaptic patch solution to either low or high basal Ca²⁺ concentrations by adding different concentrations of Ca²⁺ and the Ca²⁺ chelator EGTA (see Materials and methods). Two-photon quantitative Ca²⁺ imaging with the dual-indicator method using Fluo-5F as the Ca²⁺ indicator (Delvendahl et al., 2015; Sabatini et al., 2002) revealed the free Ca²⁺ concentration of the presynaptic intracellular solution to be 28 ± 3 and 183 ± 8 nM, for the low and high basal Ca²⁺ conditions (n = 4 and 4), respectively (Figure 1A). In both solutions, the free EGTA concentration was 4.47 mM (see Materials and methods). In response to triggering a single action potential in the presynaptic terminal, the recorded excitatory postsynaptic current (EPSC) depended strongly on the presynaptic resting Ca²⁺ concentration (Figure 1C). We found an almost threefold increase in the EPSC amplitude when elevating the resting Ca²⁺ concentration in the presynaptic terminals from 30 to 180 nM. On average, the EPSC amplitudes were 39 ± 8 and 117 ± 28 pA for the low and high basal Ca²⁺ conditions, respectively (n = 8 and 8; P_Mann-Whitney = 0.028; Figure 1D). Interestingly, the frequency of miniature currents in-between the current injections used to elicit action potentials had a tendency to increase with elevated basal Ca²⁺ concentration (median 1.1 and 3.5 Hz for the low and high basal Ca²⁺ conditions, respectively, n = 8 and 8; P_Mann-Whitney = 0.13; data not shown). The EPSC rise and decay kinetics were not significantly different (Figure 1D). No significant differences were observed in the action potential waveform including amplitude and half duration (Figure 1D) indicating that the altered synaptic strength was not caused by changes in the shape of the presynaptic action potential. These data indicate that moderate changes in the presynaptic basal Ca²⁺ concentration can alter synaptic strength up to threefold.

Figure 1

Download asset Open asset

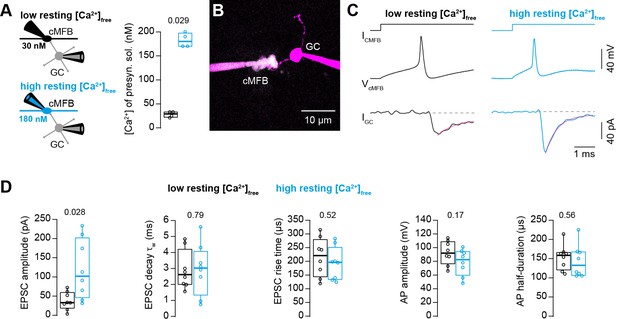
Action potential-evoked synaptic release critically depends on basal intracellular Ca²⁺ concentration.

(A) *Left:* Illustration of the cellular connectivity of the cMFB to GC synapse during simultaneous pre- and postsynaptic patch-clamp recording. The presynaptic terminal was loaded with an intracellular solution having either low or high free basal Ca²⁺ concentration (top and bottom, respectively). *Right:* Comparison of the average free Ca²⁺ concentration in the presynaptic patch pipette (quantified by two-photon Ca²⁺ imaging) for the intracellular solutions with low and high basal Ca²⁺ (n = 4 each). (B) Example two-photon microscopic image of a cMFB and a GC in the paired whole-cell configuration. (C) Example traces of a paired cMFB-GC recording with current injection (I_cMFB) (*top*) eliciting an action potential in the cMFB (*middle*) and an EPSC in the postsynaptic GC (*bottom*). Black and blue color code corresponds to low and high free basal Ca²⁺ concentration in the presynaptic solution, respectively. The decay of the EPSC was fitted with a bi-exponential function (magenta line). (D) Comparison of the properties of presynaptic action potentials and EPSCs evoked after eliciting an action potential in the presynaptic terminal using solutions having either low (black) or high (blue) free Ca²⁺ concentration. From left to right: peak amplitude of the EPSC, weighted decay time constant of the EPSC, 10-to-90% rise time of the EPSC, amplitude of the presynaptic action potential, and action potential half-duration (n = 8 and 8 paired cells for the conditions with low and high resting Ca²⁺ concentration, respectively). Boxplots show median and 1st/3rd quartiles with whiskers indicating the whole data range. Values of individual experiments are superimposed as circles. The numbers above the boxplots represent p-values of Mann-Whitney U tests.

Figure 1—source data 1 Action potential-evoked synaptic release critically depends on basal intracellular Ca²⁺ concentration.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig1-data1-v1.xlsx
Download elife-70408-fig1-data1-v1.xlsx

Ca²⁺ uncaging dose-response curve measured with presynaptic capacitance measurements

To gain a better understanding of the profound sensitivity of AP-evoked release on presynaptic basal Ca²⁺ concentration, we established presynaptic Ca²⁺ uncaging and measured the release kinetics upon step-wise elevation of Ca²⁺ concentration. We combined wide-field illumination using a high-power UV laser with previously established quantitative two-photon Ca²⁺ imaging (Delvendahl et al., 2015) to quantify the post-flash Ca²⁺ concentration (Figure 2A). This approach offers sub-millisecond control of the UV flashes and a high signal to noise ratio of the two-photon Ca²⁺ imaging deep within the brain slice. The flash-evoked artefacts in the two-photon signals, presumably due to luminescence in the light path, could be reduced to a minimum with an optimal set of spectral filters and gate-able photomultipliers (PMTs). Subtraction of the remaining artefact in the background region of the two-photon line scan resulted in artefact-free fluorescence signals (Figure 2B and C).

Figure 2 with 1 supplement see all

Download asset Open asset

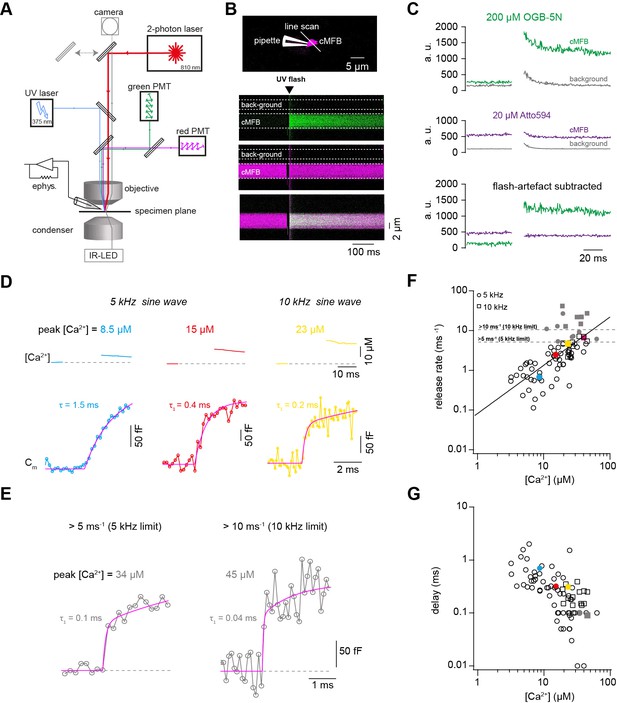
Ca²⁺ uncaging dose-response curve measured with presynaptic capacitance measurements.

(A) Illustration of the experimental setup showing the light path of the two-photon laser illumination (red line), the UV laser illumination (blue line), the electrophysiology amplifier (‘ephys.’), the red and green gate-able photomultiplier tubes (PMTs), and infrared LED illumination with oblique illumination via the condenser for visualization of the cells at the specimen plane by the camera (gray line) when the upper mirror is moved out of the light path (gray arrow). (B) *Top:* Two-photon microscopic image of a cMFB in the whole-cell configuration loaded with OGB-5N, Atto594, and DMn/ Ca²⁺. Positions of the patch pipette and line scan are indicated. *Bottom:* Two-photon line scan showing the fluorescence signal as measured through the green PMT, red PMT, and an overlay of the green and red channels. Arrow indicates the onset of the UV flash and dashed lines represent the flash-induced luminescence artefact as detected outside the cMFB. The lookup tables for the green and red channel were arbitrarily adjusted independent of the absolute values in C. (C) *Top:* change in fluorescence intensity within the cMFB for the green channel along with the corresponding flash-induced green artefact measured in the background. *Middle:* change in fluorescence intensity within the cMFB for the red channel along with the corresponding flash-induced red artefact. *Bottom:* green and red fluorescence signal after subtracting the flash-induced artefacts. (D) *Top:* Ca²⁺ signals of different concentrations elicited through Ca²⁺ uncaging in three different cells, the flash was blanked. *Bottom:* corresponding traces of capacitance recordings measured using a 5 kHz (left and middle) or 10 kHz sinusoidal stimulation (right). $τ$ represents the time constant from a mono-exponential fit, $τ_{1}$ represents the time constant of the fast component of a bi-exponential fit. (E) Traces of capacitance recordings showing the resolution limit in detecting fast release rates of >5 ms⁻¹ using 5 kHz sinusoidal stimulation or >10 ms⁻¹ using 10 kHz sinusoidal stimulation. (F) Plot of release rate versus post-flash Ca²⁺ concentration (n = 65 from 5-kHz- and from 15 10-kHz-recordings obtained from 80 cMFBs). The line represents a fit with a Hill equation (Equation 2) with best-fit values *V_max* = 1.7*10⁷ ms⁻¹, *K_D* = 7.2*10⁶ µM, and n = 1.2. Color coded symbols correspond to traces in (D – E). Gray symbols represent values above the resolution limit. (G) Plot of synaptic delay versus post-flash Ca²⁺ concentration (n = 64 from 5-kHz- and 15 from 10-kHz-recordings obtained from 79 cells). Note that one recording was removed from the analysis because the exponential fit led to a negative value of the delay. Color coded symbols correspond to traces in (D – E).

Figure 2—source data 1 Ca²⁺ uncaging dose-response curve measured with presynaptic capacitance measurements.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig2-data1-v1.xlsx
Download elife-70408-fig2-data1-v1.xlsx

To obtain a large range of post-flash Ca²⁺ concentrations within the bouton, we varied the concentration of the Ca²⁺-cage DMn (1–10 mM) and the intensity (10–100%) and the duration (100 or 200 µs) of the UV laser pulse (Table 1). The spatial homogeneity of the Ca²⁺ elevation was assessed by UV illumination of caged fluorescein mixed with glycerol (Figure 2—figure supplement 1; Schneggenburger and Neher, 2000; Bollmann et al., 2000). The resulting post-flash Ca²⁺ concentration was quantified with either high- or low-affinity Ca²⁺ indicator (Fluo-5F or OGB-5N). To measure the kinetics of neurotransmitter release independent of dendritic filtering or postsynaptic receptor saturation, vesicular fusion was quantified by measuring the presynaptic capacitance with a 5 kHz-sinusoidal stimulation (Hallermann et al., 2003). The first 10 ms of the flash-evoked capacitance increase was fitted with functions containing a baseline and mono- or bi-exponential components (magenta line in Figure 2D and E; see Equation 1 in the Materials and methods section). With increasing post-flash Ca²⁺ concentration the fast time constant decreased (τ in case of mono- and τ₁ in case of bi-exponential fits; Figure 2D). The inverse of the fast time constant represents a direct readout of the fusion kinetics of the release-ready vesicles. When plotting the inverse of the time constant as a function of post-flash Ca²⁺ concentration, we obtained a shallow dose-response curve that showed a continuous increase in the release rate with increasing post-flash Ca²⁺ concentration up to 50 µM (Figure 2F). In some experiments with high Ca²⁺ concentrations, the release was too fast to be resolved with 5 kHz capacitance sampling (i.e. time constants were smaller than 200 µs; Figure 2E). We therefore increased the frequency of the sinusoidal stimulation in a subset of experiments to 10 kHz (15 out of 80 experiments). Such high-frequency capacitance sampling is to our knowledge unprecedented at central synapses and technically challenging because exceptionally low access resistances are required (<~15 MΩ) to obtain an acceptable signal-to-noise ratio (Gillis, 1995; Hallermann et al., 2003). Despite these efforts, the time constants were sometimes faster than 100 µs, representing the resolution limit of 10 kHz capacitance sampling (Figure 2E). These results indicate that the entire pool of release-ready vesicles can fuse within less than 100 µs. Fitting a Hill equation on both 5- and 10 kHz data resulted in a best-fit K_D of >50 µM with a best-fit Hill coefficient, n, of 1.2 (Figure 2F).

Table 1

Parameters for weak, middle, and strong post-flash Ca²⁺ elevations.

	weak Ca²⁺ elevation	middle Ca²⁺ elevation	strong Ca²⁺ elevation
UV illumination
Duration (ms)	0.1 or 1	0.1	0.1 or 0.2
Intensity (%)	10–100	20–100	100
Concentration in intracellular solution (mM)
ATTO 594	0.010	0.020	0.020
Fluo 5F	0.050	0	0
OGB 5N	0	0.200	0.200
CaCl2	0.500	2.000	10.000
DM-N	0.500	2.000	10.000
Obtained peak post-flash Ca²⁺ (µM)
Min	1.1	2.7	15.7
Max	7.1	36.0	62.6
Median	2.4	8.8	25.1
Simulated uncaging fraction of DMn
α	0.08–0.5	0.15–0.55	0.14–0.25

In addition to the speed of vesicle fusion, we analyzed the delay from the onset of the UV-illumination to the onset of the rise of membrane capacitance, which was a free parameter in our fitting functions (see Equation 1). The delay was strongly dependent on the post-flash Ca²⁺ concentration and the dose-response curve showed no signs of saturation at high Ca²⁺ concentrations (Figure 2G), which is consistent with the non-saturating release rates. These data reveal that the fusion kinetics of synaptic vesicles increased up to a Ca²⁺ concentration of 50 µM without signs of saturation, suggesting a surprisingly low apparent affinity of the fusion sensor at mature cMFBs under physiological temperature conditions (K_D > 50 µM).

Ca²⁺ uncaging dose-response curve measured with deconvolution of EPSCs

Capacitance recordings are not very sensitive in detecting low release rates. We therefore performed simultaneous pre- and postsynaptic recordings and used established deconvolution techniques to calculate the presynaptic release rate by analyzing the EPSC as previously applied at this synapse (Figure 3A,B; Ritzau-Jost et al., 2014). Kynurenic acid (2 mM) and cyclothiazide (100 μM) were added to the extracellular solution in order to prevent the saturation and desensitization of postsynaptic AMPA receptors, respectively. Ca²⁺ uncaging in the presynaptic terminal evoked EPSCs with kinetics, which strongly depended on the post-flash Ca²⁺ concentration. The cumulative release obtained from deconvolution analysis of the recorded EPSCs was fitted as previously done for capacitance traces (Equation 1). At low Ca²⁺ concentrations (<5 µM), a significant amount of neurotransmitter release could be measured, which is consistent with previous reports from central synapses (Bollmann et al., 2000; Fukaya et al., 2021; Sakaba, 2008; Schneggenburger and Neher, 2000). The presynaptic release rates increased with increasing post-flash Ca²⁺ concentration and no saturation in the release rate occurred in the dose-response curve (Figure 3D). The dose-response curve for the delay from the onset of the UV illumination to the onset of the rise of the cumulative release trace (Equation 1) did not show signs of saturation of the release kinetics in the investigated range. Thus, consistent with capacitance measurements, deconvolution analysis of postsynaptic currents revealed a shallow Ca²⁺-dependence of neurotransmitter release kinetics (Figure 3D and E). Fitting a Hill equation to the deconvolution data resulted in a best-fit K_D >50 µM and a Hill coefficient of 1.6 (Figure 3D). Therefore, two independent measures of synaptic release (presynaptic capacitance measurements and postsynaptic deconvolution analysis) indicate a non-saturating shallow dose-response curve up to ~50 µM.

Figure 3 with 4 supplements see all

Download asset Open asset

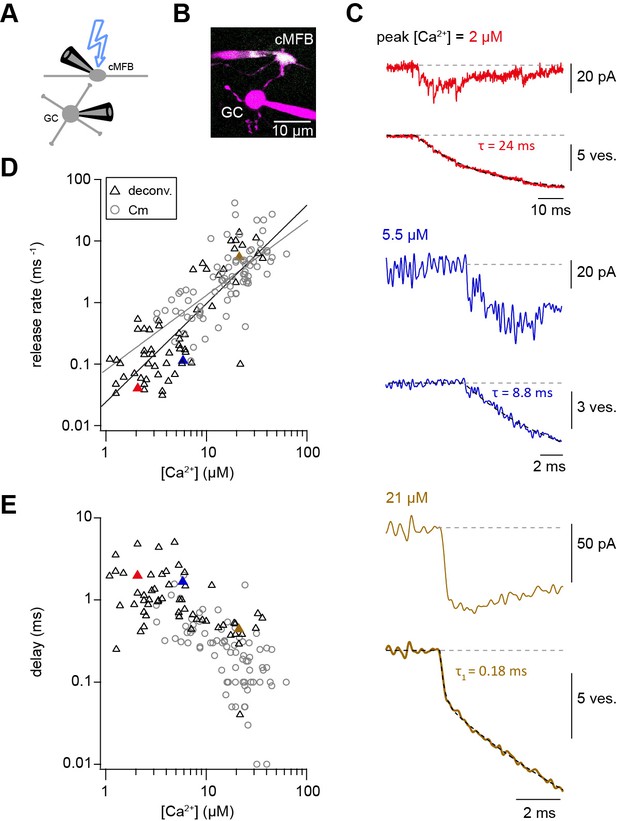
Ca²⁺ uncaging dose-response curve measured with deconvolution of EPSCs.

(A) Illustration of the cellular connectivity in the cerebellar cortex showing the pre- and postsynaptic compartments during paired whole-cell patch-clamp recordings and Ca²⁺ uncaging with UV-illumination. (B) Two-photon microscopic image of a cMFB and a GC in the paired whole-cell patch-clamp configuration. (C) Three different recordings showing UV-flash evoked EPSC (*top trace*) and cumulative release rate measured by deconvolution analysis of the EPSCs (*bottom trace*). The peak Ca²⁺ concentration, quantified with two-photon Ca²⁺ imaging, is indicated in each panel. $τ$ represents the time constant from mono-exponential fit, $τ_{1}$ represents the time constant of the fast component of bi-exponential fit. Note the different lengths of the baselines in the three recordings. (D) Plot of release rate versus post-flash Ca²⁺ concentration. Gray open circles represent data from capacitance measurements (Figure 2) and black triangles represent data from deconvolution analysis of EPSC (n = 57 recordings obtained from 42 paired cells). Gray and black lines represent fits with a Hill equation of the capacitance (as shown in Figure 1F) and the deconvolution data, respectively. The best-fit parameters for the fit on the deconvolution data were *V_max* = 6*10⁷ ms⁻¹, *K_D* = 7.6*10⁵ µM, and n = 1.6. Red, blue, and brown symbols correspond to the traces in (C). (E) Plot of synaptic delay versus post-flash Ca²⁺ concentration (n = 59 recordings obtained from 43 paired cells). Note that two recordings was removed from the analysis because the exponential fit led to a negative value of the delay Gray open circles represent data from capacitance measurements, and black triangles represent data from deconvolution analysis of EPSC. Red, blue, and brown symbols correspond to the traces in (C).

Figure 3—source data 1 Ca²⁺ uncaging dose-response curve measured with deconvolution of EPSCs.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig3-data1-v1.xlsx
Download elife-70408-fig3-data1-v1.xlsx

To rule out methodical errors that might influence the dose-response curve, we carefully determined the K_D of the Ca²⁺ indicator OGB-5N using several independent approaches including direct potentiometry (Figure 3—figure supplement 1), because this value influences the estimate of the Ca²⁺ affinity of the fusion sensors linearly. We estimated a K_D of OGB-5N of ~30 µM being at the lower range of previous estimates ranging from 20 to 180 µM (Delvendahl et al., 2015; DiGregorio and Vergara, 1997; Neef et al., 2018), arguing against an erroneously high K_D of the Ca²⁺ indicator as a cause for the non-saturation.

In addition, we used the two following independent approaches to rule out a previously described Ca²⁺ overshoot immediately following the UV illumination. Such a Ca²⁺ overshoot would be too fast to be detected by the Ca²⁺ indicators (Bollmann et al., 2000) but could trigger strong release with weak UV illumination which would predict a shallow dose-response curve. First, the time course of Ca²⁺ release from DMn was simulated (see below; Figure 6A) and no significant overshoots were observed (see below). Secondly, we experimentally compared strong and short UV illumination (100% intensity; 0.1 ms) with weak and long UV illumination (10% intensity; 1 ms), because a Ca²⁺ overshoot is expected to primarily occur with strong and short UV illumination. Comparison of these two groups of UV illumination resulted in similar post-flash concentrations but did not reveal a significant difference in the corresponding release rate indicating that undetectable Ca²⁺ overshoots did not affect the measured release rate (Figure 3—figure supplement 2). Therefore, both approaches argue against a Ca²⁺ overshoot as an explanation for the shallow dose-response curve.

Presynaptic and postsynaptic measurements reveal two kinetic processes of neurotransmitter release

In some Ca²⁺ uncaging experiments, synaptic release appeared to have two components, which could be due to heterogeneity amongst release-ready vesicles. We therefore systematically compared mono- and bi-exponential fits to the capacitance and deconvolution data (Figure 4A B). Several criteria were used to justify a bi-exponential fit (see Materials and methods). One criterion was at least a 4% increase in the quality of bi- compared with mono-exponential fits as measured by the sum of squared differences between the fit and the experimental data (χ²; Figure 4D). Consistent with a visual impression, this standardized procedure resulted in the classification of ~40% of all recordings as bi-exponential (38 out of 80 capacitance measurements and 17 out of 59 deconvolution experiments; Figure 4C D). The release rate of the fast component (1/τ₁) of the merged capacitance and deconvolution data showed no signs of saturation consistent with our previous analyses of each data set separately. Fitting a Hill equation to the merged data indicated a K_D >50 μM and a Hill coefficient of 1.6 (Figure 4C). The release rate of the slow component (1/τ₂; if existing) was on average more than 10 times smaller (black symbols, Figure 4C). These data indicate that there are at least two distinct kinetic steps contributing to release within the first 10 ms.

Figure 4

Download asset Open asset

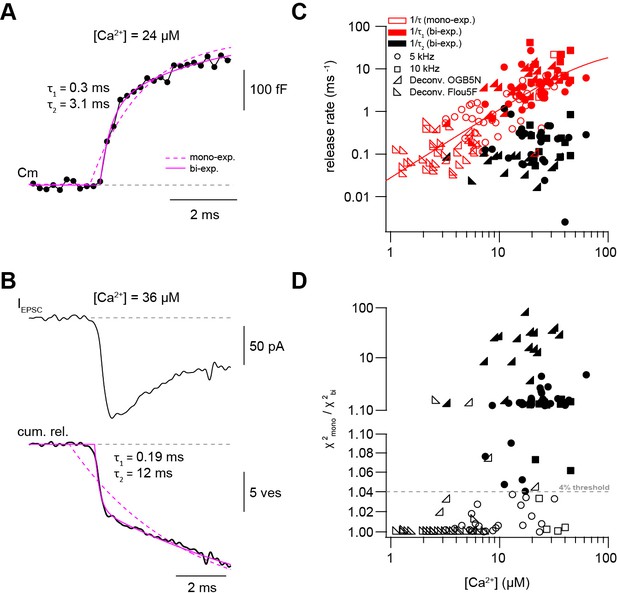
Presynaptic and postsynaptic measurements reveal two kinetic processes of neurotransmitter release.

(A) Example of a capacitance trace showing the two components of release observed within the first 10 ms in response to UV-flash-evoked increase in Ca²⁺ concentration to 24 μM. The solid magenta line represents the bi-exponential fit and the dashed magenta line represents mono-exponential fit (see Equation 1). (B) *Top:* example trace of an EPSC recording in response to UV-flash evoked increase in Ca²⁺ concentration to 36 μM. *Bottom:* the corresponding cumulative release trace obtained from deconvolution analysis, showing the two components of release observed within the first 10 ms. The solid magenta line represents the bi-exponential fit and the dashed magenta line represents mono-exponential fit (see Equation 1). (C) Top: plot of neurotransmitter release rates as a function of peak Ca²⁺ concentration (n = 80 and 59 capacitance measurements and deconvolution analysis, respectively). Data obtained from capacitance measurements with sinusoidal frequency of 5 kHz are shown as circles, data from 10 kHz capacitance measurements are shown as squares, and cumulative release data obtained from deconvolution analysis are shown as lower left- and lower right- triangles for recordings with OGB-5N and Fluo5F, respectively. Open symbols correspond to data from the mono-exponential fits and filled symbols correspond to data from the bi-exponential fits. Red symbols represent merged data of the release rates obtained from mono-exponential fit and the fast component of the bi-exponential fit, and black symbols represent the second component of the bi-exponential fit. The line represents a fit with a Hill equation with best-fit parameters V_max = 29.9 ms⁻¹, *K_D* = 75.5 µM, and n = 1.61. (D) χ² ratio for the mono-exponential compared to the bi-exponential fits. Dashed line represents the threshold of the χ² ratio used to judge the fit quality of double compared to mono-exponential fits (as one criterion for selection). 5 kHz capacitance data are shown as circles, 10 kHz capacitance data are shown as squares, and cumulative release data (obtained from deconvolution analysis) are shown as lower left- and lower right- triangles for recordings with OGB-5N and Fluo5F, respectively. Open symbols correspond to data points judged as mono-exponential and filled symbols correspond to data points judged as bi-exponential.

Figure 4—source data 1 Presynaptic and postsynaptic measurements reveal two kinetic processes of neurotransmitter release.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig4-data1-v1.xlsx
Download elife-70408-fig4-data1-v1.xlsx

Fast sustained release with very weak Ca²⁺-dependence

To gain more insights into the mechanisms of sustained vesicle release, we focused on the synaptic release within the first 100 ms after Ca²⁺ uncaging, presumably reflecting vesicle replenishment (Sakaba, 2008). Using capacitance measurements, we investigated the Ca²⁺-dependence of sustained release by estimating the number of vesicles (N_v) released between 10 and 100 ms after flash onset (Figure 5A), assuming a single vesicle capacitance of 70 aF (Hallermann et al., 2003). There was considerable variability in the release rate between 10 and 100 ms, which could be due to differences in bouton size and wash-out of proteins during whole-cell recordings. However, the release rate showed no obvious dependence on the post-flash Ca²⁺ concentration (Figure 5B). A comparable dose-response curve was obtained when investigating the rate of release between 10 and 100 ms using deconvolution analysis of postsynaptic currents, however, with a weak but significant correlation (Figure 5C). These data indicate that the slope of the sustained component of release is, if anything, weakly dependent on the intracellular Ca²⁺ concentration in the range of 1–50 µM, consistent with previously observed Ca²⁺-independent vesicle replenishment as assessed by depolarizing cMFBs to 0 mV in the absence or presence of intracellular EGTA (Ritzau-Jost et al., 2014).

Figure 5

Download asset Open asset

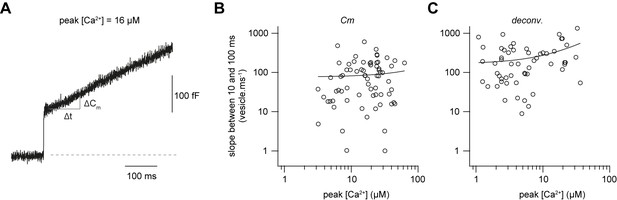
Fast sustained release with very weak Ca²⁺-dependence.

(A) Examples of a capacitance trace showing a sustained component of release. (B) Plot of the number of vesicles released between 10 and 100 ms as estimated from capacitance measurements divided by the time interval (90 ms) versus the post-flash Ca²⁺ concentration (n = 71 cMFBs). The line represents a linear fit to the data with a slope of 6 vesicles ms⁻¹ µM⁻¹ (Pearson correlation coefficient = 0.06, r² = 0.003; P_{Pearson correlation} = 0.6). (C) Plot of the number of vesicles released between 10 and 100 ms as estimated from deconvolution analysis divided by the time interval (90 ms) versus the post-flash Ca²⁺ concentration (n = 51 cMFB-GC pairs). The line represents a linear fit to the data with a slope of 10 vesicles ms⁻¹ µM⁻¹ (Pearson correlation coefficient = 0.3, r² = 0.1; P_{Pearson correlation} = 0.01).

Figure 5—source data 1 Fast sustained release with very weak Ca²⁺-dependence.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig5-data1-v1.xlsx
Download elife-70408-fig5-data1-v1.xlsx

Release schemes with five Ca²⁺ steps and fast replenishment via parallel or sequential models can explain Ca²⁺-dependence of release

To investigate the mechanisms that could explain a non-saturating and shallow dose-response curve and rapid sustained release, we performed modeling with various release schemes. First, we simulated the exact time course of the concentration of free Ca²⁺. The Ca²⁺ release from DMn and subsequent binding to other buffers and the Ca²⁺ indicator were simulated based on previously described binding and unbinding rates (Faas et al., 2005; Faas et al., 2007; Figure 6A; Table 2; see Materials and methods). In contrast to previous results, which predicted a significant overshoot of Ca²⁺ following UV illumination with short laser pulses (Bollmann et al., 2000), our simulations predict little overshoot compared to the Ca²⁺ concentration measured by the Ca²⁺ indicator (Figure 6B). The discrepancy is readily described by recent improvements in the quantification of Ca²⁺ binding and unbinding kinetics (Faas et al., 2005; Faas et al., 2007). The calculations predict an almost step-like increase in the free Ca²⁺ concentration with a 10–90% rise time below 50 µs. These simulated UV illumination-induced transients of free Ca²⁺ concentrations were subsequently used to drive the release schemes. Realistic noise was added to the resulting simulated cumulative release rate and the traces were fit with exponential functions (Equation 1) as the experimental data (Figure 6C).

Figure 6

Download asset Open asset

Release schemes with five Ca²⁺ steps and fast replenishment via parallel or sequential models can explain Ca²⁺-dependence of release.

(A) Scheme of the chemical reactions that were implemented in the model to calulate the UV-illumination-evoked increase in the free Ca²⁺ concentration. The model considered Ca²⁺ (Ca) and Mg²⁺ (Mg) binding to the indicator dye (OGB-5N or Fluo-5F), to DM-nitrophen (DMn), and to buffers (ATP and/or an endogenous buffer). The forward (k_on) and backward (k_off) rate constants differ between chemical species. Upon photolysis, a fraction α of metal bound and free DMn made a transition to different photoproducts (PP1 and PP2; Faas et al., 2005). For model parameters see Table 2. (B) The scheme in (A) was converted to a system of differential equations and the time courses of the ‘real’ free Ca²⁺ (magenta) and the free Ca²⁺ reported by Ca²⁺ dye were simulated for the indicated uncaging fractions α. Note that after less than 1 ms the dye reliably reflects the time course of Ca²⁺. (C) Traces showing the steps used in the simulation of the kinetic model of release. (D) Graphical illustration of the three models used during the simulations. For model parameters see Table 3. (E) From left to right, predictions of each model and the experimental data for the inverse of $τ_{1}$ (gray symbols, solid lines) and inverse of $τ_{2}$ (black symbols, dashed lines), delay, vesicle replenishment rate between 10 and 100 ms, and the increase in the χ² ratio for the single- compared to the bi-exponential fits. Red, yellow, and blue lines correspond to simulations of models 1, 2, and 3, respectively. For the χ² ratio (*right plot*), the experimental data and the simulations are shown separately for 5-kHz- and 10-kHz-capacitance data (C5 and C10; black and brown, respectively) and the deconvolution data (D; green).

Table 2

Parameters for simulations of Ca²⁺ release from DMN cage.

Parameters		Values	References number / Notes
Resting Ca²⁺	[Ca²⁺]_rest	227*10⁻⁹ M	Measured
Total magnesium	[Mg²⁺]_T	0.5*10⁻³ M	Pipette concentration
Fluo-5F	[Fluo]	0 or 50 *10⁻⁶ M (see Table 1)	Pipette concentration
	K_D	0.83 *10⁻⁶ M	Delvendahl et al., 2015
	k_off	249 s-1	ibid
	k_on	3*10⁸ M⁻¹s⁻¹	Yasuda et al., 2004
OGB-5N	[OGB]	0 or 200*10⁻⁶ M (see Table 1)	Pipette concentration
	K_D	31.4*10⁻⁶ M	Measured (Figure 3—figure supplement 1A)
	k_off	6000 s⁻¹	ibid.
	k_on	2.5*10⁸ M⁻¹s⁻¹	DiGregorio and Vergara, 1997
ATP	[ATP]	5 *10⁻³ M	Pipette concentration
Ca²⁺ binding	K_D	2*10⁻⁴ M	Meinrenken et al., 2002
	k_off	100 000 s⁻¹	ibid.
	k_on	5*10⁸ M⁻¹s⁻¹	ibid.
Mg²⁺ binding	K_D	100*10⁻⁶ M	Bollmann et al., 2000; MaxC
	k_off	1000 s⁻¹	ibid.
	k_on	1*10⁷ M⁻¹s⁻¹	ibid.
Endogenous buffer	[EB]	480 *10⁻⁶ M	Delvendahl et al., 2015
	K_D	32*10⁻⁶ M	ibid
	k_off	16 000 s⁻¹	ibid.
	k_on	5*10⁸ M⁻¹s⁻¹	ibid.
Total DM nitrophen	[DMn]_T	50010⁻⁶ – 1010⁻³ M (see Table 1)	Pipette concentration
Ca²⁺ binding	K_D	6.5*10⁻⁹ M	Faas et al., 2005
	k_off	0.19 s⁻¹	ibid.
	k_on	2.9*10⁷ M⁻¹s⁻¹	ibid.
Mg²⁺ binding	K_D	1.5*10⁻⁶ M	ibid.
	k_off	0.2 s⁻¹	ibid.
Uncaging fraction	α	See Table 1
Fast uncaging fraction	af	0.67	Faas et al., 2005
Photoproduct 1	[PP1]
Ca²⁺ binding	K_D	2.38*10⁻³ M	Faas et al., 2005
	k_off	69 000 s⁻¹	ibid.
	k_on	2.9*10⁷ M⁻¹s⁻¹	ibid.
Mg²⁺ binding	K_D	1.5*10⁻⁶ M	ibid.
	k_off	300 s⁻¹	ibid.
	k_on	1.3*10⁵ M⁻¹s⁻¹	ibid.
Photoproduct 2	[PP2]
Ca²⁺ binding	K_D	124.1*10⁻⁶ M	Ibid.
	k_off	3600 s⁻¹	ibid.
	k_on	2.9*10⁷ M⁻¹s⁻¹	ibid.
Mg²⁺ binding	K_D	1.5*10⁻⁶ M	ibid.
	k_off	300 s⁻¹	ibid.
	k_on	1.3*10⁵ M⁻¹s⁻¹	ibid.

We compared three different release schemes in their ability to reproduce our experimental data. In model 1, a single pool of vesicles with two Ca²⁺ binding steps was used as previously established, for example for chromaffin cells and rod photoreceptors (Duncan et al., 2010; Voets, 2000). Such an assumption would readily explain the shallow dose-response curve (Bornschein and Schmidt, 2018). The 2nd component of release could be replicated by assuming rapid vesicle replenishment from a reserve pool (V_R; Figure 6D). However, adjusting the free parameters did not allow reproducing the synaptic delay (Figure 6E). We therefore tested two more sophisticated models in which vesicle fusion is triggered via five Ca²⁺ binding steps (Schneggenburger and Neher, 2000). In model 2, onevesicle pool represents the docked vesicles (V₂) and the other pool represents a replacement pool (V₁), which can undergo rapid docking and fusion (Miki et al., 2016; Miki et al., 2018), therefore representing two kinetic steps occurring in sequence. In model 3, two pools of vesicles (V₁, V₂) with different Ca²⁺-sensitivity exist, where both types of vesicles can fuse with different Ca²⁺ affinity (Voets, 2000; Walter et al., 2013; Wölfel et al., 2007; Hallermann et al., 2010 ) therefore representing two kinetic steps occurring in parallel. Model 3 reproduced the data as good as model 2; however, the non-saturation up to 50 µM could be reproduced somewhat better in model 3. Interestingly, models 2 and 3 both replicated the observed shallow dose-response curve despite the presence of five Ca²⁺ binding steps. These results indicate that established models with five Ca²⁺-steps incorporating fast vesicle replenishment via sequential or parallel vesicle pools can replicate our data fairly well.

Ca²⁺ uncaging with different pre-flash Ca²⁺ concentrations indicates Ca²⁺-dependent vesicle priming

Finally, we aimed to obtain a mechanistic understanding that could explain both the strong dependence of action potential-evoked release on basal Ca²⁺ concentration (Figure 1) and the Ca²⁺-dependence of vesicle fusion (Figures 2–6). In principle, the action potential-evoked data in Figure 1 could be explained by an acceleration of vesicle fusion kinetics or, alternatively, an increase in the number of release-ready vesicles upon elevated basal Ca²⁺. To differentiate between these two mechanistic possibilities, we investigated the effect of basal Ca²⁺ concentration preceding the UV illumination (pre-flash Ca²⁺) on flash-evoked release. The pre-flash Ca²⁺ concentration can only be reliably determined with the Ca²⁺ indicator Fluo5F used in the experiments with weak flashes (see Table 1). We therefore grouped the deconvolution experiments with weak flashes, which elevated the Ca²⁺ concentration to less than 7 μM, into two equally sized groups of low and high pre-flash Ca²⁺ (below and above a value of 200 nM, respectively). Due to the presence of the Ca²⁺ loaded DMn cage, the pre-flash Ca²⁺ concentrations were on average higher than the resting Ca²⁺ concentration in physiological conditions of around 50 nM (Delvendahl et al., 2015). In both groups, the post-flash Ca²⁺ concentration was on average similar (~3 μM; Figure 7B). The peak EPSC amplitude of postsynaptic current was significantly larger with high compared to low pre-flash Ca²⁺ concentration (38 ± 10 and 91 ± 16 pA, n = 18 and 13, respectively, P_Mann-Whitney = 0.001; Figure 7A and C). Correspondingly, the amplitude of the fast component of release as measured from deconvolution analysis was larger with high compared to low pre-flash Ca²⁺ (18 ± 5 and 49 ± 10, n = 18 and 13, respectively, P_Mann-Whitney = 0.005; Figure 7C). However, the kinetics of vesicle fusion, measured as the inverse of the time constant of the fast component of release, were not significantly different for both conditions (0.15 ± 0.04 and 0.12 ± 0.03 ms⁻¹ for the low and high pre-flash Ca²⁺ conditions, n = 18 and 13, respectively, P_Mann-Whitney = 0.74; Figure 7C). The delay was also not significantly different (P_Mann-Whitney = 0.54; Figure 7C). These data indicate that the number of release-ready vesicles were increased upon elevating the basal Ca²⁺ concentration but the fusion kinetics were unaltered. We therefore added an additional Ca²⁺-dependent maturation step to the initial vesicle priming of the release schemes (see Materials and methods; note that this was already present in the above-described simulations of Figure 6 but it has little impact on these data). This allowed replicating the three-fold increase in the action potential-evoked release when driving the release scheme with a previously estimated local Ca²⁺ concentration during an action potential (Figure 7D; Delvendahl et al., 2015). Thus, the release schemes 2 and 3 describe all our experimental data and therefore represent to our knowledge the only release scheme explaining the priming, fusion, and replenishment of vesicles at a mature excitatory synapse in the CNS at physiological temperature.

Figure 7

Download asset Open asset

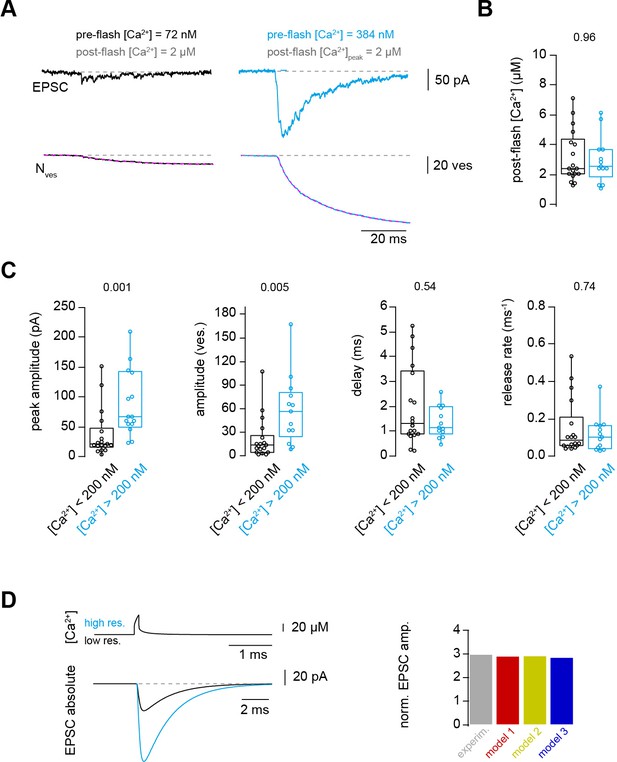
Ca²⁺ uncaging with different pre-flash Ca²⁺ concentrations indicates Ca²⁺-dependent vesicle priming.

(A) Two consecutive recordings from the same cell pair, with the same post-flash Ca²⁺ concentration but different pre-flash Ca²⁺ concentration in the presynaptic terminal. *Top:* postsynaptic current. *Bottom:* cumulative release of synaptic vesicles measured by deconvolution analysis of EPSCs superposed with a mono-exponential fit (magenta). Black and blue color represent low and high pre-flash Ca²⁺ concentration, respectively. The pre- and post-flash Ca²⁺ concentrations are indicated in each panel. (B) Comparison of the average post-flash Ca²⁺ concentration between both groups of either low (black) or high (blue) pre-flash Ca²⁺ concentration (n = 18 and 13 pairs, respectively). (C) From left to right: comparisons of the peak amplitude, the number of released vesicles measured as obtained from deconvolution analysis of EPSC, the delay of the release onset, and the release rate. Boxplots show median and 1st/3rd quartiles with whiskers indicating the whole data range. The values above the boxplots represent P-values of Mann-Whitney U tests. (D)*Top left:* simulated local action potential-evoked Ca²⁺concentrations at 20 nm from a Ca²⁺ channel taken from Delvendahl et al., 2015. Note the almost complete overlap of the two Ca²⁺ concertation traces with low and high basal Ca²⁺ concertation. *Bottom left:* predicted action potential-evoked EPSCs with low and high basal Ca²⁺ concertations. *Right:* ratio of the action potential-evoked EPSC amplitude with high and low basal Ca²⁺ concentrations for the experimental data and the model predictions.

Figure 7—source data 1 Ca²⁺ uncaging with different pre-flash Ca²⁺ concentrations indicates Ca²⁺-dependent vesicle priming.: https://cdn.elifesciences.org/articles/70408/elife-70408-fig7-data1-v1.xlsx
Download elife-70408-fig7-data1-v1.xlsx

Discussion

Here, we provided insights into the Ca²⁺-dependence of vesicle priming, fusion, and replenishment at cMFBs. The results obtained at this synapse show prominent Ca²⁺-dependent priming steps, a shallow non-saturating dose-response curve up to 50 µM, and little Ca²⁺-dependence of sustained vesicle replenishment. Our computational analysis indicates that the peculiar dose-response curve can be explained by well-established release schemes having five Ca²⁺ steps and rapid vesicle replenishment via sequential or parallel vesicle pools. Thus, we established quantitative scheme of synaptic release for a mature high-fidelity synapse, exhibiting both high- and low-affinity Ca²⁺ sensors.

Ca²⁺ affinity of the vesicle fusion sensor

The Ca²⁺-sensitivity of vesicle fusion seems to be synapse-specific. In contrast to the estimated Ca²⁺ affinity for vesicle fusion of ~100 μM at the bipolar cell of goldfish (Heidelberger et al., 1994) and the squid giant synapse (Adler et al., 1991; Llinás et al., 1992), recent studies showed that the affinity is much higher at three types of mammalian central synapses: the calyx of Held (Bollmann et al., 2000; Lou et al., 2005; Schneggenburger and Neher, 2000; Sun et al., 2007; Wang et al., 2008), the inhibitory cerebellar basket cell to Purkinje cell synapse (Sakaba, 2008), and the hippocampal mossy fiber boutons (Fukaya et al., 2021). Consistent with reports from mammalian central synapses, our data revealed prominent vesicle fusion at concentrations below 5 µM arguing for a high-affinity fusion sensor (Figures 2–4). However, the non-saturation of the dose-response curve (Figures 2–4) argues for the presence of a rather low-affinity fusion sensor at cMFBs. In our simulations, both models 2 and 3 exhibit vesicles with a Ca²⁺-affinity similar to the calyx of Held. Nevertheless, with high intracellular Ca²⁺ concentrations (>20 µM) these vesicles will fuse very rapidly and the further increase in the release kinetics (causing the non-saturating dose-response curve) can be explained by rapid vesicle replenishment from a sequential pool of vesicles exhibiting use-dependent lowering of the Ca²⁺-affinity (V₁ in model 2; Miki et al., 2018) or from a parallel pool of vesicles with lower Ca²⁺ affinity (V₁ in model 3; Hallermann et al., 2010). Our data therefore indicate that the shallow and non-saturating dose-response curve is the consequence of rapid replenishment of vesicles that still exhibit a lower Ca²⁺-affinity compared to fully recovered vesicles. Consistent with this interpretation, a lowering in the Ca²⁺-affinity of the vesicle fusion sensor has been observed at the calyx of Held with Ca²⁺ uncaging following vesicle depletion (Müller et al., 2010; Wadel et al., 2007). These newly replenished vesicles might contribute particularly to the dose-response curve at the cMFB because the cMFB has a much faster rate of vesicle replenishment compared with the calyx of Held synapse (Miki et al., 2020) providing a possible explanation why the here-reported dose-response curve differs from previous results at the calyx of Held. Furthermore, cMFBs seem to have functional similarities with ribbon-type synapses because it has recently been shown that the vesicle mobility in cMFBs is comparable to ribbon-type synapses (Rothman et al., 2016). The hallmark of ribbon-type synapses is their rapid vesicle replenishment (Lenzi and von Gersdorff, 2001; Matthews, 2000) and indeed more shallow dose-response curves were obtained at the ribbon photoreceptors and inner hair cell synapses (Duncan et al., 2010; Heil and Neubauer, 2010; Johnson et al., 2010; Thoreson et al., 2004, but see Beutner et al., 2001). The newly replenished vesicles might be molecularly immature and resemble vesicles that have only a near-linear remaining Ca²⁺ sensor when the fast Ca²⁺ sensor synaptotagmin II is lacking (Kochubey and Schneggenburger, 2011).

The here obtained dose-response curve has the following three caveats. First, the cMFB to GC synapses in lobule IX are functionally distinct based on the origin of the mossy fibers (Chabrol et al., 2015). Therefore, the here-recorded boutons in lobule IV/V could be molecularly and functionally distinct leading to the observed scatter in the dose-response curve, which could cause an apparent shallowing. Yet, the degree of scatter in the vesicular release rate at the cMFB seems comparable to studies at other synapses (Fukaya et al., 2021; Heidelberger et al., 1994; Sakaba, 2008) including the calyx of Held (Bollmann et al., 2000; Schneggenburger and Neher, 2000), although the functional heterogeneity between different types of calyces (Grande and Wang, 2011) could be explained by differences in the coupling distance (Fekete et al., 2019). Second, we could not investigate allosteric or two-sensor models (Lou et al., 2005; Sun et al., 2007; Li et al., 2021) because we did not address the release rates in the low Ca²⁺ range (<1 µM), therefore, these questions remain to be investigated at the cMFBs. Third, currently available techniques to estimate fast release rates at near-physiological temperatures in the Ca²⁺ range above 50 µM are limited by the sampling frequency of capacitance measurements and dendritic filtering, which could prevent the detection of saturation at the upper end of the dose-response curve.

Ca²⁺-sensitivity of vesicle priming

In previous reports, the Ca²⁺-dependence of vesicle priming and replenishment at cMFBs was analyzed more indirectly with the Ca²⁺ chelator EGTA (Ritzau-Jost et al., 2014; Ritzau-Jost et al., 2018) and the obtained results could be explained by Ca²⁺-dependent models but surprisingly also by Ca²⁺-independent models (Hallermann et al., 2010; Ritzau-Jost et al., 2018). Furthermore, the analysis of molecular pathways showed that the recovery from depression is independent of the Ca²⁺/calmodulin/Munc13 pathway at cMFBs (Ritzau-Jost et al., 2018). Our paired recordings and uncaging experiments (Figures 1 and 7) clearly demonstrate pronounced Ca²⁺-dependence of vesicle priming at cMFBs. Taken together, these data indicate that some priming steps are mediated by Ca²⁺-dependent mechanisms, which do not involve the Ca²⁺/calmodulin/Munc13 pathway. A potential candidate for such a Ca²⁺-dependent mechanism are the interaction of diacylgylcerol/phospholipase C or Ca²⁺/phospholipids with Munc13s (Lee et al., 2013; Lou et al., 2008; Rhee et al., 2002; Shin et al., 2010). Another candidate for a high-affinity Ca²⁺ sensor is Synaptotamin 7 (see below).

Synaptic vesicles that fuse upon single action potentials (Figure 1) and weak uncaging stimuli (post-flash Ca²⁺ concentration of ~3 µM; Figure 7) are particularly fusogenic and thus might represent the superprimed vesicles with a particular high release probability (Hanse and Gustafsson, 2001; Ishiyama et al., 2014; Kusch et al., 2018; Lee et al., 2013; Schlüter et al., 2006; Taschenberger et al., 2016) suggesting that the process of superpriming is Ca²⁺-dependent. This interpretation would also provide an explanation why in a recent report, triggering an action potential in the range of 10–50 ms before another action potential restored the synchronicity of synaptic vesicle fusion in mutant synapses which had an impaired synchronous release (Chang et al., 2018). It would be furthermore consistent with a proposed rapid, dynamic, and Ca²⁺-dependent equilibrium between primed and superprimed vesicles (Neher and Brose, 2018). However, further investigations are needed for the dissection between the Ca²⁺-dependence of priming and superpriming. Yet, our data show that some priming steps are strongly Ca²⁺-dependent with a high-affinity Ca²⁺ sensor that allow detecting changes between 30 and 180 nM at cMFBs.

Ca²⁺-sensitivity of vesicle replenishment

The upstream steps of vesicle priming, referred to as replenishment, recruitment, refilling, or reloading, remain controversial in particular with respect to their speed. The slow component of release (during prolonged depolarizations or Ca²⁺ elevations with uncaging) was initially interpreted as a sub-pool of release-ready vesicles that fuse with slower kinetics (see e.g. Sakaba and Neher, 2001a). However, recent studies indicate very fast vesicle replenishment steps (Blanchard et al., 2020; Chang et al., 2018; Doussau et al., 2017; Hallermann et al., 2010; Lee et al., 2012; Malagon et al., 2020; Miki et al., 2016; Miki et al., 2018; Saviane and Silver, 2006; Valera et al., 2012). These findings further complicate the dissection between fusion, priming, and replenishment steps. Therefore, the differentiation between ‘parallel’ release schemes with fast and slowly fusing vesicles and ‘sequential’ release schemes with fast vesicle replenishment and subsequent fusion is technically challenging at central synapses. Our data could be described by both sequential and parallel release schemes (models 2 and 3; Figure 6). The non-saturation of the release rate could be described somewhat better by the parallel model 3. However, further adjustment of the use-dependent slowing of the rates in model 2 (see k_on,plug, k_off,plug, Equations 3 and 4; Miki et al., 2018) can result in a sequential model exhibiting both fast and slowly fusing vesicles with different Ca²⁺-sensitivity (see Mahfooz et al., 2016, for an alternative description of use-dependence of vesicle fusion). Such use-dependent sequential models ultimately complicate the semantic definitions of ‘sequential’ and ‘parallel’, because the replenished vesicles of such sequential models will fuse in a molecularly different state, which could also be viewed as a parallel pathway to reach fusion. Independent of the difficulty to differentiate between sequential and parallel release schemes, the sustained component of release exhibited little Ca²⁺-dependence in the here-tested range between 1 and 50 µM (Figure 5). However, it should be mentioned that measuring the sustained release rate is prone to errors with both presynaptic capacitance and postsynaptic current recordings, because the former cannot differentiate between exo- and endocytosis occurring simultaneously, and the latter can fail to dissect direct release from spill-over current, which is prominent at this synapse (DiGregorio et al., 2002). Nevertheless, the Ca²⁺-independence of vesicle replenishment observed with capacitance measurements and the very weak Ca²⁺-dependence observed with postsynaptic techniques seem consistent with the previously observed EGTA-independent slope of the sustained release during prolonged depolarizations (Ritzau-Jost et al., 2014). Our data cannot differentiate if replenishment is mediated by a saturated Ca²⁺ sensor for priming (model 2; assumed K_dD of 2 µM; Miki et al., 2018) or a parallel Ca²⁺-independent step (model 3). Thus, during sustained activity at cMFBs, vesicle replenishment is mediated by either an apparently Ca²⁺-independent process because of a saturated high-affinity Ca²⁺ sensor or a Ca²⁺-independent process.

Implications for coupling distance

The Ca²⁺-sensitivity of vesicle fusion critically impacts the estimates of the coupling distance between Ca²⁺ channels and synaptic vesicles, mainly those obtained based on functional approaches (Neher, 1998; Eggermann et al., 2011; but not on structural approaches, see e.g. Éltes et al., 2017; Rebola et al., 2019). Our previous estimate of the coupling distance at the cMFB of 20 nm (Delvendahl et al., 2015) was based on the release scheme of Wang et al., 2008 obtained at the calyx of Held synapse at an age of (P16-P19) at room temperature and assuming a Q₁₀ factor of 2.5. The now estimated k_on and k_off rates at mature cMFBs at physiological temperature were slightly larger and smaller than the temperature-corrected values from the calyx, respectively, resulting in a slightly higher affinity of the fast releasing vesicles (V₂ in models 2 and 3). Therefore, at the cMFB, the coupling distance of the vesicles released by a single action potential is if anything even smaller than the previous estimate of 20 nm.

Implications for synaptic facilitation

Our data might contribute to a better understanding of the mechanisms of the ‘residual Ca²⁺ hypothesis’ explaining synaptic facilitation (Jackman and Regehr, 2017; Katz and Miledi, 1968; Magleby, 1987; Zucker and Regehr, 2002). The strong dependence of the action potential-evoked release on basal Ca²⁺ (Figure 1) supports the critical effect of residual Ca²⁺ on synaptic strength. Our mechanistic analysis (particularly Figure 7) indicates that the number of release-ready vesicles rather than the vesicular release probability is regulated by residual Ca²⁺. The high-affinity Ca²⁺ sensor Synaptotagmin-7 (Sugita et al., 2002) could be a sensor for the changes in basal Ca²⁺ levels and mediate the here-reported three-fold increase in synaptic strength (Figures 1 and 7). Synaptotagmin-7 has been shown to mediate vesicle recruitment (Liu et al., 2014), asynchronous release (Luo and Südhof, 2017), and synaptic facilitation (Chen et al., 2017; Jackman et al., 2016). If the recruitment and priming steps are fast enough they could provide a powerful mechanism for synaptic facilitation. Indeed, there is increasing evidence for ultra-fast Ca²⁺-dependent recruitment and priming (reviewed in Neher and Brose, 2018) as well as facilitation mediated by an increase in the number of release-ready vesicles rather than the vesicular release probability (Jackman et al., 2016; Kobbersmed et al., 2020; Vevea et al., 2021). Our data are therefore consistent with the emerging view that facilitation is mediated by rapid Synaptotagmin-7/Ca²⁺-dependent recruitment and priming of vesicles.

Implications for high-frequency transmission

Synaptic fidelity has been shown to increase with age at cMFBs (Cathala et al., 2003), neocortical synapses (Bornschein et al., 2019), and the calyx of Held (Fedchyshyn and Wang, 2005; Nakamura et al., 2015; Taschenberger and von Gersdorff, 2000). During high-frequency transmission, the residual Ca²⁺ concentration increases up to a few µM at cMFBs (Delvendahl et al., 2015) but mature cMFBs can still sustain synchronous release (Hallermann et al., 2010; Saviane and Silver, 2006). The developmental decrease in the affinity of the release sensors observed at the calyx of Held (Wang et al., 2008) and the here-reported shallow-dose-response curve at mature cMFBs could be an evolutionary adaptation of synapses to prevent the depletion of the release-ready vesicles at medium Ca²⁺ concentrations and therefore allow maintaining sustained synchronous neurotransmission with high fidelity (Matthews, 2000).

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Chemical compound, drug	NaCl	Sigma-Aldrich	Cat. # S9888
Chemical compound, drug	NaHCO₃	Sigma-Aldrich	Cat. # S6297
Chemical compound, drug	Glucose	Sigma-Aldrich	Cat. # G8270
Chemical compound, drug	AP 5	Sigma-Aldrich	Cat. # A78403
Chemical compound, drug	KCl	Sigma-Aldrich	Cat. # P9333
Chemical compound, drug	CaCl₂	Sigma-Aldrich	Cat. # C5080	For extracellular solution
Chemical compound, drug	CaCl₂	Sigma-Aldrich	Cat. # 21115	For intracellular solution
Chemical compound, drug	EGTA	Sigma-Aldrich	Cat. # E0396
Chemical compound, drug	NaH₂PO₄	Merck	Cat. # 106342
Chemical compound, drug	Tetrodotoxin	Tocris	Cat. # 1078
Chemical compound, drug	MgCl₂	Sigma-Aldrich	Cat. # M2670
Chemical compound, drug	TEA-Cl	Sigma-Aldrich	Cat. # T2265
Chemical compound, drug	HEPES	Sigma-Aldrich	Cat. # H3375
Chemical compound, drug	NaGTP	Sigma-Aldrich	Cat. # G8877
Chemical compound, drug	Na₂ATP	Sigma-Aldrich	Cat. # A2383
Chemical compound, drug	DMnitrophen	Synptic systems	Cat. # 510016
Chemical compound, drug	CsOH	Sigma-Aldrich	Cat. # C8518
Chemical compound, drug	Atto594	ATTO-TEC	Cat. # AD 594
Chemical compound, drug	OGB1	Thermo Fisher Scientific	Cat. # 06806
Chemical compound, drug	OGB-5N	Thermo Fisher Scientific	Cat. # 944034
Chemical compound, drug	Fluo-5F	Thermo Fisher Scientific	Cat. # F14221
Chemical compound, drug	KOH solution	Roth	Cat. # K017.1
Chemical compound, drug	Kynurenic acid	Sigma-Aldrich	Cat. # K3375
Chemical compound, drug	Cyclothiazide	Sigma-Aldrich	Cat. # C9847
Chemical compound, drug	Ca²⁺ Calibration Buffer Kit	Thermo Fisher Scientific	Cat. # C3008MP
Chemical compound, drug	Caged fluorescein	Sigma-Aldrich	Cat. # F7103
Chemical compound, drug	Glycerol	Sigma-Aldrich	Cat. # G5516
Chemical compound, drug	Isoflourane	Baxter	Cat. # Hdg9623
Chemical compound, drug	Aqua B. Braun	Braun	Cat. # 00882479E	For extracellular solution
Chemical compound, drug	Sterile Water	Sigma-Aldrich	W Cat. # 3500	For intracellular solution
Strain, strain background (mouse C57BL/6N)	Female, male C57BL/6N	Charles river	https://www.criver.com/
Other	Vibratome	LEICA VT 1200	https://www.leica-microsystems.com/
Other	Femto2D laser-scanning microscope	Femtonics	https://femtonics.eu/
Other	UV laser source	Rapp OptoElectronic	https://rapp-opto.com/	375 nm, 200 mW
Other	DMZ Zeitz Puller	Zeitz	https://www.zeitz-puller.com/
Other	Borocilicate glass	Science Products	https://science-products.com/en/	GB200F-10 With filament
Other	HEKA EPC10/2 amplifier	HEKA Elektronik	https://www.heka.com/
Other	Ti:Sapphire laser	MaiTai, SpectraPhysics	https://www.spectra-physics.com/
Other	Ca²⁺ sensitive electrode (ELIT 8041 PVC membrane)	NICO 2000	http://www.nico2000.net/index.htm
Other	Single junction silver chloride reference electrode (ELIT 001 n)	NICO 2000	http://www.nico2000.net/index.htm
Other	PH/Voltmeter	Metler toledo	https://www.mt.com/de/en/home.html
Other	Osmomat 3000	Gonotec	http://www.gonotec.com/de
Other	TC-324B perfusion heat controller	Warner Instruments	https://www.warneronline.com/
Software, algorithm	MES	Femtonics	https://femtonics.eu/
Software, algorithm	Igor Pro	Wavemetrics	https://www.wavemetrics.com/
Software, algorithm	Patchmaster	HEKA Elektronik	https://www.heka.com/
Software, algorithm	Adobe illustrator	Adobe	https://www.adobe.com/products/illustrator.html
Software, algorithm	Mathematica	Wolfram	https://www.wolfram.com/mathematica/
Software, algorithm	Maxchelator	Stanford University	https://somapp.ucdmc.ucdavis.edu/pharmacology/bers/maxchelator/

Preparation

Request a detailed protocol

Animals were treated in accordance with the German Protection of Animals Act and with the guidelines for the welfare of experimental animals issued by the European Communities Council Directive. Acute cerebellar slices were prepared from mature P35–P42 C57BL/6 mice of either sex as previously described (Hallermann et al., 2010). Isoflurane was used to anesthetize the mice, which were then sacrificed by decapitation. The cerebellar vermis was quickly removed and mounted in a chamber filled with chilled extracellular solution. 300-µm-thick parasagittal slices were cut using a Leica VT1200 microtome (Leica Microsystems), transferred to an incubation chamber at 35°C for ∼30 min, and then stored at room temperature until use. The extracellular solution for slice cutting and storage contained (in mM) the following: NaCl 125, NaHCO₃ 25, glucose 20, KCl 2.5, CaCl₂ 2, NaH₂PO₄ 1.25, MgCl₂1 (310 mOsm, pH 7.3 when bubbled with Carbogen [5% (vol/vol) O₂/95% (vol/vol) CO₂]). All recordings were restricted to lobules IV/V of the cerebellar vermis to reduce potential functional heterogeneity among different lobules (Straub et al., 2020).

Presynaptic recordings and flash photolysis

Request a detailed protocol

All recordings were performed at near-physiological temperature by adjusting the set temperature of the TC-324B perfusion heat controller (Warner Instruments, Hamden, CT, United States) until the temperature in the center of the recording chamber with immersed objective was between 36.0°C and 36.3°C. This process was repeated before using a new brain slice. During recordings, the thermometer was put at the side of the recording chamber and the readout was monitored to avoid potential drifts in temperature (the readout was between 32°C and 34°C, critically depending on the position of the thermometer, and changed during recording from one brain slice by less than 0.5°C). The room temperature was controlled using an air conditioner set to 24°C. Presynaptic patch-pipettes were from pulled borosilicate glass (2.0/1.0 mm outer/inner diameter; Science Products) to open-tip resistances of 3–5 MΩ (when filled with intracellular solution) using a DMZ Puller (Zeitz-Instruments, Munich, Germany). Slices were superfused with artificial cerebrospinal fluid (ACSF) containing (in mM): NaCl 105, NaHCO₃ 25, glucose 25, TEA 20, 4-AP 5, KCl 2.5, CaCl₂ 2, NaH₂PO4 1.25, MgCl₂ 1, and tetrodotoxin (TTX) 0.001, equilibrated with 95% O₂ and 5% CO₂. Cerebellar mossy fiber boutons (cMFBs) were visualized with oblique illumination and infrared optics (Ritzau-Jost et al., 2014). Whole-cell patch-clamp recordings of cMFBs were performed using a HEKA EPC10/2 amplifier controlled by Patchmaster software (HEKA Elektronik, Lambrecht, Germany). The intracellular solution contained (in mM): CsCl 130, MgCl₂ 0.5, TEA-Cl 20, HEPES 20, Na₂ATP 5, NaGTP 0.3. For Ca²⁺ uncaging experiments, equal concentrations of DM-nitrophen (DMn) and CaCl₂ were added depending on the aimed post-flash Ca²⁺ concentration, such that either 0.5, 2, or 10 mM was used for low, middle, or high target range of post-flash Ca²⁺ concentration, respectively (Table 1). To quantify post-flash Ca²⁺ concentration with a previously established dual indicator method (see below; Delvendahl et al., 2015; Sabatini et al., 2002), Atto594, OGB-5N, and Fluo-5F were used at concentrations as shown in (Table 1).

A 50 mM solution stock of DMn was prepared by neutralizing 50 mM DMn in H₂O with 200 mM CsOH in H₂O. The purity of each DMn batch was determined in the intracellular solution used for patching through titration with sequential addition of Ca²⁺ as previously described (Schneggenburger, 2005) and by measuring the Ca²⁺ concentration using the dual indicator method with 10 µM Atto594 and 50 µM OGB1 (Delvendahl et al., 2015).

After waiting for at least one minute in whole-cell mode to homogenously load the terminal with intracellular solution, capacitance measurements were performed at a holding potential of −100 mV with sine-wave stimulation (5 kHz or 10 kHz frequency and ±50 mV amplitude; Hallermann et al., 2003). Distant mossy fiber boutons on the same axon are unlikely to contaminate capacitance measurements because investigations at hippocampal mossy fiber buttons indicate that the high-frequency sine-wave techniques as used in our study are hardly affected by release from neighboring boutons on the same axon (Hallermann et al., 2003). During the ongoing sine-wave stimulation, a UV laser source (375 nm, 200 mW, Rapp OptoElectronic) was used to illuminate the whole presynaptic terminal. According to a critical illumination, the end of the light guide of the UV laser was imaged into the focal plan resulting in a homogeneous illumination in a circular area of ~30 µm diameter (Figure 2—figure supplement 1). The duration of the UV illumination was 100 µs controlled with sub-microsecond precision by external triggering of the laser source. In capacitance measurements with 10 kHz sine wave frequency, longer pulses of 200 µs were used to reach high Ca²⁺ levels. In a subset of experiments, UV pulses of 1 ms were used to rule out fast undetectable Ca²⁺ overshoots (Bollmann et al., 2000; Figure 3—figure supplement 2). The UV flash intensity was set to 100% and reduced in some experiments (10–100%) to obtain small elevations in Ca²⁺ concentrations (Table 1). To avoid photoproducts-induced cell toxicity, we applied only one flash per recording. In a subset of the paired recordings with weak UV illumination (post-flash Ca²⁺ concentration < 5 µM), we used consecutive flashes on the same cell (from 43 paired cells, 16 consecutive recordings were used).

Paired recordings between cMFBs and GCs

Request a detailed protocol

For paired pre- and postsynaptic recordings, granule cells (GCs) were whole-cell voltage-clamped with intracellular solution containing the following (in mM): K-gluconate 150, NaCl 10, K-HEPES 10, MgATP three and Na-GTP 0.3 (300–305 mOsm, pH adjusted to 7.3 with KOH). 10 μM Atto594 was included to visualize the dendrites of the GCs (Ritzau-Jost et al., 2014). After waiting sufficient time to allow for the loading of the dye, the GC dendritic claws were visualized through two-photon microscopy, and subsequently, cMFBs near the dendrites were identified by infrared oblique illumination and were patched and loaded with caged Ca²⁺ and fluorescent indicators as previously described. The reliable induction of an EPSC in the GC was used to unequivocally confirm a cMFB-GC synaptic connection. In a subset of the Ca²⁺ uncaging experiments, simultaneous presynaptic capacitance and postsynaptic EPSC recordings were performed from cMFBs and GCs, respectively.

Clamping intracellular basal Ca²⁺ concentrations

Request a detailed protocol

The intracellular solution for presynaptic recordings of the data shown in Figure 1 contained the following in mM: K-gluconate 150, NaCl 10, K-HEPES 10, MgATP 3, Na-GTP 0.3. With a combination of EGTA and CaCl₂ (5 mM EGTA / 0.412 mM CaCl₂ or 6.24 mM EGTA / 1.65 mM CaCl₂), we aimed to clamp the free Ca²⁺ concentration to low and high resting Ca²⁺ concentrations of ~50 or ~200 nM, respectively, while maintaining a free EGTA concentration constant at 4.47 mM. The underlying calculations were based on a Ca²⁺ affinity of EGTA of 543 nM (Lin et al., 2017). The resulting free Ca²⁺ concentration was quantified with the dual indicator method (see below) and was found to be to ~30 or ~180 nM, respectively (Figure 1A).

Quantitative two-photon Ca²⁺ imaging

Request a detailed protocol

For the quantification of Ca²⁺ signals elicited through UV-illumination-induced uncaging, two-photon Ca²⁺ imaging was performed as previously described (Delvendahl et al., 2015) using a Femto2D laser-scanning microscope (Femtonics) equipped with a pulsed Ti:Sapphire laser (MaiTai, SpectraPhysics) adjusted to 810 nm, a 60×/1.0 NA objective (Olympus), and a 1.4 NA oil-immersion condenser (Olympus). Data were acquired by doing line-scans through the cMFB. To correct for the flash-evoked luminescence from the optics, the average of the fluorescence from the line-scan in an area outside of the bouton was subtracted from the average of the fluorescence within the bouton (Figure 2B). Imaging data were acquired and processed using MES software (Femtonics). Upon releasing Ca²⁺ from the cage, we measured the increase in the green fluorescence signal of the Ca²⁺-sensitive indicator (OGB-5N or Fluo-5F) and divided it by the fluorescence of the Ca²⁺-insensitive Atto594 (red signal). The ratio (R) of green-over-red fluorescence was translated into a Ca²⁺ concentration through the following calculation (Yasuda et al., 2004).

[C a^{2 +}] = K_{D} \frac{(R - R_{m i n})}{(R_{m a x} - R)}

To avoid pipetting irregularities, which might influence the quantification of the fluorescence signals, pre-stocks of Ca²⁺-sensitive and Ca²⁺-insensitive indicators were used. For each pre-stock and each intracellular solution, 10 mM EGTA or 10 mM CaCl₂ were added to measure minimum (R_min) and maximum (R_max) fluorescence ratios, respectively. We performed these measurements in cMFBs and GCs as well as in cuvettes. Consistent with a previous report (Delvendahl et al., 2015), both R_min and R_max were higher when measured in cells than in cuvettes (by a factor of 1.73 ± 0.05; n = 83 and 63 measurements in situ and in cuvette; Figure 3—figure supplement 3A). The values in cMFBs and GCs were similar (Figure 3—figure supplement 3B). OGB-5N is not sensitive in detecting Ca²⁺ concentrations less than 1 μM. Therefore, we deliberately adjusted R_min of OGB-5N in the recordings where the pre-flash Ca²⁺ had negative values, to a value resulting in a pre-flash Ca²⁺ concentration of 60 nM, which corresponds to the average resting Ca²⁺ concentration in these boutons (Delvendahl et al., 2015). This adjustment of R_min resulted in a reduction of post-flash Ca²⁺ amplitudes of on average 7.5 ± 0.4% (n = 37).

The fluorescence properties of DMn change after flash photolysis, and the Ca²⁺ sensitive and insensitive dyes can differentially bleach during UV flash (Schneggenburger, 2005; Zucker, 1992). We assumed no effect of the UV flash on the K_D of the Ca²⁺-sensitive dyes (Escobar et al., 1997), and measured R_min and R_max before and after the flash for each used UV flash intensity and duration in each of the three solutions (Table 1; Schneggenburger and Neher, 2000). The flash-induced change was strongest for R_max of solutions with OGB-5N, but reached only ~20% with the strongest flashes (Figure 3—figure supplement 3F).

Deconvolution

Request a detailed protocol

Deconvolution of postsynaptic currents was performed essentially as described by Ritzau-Jost et al., 2014, based on routines developed by Sakaba and Neher, 2001b. The principle of this method is that the EPSC comprises currents induced by synchronous release and residual glutamate in the synaptic cleft due to delayed glutamate clearance and glutamate spill-over from neighboring synapses, which is prominent at the cMFB to GC synapses (DiGregorio et al., 2002). Kynurenic acid (2 mM) and Cyclothiazide (100 μM) were added to the extracellular solution to reduce postsynaptic receptor saturation and desensitization, respectively. The amplitude of the miniature EPSC (mEPSC) was set to the mean value of 10.1 pA (10.1 ± 0.2 pA; n = 8) as measured in 2 mM kynurenic acid and 100 µM cyclothiazide. Kynurenic acid has been reported to absorb UV light resulting in a reduction of the uncaging efficiency (Sakaba et al., 2005; Wölfel et al., 2007). However, kynurenic acid particularly absorbs UV light at wavelength below 370 nm (Wölfel et al., 2007) suggesting that the reduction in the uncaging efficiency at the wavelength used in this study (375 nm) might be small. In agreement with this, we were able to increase the post-flash Ca²⁺ concentrations to ~50 µM.

The deconvolution kernel had the following free parameters: the mEPSC early slope τ₀, the fractional amplitude of the slow mEPSC decay phase α, the time constant of the slow component of the decay τ₂ of the mEPSC, the residual current weighting factor β, and the diffusional coefficient d. Applying the ‘fitting protocol’ described by Sakaba and Neher, 2001b before flash experiments might affect the number of vesicles released by subsequent Ca²⁺ uncaging. On the other hand, applying the ‘fitting protocol’ after Ca²⁺ uncaging might underestimate the measured number of vesicles due to flash-induced toxicity and synaptic fatigue especially when applying strong Ca²⁺ uncaging. Therefore, we used the experiments with weak and strong flashes to extract the mini-parameters and the parameters for the residual current of the deconvolution kernel, respectively, as described in the following in more detail. To obtain the mini parameters (early slope, α, and τ₂) using weak flashes, deconvolution was first performed with a set of trial parameters for each cell pair. The mini-parameters of the deconvolution were optimized in each individual recording to yield low (but non-negative) step-like elevations in the cumulative release corresponding to small EPSCs measured from the postsynaptic terminal (the parameters for the residual current had little impact on the early phase of the cumulative release rate within the first 5 ms, therefore, some reasonable default values for the parameters of the residual current were used while iteratively adjusting the fast mini parameters for each individual recording). Next, using the average of the mini-parameters obtained from weak flashes, the deconvolution parameters for the residual current (β and d) were optimized in each recording with strong flashes until no drops occurred in the cumulative release in the range of 5–50 ms after the stimulus (while iteratively readjusting the mini parameters, if needed, to avoid any drops in the cumulative release in the window of 5–10 ms that might arise when adjusting the slow parameters based on the cumulative release in the range of 5–50 ms). Finally, we averaged the values of each parameter and the deconvolution analysis of all recordings was re-done using the average parameters values. To test the validity of this approach, cumulative release from deconvolution of EPSCs and presynaptic capacitance recordings were compared in a subset of paired recordings (n = 9 pairs) similarly as done in previous investigations (Ritzau-Jost et al., 2014). Exponential fits to the cumulative release and the presynaptic capacitance traces provided very similar time constants. On a paired-wise comparison, the difference in the time constant was always less than 40% (Figure 3—figure supplement 4). Therefore, both approaches yielded similar exponential time constants.

To combine the sustained release rate estimated from capacitance measurements (Figure 5B) and deconvolution analysis of EPSC (Figure 5C) for the modeling with release schemes (Figure 6E), we estimated the number of GCs per cMFB by comparing the product of the amplitude and the inverse of the time constant of the exponential fit of the presynaptic capacitance trace and the simultaneously measured cumulative release trace obtained by deconvolution analysis. Assuming a capacitance of 70 aF per vesicle (Hallermann et al., 2003), we obtained an average value of 90.1 GCs per MFB in close agreement with previous estimates using a similar approach (Ritzau-Jost et al., 2014). This connectivity ratio is larger than previous estimates (∼10, Billings et al., 2014; ∼50, Jakab and Hamori, 1988) which could be due to a bias toward larger terminals, ectopic vesicle release, postsynaptic rundown, or release onto Golgi cells.

Measurement of Ca²⁺ concentration using a Ca²⁺-sensitive electrode

Request a detailed protocol

A precise estimation of the binding affinity of the Ca²⁺-sensitive dyes is critical in translating the fluorescence signals into Ca² concentration. It has been reported that the K_D of fluorescent indicators differs significantly depending on the solution in which it is measured (Tran et al., 2018) due to potential differences in ionic strength, pH, and concentration of other cations. Accordingly, different studies have reported different estimates of the K_D of OGB-5N having an up to eight-fold variability (Delvendahl et al., 2015; DiGregorio and Vergara, 1997; Neef et al., 2018). In these studies, the estimation of the K_D of the Ca²⁺ sensitive dyes depended on the estimated K_D of the used Ca²⁺ chelator, which differs based on the ionic strength, pH, and temperature of the solution used for calibration. So, we set out to measure the K_D of OGB-5N, in the exact solution and temperature, which we used during patching, through direct potentiometry using an ion-selective electrode combined with two-photon Ca²⁺ imaging. An ion-selective electrode for Ca²⁺ ions provides a direct readout of the free Ca²⁺ concentration independent of the K_D of the used Ca²⁺ chelator. Using the same intracellular solution and temperature as used during experiments, the potential difference between the Ca²⁺-sensitive electrode (ELIT 8041 PVC membrane, NICO 2000) and a single junction silver chloride reference electrode (ELIT 001 n, NIC0 2000) was read out with a pH meter in voltage mode. A series of standard solutions, with defined Ca²⁺ concentration (Thermo Fisher Scientific) covering the whole range of our samples, were used to plot a calibration curve of the potential (mV) versus Ca²⁺ concentration (μM). Then, the potential of several sample solutions containing the same intracellular solution used for patching, but with different Ca²⁺ concentrations buffered with EGTA, was determined. This way, we got a direct measure of the free Ca²⁺ concentration of several sample solutions, which were later used after the addition of Ca²⁺-sensitive fluorometric indicators to plot the fluorescence signal of each solution versus the corresponding free Ca²⁺ concentration verified by the Ca²⁺-sensitive electrode, and accordingly the K_D of the Ca²⁺ indicators were obtained from fits with a Hill equation. The estimated K_D was two-fold higher than the estimate obtained using only the Ca²⁺ Calibration Buffer Kit (Thermo Fisher Scientific) without including intracellular patching solution (Figure 3—figure supplement 1). Comparable results were obtained when estimating the free Ca²⁺ concentration using Maxchelator software (https://somapp.ucdmc.ucdavis.edu/pharmacology/bers/maxchelator/). Therefore, we used two independent approaches to confirm the K_D of OGB-5N. We found that TEA increased the potential of the solutions measured through the Ca²⁺-sensitive electrode, which is consistent with a previous report showing a similar effect of quaternary ammonium ions on potassium sensitive microelectrodes (Neher and Lux, 1973). We compared the fluorescence signals of our samples with or without TEA, to check if this effect of TEA is due to an interaction with the electrode or due to an effect on the free Ca²⁺ concentration, and found no difference. Therefore, TEA had an effect on the electrode read-out without affecting the free Ca²⁺, and accordingly, TEA was removed during the potentiometric measurements (Figure 3—figure supplement 1). This resulted in a good agreement of the estimates of the free Ca²⁺ concentration measured using a Ca²⁺-sensitive electrode and those calculated via Maxchelator.

Assessment of the UV energy profile

Request a detailed protocol

The homogeneity of the UV laser illumination at the specimen plane was assessed in vitro by uncaging fluorescein (CMNB-caged fluorescein, Thermo Fisher Scientific). Caged fluorescein (2 mM) was mixed with glycerol (5% caged fluorescein/ 95% glycerol) to limit the mobility of the released dye (Bollmann et al., 2000). We did the measurements at the same plane as we put the slice during an experiment. The fluorescence profile of the dye after being released from the cage was measured at different z-positions over a range of 20 μm. The intensity of fluorescein was homogenous over an area of 10 µm x 10 µm x 10 µm which encompasses the cMFB.

Data analysis

Request a detailed protocol

The increase in membrane capacitance and in cumulative release based on deconvolution analysis was fitted with the following single or bi-exponential functions using Igor Pro (WaveMetrics) including a baseline and a variable onset.

\begin{array}{ll} f_{m o n o} (t) = {\begin{matrix} 0 & i f t < d, \\ a (1 - e x p [- \frac{(t - d)}{τ}]) & i f t \geq d \end{matrix} \\ f_{b i} (t) = {\begin{matrix} 0 & i f t < d, \\ a (1 - a_{1} e x p [- \frac{(t - d)}{τ_{1}}] - (1 - a_{1}) e x p [- \frac{(t - d)}{τ_{2}}]) & i f t \geq d \end{matrix} \end{array}

where $d$ defines the delay, $a$ the amplitude, $τ$ the time constant of the mono-exponetial fit, $τ_{1}$ and $τ_{2}$ the time constants of the fast and slow components of the bi-exponential fit, respectively, and $a_{1}$ the relative contribution of the fast component of the bi-exponential fit. The fitting of the release traces was always done with a time window of 5 ms before and 10 ms after flash onset. If the time constant of the mono-exponential fit exceeded 10 ms, a longer fitting duration of 60 ms after flash onset was used for both the experimental and the simulated data.

The acceptance of a bi-exponential fit was based on the fulfillment of the following three criteria: (1) at least 4% decrease in the sum of squared differences between the experimental trace and the fit compared with a mono-exponential fit (χ²_mono/χ²_bi > 1.04), (2) the time constants of the fast and the slow components differed by a factor >3, and (3) the relative contribution of each component was >10% (i.e. 0.1 < $a_{1}$ < 0.9). If any of these criteria was not met, a mono-exponential function was used instead. In the case of weak flashes, where we could observe single quantal events within the initial part of the EPSC, mono-exponential fits were applied. In Figure 1, bi-exponential functions were used to fit the decay of the EPSC and the amplitude-weighted time constants were used (Hallermann et al., 2010).

Hill equations were used to fit the release rate versus intracellular Ca²⁺ concentration on a double logarithmic plot according to the following equation:

H (x) = L o g [V_{m a x} \frac{1}{1 + {(\frac{K_{D}}{10^{x}})}^{n}}]

where Log is the decadic logarithm, V_max the maximal release rate, K_D the Ca²⁺ concentration at the half-maximal release rate, and n the Hill coefficient. H(x) was fit on the decadic logarithm of the release rates and x was the decadic logarithm of the intracellular Ca²⁺ concentration.

Modeling of intra-bouton Ca²⁺ dynamics

Request a detailed protocol

We simulated the intra-bouton Ca²⁺ dynamics using a single compartment model. The kinetic reaction schemes for Ca²⁺ and Mg^2+-uncaging and -binding (Figure 6A) were converted to a system of ordinary differential equations (ODEs) that was numerically solved using the NDSolve function in Mathematica 12 (Wolfram) as described previously (Bornschein et al., 2019). The initial conditions for the uncaging simulation were derived by first solving the system of ODEs for the steady state using total concentrations of all species and the experimentally determined [Ca²⁺]_rest as starting values. Subsequently, the values obtained for all free and bound species were used as initial conditions for the uncaging simulation. The kinetic properties of DMn were simulated according to Faas et al., 2005, Faas et al., 2007. The total DMn concentration ([DMn]_T) includes the free form ([DMn]), the Ca^2+-bound form ([CaDMn]), and the Mg^2+-bound form ([MgDMn]). Each of these forms is subdivided into an uncaging fraction (α) and a non-uncaging fraction (1-α). The uncaging fractions were further subdivided into a fast (af) and a slow (1-af) uncaging fraction:

[DMn]_T = [DMn]_f + [DMn]_s + [CaDMn]_f + [CaDMn]_s+ [MgDMn]_f + [MgDMn]_s
[DMn] = [DMn]_f + [DMn]_s
[DMn]_f = α af [DMn]
[DMn]_s = α (1-af) [DMn]
[CaDMn] = [CaDMn]_f + [CaDMn]_s
[CaDMn]_f = α af [CaDMn]
[CaDMn]_s = α (1-af) [CaDMn]
[MgDMn] = [MgDMn]_f + [MgDMn]_s
[MgDMn]_f = α af [MgDMn]
[MgDMn]_s = α (1-af) [MgDMn]

The suffixes ‘T’, ‘f’, and ‘s’ indicate total, fast or slow, respectively. The transition of fast and slow uncaging fractions into low-affinity photoproducts (PP) occurred with fast (τ_f) or slow (τ_s) time constants, respectively. Free Ca²⁺ or Mg²⁺-bound DMn decomposed into two photoproducts (PP1, PP2) differing with respect to their binding kinetics. The binding kinetics of all species were governed by the corresponding forward (k_on) and backward (k_off) rate constants

{\frac{d [C a D M n]}{d t}}_{x} = k_{o n} [C a] {[D M n]}_{x} - k_{o f f} {[C a D M n]}_{x} - \frac{{[C a D M n]}_{x}}{τ_{x}} H (t - t_{f l a s h}) x = f, s

{\frac{d [M g D M n]}{d t}}_{x} = k_{o n} [M g] {[D M n]}_{x} - k_{o f f} {[M g D M n]}_{x} - \frac{{[M g D M n]}_{x}}{τ_{x}} H (t - t_{f l a s h}) x = f, s

\begin{array}{ll} {\frac{d [D M n]}{d t}}_{x} = - k_{o n} [C a] {[D M n]}_{x} + k_{o f f} {[C a D M n]}_{x} - k_{o n} [M g] {[D M n]}_{x} + k_{o f f} {[M g D M n]}_{x} \\ \begin{array}{cc} - \frac{{[D M n]}_{x}}{τ_{x}} H (t - t_{f l a s h}) x = f, s \end{array} \end{array}

\begin{matrix} \frac{d [C a P P 1]}{d t} = k_{o n} [C a] [P P 1] - k_{o f f} [C a P P 1] + \frac{{[C a D M n]}_{f}}{τ_{f}} H (t - t_{f l a s h}) + \frac{{[C a D M n]}_{s}}{τ_{s}} H (t - t_{f l a s h}) \end{matrix}

\frac{d [M g P P 1]}{d t} = k_{o n} [M g] [P P 1] - k_{o f f} [M g P P 1]

\begin{matrix} \frac{d [P P 1]}{d t} = - k_{o n} [C a] [P P 1] + k_{o f f} [C a P P 1] - k_{o n} [M g] [P P 1] + k_{o f f} [M g P P 1] \\ + \frac{{[C a D M n]}_{f}}{τ_{f}} H (t - t_{f l a s h}) + \frac{{[C a D M n]}_{s}}{τ_{s}} H (t - t_{f l a s h}) \end{matrix} \begin{matrix}  \end{matrix}

\frac{d [C a P P 2]}{d t} = k_{o n} [C a] [P P 2] - k_{o f f} [C a P P 2]

\begin{matrix} \frac{d [M g P P 2]}{d t} = k_{o n} [M g] [P P 2] - k_{o f f} [M g P P 2] + \frac{{[M g D M n]}_{f}}{τ_{f}} H (t - t_{f l a s h}) \\ + \frac{{[M g D M n]}_{s}}{τ_{s}} H (t - t_{f l a s h}) \end{matrix}

\frac{d [P P 2]}{d t} = - k_{o n} [C a] [P P 2] + k_{o f f} [C a P P 2] - k_{o n} [M g] [P P 2] + k_{o f f} [M g P P 2]

+ 2 \frac{{[D M n]}_{f}}{τ_{f}} H (t - t_{f l a s h}) + \frac{{[D M n]}_{s}}{τ_{s}} H (t - t_{f l a s h})

+ \frac{{[M g D M n]}_{f}}{τ_{f}} H (t - t_{f l a s h}) + \frac{{[M g D M n]}_{s}}{τ_{s}} H (t - t_{f l a s h})

where H is the Heaviside step function and t_flash the time of the UV flash. Ca²⁺ and Mg^2+-binding to the dye, ATP, and an endogenous buffer (EB) were simulated by second-order kinetics:

\begin{matrix} {\frac{d [C a]}{d t}}_{b u f f e r} = - k_{o n, j} [C a] [B] + k_{o f f, j} [C a B] & j = d y e, A T P, E B \end{matrix}

\begin{matrix} \frac{d [M g]}{d t} = - k_{o n, j} [M g] [B] + k_{o f f, j} [M g B] & j = A T P \end{matrix}

\begin{matrix} \frac{d [B]}{d t} = - \frac{d [C a B]}{d t} - \frac{d [M g B]}{d t} & B = d y e, A T P, E B \end{matrix}

The time course of the total change in Ca²⁺ concentration or Mg²⁺ concentration is given by the sum of all the above equations involving changes in Ca²⁺ concentration or Mg²⁺ concentration, respectively. Ca²⁺ concentration as reported by the dye was calculated from the concentration of the Ca²⁺-dye complex assuming equilibrium conditions (Markram et al., 1998). The clearing of Ca²⁺ from the cytosol was not implemented in these simulations. Instead, the Ca²⁺ concentration was simulated only for 10 ms after the flash. The experimentally observed subsequent decay of the Ca²⁺ concentration was implemented by an exponential decay to the resting Ca²⁺ concentration with a time constant of 400 ms. The parameters of the model are given in Table 2.

These simulations were used to obtain Ca²⁺ transients with peak amplitudes covering the entire range of post-flash Ca²⁺ concentrations. To this end, the uncaging efficiency α was varied in each of the three experimentally used combinations of concentrations of DMn and Ca²⁺ indicators (see Table 1 for details).

Modeling of release schemes

Request a detailed protocol

Model one with two Ca²⁺ binding steps mediating fusion and one Ca²⁺-dependent priming step was defined according to the following differential equation

(\begin{matrix} d V_{0 C a} (t) / d t \\ d V_{1 C a} (t) / d t \\ d V_{2 C a} (t) / d t \\ d V_{f u s e d} (t) / d t \end{matrix}) = M (\begin{matrix} V_{0 C a} (t) \\ V_{1 C a} (t) \\ V_{2 C a} (t) \\ V_{f u s e d} (t) \end{matrix})

$V_{0 C a}$ , $V_{1 C a}$ , and $V_{2 C a}$ denote the fraction of vesicles with a fusion sensor with 0 to 2 bound Ca²⁺ ions, respectively, and $V_{f u s e d}$ denotes the fused vesicles as illustrated in Figure 6D. The reserve pool $V_{R}$ is considered to be infinite. $M$ denotes the following 4x4 matrix:

(\begin{matrix} _{- 2 k_{o n} - k_{u n p r i m} + k_{p r i m} / V_{0 C a} (t)} & _{k_{o f f}} & _{0} & _{0} \\ _{2 k_{o n}} & _{- k_{o f f} - k_{o n}} & _{2 k_{o f f} b} & _{0} \\ _{0} & _{k_{o n}} & _{- y - 2 k_{o f f} b} & _{0} \\ _{0} & _{0} & _{y} & _{0} \end{matrix})

See Table 3 for the values and Ca²⁺-dependence of the rate constants in the matrix.

Table 3

Parameters for release scheme models.

Model1		Model2		Model3
k_on	2.95*10⁹ Ca²⁺(t) M⁻¹ s⁻¹	k_on,init	5.10*10⁸ Ca²⁺(t) M⁻¹ s⁻¹	k_on1	0.5 k_on2
		k_on,plug	0.1 k_on,init	k_on2	5.10*10⁸ Ca²⁺(t) M⁻¹ s⁻¹
k_off	4.42*10⁵ s⁻¹	k_off,init	2.55*10⁴ s⁻¹	k_off1	10 k_off2
		k_off,plug	0.4 k_off,init	k_off2	2.55*10⁴ s⁻¹
b	0.25	b	0.25	b	0.25
γ	1.77*10⁴ s⁻¹	γ	1.77*10⁴ s⁻¹	γ	1.77*10⁴ s⁻¹
k_prim	0.6+30*(Ca²⁺(t)/(K_D,prim +Ca²⁺(t))) s⁻¹	k_prim1	2.5+60*(Ca²⁺(t)/(K_D,prim1 +Ca²⁺(t))) s⁻¹	k_prim1	30 s⁻¹
k_unprim	0.6+30*(Ca²⁺_Rest/(K_D,prim + Ca²⁺_Rest)) s⁻¹	k_unprim1	2.5+60*(Ca²⁺_Rest/(K_D,prim1 + Ca²⁺_Rest)) s⁻¹	k_unprim1	30 s⁻¹
K_D,prim	2 µM	K_D,prim1	2 µM
		k_prim2	100+800*(Ca²⁺(t)/(K_D,prim2 +Ca²⁺(t))) s⁻¹	k_prim2	0.5+30*(Ca²⁺(t)/(K_D,prim2 +Ca²⁺(t))) s⁻¹
		k_unprim2	100+800*(Ca²⁺_Rest/(K_D,prim2 + Ca²⁺_Rest)) s⁻¹	k_unprim2	0.5+30*(Ca²⁺_Rest/(K_D,prim2 + Ca²⁺_Rest)) s⁻¹
		K_D,prim2	2 µM	K_D,prim2	2 µM

The initial condition was defined as V_0Ca(0) = k_prim/k_unprim and V_1Ca(0), V_2Ca(0), and V_fused(0) was zero. k_prim was the sum of a Ca²⁺-dependent and Ca²⁺-independent rate constants. The Ca²⁺-dependence was implemented as a Michaelis-Menten kinetic with a maximum rate constant of 30 s⁻¹ (Ritzau-Jost et al., 2014) and a K_D of 2 µM (Miki et al., 2018). The Ca²⁺-independent rate constant was 0.6 s⁻¹, adjusted to reproduce the factor of 3 upon elevating Ca²⁺ from 30 to 180 nM (Figures 1D and 7D). k_unprim was defined such that the occupancy V_0Ca(0) = 1 for the default pre-flash resting Ca²⁺ concentration of 227 nM (Tables 2 and 3). The occupancy was set to 1 for simplicity in all models because our data did not allow determining the occupancy (but for evidence of occupancy < 1 see Pulido and Marty, 2017).

The differential equations were solved with the NDSolve function of Mathematica. The Ca²⁺ concentration, Ca²⁺(t), was obtained from the simulations as described in the previous paragraph. $V_{f u s e d} (t)$ represents the cumulative release normalized to the pool of release-ready vesicles per cMFB to GC connection. To reproduce the absolute sustained release rate (Figures 5, 6D), $V_{f u s e d} (t)$ was multiplied by a pool of release-ready vesicles per connection of 10 vesicles. The cumulative release, $V_{f u s e d} (t)$ , including a pre-flash baseline was sampled with 5 or 10 kHz. Realistic noise for 5- or 10-kHz-capacitance or deconvolution measurements was added and the data, in the 10 ms-window after the flash, were fit with mono- and bi- exponential functions (Equation 1). The selection of a bi- over a mono-exponential fit was based on identical criteria as in the analysis of the experimental data including the prolongation of the fitting duration from 10 to 60 ms if the time constant of the mono-exponential fit was >10 ms (see section Data analysis). For each peak post-flash Ca²⁺ concentration (i.e. simulated Ca²⁺(t) transient) the sampling, addition of noise, and exponential fitting were repeated 50 times. The median of these values represents the prediction of the model for each peak post flash Ca²⁺ concentration. The parameters of the r were manually adjusted to obtain best-fit results.

Model 2 was a sequential two-pool model based on Miki et al., 2018 with five Ca²⁺ binding steps mediating fusion and two Ca²⁺-dependent priming steps defined according to the following differential equations

(\begin{matrix} d V_{2, 0 C a} (t) / d t \\ d V_{2, 1 C a} (t) / d t \\ d V_{2, 2 C a} (t) / d t \\ d V_{2, 3 C a} (t) / d t \\ d V_{2, 4 a} (t) / d t \\ d V_{2, 5 C a} (t) / d t \\ d V_{2, f u s e d} (t) / d t \end{matrix}) = M (\begin{matrix} V_{2, 0 C a} (t) \\ V_{2, 1 C a} (t) \\ V_{2, 2 C a} (t) \\ V_{2, 3 C a} (t) \\ V_{2, 4 C a} (t) \\ V_{2, 5 C a} (t) \\ V_{2, f u s e d} (t) \end{matrix})

$V_{2, 0 C a}$ , $V_{2, 1 C a}$ , …, and $V_{2, 5 C a}$ denote the fraction of vesicles with a fusion sensor with 0 to 5 bound Ca²⁺ ions, respectively, and $V_{2, f u s e d}$ denotes fused vesicles as illustrated in Figure 6D. The fraction of vesicles in state $V_{1}$ is calculated according to the following differential equation

\frac{d V_{1} (t)}{d t} = k_{p r i m 1} - k_{u n p r i m 1} V_{1} (t) - k_{p r i m 2} V_{1} (t) + k_{u n p r i m 2} V_{2, 0 C a} (t)

$M$ denotes the following 7x7 matrix:

(\begin{matrix} _{- 5 k_{o n} - k_{u n p r i m 2} + k_{p r i m 2} / V_{1} (t) / V_{2, 0 C a} (t)} & _{k_{o f f}} & _{0} & _{0} & _{0} & _{0} & _{0} \\ _{5 k_{o n}} & _{- k_{o f f} - 4 k_{o n}} & _{2 k_{o f f} b} & _{0} & _{0} & _{0} & _{0} \\ _{0} & _{4 k_{o n}} & _{- 2 k_{o f f} b - 3 k_{o n}} & _{3 k_{o f f} b^{2}} & _{0} & _{0} & _{0} \\ _{0} & _{0} & _{3 k_{o n}} & _{- 3 k_{o f f} b^{2} - 2 k_{o n}} & _{4 k_{o f f} b^{3}} & _{0} & _{0} \\ _{0} & _{0} & _{0} & _{2 k_{o n}} & _{- 4 k_{o f f} b^{3} - k_{o n}} & _{5 k_{o f f} b 4} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{k_{o n}} & _{- y - 5 k_{o f f} b^{4}} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{0} & _{y} & _{0} \end{matrix})

To implement the use-dependent slowing of the release rate constants of this model (Miki et al., 2018) in a deterministic way, a site-plugging state, $P (t)$ , was defined according to

\frac{d P (t)}{d t} = (1 - P (t)) \frac{d V_{2, f u s e d}}{d t} (t) - 40 m s P (t)

$P (t)$ is approaching one during strong release and decays with a time constant of 40 ms back to zero. Similar to the implementation by Miki et al., 2018, the rate constants k_on and k_off were linearly interpolated between two values depending on $P (t)$ as

k_{o n} (t) = k_{o n, i n i t} + (k_{o n, p l u g g e d} - k_{o n, i n i t}) P (t)

k_{o f f} (t) = k_{o f f, i n i t} + (k_{o f f, p l u g g e d} - k_{o f f, i n i t}) P (t)

The reserve pool $V_{R}$ is considered to be infinite. See Table 3 for the values and Ca²⁺-dependence of the rate constants in these differential equations.

The initial condition is defined as V₁(0) = k_prim1/k_unprim1 and V_2,0Ca(0) = (k_prim1/k_unprim1)*(k_prim2/k_unprim2). The initial condition of the other state V_2,1Ca(0) to V_5,0Ca(0), V_fused(0), and $P (0)$ were zero. k_prim1 and k_prim2 were the sum of a Ca²⁺-dependent and Ca²⁺-independent rate constant defined similarly as described in Miki et al., 2018 and adjusted as described for model 1. k_unprim1 and k_unprim2 were defined such that the occupancy V₁(0) = 1 and V_2,0Ca(0) = 1 for the default pre-flash resting Ca²⁺ concentration of 227 nM (Tables 2 and 3).

Model 3 was a parallel two-pool model similar as described by Voets, 2000 and Walter et al., 2013 but with five Ca²⁺ binding steps mediating fusion of both types of vesicles and a Ca²⁺-independent priming step for V₁ vesicles and a Ca²⁺-dependent transition step from V₁ to V₂ vesicles defined according to the following differential equations

\begin{array}{ll} (\begin{matrix} d V_{1, 0 C a} (t) / d t \\ d V_{1, 1 C a} (t) / d t \\ d V_{1, 2 C a} (t) / d t \\ d V_{1, 3 C a} (t) / d t \\ d V_{1, 4 a} (t) / d t \\ d V_{1, 5 C a} (t) / d t \\ d V_{1, f u s e d} (t) / d t \end{matrix}) = M_{1} (\begin{matrix} V_{1, 0 C a} (t) \\ V_{1, 1 C a} (t) \\ V_{1, 2 C a} (t) \\ V_{1, 3 C a} (t) \\ V_{1, 4 C a} (t) \\ V_{1, 5 C a} (t) \\ V_{1, f u s e d} (t) \end{matrix}) \\ (\begin{matrix} d V_{2, 0 C a} (t) / d t \\ d V_{2, 1 C a} (t) / d t \\ d V_{2, 2 C a} (t) / d t \\ d V_{2, 3 C a} (t) / d t \\ d V_{2, 4 a} (t) / d t \\ d V_{2, 5 C a} (t) / d t \\ d V_{2, f u s e d} (t) / d t \end{matrix}) = M_{2} (\begin{matrix} V_{2, 0 C a} (t) \\ V_{2, 1 C a} (t) \\ V_{2, 2 C a} (t) \\ V_{2, 3 C a} (t) \\ V_{2, 4 C a} (t) \\ V_{2, 5 C a} (t) \\ V_{2, f u s e d} (t) \end{matrix}) \end{array}

$V_{1, 0 C a}, V_{1, 1 C a}, . . . . a n d V_{1, 5 C a}$ denote the fraction of vesicles with a low-affinity fusion sensor with 0 to 5 bound Ca²⁺ ions, respectively, and $V_{2, 0 C a}, V_{2, 1 C a}, . . . . a n d V_{2, 5 C a}$ denote the fraction of vesicles with a high-affinity fusion sensor with 0 to 5 bound Ca²⁺ ions, respectively. $V_{1, f u s e d}$ and $V_{2, f u s e d}$ denote fused vesicles as illustrated in Figure 6D.

$M_{1}$ denotes the following 7x7 matrix:

(\begin{matrix} _{- 5 k_{o n 1} - k_{u n p r i m 1} - k_{p r i m 2} + k_{p r i m 1} / V_{1, 0 C a} (t) + k_{u n p r i m 2} / V_{2, 0 C a} (t) / V_{1, 0 C a} (t)} & _{k_{o f f 1}} & _{0} & _{0} & _{0} & _{0} & _{0} \\ _{5 k_{o n 1}} & _{- k_{o f f 1} - 4 k_{o n 1}} & _{2 k_{o f f 1} b} & _{0} & _{0} & _{0} & _{0} \\ _{0} & _{4 k_{o n 1}} & _{- 2 k_{o f f 1} b - 3 k_{o n 1}} & _{3 k_{o f f 1} b^{2}} & _{0} & _{0} & _{0} \\ _{0} & _{0} & _{3 k_{o n 1}} & _{- 3 k_{o f f 1} b^{2} - 2 k_{o n 1}} & _{4 k_{o f f 1} b^{3}} & _{0} & _{0} \\ _{0} & _{0} & _{0} & _{2 k_{o n 1}} & _{- 4 k_{o f f 1} b^{3} - k_{o n 1}} & _{5 k_{o f f 1} b 4} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{k_{o n 1}} & _{- y - 5 k_{o f f 1} b^{4}} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{0} & _{y} & _{0} \end{matrix})

$M_{2}$ denotes the following 7x7 matrix:

(\begin{matrix} _{- 5 k_{o n 1} - k_{u n p r i m 2} + k_{p r i m 2} V_{1, 0 C a} (t) / V_{2, 0 C a} (t)} & _{k_{o f f 2}} & _{0} & _{0} & _{0} & _{0} & _{0} \\ _{5 k_{o n 2}} & _{- k_{o f f 2} - 4 k_{o n 2}} & _{2 k_{o f f 2} b} & _{0} & _{0} & _{0} & _{0} \\ _{0} & _{4 k_{o n 2}} & _{- 2 k_{o f f 2} b - 3 k_{o n 2}} & _{3 k_{o f f 2} b^{2}} & _{0} & _{0} & _{0} \\ _{0} & _{0} & _{3 k_{o n 2}} & _{- 3 k_{o f f 2} b^{2} - 2 k_{o n 2}} & _{4 k_{o f f 2} b^{3}} & _{0} & _{0} \\ _{0} & _{0} & _{0} & _{2 k_{o n 2}} & _{- 4 k_{o f f 2} b^{3} - k_{o n 2}} & _{5 k_{o f f 2} b 4} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{k_{o n 2}} & _{- y - 5 k_{o f f 2} b^{4}} & _{0} \\ _{0} & _{0} & _{0} & _{0} & _{0} & _{y} & _{0} \end{matrix})

The initial condition is defined as V_2,0Ca(0) = k_prim1/k_unprim1 and V_2,0Ca(0) = (k_prim1/k_unprim1)*(k_prim2/k_unprim2). The initial condition of the other state V_1,1Ca(0) to V_1,0Ca(0), V_1,fused(0), and V_2,1Ca(0) to V_2,0Ca(0), V_2,fused(0) were zero. k_prim1 was a Ca²⁺-independent rate constant and k_prim2 was the sum of a Ca²⁺-dependent and Ca²⁺-independent rate constants defined similarly as described in Hallermann et al., 2010 and adjusted as described for model 1. k_unprim1 and k_unprim2 were defined such that the occupancy V_1,0Ca(0) = one and V_2,0Ca(0) = one for the default pre-flash resting Ca²⁺ concentration of 227 nM (Tables 2 and 3).

Statistical analysis

Request a detailed protocol

Boxplots show median and 1st/3rd quartiles with whiskers indicating the whole data range (Figures 1 and 7). For statistical comparison, Mann-Whitney U tests were used, and the p-values are indicated above the boxplots.

Data availability

The code of the simulations of the release schemes (models 1 to 3) is available at https://github.com/HallermannLab/2021_eLife (copy archived at https://archive.softwareheritage.org/swh:1:rev:4cd31058945a8f1c8364d8fc21f0a2902de33365).

References

(1991)
Alien intracellular calcium chelators attenuate neurotransmitter release at the squid giant synapse

The Journal of Neuroscience 11:1496–1507.
- PubMed
- Google Scholar
1. Atwood HL
2. Karunanithi S
(2002) Diversification of synaptic strength: presynaptic elements
Nature Reviews. Neuroscience 3:497–516.

https://doi.org/10.1038/nrn876
- PubMed
- Google Scholar
(2005) Modulation of transmitter release by presynaptic resting potential and background calcium levels
Neuron 48:109–121.

https://doi.org/10.1016/j.neuron.2005.08.038
- PubMed
- Google Scholar
1. Beutner D
2. Voets T
3. Neher E
4. Moser T
(2001) Calcium dependence of exocytosis and endocytosis at the cochlear inner hair cell afferent synapse
Neuron 29:681–690.

https://doi.org/10.1016/s0896-6273(01)00243-4
- PubMed
- Google Scholar
(2014) Network structure within the cerebellar input layer enables lossless sparse encoding
Neuron 83:960–974.

https://doi.org/10.1016/j.neuron.2014.07.020
- PubMed
- Google Scholar
(2020) Differentially poised vesicles underlie fast and slow components of release at single synapses
Journal of General Physiology 152:201912523.

https://doi.org/10.1085/jgp.201912523
- Google Scholar
(2000) Calcium sensitivity of glutamate release in a calyx-type terminal
Science 289:953–957.

https://doi.org/10.1126/science.289.5481.953
- PubMed
- Google Scholar
(2019) Neocortical high probability release sites are formed by distinct Ca²⁺ Channel-to-Release Sensor Topographies during Development
Cell Reports 28:1410–1418.

https://doi.org/10.1016/j.celrep.2019.07.008
- PubMed
- Google Scholar
1. Bornschein G
2. Schmidt H
(2018) Synaptotagmin Ca²⁺ sensors and their spatial coupling to presynaptic Ca_vChannels in Central Cortical Synapses
Frontiers in Molecular Neuroscience 11:494.

https://doi.org/10.3389/fnmol.2018.00494
- PubMed
- Google Scholar
(2003)
Maturation of EPSCs and intrinsic membrane properties enhances precision at a cerebellar synapse

The Journal of Neuroscience 23:6074–6085.
- PubMed
- Google Scholar
(2015) Synaptic diversity enables temporal coding of coincident multisensory inputs in single neurons
Nature Neuroscience 18:718–727.

https://doi.org/10.1038/nn.3974
- PubMed
- Google Scholar
(2018) Synaptotagmin-1 drives synchronous Ca^₂+-triggered fusion by C₂B-domain-mediated synaptic-vesicle-membrane attachment
Nature Neuroscience 21:33–40.

https://doi.org/10.1038/s41593-017-0037-5
- PubMed
- Google Scholar
1. Chen C
2. Satterfield R
3. Young SM
4. Jonas P
(2017) Triple function of synaptotagmin 7 ensures efficiency of High-Frequency transmission at central GABAergic synapses
Cell Reports 21:2082–2089.

https://doi.org/10.1016/j.celrep.2017.10.122
- PubMed
- Google Scholar
(2015) Reduced endogenous Ca²⁺ buffering speeds active zone ^Ca2+ signaling
PNAS 112:3075–3084.

https://doi.org/10.1073/pnas.1508419112
- PubMed
- Google Scholar
(2002) Spillover of glutamate onto synaptic AMPA receptors enhances fast transmission at a cerebellar synapse
Neuron 35:521–533.

https://doi.org/10.1016/s0896-6273(02)00787-0
- PubMed
- Google Scholar
1. DiGregorio DA
2. Vergara JL
(1997) Localized detection of action potential-induced presynaptic calcium transients at a Xenopus neuromuscular junction
The Journal of Physiology 505:585–592.

https://doi.org/10.1111/j.1469-7793.1997.585ba.x
- PubMed
- Google Scholar
1. Doussau F
2. Schmidt H
3. Dorgans K
4. Valera AM
5. Poulain B
6. Isope P
(2017) Frequency-dependent mobilization of heterogeneous pools of synaptic vesicles shapes presynaptic plasticity
eLife 6:e28935.

https://doi.org/10.7554/eLife.28935
- PubMed
- Google Scholar
1. Duncan G
2. Rabl K
3. Gemp I
4. Heidelberger R
5. Thoreson WB
(2010) Quantitative analysis of synaptic release at the photoreceptor synapse
Biophysical Journal 98:2102–2110.

https://doi.org/10.1016/j.bpj.2010.02.003
- PubMed
- Google Scholar
(2011) Nanodomain coupling between Ca²⁺ channels and sensors of exocytosis at fast mammalian synapses
Nature Reviews. Neuroscience 13:7–21.

https://doi.org/10.1038/nrn3125
- PubMed
- Google Scholar
(2017) Target cell Type-Dependent differences in Ca²⁺ Channel Function Underlie Distinct Release Probabilities at Hippocampal Glutamatergic Terminals
The Journal of Neuroscience 37:1910–1924.

https://doi.org/10.1523/JNEUROSCI.2024-16.2017
- PubMed
- Google Scholar
1. Escobar AL
2. Velez P
3. Kim AM
4. Cifuentes F
5. Fill M
6. Vergara JL
(1997) Kinetic properties of DM-nitrophen and calcium indicators: rapid transient response to flash photolysis
PflüGers Archiv European Journal of Physiology 434:615–631.

https://doi.org/10.1007/s004240050444
- Google Scholar
1. Faas GC
2. Karacs K
3. Vergara JL
4. Mody I
(2005) Kinetic properties of DM-nitrophen binding to calcium and magnesium
Biophysical Journal 88:4421–4433.

https://doi.org/10.1529/biophysj.104.057745
- PubMed
- Google Scholar
1. Faas GC
2. Schwaller B
3. Vergara JL
4. Mody I
(2007) Resolving the fast kinetics of cooperative binding: ^ca2+ buffering by calretinin
PLOS Biology 5:e311.

https://doi.org/10.1371/journal.pbio.0050311
- PubMed
- Google Scholar
1. Fedchyshyn MJ
2. Wang LY
(2005) Developmental transformation of the release modality at the Calyx of held synapse
The Journal of Neuroscience 25:4131–4140.

https://doi.org/10.1523/JNEUROSCI.0350-05.2005
- PubMed
- Google Scholar
1. Fekete A
2. Nakamura Y
3. Yang YM
4. Herlitze S
5. Mark MD
6. DiGregorio DA
7. Wang LY
(2019) Underpinning heterogeneity in synaptic transmission by presynaptic ensembles of distinct morphological modules
Nature Communications 10:826.

https://doi.org/10.1038/s41467-019-08452-2
- PubMed
- Google Scholar
1. Forsythe ID
(1994) Direct patch recording from identified presynaptic terminals mediating glutamatergic EPSCs in the rat CNS, in vitro
The Journal of Physiology 479:381–387.

https://doi.org/10.1113/jphysiol.1994.sp020303
- PubMed
- Google Scholar
(2021) Rapid Ca²⁺ channel accumulation contributes to cAMP-mediated increase in transmission at hippocampal mossy fiber synapses
PNAS 118:e2016754118.

https://doi.org/10.1073/pnas.2016754118
- PubMed
- Google Scholar
Book
1. Gillis KD
(1995)
Membrane Capacitance Measurement

In: Sakmann B, Neher E, editors. Single-Channel Recording. New York: Plenum Press. pp. 155–198.
- Google Scholar
1. Grande G
2. Wang LY
(2011) Morphological and functional continuum underlying heterogeneity in the spiking fidelity at the Calyx of held synapse in vitro
The Journal of Neuroscience 31:13386–13399.

https://doi.org/10.1523/JNEUROSCI.0400-11.2011
- PubMed
- Google Scholar
(2003) A large pool of releasable vesicles in a cortical glutamatergic synapse
PNAS 100:8975–8980.

https://doi.org/10.1073/pnas.1432836100
- PubMed
- Google Scholar
(2010) Bassoon speeds vesicle reloading at a central excitatory synapse
Neuron 68:710–723.

https://doi.org/10.1016/j.neuron.2010.10.026
- Google Scholar
1. Hanse E
2. Gustafsson B
(2001) Vesicle release probability and pre‐primed pool at Glutamatergic synapses in area CA1 of the rat neonatal Hippocampus
The Journal of Physiology 531:481–493.

https://doi.org/10.1111/j.1469-7793.2001.0481i.x
- Google Scholar
(1994) Calcium dependence of the rate of exocytosis in a synaptic terminal
Nature 371:513–515.

https://doi.org/10.1038/371513a0
- PubMed
- Google Scholar
1. Heil P
2. Neubauer H
(2010) Summing across different active zones can explain the Quasi-Linear Ca-Dependencies of exocytosis by receptor cells
Frontiers in Synaptic Neuroscience 2:148.

https://doi.org/10.3389/fnsyn.2010.00148
- PubMed
- Google Scholar
1. Hosoi N
2. Sakaba T
3. Neher E
(2007) Quantitative analysis of calcium-dependent vesicle recruitment and its functional role at the Calyx of held synapse
The Journal of Neuroscience 27:14286–14298.

https://doi.org/10.1523/JNEUROSCI.4122-07.2007
- PubMed
- Google Scholar
1. Imig C
2. Min SW
3. Krinner S
4. Arancillo M
5. Rosenmund C
6. Südhof TC
7. Rhee J
8. Brose N
9. Cooper BH
(2014) The morphological and molecular nature of synaptic vesicle priming at Presynaptic active zones
Neuron 84:416–431.

https://doi.org/10.1016/j.neuron.2014.10.009
- PubMed
- Google Scholar
(2020) Ultrastructural imaging of Activity-Dependent synaptic Membrane-Trafficking events in cultured brain slices
Neuron 108:843–860.

https://doi.org/10.1016/j.neuron.2020.09.004
- PubMed
- Google Scholar
1. Ishiyama S
2. Schmidt H
3. Cooper BH
4. Brose N
5. Eilers J
(2014) Munc13-3 superprimes synaptic vesicles at granule cell-to-basket cell synapses in the mouse cerebellum
The Journal of Neuroscience 34:14687–14696.

https://doi.org/10.1523/JNEUROSCI.2060-14.2014
- PubMed
- Google Scholar
(2016) The calcium sensor synaptotagmin 7 is required for synaptic facilitation
Nature 529:88–91.

https://doi.org/10.1038/nature16507
- PubMed
- Google Scholar
1. Jackman SL
2. Regehr WG
(2017) The mechanisms and functions of synaptic facilitation
Neuron 94:447–464.

https://doi.org/10.1016/j.neuron.2017.02.047
- PubMed
- Google Scholar
1. Jakab RL
2. Hamori J
(1988) Quantitative morphology and synaptology of cerebellar glomeruli in the rat
Anatomy and Embryology 179:81–88.

https://doi.org/10.1007/BF00305102
- Google Scholar
1. Johnson SL
2. Franz C
3. Kuhn S
4. Furness DN
5. Rüttiger L
6. Münkner S
7. Rivolta MN
8. Seward EP
9. Herschman HR
10. Engel J
11. Knipper M
12. Marcotti W
(2010) Synaptotagmin IV determines the linear Ca²⁺ dependence of vesicle fusion at auditory ribbon synapses
Nature Neuroscience 13:45–52.

https://doi.org/10.1038/nn.2456
- PubMed
- Google Scholar
1. Kaplan JH
2. Ellis-Davies GC
(1988) Photolabile chelators for the rapid photorelease of divalent cations
PNAS 85:6571–6575.

https://doi.org/10.1073/pnas.85.17.6571
- PubMed
- Google Scholar
1. Katz B
2. Miledi R
(1968) The role of calcium in neuromuscular facilitation
The Journal of Physiology 195:481–492.

https://doi.org/10.1113/jphysiol.1968.sp008469
- Google Scholar
(2020) Rapid regulation of vesicle priming explains synaptic facilitation despite heterogeneous vesicle:Ca²⁺ channel distances
eLife 9:e51032.

https://doi.org/10.7554/eLife.51032
- PubMed
- Google Scholar
(2009) Developmental regulation of the intracellular Ca²⁺ sensitivity of vesicle fusion and ^Ca2+-secretion coupling at the rat Calyx of held
The Journal of Physiology 587:3009–3023.

https://doi.org/10.1113/jphysiol.2009.172387
- PubMed
- Google Scholar
(2011) Regulation of transmitter release by Ca²⁺ and synaptotagmin: insights from a large CNS synapse
Trends in Neurosciences 34:237–246.

https://doi.org/10.1016/j.tins.2011.02.006
- PubMed
- Google Scholar
1. Kochubey O
2. Schneggenburger R
(2011) Synaptotagmin increases the dynamic range of synapses by driving Ca²⁺-evoked release and by clamping a near-linear remaining Ca²+ sensor
Neuron 69:736–748.

https://doi.org/10.1016/j.neuron.2011.01.013
- PubMed
- Google Scholar
1. Kusch V
2. Bornschein G
3. Loreth D
4. Bank J
5. Jordan J
6. Baur D
7. Watanabe M
8. Kulik A
9. Heckmann M
10. Eilers J
11. Schmidt H
(2018) Munc13-3 is required for the developmental localization of Ca²⁺ Channels to Active Zones and the Nanopositioning of Ca_v2.1 Near Release Sensors
Cell Reports 22:1965–1973.

https://doi.org/10.1016/j.celrep.2018.02.010
- PubMed
- Google Scholar
1. Kusick GF
2. Chin M
3. Raychaudhuri S
4. Lippmann K
5. Adula KP
6. Hujber EJ
7. Vu T
8. Davis MW
9. Jorgensen EM
10. Watanabe S
(2020) Synaptic vesicles transiently dock to refill release sites
Nature Neuroscience 23:1329–1338.

https://doi.org/10.1038/s41593-020-00716-1
- PubMed
- Google Scholar
1. Lee JS
2. Ho WK
3. Lee SH
(2012) Actin-dependent rapid recruitment of reluctant synaptic vesicles into a fast-releasing vesicle pool
PNAS 109:765–774.

https://doi.org/10.1073/pnas.1114072109
- PubMed
- Google Scholar
1. Lee JS
2. Ho WK
3. Neher E
4. Lee SH
(2013) Superpriming of synaptic vesicles after their recruitment to the readily releasable pool
PNAS 110:15079–15084.

https://doi.org/10.1073/pnas.1314427110
- PubMed
- Google Scholar
1. Lenzi D
2. von Gersdorff H
(2001) Structure suggests function: the case for synaptic ribbons as exocytotic nanomachines
BioEssays : News and Reviews in Molecular, Cellular and Developmental Biology 23:831–840.

https://doi.org/10.1002/bies.1118
- PubMed
- Google Scholar
1. Li L
2. Liu H
3. Krout M
4. Richmond JE
5. Wang Y
6. Bai J
7. Weeratunga S
8. Collins BM
9. Ventimiglia D
10. Yu Y
11. Xia J
12. Tang J
13. Liu J
14. Hu Z
(2021) A novel dual Ca2+ sensor system regulates Ca2+-dependent neurotransmitter release
Journal of Cell Biology 220:202008121.

https://doi.org/10.1083/jcb.202008121
- Google Scholar
(2017) Dynamics of volume-averaged intracellular Ca²⁺ in a rat CNS nerve terminal during single and repetitive voltage-clamp depolarizations
The Journal of Physiology 595:3219–3236.

https://doi.org/10.1113/JP272773
- Google Scholar
1. Liu H
2. Bai H
3. Hui E
4. Yang L
5. Evans CS
6. Wang Z
7. Kwon SE
8. Chapman ER
(2014) Synaptotagmin 7 functions as a Ca²⁺-sensor for synaptic vesicle replenishment
eLife 3:e01524.

https://doi.org/10.7554/eLife.01524
- PubMed
- Google Scholar
(1992) Microdomains of high calcium concentration in a presynaptic terminal
Science 256:677–679.

https://doi.org/10.1126/science.1350109
- PubMed
- Google Scholar
(2005) Allosteric modulation of the presynaptic Ca²⁺ sensor for vesicle fusion
Nature 435:497–501.

https://doi.org/10.1038/nature03568
- PubMed
- Google Scholar
(2008) Phorbol esters modulate spontaneous and Ca²⁺-evoked transmitter release via acting on both Munc13 and protein kinase C
The Journal of Neuroscience 28:8257–8267.

https://doi.org/10.1523/JNEUROSCI.0550-08.2008
- PubMed
- Google Scholar
1. Luo F
2. Südhof TC
(2017) Synaptotagmin-7-Mediated asynchronous release boosts High-Fidelity synchronous transmission at a central synapse
Neuron 94:826–839.

https://doi.org/10.1016/j.neuron.2017.04.020
- PubMed
- Google Scholar
Book
1. Magleby KL
(1987)
Short-term changes in synaptic efficacy

In: Edelman G. M, Gall W. E, Cowan W. M, editors. Synaptic Function. New York: John Wiley & Son. pp. 21–56.
- Google Scholar
(2016) A Well-Defined readily releasable pool with fixed capacity for storing vesicles at Calyx of held
PLOS Computational Biology 12:e1004855.

https://doi.org/10.1371/journal.pcbi.1004855
- PubMed
- Google Scholar
1. Malagon G
2. Miki T
3. Tran V
4. Gomez LC
5. Marty A
(2020) Incomplete vesicular docking limits synaptic strength under high release probability conditions
eLife 9:e52137.

https://doi.org/10.7554/eLife.52137
- PubMed
- Google Scholar
(1998) Competitive calcium binding: implications for dendritic calcium signaling
Journal of Computational Neuroscience 5:331–348.

https://doi.org/10.1023/a:1008891229546
- PubMed
- Google Scholar
1. Matthews G
(2000) Vesicle fiesta at the synapse
Nature 406:835–836.

https://doi.org/10.1038/35022674
- PubMed
- Google Scholar
1. Maus L
2. Lee C
3. Altas B
4. Sertel SM
5. Weyand K
6. Rizzoli SO
7. Rhee J
8. Brose N
9. Imig C
10. Cooper BH
(2020) Ultrastructural correlates of presynaptic functional heterogeneity in hippocampal synapses
Cell Reports 30:3632–3643.

https://doi.org/10.1016/j.celrep.2020.02.083
- PubMed
- Google Scholar
(2002) Calcium secretion coupling at Calyx of held governed by nonuniform channel-vesicle topography
The Journal of Neuroscience 22:1648–1667.

https://doi.org/10.1523/JNEUROSCI.22-05-01648.2002
- PubMed
- Google Scholar
1. Miki T
2. Malagon G
3. Pulido C
4. Llano I
5. Neher E
6. Marty A
(2016) Actin- and Myosin-Dependent vesicle loading of presynaptic docking sites prior to exocytosis
Neuron 91:808–823.

https://doi.org/10.1016/j.neuron.2016.07.033
- PubMed
- Google Scholar
1. Miki T
2. Nakamura Y
3. Malagon G
4. Neher E
5. Marty A
(2018) Two-component latency distributions indicate two-step vesicular release at simple glutamatergic synapses
Nature Communications 9:3943.

https://doi.org/10.1038/s41467-018-06336-5
- PubMed
- Google Scholar
(2020) Direct imaging of rapid tethering of synaptic vesicles accompanying exocytosis at a fast central synapse
PNAS 117:14493–14502.

https://doi.org/10.1073/pnas.2000265117
- PubMed
- Google Scholar
(2005) Calcium sensitivity of neurotransmitter release differs at Phasic and tonic synapses
The Journal of Neuroscience 25:3113–3125.

https://doi.org/10.1523/JNEUROSCI.4717-04.2005
- PubMed
- Google Scholar
(2010) Interaction between facilitation and depression at a large CNS synapse reveals mechanisms of short-term plasticity
The Journal of Neuroscience 30:2007–2016.

https://doi.org/10.1523/JNEUROSCI.4378-09.2010
- PubMed
- Google Scholar
1. Nakamura Y
2. Harada H
3. Kamasawa N
4. Matsui K
5. Rothman JS
6. Shigemoto R
7. Silver RA
8. DiGregorio DA
9. Takahashi T
(2015) Nanoscale distribution of presynaptic ^ca(2+) channels and its impact on vesicular release during development
Neuron 85:145–158.

https://doi.org/10.1016/j.neuron.2014.11.019
- PubMed
- Google Scholar
1. Neef J
2. Urban NT
3. Ohn TL
4. Frank T
5. Jean P
6. Hell SW
7. Willig KI
8. Moser T
(2018) Quantitative optical nanophysiology of Ca²⁺ signaling at inner hair cell active zones
Nature Communications 9:290.

https://doi.org/10.1038/s41467-017-02612-y
- PubMed
- Google Scholar
1. Neher E
(1998) Vesicle pools and ^Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release
Neuron 20:389–399.

https://doi.org/10.1016/s0896-6273(00)80983-6
- PubMed
- Google Scholar
1. Neher E
2. Brose N
(2018) Dynamically primed synaptic vesicle states: key to understand synaptic Short-Term plasticity
Neuron 100:1283–1291.

https://doi.org/10.1016/j.neuron.2018.11.024
- PubMed
- Google Scholar
1. Neher E
2. Lux HD
(1973) Rapid changes of potassium concentration at the outer surface of exposed single neurons during membrane current flow
Journal of General Physiology 61:385–399.

https://doi.org/10.1085/jgp.61.3.385
- Google Scholar
1. Neher E
2. Sakaba T
(2008) Multiple roles of calcium ions in the regulation of neurotransmitter release
Neuron 59:861–872.

https://doi.org/10.1016/j.neuron.2008.08.019
- PubMed
- Google Scholar
1. Nusser Z
(2018) Creating diverse synapses from the same molecules
Current Opinion in Neurobiology 51:8–15.

https://doi.org/10.1016/j.conb.2018.01.001
- PubMed
- Google Scholar
1. Pan B
2. Zucker RS
(2009) A general model of synaptic transmission and short-term plasticity
Neuron 62:539–554.

https://doi.org/10.1016/j.neuron.2009.03.025
- PubMed
- Google Scholar
1. Pulido C
2. Marty A
(2017) Quantal fluctuations in central mammalian synapses: functional role of vesicular docking sites
Physiological Reviews 97:1403–1430.

https://doi.org/10.1152/physrev.00032.2016
- PubMed
- Google Scholar
1. Rebola N
2. Reva M
3. Kirizs T
4. Szoboszlay M
5. Lőrincz A
6. Moneron G
7. Nusser Z
8. DiGregorio DA
(2019) Distinct nanoscale calcium channel and synaptic vesicle topographies contribute to the diversity of synaptic function
Neuron 104:693–710.

https://doi.org/10.1016/j.neuron.2019.08.014
- PubMed
- Google Scholar
1. Rhee JS
2. Betz A
3. Pyott S
4. Reim K
5. Varoqueaux F
6. Augustin I
7. Hesse D
8. Südhof TC
9. Takahashi M
10. Rosenmund C
11. Brose N
(2002) Beta phorbol ester- and diacylglycerol-induced augmentation of transmitter release is mediated by Munc13s and not by PKCs
Cell 108:121–133.

https://doi.org/10.1016/s0092-8674(01)00635-3
- PubMed
- Google Scholar
(2014) Ultrafast action potentials mediate kilohertz signaling at a central synapse
Neuron 84:152–163.

https://doi.org/10.1016/j.neuron.2014.08.036
- PubMed
- Google Scholar
(2018) Apparent calcium dependence of vesicle recruitment
The Journal of Physiology 596:4693–4707.

https://doi.org/10.1113/JP275911
- Google Scholar
1. Rothman JS
2. Kocsis L
3. Herzog E
4. Nusser Z
5. Silver RA
(2016) Physical determinants of vesicle mobility and supply at a central synapse
eLife 5:e15133.

https://doi.org/10.7554/eLife.15133
- PubMed
- Google Scholar
(2002) The life cycle of ca(2+) ions in dendritic spines
Neuron 33:439–452.

https://doi.org/10.1016/s0896-6273(02)00573-1
- PubMed
- Google Scholar
1. Sakaba T
2. Stein A
3. Jahn R
4. Neher E
(2005) Distinct kinetic changes in neurotransmitter release after SNARE protein cleavage
Science 309:491–494.

https://doi.org/10.1126/science.1112645
- PubMed
- Google Scholar
1. Sakaba T
(2008) Two Ca²⁺-dependent steps controlling synaptic vesicle fusion and replenishment at the cerebellar basket cell terminal
Neuron 57:406–419.

https://doi.org/10.1016/j.neuron.2007.11.029
- PubMed
- Google Scholar
1. Sakaba T
2. Neher E
(2001a) Calmodulin mediates rapid recruitment of fast-releasing synaptic vesicles at a calyx-type synapse
Neuron 32:1119–1131.

https://doi.org/10.1016/s0896-6273(01)00543-8
- PubMed
- Google Scholar
1. Sakaba T
2. Neher E
(2001b) Quantitative relationship between transmitter release and calcium current at the Calyx of held synapse
The Journal of Neuroscience 21:462–476.

https://doi.org/10.1523/JNEUROSCI.21-02-00462.2001
- Google Scholar
1. Saviane C
2. Silver RA
(2006) Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse
Nature 439:983–987.

https://doi.org/10.1038/nature04509
- PubMed
- Google Scholar
(2006) Rab3 superprimes synaptic vesicles for release: implications for short-term synaptic plasticity
The Journal of Neuroscience 26:1239–1246.

https://doi.org/10.1523/JNEUROSCI.3553-05.2006
- PubMed
- Google Scholar
Book
1. Schneggenburger R
(2005)
Ca²⁺ uncaging in nerve terminals

In: Yuste R, Konnerth A, editors. Imaging in Neuroscience and Development: A Laboratory Manual. New York: Cold Spring Harbor Laboratory Press. pp. 415–419.
- Google Scholar
1. Schneggenburger R
2. Neher E
(2000) Intracellular calcium dependence of transmitter release rates at a fast central synapse
Nature 406:889–893.

https://doi.org/10.1038/35022702
- PubMed
- Google Scholar
1. Shin OH
2. Lu J
3. Rhee JS
4. Tomchick DR
5. Pang ZP
6. Wojcik SM
7. Camacho-Perez M
8. Brose N
9. Machius M
10. Rizo J
11. Rosenmund C
12. Südhof TC
(2010) Munc13 C2B domain is an activity-dependent Ca2+ regulator of synaptic exocytosis
Nature Structural & Molecular Biology 17:280–288.

https://doi.org/10.1038/nsmb.1758
- PubMed
- Google Scholar
1. Silva M
2. Tran V
3. Marty A
(2021) Calcium-dependent docking of synaptic vesicles
Trends in Neurosciences 44:579–592.

https://doi.org/10.1016/j.tins.2021.04.003
- PubMed
- Google Scholar
1. Simon SM
2. Llinás RR
(1985) Compartmentalization of the submembrane calcium activity during calcium influx and its significance in transmitter release
Biophysical Journal 48:485–498.

https://doi.org/10.1016/S0006-3495(85)83804-2
- PubMed
- Google Scholar
1. Straub I
2. Witter L
3. Eshra A
4. Hoidis M
5. Byczkowicz N
6. Maas S
7. Delvendahl I
8. Dorgans K
9. Savier E
10. Bechmann I
11. Krueger M
12. Isope P
13. Hallermann S
(2020) Gradients in the mammalian cerebellar cortex enable Fourier-like transformation and improve storing capacity
eLife 9:e51771.

https://doi.org/10.7554/eLife.51771
- PubMed
- Google Scholar
1. Südhof TC
(2004) The synaptic vesicle cycle
Annual Review of Neuroscience 27:509–547.

https://doi.org/10.1146/annurev.neuro.26.041002.131412
- PubMed
- Google Scholar
1. Südhof TC
(2013) Neurotransmitter release: the last millisecond in the life of a synaptic vesicle
Neuron 80:675–690.

https://doi.org/10.1016/j.neuron.2013.10.022
- PubMed
- Google Scholar
1. Sugita S
2. Shin OH
3. Han W
4. Lao Y
5. Südhof TC
(2002) Synaptotagmins form a hierarchy of exocytotic Ca²⁺ sensors with distinct Ca²⁺ affinities
The EMBO Journal 21:270–280.

https://doi.org/10.1093/emboj/21.3.270
- PubMed
- Google Scholar
1. Sun J
2. Pang ZP
3. Qin D
4. Fahim AT
5. Adachi R
6. SÃ¼dhof TC
7. Südhof TC
(2007) A dual-Ca²⁺-sensor model for neurotransmitter release in a central synapse
Nature 450:676–682.

https://doi.org/10.1038/nature06308
- Google Scholar
(2016) Superpriming of synaptic vesicles as a common basis for intersynapse variability and modulation of synaptic strength
PNAS 113:E4548–E4557.

https://doi.org/10.1073/pnas.1606383113
- Google Scholar
1. Taschenberger H
2. von Gersdorff H
(2000) Fine-tuning an auditory synapse for speed and fidelity: developmental changes in Presynaptic Waveform, EPSC kinetics, and synaptic plasticity
The Journal of Neuroscience 20:9162–9173.

https://doi.org/10.1523/JNEUROSCI.20-24-09162.2000
- PubMed
- Google Scholar
(2004) A highly ^Ca2+-sensitive pool of vesicles contributes to linearity at the rod photoreceptor ribbon synapse
Neuron 42:595–605.

https://doi.org/10.1016/S0896-6273(04)00254-5
- PubMed
- Google Scholar
(2018) An improved measurement of the Ca²⁺-binding affinity of fluorescent Ca²⁺ indicators
Cell Calcium 71:86–94.

https://doi.org/10.1016/j.ceca.2018.01.001
- PubMed
- Google Scholar
1. Valera AM
2. Doussau F
3. Poulain B
4. Barbour B
5. Isope P
(2012) Adaptation of granule cell to Purkinje cell synapses to high-frequency transmission
Journal of Neuroscience 32:3267–3280.

https://doi.org/10.1523/JNEUROSCI.3175-11.2012
- PubMed
- Google Scholar
(2020) Short-Term plasticity at hippocampal mossy fiber synapses is induced by natural activity patterns and associated with vesicle pool engram formation
Neuron 107:509–521.

https://doi.org/10.1016/j.neuron.2020.05.013
- PubMed
- Google Scholar
Preprint
1. Vevea JD
2. Kusick GF
3. Chen E
4. Courtney KC
5. Watanabe S
6. Chapman ER
(2021) Synaptotagmin 7 is enriched at the plasma membrane through γ-secretase processing to promote vesicle docking and control synaptic plasticity in mouse hippocampal neurons
bioRxiv.

https://doi.org/10.1101/2021.02.09.430404
- Google Scholar
1. Voets T
(2000) Dissection of three Ca²⁺-dependent steps leading to secretion in chromaffin cells from mouse adrenal slices
Neuron 28:537–545.

https://doi.org/10.1016/S0896-6273(00)00131-8
- PubMed
- Google Scholar
1. Wadel K
2. Neher E
3. Sakaba T
(2007) The coupling between synaptic vesicles and Ca²⁺ channels determines fast neurotransmitter release
Neuron 53:563–575.

https://doi.org/10.1016/j.neuron.2007.01.021
- PubMed
- Google Scholar
(2013) A sequential vesicle pool model with a single release sensor and a Ca⁽²⁺)-dependent priming catalyst effectively explains Ca⁽²⁺)-dependent properties of neurosecretion
PLOS Computational Biology 9:e1003362.

https://doi.org/10.1371/journal.pcbi.1003362
- PubMed
- Google Scholar
(2008) Synaptic vesicles in mature calyx of Held synapses sense higher nanodomain calcium concentrations during action potential-evoked glutamate release
Journal of Neuroscience 28:14450–14458.

https://doi.org/10.1523/JNEUROSCI.4245-08.2008
- PubMed
- Google Scholar
1. Wang LY
2. Kaczmarek LK
(1998) High-frequency firing helps replenish the readily releasable pool of synaptic vesicles
Nature 394:384–388.

https://doi.org/10.1038/28645
- PubMed
- Google Scholar
(2007) A mechanism intrinsic to the vesicle fusion machinery determines fast and slow transmitter release at a large CNS synapse
Journal of Neuroscience 27:3198–3210.

https://doi.org/10.1523/JNEUROSCI.4471-06.2007
- PubMed
- Google Scholar
1. Yamada WM
2. Zucker RS
(1992) Time course of transmitter release calculated from simulations of a calcium diffusion model
Biophysical Journal 61:671–682.

https://doi.org/10.1016/S0006-3495(92)81872-6
- PubMed
- Google Scholar
(2004) Imaging calcium concentration dynamics in small neuronal compartments
Science's STKE : signal transduction knowledge environment 2004:pl5.

https://doi.org/10.1126/stke.2192004pl5
- PubMed
- Google Scholar
1. Zhai RG
2. Bellen HJ
(2004) The architecture of the active zone in the presynaptic nerve terminal
Physiology 19:262–270.

https://doi.org/10.1152/physiol.00014.2004
- PubMed
- Google Scholar
1. Zucker RS
(1992) Effects of photolabile calcium chelators on fluorescent calcium indicators
Cell Calcium 13:29–40.

https://doi.org/10.1016/0143-4160(92)90027-P
- PubMed
- Google Scholar
1. Zucker RS
2. Regehr WG
(2002) Short-term synaptic plasticity
Annual Review of Physiology 64:355–405.

https://doi.org/10.1146/annurev.physiol.64.092501.114547
- PubMed
- Google Scholar

Article and author information

Author details

Abdelmoneim Eshra

Carl-Ludwig-Institute for Physiology, Medical Faculty, University of Leipzig, Leipzig, Germany

Contribution
Conceptualization, Data curation, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6579-3000
Hartmut Schmidt

Carl-Ludwig-Institute for Physiology, Medical Faculty, University of Leipzig, Leipzig, Germany

Contribution
Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-9516-423X
Jens Eilers

Carl-Ludwig-Institute for Physiology, Medical Faculty, University of Leipzig, Leipzig, Germany

Contribution
Methodology, Writing - review and editing

Competing interests
No competing interests declared
Stefan Hallermann

Carl-Ludwig-Institute for Physiology, Medical Faculty, University of Leipzig, Leipzig, Germany

Contribution
Conceptualization, Software, Investigation, Methodology, Writing - original draft, Writing - review and editing

For correspondence
stefan_jens.hallermann@uni-leipzig.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9376-7048

Funding

Deutsche Forschungsgemeinschaft (SCHM1838/2-1)

Hartmut Schmidt

Deutsche Forschungsgemeinschaft (HA6386/10-1)

Stefan Hallermann

European Research Council (CoG 865634)

Stefan Hallermann

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Erwin Neher for help with algorithms for calculating the Ca²⁺ concentration of the intracellular solutions (Figure 1) and for helpful discussions. This work was supported by a European Research Council Consolidator Grant (ERC CoG 865634) to SH and by the German Research Foundation (DFG; SCHM1838/2-1) to HS and HA6386/10-1 to SH.

Ethics

Animal experimentation: All animals were treated in accordance with the German Protection of Animals Act and with the guidelines for the welfare of experimental animals issued by the European Communities Council Directive (EU Directive 2010/63/EU). The animal killing report number is T41/16 (gov. ID: DD24-5131/347/44).

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

2,950

views
290

downloads
33

citations

Views, downloads and citations are aggregated across all versions of this paper published by eLife.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Abdelmoneim Eshra
Hartmut Schmidt
Jens Eilers
Stefan Hallermann

(2021)

Calcium dependence of neurotransmitter release at a high fidelity synapse

eLife 10:e70408.

https://doi.org/10.7554/eLife.70408

Categories and tags

Research organism

Mouse

Share this article

Cite this article

Action potential-evoked synaptic release critically depends on basal intracellular Ca2+ concentration.

Figure 1—source data 1

Ca2+ uncaging dose-response curve measured with presynaptic capacitance measurements.

Figure 2—source data 1

Parameters for weak, middle, and strong post-flash Ca2+ elevations.

Ca2+ uncaging dose-response curve measured with deconvolution of EPSCs.

Figure 3—source data 1

Presynaptic and postsynaptic measurements reveal two kinetic processes of neurotransmitter release.

Figure 4—source data 1

Fast sustained release with very weak Ca2+-dependence.

Figure 5—source data 1

Release schemes with five Ca2+ steps and fast replenishment via parallel or sequential models can explain Ca2+-dependence of release.

Parameters for simulations of Ca2+ release from DMN cage.

Ca2+ uncaging with different pre-flash Ca2+ concentrations indicates Ca2+-dependent vesicle priming.

Figure 7—source data 1

Parameters for release scheme models.

Author details

Abdelmoneim Eshra

Contribution

Competing interests

Hartmut Schmidt

Contribution

Competing interests

Jens Eilers

Contribution

Competing interests

Stefan Hallermann

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading

Action potential-evoked synaptic release critically depends on basal intracellular Ca²⁺ concentration.

Ca²⁺ uncaging dose-response curve measured with presynaptic capacitance measurements.

Parameters for weak, middle, and strong post-flash Ca²⁺ elevations.

Ca²⁺ uncaging dose-response curve measured with deconvolution of EPSCs.

Fast sustained release with very weak Ca²⁺-dependence.

Release schemes with five Ca²⁺ steps and fast replenishment via parallel or sequential models can explain Ca²⁺-dependence of release.

Parameters for simulations of Ca²⁺ release from DMN cage.

Ca²⁺ uncaging with different pre-flash Ca²⁺ concentrations indicates Ca²⁺-dependent vesicle priming.