Figures and data in Gut bacterial aggregates as living gels

Figures
Tables
Additional files

4 figures, 4 tables and 2 additional files

Figures

Figure 1

Download asset Open asset

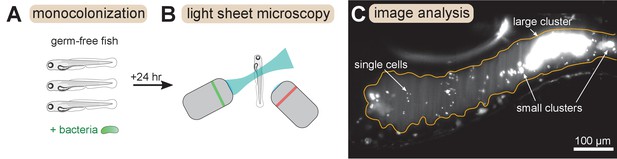
Overview of experimental methods.

Larval zebrafish were derived germ-free and then monoassociated with single bacterial species (left). After 24 hr of colonization, images spanning the entire gut were acquired with light sheet fluorescence microscopy (middle). An example image of the anterior intestine is shown on the right, with instances of single cells and multicellular aggregates marked. The image is a maximum intensity projection of a 3D image stack. The approximate boundary of the gut is outlined in orange. Sizes of bacterial clusters were estimated with image analysis by separately identifying single cells and multicellular aggregates, and then normalizing the fluorescence intensity of aggregates by the mean single cell fluorescence.

Figure 2 with 2 supplements

Download asset Open asset

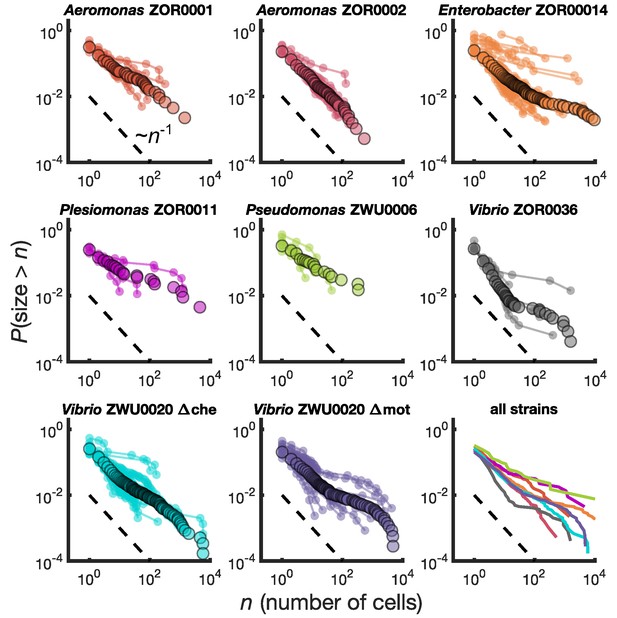
Different bacterial species exhibit similar cluster size distributions.

Reverse cumulative distributions, the probability that the cluster size is greater than $n$ as a function of $n$ , for eight bacterial strains in larval zebrafish intestines. Small circles connected by lines represent the distributions constructed from individual fish. Large circles are from pooled data from all fish. The dashed line represents $P (size > n) \sim n^{- 1}$ and is a guide to the eye. Bottom right panel shows the pooled distributions for each strain as solid lines.

Figure 2—source data 1 Spreadsheet with all cluster sizes by strain.: https://cdn.elifesciences.org/articles/71105/elife-71105-fig2-data1-v2.xlsx
Download elife-71105-fig2-data1-v2.xlsx

Figure 2—figure supplement 1

Download asset Open asset

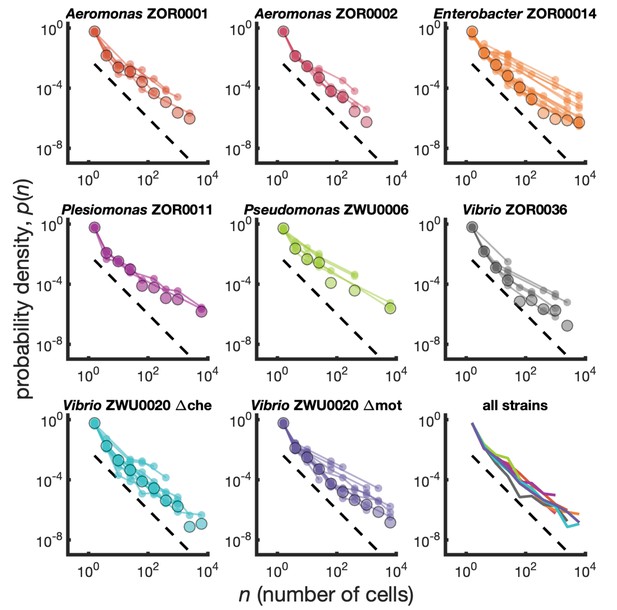
Cluster size distributions as probability densities.

Different bacterial species exhibit similar cluster size distributions. Probability densities for eight bacterial strains monoassociated in larval zebrafish intestines. Small circles connected by lines represent the distributions constructed for each fish. Large circles are the result of pooling together sizes from all fish. Dashed line represents $p (n) \sim n^{- 2}$ and is a guide to the eye. Bottom right panel shows the pooled distributions for each strain as solid lines. Summary of data is given in Table 1.

Figure 2—figure supplement 2

Download asset Open asset

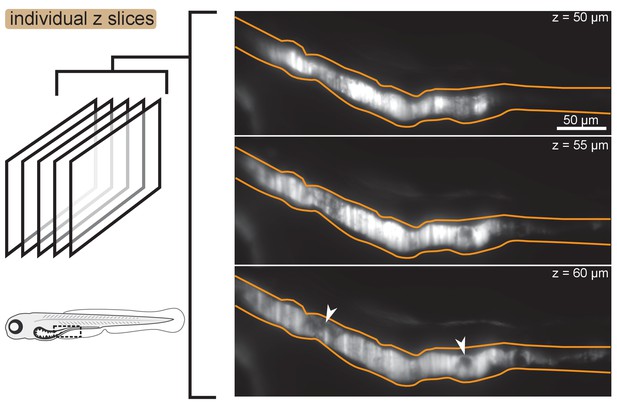
Images of individual $z$ -slices showing mild heterogeneity of fluorescence intensity within aggregates.

Fluorescence intensity is mostly homogeneous within clusters, although small dark regions do occur. Three individual z slices of a fish colonized with *Enterobacter* are shown. The approximate gut boundary is outlined in orange. Dark regions within the cluster are noted with white arrows. The approximate location of the field of view within the animal is noted with a dashed black box on the fish cartoon.

Figure 3

Download asset Open asset

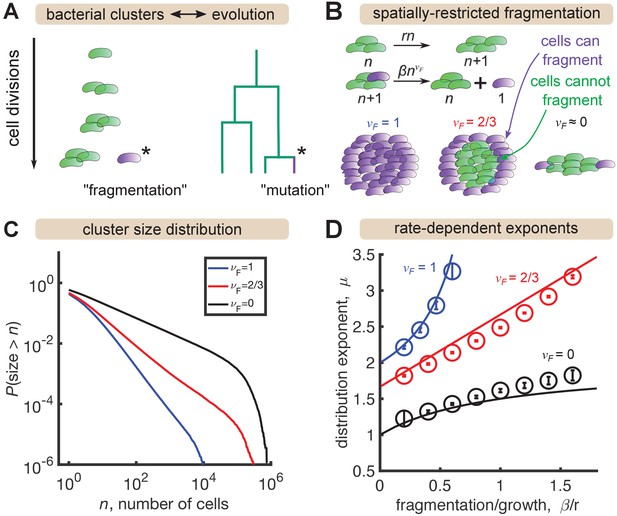
A minimal model inspired by evolutionary dynamics generates power law distributions.

(A) Fragmentation is analogous to mutation and we can construct a genealogy that mirrors the physical structure of the clusters. (B) Summary of a growth/fragmentation process that includes the effect of spatially confined clusters. (C) Examples of reverse cumulative size distributions obtained from stochastic simulations of the model for different values of the fragmentation exponent, $ν_{F}$ . The tails of the distribution are approximately power laws, defined as $P (size > n) \sim n^{- μ + 1}$ . Parameters: $r$ = 0.5 hr^-1, $β = 0.4, 0.2, 0.167$ hr^-1, for $ν_{F} =$ 0, 2/3, 1, respectively, time $t = 24$ hr, and the system was initialized with 10 single cells. (D) Dependence of the resulting distribution exponent, μ, on ratio of fragmentation to aggregation rate ( $β / r$ ) and fragmentation exponent ( $ν_{F}$ ). Markers show mean and standard deviation across 100 simulations. Solid lines are approximate analytic results (Table 2). Parameters: same as (C) with β varying.

Figure 3—source data 1 Results of power-law fits to simulated distributions.: https://cdn.elifesciences.org/articles/71105/elife-71105-fig3-data1-v2.xlsx
Download elife-71105-fig3-data1-v2.xlsx

Figure 4 with 3 supplements

Download asset Open asset

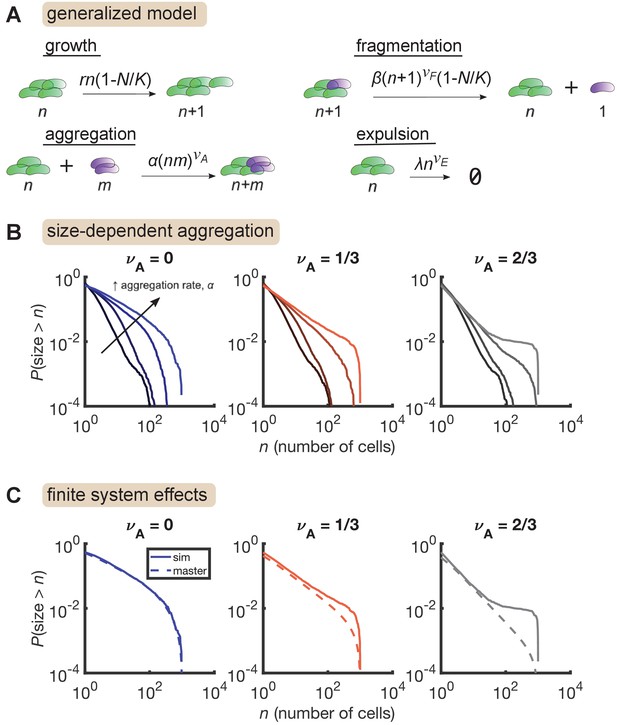
Size-dependent aggregation introduces a plateau in the size distribution.

(A) Schematic of the generalized model. Parameters summarized in Table 3. (B) Reverse cumulative distributions obtained from simulations for different values of $ν_{A}$ (left, middle, right) and $α$ (different colored lines within each panel). Increasing aggregation produces a plateau if the aggregation depends strongly enough on cluster size. (C) The plateau arises only in stochastic simulation of finite systems with size-dependent aggregation. Solid lines are stochastic simulations, dashed lines are the result of numerically integrating the master equation. Parameters: $r$ = 0.5 hr^-1, $ν_{F} = 2 / 3$ , $β = 0.5$ hr^-1, $ν_{E} = 1 / 3$ , $λ = 0.01$ hr^-1, $K = 10^{3}$ , and the number of simulation was replicates = 150 per parameter set. For each value of $ν_{A}$ , we considered $α$ values of 0 (no aggregation) and then varied α logarithmically, with the following (min, max) values for $\log_{10} α$ : (−4,–2) for $ν_{A} = 0$ , (−4.5,–2.5) for $ν_{A} = 1 / 3$ , and (−5,–3) for $ν_{A} = 2 / 3$ .

Figure 4—figure supplement 1

Download asset Open asset

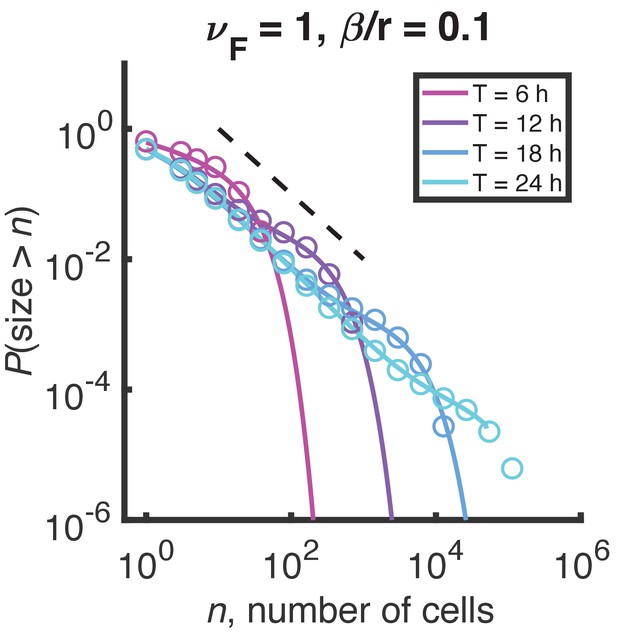
Distributions of growth/fragmentation process at short times.

Mild curvature appears in the minimal growth/fragmentation process distribution at finite time, but the result is inconsistent with experimental data. Circles are the result of stochastic simulation, solid lines are the result of numerical integration of the master equation. Color denotes simulation time. Dashed black line indicates $P (size > n) \sim n^{- 1}$ and is a guide to the eye.

Figure 4—figure supplement 2

Download asset Open asset

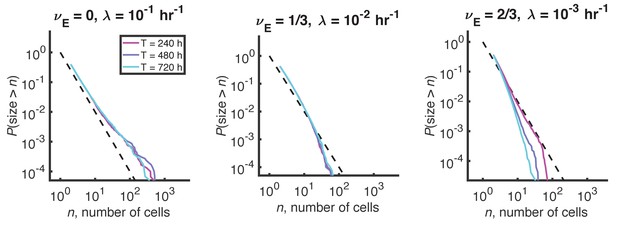
Distributions for a process with density-dependent growth, fragmentation, and expulsion.

A modified process with carrying capacity and expulsion does not produce a plateau in the stationary size distribution. Reverse cumulative distributions computed from stochastic simulations with different values of the expulsion exponent, $ν_{E}$ . For each value of $ν_{E}$ , the expulsion rate, $λ$ , was chosen such that for clusters of size $K = 1000$ cells, $λ K^{ν_{E}} = 0.1$ hr^-1, consistent with experimental data. Three different simulation times are shown in each panel in differently colored solid lines. Long simulation times are required to approach steady state when $λ$ becomes small, and the steady state is not quite reached in the right panel even after 720 hr. Dashed line indicates $P (size > n) \sim n^{- 1}$ and is a guide to the eye. Other parameters: $r = 0.5$ hr^-1, $ν_{F} = 2 / 3$ , $β = 0.5$ hr^-1, and the number of simulations = 100.

Figure 4—figure supplement 3

Download asset Open asset

Distributions for a model with only aggregation and $ν_{A} = 1$ .

Plateaus arise at the gelation transition of purely aggregating systems. Reverse cumulative distributions computed from stochastic simulations are shown. Different curves represent different simulation times, ranging linearly from 0.1 to 0.175 hr (magenta to cyan). Dashed line represents an approximate analytic prediction of $P (size > n) \sim n^{- 3 / 2}$ in the sol phase at the transition point and is a guide to the eye. Parameters: $α = 0.01$ hr^-1, number of cells = 10³, number of simulations = 100.

Tables

Table 1

Summary of cluster data by bacterial strain.

Each row corresponds to one of the bacterial strains included in this study. Entries include strain name, total number of fish colonized with that strain, total number of clusters identified across all fish, and the original publication that the data was pulled from.

Bacterial strain	Number of fish	Number of clusters	Source publication
Aeromonas ZOR0001	6	445	Schlomann et al., 2018
Aeromonas ZOR0002	6	1901	Schlomann et al., 2018
Enterobacter ZOR0014	18	3597	Schlomann et al., 2018; Schlomann et al., 2019
Plesiomonas ZOR0011	3	223	Schlomann et al., 2018
Pseudomonas ZWU0006	6	133	Schlomann et al., 2018
Vibrio ZOR0036	6	2430	Schlomann et al., 2018
Vibrio ZWU0020 Δmot	11	5888	Wiles et al., 2020
Vibrio ZWU0020 Δche	11	3551	Wiles et al., 2020

Table 2

Analytic results for the minimal growth-fragmentation process.

Distribution exponent, μ, as a function of fragmentation exponent, $ν_{F}$ , fragmentation rate, β, and growth rate, r, as plotted in Figure 3D. Results are expected to be valid for long times ( $t \to \infty$ ), large sizes ( $n \to \infty$ ), and slow fragmentation ( $β / r < 1$ ). See Appendix for details.

	$ν_{F} = 1$	$ν_{F} = 2 / 3$	$ν_{F} = 0$
distribution exponent, μ	$1 + \frac{1}{1 - β / r}$	$\frac{5}{3} + \frac{β}{r}$	$1 + \frac{β / r}{1 + β / r}$

Table 3

Summary of model variables and parameters.

Variable/parameter	Description
$n$	Cluster size (number of cells)
$p (n)$	Probability of cluster size, $n$
$P (size > n)$	Cumulative probability; probability of size being larger than $n$
μ	Exponent of power law; $p (n) \sim n^{- μ}$ , $P (size > n) \sim n^{- μ + 1}$
$r$	Cell division rate
$K$	Carrying capacity; maximum number of cells
$β$	Fragmentation rate
$ν_{F}$	Fragmentation exponent; clusters of size $n$ fragment with rate $β n^{ν_{F}}$
$α$	Aggregation rate
$ν_{A}$	Aggregation exponent; clusters of sizes $n$ and $m$ aggregate with rate $α {(n m)}^{ν_{A}}$
$λ$	Expulsion rate
$ν_{E}$	Expulsion exponent; clusters of size $n$ are expelled with rate $λ n^{ν_{E}}$

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Additional information
Software, algorithm	Analysis code	This study	see Materials and methods, Simulations
Other	Cluster size data	Schlomann and moments, 2018
Other	Cluster size data	Schlomann et al., 2019
Other	Cluster size data	Wiles et al., 2020

Additional files

Supplementary file 1 Cumulative distribution exponents of cluster size distributions by strain, with analysis of sensitivity to single-cell detection. The small size regime of the cluster size distributions were fit to a power-law model for sizes up to 100 cells using two methods: a linear fit to $P (size > n)$ and maximum likelihood estimation (Materials and methods). The fits were done for each animal and the resulting mean ± std. dev of the exponents (corresponding to $μ - 1$ , as defined in the text) are given for each strain. For each method, the fits were done twice, once including single cells, and once considering only cells of size two or greater. As discussed in the main text, the largest uncertainty in cluster size enumeration from the images occurs at small sizes. Ignoring single cells in the fit only mildly changes the average exponent, and all changes are within uncertainties. Most exponents are consistent with $μ - 1 = 1$ .: https://cdn.elifesciences.org/articles/71105/elife-71105-supp1-v2.xlsx
Download elife-71105-supp1-v2.xlsx
Transparent reporting form: https://cdn.elifesciences.org/articles/71105/elife-71105-transrepform-v2.docx
Download elife-71105-transrepform-v2.docx