1. Neuroscience

Behavioral evidence for nested central pattern generator control of Drosophila grooming

  1. Primoz Ravbar  Is a corresponding author
  2. Neil Zhang
  3. Julie H Simpson  Is a corresponding author
  1. Molecular Cellular and Developmental Biology and Neuroscience Research Institute, University of California, Santa Barbara, United States
https://doi.org/10.7554/eLife.71508
Share this article
Cite this article
  1. Primoz Ravbar
  2. Neil Zhang
  3. Julie H Simpson
(2021)
Behavioral evidence for nested central pattern generator control of Drosophila grooming
eLife 10:e71508.
https://doi.org/10.7554/eLife.71508
  2. Download BibTeX
  3. Download .RIS

Abstract

Central pattern generators (CPGs) are neurons or neural circuits that produce periodic output without requiring patterned input. More complex behaviors can be assembled from simpler subroutines, and nested CPGs have been proposed to coordinate their repetitive elements, organizing control over different time scales. Here, we use behavioral experiments to establish that Drosophila grooming may be controlled by nested CPGs. On a short time scale (5–7 Hz, ~ 200 ms/movement), flies clean with periodic leg sweeps and rubs. More surprisingly, transitions between bouts of head sweeping and leg rubbing are also periodic on a longer time scale (0.3–0.6 Hz, ~2 s/bout). We examine grooming at a range of temperatures to show that the frequencies of both oscillations increase—a hallmark of CPG control—and also that rhythms at the two time scales increase at the same rate, indicating that the nested CPGs may be linked. This relationship holds when sensory drive is held constant using optogenetic activation, but oscillations can decouple in spontaneously grooming flies, showing that alternative control modes are possible. Loss of sensory feedback does not disrupt periodicity but slow down the longer time scale alternation. Nested CPGs simplify the generation of complex but repetitive behaviors, and identifying them in Drosophila grooming presents an opportunity to map the neural circuits that constitute them.

Editor's evaluation

This study presents an intriguing example of natural rhythmic leg movement oscillations at a fast time scale embedded within a slower rhythmic behavioral oscillation and the similar effects of temperature on the rates of the two rhythms. The data and the writing are both exceptionally clear and advance our understanding,

https://doi.org/10.7554/eLife.71508.sa0

Introduction

Animals combine simpler movements into complex routines, forming behaviors with organization across multiple time scales. We have observed lobsters moving antennal segments at different speeds, and marveled at pianists playing Rachmaninoff moving their fingers blindingly fast, hands at a slower pace, while arms and body are swinging, all nearly perfectly orchestrated. We wondered how a complex behavior can be assembled from simpler movements in such a harmonious manner.

Central pattern generators (CPGs) are neural circuits that produce rhythmic motor outputs in response to a trigger without requiring ongoing descending drive or patterned sensory inputs; CPGs control short stereotypic actions in cat walking, crayfish swimming, locust flight, leech heartbeat, and the stomatogastric and pyloric rhythms of crustaceans (reviewed in Berkowitz, 2019; Harris-Warrick and Ramirez, 2017 ; Grillner, 2006; Marder and Calabrese, 1996; Mulloney and Smarandache, 2010; Selverston, 2010). However, CPGs may also contribute to control of more complex behaviors. When the movements that compose a behavior repeat, it is inefficient to initiate each step with a separate decision. Automating the sequence by calling its actions in series produces reliable execution. Increasingly complex sequences can be assembled from shorter elements, suggesting hierarchical control. When repetitive subroutines are themselves composed of simpler periodic movements, they may be controlled by nested CPGs, hierarchically organized so that a ‘high-level’ slow CPG controls the behavior on coarse scale and a ‘lower-level’ fast CPG adds the fine structure (Berkowitz, 2019). In other words, the slow CPG controls alternations between subroutines and the fast CPG controls alternations within these subroutines. Various combinations of coarse and fine oscillators could produce behaviors of arbitrary complexity while still keeping them well-timed, stereotyped, and coherent. Bird song, for example, contains sound syllables executed in sequences. The syllables are short repeating elements, and sequences of syllables make phrases or words that also repeat, creating structure over several time scales. Ingenious local cooling experiments of specific brain regions cause the whole song to slow down, indicating that it is governed by central pattern generating circuits (Long and Fee, 2008). Temporally nested, hierarchical patterns of neural activity have also recently been found during locomotion in Caenorhabditis elegans (Kaplan et al., 2020).

Here, we show that Drosophila grooming behavior contains periodic elements over several time scales of which we explore two: a fast repeat of individual leg movements (including head sweeps and front leg rubs) and a slow alternation between bouts of head cleaning and front leg rubbing. We demonstrate that both of these repeated elements show evidence of CPG control, and that the two rhythms are usually coordinated, establishing fly grooming as a model system for understanding the circuit architecture of nested CPGs.

Results

Two time scales of grooming are periodic

When flies are covered in dust, they initially groom anterior body parts using their front legs (Seeds et al., 2014). They alternate between bouts of head sweeps, where the legs move synchronously, and bouts of leg rubbing, where the legs move in opposition to each other, scraping the dust off. These movements are shown schematically in Figure 1A: the purple and orange arrows indicate synchronous in-phase head sweeps and opposing out-of-phase leg rubs, respectively; the thicker light blue arrows show alternation between these two leg coordination modes. Bouts of head sweeping (h) are indicated in purple and front leg rubbing (f) in orange on the ethogram (record of behavior actions over time) shown in Figure 1B.

Figure 1 with 4 supplements see all
Download asset Open asset
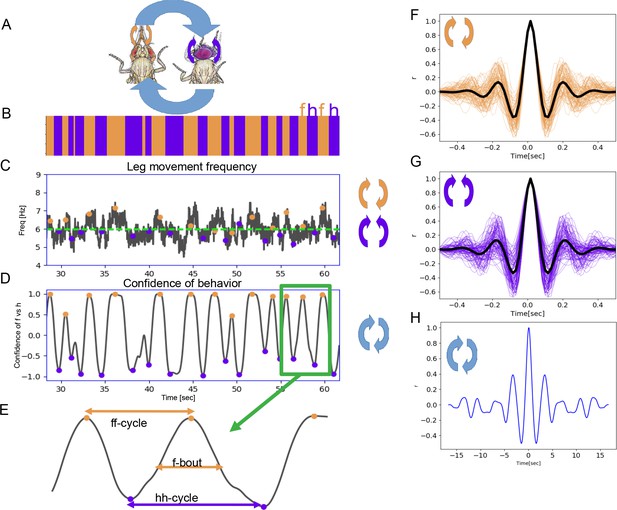
Two time scales of grooming behavior are periodic.

(A) Schematic of anterior grooming behavior. The out-of-phase motion of leg rubbing is indicated by the orange arrows and in-phase head cleaning movements are indicated by the purple arrows (the short time scale). The blue arrows indicate alternations between the leg rubbing and head cleaning subroutines (the long time scale). (B) Ethogram showing alternations between bouts of front leg rubbing (f) and head cleaning (h) in dust-covered flies recorded at 18°C. (C) Example leg sweep and rub frequencies measured in the 30 s of anterior grooming behavior shown in the ethogram above. Purple and orange dots indicate front leg rubbing (f) and head cleaning (h) as detected by the Automatic Behavior Recognition System. (D) Bouts of front leg rubbing (f) or head cleaning (h) are identified by their probabilities (from the output of the Convolutional Neural Network). When we subtract the probability of h-bouts from that of f-bouts, we obtain the confidence of behavior curve shown here (see Materials and methods). Purple and orange dots indicate maxima and minima of confidence in behavior identification, corresponding to the centers of the f- and h-bouts, respectively. (E) Enlarged segment taken from (D) showing the definitions of ff-cycle and hh-cycle and f-/h-bouts. (F) Samples of autocorrelation functions (ACFs) computed over 3 min of movies when the fly was engaged in front leg rubbing or head sweeps (G). The thick black lines indicate the average of these samples, while thinner purple and orange lines represent each individual ACF contributing to this average; see Materials and methods for details. (H) ACF of the alternation of f-bout and h-bout from the example of ff-cycles shown in (D) also reveals periodic signal.

The individual leg sweeps and rubs are stereotyped: these movements are recognizable by human observers or machine vision algorithms (Mathis et al., 2018; Ravbar et al., 2019), and they represent the short time scale we consider here. We first count individual leg movements from raw videos as they are processed for our Automatic Behavior Recognition System (ABRS) pipeline (see Materials and methods and Figure 1—figure supplement 1) and compute their frequencies. In Figure 1C, we show an example of frequencies of leg sweeps and rubs during the same one-minute period as Figure 1B. At 18°C, leg rubs and sweeps have a characteristic frequency ~6 Hz. This means that each leg movement takes approximately 150 ms to complete, which is consistent with our observations using higher resolution video recordings (see below).

Grooming is not a fixed action pattern and flies choose subroutines such as head sweeps or wing cleaning stochastically, but with different levels of prioritization (Seeds et al., 2014). During anterior grooming, flies typically make several head sweeps in a row, followed by repeated leg rubbing movements; we call these periods where a single type of action is repeated bouts. We use ABRS (Ravbar et al., 2019) to automatically classify different grooming actions and to identify the time points of maximum behavior identification confidence as the centers of bouts (orange and purple circles in the time series shown in Figure 1D). Head cleaning bouts and front leg rubbing bouts alternate: we define the time between two head cleaning bouts as a hh-cycle while the time between two consecutive front leg rubbing bouts is an ff-cycle. Either cycle will include both leg rubs and head sweeps, which is why we consider the average frequency of both types of leg movements in our analysis. These terms are illustrated in Figure 1E, and the cycles are the long time scale we investigate here.

We demonstrate the periodicity of head sweeps and leg rubs (short time scale) using autocorrelation analysis (Figure 1F and G). Although previous work revealed some syntactic organization at the bout level—both identity and duration of current action influence the identity and duration of the next (Mueller et al., 2019)—we were surprised to find that the alternation of head cleaning and front leg rubbing bouts is also periodic. Autocorrelation analysis of the time series shown in Figure 1H illustrates signal at ~0.33 Hz, corresponding to approximately 2 s between the mid-point of consecutive bouts of front leg rubbing.

To quantify the strength of periodicity, we computed the ratio between the heights of the prominent peak nearest to zero lag and the central peak (at zero lag) of the autocorrelation function (ACF) (Figure 1—figure supplement 2); we call the ratio of these peak heights the Periodicity Index (PI). More periodic movements have high shoulder peaks: a perfect sine wave would have a PI of 1, while in more weakly periodic data, this index would approach 0. The weakest periodic grooming movements we observe have values ~0.2. Non-periodic signals have poorly defined shoulder peaks and fall below our threshold for peak detection; therefore, the PI is not computed for non-periodic behaviors (see Materials and methods). Using this metric, head sweeps and leg rubbing movements of dusted flies grooming at 18°C have a mean PI of 0.31 (s.d.=0.02) and 0.31 (s.d.=0.01), respectively; the alternation between bouts (the long time scale) at 18°C has a mean PI of 0.36 (s.d.=0.02). We also quantify the amount of periodic behavior as a ratio of time spent in periodic versus non-periodic movements, as shown in Figure 1—figure supplement 2. Using these ratios, we found that overall the amount of periodic behavior for the long time scale is 80% (s.d.=8%) at 18°C. For a comprehensive comparison of PI values and the overall amounts of periodic behaviors for the different conditions evaluated throughout this project see Figure 1—figure supplement 3. Illustrative examples of animals engaged in periodic or non-periodic behaviors, sampled from different groups studied, are shown in Figure 6—figure supplement 2.

We confirm the frequency and periodicity of leg movements during grooming using Deep Lab Cut (DLC) to analyze an independent video data set. DLC is a method developed for tracking of individual body parts (Mathis et al., 2018). Figure 1—figure supplement 4 shows the changes of joint angles (resulting from leg movements) over 2 s of grooming behavior: at 18°C, the movement frequencies for the short time scale and long time scale are 4.5 Hz and 0.22 Hz, respectively, similar to our original measurements using ABRS. The PI values are ~0.34 and the prominence of shoulder peaks is above our threshold for periodic behaviors. The discovery that both short time scale and long time scale subroutines within grooming behavior show periodicity suggests the possibility that they may both be controlled by central pattern generating circuits.

The period lengths of both time scales contract with increasing temperature

A key feature of CPGs is that they oscillate faster at higher temperatures (Deliagina et al., 1983; Tang et al., 2012). To determine whether temperature affects the periodicity of leg sweeps and rubs (short time scale) or the alternation between bouts of head sweeps and leg rubs (ff/hh-cycles; long time scale), we recorded the grooming behavior of dust-covered flies at a range of temperatures between 18°C and 30°C. Examples of ethograms from the extreme temperatures are shown in Figure 2A, and ethograms from the entire data set arranged from coolest to warmest temperature of 84 individual flies at seven temperatures recorded for 13 min each are displayed in Figure 2B.

Figure 2 with 4 supplements see all
Download asset Open asset
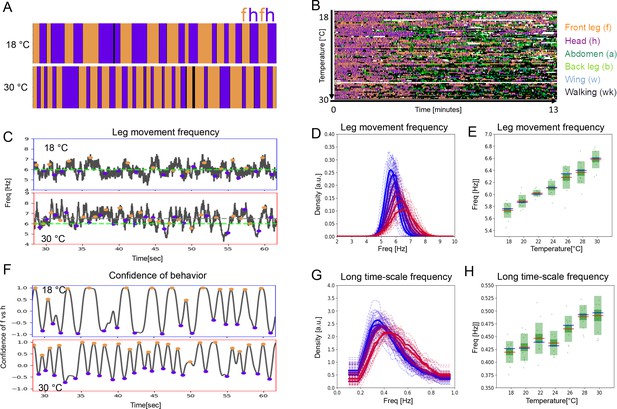
Period lengths of two time scales contract with increasing temperature in dust-stimulated flies.

(A) Examples of ethograms recorded at 18°C (top) and 30°C (bottom). (B) Ethograms of 84 dust-stimulated flies recorded at different temperatures (18–30°C). Colors represent behaviors as indicated in the color legend on the right. (C –E) The frequency of individual leg movements increases with temperature. Part (C) shows example frequency time series from 30 s of grooming at 18°C (top, blue outline) and 30°C (bottom, red outline). Gray dashed line = mean of this sample; green dashed line = reference at 6 Hz. (D) Histogram of leg movement frequencies, sampled from seven temperatures (18–30°C.) Lower temperatures are indicated in blue and higher ones in red. Thin lines—individual histograms; thick lines—average of samples at each temperature. All histograms are computed from the 84 ethograms of dust-stimulated flies in (B). (E) Box plots of leg sweep frequencies. Dots show individual fly averages, while the blue bars show the mean frequency, the red bars mark median and the green shaded areas indicate standard deviation (SD) and error (Blue/red bars in box plots – mean/median; shaded areas – SD and SE). (F–H) The frequency of the long time scale (ff-cycles + hh-cycles) also increases with temperature. (F) As described in Figure 1D, this plot shows the confidence in samples recorded at 18°C (top) and 30°C (bottom). (G , H) Similar to the panels (D , E) but showing the increase of ff-cycle frequency with temperature computed from the 84 dust-stimulated flies.

Temperature increase causes faster individual leg movements (short time scale) (Figure 2C–D) and the frequency shows a linear increase from 5.7 Hz to 6.6 Hz (R2=0.99, p<0.001; Figure 2E). This analysis combines sweeps and rubs, but when the different leg movements are considered separately, both show a similar increase with temperature (Figure 2—figure supplement 1).

The period of long time scale movements is also compressed by temperature. The ff/hh-cycle frequency increases from 0.42 Hz (s.d.=0.02) at 18°C to 0.49 Hz (s.d.=0.04) at 30°C, also in a linear manner (R2=0.96, p<0.001; Figure 2F–H). The frequencies of hh-cycles show a very similar trend (Figure 2—figure supplement 2). Autocorrelations for the long time scale are more variable at higher temperatures, but the alternation remains periodic across the entire range of temperatures (Figure 1—figure supplement 3F, Figure 2—figure supplement 3). A full spectral analysis of the effect of temperature on the ACF shows complex structure over several time scales (Figure 2—figure supplement 4).

Increasing temperature shortens the cycle period of both the short time scale leg sweeps and rubs and the long time scale alternation between bouts of head cleaning and front leg rubbing. Next, we asked if behaviors at the two time scales contract with temperature by the same amount, which could suggest a linkage between them.

Two time scales contract together with temperature elevation

Several metrics indicate that the short and long time scale oscillations contract at the same rate as temperature increases. We noticed that the number of leg movements within an ff/hh-cycle is fairly consistent, averaging ~15: means range from 13.2 to 15.8 and s.d. range from 0.75 to 1.95 across temperatures (Figure 3A). At 18°C, there are 15 leg movements of 175 ms for an ff/hh-cycle duration of 2.38 s, while at 30°C there are 15 leg movements of 152 ms for an ff/hh-cycle duration of 2.04 s. Thus, the average number of leg movements per ff/hh-cycle remains constant even as the cycle duration shortens with increasing temperature (Figure 3B).

Figure 3 with 1 supplement see all
Download asset Open asset
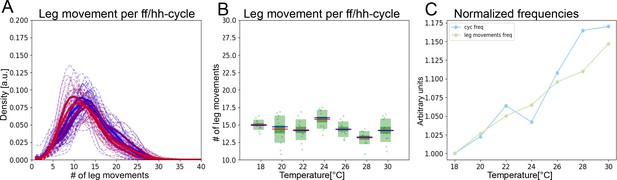
The two time scales contract together with increasing temperature.

(A) Histograms of numbers of leg movements per ff/hh-cycle in cooler temperatures (blue) and warmer temperatures (red). (B) Box plots of leg movement counts per ff/hh-cycle across the seven temperatures; statistics as in Figure 2E. (C) The frequency of individual leg movements and bout alternations (ff/hh-cycles) increases roughly linearly with temperature but over different time scales (ms vs. s; 7 Hz vs. 0.5 Hz). To see if they increase at the same rate, we compare them in arbitrary units. Frequencies were normalized by dividing each mean value from Figure 2E by the lowest value recorded: this produces the rate of change, where 1.0 means no change and values above 1.0 reflect the increased rate. See Figure 3—figure supplement 1 for similar effects in hh-cycles.

An alternative way to determine whether the two time scales contract together with temperature is to plot their contraction rates. Normalizing by their minimal frequencies, we can visualize the slope of temperature dependence for each time scale and the correlation between them is striking (R2=0.96, p<0.001; Figure 3C). Both time scales contract at the same rate, with R2 values of 0.995 and 0.956, respectively. This analysis combined both head sweeps and leg rubs for the short time scale and ff/hh-cycles for the longer one, but when only head sweeps and hh-cycles are considered, a similar correlated contraction with temperature is also observed (Figure 3—figure supplement 1).

It is possible that temperature will affect both time scales of grooming behaviors at the same rate just because increased temperature tends to speed up all behaviors through its effect on neural activity, making the apparent coupling between grooming CPGs an epiphenomenon. We consider this unlikely because the two time scales can be decoupled in spontaneously grooming flies, where they respond differently to temperature, as described below.

Periodicity and correlation between time scales persist when sensory stimulation is constant

So far, we have shown that two hallmarks of CPGs—periodicity and temperature-dependent frequency increase—hold for both short time scale leg sweeps or rubs and long time scale alternations between bouts of leg rubbing and head cleaning. An additional criterion for determining if a behavior is controlled by a CPG is that rhythmic output does not require rhythmic input. It is challenging to isolate the contribution of sensory input or feedback to the rhythms we observe in grooming. There are mechanosensory bristle neurons that detect dust and induce grooming, and proprioceptive sensors that detect limb position or movement during grooming. If these sensory inputs are rhythmic, they could contribute to both short and long time scale rhythms.

When flies are covered in dust, their own grooming actions alter sensory input stimuli. The faster their legs sweep, the more quickly dust is removed. Perhaps the coupling between time scales can be explained because faster leg sweeps result in more dust removal, which reduces sensory drive and thus shortens grooming bouts. In other words, the rhythmic behavioral output could result in similarly rhythmic sensory input—thus not excluding a reflex chain explanation of the observed periodicity (Harris-Warrick and Ramirez, 2017). What happens to the periodicity of the long time scale grooming rhythms, across temperatures, if the sensory drive is held constant? We predict that if it is indeed CPG-controlled, it should still contract with increasing temperature. We test this using optogenetic activation of all mechanosensory bristle neurons.

We previously demonstrated that this manipulation induces grooming, beginning with the anterior body parts, and causing alternation between bouts of head cleaning and front leg rubbing (Hampel et al., 2017; Zhang et al., 2020). Here, we combine optogenetic activation for constant sensory input with changing temperature to show that both individual leg movements and bout-level alternations increase in frequency with temperature and that they do so in a correlated manner. The expression pattern used to activate mechanosensory bristle neurons is shown in Figure 4—figure supplement 1. Representative ethograms at 18°C and 30°C show characteristic alternation between bouts of head cleaning and front leg rubbing (Figure 4A). The entire behavioral data set of optogenetically induced grooming over a range of temperatures is shown in Figure 4B.

Figure 4 with 3 supplements see all
Download asset Open asset
Under constant sensory stimulation, the temperature effect on both time scales persists.

Undusted flies expressing the optogenetic activator UAS-Chrimson in mechanosensory bristles were stimulated with red light to induce anterior grooming behavior. Examples ethograms recorded at 18°C (top) and 30 °C (bottom) are shown in (A), while (B) shows the whole data set of ethograms representing 56 flies across the range of temperatures, similar to Figure 2B. The green bars represent the periods of light activation, lasting 2 min each, to optogenetically induce grooming. (C) Examples of leg movement frequencies at 18°C (top) and 30°C (bottom), (D) histograms of mean frequencies at cool (blue) and warm (red) temperatures, and (E) box plots of the increase in leg movement frequency with temperature; plots and statistics as described in Figure 2C, D and E; compare to short time scale effects where grooming is induced by dust. (F–H) Long time scale ff-cycle + hh-cycle analysis same as in Figure 2F, G and H. (I) Histograms and box plots (J) of median leg movement counts per ff-cycle and hh-cycle across the seven temperatures, quantified as in Figure 3A and B. (K) The rate of temperature-driven increase in frequency is shown by normalization as in Figure 3C.

Uniform sensory input still evokes rhythmic output at both short and long time scales (Figure 4—figure supplement 2). For example, the PIs at 18°C for short and long time scales are 0.29 (s.d.=0.03) and 0.35 (s.d.=0.03), respectively (Figure 1—figure supplement 3E), and the amount of periodic behavior, considering the long time scale alterations, is 62% (s.d.=10%) (Figure 1—figure supplement 3H). This amount of periodic behavior is less than the 80% (s.d.=8%) in the dusted flies, and the long time scale rhythm also appears more ragged. We propose that sensory feedback may be needed to stabilize rhythms but not necessarily to generate them in the first place. The period of the optogenetically induced rhythms gets shorter with temperature (Figure 4C–H). The frequencies are similar to dust-induced grooming, and the average number of leg movements per ff/hh-cycle is also preserved across the range of temperatures (Figure 4I–J). As with dusted flies, the rate of contraction of the two time scales is correlated (Figure 4K), supporting the hypothesis that the short time scale leg movements and the long time scale bout alternations are both controlled by CPGs, and that these circuits are yoked together, even under constant sensory stimulation.

Optogenetic activation of mechanosensory neurons does not precisely mimic the physical stimulus of dust itself, and the response of the optogenetically stimulated flies to temperature reflects this. Both short and long time scale behaviors occur with somewhat shorter periods at lower temperature than their dust-evoked counterparts, and they stop increasing beyond 26–28°C (compare Figures 2E, H ,, 4E and H). One possible explanation is that the optogenetic stimulation is ‘maxing out’ the sensory input: it may be driving the fastest leg movements biomechanically possible, or the upper bound of the CPGs’ frequency range may be reached at a lower temperature. We investigated this possibility by activating the mechanosensory bristle neurons at a constant temperature but with a range of light intensities: the frequencies of movements induced remain constant (Figure 4—figure supplement 3). Even starting from this higher frequency baseline, the two time scales still increase with temperature at similar rates (Figure 4K), indicating that optogenetic activation does not immediately induce maximum movement speeds.

Periodicity of both time scales is preserved under reduced sensory feedback

Optogenetic activation may mask acute changes in sensory feedback as the legs contact the body or each other during grooming movements, but removing or silencing sensory neurons is a more direct test of this potential contribution to rhythmicity. To determine if leg rubs and head sweeps remain rhythmic when sensory feedback is reduced, we amputated one front leg between the femur and tibia, similar to Berendes et al., 2016. This eliminates distal proprioceptive feedback from the amputated leg, as well as the usual mechanosensation provided by contact between the legs or the leg and the head during rubs and sweeps. We then employed the DLC software to track the position of the stump and of the intact front leg (Figure 5—figure supplement 1). We found that movements of both the intact leg and the stump remained periodic, with frequencies and PIs similar to those of intact legs in dusted flies. This result further supports that at least the short time scale leg movements are indeed controlled by CPGs.

We also attempted to reduce sensory feedback using genetic reagents. We blocked chemical synaptic transmission in leg mechanosensory neurons by expressing tetanus toxin as described in Mendes et al., 2013 observed grooming behavior in response to dust. Figure 5A shows ethograms of grooming behaviors for both the experimental (TNT) and control (GFP) groups; Figure 5B–C shows the neurons that have been genetically inhibited. The frequency of rubs is lower in the TNT group than in the control (p< 0.001) (Figure 5D) while the frequency of sweeps is similar for both (Figure 5E). The long time scale oscillations are significantly slower in the TNT group (p<0.003) (Figure 5H, also ethograms in Figure 5A) and so are the numbers of leg movements per ff/hh-cycle (Figure 5F–G). Both groups exhibited periodic behaviors on both the long and short time scales (Figure 5I and J). The sensory inhibited flies also performed less overall periodic behavior on the long time scale (Figure 5K). Taken together, these results suggest that grooming behaviors do not require sensory input for periodicity, but do utilize it for timing, modulation, and perhaps stabilization of the motor output, especially on the longer time scale.

Figure 5 with 1 supplement see all
Download asset Open asset
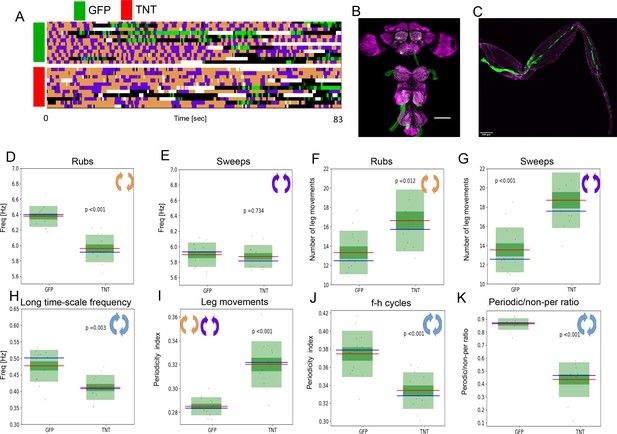
Periodicity of both time scales is preserved under reduced sensory feedback.

(A) Ethograms of grooming behavior flies with inhibited proprioception (TNT, red bar) versus the ethograms of the control group (GFP, green bar). (B) Expression pattern of the leg mechanosensory neurons driver line used in TNT inhibition experiments. Expression pattern of 540-GAL4, DacRE-flp > 10X-stop-mCD8-GFP in central nervous system. Magenta: anti-Bruchpilot. Green: anti-GFP. Scale bars, 100 μm. (C) Expression pattern of 540-GAL4, DacRE-flp > 10X-stop-mCD8-GFP in leg sensory neurons. Magenta: cuticle autofluorescence. Green: innate GFP fluorescence. Scale bars, 200 μm. (D , E) Box plots of leg-rub and head-cleaning frequencies, respectively. (F , G) Similar as in (D , E) but for the count of rubs and sweeps per ff-cycle. (H) Frequencies of the long time scale (computed from ff-cycles and hh-cycles as in Figure 2G and H) for both groups. (I) Box plots of Periodicity Indexes for the short time scale of the control (GFP) and the experimental (TNT) flies. (J) Similar as in (I) but for the long time scale. (K) Ratios of periodic versus non-periodic long time scale oscillations in control and experimental groups. See also Figure 5—figure supplement 1 for removal of sensory cues by amputation.

Nested CPGs can be decoupled in spontaneously grooming flies

Flies groom robustly in response to dust or optogenetically controlled mechanosensory stimulation, but they also groom spontaneously. The leg movements they perform are recognizable sweeps and rubs, and they occasionally produce alternating bouts of head cleaning and front leg rubbing as well (Figure 6A and B). These flies have no experimentally applied sensory stimuli—only what they generate themselves by contact between their legs and bodies, and the associated proprioceptive feedback—so these motor patterns are most likely to be generated by internal circuits. We analyzed the temperature response of both time scales of grooming movements in these spontaneously grooming flies.

Figure 6 with 2 supplements see all
Download asset Open asset
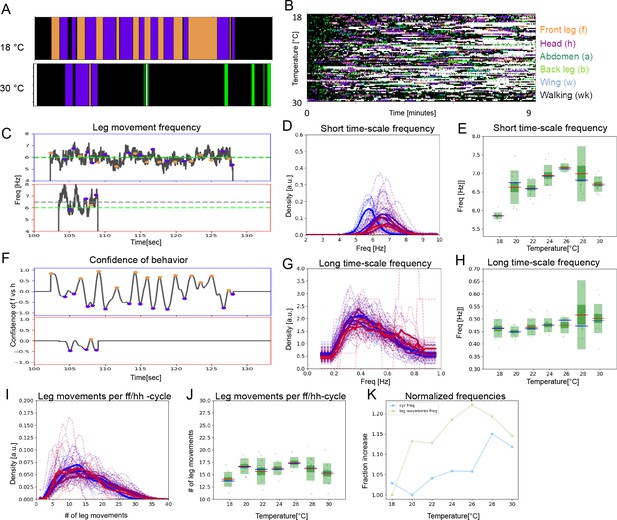
Two time scales of patterned movements can be decoupled in spontaneous grooming.

Spontaneous grooming was recorded in undusted flies at a range of temperatures between 18°C and 30 °C. Examples are shown in (A) and the whole data set of 80 flies recorded for 13 min is shown in (B). (C) Examples of spontaneous leg movement frequencies at 18°C (top) and 30°C (bottom), (D) histograms of mean frequencies at cool (blue) and warm (red) temperatures, and (E) box plots of the increase in leg movement frequency with temperature; plots and statistics as described in Figures 2, 3C and D, and (E); compare to short time scale effects where grooming is induced by dust. (F–H) Long time scale (ff-cycle + hh-cycle) analysis comparable to Figure 2, Figure 3F, G, and H. (I) Histograms and box plots (J) of median movement counts per ff-cycle and hh-cycle across the seven temperatures, quantified as in Figure 3A and B. (K) The rate of temperature-driven increase in frequency is shown by normalization as in Figure 3C. See also Figure 6—figure supplements 1 and 2, and 3 for evidence of periodicity and response to temperature.

Although these flies groom less than dusted or optogenetically activated flies, they show characteristic sweep and rub frequencies that increase with temperature, albeit with higher variance, ranging from 5.85 Hz to 7.15 Hz. (Figure 6C–E). The ff/hh-cycles are rarer, and when they occur, the temperature-dependent contraction of the long time scale is less pronounced than in the stimulated flies (R2=0.86; p=0.012) (Figure 6F–H). Perhaps most strikingly, although the number of leg movements per ff/hh-cycle is similar to stimulated flies (~17; with higher variation across the temperature range, Figure 6I and J), the correlated temperature-dependent contraction of the short and long time scales observed in the dusted and optogenetically activated flies is not seen in the spontaneously grooming ones (R2=0.43; p=0.332) (compare Figure 6K to Figures 3K and 4K). The frequency of leg rubs and sweeps increases with temperature at a greater rate than the frequency of ff/hh-cycles (Figure 6K), suggesting that the pattern-generating circuits that control the two time scales of movements may be dissociated in spontaneous grooming.

Perhaps, in spontaneously grooming flies, the two levels of nested CPG are linked only sporadically, when the flies engage in more periodic behaviors. To explore this possibility, we separated the periodic long time scale oscillations from the non-periodic ones using a threshold of ACF shoulder peak prominence (see Materials and methods and Figure 1—figure supplement 2). We hypothesized that if the periodic behaviors are CPG-driven and the non-periodic behaviors are not, then the periodic behaviors should scale with temperature more strongly than non-periodic ones. However, we found that neither periodic nor non-periodic behaviors changed frequency with temperature (Figure 6—figure supplement 1C and D) and there was no significant correlation between the two time scales (Figure 6—figure supplement 1E and F), or between the two levels of the nested CPG, in spontaneously grooming flies.

Discussion

Temperature manipulations have been instrumental in identifying behaviors controlled by CPGs and for locating where those circuits reside. Robust rhythms are retained across a range of temperatures in the crustacean stomatogastric ganglia, where the relative timing of events is preserved even as the sequence itself changes speeds (Alonso and Marder, 2020; Rinberg et al., 2013; Tang et al., 2012). Local cooling of the cat spinal cord demonstrated which segments contain locomotion control circuits (Deliagina et al., 1983), and local warming showed that cricket chirping is governed by thoracic rather than brain ganglia (Pires and Hoy, 1992a; Pires and Hoy, 1992b). The role of CPGs in bird song, and the importance of the HVC brain region for sequence timing, was shown because local cooling expands the entire song without changing the relative durations of the syllables and sub-syllabic components (Armstrong and Abarbanel, 2016; Long and Fee, 2008). In frogs (Xenopus laevis), both local cooling and ambient temperature affect the frequencies of vocalization patterns (Yamaguchi et al., 2008). Here, we follow this tradition to examine fly grooming behavior at different temperatures, demonstrating that both its short and long time scale components show evidence of CPG control. Although here we change the temperature of the whole fly, our study opens the way to use anatomical and genetic tools to map underlying neural circuits in future experiments.

Fly grooming is an innate motor sequence with both repetition and flexibility. Behavior analysis has shown organization over several time scales, from single stereotyped leg movements and alternations between bouts of repeated actions targeting specific body parts (Mueller et al., 2019), to a gradual and probabilistic progression from anterior toward posterior grooming (Seeds et al., 2014). Here, we investigate what aspects of fly grooming are periodic, demonstrating that the short time scale leg sweeps and rubs repeat at characteristic frequencies, in the absence of patterned sensory input, and in a temperature-dependent manner (Figure 2D–E), consistent with control by CPGs. Since the neural circuits that constitute the CPGs controlling these periodic leg movements are likely to overlap with those proposed to coordinate walking (Bidaye et al., 2018), this was not unexpected.

But our more surprising discovery was that the alternation between bouts of head cleaning and front leg rubbing is also periodic (Figure 1—figure supplement 4A). While this oscillation is more variable, it too, is independent of patterned sensory input, and increases in frequency with temperature (Figures 2G–H–4G–H)—suggesting that there may be an additional CPG operating at this longer time scale. This high-level, overarching, CPG can control the alternations between leg rubs and sweeps that are themselves governed by faster, low-level CPGs. The idea that multiple CPGs coordinate movements is not new: CPGs may control each leg joint, regulating the interaction between flexor and extensor muscles, governing the way coxa-trochanter and femur-tibia joints are coordinated to produce forward or backward walking, or mediating interactions among limbs (Feng et al., 2020; Mantziaris et al., 2020). In the vertebrate spinal cord, inhibitory and excitatory commissural neurons can cause the CPGs controlling the legs to synchronize for a hopping gait or operate out-of-phase for walking (Kiehn, 2016). CPGs in frogs have been shown to act on different time scales (sequentially) to govern their vocal behaviors (Zornik et al., 2010), and leeches can alternate between different CPG-driven behaviors (Esch et al., 2002). The concept of nested CPGs has recently been extended to explain the flexible coordination of behaviors ranging from fish swimming to bird song (Berkowitz, 2019). We map fly grooming behavior into this nested CPG framework as shown in Figure 7.

Figure 7
Download asset Open asset
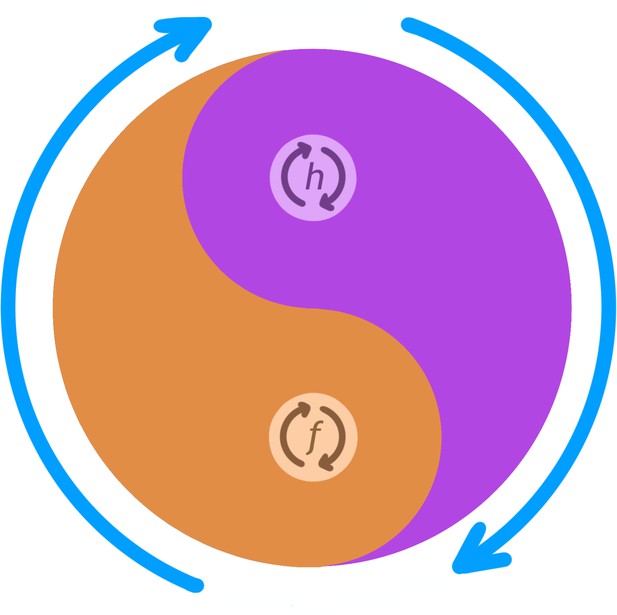
Conceptual schematic of nested CPG controlling anterior grooming behavior.

This diagram illustrates how the lower level CPG modes controlling individual leg rubbing (f) and head cleaning (h) oscillations (small orange and purple arrows) can be coordinated by an over-arching, high-level, CPG controlling the alternation between the front leg rubbing and head cleaning bouts (large blue arrows). The probability of f versus h is indicated by the thickness of their corresponding colors (orange vs. purple) at each angle of the circle. For example, at 5 o'clock the probability of f is higher than that of h and at 11 o'clock probability of h is higher than that of f, and so on. CPG, central pattern generator.

In a recent publication, nested CPGs similar to the one we are proposing here have been described in the crab stomatogastric ganglion, where fast pyloric and slow gastric mill rhythms are coupled and compensate for temperature changes (Powell et al., 2020). The combination of two rhythmic behaviors raises the possibility that the governing circuits interact, like meshed gears of different sizes, to simplify control of a repetitive behavior on multiple time scales. Just as the relative number of rotations between different gears is the same regardless of the absolute speed of the mechanism, so the phase of different components of CPGs is conserved across a range of temperatures (Harris-Warrick and Ramirez, 2017). In the case of fly grooming, this relationship between fast and slow components of the system may be reflected in the constant number of leg movements within each grooming bout across a range of temperatures (Figure 3). The fast and slow components of the nested CPG can be coupled (in stimulated flies) or decoupled (in spontaneously grooming flies). It is also possible that coupling can occur dynamically over the period of behavior execution, resulting in alternation between periodic and non-periodic behaviors on the long time scale (Figure 6—figure supplement 2B). However, in spontaneously grooming flies, we saw no coupling between the two time scales in either periodic or non-periodic behavioral episodes (Figure 6—figure supplement 1). The neural circuit implementation of nested CPGs, and the potential ‘clutch’ mechanisms that engage and disengage their connections, remain to be determined.

Dust-induced grooming can be routine, rhythmic, repetitive, and governed by CPGs, but spontaneous grooming may have more varied control architecture. Fast walking insects may be more likely to engage CPGs, while slower ones may rely more on sensory feedback and reflex chains (Mantziaris et al., 2020). Just as you can walk a straight path without thinking about it or you can carefully place each foot on icy terrain, flies may have alternative ways to produce movement sequences. Disturbing a single bristle elicits a single directed leg sweep (Kays et al., 2014; Vandervorst and Ghysen, 1980), while covering the fly in dust evokes an entire grooming program with bouts of several leg sweeps and rubs, alternation between the bouts, and slow gradual anterior-to-posterior progression (Phillis et al., 1993; Seeds et al., 2014). Our observation that spontaneous grooming shows less periodicity at the long time scale (Figure 6—figure supplement 2B) can be interpreted as effective decoupling of the two levels of the nested CPG in those flies when they engage in more sporadic and shorter episodes of grooming.

In both optogenetically stimulated flies and in flies where sensory feedback was inhibited, we observe less periodicity of the long time scale than in the dust-stimulated flies (Figure 1—figure supplement 2H and Figure 5K). We speculate that sensory feedback is needed to stabilize and modulate the rhythmic behavior, even though it is not necessary to produce it. For example, a fly could produce in-phase rhythms to provide the general control of head-cleaning movements but the sensory feedback from various parts of the head could adjust these movements to optimize the efficiency of cleaning of those parts. The concept of sensory feedback playing a role in stabilizing and adjusting rhythmic behaviors has been explored in walking mice (Mayer and Akay, 2018, Santuz et al., 2019) and flies (Mendes et al., 2013), as well as in robotics (Wang et al., 2014, Sartoretti et al., 2018) and computational modeling of CPGs (Yu and Thomas, 2021).

Nested CPGs can be implemented to generate arbitrarily complex behaviors that are also periodic and well-coordinated. Many different time scales of simple periodic movements can be combined into a more complex periodic behaviors the way different frequencies of sine waves can be combined to create arbitrarily complex shapes in Inverse Fourier Transformation. If CPGs can operate across various time scales in this fashion, then all that is needed to create arbitrarily complex yet highly reproducible behavior is to adjust the weight of each contributor to a multi-level nested CPG.

The specific neural circuits that constitute CPGs have been challenging to identify in most preparations and even the best characterized would benefit from more comparators. The electrophysiological recordings that have been so critical in CPG analysis in other preparations are possible but challenging in Drosophila, but the real strength of the system is the ability to demonstrate that specific neurons have a causal connection to rhythm generation. New anatomical resources to map neural circuits, especially the complete electron microscopy data set covering the ventral nerve cord (Phelps et al., 2021), will enable the identification of the pre-motor neurons most likely to participate in CPGs and the commissural connections that may mediate among them. Functional imaging of neural activity in dissected, fictive preparations (Pulver et al., 2015) and even in behaving flies (Chen et al., 2018) is another promising approach to identify neurons with rhythmic activity that may constitute parts of the CPGs. The genetically encoded calcium indicators and new voltage sensors have fast enough onset and offset kinetics to capture rhythmicity on the expected time scales (Simpson and Looger, 2018). For example, whole nervous system monitoring of neural activity was recently described in C. elegans to identify hierarchical and dynamic control of nested locomotion patterns (Kaplan et al., 2020).

Rhythmic activity and circuit connectivity may suggest candidate neurons, while genetic tools to target specific neurons (Jenett et al., 2012) and optogenetic methods to impose altered activity patterns (Klapoetke et al., 2014) present a way to causally connect them to control of rhythmic behaviors. The behavioral evidence presented here suggests that a two-level nested CPG can control aspects of fly grooming over at least two time scales. Identifying what circuits constitute these CPGs and mapping the neurons that coordinate their interactions is feasible, now that we know we ought to be looking for them.

Materials and methods

Fly stocks and husbandry

Request a detailed protocol

Drosophila melanogaster was reared on common cornmeal food in a 25°C incubator on a 12-hr light/dark cycle. Three to five days, CantonS males were used for dusting and spontaneous grooming experiments. For optogenetic experiments, larvae were raised on normal food. After eclosion, 1-day-old adults were transferred into food containing 0.4 mM all-trans-retinal and reared in the dark for another 2 days.

R74C07-GAL4 (Bloomington Stock Center 39847), 20XUAS-IVS-CsChrimson.mVenus (Bloomington Stock Center 55134), 5–40 GAL4 (Hughes and Thomas, 2007), DacRE-FLP (Mendes et al., 2013), UAS>stop>TNT (Stockinger et al., 2005), and 10XUAS>stop>myr-GFP (Bloomington Stock Center 55811) were used in the paper. Ten-day-old males were used in TNT inhibition experiments. Three- to five-day-old males were used in other experiments.

Behavior experiments with temperature control

Request a detailed protocol

Behavior videos were recorded inside New Brunswick I2400 incubator shaker or DigiTherm DT2-MP-47L heating/cooling incubator. Experiments were performed every 2°C between 18°C and 30°C. Temperature was monitored by a Govee H5072 Bluetooth thermometer. For dusting experiments, the room temperature was also adjusted to the target temperature to make sure flies stay at the same temperature during fly dusting. Each fly was tested once in one condition. Three types of chambers were used in fly dusting assay: dusting chamber (24-well corning tissue culture plate #3524), transfer chamber, and recording chamber. Flies were anesthetized on ice and transferred to the middle four wells of the transfer chamber. Transfer chamber with flies was then kept in the incubator set to the target temperature for 15 min. For fly dusting, around 5 mg Reactive Yellow 86 dust was added into each of the four middle wells of the dusting chamber. Transfer chamber was aligned with the dusting chamber. Flies were tapped into the dusting chamber and shaken 10 times. After dusting, flies and dust were transferred back into the transfer chamber. Transfer chamber was banged against an empty pipette tip box to remove extra dust. Dusted flies were then immediately tapped into the recording chamber for video recording. The whole dusting process was performed in a Misonix WS-6 downflow hood.

For optogenetics and spontaneous grooming experiments, ice-anesthetized flies were put into the recording chamber directly. Recording chamber with flies was then kept in the incubator set to the target temperature for 15 min before the experiment. In spontaneous grooming experiments, flies were shaken five times after the 15 min incubation. They were then rested in the incubator for another 3 min before recording.

60 Hz videos were recorded for 9 min in optogenetics experiments, 13 min in dusting, and spontaneous grooming experiments with a FLIR Blackfly S USB3 camera. Each video is recorded from the top and it captures flies in four chambers. Infrared backlight was used for all experiments. Custom-made LED panels (LXM2-PD01-0050, 625 nm) were used for optogenetic activation from below. 20 Hz 20% light duty cycle was used in optogenetics experiments. Red light intensity was adjusted to 0.85 mW/cm2. Before the video analysis, the frames were split into four quadrants corresponding to the four chambers.

For all experiments described above, 8–12 flies were used per temperature or per experimental group (for the TNT inhibition experiment). Occasionally a recording chamber was empty or the fly was visibly damaged or dead. Those chambers were excluded from further analysis. These numbers were sufficient to extract the quantities we use in this work such as ff/hh-cycle periods.

High-resolution videos recording

Request a detailed protocol

For high-resolution videos used for leg tracking, flies were put in a 10-mm diameter quartz chamber, and 100 Hz videos were recorded from below. An FLDR-i132LA3 red ring light (626 nm) was used for optogenetics activation. For leg amputation experiments, one front leg was amputated at the middle of the femur. Flies were recovered for 3 days before the experiments. The dusting procedure is the same as what is described above.

Leg movements counting from video

Request a detailed protocol

We did not track individual legs or joints so the frequencies of leg movements during grooming were estimated from frame-to-frame changes in pixel values. When flies are walking or engaged in other non-grooming behaviors, such measurements would not be very useful. However, during grooming, flies are standing in one place and the most intense pixel value differences roughly correspond to those created by leg movements (rather than whole body translations).

Regions of interest were cropped around the animals to produce 80×80 arrays of pixels (F). The F arrays were reshaped into 1600 columns and 32 rows, corresponding to 32 consecutive frames (~0.5 s window at 60 Hz), and were stacked together to obtain 32×1600 array of pixel values (W).

The derivatives of W across time were computed using Numpy.gradient() function to obtain matrix of frame-to-frame differences D. The matrix D was smoothed using Gaussian filter (scipy.ndimage.filters.gaussian_filter). Sigma=[2, 5]. This was done to denoise the signal—to remove non-biological high-frequency changes (temporal smoothing) and to reduce spatial resolution (so that more neighboring pixels capture the same signal). All the values of D where cumulative change of pixel values was less than threshold (θ=5.0) were converted to zeros to retain only those pixels where significant movement occurred. An example of D matrix is shown in Figure 1—figure supplement 1.

Notice in the figure the several non-zero columns (corresponding to pixels) that appear sinusoidal. These columns contain the signals that have been smoothed to remove the high-frequency noise and are prominent enough to ‘survive’ the thresholding. Therefore, we assume that the movements represented in these columns correspond to relatively large, periodic actions that occur while the animal is standing (otherwise the sinusoidal signals would not stay in one column over the time window). Also, only the frames where grooming behavior was detected by the ABRS were considered for leg movement counting. This assumption leads us to conclude that the periodic signals are caused by periodic leg movements during grooming. So the counting the peaks across the columns of matrix D would then result in the number of times a leg crossed a particular pixel. The peaks were found applying the scipy.signal.find_peaks() function across the rows on the matrix D. The peaks were then counted for each column in D and the median of all the counts was finally taken to be the number of leg sweeps or rubs that occurred in that time window (0.5 s). Note that at the frame rate of 60 Hz, we should be able to detect frequencies of periodic signals below 30 Hz and the highest frequency of leg movements we observed was below 7 Hz.

The number of leg movements per second was used as the leg movement frequency.

Automatic behavior recognition from videos

Request a detailed protocol

Probabilities and ethograms of grooming behaviors were extracted from raw videos using ABRS. For detailed description see Ravbar et al., 2019 and for the most updated version see ABRS (https://github.com/AutomaticBehaviorRecognitionSystem/ABRS; Ravbar, 2021; copy archived at swh:1:rev:7c558561ae82b62bfcc5337a334b07efcbb18da2).

Briefly, ABRS pre-processes video data by compressing it into spatio-temporal features in the form of three-channel space-time images (3CST images, shape=80×80×3) where the first channel [0] contains raw video frame pixel values [80×80], the second channel [1] contains spectral features of pixel value dynamics over a time window of 16 frames, and the third channel [2] contains frame-to-frame difference (frame subtraction). The 3CST images are classified into seven behavioral categories (front leg rubbing, head cleaning, back leg rubbing, abdominal cleaning, wing cleaning, and whole-body movements [walking]) by ConvNet (Covolutional Neural Network – CNN) implemented in Tensor Flow (in Python) (https://www.tensorflow.org), using a model trained with diverse set of videos of fly grooming behaviors. In the final output layer of the CNN are the probabilities of the grooming behaviors. In this work, we focus entirely on the probabilities of front leg rubbing and head cleaning behaviors: P(f) and P(h).

Behavioral confidence

Request a detailed protocol

The long time scale oscillations are quantified as probabilities of behaviors obtained from the ABRS CNN described above. Behavioral confidence (BC) is computed as:

(1) BC=P(f)−P(h)

The BC signal is smoothed two consecutive times with time window of 31 frames (0.5 s) using the scipy.signal.savgol_filter function to remove high-frequency noise.

Autocorrelation and periodicity analysis

Request a detailed protocol

ACFs were computed from a 0.5-s time window for individual leg movements (leg rubs and sweeps). The signal for autocorrelation was extracted from raw movies as follows: (1) Matrix D was obtained as described above (Leg movements counting from video); (2) ACFs were computed for every column of D (an example of the ACFs and the matrix D are shown in Figure 1—figure supplement 1); and (3) All the ACFs were averaged to obtain the mean ACF for that time window. The mean ACFs were stacked to obtain the ACF array with dimensions 60×F, where F is the number of frames in the movie. The AFCs were computed using scipy.signal.correlate function from SciPy library.

ACFs for the long time scale (the oscillations between bouts of leg rubbing and head cleaning) were computed from the BC time-traces described in Equation 1, in the time window of 999 frames (16.6 s), also using the scipy.signal.correlate function.

To quantify the periodicity of each time scale, we computed the PI from the ACFs, defined as the ratio between the height of the prominent peak nearest to zero lags and the height of the central peak (at zero lags) of an ACF (Figure 1—figure supplement 2). The peaks were detected by scipy.signal.find_peaks function. The threshold for ‘prominence’ was set at 0.2. The threshold for height was set to 0.2. We used the same method and parameter settings for both time scales to compute the PI.

We managed to separate periodic behaviors from the non-periodic by using the scipy.signal.find_peaks function. If the first neighbor of the central peak of the ACF fell below the 0.2 ‘prominence’ threshold we classified the pertaining behavior as non-periodic and as periodic otherwise. This is shown in Figure 1—figure supplement 2B.

Frequency computations for the long time scales

Request a detailed protocol

BC traces were used to compute the frequencies of the long time scale.

  • f=1/L Eq. 2.

In Eq. 2, the L is a vector containing the lengths of periods measured from the BC traces. The peaks and valleys were detected by scipy.signal.find_peaks function, where the ‘prominence’ was set at 0.1 and the minimum height was set at 0.05 (valleys were found from the same signal as the peaks but multiplied by [–1] to invert it). The periods were measured either between two peaks of the BC traces (ff-cycles) or between two valleys (hh-cycles), or we combined the periods from both, the ff-cycle and hh-cycle (also see Figure 1E for illustration). To avoid capturing very long transitions between the peaks/valleys (which occur between episodes of grooming behavior and walking or standing), we set the maximum duration of ff/hh-cycles to be 280 frames (~4.7 s). In the sensory inhibition experiment where we compare the TNT mutants to the control we increased the duration threshold to 380 frames (~6.3 s) because the ff/hh-cycles are extraordinarily long (see Figure 5A).

This produced a vector of frequencies of dimensions 1×F, where F is the number of frames in a movie, corresponding to one fly. The mean and median frequencies for each fly were computed as means/medians of vector f.

High-resolution behavior analysis

Request a detailed protocol

To confirm our observations of grooming behavior, its periodicity and the effect of temperature, we used an independent method for limb tracking, the DLC (Mathis et al., 2018) on a small sample of high-resolution videos described in the previous section. The DLC allowed us to label (virtually) three body parts on each front leg and a reference point (see Figure 5—figure supplement 1 A showing the labels on the intact front leg). We could then track these labels across time. For each leg, we computed the angle between Tibia and Femur and tracked the derivatives of these angles across time—examples are shown in Figure 1—figure supplement 4A. On these time-traces, we applied the autocorrelation analysis and FFT to compute ACFs and their spectra. (For the amputated fly, we used the relative positions of the joints and the stump instead of the angles.) We computed the PI from the ACFs.

In these analyses, we did not have access to the BC (see the section above) so, in order to examine the periodicity and frequencies of the long time scale, we computed the equivalent to BC as follows: the distance between tarsal segments was used as the ‘confidence of head cleaning’ and the angle between Tibia and Femur was used as the ‘confidence of front leg rubbing.’ We obtained the behavior confidence signal by subtracting the latter from the former. We applied autocorrelation and FFT analysis this ‘behavior confidence’ to estimate the PI and the frequency of the long time scale. Due to cumbersome nature of these analysis and the lack of behavioral recognition, we performed them only on three different movies from the dust-stimulated flies (Figure 1—figure supplement 4D-F).

Handling of outliers and missing data points

Request a detailed protocol

We found and did not eliminate an outlier in optogenetically stimulated flies (leg movement frequencies at 20°C). In cases where there were missing data points (no fly was in the recording chamber), those were not counted in the statistics.

Data availability

All data is included in the manuscript or uploaded to Dryad. All computer code is available on GitHub.

The following data sets were generated
    1. Ravbar P
    2. Zhang N
    3. Simpson J
    (2021) Dryad Digital Repository
    Behavioral probabilities and sample videos for "Behavioral evidence for nested central pattern generator control of Drosophila grooming".
    https://doi.org/10.5061/dryad/D9QW4J

References

  37. Conference
    1. Sartoretti G
    2. Shaw S
    3. Lam K
    4. Fan N
    5. Travers M
    6. Choset H
    (2018) IEEE International Conference on Robotics and Automation
    Central Pattern Generator With Inertial Feedback for Stable Locomotion and Climbing in Unstructured Terrain. pp. 5769–5775.
    https://doi.org/10.1109/ICRA.2018.8461013
    1. Selverston AI
    (2010) Invertebrate central pattern generator circuits
    Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 365:2329–2345.
    https://doi.org/10.1098/rstb.2009.0270

Decision letter

  1. K VijayRaghavan
    Senior and Reviewing Editor; National Centre for Biological Sciences, Tata Institute of Fundamental Research, India

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "Behavioral evidence for nested central pattern generator control of Drosophila grooming" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and a Senior Editor. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, the consensus view is that additional experiments would be required to address major concerns. As these experiments would likely require more than a two month timeframe, we are turning the submission dowm in its current form. If it is possible to address the major concerns outlined below, we would consider a fresh submission, if you would like to consider eLife.

The reviewers agreed that the notion of nested CPGs for coordination of grooming is important but that stronger demonstration is required that the rhythms are indeed generated by a CPG in the absence of sensory feedback. In addition, better evidence that the two rhythms are coupled would significantly strengthen the study. Key experimental suggestions are below. Full comments of the reviewers are attached to provide further guidance.

1) Better quantification of rhythms:

a) High res leg tracking will help quantify both rhythms with more accuracy. It could also be used to better describe the coupling between the two rhythms (Figure 3 and 4, what are the "leg movements" that are invariant across temp).

b) Poor confidence levels of the slow rhythm in Figure 4 and 5 need to be addressed with supporting videos, complementary analysis or new data from high res tracking.

2) Role of proprioceptive feedback in rhythm generation:

Proprioceptive feedback from the legs could be the major rhythmic input that drives both rhythms and its role should be explored by neuronal silencing (e.g. Mendes et al., 2013 eLife).

Reviewer #1:

Ravbar et al. have carried out behavioral analysis of Drosophila grooming behavior and have proposed that nested CPG modules are involved in generating the sub-routines during anterior grooming. It is a conceptually exciting hypothesis and is supported by authors' observation of two nested behavioral rhythms, a fast leg movement rhythm (5-7Hz) and a slower behavioral state switch rhythm (0.3-0.6Hz). The authors then use temperature change as a tool to prove existence and coupling of the underlying nested CPG modules that govern these rhythms.

This work is conceptually interesting with a potential for broad interest, and I'm in favor of its publication provided the authors address the major points.

1) The authors use temperature change as a tool to prove the existence and coupling of nested CPGs. Although there is a certain simplicity and elegance in this approach, it needs some more justification. Temperature directly influences neural activity (not restricted to CPGs). The authors cite important studies where temperature was used to pinpoint CPGs, but in these studies local heating/cooling of specific parts of the nervous system was used as a tool to increase/decrease neural activity in those areas and thereby locate the position of CPGs (e.g. Long and Fee 2008)). Global heating/cooling (as conducted in the current study) was only used in StG papers (Marder lab) to characterize the effect of temperature on previously well-described CPG networks. Given the pivotal role of these temperature change experiments in supporting central results of this paper, it needs more justification, both at a descriptive level as well as more characterization. E.g. it would be interesting to see how other attributes already tracked in these experiments (walking, hind grooming etc) are affected by temperature. Is there any behavior that is not proportionally affected by temperature and what does it tell us that is special about the anterior grooming rhythms? Also, given global heating will affect all neurons similarly, proportional changes in the two rhythms need not indicate "coupled" rhythms. This caveat should be discussed while discussing results from Figure 3.

2) A more direct evidence for CPGs would be to show that rhythmic motor output could be achieved without rhythmic sensory input and the authors also claim to have addressed this using optogenetics (Figure 4). The authors suggest that the changing quantity of dust on the fly's body as it grooms, could be a rhythmic input. This could be better explained. I'm guessing what matters is the difference in sensory input coming from head (H) versus front legs (F). If H>F then the fly does behavior "h", else it does "f". Doing behavior "h" reduces sensory input "H". With this assumption, the H-F input could indeed be rhythmic, and then the opto experiment rationale seems justified. However, for the fast rhythm (leg sweeps), the major rhythmic input is likely the proprioceptive input from the moving legs and not the continuously decreasing quantity of dust on the fly's body and hence this rhythm is not really addressed by the opto experiment. In fact the proprioceptive input from the legs could also be the defining input for the slower rhythm given that "number of leg movements" remain constant across temperatures (Figure 3 and 4K). One way to investigate pure centrally driven rhythms could be to eliminate rhythmic sensory feedback by leg amputation (e,g Berendes et al., J.Exp.Biol, 2016) or neuronal silencing (Mendes et al., eLife, 2013) and then apply dust/opto-stim and see if both fast and slow rhythms still persist.

3) Finally, the authors describe an interesting "decoupling" of the two rhythms during spontaneous grooming. The authors observe similar leg movement frequencies, however the longer f-f and h-h rhythms seem very rare and variable. So the "decoupling" between the two rhythms is in fact driven by "absence" of the slower rhythm in the experimental conditions. This is also interesting but should be discussed appropriately. Looking at the full ethogram in Figure 5B, it is apparent that as temperature increases, flies spend more time walking versus grooming and so the grooming bouts are likely too short to show any slow rhythms. So in theory, the rhythms could be still coupled, just now more disrupted because of a competing "walking" state.

4) The leg movement analysis needs to be justified more than what it is in the Methods section. The authors acquire videos of grooming flies at 60 Hz, then select frames containing anterior grooming bouts and in these selected frames, they then use pixel difference in consecutive frames and use the frames depicting the largest movement for quantifying frequency. It is unclear what aspect of leg movement the authors are quantifying in this analysis and whether it is affected by video frame-rate or camera angle. What motor action is represented by the "leg movement" frequency? Why is this frequency value higher for "f" bouts versus "h" bouts? Would the authors get the same results if videos were captured at a higher frame rate? It is important to disambiguate this, because the authors use "number of leg movements" as an attribute in Figure 3 to prove coupling between the CPGs. The authors could acquire some additional videos, preferably at a high frame rate, and use one of the recent tools (Pereira et al., 2019, Mathis et al., 2018) to track the legs during anterior grooming, as has been done for leg movement rhythm quantification during walking. If this type of high resolution analysis also suggests a similar leg sweep frequency, the current analysis framework of the authors will be justified. Moreover, it could provide a better understanding of results in Figure 3 and 4K.

5) For the slow f-f and h-h rhythm quantification the authors use an interesting approach (P(f)-P(h)). Although this looks promising in Figures 1D, 2F and supp Figure 2, many of the peak/trough values tend to be very close to zero in Figures 4F, 5F making it unclear what rhythms does this really represent in terms of actual behavior. Are we still talking about clear rhythms between 2 states as depicted in Figure 1A? Performing oscillation analysis using confidence values between artificially defined binary states can enforce the output to look like an oscillation and hence it is important to explicitly discuss this.

Reviewer #2:

This manuscript uses temperature and optogenetic manipulations to alter the speed of grooming behaviors and examines the resulting changes in fast- and slow-time scale behavioral structure. The authors find that temperature increases the frequency both of individual leg movements, and the alteration between bouts leg rubbing and head grooming, such that the number of leg cycles per bout is approximately the same across a range of temperatures. A similar results is found when grooming is elicited by optogenetic stimulation of mechanosensory bristles, rather than by dust. Finally, the authors show that coordination between these two levels of behavioral organization breaks down during spontaneous grooming. The authors draw conclusions about the control of these behaviors by nested central patterns generators. The behavioral observations presented here are interesting but I felt that more analysis of genetic or circuit manipulations would be required to firmly draw the conclusions the authors would like to about the neural control of these behaviors.

A central claim of the manuscript is that Drosophila grooming may be controlled by nested CPGs. As currently presented the evidence is not especially strong, as it is not clear what the alternative to central pattern generator control of these behaviors would be. The manuscript would be stronger if the authors identified neurons whose activation or inactivation altered behavioral rhythms or the coupling between fast and slow-time scale structure in the behavior.

In the case of high temperature + constant sensory stimulation the behaviors seem much more variable and irregular but this is not noted or discussed.

Line 35-36: "Automating the sequence by calling it actions in series produces reliable control" This seems like a bit of straw man. Most rhythmic behaviors such as walking, breathing, etc, are assumed or known to arise from central pattern generators, and not from individual cycle-by-cycle decision, although of course each behavior can be modulated on a cycle-by-cycle basis.

Line 73: "characteristic frequency of 6Hz." It seems in 1C that the characteristic frequency of head grooming and leg rubbing are slightly different. Can those averages be shown or given here and are they significantly different?

Line 125 + figure 2C/4C. The authors note that the behavior becomes more ragged at high temperatures and stronger deviations from the characteristic frequency are seen at 30{degree sign}, especially in figure 4C. The authors should discuss how these deviations impact their analysis of characteristic frequency.

Line 124 and 132: "suggests that CPGs may be involved…both time-scales are controlled by two nested levels of CPGs" these both seem like interpretations of the data and not things that are directly demonstrated by the data shown.

Figure 4A: It seems in this example that the relative durations of head grooming and leg rubbing, as well as the regularity of the behavior are altered at 30{degree sign}. The authors should address this. Behavioral confidence is also much lower under these conditions- is this an issue?

Line 248: "Our more surprising discovery was that the alternation between bouts of head cleaning and front leg rubbing is also periodic." I am not sure quite how surprising this is. I think it would equally surprising if there were no correlations in these measurements. I think it would help to have some measure of regularity/irregularity in these alterations.

Reviewer #3:

This study presents an intriguing example of rhythmic behavioral oscillations at a fast time scale embedded within a slower rhythmic behavioral oscillation and the similar effects of temperature on the rates of the two rhythms. The data and the writing are both exceptionally clear.

1) It is not clear why the authors use an unpublished example of different rates of oscillation in the first paragraph of the Introduction instead of using a published example, of which there are probably many to choose from.

2) At first, I was somewhat concerned that the temperature manipulation could not be used to assess the contribution of CPGs to the behaviors because temperature changes in these experiments affect both the CNS and the legs, the latter of which contain sensory neurons activated by leg movements. But then I realized that the "movement-related sensory feedback" for the slow rhythm would not be leg sensory feedback, but instead (possibly) the amount of dust on the head. I now think that generating constant bristle stimulation optogenetically indeed should make the likely sensory feedback for the slow rhythm constant, so the effect of temperature on the slow rhythm in this experiment does suggest a CPG for the slow rhythm.

3) Nonetheless, I think the first paragraph of the Discussion obscures rather than clarifies distinctions between effects on the CNS and PNS. It cites a series of studies that used localized cooling to implicate a CPG within a particular part of the CNS, as if the current experimental design is comparable to this, though in the current experiments the entire animal was warmed or cooled. It might be helpful to explicitly acknowledge that in the current study temperature was simultaneously manipulated in both the central and the peripheral nervous system, so the change in rhythm rate does not in itself eliminate the possibility that movement-related sensory feedback contributes to the rate, at least for the fast rhythm.

4) The sentence (lines 202-203), "These flies have no sensory stimuli except what they generate themselves by contact between their legs and bodies…" also seems misleading because it leaves out 1) any dust, etc. that happens to collect on their heads that was not put there by the experimenters and 2) leg proprioceptive input (i.e., not from contact).

5) Also, on line 241, the authors assert that the fast rhythm occurs "in the absence of patterned sensory input." This is misleading, because leg proprioceptors presumably provide patterned sensory feedback that could be used on this time scale. These statements should probably be revised to clarify.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Behavioral evidence for nested central pattern generator control of Drosophila grooming" for consideration by eLife. Your article has been reviewed by 2 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and K VijayRaghavan as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission. This is a strong paper now and the revisions are for enhancing clarity and presentation.

Essential revisions:

1) The apparent finding that the leg mechanosensory genetic ablation slows the slow rhythm, but not the fast rhythms, is intriguing, if true because it would indicate that the two rhythms can be independently modulated, which would suggest that they are independent CPGs, even though the slow one may trigger the fast one. (The differential effects of temperature on aspects of spontaneous grooming also suggest this.) But this conclusion rests on Figure 5D-E and H. Figure 5E shows what looks like no change in sweep frequency, but 5D shows what looks like a slowing of rub frequency; whether this apparent slowing is statistically significant or not is unclear. Figure 5H, for the slow rhythm, is a different kind of plot, so we have an "apples-to-oranges" comparison-there is no frequency power spectrum plot for the slow rhythm and no box plot of frequency for rubbing. So we are not certain that the slow rhythm slowed without the rub frequency also slowing. It would help to add the missing plots, allowing "apples-to-apples" comparisons, as well as statistical comparisons between control and tetanus toxin for each measure. This would be important for readers to be persuaded that the slow and fast rhythms can be independently modulated.

2) In this revised submission the authors introduce a new metric, Periodicity Index (PI) to quantify the periodicity of a time series (ratio of highest peak and most prominent shoulder). Although this seems intuitively logical it would help if there was a reference or (mathematical) justification for its use as a measure of periodicity.

3) Authors define a threshold (most prominent shoulder peak in ACF >0.2) for calling a behavior as periodic. This seems reasonable. But looking at the selected ACF samples for fast rhythms in Figure 1F and G, it seems like most of the prominent shoulder peaks fall below the 0.2 threshold. Unless we are mistaken, the authors seem to have chosen a particularly bad example to depict fast rhythms in Figure 1 of the paper.

4) The usage of P(f)-P(h) as explained by the authors in the rebuttal is understood; but not what the fly would be actually doing when this value approaches 0 (as happens a lot in Figures 4F and 6F). It would really help if the authors included sample videos corresponding to Figures 1D, 4F, and 6F.

Reviewer #1:

This study demonstrates that fruit flies have regular rhythms of head and leg grooming movements when dust is applied to the head and that they also alternate head and leg grooming with a regular, slower rhythm. These rhythms all increase with temperature and continue when head bristle stimulation is constant and when sensory feedback from the moving legs is reduced or eliminated. All of this suggests that the fly's central nervous system contains circuits-central pattern generators-for both the fast leg movements during grooming of either the head or the other leg and for the slow alternation between these two kinds of grooming. This suggests that central pattern generators can be nested within another central pattern generator at a higher hierarchical level, which is important for understanding how central nervous systems control movements generally.

from 2020: It is not clear why the authors use an unpublished example of different rates of oscillation in the first paragraph of the Introduction instead of using a published example, of which there are probably many to choose from.

Authors' response: We looked for an appropriate published example but came up blank. Crustacean antenna have historical contributions to ethology including grooming behavior, e.g.Vedel, J. P., 1982 and Barbato, J. C, 1997, and seemed an aesthetic example to illustrate how simple oscillators with different frequencies (and amplitudes) can create beautiful complex behaviors. This is anecdotal but reflects one author's fieldwork living next to the ocean. We can delete this example or exchange for a substitute if an alternative is proposed. Barbato, J. C., and Daniel, P. C. (1997). Chemosensory activation of an antennular grooming behavior in the spiny lobster, Panulirus argus, is tuned narrowly to L-glutamate. The Biological Bulletin, 193(2), 107-115. VEDEL, J. P. (1982). Reflex reversal resulting from active movements in the antenna of the rock lobster. Journal of Experimental Biology, 101(1), 121- 133.

My response to the authors' response:

FYI, some other examples of pairs of slow and fast CPG-driven (or apparently CPG-driven) rhythms that are coordinated across time scales (though this does not mean that one CPG triggers the other) are in:

Brown (1911) Quart J Exp Physiol 4:151-182 (rabbit hopping and scratching)

Carter and Smith (1986) J Neurophysiol 56:171-183 and 56:184-195 (cat walking and paw-shaking)

Weimann et al. (1991) J Neurophysiol 65:111-122 (crab gastric mill and pyloric rhythms)

Bartos et al. (1999) J Neurosci 19:6650-6660 (crab gastric mill and pyloric rhythms)

Esch et al. (2002) J Neurosci 22:11045-54 (leech crawling and swimming)

Zornik et al. (2010) J Neurophysiol 103: 3501-3515 (frog advertisement call sequence of fast and slow trills)

https://doi.org/10.7554/eLife.71508.sa1

Author response

[Editors’ note: the authors resubmitted a revised version of the paper for consideration. What follows is the authors’ response to the first round of review.]

The reviewers agreed that the notion of nested CPGs for coordination of grooming is important but that stronger demonstration is required that the rhythms are indeed generated by a CPG in the absence of sensory feedback. In addition, better evidence that the two rhythms are coupled would significantly strengthen the study. Key experimental suggestions are below. Full comments of the reviewers are attached to provide further guidance.

1) Better quantification of rhythms:

a) High res leg tracking will help quantify both rhythms with more accuracy. It could also be used to better describe the coupling between the two rhythms (Figure 3 and 4, what are the "leg movements" that are invariant across temp).

b) Poor confidence levels of the slow rhythm in Figure 4 and 5 need to be addressed with supporting videos, complementary analysis or new data from high res tracking.

We now confirm the existence of rhythms in the fast leg sweep/rub movements and in the slower alternation between bouts of head cleaning and front leg rubbing by analyzing new videos of grooming flies with higher spatial and temporal resolution. This required establishing a new behavior recording rig with a way to film the flies from below and implementation of Deep Lab Cut (DLC) software to track multiple leg joints. The new dataset includes recordings at 18º, 24º, and 30ºC; the results are included in the revised manuscript new Figure 1—figure supplement 4. We detect leg rub and sweep rhythms with frequencies increasing from ~5 Hz to 7 Hz, in agreement with our initial results as calculated from leg movement counts using the method described in new Figure 1—figure supplement 1.

Analysis using ABRS has sufficient temporal resolution to identify bouts of head sweeps and leg rubs, the time scale required to characterize the slower rhythm. The big advantage of ABRS is its ability to analyze large amounts of behavioral data to detect rhythms, patterns and correlations in noisy or variable signals, which was critical to detect the longer time-scale rhythm in the first place. We now confirm the periodicity of this long timescale bout alternation with the new videos analyzed using DLC in Figure 1—figure supplement 4D-F.

We quantify the periodicity of both short and long time-scale repeats using a new metric, the Periodicity Index, based on the auto-correlation function (Figure 1—figure supplement 2). The fact that there is periodicity at all on the long time-scale suggests a layer of behavioral organization, and the potential for an over-arching CPG, that is surprising. We acknowledge the greater variability and more ragged appearance of the longer-time-scale rhythm in optogenetically stimulated flies and include possible explanations in the revised Results and Discussion sections pertaining to these flies.

2) Role of proprioceptive feedback in rhythm generation:

Proprioceptive feedback from the legs could be the major rhythmic input that drives both rhythms and its role should be explored by neuronal silencing (e.g. Mendes et al., 2013 eLife).

We address the potential role of proprioceptive feedback in rhythm generation by two additional experiments: single limb amputation and selective neuronal silencing. These approaches were inspired by Berendes et al. J Exp Bio 2016 and Mendes et al. eLife 2013, as suggested by Reviewer 1. Reducing or removing proprioceptive feedback by these experimental approaches slows the long time-scale alternation but does not eliminate the periodicity of either time-scale. These data are now included in the revised manuscript.

Grooming behavior is produced by a combination of internal pattern generating circuits initiated and modulated by responses to sensory cues. It is tricky to disentangle the relative contributions of these factors. The mechanosensory and proprioceptive cues that may contribute to grooming are also involved in other coordinated limb movements such as walking and postural control. Experiments presented in the original manuscript make the sensory experience more uniform using optogenetic activation. We now include new experiments that reduce sensory contributions by physical perturbations or genetic silencing. Together, these data allow us to estimate the contribution of this sensory information to rhythmic grooming behaviors (Figure 5, Figure 5—figure supplement 1).

Patterned proprioceptive input might be produced by and contribute to fast rhythmic leg movements. We reduced this feedback by amputating one front leg and tracking the stump using DLC. We find that movement of the truncated limb is still rhythmic on the short time-scale and very similar in frequency to that of intact legs, supporting the concept of CPG control (Figure 5—figure supplement 1). It was more difficult to assess the effect of amputation on the longer-time scale alternation because identification of head sweeps and leg rubs depends on detecting synchronization of the truncated limb with the intact one and their coordination is now less precise, as was previously reported for walking gaits (Berendes et al. 2016).

To block proprioceptive neuron activity, we used the same genetic combination as Mendes et al. 2013 (dacFlp, TubP>GAL80>; 5-40-GAL4, UAS-TNT) and a new split-GAL4 combination that targets leg proprioceptors (Figure 5B-C). These flies are somewhat uncoordinated but capable of producing rhythmic sweeps and rubs (Figure 5I). The long time-scale alternations are also rhythmic but slower than those of controls (Figure 5H), consistent with the slower rhythms observed in larval crawling in the absence of normal sensory feedback (Hughes and Thomas Mol Cell Neurosci 2007, Song et al. PNAS 2007, Pulver et al. J. Neurophys 2015).

Reviewer #1:

Ravbar et al. have carried out behavioral analysis of Drosophila grooming behavior and have proposed that nested CPG modules are involved in generating the sub-routines during anterior grooming. It is a conceptually exciting hypothesis and is supported by authors' observation of two nested behavioral rhythms, a fast leg movement rhythm (5-7Hz) and a slower behavioral state switch rhythm (0.3-0.6Hz). The authors then use temperature change as a tool to prove existence and coupling of the underlying nested CPG modules that govern these rhythms.

This work is conceptually interesting with a potential for broad interest, and I'm in favor of its publication provided the authors address the major points.

1) The authors use temperature change as a tool to prove the existence and coupling of nested CPGs. Although there is a certain simplicity and elegance in this approach, it needs some more justification. Temperature directly influences neural activity (not restricted to CPGs). The authors cite important studies where temperature was used to pinpoint CPGs, but in these studies local heating/cooling of specific parts of the nervous system was used as a tool to increase/decrease neural activity in those areas and thereby locate the position of CPGs (e.g. Long and Fee 2008)). Global heating/cooling (as conducted in the current study) was only used in StG papers (Marder lab) to characterize the effect of temperature on previously well-described CPG networks. Given the pivotal role of these temperature change experiments in supporting central results of this paper, it needs more justification, both at a descriptive level as well as more characterization. E.g. it would be interesting to see how other attributes already tracked in these experiments (walking, hind grooming etc) are affected by temperature. Is there any behavior that is not proportionally affected by temperature and what does it tell us that is special about the anterior grooming rhythms? Also, given global heating will affect all neurons similarly, proportional changes in the two rhythms need not indicate "coupled" rhythms. This caveat should be discussed while discussing results from Figure 3.

Temperature does affect neural activity in general, potentially speeding up all behaviors. We expand our discussion of this possible explanation for the temperature-dependent increase in rhythm frequencies that we observe, but we do not think that the coupled increase in frequency of short and long time-scale rhythms is an epiphenomenon of generally faster neural activity because periodic behaviors are affected differently by temperature in spontaneous grooming. This caveat is now mentioned in the Results section Two time-scales contract together with temperature elevation and the counter-evidence described in section Nested CPGs can be decoupled in spontaneously grooming flies.

We reviewed the literature for fly behaviors but characterization of walking, courtship, or “fly-bowl” open-field data at multiple temperatures has not been reported to our knowledge. (This lack actually prompted us to initiate a collaboration to investigate the effects of temperature on courtship song.) Temperature dependent acceleration of oscillation has been used in several systems to provide evidence for the existence of Central Pattern Generator (CPG) circuits, as well as to investigate their anatomical locations, for example in frog vocalizations (Yamagouchi et al. 2008 and references within). This relationship between temperature and frequency prompts us to reason that behaviors that are triggered by acute sensory stimuli should be less affected by temperature than those governed by CPGs. In the revised manuscript we separate rhythmic from non-rhythmic behaviors on the long time-scale using a newly-devised Periodicity Index see Figure 1—figure supplement 2. We find that periodic long time-2 scale behaviors correlate better with temperature (R=0.83, p=0.02) than 2 non-periodic ones (R=0.70; p=0.08): new Figure 6—figure supplement 1. Taken together this new analysis shows that while all behaviors, acute and periodic, become faster with temperature, the latter show stronger temperature effect, as we would predict for CPG-driven behaviors.

Temperature-dependent acceleration of short and long time-scale rhythm frequency in grooming is one piece of evidence that these behaviors may be controlled by central pattern generator circuits, complementing our quantification of their periodicity and demonstration of their sensory independence.

2) A more direct evidence for CPGs would be to show that rhythmic motor output could be achieved without rhythmic sensory input and the authors also claim to have addressed this using optogenetics (Figure 4). The authors suggest that the changing quantity of dust on the fly's body as it grooms, could be a rhythmic input. This could be better explained. I'm guessing what matters is the difference in sensory input coming from head (H) versus front legs (F). If H>F then the fly does behavior "h", else it does "f". Doing behavior "h" reduces sensory input "H". With this assumption, the H-F input could indeed be rhythmic, and then the opto experiment rationale seems justified. However, for the fast rhythm (leg sweeps), the major rhythmic input is likely the proprioceptive input from the moving legs and not the continuously decreasing quantity of dust on the fly's body and hence this rhythm is not really addressed by the opto experiment. In fact the proprioceptive input from the legs could also be the defining input for the slower rhythm given that "number of leg movements" remain constant across temperatures (Figure 3 and 4K). One way to investigate pure centrally driven rhythms could be to eliminate rhythmic sensory feedback by leg amputation (e,g Berendes et al., J.Exp.Biol, 2016) or neuronal silencing (Mendes et al., eLife, 2013) and then apply dust/opto-stim and see if both fast and slow rhythms still persist.

The initial optogenetic stimulation experiments, activating mechanosensory bristle neurons over the body surface to mimic dust, were designed to eliminate the changing sensory drive that occurs as dust is removed from anterior body parts during sustained grooming, flattening the normal anterior-to-posterior grooming progression. This optogenetic stimulus likely also masks potential sensory contributions to the long time-scale rhythmic alternation of bouts of head-sweeps and front-leg rubs from acute evaluation of dust load on the legs. The reviewer is correct that mechanosensory bristle activation by Chrimson does not eliminate the proprioceptive and self-generated sensory stimulation produced by the movement of the legs or their contact with the body. If this contact is rhythmic, it could contribute to maintaining the head sweep or leg rub rhythms on the short time-scale.

As the reviewer suggests, we now use alternative methods to reduce sensory feedback, assessing short and long time-scale periodicity in flies with an amputated leg or genetically silenced proprioceptive sensory neurons. We analyzed grooming rhythms using both ABRS and limb tracking with Deep Lab Cut. The results are described above in the response to the Editors’ summary, but in brief, we see that the short timescale movements remain rhythmic, and the head sweep/leg rub cycles also remain periodic but less so, and become much slower than those in the control group. These data are now included in a new Figure 5 and Figure 5 —figure supplement 1.

We also observe and quantify a reduction in the amount of periodic behavior in the optogenetically stimulated flies, especially at higher temperatures (Figure 1—figure supplement 4H), suggesting the possibility that appropriate sensory feedback supports the stability of the rhythms. These results suggest that while the basic rhythms may be CPG generated, sensory information contributes to speed and stability of both time-scales. We now mention this possibility in an expanded in the Results section Two time-scales contract together with temperature elevation and in the Discussion where we provide examples from other systems.

3) Finally, the authors describe an interesting "decoupling" of the two rhythms during spontaneous grooming. The authors observe similar leg movement frequencies, however the longer f-f and h-h rhythms seem very rare and variable. So the "decoupling" between the two rhythms is in fact driven by "absence" of the slower rhythm in the experimental conditions. This is also interesting but should be discussed appropriately. Looking at the full ethogram in Figure 5B, it is apparent that as temperature increases, flies spend more time walking versus grooming and so the grooming bouts are likely too short to show any slow rhythms. So in theory, the rhythms could be still coupled, just now more disrupted because of a competing "walking" state.

The f-f and h-h oscillations are indeed less frequent in spontaneous grooming. They are less robust at room temperature, and they become increasingly “ragged” at high temperature, when flies do spend more time walking. This does make it harder to get a large enough sample to analyze the periodicity of the long time-scale alternation or whether its rate increase is coupled that of the short time-scale rhythms as temperature increases.

But when spontaneous grooming does occur, its long time-scale frequency does increase, and not at the same rate as the short time-scale frequency. The fact that we observe this lesser but significant increase in ff- and hh-cycle oscillations in these flies suggests that the low sample size is not the only explanation for the “decoupling.” We propose that the short time-scale CPG is always ON (during grooming) whereas the long timescale CPG can be either ON or OFF. We show the overall lower amount of periodic long time-scale behavior in spontaneously grooming flies across all temperatures in a newly added Figure 1—figure supplement 3G and an example of the switching between periodic and non-periodic behaviors in these flies is shown in Figure 6—figure supplement 2B. As we described above, we can now separate the periodic from non-periodic behaviors (on the long time-scale) in these flies (Figure 6—figure supplement 1). On average the ff- and hh-cycles in spontaneously grooming flies do not scale with temperature to the same extent as in the dust-stimulated flies; however, if we only sample from the periodic behaviors (CPG is ON), the temperature correlation is closer to that of the 2 dust-stimulated flies (R=0.83, p<0.02) while non-periodic behaviors 2 correlate with temperature less significantly (R=0.70, p<0.07) (Figure 6— figure supplement 1). We interpret that as flies alternating between periodic CPG-driven and non-periodic behaviors.

The competition between grooming and walking is an interesting future direction for research: perhaps the two rhythmic leg movement-based behaviors share CPG components.

4) The leg movement analysis needs to be justified more than what it is in the Methods section. The authors acquire videos of grooming flies at 60 Hz,then select frames containing anterior grooming bouts and in these selected frames, they then use pixel difference in consecutive frames and use the frames depicting the largest movement for quantifying frequency. It is unclear what aspect of leg movement the authors are quantifying in this analysis and whether it is affected by video frame-rate or camera angle. What motor action is represented by the "leg movement" frequency? Why is this frequency value higher for "f" bouts versus "h" bouts? Would the authors get the same results if videos were captured at a higher frame rate? It is important to disambiguate this, because the authors use "number of leg movements" as an attribute in Figure 3 to prove coupling between the CPGs. The authors could acquire some additional videos, preferably at a high frame rate, and use one of the recent tools (Pereira et al., 2019, Mathis et al., 2018) to track the legs during anterior grooming, as has been done for leg movement rhythm quantification during walking. If this type of high resolution analysis also suggests a similar leg sweep frequency, the current analysis framework of the authors will be justified. Moreover, it could provide a better understanding of results in Figure 3 and 4K.

We have expanded our description of how we initially analyzed leg movements in the Methods section and justify why the 60Hz frame rate is sufficient to count leg sweeps and rubs (Figure 1 —figure supplement 1), but to address the core concern, we collected new data with a different camera that enables high resolution limb tracking using DeepLabCut (DLC) at 100Hz frame rate as suggested. This analysis detects leg movement frequencies of ~5-7Hz at temperatures from 18-30ºC, which is in good agreement with our previous measurements. This new analysis also confirms the periodicity of both the short and the long time-scales of grooming behaviors. These results are now shown in Figure 1—figure supplement 4.

The frequency of f-bouts appears slightly higher than that of h-bouts in the original analysis (Figure 2—figure supplement 1) although we couldn’t detect a significant difference between them with the DLC analysis. This may be because the legs have to travel a greater distance during a head sweep than during a leg rub, or because head sweeps are differently affected by sensory feedback, as suggested by (Figure 5D-E). Head sweeps and leg rubs are likely controlled by the same CPG but modulated differently by their sensory feedback, a possibility we plan to explore in future experiments.

5) For the slow f-f and h-h rhythm quantification the authors use an interesting approach (P(f)-P(h)). Although this looks promising in Figures 1D, 2F and supp Figure 2, many of the peak/trough values tend to be very close to zero in Figures 4F, 5F making it unclear what rhythms does this really represent in terms of actual behavior. Are we still talking about clear rhythms between 2 states as depicted in Figure 1A? Performing oscillation analysis using confidence values between artificially defined binary states can enforce the output to look like an oscillation and hence it is important to explicitly discuss this.

We expand the description of the approach in the Methods section. As the reviewer said, we identify the two states (h- and f-bouts) by their probability (our detection confidence). To measure the frequency of bout alternations, we use the time distance between local confidence minima and maxima of P(f) – P(h) (the bout centroids shown in Figure 1D-E) rather than bout durations because the former is less error-prone than the positions of onsets and offsets (edges) of bouts. Therefore, our measurement is not affected by our definition of the binary states.

Reviewer #2:

This manuscript uses temperature and optogenetic manipulations to alter the speed of grooming behaviors and examines the resulting changes in fast- and slow-time scale behavioral structure. The authors find that temperature increases the frequency both of individual leg movements, and the alteration between bouts leg rubbing and head grooming, such that the number of leg cycles per bout is approximately the same across a range of temperatures. A similar results is found when grooming is elicited by optogenetic stimulation of mechanosensory bristles, rather than by dust. Finally, the authors show that coordination between these two levels of behavioral organization breaks down during spontaneous grooming. The authors draw conclusions about the control of these behaviors by nested central patterns generators. The behavioral observations presented here are interesting but I felt that more analysis of genetic or circuit manipulations would be required to firmly draw the conclusions the authors would like to about the neural control of these behaviors.

A central claim of the manuscript is that Drosophila grooming may be controlled by nested CPGs. As currently presented the evidence is not especially strong, as it is not clear what the alternative to central pattern generator control of these behaviors would be. The manuscript would be stronger if the authors identified neurons whose activation or inactivation altered behavioral rhythms or the coupling between fast and slow-time scale structure in the behavior.

In the case of high temperature + constant sensory stimulation the behaviors seem much more variable and irregular but this is not noted or discussed.

The longer-time-scale rhythms, alternating bouts of head sweeps and front leg rubbing, are indeed more variable at higher temperature and under optogenetic stimulation. This is now quantified in the new Figure 1— figure supplement 3 where we show the amounts of periodic behaviors on the long time-scale across the temperatures and for different datasets, including the optogenetically stimulated flies. We also observe this effect in the new data where we genetically reduce proprioceptive inputs as shown in the new Figure 5. We developed a metric to quantify the amount of periodicity in all genotypes and conditions, as described in Figure 1 —figure supplement 2, and we include possible explanations in the Results as well as in a new paragraph in the Discussion section. For the optogenetically-stimulated flies, in particular, we speculate that normal sensory feedback may be dispensable for basic rhythmicity but contribute to appropriate timing and stability, as has been reported in other systems as we now mention the Discussion.

Line 35-36: "Automating the sequence by calling it actions in series produces reliable control" This seems like a bit of straw man. Most rhythmic behaviors such as walking, breathing, etc, are assumed or known to arise from central pattern generators, and not from individual cycle-by-cycle decision, although of course each behavior can be modulated on a cycle-by-cycle basis.

We did start from the assumption that the short time-scale rhythm of individual leg movements for grooming would be CPG generated, but this had yet to be formally demonstrated. Our discovery that the alternation between bouts, the longer time-scale, was also rhythmic was a genuine surprise.

Line 73: "characteristic frequency of 6Hz." It seems in 1C that the characteristic frequency of head grooming and leg rubbing are slightly different. Can those averages be shown or given here and are they significantly different?

Head sweeps are slightly slower than leg rubs. We quantify this in Figure 2—figure supplement 1. The frequencies are corroborated using DeepLabCut on new video as shown in Figure 1 —figure supplement 4.

Line 125 + figure 2C/4C. The authors note that the behavior becomes more ragged at high temperatures and stronger deviations from the characteristic frequency are seen at 30{degree sign}, especially in figure 4C. The authors should discuss how these deviations impact their analysis of characteristic frequency.

We have quantified the periodicity of the longer-time scale under various conditions and include a discussion of the potential role of sensory feedback in maintaining more regular rhythmicity as discussed in the response to major comments above.

Using the new quantification, we can see a sharp decrease in periodicity index and in the proportion of periodic behavior at 30º in the optogenetically stimulated flies (Figure 1—figure supplement 3E and H). We believe that some sensory feedback may be necessary to stabilize the rhythmic output of the CPGs, since this is consistent with our new data reducing sensory feedback, and we now mention this possibility in the Discussion.

Line 124 and 132: "suggests that CPGs may be involved…both time-scales are controlled by two nested levels of CPGs" these both seem like interpretations of the data and not things that are directly demonstrated by the data shown.

The core proposal of the manuscript is that nested CPGs are the model that best explains our data. We have reviewed the division of Results and Discussion carefully to separate descriptions of behavior from interpretation. Since the hypothesis that CPGs may contribute to grooming guides our experiments, we do mention this in the experimental design, but we have tried to reserve interpretation for the Discussion.

Figure 4A: It seems in this example that the relative durations of head grooming and leg rubbing, as well as the regularity of the behavior are altered at 30{degree sign}. The authors should address this. Behavioral confidence is also much lower under these conditions- is this an issue?

The duration of individual leg movements and the lengths of bouts are reduced at higher temperature. The rhythmicity of leg movements remains strong but the alternation between bouts does become less precise. We now quantify the strength and the amount of periodicity in Figure 1— figure supplement 3 E and H. The overall result, that there is temperature-dependent contraction of the long time-scale, remains robust.

Line 248: "Our more surprising discovery was that the alternation between bouts of head cleaning and front leg rubbing is also periodic." I am not sure quite how surprising this is. I think it would equally surprising if there were no correlations in these measurements. I think it would help to have some measure of regularity/irregularity in these alterations.

We expected periodicity of leg rubbing and head sweeps; these highly repetitive movements seemed characteristic of CPG control. Our previous work revealed that both behavior identity and duration affect the choice of next movement (Mueller et al. 2019), but prior to this study, we had not identified rhythmic alternation between anterior grooming bouts.

The long time-scale alternation is more variable that the short time-scale, especially at higher temperatures, under optogenetic stimulation, or in the absence of sensory feedback. We now quantify the regularity/irregularity of these alternations by the Periodicity Index, described in Figure 1 —figure supplement 2. We can also separate periodic from non-periodic alternations and estimate the overall amount of periodic behavior in different conditions (Figure 1 —figure supplement 3H).

Reviewer #3:

This study presents an intriguing example of rhythmic behavioral oscillations at a fast time scale embedded within a slower rhythmic behavioral oscillation and the similar effects of temperature on the rates of the two rhythms. The data and the writing are both exceptionally clear.

1) It is not clear why the authors use an unpublished example of different rates of oscillation in the first paragraph of the Introduction instead of using a published example, of which there are probably many to choose from.

We looked for an appropriate published example but came up blank. Crustacean antenna have historical contributions to ethology including grooming behavior, e.g.Vedel, J. P., 1982 and Barbato, J. C, 1997, and seemed an aesthetic example to illustrate how simple oscillators with different frequencies (and amplitudes) can create beautiful, complex behaviors. This is anecdotal but reflects one author’s fieldwork living next to the ocean. We can delete this example or exchange for substitute if an alternative is proposed.

Barbato, J. C., and Daniel, P. C. (1997). Chemosensory activation of an antennular grooming behavior in the spiny lobster, Panulirus argus, is tuned narrowly to L-glutamate. The Biological Bulletin, 193(2), 107-115.

Vedel, J. P. (1982). Reflex reversal resulting from active movements in the antenna of the rock lobster. Journal of Experimental Biology, 101(1), 121133.

2) At first, I was somewhat concerned that the temperature manipulation could not be used to assess the contribution of CPGs to the behaviors because temperature changes in these experiments affect both the CNS and the legs, the latter of which contain sensory neurons activated by leg movements. But then I realized that the "movement-related sensory feedback" for the slow rhythm would not be leg sensory feedback, but instead (possibly) the amount of dust on the head. I now think that generating constant bristle stimulation optogenetically indeed should make the likely sensory feedback for the slow rhythm constant, so the effect of temperature on the slow rhythm in this experiment does suggest a CPG for the slow rhythm.

This was also our reasoning on the optogenetic stimulation of mechanosensory bristles. It should make the competing sensory drives between body parts more uniform and flatten out external sensory contributions to the periodicity, revealing possible CPG control, accelerated by temperature. We clarified our description of the goals of the optogenetic activation in the corresponding Results section, Periodicity and correlation between time-scales persist when sensory stimulation is constant.

3) Nonetheless, I think the first paragraph of the Discussion obscures rather than clarifies distinctions between effects on the CNS and PNS. It cites a series of studies that used localized cooling to implicate a CPG within a particular part of the CNS, as if the current experimental design is comparable to this, though in the current experiments the entire animal was warmed or cooled. It might be helpful to explicitly acknowledge that in the current study temperature was simultaneously manipulated in both the central and the peripheral nervous system, so the change in rhythm rate does not in itself eliminate the possibility that movement-related sensory feedback contributes to the rate, at least for the fast rhythm.

We have modified the Discussion according to this suggestion: “Although here we change the temperature of the whole fly…” We are indeed changing the temperature of the whole animal to argue for internal CPG control of rhythmicity over two time-scales. We now also perform new experiments that disrupt proprioceptive sensory feedback to address possible contributions from the PNS (Figure 5 and Figure 5—figure supplement 1).

4) The sentence (lines 202-203), "These flies have no sensory stimuli except what they generate themselves by contact between their legs and bodies…" also seems misleading because it leaves out 1) any dust, etc. that happens to collect on their heads that was not put there by the experimenters and 2) leg proprioceptive input (i.e., not from contact).

In the revised manuscript section on spontaneously grooming flies, we rewrote this statement as follows: “These flies have no experimentally applied sensory stimuli - only what they generate themselves by contact between their legs and bodies, and the associated proprioceptive feedback - so these motor patterns are most likely to be generated by internal circuits.” We hope this acknowledges the limits of our control: there may be external or internal stimuli the flies sense that the experimenters did not intend. (We address the proprioceptive input below.)

5) Also, on line 241, the authors assert that the fast rhythm occurs "in the absence of patterned sensory input." This is misleading, because leg proprioceptors presumably provide patterned sensory feedback that could be used on this time scale. These statements should probably be revised to clarify.

In the revised manuscript, we attempt to address potential proprioceptive contributions through additional amputation and genetic silencing experiments, finding that proprioceptive feedback is not essential for short time-scale rhythmicity but makes long time-scale rhythms slower (Figure 5). Even with an amputated leg the frequency of the stump is nearly identical to that of the intact leg (Figure 5—figure supplement 1).

We retained this statement in the Discussion: “Here we investigate what aspects of fly grooming are periodic, demonstrating that the short timescale leg sweeps and rubs repeat at characteristic frequencies, in the absence of patterned sensory input, and in a temperature-dependent manner (Figure 2D-E), consistent with control by central pattern generators.” We hope that the optogenetic activation, amputation, and genetic silence experiments, as well as the spontaneous grooming analysis, now provide enough evidence to support this assertion.

[Editors’ note: what follows is the authors’ response to the second round of review.]

Essential revisions:

1) The apparent finding that the leg mechanosensory genetic ablation slows the slow rhythm, but not the fast rhythms, is intriguing, if true because it would indicate that the two rhythms can be independently modulated, which would suggest that they are independent CPGs, even though the slow one may trigger the fast one. (The differential effects of temperature on aspects of spontaneous grooming also suggest this.) But this conclusion rests on Figure 5D-E and H. Figure 5E shows what looks like no change in sweep frequency, but 5D shows what looks like a slowing of rub frequency; whether this apparent slowing is statistically significant or not is unclear. Figure 5H, for the slow rhythm, is a different kind of plot, so we have an "apples-to-oranges" comparison-there is no frequency power spectrum plot for the slow rhythm and no box plot of frequency for rubbing. So we are not certain that the slow rhythm slowed without the rub frequency also slowing. It would help to add the missing plots, allowing "apples-to-apples" comparisons, as well as statistical comparisons between control and tetanus toxin for each measure. This would be important for readers to be persuaded that the slow and fast rhythms can be independently modulated.

We now use the same type of plotting (the box plots) for all the measures in Figure 5 (D-K). We also added the missing statistics (p-values) to each panel. The slowing of the rub frequency shown in Figure 5D is statistically significant (p < 0.001) as is the slowing down of the long time-scale (p = 0.003) shown if Figure 5H.

2) In this revised submission the authors introduce a new metric, Periodicity Index (PI) to quantify the periodicity of a time series (ratio of highest peak and most prominent shoulder). Although this seems intuitively logical it would help if there was a reference or (mathematical) justification for its use as a measure of periodicity.

We explored metrics that could be used to quantify periodicity but did not find a more formal, mathematical solution. The ACF itself, of course, can be used to detect cycles in the data. We use the π as a threshold to determine which behaviors are periodic, rather than as an optimal estimate of the strength of periodicity.

3) Authors define a threshold (most prominent shoulder peak in ACF >0.2) for calling a behavior as periodic. This seems reasonable. But looking at the selected ACF samples for fast rhythms in Figure 1F and G, it seems like most of the prominent shoulder peaks fall below the 0.2 threshold. Unless we are mistaken, the authors seem to have chosen a particularly bad example to depict fast rhythms in Figure 1 of the paper.

Thank you for spotting this. We had plotted slightly smoothed (to remove high frequency noise) examples of ACFs but had not normalized them afterwards (the autocorrelation at t=0 should be 1). We revised the figures that show the ACFs accordingly and this does not affect the π measurements.

4) The usage of P(f)-P(h) as explained by the authors in the rebuttal is understood; but not what the fly would be actually doing when this value approaches 0 (as happens a lot in Figures 4F and 6F). It would really help if the authors included sample videos corresponding to Figures 1D, 4F, and 6F.

We now include example videos of the critical transitions. When the value approaches 0, the flies are switching between leg rubbing and head sweeping behaviors and ABRS does not assign the spatiotemporal feature to either category.

In response to this critique, we carefully reviewed the raw videos of the flies from Figures 1D, 4F, and 6F and concluded that the threshold for which events should be assigned to either f- or h- peaks (or valleys) was set too liberally. We adjusted the threshold so that the absolute value should be at least 0.05 and recomputed the ff/hh cycles. This change affected the long time-scale analysis in Figures 1D, 4F, and 6F, resulting in smaller sample sizes. We now combine ff and hh cycles into a single value, and repeated our analysis of the temperature dependence of the long-time scale. The core conclusions remain the same, with the exception of Figure 6 Supplement 1, where the infrequent long time-scale periodic behaviors no longer show a temperature effect.

Reviewer #1:

This study demonstrates that fruit flies have regular rhythms of head and leg grooming movements when dust is applied to the head and that they also alternate head and leg grooming with a regular, slower rhythm. These rhythms all increase with temperature and continue when head bristle stimulation is constant and when sensory feedback from the moving legs is reduced or eliminated. All of this suggests that the fly's central nervous system contains circuits-central pattern generators-for both the fast leg movements during grooming of either the head or the other leg and for the slow alternation between these two kinds of grooming. This suggests that central pattern generators can be nested within another central pattern generator at a higher hierarchical level, which is important for understanding how central nervous systems control movements generally.

from 2020: It is not clear why the authors use an unpublished example of different rates of oscillation in the first paragraph of the Introduction instead of using a published example, of which there are probably many to choose from.

Authors' response: We looked for an appropriate published example but came up blank. Crustacean antenna have historical contributions to ethology including grooming behavior, e.g.Vedel, J. P., 1982 and Barbato, J. C, 1997, and seemed an aesthetic example to illustrate how simple oscillators with different frequencies (and amplitudes) can create beautiful complex behaviors. This is anecdotal but reflects one author's fieldwork living next to the ocean. We can delete this example or exchange for a substitute if an alternative is proposed. Barbato, J. C., and Daniel, P. C. (1997). Chemosensory activation of an antennular grooming behavior in the spiny lobster, Panulirus argus, is tuned narrowly to L-glutamate. The Biological Bulletin, 193(2), 107-115. VEDEL, J. P. (1982). Reflex reversal resulting from active movements in the antenna of the rock lobster. Journal of Experimental Biology, 101(1), 121- 133.

My response to the authors' response:

FYI, some other examples of pairs of slow and fast CPG-driven (or apparently CPG-driven) rhythms that are coordinated across time scales (though this does not mean that one CPG triggers the other) are in:

Brown (1911) Quart J Exp Physiol 4:151-182 (rabbit hopping and scratching)

Carter and Smith (1986) J Neurophysiol 56:171-183 and 56:184-195 (cat walking and paw-shaking)

Weimann et al. (1991) J Neurophysiol 65:111-122 (crab gastric mill and pyloric rhythms)

Bartos et al. (1999) J Neurosci 19:6650-6660 (crab gastric mill and pyloric rhythms)

Esch et al. (2002) J Neurosci 22:11045-54 (leech crawling and swimming)

Zornik et al. (2010) J Neurophysiol 103: 3501-3515 (frog advertisement call sequence of fast and slow trills)

We chose to keep the lobster example but have made it clear that it is an inspirational observation that motivated our study; we add a description of a piano player to illustrate the general question that fascinates us. We thank the reviewer for pointing out these relevant references, some of which we now include in the Discussion.

https://doi.org/10.7554/eLife.71508.sa2

Article and author information

Author details

  1. Primoz Ravbar

    Molecular Cellular and Developmental Biology and Neuroscience Research Institute, University of California, Santa Barbara, Santa Barbara, United States
    Contribution
    Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft
    For correspondence
    primoz.ravbar@gmail.com
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-7769-8687

  2. Neil Zhang

    Molecular Cellular and Developmental Biology and Neuroscience Research Institute, University of California, Santa Barbara, Santa Barbara, United States
    Contribution
    Investigation
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-3397-5974

  3. Julie H Simpson

    Molecular Cellular and Developmental Biology and Neuroscience Research Institute, University of California, Santa Barbara, Santa Barbara, United States
    Contribution
    Conceptualization, Funding acquisition, Project administration, Supervision, Writing – review and editing
    For correspondence
    jhsimpson@ucsb.edu
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-6793-7100

Funding

National Institute of Neurological Disorders and Stroke (R01NS110866)

  • Julie H Simpson

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors thank members of the Simpson, Louis, and Kim labs for feedback, and especially Li Guo and Dr. Josh Mueller for excellent suggestions. The authors thank Carla Ladd for creative input with figure design and Aleks Labuda for instrument design for high-resolution video recording. This research was supported by NIH-R01NS110866 and HHMI Janelia transition funding.

Senior and Reviewing Editor

  1. K VijayRaghavan, National Centre for Biological Sciences, Tata Institute of Fundamental Research, India

Version history

  1. Preprint posted: September 15, 2020 (view preprint)
  2. Received: June 22, 2021
  3. Accepted: December 8, 2021
  4. Version of Record published: December 22, 2021 (version 1)

Copyright

© 2021, Ravbar et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 1,060
    Page views
  • 131
    Downloads
  • 6
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Primoz Ravbar
  2. Neil Zhang
  3. Julie H Simpson
(2021)
Behavioral evidence for nested central pattern generator control of Drosophila grooming
eLife 10:e71508.
https://doi.org/10.7554/eLife.71508

Categories and tags

Research organism

Further reading

    1. Evolutionary Biology
    2. Neuroscience

    Diversity and evolution of cerebellar folding in mammals

    Katja Heuer, Nicolas Traut ... Roberto Toro
    Research Article

    The process of brain folding is thought to play an important role in the development and organisation of the cerebrum and the cerebellum. The study of cerebellar folding is challenging due to the small size and abundance of its folia. In consequence, little is known about its anatomical diversity and evolution. We constituted an open collection of histological data from 56 mammalian species and manually segmented the cerebrum and the cerebellum. We developed methods to measure the geometry of cerebellar folia and to estimate the thickness of the molecular layer. We used phylogenetic comparative methods to study the diversity and evolution of cerebellar folding and its relationship with the anatomy of the cerebrum. Our results show that the evolution of cerebellar and cerebral anatomy follows a stabilising selection process. We observed 2 groups of phenotypes changing concertedly through evolution: a group of 'diverse' phenotypes - varying over several orders of magnitude together with body size, and a group of 'stable' phenotypes varying over less than 1 order of magnitude across species. Our analyses confirmed the strong correlation between cerebral and cerebellar volumes across species, and showed in addition that large cerebella are disproportionately more folded than smaller ones. Compared with the extreme variations in cerebellar surface area, folial anatomy and molecular layer thickness varied only slightly, showing a much smaller increase in the larger cerebella. We discuss how these findings could provide new insights into the diversity and evolution of cerebellar folding, the mechanisms of cerebellar and cerebral folding, and their potential influence on the organisation of the brain across species.

    1. Neuroscience

    Hunger- and thirst-sensing neurons modulate a neuroendocrine network to coordinate sugar and water ingestion

    Amanda J González Segarra, Gina Pontes ... Kristin Scott
    Research Article

    Consumption of food and water is tightly regulated by the nervous system to maintain internal nutrient homeostasis. Although generally considered independently, interactions between hunger and thirst drives are important to coordinate competing needs. In Drosophila, four neurons called the interoceptive subesophageal zone neurons (ISNs) respond to intrinsic hunger and thirst signals to oppositely regulate sucrose and water ingestion. Here, we investigate the neural circuit downstream of the ISNs to examine how ingestion is regulated based on internal needs. Utilizing the recently available fly brain connectome, we find that the ISNs synapse with a novel cell-type bilateral T-shaped neuron (BiT) that projects to neuroendocrine centers. In vivo neural manipulations revealed that BiT oppositely regulates sugar and water ingestion. Neuroendocrine cells downstream of ISNs include several peptide-releasing and peptide-sensing neurons, including insulin producing cells (IPCs), crustacean cardioactive peptide (CCAP) neurons, and CCHamide-2 receptor isoform RA (CCHa2R-RA) neurons. These neurons contribute differentially to ingestion of sugar and water, with IPCs and CCAP neurons oppositely regulating sugar and water ingestion, and CCHa2R-RA neurons modulating only water ingestion. Thus, the decision to consume sugar or water occurs via regulation of a broad peptidergic network that integrates internal signals of nutritional state to generate nutrient-specific ingestion.

    1. Neuroscience

    Dynamic top-down biasing implements rapid adaptive changes to individual movements

    Lucas Y Tian, Timothy L Warren ... Michael S Brainard
    Research Article

    Complex behaviors depend on the coordinated activity of neural ensembles in interconnected brain areas. The behavioral function of such coordination, often measured as co-fluctuations in neural activity across areas, is poorly understood. One hypothesis is that rapidly varying co-fluctuations may be a signature of moment-by-moment task-relevant influences of one area on another. We tested this possibility for error-corrective adaptation of birdsong, a form of motor learning which has been hypothesized to depend on the top-down influence of a higher-order area, LMAN (lateral magnocellular nucleus of the anterior nidopallium), in shaping moment-by-moment output from a primary motor area, RA (robust nucleus of the arcopallium). In paired recordings of LMAN and RA in singing birds, we discovered a neural signature of a top-down influence of LMAN on RA, quantified as an LMAN-leading co-fluctuation in activity between these areas. During learning, this co-fluctuation strengthened in a premotor temporal window linked to the specific movement, sequential context, and acoustic modification associated with learning. Moreover, transient perturbation of LMAN activity specifically within this premotor window caused rapid occlusion of pitch modifications, consistent with LMAN conveying a temporally localized motor-biasing signal. Combined, our results reveal a dynamic top-down influence of LMAN on RA that varies on the rapid timescale of individual movements and is flexibly linked to contexts associated with learning. This finding indicates that inter-area co-fluctuations can be a signature of dynamic top-down influences that support complex behavior and its adaptation.