Modular, robust, and extendible multicellular circuit design in yeast
Figures
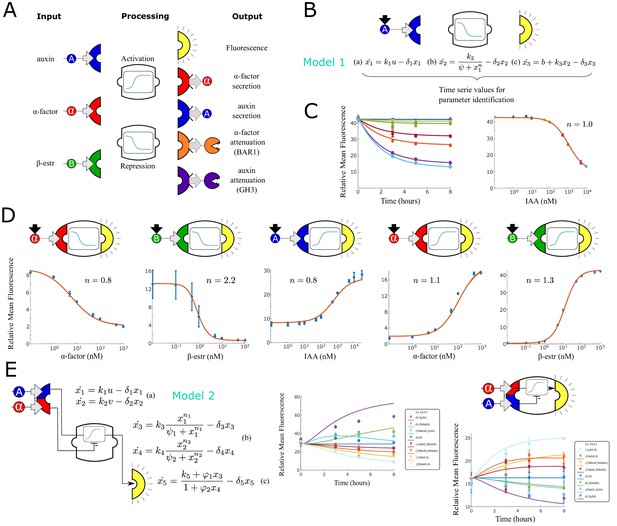
Modular components for engineering multi-cellular signaling circuits.
(A) Three input signals, two transfer functions and five outputs are used to assemble 24 distinct strains. (B) Differential equations are used to model and predict behavior of all strains and strain combinations in the paper. In this example, a model (Model 1) and symbolic representation for a fluorescent reporter repressed by high auxin concentration are shown. (C) Left: Time course fluorescence data for different auxin concentrations for the sensor strain shown in (B). Full lines are model simulations. Right: End point fluorescence data is shown as a function of auxin concentration color-matching the time series on the left. The steady-state simulation is shown in orange. (D) Symbolic representation, steady state data and model fit for all other single input reporter strains. (E) Modeling framework (Model 2) and fluorescence kinetics data for two different two-input reporter strains. Error bars represents the s.d. of three biological replicates.
-
Figure 1—source data 1
The data used for plotting Figure 1 and supplements.
- https://cdn.elifesciences.org/articles/74540/elife-74540-fig1-data1-v3.xlsx
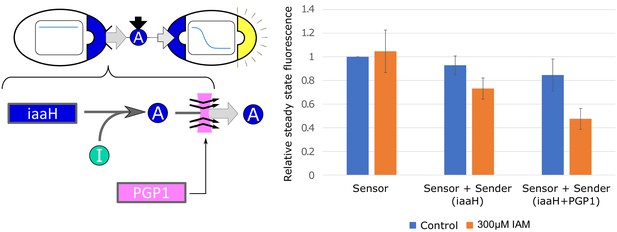
Effect of PGP1 on auxin secretion and sensing.
We integrated the auxin-pump PGP1 from A. thaliana into our yeast strains. Yeast strains expressing PGP1 have been shown to increase auxin efflux up to seven times Geisler et al., 2005. We observe a statistically (, Welch t-test) significant IAA-efflux increase in our sender/receiver co-culture, where the sender is constitutively synthesizing IAA from the IAM intermediate (labeled ’I’ in the left panel). No improvements were detected with multiple integration of PGP1 (data not shown). Error bars represents the standard deviation of three biological replicates.
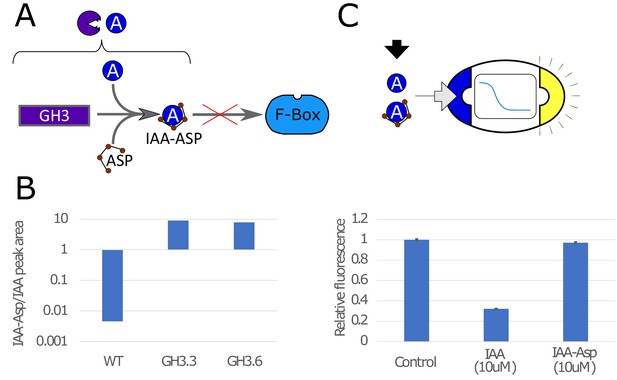
Auxin conjugation to Asp mediated by the GH3 protein in yeast.
(A) GH3 mediates binding of IAA to aspartic acid (Asp), making it not viable to bind to the F-box, which prevents auxin-induced degradation. (B) Using mass-spectrometry (Figure 1—figure supplement 1), we tested the effectiveness of GH3.3 and GH3.6 proteins of the GH3 family to bind IAA to Asp. Peak areas for IAA-Asp and IAA were detected with mass spectrometry and ratio is here reported for WT strain and strains expressing constitutively GH3.3 and GH3.6. The concentration of IAA-Asp is about 10 times higher than IAA for GH3-expressing strains. (C) We tested for fluorescence response in strains that sense IAA and repress GFP for IAA-Asp, and we could detect a statistically significant (p-value = 0.012, T-test) but minor difference with respect to control. The bars are normalized so that Control is equal to 1. Error bars represents the standard deviation of three biological replicates.

Mass spectrometry data for IAA-Asp synthesis from IAA in GH3-expressing strains.
We detected IAA and IAA-Asp peaks for WT strains and strains expressing GH3.3, GH3.6 and both proteins. Strains were exposed to 1 µM IAA from low dilution till saturation (approximately 20 hr). Then cells were harvested, spun down and the supernatant was removed. After adding 250 µL of methanol and boiled at 95°C for 15 minutes (vortexed twice during incubation) (Lee et al., 2013). After spinning the cells down, we took the supernatant to perform IAA extraction through phase separation. We used the protocol outlined in Kriechbaumer, 2016 using ethyl acetate phase separation. We expected a peak between 6-7 for IAA-Asp and between 8-9 for IAA. The label on the left-hand side shows the strain used, while the label on the right side shows the measured compound (IAA-22 or IAA-Asp). The number coming off the peak represent the area measurements used to generate plot (B) of Figure 1—figure supplement 1.
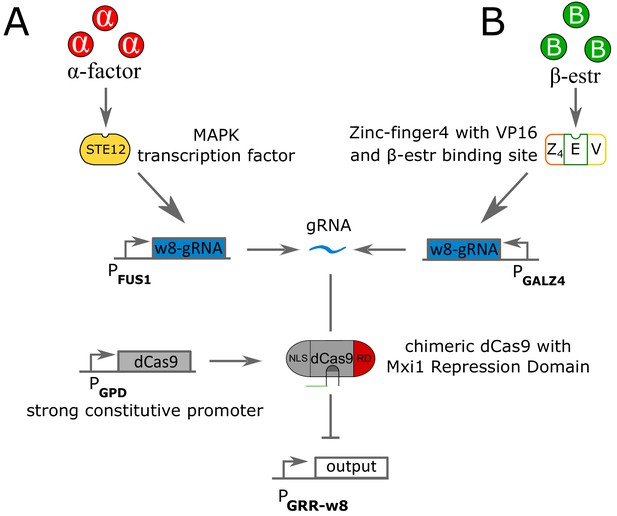
Circuit pathways for repressing strains using α-factor and β-estradiole as inputs.
(A) The signaling molecule α-factor binds to the surface protein STE2, which activates a phosphorylation cascade that ends up activating the transcription factor STE12. Active STE12 then binds to the pFUS1 promoter, here rewired to synthesize gRNA (labeled as in Gander et al., 2017). The gRNA binds to dCas9 fused with the Mxi1 repressing domain (RD) and a Nuclear Localization Signal. dCas9 is under a strongly constitutive promoter GPD. The gRNA-dCas9 complex binds to the pGRR- promoter to stop transcription of the output gene. (B) The signaling molecule β-estr penetrates the cell wall and binds to the chimeric protein Z4EV, constituted of a zinc-finger4 DNA-binding domain, a VP16 activation domain and binding pocket for β-estradiole. Upon β-estradiole binding, Z4EV induce transcription of the -gRNA gene under the pGALZ4 promoter. The rest of the pathway is identical to (A).
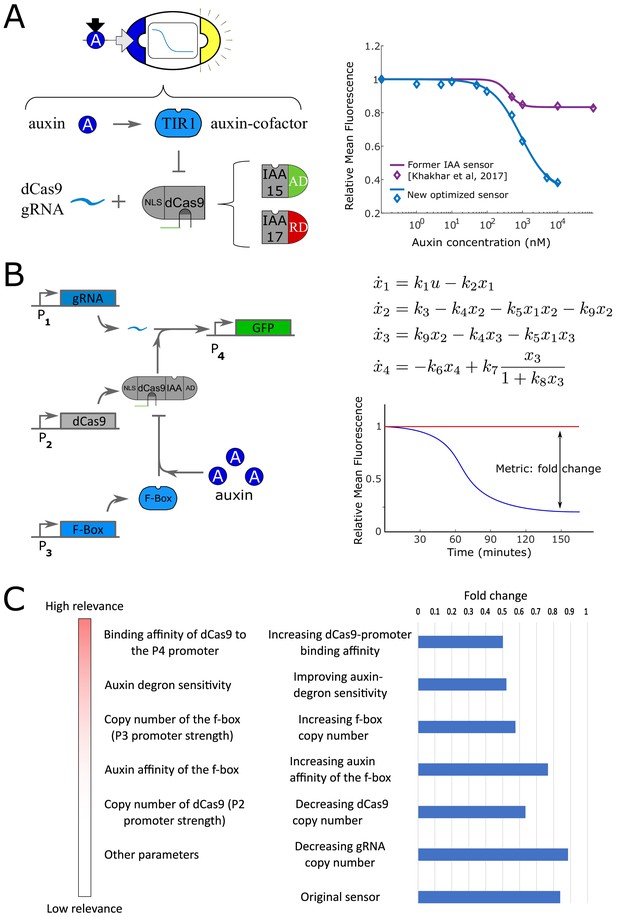
Pathway optimization for IAA-sensing strains.
(A) The repressing circuit driving GFP proposed in Khakhar et al., 2016 has low sensitivity and ON/OFF fold change (purple line in the steady-state plot). Hence, we optimized the pathway for higher sensitivity and fold change (blue line in the steady-state plot). A similar study was conducted for the IAA-activating pathway. (B) To optimize the response, we minimized a metric defined as the L2-norm of the inverse of the fold-change. The fold change was computed by simulating the mechanistic model proposed in Pierre-Jerome et al., 2014, with constrained parameters , .. (C) We order the parameters according to their effect on the metric using sensitivity analysis. We then tested the effect of some of these perturbations in vivo and measured the fold-change between ON and OFF state (blue histogram to the right). Since the results agree with our predictions, we constructed a strain with three copies of TIR1DM (f-box mutated for higher sensitivity), high affinity gRNA-promoter pair ( gRNA and pGRR-/pCYC1- promoter, RD/AD) from Gander et al., 2017, and IAA17/IAA15 (RD/AD) auxin degron for higher auxin sensitivity.
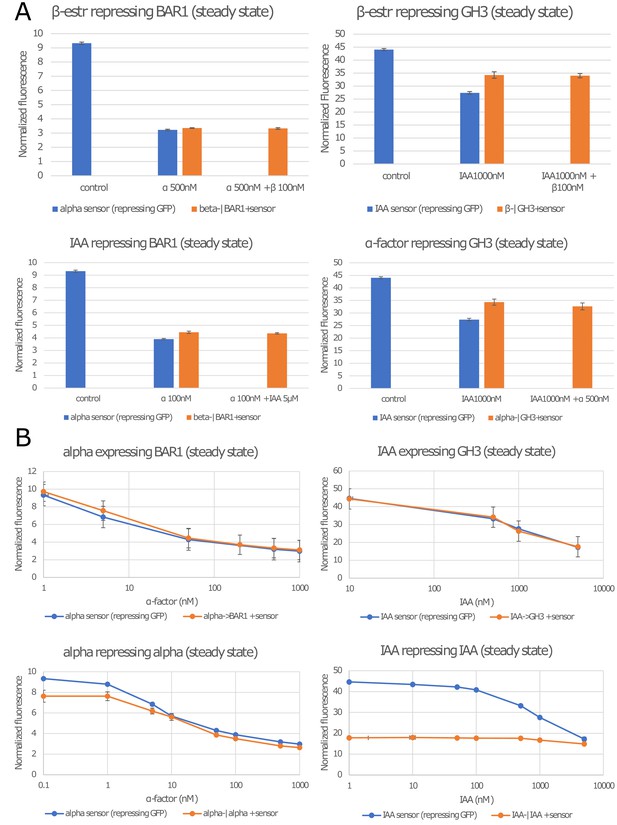
Strains constructed but not used in this study.
(A) The four strains repressing expression of BAR1 or GH3 that are not positive feedbacks did not respond to their inputs significantly enough for us to include them in this study. They either do not affect the signaling molecule (the sensor response is identical to treatment whether the repressing strain is present of not), or they do not display a significant response range (no difference between the two orange bars). (B) Top: these two negative feedback topologies do not significantly differ from the sensor alone in response to α-factor and IAA induction. Bottom: these strains present a significant functional range for negative feedback. Since, no circuits was built using these strains, they are not presented in the main manuscript. Error bars represents the standard deviation of three biological replicates.
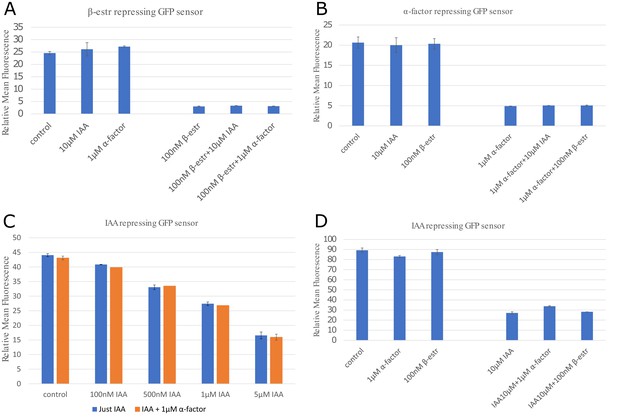
Orthogonality between signaling molecules.
To test the effect of crosstalk between the three signaling molecules, we measured the ON and OFF steady states (8 hours) of the three repressive sensors (IAA, α-factor, and β-estradiole) with and without the alternative signaling molecules (induction here is always at the saturation level). The data suggests that the signaling pathways are fairly orthogonal for the β-estradiole and (A) and α-factor (B) pathways. We tested the IAA pathway for different concentrations of auxin and with or without 1 µM of α-factor (C), detecting variation always contained within. 5% A maximum increase of 24% above the baseline is observed for the IAA-sensor in a regime where both alpha factor and auxin are at or above saturating concentrations (D). This apparent cross-talk could also be the result of toxicity of signal added at very high concentrations. However, this combination is not used in any circuit experiment. Data were collected with two different BD Accuri C6 flow cytometers with different voltage setting. Hence, fluorescence values for (A), (B) and (D) have absolute values about twice as high than presented in the rest of this study. Error bars represents the standard deviation of three biological replicates.

Multi-strain signaling cascades.
(A) Symbolic representation of a two-strain cascade that uses α-factor as the input and auxin as an intermediate signal. To model multi-strain cascades, models for individual strains are concatenated and only the last differential equation of the first model is fit: the GFP output (dashed yellow semi-circle) is substituted with IAA (solid blue semi-circle). End-point fluorescence data and fit are shown for the example cascade. (B) By varying the concentration of the upstream strain, the strength of the signal seen by the downstream strain can be predictably controlled. This change in signal is modeled with a single parameter K. Right: data and model predictions for three experiments with the same strains but varying concentrations of the upstream strain. (C) Symbolic representation, model and data for a two strain cascade wherein the upstream strain removes a signal rather than secreting it. (D) Symbolic representation, model and data for all two strain cascades where the upstream input is activating the production of the intermediate signal. (E) Symbolic representation, model and data for all two strain cascades where the upstream input is repressing the production of the intermediate signal. (F) Symbolic representation, model and data for three-layer signaling cascades. Error bars represents the s.d. of three biological replicates.
-
Figure 2—source data 1
The data used for plotting Figure 2.
- https://cdn.elifesciences.org/articles/74540/elife-74540-fig2-data1-v3.xlsx
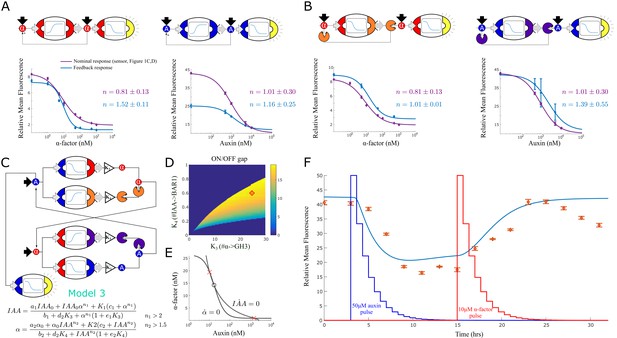
Feedback strains and bistability.
(A) Symbolic representation, model and data for two self-activating positive feedback circuits using alpha factor (left) and auxin (right) as the activating signal. (B) Symbolic representation, model and data for two positive feedback circuits that act through double repression. (C) Architecture and model for a bistable switch assembled from four separate strains. (D) Area of bistability as a function of strain concentrations, where the dark blue color represents one stable equilibrium and color shades report predicted fold-change between ON and OFF states. The coordinates of the red diamond are the concentrations chosen for experimental testing. (E) For the chosen solution, the nullclines show the IAA and alpha-factor concentration for the three equilibria (× = stable, ο = unstable) (F) Experimental data for the bistable switch. Full line is Model 3 simulation, and exogenous auxin and alpha-factor concentrations are reported as a function of dilution over time,depicted in the figure as jagged blue and red lines (the peaks are normalized to simplify their graphical representation). Error bars represents the s.d. of three biological replicates.
-
Figure 3—source data 1
The data used for plotting Figure 3 and supplements.
- https://cdn.elifesciences.org/articles/74540/elife-74540-fig3-data1-v3.xlsx
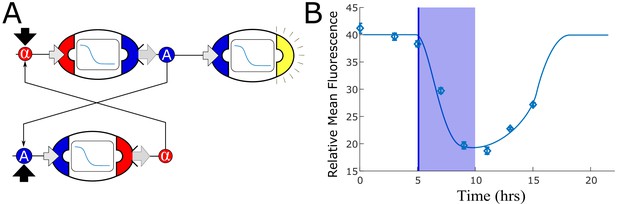
Mutually repressing strains do not generate bistability.
(A) We tested a naive realization of a potential bistable network using two strains that mutually repress each other’s inputs: a strain that senses α-factor and represses auxin synthesis, and a strain that senses auxin and represses α-factor synthesis. (B) We computed the optimal concentration of each of these strains using model simulation, but no combination generated two stable equilibria of α-factor and IAA concentrations. We experimentally tested the combination of these two strains with an auxin repression sensor strain to detect auxin concentration. Samples were taken every 2 hr along with dilution to restore the original cell concentration. After five hours, we inoculated 10µM IAA and diluted the samples of one third every 40 min, so that the IAA concentration became negligible after 5 hr (150 nM). The experimental data confirm that, while a lower value is reached when IAA is exogenously added, no stable equilibrium is reached and the system returns to the original equilibrium (low IAA concentration) after dilution. The diamonds are data, while the smooth line is the simulation; the transparent blue bar represents IAA inoculation starting at 5 hr, being reduced to below detection at hour 10. Error bars represents the standard deviation of three biological replicates.
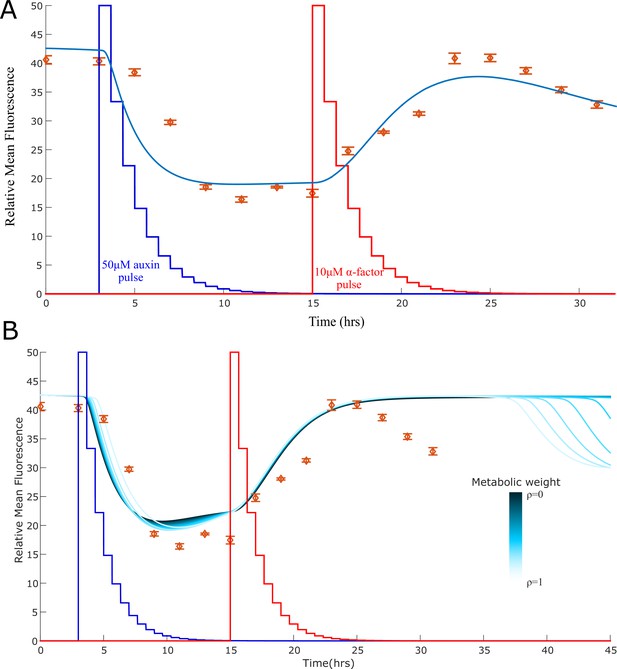
Model explanation for the stable-to-unstable shift.
(A) The experimental data for the bistable switch constructed as in Figure 3C appear to exit its stable orbit after 25 hr, as one can see from the steady decrease in fluorescence. One potential explanation is that the ratio between the strains is no longer maintained due to small difference in strain growth rate that we did not detect over 10 or 12 hr in this study. To test this hypothesis, we simulated the system and allowed the strain that synthesis BAR1 to slightly increase in concentration over time (reaching 0.8 at time 25 hr from a starting concentration of 0.7). With this minor correction, the simulation predicts loss of stability as observed in the data, with the three equilibria becoming a single stable equilibrium with high IAA and low α-factor concentration. (B) Another possible explanation is that the loss of stability is caused by the effect of metabolic load on the strain growth. According to this explanation, active strains grow more slowly affecting the strain ratio that is necessary for bistability to arise. We simulated the effect of increasing metabolic load (represented by variation of the parameter ρ from 0 to 1) using the model described in Appendix 1. We observe a loss of stability for high metabolic weight, although at a later time (36 hrs) than what measured in the experiments (25 hrs). Error bars represents the standard deviation of three biological replicates.

Growth rate of the five strains in the bistable switch.
Data collected with a plate reader over the course of 12 hr, 3 experimental repeats for each of the five strains in the bistable switch topology. Data were collected as, sampling every 15 min at,30°C starting from an initial concentration of 30 events/μl. Growth rate was estimated fitting an exponential curve and the value here reported is average and standard deviation over fitting each of the three replicates. To account for the lower sensitivity threshold of the plate reader, each time series was set to be the minimum detectable till a 25% increase was detected. The ANOVA Table shows that one cannot reject the hypothesis that the five growth parameters are different with 90% confidence. Pairwise t-tests show that the only the IAA sensor growth is different from the other parameters with 95% confidence (p-value = 0.0466), while there is no statistical difference between any other pair.
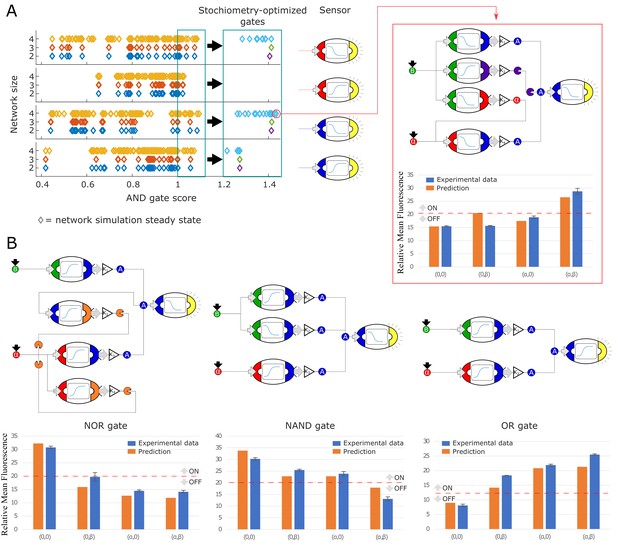
Model-generated implementation of Boolean logic gates.
(A) We used an automated search algorithm to screen all possible strain combinations up to size four (and including exactly one sensor strain) for their ability to realize a set of logic functions. In the example, each strain combination is scored according to how close the combination is to realizing an ideal Boolean AND gate. Each colored diamond corresponds to one strain combination. Circuits consisting of two strains (+ a sensor) are shown in blue, three-strain gates are shown in red, and four-strain gates in yellow. All strains in these simulations are at equal stoichiometry. Higher scores indicate more AND-like behavior. The top-performing strains (score >1, teal box) are selected for further computational optimization of strain stoichiometry. Optimized strain combinations have higher AND scores. Optimized circuits consisting of two strains are shown in light blue, three-strain gates are shown in green, and four-strain gates in purple. Simulations are separated according to which sensor strain is used. A specific high-scoring four-strain combination was chosen for experimental testing (red box). The experimental data (blue bars) show good quantitative agreement with the predictions (orange bars). (B) Similar optimization procedures to the ones shown in (A) were used to identify strain combinations that realize NOR, NAND, and OR logic functions. Example implementations, model predictions and experimental data are shown for all three logic functions. Error bars represents the s.d. of three biological replicates.
-
Figure 4—source data 1
The data used for plotting Figure 4 and supplements.
- https://cdn.elifesciences.org/articles/74540/elife-74540-fig4-data1-v3.xlsx

Optimal circuits, simulation, and experimental realization of the AND gate for 2, 3, and 4-node topologies.
Error bars represents the standard deviation of three biological replicates.
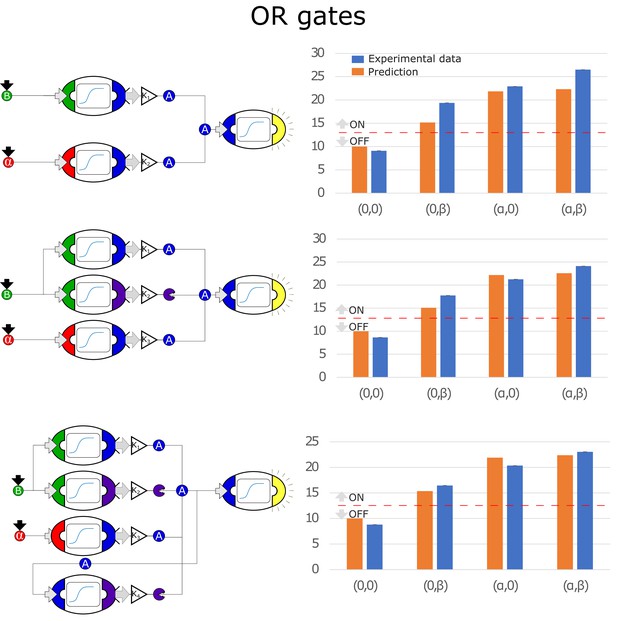
Optimal circuits, simulation, and experimental realization of the OR gate for 2, 3, and 4-node topologies.
Optimal circuits, simulation, and experimental realization of the OR gate for 2, 3, and 4-node topologies. Error bars represents the standard deviation of three biological replicates.
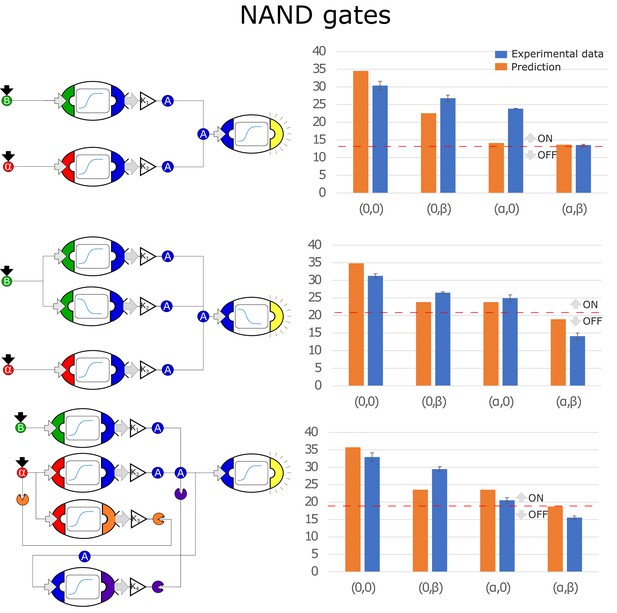
Optimal circuits, simulation, and experimental realization of the NAND gate for 2, 3, and 4-node topologies.
Optimal circuits, simulation, and experimental realization of the NAND gate for 2, 3, and 4-node topologies. Error bars represents the standard deviation of three biological replicates.
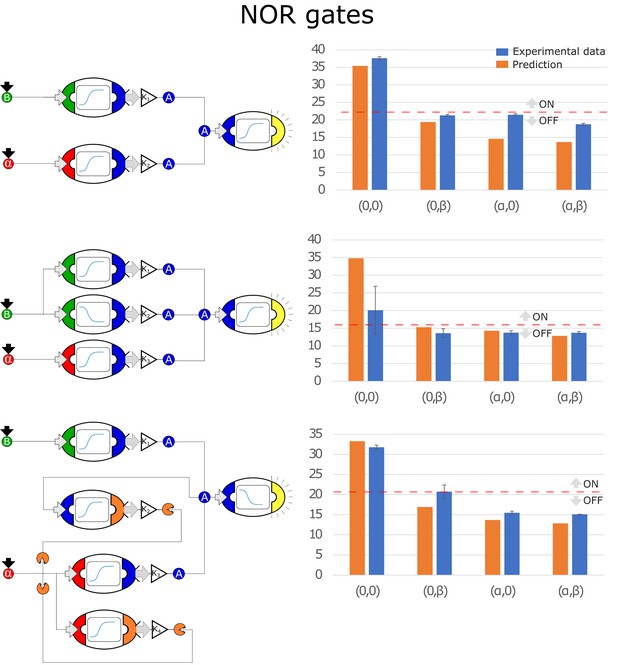
Optimal circuits, simulation, and experimental realization of the NOR gate for 2, 3, and 4-node topologies.
Optimal circuits, simulation, and experimental realization of the NOR gate for 2, 3, and 4-node topologies. Error bars represents the standard deviation of three biological replicates.
Model generated implementations of analog functions.
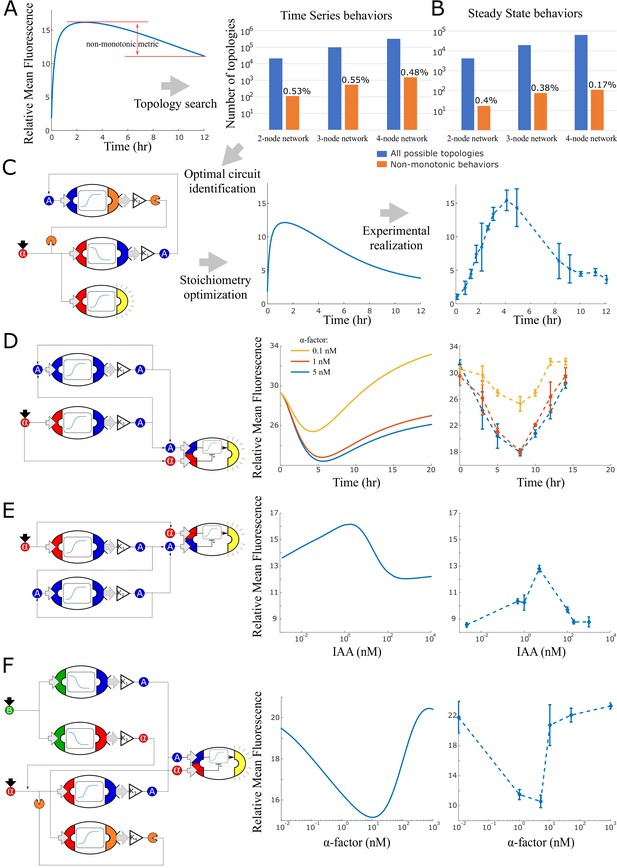
(A) An automated search algorithm was used to screen all possible strain combinations up to size four (plus one sensor strain) for non-monotonic behaviors. Specifically, we set up the search to find combinations that result in a pulse as a function of time or as a function of concentration (B). Top row: We define a non-monotonicity metric and rank all combinations according to that score. Bar graphs show the total number of possible strain combinations (blue) and the percentage that show non-linear behaviors. Results are organized by size of the strain combination and the type of target behavior. (C) Strain stoichiometries are optimized for the most promising strains to obtain more extreme maxima or minima. Left: a diagram of the highest scoring circuit for time pulses selected for testing. Center: behavior prediction after circuit stoichiometry optimization. Right: Experimental data for the time pulse circuits is shown. (D) Strain combination, model prediction, and experimental data for a system that results in a dip in fluorescence as a function of time rather than a peak. (E) Strain combination, model prediction and experimental data for a system that generates a peak at intermediate auxin concentration thus realizing a band-pass filter. (F) Strain combination, model prediction and experimental data for a system that generates a dip at intermediate alpha-factor concentrations. This system realizes a ‘band-stop’ filter, which is a combination of a low and a high-pass filter. Error bars represents the s.d. of three biological replicates.
-
Figure 5—source data 1
The data used for plotting Figure 5.
- https://cdn.elifesciences.org/articles/74540/elife-74540-fig5-data1-v3.xlsx





