Epithelial-to-mesenchymal transition proceeds through directional destabilization of multidimensional attractor

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: March 14, 2022 (This version)
Accepted Manuscript published: February 21, 2022 (Go to version)
Accepted: February 6, 2022
Received: October 20, 2021
Preprint posted: January 28, 2020 (Go to version)

1. Of interest
Vasculature: Exploring the dynamics of vascular adaptation

Thomas S Shimizu, E Toby Kiers, Howard A Stone

Insight May 25, 2023
Further reading

Article
Figures and data
Abstract
Editor's evaluation
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

How a cell changes from one stable phenotype to another one is a fundamental problem in developmental and cell biology. Mathematically, a stable phenotype corresponds to a stable attractor in a generally multi-dimensional state space, which needs to be destabilized so the cell relaxes to a new attractor. Two basic mechanisms for destabilizing a stable fixed point, pitchfork and saddle-node bifurcations, have been extensively studied theoretically; however, direct experimental investigation at the single-cell level remains scarce. Here, we performed live cell imaging studies and analyses in the framework of dynamical systems theories on epithelial-to-mesenchymal transition (EMT). While some mechanistic details remain controversial, EMT is a cell phenotypic transition (CPT) process central to development and pathology. Through time-lapse imaging we recorded single cell trajectories of human A549/Vim-RFP cells undergoing EMT induced by different concentrations of exogenous TGF-β in a multi-dimensional cell feature space. The trajectories clustered into two distinct groups, indicating that the transition dynamics proceeds through parallel paths. We then reconstructed the reaction coordinates and the corresponding quasi-potentials from the trajectories. The potentials revealed a plausible mechanism for the emergence of the two paths where the original stable epithelial attractor collides with two saddle points sequentially with increased TGF-β concentration, and relaxes to a new one. Functionally, the directional saddle-node bifurcation ensures a CPT proceeds towards a specific cell type, as a mechanistic realization of the canalization idea proposed by Waddington.

Editor's evaluation

This is a multifaceted study of the epithelial to mesenchymal transition (EMT) in live cells. EMT is relevant for cancer, development, and wound healing. The authors were able to discern two possible cell transition path categories without multi-color labeling or other advanced experimental approaches, which could be impactful for other studies. The study draws on a wide range of experimental, data science, and modelling tools and techniques.

https://doi.org/10.7554/eLife.74866.sa0

eLife digest

Cells with the same genetic code can take on many different formss, or phenotypes, which have distinct roles and appearances. Sometimes cells switch from one phenotype to another as part of healthy growth or during disease. One such change is the epithelial-to-mesenchymal transition (EMT), which is involved in fetal development, wound healing and the spread of cancer cells.

During EMT, closely connected epithelial cells detach from one another and change into mesenchymal cells that are able to migrate. Cells undergo a number of changes during this transition; however, the path they take to reach their new form is not entirely clear. For instance, do all cells follow the same route, or are there multiple ways that cells can shift from one state to the next?

To address this question, Wang et al. studied individual lung cancer cells that had been treated with a protein that drives EMT. The cells were then imaged at regular intervals over the course of two to three days to see how they changed in response to different concentrations of protein. Using a mathematical analysis designed to study chemical reactions, Wang et al. showed that the cells transform into the mesenchymal phenotype through two main routes.

This result suggests that attempts to prevent EMT, in cancer treatment for instance, would require blocking both paths taken by the cells. This information could be useful for biomedical researchers trying to regulate the EMT process. The quantitative approach of this study could also help physicists and mathematicians study other types of transition that occur in biology.

Introduction

Cells of multicellular organisms assume different phenotypes that can have drastically different functions, morphologies, and gene expression patterns, and can undergo distinct changes when subjected to specific stimuli and microenvironments. Examples of cell phenotypic transitions (CPTs) include cell differentiation during development and induced and spontaneous cell fate transition such as reprogramming and trans-differentiation. Epithelial-to-mesenchymal transition (EMT) is a prototypic progress that has been extensively studied due to its significance in cell and developmental biology as well as in biomedical research (Figure 1a). Recent advances in single-cell techniques have further accelerated the long-term efforts on unraveling the mechanisms of CPTs, for understanding processes such as differentiation and reprogramming in developmental and cell biology, and for potential biomedical implications of modulating cell phenotypes in regenerative medicine and diseases such as cancer and chronic diseases (Wagner and Klein, 2020; Weinreb et al., 2020).

Figure 1

Download asset Open asset

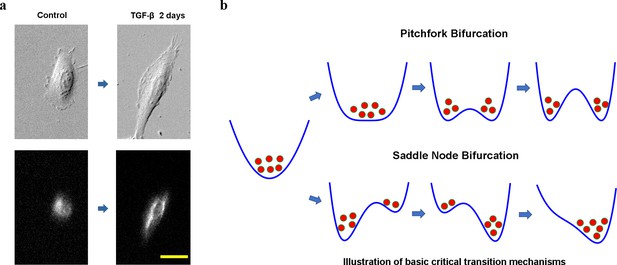
Cell phenotypic transitions as critical state transitions.

(a) Transmission light and fluorescence (Vimentin-RFP) images showing an A549/Vim-RFP cell undergoing epithelial-to-mesenchymal transition. Scale bar: 30 µm. (b) Possible critical transition mechanisms in EMT. This is an illustration of pitchfork (top) and saddle-node (bottom) bifurcations using 1-D potential systems.

Considering cell as a dynamical system, understanding the CPT process from a dynamical systems theory perspective is an intriguing long-standing question in mathematical and systems biology. Mathematically, at any time a cell state can be specified by a set of state variables, such as gene expression levels, or other collective cell feature variables. A stable cell phenotype is an attractor in a high-dimensional cell state space formed by the state variables (Huang et al., 2005), and a CPT is a transition between different attractors. Waddington famously made an analogy comparing developmental processes to a ball sliding down a potential landscape, and diverging into multiple paths at some bifurcation points (Rand et al., 2021). This picture exemplifies a pitchfork bifurcation, where an original stable attractor turns to an unstable saddle point together with the emergence of two new attractors (Figure 1b top). Another well-discussed mechanism for attractor-to-attractor transition is through a series of saddle-node bifurcations, where first a new fixed point emerges, splits into a saddle point and attractor, then the saddle point separating the two attractors moves toward and eventually collides with the old attractor to destabilize the latter (Figure 1b bottom). A notable difference between the two types of bifurcations is that after a pitchfork bifurcation the original state can relax to multiple new stable states, while the saddle-node bifurcation the system is directed to relax to one attractor. A fundamental theoretical question is which mechanism a CPT process assumes, and why.

Pitchfork and saddle-node bifurcation are two important theoretical mechanisms of critical state transition and have been discussed in the context of CPTs (Mojtahedi et al., 2016). A new challenge then is how to evaluate various mathematical models experimentally at single cell levels. Several studies have suggested that analyzing snapshot single-cell genomics data (Mojtahedi et al., 2016; Chen et al., 2012), fixed cell data, to understand critical state transitions cannot provide temporal information on how individual cells transition. In addition, information from fluorescence-based live cell imaging is typically restricted to a small number of molecular species. Thus, tracking a small number of molecular species through live cell imaging cannot provide the collective transition dynamics due to the intrinsic high-dimensional nature.

Specifically in the context of EMT, theoretical studies suggest that EMT proceeds as a saddle-node bifurcation (Tian et al., 2013); however, there is no direct experimental study on the single-cell transition dynamics. As recognized in a consensus statement from researchers in the EMT field, several open questions and challenges exist on understanding the mechanisms of the EMT process (Yang et al., 2020). For example, it is unclear whether the process proceeds as hopping among a small number of discrete and distinct intermediate states, or a continuum of such states with no clear boundary. The transition may proceed either along a linear array of states or through multiple parallel paths. Pseudo-time analyses of high throughput single cell genomics studies infer that EMT proceeds through a 1-D continuum path (McFaline-Figueroa et al., 2019), consistent with a prevalent EMT axis concept with the epithelial and the mesenchymal states as the two end states (Nieto et al., 2016). These predictions, which are indirectly inferred from snapshot single-cell data, require direct testing by tracking single cells over time. However, live cell imaging studies are impeded because EMT status cannot be assessed based on only a small number of molecular markers such as key transcriptional factors (Yang et al., 2020).

To address the above challenge when studying EMT dynamics, recently we developed a platform of tracking cell state change in a composite cell feature space that is accessible for multiplex and long-term live cell imaging (Wang et al., 2020). Here, we first apply the platform to study EMT in a human A549 derivative cell line with endogenous vimentin-RFP labeling (ATCC CCL-185EMT, denoted as A549/Vim-RFP in later discussions) induced by different concentrations of TGF-β. Then we analyze an ensemble of recorded multi-dimensional single-cell trajectories within the framework of reaction rate theories that have been a focused subject in the context of physics and chemistry.

Results

Single-cell trajectories are mathematically represented in a collective morphology/texture feature space

For quantitative studies of CPT dynamics, one first needs to establish a mathematical representation of the cell states and cell trajectories. Mathematically, one can represent a cell state by a point in a multi-dimensional space defined by gene expression (Ye and Sarkar, 2018) or other cell properties (Gordonov et al., 2016; Chang and Marshall, 2019; Kimmel et al., 2018). Noticing that cells have phenotype-specific morphological features that can be monitored even with transmission light microscopes, recently we developed a framework that defines cell states in a combined morphology and texture feature space (Wang et al., 2020). The framework allows one to trace individual cell trajectories during a CPT process through live-cell imaging. We applied the framework to study the TGF-β induced EMT with the A549/Vim-RFP cells (Figure 2; Wang et al., 2020). Vimentin is a type of intermediate filament protein commonly used as a mesenchymal marker, and changes its expression and spatial distribution during EMT (Zhang et al., 2014). Furthermore, during EMT cells undergo dramatic change of cell morphology accompanying gene expression change (Figure 1a; Zhang et al., 2014; Zhang et al., 2019). Accordingly, we used a combination of vimentin texture and cell shape features to specify a cell state.

Figure 2

Download asset Open asset

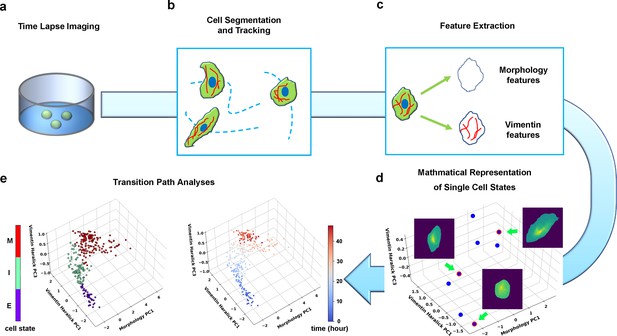
Summary of pipeline for recording and analyzing single-cell trajectories in composite multi-dimensional cell feature space.

(a) Time-lapse imaging of A549/Vim-RFP cells treated with TGF-β. (b) Deep-learning aided single-cell segmentation and tracking on the acquired time-lapse images. (c) Extraction of morphology and vimentin features of single cells. (d) Representation of single cell states in a multidimensional morphology/texture feature space. (e) Transition path analyses over recorded trajectories. Right: A representative single cell trajectory of EMT in the feature space. Color represents time (unit: hour). Left: the same trajectory colored by the regions in the feature space (E, I, and M, for epithelial, intermediate, and mesenchymal regions, respectively) each data point resides. Reduced units are used in this and all other figures.

We first performed time-lapse imaging of the EMT process of A549/Vim-RFP induced with 4 ng/ml TGF-β (Figure 2a, Materials and methods Wagner and Klein, 2020; Weinreb et al., 2020), then performed single-cell segmentation and tracking on the acquired images (Figure 2b, Materials and methods Huang et al., 2005). We quantified the images with an active shape model (Cootes et al., 1995) and performed principal component analysis (PCA) to form a set of orthonormal basis vectors of collective variables, which include cell body shape of 296 degrees of freedom (DoF) quantified by an active shape model (Cootes et al., 1995), and texture features of cellular vimentin distribution quantified by 13 Haralick features (Haralick, 1979; Figure 2c, Materials and methods Huang et al., 2005). Then the state of a cell at a given instant is represented as a point in the 309-dimensional composite morphology/texture feature space (Figure 2d), and the temporal evolution of the state forms a continuous trajectory in the space subject to further theoretical analyses (Figure 2e).

Transition path analyses identify an ensemble of reactive single-cell trajectories

Before TGF-β treatment, a population of cells assume a localized stationary distribution in this 309-dimensional composite space, and most cells are epithelial (Figure 3a, blue). TGF-β treatment destabilizes such distribution, and the cells relax into a new stationary distribution dominated by mesenchymal cells (Figure 3a red). We recorded 204 continuous trajectories in the state space. A representative trajectory shown in Figure 2e (right) (also in Video 1) reveals how a cell transits step-by-step from an epithelial cell with convex polygon shapes and a localized intracellular vimentin distribution, to the mesenchymal phenotype with elongated spear shapes and a dispersive vimentin distribution.

Figure 3 with 1 supplement see all

Download asset Open asset

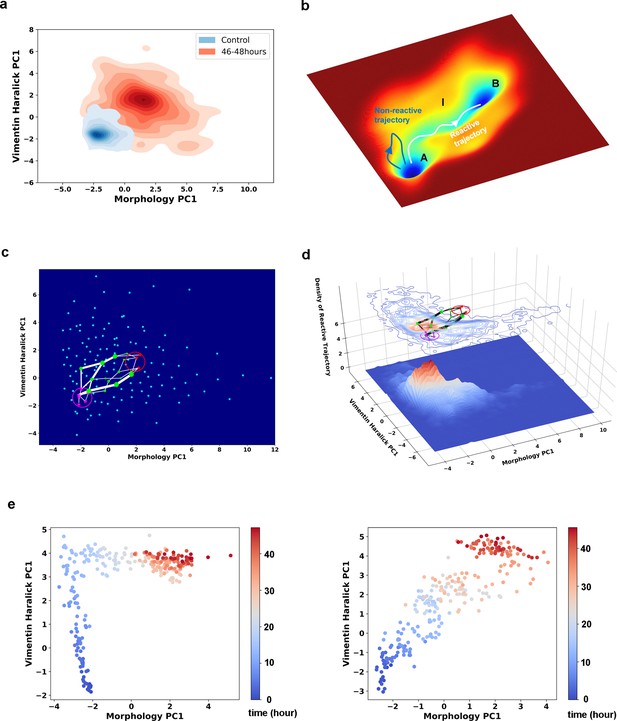
Single cell trajectories of EMT form two distinct groups.

(a) Kernel density estimation of cells in control condition (Blue) and cells after being treated with 4 ng/ml TGF-β for 46–48 hours (Red). (b) Schematic example reactive and nonreactive trajectories in a potential system. Also shown is a valley connecting regions A and B that most reactive trajectories fall in and form a reaction tube. (c) Discretization of the whole single cell data set with self-organizing map into 12 × 12 discrete states (clusters) in the state space. Directed network generated base on the self-organizing map and the transitions between states. The distance between two states is defined as the negative logarithm of transition probability. White lines are shortest between epithelial states (purple stars) and mesenchymal states (red stars). Green dots are states that the shorted paths pass by. The size of a dot stands for the frequency of this dot passed by shortest paths. The width of a white line represents the frequency that these shortest paths pass by. (d) Contour map (top, superimposed with the shortest paths in panel c) and 3D surface-plot (bottom) of density of reactive trajectories in the plane of morphology PC1 and vimentin Haralick PC1. (e) Representative trajectories from the two groups. Left: Vimentin varies first. Right: Concerted variation.

Video 1

Download asset

posterframe for video — Recorded live cell trajectory in Figure 2e.

Each frame is a segmented cell mask cropped from the original vimentin fluorescence image.

Next, we applied rate theory analyses on the recorded single-cell trajectories. Rate theory studies how a system escapes from a metastable state, or relaxation from one stationary distribution to a new one (Hänggi et al., 1990). Specifically, transition path theory (TPT) is a modern development in the field (Weinan et al., 2005; Rohrdanz et al., 2013; Bolhuis et al., 2002; Weinan and Vanden-Eijnden, 2010). Within the TPT framework, one divides the state space into regions containing the initial (A) and final (B) attractors, and an intermediate (I) region. A reactive trajectory is one that originates from region A, and enters region I then B before re-entering region A (Figure 3b). The reactive trajectories form an ensemble of transition paths that connect regions A and B.

Accordingly, we divided the four-dimensional principal component subspace into epithelial (E), intermediate (I), and mesenchymal (M) regions (Figure 2e left) (Wang et al., 2020). With this division of space, we identified a subgroup of 135 recorded single-cell trajectories that form an ensemble of reactive trajectories that connect E and M by day 2. It should be noted that the practical definition of reactive trajectories here differs from the theoretical definition in classical TPT. In classical TPT, one runs a trajectory of infinite length that travel back and forth between the initial and final regions numerous times, and a reactive trajectory refers to a segment that starts from the initial region and ends in the final region.

TGF-β induced EMT in A549/Vim-RFP cells proceeds through parallel transition paths

We first examined whether EMT proceeds through one or multiple types of paths by analyzing the ensemble of reactive trajectories using self-organizing map (SOM) (Materials and methods Rand et al., 2021). SOM is an unsupervised artificial neural network that utilizes a neighborhood function to represent the topology structure of input data (Kohonen, 1982). The algorithm clusters the recorded cell states into 144 discrete states, and represents the EMT process as a Markovian transition process among these states (Figure 3—figure supplement 1). Shortest path analysis using the Dijkstra algorithm (Dijkstra, 1959) over the transition matrix reveals two groups of paths: vimentin Haralick PC1 varies first, and concerted variation of morphology PC1 and vimentin Haralick PC1, with finite probabilities of transition between the two groups (Figure 3c). This result is consistent with our previous trajectory clustering analysis using dynamics time warping (DTW) distance between reactive trajectories (Wang et al., 2020). To further support this conclusion, we examined the density of reactive trajectories ρ_R, in the plane of morphology PC1 and vimentin Haralick PC1 (Materials and methods Mojtahedi et al., 2016). The contour map of ρ_R shows two peaks corresponding to the two groups of shorted paths in the directed network (Figure 3d). The peak where vimentin Haralick PC1 varies first is higher than the peak of concerted variation, indicating more reactive trajectories along this path. The distinct features of the two types of trajectories are apparent from the two representative single-cell trajectories shown in Figure 3e.

A revised string method is developed to reconstruct reaction coordinate from single-cell trajectories

Due to the continuous and stochastic nature of the system dynamics there are infinite number of reactive trajectories, which mainly concentrate within a tube in the state space that connects regions A and B (Figure 3b; Weinan and Vanden-Eijnden, 2010). The center of the tube has been used to define a reaction coordinate (RC), a concept central to rate theories (Figure 4a; Vanden-Eijnden and Venturoli, 2009). A RC is a one-dimensional geometric parameter (denoted as s in the subsequent discussions) that describes the progression along a continuous reaction path defined in the state space (Rohrdanz et al., 2013). A good choice of RC can provide mechanistic insight on how the transition process proceeds.

Figure 4 with 1 supplement see all

Download asset Open asset

Reaction coordinate reconstruction of two parallel paths from reactive A549/Vim-RFP EMT trajectory ensemble with a modified string method.

(a) Discrete representation of a 1-D reaction coordinate (i.e. image points, represented as colored dots) on the filled contour map with corresponding Voronoi cells. The cyan line is a reactive trajectory that starts from A and ends in B. (b) Reconstructed RCs from reactive single cell EMT trajectories using a revised finite temperature string method. Single cell images represent typical cell states in their locations (Epithelial state, mesenchymal state, in mid-transition with vimentin varies first and in mid-transition with concerted variation) (c) Separate representation of the RCs overlaid with representative reactive single-cell trajectories. Top: vimentin varies first; Bottom: concerted variation. For visual clarity, the trajectories were plotted with data points separated by 50 min. (d) Cell shape (left), Haralick feature (right) along RC s₁. The colors of the cell shapes in b/c left represent progression of EMT (starts from blue and ends in red). Haralick feature 1: Angular Second Moment; 2: Contrast; 3: Correlation; 4: Sum of Squares: Variance; 5: Inverse Difference Moment; 6: Sum Average; 7: Sum Variance; 8: Sum Entropy; 9: Entropy; 10: Difference Variance; 11: Difference Entropy; 12: Information Measure of Correlation 1; 13: Information Measure of Correlation 2. (e) Similar to panel e but along RC s₂.

Therefore, we set to reconstruct the RC for each path with the recorded reactive trajectories using a revised finite temperature string method, which was originally designed for RC reconstruction for theoretical and computational modeling systems (Vanden-Eijnden and Venturoli, 2009; Allen et al., 2005; Dickson et al., 2009). The method first approximates the RC by a set of discrete image points that are uniformly distributed along the arc length of the RC, so the multi-dimensional state space can be divided by a 1-D array of Voronoi polyhedra containing individual images, and the data points can be assigned to individual Voronoi cells (Figure 4a). Starting with a trial RC to define the initial division of the Voronoi cells, one optimizes the trial RC iteratively by minimizing the distance dispersion between the string point and sample points within each Voronoi cell (Figure 4—figure supplement 1). Since here we have an ensemble of continuous trajectories, we modified the iteration procedure slightly. Specifically, we minimized both the distance between the ensemble of measured reactive trajectories and the image point within each individual Voronoi cell, as well as the overall distance between each individual trajectory and the trial RC (Materials and methods Chen et al., 2012).

Therefore, we grouped the reactive trajectories based on the DTW distance, then identified the RCs for each group separately following the modified string method. The iteration procedure gives the RC of each path ( $s_{1}$ and $s_{2}$ ) that characterizes common features of the reactive trajectories for the TGF-β induced EMT in A549/Vim-RFP cells (Figure 4b). The recorded trajectories fluctuate around the RCs and form reaction tubes as expected from the TPT theory (Figure 4c). Along each RC, the cell shape changes dominantly through elongation and growth (Figure 4d & e, left), and most of the 13 vimentin Haralick features increase or decrease monotonically and continuously over time (Figure 4d & e, right) (Materials and Methods Tian et al., 2013). The two RCs first diverge from the E region to follow two distinct paths, then converge within the M region. In one group (Figure 4d), most of the Haralick feature changes take place before major morphology change. For the group with concerted dynamics (Figure 4e), both cell shape and Haralick features vary gradually along the RC.

Reconstructed reaction coordinate and quasi-potentials reveal EMT as relaxation along continuum manifolds

Considering a cell as a dynamical system, with the single-cell trajectories one may formulate an inverse problem to reconstruct the underlying dynamical equations governing the EMT transition. Let’s take a minimal ansatz that assumes the dynamics of the collective variables (x) can be described by a set of Langevin equations in the morphology/texture feature space, $d x / d t = F (x) + η (x, t)$ , where F(x) is a governing vector field, and η are white Gaussian noises with zero mean. Then in principle one can reconstruct F(x) from the single-cell trajectory data, $F (x) = ⟨ d x / d t ⟩$ , averaged over the neighborhood of each x. Notice for the ensemble average one needs to use all the reactive and nonreactive trajectories.

For mathematical simplicity and better numerical convergence, here we restricted to reconstructing the dynamics along the RC (Figure 5a). The ansatz becomes a 1-D convection-diffusion process, $d s / d t = - d ϕ / d s + η$ . Notice that for a 1-D system even without detailed balance one can define a quasi-scalar potential ϕ (Xing, 2010; Xing and Kim, 2011; Risken, 1996). This quasi-potential corresponds to a potential of mean force in the case of a conserved system. To confirm that the ansatz of using a memory-less 1-D Langevin equation is a good approximation for the EMT dynamics along a RC, we performed the Chapman-Kolmogorov Test (CK-test). The test shows that the one-step transition matrix can indeed predict the dynamics on longer time scales, and thus the Markovian assumption is a good zero^th-order approximation of the EMT dynamics (Figure 5—figure supplement 1, Materials and Methods Yang et al., 2020).

Figure 5 with 7 supplements see all

Download asset Open asset

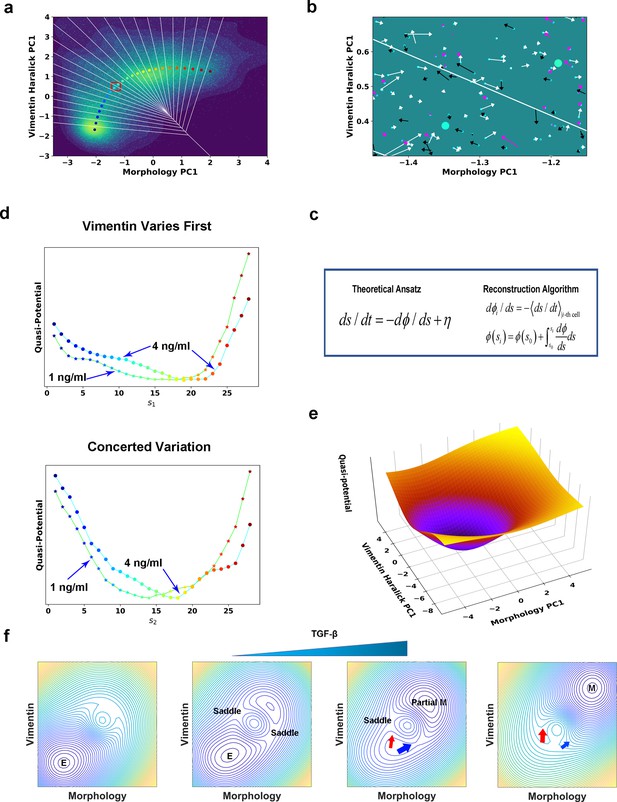
Quantification of dynamics along the two RCs suggests a mechanism of forming two EMT paths through sequential saddle-node collisions.

(a) Reconstructed RC s₁ on density plot of single cell trajectories data. Cyan dots are single cell data points. (b) Enlarged view of the red box region in (a). The arrow associated with each data point (cyan dot) represents the value of ds/dt (white: > 0, magenta: = 0, black: < 0). (c) Theoretical framework of dynamics reconstruction along the RC. (d) Comparison of reconstructed quasi-potentials along the RC with 1 ng/ml (star) and 4 ng/ml (circle) TGF-β treatment. Top: Reconstructed quasi-potentials along RC s₁. Bottom: Reconstructed quasi-potentials along RC s₂. (e) Quasi-potential of the control cells based on kernel density estimation. (f) A metaphorical potential system to illustrate a plausible mechanism for generating the two paths through sequential collision between a stable attractor and two saddle points when the concentration of TGF-β increases. The width of the arrows represents the probabilities that single-cell trajectories follow corresponding paths. E: epithelial attractor; Partial M: partial EMT attractor; M: mesenchymal attractor.

To reconstruct the dynamical equations, we used the measured trajectories and instant velocities (along the RC direction) as input. An enlarged view in Figure 5b shows the instant velocities (ds/dt) of various trajectories segments within Voronoi cells. Numerically, we related the potential gradient dϕ/ds with the mean velocity within the i_th Voronoi cell through averaging over all recorded reactive and nonreactive trajectory segments that locate within the Voronoi cell at any time t (Figure 5a & c, Materials and methods McFaline-Figueroa et al., 2019; Nieto et al., 2016). On the obtained curve of dϕ/ds vs. s (Figure 5—figure supplement 2), the zeroes correspond to stationary points of the potential. We then reconstructed the quasi-potential through integrating over s, $ϕ (s_{i}) = ϕ (s_{0}) + \int_{s_{0}}^{s_{i}} (d ϕ / d s) d s$ (Figure 5d). We also obtained the quasi-potential of the untreated cells (Figure 5e) from the steady state distribution of untreated cells along the RC, $ϕ_{0} \propto - \log p_{s s}$ .

The reconstructed RCs and quasi-potentials provide mechanistic insight on the transition. Before TGF-β induction, cells reside on the untreated cell potential centered with a potential well corresponding to the epithelial attractor (Figure 5e). After induction, the system relaxes following the new potential into a new well corresponding to the mesenchymal attractor. Notably, in the new potential the original epithelial attractor disappears, reflecting that the epithelial phenotype is destabilized under the applied 4 ng/ml TGF-β concentration.

With the reconstructed quasi-potentials and variance of dϕ/ds obtained from experiment, we solved the Fokker-Planck (FP) equation corresponding to the Langevin equation to predict the steady distribution vs. RC (Materials and methods Wang et al., 2020). While the dynamical equations were reconstructed from trajectories during the transition process and with a minimal Langevin equation ansatz, the predicted stationary distribution have average values and standard deviations, (17.2, 4.6) and (14.7, 4.4) for the two paths, respectively, close to those calculated from the distributions sampled from cells after 39 h TGF-β treatment, (16.0, 5.0) and (16.2, 4.0), respectively (Figure 5—figure supplement 3a and b).

Lowering TGF-β concentration leads to relaxation to a new partial EMT attractor through two parallel paths

Notice that quasi-potential with 4 ng/ml TGF-β for the Vimentin varies first path shows a plateau around s₁ = 8 (Figure 5d). We hypothesized that this plateau is a remnant of the original epithelial attractor, and if so we expect to observe a flatter plateau or even a metastable attractor with a lower TGF-β concentration. Therefore, we treated A549/Vim-RFP cells with 1 ng/ml TGF-β and recorded 135 3-day long single-cell trajectories. Among the recorded trajectories 65 indeed reached the M region. The reactive trajectories also cluster into two groups (Figure 5—figure supplement 4). For the purpose of comparison, we projected the trajectories onto the RCs obtained from the 4 ng/ml TGF-β and reconstructed the quasi-potentials in the case of 1 ng/ml of TGF-β. Indeed, the quasi-potential for the path with vimentin varying first has a plateau flatter than that of the 4 ng/ml TGF-β-treated cells. The quasi-potential of another path, however, does not show such flattening.

In the EMT field, it is under debate whether EMT has a discrete or continuum spectrum of intermediate states (Yang et al., 2020). Single-cell transcriptomic studies reveal intermediate states (Cook and Vanderhyden, 2020). If EMT proceeds through a set of discrete and definite states, we expect to observe attractors, i.e., potential wells, corresponding to these states. In addition, lowering the TGF-β concentration would lead to an increased barrier between neighboring wells and cells trapped at some intermediate state for a long time. While all the quasi-potentials at the two TGF-β concentrations reveal destabilization of the epithelial attractor, they do not have multiple attractors anticipated for discrete EMT states (Figure 5e dϕ/ds in Figure 5—figure supplement 5a, b). Compared to those at 4 ng/ml TGF-β, both quasi-potentials at 1 ng/ml TGF-β have the new attractor closer to the epithelial state. Examination of individual trajectories also reveals that cells with 1 ng/ml TGF-β treatment leave the E region and mostly reside around a new attractor in the I region (Figure 5—figure supplement 5c, d). Some trajectories fluctuate within the attractor and only transiently reach the M region. That is, cells reach a new stable phenotype whose degree of mesenchymal features depends on the TGF-β concentration, which is consistent with previous studies on MCF10A cells treated with different concentrations of TGF-β (Zhang et al., 2014). Fluctuations of single-cell trajectories limit the state resolution in the cell feature space and prevent us from telling whether the two paths reach one common intermediate state or two distinct ones. To examine how the number of Voronoi cells affects the quasi-potential properties, we varied the number of discretization points along the RCs and did the same analysis to reconstruct the quasi-potential (Figure 5—figure supplement 6a and b). The reconstructed potentials have similar shapes, although show different smoothness.

Discussion

Cell type regulation is an important topic in mathematical and systems biology, and several theoretical and computational studies on modeling CPT systems have been performed in the context of rate theories (Aurell and Sneppen, 2002; Brackston et al., 2018; Morelli et al., 2008; Wang et al., 2014; Ge et al., 2015; Wang et al., 2011; Tse et al., 2018). Recent advances in single-cell techniques have catalyzed quantitative measurements on the dynamics of CPTs, and have opened new questions on how to quantify and analyze single-cell data in the framework of dynamical systems theory and how it compares with theoretical results. In our previous studies (Wang et al., 2020), we developed an integrated live cell imaging and image analysis framework for quantifying and representing live cell imaging data. In this work, we further showed that the mathematical representation allows one to analyze the single cell trajectories and study CPT dynamics using rate theories for quantitative mechanistic insights (Figure 5—figure supplement 7).

A long-held concept in cell and developmental biology is that cells exist as discrete and distinct phenotypes. Single cell genomics measurements have challenged such views and have revealed that cells move along continuum manifolds. The live cell imaging studies presented here support such a picture by demonstrating EMT as a relaxation along a continuum manifold, which is also supported by single cell RNA-seq studies (McFaline-Figueroa et al., 2019).The high-throughput single-cell data provides high dimensional information, but identifying the intermediate states in the snap-shot data requires the development of new dimension reduction and clustering methods (MacLean et al., 2018). Compared to the snapshot studies, live cell trajectories reveal that the EMT trajectories can be clustered as fluctuating around two distinct paths that connect the epithelial and mesenchymal phenotypes. The existence of two types of transition paths suggest that the previously proposed conceptual 1D EMT axis (Nieto et al., 2016) is insufficient for understanding how EMT proceeds, and puts dynamics inferred indirectly from snapshot data questionable (McFaline-Figueroa et al., 2019). Extracting multi-dimensional features from live cell imaging data provides a complementary strategy, and further development along this direction will benefit from advances of imaging technology and algorithm (Christiansen et al., 2018; Ounkomol et al., 2018).

In rate theories, identifying an appropriate RC provides mechanistic insights of a transition process. For example, recognizing collective solvent reorganization as part of the reaction coordinate is a key part of Marcus’s electron transfer theory (Marcus, 1993). Adopting the fraction of native contacts as a RC also historically plays a key role in the development of protein folding theories. Therefore, continuous efforts have been made on defining an optimal RC for a complex dynamical system (Li and Ma, 2014; Best and Hummer, 2005; Fukui, 2002), and it is even questionable to assume that the system dynamics can be well presented by a 1-D RC, as suggested by theoretical analysis on protein folding (Udgaonkar, 2008). Indeed, the analyses presented in this study shows such a breakdown of this basic assumption.

In the introduction, we discussed two basic mechanisms of critical state transitions. For TGF-β induced EMT in A549 cells, analysis of the trajectories reveals that mathematically multiple paths may originate from destabilization of a multi-dimensional epithelial attractor through colliding with multiple saddle points sequentially. We illustrated such a mechanism in Figure 5f and in Video 2 schematically with a metaphorical potential system. With no or low TGF-β, the system resides in the epithelial attractor (Figure 5f, first). Adding TGF-β leads to the appearance of a new (mesenchymal) attractor, and elevation of the epithelial attractor (Figure 5f, second). The epithelial attractor approaches and collides first with a saddle point to form a barrier-less (concerted-variation) path to the new attractor (Figure 5f, third). At this TGF-β concentration (e.g. 1 ng/ml), some barrier still exists along an alternative (vimentin-first) path, which then disappears with the increase of TGF-β concentration again (as revealed in Figure 5d) through saddle node collision (Figure 5f, fourth). Indeed, we observed the reactive trajectories predominantly assume the concerted-variation path under 1 ng/ml TGF-β treatment (Figure 5—figure supplement 4a), while the vimentin-first path becomes dominant under 4 ng/ml TGF-β treatment (Figure 5—figure supplement 4b). It should be pointed out that this sequential saddle-node bifurcation mechanism is only a plausible one that can explain the experimental data. Multidimensional systems can show complex bifurcation patterns (Rand et al., 2021; Kheir Gouda et al., 2019). With sufficient single-cell trajectories, one can extend the procedure described in this work and in Qiu et al., 2022 to reconstruct the multi-dimensional vector field and the full governing Fokker-Planck equations directly. The full model will help address questions on the role of noise in CPTs (Balázsi et al., 2011).

Video 2

Download asset

One major limitation of the minimal Langevin equation ansatz used in this work is that the dynamics is assumed to be Markovian, that is, the temporal evolution of the system depends only on the current but not previous cell state. A cell has a much larger number of degrees of freedom than what can be measured explicitly through live-cell imaging, and these implicit degrees of freedom result in possible non-Markovian dynamics. Future studies may use the generalized Langevin equation formalism that takes into account the non-Markovian effects. In addition, we used the added exogenous TGF-β concentration as a control parameter, as in previous studies (Tian et al., 2013; Zhang et al., 2014). Cells also secrete endogenous TGF-β, and interact with other cells, so the extracellular microenvironment for individual cells is in general spatially and temporally changing. In future studies, one can relax the mean-field approximation assumed in this work. Experimentally, one can use microfluidic chambers for more precise control of extracellular environments. Furthermore, one needs to identify the expression profiles of cell states along the two paths for deeper mechanistic understanding how the two paths emerge and how one can modulate the EMT dynamics, possibly through combining live cell imaging and fixed-cell measurements.

In summary, through an integrated framework of live cell imaging and single-cell trajectories with dynamical systems theories we obtained quantitative mechanistic insights of TGF-β induced EMT as a prototype for CPTs in general. Since a cell is a complex dynamical system with many strongly coupled degrees of freedom and a broad range of relevant time scales, further development will benefit from a finer resolution of cell state through including additional measurable cell features.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Cell line (Homo sapiens, human)	A-549 VIM RFP	American Type Culture Collection(ATCC)	Cat# CCL-185EMTRRID:SCR_007358
Peptide, recombinant protein	TGF-β (Recombinant Human TGF-beta 1 Protein)	R&D Systems	Cat#240-B
Software, algorithm	CellProfiler	Broad Institute	RRID:SCR_007358
Software, algorithm	Scipy	PMID:32015543	RRID:SCR_008058	https://scipy.org/

Cell line

Request a detailed protocol

A549/VIM-RFP cells were obtained from (ATCC CCL-185EMT, RRID:CVCL_LI35), and cells within 5–15 generations were used in the studies. Cells were cultured in F-12K medium (Corning) with 10% fetal bovine serum (FBS) in MatTek glass bottom culture dishes (P35G-0–10 C) in a humidified atmosphere at 37 °C and 5% CO2, as detailed in Wang et al., 2020. The cell line was authenticated as A549 cells with short tandem repeat (STR) analysis by University of Arizona Genetics Core (UAGC). The result of mycoplasma contamination test (MycoFluor Mycoplasma Detection Kit Molecular Probes, M-7006) was negative.

Time-lapse imaging

Request a detailed protocol

Time-lapse images were taken with a Nikon Ti2-E microscope with differential interference contrast (DIC) and TRITC channels (Excitation wavelength is 555 nm and Emission wavelength is 587) (20× objective, N.A. = 0.75). The cell culture condition was maintained with Tokai Hit Microscope Stage Top Incubator. For the 4 ng/ml TGF-β (R&D Systems 240-B) experiment, cells were imaged every 5 min with the DIC channel and every 10 min with the TRITC channel for 2 days. The exposure time for DIC was 100 ms and the exposure time for the TRITC channel was 30 ms. For the 1 ng/ml TGF-β experiment, cells were imaged every 5 min with the DIC channel and every 15 min with the TRITC channel for 3 days. The exposure time for DIC was 100ms and the exposure time for the TRITC channel was 30ms. While taking the images, all the imaging fields were chosen randomly.

Trajectory analyses

Request a detailed protocol

After single-cell segmentation, we performed single cell tracking with CellProfiler (RRID:SCR_007358) using a linear assignment problem (LAP) method (Jaqaman et al., 2008; Carpenter et al., 2006). To reduce the influence of over- and under-segmentation on the trajectory analysis, we utilized the cell tracking to detect these false segmentations through calculating the overlap relationship between single cells in the consecutive frames. If a cell in one frame and its maximum overlap cell in the next frame do not belong to the same trajectory, cells that overlap with the two cells were manually checked. Specifically, we trained an CNN (ResNet) to identify the over- and under-segmented cells (He et al., 2016). To increase accuracy, we used both the prediction results from this CNN, and other criteria. For instance, falsely segmented cells usually do not exist for a long duration. We used the lasting duration (30 minutes) to identify possible over- and under-segmentation. The identified falsely segmented cells were removed from the trajectories, and the broken trajectories were relinked using the LAP method.

We represented the state of a cell by its morphology and Vimentin Haralick features (Wang et al., 2020). The morphology was described with the active shape model (Pincus and Theriot, 2007). Calculation of Haralick features was based on the gray-level co-occurrence matrix G. $G_{i j}$ is the frequency of observing the gray-levels values of two neighboring pixels i and j, respectively. It was normalized by the total counts. In 2D images, there are four directions of such neighbors (0°, 45°, 90°, and 135°). To be rotation invariant, each feature was calculated on all the four directions of G matrix and averaged over them. Haralick features include the following features: 1 Angular Second Moment; 2: Contrast; 3: Correlation; 4: Sum of Squares: Variance; 5: Inverse Difference Moment; 6: Sum Average; 7: Sum Variance; 8: Sum Entropy; 9: Entropy; 10: Difference Variance; 11: Difference Entropy; 12: Information Measure of Correlation 1; 13: Information Measure of Correlation 2.

Self-organizing map and shortest transition paths in the directed network

Request a detailed protocol

The self-organizing map is an unsupervised machine learning method to represent the topology structure of date sets. We used a 12 × 12 grid (neurons) to perform space approximation of all reactive trajectories. The SOM was trained for 50 epochs on the data with Neupy (http://neupy.com/pages/home.html). We set the learning radius as one and standard deviation 1. These neurons divide the data into 144 micro-clusters ( ${ψ}$ ). With the single-cell trajectory data, we counted the transition probabilities from cluster i to cluster j (including self), with $\sum_{j} p_{i j} = 1$ . If the transition probability is smaller than 0.01, the value is then reset as 0. With the transition probability matrix, we built a directed network of these 144 neurons (Figure 3—figure supplement 1). The distance (weight) of the edge between neuron $ψ_{i}$ and neuron $ψ_{j}$ is defined as the negative logarithm of transition probability ( $- l o g p_{i j}$ ). We set the neurons that close to the center of epithelial and mesenchymal state (sphere with radius = 0.7) as epithelial community and mesenchymal community, respectively, and used Dijkstra algorithm to find the shortest path between each pair of epithelial and mesenchymal neurons (Dijkstra, 1959) with NetworkX (Hagberg et al., 2008). We recorded the frequency of neurons and edge between these neurons that were past by these shortest paths.

Calculation of density of reactive trajectories

Request a detailed protocol

The density of reactive trajectory on the plane of morphology PC1 and vimentin Haralick PC1 was calculated with the following procedure:

Divide the whole plane into 200 × 200 grids.
In each grid, count the number of reactive trajectory (only the parts of each reactive trajectory that were in the intermediate region were taken into consideration) that enters and leaves it. If a reactive trajectory passes certain grid multiple times, only one was added in this grid’s density. Thus, the density matrix was obtained.
Use Gaussian filter to smooth the obtained density matrix. The standard deviation was set to be two and the truncation was two (i.e., truncate at twice of the standard deviation).

Procedure for determining a reaction coordinate

Request a detailed protocol

We followed a procedure adapted from what used in the finite temperature string method for numerical searching of reaction coordinate and non-equilibrium umbrella sampling (Vanden-Eijnden and Venturoli, 2009; Dickson et al., 2009), with a major difference that we used experimentally measured single-cell trajectories (Figure 4—figure supplement 1).

Identify the starting and ending points of the reaction path as the means of data points in the epithelial and mesenchymal regions, respectively. The two points are fixed in the remaining iterations.
Construct an initial guess of the reaction path that connects the two ending points in the feature space through linear interpolation. Discretize the path with N ( = 30) points (called images, and the k_th image denoted as $s_{k}$ with corresponding coordinate X(s_k)) uniformly spaced in arc length.
Collect all the reactive single-cell trajectories that start from the epithelial region and end in the mesenchymal region.
For a given trial RC, divide the multi-dimensional state space by a set of Voronoi polyhedra containing individual images, and calculate the score function F given in the main text (with w = 10 in our calculations). We carried out the minimization procedure through an iterative process. For a given trial path defined by the set of image points, we calculated a set of average points using the following equations, $\bar{X} (s_{k}) = \frac{⟨ \sum_{u} \sum_{α} {X_{u, t_{α}} | X_{u, t_{α}} \in s_{k}} ⟩ + w ⟨ \sum_{u} X_{u, a r g m i n ‖ X (s_{k}) - X_{u, t_{α}} ‖^{2}} ⟩}{1 + w}$ . Next we updated the continuous reaction path through cubic spline interpolation of the average positions (Virtanen et al., 2020), and generated a new set of N images ${X (s_{k})}$ that are uniformly distributed along the new reaction path. We set a smooth factor, that is, the upper limit of $\sum_{k = 1}^{N} (\bar{X} (s_{_{k}}) - X (s_{_{k}}))$ , as one for calculating the RC in Figure 4.
We iterated the whole process in step three until there was no further change of Voronoi polyhedron assignments of the data points.
For obtaining the quasi-potential of a larger range of s, extrapolate the obtained reaction path forward and backward by adding additional image points (three for the two parallel reaction paths) beyond the two ends of the path linearly, respectively. These new image points are also uniformly distributed along s as the old image sets do. Re-index the whole set of image points as ${s_{0}, s_{1}, . . ., s_{i}, . . . s_{N}, s_{N + 1}}$ .

Calculation of dynamics of morphology and Haralick features along reaction path

Request a detailed protocol

The reaction path is calculated in the principal component (PC) space of morphology PC1, vimentin Haralick PC1, PC3, and PC4. Distribution of cells show significant shift before and after TGF-β treatment in these dimensions (Wang et al., 2020). To reconstruct dynamics in the original features space from PCs, the reaction path’s coordinates on the other dimensions of PC are set as means of data in the corresponding Voronoi cell of each point on the reaction path. We obtain the reaction path in full dimension of PC space. The dynamics of morphology and Haralick features are calculated by inverse-transform of coordinates of PCs.

Markov property test

Request a detailed protocol

We examined the Markov property of the RC trajectories with Chapman-Kolmogorov Test (CK-test) (Figure 5—figure supplement 1). The CK-test compares the left and right sides of Chapman-Kolmogorov equation ( $P (k τ) = p^{k} (τ)$ ). The $k$ -step transition matrix should equal to the $k_{t h}$ power of 1-step transition matrix if the process is Markovian. We estimated the transition matrix with PyEMMA (Scherer et al., 2015).

Reconstruction of quasi-potential along the reaction coordinate

Request a detailed protocol

Based on the theoretical framework in Figure 5c, we followed the procedure below:

The N + 2 image points of an identified RC divide the space in N + 2 Voronoi cells that data points can assign to. Ignore the first and last Voronoi cells, and use the remaining N cells for the remaining analyses.
Within the i_th Voronoi cell, calculate the mean drift speed (and thus $d ϕ / d s$ ) at $s_{i}$ approximately by $\frac{d ϕ}{d s} {|_{s_{i}} = - ⟨ \frac{d s_{i}}{d t} ⟩ \approx ⟨ \frac{s ⟮ X (t + Δ t) ⟯ - s_{i}}{Δ t} ⟩ |}_{s (X (t)) = s_{i}}$ where s(X) is the assumed value along s for a cell state X in the morphology/texture feature space. The sum $s (X (t)) = s_{i}$ is over all time and all data points from all the recorded trajectories that lie within the i_th Voronoi cell ( $s (X (t)) = s_{i}$ ), and Δt = 1 is one recording time interval. Using data points from all instead of just reactive trajectories is necessary for unbiased sampling within each Voronoi cell with ${⟨ η ⟩}_{s_{i}} = 0$ .
Calculate the quasi-potential through numerical integration, $ϕ (s_{i}) = ϕ (s_{0}) + \int_{s_{0}}^{s_{i}} \frac{d ϕ}{d s} d s \approx ϕ (s_{0}) + Δ s \sum_{j = 1}^{i} \frac{d ϕ}{d s} |_{s_{j}}$ . The exact value of ϕ(s₀) does not affect the quasi-potential shape.

Reconstruction of quasi-potential along parallel paths

Request a detailed protocol

We followed the same mapping procedure for trajectories of cells treated with different TGF-β concentration. We used tslearn to calculate the DTW distance between two reactive trajectories, then performed K-Means clustering (Sammut and Webb, 2017) on the DTW distance matrix (Sakoe and Chiba, 1978) to cluster the reactive trajectories into two groups. We then followed the procedure in Materials and methods (McFaline-Figueroa et al., 2019) to reconstruct the RC for each group. We reconstructed the quasi-potentials using all trajectories.

For a single-cell trajectory, it is possible that the cell jumps out its original path due to fluctuation. For example, for a trajectory that mainly follows RC1, certain parts of it may transit into the range of RC2. So we used a part-aligning method to map all the trajectories to the RCs.

For a trajectory not belonging to the reactive trajectory ensemble, we assigned it to one of the two group associated to the two RCs, ${s_{1}} = {s_{1, 1}, . . ., s_{1, i}, . . . s_{1, N}}$ and ${s_{2}} = {s_{2, 1}, . . ., s_{2, i}, . . . s_{2, N}}$ by using sub-sequence DTW distance (Sammut and Webb, 2017). We first calculate the sub-sequence DTW distance of this trajectory to the Voronoi cells of ${S_{1}}$ and ${S_{2}}$ , respectively, and identified its matching coordinates ${s_{1, a}, . . ., s_{1, i}, . . ., s_{1, b}}$ , and ${s_{2, c}, . . ., s_{2, i}, . . . s_{2, d}}$ on the RCs. Each point on the trajectory was assigned to the RCs based on minimum Euclidean distance. Then the consecutive parts of this trajectory along each RC were used to calculate the drift speed $⟨ d s / d t ⟩$ and quasi-potential $ϕ (s)$ following the definition and procedure described in Materials and methods (McFaline-Figueroa et al., 2019).

Numerical solution of the Fokker-Planck equation

Request a detailed protocol

The Langevin equation, $d s / d t = F (s) + η (s, t)$ , describes how one cell evolves along a reaction coordinate s in the state space. Equivalently under the Ito interpretation the Fokker-Planck equation describes on the probability density of observing cells at a specific point s, $ρ (s, t)$ changes over time (Kubo et al., 1991; Schnoerr et al., 2017),

\partial_{t} ρ (s, t | s_{0}, t_{0}) = \nabla \cdot [D (\nabla - \frac{F (s)}{k_{B} T}) ρ (s, t | s_{0}, t_{0})] .

In the equation, the spatially dependent diffusion constant D was estimate from the experiment data, $D_{s_{i}} = V a r (\frac{d s}{d t} | {_{s}}_{_{i}})$ , the variance of $\frac{d s}{d t} | {_{s}}_{_{i}}$ calculated from experiment data in corresponding Voronoi cells. The term $F (s) = - \nabla U$ , where $U$ is the quasi-potential obtained from experiment data, the pseudo-temperature T was set as $\frac{1}{2 k_{B}}$ , where $k_{B}$ is the Boltzmann constant. With these inputs, we solved the equations numerically (Holubec et al., 2019).

Data availability

Request a detailed protocol

The scripts and single-cell trajectory data can be found in the link https://github.com/opnumten/trajectory_analysis (Wang, 2022 copy archived at swh:1:rev:1153076f88acab6f1030eefa119f4e6bd49cbb97).

Data availability

The computer code are shared on GitHub, so other researchers can run to reproduce Figure 3, 4, and 5. The processed single cell trajectory data are on Dryad.

The following data sets were generated

1. Wang W
(2022) Dryad Digital Repository
A549 VIM-RFP EMT single cell trajectory data.
https://doi.org/10.5061/dryad.7h44j0zvp

References

(2005) Sampling rare switching events in biochemical networks
Physical Review Letters 94:018104.
https://doi.org/10.1103/PhysRevLett.94.018104
- PubMed
- Google Scholar
1. Aurell E
2. Sneppen K
(2002) Epigenetics as a first exit problem
Physical Review Letters 88:048101.
https://doi.org/10.1103/PhysRevLett.88.048101
- PubMed
- Google Scholar
(2011) Cellular decision making and biological noise: from microbes to mammals
Cell 144:910–925.
https://doi.org/10.1016/j.cell.2011.01.030
- PubMed
- Google Scholar
1. Best RB
2. Hummer G
(2005) Reaction coordinates and rates from transition paths
PNAS 102:6732–6737.
https://doi.org/10.1073/pnas.0408098102
- PubMed
- Google Scholar
(2002) Transition path sampling: throwing ropes over rough mountain passes, in the dark
Annual Review of Physical Chemistry 53:291–318.
https://doi.org/10.1146/annurev.physchem.53.082301.113146
- PubMed
- Google Scholar
(2018) Transition state characteristics during cell differentiation
PLOS Computational Biology 14:e1006405.
https://doi.org/10.1371/journal.pcbi.1006405
- PubMed
- Google Scholar
1. Carpenter AE
2. Jones TR
3. Lamprecht MR
4. Clarke C
5. Kang IH
6. Friman O
7. Guertin DA
8. Chang JH
9. Lindquist RA
10. Moffat J
11. Golland P
12. Sabatini DM
(2006) CellProfiler: image analysis software for identifying and quantifying cell phenotypes
Genome Biology 7:R100.
https://doi.org/10.1186/gb-2006-7-10-r100
- PubMed
- Google Scholar
1. Chang AY
2. Marshall WF
(2019) Dynamics of living cells in a cytomorphological state space
PNAS 116:21556–21562.
https://doi.org/10.1073/pnas.1902849116
- PubMed
- Google Scholar
1. Chen L
2. Liu R
3. Liu ZP
4. Li M
5. Aihara K
(2012) Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers
Scientific Reports 2:342.
https://doi.org/10.1038/srep00342
- PubMed
- Google Scholar
1. Christiansen EM
2. Yang SJ
3. Ando DM
4. Javaherian A
5. Skibinski G
6. Lipnick S
7. Mount E
8. O’Neil A
9. Shah K
10. Lee AK
11. Goyal P
12. Fedus W
13. Poplin R
14. Esteva A
15. Berndl M
16. Rubin LL
17. Nelson P
18. Finkbeiner S
(2018) In Silico Labeling: Predicting Fluorescent Labels in Unlabeled Images
Cell 173:792–803.
https://doi.org/10.1016/j.cell.2018.03.040
- PubMed
- Google Scholar
1. Cook DP
2. Vanderhyden BC
(2020) Context specificity of the EMT transcriptional response
Nature Communications 11:2142.
https://doi.org/10.1038/s41467-020-16066-2
- PubMed
- Google Scholar
(1995) Active Shape Models-Their Training and Application
Computer Vision and Image Understanding 61:38–59.
https://doi.org/10.1006/cviu.1995.1004
- Google Scholar
(2009) Nonequilibrium umbrella sampling in spaces of many order parameters
The Journal of Chemical Physics 130:074104.
https://doi.org/10.1063/1.3070677
- PubMed
- Google Scholar
1. Dijkstra EW
(1959) A note on two problems in connexion with graphs
Numerische Mathematik 1:269–271.
https://doi.org/10.1007/BF01386390
- Google Scholar
1. Fukui K
(2002) The path of chemical reactions - the IRC approach
Accounts of Chemical Research 14:363–368.
https://doi.org/10.1021/ar00072a001
- Google Scholar
1. Ge H
2. Qian H
3. Xie XS
(2015) Stochastic phenotype transition of a single cell in an intermediate region of gene state switching
Physical Review Letters 114:078101.
https://doi.org/10.1103/PhysRevLett.114.078101
- PubMed
- Google Scholar
(2016) Time series modeling of live-cell shape dynamics for image-based phenotypic profiling
Integrative Biology 8:73–90.
https://doi.org/10.1039/c5ib00283d
- PubMed
- Google Scholar
Book
(2008)
Exploring Network Structure, Dynamics, and Function Using NetworkX

Los Alamos National Lab.(LANL), Los Alamos, NM (United States.
- Google Scholar
(1990) Reaction-rate theory: fifty years after Kramers
Reviews of Modern Physics 62:251–341.
https://doi.org/10.1103/RevModPhys.62.251
- Google Scholar
1. Haralick RM
(1979) Statistical and structural approaches to texture
Proceedings of the IEEE 67:786–804.
https://doi.org/10.1109/PROC.1979.11328
- Google Scholar
Conference
1. He K
2. Zhang X
3. Ren S
4. Sun J
(2016) Deep Residual Learning for Image Recognition
2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 770–778.
https://doi.org/10.1109/CVPR.2016.90
- Google Scholar
(2019) Physically consistent numerical solver for time-dependent Fokker-Planck equations
Physical Review. E 99:032117.
https://doi.org/10.1103/PhysRevE.99.032117
- PubMed
- Google Scholar
1. Huang S
2. Eichler G
3. Bar-Yam Y
4. Ingber DE
(2005) Cell Fates as High-Dimensional Attractor States of a Complex Gene Regulatory Network
Physical Review Letters 94:12.
https://doi.org/10.1103/PhysRevLett.94.128701
- PubMed
- Google Scholar
1. Jaqaman K
2. Loerke D
3. Mettlen M
4. Kuwata H
5. Grinstein S
6. Schmid SL
7. Danuser G
(2008) Robust single-particle tracking in live-cell time-lapse sequences
Nature Methods 5:695–702.
https://doi.org/10.1038/nmeth.1237
- PubMed
- Google Scholar
(2019) Evolutionary regain of lost gene circuit function
PNAS 116:25162–25171.
https://doi.org/10.1073/pnas.1912257116
- PubMed
- Google Scholar
(2018) Inferring cell state by quantitative motility analysis reveals a dynamic state system and broken detailed balance
PLOS Computational Biology 14:e1005927.
https://doi.org/10.1371/journal.pcbi.1005927
- PubMed
- Google Scholar
1. Kohonen T
(1982) Self-organized formation of topologically correct feature maps
Biological Cybernetics 43:59–69.
https://doi.org/10.1007/BF00337288
- Google Scholar
Book
(1991) Statistical Physics II
In: Kubo R, editors. Statistical Physics II: Nonequilibrium Statistical Mechanics (2nd Ed). Berlin, Heidelberg: Springer. pp. 1–279.
https://doi.org/10.1007/978-3-642-58244-8
- PubMed
- Google Scholar
1. Li W
2. Ma A
(2014) Recent developments in methods for identifying reaction coordinates
Molecular Simulation 40:784–793.
https://doi.org/10.1080/08927022.2014.907898
- PubMed
- Google Scholar
1. MacLean AL
2. Hong T
3. Nie Q
(2018) Exploring intermediate cell states through the lens of single cells
Current Opinion in Systems Biology 9:32–41.
https://doi.org/10.1016/j.coisb.2018.02.009
- PubMed
- Google Scholar
1. Marcus RA
(1993) Electron transfer reactions in chemistry
Theory and Experiment. Reviews of Modern Physics 65:599–610.
https://doi.org/10.1103/RevModPhys.65.599
- Google Scholar
(2019) A pooled single-cell genetic screen identifies regulatory checkpoints in the continuum of the epithelial-to-mesenchymal transition
Nature Genetics 51:1389–1398.
https://doi.org/10.1038/s41588-019-0489-5
- PubMed
- Google Scholar
1. Mojtahedi M
2. Skupin A
3. Zhou J
4. Castaño IG
5. Leong-Quong RYY
6. Chang H
7. Trachana K
8. Giuliani A
9. Huang S
(2016) Cell Fate Decision as High-Dimensional Critical State Transition
PLOS Biology 14:12.
https://doi.org/10.1371/journal.pbio.2000640
- PubMed
- Google Scholar
(2008) Reaction coordinates for the flipping of genetic switches
Biophysical Journal 94:3413–3423.
https://doi.org/10.1529/biophysj.107.116699
- PubMed
- Google Scholar
(2016) EMT: 2016
Cell 166:21–45.
https://doi.org/10.1016/j.cell.2016.06.028
- PubMed
- Google Scholar
(2018) Label-free prediction of three-dimensional fluorescence images from transmitted-light microscopy
Nature Methods 15:917–920.
https://doi.org/10.1038/s41592-018-0111-2
- PubMed
- Google Scholar
1. Pincus Z
2. Theriot JA
(2007) Comparison of quantitative methods for cell-shape analysis
Journal of Microscopy 227:140–156.
https://doi.org/10.1111/j.1365-2818.2007.01799.x
- PubMed
- Google Scholar
1. Qiu X
2. Zhang Y
3. Martin-Rufino JD
4. Weng C
5. Hosseinzadeh S
6. Yang D
7. Pogson AN
8. Hein MY
9. Hoi Joseph Min K
10. Wang L
11. Grody EI
12. Shurtleff MJ
13. Yuan R
14. Xu S
15. Ma Y
16. Replogle JM
17. Lander ES
18. Darmanis S
19. Bahar I
20. Sankaran VG
21. Xing J
22. Weissman JS
(2022) Mapping transcriptomic vector fields of single cells
Cell 185:690–711.
https://doi.org/10.1016/j.cell.2021.12.045
- PubMed
- Google Scholar
1. Rand DA
2. Raju A
3. Sáez M
4. Corson F
5. Siggia ED
(2021) Geometry of gene regulatory dynamics
PNAS 118:e2109729118.
https://doi.org/10.1073/pnas.2109729118
- PubMed
- Google Scholar
Book
1. Risken H
(1996) The Fokker-Planck Equation
In: Risken H, editors. The Fokker-Planck Equation: Methods of Solutions and Applications (2nd Ed). Berlin, Heidelberg: Springer-Verlag. pp. 1–474.
https://doi.org/10.1007/978-3-642-61544-3
- Google Scholar
(2013) Discovering mountain passes via torchlight: methods for the definition of reaction coordinates and pathways in complex macromolecular reactions
Annual Review of Physical Chemistry 64:295–316.
https://doi.org/10.1146/annurev-physchem-040412-110006
- PubMed
- Google Scholar
1. Sakoe H
2. Chiba S
(1978) Dynamic programming algorithm optimization for spoken word recognition
IEEE Transactions on Acoustics, Speech, and Signal Processing 26:43–49.
https://doi.org/10.1109/TASSP.1978.1163055
- Google Scholar
Book
1. Sammut C
2. Webb GI
(2017) Encyclopedia of Machine Learning and Data Mining
Springer.
https://doi.org/10.1007/978-1-4899-7687-1
- Google Scholar
(2015) PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models
Journal of Chemical Theory and Computation 11:5525–5542.
https://doi.org/10.1021/acs.jctc.5b00743
- PubMed
- Google Scholar
(2017) Approximation and inference methods for stochastic biochemical kinetics—a tutorial review
Journal of Physics A 50:093001.
https://doi.org/10.1088/1751-8121/aa54d9
- Google Scholar
1. Tian XJ
2. Zhang H
3. Xing J
(2013) Coupled reversible and irreversible bistable switches underlying TGFβ-induced epithelial to mesenchymal transition
Biophysical Journal 105:1079–1089.
https://doi.org/10.1016/j.bpj.2013.07.011
- PubMed
- Google Scholar
1. Tse MJ
2. Chu BK
3. Gallivan CP
4. Read EL
(2018) Rare-event sampling of epigenetic landscapes and phenotype transitions
PLOS Computational Biology 14:e1006336.
https://doi.org/10.1371/journal.pcbi.1006336
- PubMed
- Google Scholar
1. Udgaonkar JB
(2008) Multiple routes and structural heterogeneity in protein folding
Annual Review of Biophysics 37:489–510.
https://doi.org/10.1146/annurev.biophys.37.032807.125920
- PubMed
- Google Scholar
1. Vanden-Eijnden E
2. Venturoli M
(2009) Revisiting the finite temperature string method for the calculation of reaction tubes and free energies
The Journal of Chemical Physics 130:194103.
https://doi.org/10.1063/1.3130083
- PubMed
- Google Scholar
1. Virtanen P
2. Gommers R
3. Oliphant TE
4. Haberland M
5. Reddy T
6. Cournapeau D
7. Burovski E
8. Peterson P
9. Weckesser W
10. Bright J
11. van der Walt SJ
12. Brett M
13. Wilson J
14. Millman KJ
15. Mayorov N
16. Nelson ARJ
17. Jones E
18. Kern R
19. Larson E
20. Carey CJ
21. Polat İ
22. Feng Y
23. Moore EW
24. VanderPlas J
25. Laxalde D
26. Perktold J
27. Cimrman R
28. Henriksen I
29. Quintero EA
30. Harris CR
31. Archibald AM
32. Ribeiro AH
33. Pedregosa F
34. van Mulbregt P
35. SciPy 1.0 Contributors
(2020) SciPy 1.0: fundamental algorithms for scientific computing in Python
Nature Methods 17:261–272.
https://doi.org/10.1038/s41592-019-0686-2
- PubMed
- Google Scholar
1. Wagner DE
2. Klein AM
(2020) Lineage tracing meets single-cell omics: opportunities and challenges
Nature Reviews Genetics 21:410–427.
https://doi.org/10.1038/s41576-020-0223-2
- PubMed
- Google Scholar
1. Wang J
2. Zhang K
3. Xu L
4. Wang E
(2011) Quantifying the Waddington landscape and biological paths for development and differentiation
PNAS 108:8257–8262.
https://doi.org/10.1073/pnas.1017017108
- PubMed
- Google Scholar
1. Wang P
2. Song C
3. Zhang H
4. Wu Z
5. Tian X-J
6. Xing J
(2014) Epigenetic state network approach for describing cell phenotypic transitions
Interface Focus 4:20130068.
https://doi.org/10.1098/rsfs.2013.0068
- PubMed
- Google Scholar
1. Wang W
2. Douglas D
3. Zhang J
4. Kumari S
5. Enuameh MS
6. Dai Y
7. Wallace CT
8. Watkins SC
9. Shu W
10. Xing J
(2020) Live-cell imaging and analysis reveal cell phenotypic transition dynamics inherently missing in snapshot data
Science Advances 6:36.
https://doi.org/10.1126/sciadv.aba9319
- PubMed
- Google Scholar
Software
1. Wang W
(2022) trajectory_analysis, version swh:1:rev:1153076f88acab6f1030eefa119f4e6bd49cbb97
Software Heritage.

https://archive.softwareheritage.org/swh:1:dir:9461041d0ae4fa4e2a7eb83c4d3c8db1aa2c7f32;origin=https://github.com/opnumten/trajectory_analysis;visit=swh:1:snp:f9dea6f257650f495f93afe89dc9bf241b091648;anchor=swh:1:rev:1153076f88acab6f1030eefa119f4e6bd49cbb97
(2005) Finite temperature string method for the study of rare events
The Journal of Physical Chemistry. B 109:6688–6693.
https://doi.org/10.1021/jp0455430
- PubMed
- Google Scholar
1. Weinan E
2. Vanden-Eijnden E
(2010) Transition-path theory and path-finding algorithms for the study of rare events
Annual Review of Physical Chemistry 61:391–420.
https://doi.org/10.1146/annurev.physchem.040808.090412
- PubMed
- Google Scholar
(2020) Lineage tracing on transcriptional landscapes links state to fate during differentiation
Science (New York, N.Y.) 367:6479.
https://doi.org/10.1126/science.aaw3381
- PubMed
- Google Scholar
1. Xing J
(2010) Mapping between dissipative and Hamiltonian systems
Journal of Physics A 43:375003.
https://doi.org/10.1088/1751-8113/43/37/375003
- Google Scholar
1. Xing J
2. Kim KS
(2011) Application of the projection operator formalism to non-hamiltonian dynamics
The Journal of Chemical Physics 134:044132.
https://doi.org/10.1063/1.3530071
- PubMed
- Google Scholar
1. Yang J
2. Antin P
3. Berx G
4. Blanpain C
5. Brabletz T
6. Bronner M
7. Campbell K
8. Cano A
9. Casanova J
10. Christofori G
11. Dedhar S
12. Derynck R
13. Ford HL
14. Fuxe J
15. García de Herreros A
16. Goodall GJ
17. Hadjantonakis AK
18. Huang RYJ
19. Kalcheim C
20. Kalluri R
21. Kang Y
22. Khew-Goodall Y
23. Levine H
24. Liu J
25. Longmore GD
26. Mani SA
27. Massagué J
28. Mayor R
29. McClay D
30. Mostov KE
31. Newgreen DF
32. Nieto MA
33. Puisieux A
34. Runyan R
35. Savagner P
36. Stanger B
37. Stemmler MP
38. Takahashi Y
39. Takeichi M
40. Theveneau E
41. Thiery JP
42. Thompson EW
43. Weinberg RA
44. Williams ED
45. Xing J
46. Zhou BP
47. Sheng G
48. EMT International Association TEMTIA
(2020) Guidelines and definitions for research on epithelial-mesenchymal transition
Nature Reviews. Molecular Cell Biology 21:341–352.
https://doi.org/10.1038/s41580-020-0237-9
- PubMed
- Google Scholar
1. Ye Z
2. Sarkar CA
(2018) Towards a Quantitative Understanding of Cell Identity
Trends in Cell Biology 28:1030–1048.
https://doi.org/10.1016/j.tcb.2018.09.002
- PubMed
- Google Scholar
1. Zhang J
2. Tian X-J
3. Zhang H
4. Teng Y
5. Li R
6. Bai F
7. Elankumaran S
8. Xing J
(2014) TGF-β-induced epithelial-to-mesenchymal transition proceeds through stepwise activation of multiple feedback loops
Science Signaling 7:ra91.
https://doi.org/10.1126/scisignal.2005304
- PubMed
- Google Scholar
1. Zhang J
2. Chen H
3. Li R
4. Taft DA
5. Yao G
6. Bai F
7. Xing J
(2019) Spatial clustering and common regulatory elements correlate with coordinated gene expression
PLOS Computational Biology 15:e1006786.
https://doi.org/10.1371/journal.pcbi.1006786
- PubMed
- Google Scholar

Decision letter

Wenying Shou

Reviewing Editor; University College London, United Kingdom
Aleksandra M Walczak

Senior Editor; CNRS LPENS, France
Gabor Balazsi

Reviewer; Stony Brook University, United States
Michael Stumpf

Reviewer; University of Melbourne, Australia
Jian Liu

Reviewer; Cell Biology, Johns Hopkins Medicine, United States

Our editorial process produces two outputs: i) public reviews designed to be posted alongside the preprint for the benefit of readers; ii) feedback on the manuscript for the authors, including requests for revisions, shown below. We also include an acceptance summary that explains what the editors found interesting or important about the work.

Decision letter after peer review:

Thank you for submitting your article "Epithelial-to-mesenchymal transition proceeds through directional destabilization of multidimensional attractor" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Gabor Balazsi (Reviewer #1); Michael Stumpf (Reviewer #2); Jian Liu (Reviewer #3).

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Overall, all three reviewers are positive about your work. However, there are items that need to be addressed, which are summarised below. Note that the three reviews are attached in their entirety to assist your revision.

Essential points to be addressed:

1. How the existence of multiple reaction paths is or is not robust to e.g. multiplicative noise and other factors in the analysis.

2. What is the method's applicability to other cell lines, proteins, and cellular transitions.

3. Whether a simpler analysis would have given the same results.

4. Clearly state what the advance this paper has over the previous Science Advance paper (Ref. 11).

5. Improve clarity of your writing, including tidying up typos and references, explaining to biology audience the difference between Langevin and Fokker-Planck equations, providing justification of using Langevin, discussing how this system's transition is different from the typical analysis, explaining the plethora of computational methods deployed, and providing better illustration of morphological and textural features.

Reviewer #1 (Recommendations for the authors):

(1) In the Introduction, the definition of the saddle-node bifurcation is unusual. Specifically, the saddle-node bifurcation is described here as both the appearance of a saddle point and a new steady state, and then the merger of the saddle point with the original steady state. Typically, however, these are considered two different saddle-node bifurcations. In fact, there are systems exhibiting a single saddle-node bifurcation, when the saddle point never merges with the original steady state, so the system remains bistable even as the bifurcation parameter tends to infinity. See the wild-type circuit in PMID: 31754027 for an example.

(2) The way the system's transition is induced here is different from the way typical bifurcations are realized mathematically. Specifically, in mathematics the system's steady states are investigated while a bifurcation parameter is scanned – but each particular value of the bifurcation parameter is considered fixed. In contrast, in this experimental system the bifurcation parameter is time-dependent: intracellular TGF-β concentrations change as they equilibrate with the extracellular TGF-β levels. This difference should be mentioned and discussed, regarding the influx rate of TGF-β and membrane permeability. About how long does it take for intracellular and extracellular TGF-β to equilibrate?

(3) Related to the previous point, an experiment closer to the mathematical studies would keep cells in microfluidic chambers, perfusing media with constant TGF-β concentration that does not depend on time but may increase from chamber to chamber. This should be mentioned as a possibility for future studies.

(4) The analysis involves a plethora of computational and mathematical methods: PCA, active shape model, Haralick features, SOM, Dijkstra algorithm, Onsager-Machlup action, dynamics time warping, Focker-Planck equation, pseudopotential, Voronoi partitioning, finite temperature string method, etc. While all of this is impressive, there is a concern. Some parts of the text are difficult to follow, and the overall procedure is not easy to comprehend. To make this approach really useful to the EMT community, a knowledgeable biologist should be able to comprehend and reproduce the results. So, is it possible to get to the same conclusion with fewer and/or simpler computational steps? Are all the steps employed here necessary to uncover the two cell transition path categories? Moreover, how transferable is the methodology to other cell lines, other CPTs and other proteins? A highly sophisticated, multistep approach is probably less likely to transfer and generalize than a simpler one. All of this should be at least discussed, and possibly addressed by an attempt to simplify the steps, accordingly simplifying the text of the manuscript by reducing some of the jargon.

(5) Most of the methods are introduced and similar conclusions about the CPT paths are reached in the earlier Science Advances paper (Ref. 11.) using the same cell line, the same markers, and the same CPT. The authors should clearly state what is distinguishingly novel in this manuscript compared to their earlier publication.

(6) A more intuitive illustration of the morphology and texture features is needed. What cellular aspects do the main Principal Components contain? Are any morphology and texture aspects overrepresented in the first PCs? For example, it would be very helpful to illustrate the morphology and texture extracted, along with their computational analysis to obtain the numbers for a few cells: (i) in the E state; (ii) in the M state; (iii) in mid-transition with vimentin increases first; (iv) in mid-transition with concordant increase. This could be addressed by altering the current Figure 4, similar to Figures 3 and 4 in the Science Advances paper (Ref. 11.).

(7) The Langevin approach assumes uncorrelated Gaussian noise. However, most fluctuations of cellular molecules are neither Gaussian, nor uncorrelated. Moreover, the noise properties can depend on the deterministic components of the Langevin approach: F, x and t. What justifies the applicability of the approach? This should be discussed.

(8) For the 1 ng/mL TGF-β treatment, what would the actual reaction path look like (compared to the 4 ng/mL treatment)? Here the new trajectories are projected onto the RCs for the 4 ng/mL treatment "for comparison". What does this projection imply compared to a separate analysis of the 1 ng/mL treatment? What if the reverse is done: the trajectories of the 4 ng/mL treatment are projected onto the RCs of the 1 ng/mL treatment?

(9) Related to the above question, it is interesting that the new M attractor for 1 ng/mL treatment is closer to the E state. Does this mean that the attractor-based definition of the "M" state is stimulus-dependent? So how can we be sure there is an "E" and an "M" state if their definition changes according to the environment? Shouldn't these states be independent of the environment?

(10) It is interesting that some cells become mesenchymal in low TGF-β, and possibly even without TGF-β. Do any of these cells revert? It is understood that high TGF-β prevents reversion, but the plateau in Figure 5 implies that reversions may be possible at low or zero TGF-β.

(11) Are there any "early signs" of cells that will become mesenchymal? Could this be predicted based on the values, or fluctuations of numerical features or their correlation analysis?

(12) This manuscript is about environment-induced CPTs. On the other hand, CPTs can also occur stochastically in a constant environment. This distinction would be worth making to place the research in context, citing PMID:21414483.

(13) A reference is needed for TPT in line 151 and also for the Onsager-Machlup action in line 200.

(14) The phrase "round polygon" probably means convex polygon?

(15) CPT appears in the Abstract without a prior definition.

(16) References (16) and (17) are identical.

(17) Please watch the grammar! There are some missing or extra words, e.g., "instant OF time", "towards TO", etc.

Reviewer #2 (Recommendations for the authors):

Specific points:

Figure 1: The figure legend could be made clearer. The figure might give the impression that the data is sufficient to distinguish between saddle node and pitchfork bifurcation.

line 135: I would like to see an outline of what Haralick features are.

line 199-200: It would help to define in general terms what an action is.

line 203: reference 22 has nothing to do with reaction coordinates as far as I can make out. Did the bibliography get mixed up here?

line 262: in 1D all dynamical systems are gradient systems. References 28 and 29 are not the most appropriate references in this context. Most introductory dynamical systems books would suffice.

line 283-284: It may help some readers to learn more about the differences between Langevin and Fokker-Planck equations. Schnoerr et al., Journal of Physics A (2017) 50:093001 is a reference that I find very useful.

line 287: Is it possible to do better than "matches reasonably well"? Are there statistical measures by which this can be quantified? Or is it possible to explain why there is a mismatch.

line 319-323: I found the discussion about the intermediate states fascinating: I was wondering if this could be extended to include some of the arguments of PMC6238957 or similar? More generally, mathematically, for the systems considered here (in a deterministic regime) the Palais-Smale conditions or the mountain pass theorem would hold. MacLean et al., make such arguments less formally and more intuitive.

Finally, most other previous authors appear to have used the term quasi-potential to denote landscapes of differentiating systems. In solid-state theory and chemistry pseudo-potential appears to be favoured to describe e.g. effective electron potentials. I would recommend the terminology "quasi-potential" here.

Reviewer #3 (Recommendations for the authors):

1. The writing needs to be greatly improved. While some parts are arguably a subject of style/taste, the rest of the manuscript is littered with grammar mistakes. For instance, the "CPT" in Abstract needs to be defined first. On Lines 37-38: "different function, morphology, …" should be "different functions, morphologies…". On Line 48-49: "A cell is a dynamical system, and understanding a CPT process from dynamical systems theory …" should be something like "Considering cell as a dynamical system, understanding a CPT process from dynamical systems theory…".

2. Any results from deep learning critically hinge on the quality of the training set; otherwise, the automation can easily go wrong. In automatically characterizing the live-cell time-lapsed images, the authors need to provide the necessary baseline or the control in their deep learning method. If it is already done in their previous work, then the authors need to explicitly state and refer to it in the current paper. If not, then such a control measure in deep learning needs to be included in the Method.

3. Using time-lapsed images to reconstruct pseudopotential is a great improvement over the previous work. The question: How does the number of images points or the time-resolution along the reaction coordinate affect the reconstructed potential? The authors need to at least discuss the potential effects.

4. With the high-dimensional parameter space, the authors reconstructed the common transition paths of EMT. It is well known that cells exhibit large heterogeneity in terms of gene expression and dynamics. The question is: How can we reconcile the two opposing features?

5. The authors demonstrated the two parallel pathways in EMT with the same starting and ending states (e.g., Figure 3e). While the reaction coordinates of transition state along one pathway (vimentin PC1 and morphology PC1) are intermediate between the E and the M states (the right panel of Figure 3e), those along the other pathway are not (the left panel of Figure 3e). What is the physical nature of this largely non-monotonic change? And if possible, what is the functional role? In perspective, cell operates in the multi-dimensional parameter space. What the authors have characterized is only the subset. Possibly, there exist additional but essential parameters that remain to be explored. This way, the non-monotonic change in the reaction coordinates may reflect the projection from a higher dimensional space onto the two-dimensional parameter plane. For instance, cell mechanics may be another set of key parameters that underlie EMT, which has been demonstrated to display non-monotonic changes during EMT (see Margaron et al., Biophysical properties of intermediate states of EMT outperform both epithelial and mesenchymal states (bioRxiv, 2019)). I'd suggest the authors discuss the finding in a broader context.

https://doi.org/10.7554/eLife.74866.sa1

Author response

Essential points to be addressed:

1. How the existence of multiple reaction paths is or is not robust to e.g. multiplicative noise and other factors in the analysis.

The existence of the two paths was revealed from clustering the trajectories. We obtained the two paths with several different clustering approaches. All these analyses do not require any assumption on the underlying dynamics.

2. What is the method's applicability to other cell lines, proteins, and cellular transitions.

This method is general for studying cell phenotypic transitions, and can be used on other cell lines and cellular processes. In a separate work (Wang et al., BioRxiv, 2021.09.21.461257, doi: https://doi.org/10.1101/2021.09.21.461257), we also applied the transition path analyses on scRNA-seq data.

3. Whether a simpler analysis would have given the same results.

This work has two parts.

In part 1, we analyzed the single cell trajectories using some standard clustering algorithms (used in different contexts), and the analyses revealed two parallel transition paths. As discussed in point 1, the analyses are standard in data sciences.

In part 2, we applied the transition path analyses to the single cell trajectories, and this part also has two steps:

1) We adapted the finite temperature string method widely used in studying chemical reactions to reconstruct the reaction coordinates for the two paths. Notice up to this step (i.e., part 1 and step 1 of part2) we had not made any assumption on the system dynamics. Here we mentioned Onsager-Machlup action only to give a qualitative theoretical explanation on why cells form concentrated reaction tubes in the state space. In this revised version we removed this part to avoid reference to unnecessary theoretical discussions.

2) We reconstructed the equations of motion along the reaction coordinates under a minimal ansatz of Langevin dynamics.

Indeed some of the theoretical concepts and approaches are from chemical physics, and may not be familiar to the quantitative cell biology field. Introduction of these approaches is an important and exciting aspect of this work to demonstrate that these theoretical and computational tools conventionally used in chemical physics can also be applied to analyze single cell live cell imaging data; compared to typical comprehensive and often very expensive experimental measurements such as single cell genomics studies, we show how these tools can reveal quantitative mechanistic information from the often-regarded-as-less-informative imaging data. That is, our integrated live cell imaging and analysis platform provides dynamical information complements and corroborates with what one can get from snapshot single cell data, which can only provide partial dynamical information due to the destructive nature of the techniques used.

4. Clearly state what the advance this paper has over the previous Science Advance paper (Ref. 11).

We added in paragraph 1 of the Discussion section. In the Science Advance paper, we established a live cell imaging and image analysis procedure so one can represent cell phenotypic transitions mathematically as trajectories in a composite cell feature space, analogous to how one represents molecular motions in a phase space. In this work, with the mathematical representation of live cell imaging data we applied concepts and techniques developed in chemical physics for studying molecular processes to investigate cell phenotypic transitions. With the quantitative approaches we reconstructed the reaction coordinates and the equations of motion along the transition paths, and the quantitative results suggest a sequential saddle-node bifurcation mechanism for TGF-β induced EMT in A549 cells.

5. Improve clarity of your writing, including tidying up typos and references, explaining to biology audience the difference between Langevin and Fokker-Planck equations, providing justification of using Langevin, discussing how this system's transition is different from the typical analysis, explaining the plethora of computational methods deployed, and providing better illustration of morphological and textural features.

Thanks for the suggestions. We have made corresponding changes.

Reviewer #1 (Recommendations for the authors):

(1) In the Introduction, the definition of the saddle-node bifurcation is unusual. Specifically, the saddle-node bifurcation is described here as both the appearance of a saddle point and a new steady state, and then the merger of the saddle point with the original steady state. Typically, however, these are considered two different saddle-node bifurcations. In fact, there are systems exhibiting a single saddle-node bifurcation, when the saddle point never merges with the original steady state, so the system remains bistable even as the bifurcation parameter tends to infinity. See the wild-type circuit in PMID: 31754027 for an example.

Thanks for pointing out. Indeed our previous wording is not precise. We have modified the discussions.

(2) The way the system's transition is induced here is different from the way typical bifurcations are realized mathematically. Specifically, in mathematics the system's steady states are investigated while a bifurcation parameter is scanned – but each particular value of the bifurcation parameter is considered fixed. In contrast, in this experimental system the bifurcation parameter is time-dependent: intracellular TGF-β concentrations change as they equilibrate with the extracellular TGF-β levels. This difference should be mentioned and discussed, regarding the influx rate of TGF-β and membrane permeability. About how long does it take for intracellular and extracellular TGF-β to equilibrate?

This is a good question, and we added discussions in the paragraph (lines 406-411). The bifurcation parameter here is the extracellular concentration of the exogenous TGF-β, as in our previous studies and typical bifurcation analyses. As the reviewer pointed out, intracellular TGF-β levels are more complex and difficult to use as a bifurcation parameter. The transduction of TGF-β requires time. The time scale of dynamics of tyrosine kinase receptor is in minutes level (1). But the downstream like Smad phosphorylation and translocation to nucleus need several hours(2, 3). Since the exogenous TGF-β is externally controlled and is in large excess, to a good approximation we treated its level as a constant.

(3) Related to the previous point, an experiment closer to the mathematical studies would keep cells in microfluidic chambers, perfusing media with constant TGF-β concentration that does not depend on time but may increase from chamber to chamber. This should be mentioned as a possibility for future studies.

Thanks. We added discussions in the paragraph (lines 406-411). One should be aware of one complexity though. Cells also secrete endogenous TGF-β. So such a microfluidic experiment corresponds to the condition of a constant total TGF-β concentration.

(4) The analysis involves a plethora of computational and mathematical methods: PCA, active shape model, Haralick features, SOM, Dijkstra algorithm, Onsager-Machlup action, dynamics time warping, Focker-Planck equation, pseudopotential, Voronoi partitioning, finite temperature string method, etc. While all of this is impressive, there is a concern. Some parts of the text are difficult to follow, and the overall procedure is not easy to comprehend. To make this approach really useful to the EMT community, a knowledgeable biologist should be able to comprehend and reproduce the results. So, is it possible to get to the same conclusion with fewer and/or simpler computational steps? Are all the steps employed here necessary to uncover the two cell transition path categories? Moreover, how transferable is the methodology to other cell lines, other CPTs and other proteins? A highly sophisticated, multistep approach is probably less likely to transfer and generalize than a simpler one. All of this should be at least discussed, and possibly addressed by an attempt to simplify the steps, accordingly simplifying the text of the manuscript by reducing some of the jargon.

From the perspective of methodology, active shape model and Haralick features are what we use to represent the single cell dynamics mathematically. We believe that there are other ways to represent the single cell dynamics. For example, researchers can use other morphology features like area, major axis length and perimeter. But as mentioned in a systematic study of Pincus et al(4)., the active shape mode with PCA is one of the best representations of cell morphology. While active shape model is abstract, the PCA can reveal the general feature of variation In active shape model. For instance, our analysis show that the first principal component mode in EMT of A549 treated with TGF-β is close to the variation of major axis length. Haralick features are one type of texture features. Researchers can use other types of texture features like wavelet features, moment features (5). For this step, one just needs find the representation that is suitable for their data.

The active shape mode and Haralick features can be used on other types of cell phenotype transition. We also have applied the analysis pipeline including the Dijkstra algorithm, finite temperature string method and Voronoi partitioning on single cell RNA sequencing data (https://www.biorxiv.org/content/biorxiv/early/2021/09/24/2021.09.21.461257.full.pdf).

Dynamic time warping has been commonly used method in time series analysis. SOM and Dijkstra algorithm are alternative to the dynamic time warping method. We recovered two parallel EMT paths using these two different analysis approaches. The finite temperature string method, Voronoi partitioning and reconstruction of pseudopotential are chemical physics approaches typically in studying chemical reactions.

An important part of the present work is to show applying these analysis tools originally developed in various fields, one can extract quantitative mechanistic information from simple bright field/fluorescent images, as compared the much more complex and expensive single cell genomics approaches. We summarize the analysis pipeline using one schematic single cell trajectory (Figure 5—figure supplement 7). The code will be publicly available on Github.

(5) Most of the methods are introduced and similar conclusions about the CPT paths are reached in the earlier Science Advances paper (Ref. 11.) using the same cell line, the same markers, and the same CPT. The authors should clearly state what is distinguishingly novel in this manuscript compared to their earlier publication.

We added discussions in the paragraph (lines 348-357). In the Sci Adv paper we established a framework of recording and representing mathematically single cell trajectories in multi-dimensional composite feature space. In this work we developed a downstream theoretical framework of analyzing the recorded single cell trajectories. Through experimenting on A549 cells without any treatment and A549 cells treated with 1, 4 ng/ml TGF-β, we revealed a sequential saddle-node bifurcation mechanism.

(6) A more intuitive illustration of the morphology and texture features is needed. What cellular aspects do the main Principal Components contain? Are any morphology and texture aspects overrepresented in the first PCs? For example, it would be very helpful to illustrate the morphology and texture extracted, along with their computational analysis to obtain the numbers for a few cells: (i) in the E state; (ii) in the M state; (iii) in mid-transition with vimentin increases first; (iv) in mid-transition with concordant increase. This could be addressed by altering the current Figure 4, similar to Figures 3 and 4 in the Science Advances paper (Ref. 11.).

Thanks for the advice and we modified Figure 4 accordingly. We added representative single cell images of different types (E state, M state, in mid-transition with vimentin increases first and in mid-transition with concordant increase).

For the morphology space, the first principal component of morphology mainly reflects the variation of major axis length. And the second principal component reflects the variation in the minor axis length. Both PCs are related to cell area.

For Haralick features, the coefficients of different features in the first component are quite similar. In the third principal component, correlation and information measure of correlation 2 count for large proportion. In the fourth principal component, entropy and information measure of correlation 1 play important roles.

(7) The Langevin approach assumes uncorrelated Gaussian noise. However, most fluctuations of cellular molecules are neither Gaussian, nor uncorrelated. Moreover, the noise properties can depend on the deterministic components of the Langevin approach: F, x and t. What justifies the applicability of the approach? This should be discussed.

Thanks. The Langevin ansatz used in this work assumes multiplicative noises in general. We made it clear by explicitly adding the x-dependence in the equation. See also description in the method section 9. Notice we performed CK tests to validate the Markovian property. Given the noisy data and a limited number of trajectories we could obtain with the current experimental setup, in this study we restrict our analysis to this minimal model, and leave more complex models to future studies.

(8) For the 1 ng/mL TGF-β treatment, what would the actual reaction path look like (compared to the 4 ng/mL treatment)? Here the new trajectories are projected onto the RCs for the 4 ng/mL treatment "for comparison". What does this projection imply compared to a separate analysis of the 1 ng/mL treatment? What if the reverse is done: the trajectories of the 4 ng/mL treatment are projected onto the RCs of the 1 ng/mL treatment?

We calculated the RCs for the 1 ng/ml case (Author response image 1). Compare with the 4ng/ml treatment, the final state of 1 ng/ml treatment is closer to the initial epithelial state. The corresponding quasi-potentials are qualitatively similar to what shown in Figure 5d. We decide not to include in the manuscript given that there is already lot of information.

Author response image 1

Download asset Open asset

Transition path analyses of single cell trajectories along the RCs obtained from 1 and 4 ng/ml trajectories, respectively.

(a) RCs in the 2-D state space plane. (b) Quasi-potentials of 1 ng/ml trajectories reconstructed along the 1 ng/ml RCs. Left: Vimentin varies first. Right: Concerted variation.

The reason we projected the 1 ng/ml trajectory data is to compare the two different situations on the same coordinates. The reverse analysis is less meaningful because that a large part of the data points in 4 ng/ml treatment will be projected to the final coordinate of 1 ng/ml. This will give a result that cells in 4 ng/ml will locate in the final state of 1 ng/ml treatment, which is not the case.

(9) Related to the above question, it is interesting that the new M attractor for 1 ng/mL treatment is closer to the E state. Does this mean that the attractor-based definition of the “M” state is stimulus-dependent? So how can we be sure there is an“E” and an“M" state if their definition changes according to the environment? Shouldn't these states be independent of the environment?

This is really a good question. Yes, the attractor-based definition is stimulus-dependent. It is apparent from a mathematics perspective, for example, the state on a branch of a bifurcation diagram generally changes with the bifurcation parameter. This dependence has been also gradually accepted in the EMT field, and researchers use quantities like EMT score to describe the continuum spectrum of EMT. As suggested in (6), one may use some cellular features and properties to define different EMT phenotypes. In this work we showed that cells with and without TGF-β occupy distinct regions in the vimentin texture feature – morphological feature space. In our Science Advance paper, we also showed corresponding changes of selected EMT markers and transcription factors.

(10) It is interesting that some cells become mesenchymal in low TGF-β, and possibly even without TGF-β. Do any of these cells revert? It is understood that high TGF-β prevents reversion, but the plateau in Figure 5 implies that reversions may be possible at low or zero TGF-β.

It is a question we would like to explore. From our recorded single cell trajectories, some of the cells jumping out of the epithelial region will transit back into the epithelial region we defined in the composite feature spaces. Author response image 2 shows one representative 1 ng/ml trajectory. Several studies in other systems suggest such dynamic equilibrium among different sub-phenotypes(7-9), and it is a problem our integrated live cell imaging and image analysis platform can provide quantitative information.

Author response image 2

Download asset Open asset

A representative reactive trajectory which transits back into the epithelial region.

The arrow indicates the end point.

(11) Are there any“"early sign”" of cells that will become mesenchymal? Could this be predicted based on the values, or fluctuations of numerical features or their correlation analysis?

Thanks for the advice. This is a question that we are currently investigating. We compared the initial distribution of cells transiting into mesenchymal state and that of cells failing to transit into mesenchymal state. We found no difference between distributions of their initial conditions (Author response image 3).

Author response image 3

Download asset Open asset

Distribution of initial values of EMT trajectory and failed EMT trajectory.

a: Distribution of initial morphology PC1; b: Distribution of initial vimentin Haralick PC1.

For bulk data, there are studies on identifying the early warning signals of critical transitions. We utilized the critical index of Mojtahedi et al., (10). This critical index is defined as $I_{c} = \frac{⟨ │ R (f_{i}, f_{j}) │ ⟩}{⟨ R (S^{k}, S^{l}) ⟩}$ , where $f$ are the feature (or gene) vectors, are the cell state vectors at sampling time t, and $R$ are the Pearson’s correlation coefficients. As shown in Author response image 4, we can identify the time when transition in population level happens (peak). We also modified it to apply on the single trajectories with a sliding window method. But the limitation is that frequency of the experiment data is not high enough to support such analysis, so we are working on improving it.

Most of existing methods on early warning signs can only be used on 1-D time series (11). We are working on finding a method to identify the early sign of critical transition in multi-dimensional trajectories. We also hypothesize that our cell state resolution may not be sufficient to distinguish the two populations. Currently we are using a cell line with additional cell cycle reporter and microscopes that can provide more cell feature information.

Author response image 4

Download asset Open asset

Critical state index along time.

The critical state index shows a peak around 24 hour, which indicates the transition from epithelial state to mesenchymal state.

(12) This manuscript is about environment-induced CPTs. On the other hand, CPTs can also occur stochastically in a constant environment. This distinction would be worth making to place the research in context, citing PMID:21414483.

Thanks for pointing this out. We added the reference in our discussion.

(13) A reference is needed for TPT in line 151 and also for the Onsager-Machlup action in line 200.

Thanks. We add TPT references in the manuscript, and removed reference to the Onsager-Machlup action.

(14) The phrase "round polygon" probably means convex polygon?

Yes. Thanks for pointing this out. We modified it.

(15) CPT appears in the Abstract without a prior definition.

Thanks. We modified it.

(16) References (16) and (17) are identical.

Thanks. We modified it.

(17) Please watch the grammar! There are some missing or extra words, e.g., "instant OF time", "towards TO", etc.

Thanks. We modified the manuscript.

Reviewer #2 (Recommendations for the authors):

Specific points:

Figure 1: The figure legend could be made clearer. The figure might give the impression that the data is sufficient to distinguish between saddle node and pitchfork bifurcation.

Thanks. We modified the figure caption.

line 135: I would like to see an outline of what Haralick features are.

We provided the definition of Haralick features in the caption of Figure 4.

We described the calculation of Haralick features in Materials and methods (3). The calculation is based on the gray-level co-occurrence matrix G. $G_{ij}$ is the frequency when two neighbor pixels’ values are i and j. It is normalized by the total counts. In 2D images, there are four directions of such neighbors (0°, 45°, 90°, and 135°). To be rotation invariant, each feature is calculated on all the four directions of G matrix and averaged over them. Haralick features include the following features: 1 Angular Second Moment; 2: Contrast; 3: Correlation; 4: Sum of Squares: Variance; 5: Inverse Difference Moment; 6: Sum Average; 7: Sum Variance; 8: Sum Entropy; 9: Entropy; 10: Difference Variance; 11: Difference Entropy; 12: Information Measure of Correlation 1; 13: Information Measure of Correlation 2.

line 199-200: It would help to define in general terms what an action is.

We deleted discussions about actions since the concept was mentioned in the previous version only for understanding the transition tubes.

line 203: reference 22 has nothing to do with reaction coordinates as far as I can make out. Did the bibliography get mixed up here?

Thanks for point this out. We modified this reference.

line 262: in 1D all dynamical systems are gradient systems. References 28 and 29 are not the most appropriate references in this context. Most introductory dynamical systems books would suffice.

Thanks. We modified it and added more references.

line 283-284: It may help some readers to learn more about the differences between Langevin and Fokker-Planck equations. Schnoerr et al., Journal of Physics A (2017) 50:093001 is a reference that I find very useful.

Thanks. We added a brief introduction of both equations in Materials and methods (11).

line 287: Is it possible to do better than "matches reasonably well"? Are there statistical measures by which this can be quantified? Or is it possible to explain why there is a mismatch.

We compared the predicted steady distributions with the experiment data distributions of both paths. For the path that vimentin varies first, the mean value and standard deviation of the predicted steady distribution are 17.2 and 4.6. And the mean value and standard deviation of distribution of experiment data are 16.0 and 5.0. For the path of concerted variation, the mean value and standard deviation of the predicted steady distribution are 14.7 and 4.4. And the mean value and standard deviation of distribution of experiment data are 16.2 and 4.0. From the perspective of data analysis, the discretization of state space is one source of this error. If we use a smaller number of reaction coordinate, the mean squared error will increase. A more coarse-grained Voronoi separation increase this error when discretizing the trajectory progression. More importantly, our analysis is based on two 1-D paths analysis instead of direct 2D analysis. We assign the data points by their dynamics (dynamic time warping) to their corresponding path. But the probable wrong assignment would affect the calculation of the potential.

line 319-323: I found the discussion about the intermediate states fascinating: I was wondering if this could be extended to include some of the arguments of PMC6238957 or similar? More generally, mathematically, for the systems considered here (in a deterministic regime) the Palais-Smale conditions or the mountain pass theorem would hold. MacLean et al., make such arguments less formally and more intuitive.

Thanks. We added some discussion on the intermediate states in the manuscript. The papers you raised are highly relevant. We are in the process of reconstructing the multi-dimensional vector field, and from examining these vector fields we may get more insights on addressing the question. In a separate study (12), we reconstructed the vector field in the expression space, and were able to perform topological characterizations.

Finally, most other previous authors appear to have used the term quasi-potential to denote landscapes of differentiating systems. In solid-state theory and chemistry pseudo-potential appears to be favoured to describe e.g. effective electron potentials. I would recommend the terminology "quasi-potential" here.

Thanks. We modified all the pseudo-potential to quasi-potential.

Reviewer #3 (Recommendations for the authors):

1. The writing needs to be greatly improved. While some parts are arguably a subject of style/taste, the rest of the manuscript is littered with grammar mistakes. For instance, the "CPT" in Abstract needs to be defined first. On Lines 37-38: "different function, morphology, …" should be "different functions, morphologies…". On Line 48-49: "A cell is a dynamical system, and understanding a CPT process from dynamical systems theory …" should be something like "Considering cell as a dynamical system, understanding a CPT process from dynamical systems theory…".

Thanks. We modified these errors and the writing of the manuscript.

2. Any results from deep learning critically hinge on the quality of the training set; otherwise, the automation can easily go wrong. In automatically characterizing the live-cell time-lapsed images, the authors need to provide the necessary baseline or the control in their deep learning method. If it is already done in their previous work, then the authors need to explicitly state and refer to it in the current paper. If not, then such a control measure in deep learning needs to be included in the Method.

Thanks for pointing this out. We also realized this when performing tracking on live cells. To reduce the influence of false segmentation on the trajectory analysis, we used a method to filter out those probable over- and under-segmentation. We calculated the overlap between cells in consecutive frames. The cells that have abnormal overlap values were detected. And their trajectories were analyzed. We filtered out those over- and under-segmented cells and relinked the broken trajectories with linear assignment algorithm. We added this part in Material and Methods.

3. Using time-lapsed images to reconstruct pseudopotential is a great improvement over the previous work. The question: How does the number of images points or the time-resolution along the reaction coordinate affect the reconstructed potential? The authors need to at least discuss the potential effects.

In a wide range of image point numbers, the reconstructed potentials of 4ng/ml and 1ng/ml keep the same (see new Figure 5—figure supplement 6). While more image points lead to smoother reconstructed quasi-potential, the number is compromised by keeping the number of sampling points in each Voronoi cell sufficient.

4. With the high-dimensional parameter space, the authors reconstructed the common transition paths of EMT. It is well known that cells exhibit large heterogeneity in terms of gene expression and dynamics. The question is: How can we reconcile the two opposing features?

The reviewer asked a very deep and fundamental question in studying complex systems, which have the characteristics of many coupled degrees of freedom with no clear time scale separation, and sometime not at thermodynamic equilibrium (e.g., for cells). Another example of such heterogeneity, has been also noticed in studying reactions of complex molecular systems such as enzymatic reactions (e.g., the single molecule enzymology studies of Sunney Xie), and is termed dynamic disorder in the chemical physics field (13). Existence of heterogeneity indicates existence of one or more other slow degrees of freedom that couples to the transition process under study. Therefore it is still an active research area whether and how one can use one or a few 1D transition paths to represent a transition process:

a) Different cells (or molecules in chemical reactions) share common transition mechanisms. Intuitively, for EMT while cells show large heterogeneity in their cell sizes, etc, it is straightforward to tell whether individual cells undergo EMT. One can identify common characteristic changes in terms of cell morphological features (enlarged and elongated shape), and vimentin texture features (increased expression with a change from localized to dispersive distribution).

b) Proper choice of the coordinates is essential. For a given transition process, it is known in transition path theory that a localized transition tube exists in one coordinate frame, but may not in another one (14). In our study, we used scaled coordinates to measure the relative changes of individual cells during EMT, which partially remove cell heterogeneity (e.g., cells with different initial cell size). In other contexts such as signal transduction studies people also use the fold-change scheme to remove cell heterogeneity (i.e., variation of basal expression levels of the signal transduction molecules).

c) Existence of slow degrees of freedom may complicate the dynamics along the projected coordinate to be non-Markovian. We performed Chapman-Kolmogorov test, which indicates that the dynamics along the 1D reaction coordinates is largely Markovian. In the revised Discussions, we suggest that more systematic studies would be needed, especially expanding the state space dimensionality will shed light on the coupling between the transition process and other cellular processes. It will be an exciting future direction. Notice that it is practically straightforward to record multi-dimensional single cell trajectories from the live cell imaging platform presented here, which would be generally very challenging or not feasible for a molecular system. We suggest that the quantitative imaging/analysis approaches and the experimental data will inspire further theoretical development of transition rate theories.

As a side note, Neupane et al.,(15) showed that “Protein folding trajectories can be described quantitatively by one-dimensional diffusion over measured energy landscapes”.

5. The authors demonstrated the two parallel pathways in EMT with the same starting and ending states (e.g., Figure 3e). While the reaction coordinates of transition state along one pathway (vimentin PC1 and morphology PC1) are intermediate between the E and the M states (the right panel of Figure 3e), those along the other pathway are not (the left panel of Figure 3e). What is the physical nature of this largely non-monotonic change? And if possible, what is the functional role? In perspective, cell operates in the multi-dimensional parameter space. What the authors have characterized is only the subset. Possibly, there exist additional but essential parameters that remain to be explored. This way, the non-monotonic change in the reaction coordinates may reflect the projection from a higher dimensional space onto the two-dimensional parameter plane. For instance, cell mechanics may be another set of key parameters that underlie EMT, which has been demonstrated to display non-monotonic changes during EMT (see Margaron et al., Biophysical properties of intermediate states of EMT outperform both epithelial and mesenchymal states (bioRxiv, 2019)). I'd suggest the authors discuss the finding in a broader context.

Thanks. The physical nature of this change might be that in some of the cells, the variation of morphology probably relies on the variation of vimentin. It is reported that vimentin can regulate the morphology through several ways. Vimentin is required for the mediation of Slug and Axl (16-19), and it can induce variation of cell morphology, motility and adhesion (19). Vimentin fibers regulate cytoskeleton architecture (18).

Though we can represent single cell trajectories in a very high dimensional composite feature space, this might be still insufficient to resolve the state of a cell. As you suggested, the two paths are probably the projection of higher dimensional space. We are going to explore it by including more features. And we add some discussion on this topic in the manuscript.

References

1. Zi Z, Chapnick DA, and Liu X (2012) Dynamics of TGF-β/Smad signaling. FEBS Lett 586(14):1921-1928.

2. Zhang J, et al. (2018) Pathway crosstalk enables cells to interpret TGF-β duration. npj Systems Biology and Applications 4(1):18.

3. Vizán P, et al. (2013) Controlling long-term signaling: receptor dynamics determine attenuation and refractory behavior of the TGF-β pathway. Science signaling 6(305):ra106.

4. Pincus Z & Theriot J (2007) Comparison of quantitative methods for cell‐shape analysis. Journal of microscopy 227(2):140-156.

5. Wang J, et al. (2008) Cellular phenotype recognition for high-content RNA interference genome-wide screening. Journal of Biomolecular Screening 13(1):29-39.

6. Yang J, et al. (2020) Guidelines and definitions for research on epithelial–mesenchymal transition. Nat Rev Mol Cell Biol 21:341-352.

7. Chang HH, Hemberg M, Barahona M, Ingber DE, and Huang S (2008) Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature 453(7194):544-547.

8. Gupta PB, et al. (2011) Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 146(4):633-644.

9. Wang W, et al. (2014) Dynamics between Cancer Cell Subpopulations Reveals a Model Coordinating with Both Hierarchical and Stochastic Concepts. PLoS ONE 9(1):e84654.

10. Mojtahedi M, et al. (2016) Cell Fate Decision as High-Dimensional Critical State Transition. PLOS Biology 14(12):e2000640.

11. Scheffer M, et al. (2009) Early-warning signals for critical transitions. Nature 461(7260):53-59.

12. Qiu X, et al. (2022) Mapping Transcriptomic Vector Fields of Single Cells. Cell (in press).

13. Zwanzig R (1992) Dynamic Disorder - Passage through a Fluctuating Bottleneck. J. Chem. Phys. 97(5):3587-3589.

14. E W & Vanden-Eijnden E (2010) Transition-path theory and path-finding algorithms for the study of rare events. Annu Rev Phys Chem 61:391-420.

15. Neupane K, Manuel AP, and Woodside MT (2016) Protein folding trajectories can be described quantitatively by one-dimensional diffusion over measured energy landscapes. Nature Physics 12(7):700-703.

16. Vuoriluoto K, et al. (2011) Vimentin regulates EMT induction by Slug and oncogenic H-Ras and migration by governing Axl expression in breast cancer. Oncogene 30(12):1436.

17. Ivaska J (2011) Vimentin: Central hub in EMT induction? Small GTPases 2(1):1436-1448.

18. Liu C-Y, Lin H-H, Tang M-J, and Wang Y-K (2015) Vimentin contributes to epithelial-mesenchymal transition cancer cell mechanics by mediating cytoskeletal organization and focal adhesion maturation. Oncotarget 6(18):15966.

19. Mendez MG, Kojima S-I, and Goldman RD (2010) Vimentin induces changes in cell shape, motility, and adhesion during the epithelial to mesenchymal transition. The FASEB Journal 24(6):1838-1851.

https://doi.org/10.7554/eLife.74866.sa2

Article and author information

Author details

Weikang Wang

Department of Computational and Systems Biology, University of Pittsburgh, Pittsburgh, United States

Contribution
Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing

For correspondence
weikang@pitt.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4783-7540
Dante Poe
1. Department of Computational and Systems Biology, University of Pittsburgh, Pittsburgh, United States
2. Joint CMU-Pitt Ph.D. Program in Computational Biology, University of Pittsburgh, Pittsburgh, United States
Contribution
Investigation, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4813-3035
Yaxuan Yang

Department of Computational and Systems Biology, University of Pittsburgh, Pittsburgh, United States

Contribution
Investigation, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-3077-2813
Thomas Hyatt

Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, United States

Contribution
Investigation, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-7536-0850
Jianhua Xing
1. Department of Computational and Systems Biology, University of Pittsburgh, Pittsburgh, United States
2. Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, United States
3. UPMC-Hillman Cancer Center, University of Pittsburgh, Pittsburgh, United States
Contribution
Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Visualization, Writing – original draft, Writing – review and editing

For correspondence
xing1@pitt.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3700-8765

Funding

National Institute of Diabetes and Digestive and Kidney Diseases (R01DK119232)

Jianhua Xing

National Cancer Institute (R37 CA232209)

Jianhua Xing

National Institutes of Health (NIBIB T32EB009403)

Dante Poe

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This work was partially supported by National Cancer Institute (R37 CA232209), National Institute of Diabetes and Digestive and Kidney Diseases (R01DK119232) to JX, and National Institutes of Health (NIBIB T32EB009403) to DP. This work used the Extreme Science and Engineering Discovery Environment (XSEDE) at SDSC Dell Cluster with NVIDIA V100 GPUs NVLINK and HDR IB (Expanse GPU) through allocation BIO200085. We thank Eric Siggia, John J Tyson, and Sophia Hu for critical reading of the manuscript and constructive comments.

Senior Editor

Aleksandra M Walczak, CNRS LPENS, France

Reviewing Editor

Wenying Shou, University College London, United Kingdom

Reviewers

Gabor Balazsi, Stony Brook University, United States
Michael Stumpf, University of Melbourne, Australia
Jian Liu, Cell Biology, Johns Hopkins Medicine, United States

Publication history

Preprint posted: January 28, 2020 (view preprint)
Received: October 20, 2021
Accepted: February 6, 2022
Accepted Manuscript published: February 21, 2022 (version 1)
Version of Record published: March 14, 2022 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

1,528

Page views
282

Downloads
4

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Weikang Wang
Dante Poe
Yaxuan Yang
Thomas Hyatt
Jianhua Xing

(2022)

Epithelial-to-mesenchymal transition proceeds through directional destabilization of multidimensional attractor

eLife 11:e74866.

https://doi.org/10.7554/eLife.74866

Share this article

Cite this article

Cell phenotypic transitions as critical state transitions.

Summary of pipeline for recording and analyzing single-cell trajectories in composite multi-dimensional cell feature space.

Single cell trajectories of EMT form two distinct groups.

Recorded live cell trajectory in Figure 2e.

Reaction coordinate reconstruction of two parallel paths from reactive A549/Vim-RFP EMT trajectory ensemble with a modified string method.

Quantification of dynamics along the two RCs suggests a mechanism of forming two EMT paths through sequential saddle-node collisions.

A metaphorical potential system illustrating how TGF-β treatment modifies the cell dynamics.

Transition path analyses of single cell trajectories along the RCs obtained from 1 and 4 ng/ml trajectories, respectively.

A representative reactive trajectory which transits back into the epithelial region.

Distribution of initial values of EMT trajectory and failed EMT trajectory.

Critical state index along time.

Author details

Weikang Wang

Contribution

For correspondence

Competing interests

Dante Poe

Contribution

Competing interests

Yaxuan Yang

Contribution

Competing interests

Thomas Hyatt

Contribution

Competing interests

Jianhua Xing

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading