Design of an optimal combination therapy with broadly neutralizing antibodies to suppress HIV-1
- Max Planck Institute for Dynamics and Self-Organization, Germany
- Laboratory of Experimental Immunology, Institute of Virology Faculty of Medicine and University Hospital Cologne, University of Cologne, Germany
- Department of Physics, University of Washington, United States
- Fred Hutchinson Cancer Research Center, United States
Figures
Figure 1
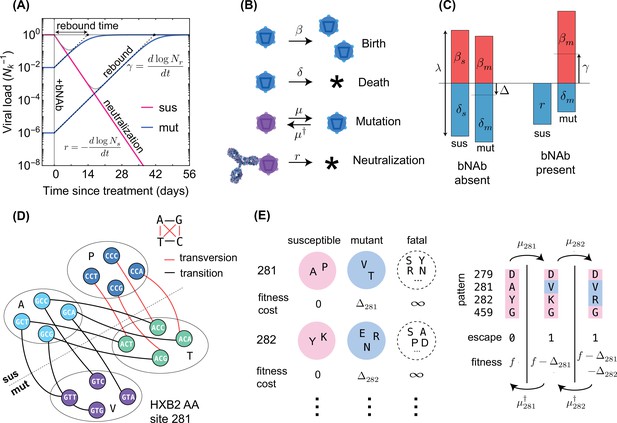
Schematics for the evolutionary dynamics of viral rebound.
(A) The viral dynamics after the initiation of a treatment with bNAb infusion () is determined by two competing processes. Susceptible strains (sus) undergo exponential decay (red line) with decay rate given by , while the resistant mutants (mut) undergo logistic growth back up to the carrying capacity () of the patient. In the deterministic limit (Equation 1), the rebound time is linearly related to the log-frequency of the mutant fraction. (B) The schematic shows the four stochastic processes of birth, death, mutation, and neutralization with their respective rates for susceptible (purple) and resistant (blue) variants. These processes define the evolution of a viral population. Note that both the susceptible and the resistant variants are subject to birth and death with their respective rates. (C) The birth and death rates can be visualized as a region of size which is partitioned into birth and death events. In the absence of antibodies, the susceptible population has balanced birth and death rates, , while the resistant population has a negative net birth rate equal to the fitness difference . After introduction of the antibody, the susceptible population decays at rate , and without competition from the susceptible population, the resistant population grows at the free growth-rate . (D) Mutational target size is inferred a priori from the genotype-phenotype mapping, which can be visualized as a bipartite graph. The nodes correspond to codons, while the edges are the mutations which link one codon to another, weighted according to the respective mutation rates. The average edge weight from codons of susceptible variants to the escape mutants determines the rate of escape mutations . Mutations can be divided into two types: transitions (black) are within-class, and transversions (red) are out of class nucleotide changes. Transitions occur at about 8 times higher rate than transversions (Figure 2). (E) A coarse grained fitness and mutation model for two of the escape sites (281 and 282) against antibody 3BNC117 are shown. Left: At each escape mediating site, amino acids fall into one of three groups: (i) susceptible (wild-type), (ii) escape mutant, and (iii) fatal. For an escape-class amino acid at site the virus incurs a fitness cost , and these costs are additive across sites. Right: Mutations at a given site occur with (independent) forward and backward rates which govern the substitution events between amino acid classes.
Figure 2 with 1 supplement
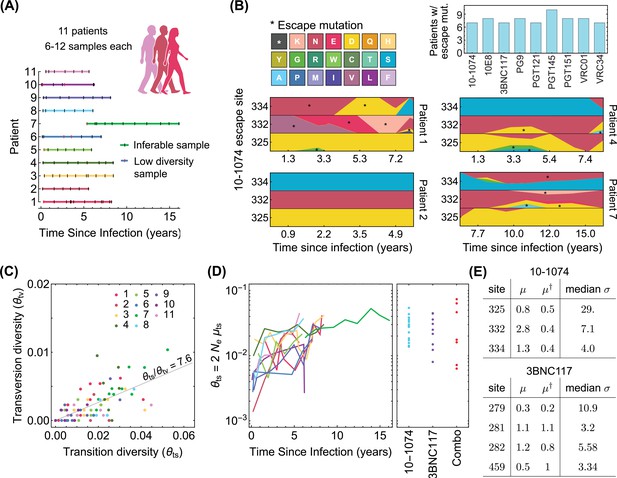
Statistics of viral genome sequences from bNAb-naive HIV-1 patients.
(A) Statistics of the high-throughput longitudinal data collected from HIV-1 populations in 11 ART-naive patients from Zanini et al., 2015, is shown. Some of the have low diversity (vertical red lines) and were not usable for our study. Usable samples (vertical black lines) amount to 4–10 samples per patient, collected over 5–10 years of infection. (B) Lower panels show the relative frequencies (cube-root transformed for legibility) of different amino acids in four patients at the 3 escape sites against the 10–1074 bNAb, estimated from the polymorphism data at the nucleotide level in each patient over time. Despite 10–1074 being a broadly neutralizing antibody, mutations associated with escape (indicated by a *) are commonly observed in untreated patients. The upper right panel shows the number of individuals (out of the cohort of 11 bNAb-naive HIV-1 patients) that carry mutations associated with escape against the indicated bNAbs. (C) The nucleotide diversity associated with transversion is shown against the transition diversity for all patients (colors) and all time points. The covariance of these two diversity measurements yields an estimate for the transition/transversion ratio . (D) Left: The transition diversity is shown to grow as a function of time since infection in all the 11 patients (colors according to (A)). Right: The neutral diversity of viral populations in patients (points) from the three different clinical trials (Caskey et al., 2015; Caskey et al., 2017; Baron et al., 2018) analyzed in this study resemble the larger diversities of long-established viral populations in untreated patients. (E) The inferred forward and backward mutation rates (), relative to the transition rate, and the median selection strength at each escape site against the two bNAbs (10–1074, and 3BNC117) from the trial data used in this study are shown. Compared to the 10–1074 bNAb, escape from the 3BNC117 bNAb appears to be less costly, and is associated with a smaller mutational target.
Figure 2—figure supplement 1
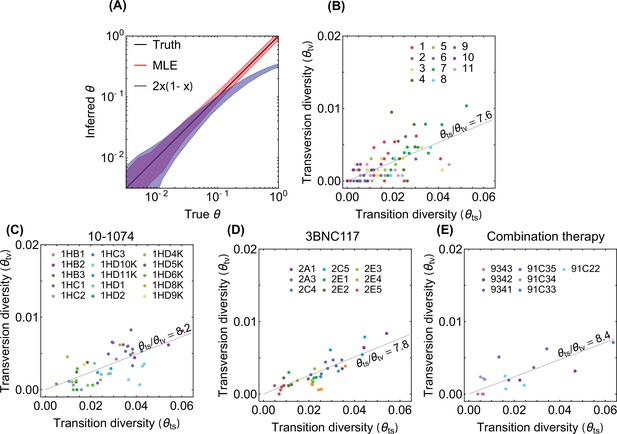
Inference of neutral diversity from genetic data.
(A) The inter-decile ranges of neutral diversity estimates for 103 simulations of genomes of 102 independent neutral sites are shown. The true values of the diversity used for simulations are shown in black. Inter-decile maximum likelihood estimate (MLE) for the diversity from Equation 22 are shown in red, and the observed variance of allele frequency as a measure of diversity is shown in blue. The inferred diversity associated with transversions is shown against that of the transition for patients (colors) enrolled in (B) the longitudinal study with high throughput HIV-1 sequence data (Zanini et al., 2015), and in the bNAB trials with (C) 10–1074 (Caskey et al., 2017), (D) 3BNC117 (Caskey et al., 2015), and (E) combination of 10–1074 and 3BNC117 (Baron et al., 2018). We find that all four diversity distributions share similar ratios , indicated in each panel.
Figure 3 with 3 supplements
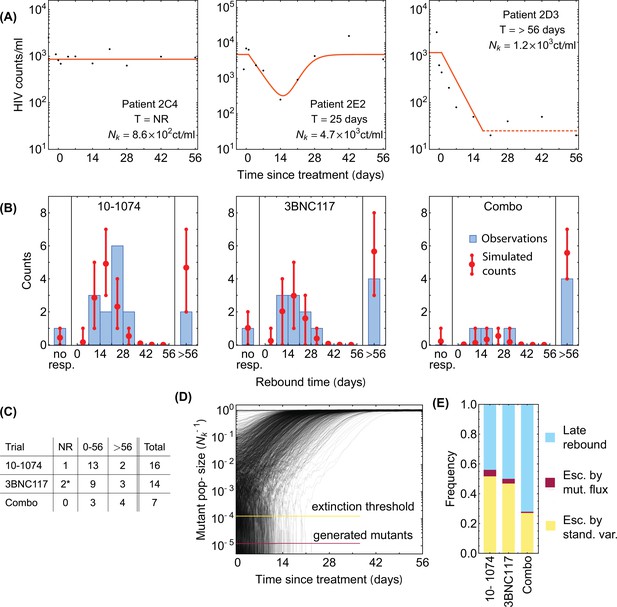
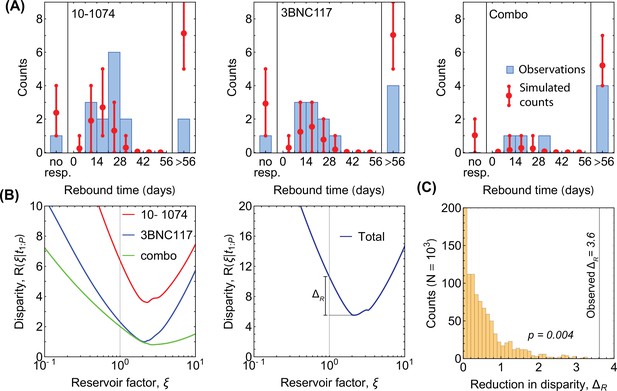
Statistics of viral rebound in clinical trials with bNAbs.
(A) Panels show viremia of three patients from the 3BNC117 trial over time (black circles) and the fitted model of the viral decay and rebound processes from Equation 1 (orange line). The viral rebound time and the fitted carrying capacity is shown in each panel. Shown are examples of a non-responder (NR; left), a rebound occurring during the trial window ( days; center), and a late rebound ( days; right). (B) We compare the distribution of rebound times in patients from the three clinical trials with 10–1074 Caskey et al., 2017, 3BNC117 Scheid et al., 2016, and the combination of the two bNAbs Baron et al., 2018 to the predictions from the simulations based on our evolutionary model (Figure 1, and Methods). The error bars show the inter decile range (0.1–0.9 quantiles) generated by the simulations for the corresponding trial. (C) The summary table shows the number of patients for whom the infecting HIV-1 population shows no response (NR), rebound during the trial window , and a late rebound ( days) in each trial. Note that three patients were excluded from the 3BNC117 trial (*) because of insufficient dosage leading to weak viral response: compared to the in the other treatment groups. (D) Plotted are 1,200 trajectories of the mutant viral population simulated using our individual based model. Due to the individual birth-death events, fluctuations are larger when the population size is smaller. At a critical threshold, , fluctuations are large enough to lead to almost certain extinction in the existing viral population. The critical threshold (yellow line) is an order of magnitude larger than the post-treatment spontaneously-generated mutant fraction (red line). (E) The predicted fraction of escape events associated with post-treatment spontaneous mutations (red) and the pre-treatment standing variation (yellow) are shown for the three trials. Late rebound events are indicated in blue. Because the spontaneously-generated mutant fraction is smaller than the extinction threshold, these mutations contribute to less than 4% of escape events (red), and escape is likely primarily driven driven by standing variation (yellow), that is, pre-existing escape variants.
Figure 3—figure supplement 1
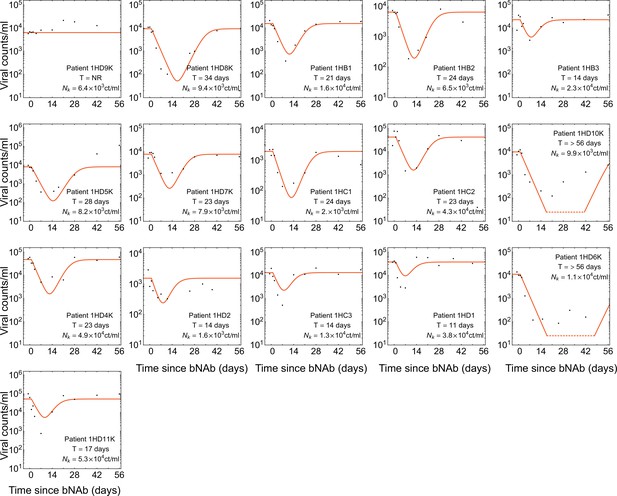
Dynamics of viremia in patients from the 10–1074 trial.
Panels shows the measured viremia over time (black dots) and the fitted deterministic dynamics from Equation 5 (red line) for all patients off ART in the 10–1074 trial Caskey et al., 2017. Patient-specific fitted carrying capacity and the estimated rebound times are reported in each panel. A common decay rate is fitted to all patient data in this trial, and growth rate is set to .
Figure 3—figure supplement 2
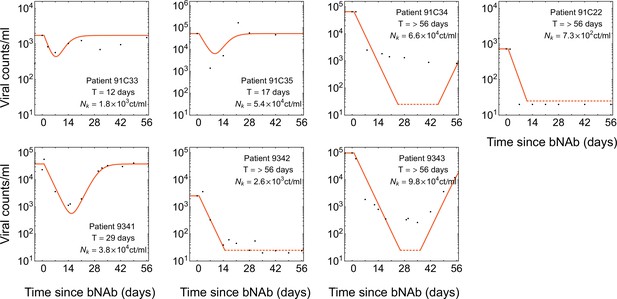
Dynamics of viremia in patients from the 3BNC117 trial.
Similar to Figure 3—figure supplement 1 but for the 3BNC117 trial Caskey et al., 2015. The cohort treated with a low dosage of bNAb ( as opposed to ) is shown in yellow; these patients exhibited a very weak response to there treatment and were excluded from our analysis. A common decay rate is fitted to all patient data in this trial, and growth rate is set to .
Figure 3—figure supplement 3
Dynamics of viremia in patients from the combination therapy trial.
Similar to Figure 3—figure supplement 1 but for the combination therapy with 10–1074 and 3BNC117 Baron et al., 2018. A common decay rate is fitted to all patients off ART in this trial, and growth rate is set to .
Figure 4 with 4 supplements
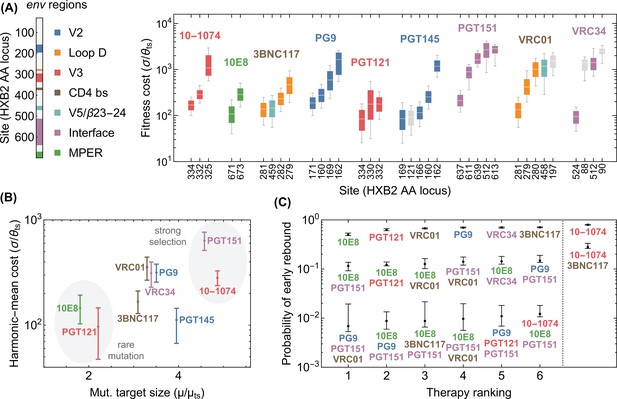
Statistics of viral escape for optimal combination therapy with bNAbs.
(A) The posterior distribution for inferred selection strength on the escape-mediating sites associated with each of the 9 bNAbs in this study is shown (right); white line: median, box: 50% around the median, bar: 80% around median. Each escape site is color coded by its location on the env gene (left) and each antibody by its associated epitope location. (B) The harmonic mean of the selection strength associated with cost of escape (scaled by transition diversity ) is shown against the mutational target size for each bNAb; error bars indicate 50% around the median. For antibodies to be broadly neutralizing, it is sufficient that viral escape from them to be associated with a small mutational target size or a large fitness cost. The mutational target size is found to be weakly correlated with the average cost of escape from a given bNAb. We identify two distinct strategies for antibody breadth—selection limited and mutational-target-size limited escape pathways each highlighted in gray. (C) bNAb therapies with 1, 2, and 3 antibodies are ranked based on the predicted probability of early viral rebound, and in each case, six therapies with highest efficacies are shown; best ranked therapy is associated with the lowest probability of early rebound (lt56 days); indicate 50% around the median. Also for reference, the probability of early viral rebound two therapies from the trials in this study (10–1074 and 10–1074+3BNC117) are shown.
Figure 4—figure supplement 1
Robustness of selection inference to intra-patient temporal correlations of HIV-1 alleles and clade-specific sampling.
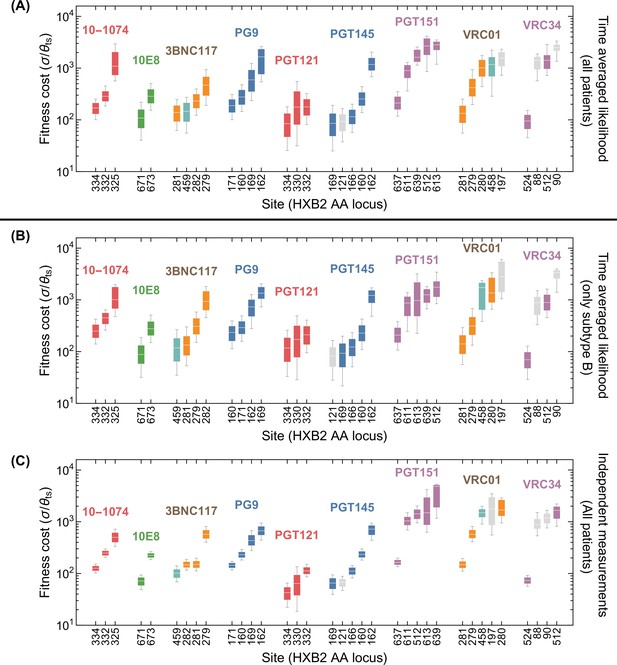
Fitness cost for escape mediating sites of different bNAbs is shown based on the selection inference using (A) the time-averaged likelihood (Equation 40 -averaged) with data from all patients, as a reference (similar to Figure 4A), (B) the time-averaged likelihood (Equation 40 -averaged) with data from patients infected with HIV-1 clade B only, and (C) independent time likelihood (Equation 40 -independent) with data from all patients. Limiting the inference to patients infected with clade B virus in (B) result in minor changes in the inferred selection strength and a slight increase in uncertainties due to a smaller data. However, the general structure of the posteriors remain similar to (A). Treating all time points as independent in (C) increases the effective sample-size of the data and reduces model uncertainty. Nonetheless, except for slight changes on the selection ordering of escape sites against 3BNC117, the median of the selection posteriors remain similar to (A). The color code is similar to Figure 4A and is determined by the env region associated with each site.
Figure 4—figure supplement 2
Robustness of selection inference to genetic linkage and hitchhiking.
Results of selection inference for simulated populations that carry escape mediating sites linked with other selected sites in the genome are shown. The blue shading shows the interdecile ranges (0.1–0.9 quantiles) for the inferred maximum likelihood estimates (MLE) of scaled selection on the escape mediating sites versus the true values used in the simulations, for different genetic linkage effects (columns) and different values of population diversity (rows). Each inferred value is based on 10 realizations of simulations (in-silico patients) for populations evolving over time, with samples taken at 10 time points spaced at 100 days. Simulations are done on whole genomes of length 512, in which 32 sites under strong selection are equally spaced throughout the genome; f0 is the base growth rate of . Each day, the preferred allele in one of the 32 sites is swapped (selection changes sign) with probability . The rate of selection fluctuation and the recombination rate are given in each panel. The carrying capacity is set to , and the event rate is ; see Algorithm 3 (Appendix 5). To initialize, we let the populations equilibrate for generations, and then gather data for maximum likelihood inference of selection at the escape mediating sites. In all panels, the median MLE for selection (black line) closely matches the true selection strength (redline). Quantile lines are smoothened by a Gaussian kernel. Variation is largest when diversity is low and when mutants are rare, which concords with the results from the Bayesian inference procedure.
Figure 4—figure supplement 3
Minimum disparity estimation for adjustment of diversity.
(A) The predicted rebound times without including an increase in diversity due to reservoirs (i.e. in Equation 42) qualitatively matches the data from the three trials (histograms in each panel), with an overestimation in the number of non-responders and patients with late rebound. For comparison, the predictions with reservoir-corrected diversity is shown in Figure 3A. (B) The disparity (Equation 35) is shown as a function of the reservoir factor for the three trials (colors; left panel). The total disparity over all trials is shown in the right panel, where indicates the reduction in disparity by using the optimal reservoir factor . (C) The distribution for the reduction in disparity (Equation 41) is shown for 1000 realizations of simulated data under the null hypothesis with . The large reduction in disparity indicates that the null hypothesis can be rejected with (Equation 42).
Figure 4—figure supplement 4
Disparity analysis for robustness of selection inference.
(A) The disparity (Equation 35) is shown as a function of rescaling of the selection strength by a multiplicative factor . The total disparity over all trials is shown in the right panel, where indicates the reduction in disparity by using the optimal selection factor . In this case the null hypothesis is that the inferred selection by the Bayesian procedure in Equation 31 requires no further rescaling for the model to fit the distribution of the rebound times (i.e. ). The large shown in (B) indicates that the null hypothesis cannot be rejected and we have no statistical justification for adding an adjustment factor for selection inferred from untreated patients.
Appendix 3—figure 1
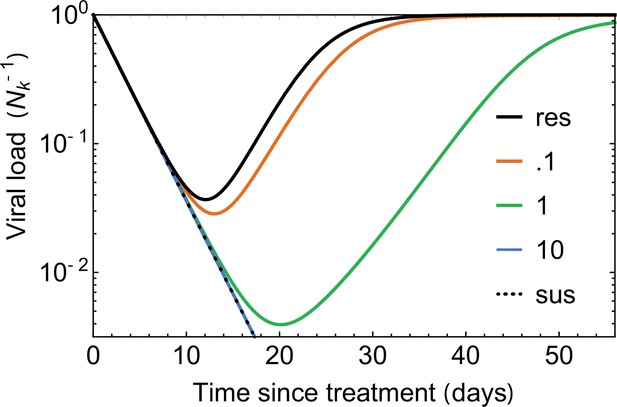
The effect of incomplete neutralization.
Viral load curves, simulated under the noise-averaged model (deterministic limit) Equation 4, are plotted under the assumption of incomplete neutralization for different values of (colors); incomplete neutralization is defined by a changing growth rate given by Equation 53. Small values of (red) lead to similar trajectories to the perfectly resistant variant (solid black line), while large (green line) is indistinguishable from the fully susceptible variants (dotted black line). For all curves, the escaping virus has an initial frequency , with decay rate and free growth rate , days.
Appendix 3—figure 2
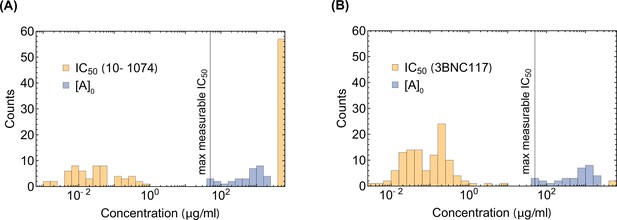
The distribution of and .
The distribution of IC50for envelope proteins derived from circulating viruses in patients after 10–1074 infusion is shown against (A) 10–1074, (B) 3BNC117 as a control. For comparison, the distribution of the maximum (initial) 10–1074 bNAb concentration used in the trial is shown in blue. The maximum measurable associated with the TZM-bl neutralization assays used in these experiments is indicated in each panel.
Appendix 4—figure 1
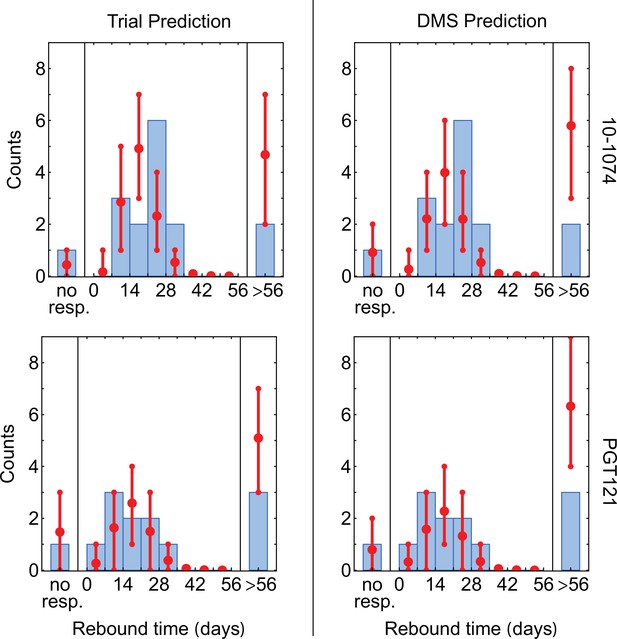
Statistics of viral rebound with using escape pathways inferred from the DMS and the trial data.
We compare the distribution of rebound times in patients from the clinical trials with 10–1074 Caskey et al., 2017 (top) and PGT121 Stephenson et al., 2021 (bottom) bNAbs, using escape pathways inferred from the respective trial data (left) and the DMS data Dingens et al., 2017 (right). The error bars show the inter decile range (0.1–0.9 quantiles) generated by the simulations for the corresponding trial. The PGT121 trial predictions relied on the neutral diversity estimates from the other three trials Caskey et al., 2015; Caskey et al., 2017; Baron et al., 2018 due to the relatively limited genetic data available from this study. The fitted reservoir value of is used for all predictions.
Tables
Appendix 1—table 1
Selection and mutational target size for escape-mediating sites against each bNAb.
Shown are the sites (column 1) and the susceptible and the escape amino acids (column 2) for each bNAb. We called patterns for 10–1074 and CD4 binding site targetting antibodies VRC01 and 3BNC117 using genetic trial data and the remainder using DMS data. The inferred mutational target size of escape at each site (forward and backward mutation rates) is shown in column 3. The major quantiles ( associated with the inferred site-specific Bayesian posterior of the scaled selection strength are shown in column 4. The corresponding quantiles for the strength of selection, after convolving the posterior for the scaled selection with the reservoir-corrected intra-patient diversity of HIV-1 are shown in column 5.
| quantiles | quantiles | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| bNAb | site | susceptible AA | escape AA | 0.1 | 0.5 | 0.9 | 0.1 | 0.5 | 0.9 | ||
| 10–1074 | 325 | DN | EGK | 0.76 | 0.51 | 560 | 1,100 | 2,900 | 8.8 | 29 | 93 |
| 332 | N | DHIKSTY | 2.8 | 0.4 | 190 | 290 | 450 | 2.6 | 7.1 | 16 | |
| 334 | S | AFGINRY | 1.3 | 0.44 | 100 | 170 | 250 | 1.4 | 4 | 9.5 | |
| 10E8 | 671 | KNS | RT | 0.41 | 0.51 | 38 | 110 | 220 | 0.68 | 2.5 | 7.3 |
| 673 | F | LV | 1.4 | 0.47 | 150 | 290 | 510 | 2.4 | 7 | 18 | |
| 3BNC117 | 279 | DN | AHK | 0.33 | 0.22 | 190 | 470 | 930 | 3.4 | 11 | 31 |
| 281 | AP | TV | 1.1 | 1.1 | 62 | 140 | 250 | 0.97 | 3.2 | 8.6 | |
| 282 | KY | ENR | 1.2 | 0.8 | 120 | 230 | 400 | 1.9 | 5.6 | 14 | |
| 459 | G | DN | 0.5 | 1 | 54 | 140 | 270 | 0.91 | 3.3 | 9.5 | |
| PG9 | 160 | N | KY | 0.4 | 0.2 | 150 | 280 | 480 | 2.3 | 6.7 | 17 |
| 162 | ST | AIP | 1.2 | 1.1 | 540 | 1600 | 2600 | 9.5 | 34 | 98 | |
| 169 | GIKMRVW | ELT | 0.53 | 0.92 | 240 | 590 | 1200 | 4.1 | 14 | 41 | |
| 171 | KPR | AEGHNQST | 1.4 | 0.62 | 100 | 190 | 310 | 1.5 | 4.5 | 11 | |
| PGT121 | 330 | FHLRSY | Q | 0.12 | 1.4 | 7.4 | 160 | 530 | 0.15 | 3.6 | 16 |
| 332 | AENV | DIKT | 1.1 | 1.2 | 80 | 180 | 320 | 1.3 | 4.2 | 11 | |
| 334 | DS | GN | 1 | 2 | 15 | 80 | 170 | 0.26 | 1.8 | 5.9 | |
| PGT145 | 121 | K | E | 1 | 1 | 34 | 92 | 170 | 0.58 | 2.1 | 5.8 |
| 160 | N | KY | 0.4 | 0.2 | 140 | 250 | 440 | 2.1 | 6.2 | 15 | |
| 162 | ST | AIP | 1.2 | 1.1 | 680 | 1200 | 2000 | 11 | 29 | 73 | |
| 166 | KR | AEGST | 0.73 | 0.58 | 58 | 120 | 200 | 0.9 | 2.8 | 7.2 | |
| 169 | GIKLTV | EMRW | 0.59 | 1.4 | 8.8 | 80 | 190 | 0.16 | 1.8 | 6.1 | |
| PGT151 | 512 | A | GT | 1.1 | 0.57 | 860 | 2,700 | 4100 | 16 | 59 | 160 |
| 611 | GN | DS | 1.3 | 2 | 360 | 890 | 1300 | 6.5 | 20 | 50 | |
| 613 | ST | CN | 0.28 | 0.7 | 1200 | 2,800 | 3500 | 21 | 58 | 140 | |
| 637 | DN | EKST | 0.83 | 0.41 | 120 | 210 | 350 | 1.8 | 5.1 | 13 | |
| 639 | T | IM | 1 | 1 | 1100 | 1600 | 2600 | 16 | 42 | 96 | |
| VRC01 | 197 | DN | S | 0.5 | 1 | 730 | 1600 | 2300 | 12 | 35 | 88 |
| 279 | DN | AHK | 0.33 | 0.22 | 200 | 420 | 940 | 3.2 | 10 | 30 | |
| 280 | N | D | 1 | 1 | 440 | 1000 | 1800 | 7.3 | 24 | 63 | |
| 281 | AP | TV | 1.1 | 1.1 | 52 | 130 | 250 | 0.9 | 3.1 | 8.6 | |
| 458 | G | D | 0.5 | 1 | 290 | 1200 | 2200 | 6 | 26 | 75 | |
| VRC34 | 512 | A | GT | 1.1 | 0.57 | 720 | 1400 | 2900 | 11 | 34 | 92 |
| 524 | GP | AERS | 1.5 | 0.67 | 45 | 95 | 150 | 0.71 | 2.2 | 5.6 | |
| 88 | N | K | 0.26 | 0.26 | 570 | 1400 | 1900 | 9.8 | 30 | 74 | |
| 90 | ST | AEK | 0.48 | 0.8 | 1400 | 2500 | 3300 | 19 | 57 | 130 | |
Appendix 4—table 1
Escape variants inferred from trial and DMS data.
Tables show the sites mediating escape of HIV-1 from the 10–1074 and the PGT121 bNAbs, using the respective trial data Caskey et al., 2017; Stephenson et al., 2021 (left) and the DMS data Dingens et al., 2017 (right). The susceptible (sus) and resistant (res) variants at each site are identified according to the procedure detailed in the Methods. Sites that are identified as escape-mediating by only one of the methods are marked with (*). While substitutions at site 325 were called as escape mediating based on the PGT121 trial data Stephenson et al., 2021 but are missed by the DMS data, this site was only inconsistently associated with escape, and its associated escape variants usually co-occur with other escape substitutions; see the Extended Data Figure 3 in Stephenson et al., 2021. Sites are numbered according to HXB2.
| 10–1074 trial | 10–1074 trial | |||||
|---|---|---|---|---|---|---|
| HXB2 site | sus | res | HXB2 site | sus | res | |
| 325 | DN | EGK | 325 | DN | EGK | |
| 330* | FHLQSYR | *1,731 | 330 | FHLQSYR | R | |
| 332 | N | DHIKSTY | 332 | N | ADEIKTV | |
| 334 | S | AFGINRY | 334 | S | DGN | |
| PGT121 trial | PGT121 DMS | |||||
| HXB2 site | sus | res | HXB2 site | sus | res | |
| 325 | D | NKT | 325* | DNKT | * | |
| 330* | FHLQSYR | *1,733 | 330 | FHLRSY | Q | |
| 332 | NV | DSRTI | 332 | AENV | DIKT | |
| 334 | TS | RND | 334 | DS | GN | |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Design of an optimal combination therapy with broadly neutralizing antibodies to suppress HIV-1
eLife 11:e76004.
https://doi.org/10.7554/eLife.76004
