Figures and data in Glycan processing in the Golgi as optimal information coding that constrains cisternal number and enzyme specificity

Figures
Tables
Additional files

16 figures, 3 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

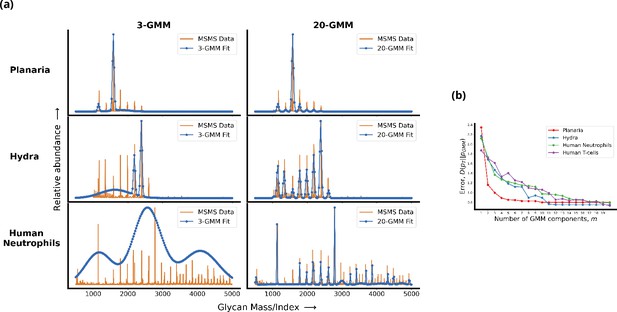
Living cells display a complex glycan distribution.

(a) 3-Gaussian mixture model (GMM) and 20-GMM approximation for the relative abundance of glycans taken from mass spectrometry coupled with determination of molecular structure (MSMS) data of planaria *Schmidtea mediterranea*, *Hydra magnipapillata,* and *human* neutrophils. (b) The change in the Kullback–Leibler (KL) divergence $D (p_{T} ∥ p_{G M M}^{(m)})$ as a function of the number of GMM components $m$ . The KL divergence for planaria saturates at $m = 5$ , for hydra at $m = 11$ , and for *human* cells at $m = 20$ . Thus, the number of components required to approximate the glycan profile correlates well with the complexity of the organism. Details are given in Appendix 1.

Figure 2

Download asset Open asset

Enzymatic reaction and transport network in the secretory pathway.

Represented here is the array of Golgi cisternae (blue) indexed by $j = 1, \dots, N_{C}$ situated between the endoplasmic reticulum (ER) and plasma membrane (PM). Glycan-binding proteins $P c_{1}^{(1)}$ are injected from the ER to cisterna-1 at rate $q$ . Superimposed on the Golgi cisternae is the transition network of chemical reactions (column) – inter-cisternal transfer (rows), the latter with rates $μ^{(j)}$ . $P c_{1}^{(1)}$ denotes the acceptor substrate in compartment $j$ and the glycosyl donor $c_{0}$ is chemostated in each cisterna. This results in a distribution (relative abundance) of glycans displayed at the PM (red curve), which is representative of the cell type.

Figure 3

Download asset Open asset

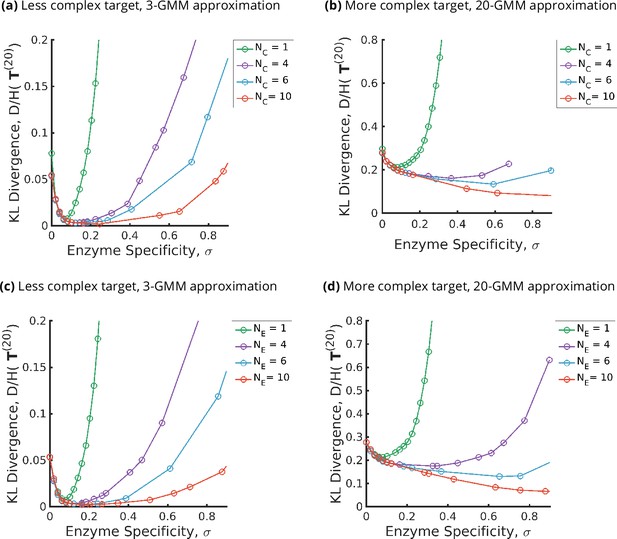
Trade-offs amongst the glycan synthesis parameters, enzyme specificity $σ$ , cisternal number $N_{C}$ , and enzyme number $N_{E}$ to achieve a complex target distribution $c^{*}$ .

(**a, b**) Normalised Kullback–Leibler distance $\bar{D} (σ, N_{E}, N_{C}, c^{*})$ as a function of $σ$ and $N_{C}$ (for fixed $N_{E} = 3$ ), (**c, d**) $\bar{D} (σ, N_{E}, N_{C}, c^{*})$ as a function of $σ$ and $N_{E}$ (for fixed $N_{C} = 3$ ), with the target distribution $c^{*}$ set to the 3-Gaussian mixture model (GMM) (less complex) and 20-GMM (more complex) approximations for the *human* T-cell mass spectrometry coupled with determination of molecular structure (MSMS) data. $\bar{D} (σ, N_{E}, N_{C}, c^{*})$ is a convex function of $σ$ for each $(N_{E}, N_{C}, c^{*})$ , decreasing in $N_{C}, N_{E}$ for each $(σ, c^{*})$ , increasing in the complexity of $c^{*}$ for fixed $(σ, N_{E}, N_{C})$ . The specificity $σ_{\min} (c^{*}, N_{E}, N_{C}) = {argmin}_{σ} {\bar{D} (σ, N_{E}, N_{C}, c^{*})}$ that minimizes the error for given $(N_{E}, N_{C}, c^{*})$ is an increasing function of $N_{C}, N_{E}$ and the complexity of the target distribution $c^{*}$ .

Figure 4

Download asset Open asset

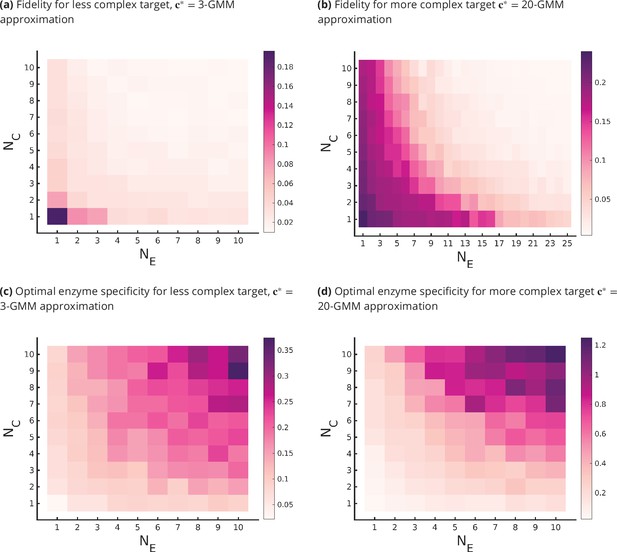
Fidelity of glycan distribution and optimal enzyme properties to achieve a complex target distribution.

The target $c^{*}$ is taken from 3-Gaussian mixture model (GMM) (less complex) and 20-GMM (more complex) approximations of the *human* T-cell mass spectrometry coupled with determination of molecular structure (MSMS) data. (**a, b**) Optimum fidelity $\min_{σ} {\bar{D} (σ, N_{C}, N_{E}, c^{*})}$ as a function of $(N_{E}, N_{C})$ . More complex distributions require either a larger $N_{E}$ or $N_{C}$ . The marginal impact of increasing $N_{E}$ and $N_{C}$ on the fidelity $\bar{D}$ is approximately equal. (**c, d**) Enzyme specificity $σ_{\min}$ that achieves $\min_{σ} {\bar{D} (σ, N_{C}, N_{E}, c^{*})}$ as a function of $(N_{E}, N_{C})$ . $σ_{m i n}$ increases with increasing $N_{E}$ or $N_{C}$ . To synthesize the more complex 20-GMM approximation with high fidelity requires enzymes with higher specificity $σ_{\min}$ compared to those needed to synthesize the broader, less complex 3-GMM approximation.

Figure 5

Download asset Open asset

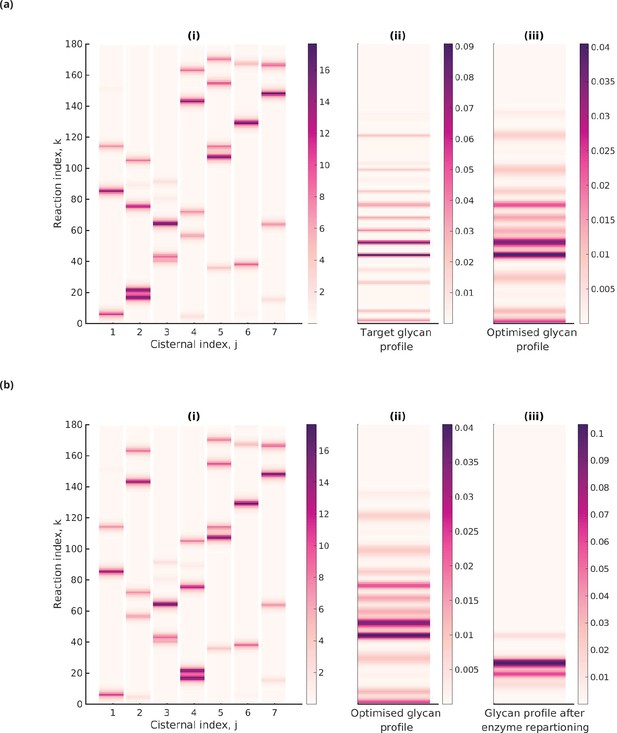
Optimal enzyme partitioning in cisternae.

(a) Heat map of the effective reaction rates in each cisterna (representing the optimal enzyme partitioning) and the steady-state concentration in the last compartment ( $c^{(N_{C})}$ ) for the 20-Gaussian mixture model (GMM) target distribution. Here, $N_{E} = 5$ , $N_{C} = 7$ , normalized $D (T^{(20)} ∥ c^{(N_{C})}) / H (T^{(20)}) = 0.11$ . (b) Effective reaction rates after swapping the optimal enzymes of the fourth and second cisternae. The displayed glycan profile is considerably altered from the original profile.

Figure 6

Download asset Open asset

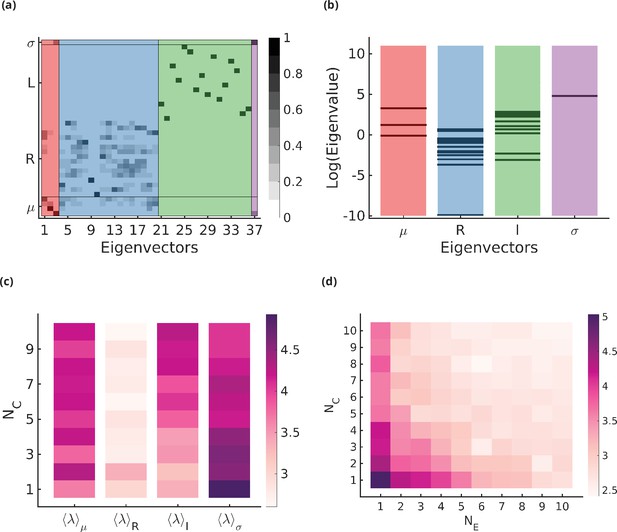
Stiff and sloppy directions in the optimization parameters.

(a) Eigenvectors of the Hessian matrix $\frac{\partial^{2}}{\partial X_{i} \partial X_{j}} F |_{X_{\min}}$ for $(N_{E}, N_{C}) = (4, 4)$ . The x-axis indexes the $N_{C} + 2 N_{E} N_{C} + 1 = 37$ eigenvectors, the y-axis indexes the $N_{C} + 2 N_{E} N_{C} + 1$ *components* of the eigenvectors, and the greyscale denotes the absolute value of the component in the range $[0, 1]$ . The components are grouped according to ( $μ, R, L, σ$ ), and the eigenvectors are ordered according to the most dominant component in the eigenvector ( $μ$ , orange; $R$ , blue; $L$ , green; $σ$ , purple). There is some mixing of the different components ( $R$ and $μ$ or $σ$ and $μ$ ) but this is usually small. (b) The distribution of eigenvalues $λ_{i}$ of the Hessian matrix $\frac{\partial^{2}}{\partial X_{i} \partial X_{j}} F |_{X_{\min}}$ . Each stripe represents an eigenvalue, and the location of the stripe on the x-axis represents whether the dominant component of the associated eigenvector belongs to $μ$ , $R$ , $L$ , or $σ$ direction. (c) The average stiffness along $μ$ , $R$ , $L$ , or $σ$ directions, defined by the log of the average of eigenvalues corresponding to the eigenvectors in the respective group, as a function of $N_{C}$ for fixed $N_{E} = 4$ . (d) Total average stiffness $⟨ λ ⟩ = \log (\frac{\sum λ_{i}}{N_{C} + 2 N_{E} N_{C} + 1})$ as a function of $N_{E}, N_{C}$ .

Figure 7

Download asset Open asset

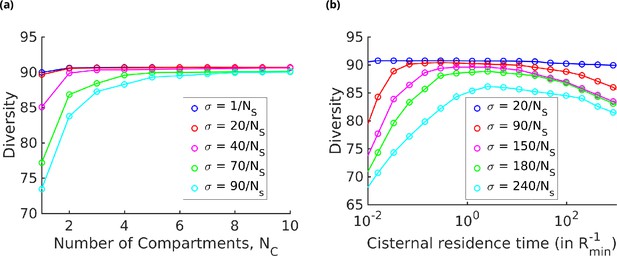
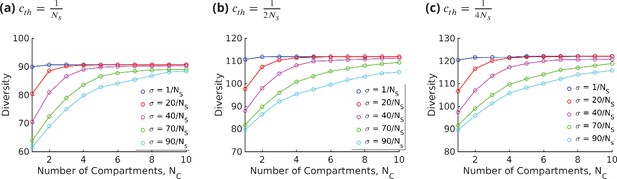
Strategies for achieving high glycan diversity.

Diversity versus $N_{C}$ and transport rate $μ$ at various values of specificity $σ$ for fixed $N_{E} = 3$ . (a) Diversity vs. $N_{C}$ at optimal transport rate $μ$ . Diversity initially increases with $N_{C}$ , but eventually levels off. The levelling off starts at a higher $N_{C}$ when $σ$ is increased. These curves are bounded by the $σ = 0$ curve. (b) Diversity vs. cisternal residence time ( $μ^{- 1}$ ) in units of the reaction time ( $R_{\min}^{- 1}$ ) at various value of $σ$ , for fixed $N_{C} = 4$ and $N_{E} = 10$ .

Appendix 1—figure 1

Download asset Open asset

The binned mass spectroscopy (MS) data (blue) approximates the raw MS data (red) very well.

We use this binned data for Gaussian mixture model (GMM) approximation of the MS data.

Appendix 1—figure 2

Download asset Open asset

Log likelihood vs. number of components ( $N$ ) in the Gaussian mixture model (GMM).

We see that the log likelihood saturates at around, $N = 20$ , thus 20-GMM is a very good representation of the mass spectroscopy (MS) data from *human* T-cells. The different symbols are for (a) different values of the maximum intensity $I_{m a x} = 50, 100, 200$ and (b) different values of the number of i.i.d. samples, $N_{i} = 500, 1000, 2000$ showing the insensitivity of the log likelihood to the value of $I_{m a x}$ and. $N_{i}$

Appendix 4—figure 1

Download asset Open asset

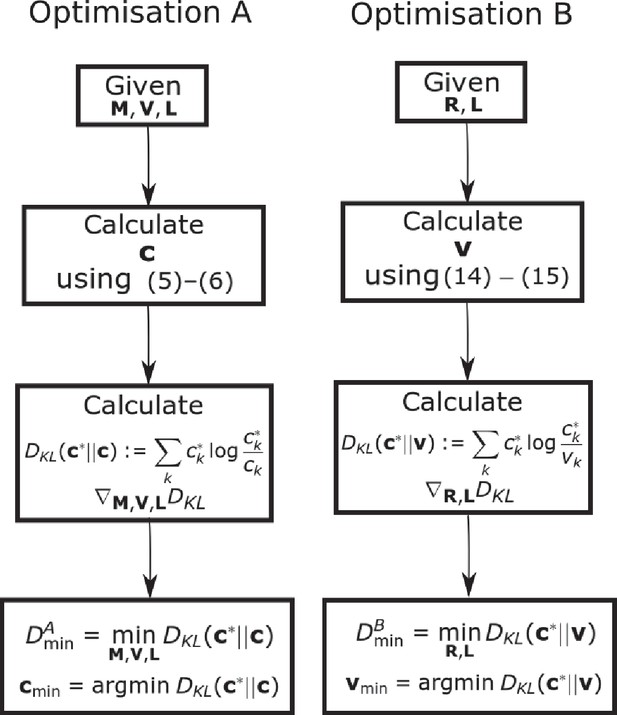
Flow chart showing the optimization schemes for Optimization A and B.

We prove that $D_{\min}^{A} = D_{\min}^{B}$ by showing the set of all $c$ is equal to the set of all $v$ . We additionally establish that the optimum $v_{\min} = c_{\min}$ .

Appendix 6—figure 1

Download asset Open asset

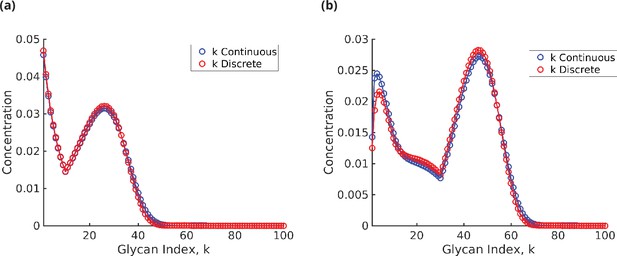
Glycan concentration profile calculated from the model using (a) formula (31) for $N_{E} = N_{C} = 1$ and (b) formulae (32)–(36) for $N_{E} = 1, N_{C} = 2$ .

Appendix 6—figure 2

Download asset Open asset

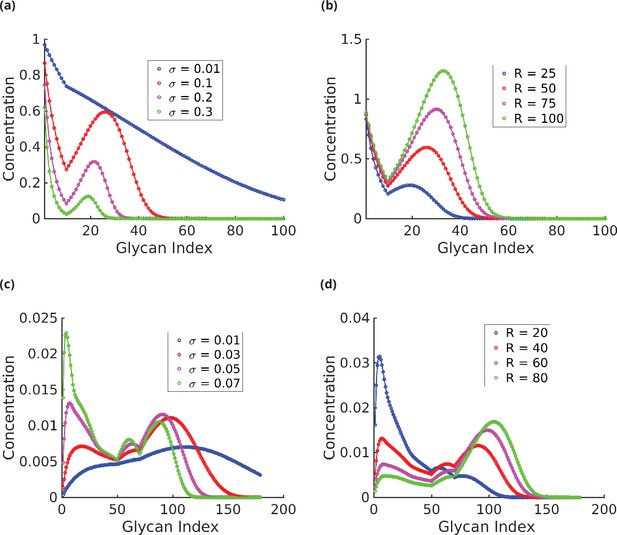
Glycan profile ${c_{k} : k = 1, \dots, N_{s}}$ as a function of specificity $σ$ (a, c) and reaction rates $R$ (b, d).

(a) $N_{E} = N_{C} = 1, (R = 50, μ = 1, l = 10)$ . c_k decreases exponentially with $k$ for very low and very high $σ$ ; however, the decay rate is lower at low $σ$ . For intermediate values of $σ$ , the distribution has *exactly* two peaks, one of which is at $k = 0$ , and eventually decays exponentially. The width of the distribution is a decreasing function of $σ$ . (b) $N_{E} = N_{C} = 1, (σ = 0.1, μ = 1, l = 10)$ . At low $R$ , c_k is concentrated at low $k$ . The proportion of higher index glycans in an increasing function of $R$ . (c) $N_{E} = N_{C} = 2, (R = 40, μ = 1, [l_{1}^{(1)}, l_{2}^{(1)}, l_{1}^{(2)}, l_{2}^{(2)}] = [10, 30, 50, 70])$ . As $σ$ increases, the distribution becomes more complex – from a single-peaked distribution at low $σ$ to a maximum of four-peaked distribution at high $σ$ . The peaks gets sharper, and more well defined as $σ$ increases. (d) $N_{E} = N_{C} = 2, (R = 40, μ = 1, [l_{1}^{(1)}, l_{2}^{(1)}, l_{1}^{(2)}, l_{2}^{(2)}] = [10, 30, 50, 70])$ . As in the plots in (b), increasing $R$ shifts the peaks towards higher index glycans and the proportion of higher index glycan increases.

Appendix 7—figure 1

Download asset Open asset

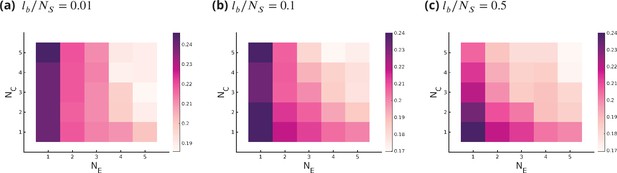
Optimum fidelity ${\bar{D}}_{K L}$ as a function of $(N_{E}, N_{C})$ for different values of $ℓ_{b} / N_{s}$ , where $ℓ_{b}$ bounds the deformation in the ideal length $ℓ_{α}^{(0)}$ of an enzyme $α = 1, \dots, N_{E}$ .

Small values of $ℓ_{b}$ restrict all enzymes from working in all cisternae and all substrates, where large value of $ℓ_{b}$ removes this constraint.

Appendix 8—figure 1

Download asset Open asset

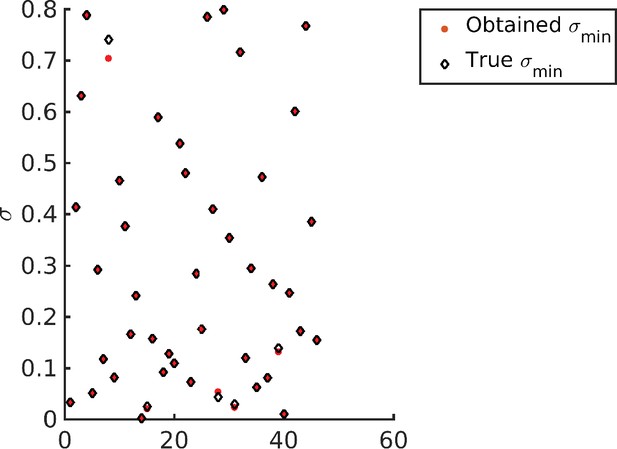
Recovering the $σ$ values for different target distribution.

Note that barring four data points all other optimized $σ$ values (red dots) exactly overlap with the corresponding target $σ$ (diamonds).

Appendix 8—figure 2

Download asset Open asset

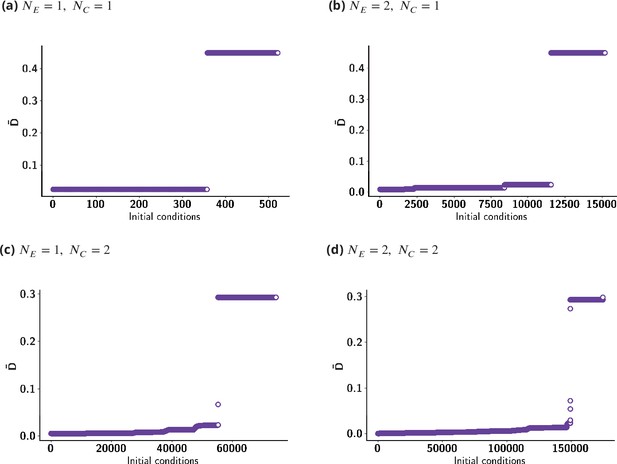
$\bar{D}$ for various initial conditions, sorted in increasing order for clarity.

This clearly shows the fraction of initial conditions for which the optimized $\bar{D}$ is small (see Appendix 8—table 1).

Appendix 10—figure 1

Download asset Open asset

Diversity vs. $N_{C}$ for different values of $σ$ keeping $N_{E} = 1$ fixed, for three different values of the threshold, $c_{t h} = \frac{1}{N_{s}}, \frac{1}{2 N_{s}}, \frac{1}{4 N_{s}}$ .

Changing the value of the threshold $c_{t h}$ only changes the saturation value of the diversity curve.

Tables

Appendix 2—table 1

Enzyme parameters taken from Table 3 in Umaña and Bailey, 1997 that we use to calculate the bounds on the reaction rate $R$ .

Here, $K_{M}^{(α)}$ and $V_{\max}^{(α)}$ denote the Michaelis constant and $V_{\max}$ of the αth enzyme.

$α$	$K_{M}^{(α)}$ (µmol)	$V_{\max}^{(α)}$ (pmol/10⁶ cell-min)
$α$	$K_{M}^{(α)}$ (µmol)	$V_{\max}^{(α)}$ (pmol/10⁶ cell-min)	1	100	5
2	260	7.5
3	200	5
4	100	5
5	190	2.33
6	130	.16
7	3400	.16
8	4000	9.66

Appendix 8—table 1

Distribution of local minima.

$N_{E}$	$N_{C}$	$\min {\bar{D}}_{K L}$	$\max {\bar{D}}_{K L}$	Fraction of initial conditions within ${\bar{D}}_{K L} \leq 0.0228$
$N_{E}$	$N_{C}$	$\min {\bar{D}}_{K L}$	$\max {\bar{D}}_{K L}$		1	1	0.0228	0.44	0.56
2	1	0.0081	0.44	0.73
1	2	0.0051	0.29	0.70
2	2	1.17e-4	0.29	0.84

Appendix 11—table 1

Table of symbols and their definitions.

Symbol	Definition
$c_{k}^{(j)}$	Concentration of $k$ th glycan in $j$ th compartment
$μ^{(j)}$	Transport rate from $j$ th to $j + 1$ compartment
$σ$	Specificity of the enzymes
$ℓ_{α}^{(j)}$	Ideal substrate length for αth enzyme in $j$ th compartment
$M (j, k, α)$	Enzyme parameter related to the Michaelis constant $K_{M}$
$V (j, k, α)$	Enzyme parameter related to $V_{m a x}$
$R (j, α)$	Reaction parameter for Optimization B
$D (c^{*} ∥ c)$	KL divergence between $c^{*}$ and $c$
$F (c^{*} \| \| c)$	Fidelity, KL divergence normalized by the entropy of the target $c^{*}$
$\bar{D} (σ, N_{E}, N_{C}, c^{*})$	$m i n_{μ, R, L} F (c^{*} \| \| c)$
$R_{e f f} (j, k)$	Effective reaction rate of $k$ th reaction in $j$ th compartment

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/76757/elife-76757-transrepform1-v2.pdf
Download elife-76757-transrepform1-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Alkesh Yadav
Quentin Vagne
Pierre Sens
Garud Iyengar
Madan Rao

(2022)

Glycan processing in the Golgi as optimal information coding that constrains cisternal number and enzyme specificity

eLife 11:e76757.

https://doi.org/10.7554/eLife.76757

Share this article

Cite this article

Living cells display a complex glycan distribution.

Enzymatic reaction and transport network in the secretory pathway.

Trade-offs amongst the glycan synthesis parameters, enzyme specificity σ, cisternal number NC, and enzyme number NE to achieve a complex target distribution c∗.

Fidelity of glycan distribution and optimal enzyme properties to achieve a complex target distribution.

Optimal enzyme partitioning in cisternae.

Stiff and sloppy directions in the optimization parameters.

Strategies for achieving high glycan diversity.

The binned mass spectroscopy (MS) data (blue) approximates the raw MS data (red) very well.

Log likelihood vs. number of components (N) in the Gaussian mixture model (GMM).

Flow chart showing the optimization schemes for Optimization A and B.

Glycan concentration profile calculated from the model using (a) formula (31) for NE=NC=1 and (b) formulae (32)–(36) for NE=1,NC=2.

Glycan profile {ck:k=1,…,Ns} as a function of specificity σ (a, c) and reaction rates R (b, d).

Optimum fidelity D¯K⁢L as a function of (NE,NC) for different values of ℓb/Ns, where ℓb bounds the deformation in the ideal length ℓα(0) of an enzyme α=1,…,NE.

Recovering the σ values for different target distribution.

D¯ for various initial conditions, sorted in increasing order for clarity.

Diversity vs. NC for different values of σ keeping NE=1 fixed, for three different values of the threshold, ct⁢h=1Ns,12⁢Ns,14⁢Ns.

Enzyme parameters taken from Table 3 in Umaña and Bailey, 1997 that we use to calculate the bounds on the reaction rate R.

Distribution of local minima.

Table of symbols and their definitions.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Trade-offs amongst the glycan synthesis parameters, enzyme specificity $σ$ , cisternal number $N_{C}$ , and enzyme number $N_{E}$ to achieve a complex target distribution $c^{*}$ .

Log likelihood vs. number of components ( $N$ ) in the Gaussian mixture model (GMM).

Glycan concentration profile calculated from the model using (a) formula (31) for $N_{E} = N_{C} = 1$ and (b) formulae (32)–(36) for $N_{E} = 1, N_{C} = 2$ .

Glycan profile ${c_{k} : k = 1, \dots, N_{s}}$ as a function of specificity $σ$ (a, c) and reaction rates $R$ (b, d).

Optimum fidelity ${\bar{D}}_{K L}$ as a function of $(N_{E}, N_{C})$ for different values of $ℓ_{b} / N_{s}$ , where $ℓ_{b}$ bounds the deformation in the ideal length $ℓ_{α}^{(0)}$ of an enzyme $α = 1, \dots, N_{E}$ .

Recovering the $σ$ values for different target distribution.

$\bar{D}$ for various initial conditions, sorted in increasing order for clarity.

Diversity vs. $N_{C}$ for different values of $σ$ keeping $N_{E} = 1$ fixed, for three different values of the threshold, $c_{t h} = \frac{1}{N_{s}}, \frac{1}{2 N_{s}}, \frac{1}{4 N_{s}}$ .

Enzyme parameters taken from Table 3 in Umaña and Bailey, 1997 that we use to calculate the bounds on the reaction rate $R$ .