Figures and data in Coevolutionary dynamics via adaptive feedback in collective-risk social dilemma game

Figures
Tables
Additional files

8 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

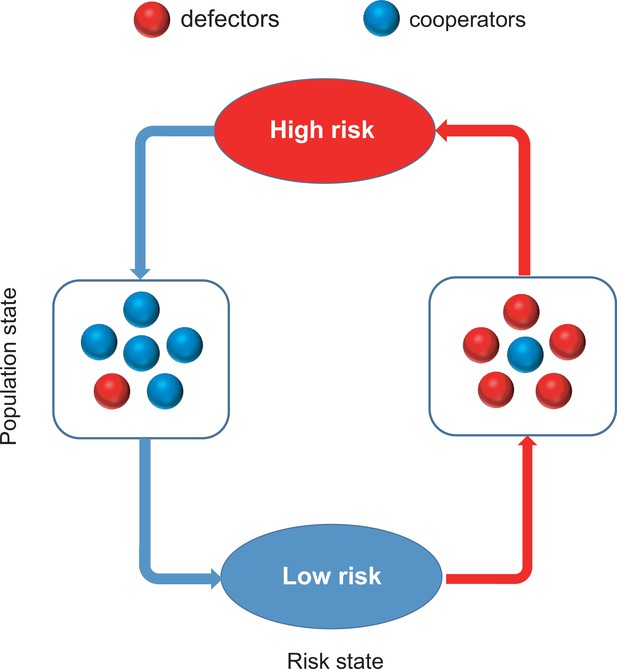
Coevolutionary feedback loop of population and risk states in the coupled game system.

The meaning of colors is explained in the legend on the top.

Figure 2

Download asset Open asset

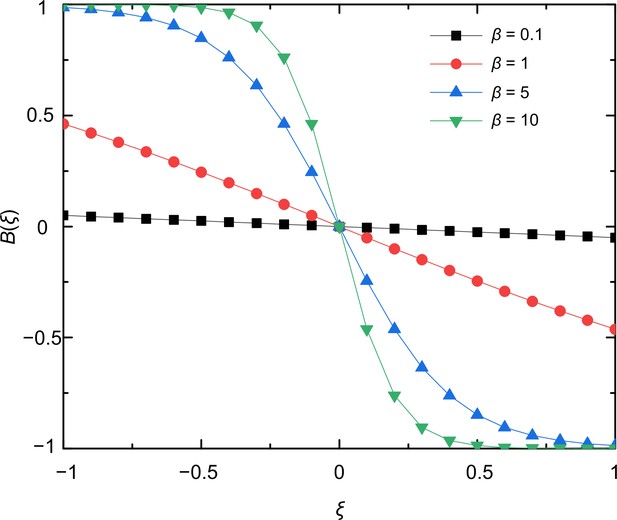
Feedback equation $B (ξ)$ varies with $ξ$ for different values of $β$ .

The parameter $β$ determines the steepness of the curves. When the value of $β$ is small, the $B (ξ)$ function is almost constant or decays linearly by increasing $ξ$ . For larger $β$ values, the shape of $B (ξ)$ approaches a step-like form. In this parameter area, the risk level depends sensitively on whether the group cooperation exceeds the threshold $T$ value or not.

Figure 3

Download asset Open asset

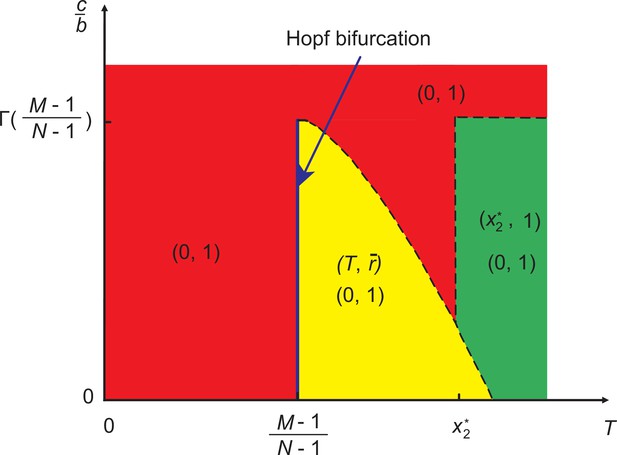
Representative plot of stable evolutionary outcomes in System I when linear strategy feedback on risk level is assumed.

Different colors are used to distinguish the stability of different equilibrium points in the parameter space ( $u, \frac{c}{b}$ ). The blue line indicates that the system undergoes a Hopf bifurcation at $u = \frac{M - 1}{N - M}$ . Here, $x_{2}^{*}$ is the real root of the equation $Γ (x) = \frac{c}{b}$ , where $Γ (x) = (\binom{N - 1}{M - 1}) x^{M - 1} {(1 - x)}^{N - M}$ , and $(\frac{u}{1 + u}, r^{*})$ is the interior fixed point where $r^{*} = \frac{c}{(\binom{N - 1}{M - 1}) (\frac{u}{1 + u})^{M - 1} (\frac{1}{1 + u})^{N - M} b}$ . The dashed curve represents that the value of $Γ (\frac{u}{1 + u})$ changes with $u$ when $u > \frac{M - 1}{N - M}$ . The horizontal dashed line represents that $Γ (\frac{M - 1}{N - 1}) = \frac{c}{b}$ when $u > \frac{x_{2}^{*}}{1 - x_{2}^{*}}$ . The vertical dashed line represents that $u = \frac{x_{2}^{*}}{1 - x_{2}^{*}}$ when $Γ (x_{2}^{*}) < \frac{c}{b} < Γ (\frac{M - 1}{N - 1})$ .

Figure 4

Download asset Open asset

Coevolutionary dynamics on phase planes and temporal dynamics of System I when linear feedback is considered.

Filled circles represent stable and open circles denote unstable fixed points. The arrows provide the most likely direction of evolution and the continuous color code depicts the speed of convergence in which red denotes the highest speed, while purple represents the lowest speed of transition. On the right-hand side, blue solid line and red dash line respectively denote the fraction of cooperation and the risk level, as indicated in the legend. The first three rows show the coevolutionary dynamics when $u > \frac{M - 1}{N - M}$ , $u = \frac{M - 1}{N - M}$ , and $u < \frac{M - 1}{N - M}$ , respectively. The bottom row shows coevolutionary dynamics when $(\binom{N - 1}{M - 1}) (\frac{u}{1 + u})^{M - 1} (\frac{1}{1 + u})^{N - M} b < c$ . Parameters are $N = 6, c = 0.1, b = 1, u = 2, ε = 0.1, M = 3$ in panel (a). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (b) and $(x, r) = (0.1, 0.1)$ in panel (c). $N = 6, c = 0.1, b = 1, u = \frac{2}{3}, ε = 0.1, M = 3$ in panel (d). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (e) and $(x, r) = (0.4, 0.5)$ in panel (f). $N = 6, c = 0.1, b = 1, u = 0.5, ε = 0.1, M = 3$ in panel (g). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (h). $N = 6, c = 0.1, b = 1, u = 4$ , $ε = 0.1, M = 3$ in panel (i). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (j) and $(x, r) = (0.1, 0.1)$ in panel (k).

Figure 5

Download asset Open asset

A representative diagram about stable solutions of System II when strategy feedback on risk level is exponential.

We use different colors to distinguish the stability of equilibrium points in the parameter space ( $T, \frac{c}{b}$ ). The blue line indicates that the system undergoes a Hopf bifurcation at $T = \frac{M - 1}{N - 1}$ . Here, $(T, \bar{r})$ is the interior fixed point where $\bar{r} = \frac{c}{(\binom{N - 1}{M - 1}) T^{M - 1} {(1 - T)}^{N - M} b}$ . The dashed curve represents that the value of $Γ (T)$ changes with $T$ when $T > \frac{M - 1}{N - 1}$ . The horizontal dashed line represents that $Γ (\frac{M - 1}{N - 1}) = \frac{c}{b}$ when $T > x_{2}^{*}$ . The vertical dashed line represents that $T = x_{2}^{*}$ when $Γ (x_{2}^{*}) < \frac{c}{b} < Γ (\frac{M - 1}{N - 1})$ .

Figure 6

Download asset Open asset

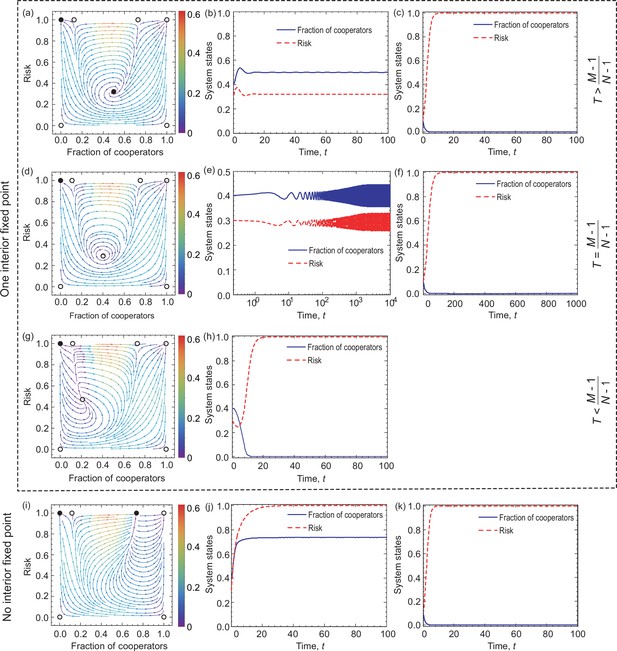
Coevolutionary dynamics on phase planes and temporal dynamics of System II when exponential feedback is assumed.

Filled circles represent stable and open circles denote unstable fixed points. The arrows provide the most likely direction of evolution and the continuous color code depicts the speed of convergence in which red denotes the highest speed, while purple represents the lowest speed of transition. Blue solid line and red dash line respectively denote the fraction of cooperation and the risk level, as indicated in the legend. The first three rows show the coevolutionary dynamics when $T > \frac{M - 1}{N - 1}$ , $T = \frac{M - 1}{N - 1}$ , and $T < \frac{M - 1}{N - 1}$ , respectively. The bottom row shows the case when $c > (\binom{N - 1}{M - 1}) T^{M - 1} (1 - T)^{N - M} b$ . Parameters are $N = 6, c = 0.1, b = 1, T = 0.5, ε = 0.1, M = 3$ in panel (a). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (b) and $(x, r) = (0.1, 0.1)$ in panel (c). $N = 6, c = 0.1, b = 1, T = 0.4, ε = 0.1, M = 3$ in panel (d). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (e) and $(x, r) = (0.4, 0.5)$ in panel (f). $N = 6, c = 0.1, b = 1, T = 0.2, ε = 0.1, M = 3$ in panel (g). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (h). $N = 6, c = 0.1, b = 1, T = 0.8$ , $ε = 0.1, M = 3$ in panel (i). The initial conditions are $(x, r) = (0.4, 0.3)$ in panel (j) and $(x, r) = (0.1, 0.1)$ in panel (k).

Appendix 1—figure 1

Download asset Open asset

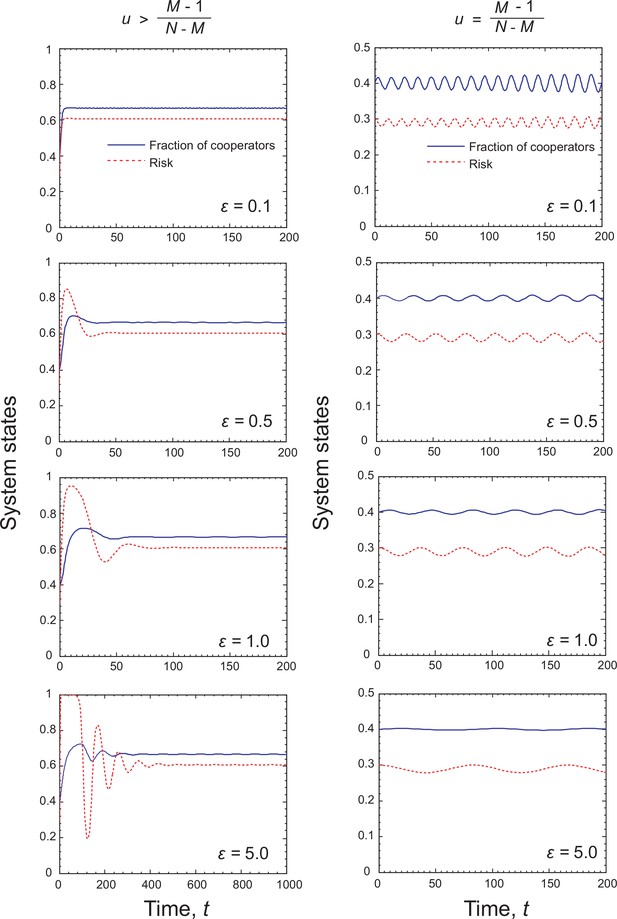
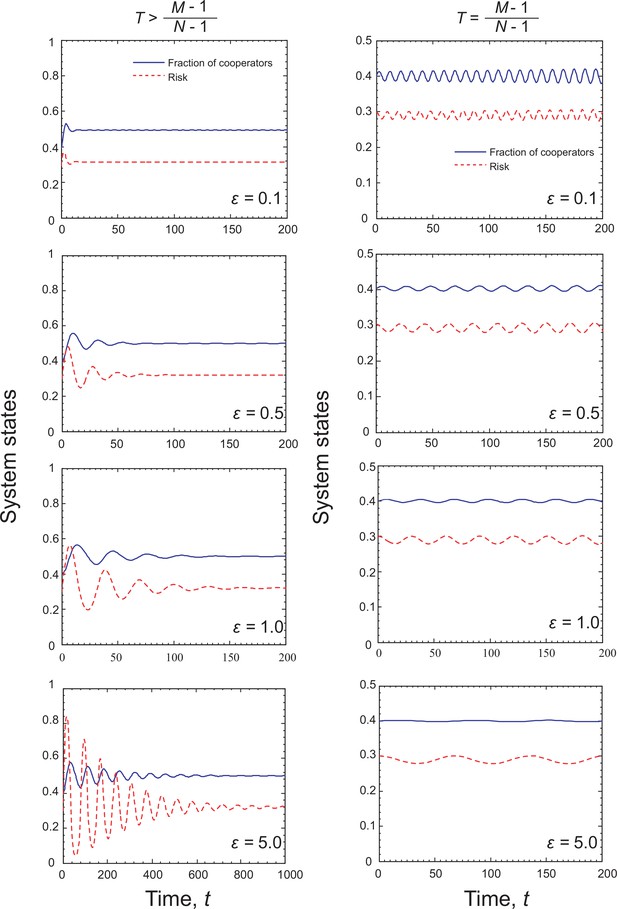
Coevolutionary dynamics of System I for different $ε$ values when linear feedback effect of strategy on risk level is considered.

Parameters are $N = 6, c = 0.1, b = 1$ , and $M = 3$ in left column and $u = 2 / 3$ in right column. The initial conditions are $(x, r) = (0.4, 0.3)$ .

Appendix 2—figure 1

Download asset Open asset

Coevolutionary dynamics of System II for different $ε$ values when the strategy feedback on risk is exponential.

Parameters are $N = 6, c = 0.1, b = 1$ , and $M = 3$ in the left column and $T = 0.4$ in the right column. The initial condition is $(x, r) = (0.4, 0.3)$ .

Tables

Table 1

Notation symbols and meanings in our work.

Symbol	Meaning
$N$	Group size
$b$	Initial endowment
$c$	Cost of cooperation
$r$	Risk
$M$	Collective goal
$ε$	Feedback speed
$u$	Growth rate of risk with the proportion of defectors
$T$	Threshold value of cooperation
$β$	Steepness parameter
$x$	Frequency of cooperation

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/82954/elife-82954-mdarchecklist1-v1.docx
Download elife-82954-mdarchecklist1-v1.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Linjie Liu
Xiaojie Chen
Attila Szolnoki

(2023)

Coevolutionary dynamics via adaptive feedback in collective-risk social dilemma game

eLife 12:e82954.

https://doi.org/10.7554/eLife.82954

Share this article

Cite this article

Coevolutionary feedback loop of population and risk states in the coupled game system.

Feedback equation B⁢(ξ) varies with ξ for different values of β.

Representative plot of stable evolutionary outcomes in System I when linear strategy feedback on risk level is assumed.

Coevolutionary dynamics on phase planes and temporal dynamics of System I when linear feedback is considered.

A representative diagram about stable solutions of System II when strategy feedback on risk level is exponential.

Coevolutionary dynamics on phase planes and temporal dynamics of System II when exponential feedback is assumed.

Coevolutionary dynamics of System I for different ε values when linear feedback effect of strategy on risk level is considered.

Coevolutionary dynamics of System II for different ε values when the strategy feedback on risk is exponential.

Notation symbols and meanings in our work.

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Feedback equation $B (ξ)$ varies with $ξ$ for different values of $β$ .

Coevolutionary dynamics of System I for different $ε$ values when linear feedback effect of strategy on risk level is considered.

Coevolutionary dynamics of System II for different $ε$ values when the strategy feedback on risk is exponential.