Neural population dynamics underlying evidence accumulation in multiple rat brain regions
- Princeton Neuroscience Institute, Princeton University, United States
- Howard Hughes Medical Institute, Princeton University, United States
- Department of Psychology, Princeton University, United States
Figures
Figure 1 with 2 supplements
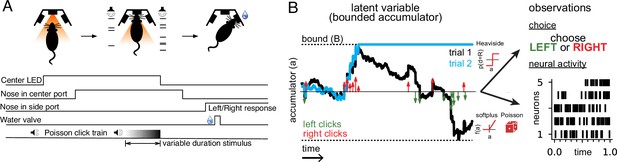
Accumulating evidence task and latent variable model.
(A) Rats performed a pulse-based evidence accumulation task. A central LED illuminates indicating that the rat can begin a trial by poking its nose in a central port. After a delay of random duration, an auditory stimulus of variable duration is delivered—a series of brief auditory pulses played from a left and a right speaker. Upon cessation of the stimulus, the rat must orient to the direction of the greater number of pulses to receive a water reward. (B) The model relates the click-based sensory stimulus to two types of observations—the animal’s choice and neural activity observed during the task. The latent variable model is a bounded accumulator. Left and right clicks (green and red arrows, respectively) push the variable to one side or the other; if the accumulator variable reaches the bound B (dotted line) accumulation ceases. Seven parameters govern the dynamics of a(t) (see main text). Two different hypothetical trajectories of a(t) are illustrated (black and blue) for the same click stimulus; the two trajectories differ due to the diffusive and stimulus noise in the model. a(t) relates to the animal’s choice by a Heaviside step function and to neural activity by way of a softplus nonlinearity and a Poisson distribution. a(t) is common for all simultaneously recorded neurons and each neuron has its own parameters that determine its tuning curve.
Figure 1—figure supplement 1
Recovering the parameters of synthetic data.
Synthetic data was generated with parameters , B=15, , , , , . Two synthetic ’sessions’ were generated, with 400 trials and 3 neurons each. Softplus gain parameters were randomly generated between –2 and 2. Parameters for decisions were c=1 (bias), (lapse). (A) Peri-stimulus time histograms (PSTHs) for two example neurons for synthetic data and simulated data after model fitting. Trials were averaged for strong evidence to the right (red) and left (brown). (B) Psychometric curves for synthetic data and simulated data after model fitting. (C) Optimization was initialized at a random set of parameters (‘initial’). Maximum likelihood parameters (‘final’) converged to within two standard deviations (error bars computed by Laplace approximation) of the parameters used to generate the data (dotted lines). refers to the neuron parameters for the jth neuron from the ith session.
Figure 1—figure supplement 2
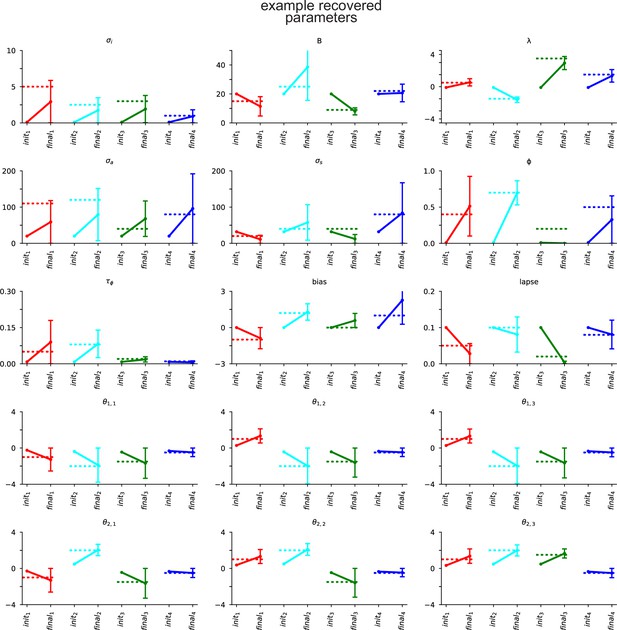
Recovering the parameters of synthetic data for multiple datasets.
Four synthetic datasets with different model parameters (red, cyan, green, blue) were generated as in Figure 1—figure supplement 1 (two sessions per dataset, with three neurons in each session). Dotted lines in each panel indicate the generative parameters. Optimization was initialized at a random set of parameters (‘init.’). Maximum likelihood parameters (‘final’) almost always converge to within two standard deviations (error bars computed by Laplace approximation) of the parameters used to generate the data. refers to the neuron parameters for the jth neuron from the ith session.
Figure 2
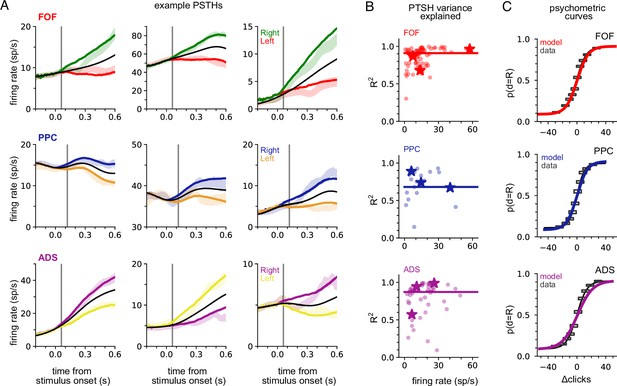
A shared accumulator model captures neural response and choice for each brain region.
(A) Peri-stimulus time histograms (PSTHs) of three example neurons for each brain region (each row; frontal orienting fields [FOF]: red/green, posterior parietal cortex [PPC]: blue/orange, anterior-dorsal striatum [ADS]: purple/yellow). Spike trains were binned, filtered with a Gaussian kernel (std = 50 ms), grouped based on the strength of evidence, and averaged. Transparent shaded regions are ±1 standard error of the mean for the empirical data for each grouping. Colored curves are the mean of synthetic data simulated from the model with the parameters that maximize the likelihood of the data, grouped in a similar fashion. The black curve shows the trial-averaged firing rate, for all evidence strengths. Gray vertical lines indicate the average delay between the stimulus and the response for each brain region (see Methods). (B) Coefficient of determination (R2) between empirical PSTH and synthetic data PSTH, for each neuron in each brain region. The data are plotted as a function of average firing rate. The median across the population is shown as a line. Points indicated with a ‘star’ refer to the data plotted in (A). (C) Probability of making a rightward choice as a function of cumulative difference in the number of clicks (psychometric curves) for empirical data (black lines) and data simulated from the model with the best fitting parameters (colored curves; FOF: red, PPC: blue, ADS: purple). Each curve is the curve of best fit, as computed by logistic regression. Rectangles indicate 25-th and 75-th quantiles of the data.
Figure 3 with 4 supplements
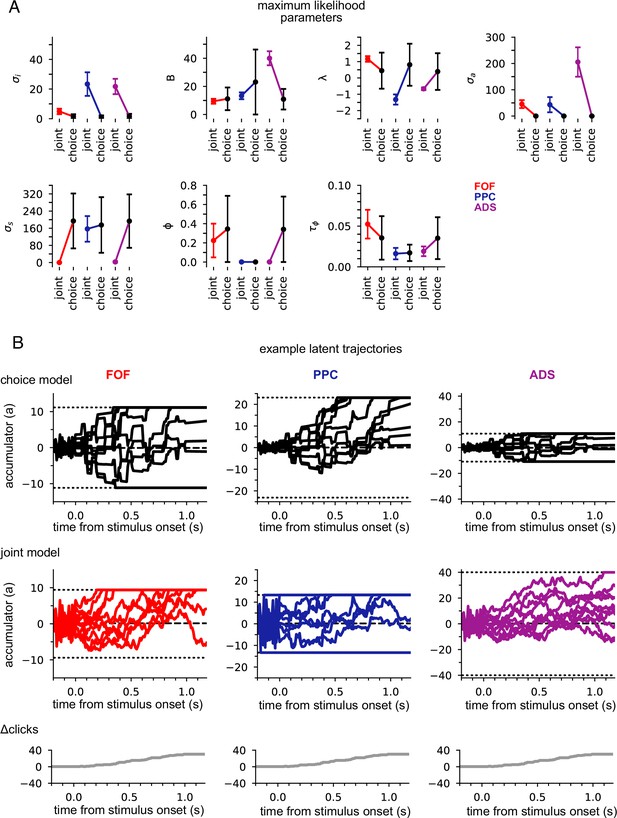
Data from different regions is best fit by different accumulator models.
(A) Maximum likelihood parameters that govern a(t) for the joint neural-behavioral model and the choice-only model. Error bars, computed by the Laplace approximation (Methods), are ±2 standard deviations. Parameters are σi: initial variance, B: accumulation bound, λ: drift, σa: accumulation noise variance, σs: click noise variance, φ: adaptation strength, τɸ: adaptation timescale. (B) 10 example trajectories with different noise instantiations for one trial for the choice model (top) and the joint model (middle) for each brain region, and cumulative sum of the click stimulus for each trial (bottom). The dotted black lines (top and middle) indicate the accumulation boundary value for each model.
Figure 3—figure supplement 1
Model comparison using Poisson or negative binomial observation model.
(A) Parameters are : initial variance, B: accumulation bound, λ: drift, : accumulation noise variance, : click noise variance, φ: adaptation strength, : adaptation timescale. Each point is a data fold (1 of 5). Maximum likelihood parameters were similar for the two observation models. Cross-validated log-likelihood was statistically indistinguishable (frontal orienting fields [FOF]: p=0.99; posterior parietal cortex [PPC]: 0.93; anterior-dorsal striatum [ADS]: 0.98) and the average difference in cross-validated log-likelihood was small (FOF: 1.11e-5; PPC: –0.036; ADS: –0.035). (B) Histogram of the negative binomial dispersion parameter (r) across all neurons for each region. For large values of r, as seen here, the negative binomial approaches the Poisson distribution.
Figure 3—figure supplement 2
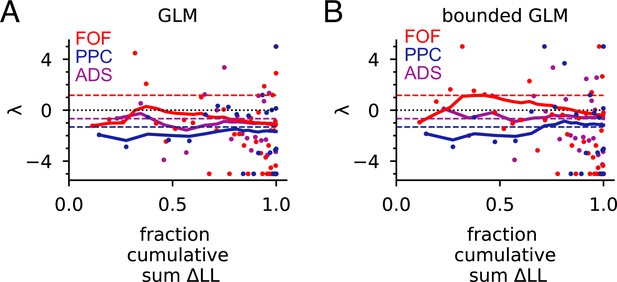
Generalized linear model (GLM) analysis of individual sessions.
(A) Poisson GLM with a softplus nonlinearity was fit with exponentially filtered clicks as the regressors (see Methods), using the same data as in Figure 2 and Figure 3. Each dot is the maximum likelihood drift (λ) parameter for a session. Sessions are ordered (from left to right) based on the fraction of the cumulative sum (across all sessions for a brain region) of the change in log-likelihood (LL) over the null model (see Methods for null model). For example, the leftmost dot for each brain region is the session with the largest change in LL. Dots on the right were from sessions with the smallest change in LL over the null. The colored lines are the cumulative mean of λ weighted by that session’s normalized change in LL. Dots on the far right have little change in LL and thus contribute to this mean only weakly. (B) GLM as in (A) but fit with a boundary, such that if the filtered clicks crossed a boundary B, the value of the regressors remained equal to B henceforth in a trial (see Methods). In each plot, the dashed colored lines are the values of λ from the full model fit (as in Figure 2 and Figure 3).
Figure 3—figure supplement 3
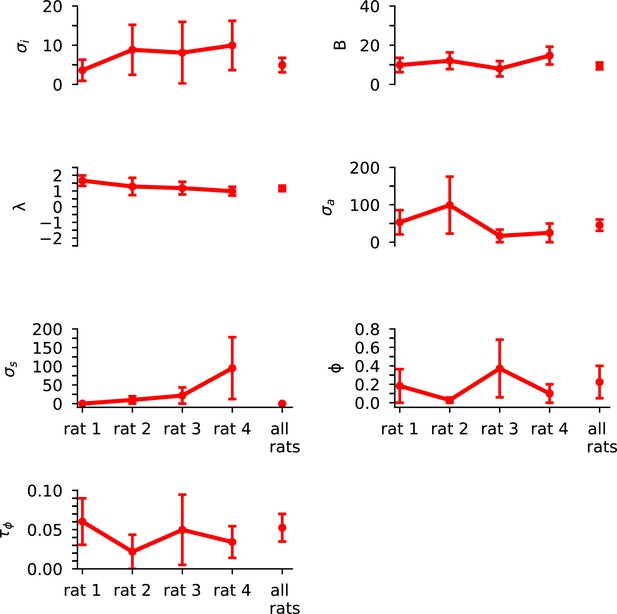
Maximum likelihood parameters of joint model for each frontal orienting fields (FOF) rat individually.
Error bars, computed by the Laplace approximation (Methods), are ±2 standard deviations. Parameters are : initial variance, B: accumulation bound, λ: drift, : accumulation noise variance, : click noise variance, φ: adaptation strength, : adaptation timescale.
Figure 3—figure supplement 4
Comparison of maximum likelihood parameters for three models: joint (neural/choice) model, choice-only model, and independent-noise joint model, when fit to all data, or using cross-validation data.
(A) Circles with error bars are for models fit to all data. Error bars for models fit to full data computed by the Laplace approximation (Methods) are ±2 standard deviations. ‘Plus (+) ’ marks are models (five for each model type) fit to cross-validation data (fivefold). Parameters are : initial variance, B: accumulation bound, λ: drift, : accumulation noise variance, : click noise variance, φ: adaptation strength, : adaptation timescale. (B) Test log-likelihood for models fit to all data (i.e., using trials reserved as testing trials when cross-validation is done) plotted against test log-likelihood for cross-validation models, for each model type (joint, choice, joint (ind.)), for all three brain regions.
Figure 4 with 2 supplements
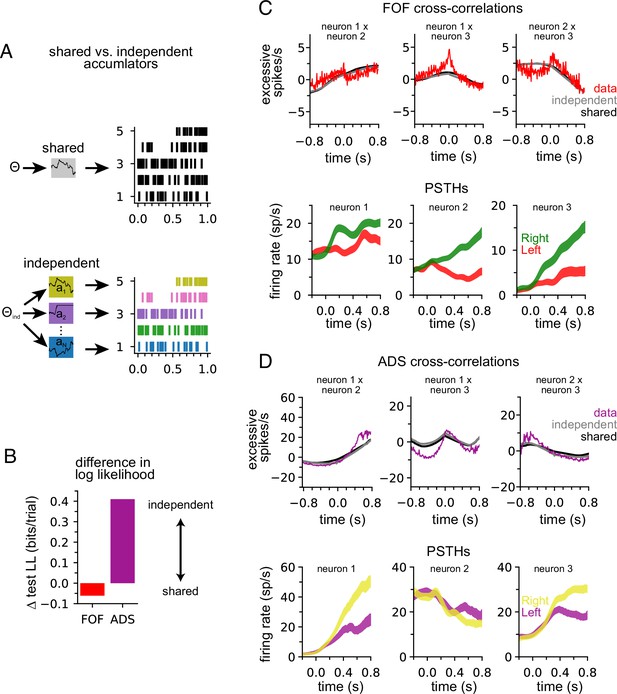
Anterior-dorsal striatum (ADS) is better described by independent accumulators.
(A) For the shared-noise accumulator model (top), a set of parameters defines the dynamics of a single accumulator, which drives the spiking activity of the entire population. In the independent-noise accumulator model, a set of parameters defines the dynamics of an ensemble of independent accumulator models, which each individually determine the spiking of a single neuron. (B) Difference in test log-likelihood (bits/trial) for the shared-noise vs. independent-noise accumulator models. (C) Empirical (red) and synthetic (shared: black; independent; gray) shuffle-corrected cross-correlation function for three simultaneously recorded neurons from the frontal orienting fields (FOF). Corresponding peri-stimulus time histograms (PSTHs) are shown below for reference. (D) Same as (C) for three (of five) simultaneously recorded neurons from the ADS.
Figure 4—figure supplement 1
Maximum likelihood parameters for the joint (neural/choice, i.e., shared-noise) model and independent (‘ind.’) noise joint model.
Error bars, computed by the Laplace approximation (Methods), are ±2 standard deviations. Parameters are : initial variance, B: accumulation bound, λ: drift, : accumulation noise variance, : click noise variance, φ: adaptation strength, : adaptation timescale.
Figure 4—figure supplement 2
between the shared-noise and independent-noise accumulator model.
(A) Difference in log-likelihood for each session for frontal orienting fields (FOF) and anterior-dorsal striatum (ADS) data plotted as a function of the number of neurons in each session. (B) When the number of neurons in each session for the ADS dataset was subsampled to match the maximum number of neurons in an FOF session (three neurons) the ADS was still favored by an independent-noise accumulator model (purple, no fill; averaged across two subsample permutations of the ADS recordings). (C) Same as (A) but plotted as a function of dimension, as computed by the participation ratio (see Methods). Sessions in the ADS with higher dimension favored the independent-noise accumulator model, leading to the net effect seen in Figure 4B. (D) The difference in log-likelihood was similar when the choice data was omitted from both models.
Figure 5
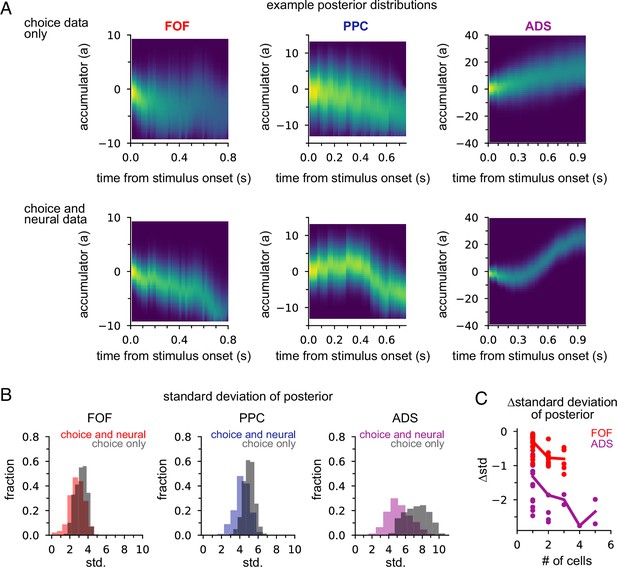
Neural data provides more information about accumulated evidence on single trials than choice alone.
(A) Posterior distribution of a(t) under the joint model (excluding captured mass at the boundary) given only the choice (top row) and given spike times and choice (bottom row), for a single example trial. Columns show example trials for different brain regions. (B) Histogram of joint model posterior standard deviations given choice data (black) or both neural and choice data (colors) for all three brain regions. (C) Difference in choice-conditioned joint posterior standard deviation and neural- and choice-conditioned joint posterior standard deviation as a function of the number of simultaneously recorded neurons. Each point is the difference in the average posterior standard deviation for a session. Negative values indicate that the neural- and choice-conditioned posterior had smaller average standard deviation than the choice-conditioned posterior.
Figure 6 with 2 supplements
Joint neural-behavioral model improves choice decoding.
(A) Choice-prediction accuracy, quantified with log-likelihood (left) and percent correct (right) on test choice data for four models: joint neural-behavioral model, choice-only model, and two logistic regression models (Methods). Values greater than zero indicate that the model can predict choices better than a baseline model that only knows the marginal probability of a rightward choice. (B) Posterior mean of a(t) conditioned on the neural activity for the joint model (colors), the distribution of a(t) for the choice-only model (black), and the cumulative click difference (gray) for three example trials (one for each brain region). ‘Animal’s choice’ arrow indicates the choice (left or right) the animal made on that trial. (C) Putative change of mind events, where the posterior mean of the joint model crossed the decision threshold. The corresponding distribution of a(t) for the choice-only model (black) and the cumulative click difference (gray) for the same trial are shown for comparison. ‘Animal’s choice’ arrow indicates the choice (left or right) the animal made on that trial. (D) Fraction of trials that contain at least one putative change of mind event for the cumulative click difference, the choice model, and the joint model, for each brain region. (E) Fraction of trials for which a putative change of mind event occurs at the specified time relative to the end of the stimulus for the joint model (color) and the cumulative click difference (black) for each brain region. (F) Choice response latency as a function of timing of putative change of mind events relative to stimulus offset for each brain region. Bar plots show the 25–75 percentiles of the choice response latency for putative change of mind events occurring at similar times. The colored lines indicate the line of best fit for each brain region computed by linear regression.
Figure 6—figure supplement 1
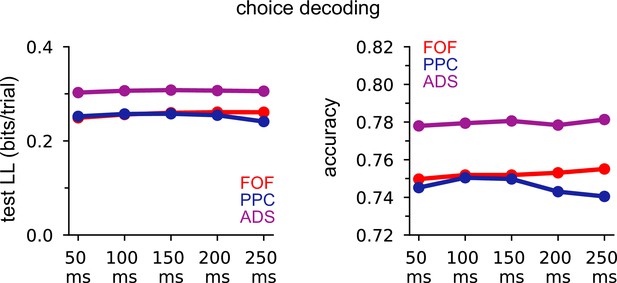
Generalized linear model (GLM) choice decoding (as in Figure 6A) using spikes in different time windows relative to stimulus offset.
Figure 6—figure supplement 2
Accuracy on putative change of mind event trials and non-event trials.
(A) Accuracy of the rat for data from each brain region for putative change of mind event trials and trials that lacked events (‘no event’). (B) Same as (A) but for accuracy of the joint model for each brain region.
Author response image 1
Author response image 2
Tables
Table 1
Number of neurons, sessions, and trials for each rat.
| Rat | Region | Sessions | Neurons | Trials | Sessions with greater than 1 neuron | Max. # of simultaneously recorded neurons |
|---|---|---|---|---|---|---|
| B068 | FOF | 11 | 13 | 5859 | 2 | 2 |
| T034 | FOF | 9 | 10 | 4138 | 1 | 2 |
| T036 | FOF | 8 | 12 | 3026 | 4 | 2 |
| T063 | FOF | 17 | 32 | 4002 | 9 | 3 |
| T030 | FOF | 1 | 1 | 357 | 0 | 1 |
| T035 | PPC | 15 | 16 | 5919 | 1 | 2 |
| T011 | PPC | 7 | 7 | 2235 | 0 | 1 |
| B053 | PPC | 2 | 2 | 883 | 0 | 1 |
| T080 | ADS | 5 | 6 | 1731 | 1 | 2 |
| T103 | ADS | 19 | 38 | 8332 | 9 | 5 |
| E021 | ADS | 3 | 4 | 697 | 1 | 2 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Neural population dynamics underlying evidence accumulation in multiple rat brain regions
eLife 13:e84955.
https://doi.org/10.7554/eLife.84955
