Basolateral amygdala oscillations enable fear learning in a biophysical model

Reviewer #1 (Public Review):

Plasticity in the basolateral amygdala (BLA) is thought to underlie the formation of associative memories between neutral and aversive stimuli, i.e. fear memory. Concomitantly, fear learning modifies the expression of BLA theta rhythms, which may be supported by local interneurons. Several of these interneuron subtypes, PV+, SOM+, and VIP+, have been implicated in the acquisition of fear memory. However, it was unclear how they might act synergistically to produce BLA rhythms that structure the spiking of principal neurons so as to promote plasticity. Cattani et al. explored this question using small network models of biophysically detailed interneurons and principal neurons.

Using this approach, the authors had four principal findings:

(1) Intrinsic conductances in VIP+ interneurons generate a slow theta rhythm that periodically inhibits PV+ and SOM+ interneurons, while disinhibiting principal neurons.
(2) A gamma rhythm arising from the interaction between PV+ and principal neurons establishes the precise timing needed for spike-timing-dependent plasticity.
(3) Removal of any of the interneuron subtypes abolishes conditioning-related plasticity.
(4) Learning-related changes in principal cell connectivity enhance expression of slow theta in the local field potential.

The strength of this work is that it explores the role of multiple interneuron subtypes in the formation of associative plasticity in the basolateral amygdala. The authors use biophysically detailed cell models that capture many of their core electrophysiological features, which helps translate their results into concrete hypotheses that can be tested in vivo. Moreover, they try to align the connectivity and afferent drive of their model with those found experimentally.

Deficient in this study is the construction of the afferent drive to the network, which does elicit activities that are consistent with those observed to similar stimuli. It still remains to be demonstrated that their mechanism promotes plasticity for training protocols that emulate the kinds of activities observed in the BLA during fear conditioning.

Setting aside the issues with the conditioning protocol, the study offers a model for the generation of multiple rhythms in the BLA that is ripe for experimental testing. The most promising avenue would be in vivo experiments testing the role of local VIP+ neurons in the generation of slow theta. That would go a long way to resolving whether BLA theta is locally generated or inherited from medial prefrontal cortex or ventral hippocampus afferents.

The broader importance of this work is that it illustrates that we must examine the function of neurons not just in terms of their behavioral correlates, but by their effects on the microcircuit they are embedded within. No one cell type is instrumental in producing fear learning in the BLA. Each contributes to the orchestration of network activity to produce plasticity. Moreover, this study reinforces a growing literature highlighting the crucial role of theta and gamma rhythms in BLA function.

Reviewer #2 (Public Review):

The authors of this study have investigated how oscillations may promote fear learning using a network model. They distinguished three types of rhythmic activities and implemented an STDP rule to the network aiming to understand the mechanisms underlying fear learning in the BLA.

After the revision, the fundamental question, namely, whether the BLA networks can or cannot intrinsically generate any theta rhythms, is still unanswered. The author added this sentence to the revised version: "A recent experimental paper, (Antonoudiou et al., 2022), suggests that the BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings under certain conditions, such as reduced inhibitory tone." In the cited paper, the authors studied gamma oscillations, and when they applied 10 uM Gabazine to the BLA slices observed rhythmic oscillations at theta frequencies. 10 uM Gabazine does not reduce the GABA-A receptor-mediated inhibition but eliminates it, resulting in rhythmic populations burst driven solely by excitatory cells. Thus, the results by Antonoudiou et al., 2022 contrast with, and do not support, the present study, which claims that rhythmic oscillations in the BLA depend on the function of interneurons. Thus, there is still no convincing evidence that BLA circuits can intrinsically generate theta oscillations in intact brain or acute slices. If one extrapolates from the hippocampal studies, then this is not surprising, as the hippocampal theta depends on extra-hippocampal inputs, including, but not limited to the entorhinal afferents and medial septal projections (see Buzsaki, 2002). Similarly, respiratory related 4 Hz oscillations are also driven by extrinsic inputs. Therefore, at present, it is unclear which kind of physiologically relevant theta rhythm in the BLA networks has been modelled.

Author response:

The following is the authors’ response to the current reviews.

eLife assessment:

This useful modeling study explores how the biophysical properties of interneuron subtypes in the basolateral amygdala enable them to produce nested oscillations whose interactions facilitate functions such as spike-timing-dependent plasticity. The strength of evidence is currently viewed as incomplete because of insufficient grounding in prior experimental results and insufficient consideration of alternative explanations. This work will be of interest to investigators studying circuit mechanisms of fear conditioning as well as rhythms in the basolateral amygdala.

We disagree with the overall assessment of our paper. The current reviews published below focus on two kinds of perceived inadequacies. Reviewer 1 (R1) was concerned that the fear conditioning paradigm used in the model is not compatible with some of the experiments we are modeling. The reviewer helpfully suggested in the Recommendations for the Authors some papers, which R1 believed exposed this incompatibility. In our reading, those data are indeed compatible with our hypotheses, as we will explain in our reply. Furthermore, the point raised by R1 is an issue for the entire field. We will suggest a solution to that issue based on published data.

Reviewer 2 (R2) said that there is no evidence that the BLA is capable of producing, by itself, the rhythms that have been observed during fear conditioning in BLA and, furthermore, that the paper we cited to support such evidence, in fact, refutes our argument. We believe that the reasoning used by reviewer 2 is wrong and that the framework of R2 for what counts as evidence is inadequate. We spell out our arguments below in the reply to the reviewers.

Finally, we believe this work is of interest far beyond investigators studying fear conditioning. The work shows how rhythms can create the timing necessary for spike-timing-dependent plasticity using multiple time scales that come from multiple different kinds of interneurons found both in BLA and, more broadly, in cortex. Thus, the work is relevant for all kinds of associative learning, not just fear conditioning. Furthermore, it is one of the first papers to show how rhythms can be central in mechanisms of higher-order cognition.

Reviewer #1

We thank Reviewer 1 for his kind remarks about our first set of responses and their understanding of the importance of the work. There was only one remaining point to be addressed:

Deficient in this study is the construction of the afferent drive to the network, which does elicit activities that are consistent with those observed to similar stimuli. It still remains to be demonstrated that their mechanism promotes plasticity for training protocols that emulate the kinds of activities observed in the BLA during fear conditioning.

It is true that some fear conditioning protocols involve non-overlapping US and CS, raising the question of how plasticity happens or whether behavioral effects may happen without plasticity. This is an issue for the entire field (Sun et al., F1000Research, 2020). Several papers (Quirk, Repa and LeDoux, 1995; Herry et al, 2007; Bordi and Ledoux 1992) show that the pips in auditory fear conditioning increase the activity of some BLA neurons: after an initial transient, the overall spike rate is still higher than baseline activity. The question remains as to whether the spiking is sustained long enough and at a high enough rate for STDP to take place when US is presented sometime after the stop of the CS.

Experimental recordings cannot speak to the rate of spiking of BLA neurons during US due to recording interference from the shock. However, evidence seems to suggest that ECS activity should increase during the US due to the release of acetylcholine (ACh) from neurons in the basal forebrain (BF) (Rajebhosale et al., 2024). Pyramidal cells of the BLA robustly express M1 muscarinic ACh receptors (Muller et al., 2013; McDonald and Mott, 2021) and M1 receptors target spines receiving glutamatergic input (McDonald et al., 2019). Thus, ACh from BF should elicit a long-lasting depolarization in pyramidal cells. Indeed, the pairing of ACh with even low levels of spiking of BLA neurons results in a membrane depolarization that can last 7 – 10 s (Unal et al., 2015). This implies that the release of ACh can affect the consequences of the CS in successive trials. This should include higher spiking rates and more sustained activity in the ECS neurons after the first presentation of US, thus ensuring a concomitant activation of ECS and fear (F) neurons necessary for STDP to take place. Hence, we suggest that a solution to the problem raised by R1 may be solved by considering the role of ACh release by BF. To the best of our knowledge, there is nothing in the literature that contradicts this potential solution. The model we have may be considered a “minimal” model that puts in by hand the higher frequency due to the cholinergic drive without explicitly modeling it. As R1 says, it is important for us to give the motivation of that higher frequency; in the next revision, we will be explicit about how the needed adequate firing rate can come about without an overlap of CS and US in any given trial.

Reviewer #2

The authors of this study have investigated how oscillations may promote fear learning using a network model. They distinguished three types of rhythmic activities and implemented an STDP rule to the network aiming to understand the mechanisms underlying fear learning in the BLA.

After the revision, the fundamental question, namely, whether the BLA networks can or cannot intrinsically generate any theta rhythms, is still unanswered. The author added this sentence to the revised version: "A recent experimental paper, (Antonoudiou et al., 2022), suggests that the BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings under certain conditions, such as reduced inhibitory tone." In the cited paper, the authors studied gamma oscillations, and when they applied 10 uM Gabazine to the BLA slices observed rhythmic oscillations at theta frequencies. 10 uM Gabazine does not reduce the GABA-A receptor-mediated inhibition but eliminates it, resulting in rhythmic populations burst driven solely by excitatory cells. Thus, the results by Antonoudiou et al., 2022 contrast with, and do not support, the present study, which claims that rhythmic oscillations in the BLA depend on the function of interneurons. Thus, there is still no convincing evidence that BLA circuits can intrinsically generate theta oscillations in intact brain or acute slices. If one extrapolates from the hippocampal studies, then this is not surprising, as the hippocampal theta depends on extra-hippocampal inputs, including, but not limited to the entorhinal afferents and medial septal projections (see Buzsaki, 2002). Similarly, respiratory related 4 Hz oscillations are also driven by extrinsic inputs. Therefore, at present, it is unclear which kind of physiologically relevant theta rhythm in the BLA networks has been modelled.

Reviewer 2 (R2) says “the fundamental question, namely, whether the BLA networks can or cannot intrinsically generate any theta rhythms, is still unanswered.” In our revision, we cited (Antonoudiou et al., 2022), who showed that BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings. R2 pointed out that this paper produces such theta under conditions in which the inhibition is totally removed. R2 then states that the resulting rhythmic populations burst at theta “are driven solely by excitatory cells. Thus, the results by (Antonoudiou et al., 2022) contrast with, and do not support, the present study, which claims that rhythmic oscillations in the BLA depend on the function of interneurons. Thus, there is still no convincing evidence that BLA circuits can intrinsically generate theta oscillations in intact brain or acute slices.”

This reasoning of R2 is faulty. With all GABAergic currents omitted, the LFP is composed of excitatory currents and intrinsic currents. Our model of the LFP includes all synaptic and membrane currents. In our model, the high theta comes from the spiking activity of the SOM cells, which increase their activity if the inhibition from VIP cells is removed. We are including a new simulation, which models the activity of the slice in the presence of kainate (as done in Antonoudiou et al., 2022), providing additional excitation to the network. If the BLA starts at high excitation, our model produces an ongoing gamma in the VIP cells that suppress SOM cells and allows a PING gamma to form between PV and F cells; with Gabazine (modeled as the removal of all the GABAergic synapses), this PING is no longer possible and so the gamma rhythm disappears. As expected, the simulation shows that the model produces theta with Gabazine; the model also shows that a PING rhythm is produced without Gabazine, and that this rhythm goes away with Gabazine because PING requires feedback inhibition (see Author response image 1). Thus, the theta increase with Gabazine in the (Antonoudiou et al., 2022) paper can be reproduced in our model, so that paper does support the model.

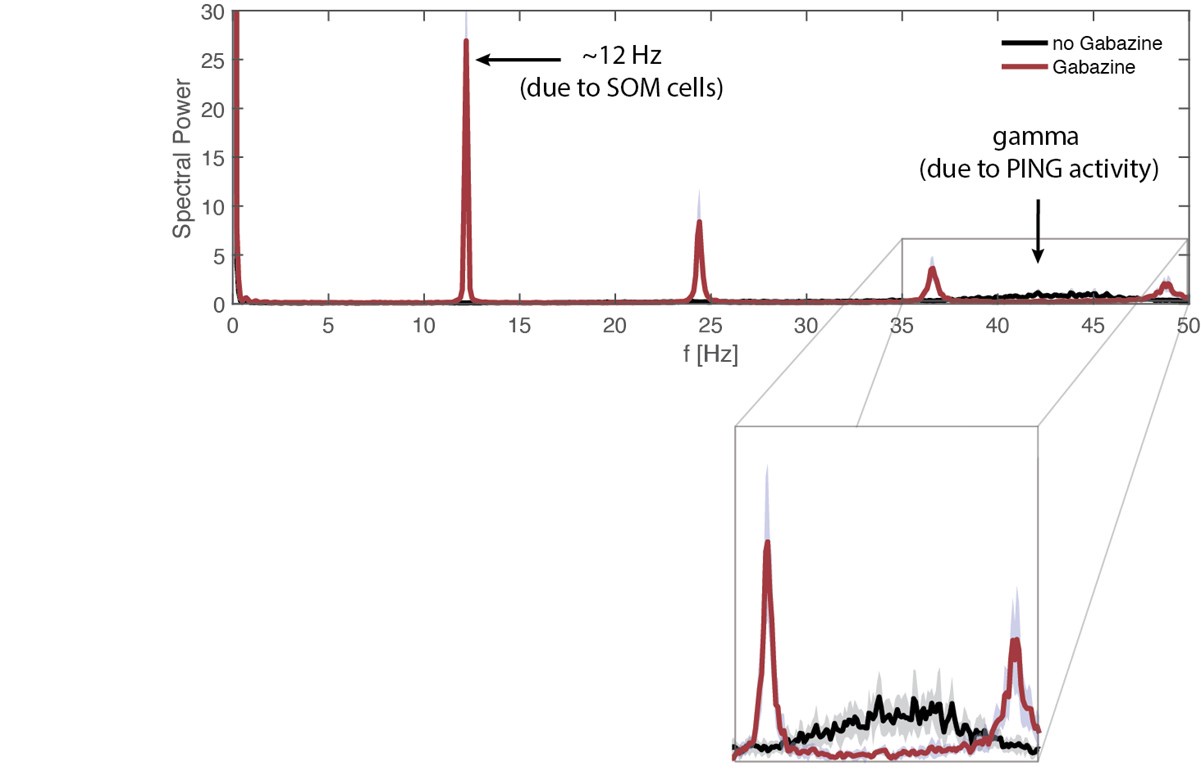
Author response image 1.

Spectral properties of the BLA network without (black) versus with Gabazine (magenta). Power spectra of the LFP proxy, which is the linear sum of AMPA, GABA (only present in the absence of Gabazine, D-, NaP-, and H-currents. Both power spectra are represented as mean and standard deviation across 10 network realizations. Bottom: inset between 35 and 50 Hz.

Nevertheless, we agree that this paper alone is not sufficient evidence that the BLA can produce a low theta. We have recently learned of a new paper (Bratsch-Prince et al., 2024) that is directly related to the issue of whether the BLA by itself can produce low theta, and in what circumstances. In this study, intrinsic BLA theta is produced in slices with ACh stimulation (without needing external glutamate input) which, in vivo, would be produced by the basal forebrain (Rajebhosale et al., eLife, 2024) in response to salient stimuli. The low-theta depends on muscarinic activation of CCK interneurons, a group of interneurons that overlaps with the VIP neurons in our model (Krabbe 2017; Mascagni and McDonald, 2003).

We suspect that the low theta produced in (Bratsch-Prince et al., 2024) is the same as the low theta in our model. We do not explicitly include ACh modulation of BLA in our paper, but in current work with experimentalists, we aim to show that ACh is essential to the theta by activating the BLA VIP cells. In our re-revised version, we will discuss Bratsch-Prince et al., 2024 and its connection to our hypothesis that the theta oscillations can be produced within the BLA.

Note that we have already included a paragraph stating explicitly that our hypothesis in no way contradicts the idea that inputs to the BLA may include theta oscillations. Indeed, the following paragraphs in the revised paper describe the complexity of trying to understand the origin of brain rhythms in vivo. R2 did not appear to take this complexity, and the possible involvement of neuromodulation, into account in their current position that the theta rhythms cannot be produced intrinsically in the BLA.

From revised paper: “Where the rhythms originate, and by what mechanisms. A recent experimental paper, (Antonoudiou et al. 2022), suggests that the BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings under certain conditions, such as reduced inhibitory tone. They draw this conclusion in mice by removing the hippocampus, which can volume conduct to BLA, and noticing that other nearby brain structures did not display any oscillatory activity. Our model also supports the idea that intrinsic mechanisms in the BLA can support the generation of the low theta, high theta, and gamma rhythms.

Although the BLA can produce these rhythms, this does not rule out that other brain structures also produce the same rhythms through different mechanisms, and these can be transmitted to the BLA. Specifically, it is known that the olfactory bulb produces and transmits the respiratory-related low theta (4 Hz) oscillations to the dorsomedial prefrontal cortex, where it organizes neural activity (Bagur et al., 2021). Thus, the respiratory-related low theta may be captured by BLA LFP because of volume conduction or through BLA extensive communications with the prefrontal cortex. Furthermore, high theta oscillations are known to be produced by the hippocampus during various brain functions and behavioral states, including during spatial exploration (Vanderwolf, 1969) and memory formation/retrieval (Raghavachari et al., 2001), which are both involved in fear conditioning. Similarly to the low theta rhythm, the hippocampal high theta can manifest in the BLA. It remains to understand how these other rhythms may interact with the ones described in our paper.”

We believe our current paper is important to show how detailed biophysical modeling can unearth the functional implications of physiological details (such as the biophysical bases of rhythms), which are often (indeed, usually) ignored in models, and why rhythms may be essential to some cognitive processes (including STDP). Indeed, for evaluating our paper it is necessary to go back to the purpose of a model, especially one such as ours, which is “hypothesis/data driven”. The hypotheses of the model serve to illuminate the functional roles of the physiological details, giving meaning to the data. Of course, the hypotheses must be plausible, and we think that the discussion above easily clears that bar. Hypotheses should also be checked experimentally, and a model that explains the implications of a hypothesis, such as ours, provides motivation for doing the hard work of experimental testing. We think that R1 understands this and has been very helpful.

—————

The following is the authors’ response to the original reviews.

eLife assessment

This useful modeling study explores how the biophysical properties of interneuron subtypes in the basolateral amygdala enable them to produce nested oscillations whose interactions facilitate functions such as spike-timing-dependent plasticity. The strength of evidence is currently viewed as incomplete because the relevance to plasticity induced by fear conditioning is viewed as insufficiently grounded in existing training protocols and prior experimental results, and alternative explanations are not sufficiently considered. This work will be of interest to investigators studying circuit mechanisms of fear conditioning as well as rhythms in the basolateral amygdala.

Most of our comments below are intended to rebut the sentence: “The strength of evidence is currently viewed as incomplete because the relevance to plasticity induced by fear conditioning is viewed as insufficiently grounded in existing training protocols and prior experimental results, and alternative explanations are not sufficiently considered”.

We believe this work will be interesting to investigators interested in dynamics associated with plasticity, which goes beyond fear learning. It will also be of interest because of its emphasis on the interactions of multiple kinds of interneurons that produce dynamics used in plasticity, in the cortex (which has similar interneurons) as well as BLA. We note that the model has sufficiently detailed physiology to make many predictions that can be tested experimentally. Details are below in the answer to reviewers.

Reviewer #1 (Public Comments):

(1) … the weakness is that their attempt to align with the experimental literature (specifically Krabbe et al. 2019) is performed inconsistently. Some connections between cell types were excluded without adequate justification (e.g. SOM+ to PV+).

In order to constrain our model, we focused on what is reported in (Krabbe et al., 2019) in terms of functional connectivity instead of structural connectivity. Thus, we included only those connections for which there was strong functional connectivity. For example, the SOM to PV connection is shown to be small (Krabbe et al., 2019, Supp. Fig. 4, panel t). We also omitted PV to SOM, PV to VIP, SOM to VIP, VIP to excitatory projection neurons; all of these are shown in (Krabbe et al. 2019, Fig. 3 (panel l), and Supp. Fig. 4 (panels m,t)) to have weak functional connectivity, at least in the context of fear conditioning.

We reply with more details below to the Recommendations for the Authors, including new text.

(2) The construction of the afferent drive to the network does not reflect the stimulus presentations that are given in fear conditioning tasks. For instance, the authors only used a single training trial, the conditioning stimulus was tonic instead of pulsed, the unconditioned stimulus duration was artificially extended in time, and its delivery overlapped with the neutral stimulus, instead of following its offset. These deviations undercut the applicability of their findings.

Regarding the use of a single long presentation of US rather than multiple presentations (i.e., multiple trials): in early versions of this paper, we did indeed use multiple presentations. We were told by experimental colleagues that the learning could be achieved in a single trial. We note that, if there are multiple presentations in our modeling, nothing changes; once the association between CS and US is learned, the conductance of the synapse is stable. Also, our model does not need a long period of US if there are multiple presentations.

We agree that, in order to implement the fear conditioning paradigm in our in-silico network, we made several assumptions about the nature of the CS and US inputs affecting the neurons in the BLA and the duration of these inputs. A Poisson spike train to the BLA is a signal that contains no structure that could influence the timing of the BLA output; hence, we used this as our CS input signal. We also note that the CS input can be of many forms in general fear conditioning (e.g., tone, light, odor), and we wished to de-emphasize the specific nature of the CS. The reference mentioned in the Recommendations for authors, (Quirk, Armony, and LeDoux 1997), uses pulses 2 seconds long. At the end of fear conditioning, the response to those pulses is brief. However, in the early stages of conditioning, the response goes on for as long as the figure shows. The authors do show the number of cells responding decreases from early to late training, which perhaps reflects increasing specificity over training. This feature is not currently in our model, but we look forward to thinking about how it might be incorporated. Regarding the CS pulsed protocol used in (Krabbe et al., 2019), it has been shown that intense inputs (6kHz and 12 kHz inputs) can lead to metabotropic effects that last much longer than the actual input (200 ms duration) (Whittington et al., Nature, 1995). Thus, the effective input to the BLA may indeed be more like Poisson.

Our model requires the effect of the CS and US inputs on the BLA neuron activity to overlap in time in order to instantiate fear learning. Despite paradigms involving both overlapping (delay conditioning, where US coterminates with CS (Lindquist et al., 2004), or immediately follows CS (e.g., Krabbe et al., 2019)) and non-overlapping (trace conditioning) CS/US inputs existing in the literature, we hypothesized that concomitant activity in CS- and US-encoding neuron activity should be crucial in both cases. This may be mediated by the memory effect, as suggested in the Discussion of our paper, or by metabotropic effects as suggested above, or by the contribution from other brain regions. We will emphasize in our revision that the overlap in time, however instantiated, is a hypothesis of our model. It is hard to see how plasticity can occur without some memory trace of US. This is a consequence of our larger hypothesis that fear learning uses spiketiming-dependent plasticity; such a hypothesis about plasticity is common in the modeling literature.

We reply with more details below to the Recommendations for the Authors, including new text.

Reviewer #1 (Recommendations For The Authors):

Major points:

(1) This paper draws extensively from Krabbe et al. 2019, but it does not do so consistently. The paper would be strengthened if it tried to better match the circuit properties and activations.

Specifically:

a. Krabbe found that PV interneurons were comparably activated by the US (see Supp Fig 1). Your model does not include that. The basis for the Krabbe 2019 claim that PV US responses are weaker is that they have a slightly larger proportion of cells inhibited by the US, but this is not especially compelling. In addition, their Fig 2 showed that VIP and SOM cells receive afferents from the same set of upstream regions.

b. The model excluded PV-SOM connections, but this does not agree with Krabbe et al. 2019, Table 2. PV cells % connectivity and IPSC amplitudes were comparable to those from VIP interneurons.

c. ECS to PV synapses are not included. This seems unlikely given the dense connectivity between PV interneurons and principal neurons in cortical circuits and the BLA (Woodruff and Sah 2007 give 38% connection probability in BLA).

We thank the Reviewer for raising these points, which allow us to clarify how we constrained our model and to do more simulations. Specifically:

a. (Wolff et al., Nature, 2014), cited by (Krabbe et al. 2018), reported that PV and SOM interneurons are on average inhibited by the US during the fear conditioning. However, we agree that (Krabbe et al., 2019) added to this by specifying that PV interneurons respond to both CS+ and US, although the fraction of US-inhibited PV interneurons is larger. As noted by the Reviewer, in the model we initially considered the PV interneurons responding only to CS+ (identified as “CS” in our manuscript). For the current revision, we ran new simulations in which the PV interneuron receives the US input, instead of CS+. It turned out that this did not affect the results, as shown in the figure below: all the network realizations learn the association between CS and fear. In the model, the PING rhythm between PV and F is the crucial component for establishing fine timing between ECS and F, which is necessary for learning. Having PV responding to the same input as F, i.e., US, facilitates their entrainment in PING and, thus, successful learning.

As for afferents of VIP and SOM from upstream regions, in (Krabbe et al., 2019) is reported that “[…] BLA SOM interneurons receive a different array of afferent innervation compared to that of VIP and PV interneurons, which might contribute to the differential activity patterns observed during fear learning.” Thus, in the model, we are agnostic about inputs to SOM interneurons; we modeled them to fire spontaneously at high theta.

To address these points in the manuscript, we added some new text in what follows:

(1) New Section “An alternative network configuration characterized by US input to PV, instead of CS, also learns the association between CS and fear” in the Supplementary information:

“We constrained the BLA network in Fig. 2 with CS input to the PV interneuron, as reported in (Krabbe et al., 2018). However, (Krabbe et al., 2019) notes that a class of PV interneurons may be responding to US rather than CS. Fig. S3 presents the results obtained with this variation in the model (see Fig. 3 A,B for comparison) and shows that all the network realizations learn the association between CS and fear. In the model, the PING rhythm between PV and F is the crucial component for establishing fine timing between ECS and F, which is necessary for learning. Having PV responding to the same input as F, i.e., US, facilitates their entrainment in PING and, thus, successful fear learning.

We model the VIP interneuron as affected by US; in addition, (Krabbe et al. 2019) reports that a substantial proportion of them is mildly activated by CS. Replacing the US by CS does not change the input to VIP cells, which is modeled by the same constant applied current. Thus, the VIP CS-induced activity is a bursting activity at low theta, similar to the one elicited by US in Fig. 2.”

(2) Section “With the depression-dominated plasticity rule, all interneuron types are needed to provide potentiation during fear learning” in Results: “Finally, since (Krabbe et al., 2019) reported that a fraction of PV interneurons are affected by US, we have also run the simulations for single neuron network with the PV interneuron affected by US instead of CS. In this case as well, all the network realizations are learners (see Fig. S3). ”

(3) Section “Conditioned and unconditioned stimuli” in Materials and Methods: “To make Fig. S3, we also considered a variation of the model with PV interneurons affected by US, instead of CS, as reported in (Krabbe et al. 2019).”

b. Re the SOM to PV connection: As reported in the reply to the public reviews, we considered the prominent functional connections reported in (Krabbe et al., 2019), instead of structural connections. That is, we included only those connections for which there was strong functional connectivity. For example, the SOM to PV connection is shown to be small (Supp. Fig. 4, panel t, in (Krabbe et al., 2019)). We also omitted PV to SOM, PV to VIP, SOM to VIP, and VIP to excitatory projection neurons; all of these are shown in (Krabbe et al. 2019, Fig. 3 (panel l), and Supp. Fig. 4 (panels m,t)) to have weak functional connectivity, at least in the context of fear conditioning.

In order to clarify this point, in Section “Network connectivity and synaptic currents” in Materials and Methods, we now say:

“We modeled the network connectivity as presented in Fig. 2B, derived from the prominent functional, instead of structural, connections reported in (Krabbe et al., 2019).”

c. Re the ECS to PV synapses: We thank the Reviewer for the reference provided; as the Reviewer says, the ECS to PV synapses are not included. Upon adding this connection in our network, we found that, unlike the connection suggested in part a above, introducing these synapses would, in fact, change the outcome. Thus, the omission of this connection must be considered an implied hypothesis. Including those synapses with a significant strength would alter the PING rhythm created by the interactions between F and PV, which is crucial for ECS and F fine timing. Thanks very much for showing us that this needs to be said. Our hypothesis does not contradict the dense connections mentioned by the Reviewer; such dense connectivity does not mean that all pyramidal cells connect to all interneurons. This hypothesis may be taken as a prediction of the model.

The absence of this connection is now discussed at the end of a new Section of the Discussion entitled “Assumptions and predictions of the model”, which reads as follows:

“Finally, the model assumes the absence of significantly strong connections from the excitatory projection cells ECS to PV interneurons, unlike the ones from F to PV. Including those synapses would alter the PING rhythm created by the interactions between F and PV, which is crucial for ECS and F fine timing. We note that in (Woodruff and Sah, 2007) only 38% of the pyramidal cells are connected to PV cells. The functional identity of the connected pyramidal cells is unknown. Our model suggests that successful fear conditioning requires F to PV connections and that ECS to PV must be weak or absent.”

(2) Krabbe et al. 2019 and Davis et al. 2017 were referenced for the construction of the conditioned and unconditioned stimulus pairing protocol. The Davis citation is not applicable here because that study was a contextual, not cued, fear conditioning paradigm. Regarding Krabbe, the pairing protocol was radically different from what the authors used. Their conditioned stimulus was a train of tone pips presented at 0.9 Hz, which lasted 30 s, after which the unconditioned stimulus was presented after tone offset. The authors should determine how their network behaves when this protocol is used. Also, note that basolateral amygdala responses to tone stimuli are primarily brief onset responses (e.g. Quirk, Armony, and LeDoux 1997), and not the tonic activation used in the model.

We replied to this point in our responses to the Reviewer’s Public Comments as follows:

“We agree that, in order to implement the fear conditioning paradigm in our in-silico network, we made several assumptions about the nature of the CS and US inputs affecting the neurons in the BLA and the duration of these inputs. A Poisson spike train to the BLA is a signal that contains no structure that could influence the timing of the BLA output; hence, we used this as our CS input signal. We also note that the CS input can be of many forms in general fear conditioning (e.g., tone, light, odor), and we wished to de-emphasize the specific nature of the CS. The reference mentioned in the Recommendations for authors, (Quirk, Armony, and LeDoux 1997), uses pulses 2 seconds long. At the end of fear conditioning, the response to those pulses is brief. However, in the early stages of conditioning, the response goes on for as long as the figure shows. The authors do show the number of cells responding decreases from early to late training, which perhaps reflects increasing specificity over training. This feature is not currently in our model, but we look forward to thinking about how it might be incorporated. Regarding the CS pulsed protocol used in (Krabbe et al., 2019), it has been shown that intense inputs (6kHz and 12 kHz inputs) can lead to metabotropic effects that last much longer than the actual input (200 ms duration) (Whittington et al., Nature, 1995). Thus, the effective input to the BLA may indeed be more like

Poisson.”

Current answer to the Reviewer:

There are several distinct issues raised by the Reviewer in the more detailed critique. We respectfully disagree that the model is not applicable to context-dependent fear learning where the context acts as a CS, though we should have been more explicit. Specifically, our CS input can describe both the cue and the context. We included the following text in the Results section “Interneuron rhythms provide the fine timing needed for depression-dominated STDP to make the association between CS and fear”:

“In our simulations, the CS input describes either the context or the cue in contextual and cued fear conditioning, respectively. For the context, the input may come from the hippocampus or other non-sensory regions, but this does not affect its role as input in the model.”

The second major issue is whether the specific training protocols used in the cited papers need to be exactly reproduced in the signals received by the elements of our model; we note that there are many transformations that can occur between the sensory input and the signals received by the BLA. In the case of auditory fear conditioning, a series of pips, rather than individual pips, are considered the CS (e.g., (Stujenske et al., 2014; Krabbe et al. 2019)). Our understanding is that a single pip does not elicit a fear response; a series of pips is required for fear learning. This indicates that it is not the neural code of a single pip that matters, but rather the signal entering the amygdala that incorporates any history-dependent signaling that could lead to spiking throughout the sequence of pips. Also, as mentioned above, intense inputs at frequencies about 6kHz and 12kHz can lead to metabotropic effects that last much longer than each brief pip (~200 ms), thus possibly producing continuous activity in neurons encoding the input. Thus, we believe that our use of the Poisson spike train is reasonable.

However, we are aware that the activity of neurons encoding CS can be modulated by the pips: neurons encoding auditory CS display a higher firing rate when each pip is presented and a Poisson-like spike train between pips (Herry et al., Journal of Neuroscience, 2007). Here we confirm that potentiation is present even in the presence of the fast transient response elicited by the pips. We said in the original manuscript that there is learning for a Poisson spike train CS input at ~50 Hz; this describes the neuronal activity in between pips. For the revision, we asked whether learning is preserved when CS is characterized by higher frequencies, which would describe the CS during and right after each pip. We show in the new Fig. S4 that potentiation is ensured for a range of CS frequencies. The figure shows the learning speed as a function of CS and US frequencies. For all the CS frequencies considered, i) there is learning, ii) learning speed increases with CS frequency. Thus, potentiation is present even when pips elicit a faster transient response.

To better specify this in the manuscript,

We added the following sentences in the Results section “With the depressiondominated plasticity rule, all interneuron types are needed to provide potentiation during fear learning”:

“We note that the CS and US inputs modeled as independent Poisson spike trains represent stimuli with no structure. Although we have not explicitly modeled pulsating pips, as common in auditory fear conditioning (e.g., (Stujenske 2014; Krabbe 2019)), we show in Fig. S4 that potentiation can be achieved over a relatively wide range of gamma frequencies. This indicates that overall potentiation is ensured if the gamma frequency transiently increases after the pip.”

We added the section “The full network potentiates for a range of CS frequencies“ and figure S4 in the Supplementary Information:

We included in Materials and Methods “Conditioned and unconditioned stimuli” the following sentences:

“Finally, for Fig.S4, we considered a range of frequencies for the CS stimulus. To generate the three Poisson spike trains with average frequencies from 48 to 64 Hz in Fig. S4, we set 𝜆 = 800, 1000, 1200.”

Finally, to address the comment about the need for CS and US overlapping in time to instantiate fear association, we added the following text in the Results section “Assumptions and predictions of the model”:

“Finally, our model requires the effect of the CS and US inputs on the BLA neuron activity to overlap in time in order to instantiate fear learning. Despite paradigms involving both overlapping (delay conditioning, where US co-terminates with CS (e.g., (Lindquist et al., 2004)), or immediately follows CS (e.g., Krabbe et al., 2019)) and non-overlapping (trace conditioning) CS/US inputs exist, we hypothesized that concomitant activity in CS- and US-encoding neuron activity should be crucial in both cases. This may be mediated by the memory effect due to metabotropic effects (Whittington et al., Nature, 1995) as suggested above, or by the contribution from other brain regions (see section “Involvement of other brain structures” in the Discussion). The fact that plasticity occurs with US memory trace is a consequence of our larger hypothesis that fear learning uses spike-timing-dependent plasticity; such a hypothesis about plasticity is common in the modeling literature.”

(3) As best as I could tell, only a single training trial was used in this study. Fair enough, especially given that fear learning can occur with a single trial. However, most studies of amygdala fear conditioning have multiple trials (~5 or more). How does the model perform when multiple trials are given?

The association between CS and fear acquired after one trial, i.e., through a potentiated ECS to F connection, is preserved in the presence of multiple trials. Indeed, the association would be weakened or erased (through depression of the ECS to F connection) only if ECS and F did not display good fine timing, i.e., F does not fire right after ECS most of the time. However, the implemented circuit supports the role of interneurons in providing the correct fine timing, thus preventing the association acquired from being erased.

In the second paragraph of the Results section “With the depression-dominated plasticity rule, all interneuron types are needed to provide potentiation during fear learning”, we made the above point by adding the following text:

“We note that once the association between CS and fear is acquired, subsequent presentations of CS and US do not weaken or erase it: the interneurons ensure the correct timing and pauses in ECS and F activity, which are conducive for potentiation.”

(4) The LFP calculations are problematic. First, it is unclear how they were done. Did the authors just take the transmembrane currents they included and sum them, or were they scaled by distance from the 'electrode' and extracellular conductivity (as one would derive from the Laplace equation)? Presumably, the spatial arrangement of model neurons was neglected so distance was not a factor.

Second, if this is the case, then the argument for excluding GABAergic conductances seems flawed. If the spatial arrangement of neurons is relevant to whether to include or exclude GABAergic conductances, then wouldn't a simulation without any spatial structure not be subject to the concern of laminar vs. nuclear arrangement?

Moreover, to the best I can tell, the literature the authors use to justify the exclusion of

GABAergic currents does not make the case for a lack of GABAergic contribution in non-laminar structures. Instead, those studies only argue that in a non-laminar structure, AMPA currents are detectable, not that GABA cannot be detected. Thus, the authors should either include the GABAergic currents when calculating their simulated LFP, or provide a substantially better argument or citation for their exclusion.

We thank the Reviewer for pointing this out; this comment helped us rethink how to model the LFP. The origin of the LFP signal in BLA has not been fully determined, but factors thought to be important include differences in the spatial extension of the arborization in excitatory and inhibitory neurons, in the number of synaptic boutons, and spatial distributions of somata and synapses (Lindén et al 2011; Łęski 2013; Mazzoni et al. 2015). In the first version of the manuscript, we excluded the GABAergic currents because it is typically assumed that they add very little to the extracellular field as the inhibitory reversal potential is close to the resting membrane potential. For the revision, we re-ran the simulations during pre and post fear conditioning and we modeled the LFP as the sum of the AMPA, GABA and NaP-/H-/D- currents. With this new version of the LFP, we added a new Fig. 6 showing that there is a significant increase in the low theta power, but not in the high theta power, with fear learning (Fig. 6 C, D, E). This increase in the low theta power was mainly due to the AMPA currents created by the newly established connection from ECS to F, which allowed F to be active after fear conditioning in response to CS.

However, as the Reviewer mentioned, our network has no spatial extent: neurons are modeled as point cells. Thus, our current model does not include the features necessary to model some central aspects of the LFP. Despite that, our model does clearly demonstrate how rhythmic activity in the spike timing of neurons within the network changes due to fear learning (Fig. 6B). The spiking outputs of the network are key components of the inputs to the LFP, and thus we expect the rhythms in the spiking to be reflected in more complex descriptions of the LFP. But we also discovered that different LFP proxies provide different changes in rhythmic activity comparing pre- and post-fear learning; although we have no principled way to choose a LFP proxy, we believe that the rhythmic firing is the essential finding of the model.

We have added the following to the manuscript:

(1) In the new version of Fig. 6, we present the power spectra of the network spiking activity (panel B), along with the power spectra of the LFP proxy that includes the GABA, AMPA, and NaP-/H-/D- currents (panels C, D, E).

(2) We modified the conclusion of the Results section entitled “Increased low-theta frequency is a biomarker of fear learning” by saying:

“In this section, we explore how plasticity in the fear circuit affects the network dynamics, comparing after fear conditioning to before. We first show that fear conditioning leads to an increase in low theta frequency power of the network spiking activity compared to the pre-conditioned level (Fig. 6 A,B); there is no change in the high theta power. We also show that the LFP, modeled as the linear sum of all the AMPA, GABA, NaP-, D-, and H- currents in the network, similarly reveals a low theta power increase and no significant variation in the high theta power (Fig. 6 C,D,E). These results reproduce the experimental findings in (Davis et al., 2017), and (Davis et al., 2017), and Fig 6 F,G show that the low theta increase is due to added excitation provided by the new learned pathway. The additional unresponsive ECS and F cells in the network were included to ensure we had not biased the LFP towards excitation. Nevertheless, although both the AMPA and GABA currents contribute to the power increase in the low theta frequency range (Fig. 6F), the AMPA currents show a dramatic power increase relative to the baseline (the average power ratio of AMPA and GABA post- vs pre-conditioning across 20 network realizations is 3*103 and 4.6, respectively). This points to the AMPA currents as the major contributor to the low theta power increase. Specifically, the newly potentiated AMPA synapse from ECS to F ensures F is active after fear conditioning, thus generating strong currents in the PV cells to which it has strong connections (Fig. 6G). Finally, the increase in power is in the low theta range because ECS and F are allowed to spike only during the active phase of the low theta spiking VIP neurons. We have also explored another proxy for the LFP (see Supplementary Information and Fig. S6).”

In the Supplementary Information, we included a figure and some text in the new section entitled “A higher low theta power increase emerges in LFP approximated with the sum of the absolute values of the currents compared to their linear sum”:

“Given that our BLA network comprises a few neurons described as single-compartment cells with no spatial extension and location, the LFP cannot be computed directly from our model’s read-outs. In the main text, we choose as an LFP proxy the linear sum of the AMPA, GABA, and P-/H-/D-currents. We note that if the LFP is modeled as the sum of the absolute value of the currents, as suggested by (Mazzoni et al. 2008; Mazzoni et al. 2015), an even higher low theta power increase arises after fear conditioning compared to the linear sum. Differences in the power spectra also arise if other LFP proxies (e.g., only AMPA currents, only GABA currents) are considered. A principled description of an LFP proxy would require modeling the three-dimensional BLA anatomy, including that of the interneurons VIP and SOM; this is outside the scope of the current paper. (See (Feng et al. 2019) for a related project in the BLA.)”

(3) We updated the Materials and Methods section “Local field potentials and spectral analysis” to explain how we compute the LFP in the revised manuscript:

“We considered as an LFP proxy as the linear sum of all the AMPA, GABA, NaP, D, and H currents in the network. The D-current is in the VIP interneurons, and NaP-current and H-current are in SOM interneurons.”

Although it is beyond the scope of the current work, an exploration of the most accurate proxy of the LFP in the amygdala is warranted. Such a study could be accomplished by adopting a similar approach as in (Mazzoni et al., 2015), where several LFP proxies based on point-neuron leaky-integrate and fire neuronal network were compared with a “groundtruth” LFP obtained in an analogous realistic three-dimensional network model.

To explicitly mention this issue in the paper, we add a paragraph in the “Limitations and caveats” section in the Discussion, which reads as follows:

“LFPs recorded in the experiments are thought to be mainly created by transmembrane currents in neurons located around the electrode and depend on several factors, including the morphology of the arborization of contributing neurons and the location of AMPA and GABA boutons (Katzner et al. 2009; Lindén et al 2011; Łęski 2013; Mazzoni et al. 2015). Since our model has no spatial extension, we used an LFP proxy; this proxy was shown to reflect the rhythmic output of the network, which we believe to be the essential result (for more details see Results “Increased low-theta frequency is a biomarker of fear learning”, and Supplementary Information “A higher low theta power increase emerges in LFP approximated with the sum of the absolute values of the currents compared to their linear sum”).”

(4) We have removed the section “Plasticity between fear neuron and VIP slows down overall potentiation” in Results and sections “Plasticity between the fear neuron (F) and VIP slows down overall potentiation” and “Plastic F to VIP connections further increase lowtheta frequency power after fear conditioning” in the Supplementary Information. This material is extraneous since we are using a new proxy for LFP.

Minor points:

(1) In Figure 3C, the y-axis tick label for 0.037 is written as "0.37."

We thank the reviewer for finding this typo; we fixed it.

(2) Figure 5B is unclear. It seems to suggest that the added ECS and F neurons did not respond to either the CS or UCS. Is this true? If so, why include them in the model? How would their inclusion change the model behavior?

It is correct that the added ECS and F neurons did not respond to the CS or US (UCS); they are constructed to be firing at 11 Hz in the absence of any connections from other cells. These cells were included to be part of our computation of the LFP. Specifically, adding in those cells would make the LFP take inhibition into account more, and we wanted to make sure that were not biasing our computation away from the effects of inhibition. As shown in the paper (Fig. 6B), even with inhibition onto these non-responsive cells, the LFP has the properties claimed in the paper concerning the changes in the low theta and high-theta power, because the LFP is dominated by new excitation rather than the inhibition.

First, in the Results section “Network with multiple heterogeneous neurons can establish the association between CS and fear”, we commented on the added ECS and F neurons that do not respond to either CS or US by saying the following:

“The ECS cells not receiving CS are inhibited by ongoing PV activity during the disinhibition window (Fig. 5B); they are constructed to be firing at 11 Hz in the absence of any connections from other cells. The lack of activity in those cells during fear conditioning implies that there is no plasticity from those ECS cells to the active F. Those cells are included for the calculation of the LFP (see below in “Increased low-theta frequency is a biomarker of fear learning”.)”

Furthermore, we add the following sentence in the Results section “Increased low-theta frequency is a biomarker of fear learning”:

“The additional unresponsive ECS and F cells in the network were included to ensure we had not biased the LFP towards excitation.”

(3) Applied currents are given as current densities, but these are difficult to compare with current levels observed from whole-cell patch clamp recordings. Can the currents be given as absolute levels, in pA/nA.

In principle, it is possible to connect current densities with absolute levels, as requested. However, we note that the number of cells in models is orders of magnitude smaller than the number being modeled. It is common in modeling to adjust physiological parameters to achieve the qualitative properties that are important to the model, rather than trying to exactly match particular recordings.

We added to the Methods description why we choose units per unit area, rather than absolute units.

“All the currents are expressed in units per area, rather than absolute units, to avoid making assumptions about the size of the neuron surface.”

(4) Regarding: "We note that the presence of SOM cells is crucial for plasticity in our model since they help to produce the necessary pauses in the excitatory projection cell activity. However, the high theta rhythm they produce is not crucial to the plasticity: in our model, high theta or higher frequency rhythms in SOM cells are all conducive to associative fear learning. This opens the possibility that the high theta rhythm in the BLA mostly originates in the prefrontal cortex and/or the hippocampus (Stujenske et al., 2014, 2022)." The chain of reasoning in the above statement is unclear. The second sentence seems to be saying contradictory things.

We agree that the sentence was confusing; thank you for pointing it out. We have revised the paragraph to make our point clearer. The central points are: 1) having the SOM cells in the BLA is critical to the plasticity in the model, and 2) these cells may or may not be the source of the high theta observed in the BLA during fear learning.

We deleted from the discussion the text reported by the Reviewer, and we added the following one to make this point clearer:

“We note that the presence of SOM cells is crucial for plasticity in our model since they help to produce the necessary pauses in the excitatory projection cell activity. The BLA SOM cells do not necessarily have to be the only source of the high theta observed in the BLA during fear learning; the high theta detected in the LFP of the BLA also originates from the prefrontal cortex and/or the hippocampus (Stujenske et al., 2014, 2022).”

(5) Regarding: "This suggests low theta power change is not just an epiphenomenon but rather a biomarker of successful fear conditioning." Not sure this is the right framing for the above statement. The power of the theta signal in the LFP reflects the strengthening of connections, but it itself does not have an impact on network activity. Moreover, whether something is epiphenomenal is not relevant to the question of whether it can serve as a successful biomarker. A biomarker just needs to be indicative, not causal.

We intended to say why the low theta power change is a biomarker in the sense of the Reviewer. That is: experiments have shown that, with learning, the low theta power increases. The modeling shows in addition that, when learning does not take place, the low power does not increase. That means that the low theta power increases if and only if there is learning, i.e., the change in low theta power is a biomarker. To make our meaning clearer, we have changed the quoted sentences to read:

“This suggests that the low theta power change is a biomarker of successful fear conditioning: it occurs when there is learning and does not occur when there is no learning.”

Reviewer #2 (Public Comments):

We thank the Reviewer for raising these interesting points. Below are our public replies and the changes we made to the manuscript to address the Reviewer’s objections.

(1) Gamma oscillations are generated locally; thus, it is appropriate to model in any cortical structure. However, the generation of theta rhythms is based on the interplay of many brain areas therefore local circuits may not be sufficient to model these oscillations.

Moreover, to generate the classical theta, a laminal structure arrangement is needed (where neurons form layers like in the hippocampus and cortex)(Buzsaki, 2002), which is clearly not present in the BLA. To date, I am not aware of any study which has demonstrated that theta is generated in the BLA. All studies that recorded theta in the BLA performed the recordings referenced to a ground electrode far away from the BLA, an approach that can easily pick up volume conducted theta rhythm generated e.g., in the hippocampus or other layered cortical structure. To clarify whether theta rhythm can be generated locally, one should have conducted recordings referenced to a local channel (see Lalla et al., 2017 eNeuro). In summary, at present, there is no evidence that theta can be generated locally within the BLA. Though, there can be BLA neurons, firing of which shows theta rhythmicity, e.g., driven by hippocampal afferents at theta rhythm, this does not mean that theta rhythm per se can be generated within the BLA as the structure of the BLA does not support generation of rhythmic current dipoles. This questions the rationale of using theta as a proxy for BLA network function which does not necessarily reflect the population activity of local principal neurons in contrast to that seen in the hippocampus.

In both modeling and experiments, a laminar structure does not seem to be needed to produce a theta rhythm. A recent experimental paper, (Antonoudiou et al. 2022), suggests that the BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings under certain conditions, such as reduced inhibitory tone. The authors draw this conclusion by looking at mice ex vivo slices. The currents that generate these rhythms are in the BLA, since the hippocampus was removed to eliminate hippocampal volume conduction and other nearby brain structures did not display any oscillatory activity. Also, in the modeling literature, there are multiple examples of the production of theta rhythms in small networks not involving layers; these papers explain the mechanisms producing theta from non-laminated structures (Dudman et al., 2009, Kispersky et al., 2010, Chartove et al. 2020). We are not aware of any model description of the mechanisms of theta that do require layers.

We added the following text in the introduction of the manuscript to make this point clearer: “A recent rodent experimental study (Antonoudiou et al. 2022) suggests that BLA can intrinsically generate theta oscillations (3-12 Hz).”

(2) The authors distinguished low and high theta. This may be misleading, as the low theta they refer to is basically a respiratory-driven rhythm typically present during an attentive state (Karalis and Sirota, 2022; Bagur et al., 2021, etc.). Thus, it would be more appropriate to use breathing-driven oscillations instead of low theta. Again, this rhythm is not generated by the BLA circuits, but by volume conducted into this region. Yet, the firing of BLA neurons can still be entrained by this oscillation. I think it is important to emphasize the difference.

Many rhythms of the nervous system can be generated in multiple parts of the brain by multiple mechanisms. We do not dispute that low theta appears in the context of respiration; however, this does not mean that other rhythms with the same frequencies are driven by respiration. Indeed, in the response to question 1 above, we showed that theta can appear in the BLA without inputs from other regions. In our paper, the low theta is generated in the BLA by VIP neurons. Using intrinsic currents known to exist in VIP neurons (Porter et al., 1998), modeling has shown that such neurons can intrinsically produce a low theta rhythm. This is also shown in the current paper. This example is part of a substantial literature showing that there are multiple mechanisms for any given frequency band.

To elaborate more on this in the manuscript, we added the following new section in the discussion:

“Where the rhythms originate, and by what mechanisms. A recent experimental paper, (Antonoudiou et al. 2022), suggests that the BLA can intrinsically generate theta oscillations (3-12 Hz) detectable by LFP recordings under certain conditions, such as reduced inhibitory tone. They draw this conclusion in mice by removing the hippocampus, which can volume conduct to BLA, and noticing that other nearby brain structures did not display any oscillatory activity. Our model also supports the idea that intrinsic mechanisms in the BLA can support the generation of the low theta, high theta, and gamma rhythms.

Although the BLA can produce these rhythms, this does not rule out that other brain structures also produce the same rhythms through different mechanisms, and these can be transmitted to the BLA. Specifically, it is known that the olfactory bulb produces and transmits the respiratory-related low theta (4 Hz) oscillations to the dorsomedial prefrontal cortex, where it organizes neural activity (Bagur et al., 2021). Thus, the respiratory-related low theta may be captured by BLA LFP because of volume conduction or through BLA extensive communications with the prefrontal cortex. Furthermore, high theta oscillations are known to be produced by the hippocampus during various brain functions and behavioral states, including during spatial exploration (Vanderwolf, 1969) and memory formation/retrieval (Raghavachari et al., 2001), which are both involved in fear conditioning. Similarly to the low theta rhythm, the hippocampal high theta can manifest in the BLA. It remains to understand how these other rhythms may interact with the ones described in our paper.”

We also note that the presence of D-currents in the BLA VIP interneurons should be confirmed experimentally, and that the ability of VIP interneurons to generate the BLA low theta rhythm constitutes a prediction of our computational model. These points are specified in the first paragraph in the Discussion entitled “Assumptions and predictions of the model”:

“The interneuron descriptions in the model were constrained by the electrophysiological properties reported in response to hyperpolarizing currents (Sosulina et al., 2010). Specifically, we modeled the three subtypes of VIP, SOM, and PV interneurons displaying bursting behavior, regular spiking with early spike-frequency adaptation, and regular spiking without spike-frequency adaptation, respectively. Focusing on VIP interneurons, we were able to model the bursting behavior by including the D-type potassium current. This current is thought to exist in the VIP interneurons in the cortex (Porter et al., 1998), but whether this current is also found in the VIP interneurons the BLA is still unknown. Similarly, we endowed the SOM interneurons with NaP- and H-currents, as the OLM cells in the hippocampus. Due to these currents, the VIP and SOM cells are able to show low- and high-theta oscillations, respectively. The presence of these currents and the neurons’ ability to exhibit oscillations in the theta range during fear conditioning and at baseline in BLA, which are assumptions of our model, should be tested experimentally.”

(3) The authors implemented three interneuron types in their model, ignoring a large fraction of GABAergic cells present in the BLA (Vereczki et al., 2021). Recently, the microcircuit organization of the BLA has been more thoroughly uncovered, including connectivity details for PV+ interneurons, firing features of neurochemically identified interneurons (instead of mRNA expression-based identification, Sosulina et al., 2010), synaptic properties between distinct interneuron types as well as principal cells and interneurons using paired recordings. These recent findings would be vital to incorporate into the model instead of using results obtained in the hippocampus and neocortex. I am not sure that a realistic model can be achieved by excluding many interneuron types.

The interneurons and connectivity that we used were inspired by the functional connectivity reported in (Krabbe et al., 2019) (see above answer to Reviewer #1). As reported in (Vereczki et al., 2021), there are multiple categories and subcategories of interneurons; that paper does not report on which ones are essential for fear conditioning. We did use all the highly represented categories of the interneurons, except NPYcontaining neurogliaform cells.

The Reviewer says “I am not sure that a realistic model can be achieved by excluding many interneuron types”. We agree with the Reviewer that discarding the introduction of other interneurons subtypes and the description of more specific connectivity (soma-, dendrite-, and axon-targeting connections) may limit the ability of our model to describe all the details in the BLA. However, this work represents a first effort towards a biophysically detailed description of the BLA rhythms and their function. As in any modeling approach, assumptions about what to describe and test are determined by the scientific question; details postulated to be less relevant are omitted to obtain clarity. The interneuron subtypes we modeled, especially VIP+ and PV+, have been reported to have a crucial role in fear conditioning (Krabbe et al., 2019). Other interneurons, e.g. cholecystokinin and SOM+, have been suggested as essential in fear extinction. Thus, in the follow-up of this work to explain fear extinction, we will introduce other cell types and connectivity. In the current work, we have achieved our goals of explaining the origin of the experimentally found rhythms and their roles in the production of plasticity underlying fear learning. Of course, a more detailed model may reveal flaws in this explanation, but this is science that has not yet been done.

We elaborate more on this in a new section in the Discussion entitled “Assumptions and predictions of the model”. The paragraph related to this point reads as follows:

“Our model, which is a first effort towards a biophysically detailed description of the BLA rhythms and their functions, does not include the neuron morphology, many other cell types, conductances, and connections that are known to exist in the BLA; models such as ours are often called “minimal models” and constitute the majority of biologically detailed models. Such minimal models are used to maximize the insight that can be gained by omitting details whose influence on the answers to the questions addressed in the model are believed not to be qualitatively important. We note that the absence of these omitted features constitutes hypotheses of the model: we hypothesize that the absence of these features does not materially affect the conclusions of the model about the questions we are investigating. Of course, such hypotheses can be refuted by further work showing the importance of some omitted features for these questions and may be critical for other questions. Our results hold when there is some degree of heterogeneity of cells of the same type, showing that homogeneity is not a necessary condition.”

(4) The authors set the reversal potential of GABA-A receptor-mediated currents to -80 mV. What was the rationale for choosing this value? The reversal potential of IPSCs has been found to be -54 mV in fast-spiking (i.e., parvalbumin) interneurons and around -72 mV in principal cells (Martina et al., 2001, Veres et al., 2017).

A GABA-A reversal potential around -80 mV is common in the modeling literature (Jensen et al., 2005; Traub et al., 2005; Kumar et al., 2011; Chartove et al., 2020). Other computational works of the amygdala, e.g. (Kim et al., 2016), consider GABA-A reversal potential at -75 mV based on the cortex (Durstewitz et al., 2000). The papers cited by the reviewer have a GABA-A reversal potential of -72 mV for synapses onto pyramidal cells; this is sufficiently close to our model that it is not likely to make a difference. For synapses onto PV+ cells, the papers cited by the reviewer suggest that the GABA-A reversal potential is -54 mV; such a reversal potential would lead these synapses to be excitatory instead of inhibitory. However, it is known (Krabbe et al., 2019; Supp. Fig. 4b) that such synapses are in fact inhibitory. Thus, we wonder if the measurements of Martina and Veres were made in a condition very different from that of Krabbe. For all these reasons, we consider a GABA-A reversal potential around -80 mV in amygdala to be a reasonable assumption.

In section “Network connectivity and synaptic currents” in “Materials and Methods” we provided references to motivate our choice of considering a GABA-A reversal potential around -80 mV:

“The GABAa current reversal potential (𝐸!) is set to −80 𝑚𝑉, as common in the modeling literature (Jensen et al., 2005; Traub et al., 2005; Kumar et al., 2011; Chartove et al., 2020).”

(5) Proposing neuropeptide VIP as a key factor for learning is interesting. Though, it is not clear why this peptide is more important in fear learning in comparison to SST and CCK, which are also abundant in the BLA and can effectively regulate the circuit operation in cortical areas.

Other peptides seem to be important in overall modulation of fear, but VIP is especially important in the first part of fear learning, the subject of our paper. Re SST: we hypothesize that SST interneurons are critical in fear extinction and preventing fear generalization, but not to initial fear learning. The peptide of the CCK neurons, which overlap with VIP cells, has been proposed to promote the switch between fear and safety states after fear extinction (Krabbe al. 2018). Thus, these other peptides are likely more important for other aspects of fear learning.

In the Discussion, we have added:

“We hypothesize that SST peptide is critical in fear extinction and preventing fear generalization, but not to initial fear learning. Also, the CCK peptide has been proposed to promote the switch between fear and safety states after fear extinction (Krabbe al. 2018).”

Reviewer #2 (Recommendations For The Authors):

We note that Reviewer #2’s Recommendations For The Authors have the same content as the Public Comments. Thus, the changes to the manuscript we implemented above address also the private critiques listed below.

(1) As the breathing-driven rhythm is a global phenomenon accompanying fear state, one might restrict the analysis to this oscillation. The rationale beyond this restriction is that the 'high' theta in the BLA has an unknown origin (since it can originate from the ventral hippocampus, piriform cortex etc.).

In response to point 4 made by Reviewer 1 (Recommendations for the Authors) (p. 13), referring to high theta in the BLA, we previously wrote: 1) having the SOM cells in the BLA is critical to the plasticity in the model, and 2) these cells may or may not be the source of the high theta observed in the BLA during fear learning.

In the Public Critiques, Reviewer 2 relates the respiratory rhythm to the low theta. We answered this point in point 2 of the Reviewer’s Public Comments (at p. 15).

(2) I would include more interneurons in the network model incorporating recent findings.

This point was answered in our response to point 3 of the Reviewer’s Public Comments.

(3) The reversal potential for GABA-A receptor-mediated currents would be good to set to measured values. In addition, I would use AMPA conductance values that have been measured in the BLA.

We addressed this objection in our response to point 4 of the Reviewer’s Public Comments.

Reviewer #3 (Public comments):

Weaknesses:

(1) The main weakness of the approach is the lack of experimental data from the BLA to constrain the biophysical models. This forces the authors to use models based on other brain regions and leaves open the question of whether the model really faithfully represents the basolateral amygdala circuitry.

(2) Furthermore, the authors chose to use model neurons without a representation of the morphology. However, given that PV+ and SOM+ cells are known to preferentially target different parts of pyramidal cells and given that the model relies on a strong inhibition form SOM to silence pyramidal cells, the question arises whether SOM inhibition at the apical dendrite in a model representing pyramidal cell morphology would still be sufficient to provide enough inhibition to silence pyramidal firing.

1. Lastly, the fear learning relies on the presentation of the unconditioned stimulus over a long period of time (40 seconds). The authors justify this long-lasting input as reflecting not only the stimulus itself but as a memory of the US that is present over this extended time period. However, the experimental evidence for this presented in the paper is only very weak.

We are repeating here the answers we gave in response to the public comments, adding further relevant points.

(1) Our neurons were constrained by electrophysiology properties in response to hyperpolarizing currents in the BLA (Sosulina et al., 2010). We can reproduce these electrophysiological properties by using specific membrane currents known to be present in similar neurons in other brain regions (D-current in VIP interneurons in the cortex, and NaP- and H-currents in OLM/SOM cells in the hippocampus). Also, though a much more detailed description of BLA interneurons was given in (Vereczki et al., 2021), it is not clear that this level of detail is relevant to the questions that we were asking, especially since the experiments described were not done in the context of fear learning.

(2) It is true that we did not include the morphology, which undoubtedly makes a difference to some aspects of the circuit dynamics. Furthermore, it is correct that the model relies on a strong inhibition from SOM and PV to silence the excitatory projection neurons. We agree that the placement of the SOM inhibition on the pyramidal neurons can make a difference on some aspects of the circuit behavior. We are assuming that the inhibition from the SOM cells can inhibit the pyramidal cells firing, which can be seen as a hypothesis of our model. It is well known that VIP cells disinhibit pyramidal cells through inhibition of SOM and PV cells (Krabbe et al. 2019); hence, this hypothesis is generally believed. This choice of parameters comes from using simplified models: it is standard in modeling to adjust parameters to compensate for simplifications.

Re points 1) and 2), in a new paragraph (“Assumptions and predictions of the model”) in the Discussion reported in response to Reviewer #2 (public comments)’s point 3, we stated that modeling requires the omission of many details to bring out the significance of other details.

(3) 40 seconds is the temporal interval we decided to use to present the results. In the Results, we also showed that there is learning over a shorter interval of time (15 seconds) where CS and US/memory of US should both be present. Thus, our model requires 15 seconds over a single or multiple trials for associative learning to be established. We included references to additional experimental papers to support our reasoning in the last paragraph of section “Assumptions and predictions of the model” in the Discussion, also reported in response to Reviewer #1 point 2 (Recommendations for the Authors). We said there that some form of memory or overlap in the activity of the excitatory projection neurons is necessary for spike-timing-dependent plasticity.

The authors achieved the aim of constructing a biophysically detailed model of the BLA not only capable of fear learning but also showing spectral signatures seen in vivo. The presented results support the conclusions with the exception of a potential alternative circuit mechanism demonstrating fear learning based on a classical Hebbian (i.e. non-depression-dominated) plasticity rule, which would not require the intricate interplay between the inhibitory interneurons. This alternative circuit is mentioned but a more detailed comparison between it and the proposed circuitry is warranted.

Our model accounts for the multiple rhythms observed in the context of fear learning, as well as the known involvement of multiple kinds of interneurons. We did not say explicitly enough why our complicated model may be functionally important in ways that cannot be fulfilled with a simpler model with the non depression-dominated Hebbian rule. To explain this, we have added the following in the manuscript discussion:

“Although fear learning can occur without the depression-dominated rule, we hypothesize that it is necessary for other aspects of fear learning and regulation. That is, in pathological cases, there can be overgeneralization of learning. We hypothesize that the modulation created by the involvement of these interneurons is normally used to prevent such overgeneralization. However, this is beyond the scope of the present paper.”

We have also written an extra paragraph about generalization in the Discussion “Synaptic plasticity in our model”:

“With the classical Hebbian plasticity rule, we show that learning can occur without the involvement of the VIP and SOM cells. Although fear learning can occur without the depressiondominated rule, we hypothesize that the latter is necessary for other aspects of fear learning and regulation. Generalization of learning can be pathological, and we hypothesize that the modulation created by the involvement of VIP and SOM interneurons is normally used to prevent such overgeneralization. However, in some circumstances, it may be desirable to account for many possible threats, and then a classical Hebbian plasticity rule could be useful. We note that the involvement or not of the VIP-SOM circuit has been implicated when there are multiple strategies for solving a task (Piet et al., 2024). In our situation, the nature of the task (including reward structure) may determine whether the learning rule is depression-dominated and therefore whether the VIP-SOM circuit plays an important role.”

Reviewer #3 (Recommendations For The Authors):

We thank the Reviewer for all the recommendations. We replied to each of them below.

In general, there are some inconsistencies in the naming (e.g. sometimes you write PV sometimes PV+,...), please use consistent abbreviations throughout the manuscript. You also introduce some of the abbreviations multiple times.

We modified the manuscript to remove all the inconsistencies in the naming.

Introduction:

- In the last section you speak about one recent study but actually cite two articles.

We removed the reference to (Perrenoud and Cardin, 2023), which is a commentary on the Veit et al. article.

Results:

- 'Brain rhythms are thought to be encoded and propagated largely by interneurons' What do you mean by encoded here?

We agree with the Reviewer that the verb “to encode” is not accurate. We modified the sentence as follows:

“Brain rhythms are thought to be generated and propagated largely by interneurons”.

- The section 'Interneurons interact to modulate fear neuron output' could be clearer. Start with describing the elements of the circuit, then the rhythms in the baseline.

We reorganized the section as follows:

“Interneurons interact to modulate fear neuron output. Our BLA network consists of interneurons, detailed in the previous section, and excitatory projection neurons (Fig. 2A). Both the fear-encoding neuron (F), an excitatory projection neuron, and the VIP interneuron are activated by the noxious stimulus US (Krabbe et al., 2019). As shown in Fig. 2A (top, right), VIP disinhibits F by inhibiting both SOM and PV, as suggested in (Krabbe et al., 2019). We do not include connections from PV to SOM and VIP, nor connections from SOM to PV and VIP, since those connections have been shown to be significantly weaker than the ones included (Krabbe et al., 2019). The simplest network we consider is made of one neuron for each cell type. We introduce a larger network with some heterogeneity in the last two sections of the Results.

Fig. 2A (bottom) shows a typical dynamic of the network before and after the US input onset, with US modeled as a Poisson spike train at ~50 Hz; the network produces all the rhythms originating from the interneurons alone or through their interactions with the excitatory projection neurons (shown in Fig. 1). Specifically, since VIP is active at low theta during both rest and upon the injection of US, it then modulates F at low theta cycles via SOM and PV. In the baseline condition, the VIP interneuron has short gamma bursts nested in low theta rhythm. With US onset, VIP increases its burst duration and the frequency of low theta rhythm. These longer bursts make the SOM cell silent for long periods of each low theta cycle, providing F with windows of disinhibition and contributing to the abrupt increase in activity right after the US onset. Finally, in Fig. 2A, PV lacks any external input and fires only when excited by F. Thanks to their reciprocal interactions, PV forms a PING rhythm with F, as depicted in Fig.1C.”

- Figure 3C: The lower dashed line has the tick label '0.37' which should read '0.037'.

We fixed it.

- The section describing the network with multiple neurons could be clearer, especially, it is not really clear how these different ECS and F neurons receive their input.

We answered the same objection in the reply to Reviewer #1 in point 2 under “minor issues.”

Discussion:

- The paragraph 'It has also been suggested that ventral tegmental area has a role in fear expression (Lesas et al.,2023). Furthermore, it has been reported that the prelimbic cortex (PL) modulates the BLA SOM cells during fear retrieval, and the latter cells are crucial to discriminate non-threatening cues when desynchronized by the PL inputs (Stujenske et al., 2022).' is merely stating facts but I don't see how they relate to the presented work.

We thank the Reviewer for pointing out that this was confusing. What we meant to emphasize was that later stages of fear conditioning and extinction appear to require more than the BLA. We specifically mention the discrimination of non-threatening cues at the end of the paragraph, which now reads as follows:

“Other brain structures may be involved in later stages of fear responsiveness, such as fear extinction and prevention of generalization. It has been reported that the prelimbic cortex (PL) modulates the BLA SOM cells during fear retrieval, and the latter cells are crucial to discriminate non-threatening cues when desynchronized by the PL inputs (Stujenske et al., 2022). Brain structures such as the prefrontal cortex and hippocampus have been documented to play a crucial role also in fear extinction, the paradigm following fear conditioning aimed at decrementing the conditioned fearful response through repeated presentations of the CS alone. As reported by several studies, fear extinction suppresses the fear memory through the acquisition of a distinct memory, instead of through the erasure of the fear memory itself (Harris et al., 2000; Bouton, 2002; Trouche et al., 2013; Thompson et al., 2018). Davis et al., 2017 found a high theta rhythm following fear extinction that was associated with the suppression of threat in rodents. Our model can be extended to include structures in the prefrontal cortex and the hippocampus to further investigate the role of rhythms in the context of discrimination of non-threatening cues and extinction. We hypothesize that a different population of PV interneurons plays a crucial role in mediating competition between fearful memories, associated with a low theta rhythm, and safety memories, associated with a high theta rhythm; supporting experimental evidence is in (Lucas et al., 2016; Davis et al., 2017; Chen et al., 2022).”

- The comparison to other models BLA is quite short and seems a bit superficial. A more indepth comparison seems warranted.

We thank the reviewer for suggesting that a more in-depth comparison between our and other models in the literature would improve the manuscript. We rewrote entirely the first paragraph of that section. The new content reads as follows:

“Comparison with other models. Many computational models that study fear conditioning have been proposed in the last years; the list includes biophysically detailed models (e.g., (Li 2009; Kim et al., 2013a)), firing rate models (e.g., Krasne 2011; Ball 2012; Vlachos 2011), and connectionist models (e.g., Moustafa 2013; Armony 1997; Edeline 1992) (for a review see (Nair et al., 2016)). Both firing rate models and connectionist models use an abstract description of the interacting neurons or regions. The omission of biophysical details prevents such models from addressing questions concerning the roles of dynamics and biophysical details in fear conditioning, which is the aim of our model. There are also biophysically detailed models (Li 2009; Kim 2013; Kim 2016; Feng 2019), which differ from ours in both the physiology included in the model and the description of how plastic changes take place. One main difference in the physiology is that we differentiated among types of interneurons, since the fine timing produced for the latter was key to our use of rhythms to produce spike-time dependent plasticity. The origin of the gamma rhythm (but not the other rhythms) was investigated in Feng et al 2019, but none of these papers connected the rhythms to plasticity.

The most interesting difference between our work and that in (Li 2009; Kim 2013; Kim 2016) is the modeling of plasticity. We use spike-time dependent plasticity rules. The models in (Li 2009; Kim 2013; Kim 2016) were more mechanistic about how the plasticity takes place, starting with the known involvement of calcium with plasticity. Using a hypothesis about back propagation of spikes, the set of papers together come up with a theory that is consistent with STDP and other instantiations of plasticity (Shouval 2002a; Shouval 2002b). For the purposes of our paper, this level of detail, though very interesting, was not necessary for our conclusions. By contrast, in order for the rhythms and the interneurons to have the dynamic roles they play in the model, we needed to restrict our STDP rule to ones that are depression-dominated. Our reading of (Shouval 2002) suggests to us that such subrules are possible outcomes of the general theory. Thus, there is no contradiction between the models, just a difference in focus; our focus was on the importance of the much-documented rhythms (Seidenbecher et al., 2003; Courtin et al., 2014b; Stujenske et al., 2014; Davis et al., 2017) in providing the correct spike timing. We showed in the Supplementary Information (“Classical Hebbian plasticity rule, unlike the depression-dominated one, shows potentiation even with no strict pre and postsynaptic spike timing”) that if the STDP rule was not depression dominated, the rhythms need not be necessary. We hypothesize that the necessity of strict timing enforced by the depression-dominated rule may foster the most appropriate association with fear at the expense of less relevant associations.”

- The paragraph 'This could happen among some cells responding to weaker sensory inputs that do not lead to pre-post timing with fear neurons. This timing could be modified by the "triconditional rule", as suggested in (Grewe et al., 2017).' is not very clear. What exactly is 'this' in the first sentence referring to? If you mention the 'tri-conditional rule' here, please briefly explain it and how it would solve the issue at hand here.

We apologize that the sentence reported was not sufficiently clear. “This” refers to “depression”. We meant that, in our model, depression during fear conditioning happens every time there is no pre-post timing between neurons encoding the neutral stimuli and fear cells; poor pre-post timing can characterize the activity of neurons responding to weaker sensory inputs and does not lead to associative learning. We modified that paragraph as follows:

“The study in (Grewe et al., 2017) suggests that associative learning resulting from fear conditioning induces both potentiation and depression among coactive excitatory neurons; coactivity was determined by calcium signaling and thus did not allow measurements of fine timing between spikes. In our model, we show how potentiation between coactive cells occurs when strict pre-post spike timing and appropriate pauses in the spiking activity arise. Depression happens when one or both of these components are not present. Thus, in our model, depression represents the absence of successful fear association and does not take part in the reshaping of the ensemble encoding the association, as instead suggested in (Grewe et al., 2017). A possible follow-up of our work involves investigating how fear ensembles form and modify through fear conditioning and later stages. This follow-up work may involve using a tri-conditional rule, as suggested in (Grewe et al. 2017), in which the potential role of neuromodulators is taken into account in addition to the pre- and postsynaptic neuron activity; this may lead to both potentiation and depression in establishing an associative memory.”

- In the limitations and caveats section you mention that the small size of the network implies that they represent a synchronous population. What are the potential implications for the proposed rhythm-dependent mechanism? What are your expectations for larger networks?

We apologize if we were not adequately clear. We are guessing that the Reviewer thought we meant the entire population was synchronous, which it is not. We meant that, when we use a single cell to represent a subpopulation of cells of that type, that subpopulation is effectively synchronous. For larger networks in which each subtype is represented by many cells, there can be heterogeneity within each subtype. We have shown in the paper that the basic results still hold under some heterogeneity; however, they may fail if the heterogeneity is too large.

We mentioned in a new section named “Assumptions and predictions of the model” in response to point 3 made by Reviewer #2.

- The discussion is also missing a section on predictions/new experiments that can be derived from the model. How can the model be confirmed, what experiments/results would break the model?

To answer this question, we put in a new section in the Discussion entitled “Assumptions and predictions of the model”. The first paragraph of this section is in the reply to Reviewer #2 point 2; the second paragraph is in the reply to Reviewer #2 point 3; the last paragraph is in the Reply to Reviewer #1 point c; the rest of the section reads as follows:

“Our study suggests that all the interneurons are necessary for associative learning provided that the STDP rule is depression-dominated. This prediction could be tested experimentally by selectively silencing each interneuron subtype in the BLA: if the associative learning is hampered by silencing any of the interneuron subtypes, this validates our study. Finally, the model prediction could be tested indirectly by acquiring more information about the plasticity rule involved in the BLA during associative learning. We found that all the interneurons are necessary to establish fear learning only in the case of a depression-dominated rule. This rule ensures that fine timing and pauses are always required for potentiation: interneurons provide both fine timing and pauses to pyramidal cells, making them crucial components of the fear circuit.

The modeling of the interneurons assumes the involvement of various intrinsic currents; the inclusion of those currents can be considered hypotheses of the model. Our model predicts that blockade of D-current in VIP interneurons (or silencing VIP interneurons) will both diminish low theta and prevent fear learning. Finally, the model assumes the absence of significantly strong connections from the excitatory projection cells ECS to PV interneurons, unlike the ones from F to PV. Including those synapses would alter the PING rhythm created by the interactions between F and PV, which is crucial for fine timing between ECS and F needed for LTP.”