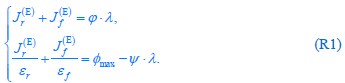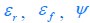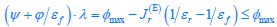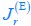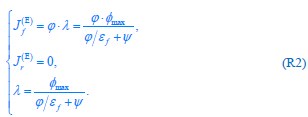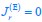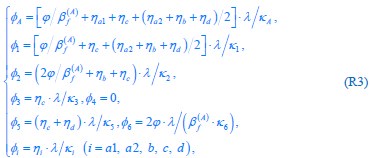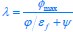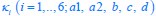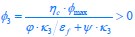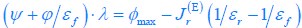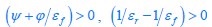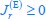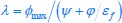Overflow metabolism originates from growth optimization and cellheterogeneity

Reviewer #1 (Public review):

Summary:

Cell metabolism exhibits a well-known behavior in fast-growing cells, which employ seemingly wasteful fermentation to generate energy even in the presence of sufficient environmental oxygen. This phenomenon is known as Overflow Metabolism or the Warburg effect in cancer. It is present in a wide range of organisms, from bacteria and fungi to mammalian cells.

In this work, starting with a metabolic network for Escherichia coli based on sets of carbon sources, and using a corresponding coarse-grained model, the author applies some well-based approximations from the literature and algebraic manipulations. These are used to successfully explain the origins of Overflow Metabolism, both qualitatively and quantitatively, by comparing the results with E. coli experimental data.

By modeling the proteome energy efficiencies for respiration and fermentation, the study shows that these parameters are dependent on the carbon source quality constants K_i (p.115 and 116). It is demonstrated that as the environment becomes richer, the optimal solution for proteome energy efficiency shifts from respiration to fermentation. This shift occurs at a critical parameter value K_A(C).
This counter intuitive results qualitativelly explains Overflow Metabolism.

Quantitative agreement is achieved through the analysis of the heterogeneity of the metabolic status within a cell population. By introducing heterogeneity, the critical growth rate is assumed to follow a Gaussian distribution over the cell population, resulting in accordance with experimental data for E. coli. Overflow metabolism is explained by considering optimal protein allocation and cell heterogeneity.

The obtained model is extensively tested through perturbations: 1) Introduction of overexpression of useless proteins; 2) Studying energy dissipation; 3) Analysis of the impact of translation inhibition with different sub-lethal doses of chloramphenicol on Escherichia coli; 4) Alteration of nutrient categories of carbon sources using pyruvate. All model perturbations results are corroborated by E. coli experimental results.

Strengths:

In this work, the author effectively uses modeling techniques typical of Physics to address complex problems in Biology, demonstrating the potential of interdisciplinary approaches to yield novel insights. The use of Escherichia coli as a model organism ensures that the assumptions and approximations are well-supported in existing literature. The model is convincingly constructed and aligns well with experimental data, lending credibility to the findings. In this version, the extension of results from bacteria to yeast and cancer is substantiated by a literature base, suggesting that these findings may have broad implications for understanding diverse biological systems.

Weaknesses:

The author explores the generalization of their results from bacteria to cancer cells and yeast, adapting the metabolic network and coarse-grained model accordingly. In previous version this generalization was not completedly supported by references and data from the literature. This drawback, however, has been treated in this current version, where the authors discuss in much more detail and give references supporting this generalization.

Reviewer #2 (Public review):

In this version of manuscript, the author clarified many details and rewrote some sections. This substantially improved the readability of the paper. I also recognized that the author spent substantial efforts in the Appendix to answer the potential questions.

Unfortunately, I am not currently convinced by the theory proposed in this paper. In the next section, I will first recap the logic of the author and explain why I am not convinced. Although the theory fits many experimental results, other theories on overflow metabolism are also supported by experiments. Hence, I do not think based on experimental data we could rule in or rule out different theories.

Recap: To explain the origin of overflow metabolism, the author uses the following logic:

(1) There is a substantial variability of single-cell growth rate
(2) The flux (J_r^E) and (J_f^E) are coupled with growth rate by Eq. 3
(3) Since growth rate varies from cells to cells, flux (J_r^E) and (J_f^E) also varies
(4) The variabilities of above fluxes in above create threshold-analog relation, and hence overflow metabolism.

My opinion:

The logic step (2) and (3) have caveats. The variability of growth rate has large components of cellular noise and external noise. Therefore, variability of growth rate is far from 100% correlated with variability of flux (J_r^E) and (J_f^E) at the single-cell level. Single-cell growth rate is a complex, multivariate functional, including (Jr^E) and (J_f^E) but also many other variables. My feeling is the correlation could be too low to support the logic here.

One example: ribosomal concentration is known to be an important factor of growth rate in bulk culture. However, the "growth law" from bulk culture cannot directly translate into the growth law at single-cell level [Ref1,2]. This is likely due to other factors (such as cell aging, other muti-stability of cellular states) are involved.

Therefore, I think using Eq.3 to invert the distribution of growth rate into the distribution of (Jr^E) and (J_f^E) is inapplicable, due to the potentially low correlation at single-cell level. It may show partial correlations, but may not be strong enough to support the claim and create fermentation at macroscopic scale.

Overall, if we track the logic flow, this theory implies overflow metabolism is originated from variability of k_cat of catalytic enzymes from cells to cells. That is, the author proposed that overflow metabolism happens macroscopically as if it is some "aberrant activation of fermentation pathway" at the single-cell level, due to some unknown partially correlation from growth rate variability.

Compared with other theories, this theory does not involve any regulatory mechanism and can be regarded as a "neutral theory". I am looking forward to seeing single cell experiments in the future to provide evidences about this theory.

[Ref1] https://www.biorxiv.org/content/10.1101/2024.04.19.590370v2
[Ref2] https://www.biorxiv.org/content/10.1101/2024.10.08.617237v2

Author response:

The following is the authors’ response to the original reviews.

Reviewer #1 (Public Review):

Summary:

Cell metabolism exhibits a well-known behavior in fast-growing cells, which employ seemingly wasteful fermentation to generate energy even in the presence of sufficient environmental oxygen. This phenomenon is known as Overflow Metabolism or the Warburg effect in cancer. It is present in a wide range of organisms, from bacteria and fungi to mammalian cells.

In this work, starting with a metabolic network for Escherichia coli based on sets of carbon sources, and using a corresponding coarse-grained model, the author applies some well-based approximations from the literature and algebraic manipulations. These are used to successfully explain the origins of Overflow Metabolism, both qualitatively and quantitatively, by comparing the results with E. coli experimental data.

By modeling the proteome energy efficiencies for respiration and fermentation, the study shows that these parameters are dependent on the carbon source quality constants K_i (p.115 and 116). It is demonstrated that as the environment becomes richer, the optimal solution for proteome energy efficiency shifts from respiration to fermentation. This shift occurs at a critical parameter value K_A(C).

This counterintuitive result qualitatively explains Overflow Metabolism.

Quantitative agreement is achieved through the analysis of the heterogeneity of the metabolic status within a cell population. By introducing heterogeneity, the critical growth rate is assumed to follow a Gaussian distribution over the cell population, resulting in accordance with experimental data for E. coli. Overflow metabolism is explained by considering optimal protein allocation and cell heterogeneity.

The obtained model is extensively tested through perturbations: 1) Introduction of overexpression of useless proteins; 2) Studying energy dissipation; 3) Analysis of the impact of translation inhibition with different sub-lethal doses of chloramphenicol on Escherichia coli; 4) Alteration of nutrient categories of carbon sources using pyruvate. All model perturbation results are corroborated by E. coli experimental results.

We appreciate the reviewer's highly positive comments and the accurate summary of our manuscript.

Strengths:

In this work, the author employs modeling methods typical of Physics to address a problem in Biology, standing at the interface between these two scientific fields. This interdisciplinary approach proves to be highly fruitful and should be further explored in the literature. The use of Escherichia coli as an example ensures that all hypotheses and approximations in this study are well-founded in the literature. Examples include the approximation for the Michaelis-Menten equation (line 82), Eq. S1, proteome partition in Appendix 1.1 (lines 68-69), and a stable nutrient environment in Appendix 1.1 (lines 83-84). The section "Testing the model through perturbation" heavily relies on bacterial data. The construction of the model and its agreement with experimental data are convincingly presented.

We appreciate the reviewer's highly positive comments. We have incorporated many of the reviewer's insightful suggestions and added citations in the appropriate contexts, which have significantly improved our manuscript.

Weaknesses:

In Section Appendix 6.4, the author explores the generalization of results from bacteria to cancer cells, adapting the metabolic network and coarse-grained model accordingly. It is argued that as a consequence, all subsequent steps become immediately valid. However, I remain unconvinced, considering the numerous approximations used to derive the equations, which the literature demonstrates to be valid primarily for bacteria. A more detailed discussion about this generalization is recommended. Additionally, it is crucial to note that the experimental validation of model perturbations heavily relies on E. coli data.

We appreciate the reviewer's insightful suggestions. We apologize for not clearly illustrating the generalization of results from bacteria to cancer cells in the previous version of our manuscript. Indeed, in our earlier version, there was no experimental validation of model results related to cancer cells.

Following the reviewer’s suggestions, we have now added Fig. 5 and Appendix-fig. 5, fully expanded the previous Appendix 6.4 into Appendix 9 in our current version, and added a new section entitled “Explanation of the Crabtree effect in yeast and the Warburg effect in cancer cells” in our main text to provide a detailed discussion of the generalization from bacteria to yeast and cancer cells. Through the derivations shown in Appendix 9 (Eqs. S180-S189), we arrived at Eq. 6 (or Eq. S190 in Appendix 9) to facilitate the comparison of our model results with experimental data in yeast and cancer cells. This comparison is presented in Fig. 5, where we demonstrate that our model can quantitatively explain the data for the Crabtree effect in yeast and the Warburg effect in cancer cells (related experimental data references: Shen et al., Nature Chemical Biology 20, 1123–1132 (2024); Bartman et al., Nature 614, 349-357 (2023)). These additions have significantly strengthened our manuscript.

Reviewer #2 (Public Review):

Summary

This paper has three parts. The first part applied a coarse-grained model with proteome partition to calculate cell growth under respiration and fermentation modes. The second part considered single-cell variability and performed population average to acquire an ensemble metabolic profile for acetate fermentation. The third part used model and simulation to compare experimental data in literature and obtained substantial consistency.

We thank the reviewer for the accurate summary and positive comments on our manuscript.

Strengths and major contributions

(i) The coarse-grained model considered specific metabolite groups and their interrelations and acquired an analytical solution for this scenario. The "resolution" of this model is in between the Flux Balanced Analysis/whole-cell simulation and proteome partition analysis.

(ii) The author considered single-cell level metabolic heterogeneity and calculated the ensemble average with explicit calculation. The results are consistent with known fermentation and growth phenomena qualitatively and can be quantitatively compared to experimental results.

We appreciate the reviewer’s highly positive comments.

Weaknesses

(i) If I am reading this paper correctly, the author's model predicts binary (or "digital") outcomes of single-cell metabolism, that is, after growth rate optimization, each cell will adopt either "respiration mode" or "fermentation mode" (as illustrated in Figure Appendix - Figure 1 C, D). Due to variability enzyme activity k_i^{cat} and critical growth rate λ_C, each cell under the same nutrient condition could have either respiration or fermentation, but the choice is binary.

The binary choice at the single-cell level is inconsistent with our current understanding of metabolism. If a cell only uses fermentation mode (as shown in Appendix - Figure 1C), it could generate enough energy but not be able to have enough metabolic fluxes to feed into the TCA cycle. That is, under pure fermentation mode, the cell cannot expand the pool of TCA cycle metabolites and hence cannot grow.

This caveat also appears in the model in Appendix (S25) that assumes J_E = r_E*J_{BM} where r_E is a constant. From my understanding, r_E can be different between respiration and fermentation modes (at least for real cells) and hence it is inappropriate to conclude that cells using fermentation, which generates enough energy, can also generate a balanced biomass.

We thank the reviewer for raising this question. Indeed, regarding energy biogenesis between respiration and fermentation, our model predicts binary outcomes at the single-cell level. However, this outcome does not hinder cell growth, as there are three independent possible fates for the carbon source (e.g., glucose) in metabolism: fermentation, respiration for energy biogenesis, and biomass generation. Each fate is associated with a distinct fraction of the proteome, with no overlap between them (see Appendix-figs. 1 and 5). Consequently, in a purely fermentative mode, a cell can still use the proteome dedicated to the biomass generation pathway to produce biomass precursors via the TCA cycle.

The classification of the carbon source’s fates into three independent pathways was initially introduced by Chen and Nielsen (Chen and Nielsen, PNAS 116, 17592-17597 (2019)). We apologize for the oversight in not citing their paper in this context in the previous version of our manuscript (although it was cited elsewhere). We have now included the citation in all appropriate places.

To illustrate this issue more clearly, we explicitly present the proteome allocation results for optimal growth in a fermentation mode below, where the proteome efficiency (i.e., the proteome energy efficiency in our previous version) in fermentation is higher than in respiration (i.e., ). We use the model shown in Fig. 1B as an example, with the relevant equations being Eqs. S26 and S28 in Appendix 2.1. By substituting Eq. S28 into Eq. S26, we arrive at Eq. 3 (or Eq. S29 in Appendix 2.1), which we restate here as Eq. R1:

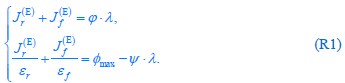
For a given nutrient condition, i.e., for a specific value of κ_A at the single-cell level, the values of 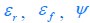are determined (see Eqs. S20, S27, S31 and S32), while ϕ and φ_max are constants (see Eq. S33 and Appendix 1.1). Therefore, if , then 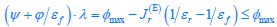, since all coefficients are positive (i.e., 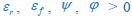) and 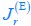takes non-negative values. Hence, the solution for optimal growth is (see Eqs. S35-S36 in Appendix 2.2):

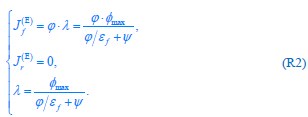
Here, the result 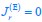signifies a pure fermentation mode with no respiration flux for energy biogenesis. Then, by combining Eq. R2 with Eqs. S28 and S30 from Appendix 2.1, we obtain the optimal proteome allocation results for this case:

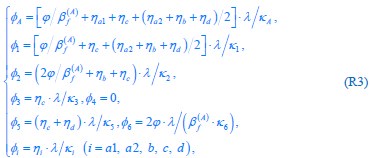
where 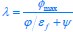, while κ_A and 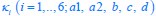take given values (see Eqs. S20 and S27). In Eq. R3, φ₃ corresponds to the fraction of the proteome devoted to carrying the carbon flux from Acetyl-CoA (the entry point of Pool b, see Fig. 1B and Appendix 1.2) to α-Ketoglutarate (the entry point of Pool c), with all of these being enzymes within the TCA cycle. The optimal growth solution is 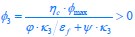, which demonstrates that in a pure fermentation mode, the optimal growth condition includes the presence of enzymes within the TCA cycle capable of carrying the flux required for biomass generation.

Regarding Eq. S25, J_E represents the energy demand for cell proliferation, expressed as the stoichiometric energy flux in ATP. Although the influx of carbon sources (e.g., glucose) varies significantly between fermentation and respiration modes, J_BM and J_E are the biomass and energy fluxes used to build cells, respectively. In bacteria, whether in fermentation or respiration mode, the proportion of maintenance energy used for protein degradation is roughly negligible (see Locasale and Cantley, BMC Biol 8, 88 (2010)). Consequently, the energy demand represented by _J_E scales approximately linearly with the biomass production rate J_BM (related experimental data reference: Ebenhöh et al., Life 14, 247 (2024)), regardless of the energy biogenesis mode. Therefore, _r_E can be regarded as roughly constant for bacteria. However, in eukaryotic cells such as yeast and mammalian cells, the proportion of maintenance energy is much more significant (see Locasale and Cantley, BMC Biol 8, 88 (2010)). Therefore, we have explicitly considered the contribution of maintenance energy in these cases and have extended the previous Appendix 6.4 into Appendix 9 in the current version.

(ii) The minor weakness of this model is that it assumes a priori that each cell chooses its metabolic strategy based on energy efficiency. This is an interesting assumption but there is no known biochemical pathway that directly executes this mechanism. In evolution, growth rate is more frequently considered for metabolic optimization. In Flux Balanced Analysis, one could have multiple objective functions including biomass synthesis, energy generation, entropy production, etc. Therefore, the author would need to justify this assumption and propose a reasonable biochemical mechanism for cells to sense and regulate their energy efficiency.

We thank the reviewer for raising this question and apologize for not explaining this point clearly enough in the previous version of our manuscript. Just as the reviewer mentioned, growth rate should be considered for metabolic optimization under the selection pressure of the evolutionary process. In fact, in our model, the sole optimization objective is exactly the cell growth rate. The determination of whether to use fermentation or respiration based on proteome efficiency (i.e., the proteome energy efficiency in our previous version) is not an a priori assumption in our model; rather, it is a natural consequence of growth rate optimization, as we detail below.

For a given nutrient condition with a determined value of κ_A , as we have explained in the aforementioned responses, the constraint on the fluxes is summarized in Eq. 3 and is restated as Eq. R1. Mathematically, we can obtain the solution for the optimal growth strategy by combining Eq. R1 (i.e., Eq. 3) with the optimization on cell growth rate λ, and the solution can be obtained as follows: If the proteome efficiency in fermentation is larger than that in respiration, i.e., , then from Eq. R1, we obtain 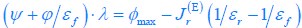, since the values of ε_r , ε_f , Ψ, ϕ and φ_max are all fixed for a given κA , with ε_r , ε_f , Ψ, ϕ, φ_max > 0 . Hence, 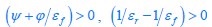(since ), and note that 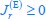. Therefore 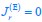is the solution for optimal growth, where the growth rate can take the maximum value of 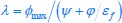. Similarly, for the case where the proteome efficiency in respiration is larger than that in fermentation (i.e ), 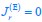is the solution for optimal growth. With this analysis, we have demonstrated that the choice between fermentation and respiration based on proteome efficiency is a natural consequence of growth rate optimization.

We have now revised the related content in our manuscript to clarify this point.

My feeling is that the mathematical structure of this model could be correct, but the single-cell interpretation for the ensemble averaging has issues. Each cell could potentially adopt partial respiration and partial fermentation at the same time and have temporal variability in its metabolic mode as well. With the modification of the optimization scheme, the author could have a revised model that avoids the caveat mentioned above.

We thank the reviewer for raising this question. In fact, in the above two responses, we have addressed the issues raised here, clarifying that the binary mode between respiration and fermentation does not hinder cell growth and that the sole optimization objective is the cell growth rate, as the reviewer suggested. Regarding temporal variability, due to factors such as cell cycle stages and the intrinsic noise arising from stochastic processes, temporal variability in the fermentation or respiration mode is indeed likely. However, at any given moment at the single-cell level, a binary choice between fermentation and respiration is what our model predicts for the optimal growth strategy.

Discussion and impact for the field

Proteome partition models and Flux Balanced Analysis are both commonly used mathematical models that emphasize different parts of cellular physiology. This paper has ingredients for both, and I expect after revision it will bridge our understanding of the whole cell.

We appreciate the reviewer’s very positive comments. We have followed many of the good suggestions raised by the reviewer, and our revised manuscript is much improved as a result.

Reviewer #3 (Public Review):

Summary:

In the manuscript "Overflow metabolism originates from growth optimization and cell heterogeneity" the author Xin Wang investigates the hypothesis that the transition into overflow metabolism at large growth rates actually results from an inhomogeneous cell population, in which every individual cell either performs respiration or fermentation.

We thank the reviewer for carefully reading our manuscript and the accurate summary.

Weaknesses:

The paper has several major flaws. First, and most importantly, it repeatedly and wrongly claims that the origins of overflow metabolism are not known. The paper is written as if it is the first to study overflow metabolism and provide a sound explanation for the experimental observations. This is obviously not true and the author actually cites many papers in which explanations of overflow metabolism are suggested (see e.g. Basan et al. 2015, which even has the title "Overflow metabolism in E. coli results from efficient proteome allocation"). The paper should be rewritten in a more modest and scientific style, not attempting to make claims of novelty that are not supported. In fact, all hypotheses in this paper are old. Also the possiblility that cell heterogeneity explains the observed 'smooth' transition into overflow metabolism has been extensively investigated previously (see de Groot et al. 2023, PNAS, "Effective bet-hedging through growth rate dependent stability") and the random drawing of kcat-values is an established technique (Beg et al., 2007, PNAS, "Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity"). Thus, in terms of novelty, this paper is very limited. It reinvents the wheel and it is written as if decades of literature debating overflow metabolism did not exist.

We thank the reviewer for both the critical and constructive comments. Following the reviewer’s suggestion, we have revised our manuscript to adopt a more modest style. However, we respectfully disagree with the criticism regarding the novelty of our study, as detailed below.

First, while many explanations for overflow metabolism have been proposed, we have cited these in both the previous and current versions of our manuscript. We apologize for not emphasizing the distinctions between these previous explanations and our study in the main text of our earlier version, though we did provide details in Appendix 6.3. In fact, most of these explanations (e.g., Basan et al., Nature 528, 99-104 (2015); Chen and Nielsen, PNAS 116, 17592-17597 (2019); Majewski and Domach, Biotechnol. Bioeng. 35, 732-738 (1990); Niebel et al., Nat. Metab. 1, 125-132 (2019); Shlomi et al., PLoS Comput. Biol. 7, e1002018 (2011); Varma and Palsson, Appl. Environ. Microbiol. 60, 3724-3731 (1994); Vazquez et al., BMC Syst. Biol. 4, 58 (2010); Vazquez and Oltvai, Sci. Rep. 6, 31007 (2016); Zhuang et al., Mol. Syst. Biol. 7, 500 (2011)) heavily rely on the assumption that cells optimize their growth rate for a given rate of carbon influx under each nutrient condition (or certain equivalents) to explain the growth rate dependence of fermentation flux. However, this assumption—that cell growth rate is optimized for a given rate of carbon influx—is questionable, as the given factors in a nutrient condition are the identity and concentration of the carbon source, rather than the carbon influx itself.

Consequently, in our model, we purely optimize cell growth rate without imposing a special constraint on carbon influx. Our assumption that the given factors in a nutrient condition are the identity and concentration of the carbon source aligns with the studies by Molenaar et al. (Molenaar et al., Mol. Syst. Biol. 5, 323 (2009)), where they specified an identical assumption on page 5 of their Supplementary Information (SI); Scott et al. (Scott et al., Science 330, 1099-1102 (2010)), where the growth rate formula was derived for a culturing condition with a given nutrient quality; and Wang et al. (Wang et al., Nat. Comm. 10, 1279 (2019)), our previous study on microbial growth. Among these three studies, only Molenaar et al. addresses overflow metabolism. However, Molenaar et al. did not consider cell heterogeneity, resulting in their model predictions on the growth rate dependence of fermentation flux being a digital response, which is inconsistent with experimental data.

Furthermore, prevalent explanations such as those by Basan et al. (Basan et al., Nature 528, 99-104 (2015)) and Chen and Nielsen (Chen and Nielsen, PNAS 116, 17592-17597 (2019)) suggest that overflow metabolism originates from the proteome efficiency in fermentation always being higher than in respiration. However, Shen et al. (Shen et al., Nature Chemical Biology 20, 1123–1132 (2024)) recently discovered that the proteome efficiency measured at the cell population level in respiration is higher than in fermentation for many yeast and cancer cells, despite the presence of fermentation fluxes through aerobic glycolysis. This finding clearly contradicts the studies by Basan et al. (2015) and Chen and Nielsen (2019).

Nevertheless, our model may resolve this puzzle by incorporating two important features. First, in our model, the proteome efficiency (i.e., the proteome energy efficiency in our previous version) in respiration is larger than that in fermentation when nutrient quality is low (Eqs. S174-S175 in Appendix 9). Second, and crucially, due to the incorporation of cell heterogeneity in our model, there could be a proportion of cells with higher proteome efficiency in fermentation than in respiration, even when the overall proteome efficiency at the cell population level is higher in respiration than in fermentation. As shown in the newly added Fig. 5A-B, our model results can quantitatively illustrate the experimental data from Shen et al., Nature Chemical Biology 20, 1123–1132 (2024).

Finally, regarding the criticism of the novelty of our hypothesis: As specified in our main text, cell heterogeneity has been widely reported experimentally in both microbes (e.g., Ackermann, Nat. Rev. Microbiol. 13, 497-508 (2015); Bagamery et al., Curr. Biol. 30, 4563-4578 (2020); Balaban et al., Science 305, 1622-1625 (2004); Nikolic et al., BMC Microbiol. 13, 1-13 (2013); Solopova et al., PNAS 111, 7427-7432 (2014); Wallden et al., Cell 166, 729-739 (2016)) and tumor cells (e.g., Duraj et al., Cells 10, 202 (2021); Hanahan and Weinberg, Cell 164, 681-694 (2011); Hensley et al., Cell 164, 681-694 (2016)). However, to the best of our knowledge, cell heterogeneity has not yet been incorporated into theoretical models for explaining overflow metabolism or the Warburg effect. The reviewer mentioned the study by de Groot et al. (de Groot et al., PNAS 120, e2211091120 (2023)) as studying overflow metabolism similarly to our work. We have carefully read this paper, including the main text and SI, and found that it is not directly relevant to either overflow metabolism or the Warburg effect. Instead, their model extends the work of Kussell and Leibler (Kussell and Leibler, Science 309, 2075-2078 (2005)), focusing on bet-hedging strategies of microbes in changing environments.

Regarding the criticism that random drawing of kcat-values is an established technique (Beg et al., PNAS 104, 12663-12668 (2007)), we need to stress that the distribution noise on kcat-values considered in our model is fundamentally different from that in Beg et al. In Beg et al., their model involved 876 reactions (see Dataset 1 in Beg et al.), of which only 109 had associated biochemical experimental data. Thus, their distribution of kcat-values pertains to different enzymes within the same cell. In contrast, we have the mean of the kcat-values from experimental data for each relevant enzymes, with the distribution of kcat-values representing the same enzyme in different cells.

Moreover, the manuscript is not clearly written and is hard to understand. Variables are not properly introduced (the M-pools need to be discussed, fluxes (J_E), "energy coefficients" (eta_E), etc. need to be more explicitly explained. What is "flux balance at each intermediate node"? How is the "proteome efficiency" of a pathway defined? The paper continues to speak of energy production. This should be avoided. Energy is conserved (1st law of thermodynamics) and can never be produced. A scientific paper should strive for scientific correctness, including precise choice of words.

We thank the reviewer for the constructive comments. Following these, we have provided more explicit information and revised our manuscript to enhance readability. In our initially submitted version, the phrase "energy production" was borrowed from Nelson et al. (Nelson et al., Lehninger principles of biochemistry, 2008) and Basan et al. (Basan et al., Nature 528, 99-104 (2015)), and we chose to follow this terminology. We appreciate the reviewer’s suggestion and have now revised the wording to use more appropriate expressions.

The statement that the "energy production rate ... is proportional to the growth rate" is, apart from being incorrect - it should be 'ATP consumption rate' or similar (see above), a non-trivial claim. Why should this be the case? Such statements must be supported by references. The observation that the catabolic power indeed appears to increase linearly with growth rate was made, based on chemostat data for E.coli and yeast, in a recent preprint (Ebenhöh et al, 2023, bioRxiv, "Microbial pathway thermodynamics: structural models unveil anabolic and catabolic processes").

We thank the reviewer for the insightful suggestions. Following these, we have revised our manuscript and cited the suggested reference (i.e., Ebenhöh et al., Life 14, 247 (2024)).

All this criticism does not preclude the possibility that cell heterogeneity plays a role in overflow metabolism. However, according to Occam's razor, first the simpler explanations should be explored and refuted before coming up with a more complex solution. Here, it means that the authors first should argue why simpler explanations (e.g. the 'Membrane Real Estate Hypothesis', Szenk et al., 2017, Cell Systems; maximal Gibbs free energy dissipation, Niebel et al., 2019, Nature Metabolism; Saadat et al., 2020, Entropy) are not considered, resp. in what way they are in disagreement with observations, and then provide some evidence of the proposed cell heterogeneity (are there single-cell transcriptomic data supporting the claim?).

We thank the reviewer for raising these questions and providing valuable insights. Regarding the shortcomings of simpler explanations, as explained above, most proposed explanations (including the references mentioned by the reviewer: Szenk et al., Cell Syst. 5, 95-104 (2017); Niebel et al., Nat. Metab. 1, 125-132 (2019); Saadat et al., Entropy 22, 277 (2020)) rely heavily on the assumption that cells optimize their growth rate for a given rate of carbon influx under each nutrient condition (or its equivalents). However, this assumption is questionable, as the given factors in a nutrient condition are the identities and concentrations of the carbon sources, rather than the carbon influx itself.

Specifically, Szenk et al. is a perspective paper, and the original “membrane real estate hypothesis” was proposed by Zhuang et al. (Zhuang et al., Mol. Syst. Biol. 7, 500 (2011)). Zhuang et al. specified in Section 7 of their SI that their model’s explanation of the experimental results shown in Fig. 2C of their manuscript relies on the assumption of restrictions on carbon influx. In Niebel et al. (Niebel et al., Nat. Metab. 1, 125-132 (2019)), the Methods section specifies that the glucose uptake rate was considered a given factor for a growth condition. In Saadat et al. (Saadat et al., Entropy 22, 277 (2020)), Appendix A notes that their model results depend on minimizing carbon influx for a given growth rate, which is equivalent to the assumption mentioned above (see Appendix 6.3 in our manuscript for details).

Regarding the experimental evidence for our proposed cell heterogeneity, Bagamery et al. (Bagamery et al., Curr. Biol. 30, 4563-4578 (2020)) reported non-genetic heterogeneity in two subpopulations of Saccharomyces cerevisiae cells upon the withdrawal of glucose from exponentially growing cells. This strongly indicates the coexistence of fermentative and respiratory modes of heterogeneity in S. cerevisiae cultured in a glucose medium (refer to Fig. 1E in Bagamery et al.). Nikolic et al. (Nikolic et al., BMC Microbiol. 13, 1-13 (2013)) reported a bimodal distribution in the expression of the acs gene (the transporter for acetate) in an E. coli cell population growing on glucose as the sole carbon source within the region of overflow metabolism (see Fig. 5 in Nikolic et al.), indicating the cell heterogeneity we propose. For cancer cells, Duraj et al. (Duraj et al., Cells 10, 202 (2021)) reported a high level of intra-tumor heterogeneity in glioblastoma using optical microscopy images, where 48%~75% of the cells use fermentation and the remainder use respiration (see Fig. 1C in Duraj et al.), which aligns with the cell heterogeneity picture of aerobic glycolysis predicted by our model.

We have now added related content to the discussion section to strengthen our manuscript.

Reviewer #1 (Recommendations For The Authors):

Some minor corrections:

(1) Adjusted the reference: (García-Contreras et al., 2012)

(2) Corrected line 255: Removed the duplicate "the genes"

We thank the reviewer for the suggestions and have implemented each of them to revise our manuscript. The reference in the form of García-Contreras et al., 2012, although somewhat unusual, is actually correct, so we have kept it unchanged.

General comment to the author:

Considering that this work exists at the interface between Physics and Biology, where a significant portion of the audience may not be familiar with the mathematical manipulations performed, it would enhance the paper's readability to provide more explicit indications in the text. For example, in line 91, explicitly define phi_A as phi_R; or in line 115, explain the K_i parameter in the text for better readability.

We thank the reviewer for the suggestion. Following this, we have now provided more explicit information for the definition of mathematical symbols to enhance readability.

Reviewer #2 (Recommendations For The Authors):

The current form of this manuscript is difficult to read for general readers. In addition, the model description in the Appendix can be improved for biophysics readers to keep track of the variables. Here are my suggestions:

a) In the main text, the author should give the definition of "proteome energy efficiency" explicitly both in English and mathematical formula - since this is the central concept of the paper. The biological interpretation of formula (4) should also be stated.

We thank the reviewer for the suggestion. Following this, we have now added definitions and biological interpretations to fix these issues.

b) I feel the basic model of the reaction network in the Appendix could be stated in a more concise way, by emphasizing whether a variable is extensive (exponential growing) or intensive (scale-invariant under exponential growth).

From my understanding, this work assumes balanced exponential growth and hence there is a balanced biomass vector Y* (a constant unit vector with all components sum to 1) for each cell. The steady-state fluxes {J} are extensive and all have growth rate λ. The proteome partition and relative metabolite fractions are ratios of different components of Y* and hence are intensive.

The normalized fluxes {J^(n)} (with respect to biomass) are a function of Y* and are all kept as constant ratios with each other. They are also intensive.

The biomass and energy production are linear combinations of {J} and hence are extensive and follow exponential growth. The biomass and energy efficiency are ratios between flux and proteome biomass, and hence are intensive.

We thank the reviewer for the insightful suggestion. Following this, we have now added the intensive and extensive information for all relevant variables in the newly added Appendix-table 3.

c) In the Appendix, the author should have a table or list of important variables, with their definition, units, and physiological values under respiration and fermentation.

We thank the reviewer for the very useful suggestion. Following this, we have now added Appendix-table 3 (pages 54-57 in the appendices) to illustrate the symbols used throughout our manuscript, as well as the model variables and parameter settings.

d) Regarding the single-cell variability, the author ignored recent experimental measurements on single-cell metabolism. This includes variability on ATP, NAD(P)H in E. coli, which will be useful background for the readers, see below.

https://pubmed.ncbi.nlm.nih.gov/25283467/

https://pubmed.ncbi.nlm.nih.gov/29391569/

We thank the reviewer for the very useful suggestion. We have now cited these relevant studies in our manuscript.

e) The choice between 100% respiration and 100% fermentation is based on the optimization of proteome energy efficiency, while the intermediate strategies are not favored in this model. This is similar to a concept in control theory called the bang-bang principle. This can be added to the Discussion.

We thank the reviewer for this suggestion. We have reviewed the concept and articles on the bang-bang principle. While the bang-bang principle is indeed relevant to binary choices, it is somewhat distant from the topic of metabolic strategies related to optimal growth. The elementary flux mode (see Müller et al., J. Theor. Biol. 347, 182190 (2014); Wortel et al., FEBS J. 281, 1547-1555 (2014)) is more pertinent to this topic, as it may lead to diauxic microbial growth (another binary metabolic strategy) in microbes grown on a mixture of two carbon sources from Group A (see Wang et al., Nat. Comm. 10, 1279 (2019)). Therefore, we have cited and mentioned only the elementary flux mode (Müller et al., J. Theor. Biol. 347, 182-190 (2014); Wortel et al., FEBS J. 281, 1547-1555 (2014)) in the introduction and discussion sections of our manuscript.