Side-binding proteins modulate actin filament dynamics
- Ludwig-Maximilians-Universität München, Germany
- Max Planck Institute of Biochemistry, Germany
- Technische Universität München, Germany
- Helmholtz Zentrum München, Germany
- Cells-in-Motion Cluster of Excellence (EXC 1003 – CiM), University of Münster, Germany
Figures
Figure 1 with 1 supplement
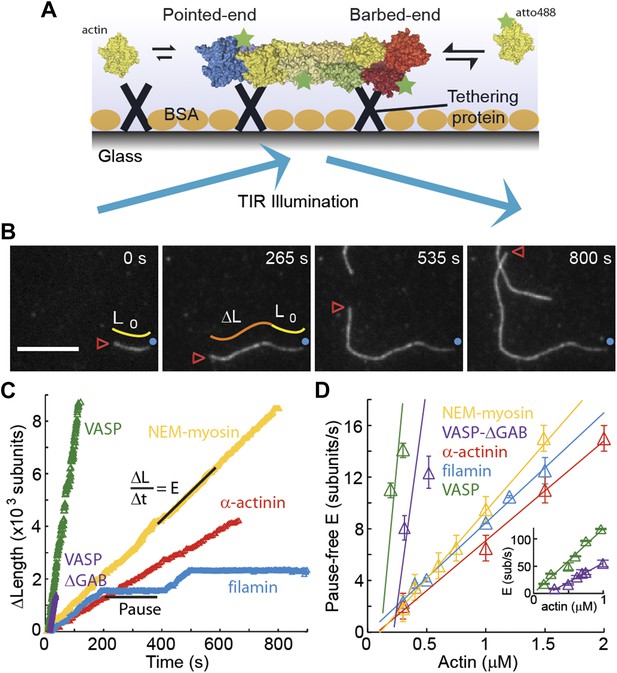
The dependence of the barbed-end kinetics on the side-binding protein.
(A) A schematic of total internal reflection illumination and single actin filament imaging of filaments tethered to a glass surface. Filaments grow from the addition of subunits at either the …
Figure 1—figure supplement 1
Comparison of algorithms for end-detection and filament growth.
(A) An image from a TIRF measurement of the elongation of an actin filament tethered to the surface using filamin. From the movie, an automated filament tracing analysis, developed by Kuhn and …
Figure 2
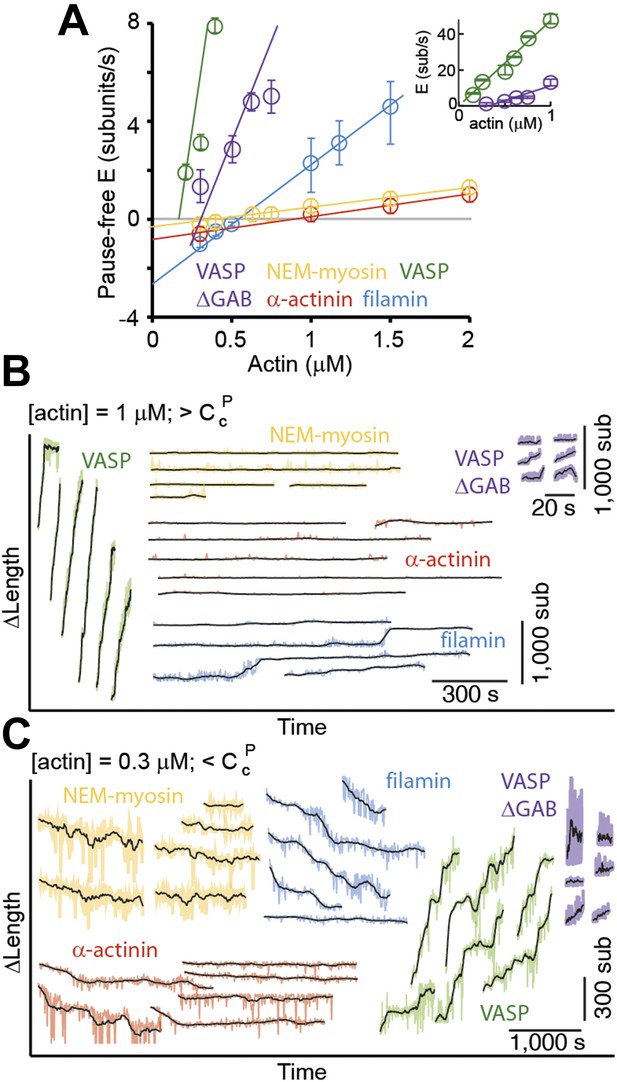
Pointed-end elongation and depolymerization kinetics as a function of the associated side-binding protein.
(A) The elongation velocity (E) is plotted as a function of free actin concentration. Error bars are s.e.m. (n > 20). (B–C) A gallery of traces of ΔL as a function of time for pointed-ends observed …
Figure 3 with 5 supplements
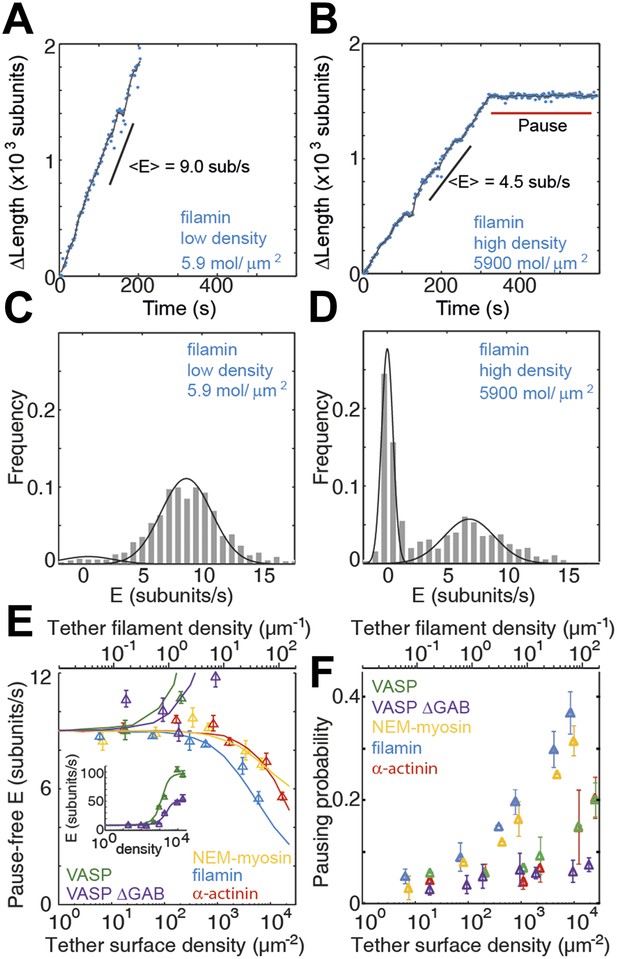
Barbed-end actin filament elongation as a function of the surface density of side-binding proteins.
(A–B) The change in length, ΔL, of actin filaments as a function of time when using filamin as the surface tethering protein at the (A) lowest (5.9 molecules/μm2 or 0.03 molecules per micron of …
Figure 3—figure supplement 1
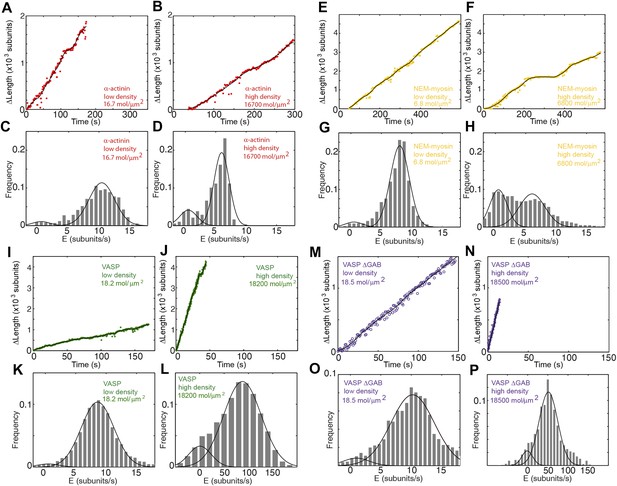
Actin filament elongation as a function of the surface density of side-binding proteins.
(A–B) The change in length, ΔL, as a function of time for a filament tether to the surface using α-actinin at (A) low (16.7 molecules/μm2 or 0.1 molecules per micron of filament) or (B) high (16,700 …
Figure 3—figure supplement 2
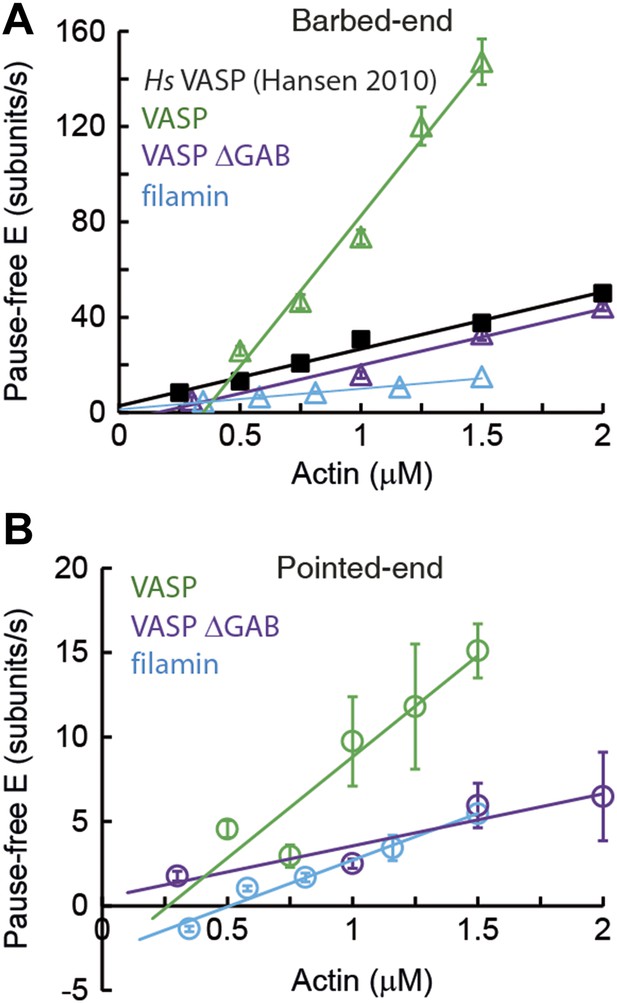
Barbed- and pointed-end actin filament elongation kinetics.
Barbed-end (A) and pointed-end (B) pause-free elongation velocities (E) as a function of free actin concentration in solution in the presence, also in solution, of different tethering proteins. …
Figure 3—figure supplement 3
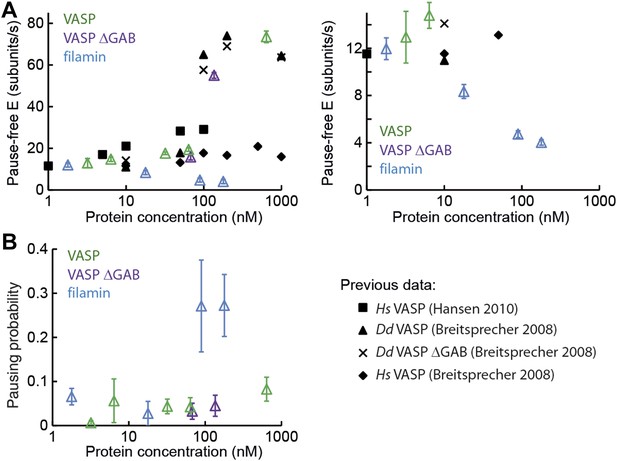
Barbed-end actin filament elongation as a function of side-binding proteins concentration.
(A) Elongation velocity of 1 μM actin (30% atto488 labeled) as a function of side-binding protein concentration in solution from kinetically active phases. A surface density of <100 molecules/μm2 of …
Figure 3—figure supplement 4
Schematic of the proposed model.
Interaction of a lattice-binding protein (red square) with the actin filament (blue) alters the basal elongation rate (kon0) of successive association events by a factor α over a characteristic …
Figure 3—figure supplement 5
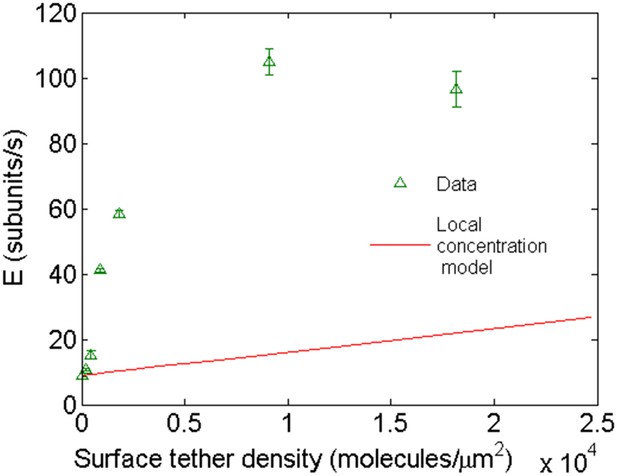
Comparison of the expected behavior using a higher local concentration mechanism with experimental results.
Open green triangles are experimental data of barbed-end elongation as a function of VASP surface density in the presence of 1 μM-free actin in solution. The solid line is the expected average E …
Figure 4 with 3 supplements
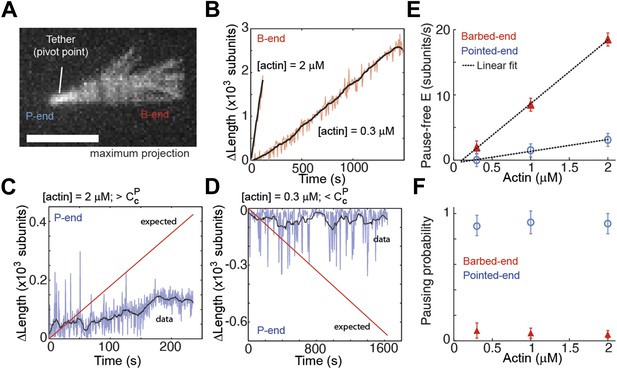
Intrinsic filament dynamics.
(A) A maximum projection image from a movie of an actin filament tethered to a glass surface via a single α-actinin molecule where the tethering position about which the filament swivels is visible …
Figure 4—figure supplement 1
Pointed-end pausing on freely swiveling ends for various tethering proteins.
(A–B) The change in length of the pointed-end of actin filaments as a function of time at 1 μM-free actin concentration are shown when using (A) α-actinin, NEM-myosin, filamin, and (B) VASP as …
Figure 4—figure supplement 2
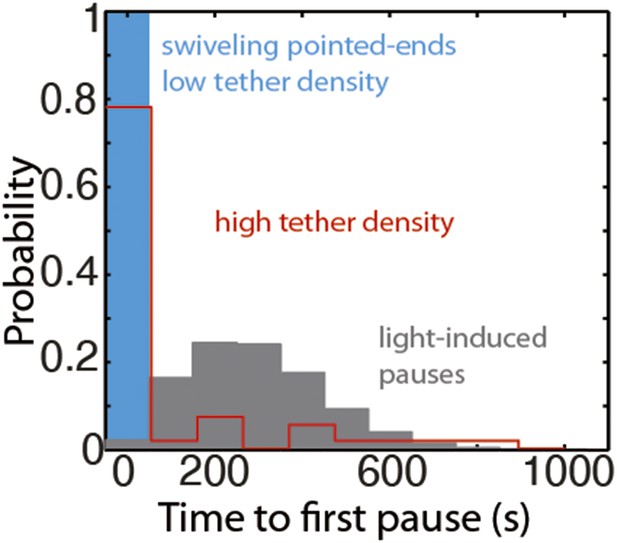
The distribution of the time to the first elongation pause at 300 nM free actin concentration.
The distribution of the observed time to the first pause for depolymerizing pointed-ends at the lowest tether density (blue bar), at medium to high tether density (pooled data, red bars), or …
Figure 4—figure supplement 3
Two-color seeded assay for visualizing pointed-end growth from an actin filament seed.
A schematic of the assay is shown. Actin filament fragments labeled in red with atto565 were used as seeds for filament growth in a solution of atto488-labeled (green) actin monomers. After 15 min, …
Figure 5
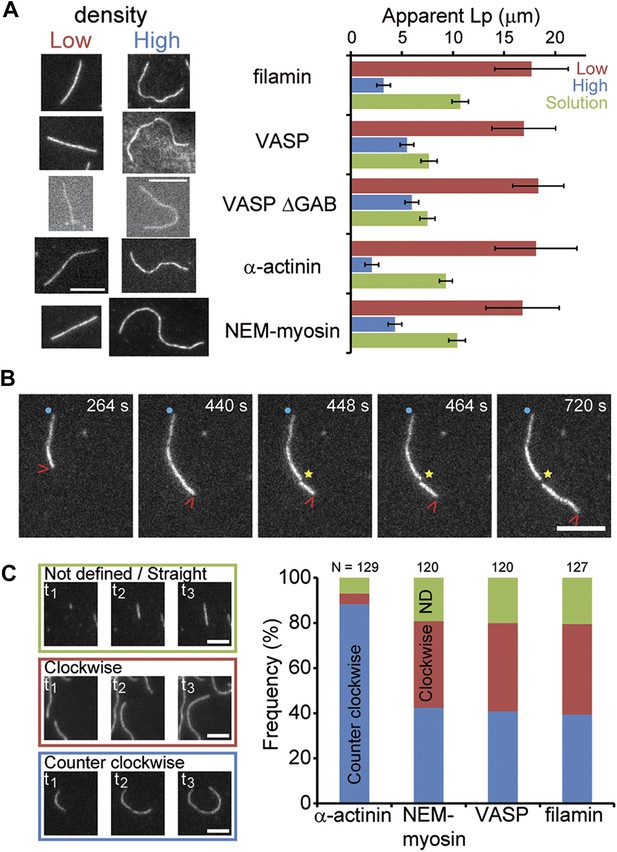
Side-binding proteins alter filament structure.
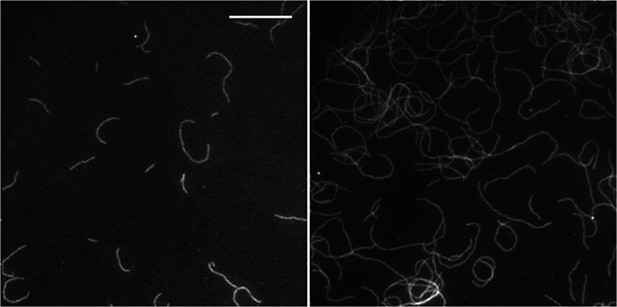
(A) (left panels) Images of individual filaments attached to the surface using different side-binding proteins at the lowest or highest surface density of tethering protein. Scale bar: 5 μm. (right …
Author response image 1
Tables
Table 1
Rate constants of Mg-ATP-actin monomer association and dissociation at both ends of the actin filament in the absence and presence of side-binding proteins
| End | kon (sub·μM−1·s−1) | koff (sub·s−1)† | koff/kon (μM) | Reference | |
|---|---|---|---|---|---|
| actin alone | Barbed | 11.6 ± 1.2 | 1.4 ± 0.8 | 0.12 ± 0.07 | (Pollard, 1986) |
| Pointed | 1.3 ± 0.2 | 0.8 ± 0.3 | 0.6 ± 0.17 | (Pollard, 1986) | |
| Barbed | 9.7 ± 2* | 1 ± 0.3 | 0.1 ± 0.04 | this work | |
| Pointed | 2.1 ± 0.8 | 0.8 ± 0.4 | 0.4 ± 0.35 | this work | |
| Surface adsorbed | |||||
| NEM-myosin | Barbed | 11 ± 1 | 1.6 ± 0.7 | 0.15 ± 0.03 | this work |
| Pointed | 0.8 ± 0.1 | 0.4 ± 0.1 | 0.5 ± 0.2 | this work | |
| Dd VASP | Barbed | 120 ± 30 | 1 ± 3 | 0.01 ± 0.03 | this work |
| Pointed | 48 ± 10 | 0.5 ± 2 | 0.01 ± 0.05 | this work | |
| filamin | Barbed | 8.5 ± 1.3 | 0.1 ± 0.4 | 0.012 ± 0.002 | this work |
| Pointed | 5.3 ± 0.1 | 2.6 ± 0.2 | 0.5 ± 0.04 | this work | |
| α-actinin | Barbed | 7.7 ± 1.5 | 0.7 ± 1 | 0.1 ± 0.2 | this work |
| Pointed | 0.9 ± 0.3 | 0.9 ± 0.3 | 1 ± 1 | this work | |
| Dd VASP ΔGAB | Barbed | 70 ± 13 | 14 ± 9 | 0.2 ± 0.2 | this work |
| Pointed | 16 ± 12 | 5 ± 8 | 0.3 ± 0.2 | this work | |
| In solution | |||||
| Dd VASP | Barbed | 126 ± 30 | 43 ± 33 | 0.3 ± 0.2 | this work |
| Pointed | 12 ± 8 | 3 ± 8 | 0.3 ± 2 | this work | |
| filamin | Barbed | 8.6 ± 1.1 | −1.3 ± 2 | 0.0 ± 0.1 | this work |
| Pointed | 5.5 ± 1.5 | 2.8 ± 1.6 | 0.5 ± 0.4 | this work | |
| Dd VASP ΔGAB | Barbed | 24 ± 11 | 4 ± 15 | 0.2 ± 1 | this work |
| Pointed | 3 ± 2.5 | 0.5 ± 4.5 | 0.2 ± 7 | this work | |
| Hs VASP | Barbed | 24 ± 4 | −3 ± 5 | 0 ± 0.1 | (Hansen and Mullins, 2010) |
| Pointed | Not reported | Not reported | Not reported | (Hansen and Mullins, 2010) |
-
*
All reported errors from this work are 95% confidence intervals whereas those of (Pollard, 1986) represent SD.
-
†
All reported dissociation constants from this work are inferred from extrapolation of the elongation velocity as a function of actin concentration to zero concentration, data from Figures 1, 2 and 4.
Table 2
Results of a Monte Carlo simulation describing the affect of lattice protein binding to the association rate of actin monomer binding to filaments
| α | LC (monomers) | |
|---|---|---|
| VASP | 9* (7–10)† | 160* (145–175)† |
| VASP ΔGAB | 5.1 (5.0–5.1) | 76 (74–76) |
| α-actinin | 0.4 (0.4–0.7) | 1 (1–11) |
| Filamin | 0.4 (0.2–0.8) | 11 (1–101) |
| NEM-myosin | 0.7 (0.3–0.9) | 11 (1–201) |
-
The binding of an actin-binding protein onto the lattice of a filament leads to changes (with magnitude α) in association kinetics that are propagated over a certain characteristic length LC, as a number of monomers.
-
*
The value obtained by minimizing the χ2.
-
†
The values in parenthesis represent the 68% confidence interval.
