Cortical flow aligns actin filaments to form a furrow
- Technische Universität Dresden, Germany
- Max Planck Institute of Molecular Cell Biology and Genetics, Germany
- Max Planck Institute for the Physics of Complex Systems, Germany
- The Francis Crick Institute, United Kingdom
Figures
Figure 1 with 1 supplement
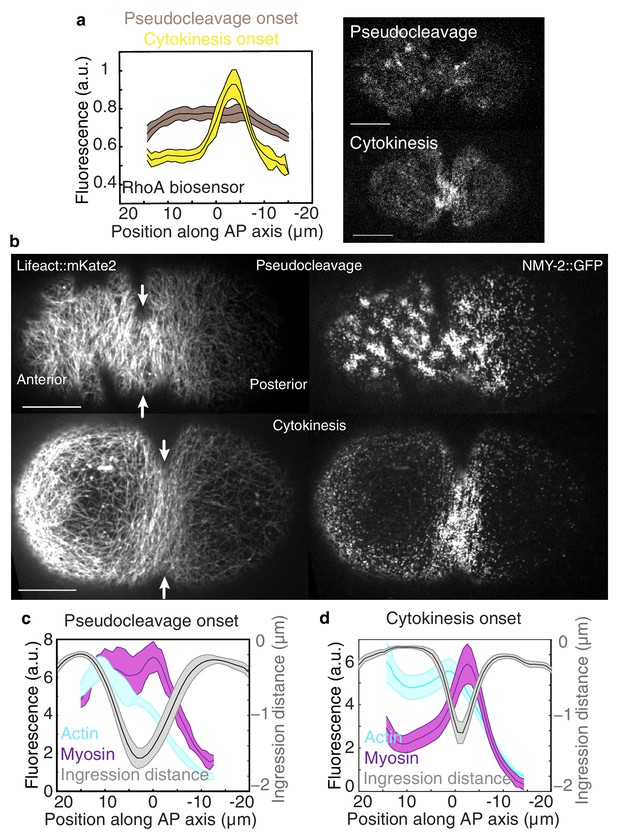
Flow and ingression during pseudocleavage and cytokinesis.
(a) Average active RhoA biosensor intensity profiles along the AP axis (0 represents the embryo center; N = 14 embryos for pseudocleavage and N = 7 for cytokinesis; errors represent the standard error of the mean). (b) Actomyosin cortical organization at the onset of pseudocleavage and cytokinesis in embryos expressing both Lifeact::mKate2 and NMY-2::GFP. (c–d) Average actin, myosin and ingression profiles as a function of position along the AP axis (N = 10 embryos for pseudocleavage and N = 22 for cytokinesis; errors represent the standard error of the mean). Scale bars, 10 μm. The following figure supplement is available for Figure 1:
Figure 1—figure supplement 1
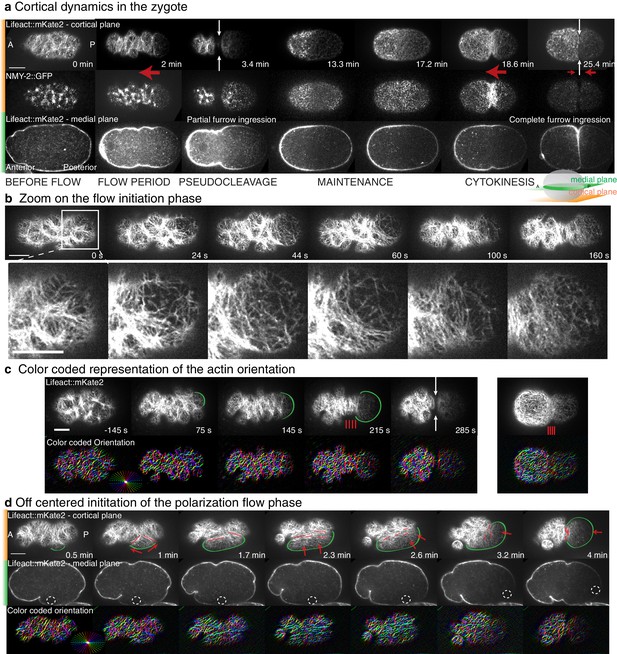
Details of actin organization during the polarization flow phase.
(a) Actomyosin gel dynamics in the C. elegans zygote. Single cortical and medial planes from a timelapse sequence of a representative embryo expressing both Lifeact::mKate2 and NMY-2::GFP. Anterior is to the left, posterior to the right. White arrows indicate the position of pseudocleavage and cytokinesis ingressions. Red arrows indicate flow directions. (b) Close up look at the filaments dynamics near the site of flow initiation. Cortical plane from a timelapse sequence of an embryo expressing both Lifeact::mKate2 and NMY-2::GFP. (c) Top: Actin network organization from an embryos expressing Lifeact::mKate2. Times rescaled to 0 at flow initiation. Green arcs indicate the smooth cleared zone during the polarization process. Red lines schematize filaments maximum vertical alignment positions. White arrows underlie pseudocleavage ingression. Bottom: color-coded representation of the orientation of filaments. (d) Example from an embryo for which the polarization process starts off centered from the physical pole of the embryo due to a mispositioning of the sperm pronucleus (dashed circle on medial plane). Alignment direction is observed to follow perpendicularly to the direction of the flow as it reorients along the long axis of the embryo (also see Appendix). Red arrows represent flow direction, red lines filaments main orientation. Scale bars, 10 μm.
Figure 2 with 5 supplements
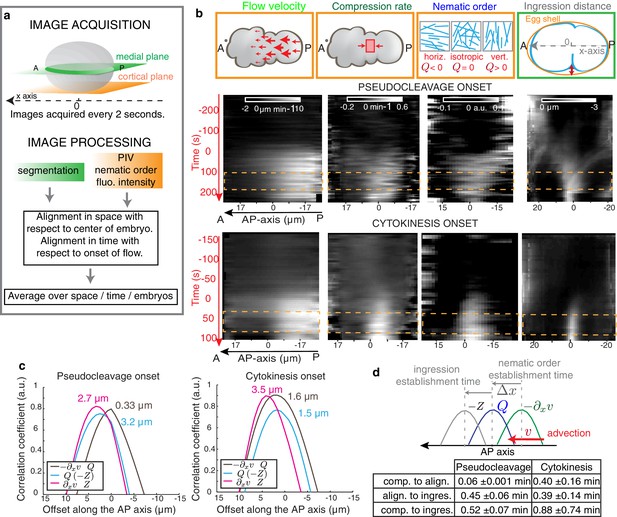
Cortical flows compress the gel to generate alignment.
(a) Filament orientation is quantified by a nematic order parameter; flow fields are obtained from Particle Image Velocimetry (PIV) analysis. (b) Gel flow, compression rate, filament orientation and cell ingression fields. Top row, schematic representations. Middle row, kymographs of the time evolution of the profiles along the AP axis of flow velocity, compression rate, nematic order parameter and outer ingression distance for pseudocleavage (N = 10). Bottom row, cytokinesis (N = 12). Orange dashed lines indicate the times where all four fields are stationary. Flow, compression and nematic order were determined from bottom-section and ingression from mid-section views of Lifeact::mKate2 labelled embryos (see Materials and methods and Appendix). (c) Spatial correlation between compression, alignment and ingression (see Materials and methods). Peak value positions (estimated by a Gaussian fitting of the 1D correlation curve) are indicated. See Figure 2—figure supplement 2 for spatiotemporal correlation functions. (d) Table of the temporal delays obtained from the correlation peak value positions using the mean values of the velocity in the 10 μm central region (mean values for pseudocleavage: = 6.16 ±1.23 μm/min; for cytokinesis: = 4.01±1.92 μm/min; mean ± SD).
Figure 2—figure supplement 1
Quantification methods developed.
(a) Example of the filaments alignment quantification (red lines) and the flow velocity field (yellow arrows), as well as nematic order parameters conventions. (b) Time evolution of flow (light green) and compression rate (dark green) as well as ingression (grey) measured at a fixed position along the AP axis (−20 μm for velocity, 0 μm or central position of the embryo for compression and 3 μm for ingression, measured from the center). Error bars represent the standard error of the mean. Bottom, fit using the error function (red line) of the time evolution of the velocity from a single embryo (blue dots) used to determine the reference time point (Time = 0). (c) Time evolution of the mean velocity and compression rate along the AP axis and nematic order parameter, all taken at fixed positions along the AP axis. Error bars represent the standard error of the mean. In orange is represented the period chosen as stationary flow phase. (d) Mean profiles along the AP axis of the velocities (vx light green and vy yellow), compression rate and nematic order parameters (Q = −Qxx in dark blue and Qxy in cyan) during the stationary flow phase. (See Appendix for further explanations.)
Figure 2—figure supplement 2
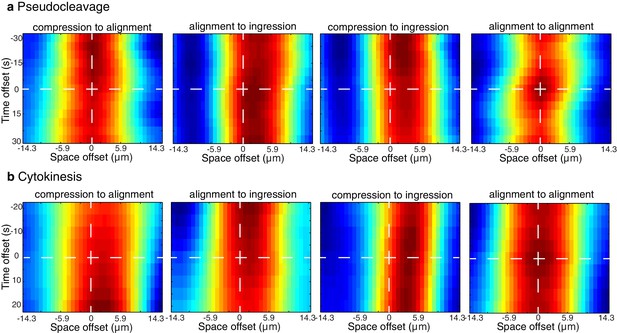
Spatiotemporal correlations.
Plots of the spatiotemporal correlations between the compression, alignment and ingression data sets taken during the pseudocleavage stationary phase (a) and cytokinesis onset stationary phase (b). Data is restricted to the 30 μm central region of the embryo.
Figure 2—figure supplement 3
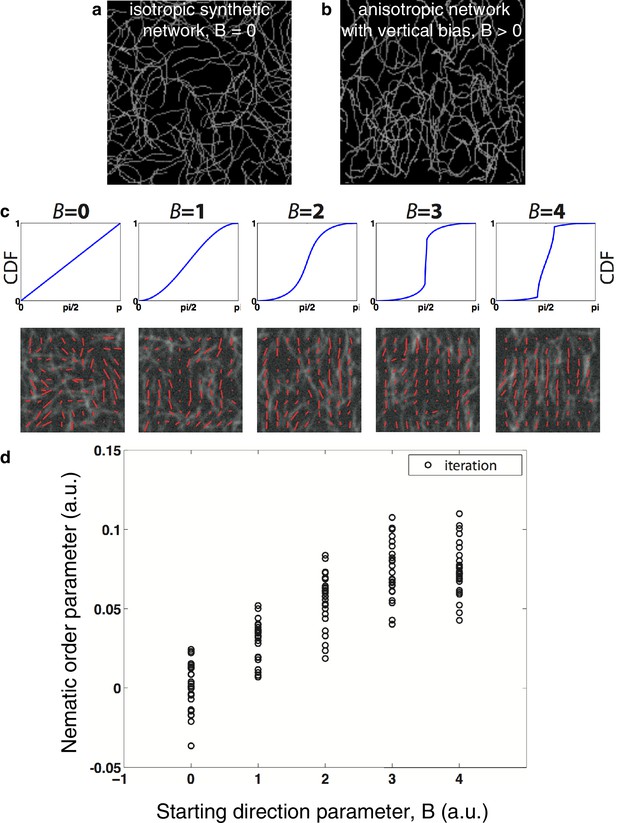
Nematic order parameter quantification of artificial images with and without directional bias.
(a) Example of a simulated isotropic actin meshwork (see Appendix for details). (b) Example of a simulated actin meshwork for which the angle of the starting direction is biased toward vertical (see Appendix). (c) Cumulative distribution function (CDF) used and example of an image and its nematic order map (red lines indicate the preferential orientation inside a template or orientation vector) obtained for different values of the starting parameter B that controls the bias of the filaments orientation. B = 0 leads to an isotropic orientation. (d) Variation of the average nematic order parameter obtained for several synthetic meshworks while increasing the vertical bias of the filaments orientation. The saturation is caused by the fact that we here bias only the initial direction of growth.
Figure 2—figure supplement 4
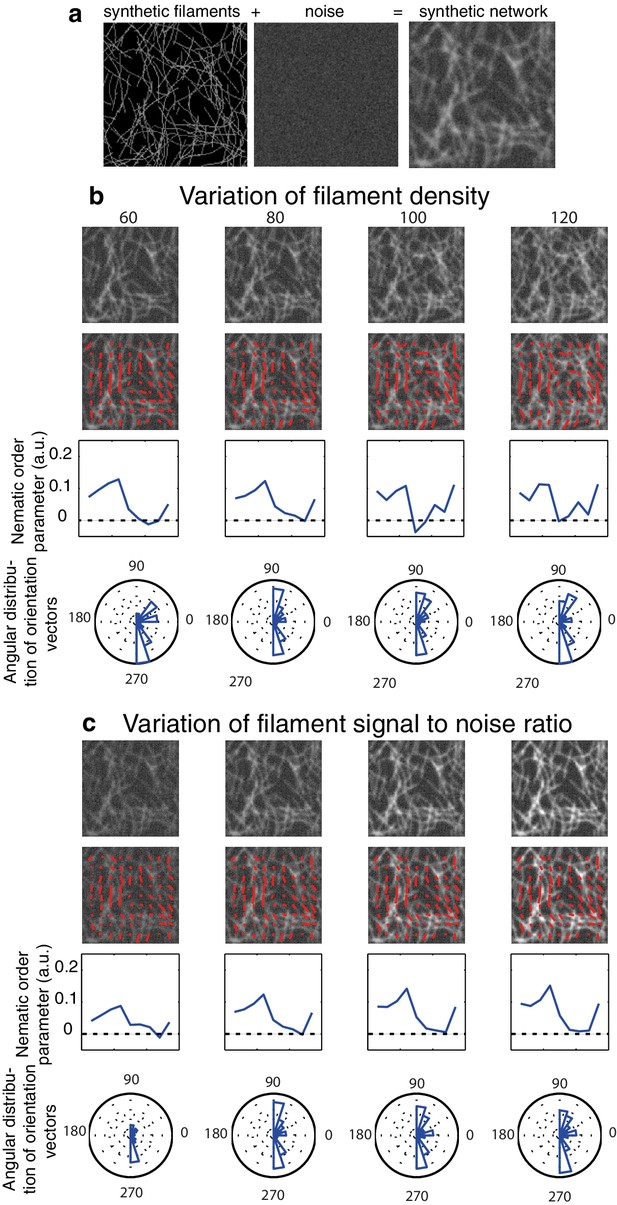
Impact of image quality on the nematic order parameter quantification.
(a) An artificial filamentous network is obtained by a random iteration process with controllable parameters in Matlab (see Appendix for more details). (b-d) We chose to maintain a vertical bias in the orientation of the filaments in all the following cases (B = 1). Red lines indicate the preferential orientation inside a template or orientation vector. A profile of the mean nematic order parameter along the x-axis as well as the angular distribution are shown in all cases. Note that as we do not measure the directionality of filaments thus we obtain values modulo π. (b) Impact of the filament density (ranging from 60 to 120 filaments per image) on the nematic order parameter quantification. The profile of nematic order is to first order independent of network density. (c) Impact of the signal to noise ratio. High signal to noise ratio leads to higher values of the nematic order parameter, low signal to noise ratio leads to a poor detection of the direction of the filaments and artificially small values of the nematic order parameter.
Figure 2—figure supplement 5
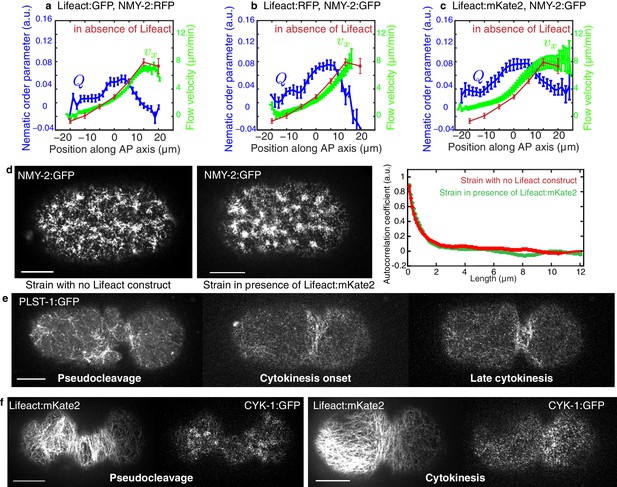
Comparison of different actin labeling strains and actin-binding protein localization.
(a–c) Average AP profiles of flow velocity (light green) and nematic order parameter (blue) at the time of stationary flow during pseudocleavage of respectively 22 embryos expressing Lifeact:GFP, NMY:RFP, 9 embryos expressing Lifeact:RFP, NMY-2:GFP and 16 embryos expressing Lifeact:mKate2, NMY-2:GFP. Overlaid in red is the velocity profile of worms expressing only labeled NMY-2 (N = 5). Error bars represent the standard error of the mean. (d) Images of NMY-2:GFP in the early zygote. Left strain without Lifeact, right strain expressing Lifeact:mKate2. The density, size and dynamics are similar in both strains. Right panel, the average radial autocorrelation coefficient of the myosin intensity over a minute in early embryos gives an average myosin foci size. (e) Localization of the actin bundling protein plastin during pseudocleavage and cytokinesis. Plastin localizes in dense bundles of actin filaments and is particularly abundant in the cytokenetic ring and could act to stabilize actin bundles in these regions. (f) Localization of the actin nucleating agent formin during pseudocleavage and cytokinesis. CYK-1 is present throughout the cell cortex during pseudocleavage, with higher densities in foci regions. It is recruited to the cell equator during cytokinetic ring formation and ingression. Scale bars, 10 μm.
Figure 3 with 4 supplements
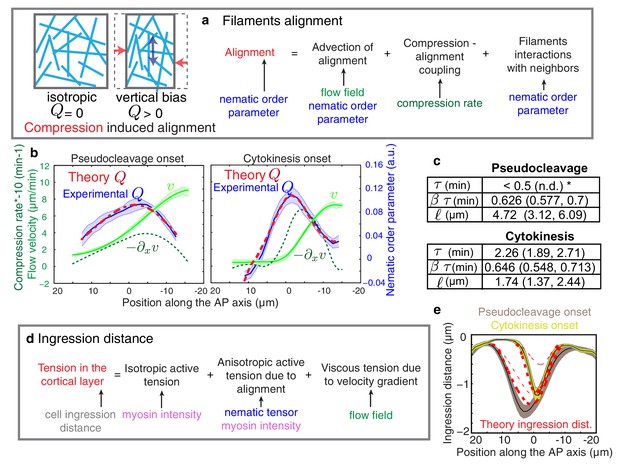
Theory predicts an alignment peak.
(a) Schematic representation of flow-based alignment. For full theory refer to Appendix. (b) Average AP profiles of gel flow (light green, smoothened), compression rates (dark green) and nematic order parameter (blue) at the time of stationary flow (Figure 2C) during pseudocleavage (left, N = 16) and cytokinesis onset (right, N = 32). Error bars represent the standard error of the mean. Dashed red line indicates the respective best-fit theory predictions for the nematic order parameter (blue). (c) Table of the material parameters. See also Figure 3—figure supplement 1 and Table 1, Table 2. (d) Illustration of the cortical tension related to the ingression distance. (e) Outer ingression profiles at the onset of pseudocleavage (brown) and cytokinesis (yellow). The theoretical profiles (thick dashed red lines: active tension depends on alignment and can be anisotropic; thin dashed lines: active tension is isotropic) are determined by simultaneous fitting of both the pseudocleavage and cytokinesis datasets with a single fit parameter (see Appendix) using the myosin density, flow velocity and nematic order parameter fields.
Figure 3—figure supplement 1
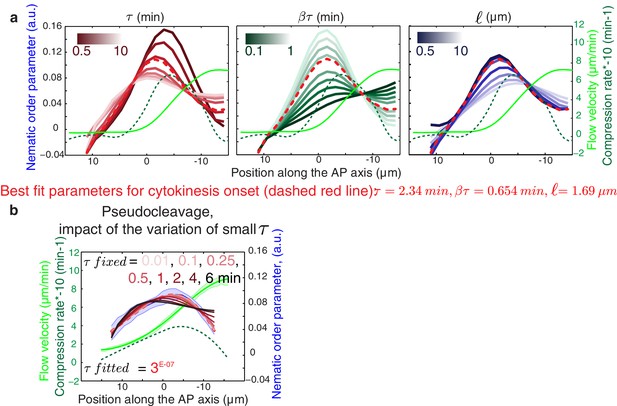
Influence of the gel material parameters for the nematic order parameter.
(a) Nematic order parameter profiles obtained when varying independently each of the fitting parameters , , away from their the best fit values obtained for cytokinesis. Dashed red line, best fit result ( = 2.34 min, = 0.654 min, =1.69 μm). For each set of parameters , , a fit is performed for the fitting parameters C1 and C2 only (see Appendix). (b) Nematic order parameter profiles obtained when varying the fitting parameter while keeping , fixed and equal to their best-fit values. Appropriate fits to experimental curve are obtained for all values of < 0.5 min. For each value of , a fit is performed for the fitting parameters C1 and C2 only.
Figure 3—figure supplement 2
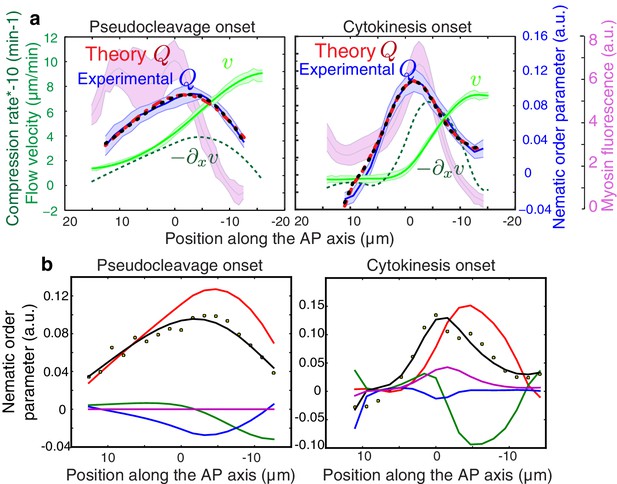
Contribution of active alignment to the nematic order parameter profile.
(a) Average AP profiles of gel flow (light green), compression rates (dashed dark green), nematic order parameter (blue) and myosin fluorescence (magenta) at the time of stationary flow during pseudocleavage (left, N = 16) and cytokinesis onset (right, N = 32). Error bars represent the standard error of the mean. Dashed red lines indicate the best-fit theory predictions for the nematic order parameter in absence of active alignment, dashed black lines are the fits obtained while including the myosin-based active alignment, with for pseudocleavage and for cytokinesis. (b) Contribution of the individual terms from Equation 3 in the main text (red: , green: , blue: , magenta: ). Note that myosin-based active alignment (magenta) is insignificant for pseudocleavage and is low for cytokinesis compared to compression-based alignment (red). The theoretical alignment profile (sum of all the terms shown in black) overlays the experimental data points (dots).
Figure 3—figure supplement 3
Ingression through anisotropic stress generation in the aligned gel.
(a) Top, a representative embryo is used to visualize the time course of ingression. Bottom, Kymograph obtained from the region specified by the dashed white box in the upper pannel. The pseudocleavage and cytokinesis ingressions are visible. Yellow arrow indicates the inner ingression distance during polarizing flow phase, magenta dashed line indicates the ingressing membrane and blue arrow indicates the outer ingression. Red doted lines represent the position of the eggshell. Scale bar 10 μm. (b) Top, illustration of the cortical tension during ingression. Bottom, outer ingression profiles (grey) averaged over the time periods indicated by the thin horizontal white lines in (a, bottom) during pseudocleavage (left) and cytokinesis (right). The theoretical profiles (dashed red lines) are determined by simultaneous fitting of both the pseudocleavage and cytokinesis datasets with a single fit parameter (see Appendix) using the myosin density (magenta), flow velocity (green) and nematic order parameter (blue) fields. (c) and (d) Illustration of the coordinate and reference systems used for this theoretical description. (e) Comparison of the theoretically obtained profile of the outer ingression without the anisotropic stress induced by nematic order (dashed red, obtained by imposing p3 = 0) during pseudocleavage and cytokinesis phases with the experimental data (black).
Figure 3—figure supplement 4
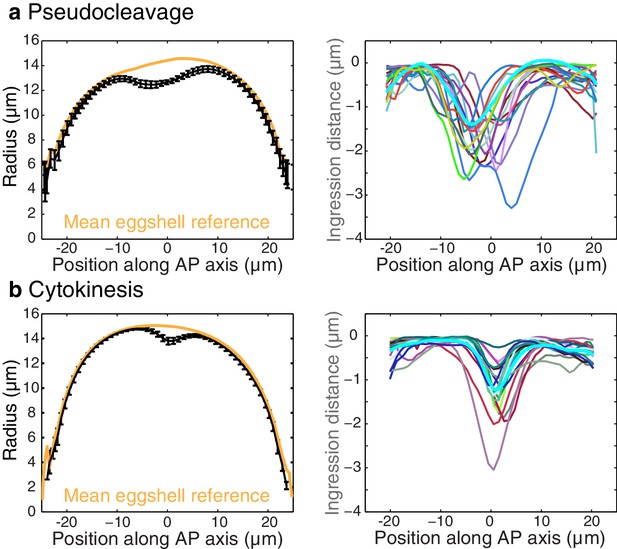
Shape and ingression distance quantification.
Left column, plots of the cell shape (mean radius for all embryos during the stationary flow phase and eggshell reference) for pseudocleavage (a) and cytokinesis (b). Error bars, the standard error of the mean. Right column, ingression distance for several embryos and mean value (cyan) during the stationary phase of pseudocleavage and cytokinesis.
Figure 4 with 2 supplements
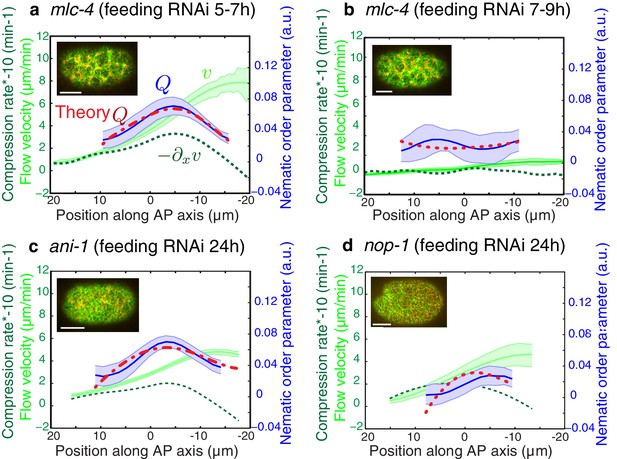
Flows and compression are required to generate alignment.
(a-d) Average AP profiles of gel flow (light green, smoothened), compression rates (dark green) and nematic order parameter (blue) at the time of stationary flow during pseudocleavage onset for mlc-4 5–7 hr and 7–9 hr, nop-1 and ani-1 RNAi. Error bars represent the standard error of the mean (N = 17, 14, 10, 22 for a-d, respectively). Dashed red line indicate the respective best-fit theory predictions for the nematic order parameter (blue). For ani-1 and mlc-4 (5–7 hr), is small and is determined to be smaller than 0.5 min. For nop-1 and mlc-4 (7–9 hr), theory profiles were generated using the parameters obtained for the unperturbed non-RNAi pseudocleavage, since insufficient compression rates did not constrain the physical parameters. Scale bar, 10 μm.
Figure 4—figure supplement 1
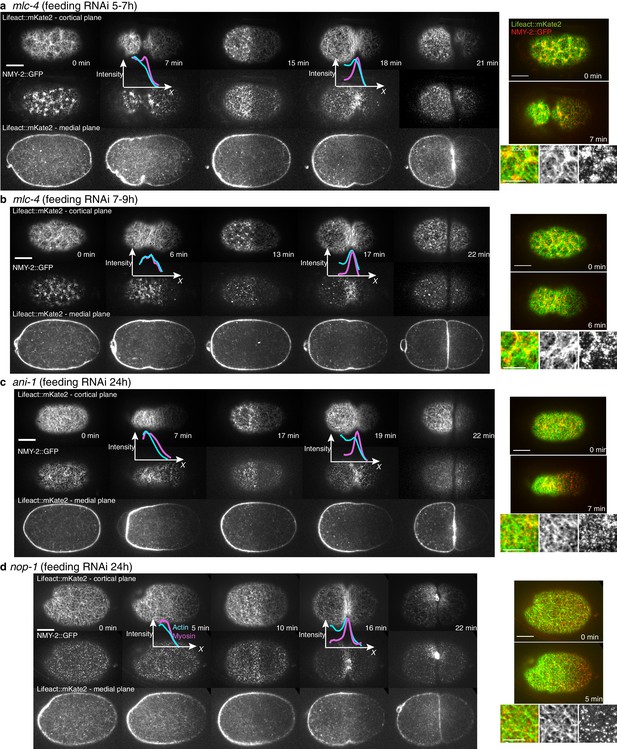
Cytoskeletal organization under RNAi perturbation.
(a-d) Actin organization and myosin distribution under nop-1(RNAi), ani-1(RNAi) and mlc-4(RNAi). Inserts with fluorescence intensity profiles during pseudocleavage and cytokinesis onset are overlaid next to the corresponding images (actin in blue, myosin in magenta). Note that ANI-1 depleted embryos had more elongated and thin anterior halves, with no localized dense actin ring like structure and no clear and stable central furrow with membrane overlapping. Also note that the asymmetry in the distribution of actin (usually denser in the anterior half of the embryo) during cytokinesis was reduced for both nop-1 and long mlc-4(RNAi). Right, combined images and zoom (green Lifeact, red NMY-2). Scale bar, 10 μm (full images); 5 μm (zoom).
Figure 4—figure supplement 2
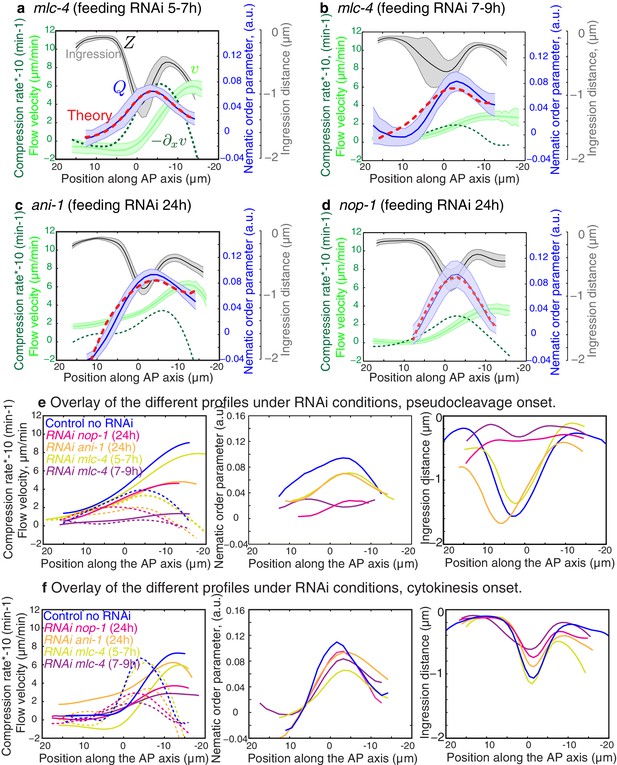
Flows, compression and alignment at cytokinesis onset.
(a-d) Results of nop-1(RNAi), ani-1(RNAi) and mlc-4(RNAi). Average AP profiles of gel flow (light green, smoothened), compression rates (dark green) and nematic order parameter (blue) at the time of stationary flow during cytokinesis onset. Error bars represent the standard error of the mean (for nop-1, ani-1, mlc-4 5–7 hr and 7–9 hr, N = 9, 18, 9, 13, respectively). Dashed red line indicates the respective best-fit theory predictions for the nematic order parameter (blue). For cytokinesis mlc-4 (7–9 hr) tau is small and is determined to be smaller than 0.5 min. (e-f) Overlay of the different profiles at pseudocleavage and cytokinesis onset, non-RNAi is shown in blue and compression rates in dashed lines. Note that the level of outer ingression was similar to the non-RNAi case for ani-1(RNAi) pseudocleavage, but with improper location and no membrane overlapping, thus no full pseudocleavage furrowing was obtained but a remaining initial anterior ingression was achieved in the presence of some filaments alignment.
Figure 5
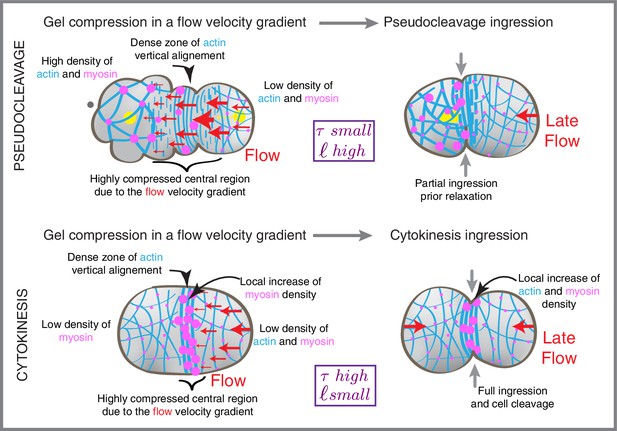
Compression drives alignment for furrowing.
Schematic illustration of flows, cytoskeletal organization and cell shape changes during pseudocleavage and at the onset of cytokinesis.
Author response image 1
Actomyosin ring closure dynamics.
https://doi.org/10.7554/eLife.17807.029Videos
Video 1
Actomyosin gel dynamics in the C. elegans zygote.
Cortical and medial planes of an embryo expressing both Lifeact::mKate2 and endogenous NMY-2::GFP. Left panel, medial plane Lifeact:mKate2, center, cortical NMY-2::GFP, right panel, cortical Lifeact:mKate2 (min:s).
Video 2
Three-dimensional reconstruction of an early one-cell embryo of C. elegans expressing Lifeact::mKate2.
The back of the embryo is dimmer due to imaging.
Video 3
Cortical dynamics at flow initiation.
Left panel, cortical NMY-2::GFP, center cortical Lifeact:mKate2 and a zoom is shown in the right panel (min:s).
Video 4
Cortical dynamics of an embryo in which flow was initiated at the side (bottom) and far from the posterior pole of the embryo.
Actin filament alignment follows flow and compression, thus transitions from a horizontal to a vertical direction (min:s).
Video 5
Actomyosin gel dynamics in the C. elegans zygote after 24 hr nop-1(RNAi).
Cortical and medial planes of an embryo expressing both Lifeact::mKate2 and endogenous NMY-2::GFP. Left panel, medial plane Lifeact:mKate2, center, cortical NMY-2::GFP, right panel, cortical Lifeact:mKate2 (min:s).
Video 6
Actomyosin gel dynamics in the C. elegans zygote after 26 hr ani-1(RNAi).
Cortical and medial planes of an embryo expressing both Lifeact::mKate2 and endogenous NMY-2::GFP. Left panel, medial plane Lifeact:mKate2, center, cortical NMY-2::GFP, right panel, cortical Lifeact:mKate2 (min:s).
Video 7
Actomyosin gel dynamics in the C. elegans zygote after 14 hr mlc-4(RNAi).
Cortical and medial planes of an embryo expressing both Lifeact::mKate2 and endogenous NMY-2::GFP. Left panel, medial plane Lifeact:mKate2, center, cortical NMY-2::GFP, right panel, cortical Lifeact:mKate2 (min:s).
Tables
Table 1
Best fit gel material parameters, bootstrapping. The median values together with the standard 68% confidence bounds of the distribution of the bootstrap data are given.
Pseudocleavage | Cytokinesis | |
|---|---|---|
non RNAi | non RNAi | |
, min | < 0.5 (n.d.) † | 2.26 (1.89, 2.71) |
, min | 0.626 (0.577, 0.7) | 0.646 (0.548, 0.713) |
, μm | 4.72 (3.12, 6.09) | 1.74 (1.37, 2.44) |
nop-1 RNAi | nop-1 RNAi | |
, min | n.d. * | < 0.5 (n.d.) † |
, min | n.d. * | 0.771 (0.694, 2.75) |
, μm | n.d. * | 2.67 (1.7, 11.5) |
ani-1 RNAi | ani-1 RNAi | |
, min | < 0.5 (n.d.) † | 0.989 (0.555, 1.79) |
, min | 1.45 (0.969, 18) ‡ | 0.724 (0.636, 0.929) |
, μm | 12.3 (6.39, 58.4) ‡ | 3.38 (2.97, 6.16) |
mlc-4 (5–7 hr) RNAi | mlc-4 (5–7 hr) RNAi | |
, min | < 0.5 (n.d.) † | 4.76 (3.67, 6.6) |
, min | 0.467 (0.451, 0.503) | 0.637 (0.567, 0.768) |
, μm | 2.75 (2.38, 4.1) | 6.58 (5.31, 6.85) |
mlc-4 (7–9 hr) RNAi | mlc-4 (7–9 hr) RNAi | |
, min | n.d. * | < 0.5 (n.d.) † |
, min | n.d. * | 0.916 (0.82, 1.04) |
, μm | n.d. * | 3.12 (2.49, 4.18) |
-
*n.d. denotes parameters which could not be determined,
-
†< 0.5 (n.d.) denotes parameters which could not be determined, but could be determined to be below 0.5 (see Figure 3—figure supplement 1b),
-
‡denotes values that could be determined but that were not well constrained.
Table 2
Best fit gel material parameters, no bootstrapping. The mean values together with its 95% confidence bounds are given.
Pseudocleavage | Cytokinesis | |
|---|---|---|
non RNAi | non RNAi | |
, min | < 0.5 (n.d.) † | 2.34 (1.74, 3.14) |
, min | 0.59 (0.513, 0.806) | 0.652 (0.541, 0.764) |
, μm | 5.38 (3.27, 8.85) | 1.69 (1.04, 2.75) |
nop-1 RNAi | nop-1 RNAi | |
, min | n.d. * | < 0.5 (n.d.) † |
, min | n.d. * | 0.738 (0.0.614, 0.862) |
, μm | n.d. * | 1.79 (0.64, 5.03) |
ani-1 RNAi | ani-1 RNAi | |
, min | < 0.5 (n.d.) † | 1.01 (0.989, 1.03) |
, min | 1.31 (0.428, 2.19) | 0.74 (0.588, 0.892) |
, μm | 10.4 (4.91, 21.9) ‡ | 4.08 (2.68, 6.2) |
mlc-4 (5–7 hr) RNAi | mlc-4 (5–7 hr) RNAi | |
, min | < 0.5 (n.d.) †** | 4.37 (3.08, 6.21) |
, min | 0.454 (0.437, 0.47) | 0.614 (0.501, 0.727) |
, μm | 2.24 (1.87, 2.67) | 5.81 (5.02, 6.72) |
mlc-4 (7–9 hr) RNAi | mlc-4 (7–9 hr) RNAi | |
, min | n.d. * | < 0.5 (n.d.) † |
, min | n.d. * | 0.97 (0.931, 1.01) |
, μm | n.d. * | 2.98 (2.88, 3.08) |
-
*n.d. denotes parameters which could not be determined,
-
†< 0.5(n.d.) denotes parameters which could not be determined, but could be determined to be below 0.5 (see Figure 3—figure supplement 1b),
-
‡denotes values that could be determined but that were not well constrained. Caption for Videos 1Videos 1 to 7
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Cortical flow aligns actin filaments to form a furrow
eLife 5:e17807.
https://doi.org/10.7554/eLife.17807
