Controlling contractile instabilities in the actomyosin cortex

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record updated: July 27, 2017 (This version)
Version of Record updated: July 19, 2017 (Go to version)
Version of Record published: March 16, 2017 (Go to version)
Accepted Manuscript updated: January 28, 2017 (Go to version)
Accepted Manuscript published: January 24, 2017 (Go to version)
Accepted: January 14, 2017
Received: July 12, 2016

1. Of interest
A mechanosensing mechanism controls plasma membrane shape homeostasis at the nanoscale

Xarxa Quiroga, Nikhil Walani ... Pere Roca-Cusachs

Research Article Sep 25, 2023
Further reading

Abstract
Introduction
Results and discussion
Materials and methods
Appendix
References
Decision letter
Author response
Article and author information
Metrics

Abstract

The actomyosin cell cortex is an active contractile material for driving cell- and tissue morphogenesis. The cortex has a tendency to form a pattern of myosin foci, which is a signature of potentially unstable behavior. How a system that is prone to such instabilities can rveliably drive morphogenesis remains an outstanding question. Here, we report that in the Caenorhabditis elegans zygote, feedback between active RhoA and myosin induces a contractile instability in the cortex. We discover that an independent RhoA pacemaking oscillator controls this instability, generating a pulsatory pattern of myosin foci and preventing the collapse of cortical material into a few dynamic contracting regions. Our work reveals how contractile instabilities that are natural to occur in mechanically active media can be biochemically controlled to robustly drive morphogenetic events.

https://doi.org/10.7554/eLife.19595.001

Introduction

Alan Turing described in his seminal 1952 paper the ability of an initially homogeneous spatial system that contains diffusing and chemically interacting species to form a self-organized pattern (Turing, 1952). Turing’s original conjecture was that such processes contribute to the patterning of developing organisms. While many examples have been found that are compatible with this idea (Kondo and Asal, 1995; Müller et al., 2012; Sheth et al., 2012; Raspopovic et al., 2014), self-organized patterning in morphogenesis, however, is known to not only rely on biochemical regulation but also depend on cell-and tissue scale active mechanical processes (Turing, 1952; Howard et al., 2011). General physical mechanisms by which the interplay between regulatory and mechanical processes endows active biological materials to form self-organized spatiotemporal patterns have remained largely unexplored.

Actomyosin contractility (Bray and White, 1988; Salbreux et al., 2012) is an essential cellular mechanical process, responsible for driving many cell- and tissue scale morphogenetic events (Murrell et al., 2015; Levayer and Lecuit, 2012). The cortex consists to a large extent of actin filaments and myosin motor proteins, forming a thin layer underneath the cell membrane that can be thought of as a thin film of an active gel (Salbreux et al., 2012; Jülicher et al., 2007). Contractility by myosin motor proteins generates active tension in the gel, and gradients in active tension are known to generate cortical flows of this layer (Mayer et al., 2010). Cortical flow participates in forming the cytokinetic furrow (Bray and White, 1988; Benink et al., 2000; Yumura, 2001; Eggert et al., 2006), and drives polarization of the one-cell stage C. elegans embryo (Hird and White, 1993; Guo and Kemphues, 1996; Cheeks et al., 2004; Munro et al., 2004; Goehring et al., 2011). Highly contractile cortices, like the one driving polarization in C. elegans, tend to exhibit transient accumulations of myosin that form a pulsatile pattern. Pulsatile actomyosin patterns are ubiquitous in development (Munro et al., 2004; Martin et al., 2009; Solon et al., 2009; Rauzi et al., 2010; Roh-Johnson et al., 2012; Maître et al., 2015), and it has been suggested that they result from positive feedback and contractile instabilities (Kruse and Jülicher, 2000; Bois et al., 2011; Gowrishankar et al., 2012; Kumar et al., 2014; Munjal et al., 2015; Hannezo et al., 2015). A contractile instability causes the cortex to become inhomogeneous over space, with cortical material collapsing into contracting regions (Bois et al., 2011; Alvarado et al., 2013). Theoretical work has shown that contractile instabilities are inevitable when contractility is high enough (Bois et al., 2011), raising the question of how a system that is prone to such instabilities can reliably drive morphogenesis. Here we show that there indeed exists a contractile instability in the actomyosin cortical layer of the C. elegans zygote, and we discover that this instability is controlled by a RhoA oscillator.

Results and discussion

In order to investigate spatiotemporal patterns in the C. elegans cortex, we first sought to see whether non-muscle myosin II (NMY-2) in the C. elegans zygote displays pulsatile dynamics (Munro et al., 2004). For this, we determined the temporal derivative of the average NMY-2 intensity (Figure 1A, averaging over a region in the posterior indicated by a white box), as a proxy of myosin foci assembly and disassembly behavior (Figure 1A–C). We also quantified the time-dependence of the average speed of cortical flow in this region as determined by Particle Image Velocimetry (PIV, see Appendix for detail) (Figure 1B,C). Notably, both quantities exhibited signs of oscillatory behavior (Figure 1C) and an auto-correlation analysis revealed periodic changes in both quantities with a time constant of approximately 30 s (Figure 1D,E). To conclude, the myosin foci pattern in the C. elegans zygote exhibits pulsatile, oscillatory dynamics.

Figure 1 with 3 supplements see all

Download asset Open asset

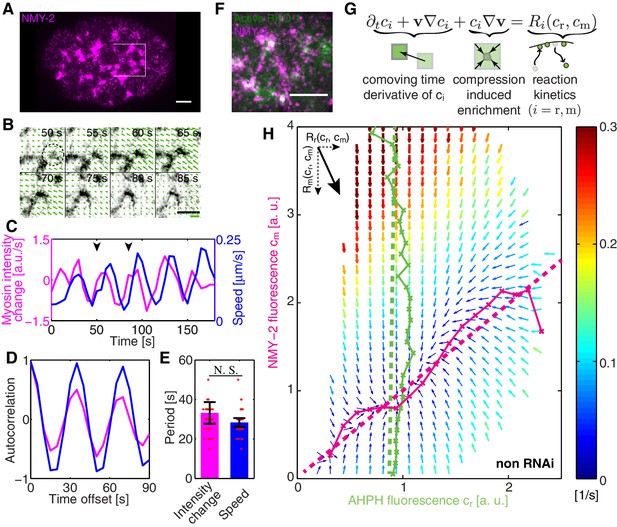
COMBI of active RhoA and NMY-2.

(A) A representative image of NMY-2::GFP showing the NMY-2 foci pattern (magenta) in the *C. elegans* zygote. Anterior is to the left throughout, white box denotes region shown in B. (B) Myosin focus assembly and disassembly time-course from A in inverted contrast; dashed circle indicates a myosin focus. Arrows denote the velocity field determined by PIV; thick green line: velocity scale bar 0.4 $μ m / s$ . (C) The temporal dynamics of NMY-2 fluorescence intensity time-rate change (magenta) and cortical flow speed (blue, obtained by PIV) for the region in (B), arrowheads indicate the time interval shown in (B). (D) Normalized autocorrelation of NMY-2 intensity change and flow speed timecourses in (C) and (E) respective oscillation periods. (F) NMY-2::RFP (magenta) and AHPH::GFP (green), a probe for active RhoA, co-localize at myosin foci. (G) COMBI analysis schematic. (H) Effective reaction terms of NMY-2 and active RhoA in the phase plane of normalized NMY-2 and active RhoA concentrations (N = 25 embryos). Arrows represent concentration changes, colors indicate the magnitude of change. Thin solid magenta (NMY-2) and green (RhoA) lines, numerically determined nullclines. Thick dashed lines, linearized nullclines (see Appendix). Scale bars; $5 μ m$ .

https://doi.org/10.7554/eLife.19595.002

We next sought to understand where this oscillatory behavior comes from. One possibility is that positive feedback mediated by RhoA (RHO-1 in C. elegans) (Bement et al., 2015), a key activator of myosin (Jenkins et al., 2006; Motegi and Sugimoto, 2006; Schonegg and Hyman, 2006), plays a role in generating this pulsatile pattern (Munjal et al., 2015). We investigated the dynamics of active RhoA by use of a GFP fused anillin homology domain (AHPH) probe, to image the GTP-bound active form of RhoA (Tse et al., 2012). We find that active RhoA forms a dynamic, pulsatile pattern that is similar to that of myosin, with both active RhoA and myosin co-localizing in pulsatile foci (Figure 1F, Figure 1—figure supplement 1, and Video 1). We speculated that flow-based transport of an activator of myosin could give rise to positive feedback and a contractile instability (Bois et al., 2011), favouring the spontaneous formation of self-organized pulsatory patterns (Munjal et al., 2015). However, testing for this possibility requires knowledge of the kinetics of active RhoA mediated myosin recruitment coupled with a hydrodynamic description of active cortical mechanics, for evaluating if the full mechanochemically coupled system indeed is unstable.

Video 1

Download asset

posterframe for video — Active RhoA and myosin co-localization in pulsatile foci.

Time lapse movie shows the cortical plane of embryo that expresses both AHPH::GFP (green) and NMY-2::tagRFP-T (magenta) in non-RNAi condition. Scale bar, 5 $μ m$ .

https://doi.org/10.7554/eLife.19595.006

We set out to test if coupling RhoA mediated myosin recruitment to gel flow and advection results in an intrinsically unstable cortex (Figure 2A). To this end, we sought to determine the effective reaction kinetics of the regulatory interaction between active RhoA and myosin in vivo. We developed a method of measuring the kinetic diagram of active RhoA mediated myosin recruitment (CO-moving Mass Balance Imaging; COMBI): We investigated the mass balance of both species in the comoving frame of reference of the flowing cortex, under consideration of the effects of dilution/enrichment by divergent/convergent gel flow (Figure 1G) (Vallotton et al., 2004). In the frame of reference of the embryo, concentrations of myosin and active RhoA can change due to transport by flow (advective fluxes) or due to association/dissociation (chemical fluxes). The chemical fluxes $R_{r}$ and $R_{m}$ , where r denote active RhoA and m denotes myosin, correspond to reaction terms that capture turnover and biochemically regulated recruitment effects. They can depend on the concentrations of both species.

Figure 2 with 2 supplements see all

Download asset Open asset

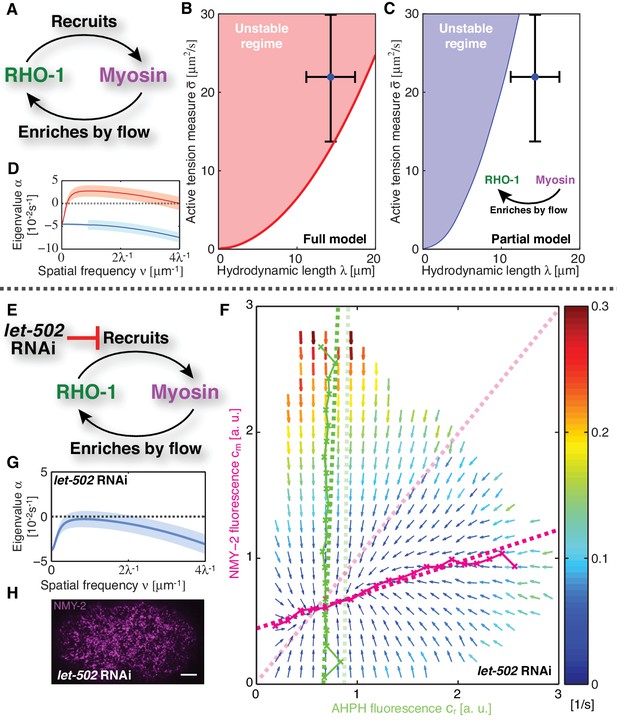
Linear stability analysis reveals that the actomyosin cortex in *C. elegans* is unstable.

(A) Schematic of the full mechanochemical patterning system. (B) Stability diagram of the homogeneous state in the plane of hydrodynamic length $λ$ and active tension measure $\bar{σ}$ (see Appendix). The homogeneous state is unstable within the red region. Blue dot represents the parameter values of the non-RNAi *C. elegans* cortex; error bars denote 95% confidence intervals. (C) Stability diagram for a partial model without NMY-2 recruitment by RhoA; inset: corresponding schematic. The homogeneous state is unstable within the blue region. (D) Dispersion relations of the full mechanochemical patterning system with (red) and without (blue) RhoA mediated NMY-2 recruitment. Lighter shared areas represent 95% confidence intervals. (E) *let-502* RNAi suppresses RhoA mediated recruitment of NMY-2. (F) COMBI diagram for *let-502* RNAi (30 hr), N = 12 embryos. Thin solid magenta (NMY-2) and green (RhoA) lines; numerically determined nullclines. Thick solid dashed lines, linearized nullclines. Light dashed lines, linearized nullclines for the non-RNAi condition (Figure 1H) for comparison. (G) Dispersion relation for *let-502* RNAi, lighter blue area indicates the 95% confidence interval. (H) NMY-2 distribution under *let-502* RNAi. Scale bar; $5 μ m$ .

https://doi.org/10.7554/eLife.19595.007

COMBI determines the average changes of per area myosin concentration ( $c_{m}$ ) and of active RhoA concentration ( $c_{r})$ due to turnover/regulation and as a function of the concentrations of both species. This provides us with information of the reaction kinetics of RhoA $(R_{r} (c_{r}, c_{m}))$ and myosin $(R_{m} (c_{r}, c_{m}))$ in the myosin and active RhoA concentration phase space (Figure 1G). We determined $c_{m}$ and $c_{r}$ every 5 s by spinning-disk confocal microscopy (Materials and methods). Advective fluxes account for the effects of dilution/enrichment by divergent/convergent gel flow, and these were determined by measuring the velocity field of cortical flow by particle image velocimetry (PIV), an image-based crosscorrelation analysis (Mayer et al., 2010; Raffel et al., 2007) that quantifies the movement of interrogation areas between two sequential timelapse images (Materials and methods). The spatial resolution of the velocity field is determined by the spacing of the interrogation areas which we choose as $1.26 μ m$ . This is sufficiently smaller than the correlation length of cortical flow (the hydrodynamic length is ∼14 μm [Mayer et al., 2010; Saha et al., 2016]), hence, COMBI can provide information on actomyosin homeostasis by determining the average reaction kinetics on a timescale of seconds and a length scale of microns.

We visualize the reaction terms determined by COMBI in a vector field that illustrates the average evolution of concentrations of both species (Figure 1H). This reveals interesting features, for example a trajectory that starts with high active RhoA and low myosin levels will overshoot in its level of myosin prior to approaching the single stable fixed point (thick black line in Figure 1—figure supplement 2A). Key aspects of these dynamics can be captured by a nullcline analysis (Izhikevich, 2007). Reaction terms are zero on a nullcline ( $R_{r} = 0$ for active RhoA, Figure 1H, solid green line; and $R_{m} = 0$ for myosin, Figure 1H, solid magenta line), which describes the concentration that a species would achieve when the concentration of the other species is fixed. This reveals that active RhoA recruits myosin (Figure 1H, solid magenta line) (Motegi and Sugimoto, 2006; Schonegg and Hyman, 2006) while RhoA activation kinetics is essentially independent of myosin levels (Figure 1H, solid green line). The full kinetic landscape can be linearized over its entire range (Figure 1H, dashed lines; Figure 1—figure supplement 2B–D), capturing global aspects of RhoA-based myosin recruitment. To conclude, COMBI can provide insight into the cortical kinetics over a broad range of myosin and active RhoA concentrations.

Given our kinetic analysis, we next sought to test if the full mechanochemically coupled system is indeed unstable. We describe the actomyosin cortex as a thin film of an active gel (Simha and Ramaswamy, 2002; Kruse et al., 2004; Ahmadi et al., 2006; Salbreux et al., 2009), with active tension generation by myosin under control of RhoA (Figure 2A; see Appendix for details). We measured the relevant material parameters of the gel in vivo directly from laser ablation experiments (hydrodynamic length: $λ = 14.3 μ m$ , and a conversion factor from NMY-2 intensity to active tension, $ζ^{'} = 24.9 μ m^{2} / s$ )(Saha et al., 2016). This allowed us to perform a linear stability analysis of the homogeneous state for the full model of the mechanochemical patterning system, with the above determined and linearized reaction kinetics between active RhoA and NMY-2 (Figure 1H). Figure 2B shows the corresponding stability diagram as a function of both the hydrodynamic length of the cortex $λ$ and the active tension measure $\bar{σ}$ (see Appendix for detail). Notably, the homogeneous state, in which all concentrations are constant in space, always becomes unstable above a critical value of the active tension. Furthermore, we find that the parameter values of the C. elegans cortex are such that the system is close to the transition line between stable and unstable, but placed within the unstable regime (Figure 2B). Hence, our analysis is consistent with the actomyosin cortex in C. elegans being unstable and poised to form a spatial pattern.

Our theory predicts that the contractile instability depends on the strength of positive feedback, and thus the amount of recruitment of myosin by active RhoA (Figure 2C,D). Hence, we asked if suppression of RhoA mediated recruitment of myosin in the C. elegans zygote prevents the instability and results in a homogeneous NMY-2 distribution. LET-502 is the Rho-associated protein kinase that phosphorylates the regulatory myosin light chain, MLC-4, to activate NMY-2 (Piekny and Mains, 2002). Hence, reducing the concentration of LET-502 by RNAi should suppress RhoA mediated recruitment of myosin to the cortex. Indeed, COMBI analysis of let-502 RNAi embryos (30 hr) revealed that RhoA mediated recruitment of NMY-2 to the cortex is reduced, since the myosin nullcline displays a significantly decreased slope as compared to the non-RNAi condition (Figure 2E,F; see Table 1). Using the non-RNAi values of $λ$ and $ζ^{'}$ and the linearized reaction kinetics between active RhoA and NMY-2 measured by COMBI in let-502 RNAi (dark dashed lines in Figure 2F), we find that the cortex is predicted to be stable because all eigenvalues are negative (Figure 2G, compare to D; see Appendix for detail). Consistent with this prediction, we observed that let-502 RNAi embryos display a homogeneous NMY-2 distribution without pulsatory myosin foci (Figure 2H, compare to Figure 1A; Video 2). We conclude that, consistent with COMBI and theory, the actomyosin cortex can be brought into a stable regime by reducing positive feedback via suppressing myosin recruitment by active RhoA.

Table 1

Parameter values.

https://doi.org/10.7554/eLife.19595.010

Parameters*^,†	Value
Determined in this study
Kinetic parameter for non RNAi
$k_{on}^{r}$	$3.96 \pm 0.21 [10^{- 2} / s]$
$k_{off}^{r}$	$4.54 \pm 0.244 [10^{- 2} / s]$
$k_{on}^{mr}$	$0.0576 \pm 0.0934 [10^{- 2} / s]$
$k_{on}^{m}$	$0.126 \pm 0.389 [10^{- 2} / s]$
$k_{on}^{rm}$	$9.94 \pm 0.435 [10^{- 2} / s]$
$k_{off}^{m}$	$10.1 \pm 0.269 [10^{- 2} / s]$
Kinetic parameter for let-502 RNAi
$k_{on}^{r}$	$2.87 \pm 0.105 [10^{- 2} / s]$
$k_{off}^{r}$	$4.39 \pm 0.0979 [10^{- 2} / s]$
$k_{on}^{mr}$	$0.178 \pm 0.178 [10^{- 2} / s]$
$k_{on}^{m}$	$3.56 \pm 0.165 [10^{- 2} / s]$
$k_{on}^{rm}$	$1.81 \pm 0.0938 [10^{- 2} / s]$
$k_{off}^{m}$	$7.49 \pm 0.106 [10^{- 2} / s]$
$D_{r}, D_{m}$	$0.01 [μ m^{2} / s]$
Determined in Saha et al.,
$λ$	$14.3 \pm 2.94 [μ m]$
$ζ / γ$	$24.8 \pm 8.62 [μ m^{2} / s]$
Parameter values for complex Swift-Hohenberg equation
$a$	$0.25$
$b$	$0.0000490$
$d_{1}$	$1.00 + 0.2 i$
$d_{2}$	$0.0297 + 0.00400 i$
$f_{0}$	$0.4$
$f_{1}$	$0.00247$
$q_{0}$	$10.1$

*Parameter values are shown with 95 % confidence intervals.
^†Active RhoA and NMY-2 densities are normalized by their average concentrations, and reported in dimensionless units of fluorescence intensities per unit area of $1 {[pixel]}^{2}$ , corresponding to $0.0110 μ m^{2}$ .

Video 2

Download asset

We next asked if the patterns that are formed in the unstable regime in our theory correspond to the pattern of myosin foci observed in the embryo. Earlier work that considers a cortical gel with a diffusible activator of myosin (Bois et al., 2011; Kumar et al., 2014) suggests that a contractile instability results in a myosin foci pattern with a spacing that is determined by the hydrodynamic length $λ$ . Indeed, a numerical solution of the full mechanochemical patterning system (Figure 2A) reveals the formation of a few dynamic contracting regions which travel and are spaced about $2 λ$ apart (Figure 3—figure supplement 1, Video 3). These traveling peaks have rapid flows converging upon them (peak flow speed: $0.7 μ m / s$ ), and they persist and are not pulsatile. This pattern is different from the myosin foci pattern observed in the C. elegans zygote, which is pulsatile and exhibits a shorter spacing between foci ( $\sim 5 μ m$ , compare to $λ = 14.3 μ m$ ; see Figure 3—figure supplement 1) (Munro et al., 2004; Mayer et al., 2010). This suggests that our model is missing an essential feature, which is responsible for determining the myosin pattern beyond the contractile instability.

Video 3

Download asset

To identify the element missing in our model, we note that our theory predicts that reducing myosin recruitment by let-502 RNAi should cause both myosin and RhoA to be homogeneous and non-pulsatile (all eigenvalues are negative, see Figure 2G). However, imaging active RhoA under let-502 RNAi revealed that while the pulsatile myosin pattern is lost, the pulsatile active RhoA pattern is still present (Figure 3A,C; Video 4). Similarly, we find that 16 hr of RNAi of nmy-2 led to an almost complete loss of cortical myosin with, however, active RhoA still forming pulsatile foci (Figure 3B,D; Video 5). We conclude that, in contrast to the scenario in Drosophila germband extension (Munjal et al., 2015), active RhoA in C. elegans exhibits pulsatile foci dynamics independently of NMY-2 function. Importantly, both the characteristic spacing of the myosin-independent active RhoA pattern and its characteristic timescale were similar between nmy-2 RNAi, let-502 RNAi, and the non-RNAi condition (Figure 3E,F). Given that active RhoA in the wild-type acts to recruit myosin (Figure 1H), this raises the possibility that the myosin-independent dynamic active RhoA pattern is responsible for setting the myosin spatiotemporal pattern beyond the contractile instability. We conclude that the dynamic active RhoA pattern is generated in a manner that is independent of the myosin foci pattern, possibly through an independent RhoA spatiotemporal oscillator.

Oscillatory activities of Rho GTPases have previously been observed (Hwang et al., 2005; Miller and Bement, 2009; Das et al., 2012; Antoine-Bertrand et al., 2016). We next asked if this spatiotemporal oscillator requires ect-2, a RhoGEF, responsible in the early morphogenesis (Motegi and Sugimoto, 2006; Schonegg and Hyman, 2006). Indeed, RNAi of ect-2 leads to a complete absence of RhoA pulsation (Video 6). Furthermore, it is interesting to speculate if the myosin-independent active RhoA oscillator that we identify here is related to the RhoA/actin-based excitable oscillatory system reported previously (Bement et al., 2015; Westendorf et al., 2013). To test if the underlying mechanism to generate myosin-independent active RhoA oscillator is shared between C. elegans single-cell embryo and Xenopus embryo, we used COMBI to investigate the effective kinetic regulation between active RhoA and actin. We used LifeAct tagRFP-T as a probe for filamentous actin in the cortex (Riedl et al., 2008; Reymann et al., 2016). We determined the kinetic diagram in the active RhoA and actin concentration phase plane, to quantitatively evaluate the rate constants in the effective kinetic equations (Figure 1—figure supplement 3A). We find that the active RhoA nullcline is nearly vertical and inconsistent with actin behaving as a negative regulator of RhoA. Note that this does not exclude the general possibility of negative feedback between actin and RhoA (Robin et al., 2016), but suggests that the C. elegans cortex is normally operating in a regime where no such negative feedback is accessed. While the detailed mechanism as well as the kinetic interactions that underlie RhoA pulsation in C. elegans remain to be determined, the RhoGEF ect-2 is involved and the system appears to undergo spatiotemporal oscillations in the absence of negative feedback between actin and RhoA.

Figure 3 with 2 supplements see all

Download asset Open asset

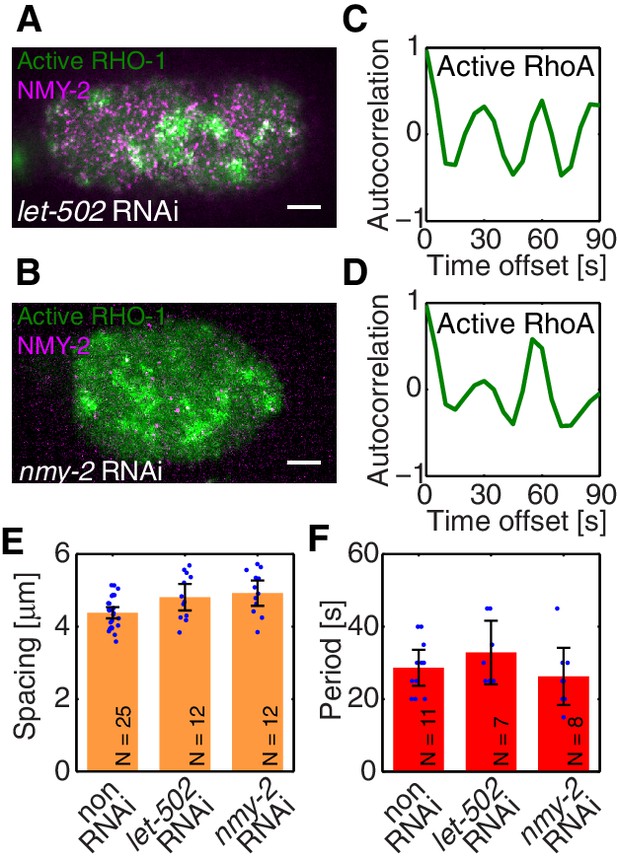
Active RhoA exhibits pulsatory dynamics under conditions of reduced myosin activity.

(**A,B**) AHPH::GFP (green) and NMY-2::RFP (magenta) in (A) a representative *let-502* RNAi and (B) a representative *nmy-2* RNAi embryo. (**C,D**) Normalized AHPH::GFP intensity change autocorrelation (C) for (A) and (D) for B, obtained within the posterior. (**E,F**) Characteristic (E) spacing of AHPH patterns and (F) period of AHPH intensity change in non-RNAi, *nmy-2* RNAi, and *let-502* RNAi embryos. Scale bars, $5 μ m$ .

https://doi.org/10.7554/eLife.19595.013

Video 4

Download asset

Video 5

Download asset

Video 6

Download asset

We next sought to test in our theory if it is possible that an active RhoA spatiotemporal oscillator sets the myosin pattern beyond the contractile instability (Figure 4A, left). To this end, we described the dynamical behavior of an active RhoA pacemaker by use of a generic model of spatiotemporal oscillating patterns, the complex Swift-Hohenberg Equation (Figure 4—figure supplement 1A) (Sakaguchi, 1997). Importantly, coupling in our model this generic spatiotemporal oscillator ( $30 s$ characteristic timescale, $5 μ m$ characteristic length scale, Figure 3E,F; see Appendix for detail) to the full mechanochemical patterning system does not destroy the active RhoA spatiotemporal oscillator pattern. Instead our model predicts that the myosin pattern (which in the absence of the generic oscillator formed a single traveling peak, see Figure 3—figure supplement 1) now follows that of the active RhoA spatiotemporal oscillator (Figure 4B left). Hence, the active RhoA oscillator can determine the myosin pattern in the unstable regime (Video 7). As a consequence, controlling the myosin pattern also results in reduced cortical flow speeds (peak flow speed: $0.17 μ m / s$ ) as compared to the case where the RhoA oscillator is absent ( $0.7 μ m / s$ , see above). However, we find that the ability of the RhoA oscillator to control the myosin pattern critically depends on the level of mechanochemical feedback. We demonstrate this by reducing the hydrodynamic length in our model, which increases overall flow speeds and advection, and thereby increases the mechanochemical feedback strength. We find in our model that this change destroys the pattern of the active RhoA spatiotemporal oscillator. Both the myosin and active RhoA pattern no longer form a regular spatiotemporal oscillation (Figure 4—figure supplement 1, $λ$ is reduced by $5 μ m$ to $9 μ m$ ). Instead, the system displays a dynamical state that is characterized by an irregular spatiotemporal pattern of dynamic contracting regions that move rapidly (Figure 4B right; Figure 4—figure supplement 1; Video 8). In this state, the pattern of active RhoA now depends on myosin and flows and is essentially under control of the contractile instability. Finally, flow speeds are again increased and comparable to the case when the RhoA oscillator is absent (peak flow speed: $0.94 μ m / s$ ). In conclusion, theory indicates that the active RhoA oscillator can act as a pacemaker for the system, to control the contractile instability and to prevent the formation of large and irregularly moving contracting regions of myosin.

Figure 4 with 1 supplement see all

Download asset Open asset

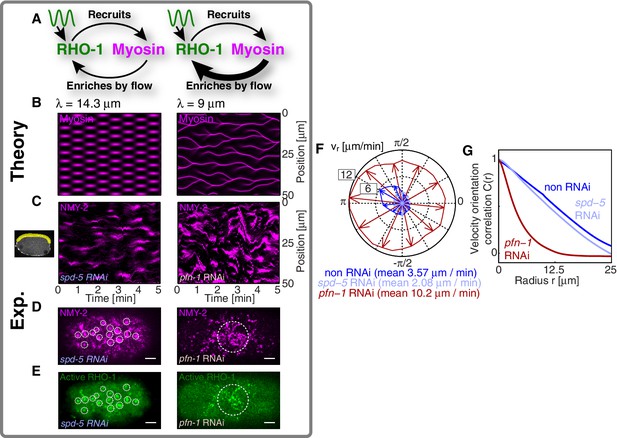
A RhoA pacemaking oscillator controls the contractile instability.

(A) Schematic of a mechanochemical patterning system under control of a RhoA pacemaker, with (left) normal conditions and (right) with increased mechanochemical feedback and with faster flows. (B) Numerically obtained space time plots of the myosin distribution, for normal conditions ( $λ = 14.3 μ m$ ; left) and for a weakened cortex with increased mechanochemical feedback ( $λ = 9 μ m$ ; right); see Appendix. (C) Kymographs of NMY-2 intensity under normal conditions (*spd-5* RNAi; left) and under conditions of a weakened cortex (*pfn-1* RNAi; right) obtained in mid-plane images and from the yellow region illustrated in the inset image on the right. (**D,E**) Representative cortical plane images of (D) NMY-2::tagRFP-T and (E) RhoA::GFP, dotted circles indicate foci. (F) Average cortical flow speed as a function of direction under conditions of a normal cortex (dark blue: non-RNAi; light blue: *spd-5* RNAi) as well as for a weakened cortex (red: *pfn-1* RNAi). (G) Radially averaged velocity orientation correlation function (Materials and methods) for the same three conditions, note that the *pfn-1* RNAi embryo cannot drive coherent flow over large distances. Scale bars, $5 μ m$ .

https://doi.org/10.7554/eLife.19595.019

Video 7

Download asset

Video 8

Download asset

We next sought to seek experimental evidence that the myosin pattern in the C. elegans zygote is under control of the RhoA pacemaker. To this end, we tested if increasing the level of mechanical feedback in C. elegans destroys the pattern of the active RhoA spatiotemporal oscillator as predicted from theory. For this we recorded space-time patterns of myosin in a midplane section under conditions of spd-5 RNAi. SPD-5 is a centriole constituent that is essential for centriole maturation (Hamill et al., 2002), and its RNAi leads to a delay of polarizing flows which gives us more time for an analysis of the pulsatory dynamics. To increase mechanochemical feedback we recorded space-time patterns of myosin under RNAi of the actin nucleator pfn-1 (Severson et al., 2002) for which the cortex is weakened and flow speeds are increased by a factor of three to five (Figure 4F) and for which the hydrodynamic length is decreased by $5 μ m$ to $9 μ m$ (Severson et al., 2002; Naganathan, unpublished). For spd-5 RNAi, we observed the ’normal’ pulsating pattern of myosin foci (Figure 4C left; Video 9 and Video 10). In contrast, for pfn-1 RNAi we observed large contracting regions of myosin that rapidly move in an irregular fashion (Figure 4C right, D right; Videos 9 and 11). Importantly, in pfn-1 RNAi active RhoA assembles in large and irregularly moving foci structures (Figure 4E right, compare to Figure 4E left and Figure 3A,C; Video 11). This suggests that the normal pattern of the active RhoA spatiotemporal oscillator is destroyed, and the distribution of active RhoA is now governed by the irregular dynamics of myosin. Note that pfn-1 RNAi does not destroy the general ability of RhoA to generate a pulsating pacemaker pattern, as revealed by double RNAi of pfn-1 and nmy-2 (Video 12). We conclude that reducing the hydrodynamic length increases mechanochemical feedback and advection. This causes the RhoA pacemaker to lose the ability to control the contractile instability. Consistent with the predictions of our theory, this destroys the RhoA pacemaker pattern and causes the system to undergo a transition to irregular behavior with large and rapidly moving contracting regions (Figure 4C–E). Interestingly, the uncontrolled gel is no longer capable to drive coherent flows of the cortex over large distances (Figure 4G), and the embryo fails to polarize (Severson et al., 2002). Taken together, our quantitative analysis is consistent with the interpretation that the spatiotemporal RhoA oscillator acts as a pacemaker in C. elegans, controlling the contractile instability of the actomyosin cortex.

Video 9

Download asset

Video 10

Download asset

Video 11

Download asset

Video 12

Download asset

We have here investigated the mechanisms of pattern formation in an active system that combines the contractile force generation and flow with regulation and advection. For this, we introduced the COMBI method to directly infer reaction kinetics without relying for example on photobleaching (Sprague et al., 2004). We determined the effective reaction kinetics of myosin and active RhoA in the actomyosin cortex with COMBI. This allowed us to build a quantitative model of mechanochemical patterning in the actomyosin layer. By use of linear stability analysis, we found that the actomyosin cortex is unstable and spontaneously forms a self-organized pattern. We speculate that during embryogenesis cells need high cortical contractility to drive morphological changes. This can lead them near or beyond contractile instabilities, leading to dynamics characterized by strong fluctuations and irregular behavior, possibly exhibiting active turbulence (Giomi, 2015). We suggest that such instabilities are inevitable in dynamic systems that are highly contractile. We discovered a spatiotemporal RhoA oscillator that determines the myosin pattern even beyond the contractile instability, thereby controlling the contractile instability. The independent biochemical RhoA oscillator endows the cell with the ability to use an intrinsically unstable active contractile medium for driving morphogenetic processes such as polarization. To conclude, our work paves the way for understanding pattern formation in active biological materials that utilize potentially unstable contractile processes.

Materials and methods

Worm strains, maintenance, and sample preparation

Request a detailed protocol

The following transgenic lines were used in this study. SWG003: nmy-2(cp8[nmy-2::GFP + unc-119(+)]) I; unc-119(ed3) III; gesIs002[Ppie-1::Lifeact::tagRFP-T::pie-1UTR + unc-119(+)], for imaging of GFP labelled NMY-2 (the images shown in Figure 1A and B and in Figure 4C). SWG012: nmy-2(ges6[nmy-2::tagRFP-T + unc-119(+)]) I; xsSi5[cb-UNC-119 (+) GFP:: ANI-1 (AH+PH)] II; unc-119(ed3) III, for imaging of tagRFP-T labelled NMY-2 and GFP labelled AHPH for a probe of active RhoA in the cortex (the images shown in Figure 1F, in Figure 2H, and in Figure 3A and B).

Worm strains were maintained at 20°C, and shifted to 24°C for 24 hr before imaging. Embryos were dissected in M9 buffer and mounted onto agar pads (2% agarose in water) to squish the embryos gently. All experiments were performed at 23–24°C. RNA interference experiments were performed by feeding as described in Naganathan et al. (2014). Feeding times for RNAi experiments were 16–18 hr for nmy-2, 23–25 hr for spd-5, 19–21 hr for pfn-1, 19–21 hr for pfn-1;nmy-2 double knockdown and 29–31 hr for let-502. Feeding clones were obtained from the Hyman lab (MPI-CBG, Dresden, Germany).

Imaging

Request a detailed protocol

One-cell stage embryos were observed under the inverted fluorescence microscope (Axio Observer Z1, Zeiss) using a Zeiss C-Apochromat 63 $\times$ water immersion lens, equipped with a spinning disc confocal unit (Yokogawa, CSU-X1) and AOTF laser combiner (Andor, ALC). Fluorescence images were acquired by a sCMOS camera (Hamamatsu, ORCA flash 4.0) at 5 s time intervals for non-RNAi, let-502 RNAi, nmy-2 RNAi, and pfn-1;nmy-2 RNAi embryos. For pfn-1 RNAi embryos, images were taken every 3 s. Pixel size was 0.105 $\times$ 0.105 $μ m^{2}$ , all devices were controlled through $μ -$ manager(Edelstein et al., 2014). Fluorescence images of GFP and tagRFT-T labeled proteins in the embryos were excited by 488 and 561 nm lasers, respectively.

Image analysis

Request a detailed protocol

Prior to COMBI analysis, images were filtered using the nonlocal means method (Buades et al., 2005), reducing spatially uncorrelated noise while preserving finer structures. Filtering was performed by averaging fluorescence intensities on the basis of the similarity between the fluorescence intensity profile in the interrogation area and the intensity profile in the neighboring region, i.e., a searching window. We set the size of the interrogation area and the searching window, to be $5 \times 5$ pixels and $25 \times 25$ pixels, corresponding to 0.525 $\times$ 0.525 $μ m^{2}$ and 2.625 $\times$ 2.625 $μ m^{2}$ , respectively. A filtering parameter, $h$ , was set to be $0.1 s$ for NMY-2 images, $0.3 s$ for AHPH images, where $s$ denotes the standard deviation of the fluorescence intensity in each image. We performed the filtering using a freely available code from MATLAB central (Fast Non-Local Means 1D, 2D Color and 3D by Kroon). Note that it is important to remove spatially uncorrelated noise prior to the computation of the spatial derivatives, since differential value is affected by spatially uncorrelated noises.

To perform COMBI, we first determined the cortical flow velocity, $𝐯 (x, y)$ , by Particle Image Velocimetry (PIV) using a freely available PIV algorithm, PIVlab 1.32 (available from http://pivlab.blogspot.de/). PIV was performed on NMY-2 images by setting the interrogation area as 24 pixels with a step of 12 pixels. Velocity vectors were then interpolated to single pixel resolution for determining $R_{r}$ and $R_{m} .$ $\partial_{t} C_{i}, C_{i} \nabla v$ and $𝐯 \nabla C_{i}$ for both the background subtracted, active RhoA and myosin intensities (denoted by $C_{r}$ and $C_{m}$ , respectively). Intensity background levels were obtained by averaging the intensity in the region outside the embryo. $R_{r}$ and $R_{m}$ were then determined for each pixel throughout the cortical plane, by the use of the mass balance equations given in Figure 1G. We obtained a kinetic diagram (Figure 1H) by averaging $R_{r}$ and $R_{m}$ in $10 \times 10 μ m^{2}$ boxes located in the anterior region. We determined average values for each embryo by averaging over the first 36 frames after the start of polarizing flow. For the non-RNAi case (Figure 1H), we report the average kinetic diagram from $N = 25$ embryos, for let-502 RNAi (Figure 2F) we averaged over $N = 12$ embryos. Note that the active RhoA and NMY-2 concentrations were normalized by the respective mean intensities of active RhoA and NMY-2 under non-RNAi conditions.

Correlation analysis

Request a detailed protocol

To characterize the myosin intensity change, $Δ I (t)$ and the cortical flow speed $v_{r} (t)$ in a box of size $10 \times 10 μ m^{2}$ in the posterior region, we determined the spatial average over the box. We then computed the autocorrelation function

C_{t} (τ) = \frac{{⟨ [f (t)^{2} - \bar{f}] [f (t + τ)^{2} - \bar{f}] ⟩}_{t}}{σ_{f}^{2}},

where $f (t) = Δ I (t)$ or $v_{r} (t)$ , $σ_{f}$ denote the standard deviation of $f (t)$ , and $\bar{f}$ denotes the mean of $f (t)$ , averaged over time $t$ , where ${⟨ ⟩}_{t}$ represents an average over time. $C_{t}$ is mean-subtracted and normalized by the variance of $f (t)$ . The period of oscillation was determined by the peak position in the autocorrelation function. For a precise detection of oscillatory behavior, we removed from our analysis embryos in which the second peak in the autocorrelation function of the time course was undetectable (12 out of 25 cases for non-RNAi embryos, 5 out of 12 cases in let-502 embryos, 4 out of 12 embryos for nmy-2 RNAi embryos, respectively).

We obtained the characteristic length of the spatial pattern of myosin and RhoA by detecting the location of the first peak in the radial spatial intensity correlation function. The spatial intensity autocorrelation function of intensity, $f (x, y, t)$ , was obtained by

C_{s p} (ξ, η, t) = \frac{{⟨ [f (x, y, t)^{2} - \bar{f} (t)] [f (x + ξ, y + η, t)^{2} - \bar{f}] ⟩}_{x, y}}{σ_{f}^{2}},

where $\bar{f} (t)$ denotes the spatial average of $f (x, y, t)$ , see Figure 3—figure supplement 2C. This function was radially averaged, and the first peak was detected (Figure 3—figure supplement 2D) in each time point. The radii of first peak were then averaged over time in each embryo. For the determination of the spacing in AHPH foci, the contrast of the fluorescence images was enhanced using the Contrast Limited Adaptive Histogram Equalization method using Matlab (Mathworks)(see Figure 3—figure supplement 2).

To characterize the spatial coherence of the velocity field, we evaluated the spatial correlation of the normalized velocity vectors, $n (x, y, t) = v (x, y, t) / | | v (x, y, t) | |$ . The spatial correlation function was computed by,

C_{o r i} (ξ, η) = {⟨ n (x, y, t) \cdot n (x + ξ, y + η, t) ⟩}_{x, y, t},

where $\cdot$ represents scalar product, and ${⟨ ⟩}_{x, y}$ denotes the spatial average. Note that the coordinate transformation from Cartesian to polar coordinates of the orientation vectors, $𝐧 (x, y, t)$ , provides a simpler representation of $C_{ori} (ξ, η)$ as,

C_{o r i} (ξ, η) = ⟨ \cos [θ (x, y, t) - θ (x + ξ, y + η, t)] ⟩,

where $θ (x, y, t)$ denotes the anti-clockwise angle from x-axis of $𝐧 (x, y, t)$ . The above expression shows that the $C_{ori} (ξ, η)$ provides spatial correlation of the cosine similarity between $θ (x, y, t)$ and $θ (x + ξ, y + η, t)$ . Therefore, the characteristic length of the decay of $C_{ori} (ξ, η)$ represents the loss of correlation between the directions of velocity vectors, $(ξ, η)$ away. Larger characteristic length of the decay demonstrates the large-scale flow of the cortex.

For visualizing purpose, we transformed the coordinate system from $(ξ, η)$ to polar $(r, ϕ)$ and then determined the average over the angle, $ϕ$ , to plot $C_{ori}$ as a function of the radius, $r$ , e.g. Figure 4G.

Appendix

Active gel description of the cortex

We described the dynamics of the cortical layer on the surface of the zygote by use of a full mechanochemically coupled system containing an active gel description for the cortical layer(Bois et al., 2011; Kumar et al., 2014) together with a reaction-diffusion-advection equation system for active RhoA and NMY-2. For the latter, the concentrations of active RhoA and NMY-2 in one dimension are given by $ρ_{m} (x, t)$ and $ρ_{r} (x, t)$ , respectively, where $x$ denotes position and $t$ denotes time. The dynamics of the 1-D surface concentration vector $𝝆 (x, t) = {[ρ_{m} (x, t), ρ_{r} (x, t)]}^{t}$ is given by

\begin{aligned} (4) & \partial_{t} ρ_{i} (x, t) + \partial_{x} j_{i} (x, t) & = R_{i} (ρ (x, t)) \\ (5) & j_{i} (x, t) = v (x, t) ρ_{i} (x, t) & - D_{i} \partial_{x} ρ_{i} (x, t), \end{aligned}

where $i \in {m, r}$ , with $m$ denoting NMY-2 and $r$ denoting active RhoA. Here, $v (x, t)$ represents the gel velocity field determined by active cortical mechanics, see below. $R_{m} (𝝆 (x, t))$ and $R_{r} (𝝆 (x, t))$ denote the respective fluxes of NMY-2 and active RhoAand from the cytosol onto the surface via turnover and recruitment. $D_{m}$ and $D_{r}$ denote the respective diffusion coefficients of active RhoA and NMY-2. We estimated the surface diffusion coefficients of both active RhoA and myosin, by analyzing FRAP recovery in ANI-1::GFP and NMY-2::GFP by use of a method considers of both turnover and lateral diffusion (Goehring et al., 2010). This revealed in both cases that lateral (surface) diffusion was below the detection limit and undistinguishable from zero. Hence, we expect surface diffusion of myosin and active RhoA to not significantly impact the dynamics of the cortical layer. However, for the purpose of preventing sharp peaks in concentration fields in our numerical simulations, we here set $D_{r} = D_{m} = 0.01 μ m^{2} / s$ . Note that the general results of our numerical analysis do not change when increasing or decreasing either diffusion constant by a factor of 10. Importantly, the fastest growing mode occurs for wavelengths of the order of $λ$ in all cases (Figure 2—figure supplement 1).

We describe forces and flows within the cortical layer in the framework of active gel theory (Bois et al., 2011; Kumar et al., 2014; Kruse et al., 2005; Mayer et al., 2010). We consider the cortex to be a thin film active viscous fluid in 1D, where NMY-2 generates active tension (Bois et al., 2011; Kumar et al., 2014; Mayer et al., 2010). Hence, total tension

$σ$ in the layer is given by a sum of viscous tension arising characterized by a bulk viscosity $η$ , and active tension (or contractility) $σ^{a}$ that depends on myosin concentration acording to $σ^{a} = ζ f (ρ_{m})$ , with $f (ρ_{m})$ and increasing function of the concentration $ρ_{m}$ and $ζ$ a coefficient that determines the magnitude of active tension.

The constitutive equation for an active viscous fluid is then given by Mayer et al. (2010)

σ = η \partial_{x} v (x, t) + σ^{a} (ρ_{m}) .

We choose for $f (ρ_{m})$ a saturating Hill-function, $f (ρ_{m}) = ρ_{m} (ρ_{m0} + 1) / (ρ_{m} + 1)$ (Bois et al., 2011; Kumar et al., 2014), to limit the active stress in our numerical simulations. Here, $ρ_{m0}$ denotes the stationary concentration of NMY-2. Note that choosing a linear dependence without saturation does not significantly change the stability diagram, see Figure 2—figure supplement 2.

The force balance equation for an active viscous fluid in the presence of friction with a coefficient $γ$ between the cortex and its surrounding cytoplasm and cell membrane (Mayer et al., 2010; Bois et al., 2011; Kumar et al., 2014) is given by

\partial_{x} σ = γ v .

Equations 6 and 7 provide an equation of motion

λ \partial_{x}^{2} v + \frac{ζ^{'}}{λ} \partial_{x} f (ρ_{m}) - \frac{1}{λ} v = 0,

where $λ = \sqrt{η / γ}$ represents the hydrodynamic length of the cortex, which sets a correlation length for the velocity field. We determined the parameters $λ$ and $ζ^{'} = \frac{ζ}{γ}$ that characterize the active viscous fluid with a method that compares the relaxation dynamics of the cortex in response to cortical laser ablation (COLA) between experiment and theoretical predictions ( $λ = 14.3 μ m$ , $ζ^{'} = 24.9 μ m^{2} / s$ ) (Saha et al., 2016). Note that we ignored the polar or nematic order of actin filament in the cortex, which can introduce the tension anisotropy. Based on the recent study by Reymann et al. (Reymann et al., 2016), the alignment is mainly due to large-scale cortical flow in one-cell stage C. elegans embryo, which has the highest compressible component and nematic order parameter in the mid-zone of posterior.

Rescaling

We rescale the spatial coordinate with respect to $λ$ , and rewrite Equations 5–7 according to

\begin{array}{l} \tilde{σ} = \partial_{\tilde{x}} \tilde{v} + \tilde{σ^{a}} \\ \partial_{\tilde{x}} \tilde{σ} = \tilde{v} \\ \partial_{t} ρ_{i} + \partial_{\tilde{x}} \tilde{v} ρ_{i} - {\tilde{D}}_{i} \partial_{\tilde{x}}^{2} ρ_{i} = R_{i} (ρ_{m}, ρ_{r}), \end{array}

with the following rescaled quantities

\begin{array}{ll} \tilde{x} & = x / λ \\ \tilde{v} & = \frac{v}{λ} \\ \tilde{σ} & = \frac{σ}{λ^{2} γ} \\ \tilde{σ^{a}} & = \frac{ζ}{λ^{2} γ} f (ρ_{m}) \\ {\tilde{D}}_{i} & = \frac{D}{λ^{2}} . \end{array}

We performed numerical integrations of Equation 9 with periodic boundary conditions by use of the pseudospectral method (Boyd, 2001).

Linear stability analysis

The homogeneous state with the concentrations $𝝆_{𝟎} = {(ρ_{r0}, ρ_{m0})}^{t}$ and a vanishing flow field $v (x, t) = 0$ can be a stationary state of the system. To test the stability of this stationary state, we apply a small perturbation of $δ ρ = ρ_{0} + δ ρ_{0} e^{2 π i ν x + α (ν) t}$ , where $ν$ and $α$ denote spatial frequency and eigenvalue, respectively. Inserting $𝜹 𝝆$ into Equation 9 and retaining linear terms only, the linear stability matrix $𝐀$ with respect to the perturbation $𝜹 𝝆$ becomes

\begin{aligned} (10) & A = & 4 π^{2} ν^{2} [\begin{matrix} - {\tilde{D}}_{r} & 0 \\ 0 & - {\tilde{D}}_{m} \end{matrix}] + \frac{4 π^{2} ν^{2} \tilde{ζ} \partial_{ρ_{m}} f (ρ_{m 0})}{4 π^{2} ν^{2} + 1} [\begin{matrix} 0 & ρ_{r 0} \\ 0 & ρ_{m 0} \end{matrix}] + Ω \\ (11) & Ω = & [\begin{matrix} \partial_{ρ_{r}} R_{r} (ρ_{0}) & \partial_{ρ_{m}} R_{r} (ρ_{0}) \\ \partial_{ρ_{r}} R_{m} (ρ_{0}) & \partial_{ρ_{m}} R_{m} (ρ_{0}) \end{matrix}], \end{aligned}

where $\tilde{ζ} = ζ / λ^{2} γ$ . To determine the linearized matrix $𝛀$ that characterizes biochemical regulation of NMY-2 and active RhoA, we performed a linear regression over the whole range of $R_{r}$ and $R_{m}$ values determined by COMBI (Figure 1H in main text) using

\begin{array}{ll} R_{r} (c_{r}, c_{r m}) & = k_{o n}^{r} - k_{o f f}^{r} c_{r} + k_{o n}^{m r} c_{m} \\ R_{m} (c_{r}, c_{r m}) & = k_{o n}^{m} + k_{o n}^{r m} c_{r} - k_{o f f}^{m} c_{m} . \end{array}

Here, $c_{r}$ and $c_{m}$ denote the normalized intensities of AHPH and NMY-2, respectively, with $[c_{r}, c_{m}] = [ρ_{r}, ρ_{m}]$ . We get

𝛀 = [\begin{matrix} - k_{off}^{r} & k_{on}^{mr} \\ k_{on}^{rm} & - k_{off}^{m} \end{matrix}] .

We determined the matrix $𝛀$ directly from our experimental data (Figure 1H in main text) by robust regression and using standard deviations for weights, and find

𝛀 = [\begin{matrix} - 0.0454 & 0.000576 \\ 0.0994 & - 0.101 \end{matrix}] .

Please see Figure 1—figure supplement 2 for a comparison between the linearized and full landscapes. The corresponding eigenvalues of $𝛀$ are $α = - 0.102, - 0.0444$ . Both of these are negative and real, indicating that the fixpoint is a sink.

The stability diagram shown in Figure 2B in the main text was obtained in the plane of hydrodynamic length $λ$ and the active tension (or contractility) measure $\bar{σ} = ζ^{'} f (c_{m}^{⋆})$ , where $c_{m}^{⋆}$ denotes the stationary concentration of $c_{m}$ in the homogeneous state.

Pulsatile dynamics of active RhoA

Phenomenological description of the pulsatory dynamics

To investigate if an active RhoA pacemaking oscillator can control the contractile instability and determine the myosin pattern, we describe active RhoA pulsation dynamics by an oscillating standing wave. For this, we utilize a generic spatiotemporal oscillator, the complex Swift-Hohenberg equation (Cross and Hohenberg, 1993; Sakaguchi, 1997). We introduce a complex variable $ψ (x, t)$ , the real part of which represents the concentration of active RhoA, $ℜ [ψ (x, t)] = ρ_{r} (x, t)$ . We write a conservation law for $ψ (x, t)$ according to

\begin{array}{ll} \partial_{t} ψ (x, t) & = - \partial_{x} j_{r} + R_{S H} (ψ (x, t) - ρ_{r 0} (x, t)), \\ j_{r} = ℜ [ψ (x, t)] v + D_{r} \partial_{x} ℜ [ψ (x, t)] \end{array}

with

\begin{array}{ll} R_{S H} (ψ (x, t)) = & (a + i f_{0}) ψ (x, t) - b (q_{0}^{2} + \partial_{x}^{2})^{2} ψ (x, t) \\ + i f_{1} \partial_{x}^{2} ψ (x, t) - d_{1} | ψ (x, t) |^{2} ψ (x, t) \\ - d_{2} | \partial_{x} ψ (x, t) |^{2} ψ (x, t) . \end{array}

Here, $R_{SH}$ is the pacemaking oscillator term using the complex Swift-Hohenberg equation, while $a, b, d_{1}, d_{2}, f_{0}, f_{1}$ and $q_{0}$ are phenomenological coefficients that determine the spatiotemporal dynamics of $ψ (x, t)$ .

We chose a set of parameter values that is based on (Sakaguchi, 1997) and that gives rise to an oscillating pattern that is similar to the active RhoA oscillation shown in Figure 3 of the manuscript, with a characteristic length-scale of $5 μ m$ and a characteristic time-scale of 60 s ( i,e. the half-period corresponds to the active RhoA oscillation period). We find that the occurrence of a transition from a pacemaker- entrained state (i.e. the myosin pattern is determined by the pattern of the active RhoA pacemaker) to a detrained state (i.e. the active RhoA pattern is destroyed and now determined by cortical mechanics and myosin) is not sensitive to the detailed characteristics of the pacemaking oscillator, e.g. its amplitude, period, and spacing. For large hydrodynamic lengths $λ$ , the myosin pattern is entrained to the active RhoA pulsatility. As we decrease $λ$ , the period of myosin pattern oscillation increases, due to increasing amounts of accumulation of myosin and active RhoA at the myosin foci by advection. At intermediate values of $λ$ around $\sim 12 μ m$ , we observed a transition from the entrained state to the detrained state. Here, the dynamical pattern is characterized by irregular movements and ‘mechanochemical turbulence’ (Figure 4 in main text, Figure 4—figure supplement 1), and depends on a both flow and advection as well as the active RhoA pacemaking activity.

Associated time-scales

To provide an intuitive understanding of entrainment-detrainment transition, we compare characteristic time-scales of advection and biochemical regulations. First we obtain an advection time-scale, $τ_{adv}$ , by solving Equation 8 for $\partial_{x} f (ρ_{m}) = δ (x - x_{0})$ , where $δ (x)$ is Dirac’s delta function. For the infinite interval, $- \infty < x < \infty$ , and a no-flux boundary condition, $v (\pm \infty, t) = 0$ , the velocity profile, $v_{0} (x)$ , is given by

v_{0} (x) = \frac{ζ}{2 λ γ} \exp (- \frac{| x - x_{0} |}{λ}) .

hence, the velocity decay over space is characterized by the hydrodynamic length $λ$ , while the magnitude of velocity is set by $V_{c} = \frac{ζ}{2 λ γ}$ . We obtain a time-scale for advection as

τ_{adv} \sim \frac{λ}{V_{c}} = \frac{2 γ λ^{2}}{ζ},

which specifies the time required for the thin film active fluid to advect biochemical regulators over the characteristic length $λ$ .

Next, we introduce a characteristic time-scale of biochemical regulation as $τ_{R} = {(\partial R_{m} / \partial ρ_{r})}^{- 1} = {k_{o n}^{r m}}^{- 1} \sim 10 s$ . If $τ_{adv} ≫ τ_{R}$ , the RhoA pacemaking oscillator controls the dynamics of the full mechanochemical patterning system, and advection plays a minor role. In this case, NMY-2 dynamics are entrained to the pulsatory dynamics of the active RhoApacemaker. In contrast to this, flow and advection dominate the dynamics of the full mechanochemical patterning system when $τ_{adv} ≪ τ_{r}$ . Here, the regularly oscillating pacemaker pattern of active RhoAis destroyed due to increased advection, leading to irregular spatiotemporal dynamics and ‘mechanochemical turbulence’.

In the zygote, we find that for the non-RNAi case that $τ_{a d v} = 16.5 s$ is larger than $τ_{R} \sim 10 s$ . Thus the myosin pattern is entrained to the active RhoA pulsatory dynamics. On the other hand, we find that for the pfn-1 RNAi case that $τ_{a d v} = 6.5 s$ , which is smaller than $τ_{R}$ . Hence, we observe irregular behavior (Figure 4B, right, in the main text).

References

1. Aditi Simha R
2. Ramaswamy S
(2002) Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles
Physical Review Letters 89:058101.
https://doi.org/10.1103/PhysRevLett.89.058101
- PubMed
- Google Scholar
(2006) Hydrodynamics of isotropic and liquid crystalline active polymer solutions
Physical Review E 74:061913.
https://doi.org/10.1103/PhysRevE.74.061913
- Google Scholar
(2013) Molecular motors robustly drive active gels to a critically connected state
Nature Physics 9:591–597.
https://doi.org/10.1038/nphys2715
- Google Scholar
(2016) Direct measurement of oscillatory RhoA activity in embryonic cortical neurons stimulated with the axon guidance cue netrin-1 using fluorescence resonance energy transfer
Biology of the Cell 108:115–126.
https://doi.org/10.1111/boc.201500077
- PubMed
- Google Scholar
1. Bement WM
2. Leda M
3. Moe AM
4. Kita AM
5. Larson ME
6. Golding AE
7. Pfeuti C
8. Su KC
9. Miller AL
10. Goryachev AB
11. von Dassow G
(2015) Activator-inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium
Nature Cell Biology 17:1471–1483.
https://doi.org/10.1038/ncb3251
- PubMed
- Google Scholar
(2000) Analysis of cortical flow models in vivo
Molecular Biology of the Cell 11:2553–2563.
https://doi.org/10.1091/mbc.11.8.2553
- PubMed
- Google Scholar
(2011) Pattern formation in active fluids
Physical Review Letters 106:028103.
https://doi.org/10.1103/PhysRevLett.106.028103
- PubMed
- Google Scholar
Book
1. Boyd JP
(2001)
Chebyshev and fourier spectral methods

Courier Corporation.
- Google Scholar
1. Bray D
2. White JG
(1988) Cortical flow in animal cells
Science 239:883–888.
https://doi.org/10.1126/science.3277283
- PubMed
- Google Scholar
Conference
1. Buades A
2. Coll B
3. More J
(2005) A non-local algorithm for image denoising
IEEE Computer Society Conference on Computer Vision and Pattern Recognition. pp. 60–65.
https://doi.org/10.1109/CVPR.2005.38
- Google Scholar
1. Cheeks RJ
2. Canman JC
3. Gabriel WN
4. Meyer N
5. Strome S
6. Goldstein B
(2004) C. elegans PAR proteins function by mobilizing and stabilizing asymmetrically localized protein complexes
Current Biology 14:851–862.
https://doi.org/10.1016/j.cub.2004.05.022
- PubMed
- Google Scholar
1. Cross MC
2. Hohenberg PC
(1993) Pattern formation outside of equilibrium
Reviews of Modern Physics 65:851–1112.
https://doi.org/10.1103/RevModPhys.65.851
- Google Scholar
1. Das M
2. Drake T
3. Wiley DJ
4. Buchwald P
5. Vavylonis D
6. Verde F
(2012) Oscillatory dynamics of Cdc42 GTPase in the control of polarized growth
Science 337:239–243.
https://doi.org/10.1126/science.1218377
- PubMed
- Google Scholar
(2014) Advanced methods of microscope control using μmanager software
Journal of Biological Methods 1:e10.
https://doi.org/10.14440/jbm.2014.36
- PubMed
- Google Scholar
(2006) Animal cytokinesis: from parts list to mechanisms
Annual Review of Biochemistry 75:543–566.
https://doi.org/10.1146/annurev.biochem.74.082803.133425
- PubMed
- Google Scholar
1. Giomi L
(2015) Geometry and topology of turbulence in active nematics
Physical Review X 5:031003.
https://doi.org/10.1103/PhysRevX.5.031003
- Google Scholar
(2010) FRAP analysis of membrane-associated proteins: lateral diffusion and membrane-cytoplasmic exchange
Biophysical Journal 99:2443–2452.
https://doi.org/10.1016/j.bpj.2010.08.033
- PubMed
- Google Scholar
1. Goehring NW
2. Trong PK
3. Bois JS
4. Chowdhury D
5. Nicola EM
6. Hyman AA
7. Grill SW
(2011) Polarization of PAR proteins by advective triggering of a pattern-forming system
Science 334:1137–1141.
https://doi.org/10.1126/science.1208619
- PubMed
- Google Scholar
1. Gowrishankar K
2. Ghosh S
3. Saha S
4. Rumamol C
5. Mayor S
6. Rao M
(2012) Active remodeling of cortical actin regulates spatiotemporal organization of cell surface molecules
Cell 149:1353–1367.
https://doi.org/10.1016/j.cell.2012.05.008
- PubMed
- Google Scholar
1. Guo S
2. Kemphues KJ
(1996) A non-muscle myosin required for embryonic polarity in Caenorhabditis elegans
Nature 382:455–458.
https://doi.org/10.1038/382455a0
- PubMed
- Google Scholar
(2002) Centrosome maturation and mitotic spindle assembly in C. elegans require SPD-5, a protein with multiple coiled-coil domains
Developmental Cell 3:673–684.
https://doi.org/10.1016/S1534-5807(02)00327-1
- PubMed
- Google Scholar
1. Hannezo E
2. Dong B
3. Recho P
4. Joanny JF
5. Hayashi S
(2015) Cortical instability drives periodic supracellular actin pattern formation in epithelial tubes
PNAS 112:8620–8625.
https://doi.org/10.1073/pnas.1504762112
- PubMed
- Google Scholar
1. Hird SN
2. White JG
(1993) Cortical and cytoplasmic flow polarity in early embryonic cells of Caenorhabditis elegans
The Journal of Cell Biology 121:1343–1355.
https://doi.org/10.1083/jcb.121.6.1343
- PubMed
- Google Scholar
(2011) Turing's next steps: the mechanochemical basis of morphogenesis
Nature Reviews Molecular Cell Biology 12:400–406.
https://doi.org/10.1038/nrm3120
- PubMed
- Google Scholar
1. Hwang JU
2. Gu Y
3. Lee YJ
4. Yang Z
(2005) Oscillatory ROP GTPase activation leads the oscillatory polarized growth of pollen tubes
Molecular Biology of the Cell 16:5385–5399.
https://doi.org/10.1091/mbc.E05-05-0409
- PubMed
- Google Scholar
Book
1. Izhikevich EM
(2007)
Dynamical Systems in Neuroscience

MIT press.
- Google Scholar
(2006) CYK-4/GAP provides a localized cue to initiate anteroposterior polarity upon fertilization
Science 313:1298–1301.
https://doi.org/10.1126/science.1130291
- PubMed
- Google Scholar
1. Jülicher F
2. Kruse K
3. Prost J
4. Joanny J
(2007) Active behavior of the cytoskeleton
Physics Reports 449:3–28.
https://doi.org/10.1016/j.physrep.2007.02.018
- Google Scholar
1. Kondo S
2. Asal R
(1995) A reaction-diffusion wave on the skin of the marine angelfish Pomacanthus
Nature 376:765–768.
https://doi.org/10.1038/376765a0
- PubMed
- Google Scholar
1. Kruse K
2. Joanny JF
3. Jülicher F
4. Prost J
5. Sekimoto K
(2004) Asters, vortices, and rotating spirals in active gels of polar filaments
Physical Review Letters 92:078101.
https://doi.org/10.1103/PhysRevLett.92.078101
- PubMed
- Google Scholar
1. Kruse K
2. Joanny JF
3. Jülicher F
4. Prost J
5. Sekimoto K
(2005) Generic theory of active polar gels: a paradigm for cytoskeletal dynamics
The European Physical Journal E 16:5–16.
https://doi.org/10.1140/epje/e2005-00002-5
- Google Scholar
1. Kruse K
2. Jülicher F
(2000) Actively contracting bundles of polar filaments
Physical Review Letters 85:1778–1781.
https://doi.org/10.1103/PhysRevLett.85.1778
- PubMed
- Google Scholar
1. Kumar KV
2. Bois JS
3. Jülicher F
4. Grill SW
(2014) Pulsatory patterns in active fluids
Physical Review Letters 112:208101.
https://doi.org/10.1103/PhysRevLett.112.208101
- Google Scholar
1. Levayer R
2. Lecuit T
(2012) Biomechanical regulation of contractility: spatial control and dynamics
Trends in Cell Biology 22:61–81.
https://doi.org/10.1016/j.tcb.2011.10.001
- PubMed
- Google Scholar
(2009) Pulsed contractions of an actin-myosin network drive apical constriction
Nature 457:495–499.
https://doi.org/10.1038/nature07522
- PubMed
- Google Scholar
1. Mayer M
2. Depken M
3. Bois JS
4. Jülicher F
5. Grill SW
(2010) Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows
Nature 467:617–621.
https://doi.org/10.1038/nature09376
- PubMed
- Google Scholar
(2015) Pulsatile cell-autonomous contractility drives compaction in the mouse embryo
Nature Cell Biology 17:849–855.
https://doi.org/10.1038/ncb3185
- PubMed
- Google Scholar
1. Miller AL
2. Bement WM
(2009) Regulation of cytokinesis by Rho GTPase flux
Nature Cell Biology 11:71–77.
https://doi.org/10.1038/ncb1814
- PubMed
- Google Scholar
1. Motegi F
2. Sugimoto A
(2006) Sequential functioning of the ECT-2 RhoGEF, RHO-1 and CDC-42 establishes cell polarity in Caenorhabditis elegans embryos
Nature Cell Biology 8:978–985.
https://doi.org/10.1038/ncb1459
- PubMed
- Google Scholar
1. Munjal A
2. Philippe JM
3. Munro E
4. Lecuit T
(2015) A self-organized biomechanical network drives shape changes during tissue morphogenesis
Nature 524:351–355.
https://doi.org/10.1038/nature14603
- PubMed
- Google Scholar
(2004) Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo
Developmental Cell 7:413–424.
https://doi.org/10.1016/j.devcel.2004.08.001
- PubMed
- Google Scholar
1. Murrell M
2. Oakes PW
3. Lenz M
4. Gardel ML
(2015) Forcing cells into shape: the mechanics of actomyosin contractility
Nature Reviews Molecular Cell Biology 16:486–498.
https://doi.org/10.1038/nrm4012
- PubMed
- Google Scholar
1. Müller P
2. Rogers KW
3. Jordan BM
4. Lee JS
5. Robson D
6. Ramanathan S
7. Schier AF
(2012) Differential diffusivity of nodal and Lefty underlies a reaction-diffusion patterning system
Science 336:721–724.
https://doi.org/10.1126/science.1221920
- PubMed
- Google Scholar
(2014) Active torque generation by the actomyosin cell cortex drives left-right symmetry breaking
eLife 3:e04165.
https://doi.org/10.7554/eLife.04165
- PubMed
- Google Scholar
1. Piekny AJ
2. Mains PE
(2002)
Rho-binding kinase (LET-502) and myosin phosphatase (MEL-11) regulate cytokinesis in the early Caenorhabditis elegans embryo

Journal of Cell Science 115:2271–2282.
- PubMed
- Google Scholar
Book
(2007)
Particle image velocimetry - a practical guide

Springer Berlin Heidelberg.
- Google Scholar
(2014) Modeling digits. Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients
Science 345:566–570.
https://doi.org/10.1126/science.1252960
- PubMed
- Google Scholar
(2010) Planar polarized actomyosin contractile flows control epithelial junction remodelling
Nature 468:1110–1114.
https://doi.org/10.1038/nature09566
- PubMed
- Google Scholar
(2016) Cortical flow aligns actin filaments to form a furrow
eLife 5:e17807.
https://doi.org/10.7554/eLife.17807
- PubMed
- Google Scholar
1. Riedl J
2. Crevenna AH
3. Kessenbrock K
4. Yu JH
5. Neukirchen D
6. Bista M
7. Bradke F
8. Jenne D
9. Holak TA
10. Werb Z
11. Sixt M
12. Wedlich-Soldner R
(2008) Lifeact: a versatile marker to visualize F-actin
Nature Methods 5:605–607.
https://doi.org/10.1038/nmeth.1220
- PubMed
- Google Scholar
Preprint
(2016) Excitable RhoA dynamics drive pulsed contractions in the early C. elegans embryo.
bioRxiv.
https://doi.org/10.1101/076356
- Google Scholar
1. Roh-Johnson M
2. Shemer G
3. Higgins CD
4. McClellan JH
5. Werts AD
6. Tulu US
7. Gao L
8. Betzig E
9. Kiehart DP
10. Goldstein B
(2012) Triggering a cell shape change by exploiting preexisting actomyosin contractions
Science 335:1232–1235.
https://doi.org/10.1126/science.1217869
- PubMed
- Google Scholar
(2016) Determining physical properties of the cell cortex
Biophysical Journal 110:1421–1429.
https://doi.org/10.1016/j.bpj.2016.02.013
- PubMed
- Google Scholar
1. Sakaguchi H
(1997) Standing wave patterns for the complex Swift-Hohenberg equation
Progress of Theoretical Physics 98:577–585.
https://doi.org/10.1143/PTP.98.577
- Google Scholar
(2012) Actin cortex mechanics and cellular morphogenesis
Trends in Cell Biology 22:536–545.
https://doi.org/10.1016/j.tcb.2012.07.001
- PubMed
- Google Scholar
(2009) Hydrodynamics of cellular cortical flows and the formation of contractile rings
Physical Review Letters 103:058102.
https://doi.org/10.1103/PhysRevLett.103.058102
- PubMed
- Google Scholar
1. Schonegg S
2. Hyman AA
(2006) CDC-42 and RHO-1 coordinate acto-myosin contractility and PAR protein localization during polarity establishment in C. elegans embryos
Development 133:3507–3516.
https://doi.org/10.1242/dev.02527
- PubMed
- Google Scholar
(2002) A formin homology protein and a profilin are required for cytokinesis and Arp2/3-independent assembly of cortical microfilaments in C. elegans
Current Biology 12:2066–2075.
https://doi.org/10.1016/S0960-9822(02)01355-6
- PubMed
- Google Scholar
1. Sheth R
2. Marcon L
3. Bastida MF
4. Junco M
5. Quintana L
6. Dahn R
7. Kmita M
8. Sharpe J
9. Ros MA
(2012) Hox genes regulate digit patterning by controlling the wavelength of a Turing-type mechanism
Science 338:1476–1480.
https://doi.org/10.1126/science.1226804
- PubMed
- Google Scholar
(2009) Pulsed forces timed by a ratchet-like mechanism drive directed tissue movement during dorsal closure
Cell 137:1331–1342.
https://doi.org/10.1016/j.cell.2009.03.050
- PubMed
- Google Scholar
(2004) Analysis of binding reactions by fluorescence recovery after photobleaching
Biophysical Journal 86:3473–3495.
https://doi.org/10.1529/biophysj.103.026765
- PubMed
- Google Scholar
1. Tse YC
2. Werner M
3. Longhini KM
4. Labbe JC
5. Goldstein B
6. Glotzer M
(2012) RhoA activation during polarization and cytokinesis of the early Caenorhabditis elegans embryo is differentially dependent on NOP-1 and CYK-4
Molecular Biology of the Cell 23:4020–4031.
https://doi.org/10.1091/mbc.E12-04-0268
- PubMed
- Google Scholar
1. Turing AM
(1952) The chemical basis of morphogenesis
Philosophical Transactions of the Royal Society B: Biological Sciences 237:37–72.
https://doi.org/10.1098/rstb.1952.0012
- Google Scholar
(2004) Simultaneous mapping of filamentous actin flow and turnover in migrating cells by quantitative fluorescent speckle microscopy
PNAS 101:9660–9665.
https://doi.org/10.1073/pnas.0300552101
- PubMed
- Google Scholar
1. Westendorf C
2. Negrete J
3. Bae AJ
4. Sandmann R
5. Bodenschatz E
6. Beta C
(2013) Actin cytoskeleton of chemotactic amoebae operates close to the onset of oscillations
PNAS 110:3853–3858.
https://doi.org/10.1073/pnas.1216629110
- PubMed
- Google Scholar
1. Yumura S
(2001) Myosin II dynamics and cortical flow during contractile ring formation in Dictyostelium cells
The Journal of Cell Biology 154:137–146.
https://doi.org/10.1083/jcb.200011013
- PubMed
- Google Scholar

Decision letter

Matthieu Piel

Reviewing Editor; Institut Curie, France

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Controlling contractile instabilities in the actomyosin cortex" for consideration by eLife. Your article has been favorably evaluated by Marianne Bronner (Senior Editor) and three reviewers, one of whom is a member of our Board of Reviewing Editors. The following individuals involved in review of your submission have agreed to reveal their identity: Matthieu Piel (Reviewer #2); Jean-Francois Joanny (Reviewer #3).

The reviewers have discussed the reviews (see below) with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

In this article, Masatochi and colleagues combine quantitative imaging, advanced image analysis and modeling to study the formation of patterns in the acto-myosin cortex of a C. elegans zygote during the initial polarization event. They show that the observed Myosin II oscillatory patterns are driven by a RhoA oscillator that does not depend on the contractility of the cortex. They propose that this RhoA 'pacemaker' driving the acto-myosin patterns could be important to prevent large contractility occurring during polarization of whole cells, to lead to an instability of the cortex that would prevent it to exert the large forces needed, or to produce a cell-scale pattern. This is a very original and interesting idea.

As can be seen in the attached reviews, the reviewers have very different points of view on this paper. While all agree that the notion that contractile oscillations in the cortex "dampen" large instabilities is a new idea and the data analysis and modelling are novel and well done, reviewer 1 has concerns about the biological significance and the lack of new mechanistic insight into phenomenon of study, and reviewer 2 is not convinced, with the data provided, that the parameters measured in the experiments can really be used to fit the model.

The consensus of the reviewers, after discussion of their dissenting points of view, is that the manuscript could in principle be acceptable for publication in eLife, pending major revisions specifically addressing the following major points.

With regard to biological significance and/or mechanism, the authors would either need to provide some demonstration that RhoA oscillations mediating the damping of large contractile instabilities are a general phenomenon underlying other biological processes in which contractile pulses are known to occur, or provide some mechanistic dissection of the driver of Rho pulses. Other biological systems in which contractile pulses occur include several tissues in developing Drosophila as wells as Xenopus and mouse. Demonstration of myosin II-independent Rho activity oscillations in these systems would provide evidence of generality. The candidates for mechanistic insight into the Rho pulse driver/terminator include actin (see Nat Cell Biol. 2015; 17:1471-83. Bement WM. et al), or perhaps whatever lies between actin polymerization and Rho, likely some Rho-Gef. As noted by both reviewers, imaging and analysis of actin dynamics and application of drugs or mutants that stabilize the actin and thus inhibit its assembly/disassembly cycle are needed both to determine if the oscillations are driven by the same mechanism seen in the previous publication and to also better inform the parameters used in their model. The authors alternatively could screen known RhoGef mutants to determine their involvement in driving Rho oscillations.

With regard to better delineating the model parameters, results and interpretations, the authors need to rewrite the descriptions of the approaches, results and reasoning behind the conclusions more explicitly and in more detail.

Reviewer 1:

In this manuscript, the authors describe the regulation of actomyosin activity in the cortex of C. elegans zygotes. They use fluorescence microscopy, advanced image analysis, and theoretical modelling to try to understand the mechanism of the localized, pulsed assembly and movement of myosin 2 foci that occurs prior to and during establishment of embryonic polarity at the 1-cell stage. In the past several years, this pulsed activity of myosin 2 has been observed during developmental morphogenesis in worms, flies, frogs, and mice.

The authors show that the pulsed assembly of myosin 2 is driven by localized cortical pulses of RhoA activity, as reported by the Bement biosensor, and that RhoA pulses occur independently of myosin 2. Using previously characterized mutants, they show that the Rho kinase let-502, the centrosome-associated protein spd-5, and the profilin pfn1 all regulate the ability of myosin 2 to pulse or form its normal pattern of pulsing, but have little effect on the pulsing of RhoA. The authors develop a theoretical model of the mechanochemical feedback between myosin 2 and RhoA based on a thin active gel, utilizing parameters for the temporal relationship between myosin 2 and RhoA pulses that they measure here, together with their previous measurements of cortical mechanical properties. This model predicts that in its wild type state, the zygote cortex verges just over the line between stability and instability. They predict that the rate of myosin 2 recruitment by RhoA and the hydrodynamic length of the cortex material determine the transition from stable and homogenous to unstable and pulsing. They show that perturbing the ability of RhoA pulses to recruit myosin 2 to the cortex with the let-502 mutant abolishes myosin 2 pulses and makes the cortex homogeneous, while perturbing the integrity of the cortex with the pfn-1 mutant induces greater instability and increases the dynamics of the myosin 2 pulses.

The phenomenon of pulsed or wave-like patterns of cortical activity has begun to be studied in depth. Previous studies by the Bement, Martin and Zallen labs have shown that Rho GTPases and their downstream effectors exhibit pulsed or wave-like dynamics in other embryonic systems, and that pulsing requires formin-mediated actin assembly, cortical integrity, and Rho-mediated myosin 2 phosphoregulation. The Bement lab has also demonstrated that Rho waves occur independent of myosin 2 activity, but their termination requires Rho-mediated actin assembly, thus placing actin at the hub of a mechanochemical negative feedback driving pulses. Whether actin assembly or some other mechanism is required for driving or terminating RhoA pulses in the C. elegans zygote was not explored in the current paper. Thus, the main contribution of the current study is the development of analysis methods and a theoretical model of cortical mechanics and dynamics that agrees with the notion that cortical integrity is a key driver of cytoskeletal pulses, and the finding from this model that the natural state of the cortical cytoskeleton in the C. elegans zygote verges on instability.

In spite of the flurry of studies of pulsed/wave-like cortical cytoskeleton behavior in the past several years, it is unclear whether the behavior is actually required for biological function, or is an epiphenomenon that occurs at a certain level of cortical contractility. The current paper suggests the latter. Indeed, they show here that C. elegans zygotes can undergo polarization in the absence of myosin 2 pulses, i.e. when the myosin 2 is homogeneously distributed in the cortex in the let-502 mutant (although this mutant has other major defects in later stages of development). In addition, work from the Martin lab shows that in embryos that express a phosphomimetic myosin (with the endogenous myosin strongly reduced but not eliminated), apical constriction during mesoderm invagination in Drosophila occurs continuously (not in pulses), and yet the cells apically constrict and internalize just fine. Thus, the lack of advance into understanding the upstream regulation of the RhoA pulses together with the questionable biological significance of the pulses, unfortunately precludes publication of the paper in eLife.

Reviewer 2:

In this article, Masatoshi and colleagues combine quantitative imaging, advanced image analysis and modeling to study the formation of patterns in the acto-myosin cortex of a C. elegans zygote during the initial polarization event. They show that the observed Myosin II oscillatory patterns are driven by a RhoA oscillator that does not depend on the contractility of the cortex. They propose that this RhoA 'pacemaker' driving the acto-myosin patterns could be important to prevent large contractility occurring during polarization of whole cells, to lead to an instability of the cortex that would prevent it to exert the large forces needed, or to produce a cell-scale pattern. This is a very original and interesting idea. Experimentally estimated parameters are used in the frame of a mechanochemical model of the acto-myosin cortex which predicts an instability and formation of a spatial pattern. While the initial model proposed predicts the instability, it fails to predict the correct pattern and the pulsatile behavior. This behavior can be obtained by adding a driving pulsatile pattern in the modeling, which would correspond to the observed Myosin II independent pulsatile pattern of active RhoA. The origin of this RhoA pacemaker is not addressed in the paper, neither experimentally nor theoretically. Some perturbation experiments are performed to test predictions of the driven mechanochemical model. They suggest that the RhoA pacemaker might be essential to control the instability of the actomyosin cortex and form the observed pulsatile pattern instead of large clusters and flows. The final conclusion is new and represents an important step in the understanding of how the acto-myosin cortex works and contributes to morphogenesis. The experiments are well done and analysed, and there is no issue with the modeling proposed, which builds upon a large body of theoretical work and experiments – the modeling part was reviewed by my colleague Raphael Voituriez, who found no issue in the modeling proposed and commented that the part on the driving by the RhoA pacemaker, although leading to expected results, is new and well done. As a conclusion, the article should be published and will be an important contribution to the field.

I have a main concern, which might be solved mostly by a major effort in rewriting the article, if the authors are willing to do so. Indeed, my general feeling after many hours of work on this article, is that, despite all its qualities listed above, it does not convey its central message in a very convincing manner. The general feeling is that the authors tend to rush to the conclusions and leave the reader unsatisfied or feeling 'dumb' – asking the reader to be a believer rather than a critical thinker. The article is using a large number of sophisticated methods, from a number of different fields – developmental biology, imaging, physics – and if the authors want to be understood and trusted by scientists beyond the 'biophysicists of the acto-myosin cortex in C. elegans', they have to make a special effort in the presentation of their work.

Reviewer 3:

The manuscript of Nishikawa et al. studies both experimentally and theoreticallythe pulsatile contractile instability of the C. elegans actin cortex. The strength of this paper is the combination an original experimental technique to measure the kinetics of the actin cortex – that they call COMBI – to a theoretical analysis based on active gel theory. Each step of the theory is carefully checked experimentally and the authors get this way a very precise description of the cortical kinetics from which they describe the cortical instability. The instability is explained by an interplay between myosin molecular motors and the G protein RhoA. In order to explain the experimental results, the authors describe the dynamics of RhoA by introducing a RhoA pacemaker oscillator through the very generic Swift-Hohenberg equation.

This is a beautiful and very original manuscript and I certainly recommend its publication in eLife. The authors should consider the following comments prior to publication.

Throughout the manuscript the authors switch between RhoA and Rho1,which are if I understand well the same protein. It would be clearer for the reader if they were always using the same name.

The authors introduce a pacemaker dynamics of RhoA via the very general Swift-Hohenberg equation. This explains well the experimental results. However, they do not discuss the origin of this dynamics. Is there any information on that, which proteins are involved for instance?

The model proposed is only one-dimensional, it ignores the thickness of the cortex and restricts the description to one dimension along the cortex. It would of course be useful to extend the model to two dimensions to compare the observed patterns of each components with the prediction of the theory. That probably could be done numerically and would provide a stronger test of the theory.

One of the simplifications that the model makes is that it considers only an isotropic cortex. However, the active stress is not isotropic and depend on actin polarization. Does actin polarization play any role? What would it change to the theory?

One could also worry whether the instability described in this manuscript is generic. The main ingredient is the regulation of the myosin motors by Rho A, which to my knowledge is a very general feature and the pacemaking oscillations of RhoA. Would a similar instability be observed in any cortex?

https://doi.org/10.7554/eLife.19595.027

Author response

[…]

With regard to biological significance and/or mechanism, the authors would either need to provide some demonstration that RhoA oscillations mediating the damping of large contractile instabilities are a general phenomenon underlying other biological processes in which contractile pulses are known to occur, or provide some mechanistic dissection of the driver of Rho pulses. Other biological systems in which contractile pulses occur include several tissues in developing Drosophila as wells as Xenopus and mouse. Demonstration of myosin II-independent Rho activity oscillations in these systems would provide evidence of generality. The candidates for mechanistic insight into the Rho pulse driver/terminator include actin (see Nat Cell Biol. 2015; 17:1471-83. Bement WM. et al), or perhaps whatever lies between actin polymerization and Rho, likely some Rho-Gef. As noted by both reviewers, imaging and analysis of actin dynamics and application of drugs or mutants that stabilize the actin and thus inhibit its assembly/disassembly cycle are needed both to determine if the oscillations are driven by the same mechanism seen in the previous publication and to also better inform the parameters used in their model. The authors alternatively could screen known RhoGef mutants to determine their involvement in driving Rho oscillations.

We thank the reviewer and the editor for these suggestions. The mechanistic basis for the RhoA pacemaking oscillator itself was not the main interest of our study. However, we agree that more information on the mechanism of pulse generation by RhoA would strengthen our work, and we addressed this issue in two ways.

First, we investigated the interaction between active RhoA and actin, by generating a transgenic line that expresses both the active RhoA probe and tagRFP-T labeled LifeAct, a probe for filamentous actin in cortex. We utilized this new line to determine a kinetic interaction diagram by using COMBI, as was done for the myosin and active RhoA in Figure 1H in the main text. As you can see in Figure 1—figure supplement 3, we did not detect negative feedback from actin onto RhoA, which is in contrast to what is seen by Bill Bement in the recent Nature Cell Biology paper (Figure 5C in Bement et al). Instead, the nullcline of RhoA kinetics (Figure 1—figure supplement 3A, green line) displays a positive slope (i.e. active RhoA increases with increasing actin concentration), consistent with actin operating only as a positive regulator of active RhoA. This does not mean that there is no negative feedback at all between actin and RhoA, but suggests that the C. elegans cortex, in which there exists a dense network of actin, is normally operating in a regime where only positive feedback is accessed. To conclude, we do not observe quite as strong an interaction between actin and active RhoA in C. elegans as was reported for Xenopus.

Second, following the advice from the editor we set out to determine if known RhoGEFs are involved in driving the RhoA pacemaking oscillator. Previous work has shown that the C. elegans RhoGEF ECT-2 positively regulates RHO-1 (see e.g. Schonegg and Hyman, 2006), and we now demonstrate that RNAi of this RhoGEF leads to the absence of RhoA pulsation (Video 6). This allows us to identify ECT-2 as a positive regulator of RhoA, even if the kinetics aren’t clear yet. This is now properly discussed in the revised manuscript.

While these additional experiments strengthen our work, we hope that the referees and the editor agree that an analysis of the full kinetics of recruitment and activation underlying active RhoA pulsation, which is required for understanding how they arise, is beyond the scope of the work here. This is the focus of ongoing research and (hopefully) a future publication from our lab.

We agree and have added better descriptions throughout. We have also taken most of the criticism raised below into account in our revised manuscript. Please also note our responses to the detailed concerns given below.

Reviewer 1:

[…] The phenomenon of pulsed or wave-like patterns of cortical activity has begun to be studied in depth. Previous studies by the Bement, Martin and Zallen labs have shown that Rho GTPases and their downstream effectors exhibit pulsed or wave-like dynamics in other embryonic systems, and that pulsing requires formin-mediated actin assembly, cortical integrity, and Rho-mediated myosin 2 phosphoregulation. The Bement lab has also demonstrated that Rho waves occur independent of myosin 2 activity, but their termination requires Rho-mediated actin assembly, thus placing actin at the hub of a mechanochemical negative feedback driving pulses. Whether actin assembly or some other mechanism is required for driving or terminating RhoA pulses in the C. elegans zygote was not explored in the current paper. Thus, the main contribution of the current study is the development of analysis methods and a theoretical model of cortical mechanics and dynamics that agrees with the notion that cortical integrity is a key driver of cytoskeletal pulses, and the finding from this model that the natural state of the cortical cytoskeleton in the C. elegans zygote verges on instability.

Indeed, the focus of our work is the investigation of cortical integrity, and the mechanisms by which a contractile instability can be controlled. An in-depth investigation of the mechanisms by which the RhoA oscillator is generated was not the core focus of our study, since this has been worked on before. However, this referee, together with referee #2, requested additional information on which mechanisms contribute to positive and/or negative feedback in RhoA. We have taken these comments seriously, and have added two pieces of additional data. First, we performed a kinetic COMBI analysis of active RhoA vs. actin, and find that in contrast to Xenopus, actin does not appear to be contributing to the termination of RhoA pulses. Second, we show that RhoA pulses require the Rho-GEF ECT-2 (see our answer above for more detail). Together, these results shed further light on the RhoA oscillator, which in turn, as we show here, provides increased cortical integrity by controlling the contractile instability.

In spite of the flurry of studies of pulsed/wave-like cortical cytoskeleton behavior in the past several years, it is unclear whether the behavior is actually required for biological function, or is an epiphenomenon that occurs at a certain level of cortical contractility. The current paper suggests the latter. Indeed, they show here that C. elegans zygotes can undergo polarization in the absence of myosin 2 pulses, i.e. when the myosin 2 is homogeneously distributed in the cortex in the let-502 mutant (although this mutant has other major defects in later stages of development). In addition, work from the Martin lab shows that in embryos that express a phosphomimetic myosin (with the endogenous myosin strongly reduced but not eliminated), apical constriction during mesoderm invagination in Drosophila occurs continuously (not in pulses), and yet the cells apically constrict and internalize just fine. Thus, the lack of advance into understanding the upstream regulation of the RhoA pulses together with the questionable biological significance of the pulses, unfortunately precludes publication of the paper in eLife.

Any contractile medium is prone to contractile instabilities, this is one of the points we are making in our work. If the material is too contractile, it will tend to pull itself apart, this is inevitable. Thus, one might refer to this behaviour as an epiphenomenon, however, we don’t think that this terminology does justice to the problem at hand. Controlling this instability allows the material to remain highly contractile overall to successfully, rapidly and robustly drive morphogenetic events, this is our conclusion. Submitting to the contractile instability gives rise to a lethal phenotype, as we show via pfn-1 RNAi. Hence, our work assigns a potential function to the RhoA/myosin pulses, which is to control the instability and allow the cortex to operate in a regime of high contractility that is otherwise not accessible. Removing pulsation does not appear to generally give rise to lethal phenotypes, this is correct. However, as stated above our suggestion is that overall contractility will necessarily be lower, leading to less rapid and probably less robust morphogenetic transitions. This is now more explicitly discussed in our revised manuscript. We hope that the referee now agrees that our work provides a significant step forward both for the biology and the physical mechanism of myosin pulsation.

Reviewer 2:

[…] I have a main concern, which might be solved mostly by a major effort in rewriting the article, if the authors are willing to do so. Indeed, my general feeling after many hours of work on this article, is that, despite all its qualities listed above, it does not convey its central message in a very convincing manner. The general feeling is that the authors tend to rush to the conclusions and leave the reader unsatisfied or feeling 'dumb' – asking the reader to be a believer rather than a critical thinker. The article is using a large number of sophisticated methods, from a number of different fields – developmental biology, imaging, physics – and if the authors want to be understood and trusted by scientists beyond the 'biophysicists of the acto-myosin cortex in C. elegans', they have to make a special effort in the presentation of their work.

We thank the referee for this feedback, which we have taken seriously in our re- vision.

Reviewer 3: […] Throughout the manuscript the authors switch between RhoA and Rho1,which are if I understand well the same protein. It would be clearer for the reader if they were always using the same name.

This has been changed.

This concern resonates well with similar concerns from the other referees. We have done additional experiments and now report on the involvement of Rho GEF, ect-2 in generating the oscillatory dynamics of the active RhoA. Please see the response to the editor above for detail.

A precise comparison between 2D foci dynamics with the RhoA oscillator in place in theory and simulation is beyond what we are aiming to do in our manuscript. We have put in place a generic spatiotemporal oscillator for the RhoA dynamics that will differ from the actual dynamics, and consequently we are not expecting that the dynamics of the full system in 2D will be quantitatively reproduced with our approach here. Indeed, we had and have done 2D simulations and they show similar general behavior. Given that a 2D analysis might raise false hope that the 2D RHoA-myosin patterns are quantitatively reproduced in theory (which they are not given the uncertainties underlying the nature of the RhoA oscillator, neither for 1D nor for 2D), we have chosen not to add this to the manuscript. We have also added a clarification that our theory remains qualitative and does not quantitatively reproduce the patterns.

This is a very good point that also relates to the point just above (2D simulation). We have considered isotropic active stresses only, which we know is a simplification (see our recent eLife paper Reymann et al.). Introducing a coupling between active tension and alignment would alter the theory, however, we think this will be an effect that will mildly impact the dynamics in a 2D simulation. This type of comparison is beyond what we are aiming to do here and we have chosen to remain qualitative and have not added 2D simulations (see our answer to the point above). Finally, moving from nematic to polar order will again change the dynamics, but we have no experimental access to the local state of polarization of the cortex so this is currently not really feasible.

We think the instability is generic. First of all, any cortex that is overly contractile will undergo a contractile instability. Perhaps the referee is more concerned with the actual feedback we are reveling for C. elegans, which is more system-specific. While the kinetics will be different in other systems, RhoA is a general master-regulator of the cortex, and we expect a similar feedback to exist in essentially every animal cortex. And the ability to cross the contractile instability critically depends on the level of mechanochemical feedback and myosin recruitment, and as such the mechanism should be generic.

https://doi.org/10.7554/eLife.19595.028

Article and author information

Author details

Masatoshi Nishikawa
1. Biotechnology Center, Technical University Dresden, Dresden, Germany
2. Max Planck Institute for the Physics of Complex Systems, Dresden, Germany
3. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
Present address
Department of Frontier Bioscience, Hosei University, Koganei, Japan

Competing interests
No competing interests declared.

"This ORCID iD identifies the author of this article:" 0000-0001-6502-7907
Sundar Ram Naganathan
1. Biotechnology Center, Technical University Dresden, Dresden, Germany
2. Max Planck Institute for the Physics of Complex Systems, Dresden, Germany
3. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
Present address
The Francis Crick Institute, London, United Kingdom

Competing interests
No competing interests declared.
Frank Jülicher

Max Planck Institute for the Physics of Complex Systems, Dresden, Germany

Competing interests
FJ: Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0003-4731-9185
Stephan W Grill
1. Biotechnology Center, Technical University Dresden, Dresden, Germany
2. Max Planck Institute for the Physics of Complex Systems, Dresden, Germany
3. Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany
For correspondence
stephan.grill@tu-dresden.de

Competing interests
No competing interests declared.

"This ORCID iD identifies the author of this article:" 0000-0002-2290-5826

Funding

Deutsche Forschungsgemeinschaft (SPP 1782)

Stephan W Grill

European Research Council (281903)

Stephan W Grill

Human Frontier Science Program (RGP0023/2014)

Stephan W Grill

European Commission (ITN grant - 281903)

Stephan W Grill

Max-Planck-Gesellschaft

Stephan W Grill

European Commission (ITN grant - 641639)

Stephan W Grill

Deutsche Forschungsgemeinschaft (GSC 97)

Stephan W Grill

Deutsche Forschungsgemeinschaft (GR 3271/2)

Stephan W Grill

Deutsche Forschungsgemeinschaft (GR 3271/3)

Stephan W Grill

Deutsche Forschungsgemeinschaft (GR 3271/4)

Stephan W Grill

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We are grateful to Michael Glotzer and Daniel Dickinson for providing C. elegans strains. We acknowledge Stefan Eimer for the gift of tagRFP-T gene. We thank G Salbreux, JS Bois, PGross and P Gönczy for fruitful discussions. SWG was supported by the DFG (SPP 1782, GSC 97, GR 3271/2, GR 3271/3, GR 3271/4), the European Research Council (grant No 281903), ITN grants 281903 and 641639 from the EU, the Max-Planck-Society as a Max-Planck-Fellow, and the Human Frontier Science Program (RGP0023/2014).

Reviewing Editor

Matthieu Piel, Institut Curie, France

Version history

Received: July 12, 2016
Accepted: January 14, 2017
Accepted Manuscript published: January 24, 2017 (version 1)
Accepted Manuscript updated: January 28, 2017 (version 2)
Version of Record published: March 16, 2017 (version 3)
Version of Record updated: July 19, 2017 (version 4)
Version of Record updated: July 27, 2017 (version 5)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.