1. Cell Biology
  2. Developmental Biology

Patterned cortical tension mediated by N-cadherin controls cell geometric order in the Drosophila eye

  1. Eunice HoYee Chan  Is a corresponding author
  2. Pruthvi Chavadimane Shivakumar
  3. Raphaël Clément
  4. Edith Laugier
  5. Pierre-François Lenne  Is a corresponding author
  1. Aix Marseille Univ, CNRS, IBDM, France
https://doi.org/10.7554/eLife.22796
Share this article
Cite this article
  1. Eunice HoYee Chan
  2. Pruthvi Chavadimane Shivakumar
  3. Raphaël Clément
  4. Edith Laugier
  5. Pierre-François Lenne
(2017)
Patterned cortical tension mediated by N-cadherin controls cell geometric order in the Drosophila eye
eLife 6:e22796.
https://doi.org/10.7554/eLife.22796
  2. Download BibTeX
  3. Download .RIS

Abstract

Adhesion molecules hold cells together but also couple cell membranes to a contractile actomyosin network, which limits the expansion of cell contacts. Despite their fundamental role in tissue morphogenesis and tissue homeostasis, how adhesion molecules control cell shapes and cell patterns in tissues remains unclear. Here we address this question in vivo using the Drosophila eye. We show that cone cell shapes depend little on adhesion bonds and mostly on contractile forces. However, N-cadherin has an indirect control on cell shape. At homotypic contacts, junctional N-cadherin bonds downregulate Myosin-II contractility. At heterotypic contacts with E-cadherin, unbound N-cadherin induces an asymmetric accumulation of Myosin-II, which leads to a highly contractile cell interface. Such differential regulation of contractility is essential for morphogenesis as loss of N-cadherin disrupts cell rearrangements. Our results establish a quantitative link between adhesion and contractility and reveal an unprecedented role of N-cadherin on cell shapes and cell arrangements.

https://doi.org/10.7554/eLife.22796.001

Introduction

Cells acquire different shapes and arrangements to form tissues, depending on their functions and microenvironment. During tissue morphogenesis, cells actively form and remodel their cell contacts, generating forces to drive various morphogenetic events (Lecuit and Lenne, 2007). In epithelia, cell division (Herszterg et al., 2013; Guillot and Lecuit, 2013; Founounou et al., 2013), cell intercalation (Bertet et al., 2004; Blankenship et al., 2006) and cell delamination (Marinari et al., 2012) are basic mechanisms of morphogenesis, which all involve gain or loss of cell contacts (Heisenberg and Bellaïche, 2013). Two systems contribute to changes in cell contacts: Cadherin complexes and actomyosin networks (Harris, 2012; Baum and Georgiou, 2011).

At the level of a single cell contact, formation of cadherin-cadherin bonds favors contact expansion. Actomyosin contractility acts antagonistically by reducing cell contact size (Lecuit and Lenne, 2007; Winklbauer, 2015). There is numerous evidence in vivo that shows actomyosin-generated tension regulates cell shape (Rauzi et al., 2008; Martin et al., 2009). In vitro, contact size is mainly determined by actomyosin contractility but not cadherin engagement (Maître et al., 2012). However, in Drosophila retina, N-cadherin mutants show drastic alteration of contact size and cell shape (Hayashi and Carthew, 2004), which suggests that cadherin-associated adhesion cannot be discounted. Even though the forces produced by cadherins and actomyosin networks act antagonistically, both systems are interconnected as cadherins are associated with intracellular actomyosin networks via catenins and other actin-binding proteins (Priya et al., 2013; Röper, 2015).

Due to the intrinsic links between cadherin-dependent adhesion and actomyosin contractility, it is challenging to address whether and how cadherin adhesion regulates cell shape. What is the direct contribution of cadherin-cadherin bonds to cell shape? Do cadherins influence cell shape through actomyosin contractility? To address these questions, we investigated the origin of cell shapes in vivo in the highly organized Drosophila retina, which features differential expression of cadherin molecules and is amenable to quantification of cell shapes and mechanical measurements. In particular, the Drosophila retina is an ideal system to study heterotypic contacts, and their differences with homotypic contacts.

Drosophila retina is composed of approximately 750 facets called ommatidia (Cagan and Ready, 1989; Tepass and Harris, 2007), each of which includes four cone cells (C) embedded in two primary pigment cells (P), along with other cell types shared by neighboring ommatidia (Figure 1A,B). The pattern of cone cells arrangement is strikingly similar to that of soap bubbles (Hayashi and Carthew, 2004). While this visual resemblance suggests that cells might minimize their surface of contact, both contractility and adhesion have to be considered for cell shape and cell arrangements (Lecuit and Lenne, 2007), as indicated by physical models (Käfer et al., 2007; Hilgenfeldt et al., 2008). Two classical Type I cadherins, E-cadherin (Ecad) and N-cadherin (Ncad) are expressed in the retina and specific expression of N-cadherin solely in cone cells governs the cone cell shape and arrangements (Hayashi and Carthew, 2004). In silico predictions based on energy minimization reproduce well the cone cell shapes but have limited experimental support (Käfer et al., 2007; Hilgenfeldt et al., 2008). In particular, the contributions of Ncad-mediated actomyosin contractility, as well as the interfacial tension in cone cell shape control, have not been explored.

Figure 1 with 1 supplement see all
Download asset Open asset
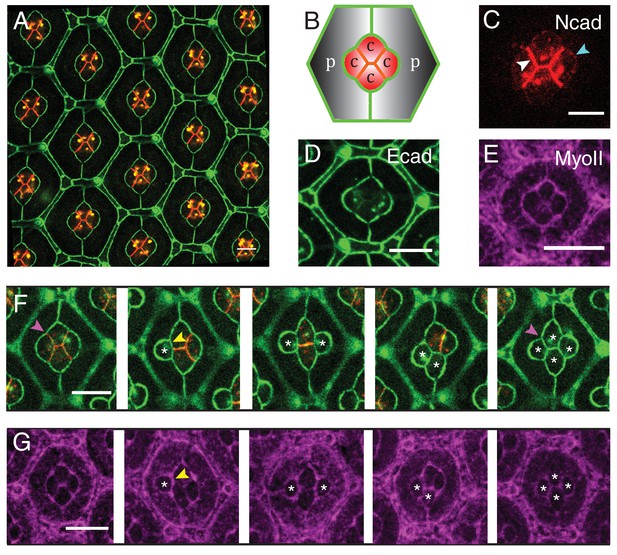
Patterns of Drosophila eye with the distributions of cadherins and Myosin-II (MyoII) in wildtype and NcadM19 mosaic ommatidia.

(A) Image of pupal retina at 41 hr after puparium formation (APF) consisting of repeating lattice structure called ommatidia labeled with Ecad::GFP (green) and Ncad::mKate2 (red). (B) A schematic of the most apical view of an ommatidium, which contains four cone cells (C) and two primary pigment cells (P), and the localization of cadherins (Ecad in green and Ncad in red). (C–E) An individual ommatidium with Ncad::GFP in red (C), Ecad::GFP in green (D), Zip::YFP in magenta (E). (F–G) Wildtype and NcadM19 mosaic ommatidia labelled with Ecad::GFP (green), Ncad (red) and Zip::YFP (magenta). NcadM19 cone cells are marked by white asterisks. Magenta arrowheads in (F) shows the angle change in full NcadM19 cone cells compared to wildtype. White arrowhead indicates the C|C contact with homophilic complexes and cyan arrowhead indicates the C|P contact in (C). Yellow arrowheads indicate one of the contacts at the interface between wildtype and NcadM19 cells to highlight the absence of Ncad adhesion in (F) and significant increase in MyoII levels in (G). Scale bar, 10 µm.

https://doi.org/10.7554/eLife.22796.002

Ncad is involved in numerous morphogenetic processes including cell migration, neural tube formation, and axon guidance (Derycke and Bracke, 2004; Hirano and Takeichi, 2012; Lee et al., 2001). To date, the direct implication of Ncad and actomyosin complexes on cell sorting and patterning during development is unclear. Ncad depletion in Xenopus neural plate leads to the loss of activated form of myosin light chain (Nandadasa et al., 2009). Actin cytoskeleton remodelling in Drosophila glial cells is tightly regulated by Ncad levels (Kumar et al., 2015). In cell culture, a dynamic interaction was reported between Ncad and actomyosin complexes in myocytes (Comunale et al., 2007; Ladoux et al., 2010; Shih and Yamada, 2012; Chopra et al., 2011), neurons (Bard et al., 2008; Luccardini et al., 2013; Garcia et al., 2015; Okamura et al., 2004; Chazeau et al., 2015) and fibroblasts (Ouyang et al., 2013).

Here we combine mechanical measurements, quantitative microscopy and modelling to revisit the role of Ncad in cell shapes and cell arrangement. We show that Ncad bonds contribute two fold less than Myosin-II (MyoII) to interfacial tension, but that Ncad also affects localization and levels of MyoII, and thus cell shapes. We reveal that heterotypic interfaces between Ncad-expressing and non-Ncad-expressing cells accumulate MyoII more than homotypic interfaces, thereby stabilizing specific cell configurations. Our results emphasize the interplay between cadherins and actomyosin networks, which determines cell shape and cell arrangements during morphogenesis.

Results

Cadherins and Myosin-II distribution in pupal retinas

To visualize the patterns of cadherins in ommatidia, we analyzed their expression in Ncad::GFP (Figure 1C) and Ecad::GFP knock-in retinas (Figure 1D) (See Material and methods for details). As previously reported (Hayashi and Carthew, 2004), Ncad is localized at cone cell-cone cell contacts (C|C), where it forms homophilic complexes (Figure 1C, white arrowhead). Ncad is also found at low level at the junctions between cone cell and primary pigment cell (C|P) (Figure 1C, cyan arrowhead and Figure 1—figure supplement 1A). At C|P contacts, Ncad cannot form trans-homophilic bonds but cis-homophilic bonds, as it is expressed in cone cells but not in primary pigment cells. In addition, Ncad-Ecad trans-heterotypic bonds appear to be absent, as Ecad mutant cone cell loses contact from the neighbouring Ecad expressing primary pigment cell (Hayashi and Carthew, 2004). Ecad is present in all cell contacts albeit at different levels. Ecad concentration is lower at C|C relative to C|P and at primary pigment cell and primary pigment cell contacts (P|P) (Figure 1D). To visualize the pattern of MyoII, we imaged Myosin heavy chain (Zip)::YFP knock-in retinas (Figure 1E), and Myosin light chain (Sqh)::GFP flies driven by Sqh promotor in Sqh mutant background (Figure 1—figure supplement 1B). We also stained Zip::YFP or Sqh::GFP retinas with Phospho-Myosin-II light chain antibodies which labels active MyoII to check how well they correlate with each other (Figure 1—figure supplement 1C,D). As reported earlier (Warner and Longmore, 2009; Yashiro et al., 2014; Deng et al., 2015), Phospho-Myosin-II light chain antibodies show a punctate distribution, but overall the three markers indicate that MyoII is enriched at cell contacts and is also present as apical mesh at a lower concentration. ​

Loss of N-cadherin not only affects cone cell shape but also Myosin-II levels

To assess the impact of Ncad on cone cell shapes, we performed mosaic analysis to generate Ncad loss of function (NcadM19) clones in pupal retinas. Ncad mutation in one or multiple cone cells results in significant cell shape changes (Figure 1F), as reported earlier (Hayashi and Carthew, 2004). Shape variations are dependent on the numbers and combinations of wildtype and NcadM19 cone cells in the mosaic ommatidia (Figure 1F). In a full NcadM19 ommatidium, the four cone cells acquire a cruciform shape rather than the normal diamond shape (last and first image respectively in Figure 1F). Reduction in cell contact length (Figure 1F, yellow arrowhead) and change in angles (compare first and the last image of Figure 1F, magenta arrowhead) suggests that adhesion by homophilic bonding of Ncad causes a significant expansion of contacts between cone cells. Apart from the cell shape changes, there are variations in MyoII levels at mosaic NcadM19 ommatidium. For instance, at wildtype and NcadM19 cone cell contact, there is a significant increase in MyoII level (Figure 1G, yellow arrowhead). So, the loss of Ncad induces change in MyoII concentrations, suggesting a possible contribution of MyoII contractility in shaping cone cell patterns (Figure 1G).

Differential Myosin-II levels and interfacial tension

To explore the role of contractile forces in cone cell shapes, we determined the distribution of MyoII, a proxy for contractility, and measured interfacial tension acting at cell contacts in wildtype and NcadM19 mosaic ommatidia.

We used Zip::YFP fluorescence intensity as a readout of MyoII concentration. We observed different levels of MyoII at cell contacts, depending on whether (i) the two cells, for example cell 1 and cell 2 in contact express both Ecad and Ncad (1(E,N)|2(E,N)), (ii) the two cells in contact express only Ecad (1(E)|2(E)), (iii) one of the two cells in contact expresses only Ecad and another expresses both Ecad and Ncad (1(E)|2(E,N)) (Figure 1G, yellow arrowhead and Figure 1F,G).

In wildtype ommatidia, MyoII level was found 2.2-fold higher at the contact between cone cell and primary pigment cell, C(E,N)|P(E), than at C(E,N)|C(E,N) contacts. MyoII at contacts between primary pigment cells, P(E)|P(E), was found 1.8-fold higher than at C(E,N)|C(E,N) contacts (Figure 2A–C, Supplementary file 1 - table 1). A same trend in MyoII concentration is also observed when using Sqh::GFP as marker (Figure 2—figure supplement 1A–C, Supplementary file 1 -table 1). Interestingly, in NcadM19 mosaic ommatidium comprised of two NcadM19 cone cells, we again observed three distinct levels of MyoII depending on the genotype of the two cone cells in contact (WT and WT (C(E,N)|C(E,N)), WT and NcadM19 (C(E,N)|C(E)), NcadM19 and NcadM19 (C(E)|C(E))) (Figure 2D–F and Figure 2—figure supplement 1D–H, Supplementary file 1 -table 1). These data revealed a simple gradation in MyoII concentration cMyo, similar to the wildtype at C(E,N)|C(E,N), P(E)|P(E) and C(E,N)|P(E) contacts: cMyo(C(E,N)|C(E,N))=1, cMyo(C(E)|C(E))=1.6, and cMyo(C(E,N)|C(E))=2.3 (in arbitrary units). Our data indicates that differences in MyoII concentrations at contact are dependent on Ncad expression in the cells.

Figure 2 with 2 supplements see all
Download asset Open asset
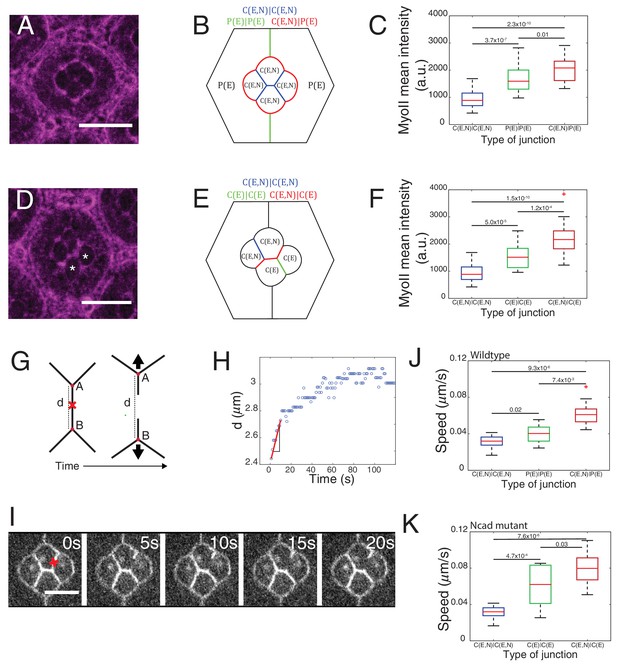
Differential MyoII levels and interfacial tensions at various cell contacts.

(A) Wildtype ommatidium with Zip::YFP represented by (B) a schematic that highlights three different types of contacts at cell interfaces that express Ecad or Ncad or both E and Ncad. C(E,N)|C(E,N) contact (blue) shared by two cone cells, P(E)|P(E) contact (green) shared by two primary pigment cells and C(E,N)|P(E) contact (red) shared by a cone and a primary pigment cell. Scale bar, 10 µm. (C) Quantification of MyoII intensity in C(E,N)|C(E,N) (n = 30), P(E)|P(E) (n = 22) and C(E,N)|P(E) (n = 36) contacts. P-values are shown above the black horizontal lines (non-parametric Mann-Whitney U test on pairs and Bonferroni correction). (D) A NcadM19 mosaic ommatidium with Zip::YFP. NcadM19 cells are marked by white asterisks. Scale bar, 10 µm. (E) A schematic represents the corresponding NcadM19 mosaic mutants highlighting C(E,N)|C(E,N) (blue), C(E)|C(E) (green) and C(E,N)|C(E) contacts (red). (F) Quantification of MyoII intensity in C(E,N)|C(E,N) (n = 30), C(E)|C(E) (n = 22) and C(E,N)|C(E) (n = 36) contacts. P-values are shown above the black horizontal lines. (G)-(K) Laser nanoablation experiments to estimate interfacial tension. (G) Schematic of a contact before (left) and after (right) ablation. Red cross represents the point of the ablation. Vertex A and B recoil changing distance 'd' after ablation. (H) Opening curve plots the distance’ d’ over time with a linear fit for initial time points to get the initial recoil speed. (I) Snapshot of an ablation at C(E,N)|C(E,N) contact in wildtype ommatidium, red cross indicates the ablation point. (J) Quantification of initial recoil speed of C(E,N)|C(E,N) (n = 14), P(E)|P(E) (n = 18) and C(E,N)|P(E) (n = 19) contacts in wildtype ommatidia. P-values are shown above the black horizontal lines. (K) Quantification of initial recoil speed in C(E,N)|C(E,N) (n = 14), C(E)|C(E) (n = 18) and C(E,N)|C(E) (n = 17) contacts in NcadM19 mosaic mutants. Scale bar, 5 µm. P-values are shown above the black horizontal lines.

https://doi.org/10.7554/eLife.22796.005
Figure 2—source data 1

Dataset for Figure 2C,F,J and K.

https://doi.org/10.7554/eLife.22796.006

Apart from MyoII, we also observed differences in Ecad levels when comparing C(E,N)|C(E,N), C(E)|C(E), C(E,N)|C(E) contacts (Figure 2—figure supplement 1F,G,H, Supplementary file 1 -table 2), raising the possibility that the changes in MyoII levels might be a consequence of Ecad homotypic interactions. However, MyoII levels are uncorrelated with Ecad levels, ruling out this possibility (Figure 2—figure supplement 1G and H).

MyoII level anti-correlates with cell contact length (Figure 2—figure supplement 1G,H), which is consistent with the idea that MyoII regulates length. One can argue that the knowledge of MyoII distribution is not sufficient to characterize contractility and that F-actin distribution and organization might also be an important determinant (Reymann et al., 2012). Thus, we stained for F-actin using phalloidin and found that F-actin is mostly apical and junctional like MyoII, but its distribution does not strictly correlate with that of MyoII; homotypic C(E,N)|C(E,N) contacts show higher F-actin level than C(E,N)|P(E), C(E,N)|C(E), P(E)|P(E) and C(E)|C(E) contacts (Figure 2—figure supplement 2A–C).

In an attempt to determine the relationship between MyoII-dependent contractility and tensile forces at cell contacts, we performed laser nano-dissection experiments (Rauzi et al., 2008). The initial recoil speed after the cell contact ablation served as a proxy for interfacial tension (Figure 2G–I, Figure 2—figure supplement 2D, Videos 1 and 2). We found that tension at C(E,N)|C(E) contacts was the highest while tension at C(E,N)|C(E,N) contacts was the lowest (Figure 2J,K). These values correlate with the levels of MyoII (compare Figure 2C and J or Figure 2F and K) and are consistent with the hypothesis that MyoII is a major determinant of interfacial tension.

Video 1
Download asset
Laser nano-ablation of C(E,N)|C(E,N) contact in wildtype ommatidium.

Ablation at 00:00:00. Frame rate is 1 s/frame. Labelling: β-cat::GFP. Scale bar, 5 μm.

https://doi.org/10.7554/eLife.22796.011
Video 2
Download asset
Laser nano-ablation of C(E,N)|C(E) contact in NcadM19 mosaic ommatidium with polar (Pl) and posterior (P) cone cells(see Figure 5A for cone cell axes of polarity) lacking Ncad.

Ablation at 00:00:00. Frame rate is 250 ms/frame. Labelling: Ecad::GFP. Scale bar, 5 μm.

https://doi.org/10.7554/eLife.22796.012

Bound and unbound N-cadherin differentially impact on Myosin–II junctional localization

To determine whether and how Ncad might control cell shape through MyoII regulation, we focused on the links between Ncad and MyoII localization. We observed high level of Ncad at homotypic contacts (C(E,N)|C(E,N)) which also exhibit the lowest concentration of MyoII, by 1.8 fold lower than the P(E)|P(E) cell contacts. This suggests that homophilic Ncad at homotypic contact reduces MyoII levels (Figure 2A,C), in agreement with the idea that cadherin lowers interfacial tension at cell contacts (Maître and Heisenberg, 2013). At heterotypic contacts (C(E,N)|P(E)), where Ncad cannot form transhomophilic bond, Ncad was found at very low level (Figure 1C, Figure 1—figure supplement 1A) and MyoII at a higher level than at any other contact (Figure 2A,C). This suggests that unbound Ncad at heterotypic contact signals to MyoII and induces its accumulation. To confirm this hypothesis, we took advantage of the fact that the primary pigment cells do not express Ncad and asked if we could modify MyoII level at different cell contacts by Ncad misexpression.

Ncad misexpression in one of the primary pigment cell affected the shape of cone cells in contact with it (Figure 3A,B). Homophilic Ncad was detected at the C(E,N)|P(E,N+) contacts (Figure 3—figure supplement 1A and A’, yellow arrowhead) and MyoII levels at these modified contacts (C(E,N)|P(E,N+), Figure 3A,B, yellow arrowhead) were significantly reduced compared to wildtype C|P contacts (C(E,N)|P(E), Figure 3A,B, green arrowhead, Supplementary file 1 - table 1). This confirms our hypothesis that homophilic Ncad reduces MyoII level (Figure 3C). In addition, higher level of MyoII was detected at contacts between primary pigment cells with one of them misexpressing Ncad (P(E)|P(E,N+)) (Figure 3A,D red arrowhead) than at contacts between wildtype primary pigment cells expressing only Ecad (P(E)|P(E)) (Figure 3A,B,D, Supplementary file 1 -table 1).

Figure 3 with 3 supplements see all
Download asset Open asset
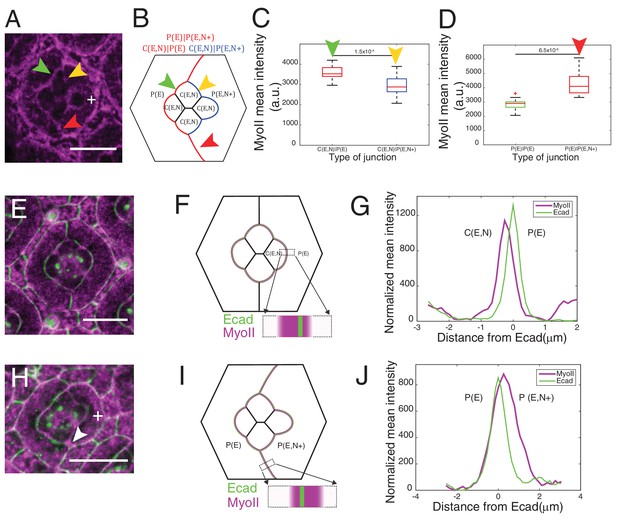
Misexpression of Ncad in primary pigment cells and MyoII accumulation and MyoII asymmetry at cell contacts.

(A) An ommatidium with Ncad misexpressed in one of the primary pigment cells (white +) with Zip::YFP in magenta. Green arrowhead indicates the C(E,N)|P(E) contact. Yellow and red arrowheads indicate the modified C(E,N)|P(E,N+) and P(E)|P(E,N+) contacts respectively. (B) A schematic of Ncad misexpression ommatidium with the modified C(E,N)|P(E,N+) (blue), wildtype C(E,N)|P(E) and modified P(E)|P(E,N+) (red) contacts. (C) Quantification of MyoII intensity in C(E,N)|P(E) (n = 20) and C(E,N)|P(E,N+) (n = 20) contacts. P-value is shown above the black horizontal line. (D) Quantification of MyoII intensity in P(E)|P(E) (n = 16) and P(E)|P(E,N+) (n = 16) contacts. P-value is shown above the black horizontal line. (E) Wildtype ommatidium with Ecad::GFP (green) and Sqh::Ch (magenta). (F) Schematic with a zoom-in of a C(E,N)|P(E) contact shared by cone cell and primary pigment cell representing the asymmetric distribution of MyoII. (G) Average linescan of Sqh::Ch (magenta) intensity with respect to Ecad::GFP intensity (green) normal to interfaces (n = 10 interfaces). (H) An ommatidium with Ncad misexpressed in one of the primary pigment cell (white +) with Sqh::Ch (magenta). White arrowhead indicates the modified P(E)|P(E,N+) contact. (I) Schematics with a zoom-in of a modified P(E)|P(E,N+) contact shared by primary pigment cell and Ncad misexpressed primary pigment cell representing the asymmetric distribution of MyoII. (J) Average linescan of Sqh::Ch intensity (magenta) with respect to Ecad::GFP intensity (green) (n = 13 interfaces). Scale bar 10 µm.

https://doi.org/10.7554/eLife.22796.013
Figure 3—source data 1

Dataset for Figure 3C,D,G and H.

https://doi.org/10.7554/eLife.22796.014

To test whether such property of Ncad is specific to the retinal epithelium or more general, we performed clonal misexpression of Ncad in the larval wing pouch which cells express only Ecad. We noticed higher level of MyoII at the boundary of clones compared to MyoII inside the clones or to the surrounding wildtype tissue (Figure 3—figure supplement 1B,C, cyan arrowheads). This indicates that MyoII regulation by Ncad is not specific to the retina.

At C(E,N)|P(E) contacts, Ncad is asymmetrically localized as it is expressed only in one of the two apposed cells. We thus wondered whether MyoII could also be asymmetrically localized. To address this, we measured the intensity profile of MyoII perpendicular to C(E,N)|P(E) contacts, using Ecad intensity as a marker for the contact position. Localization of Ecad::GFP, and thus the contact position, can be determined with a precision better than the diffraction limit given the high signal/noise ratio (5–22 nm) (Figure 3—figure supplement 2, See Materials and methods). We found that MyoII maximum intensity was systematically shifted towards the cell that expressed both Ecad and Ncad (Figure 3—figure supplement 2A,B). Importantly, the distance between MyoII and Ecad intensity peaks (Figure 3—figure supplement 2C) was found larger than the imprecision in peaks’ localization (Figure 3—figure supplement 2D, See Material and methods). This significant and systematic shift indicates that MyoII is enriched in the cortex of an Ecad- and Ncad-expressing cell when it is apposed to an Ecad-expressing cell (Figure 3E–G). Using Starry night (Stan), a membrane marker that has a higher signal/noise ratio than Ecad at C(E,N)|C(E,N) contacts (Figure 3—figure supplement 2E), we confirmed the asymmetry of MyoII at C(E,N)|P(E) contacts (Figure 3—figure supplement 2F,G). In contrast, we observed a symmetric localization of MyoII at C(E,N)|C(E,N) contacts (Figure 3—figure supplement 2F,H).

This increase in MyoII level is cell contact autonomous: we observed higher MyoII intensity at C(E,N)|P(E) contacts, irrespective of the other contacts of the cell (for instance, C(E,N)|C(E,N)). This increase is striking in NcadM19 mosaic ommatidia in which a single Ecad- and Ncad-expressing cell is surrounded by Ecad-expressing cells: we noticed an intense ring of MyoII at the cortex (Figure 3—figure supplement 3A,B,C, compare cells marked by white and green arrowheads, Figure 3—figure supplement 3C). To further confirm the above observation, Ncad was again misexpressed in primary pigment cells to check if it could induce MyoII asymmetry at the modified P(E)|P(E,N+) contacts. An asymmetric localization of MyoII in cells that express both Ecad and Ncad was observed at the P(E)|P(E,N+) contacts (Figure 3H–J).

To further explore how Ncad at heterotypic contacts could induce MyoII contractility, we expressed only the extracellular part of Ncad in one primary pigment cell (Figure 4A, white +). Such truncated Ncad can form adhesion bonds but cannot interact with the actomyosin network (Figure 4A, white arrowhead). We observed a change in contact shape and MyoII levels at the interface between the wildtype cone cell and primary pigment cell that misexpressed extracellular Ncad (Figure 4B–D, compare blue and red arrowheads, Supplementary file 1 -table 1), which confirms a role for homophilic Ncad bonds in the downregulation of MyoII contractility. However, MyoII levels at the contact between primary pigment cells, which included one cell that misexpressed extracellular Ncad showed no change in MyoII, when compared to full-length Ncad (Figure 4B,C,E, green arrowhead, Supplementary file 1 -table 1). This result suggested that cytoplasmic part of Ncad is required for the accumulation of MyoII at the C(E,N)|P(E) contacts.

Figure 4
Download asset Open asset
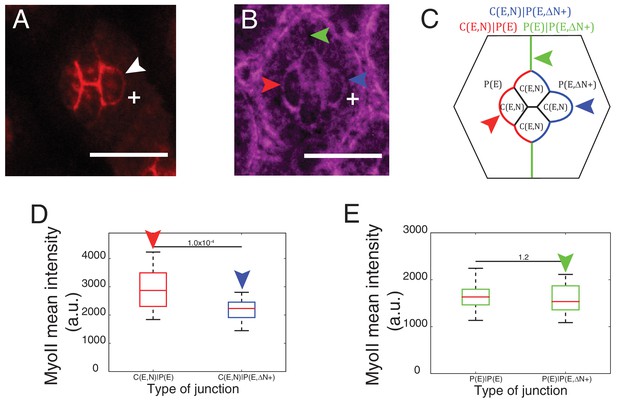
Cytoplasmic part of Ncad is required for MyoII accumulation in heterotypic contacts.

(A–B) An ommatidium misexpressing extracellular part of Ncad in one of the primary pigment cells (white +) with Ncad (A) and Zip::YFP (B). White arrowhead indicates the C(E,N)|P(E,ΔN+) cell contact with homophilic Ncad in (A), red arrowhead indicates C(E,N)|P(E,ΔN+) wildtype cell contact, blue arrowhead indicates modified C(E,N)|P(E) cell contact and green arrowhead indicates the unchanged P(E)|P(E,ΔN+) cell contact. (C) Schematic of ommatidium misexpressing extracellular part of Ncad shows the modified cell contacts, C(E,N)|P(E) contact (blue), wildtype C(E,N)|P(E) contact (red) and unaffected P(E)|P(E,ΔN+) contact (green). (D) Quantification of MyoII intensity in C(E,N)|P(E) (n = 28) and C(E,N)|P(E,ΔN+) (n = 28). P-value is shown above the black horizontal line. (E) Quantification of MyoII intensity in wildtype P(E)|P(E) (n = 19) and unaffected P(E)|P(E,ΔN+) contact (n = 19). Scale bar, 10 µm. P-value is shown above the black horizontal line.

https://doi.org/10.7554/eLife.22796.020
Figure 4—source data 1

Dataset for Figure 4D and E.

https://doi.org/10.7554/eLife.22796.021

The above data suggest that while homophilic Ncad reduces MyoII contractility at homotypic contacts, unbound Ncad is able to activate MyoII, and locally enhance contractility at heterotypic contacts through its cytoplasmic part.

Both local tension and cell-scale contractility determine ommatidia shape

To understand how tensions at cell contacts determine ommatidia shape, we sought to build a simple mechanical model integrating both local tension and cell-scale contractility. Following earlier works, we thus designed a 2D model based on the minimization of a tension-based energy function (Käfer et al., 2007; Hilgenfeldt et al., 2008; Farhadifar et al., 2007). Although retina is obviously a 3D system, we treat the plane of adherens junctions, where both adhesion and MyoII molecules are recruited, as a 2D system. Since retinal cells have a complex shape and are variant in the z-direction, the relevance of the model is therefore limited to the junctional plane. Such an energy-based model assumes that the system settles to a configuration of minimum potential energy, which is likely to be the case in vivo since the developmental process is very slow and quasi-static. We then assume that individual contacts have a local tension γloc. As shown by our experiments, γloc is likely to be determined by the concentration of MyoII and cadherins engaged at the contact. The contribution of γloc at each contact to the total energy of the system is simply γlocl, where l is the contact length. In addition, and as shown by others (Käfer et al., 2007; Hilgenfeldt et al., 2008; Farhadifar et al., 2007), the contractile cortical network and the 3D cell volume constraint are likely to impose a 2D geometry constraint at the cell level. We encapsulate this in a perimeter elasticity term, in which deviations Δp of the cell perimeter p from a preferred cell perimeter p0 yield an energy penalty K2(p−p0)2p0. The elastic constant K, which we assume is the same for all cells, determines how big this penalty is. In two-dimension, the mechanical energy of the ommatidium thus writes:

E=∑contactijγlocijlij+∑cellsiK2(pi−p0i)2p0i

While cell area can vary experimentally, in a range which is likely to be determined by volume constraint and cell elasticity, in the model we chose to fix the area using a Lagrange multiplier. This choice is driven by simplicity arguments. Unlike perimeter elasticity, area elasticity is not crucial to select a shape or configuration, but mostly set the cell size (Hilgenfeldt et al., 2008). Interfacial tension at a cell junction is, by definition, the derivative of the energy function with respect to junction length, and writes:

(1) γij=γlocij+KΔpip0i+KΔpjp0j

Interfacial tension γ is thus the sum of the local term, γloc, and of a cell-scale elastic term, γel=KΔpip0i+KΔpjp0j. Note that ablation experiments reveal the global interfacial tension γ.

The parameters of the model are the target perimeters, the local tensions, and K. We sought to determine as many parameters as possible from experiments. We reasoned that in the absence of forces applied by surrounding cells, cells should acquire their preferred (target) perimeter (Figure 5—figure supplement 1A). We thus performed circular ablations, separating a cell from all its neighboring cells to measure the target perimeter. After ablation, cells relaxed towards a circular shape in the plane of adherens junctions (Video 3). Note that the perimeter after relaxation was found to be typically 8% smaller (8.4 ± 1.2, n = 7) than prior to ablation (Figure 5—figure supplement 1B,C). In addition, laser ablation experiments in Figure 2 provided us with relative estimates of the interfacial tensions (γ) for the different contact types (C(E,N)|C(E,N), P(E)|P(E) and C(E,N)|P(E)). Note that all tensions (including K, which has the dimension of γ) were normalized by the interfacial tension measured for C(E,N)|C(E,N) contacts, and therefore are given in units of C(E,N)|C(E,N)=1. Using that γloc≈γ−2KΔppo and having determined Δppo,K is the only free parameter remaining in the model. To determine its value, we minimized the energy function using the Surface Evolver software starting from an unrealistic configuration (Figure 5—figure supplement 2A), until the equilibrium configuration was reached. We then fitted the resulting ommatidia shapes to experimental shapes using K as a fit parameter. To fit simulations to experimental geometries, we chose two geometrical descriptors: the angle formed by adjacent C|P contacts and the length ratio between two contacts (polar-equatorial (Lm) over polar-posterior (Ls) contacts) (Figure 5A). We simulated the wildtype and four different NcadM19 mosaic ommatidia, and applied a weighted least squares method to fit them altogether (Figure 5—figure supplement 2B). The best fit corresponds to K = 4.2 (in units of γC(E,N)|C(E,N)=1). The cell patterns obtained in silico for this value are in very good agreement with the cell patterns observed in vivo, for wildtype ommatidia and for NcadM19 mosaic ommatidia with different numbers and combinations of wildtype and NcadM19 cone cells (Figure 5B, Figure 5—figure supplement 2C,D). Interestingly, our estimate of K also indicates that elastic tension contributes to 1/3 to 1/2 of the total interfacial tension, depending on the cell contacts considered (Figure 5—figure supplement 2E).

Figure 5 with 4 supplements see all
Download asset Open asset
Simulations of cone cell shapes and contribution of cadherins and MyoII to cell shapes.

(A) Schematics of two axes of polarity, A-P and Eq-Pl, of cone cells (bottom) and fit parameters measured in experiments and simulations, contact angle between cone cell and primary pigment cell (θ), ratio of contact length shared by A/P and Eq/Pl cell (Ls) to contact length shared by Eq and Pl cells (Lm) (top). (B) Comparison of experimental images (lower panel) to the simulations (upper panel), NcadM19 cells are marked by white asterisks. (C) Schematic of force balance resulting from adhesion of Ecad (ωE, green) and Ncad (ωN, red), MyoII dependent cortical tension at the cell contact (σ) and cortex elasticity due to actomyosin at the cell perimeter (γel) (both in magenta). (D) Relative contribution of MyoII dependent cortical tension (σ), Ecad adhesion (wE) and Ncad adhesion (wN) to the local tension term γloc for all contact types in wildtype and NcadM19 mosaic mutants. (E–E') Image of the ommatidium with (E) Eq and (E') Eq and Pl cone cells SqhAx3 mutant (white -). β-catenin staining in green. (F–F') Image of the ommatidium with (F) Eq and (F') Eq and Pl cone cells expressing constitutively active form of Sqh, SqhT20ES20E (white +), β-catenin staining in red. Scale bar, 10 µm.

https://doi.org/10.7554/eLife.22796.022
Video 3
Download asset
Laser nano-ablation of target perimeter measurement (Δp/po).

Ablation at 00:00. Frame rate is 250 ms/frame. Labelling: β-cat::GFP. Scale bar, 5 μm.

https://doi.org/10.7554/eLife.22796.031

The balance of cortical tension and adhesion determines local tension

The rationale of the model presented above is to predict ommatidia shapes from tensions at the cell contacts measured by ablations, irrespective of MyoII or cadherin levels. Yet, local tension is likely to result from the balance between MyoII-dependent cortical tension and cadherin-based adhesion (Lecuit and Lenne, 2007), and we were interested in weighing their respective (direct) contributions. To do so, we measured concentrations of cadherin and MyoII molecules in different configurations for which we knew the local tension.

We assumed that adhesion molecules and motor molecules have an additive and antagonistic contribution to local tension (Maître et al., 2012). Hence, MyoII cortical tension σ is balanced by cadherin based adhesion ω, so that γloc= σ - ω (Figure 5C). At C(E,N)|C(E,N) contacts, both Ecad and Ncad contribute to the adhesion term, so that ω = ωE + ωN, while at C(E,N)|P(E) and P(E)|P(E) contacts, only Ecad contributes to adhesion, and ω = ωE. For the sake of simplicity, we assumed that adhesion and MyoII-dependent cortical tension were proportional to the concentrations of cadherins and MyoII, respectively. It should be noted that whether MyoII molecules are recruited through an Ncad feedback or any other pathway is not relevant to how they contribute to local tension. Hence the feedback between MyoII and Ncad is not considered to estimate the respective contribution of cadherin and MyoII molecules to tension. From there, we could use the molecular concentrations (Figure 2C,F, Figure 5—figure supplement 3A,B and E,F) and local tensions γloc obtained from ablation experiments combined to numerical modelling (Figure 2J,K and Figure 5—figure supplement 2E) to infer the contributions of Ecad, Ncad and MyoII to the local tension of the different contact types (See Materials and methods). We found that MyoII has a very significant contribution to local tension, which is about two to five times higher than that of Ncad or Ecad depending on the contact type (Figure 5D). This data, in agreement with in vitro experiments on cell doublets (Maître et al., 2012), emphasizes the quantitative role of MyoII on cell shapes in vivo. It also indicates that control of cell shape by adhesion is mostly indirect, through the regulation of MyoII level by unbound Ncad. This is again exemplified by the higher contribution of MyoII to local tension in C(E,N)|P(E) and C(E,N)|C(E) contacts than in P(E)|P(E) and C(E)|C(E) contacts (Figure 5D, middle and bottom panels).

To confirm the importance of MyoII on cone cell shapes, we manipulated MyoII activity in cone cells. We first decreased MyoII contractility using Myosin-II light chain loss of function (SqhAx3) mutant (Figure 5E,E’), and observed a massive increase in cell apical area in the mutant cells and change in cell contact length (Figure 5—figure supplement 4A Supplementary file 1 - table 2). Conversely, misexpression of constitutively active form of MyoII (SqhT20E.S21E) leads to a reduction of cell apical area (Figure 5F,F’) and change in cell contact length (Figure 5—figure supplement 4B). These changes in apical area suggest that shape changes resulting from MyoII loss of function or misexpression are dominated by cell-scale (apical MyoII) rather than cell contact-scale contribution of MyoII. This is exemplified by our simulations, in which a simple change of the (fixed) area yields a qualitatively good prediction of cone cell shapes in different mutant configurations (Figure 5—figure supplement 4, See Materials and methods). A more quantitative assessment on these experiments would most likely require additional terms of area elasticity. Note that to exemplify experimentally the contribution of MyoII to local tension, one would ideally want to selectively downregulate or upregulate MyoII at cell contacts only, which is technically very challenging.

Myosin-II localization mediated by N-cadherin regulates cell arrangement

Lastly, to test the relevance of our data for tissue morphogenesis, we analyzed ommatidia morphogenesis in wildtype and NcadM19 mosaic retinas, 21 hr after pupal formation (APF) for 5 and 9 hr, respectively (Figure 6A,B and Videos 4 and 5). Wildtype cone cells undergo stereotypic neighbor exchanges (Figure 6A). Anterior and posterior cells lose A-P contact, while equatorial and polar cells intercalate and form a new Eq-Pl contact (A-P to Eq-Pl contact transition) (Figure 5A). However, when imaging the NcadM19 mosaic mutants, we observed defects of this A-P to Eq-Pl transition. 98,2% of analyzed ommatidia where Ncad was mutated in either the equatorial or polar cell failed to transit (Figure 6B, red arrowheads, Figure 6C, n = 114). 100% of analyzed ommatidia where Ncad was mutated in both equatorial and polar cells failed to transit (Figure 6D, n = 16). We reasoned that this transition might be prevented due to the increase in tension at the transverse cell contacts where C(E,N)|C(E,N) contacts are transformed into C(E,N)|C(E) contacts, and indeed observed increased levels of MyoII in these contacts (Figure 6E,F). To further test this hypothesis, we estimated the energy of the system as a function of the central junction length in both vertical and horizontal configurations (Figure 6G,H). Note that this required to fix that length during the minimization process. We found that the model predicts an energy minimum in the vertical configuration in both cases (when either 1 or 2 of the polar and equatorial cells are Ncad mutants), consistent with our experimental observations. Thus, cell mechanical properties, indirectly controlled by Ncad expression, not only impact on cell shapes but also on cell arrangement.

Figure 6
Download asset Open asset
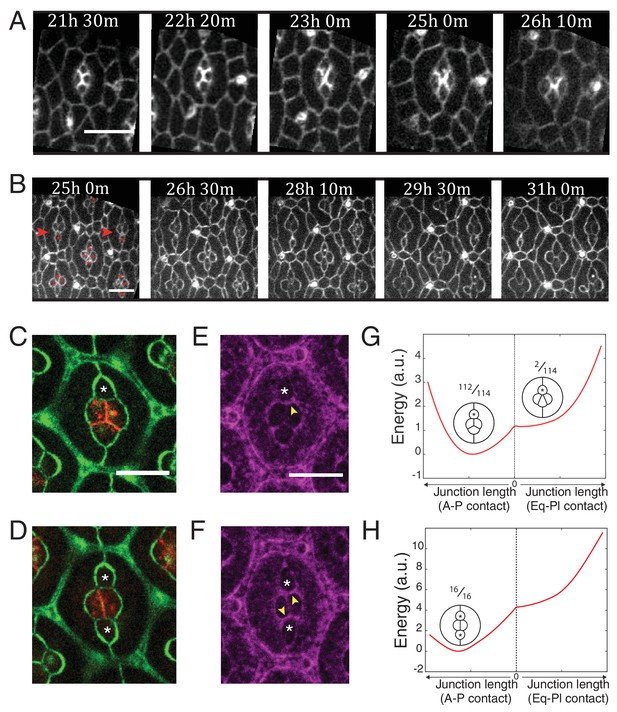
Ncad mediated MyoII contractility impacts on cone cell arrangements.

(A) Snapshots of a movie at different APF from wildtype retina labelled with β-cat::GFP. Scale bar, 5 µm. (B) Snapshots of a movie at different APF from NcadM19 mosaic mutant with Ecad::GFP and NcadM19 cells (red asterisks). Mosaic ommatidia that failed to undergo normal cell rearrangement are indicated by red arrowheads. Scale bar, 5 µm. (C), (E) Equatorial NcadM19 cone cell (white asterisk) in mosaic mutant with Ecad::GFP (green) and Ncad (red) in (C) and Zip::YFP (magenta) in (E) (both (C) and (E) total n = 112). (D), (F) Image of equatorial and polar NcadM19 cone cells (white asterisks) with Ecad::GFP (green) and Ncad (red) in (D) and Zip::YFP (magenta) in (F) (both (D) and (F) total n = 16). (G) Energy profile of ommatidia with an equatorial NcadM19 cone cell as a function of the central contact length (left direction: vertical contact length, right direction: horizontal contact length). Diagrams show corresponding simulations, with occurrence numbers observed experimentally. (H) Energy profile of ommatidia with equatorial and polar NcadM19 cone cells as a function of the central contact length (left direction: vertical contact length, right direction: horizontal contact length). Diagrams show corresponding simulations, with occurrence numbers observed experimentally.

https://doi.org/10.7554/eLife.22796.032
Video 4
Download asset
A-P to Eq-Pl transition in wildtype retina.

Movies starting from 21:30:00 APF. Frame rate is 10 min/frame. Labelling: β-cat::GFP. Scale bar, 5 μm.

https://doi.org/10.7554/eLife.22796.033
Video 5
Download asset
Defects in cell rearrangements in NcadM19 mosaic mutants.

Movies starting from 25:00:00 APF. Frame rate is 10 min/frame. Labelling: Ecad::GFP. Scale bar, 5 μm.

https://doi.org/10.7554/eLife.22796.034

Discussion

We showed that the adhesion provided by Ecad and Ncad homophilic bonds have a moderate direct contribution to interfacial tension as compared to MyoII dependent contractile forces. Our in vivo findings are consistent with in vitro measurements using the shapes of cell doublets to infer the relative contribution of adhesion and cortical tension to interfacial tension (Maître et al., 2012). Here we demonstrate that in vivo, the contribution of adhesion to interfacial tension is roughly half of MyoII cortical tension. Our data indicate that the hypotheses of differential contractility (Harris, 1976; Brodland, 2002) or differential adhesion (Steinberg, 1963) are not mutually exclusive, and the balance of contractility and adhesion determines cell shapes, cell arrangement (Lecuit and Lenne, 2007; Käfer et al., 2007; Hilgenfeldt et al., 2008) and cell sorting (Krieg et al., 2008). The moderate contribution of adhesion bonds to interfacial tension might explain why cadherin binding affinities are not predictive of cell sorting outcomes in vivo and in vitro (Shi et al., 2008; Leckband and Sivasankar, 2012).

Our work unravels a cell-scale (autonomous) and a junction-scale (non-autonomous) control of cell shape through actomyosin contractility. Following previous models of epithelial mechanics (Käfer et al., 2007; Hilgenfeldt et al., 2008), we confirm that actomyosin contractility generates a cell-scale elastic tension at the cell periphery, which restricts cell deformation. This elastic tension is likely to be dependent on the stiffness of the actomyosin network bound to the membrane (Salbreux et al., 2012). Our data constrain the model and reduce the number of free parameters down to one, an effective elastic constant. Our model shows that the cell-scale elasticity is crucial to stabilizing the four-cone cell arrangement and it is possible that cell elasticity also ensures correct global patterning of the retina. Analysis of our measurements of mechanical properties and quantification of molecular distribution demonstrate that MyoII contractility also contributes locally to tension at cell contacts (cortical tension) to shape cone cell arrangement. This local contribution of MyoII to tension was not considered in previous works (Käfer et al., 2007; Hilgenfeldt et al., 2008). The cell-scale elasticity and junction-scale cortical tension contributions are on the same order of magnitude (Figure 5—figure supplement 2E) and are both crucial to predicting cell shape.

MyoII distribution and thus contractility is strongly dependent on cadherins. While the role of Ecad on contractility during tissue morphogenesis is well documented (Lecuit and Yap, 2015), the role of Ncad is poorly known. We identified a dual role of Ncad on cell shapes and cell arrangement. Junctional N-cadherin bonds yield contact expansion between Ncad-expressing cells. However, this effect is moderate and cannot alone account for the shapes of cells in the ommatidia. Through the determination of MyoII distributions at cell contacts, we uncovered another mechanism mediated by Ncad at heterotypic cell contacts, where a low level of Ncad is detected at junctional plane (unbound). Heterotypic contacts between cells expressing Ecad and Ncad and cells expressing Ecad only exhibit increased local contractility as compared to homotypic contacts. This difference in contractility cannot be explained only by differences in adhesion contributed by both Ecad and Ncad. This is a junction-autonomous property, as in an Ecad- and Ncad-expressing cell (C), we observed increased contractility at heterotypic contacts irrespective of the other contacts of the cell (heterotypic and/or homotypic). Our data suggest that unbound Ncad has the ability to redirect MyoII at heterotypic contacts via its signaling intracellular region. Interestingly, this does not seem to be specific to the retina and might be a more general mechanism, as suggested by our observations in the larval wing disc. N-cadherin was found to polarize MyoII contractility directly through it cytoplasmic partners such as β-catenin (Ouyang et al., 2013) or indirectly through its interplay with Ecad (Scarpa et al., 2015), presumably through an indirect mechanism. Cadherin-mediated adhesion is tightly coupled to actomyosin through small GTPase including Rho and antagonistic Rac (Takeichi et al., 1997; Ratheesh et al., 2013). Homophilic N-cadherin dimerization activates Rho (Comunale et al., 2007; Charrasse et al., 2002; Marrs et al., 2009; Taulet et al., 2009; Puvirajesinghe et al., 2016) and Rac (Matsuda et al., 2006). Also, actin organisation has been shown to be able to affect MyoII (Reymann et al., 2012). We did not detect any significant variation in Rho activities among different contacts of the ommatidia using a biosensor which detects active Rho1 (Munjal et al., 2015)(data not shown). Further experiments will be required to resolve the mechanism by which unbound Ncad could activate MyoII.

High MyoII contractility induced by cell contact molecules at tissue boundary has a significant impact on tissue separation (Dahmann et al., 2011; Major and Irvine, 2006; Fagotto, 2014). In Drosophila, supracellular actomyosin structures are found at boundaries in wing imaginal discs (Major and Irvine, 2006; Landsberg et al., 2009; Monier et al., 2010; Umetsu et al., 2014; Bielmeier et al., 2016) and embryos (Monier et al., 2010; Röper, 2013; Laplante and Nilson, 2011). We show here that the four cone cells in ommatidia form a boundary with primary pigment cells through increased MyoII contractility at the C(E,N)|P(E) heterotypic contacts. This MyoII cable is reminiscent of that triggered by Crumbs anisotropy at the border of placodes in the Drosophila (Röper, 2012). Cells inside the placodes have higher levels of Crumbs than cells outside placodes. In the peripheral placode cells, Crumbs homophilic interactions, which are thought to negatively regulate MyoII, lead to the selective accumulation of the Myosin cable at the boundary depleted of Crumbs. One could envision that Ecad anisotropy could lead to the accumulation of MyoII at the cell contacts having a high level of Ecad. We ruled out this possibility here as we found conditions where MyoII and Ecad anisotropy do not correlate (Figure 2—figure supplement 1G). In the retina, we showed that accumulation of MyoII is junction-autonomous and determined by the expression of adhesive molecules in the apposed cells.

At the heterotypic contacts, MyoII is asymmetrically distributed: it is mainly localized at the cortex of the Ecad and Ncad expressing cells. A recent study on the localization of polarity proteins on either side of cell interfaces made a similar observation (Aigouy and Le Bivic, 2016). From a mechanical point of view, the asymmetry of MyoII is an interesting observation as it suggests that tension can be set and modified asymmetrically. As a consequence, shrinkage or extension of a junction might be driven unilaterally from one of the two apposed cells. So far mechanical models of epithelia, including ours, do not take asymmetry into account, a property which would be interesting to explore further in the future. The adhesion molecules that are engaged in trans-bonds at cell contacts are symmetric in the apposed membranes. Thus, they cannot be the direct cause of this asymmetry. Instead, our data suggest that asymmetrically distributed unbound Ncad could signal to MyoII and cause its asymmetry. While asymmetric localization is an essential feature of planar polarity components (Goodrich and Strutt, 2011), it is largely unexplored for other junction constituents. It will be important to determine whether cytoskeletal components and regulators and members of adhesion complexes, also show asymmetric localization.

High MyoII contractility at contacts between two cell types might represent a general mechanism, which could be important for lineage sorting and elimination of misspecified cells (Bielmeier et al., 2016). Given the importance of E- to N-cadherin switch in epithelial-mesenchyme transition (Wheelock et al., 2008), our findings may also have implications in other developmental processes.

Materials and methods

Drosophila stocks and genotypes

Request a detailed protocol

To visualize Myosin-II in wildtype retinas, we used Zip::YFP(CPTI-100036) and SqhAX3 /FM7; sqh-Sqh ::GFP flies (Karess et al., 1991). To quantify the levels and asymmetry of Myosin-II at contacts in both NcadM19 mutant and misexpression background, we used Zip::YFP (RRID:DGGR_115082) and Sqh-Sqh::Cherry (Martin et al., 2009) as probes respectively. FRT40A, NcadM19 mutants and UAS-Ncad flies were gifts from Tadashi Uemura (Iwai et al., 1997). UAS-NcadΔcyto flies was a gift from C.H. Lee (Yonemura et al., 2010). UAS-SqhT20ES20E flies (RRID:BDSC_64411) was a gift from R. Karess (Jordan and Karess, 1997). SqhAx3 FRT19A/FM7 flies (RRID:BDSC_25712) are from Bloomington Drosophila stock centre. In laser ablation experiments, Ecad::GFP (RRID:BDSC_60584) (Huang et al., 2009) and β-catenin::GFP (Huang et al., 2011) knock-in flies used for visualizing the AJs were gifts from Y. Hong. Ncad::mKate2 flies are generated in house using the CRISPR/Cas9 technique (Port et al., 2014). Ncad::GFP flies are from the service of inDROSO. See belows for details of both Ncad knockin flies.

Genotypes used in experiments were as followed:

Figure 1A: Ncad::mKate2, Ecad::GFP

Figure 1C: Ncad::GFP

Figure 1D: Ecad::GFP

Figure 1E: Zip::YFP/ +

Figure 1F: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 1G: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 1- figure supplement 1A: Ncad::GFP

Figure 1- figure supplement 1B: SqhAx3; sqh-Sqh::GFP/ sqh-Sqh::GFP

Figure 1- figure supplement 1C: Zip::YFP/ +

Figure 1- figure supplement 1D: SqhAx3; sqh-Sqh::GFP/ sqh-Sqh::GFP

Figure 2A-C: Zip::YFP/ +

Figure 2D-F: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 2I-J: β-catenin::GFP

Figure 2K: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 2- figure supplement 1A-C: SqhAx3; sqh-Sqh::GFP/ sqh-Sqh::GFP

Figure 2- figure supplement 1E: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A NcadM19

Figure 2- figure supplement 1F: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 2- figure supplement 2A-C: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 2- figure supplement 2D: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 3A-D: hsFLP; Zip::YFP/ UAS-Ncad; ActGal4, UAS-RFP/ +

Figure 3E-G: SqhAx3; Ecad::GFP; sqh-Sqh::mCherry

Figure 3H-J: hsFLP; UAS-Ncad/ ActGal4 UAS-GFP, sqh-Sqh:mCherry/ +

Figure 3- figure supplement 1A-A’: hsFLP; Ecad::GFP/ UAS-Ncad; ActGal4, UAS-RFP/ +

Figure 3- figure supplement 1B-C: hsFLP; UAS-Ncad/ActGal4, UAS-GFP/; Sqh::Ch/+

Figure 3- figure supplement 2A-D: SqhAx3; Ecad::GFP; sqh-Sqh::mCherry

Figure 3- figure supplement 2E-H: w

Figure 3- figure supplement 3A-C: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 4A-E: hsFLP; UAS-NcadΔcyto/ Zip::YFP; Act-Gal4 UAS-RFP/ +

Figure 5B: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 5E-E’: Ubi-mRFP.nls, FRT19A/ FRT19A, SqhAx3;; eyFLP/ +

Figure 5F-F’: hsFLP; UAS-SqhT20ES20E/+; ActGal4, UAS-RFP/ +

Figure 5- figure supplement 3A-B: Ecad::GFP

Figure 5- figure supplement 3E-F: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 5- figure supplement 4C’: Ubi-mRFP.nls, FRT19A/ FRT19A, SqhAx3;; eyFLP/ +

Figure 5- figure supplement 4D’: hsFLP; UAS-SqhT20ES20E/+; ActGal4, UAS-RFP/ +

Figure 6A: β-catenin::GFP

Figure 6B-D: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Figure 6E-F: eyFLP; Zip::YFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Movie 1, 3, 4: β-catenin::GFP

Movie 2, 5: eyFLP; Ecad::GFP, FRT40A, GMR-Gal4 myr-RFP/ FRT40A, NcadM19

Genetics and immunochemistry

Request a detailed protocol

FLP/FRT system with eyFLP was used to create mosaic mutant tissues. Gal4-UAS system with hsFLP was used to induce targeted gene expression. 10 min heat-shock was performed 72 hr after egg deposition. Pupae were staged by collecting white prepupae and incubating at 25°C for the indicated times. Retinas were fixed in 4% of paraformaldehyde (PFA) in PBS for 20 mins, washed three times with PBS, permeabilised with PBT (PBS + 0.3% Triton x100), blocked with PBS + 10% NGS (Cat#50197Z, Life technology, CA, USA), immunostained with the indicated primary antibodies in PBS + 10% NGS at 4°C overnight and secondary antibodies for 2 hr at room temperature.

Primary antibodies used rat anti N-cadherin (DSHB Cat# DN-Ex 8 RRID:AB_528121) 1:20, rat anti E-cadherin (DSHB Cat# DCAD2 RRID:AB_528120) 1:20, mouse anti-β-catenin (DSHB Cat# N2 7A1 ARMADILLO RRID:AB_528089), 1:10 and mouse anti-stan #74 (DSHB Cat# Flamingo #74 RRID:AB_2619583), 1:10 (Developmental Studies Hybridoma Bank [DSHB]) and rabbit anti-Phospho-Myosin light Chain-II (Ser19) Antibody, 1:100 (RRID:AB_330248, #3671, Cell Signalling Technology, MA, USA). Secondary antibodies used were goat anti-mouse Alexa 488, goat anti-rabbit Alexa 555 and goat anti-rat/mouse Alexa 633 (1/500) (ThermoFischer Scientific, MA, USA). Fluorescence images were acquired with a Zeiss LSM780 confocal microscope with ×63, 1.4 N.A oil immersion objective. Images typically have 5–6 stacks, 0.5 μm apart.

Time-lapse imaging of living pupal retinas

Request a detailed protocol

Pupae at indicated time after pupal formation were dissected and mounted on glass slides as described previously (Corrigall et al., 2007). Prepared samples in a temperature control chamber at 25°C were imaged using a Nikon spinning-disc Eclipse Ti inverted microscope with ×100, 1.4 N.A oil immersion objective. MetaMorph software was used and images were acquired every 10 min for 12 hr. Every image has ~10 stacks, 1 μm apart and stacks featuring the apical junctions were registered using Fiji. Wildtype retinas live imaging was performed with β-cat::GFP flies and NcadM19 mosaic mutant live imaging was with Ecad::GFP flies.

Laser ablation experiment and analysis

Request a detailed protocol

Laser ablation experiments were performed as previously described (Rauzi et al., 2008). Experiments were performed in NcadM19 mosaic mutants labelled with Ecad::GFP, NcadM19 mutant cells were differentiated from wildtype cells by RFP signal. Ablations in wildtype were performed on flies labelled with β-catenin. For C(E,N)|P(E) ablation experiments, contacts shared by equatorial or polar with primary pigments cells were used.

The recorded images of ablation were analysed in ImageJ by measuring the opening distance between vertices of the ablated junction. This opening distance was plotted over time and linear fit over the first 10 points was used to the recoil speed, which is used as an estimate of interfacial tension.

Quantification of MyoII intensity

Request a detailed protocol

PFA-fixed retinas with Zip::YFP or Sqh::Ch to mark MyoII were imaged with Zeiss LSM780 confocal microscope and images were quantified by Fiji. Fluorescence signal at C(E,N)|P(E) contact can be clearly marked by ROI (generally of Linewidth 4 (0.439 µm) of the segmented ‘selection’ tool). Once the Line width is chosen for C(E,N)|P(E) contact same is used for the P(E)|P(E) and C(E,N)|C(E,N). To localize the P(E)|P(E) and C(E,N)|C(E,N)contacts, marked RFP signal was used (Figure 2—figure supplement 2A, right panels). Background was measured from the lowest frame of the image (~2.5 μm below from the adherens junction). Remaining stacks were summed on Z project (images were taken with 4–5 Z slices of 0.5 μm). Then, with chosen ROI junctional Myosin-II intensity at various contact type i. e. C(E,N)|C(E,N), C(E,N)|P(E), P(E)|P(E), C(E)|C(E) and C(E,N)|C(E), excluding the vertices, were measured. Mean intensity was measured using ‘measure’ tool of Fiji and background was subtracted from each.

Quantification of asymmetric localization of MyoII

Request a detailed protocol

To determine MyoII localization with respect to cell contacts, we imaged retinas with Zip::YFP or Sqh::Ch to mark MyoII and Ecad::GFP to mark Ecad as a proxy for contact position. The images were acquired with a Zeiss LSM780 confocal microscope and quantified using Fiji. Intensity plot profiles (‘Plot profile tool’) for MyoII and Ecad were drawn from line segments of about 5 µm (generally of Linewidth 8 (1.05µm) of the segmented ‘selection’ tool) intersecting cell contacts orthogonally and at their middle. Mean intensities values were plotted for MyoII and Ecad. We used Gaussian fits to determine the position of intensity peaks and the signal to noise ratio of individual intensity line traces to estimate the precision in localization (Bobroff, 1986). We used multicolour Tetraspek microspheres 200 nm diameter (Invitrogen/Life Technologies, CA, USA) to measure the chromatic shift between red and green channels, which was found to be 50 and 70 nm in x, y directions, respectively.

Angle θ measurement and ratio Lm/Ls measurement

Request a detailed protocol

The ‘Angle’ tool in Fiji was used to measure the angle θ. The brightest pixel at the contact point was used as the angle vertex. Angles are measured for different types of cell contacts between cone cells and primary pigment cell, in wildtype as well as in NcadM19 mosaic conditions. The lengths are measured using the straight line ‘Selection’ tool of Fiji.

Statistics

All the statistical analyzis was done in Matlab. We used the non-parametric Mann-Whitney U test on pairs and systematically applied a Bonferroni correction for multiple comparisons. Note that P-values shown in graphs include the Bonferroni correction (p>0.5, N.S). Summary for all the statistical value is in Supplementary file 1 – table 3.

Simulations

Request a detailed protocol

Simulations were performed with Surface Evolver version 2.7 (Brakke, 1992). Mesh grooming was implemented during minimization by refinement, and various refinement lengths have been tested to ensure that the system had really reached energy minima. The perimeter elasticity term in the energy function (Equation 1) was programmed by method instance, which can be defined in the datafile. Tension was specifically set for each contact depending on its type (See parameter measurements and model simulations section).

Parameters measurements and model simulations

Request a detailed protocol

Simulations of ommatidia rely on the minimization of the energy function using Surface Evolver. Surface Evolver is a freely available software (Brakke, 1992) designed for the study of objects maintained by surface energy (in our 2D case, line energy) and other customizable forms of energy (in our case, perimeter elasticity). Surface Evolver evolves the given surface towards its minimal energy by a gradient descent method. Area of each cell is fixed in the model, even though the apical area can change experimentally. This choice is driven by simplicity arguments. Indeed, area variations could be accounted for with an area elasticity term (in the form KA(A−A0)2, where KA is the area elastic constant, and A and A0 are the actual and preferred area, respectively). Yet, and unlike perimeter elasticity, area elasticity is not crucial to select a shape or configuration (Hilgenfeldt et al., 2008) but mostly to set cell area. Hence, we chose to fix the area so that it matches the experimentally measured one, which spared us from having additional free parameters (KA and A0). In MyoII perturbation experiments, in which cell area is significantly modified, we changed the fixed area to that measured in experiments.

The simulation parameters are γloc, which depends on the cell contact type, the elastic constant K, which we assume constant for all cells, and the preferred perimeters p0. Using our circular ablation experiments to determine preferred perimeters, our measurements of γ for the different contact types, and the fact that γloc≈γ−2KΔpp0, K is the only free parameter remaining. We ran simulations with K ranging from 0.1 to 6 and fitted the resulting shapes to wildtype and Ncad mosaic ommatidia. The geometrical descriptors that we used for the fit are i) the contact angle θ between cone cells and primary pigment cells, and ii) the ratio Ls/Lm. Ls is the length of the junction shared by the posterior/anterior cone cell and the polar/equatorial cell, and Lm is the length of the junction shared by equatorial and polar cells (Figure 5A). To actually perform the fit, we calculated the sum of residuals for the measured angles and ratios in five configurations (one wildtype +4 different NcadM19 mosaic configurations), hence 2 x 5 = 10 residuals. We used a weighted least square method to take into account that the descriptors (an angle and a length ratio) are different quantities. Note that to simulate Ncad mosaic ommatidia, we only changed the parameter γloc according to the contact type. For example, if the anterior cone cell lacks Ncad, then its contacts shared with equatorial and polar cone cells become C(E,N)|C(E) and its contact shared with the primary pigment cell becomes C(E)|P(E). Tensions were set according to the ablation experiments performed for each contact type.

Estimation of the contribution of adhesion and cortical tension to γloc

Request a detailed protocol

Local tension γloc results from the balance between MyoII contractility σ and cadherin-based adhesion ωN, and we were interested in weighing their respective (direct) contributions. In order to do so, we assumed that adhesion molecules and motor molecules have an additive and antagonistic role. Hence we have γloc= σ - ω. ω = ωE + ωN if both Ecad and Ncad are present at the contact, and ω = ωE if only Ecad is present. We assumed that σ is proportional to MyoII intensity (σ = αCM) and ω proportional to Cadherin intensity (ωE = βCE for Ecad and ωN = δCN for Ncad). Tension measurements combined to intensity measurements provide an equation for each contact type (C(E,N|C(E,N), C(EN)|P(E), P(E)|P(E), C(E,N)|C(E) and C(E)|C(E)), so that we have 5 equations for 3 unknowns (α, β, and δ). We use a least square fit method to find the best solution to this overdetermined system, thus estimate (α, β, δ) and consequently determine the relative contributions of MyoII (σ), Ecad (ωE) and Ncad (ωN) to γloc for the different contact types (Figure 5D).

Simulations of MyoII mutants and MyoII overexpression

Request a detailed protocol

MyoII manipulation experiments changed the apical areas of the cone cells and length of the cell contacts (Figure 5—figure supplement 4A,B). Myosin-II light chain (SqhAx3) mutant cone cells showed larger apical surface area than their wildtype counterparts. Cone cells misexpressing the constitutively active Myosin-II light chain (UAS-SqhT20ES21E) showed smaller apical surface area than their wildtype counterparts. To simulate the shape of these perturbed cells, we measured the area (A) of these cells to fix it in the simulations and the target perimeter by p0=2Aπ. The in silico patterns obtained for this simple change in area and target perimeter are in good agreement with the in vivo cell patterns (Figure 5—figure supplement 4C,C’, D,D’, E).

Cell contact length measurement in ommatidium with two NcadM19 cone cells

Request a detailed protocol

PFA-fixed retinas with Ecad::GFP and RFP to differentiate wildtype from NcadM19 mutant cells were used to measure the junction length of C(E,N)|C(E,N), C(E)|C(E), C(E,N)|C(E) cell contacts in ommatidia with two adjacent cone cells NcadM19 mutants. Lengths were measured using ‘line tool’ of Fiji. Different types of lengths measured in an ommatidum is normalized to its C(E,N)|C(E,N) length.

Quantification of Ecad intensity

Request a detailed protocol

PFA-fixed retinas with Ecad::GFP and RFP to differentiate wildtype from NcadM19 mutant cells. Images were obtained with Zeiss LSM780 confocal microscopy and Fiji was used for quantification. Background subtraction was not used since the background was nearly zero. Stacks were summed on ‘Z project’. Linewidth 4 (0.659µm) of the segmented ‘selection’ tool was used to measure the mean intensity of junctional Ecad according to the contact type.

Quantification of MyoII intensity in NcadM19 mosaic ommatidia with only one wildtype Ecad and Ncad expressing cone cell

Request a detailed protocol

PFA-fixed retinas with Zip::YFP to mark MyoII and RFP to differentiate wildtype from NcadM19 cells were imaged with Zeiss LSM780 confocal microscope and images were quantified by Fiji. Stacks were summed on ‘Z project’ for all the images. Background was measured from the center (apical region) of any cone cell. Linewidth 4 of the segmented ‘selection’ tool was used to measure mean intensity around wildtype cell and around NcadM1 mutant cell. Background was subtracted from wildtype and mutant mean intensities for each image. After background subtraction, intensities were compared (wildtype n = 41, mutant n = 41).

Quantification of F-Actin intensity

Request a detailed protocol

PFA-fixed retinas with Zip::YFP to mark MyoII, RFP to differentiate wildtype from NcadM19 mutant cells and phalloidin staining for F-actin. Images were obtained with Zeiss LSM780 confocal microscopy and Fiji was used for quantification. Stacks were summed on ‘Z project’. Linewidth 7 (0.615µm) of the segmented ‘selection’ tool was used to measure the mean intensity of junctional F-Actin according to the contact type (junctional Zip::YFP was used for the reference).

Quantification of Ncad intensity

Request a detailed protocol

PFA-fixed retinas with Ncad::GFP were obtained with Zeiss LSM780 confocal microscopy and Fiji was used for quantification. Line width 5 (0.659µm) of the segmented ‘selection’ tool was used to measure the mean intensity. For each measurement at the C(E,N)|C(E,N) and C(E,N)|P(E) contacts, background is measured adjacent to the contact and subtracted from the signal at junctions.

Analysis of localization error in Ecad or MyoII peaks

Request a detailed protocol

The localization precision ΔX of Ecad or MyoII peaks was evaluated using (Bobroff, 1986) ΔX∼1.8SNRΓδx, where Γ is the standard deviation of the Gaussian fit of the intensity profiles, SNR is the signal to noise ratio, and δx is the pixel size. Typical values were ΓEcad~250 nm, ΓMyoII~300 nm, SNREcad~34 and SNRMyoII~10 and δx=131 nm. The analysis of multiple intensity profiles (n=10) led to ΔXEcad = 5–22 nm and ΔXMyoII = 18–77 nm.

Generation of CRISPR/Cas9 mediated Ncad::eGFP flies

Request a detailed protocol

Ncad::eGFP flies were designed and generated by inDROSO functional genomics (France). eGFP was inserted just before the stop codon of Ncad with a flexible linker GVG and the resulting flies was validated by sequencing. Homozygous flies are viable and occasionally exhibit islets of black cells.

Generation of CRISPR/Cas9 mediated Ncad:mKate2 flies

Plasmid construction

Request a detailed protocol

Cloning was performed with the Gibson assembly Mix (New England Biolabs, Ipswich, MA, USA). PCR products were produced with the Phusion Hot Start II HF DNA Polymerase (ThermoFischer Scientific, MA, USA). All inserts were verified by sequencing. Primers used for plasmid construction are listed in Supplementary file 1 - table 4. Primers gRNA-NCadFw and gRNA-NCadRev were used to obtain the Ncad-gRNA from pACMAN BAC DN.CAD CH321-57H14. pCFD3 plasmid containing the U6:3 promoter (from Addgene no. 49410; Port et al., 2014) was used to clone annealed complementary Ncad oligo-nucleotides into the BbsI digested backbone using standards procedures to produce the following 5'-to-3' configuration: U6 promoter-gRNA-Ncad-gRNA core sequence. The construct was inserted in the attP2 site on chromosome three to generate transgenic flies (BestGene Inc., Chino Hills, CA, USA).

Ncad::mKate2 donor plasmid production

Request a detailed protocol

The donor plasmid was designed to introduce a mKate2-coding sequence before the stop codon of Ncad. The exogenous sequence is flanked by homology arms of 2.31 kb (5' homology) and 1.46 kb (3' homology). The 5' homology arm contains a synonymous mutation that removes the protospacer-adjacent motif (PAM) sequence for g-RNA-NCAD to prevent mutagenesis after the integration of donor-derived sequences. The 5' and 3' homology arms were PCR amplified from genomic DNA from the clone pACMAN BAC DN.CAD CH321-57H14 using primers Ncad5'. For, Ncad5'.Rev, Ncad3'-For, Ncad3'-Rev. The mKate2 coding sequence was amplified from a mKate2-containing plasmid (Shcherbo et al., 2009) using the primers mKate2For and mKate2Rev. The sequences of all the primers can be found in Supplementary file 1- table 4. All fragments were assembled by Gibson assembly Mix into pBluescript SK(+) (Stratagene, La Jolla, CA, USA) that was digested with XhoI and NotI.

Embryo injections

Request a detailed protocol

Embryos from crosses between transgenic nos-cas9 (BL 54591) virgin females and U6:3-gRNA-NCAD-expressing males were injected using standard procedures. Plasmid DNA for homologous recombination-mediated integration of mKate2 into the NCAD locus was injected at a concentration of 300 ng/µl into the nos-cas9/+;U6:3-gRNA-NCAD/+ embryos. After injection of plasmids, embryos were transferred on their coversplips to a plastic box containing wet paper towel at 25°C until they hatched as larvae. Larvae were collected with forceps and transferred to a food vial with fresh yeast, followed by culture at 25°C.

Drosophila genetics and screen

Request a detailed protocol

Approximately 2% of the injected Nos-cas9/+; gRNA-NCAD/+ larvae survived the injection and were crossed to a w; Sp/CyO balancer strain. In the next generation (F1), the males were conserved at 18°C and five females were pooled for genomic extraction and PCR screen. The quality of the DNA extraction was tested with the TIO-F and TIO-R primers. The presence of mKate2 insertion in the genome was detected by PCR using the m-Kate2-Fw and m-Kate2-Rv primers. When an amplification was obtained for mKate2, 30 F1 males were crossed individually with w; Sp/CyO females. When the F2 generation is well developed, the F1 male was sacrified to extract the genomic DNA and screen for the presence of mKate2. Then, the progeny of positive male was amplified and stored. To confirm that the sequences remain in-frame after the CRISPR integration, the DNA sequence surrounding the fusion was amplified by PCR using primers NCAD-F2 and mKate2R2 (Supplementary file 1 - table 4) and checked by sequencing. The resulting Ncad::mKate2 flies are homozygous viable.

References

Decision letter

  1. Frank Jülicher
    Reviewing Editor; Max Planck Institute for the Physics of Complex Systems, Germany

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Patterned cortical tension mediated by N-cadherin controls cell geometric order in the Drosophila eye" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by K VijayRaghavan as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

This work is a timely addition to older studies that focused on the mechanics of cell shape and arrangement in the fly eye. Earlier work revealed the importance of mechanical cell bond tension for tissue morphology and implicated differences of adhesion strength between different cell types as a significant factor for tissue morphology. Lenne and colleagues have now taken this a step further and looked at cell bond contractility and separated contributions from adhesion and myosin contractility to effective bond tension. They found evidence for differences of contractility at different cell bonds and a role of both adhesion and myosin mediated contractility. Interestingly, levels of N-cadherin adhesion molecules appear to down regulate myosin levels and thereby cell bond tension. This work provides an important step forward to our understanding of cell packings in the fly eye. However the present manuscript has a number of problems and shortcomings. Some of the experimental evidence presented is not sufficiently clear and the authors need to be more comprehensive in the way they present the data and provide more information. Also, the analysis of the data using a simple model of cell bond mechanics is rather murky and remains in parts unclear and unconvincing. Overall the presentation of the work needs to be significantly improved before this manuscript could be suitable for publication in eLife.

Essential revisions:

Experimental Analysis

Experiments are well controlled and quantified using excellent reagents. However, some of the analysis requires improvement or better explanation.

1) The authors fail to properly highlight a major feature of the system in the main text. As the authors show, loss of N-Cadherin leads to the accumulation of high levels of E-Cadherin at junctions that were previously high in N-Cadherin. Similar crosstalk between these two adhesion molecules is observed in many other systems. Because of this, and because of the very low levels of N-Cadherin present at C/P interfaces in the wildtype, I do not think the paper does enough to show that low level N-Cadherin functions in the absence of homotypic interactions to modify MyoII levels at junctions. While the authors are careful in their discussion to avoid suggesting that there is a direct link between N-Cadherin and MyoII, to make this clearer the authors should modify the Results section and should present the complete data set (all data points) for each type of cell-cell interface in the wildtype, N-cadherin and Squash mutant condition. In each case, it would be best to provide the full set of primary data for: E and N cadherin levels, ii) MyosinII levels, and iii) junction lengths. This would help the reader to determine, for example, the extent to which the amounts of MyoII and E-Cadherin between cells in an N-cadherin mutant are independent of junctional curvature, variance in the system, and how loss/gain of MyoII changes the lengths of different type of cell-cell junction. In this vein, I think the nomenclature is confusing. After all, there is very little N-cadherin at an EN/E interface.

2) The analysis of localized Myo2 activity is tricky and could be prone to error. The authors use three proxies: Zip, Sqh and anti-phospho-Myo. Zip and Sqh signals are more frequently used, but choosing where to measure fluorescence instensity in the images is problematic. The signal is fairly diffuse and except for CP interfaces, not noteceably concentrated at membranes. How they choose the ROI to measure will be error-prone. Likewise, the P-Myo signal is highly punctated and therefore, ROI choice will introduce variation. For example, the difference between E/E and EN/EN intensity is pretty small for P-Myo and much bigger for Sqh, yet both are supposed to be proxies of the same thing. Did the authors use a control membrane marker to guide choice of ROI (eg myr-RFP) and act as a normalization agent? Since much of the data is analyzed this way, some clearer sense of how much measurement error exists should be made and shown. They should also test how well co-imaged P-Myo, Zip, and Squ measurements correlate with one another across all interfaces.

3) The analysis shown in Figure 4 is very tricky, where the authors attempt to see if Myo2 localization is biased with respect to the membrane interface. Images shown in the figure suggest that is difficult to analyze. Since the diffraction limit of detected light is much bigger than distance across an adherens junction interface, which is 100 nm, this is a technical stretch. They aligned Myo intensity traces with respect to the supposed peak of E-cad localization, but the E-cad traces are not shown. They need to also show the traces of E-cad, centering peaks and registering Myo2. In other words, how much uncertainty is there in assigning peak position to E-cad? Another problem is the low sampling number n=10. 10 scans across same cell? How did they choose the place to transect the membrane? No description of this analysis is provided in the methods. Was it done by line scan? It should be an area scan. This analysis requires elaboration. They should do the same with N-cad and Myo2 at EN/E interfaces. If their interpretation is correct, there should be less bias in the Myo2 localization with respect to N-cad, since both are present in only one cell of the interface. They need to also scan Myo2 with E-cadherin at E/E and EN/EN interfaces. If they are right, then Myo2 will be centered. Overall, I think this is a weak line of evidence, not super crucial to the paper, and better left out or more substantiated.

4) In Figure 5D and E – the authors claim there is no difference in Myo2 levels at an EN/E PP interface with extracellular N-cad misexpression in one P cell. But the N of the analysis is smaller than the N of the other experiments, N=10, and there is a trending difference apparent, a slight reduction in Myo2 levels. They should increase the sample size and if the trend continues, it will become statistically significant. So the interpretation of this part is a bit iffy.

5) The statistical analysis employed throughout uses only a parametric t-test. The implicit assumptions of this test (normal distribution and homogeneity of variance) are not always met by the data as it appears in their box and whisker plots. There is often varied variance and skewed distributions that appear more like gammas. The authors should instead perform pair-wise or multi-group non-parametric tests to test their hypotheses. And since they are performing multiple pair-wise tests per experiment, a Bonferroni correction should be systematically applied.

6) Interpretation of N-cadherin effects on Myo2

The work nicely shows that N-cad affects Myo2 localization. But what about other way around – is it mutually dependent or epistatic? Since they made Sqh mutant C cells, instead of looking at catenin, did the authors look at effect on N-cadherin levels?

In Figure 4C – EN/EN CP ectopic interface does not have 2-fold lower Myo2 than the EN/E CC interface in Figure 2F. Unlike the EN/EN CC interface which does. It suggests something else is also at work in affecting Myo2 localization. In Figure 4D, EN/E PP interface has 33% more Myo2 than E/E PP interface. Similar to C/C situation. This is a better controlled expt to analyze.

Maybe the small amount of N-cad at C/P edges is N-cad paired to E-cad. Heterotypic pairing is known in mammalian systems. The authors claim N-cad is unpaired at these interfaces but that only assumes homotypic bonding. They should discuss and qualify.

7) The majority of MyoII in the system appears to be concentrated at three way vertices where cells meet, not along junctions as suggested. The authors should take this into consideration. This also creates problems for data analysis, since it leads to an over-estimate of the levels of MyoII at short interfaces. The authors should be explicit in explaining how they have dealt with this.

8) The authors don't comment on the effects of MyoII accumulation on one-side of a junction. On the same topic, why isnt MyoII gone from the homophilic junction EN/ENdelta in Figure 5B, given that MyoII is supposed to be on the N-Cadherin side (4F), i.e. it should be subject to N-Cadherin inhibition.

Analysis of the experiments based on the mechanical model

A simple model for cell mechanics is proposed to capture the basic features of cell packings. The model is postulated but not really tested. There are several problems with the analysis of the data based on the model and as a consequence, the conclusions taken by the authors are not fully convincing.

1) Overall the interpretation of relative impact of contractility and adhesion is unclear and muddled. At one point the authors say the effect of adhesion on shape is mostly indirect. In the Discussion, they say it is also direct. One possibility is to re-organize the manuscript to deal with the issue near the end of the results and all at once using several lines of presented evidence. Because as it stands, they hop onto the issue sporadically as new data appears. The message is very mixed. A coherent multi-pronged approach will help in clarity.

2) A related issue about clarity: the model is based on the idea that contributions to tension gamma_loc from cadherin and from myosin are linear and additive. However, a theme of the work is the idea that cadherin influences myosin levels and myosin mediated contractile tension. This is presented in a fully coherent way. Either the system is intrinsically coupled and nonlinear. Then one cannot linearly superimpose the contributions of cadherins and myosins. Or alternatively, the system is simple and linear. Then a regulation of myosin by cadherins foes not fit in the picture. This is probably mainly problem of the presentation which is confusing.

3) With their surface evolver model, they could quantify the different contributions by comparing simulations where adhesion terms are differential and contraction terms are uniform, versus simulations where both are differential. Then compare solutions to experimental data, to ask how different is each to experiment. They could repeat the modeling where contraction is always differential, and adhesion is either uniform or differential.

4) They continually interpret together analysis of C/P cell interfaces with analysis of chimeric C interfaces or chimeric P interfaces. They are assuming that the only variable in C and P cells is N-cadherin. But that is not true – they are very different cell types, occupying different positions in space. The most highly controlled situations for their experiments is where either C cells or P cells are chimeric for either N-cadherin or Sqh. The only known variable is N-cad or Sqh. When weighing on the contributions of N-cadherin versus contactility, these are the cleaner subjects for analysis.

5) I like their analysis in Figure 3G where they find contractility has about 3/4 impact on local tension and N-cad adhesion about 1/4 impact. Another way of looking at this is to normalize laser ablation retraction speed with local Myo2 intensity for the C/C interface. When I estimated this for C/C interfaces Speed/Zip (x10^-5) is EN/EN 3.3; E/E 4.6; EN/E 3.8. Tension normalized for contractility is not identical for the three interface types, yet they would be the same if tension was only affected by differential contractility. This suggests that N-cad reduces tension at interfaces independent of its effects on Myo2, and is consistent with reducing tension through adhesion. But since non-normalized tension at E/E interfaces is two-fold more than at EN/EN interfaces, clearly contractility is also important.

6) Figure 3 shows that the energy profile has two minima, separated by a large barrier. It is suggested that the lower minimum is selected by the cells and describes the observed cell packing ("the most favorable configuration" according to the authors.). However, the principle from equilibrium thermodynamic that energy minima are selected does not apply to systems out of thermodynamic equilibrium such as tissues. Therefore both energy minima could be selected by the system. It is quite unclear given the proposed model why only one of these minima is selected. The fact that the model has two competing minima but that only one configuration is observed in WT leaves some doubts about the origins of the observed packing geometry and the validity of the model. It should be noted that the question of how the system selects the equatorial-polar cone cells in contact is very interesting. The proposed mechanism however based simply on energy minimization seems incomplete at best and could be wrong.

7) The model is based on the idea that cell area is fixed. However it is quite unclear what mechanisms keep area fixed. Furthermore, some myosin perturbations do lead to area changes as the authors report. If a fixed area is considered, it would be important to show that area is indeed fixed under at least some perturbations.

8) When looking at the supplement, "simulation" is explained to be "energy minimization" which is not a simulation. It is not explained how the energy minimization is done, how accurate it is etc.

9) The authors are quite careless with physical units. The interfacial tension γ and the elasticity K have units and the text is written as if the values of these parameters are determined. However different dimensionless ratios are discussed. This is not clearly distinguished from real values and it is sometimes unclear what dimensionless ratios are actually considered (e.g. Figure 3—figure supplement 1E).

10) The key parameter gamma_loc is determined from Video 3. I would like to see a proper analysis determining this (dimensionless) parameter.

11) The authors use the term "adhesion force" to describe bond tension related to cell adhesion molecules. I have some doubts that this concept is well defined and I do not see it defined in the present paper.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Patterned cortical tension mediated by N-cadherin controls cell geometric order in the Drosophila eye" for further consideration at eLife. Your revised article has been favorably evaluated by K VijayRaghavan (Senior editor), and two reviewers, one of whom is a member of our Board of Reviewing Editors.

The manuscript has been significantly improved. Both the writing and presentation of the Results and Discussion are greatly improved over the original submission. The text is now very clear and the figures are also improved. The authors have also made good efforts to address concerns and questions. It is quite convincing that NCad influences differential myosin localization along specific interfaces, and this contributes to the differential tensions of interfaces, and ultimately sculpts the cone and primary pigment cells. This represents a significant advance of the field. There are a few remaining issues that need to be addressed before acceptance. In particular panels G and H in Figure 6 might be somewhat misleading.

Specific comment:

Figure 6G and H results appear misleading. The authors used the Surface Evolver to find minimal energy solutions to cell patterns constrained by genotype. But Surface Evolver is also constrained by cell neighbor relations: cell-cell contacts are not automatically rearranged unless a user "pushes" the program to do so. Thus, starting with Eq and Pl cones in contact with each other will not lead to their rearrangement into Ant – Post cone contact, no matter what parameter values are provided. Likewise, starting with Ant – Post cones in contact, as the authors did in Figure 6GH will result in a minimal solution with Ant-Post cones still in contact, no matter what "genotypes" the cells have, WT or mutant. This could mislead the reader into thinking that the initial conditions of cell neighbor relations are identical in the Figure 6GH solutions as those shown in previous model solutions (Figure 5). And therefore the reader might incorrectly conclude that the models use identical starting conditions for cell neighbor relations. The authors could delete the panels G and H, and simply show the results of Figure 6I and J. These compare energies for different minimizations using different starting conditions. It is not surprising that the authors do not show a comparable energy profile for a wildtype ommatium because the A-P junction valley for WT may still be lower than the Eq-Pl junction valley. If true, this would further add to doubts as to the utility of applying the surface evolver method to analyzing cell-cell rearrangements.

https://doi.org/10.7554/eLife.22796.037

Author response

Essential revisions:

Experimental Analysis

Experiments are well controlled and quantified using excellent reagents. However, some of the analysis requires improvement or better explanation.

1) The authors fail to properly highlight a major feature of the system in the main text. As the authors show, loss of N-Cadherin leads to the accumulation of high levels of E-Cadherin at junctions that were previously high in N-Cadherin. Similar crosstalk between these two adhesion molecules is observed in many other systems. Because of this, and because of the very low levels of N-Cadherin present at C/P interfaces in the wildtype, I do not think the paper does enough to show that low level N-Cadherin functions in the absence of homotypic interactions to modify MyoII levels at junctions. While the authors are careful in their discussion to avoid suggesting that there is a direct link between N-Cadherin and MyoII, to make this clearer the authors should modify the Results section and should present the complete data set (all data points) for each type of cell-cell interface in the wildtype, N-cadherin and Squash mutant condition. In each case, it would be best to provide the full set of primary data for: E and N cadherin levels, ii) MyosinII levels, and iii) junction lengths. This would help the reader to determine, for example, the extent to which the amounts of MyoII and E-Cadherin between cells in an N-cadherin mutant are independent of junctional curvature, variance in the system, and how loss/gain of MyoII changes the lengths of different type of cell-cell junction. In this vein, I think the nomenclature is confusing. After all, there is very little N-cadherin at an EN/E interface.

We thank the reviewer(s) for this constructive comment. A major feature of the system, the ommatidia, is the existence of contacts between cells differentially expressing two types of Cadherins, namely E-Cadherin and N-Cadherin. This feature makes the ommatidia an ideal system to study the mechanics of heterotypic contacts. We have now emphasized it in the main text and by revising the Result section which should highlight the main features.

In response to reviewers’ concern on the clarity of data presentation and interpretation, we now provide a complete raw dataset for E/Ncad, MyoII levels and junction length in wildtype, Ncad and Sqh mutant conditions (New Supplementary file 1-Table 1 and 2). In Ncad mosaic mutant condition, a graph showing the relationship among contact length, cadherin and MyoII is added (New Figure 2—figure supplement 1G for Ncad mosaic retinas with 2 mutant cells adjacent to each other and, H for all Ncad mosaic retinas with different combinations of NcadM19 and WT cells). In addition, we have renamed the contacts which now clarify the cell types, cone cell (C) and primary pigment cell (P), as well as the type of Cadherins, Ecad (E) and Ncad (N) expressed in the cells. We introduced and explained the new nomenclature in Figure 2. Clearer presentation of data will assist the readers from understanding the role of cadherins and MyoII in junction length/cell shapes and also resolve reviewers’ concern on the role of Ncad, in inducing MyoII at heterotypic contacts.

In fact, heterotypic contacts between cells expressing Ecad only and Ecad and Ncad exhibit increased local contractility as compared to homotypic contacts. We observed this irrespective of the type of cells in contact: wild type cone cell contacting primary pigment cell (C(E,N)|P(E)), WT cone cell contacting Ncad mutant cone cell (C(E,N)|C(E)) and primary pigment cell overexpressing Ncad contacting WT primary pigment cell (P(E,N+)|P(E)) (Supplementary file 1-Table 1).

If such increased MyoII level would be a consequence of changes in homotypic interactions of Ecad one would expect Ecad level to show a correlation with MyoII level. Figure 2—figure supplement 1G and H show this is not the case. In contrast, we observe change in MyoII when we manipulate Ncad (Figure 3A-D). This is a junction-autonomous property, as in an Ecad- and Ncad-expressing cell, we observed increased contractility at heterotypic contacts irrespective of the other contacts of the cell (Figure 3—figure supplement 3A-C). Our data suggest that unbound Ncad has the ability to redirect MyoII at heterotypic contacts, presumably via its signaling intracellular region.

To further test the generality of our observations, we also generated Ncad misexpressed clones in the larval wing pouch, a system in which cells express Ecad but not Ncad. We consistently found that the MyoII level is increased at the boundary between N+ clones and the surrounding tissue (New Figure 3—figure supplement 1B,C, cyan arrowheads).

2) The analysis of localized Myo2 activity is tricky and could be prone to error. The authors use three proxies: Zip, Sqh and anti-phospho-Myo. Zip and Sqh signals are more frequently used, but choosing where to measure fluorescence instensity in the images is problematic. The signal is fairly diffuse and except for CP interfaces, not noteceably concentrated at membranes. How they choose the ROI to measure will be error-prone. Likewise, the P-Myo signal is highly punctated and therefore, ROI choice will introduce variation. For example, the difference between E/E and EN/EN intensity is pretty small for P-Myo and much bigger for Sqh, yet both are supposed to be proxies of the same thing. Did the authors use a control membrane marker to guide choice of ROI (eg myr-RFP) and act as a normalization agent? Since much of the data is analyzed this way, some clearer sense of how much measurement error exists should be made and shown. They should also test how well co-imaged P-Myo, Zip, and Squ measurements correlate with one another across all interfaces.

We are fully aware of the fact that MyoII activity measurement could be prone to error and that’s why we tested and provided quantification from all the reporters of MyoII activity (Zip, Sqh and P-Myo) we have in hands. We now include also the raw data for the quantification (corresponding source data files). As suggested by reviewer, we also co-imaged Zip::YFP or Sqh::GFP with P-Myo (New Figure 1—figure supplement 1C,D). Note that although P-Myo antibody labelling has been validated and widely used in various studies in retinas (Warner et al., 2009, Yashiro et al., 2014, Deng et al., 2015), its staining remained punctate and fuzzy. Our P-myo staining in WT retinas (New Figure 1—figure supplement 1C,D) is consistent with P-Myo images in Yashiro et al., 2014 Figure 4, with highest P-Myo staining in C|P and lowest in C|C. To conclude, despite slight differences in the subjunctional distribution of various MyoII reporters, we show a consistent relative difference in mean intensity comparing the different types of contacts (New figure 1—figure supplement 1C and D, Supplementary file 1- Table 1) and using the same protocol for analysis (Materials and methods, subsection “Quantification of Myoll intensity”). In wildtype ommatidia, MyoII level is higher at C(E,N)|P(E) contact than at P(E)|P(E) and the latter is higher than at C(E,N)|C(E,N). The same trend is observed in Ncad- mosaic mutants at which MyoII level is higher at C(E,N)|C(E) than at C(E)|C(E) and the latter is higher than at C(E,N)|C(E,N) (Figure 2F).

3) The analysis shown in Figure 4 is very tricky, where the authors attempt to see if Myo2 localization is biased with respect to the membrane interface. Images shown in the figure suggest that is difficult to analyze. Since the diffraction limit of detected light is much bigger than distance across an adherens junction interface, which is 100 nm, this is a technical stretch. They aligned Myo intensity traces with respect to the supposed peak of E-cad localization, but the E-cad traces are not shown. They need to also show the traces of E-cad, centering peaks and registering Myo2. In other words, how much uncertainty is there in assigning peak position to E-cad? Another problem is the low sampling number n=10. 10 scans across same cell? How did they choose the place to transect the membrane? No description of this analysis is provided in the methods. Was it done by line scan? It should be an area scan. This analysis requires elaboration. They should do the same with N-cad and Myo2 at EN/E interfaces. If their interpretation is correct, there should be less bias in the Myo2 localization with respect to N-cad, since both are present in only one cell of the interface. They need to also scan Myo2 with E-cadherin at E/E and EN/EN interfaces. If they are right, then Myo2 will be centered. Overall, I think this is a weak line of evidence, not super crucial to the paper, and better left out or more substantiated.

The analysis of Myo-II localization with respect to the membrane interface is based on the localization of Ecad::GFP, which can be determined with a precision better than the diffraction limit, provided a high signal-to-noise ratio (see for example, Bobroff N, Rev Sci Ins 1986, 57:1152–1157). The new Figure 3—figure supplement 2A,B shows a linescan (width =1.05µm) of Ecad::GFP and Sqh::Ch orthogonal to junctions between P-C (between points a-b) and C-P (between points c-d).

First, we found that Myo-II intensity peaks always shifted toward C cells (n=10 different junctions), whatever the orientation of junctions. Given the signal-to-noise ratio of intensity linescan, the interface positions were localized with a precision of 5-22nm (New Figure 3—figure supplement 2C) (Bobroff N, 1986.). MyoII peaks were localized with a precision of 18-77nm (New Figure 3—figure supplement 2C). We used multicolour 200 nm diameter Tetraspeck (Invitrogen/Life Technologies) to measure the chromatic shift between red and green channels, which was found to be 50 and 70 nm in x, y directions, respectively. The distance between E-cad and MyoII peaks was found larger than the sum of the localization errors (New Figure 3—figure supplement 2D). This further proves that MyoII is predominantly localized in the CCs.

We found consistent results using Starry night (Stan) as a membrane marker (New Figure 3—figure supplement 2E,F,G,H, n=15). Scanning C|C interfaces show no significant bias of MyoII localization (Figure 3—figure supplement 2H, n=15); within the experimental error, MyoII intensity is centered on the interface.

Note that although we are able to prove the existence of a spatial bias of MyoII localization towards Ncad expressing cells at heterotypic contacts, a more detailed analysis would be required to determine the positions and thicknesses of the MyoII cortices (Clark et al.,. 2013).

Detail on image acquisition and data analysis are in Materials and methods (“Quantification of asymmetric localization of Myoll”).

4) In Figure 5D and E – the authors claim there is no difference in Myo2 levels at an EN/E PP interface with extracellular N-cad misexpression in one P cell. But the N of the analysis is smaller than the N of the other experiments, N=10, and there is a trending difference apparent, a slight reduction in Myo2 levels. They should increase the sample size and if the trend continues, it will become statistically significant. So the interpretation of this part is a bit iffy.

We have now increased the sample size of the extracellular Ncad misexpression experiments (from N=10 to N= 19) and obtained the same result of no statistical difference (New Figure 4E)

5) The statistical analysis employed throughout uses only a parametric t-test. The implicit assumptions of this test (normal distribution and homogeneity of variance) are not always met by the data as it appears in their box and whisker plots. There is often varied variance and skewed distributions that appear more like gammas. The authors should instead perform pair-wise or multi-group non-parametric tests to test their hypotheses. And since they are performing multiple pair-wise tests per experiment, a Bonferroni correction should be systematically applied.

As requested by the referee, we now use pair-wise non parametric tests (Mann-Whitney test) followed by a Bonferroni correction (Supplementary file 1- Table 3). We also increased the number of samples for some of the measurements (Figure 2J, K, Figure 2—figure supplement 1E, Figure 4D,E). P-values shown in graphs include the Bonferroni correction (P>0.5, N.S).

6) Interpretation of N-cadherin effects on Myo2

The work nicely shows that N-cad affects Myo2 localization. But what about other way around – is it mutually dependent or epistatic? Since they made Sqh mutant C cells, instead of looking at catenin, did the authors look at effect on N-cadherin levels?

We did not observe any obvious change in both Ecad and Ncad levels at different contacts in Sqh mutant and active SqhEE+ misexpressed. Thus, Cadherins and MyoII levels don’t seem to be mutually dependent.

The new data is now listed in Figure 5—figure supplement 4 and Supplementary file 1-Table 2.

In Figure 4C – EN/EN CP ectopic interface does not have 2-fold lower Myo2 than the EN/E CC interface in Figure 2F. Unlike the EN/EN CC interface which does. It suggests something else is also at work in affecting Myo2 localization. In Figure 4D, EN/E PP interface has 33% more Myo2 than E/E PP interface. Similar to C/C situation. This is a better controlled expt to analyze.

We agree with the reviewers that the change in MyoII level at interfaces (C(E,N)|P(E,N+) and (P(E)|P(E,N+)) where ectopically induced Ncad in P cell is not quantitatively comparable with their wildtype counterpart interfaces (C(E,N)|C(E,N) and (C(E,N)|P(E)). This quantitative difference is mostly likely due to the fact that when we misexpress Ncad in P cell, the amount of Ncad is much larger than in a WT cell (Figure 3—figure supplement 1A,A’). As a consequence, the amount of bound and unbound Ncad at the modified junctions is different and not really comparable with WT. In the case of C(E,N)|P(E,N+) contact, we speculate that there will be few Ncad in C cell to make adhesion with many Ncad in P cell, resulting in comparatively little reduction of MyoII level. At P(E)|P(E,N+) contacts, more unbound Ncad is available in P cell to signal MyoII and so we see more MyoII at PP (33% more MyoII). In fact, the purpose of the experiment in Figures 3 and 4 is to make clear that Ncad is able to reduce MyoII when it is engaged in adhesion and to elicit MyoII accumulation when it is unbound. We have no intention to claim those modified contacts are the same contacts as their WT counterparts. However, we would like to stress the fact that the influence of Ncad on MyoII at those modified contacts are qualitatively, if not quantitatively, similar (Supplementary file 1- Table 1). Also, the new nomenclature indicates ectopic Ncad as N+ and cell types (C, P) would clarify the situation.

Maybe the small amount of N-cad at C/P edges is N-cad paired to E-cad. Heterotypic pairing is known in mammalian systems. The authors claim N-cad is unpaired at these interfaces but that only assumes homotypic bonding. They should discuss and qualify.

Indeed, Ncad and Ecad heterophilic pairing exists in mammalian systems (Straub et al., 2011, Labernadie et al., 2017). However, in Drosophila pupal retinas, such interaction seems to be absent as Ecad mutant C cells containing only Ncad lose contact with P cells which have Ecad (Hayashi 2004, Figure 3J-l). We now mention it in Introduction.

7) The majority of MyoII in the system appears to be concentrated at three way vertices where cells meet, not along junctions as suggested. The authors should take this into consideration. This also creates problems for data analysis, since it leads to an over-estimate of the levels of MyoII at short interfaces. The authors should be explicit in explaining how they have dealt with this.

We do not include the vertices in our measurements because vertices are points where three junctions meet. Thus, vertices in fluorescence images are expected to show higher MyoII levels than junctions even in the case of a homogeneous distribution. In addition, as the forces balance at vertices, it is very likely that MyoII at vertices do not contribute to junction tension. This being said, we don’t know why MyoII is found very concentrated in some of the vertices.

8) The authors don't comment on the effects of MyoII accumulation on one-side of a junction. On the same topic, why isnt MyoII gone from the homophilic junction EN/ENdelta in Figure 5B, given that MyoII is supposed to be on the N-Cadherin side (4F), i.e. it should be subject to N-Cadherin inhibition.

From a mechanical point of view, the asymmetry of MyoII is an interesting observation as it suggests that tension can be set and modified asymmetrically. As a consequence, shrinkage or extension of a junction might be driven unilaterally from one of the two apposed cells. So far mechanical models of epithelia, including ours, do not take asymmetry into account, a property which would be interesting to explore further in the future. See new text lines in Discussion paragraph five.

Concerning the second point, MyoII is gone from the homophilic junction EN/ENdelta in Figure 5B (current Figure 4B), the respective quantification of that is shown in Figure 5D.

Analysis of the experiments based on the mechanical model

A simple model for cell mechanics is proposed to capture the basic features of cell packings. The model is postulated but not really tested. There are several problems with the analysis of the data based on the model and as a consequence, the conclusions taken by the authors are not fully convincing.

1) Overall the interpretation of relative impact of contractility and adhesion is unclear and muddled. At one point the authors say the effect of adhesion on shape is mostly indirect. In the discussion, they say it is also direct. One possibility is to re-organize the manuscript to deal with the issue near the end of the results and all at once using several lines of presented evidence. Because as it stands, they hop onto the issue sporadically as new data appears. The message is very mixed. A coherent multi-pronged approach will help in clarity.

To deal with the clarity issue, we moved the modeling part near the end of the Results section, in which we detail as much as possible the assumptions made and conclusions drawn.

In our Discussion, we now make clear statements about the role of adhesion molecules. Ncad can signal to MyoII, which makes it an indirect contributor to tension, but Ncad is also directly involved in reducing tension via adhesion bonds. See answer to next point (2) for more details about contributions of adhesion in the model.

The new modeling part is starting in subsection “The balance of local tension and cell scale contractility determines ommatidia shape”.

2) A related issue about clarity: the model is based on the idea that contributions to tension gamma_loc from cadherin and from myosin are linear and additive. However, a theme of the work is the idea that cadherin influences myosin levels and myosin mediated contractile tension. This is presented in a fully coherent way. Either the system is intrinsically coupled and nonlinear. Then one cannot linearly superimpose the contributions of cadherins and myosins. Or alternatively, the system is simple and linear. Then a regulation of myosin by cadherins foes not fit in the picture. This is probably mainly problem of the presentation which is confusing.

The rationale of the numerical model is to predict shapes from tensions at the cell contacts measured by ablations, irrespective of MyoII or Cadherin levels. Yet, local tension results from the balance between MyoII contractility and cadherin-based adhesion, and we were interested in weighing their respective (direct) contributions. To do so, we measured concentrations of adhesion and MyoII molecules in different cell contacts in which the local tension was known. Whether MyoII molecules are recruited through an Ncad feedback or any other pathway is not relevant to how they contribute to tension. Hence the weighting process does not involve the feedback between MyoII and Ncad (which could be modeled separately as a regulation network). From there, our choice of linearity was driven by simplicity, and we just assumed (as others Maitre et al., 2012) that adhesion molecules and motor molecules have an additive and antagonistic role. In the end, one can use this weighting to predict local tension, given the amount of MyoII and Cadherins measured at cell contacts.

We clarified in the text that the numerical model’s purpose is to predict shapes from a balance of local and cell-scale tension, while the purpose of the weighting process is to establish respective (direct) contributions of MyoII and Cadherin molecules to local tension. These two steps are now separated in two distinct paragraphs.

Now this can be found in subsection “The balance of cortical tension and adhesion determines local tension”.

3) With their surface evolver model, they could quantify the different contributions by comparing simulations where adhesion terms are differential and contraction terms are uniform, versus simulations where both are differential. Then compare solutions to experimental data, to ask how different is each to experiment. They could repeat the modeling where contraction is always differential, and adhesion is either uniform or differential.

In its current form, the rationale of the Surface Evolver model is to predict shapes from tensions at the cell contacts measured by ablation, irrespective of MyoII or Cadherin levels. Hence in Surface Evolver, local tension is not explicitly separated between contractility and adhesion. What the reviewer first suggests (weight the separate contributions of MyoII and Cadherins directly from Surface Evolver) is possible indeed, but requires adding free weighting parameters to the Evolver model. We thus felt it easier to determine the weight of adhesion and contractility separately using the simple linear system (see above), than to explore a huge parameter space in Surface Evolver, which is prone to get stuck in local minima.

What the reviewer then suggests (repeat the modeling with uniform contraction or adhesion) can still be done a posteriori using the weighting described earlier, and plugging it back into Surface Evolver with separate terms for adhesion and contractility. We did perform these comparisons with uniform/differential adhesion and contractility (see figure below). They indeed confirm that either uniform adhesion or contractility fail to mimic experiments/observations. Yet we feel that going back and forth between surface evolver and weighting might be very confusing to readers, and we decided not to include these in the paper.

Author response image 1
Download asset Open asset

Simulation of an ommatidium with (A) differential adhesion and differential contraction (wildtype), (B) Uniform adhesion and differential contraction, (C) Differential adhesion and uniform contraction (D) Uniform adhesion and uniform contraction.

https://doi.org/10.7554/eLife.22796.036

4) They continually interpret together analysis of C/P cell interfaces with analysis of chimeric C interfaces or chimeric P interfaces. They are assuming that the only variable in C and P cells is N-cadherin. But that is not true – they are very different cell types, occupying different positions in space. The most highly controlled situations for their experiments is where either C cells or P cells are chimeric for either N-cadherin or Sqh. The only known variable is N-cad or Sqh. When weighing on the contributions of N-cadherin versus contactility, these are the cleaner subjects for analysis.

We agree with the reviewers that C cells and P cells are fundamentally different and we should be cautious when concluding the effect of Ncad on MyoII in different cells. This point is now partly addressed by renaming the contacts to prevent confusion. In the manuscript, we have compared contacts from same type of cells, i.e. contacts among C cells in Ncad mutants (Figure 2—figure supplement 1G, H and Supplementary file 1- Table 1 and 2) and Sqh mutants (Figure 5—figure supplement 4A,B and E and Supplementary file 1-Table 2) or contacts among P cells in Ncad or extracellular Ncad misexpressed cells (Supplementary file 1- Table 1 and 2). One might argue that the misexpressing Ncad or extracellular Ncad in P cells experiments should be have been done in C cells. However, as C cells express Ncad, one will need to perform overexpression of Ncad chimera in Ncad mutant background. More sophisticated genetic manipulation, such as the MARCM technique, will have to be deployed. However, we have to emphasize that we consistently see the same trend in MyoII levels changes regardless of the cell types (Supplementary file 1-Table 1).

5) I like their analysis in Figure 3G where they find contractility has about 3/4 impact on local tension and N-cad adhesion about 1/4 impact. Another way of looking at this is to normalize laser ablation retraction speed with local Myo2 intensity for the C/C interface. When I estimated this for C/C interfaces Speed/Zip (x10^-5) is EN/EN 3.3; E/E 4.6; EN/E 3.8. Tension normalized for contractility is not identical for the three interface types, yet they would be the same if tension was only affected by differential contractility. This suggests that N-cad reduces tension at interfaces independent of its effects on Myo2, and is consistent with reducing tension through adhesion. But since non-normalized tension at E/E interfaces is two-fold more than at EN/EN interfaces, clearly contractility is also important.

The alternative method suggested by the reviewer is not completely accurate since it doesn’t take into account the elastic contribution to the tension measured by ablation. Hence we prefer to stick to our analysis.

6) Figure 3 shows that the energy profile has two minima, separated by a large barrier. It is suggested that the lower minimum is selected by the cells and describes the observed cell packing ("the most favorable configuration" according to the authors.). However, the principle from equilibrium thermodynamic that energy minima are selected does not apply to systems out of thermodynamic equilibrium such as tissues. Therefore both energy minima could be selected by the system. It is quite unclear given the proposed model why only one of these minima is selected. The fact that the model has two competing minima but that only one configuration is observed in WT leaves some doubts about the origins of the observed packing geometry and the validity of the model. It should be noted that the question of how the system selects the equatorial-polar cone cells in contact is very interesting. The proposed mechanism however based simply on energy minimization seems incomplete at best and could be wrong.

The referee is right to say that the system is likely out of equilibrium, and therefore might not systematically select the most energetically favorable configuration. Note that the system being very slow it can be considered quasi-static and very likely to sit at least in a local energy minimum (subsection “The balance of local tension and cell scale contractility determines ommatidia shape”). How the minimum is selected in the course of retinal morphogenesis is not solved, and most likely relies on the history of the system, which we barely looked at in the paper. As an example, cone cells undergo a T1 transition during retinal morphogenesis, hence transiting from one minimum to another. How this transition occurs is in itself another project that remains to be addressed.

We therefore removed the Discussion concerning the energy minimization and the corresponding subfigures (current Figure 5). We still show energy landscapes in Figure 6, where we analyze the transition defects, as they are strongly asymmetric with either only one stable minimum, or two minima with on being barely stable (subsection “Myosin-II localization mediated by N-cadherin regulates cell arrangement”).

7) The model is based on the idea that cell area is fixed. However it is quite unclear what mechanisms keep area fixed. Furthermore, some myosin perturbations do lead to area changes as the authors report. If a fixed area is considered, it would be important to show that area is indeed fixed under at least some perturbations.

In experiments, area is not fixed and can vary with MyoII levels, in a range which is likely to be determined by fixed 3D volume constraint and cell elasticity. Yet in the model, the area is fixed by a Lagrange multiplier. This choice is driven by simplicity arguments. Indeed, area variations could be accounted for with an area elasticity term (in the form k_a*(A-A0)^2). Yet, and unlike perimeter elasticity, area elasticity is not crucial to select a shape or configuration (Hilgenfeldt et al., 2008) but mostly sets cell area. Hence we chose to fix the area so that it matches the experimentally measured one, which spared us from having additional free parameters (k_a and A0). In MyoII perturbation experiments, in which cell area is significantly modified, we changed the fixed area to that measured in experiments.

Revised text: subsection “The balance of local tension and cell scale contractility determines ommatidia shape”, paragraph two and Material and methods subsection “Parameters measurements and model simulations”.

8) When looking at the supplement, "simulation" is explained to be "energy minimization" which is not a simulation. It is not explained how the energy minimization is done, how accurate it is etc.

The topology of the surface is defined in a datafile, then Surface Evolver evolves the surface towards minima of energy using a gradient descent method. Hence, the modeling process searches for energy minima in which we assume the system settles. A consequence is that the model has no time scale, but only predicts equilibrium configurations. Nonetheless, we think it could still be called simulations, in the sense that the model simulates an equilibrium shape under given modeling assumptions. Note that other papers modeling these types of systems with minimization techniques also used the “simulation” terminology (Kafer et al., 2007, Hilgenfeldt et al., 2008).

Revised text: Material and methods subsection “Parameters measurements and model simulations”.

9) The authors are quite careless with physical units. The interfacial tension γ and the elasticity K have units and the text is written as if the values of these parameters are determined. However different dimensionless ratios are discussed. This is not clearly distinguished from real values and it is sometimes unclear what dimensionless ratios are actually considered (e.g. Figure 3—figure supplement 1E).

First of all it should be noted that we do not use any absolute physical values for our parameters. This is justified by the fact that ablation experiments only provide relative values of tension. From there, our (arbitrary) choice was to normalize tensions by γC|C, so that all tensions become dimensionless and in units of γC|C. This also sets the scale of our elastic constant K, which also has the dimension of γ, and is therefore also in units of γC|C. The ratios used in figures mentioned by the reviewer were indeed confusing. Hence, we removed all these ratios and only used K in these figures (Figure 5—figure supplement 2B). We now clarify in the text that K is in units of γC|C.

Revised text in the subsection “The balance of local tension and cell scale contractility determines ommatidia shape”.

10) The key parameter gamma_loc is determined from Video 3. I would like to see a proper analysis determining this (dimensionless) parameter.

We haveγloc≈γ−2KΔPP0.γwas measured for each contact type (C|C, C|P and P|P) from ablation experiments. We also estimated ΔPP0 with circle ablation experiments (as shown in Video 3). We were left with the elastic constant K as the only free parameter. To determine it, we varied K (and accordingly calculated γloc for each contact type using that(γloc≈γ−2KΔPP0) and each time we performed a simulation. We then used a least square fit method to fit simulated shapes to experimental ones, and hence determine the best K and corresponding γloc’s (Figure 5—figure supplement 2B).

We clarified this in text (subsection “The balance of local tension and cell scale contractility determines ommatidia shape”) and Material and methods subsection “Parameters measurements and model simulations”.

11) The authors use the term "adhesion force" to describe bond tension related to cell adhesion molecules. I have some doubts that this concept is well defined and I do not see it defined in the present paper.

Indeed we meant the contribution of adhesion bonds to interfacial tension. We now have removed the term adhesion force, which was not defined.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Specific comment:

Figure 6G and H results appear misleading. The authors used the Surface Evolver to find minimal energy solutions to cell patterns constrained by genotype. But Surface Evolver is also constrained by cell neighbor relations: cell-cell contacts are not automatically rearranged unless a user "pushes" the program to do so. Thus, starting with Eq and Pl cones in contact with each other will not lead to their rearrangement into Ant – Post cone contact, no matter what parameter values are provided. Likewise, starting with Ant – Post cones in contact, as the authors did in Figure 6GH will result in a minimal solution with Ant-Post cones still in contact, no matter what "genotypes" the cells have, WT or mutant. This could mislead the reader into thinking that the initial conditions of cell neighbor relations are identical in the Figure 6GH solutions as those shown in previous model solutions (Figure 5). And therefore the reader might incorrectly conclude that the models use identical starting conditions for cell neighbor relations. The authors could delete the panels G and H, and simply show the results of Figure 6I and J. These compare energies for different minimizations using different starting conditions. It is not surprising that the authors do not show a comparable energy profile for a wildtype ommatium because the A-P junction valley for WT may still be lower than the Eq-Pl junction valley. If true, this would further add to doubts as to the utility of applying the surface evolver method to analyzing cell-cell rearrangements.

We agree with this comment and have removed Figure 6G and H. Indeed, the results in Figure 6I and J are more informative and are not misleading, as the energy profiles are determined for configurations that are depicted in the figures.

https://doi.org/10.7554/eLife.22796.038

Article and author information

Author details

  1. Eunice HoYee Chan

    Aix Marseille Univ, CNRS, IBDM, Marseille, France
    Contribution
    EHoYC, Conceptualization, Data curation, Designed and performed all the genetic experiments, IF staining, confocal microscopy, and live-imaging experiments, Formal analysis, Supervision, Validation, Investigation, Visualization, Methodology, Writing—original draft, Project administration, Writing—review and editing, Commented on manuscript
    Contributed equally with
    Pruthvi Chavadimane Shivakumar
    For correspondence
    ho-yee.chan@univ-amu.fr
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-3162-3609

  2. Pruthvi Chavadimane Shivakumar

    Aix Marseille Univ, CNRS, IBDM, Marseille, France
    Contribution
    PCS, Conceptualization, Data curation, Performed laser-ablation experiments and quantified all the images and data, Formal analysis, Designed the physical model, Performed the simulations and calculations, Validation, Investigation, Visualization, Methodology, Writing—original draft, Project administration, Writing—review and editing, Commented on manuscript
    Contributed equally with
    Eunice HoYee Chan
    Competing interests
    The authors declare that no competing interests exist.

  3. Raphaël Clément

    Aix Marseille Univ, CNRS, IBDM, Marseille, France
    Contribution
    RC, Conceptualization, Formal analysis, Designed the physical model, Supervision, Validation, Visualization, Methodology, Writing—original draft, Writing—review and editing, Commented on manuscript
    Competing interests
    The authors declare that no competing interests exist.

  4. Edith Laugier

    Aix Marseille Univ, CNRS, IBDM, Marseille, France
    Contribution
    EL, Resources, Methodology, Designed and generated the CRISPR/Cas9 Ncad::mKate2 knockin line
    Competing interests
    The authors declare that no competing interests exist.

  5. Pierre-François Lenne

    Aix Marseille Univ, CNRS, IBDM, Marseille, France
    Contribution
    P-FL, Conceptualization, Resources, Formal analysis, Designed the physical model, Supervision, Funding acquisition, Validation, Investigation, Visualization, Methodology, Writing—original draft, Project administration, Writing—review and editing, Commented on manuscript
    For correspondence
    pierre-francois.lenne@univ-amu.fr
    Competing interests
    The authors declare that no competing interests exist.
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-1066-7506

Funding

Fondation pour la Recherche Médicale (FRM DEQ20130326509)

  • Eunice HoYee Chan
  • Raphaël Clément
  • Edith Laugier
  • Pierre-François Lenne

Agence Nationale de la Recherche (ANR-11-BSV5-0008)

  • Eunice HoYee Chan
  • Pierre-François Lenne

Agence Nationale de la Recherche (ANR-11-IDEX-0001–02)

  • Pruthvi Chavadimane Shivakumar
  • Pierre-François Lenne

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We are grateful to Y Hong, R Karess, CH Lee, T Lecuit, AC Martin, D Pinheiro, N Tapon, T Uemura and Bloomington Drosophila Stock Centre for generously providing fly stocks. We thank K Brakke, for surface evolver guidance and suggestions. We thank C Chardès for development and assistance with the ablation setup. R Flores-Flores on chromatic aberration testing and JM Philippe for excellent assistance on molecular biology. We thank members of the Lenne and Lecuit groups and B Aigouy for stimulating and useful discussion during the course of this project. We thank B Aigouy, F Graner, M Labouesse, R Levayer, P Mangeol, Q Mao, P Recouvreux, C Toret for critical comments on the manuscript. We thank L Spinelli for advices on statistical analysis. This work was supported by an FRM Equipe Grant FRM DEQ20130326509 and Agence Nationale de la Recherche ANR-Blanc Grant, Morfor ANR-11-BSV5-0008 (to P-FL). P S was supported by PhD grant from the Labex INFORM (ANR-11-LABX-0054) and of the A*MIDEX project (ANR-11-IDEX-0001–02), funded by the ‘Investissements d’Avenir French Government program’. We acknowledge France‐BioImaging infrastructure supported by the French National Research Agency (ANR–10–INSB‐04‐01, «Investments for the future»).

Reviewing Editor

  1. Frank Jülicher, Max Planck Institute for the Physics of Complex Systems, Germany

Version history

  1. Received: October 29, 2016
  2. Accepted: May 8, 2017
  3. Version of Record published: May 24, 2017 (version 1)

Copyright

© 2017, Chan et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 3,886
    Page views
  • 465
    Downloads
  • 31
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, Scopus, PubMed Central.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Eunice HoYee Chan
  2. Pruthvi Chavadimane Shivakumar
  3. Raphaël Clément
  4. Edith Laugier
  5. Pierre-François Lenne
(2017)
Patterned cortical tension mediated by N-cadherin controls cell geometric order in the Drosophila eye
eLife 6:e22796.
https://doi.org/10.7554/eLife.22796

Categories and tags

Research organism

Further reading

    1. Cell Biology
    2. Medicine

    Glucagon-like peptide-1 receptor activation stimulates PKA-mediated phosphorylation of Raptor and this contributes to the weight loss effect of liraglutide

    Thao DV Le, Dianxin Liu ... Julio E Ayala
    Research Article Updated

    The canonical target of the glucagon-like peptide-1 receptor (GLP-1R), Protein Kinase A (PKA), has been shown to stimulate mechanistic Target of Rapamycin Complex 1 (mTORC1) by phosphorylating the mTOR-regulating protein Raptor at Ser791 following β-adrenergic stimulation. The objective of these studies is to test whether GLP-1R agonists similarly stimulate mTORC1 via PKA phosphorylation of Raptor at Ser791 and whether this contributes to the weight loss effect of the therapeutic GLP-1R agonist liraglutide. We measured phosphorylation of the mTORC1 signaling target ribosomal protein S6 in Chinese Hamster Ovary cells expressing GLP-1R (CHO-Glp1r) treated with liraglutide in combination with PKA inhibitors. We also assessed liraglutide-mediated phosphorylation of the PKA substrate RRXS*/T* motif in CHO-Glp1r cells expressing Myc-tagged wild-type (WT) Raptor or a PKA-resistant (Ser791Ala) Raptor mutant. Finally, we measured the body weight response to liraglutide in WT mice and mice with a targeted knock-in of PKA-resistant Ser791Ala Raptor. Liraglutide increased phosphorylation of S6 and the PKA motif in WT Raptor in a PKA-dependent manner but failed to stimulate phosphorylation of the PKA motif in Ser791Ala Raptor in CHO-Glp1r cells. Lean Ser791Ala Raptor knock-in mice were resistant to liraglutide-induced weight loss but not setmelanotide-induced (melanocortin-4 receptor-dependent) weight loss. Diet-induced obese Ser791Ala Raptor knock-in mice were not resistant to liraglutide-induced weight loss; however, there was weight-dependent variation such that there was a tendency for obese Ser791Ala Raptor knock-in mice of lower relative body weight to be resistant to liraglutide-induced weight loss compared to weight-matched controls. Together, these findings suggest that PKA-mediated phosphorylation of Raptor at Ser791 contributes to liraglutide-induced weight loss.

    1. Cell Biology
    2. Developmental Biology

    Cylicins are a structural component of the sperm calyx being indispensable for male fertility in mice and human

    Simon Schneider, Andjela Kovacevic ... Hubert Schorle
    Research Article

    Cylicins are testis-specific proteins, which are exclusively expressed during spermiogenesis. In mice and humans, two Cylicins, the gonosomal X-linked Cylicin 1 (Cylc1/CYLC1) and the autosomal Cylicin 2 (Cylc2/CYLC2) genes, have been identified. Cylicins are cytoskeletal proteins with an overall positive charge due to lysine-rich repeats. While Cylicins have been localized in the acrosomal region of round spermatids, they resemble a major component of the calyx within the perinuclear theca at the posterior part of mature sperm nuclei. However, the role of Cylicins during spermiogenesis has not yet been investigated. Here, we applied CRISPR/Cas9-mediated gene editing in zygotes to establish Cylc1- and Cylc2-deficient mouse lines as a model to study the function of these proteins. Cylc1 deficiency resulted in male subfertility, whereas Cylc2-/-, Cylc1-/yCylc2+/-, and Cylc1-/yCylc2-/- males were infertile. Phenotypical characterization revealed that loss of Cylicins prevents proper calyx assembly during spermiogenesis. This results in decreased epididymal sperm counts, impaired shedding of excess cytoplasm, and severe structural malformations, ultimately resulting in impaired sperm motility. Furthermore, exome sequencing identified an infertile man with a hemizygous variant in CYLC1 and a heterozygous variant in CYLC2, displaying morphological abnormalities of the sperm including the absence of the acrosome. Thus, our study highlights the relevance and importance of Cylicins for spermiogenic remodeling and male fertility in human and mouse, and provides the basis for further studies on unraveling the complex molecular interactions between perinuclear theca proteins required during spermiogenesis.

    1. Cell Biology
    2. Structural Biology and Molecular Biophysics

    Baited reconstruction with 2D template matching for high-resolution structure determination in vitro and in vivo without template bias

    Bronwyn A Lucas, Benjamin A Himes, Nikolaus Grigorieff
    Research Advance

    Previously we showed that 2D template matching (2DTM) can be used to localize macromolecular complexes in images recorded by cryogenic electron microscopy (cryo-EM) with high precision, even in the presence of noise and cellular background (Lucas et al., 2021; Lucas et al., 2022). Here, we show that once localized, these particles may be averaged together to generate high-resolution 3D reconstructions. However, regions included in the template may suffer from template bias, leading to inflated resolution estimates and making the interpretation of high-resolution features unreliable. We evaluate conditions that minimize template bias while retaining the benefits of high-precision localization, and we show that molecular features not present in the template can be reconstructed at high resolution from targets found by 2DTM, extending prior work at low-resolution. Moreover, we present a quantitative metric for template bias to aid the interpretation of 3D reconstructions calculated with particles localized using high-resolution templates and fine angular sampling.