Rapid transporter regulation prevents substrate flow traffic jams in boron transport
- The University of Tokyo, Japan
- John Innes Centre, United Kingdom
Figures
Figure 1 with 2 supplements
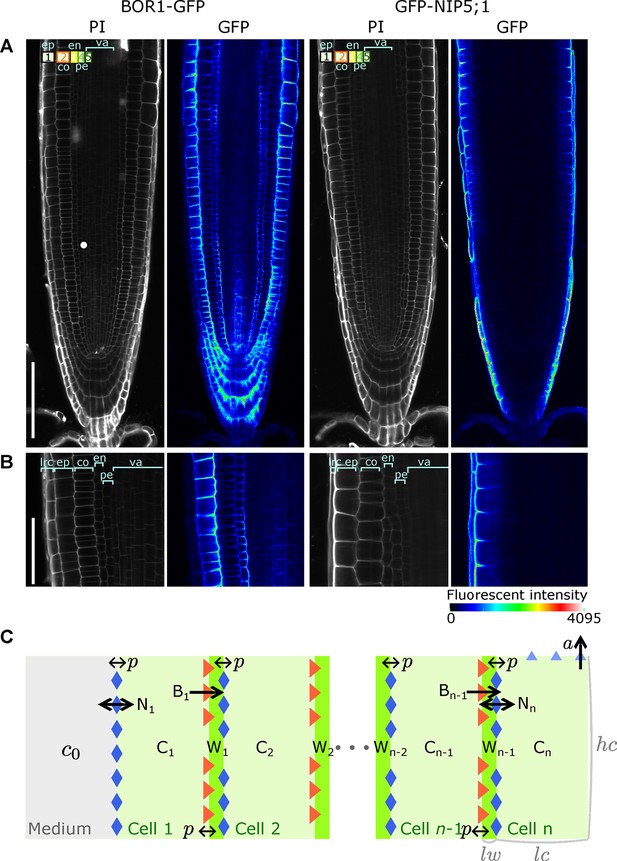
A polarised tissue model for nutrient boron transport across roots.
(A) Confocal microscope images of BOR1-GFP and GFP-NIP5;1 localisation in A. thaliana roots, revealing polar localisation of both transporters, facing inwards and outwards, respectively. Cell file identities are shown in the top-left with numbers representing, in increasing order, cell files from the outermost to the innermost cells, such as ep, epidermis; co, cortex; en, endodermis; va, vasculature. (B) Detailed view along a transversal section of the tissue at the proximal meristem. lrc, lateral root cap. (C) Schematic diagram of the NIP-BOR boron transport model, consisting of a transversal root cross-section composed of cells between the medium and the xylem. For a simplified A. thaliana model, we consider . Depicted is a generic root model consisting of cell files, not showing all cells and cell walls in between and for illustration purposes. The model includes intracellular and apoplastic compartments, as well as membrane-based properties such as transporter activity and background permeability rates. : cell wall width; : cell width; : cell height. For a full description of the parameters, see Table 1.
Figure 1—figure supplement 1
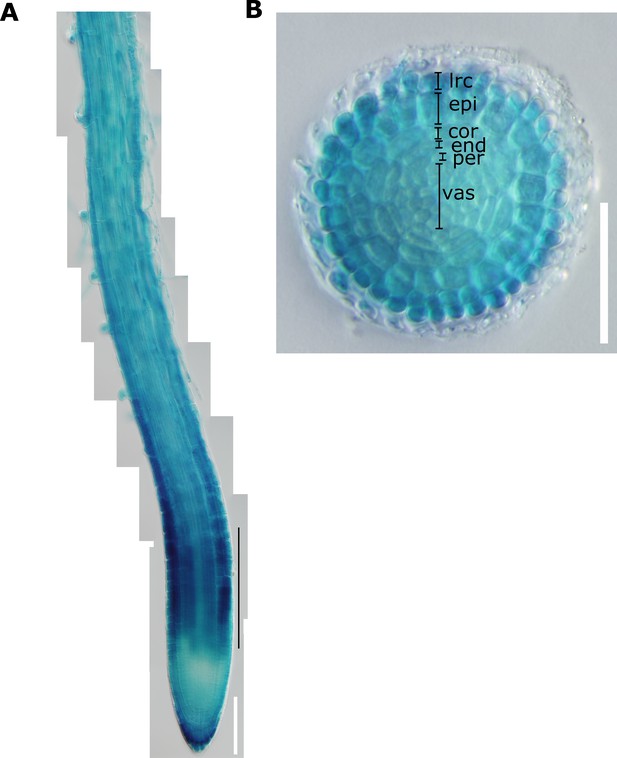
Promoter activity of NIP5;1 in roots.
Promoter activity of NIP5;1 was observed with transgenic plants expressing proNIP5;1-GUS. (A) From the root tip to differentiation zone. White bar, 100 μm. (B) Cross-section of elongation zone. Approximate root position from which the section was obtained is indicated by black line in (A). Bar, 50 μm.
Figure 1—figure supplement 2
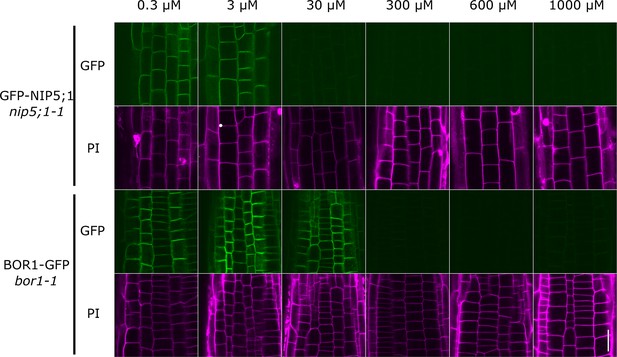
Different boron sensitivity of NIP5;1 and BOR1 with respect to the boron concentration.
Seedlings were germinated and grown on MGRL plates with various boron concentrations for seven days. GFP-NIP5;1 and BOR1-GFP in epidermis were observed with confocal microscope. Cell walls were visualised with PI staining. Scale bar is 20 μm.
Figure 2 with 1 supplement
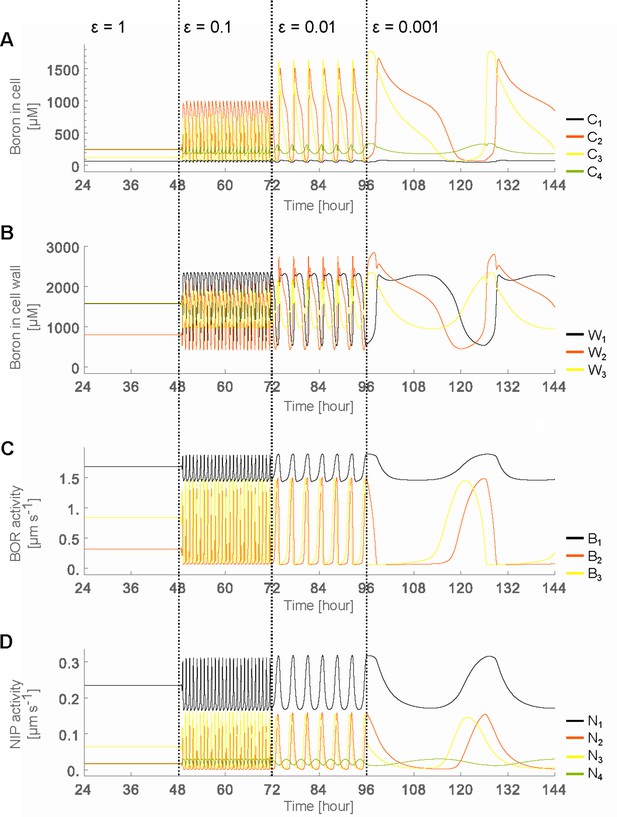
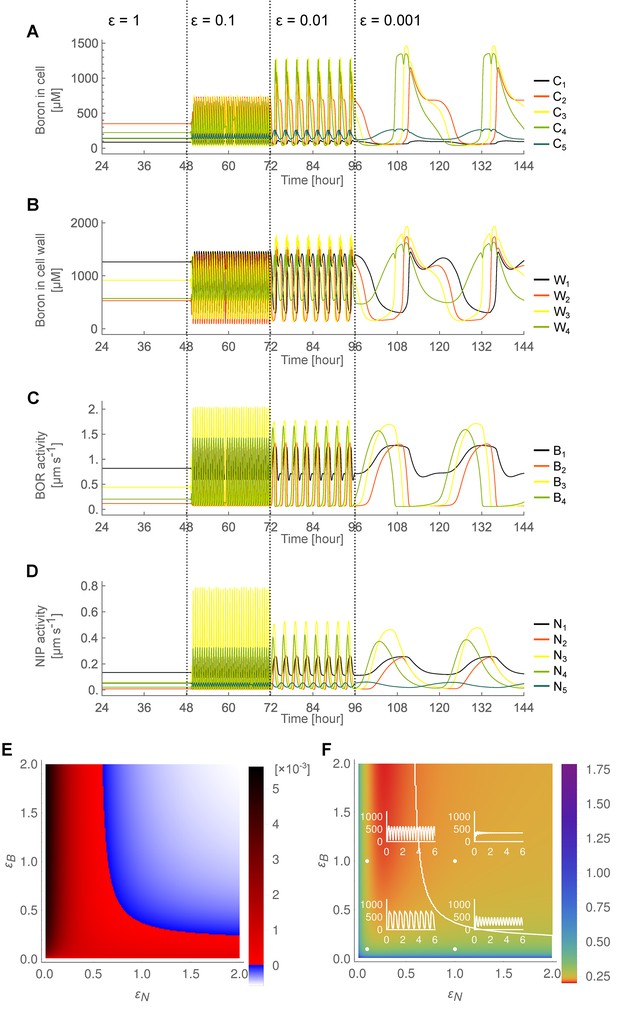
Oscillatory behaviour arises due to decreased transporter regulation swiftness.
Time development in the four-cell NIP-BOR model of the boron concentration in the cells (A) and cell walls (B), and of the transporter activity of BOR (C) and NIP (D). The simulations are started using the default parameter setting (Table 1). At the time points 48, 72 and 96 hr, the parameters determining the transporter regulation dynamics ( and ) were each time reduced to one tenth of their previous value. to are the boron concentrations in the outermost cell 1 up to the innnermost cell 4. represents boron concentration in cell wall fraction between cell and cell and are transporter activity of BOR and NIP in cell , respectively.
Figure 2—figure supplement 1
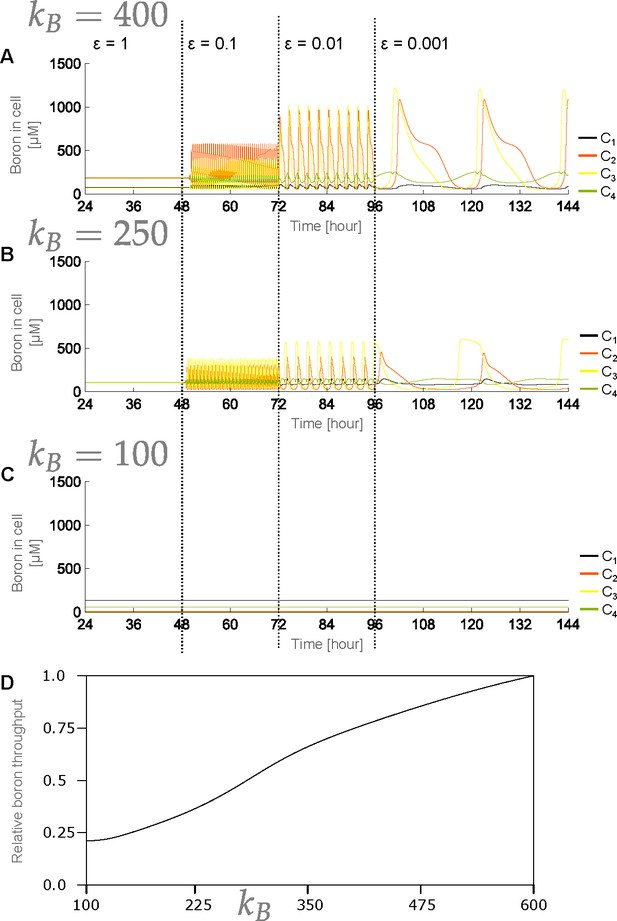
Robustness of behaviour regarding choice of parameter.
(A, B) In the standard four-cell model, cellular boron concentrations still present traffic-jam-like behaviour at reduced transporters’ regulation dynamics swiftness () when is reduced to (A) μM; or (B) μM. (C) At very low values, here μM, the concentrations remain stable even at reduced transporters’ regulation dynamics swiftness (), due to the trivial result that such low values obstruct boron uptake by the system. (D) Equilibrium relative throughput values, as a function of , with unity representing the throughput for μM. Flow stabilisation at reduced transporters’ regulation dynamics swiftness for low values is basically due to a 5-fold reduction in throughput, comparable to real traffic jams not occurring during off-peak hours. Note that for all panels μM, its standard value.
Figure 3 with 1 supplement
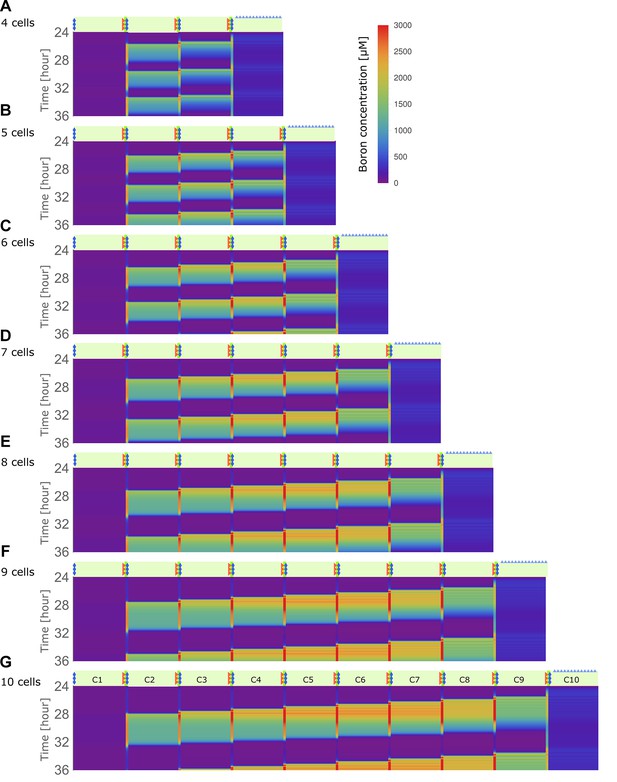
Traffic jam-like behaviour occurs for various tissue sizes.
(A–G) Kymographs of boron concentration in NIP-BOR models consisting of four (A) up to ten (G) cells. Boron concentrations in cells and cell walls are represented through a heat map colouring with development over time displayed vertically. Boron concentrations exceeding 3000 μM are displayed using the same red colour. Regions of high concentration can be observed to displace to the left, contrary to the direction of boron flow due to the transporter activity. Default parameters were used (Table 1), with exception of the transporter regulation swiftness, and , which were both set to 0.01. Above each kymograph a schematic diagram of the tissue structure is shown, corresponding to that of Figure 1C.
Figure 3—figure supplement 1
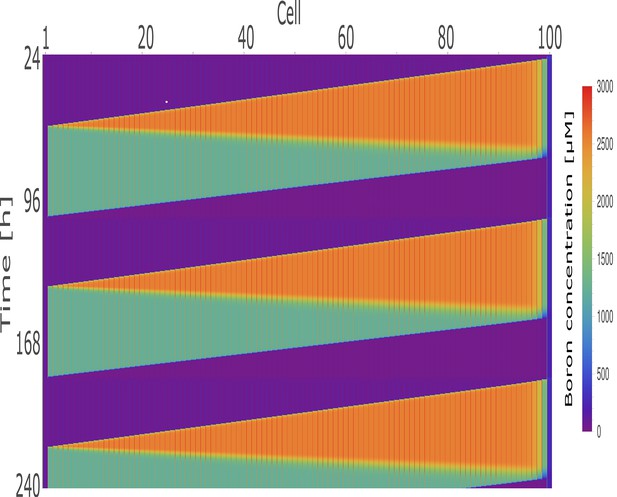
Kymographs of boron concentration in a 100-cell ring model.
Boron concentrations in the cells and cell walls of a 100-cell NIP-BOR ring model, represented through a heat map colouring and time development shown vertically. The default parameters were used (Table 1), with exception of the transporter regulation swiftness, and , which were both set to 0.01.
Figure 4 with 3 supplements
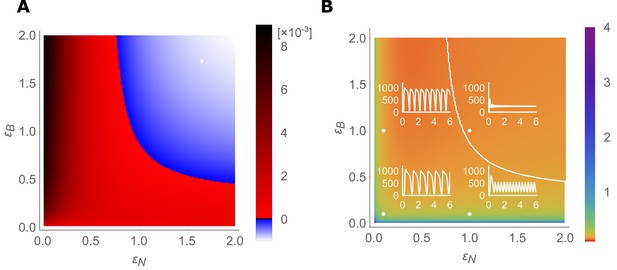
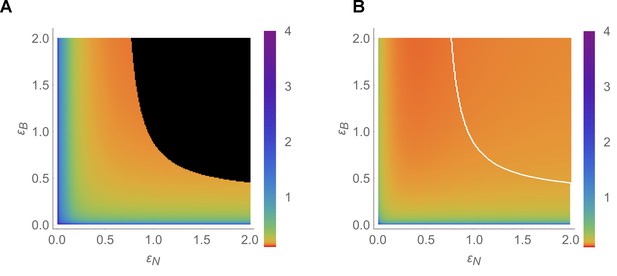
Stable- and unstable-flow regimes and their parameter dependencies.
(A) Diagram showing combinations of transporter regulation swiftness (– plane) for the four-cell NIP-BOR model for which stable flows (blue) or oscillations, that is, ‘traffic jams’, (red) ensue. (B) Oscillatory periods of the boron concentration variation. The white curved line represents the boundary between the stable and the unstable region, equivalent to the boundary between the blue and red area in (A). Four insets plot [μM] over time [hour] for the indicated parameter values (white dots), illustrating the behaviour of the model at those points within the – plane.
Figure 4—figure supplement 1
Oscillation period dependency on transporter regulation swiftness.
Numerically calculated oscillation period for the four-cell NIP-BOR model, shown on the – plane. This figure should be compared to the analytic diagram inferred from the imaginary part of the largest eigenvalue, shown in Figure 4B. Except for and , which are varied, default parameters are as given in Table 1.
Figure 4—figure supplement 2
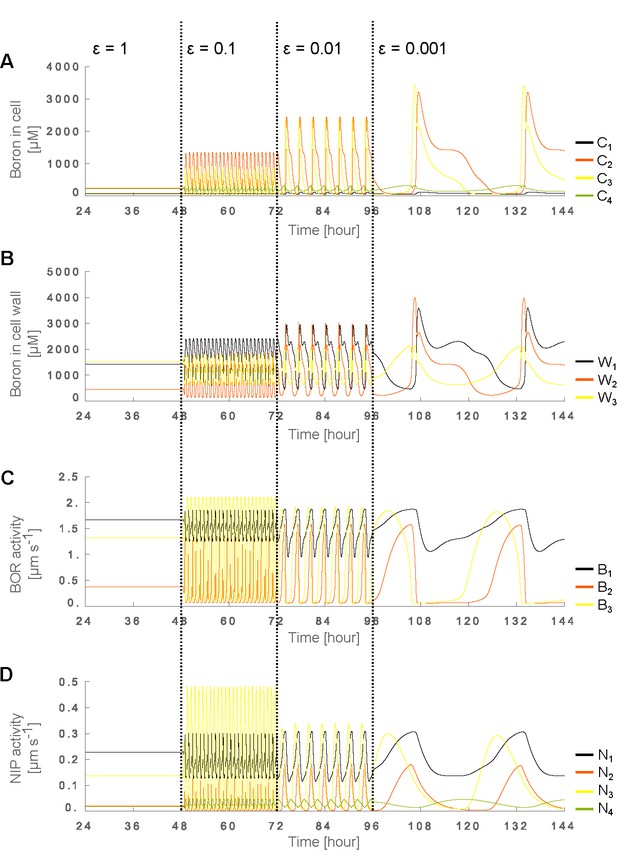
Stable and unstable flow regimes and their parameter dependencies in the five-cell model.
(A–D) Time development in the five-cell NIP-BOR model of the boron concentrations in the cells (A) and cell walls (B), and of the transporter activity of BOR (C) and NIP (D). Default parameter setting (Table 1) was used, except for , which was set to a lower value of 400 μM. At the time points 48, 72 and 96 hr, the parameters determining the transporter regulation dynamics ( and ) were each time reduced to one tenth of their previous value. to represent boron concentration in cell 1 (‘epidermis’); cell 2 (‘cortex’); cell 3 (‘endodermis’); cell 4 (‘pericycle’); and cell 5 (‘vasculature’), respectively. represents the boron concentration in the cell wall fraction between cell and cell and are the transporter activity of BOR and NIP in cell , respectively. (E) Diagram showing combinations of transporter regulation swiftness (– plane) for the 5 cell NIP-BOR model for which stable flows (blue) or oscillations, that is, ‘traffic jams’, (red) ensue. (F) Oscillatory periods of the boron concentration variation. The white curved line represents the boundary between the stable and the unstable region, equivalent to the boundary between the blue and red area in (E). Four insets plot [μM] over time [hour] for the indicated parameter value combinations (white dots), illustrating the behaviour of the model at those points within the – plane.
Figure 4—figure supplement 3
Traffic-jam-like behaviour and saturation of the BOR1 transporter permeability.
(A–D) Time development of (A) cellular and (B) cell wall boron concentrations as well as (C) BOR and (D) NIP levels in the 5 cell NIP-BOR model in which we additionally consider the saturation of BOR transporter permeability. We altered the BOR-mediated flux () as a function of BOR protein levels at the membrane () and the intracellular boron concentration (), from the standard linear regime, , into a Michaelis-Menten saturating form given by , in which is the Michaelis constant, the boron concentration at which the flux becomes half as large due to saturation, as well as the concentration at which the flux reaches its half-maximum value. The simulations use the default parameter setting (Table 1), but introduce the above saturation in BOR transport with the Michaelis constant set to μM. The time dynamics of the system’s variables (A–D) show that oscillatory behaviour remains dependent on the transporters’ regulation dynamics swiftness ( and ) in a very comparable fashion, but that the amplitude of the oscillations in these variables becomes much larger than when saturation in BOR permeability is not considered. For further details regarding this figure, see Figure 2.
Figure 5
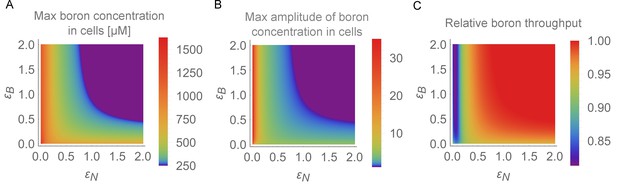
Physiological detrimental impact of the oscillations for the root.
In the BOR-NIP model with 4 cells, physiological output for the simulation period between 24 and 48 hr was displayed on the – plane. (A) Maximum boron concentration in any cell. (B) Maximum amplitude variation in boron concentration for any cell (highest boron concentration/lowest boron concentration). (C) Average throughput, measured as the output from the last cell, which represents the xylem, between 24 and 48 hr of simulation.
Figure 6
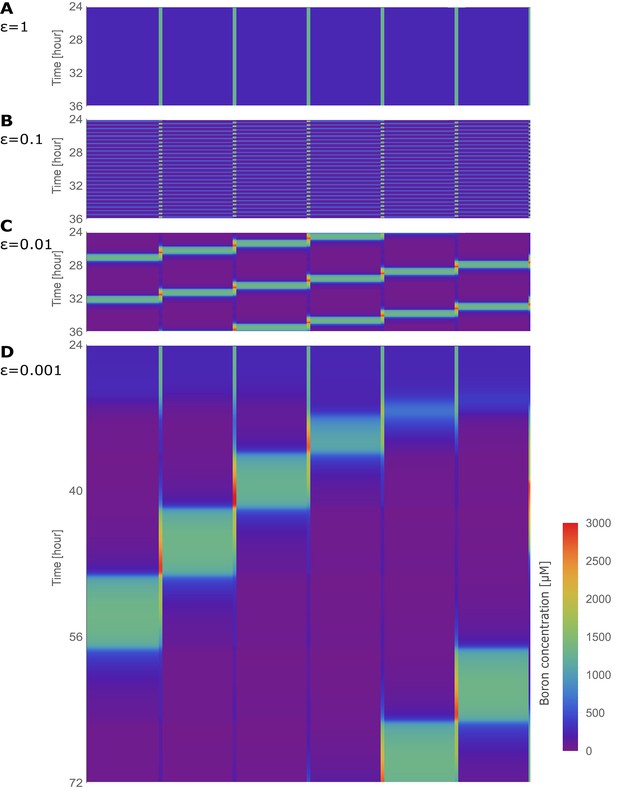
Traffic jam-like behaviour in the absence of bottlenecks: the tissue positioned in a ring.
Kymographs of the boron concentration in the cells and cell walls of the six-cell NIP-BOR ring model, represented by heat map colours and time development shown progressing vertically. The default parameters were used (Table 1), with and varied as specified for each kymograph.
Figure 7 with 1 supplement
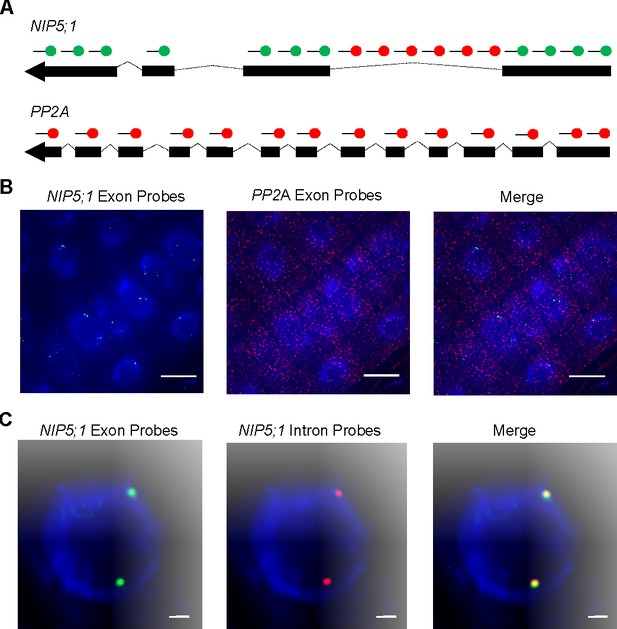
Nascent NIP5;1 RNA accumulates at sites of transcription.
(A) Schematic of probes used to detect NIP5;1 intron 1 (red), NIP5;1 exonic (green) and PP2A exonic (red) RNA. (B) Representative images of cells showing NIP5;1 (green) and PP2A (red) exonic RNA distributions. (C) Representative images showing co localisation of exons (green) and intron 1 (red) regions from NIP5;1 nascent transcripts. DNA labelled with DAPI (blue). Scale bar: 10 μm in (B) and 1 μm in (C).
Figure 7—figure supplement 1
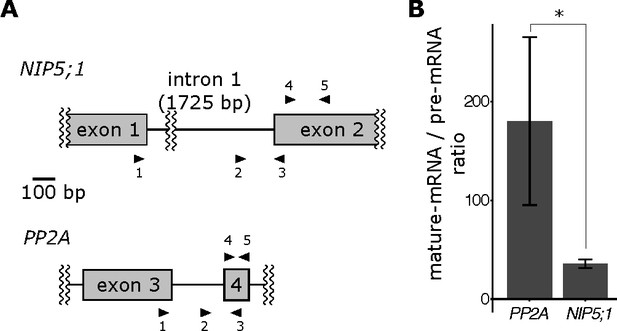
Mature and pre-mRNA abundance of NIP5;1 in root cells.
Mature mRNA and pre-mRNA abundance was separately quantified by qRT-PCR, with probes specific to mature mRNA (probe 1 and 5 for NIP5;1; 1 and 3 for PP2A) or pre-mRNA (probe 2 and 3). (A) Probe design for mature- and pre-mRNA specific qRT-PCR. Arrowheads indicate positions and directions of each probe. Probe 4 and 5 were used for normalising concentrations of standard DNA fragments. For details, see Materials and methods and Table 3. (B) Ratio of abundance of mature mRNA/pre-mRNA abundance for NIP5;1 and PP2A. Asterisk indicates significant difference at p<0.05 using Welch’s t-test.
Figure 8
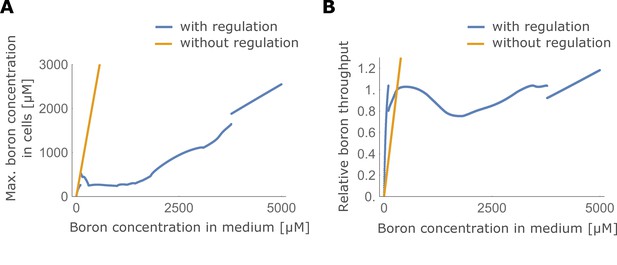
Maximum boron concentration and throughput with and without transporter regulation.
(A) Maximum boron concentration; and (B) throughput, for the four-cell NIP-BOR model, plotted for varying boron concentrations in the medium. The default parameters are used (Table 1). When transporter regulation is not considered, NIP and BOR activity were fixed to their unregulated equilibrium value in the wild type model, namely and .
Videos
Video 1
Simulation of six identical polarised cells endowed with BORs and NIPs orientated as to generate clockwise boron flows.
Time is indicated above the simulation, and dynamics show an initially constant flow, with low boron concentrations in all cells. Due to the intrinsic instability of the system, minute numerical noise generates boron peaks in the cells, a pattern which propagates counterclockwise (i.e., against the flow) through the tissue. Cytosolic boron concentrations, as well as those in the cell walls between cells, are depicted through the colour bar shown in the movie. Transporter levels (of both BORs and NIPs) are characterised through the colour changes along the radial membranes, again depicted through the colour bars shown in the movie.
Video 2
Dynamics of transporters and fluxes.
Simulation output revealing the details of boron flows over the membranes, due to transporter dynamics and background membrane permeability rates.
Tables
Table 1
Model Parameters.
https://doi.org/10.7554/eLife.27038.020| Parameter | Unit | Description | Acceptable range | Default | ||
|---|---|---|---|---|---|---|
| Max. | Min. | |||||
| BOR | - | Time constant for transporter regulation | - | - | 1 | |
| μm s-2 | Production rate of transporter activity | |||||
| s-1 | Basal degradation rate | |||||
| μM | Boron concentration for half-maximum in Hill’s function | 1000 | 1 | 600 | ||
| - | Amplitude of increased degradation rate by boron | 100 | 0 | 50 | ||
| - | Hill’s coefficient | - | - | 2 | ||
| μM | Boron concentration at which the flux reaches its half-maximum value | 500 | 1000 | |||
| NIP | - | Time constant for transporter regulation | - | - | 1 | |
| μm s-2 | Production rate of transporter activity | |||||
| s-1 | Basal degradation rate | |||||
| μM | Boron concentration for half-maximum in Hill’s function | 1000 | 1 | 20 | ||
| - | Hill’s coefficient | - | - | 2 | ||
| Cell size | μm | Cell width | 20 | 5 | 10 | |
| μm | Cell wall width | 2 | 0.2 | 0.5 | ||
| μm | Cell height | 150 | 5 | 20 | ||
| Other | μm s-1 | Membrane background permeability of boron | ||||
| μm s-1 | Xylem loading rate (in the last cell) | 500 | 0 | 0.5 | ||
| μm | Boron concentration in medium | 5000 | 0 | 300 | ||
Table 2
Probes used in the smFISH experiments.
https://doi.org/10.7554/eLife.27038.021| NIP5;1 exon probes | NIP5;1 intron 1 probes | PP2A mRNA |
|---|---|---|
| acgaaaatggagctaggact | gtagtcgattttcttacggt | ccgagcgatctatcaatcag |
| cggtttcaccaaacacaagt | attactagcacaaaccactt | gacatcctcaccaaaactca |
| gtgttttaaacttcgccagt | cggatggtgacgaatgagta | tcgggtataaaggctcatca |
| tggaggagccatcaccatta | atgcaatatgcggttatgga | tagctcgtcgataagcacag |
| cattgaatccactctcatcc | tctattgttaggtttactga | ccaagagcacgagcaatgat |
| gttggtttccgatgatcaaa | ggttcctagccagaaatttt | atcaactcttttcttgtcct |
| cggcaagcatttgcatcgag | tgtaatttttaggcttacgt | catcgtcattgttctcacta |
| atgttgaccccaagttgatc | ctttgtaaggttataacgct | atagccaaaagcacctcatc |
| gagggaaaatcggtgaagca | aacgagccattggatttctt | atacagaataaaacccccca |
| ttgcgagtgagggagacatc | cgtggattccaatgttttct | caagtttcctcaacagtgga |
| tgaatgttcccacgaactcg | ttcccaattcattattttcc | tcatctgagcaccaattcta |
| gctgtcgcggtgaatatcaa | tgtctcgatctcattttttt | tagccagaggagtgaaatgc |
| catcgtatttctggttcacg | ccctatagtacatctatatt | cattcaccagctgaaagtcg |
| gttaccgattagggtttctg | attacgatcgatttgtgagt | ggaaaatcccacatgctgat |
| tatgatcatcactgcgagtc | ttctctgtatttcagagctt | atattgatcttagctccgtc |
| cctgagatatgacctgttga | agtattatcttttggtcact | attggcatgtcatcttgaca |
| cagtgatgggtttaggtgag | ccctatgatctttttcaata | aaattagttgctgcagctct |
| cttagagcagcgaatgctat | ctcctccaagtgtgacgtaa | gctgattcaattgtagcagc |
| tatgtaagcagggacgtgtg | ctagttcatgtcgtgttaaa | ccgaatcttgatcatcttgc |
| gcgcaaatggaagctgagac | atttaattctcggttgcgac | caaccctcaacagccaataa |
| gaacactcctttaagtgcga | ttcactctctttctatttgc | ctccaacaatttcccaagag |
| caccaccggacataaaagga | ctcttagtttttcttagact | caaccatataacgcacacgc |
| tccaaggctaacagatggaa | taagttgagatcgagtgggc | agtagacgagcatatgcagg |
| tgaactcaagagcaaaggct | gagtcggtgtccattgaata | gaacttctgcctcattatca |
| cggcagttacaacaaagagg | actattagctcattgtcaca | cacagggaagaatgtgctgg |
| aacggcacgagtgtcggtag | atttacgcaacttgcgtgtt | tgacgtgctgagaagagtct |
| aacggctatacctgccaatt | agcgtgaccgttttattttt | cccattataactgatgccaa |
| aatattgagcatgaccgtgg | actttgtattcgtcattgca | tggttcacttggtcaagttt |
| atagatccaccagtcgatgg | gacctaaccaaaccatacgt | tctacaatggctggcagtaa |
| tcctagagttctcacaggat | gcttccgtcatggacagaaa | cgattatagccagacgtact |
| atagtttcctgatgcaacgg | ctaaaagaatcccatccggt | gactggccaacaagggaata |
| ccagatacacccatagtgac | aaaggacaagagccgtggat | catcaaagaagcctacacct |
| cagatatggcaccaagtgta | tccacgttaacgagcatcaa | ttgcatgcaaagagcaccaa |
| ttaacacctgtgtagaccgc | gcgtgtgatctgtctatatc | acggattgagtgaaccttgt |
| gtcagtcacgctatcgttaa | tacagtcaacggttagtatt | cttcagattgtttgcagcag |
| aaagctcctaaccggacgag | gtcattagtagttactagtt | ggaccaaactcttcagcaag |
| gtctctcactcacttaacga | agtattatttctgctgtcca | ggaactatatgctgcattgc |
| tccaaagctttttcatatca | ctagagggttctgagtcgaa | gtgggttgttaatcatctct |
| gccttttattcttcacacaa | gagatgtttcttgtctaaca | tgcacgaagaatcgtcatcc |
| tgcgtggacttatagtcaca | gtactagatgaatagaggct | ttactggagcgagaagcgat |
| aggtttatatagaccgatgc | gaacatgtgatctcggatcc | |
| aatgacgagacaagttcgca | ctctgtctttagatgcagtt | |
| agaaacccaaaccacacata | catcattttggccacgttaa | |
| ataaaaacagcctcgtctcc | cgtatcatgttctccacaac | |
| acacatgccatagattttat | atcaacatctgggtcttcac | |
| ttggagagcttgatttgcga | ||
| acacaattcgttgctgtctt | ||
| cgcccaacgaacaaatcaca |
Table 3
Primers used in qRT-PCR experiments.
https://doi.org/10.7554/eLife.27038.022| Name | Sequence | Description |
|---|---|---|
| NIP5;1_qRT-PCR-1 | caccgattttccctctcctgat | Probes for realtime PCR |
| NIP5;1_qRT-PCR-2 | ctctttcttactctctagcctc | |
| NIP5;1_qRT-PCR-3 | gaatgttcccacgaactcgg | |
| NIP5;1_qRT-PCR-4 | acattcatcttgatattcacc | |
| NIP5;1_qRT-PCR-5 | gcatgcagcgttaccgatta | |
| PP2A_qRT-PCR-1 | ccatgtttgaggatcttacgc | |
| PP2A_qRT-PCR-2 | tgtctacatctcagcttcagtgtc | |
| PP2A_qRT-PCR-3 | gctccaacaatttcccaaga | |
| PP2A_qRT-PCR-4 | caagattcggttagattattg | |
| PP2A_qRT-PCR-5 | gcgagaaattgacaatcacag | |
| NIP5;1_mRNA_F | atttaggtgacactatagtaagctcaaagactaaccaaac | For amplification of the standard DNA fragments |
| NIP5;1_mRNA_R | ttacacatgccatagattttat | |
| PP2A_mRNA_F | atttaggtgacactatagcggtctcatttctcgttcttc | |
| PP2A_mRNA_R | cacttgataagtaaattatttg |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Rapid transporter regulation prevents substrate flow traffic jams in boron transport
eLife 6:e27038.
https://doi.org/10.7554/eLife.27038
