The role of scaffold reshaping and disassembly in dynamin driven membrane fission

Abstract
eLife digest
Introduction
Results
Results and discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

The large GTPase dynamin catalyzes membrane fission in eukaryotic cells, but despite three decades of experimental work, competing and partially conflicting models persist regarding some of its most basic actions. Here we investigate the mechanical and functional consequences of dynamin scaffold shape changes and disassembly with the help of a geometrically and elastically realistic simulation model of helical dynamin-membrane complexes. Beyond changes of radius and pitch, we emphasize the crucial role of a third functional motion: an effective rotation of the filament around its longitudinal axis, which reflects alternate tilting of dynamin’s PH binding domains and creates a membrane torque. We also show that helix elongation impedes fission, hemifission is reached via a small transient pore, and coat disassembly assists fission. Our results have several testable structural consequences and help to reconcile mutual conflicting aspects between the two main present models of dynamin fission—the two-stage and the constrictase model.

https://doi.org/10.7554/eLife.39441.001

eLife digest

When cells take up material from their surroundings, they must first transport this cargo across their outer membrane, a flexible sheet of tightly organized fat molecules that act as a barrier to the environment. Cells can achieve this by letting their membrane surround the object, pulling it inwards until it is contained in a pouch that bulges into the cell. This bag is then corded up so it splits off from the outer membrane. The ‘cord’ is a protein called dynamin, which is thought to form a tight spiral around the bag’s neck, closing it over and pinching it away. The structure of dynamin is fairly well known, and yet several theories compete to explain how it may snap the bag off the outer membrane.

Here, Pannuzzo et al. have created a computer simulation that faithfully replicates the geometry and the elasticity of the membrane and of dynamin, and used it to test different ways the protein could work. The first test featured simple constriction, where the dynamin spiral contracts around the membrane to pinch it; this only separated the bag from the membrane after implausibly tight constriction. The second test added elongation, with the spiral lengthening as well as reducing its diameter, but this further reduced the ability for the protein to snap off the membrane. The final test combined constriction and rotation, whereby dynamin ‘twirls’ as it presses on the neck of the bag: this succeeded in efficiently severing the membrane once the dynamin spiral disassembled. Indeed, the simulations suggested that dynamin might start to dismantle while it constricts, without compromising its role. In fact, getting rid of excess length as the protein contracts helps to dissolve any remnants of a membrane connection.

Defects in dynamin are associated with conditions such as centronuclear myopathy and Charcot‐Marie‐Tooth peripheral neuropathy. Recent research also indicates that the protein is involved in a much wider range of neurological disorders that include Alzheimer's, Parkinson's, Huntington's, and amyotrophic lateral sclerosis. The models created by Pannuzzo et al. are useful tools to understand how dynamin and similar proteins work and sometimes fail.

https://doi.org/10.7554/eLife.39441.002

Introduction

Of the three 80% homologous mammalian isoforms of dynamin, Dyn1, highly expressed in neurons, has been studied best (Hinshaw, 2000; Praefcke and McMahon, 2004). Crystallographic analysis (Chen et al., 2004; Faelber et al., 2011; Ferguson et al., 1994; Ford et al., 2011; Zhang and Hinshaw, 2001; Chappie et al., 2010) reveals five distinct domains: an N-terminal GTPase or G-domain; a ‘stalk’ region consisting of a four helix bundle; the signaling BSE domain that links G-domain and stalk; a pleckstrin homology (PH) domain binding phosphatidylinositol-4,5-biphosphate (PIP $_{2}$ ) lipids; and a proline-rich C-terminal domain (PRD) that mediates interactions with membrane scaffolding proteins. Dynamin monomers oligomerize via their stalks in a criss-cross fashion, resulting in stable dimers (Cocucci et al., 2014) or tetramers (Ramachandran et al., 2007) in solution. Continuing this assembly path yields helical filaments (Carr and Hinshaw, 1997), which have an outer diameter of about 50 nm and a helical pitch (i.e., height increment during one complete helical turn) between 10 nm and 20 nm in the absence of GTP (Chen et al., 2004). Specific interactions among dynamin subunits are not conserved throughout the large dynamin superfamily, yet all members share similar architectural assembly properties (Praefcke and McMahon, 2004).

Dynamin helices are narrower in the presence of GTP; the strongest constriction has been seen with the point mutant $^{K 44 A} Dyn1$ : it forms a stable superconstricted 2-start helix, tightening membrane tubules to a water-filled inner lumen with a diameter as narrow as 3.7 nm, but not cutting them (Sundborger et al., 2014). Since $^{K 44 A} Dyn1$ is very inefficient in GTP hydrolysis, which however is necessary for remodeling (Zhang and Hinshaw, 2001; Chappie et al., 2011), this mutant is believed to trap the system in a pre-fission state. This leaves open the role of GTP activity, with presently two major competing scenarios: the two-stage and the constrictase model.

In the two-stage model (Bashkirov et al., 2008; Mattila et al., 2015), nucleotide-loaded dynamin assembles into highly constricted helices, whose entrapped lipid tubules spontaneously undergo hemifission; GTP hydrolysis induces subsequent detachment of the dynamin scaffold from the membrane, allowing the hemifission state to proceed to complete fission. However, neither the lack of dynamin’s cooperativity with GTP during hydrolysis (Tuma and Collins, 1994), nor the short lifetime of the post-hydrolysis GDP + P_i state (Antonny et al., 2016) are compatible with key requirements of the two-stage model. It also remains unclear why the experimentally observed superconstricted state does not reach hemifission. In the constrictase model (Chappie et al., 2011), several cycles of GTP hydrolysis induce adjacent turns (or ‘rungs’) to stepwise slide past one another, actively constricting the helix and its enclosed membrane tube until the latter fissions; disassembly is then a consequence of the vanishing lipid substrate. The problems here are that the cryo-EM density of stalks in a constricted (albeit: 2-start) helix does not match the X-ray structure of dimers, that it is not known how G-G links across rungs would unbind and step cooperatively, and that the mechanics of the final disassembly is less clear (Antonny et al., 2016).

To refine these two partially conflicting scenarios into a consistent and realistic model requires information about fast changes at the nanometer-scale. This is a challenge for all structural techniques capable of reaching the necessary resolution, and it often requires the use of mutants that might introduce artifacts. However, there is also a second problem: it is by no means obvious how a highly curved bilayer responds to the forces and torques imposed by such complex geometric constraints. Theoretical calculations have provided constraints on energetics and morphology (Kozlov, 1999; Kozlovsky and Kozlov, 2003; Bashkirov et al., 2008; McDargh et al., 2016; McDargh and Deserno, 2018), but these assume high symmetries and ignore fluctuations. Recent coarse-grained (CG) simulations, in which the dynamin helix is represented as a pair of rings, have elucidated the relevance of local torques (Fuhrmans and Müller, 2015) and the possibility of long-lived hemifission intermediates (Mattila et al., 2015; Zhang and Müller, 2017), but the implied mirror symmetry differs from the actual helicoidal one. Here we go beyond these studies and investigate the constriction of fluctuating lipid bilayer tubes by geometrically realistic dynamin helices.

We employ an implicit-solvent CG membrane model (Cooke et al., 2005; Cooke and Deserno, 2005) (see Materials and methods) in which lipids are represented by three consecutive beads, each with a diameter of $σ \sim 0.8 nm$ (Figure 1a), that assemble via tail attraction and form bilayers with a bending rigidity of $κ \approx 13 k_{B} T$ (Cooke et al., 2005; Cooke and Deserno, 2005), where the thermal energy $k_{B} T = 4.1 \times 10^{- 21} J \approx 0.6 k c a l / m o l$ provides the natural energy scale. The CG time scale maps to approximately $τ ≃ 15 ns$ , based on lipid self-diffusion, but we stress that this needs to be interpreted cautiously, since coarse-graining might speed up different dynamic processes differently. The emergent CG membranes capture not only a wide range of mesoscopic phenomena (Deserno, 2009), but also very local bilayer properties that likely play a role during leaflet-breaking fission events, such as a well-placed pivotal plane (Wang and Deserno, 2015), a correct magnitude and correlation length for lipid tilt (Wang and Deserno, 2016), and a pore-opening scenario (Cooke et al., 2005; Deserno, 2009) in agreement with previous simulations and continuum theory (Farago, 2003; Tolpekina et al., 2004). The dynamin filament is composed of similar CG beads, arranged and elastically connected to capture filament radius $r$ , helical radius $R$ and pitch $2 π p$ , and the location of an effective PH binding strip (Figure 1b and Figure 5, Materials and methods). In the present study we forgo the dynamin assembly process and start with a pre-formed helix winding around the neck of an elongated vesicle comprising about 10,000 lipids (Figure 1c). We change the scaffold geometry by tuning the equilibrium distances between its CG beads, that is by imposing internal stresses that trigger a global elastic shape relaxation, and we do this slowly enough to avoid viscous stresses in the bilayer (Figure 6, Materials and methods). All simulations were performed using the ESPResSo package (Limbach et al., 2006) and run in triplicate, leading to consistent results. Visualization was done with VMD (Humphrey et al., 1996).

Figure 1

Download asset Open asset

Ingredients of the model.

(a) CG lipids comprising three beads assemble into membranes via tail bead attractions and head bead repulsions. (b) the dynamin helix is built as a stack of disks with 19 CG beads each; it contains an adhesive membrane-binding strip (red) that represents the PH domains and that can rotate by an angle $φ$ away from the inward-pointing direction. (c) a CG filament constricts the neck of a CG vesicle consisting of $\sim 10, 000$ CG lipids.

https://doi.org/10.7554/eLife.39441.003

Results

Figure 2 with 1 supplement see all

Download asset Open asset

Dynamin shape changes and membrane response.

(a) Top and (b) Side-view of dynamin dimers assembled into an unconstricted helical filament. (c) CG representation of a constricted filament. (d) Constricted and elongated filament. (e) Constricted and rotated filament. (f) Radius of gyration $R_{g}$ of the membrane neck (see Materials and methods section) as a function of filament radius $R$ under four protocols: constriction only (blue) constriction $+$ rotation (cyan), constriction $+$ rotation $+$ elongation (dark cyan), constriction $+$ elongation (dark blue). (g) An unconstricted filament resting on a membrane of matching radius (left) creates a Darboux-torque once the (red) adhesion strip is rotated (right), inducing the membrane to asymmetrically bulge; the two arrows indicate the torque couple. (h) Cross-sectional view of a 1- and 1.5-turn helical scaffold at $R = 10.5 σ$ and a 3.5-turn scaffold at $R = 10 σ$ . The filament was constricted and rotated, only the adhesion strip is shown. Hemifission seeds are small pores, visible as breaks in bilayer continuity (arrows). (i) Cross-cut illustration of membrane shape changes triggered by a simultaneous filament constriction, rotation, and gradual disassembly (Video 5), leading to hemifission. (j) Continuation of the previous sequence from hemifission to complete fission.

https://doi.org/10.7554/eLife.39441.004

Figure 2—source data 1 Constriction-elongation trajectory.: https://doi.org/10.7554/eLife.39441.010
Download elife-39441-fig2-data1-v2.txt
Figure 2—source data 2 Constriction-rotation-elongation trajectory.: https://doi.org/10.7554/eLife.39441.011
Download elife-39441-fig2-data2-v2.txt
Figure 2—source data 3 Constriction-rotation trajectory.: https://doi.org/10.7554/eLife.39441.012
Download elife-39441-fig2-data3-v2.txt
Figure 2—source data 4 Pure constriction trajectory.: https://doi.org/10.7554/eLife.39441.013
Download elife-39441-fig2-data4-v2.txt

Pure constriction

We begin by exploring a process in which the filament constricts its helical radius $R$ but maintains both the pitch and the orientation of the PH domain with respect to the substrate (Figure 2c). At a confinement approximately corresponding to the superconstricted state, the enclosed membrane tube remains stable. The hemifission intermediate only forms at constriction levels that eliminate the inner lumen (Figure 2f, blue curve, and Video 1). This seems to contradict the findings by Kozlovsky and Kozlov (2003) that an inner lumen diameter smaller than approximately 2 nm should spontaneously proceed towards hemifission, but this is not so: in their study an approximately catenoidal neck fissions by the application of bending moments at the upper and lower edge of the neck, while in our case the neck is created by external constriction—a mechanically different scenario. It is of course conceivable that our bilayer tube is merely kinetically stable, but nothing analytical is known about the barrier towards the topologically distinct hemifission state. Indeed, the dynamin-coated superconstricted lipid tubule is stable in experiment (Sundborger et al., 2014).

Video 1

Download asset

posterframe for video — Pure filament constriction.

A dynamin filament, initially with radius $R = 18 σ$ , pitch $2 π p = 12 σ$ and rotation angle $φ = 0$ is constricted by stepwise reduction of the radius $R$ down to the critical radius $R = R_{c} = 10.5 σ$ , following the blue time-series in Figure 6. The right part of the video shows a side view, in which the 10,000 lipids of the vesicle are only rendered in stick-representation such as to permit some amount of transparency. The dynamin filament is shown as a transparent gray tube, and only the adhesive PH domain strip is explicitly shows as a sequence of red beads. The left part of the video shows a view along the helical axis of the filament, and lipids are only shown if their $z$ -distance from the filaments center of mass is within $\pm 1 σ$ , such as to follow the extent of constriction and the diameter of the luminal region.

https://doi.org/10.7554/eLife.39441.014

Constriction and elongation

Some experiments have shown that GTP hydrolysis may increase the filament’s pitch at fixed radius (Figure 2d), which has led to the suggestion that dynamin might act as an extension spring (‘poppase model’) (Stowell et al., 1999). However, since dynamin changes its shape slowly compared to a membrane’s viscoelastic time scale, believed to be shorter than about 10 ms (Camley and Brown, 2011), this putative mechanism cannot rely on viscous stresses but instead only on the reversible work being performed during elongation of the neck. To test this, we simultaneously decrease the radius and increase the pitch (Materials and methods, Figure 6). Contrary to expectation, helical elongation impedes fission: at the same helical scaffold radius $R$ , a larger pitch results in a larger effective radius $R_{g}$ of the enclosed membrane tubule, requiring further constriction to achieve hemifission. This happens because a large pitch prevents the helical filament from symmetrically confining the membrane, allowing it to ‘bulge out’ at the open groove (Figure 2f, dark blue curve). In nature this could be prevented by accessory proteins, or—if the two-start helix is physiologically relevant—by the second interlocking filament. Compared to the pure constriction case, which in all three runs transitioned into the hemifission step at the same constriction step, we here observe a slight scatter of the precise transition points between two consecutive steps—see Figure 2—figure supplement 1d. We attribute this to the reduced confinement of a membrane inside a helical scaffold with a widening groove, permitting more fluctuations that render the transition point less definite.

Constriction and rotation

Beyond changes of radius and pitch, the set of macroscopic motions available to a helical filament contains a third possibility: a ‘twirling’ motion around the local filament axis (Figure 1b and Figure 2e). Its relevance for dynamin derives from a growing number of studies that provide experimental evidence for the tilting of dynamin’s PH domains. Mehrotra et al. (2014) have shown that a change in PH domain orientation may regulate fission. Sundborger et al. (2014) fitted dynamin’s crystallographic structure to EM density maps and noticed that one of the two PH domains per dimer tilts out of the membrane, thereby breaking the symmetry of the dimer. And a very recent 3.75 Å resolution Cryo-EM reconstruction of human Dyn1 in the GMPPCP-bound state (Kong et al., 2018) shows that the bundle signaling element (BSE) is asymmetrically bent, presumably due to forces generated from the GTPase dimer interaction. These forces are further transferred across the stalk to the PH domain and onto the lipid membrane.

On mesoscopic scales, this local rearrangement of the tertiary structure can effectively be described as a net rotation of the helical scaffold around its local longitudinal axis, even if the core of the protein filament does not actually co-rotate. If the PH domains of each monomer were to tilt in the same fashion, then due to dynamin’s criss-cross assembly half of the PH domains would tilt ‘up’ while the other half would tilt ‘down’, which on average does not displace the filament’s binding surface. However, if only one of these two sets of PH domains tilts, this breaks the up-down symmetry and—at the level of our CG model—effectively rotates the average position of the adhesive strip away from the substrate. This creates a tangential torque on the membrane, because adhesion pins the filament’s local material frame to its Darboux frame on the surface (Guven et al., 2014), and therefore it has appropriately been called ‘Darboux torque’ (Fierling et al., 2016)—see Figure 2g and Box 1.

Considering that the PH domain is connected to the stalk rather flexibly, it is not obvious that it can actually transmit such a torque. However, flexibility does not preclude the transmission of stresses, provided other contacts are in place that help acting as a pivot, and these might simply be steric interactions with other parts of the assembled scaffold. We recall that Kong et al. (2018) provide structural evidence that forces are transmitted all the way from dynamin’s G-domain to the PH domain and onto the membrane, even though this is indirectly deduced by aligning the coordinates of dynamin with an unbent BSE to the structure of a bent dynamin in the Dyn^GMPPCP map at the GTPase domain. Still, neither this new structure, nor the previously observed tilting of the PH domain (Sundborger et al., 2014) unambiguously proves the existence of torques. But while elucidating the mechanical nature of this process will have to await more detailed molecular modeling, the existence of a Darboux torque as been posited and exploited in another model for dynamin-driven fission, which simplifies the complex scaffold geometry to two counter-rotating apposing rings (Fuhrmans and Müller, 2015; Shnyrova et al., 2013), a geometry that remote-pinches the membrane between the rings. Notice, though, that both geometry and symmetry are different in the latter case: counter-rotating rings have a mirror symmetry and hence exert oppositely acting Darboux torques that constructively interfere in the middle of the scaffold. Since a helix is one contiguous filament, it will rotate everywhere in the same sense, rendering torque amplification much less straightforward.

In our own simulations, which account for the full helical geometry, we find that rotation is necessary for a constricted membrane tube with a remaining aqueous lumen to transition into the hemifission intermediate. Consistent across all three simulation runs, the constriction plus rotation sequence (Figure 2f, cyan curve, Figure 2—Figure Supplement 1a, and Video 2) transitions at $R = R_{c} \approx 10.5 σ \approx 8.4 n m$ , when the inner lumen is small but has not yet vanished; we will subsequently refer to $R_{c}$ as the ‘critical constriction radius’.

Video 2

Download asset

Since rotation gradually diminishes binding between membrane and filament, a non-rotating scaffold maintains adhesion while constricting, which could hold the membrane tube open and thereby prevent it from transitioning into the hemifission case. To test this, we considered a constricted but not rotated filament at $R = 10 σ$ (which is even below the critical radius) and artificially switched off the adhesion between scaffold and membrane. As shown in Figure 3, the neck did not progress towards hemifission; in fact, the response to this change is a reduction in $R_{g}$ which, considering the error bars (determined via blocking (Flyvbjerg and Petersen, 1989)) is so small that it is not statistically significant. This suggests that the functionally important consequence of rotation is not merely a reduction of binding energy, but active stresses, likely due to the above-mentioned Darboux torque.

Box 1.

Illustration of a tangential membrane torque.

An object in contact with a membrane can exert a force on it by locally pushing or pulling. But it can also exert a tangential torque (i.e., a torque whose rotation axis is parallel to the membrane plane). This can be conceptualized as a force couple—two forces of equal magnitude but opposite direction, which do not share the same line of action. As an illustration, panel (a) shows a pen clipped to a flat piece of paper and held tangentially to its surface. Rotating the pen around its axis, as in (b), exerts a horizontal torque on the paper pinned between pen and clip, resulting in an S-shaped curvature deformation. The rotation is illustrated as a blue curve, the corresponding force couple as two red arrows. Darboux torques are tangential torques that are not triggered by an explicit external rotation (as in the pictured example) but through a mismatch between the direction of a spontaneously curved filament’s normal curvature and the direction of its adhesive strip (Fierling et al., 2016), which in our case is quantified by the angle $φ$ (see Figure 1b). Mechanical equilibrium then also requires that in the absence of any external forcing the total Darboux torque integrates to zero.

Box 1—Figure 1

Download asset Open asset

Illustration of a tangential membrane torque.
https://doi.org/10.7554/eLife.39441.016

https://doi.org/10.7554/eLife.39441.017

Figure 3

Download asset Open asset

Time evolution of $R_{g}$ .

The neck’s gyration radius is shown in the end stages of a pure constriction protocol. The time series starts when the scaffold radius is $R = R_{c} = 10.5 σ$ , which leads to $R_{g} / σ = 4.187 \pm 0.02$ (as measured over the subsequent $600 τ$ , with an error determined via blocking (Flyvbjerg and Petersen, 1989)). After that, a further constriction of the filament to $R = 10 σ$ reduces the neck’s gyration radius to $R_{g} / σ = 3.890 \pm 0.04$ but does not trigger hemifission (which corresponds to the much smaller value $R_{g} \approx 2 σ$ —see Figure 2f). Turning off the adhesion between scaffold and membrane only reduces the gyration radius by a very minor amount, $R_{g} / σ = 3.841 \pm 0.035$ , a change that is not statistically significant ( $p = 0.36$ ). Once we additionally let the scaffold disassemble into (non-adhesive) dimers (see also Video 4), the neck very rapidly doubles its radius within about $200 τ$ , after which the definition of its location becomes ambiguous.

https://doi.org/10.7554/eLife.39441.018

Figure 3—source data 1 Gyration radius as a function of time. The data are available as a text-file containing $R_{g}$ as a function of $t$ .: https://doi.org/10.7554/eLife.39441.019
Download elife-39441-fig3-data1-v2.txt

If in addition to constriction and rotation we also elongate the helix, hemifission is still reached before the inner lumen disappears, but this requires a further filament radius reduction (Figure 2f, dark cyan curve). Consistent with our observations on constriction plus elongation, this case with additional rotation also shows a greater variability across our three runs, transitioning over three consecutive constriction steps, which however fall between the bounds of constriction plus rotation and constriction only (see Figure 2—figure supplement 1b). These findings again endorse the view that rotation supports hemifission, while elongation opposes it.

Pre-hemifission disassembly of the dynamin coat

In the two-stage model the constricted state assembles from GTP-loaded dynamin, while subsequent hydrolysis-triggered depolymerization of the filament induces fission (Bashkirov et al., 2008; Mattila et al., 2015). Two pathways are conceivable: pre-hemifission coat disassembly would need to drive the membrane tube towards (at least) hemifission, while post-hemifission disassembly would only need to destabilize this hemifission state. To test the first pathway, we start with a filament at $R = R_{c}$ (induced only via constriction) and then cut it into approximately dimer-sized fragments. Irrespective of whether these retain their adhesion capability to the membrane (Video 3) or lose it and hence immediately unbind (Video 4), the membrane neck rapidly widens following scaffold rupture (see also Figure 3). Of note, even binding-capable fragments are individually not strong enough to impose their curvature on a substrate whose geometry becomes progressively unfavorable, and they ultimately detach from it. This also documents that our scaffold only binds weakly, and that rotation-driven hemifission is not the trivial result of massive forces resulting from large adhesion, or even of pulling lipids out of the membrane.

Video 3

Download asset

Video 4

Download asset

Observe that our simulation setup does not exert external membrane tension, since our implicit solvent enforces no volume constraint and permits the membrane—even though closed and constricted—to relax the area per lipid. Nevertheless, it is unlikely that a nonzero tension would prevent the widening of the neck: the value that would be needed to maintain a cylindrical membrane at the critical radius $R_{c}$ is given by $κ / 2 R_{c}^{2}$ , or a few mN/m (Deserno, 2015; Bukman et al., 1996; Hochmuth et al., 1996), which is very high. Even disregarding the question how such a large tension would arise in a physiological context, the mere fact that this approaches a membrane’s rupture stress and would hence place the system dangerously close to unspecific bilayer failure renders a recourse to such a high tension implausible.

Non-axisymmetric pathway to initiate hemifission via pores

Recent experiments have observed that fission of dynamin-coated membrane tubules occurs within the coated region (Dar et al., 2015), although earlier studies had suggested that fission occurs at the edge between the dynamin helix and the uncoated membrane (Morlot et al., 2012). We always observe that an initial hemifission seed appears in the middle of the neck for short filaments (up to 1.5 turns), or two seeds appear near the edges for longer ones (more than two turns), see Figure 2h. This suggests that two regions of highly localized stress appear slightly inwards of either edge, which overlap and may mutually amplify for sufficiently short filaments. Furthermore, since longer filaments trigger hemi-fission only at an even smaller scaffold radius ( $R_{c, l o n g} \approx 10 σ$ ), both findings indicate that short filaments induce hemifission more efficiently than long ones.

That hemifission is seeded by a small pore is unexpected, not only because fission is believed to be non-leaky (Bashkirov et al., 2008), but also because the existence of a hemifission intermediate is generally taken to exclude the need for (or even possibility of) pores. However, a tube’s inner leaflet must change topology, posing the question how a filament only in contact with the outer leaflet could promote this transition. Our simulations suggest an intriguing non-axisymmetric pathway: the filament seeds a small pore that widens around the circumference of the neck, while its top and bottom edges pull radially inward and fuse with the apposing intact membrane. This creates two defect lines at which three bilayers meet, and contracting them results in the top and bottom point singularity of the hemifission state’s cylindrical micelle. This sequence of events never involves a large pore, provided the filament stays short enough, a condition that imposes constraints on the constriction process itself.

Concomitant constriction and disassembly of the scaffold

If dynamin constricts due to GTP hydrolysis, as posited in the constrictase model, the initially unconstricted helix has to be long enough for the two rungs to meet, so that apposing G-domains can cross-catalyze hydrolysis. Constricting the radius by a factor of two then necessarily doubles the number of turns if the helical length stays fixed. We find that such long scaffolds induce rather sizable pores (Figure 2h) that would likely result in leakage. But the ends of a filament that in the constricted state only takes one turn would not be able to meet up in the preceding unconstricted state, and GTP driven constriction could not commence. This dilemma could be resolved if constriction and disassembly happen in short succession: when the two ends of the initially relaxed helical filament first meet, they hydrolyze GTP and trigger a first constriction step. This brings a new pair of GTP loaded G-domains in contact that drive the next constriction step, and so forth until full constriction. But since GTP hydrolysis enhances disassembly, a filament end comprising ever longer stretches of spent dynamin can shed its monomers concurrently with the ongoing constriction, especially if its PH domain retracted from the membrane. The helix would tighten but never extend much beyond one turn, and hence never induce large pores (Video 5). This hypothesis is compatible with the experimental evidence that, upon GTP hydrolysis, the scaffold seems to adjust to a length optimal for fission (about one full turn) (Shnyrova et al., 2013).

Video 5

Download asset

Transition from hemifission to complete fission

Without concurrent filament shortening, our hemifission state resembles a short cylindrical micelle (Figure 2f, background image), a transition state explored in two other recent investigations (Mattila et al., 2015; Zhang and Müller, 2017). These studies find that this micelle is remarkably stable, suggesting that completing fission faces a very sizable second free energy barrier. Additional tension might reduce its height, and indeed in vitro experiments by Roux et al. (2006) and Morlot et al. (2012) have found that longitudinal tension assists in producing fission (though it is interesting to note that our simulations present a tension-free pathway to fission). However, Zhang and Müller (2017) estimate that the barrier might remain as large as $30 k_{B} T$ even at the largest biologically justifiable tensions (close to uncontrolled rupture), which leads them to speculate that other factors help to complete fission, such as the high curvature in the region where the micelle merges with the bilayer.

Here we propose that this second barrier might indeed not be biologically relevant, since it is a consequence of the simulation setup in these studies, which prevents the micelle from shrinking and instead requires it to rupture mid-length. In our simulations we also never observe the micelle to break while being enclosed by the dynamin scaffold (from which it has already unbound), but we argue that this is due to the scaffold preventing the two point defects at the end of the micelle from merging. Once the scaffold disassembles (whether gradually or abruptly), they are being pulled together by a force that can be estimated to be $F ≃ π κ / 2 z_{0} \sim 𝒪 (100 pN)$ . This is the energy per unit length of creating a cylindrical micelle of curvature radius $z_{0}$ (the pivotal plane distance) out of lipids that have a monolayer leaflet rigidity of $κ / 2$ . This force pulls the two daughter membranes together, whereupon bilayer contact catalyzes micellar fission (see Video 6). This hypothesis, even though derived from a fairly coarse-grained model, is nevertheless plausible, because splitting the cylindrical micelle somewhere along its length would further raise the free energy by creating two spherical caps of even more unfavorable packing geometry (Zhang and Müller, 2017), while the contact between the daughter membranes annihilates the two already existing point defects at the micellar ends.

Video 6

Download asset

The latter scenario seems to conflict with the widely held belief that highly curved vesicles are fusogenic. However, recent experiments by François-Martin et al. (2017) paint a more nuanced picture. These authors measured the free energy barrier towards fusion between $\sim 60 nm$ diameter POPC (16:0–18:1 PC) and DOPC [18:1 ( $Δ$ 9–Cis) PC] vesicles at 37°C. On the one hand, the observed free energy barrier of $Δ F \sim 30 k_{B} T$ is at the lowest end of theoretical estimates, indicating that protein-free fusion between such vesicles is easier than previously thought. On the other hand, even when incubating such vesicles at the unusually high concentrations of 18 mM PC, only 2% had completed fusion after 30 min, which does not support the notion of spontaneous fusion—as these authors indeed conclude.

Nevertheless, the free energy pathways for events that change membrane topology remain challenging, for at least four unrelated reasons: first, the choice of boundary conditions and constraints in theory or simulations can strongly affect the outcome (for instance, whether cylindrical micelles can shrink, hemifusion diaphragms can expand, or tensions can relax); second, the key physics happens at the nanometer scale, and hence the results of highly coarse-grained models such as ours or continuum theory must be interpreted cautiously; third, a topological barrier to fusion exists, whose height depends on the Gaussian curvature modulus and is thus not well known (see the contribution of Deserno in Bassereau et al. (2018)); and fourth, additional complexity due to accessory proteins or lipid mixtures may qualitatively change the energetics, for instance by lipid sorting in very high leaflet curvature gradients (Cooke and Deserno, 2006; Tian and Baumgart, 2009). For the pathway that naturally arises in our simulations—a shrinking of the hemifission micelle post-disassembly, followed by autocatalytic cutting—the free energy barriers are not obvious, especially for solvent free models like ours (or those in the above-mentioned studies by Mattila et al. (2015) and Zhang and Müller (2017)), and hence this subject warrants more dedicated future studies.

Results and discussion

Taken together, our studies support a number of conclusions. To begin with, the poppase model (Stowell et al., 1999) faces not only kinetic but also equilibrium obstacles: extension of the helical scaffold disfavors fission, because a widening groove offsets constriction. In contrast, hemifission is promoted by tilting one of the two symmetry subsets of PH domains (Mehrotra et al., 2014; Sundborger et al., 2014; Kong et al., 2018), which effectively rotates the filament’s adhesive strip away from normal contact. The resulting Darboux torque (Fierling et al., 2016; Guven et al., 2014) has been previously invoked to explain fission (Fuhrmans and Müller, 2015; Shnyrova et al., 2013), but these earlier models pictured the dynamin scaffold as two rings, whose counter-rotation-induced torque remote-pinches the enclosed membrane tube. The effect is particularly intuitive under mirror symmetry, a geometry at odds with the actual helical one. Surprisingly, this difference appears not to be central.

We show that pre-hemifission scaffold breakage aborts fission by allowing the enclosed membrane tube to re-expand. But disassembly is still essential to complete fission, as argued in the two-stage model, because even if the severed bilayer is energetically preferable to the hemifission state (Kozlovsky and Kozlov, 2002), a substantial energy barrier is required to explicitly break the hemifission micelle (Mattila et al., 2015; Zhang and Müller, 2017). Our simulations lead us to suggest that this can be circumvented by merging and annihilating the micelle’s two endpoint defects, a process that commences once the two daughter membranes are pulled into close proximity and hence critically depends on the scaffold getting out of the way by disassembling. Notice that this mechanism is not scaffold specific and may hence apply to any other fission machinery that leads to a hemifission state involving a small stretch of a cylindrical micelle.

How hemifission is induced is experimentally less clear (Antonny et al., 2016). In our studies constriction alone, down to the smallest experimentally observed luminal radii, does not suffice. We believe this to be independent of whether the constricted state is reached passively (two-stage model) or actively (constrictase model), since our dynamic protocol could simply be viewed as a means to adiabatically prepare a highly constricted state. PH domain tilting thus emerges as a way to catalyze hemifission, and since applying a Darboux torque costs energy, we posit that the energy of GTP hydrolysis is at least in part used to drive this conformational change. This is in accord with experimental findings by Dar and Pucadyil (2017) that replacing the PH domain by a simple binding motif strongly slows down the fission rate. It is also supported by the recent Cryo-EM reconstruction by Kong et al. (2018), who suggest that forces generated from the GTPase dimer interaction are transferred across the stalk to the PH domain and from there onto the membrane. It is worth noting that in their reconstruction Dyn1 was bound to the nonhydrolyzable guanosine triphosphate analogue GMPPCP, and so the question whether GTP hydrolysis would create additional forces or torques that then could be transduced to the membrane remained open. To better understand the mechanical basis and viability of such a force transmission, it will be essential to structurally resolve the connection between the PH domain to the stalk domain.

Finally, we consistently observe that hemifission is initiated by a transient pore puncturing the constricted neck (see arrows in Figure 2h, the time sequence in Figure 4, and Video 2). This is reminiscent of likewise non-axisymmetric pathways seen in fusion simulations (Noguchi and Takasu, 2001; Noguchi and Takasu, 2002; Müller et al., 2002; Müller et al., 2003), whose implied transient leakage currents were soon after confirmed to be common in electrophysiological measurements on hemagglutinin-mediated fusion (Frolov et al., 2003). We estimate that our pores open to a diameter of no more than 2 nm, which under physiological ionic strength equips them with a conductivity on the order of 1 nS, while their lifetime is a few microseconds (mapped very roughly from our coarse-grained model via lipid self-diffusion). This would not be trivial to detect experimentally, but similarly fast transients (few microseconds) have been observed in the gating currents of Shaker potassium channels embedded in Xenopus oocytes, using an eight-pole Bessel filter and achieving a bandwidth of about 200 kHz (Bezanilla, 2018; Sigg and Bezanilla, 2003). Increasing the ionic strength in reconstituted systems to 1 M, a further gain in sensitivity by up to an order of magnitude could be obtained, provided this does not interfere with dynamin’s operation. But notice also that our leakage pores are partially covered by the dynamin scaffold (see again Figure 2h) and, under physiological conditions, possibly by additional proteins proposed to assist in dynamin-driven fission, such as BAR domains (Takei et al., 1999; Farsad et al., 2001; Itoh et al., 2005; Mim et al., 2012). Hence, a pore’s effective conductance might be significantly lower than that of a freely accessible membrane pore or channel.

Figure 4

Download asset Open asset

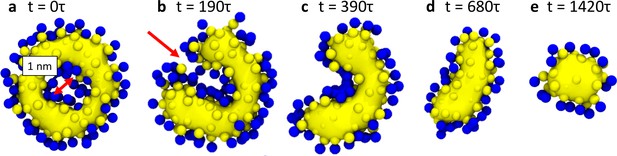
Hemifission via a transient pore.

This time sequence of simulation snapshots shows slices through the membrane neck with a width of $2 σ$ , placed symmetric around the center of mass of the scaffold (not shown for clarity). The continuity of the tail region (yellow; blue are the head groups) is emphasized by using VMD’s ‘QuickSurf’ rendering on all tail beads (Humphrey et al., 1996), which creates an isosurface extracted from a volumetric Gaussian density map. In panel (a), chosen to be time-point $0 τ$ in this sequence, the tail region is still continuous and encloses an inner lumen with a diameter of about $1 \text n m$ . In panel (b) a small pore opens (red arrow) that connects the inner lumen to the exterior region of the vesicle. As it widens through panels (c) and (d), the pore rim above and below the imaged plane fuses to the inner leaflet of the lumen, which finally leaves in panel (e) a cylindrical hemifission micelle connecting two closed vesicles. See also Video 2.

https://doi.org/10.7554/eLife.39441.024

Our simulations show that pores are larger—and hence potential leakage more severe—if hemifission is triggered at larger radii, or if the filament is longer, suggesting that a close coordination of constriction, rotation, and possibly concomitant disassembly renders fission not only more efficient but also more tight. We hence expect mutants disrupting this coordination (for instance the $Δ$ PH mutant of Dar and Pucadyil (2017)) to have larger pores. This would exacerbate leakage problems and could be experimentally observed.

While we have explicitly focused on the case of classical dynamin, several of our findings have implications beyond this particular protein and offer lessons for membrane topology remodeling that go beyond Dyn1. For instance, all members of the dynamin superfamily are believed to oligomerize (Praefcke and McMahon, 2004), likely into helices, for which our generic basic model holds. Furthermore, the mismatch between the normal curvature direction of such a helical filament and the direction of its adhesive domain (measured by $φ$ in our case) is a generic degree of freedom for such a structure. Whether directly present during assembly or only later triggered by a (possibly GTP-dependent) conformational change, it will give rise to Darboux torques on the membrane. We have explicitly shown that these support the transition into the hemifission state, and hence they provide a means to trigger a topological transition that is different from the notions of constriction or elongation. This matters because other topology remodeling proteins exist that are unlikely to work by either. Consider in particular the reverse-geometry scission driven by the ESCRT-III complex (Wollert et al., 2009), which involves the adsorption and polymerization of a helical filament on the inside of the neck to be cut. Present models (for a recent review, see Schöneberg et al. (2017)) rely on adhesion and/or geometric changes of the spiraling filaments, which result in either direct forces or boundary-induced stresses at the contact site (arising from, for instance, a contact curvature condition (Deserno et al., 2007)). But geometric rearrangements of a curved elastic filament with a finite twist rigidity, whose material frame is pinned to the membrane (Guven et al., 2014), almost invariably result in additional Darboux torques, as well as twist-induced analogs (Fierling et al., 2016), the relevance of which is only beginning to emerge (Quint et al., 2016). In this work we have explicitly demonstrated, for the particular example of Dyn1, that this geometrically elementary mechanism is remarkably effective, which suggest that it might be more common than so far realized: traces of the essential action could date back to the earliest bacterial FtsZ ancestor, which shares many of the key geometric (Erickson, 2000) and biochemical (Lu et al., 2000) features. This might hence suggest novel functional models also for other membrane remodelers (such as ESCRT-III), for which the mode of operation is much less well understood than for classical dynamin.

Materials and methods

General modeling aspects

Request a detailed protocol

Our investigation focuses on the mesoscopic effects of a constricting helical dynamin filament on a tubular lipid membrane, expressed primarily by the interplay between ( $i$ ) filament geometry and binding affinity and ( $i i$ ) membrane and filament elasticity. A long-standing aim in the dynamin field has been to develop an explanatory model for dynamin’s membrane fission mechanism within the framework of such mesoscopic emergent properties. By creating a coarse-grained (CG) model of dynamin fission that captures precisely these mesoscopic aspects, our goal is to explore the consequences of this interplay, while either disregarding much of the microscopic or chemical detail, or implicitly accounting for it in terms of effective interactions.

The fundamental degrees of freedom in our model are mesoscopic ‘beads’ with a size (diameter) $σ ≃ 0.8 nm$ , which hence correspond to $𝒪 (10)$ heavy atoms. Physics below this scale leaves its trace at larger dimensions through the collective action of effective potentials—much like the quantum mechanics of correlated electron clouds re-emerges classically as effective van der Waals interactions, or the configurational distributions of charged moieties in a molecule yield effective dipole moments and polarizabilities. A rich literature exists outlining the technique of coarse graining in a soft-matter and biophysics context (Deserno, 2009; Ingólfsson et al., 2014; Izvekov and Voth, 2005a; Izvekov and Voth, 2005b; Brini et al., 2013; Müller-Plathe, 2002; Murtola et al., 2009; Noid, 2013; Noid et al., 2008; Peter and Kremer, 2009; Riniker et al., 2012; Saunders and Voth, 2013; Voth, 2008). In the terminology of Noid (2013), we employ a ‘top down’ modeling approach.

Since we are not concerned with hydrodynamic effects, we account for the embedding water implicitly via effective attractive interactions between hydrophobic species (such as CG lipid tail beads).

The reduction of the number of degrees of freedom allows not only for a computational speed-up and a better statistical sampling; it also offers insight into the nature of the original problem: physical effects that are correctly represented in a CG model prove to be largely independent of microscopic specifics, rendering them important players in an emergent mesoscopic explanatory model.

All simulations were performed using the ESPResSo package (Limbach et al., 2006), using an integration time step $Δ t = 0.01 τ$ (where $τ$ is the simulations CG time unit). A Langevin thermostat (Grest and Kremer, 1986) with friction constant $Γ = 1.0 τ^{- 1}$ was used to keep the temperature constant. All simulations have been performed in an $N V T$ ensemble.

Lipid model

Request a detailed protocol

We use an implicit solvent lipid model (Cooke et al., 2005; Cooke and Deserno, 2005) in which a single lipid molecule is replaced by three consecutive beads, one for the hydrophilic head and two for the hydrophobic tails, which are not individually resolved (Figure 1a). In the absence of solvent, the hydrophobic effect, and hence aggregation of lipids into bilayer membranes, is driven by attractive interactions between the CG tail beads of depth $ε$ (the simulations’ energy unit) and range $w_{c}$ (the precise potential forms are detailed by Cooke et al. (2005)). The magnitude of $w_{c}$ and the temperature $T$ determine whether lipids aggregate into fluid membranes, and if so, what their material properties are. We work at the frequently employed state point $w_{c} = 1.6 σ$ and $k_{B} T = 1.1 ε$ (which also sets the energy scale). Under these conditions lipids aggregate into fluid membranes with an area per lipid of about $a_{ℓ} = 1.2 σ^{2} \approx 0.77 n m^{2}$ , an average head-bead distance from the midplane of about $d_{H} = 2.2 σ \approx 1.8 n m$ , and a separation between the half-maximum density points (a possible proxy for the Luzzati thickness (Luzzati and Husson, 1962)) of about $d_{1 / 2} = 5.6 σ \approx 4.5 n m$ . Considering the limitations of the underlying microscopic basis of nanometer-sized CG beads, these numbers are reasonably close to typical biologically relevant lipids, such as POPC ( $a_{ℓ} \approx 0.643 n m^{2}$ and $d_{1 / 2} \approx 3.91 n m$ at 30°C (Kučerka et al., 2011); still, sub-nanometer resolution should not be taken too literally in a model like this.

The membrane has a bending rigidity of $κ \approx 12.8 k_{B} T$ (Cooke et al., 2005; Cooke and Deserno, 2005; Harmandaris and Deserno, 2006; Hu et al., 2013), purposefully chosen smaller than a typically value of $20 k_{B} T$ (Kučerka et al., 2005), since this affords a significantly entropy-deprived coarse-grained system an alternative opportunity to undergo fluctuations. Wang and Deserno (2016), recently also measured the tilt modulus of this model, finding it to be $κ_{t} \approx 7 k_{B} T / n m^{2}$ . This results in the characteristic tilt decay length $ℓ_{t} = \sqrt{κ / κ_{t}} \approx 1.3 n m$ , in good agreement with experimental values (Jablin et al., 2014), indicating that the model does not merely capture overall fluidity and curvature elasticity, but also local lipid reorientation physics, which matters for the intermediate states of fission and fusion (Kozlovsky and Kozlov, 2002).

Protein

Request a detailed protocol

We model the right-handed helical dynamin scaffold by CG beads of the same diameter $σ$ as the lipid CG beads (represented by a purely repulsive Weeks-Chandler-Andersen potential that only acts between filament and lipid beads), placing them such as to represent the shape of a CG filament (Figure 1b). This first requires setting up a coordinate system that embodies helical symmetry—see Figure 5 for the following discussion.

Figure 5

Download asset Open asset

Definition of helicoidal coordinate system.

The black vertical $z$ -axis is surrounded by a cylinder, around which a helical dynamin tube winds. Its green center line with radius $R$ and pitch $2 π p$ is given by (Equation 1). On this space curve we define the (right-handed) Darboux-frame ${T, N, L}$ , consisting of a tangent vector $T$ (black), normal vector $N$ (blue) and co-normal vector $L$ (red), which are given by (Equation 2). In the $N$ - $L$ -plane we can then define the circular cross-section of the filament and place rings of CG beads at the correct distance from the green filament axis. The direction along $N$ points towards the enclosed cylinder, but it is easy to rotate it by an angle $φ$ around the $T$ axis. This is how one may rotate the beads representing the PH domain (red) off the underlying substrate.

https://doi.org/10.7554/eLife.39441.025

The arc-length ( $s$ ) parametrization of a right-handed helix of radius $R$ and pitch $2 π p$ , whose axis coincides with the $z$ -axis of the coordinate system, is given by

X (s) = (\begin{matrix} R \cos (s / \sqrt{R^{2} + p^{2}}) \\ R \sin (s / \sqrt{R^{2} + p^{2}}) \\ p s / \sqrt{R^{2} + p^{2}} \end{matrix}) .

This has a length $2 π \sqrt{R^{2} + p^{2}}$ per turn and a local (Frenet) curvature of $R / (R^{2} + p^{2})$ . The local unit tangent vector $T (s) = X^{'} (s)$ is then

T (s) = \frac{1}{\sqrt{R^{2} + p^{2}}} (\begin{matrix} - R \sin (s / \sqrt{R^{2} + p^{2}}) \\ R \cos (s / \sqrt{R^{2} + p^{2}}) \\ p \end{matrix}) .

We need to define a finite-thickness filament for which $X (s)$ is the central axis. Moreover, since we have to specify the location of an adhesive strip relative to a central cylinder that is being wrapped by the helix, it is convenient to extend the tangent vector $T$ along the helical curve into a local basis by defining two additional vectors $N$ and $L$ as follows: both have unit length and are perpendicular to $T$ , the normal vector $N$ coincides with the local surface normal of the inscribed cylinder, and the remaining co-normal vector $L$ is given by $L = T \times N$ :

\begin{aligned} (2b) & N (s) = & (\begin{matrix} - \cos (s / \sqrt{R^{2} + p^{2}}) \\ - \sin (s / \sqrt{R^{2} + p^{2}}) \\ 0 \end{matrix}) \\ (2c) & L (s) = & \frac{1}{\sqrt{R^{2} + p^{2}}} (\begin{matrix} p \sin (s / \sqrt{R^{2} + p^{2}}) \\ - p \cos (s / \sqrt{R^{2} + p^{2}}) \\ R \end{matrix}) . \end{aligned}

The thus defined triplet ${T, N, L}$ of vectors constitutes a right-handed orthonormal basis at every point along the filament. It is called the ‘Darboux frame’ (with respect to the underlying cylindrical surface on which the filament rests).

On the ${N, L}$ plane perpendicular to the filament we now place CG beads that will form one of the cross-sectional circular discs from which we build the filament slice by slice. Each disk consists of a central bead placed directly onto the filament axis, a first ring of 6 beads and radius $R_{6}$ , and a second ring of 12 beads and radius $R_{12}$ . The coordinates of the beads sitting on the 1-, 6- and 12-ring can be parametrized as

\begin{aligned} (3a) & X_{1} (s) = & X (s) \\ (3b) & X_{6} (s, n) = & X (s) + R_{6} [N (s) \cos φ_{n}^{(6)} + L (s) \sin φ_{n}^{(6)}] \\ (3c) & X_{12} (s, n) = & X (s) + R_{12} [N (s) \cos φ_{n}^{(12)} + L (s) \sin φ_{n}^{(12)}] \end{aligned}

where $n \in {0, \dots, 5}$ for the 6-ring and $n \in {0, \dots, 11}$ for the 12-ring. The angles are given by

φ_{n}^{(6)} = \frac{2 π n}{6} + φ, φ_{n}^{(12)} = \frac{2 π n}{12} + φ,

and the overall phase shift $φ$ denotes the extent to which bead 0 on the 6- and 12-ring is rotated around the local filament axis, see Figure 1b. Since we will subsequently equip bead 0 on the 12-ring with an additional adhesion towards lipid head groups, representing the inner binding region of the dynamin filament due to the PH domains, this phase angle $φ$ describes a rotation of the CG filament with which we effectively capture the asymmetric tilting of half of the PH domains. Notice that due to the way the Darboux frame is set up, $φ = 0$ corresponds to an adhesive strip that exactly sits on the enclosed cylindrical surface (and hence does not exert any Darboux torque).

We typically consider filaments consisting of 9 dynamin dimers, each comprising five discs, for a total of 45 discs. We take $R_{6} = 2 σ$ and $R_{12} = 4 σ$ , making for a filament diameter of about $8 σ \approx 6.4 n m$ . The spacing $Δ s$ between discs along the central helix is set so that a full turn in the unconstricted state ( $R = 20 σ$ and $2 π p = 11 σ$ ) comprises 40 discs, leading to $Δ s = 2 π \sqrt{R^{2} + p^{2}} / 40 = 3.1536 σ$ . The location of every bead in the filament at a given shape triplet ${R, p, φ}$ is now completely specified.

The shape is elastically fixed by introducing harmonic bonds between all beads within a cutoff distance of $r_{c u t} = 5 σ$ , whose rest length equals the equilibrium distance between the beads according to the chosen shape triplet ${R, p, φ}$ , and whose spring constant is $K = 200 ε / σ^{2}$ , which is similar to the choice for other elastic networks for coarse-grained protein models (Periole et al., 2009). This renders the filament sufficiently stiff so that it can impose its shape on an underlying membrane tube, and not vice versa.

To change the filament’s shape, we adjust the rest lengths of all elastic springs so that they represent distances in a filament at a new shape triplet, ${R, p, φ} \to {R^{'}, p^{'}, φ^{'}}$ . This introduces local stresses which the filament relaxes by transforming into the new equilibrium shape. We consider parameter ranges within $R / σ \in [6, 18]$ , $2 π p / σ \in [11, 20]$ and $φ \in [0^{\circ}, 80^{\circ}]$ . Figure 6 illustrates the time series of these parameter changes, which we use individually or in combination, as outlined in the main text. For instance, during constriction we reduce the helical radius by $1 σ$ every $300 τ$ , corresponding to about $0.18 n m / μ s$ . Albeit much faster than in reality, this is still effectively quasistatic.

Figure 6

Download asset Open asset

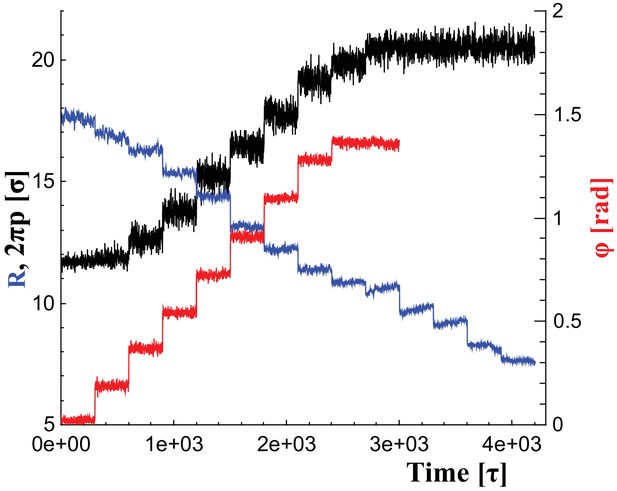
Changes of filament geometry.

Time sequence followed when driving the dynamin filament through changes in its radius $R$ , pitch $2 π p$ , and rotation angle $φ$ . As detailed in the results section, we conduct sets of simulations in which various combinations of these observables are adjusted, while others stay at their original value. For instance, in a constriction $+$ elongation simulation the radius is successively decreased from $18 σ$ to $9 σ$ , while the pitch is simultaneously tuned up from $11.5 σ$ to $20 σ$ in a way documented by the blue and black curves, respectively, while the rotation angel remains at $φ = 0$ .

https://doi.org/10.7554/eLife.39441.026

Figure 6—source data 1 Angle as a function of time. The data are available as text-files containing $R$ , $2 π p$ , and $φ$ as a function of time $t$ .: https://doi.org/10.7554/eLife.39441.027
Download elife-39441-fig6-data1-v2.txt
Figure 6—source data 2 Pitch as a function of time.: https://doi.org/10.7554/eLife.39441.028
Download elife-39441-fig6-data2-v2.txt
Figure 6—source data 3 Radius as a function of time.: https://doi.org/10.7554/eLife.39441.029
Download elife-39441-fig6-data3-v2.txt

Beads on the red adhesive strip (accounting for the PH domains) additionally experience an adhesion of strength $ε$ towards lipid head beads, represented by a standard Lennard-Jones potential that is truncated and shifted to zero at $r = 2.5 σ$ . For the beads on the two immediately adjacent neighboring strips (i.e., numbers 1 and 11 on the 12-ring) we turn off the hard core repulsion with respect to lipid head (but not tail) beads, in order to permit the adhesive domain to embed into the head group region.

The free energy of binding for dynamin dimers or larger fragments depends not only on the local chemistry, but also on the curvature of both dynamin and the membrane. We are not aware of measurements that are precise enough to help parametrizing this interaction, but in order to avoid driving fission by overly strong interactions (which could, for instance, exert unrealistically large torques or even pull lipids out of the membrane), we have opted for a lower-bound scenario, in which we made the interaction between dimer-equivalents (blocks of 5 discs) and a highly curved membrane neck just strong enough to trigger binding; but when substrate curvature decreases due to membrane tube widening, the interplay between curvature energy and adhesion increasingly disfavors binding (McDargh et al., 2016), and fragments detach (Video 3).

Measuring membrane constriction

Request a detailed protocol

Several possibilities exist to quantify the extent of tubular membrane constriction, but the two most obvious ones have significant drawbacks: the midplane radius cannot be defined once the membrane is in the hemifission state, and the radius of the inner lumen cannot distinguish between a completely closed bilayer tube and a hemifission micelle.

We hence use as a metric for constriction the cross-sectional gyration radius $R_{g}$ of beads in the vicinity of the constriction point, defined as follows:

R_{g}^{2} = \frac{1}{M} \sum_{i = 1}^{M} [(r_{i} - r_{0})_{x y}]^{2},

where the sum extends over all lipids that are at most a radial distance of $20 σ$ and an axial distance of $\pm 1 σ$ away from the filament’s center of mass, $r_{0}$ is the center of mass of these selected lipids, and the subscript ' $x y$ ' indicates that we first take the projection of $r_{i} - r_{0}$ into the $x y$ -plane.

If $R_{m}$ is the midplane radius of a cylindrical lipid tube and $w$ the monolayer width, then in continuum approximation we get

R_{g}^{2} = \frac{\int_{R_{m} - w}^{R_{m} + w} d r 2 π r r^{2}}{\int_{R_{m} - w}^{R_{m} + w} d r 2 π r} = R_{m}^{2} + w^{2},

showing that $R_{g} = R_{m} [1 + \frac{1}{2} (w / R_{m})^{2} + \dots]$ is close to $R_{m}$ , with quadratic higher order corrections in $w / R_{m}$ . Moreover, a membrane cylinder of vanishing inner lumen has $R_{m} = w$ and hence $R_{g} = \sqrt{2} w$ , while the hemifission micelle has $R_{g} = w / \sqrt{2}$ . Hence, the jump in $R_{g}$ is $w / \sqrt{2} = \frac{1}{2} \times 5.6 σ / \sqrt{2} \approx 2 σ$ , using the Luzzati width of our CG membrane. This is very close to our observed jump distance in the constriction only case (Figure 2f, blue curve), which indeed only transitions when the inner lumen disappears. For the other cases we investigate the jump tends to be higher, because hemifission occurs while the membrane tube is still water-filled.

Data availability

The simulation software used is freely available at http://espressomd.org/wordpress/. Source data for Figure 2f, the supplement figure to Figure 2f, Figure 3, and Figure 6 are also provided.

References

1. Antonny B
2. Burd C
3. De Camilli P
4. Chen E
5. Daumke O
6. Faelber K
7. Ford M
8. Frolov VA
9. Frost A
10. Hinshaw JE
11. Kirchhausen T
12. Kozlov MM
13. Lenz M
14. Low HH
15. McMahon H
16. Merrifield C
17. Pollard TD
18. Robinson PJ
19. Roux A
20. Schmid S
(2016) Membrane fission by dynamin: what we know and what we need to know
The EMBO Journal 35:2270–2284.

https://doi.org/10.15252/embj.201694613
- PubMed
- Google Scholar
(2008) GTPase cycle of dynamin is coupled to membrane squeeze and release, leading to spontaneous fission
Cell 135:1276–1286.

https://doi.org/10.1016/j.cell.2008.11.028
- PubMed
- Google Scholar
1. Bassereau P
2. Jin R
3. Baumgart T
4. Deserno M
5. Dimova R
6. Frolov VA
7. Bashkirov PV
8. Grubmüller H
9. Jahn R
10. Risselada HJ
11. Johannes L
12. Kozlov MM
13. Lipowsky R
14. Pucadyil TJ
15. Zeno WF
16. Stachowiak JC
17. Stamou D
18. Breuer A
19. Lauritsen L
20. Simon C
21. Sykes C
22. Voth GA
23. Weikl TR
(2018) The 2018 biomembrane curvature and remodeling roadmap
Journal of Physics D: Applied Physics 51:343001.

https://doi.org/10.1088/1361-6463/aacb98
- Google Scholar
1. Bezanilla F
(2018) Gating currents
The Journal of General Physiology 150:jgp.201812090.

https://doi.org/10.1085/jgp.201812090
- Google Scholar
(2013) Systematic coarse-graining methods for soft matter simulations – a review
Soft Matter 9:2108–2119.

https://doi.org/10.1039/C2SM27201F
- Google Scholar
(1996) Stability of cylindrical vesicles under axial tension
Physical Review E 54:5463–5468.

https://doi.org/10.1103/PhysRevE.54.5463
- Google Scholar
1. Camley BA
2. Brown FLH
(2011) Beyond the creeping viscous flow limit for lipid bilayer membranes: Theory of single-particle microrheology, domain flicker spectroscopy, and long-time tails
Physical Review E 84:021904.

https://doi.org/10.1103/PhysRevE.84.021904
- Google Scholar
1. Carr JF
2. Hinshaw JE
(1997) Dynamin assembles into spirals under physiological salt conditions upon the addition of GDP and gamma-phosphate analogues
Journal of Biological Chemistry 272:28030–28035.

https://doi.org/10.1074/jbc.272.44.28030
- PubMed
- Google Scholar
1. Chappie JS
2. Acharya S
3. Leonard M
4. Schmid SL
5. Dyda F
(2010) G domain dimerization controls dynamin's assembly-stimulated GTPase activity
Nature 465:435–440.

https://doi.org/10.1038/nature09032
- PubMed
- Google Scholar
1. Chappie JS
2. Mears JA
3. Fang S
4. Leonard M
5. Schmid SL
6. Milligan RA
7. Hinshaw JE
8. Dyda F
(2011) A pseudoatomic model of the dynamin polymer identifies a hydrolysis-dependent powerstroke
Cell 147:209–222.

https://doi.org/10.1016/j.cell.2011.09.003
- PubMed
- Google Scholar
1. Chen YJ
2. Zhang P
3. Egelman EH
4. Hinshaw JE
(2004) The stalk region of dynamin drives the constriction of dynamin tubes
Nature Structural & Molecular Biology 11:574–575.

https://doi.org/10.1038/nsmb762
- PubMed
- Google Scholar
(2014) Dynamin recruitment and membrane scission at the neck of a clathrin-coated pit
Molecular Biology of the Cell 25:3595–3609.

https://doi.org/10.1091/mbc.e14-07-1240
- PubMed
- Google Scholar
1. Cooke IR
2. Deserno M
(2005) Solvent-free model for self-assembling fluid bilayer membranes: stabilization of the fluid phase based on broad attractive tail potentials
The Journal of Chemical Physics 123:224710.

https://doi.org/10.1063/1.2135785
- PubMed
- Google Scholar
(2005) Tunable generic model for fluid bilayer membranes
Physical Review E 72:011506.

https://doi.org/10.1103/PhysRevE.72.011506
- Google Scholar
1. Cooke IR
2. Deserno M
(2006) Coupling between lipid shape and membrane curvature
Biophysical Journal 91:487–495.

https://doi.org/10.1529/biophysj.105.078683
- PubMed
- Google Scholar
(2015) A high-throughput platform for real-time analysis of membrane fission reactions reveals dynamin function
Nature Cell Biology 17:1588–1596.

https://doi.org/10.1038/ncb3254
- PubMed
- Google Scholar
1. Dar S
2. Pucadyil TJ
(2017) The pleckstrin-homology domain of dynamin is dispensable for membrane constriction and fission
Molecular Biology of the Cell 28:152–160.

https://doi.org/10.1091/mbc.e16-09-0640
- PubMed
- Google Scholar
(2007) Contact lines for fluid surface adhesion
Physical Review E 76:011605.

https://doi.org/10.1103/PhysRevE.76.011605
- Google Scholar
1. Deserno M
(2009) Mesoscopic membrane physics: concepts, simulations, and selected applications
Macromolecular Rapid Communications 30:752–771.

https://doi.org/10.1002/marc.200900090
- PubMed
- Google Scholar
1. Deserno M
(2015) Fluid lipid membranes: from differential geometry to curvature stresses
Chemistry and Physics of Lipids 185:11–45.

https://doi.org/10.1016/j.chemphyslip.2014.05.001
- PubMed
- Google Scholar
1. Erickson HP
(2000) Dynamin and FtsZ. missing links in mitochondrial and bacterial division
The Journal of Cell Biology 148:1103–1106.

https://doi.org/10.1083/jcb.148.6.1103
- PubMed
- Google Scholar
1. Faelber K
2. Posor Y
3. Gao S
4. Held M
5. Roske Y
6. Schulze D
7. Haucke V
8. Noé F
9. Daumke O
(2011) Crystal structure of nucleotide-free dynamin
Nature 477:556–560.

https://doi.org/10.1038/nature10369
- PubMed
- Google Scholar
1. Farago O
(2003) “Water-free” computer model for fluid bilayer membranes
The Journal of Chemical Physics 119:596–605.

https://doi.org/10.1063/1.1578612
- Google Scholar
1. Farsad K
2. Ringstad N
3. Takei K
4. Floyd SR
5. Rose K
6. De Camilli P
(2001) Generation of high curvature membranes mediated by direct endophilin bilayer interactions
The Journal of Cell Biology 155:193–200.

https://doi.org/10.1083/jcb.200107075
- PubMed
- Google Scholar
(1994) Crystal structure at 2.2 A resolution of the pleckstrin homology domain from human dynamin
Cell 79:199–209.

https://doi.org/10.1016/0092-8674(94)90190-2
- PubMed
- Google Scholar
(2016) How bio-filaments twist membranes
Soft Matter 12:5747–5757.

https://doi.org/10.1039/C6SM00616G
- PubMed
- Google Scholar
1. Flyvbjerg H
2. Petersen HG
(1989) Error estimates on averages of correlated data
The Journal of Chemical Physics 91:461–466.

https://doi.org/10.1063/1.457480
- Google Scholar
(2011) The crystal structure of dynamin
Nature 477:561–566.

https://doi.org/10.1038/nature10441
- PubMed
- Google Scholar
(2017) Low energy cost for optimal speed and control of membrane fusion
PNAS 114:1238–1241.

https://doi.org/10.1073/pnas.1621309114
- PubMed
- Google Scholar
(2003) Membrane permeability changes at early stages of influenza hemagglutinin-mediated fusion
Biophysical Journal 85:1725–1733.

https://doi.org/10.1016/S0006-3495(03)74602-5
- PubMed
- Google Scholar
1. Fuhrmans M
2. Müller M
(2015) Coarse-grained simulation of dynamin-mediated fission
Soft Matter 11:1464–1480.

https://doi.org/10.1039/C4SM02533D
- PubMed
- Google Scholar
1. Grest GS
2. Kremer K
(1986) Molecular dynamics simulation for polymers in the presence of a heat bath
Physical Review A 33:3628–3631.

https://doi.org/10.1103/PhysRevA.33.3628
- Google Scholar
(2014) Environmental bias and elastic curves on surfaces
Journal of Physics A: Mathematical and Theoretical 47:355201.

https://doi.org/10.1088/1751-8113/47/35/355201
- Google Scholar
1. Harmandaris VA
2. Deserno M
(2006) A novel method for measuring the bending rigidity of model lipid membranes by simulating tethers
The Journal of Chemical Physics 125:204905.

https://doi.org/10.1063/1.2372761
- PubMed
- Google Scholar
1. Hinshaw JE
(2000) Dynamin and its role in membrane fission
Annual Review of Cell and Developmental Biology 16:483–519.

https://doi.org/10.1146/annurev.cellbio.16.1.483
- PubMed
- Google Scholar
1. Hochmuth FM
2. Shao JY
3. Dai J
4. Sheetz MP
(1996) Deformation and flow of membrane into tethers extracted from neuronal growth cones
Biophysical Journal 70:358–369.

https://doi.org/10.1016/S0006-3495(96)79577-2
- PubMed
- Google Scholar
1. Hu M
2. Diggins P
3. Deserno M
(2013) Determining the bending modulus of a lipid membrane by simulating buckling
The Journal of Chemical Physics 138:214110.

https://doi.org/10.1063/1.4808077
- PubMed
- Google Scholar
(1996) VMD: visual molecular dynamics
Journal of Molecular Graphics 14:33–38.

https://doi.org/10.1016/0263-7855(96)00018-5
- PubMed
- Google Scholar
(2014) The power of coarse graining in biomolecular simulations
Wiley Interdisciplinary Reviews: Computational Molecular Science 4:225–248.

https://doi.org/10.1002/wcms.1169
- PubMed
- Google Scholar
1. Itoh T
2. Erdmann KS
3. Roux A
4. Habermann B
5. Werner H
6. De Camilli P
(2005) Dynamin and the actin cytoskeleton cooperatively regulate plasma membrane invagination by BAR and F-BAR proteins
Developmental Cell 9:791–804.

https://doi.org/10.1016/j.devcel.2005.11.005
- PubMed
- Google Scholar
1. Izvekov S
2. Voth GA
(2005a) A multiscale coarse-graining method for biomolecular systems
The Journal of Physical Chemistry B 109:2469–2473.

https://doi.org/10.1021/jp044629q
- PubMed
- Google Scholar
1. Izvekov S
2. Voth GA
(2005b) Multiscale coarse graining of liquid-state systems
The Journal of Chemical Physics 123:134105.

https://doi.org/10.1063/1.2038787
- PubMed
- Google Scholar
(2014) Experimental support for tilt-dependent theory of biomembrane mechanics
Physical Review Letters 113:248102.

https://doi.org/10.1103/PhysRevLett.113.248102
- PubMed
- Google Scholar
1. Kong L
2. Sochacki KA
3. Wang H
4. Fang S
5. Canagarajah B
6. Kehr AD
7. Rice WJ
8. Strub MP
9. Taraska JW
10. Hinshaw JE
(2018) Cryo-EM of the dynamin polymer assembled on lipid membrane
Nature 560:258–262.

https://doi.org/10.1038/s41586-018-0378-6
- PubMed
- Google Scholar
1. Kozlov MM
(1999) Dynamin: possible mechanism of "Pinchase" action
Biophysical Journal 77:604–616.

https://doi.org/10.1016/S0006-3495(99)76917-1
- PubMed
- Google Scholar
1. Kozlovsky Y
2. Kozlov MM
(2002) Stalk model of membrane fusion: solution of energy crisis
Biophysical Journal 82:882–895.

https://doi.org/10.1016/S0006-3495(02)75450-7
- PubMed
- Google Scholar
1. Kozlovsky Y
2. Kozlov MM
(2003) Membrane fission: model for intermediate structures
Biophysical Journal 85:85–96.

https://doi.org/10.1016/S0006-3495(03)74457-9
- PubMed
- Google Scholar
(2005) Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains
Journal of Membrane Biology 208:193–202.

https://doi.org/10.1007/s00232-005-7006-8
- PubMed
- Google Scholar
(2011) Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature
Biochimica Et Biophysica Acta (BBA) - Biomembranes 1808:2761–2771.

https://doi.org/10.1016/j.bbamem.2011.07.022
- Google Scholar
1. Limbach HJ
2. Arnold A
3. Mann BA
4. Holm C
(2006) ESPResSo—an extensible simulation package for research on soft matter systems
Computer Physics Communications 174:704–727.

https://doi.org/10.1016/j.cpc.2005.10.005
- Google Scholar
1. Lu C
2. Reedy M
3. Erickson HP
(2000) Straight and curved conformations of FtsZ are regulated by GTP hydrolysis
Journal of Bacteriology 182:164–170.

https://doi.org/10.1128/JB.182.1.164-170.2000
- PubMed
- Google Scholar
1. Luzzati V
2. Husson F
(1962) The structure of the liquid-crystalline phasis of lipid-water systems
The Journal of Cell Biology 12:207–219.

https://doi.org/10.1083/jcb.12.2.207
- PubMed
- Google Scholar
1. Mattila JP
2. Shnyrova AV
3. Sundborger AC
4. Hortelano ER
5. Fuhrmans M
6. Neumann S
7. Müller M
8. Hinshaw JE
9. Schmid SL
10. Frolov VA
(2015) A hemi-fission intermediate links two mechanistically distinct stages of membrane fission
Nature 524:109–113.

https://doi.org/10.1038/nature14509
- PubMed
- Google Scholar
(2016) Constriction by dynamin: elasticity versus adhesion
Biophysical Journal 111:2470–2480.

https://doi.org/10.1016/j.bpj.2016.10.019
- PubMed
- Google Scholar
1. McDargh ZA
2. Deserno M
(2018) Dynamin's helical geometry does not destabilize membranes during fission
Traffic 19:328–335.

https://doi.org/10.1111/tra.12555
- PubMed
- Google Scholar
(2014) Alternate pleckstrin homology domain orientations regulate dynamin-catalyzed membrane fission
Molecular Biology of the Cell 25:879–890.

https://doi.org/10.1091/mbc.e13-09-0548
- PubMed
- Google Scholar
1. Mim C
2. Cui H
3. Gawronski-Salerno JA
4. Frost A
5. Lyman E
6. Voth GA
7. Unger VM
(2012) Structural basis of membrane bending by the N-BAR protein endophilin
Cell 149:137–145.

https://doi.org/10.1016/j.cell.2012.01.048
- PubMed
- Google Scholar
1. Morlot S
2. Galli V
3. Klein M
4. Chiaruttini N
5. Manzi J
6. Humbert F
7. Dinis L
8. Lenz M
9. Cappello G
10. Roux A
(2012) Membrane shape at the edge of the dynamin helix sets location and duration of the fission reaction
Cell 151:619–629.

https://doi.org/10.1016/j.cell.2012.09.017
- PubMed
- Google Scholar
(2002) New mechanism of membrane fusion
The Journal of Chemical Physics 116:2342–2345.

https://doi.org/10.1063/1.1448496
- Google Scholar
(2003) A new mechanism of model membrane fusion determined from Monte Carlo simulation
Biophysical Journal 85:1611–1623.

https://doi.org/10.1016/S0006-3495(03)74592-5
- PubMed
- Google Scholar
1. Müller-Plathe F
(2002) Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back
ChemPhysChem 3:754–769.

https://doi.org/10.1002/1439-7641(20020916)3:9<754::AID-CPHC754>3.0.CO;2-U
- Google Scholar
(2009) Multiscale modeling of emergent materials: biological and soft matter
Physical Chemistry Chemical Physics 11:1869–1892.

https://doi.org/10.1039/b818051b
- PubMed
- Google Scholar
1. Noguchi H
2. Takasu M
(2001) Fusion pathways of vesicles: A Brownian dynamics simulation
The Journal of Chemical Physics 115:9547–9551.

https://doi.org/10.1063/1.1414314
- Google Scholar
1. Noguchi H
2. Takasu M
(2002) Adhesion of nanoparticles to vesicles: a brownian dynamics simulation
Biophysical Journal 83:299–308.

https://doi.org/10.1016/S0006-3495(02)75170-9
- PubMed
- Google Scholar
1. Noid WG
2. Chu JW
3. Ayton GS
4. Krishna V
5. Izvekov S
6. Voth GA
7. Das A
8. Andersen HC
(2008) The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models
The Journal of Chemical Physics 128:244114.

https://doi.org/10.1063/1.2938860
- PubMed
- Google Scholar
1. Noid WG
(2013) Perspective: coarse-grained models for biomolecular systems
The Journal of Chemical Physics 139:090901.

https://doi.org/10.1063/1.4818908
- PubMed
- Google Scholar
(2009) Combining an elastic network with a coarse-grained molecular force field: structure, dynamics, and intermolecular recognition
Journal of Chemical Theory and Computation 5:2531–2543.

https://doi.org/10.1021/ct9002114
- PubMed
- Google Scholar
1. Peter C
2. Kremer K
(2009) Multiscale simulation of soft matter systems – from the atomistic to the coarse-grained level and back
Soft Matter 5:4357–4366.

https://doi.org/10.1039/b912027k
- Google Scholar
1. Praefcke GJ
2. McMahon HT
(2004) The dynamin superfamily: universal membrane tubulation and fission molecules?
Nature Reviews Molecular Cell Biology 5:133–147.

https://doi.org/10.1038/nrm1313
- PubMed
- Google Scholar
(2016) Shape selection of surface-bound helical filaments: biopolymers on curved membranes
Biophysical Journal 111:1575–1585.

https://doi.org/10.1016/j.bpj.2016.08.017
- PubMed
- Google Scholar
1. Ramachandran R
2. Surka M
3. Chappie JS
4. Fowler DM
5. Foss TR
6. Song BD
7. Schmid SL
(2007) The dynamin middle domain is critical for tetramerization and higher-order self-assembly
The EMBO Journal 26:559–566.

https://doi.org/10.1038/sj.emboj.7601491
- PubMed
- Google Scholar
(2012) On developing coarse-grained models for biomolecular simulation: a review
Physical Chemistry Chemical Physics 14:12423–12430.

https://doi.org/10.1039/c2cp40934h
- PubMed
- Google Scholar
1. Roux A
2. Uyhazi K
3. Frost A
4. De Camilli P
(2006) GTP-dependent twisting of dynamin implicates constriction and tension in membrane fission
Nature 441:528–531.

https://doi.org/10.1038/nature04718
- PubMed
- Google Scholar
1. Saunders MG
2. Voth GA
(2013) Coarse-graining methods for computational biology
Annual Review of Biophysics 42:73–93.

https://doi.org/10.1146/annurev-biophys-083012-130348
- PubMed
- Google Scholar
(2017) Reverse-topology membrane scission by the ESCRT proteins
Nature Reviews Molecular Cell Biology 18:5–17.

https://doi.org/10.1038/nrm.2016.121
- PubMed
- Google Scholar
(2013) Geometric catalysis of membrane fission driven by flexible dynamin rings
Science 339:1433–1436.

https://doi.org/10.1126/science.1233920
- PubMed
- Google Scholar
1. Sigg D
2. Bezanilla F
(2003) A physical model of potassium channel activation: from energy landscape to gating kinetics
Biophysical Journal 84:3703–3716.

https://doi.org/10.1016/S0006-3495(03)75099-1
- PubMed
- Google Scholar
1. Stowell MH
2. Marks B
3. Wigge P
4. McMahon HT
(1999) Nucleotide-dependent conformational changes in dynamin: evidence for a mechanochemical molecular spring
Nature Cell Biology 1:27–32.

https://doi.org/10.1038/8997
- PubMed
- Google Scholar
1. Sundborger AC
2. Fang S
3. Heymann JA
4. Ray P
5. Chappie JS
6. Hinshaw JE
(2014) A dynamin mutant defines a superconstricted prefission state
Cell Reports 8:734–742.

https://doi.org/10.1016/j.celrep.2014.06.054
- PubMed
- Google Scholar
(1999) Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis
Nature Cell Biology 1:33–39.

https://doi.org/10.1038/9004
- PubMed
- Google Scholar
1. Tian A
2. Baumgart T
(2009) Sorting of lipids and proteins in membrane curvature gradients
Biophysical Journal 96:2676–2688.

https://doi.org/10.1016/j.bpj.2008.11.067
- PubMed
- Google Scholar
(2004) Simulations of stable pores in membranes: system size dependence and line tension
The Journal of Chemical Physics 121:8014–8020.

https://doi.org/10.1063/1.1796254
- PubMed
- Google Scholar
1. Tuma PL
2. Collins CA
(1994)
Activation of dynamin GTPase is a result of positive cooperativity

The Journal of Biological Chemistry 269:30842–30847.
- PubMed
- Google Scholar
Book
1. Voth GA
(2008)
Coarse-Graining of Condensed Phase and Biomolecular Systems

CRC Press. ISBN 978-1-4200-5955-7.
- Google Scholar
1. Wang X
2. Deserno M
(2015) Determining the pivotal plane of fluid lipid membranes in simulations
The Journal of Chemical Physics 143:164109.

https://doi.org/10.1063/1.4933074
- PubMed
- Google Scholar
1. Wang X
2. Deserno M
(2016) Determining the lipid tilt modulus by simulating membrane buckles
The Journal of Physical Chemistry B 120:6061–6073.

https://doi.org/10.1021/acs.jpcb.6b02016
- PubMed
- Google Scholar
(2009) Membrane scission by the ESCRT-III complex
Nature 458:172–177.

https://doi.org/10.1038/nature07836
- PubMed
- Google Scholar
1. Zhang P
2. Hinshaw JE
(2001) Three-dimensional reconstruction of dynamin in the constricted state
Nature Cell Biology 3:922–926.

https://doi.org/10.1038/ncb1001-922
- PubMed
- Google Scholar
1. Zhang G
2. Müller M
(2017) Rupturing the hemi-fission intermediate in membrane fission under tension: Reaction coordinates, kinetic pathways, and free-energy barriers
The Journal of Chemical Physics 147:064906.

https://doi.org/10.1063/1.4997575
- PubMed
- Google Scholar

Article and author information

Author details

Martina Pannuzzo

Department of Physics, Carnegie Mellon University, Pittsburgh, United States

Present address
Istituto Italiano di Tecnologia, Genova, Italy

Contribution
Conceptualization, Software, Formal analysis, Supervision, Funding acquisition, Investigation, Visualization, Methodology, Writing—original draft, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-8629-0173
Zachary A McDargh

Department of Physics, Carnegie Mellon University, Pittsburgh, United States

Present address
Department of Chemical Engineering, Columbia University, New York, United States

Contribution
Conceptualization, Software, Formal analysis, Investigation, Visualization, Methodology, Writing—original draft

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9022-5593
Markus Deserno

Department of Physics, Carnegie Mellon University, Pittsburgh, United States

Contribution
Conceptualization, Supervision, Funding acquisition, Investigation, Methodology, Writing—original draft, Writing—review and editing

For correspondence
deserno@andrew.cmu.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-5692-1595

Funding

National Science Foundation (NSF CHE #1464926)

Markus Deserno

Carnegie Mellon University (Center of Excellence funding)

Markus Deserno

Horizon 2020 - Research and Innovation Framework Programme (Marie Sklodowska-Curie grant agreement no. 754490)

Martina Pannuzzo

National Science Foundation (NSF CHE #1764257)

Markus Deserno

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank Marijn Ford, Aurelian Roux, Joshua Zimmerberg, Fred Lanni, Tina Lee, Adam Linstedt, Mathias Lösche, Martin Müller, and Antonio Raudino for discussions and critical comments. This work was supported by NSF Grants CHE #1464926, CHE #1764257, a Carnegie Mellon MCS/CIT Postdoctoral Fellowship, and the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement no. 754490.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.