1. Neuroscience

Using subthreshold events to characterize the functional architecture of the electrically coupled inferior olive network

  1. Yaara Lefler  Is a corresponding author
  2. Oren Amsalem  Is a corresponding author
  3. Nora Vrieler
  4. Idan Segev
  5. Yosef Yarom
  1. The Hebrew University of Jerusalem, Israel
https://doi.org/10.7554/eLife.43560
Share this article
Cite this article
  1. Yaara Lefler
  2. Oren Amsalem
  3. Nora Vrieler
  4. Idan Segev
  5. Yosef Yarom
(2020)
Using subthreshold events to characterize the functional architecture of the electrically coupled inferior olive network
eLife 9:e43560.
https://doi.org/10.7554/eLife.43560
  2. Download BibTeX
  3. Download .RIS

Abstract

The electrical connectivity in the inferior olive (IO) nucleus plays an important role in generating well-timed spiking activity. Here we combined electrophysiological and computational approaches to assess the functional organization of the IO nucleus in mice. Spontaneous fast and slow subthreshold events were commonly encountered during in vitro recordings. We show that whereas the fast events represent intrinsic regenerative activity, the slow events reflect the electrical connectivity between neurons (‘spikelets’). Recordings from cell pairs revealed the synchronized occurrence of distinct groups of spikelets; their rate and distribution enabled an accurate estimation of the number of connected cells and is suggestive of a clustered organization. This study thus provides a new perspective on the functional and structural organization of the olivary nucleus and a novel experimental and theoretical approach to study electrically coupled networks.

Introduction

In recent years, research has confirmed that electrically coupled neural networks are found in every major region of the central nervous system (Condorelli et al., 2000; Bennett and Zukin, 2004; Connors and Long, 2004; Hormuzdi et al., 2004). One common feature of these networks is their synchronized rhythmic activity (Connors and Long, 2004; Bennett and Zukin, 2004; Connors, 2017; Coulon and Landisman, 2017), which has been shown to be correlated with higher brain functions such as states of arousal, awareness, cognition and attention (Ritz and Sejnowski, 1997; Engel et al., 2001; Buzsáki, 2005; Steriade, 2006; Uhlhaas et al., 2009; Wang, 2010). Recently, it has been demonstrated that the efficiency of electrical synapses is modulated by electrical and chemical activity, very much like chemical synapses (O'Brien, 2014; Marder et al., 2017; Coulon and Landisman, 2017). It thus stands to reason that the functional architecture of these networks must undergo continuous modification to meet the system’s demands. This underscores the urgent need to determine the functional state of a network and associate it with the corresponding brain states. Since anatomical information is insufficient, this can only be done using physiological parameters that capture the functional architecture of a network at any given time.

The inferior olive network, which was among the first electrically coupled networks to be studied in the mammalian brain, provides primary excitatory input to the cerebellar cortex (Eccles et al., 1966). There is a general consensus that the function of this network is to generate synchronous activity in olivary neurons, which provide temporal information for either learning processes, motor execution, sensory predictions or expectations (Llinás and Sasaki, 1989; Lou and Bloedel, 1992; Welsh et al., 1995; Van Der Giessen et al., 2008; Llinás, 2009; De Zeeuw et al., 2011; Ohmae and Medina, 2015; Heffley et al., 2018). Temporal information is thought to be generated by the subthreshold sinusoidal-like oscillations of the membrane voltage that appear to emerge from an interplay between the membrane properties and network connectivity (Llinás and Yarom, 1986; Lampl and Yarom, 1997; Manor et al., 1997; Loewenstein et al., 2001; Devor and Yarom, 2002b). Recently, this oscillatory activity was shown to be governed by chemical synaptic inputs that partially originate in the deep cerebellar nuclei and modulate the efficacy of the coupling by defining the spatial extent of the electrically coupled network (Lefler et al., 2014; Mathy et al., 2014; Turecek et al., 2014).

Early work on the morphological organization of the IO indicated that it is organized in clusters of up to eight neurons, whose dendrites are integrated in glomerulus structures (Sotelo et al., 1974) and are innervated by both excitatory and inhibitory synaptic inputs (de Zeeuw et al., 1990; de Zeeuw et al., 1989). This presumed clustered organization has been supported by dye coupling studies showing that each olivary neuron is anatomically coupled to roughly ten other neurons (Devor and Yarom, 2002a; Leznik and Llinás, 2005; Placantonakis et al., 2006; Hoge et al., 2011; Turecek et al., 2014), and by a recent detailed morphological study demonstrating the directionality of IO neuron dendrites (Vrieler et al., 2019). Physiologically however, the organization of the network has only been addressed in a few voltage-sensitive dye imaging studies which found ensembles of synchronously active neurons corresponding to a cluster size estimation of hundreds of neurons (Devor and Yarom, 2002b; Leznik et al., 2002). The documented synchronicity of complex spike activity in tens to hundreds of cerebellar Purkinje cells during motor tasks and sensory stimulation is also in favor of such ensemble organization (Bloedel and Ebner, 1984; Welsh et al., 1995; Mukamel et al., 2009; Ozden et al., 2009; Schultz et al., 2009; De Zeeuw et al., 2011; Byk et al., 2019; Kostadinov et al., 2019).

In this study, we describe a novel method to estimate the size and connectivity of a network by analyzing the all-or-none subthreshold unitary events known as ‘spikelet’. Initially, spikelets were considered as the manifestation of an action potential transmitted via electrical synapses (Llinas et al., 1974; MacVicar and Dudek, 1981; Valiante et al., 1995; Galarreta and Hestrin, 1999; Gibson et al., 1999; Mann-Metzer and Yarom, 1999; Hughes et al., 2002; Chorev and Brecht, 2012). However other studies have also referred to spikelets as reflecting either local dendritic regenerative responses (Spencer and Kandel, 1961; Golding and Spruston, 1998; Smith et al., 2013); action potentials in the initial segment or at an ectopic site along the axon that fail to invade the soma (Stasheff et al., 1993; Avoli et al., 1998; Juszczak and Swiergiel, 2009; Sheffield et al., 2011; Dugladze et al., 2012; Michalikova et al., 2017); electrical coupling between axons (Schmitz et al., 2001; Traub et al., 2002); or extracellularly recorded activity of nearby neurons (Vigmond et al., 1997; Scholl et al., 2015). Here we show that the spontaneous unitary events recorded from olivary neurons can be classified into two groups that differ in their waveform and properties: fast events having identical waveforms with variable high amplitudes, and slow events having different waveforms and low amplitudes. We show that the low-amplitude slow events reflect the occurrence of action potentials in electrically coupled neurons, whereas the high-amplitude fast events are likely to represent internal regenerative responses. We then used slow events recorded simultaneously in pairs of neurons to estimate the size of the network (i.e. the number of neurons that are connected to each neuron) and the network connectivity profile. We found that each olivary neuron is electrically connected to an average of 19 other neurons and that the network is not randomly connected but rather composed of functional clusters of connected neurons.

Results

Spontaneous unitary events recorded in neurons of the inferior olive

The subthreshold spontaneous activity recorded from IO neurons (Figure 1A) is composed of unitary unipolar events of varying amplitudes and waveforms. Such events were observed in 74.3% of the neurons (188 out of 253) with an average rate of 0.7 ± 0.6 Hz (calculated in 70 neurons). The subthreshold events could readily be divided into two populations of small and large events (Figure 1A inset, circles vs. stars), as shown by the amplitude histogram (Figure 1B). In this example neuron, K-means clustering of the events' waveforms reveals five distinct groups (Figure 1B,C), which when normalized (Figure 1D), showed the waveform difference between the two types; one type had high amplitude and fast kinetics, and the second type had low amplitude and slow kinetics.

Figure 1
Download asset Open asset
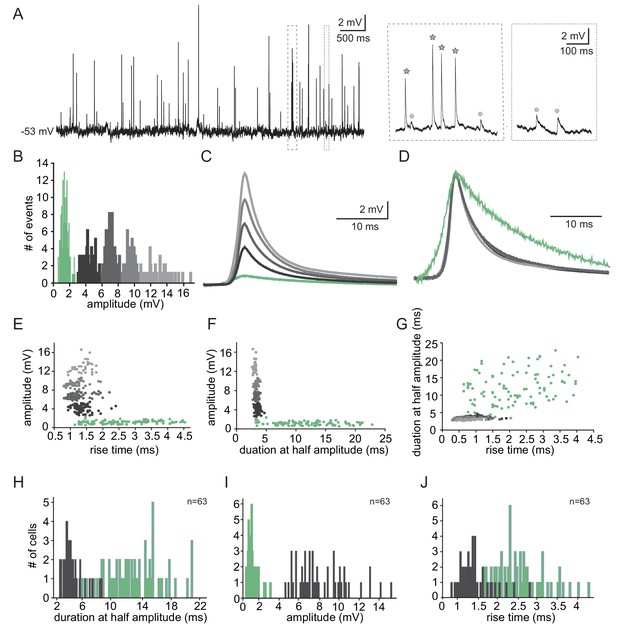
Two types of subthreshold spontaneous events recorded in olivary neurons.

(A) Spontaneous subthreshold events recorded from an olivary neuron. Right panels - higher magnification of the marked rectangles; gray stars - fast and high amplitude events; green circles - slow and small events. (B) The distribution of the events’ amplitudes in this neuron; colors were assigned according to the K-means analysis of the amplitudes. (C) Averages of the subthreshold events in each cluster, color coded as in B. (D) The normalized events shown in C. (E–G) Scatter plots for the relationships between the shape indices of the subthreshold events (color coded as in B). (E) Amplitude and rise time; (F) Amplitude and half width; (G) half width and rise time. (H–J) Histograms of the shape indices (half width (H); amplitude (I); and rise time (J)) of the subthreshold events in a population of 63 olivary neurons; green and gray bars correspond to slow and fast events respectively.

Figure 1—source data 1

Source data for Figure 1.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig1-data1-v1.xlsx
Figure 1—source data 2

Trace for Figure 1A.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig1-data2-v1.mat

To further analyze the event waveforms, we measured each event’s rise time and duration at half amplitude. The results obtained from a representative neuron are summarized in Figure 1E–G. One type (black to gray circles) had a relatively high amplitude (2.4–16.6 mV; average of 7.5 ± 3.1 mV) and fast kinetics (average rise time of 1.3 ± 0.3 ms and average half duration of 3.4 ± 0.3 ms) whereas the second type (green circles) had a relatively low amplitude (0.6–1.9 mV; average of 1.17 ± 0.3 mV) and slow kinetics (average rise time of 2.4 ± 0.4 ms and average half duration of 11.8 ± 5 ms). Plotting the duration as a function of the rise time (Figure 1G), which further supports the two-type scheme, failed to demonstrate a monotonous relationship between the rise-time and half-width that is expected from different dendritic locations of synapses (Rall’s cable theory; Rall, 1967). Thus, it seems unlikely that the two types represent signals arising from different locations along the cell's morphological structure. The distribution of rise-time and half-width in a population of 63 neurons (of which 49 neurons had the two types of events), which is summarized in Figure 1H–J, confirms that there were indeed two distinct types of events. Whereas the high-amplitude events had a fast rise time (0.8–2.8 ms; average of 1.4 ± 0.4 ms) and short duration (2.5–8.3 ms; average of 4.2 ± 1.3 ms), the low-amplitude events had a longer rise time (1.3–4.3 ms; average of 2.5 ± 0.6 ms) and a longer duration (3.6–21 ms; average of 12.7 ± 3.9 ms). For the high-amplitude events, the broad distribution of amplitudes (ranging from 4.5 to 15.3 mV) and the somewhat limited distribution of rise-times and durations strongly indicates that these groups of fast events were generated by a similar mechanism. Overall, the frequency of slow events was four times higher (0.56 ± 0.62 Hz; n = 69 neurons) than that of the fast events (0.14 ± 0.18 Hz; n = 58 neurons).

To further distinguish between these two events, we examined the effect of the membrane voltage on the occurrence and waveforms of both types of unitary events. To that end, we used DC current injection, which on average set the membrane potential to a range of −33 to −90 mV. Figure 2A–B shows the aligned superimposed traces of slow events (Figure 2A) and fast events (Figure 2B) from one neuron. Normalizing the event amplitudes (Figure 2A–B, right panels) shows that whereas the shape of the slow events was unaffected by the current injection (A), the fast events showed a slowdown of the late repolarizing phase with hyperpolarization (B). Quantifying the effect of the injected current (see Materials and methods) on the amplitude and duration at 20% of the amplitude in 16 neurons revealed no effect on the amplitude of either type of events (Figure 2C,D; R2 = 0.0057 and 0.0035, respectively). The duration of the slow events was slightly, but not significantly, affected (Figure 2E; R2 = 0.44; one-sample t-test p=0.057). In contrast, DC current injection significantly increased the duration of the fast events (Figure 2F; R2 = 0.712; one-sample t-test p=0.0005). Comparing the two sets of data revealed a significant difference (Figure 2E vs. Figure 2F; paired t-test p=0.017). Finally, we measured the effect of the DC current injection on the rate of occurrence of the subthreshold unitary events (Figure 2G–H). Whereas the frequency of the slow events remained unaffected (Figure 3G, R2 = 0.012), the frequency of the fast events increased by a factor of up to 5 (Figure 2H; R2 = 0.836). This difference between the occurrence of slow and the fast events, which was highly significant (Figure 2G vs. Figure 2H, paired t-test p=0.005), further supports our presumption that two different mechanisms generate the two types of unitary subthreshold events. Since the membrane potential did not change the amplitude of the events, it implies that neither of them represents chemical synaptic potentials.

Figure 2
Download asset Open asset
Voltage dependency of the subthreshold events.

(A) Superimposed slow events recorded during seven different DC current injections (−300 to 0 pA, color coded, left panel), and normalized by amplitude (right panel). (B) Same as A, for the fast events. (C–H) The effect of DC current injection on the amplitude (C–D), the duration measured at 20% of the amplitude (E–F) and the frequency of occurrence (G–H) measured in 16 neurons. Gray circles represent the average data from individual neurons, each fitted with a linear regression (dashed gray lines). Black circles and error bars (std) represent the average value for all the neurons in each current injection. Note that the decrease in duration (F) and the increase in frequency (H) with depolarization only occurs for fast events.

Figure 2—source data 1

Source data for Figure 2.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig2-data1-v1.xlsx
Figure 3 with 2 supplements see all
Download asset Open asset
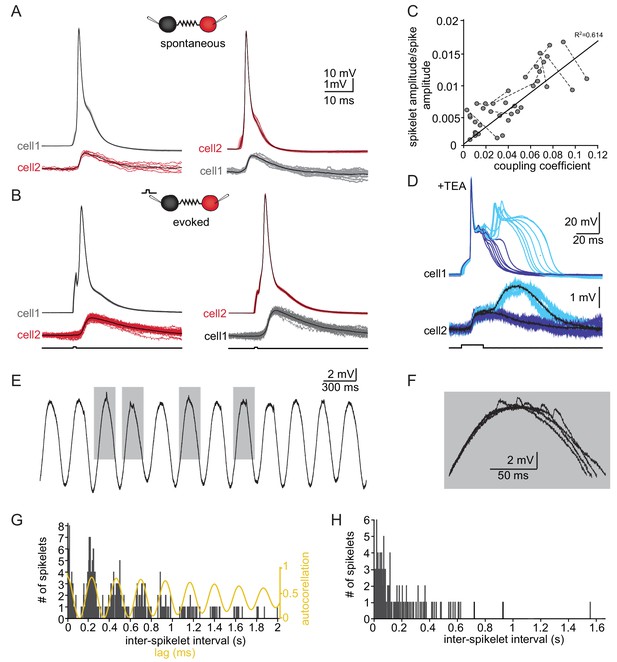
The slow events represent the electrical coupling between neurons.

(A) Superimposed traces of spontaneously occurring action potentials recorded simultaneously from a pair of coupled neurons (red and gray traces; black traces represent the average events). (B) The same as in A for action potentials evoked by 100 pA, 1 ms current pulses. (C) The linear relationship between the DC coupling coefficient and the spike coupling coefficient. Pairs of cells are connected by dashed lines. Blue line is the linear regression fit (R2 = 0.6). (D) Paired recording in the presence of 10 mM TEA. Action potentials with relatively long durations (upper panel, blue traces) were elicited in cell 1 by 50 pA, 20 ms current pulse. Occasionally they were followed by a second response (cyan traces). These action potentials elicited post junctional responses in cell 2 with corresponding waveforms (lower traces). (E) Subthreshold events recorded in oscillating olivary neuron. (F) Superposition of the gray rectangles in E, at higher magnification. Note that spikelets were only present for 50 ms along the peak of the oscillations. (G) Inter-spikelet interval (ISLI) from the same neuron (using 4 ms bins), and an autocorrelation (yellow line) of the membrane potential. (H) The ISLI distribution in a non-oscillating neuron.

Figure 3—source data 1

Source data for Figure 3.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig3-data1-v1.xlsx
Figure 3—source data 2

Trace for Figure 3A.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig3-data2-v1.mat
Figure 3—source data 3

Trace for Figure 3B.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig3-data3-v1.mat
Figure 3—source data 4

Trace for Figure 3E.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig3-data4-v1.mat

However, application of excitatory synaptic blockers (DNQX and APV) completely eliminated the presence of the fast events (frequency before application was 0.056 ± 0.066 Hz, with zero events after application in n = 5 cells). Thus, it is likely that the fast events reflect intrinsic regenerative response that is triggered by excitatory synaptic input (as for the effect on slow events, see below).

Slow events reflect electrical coupling between neurons

Whole-cell recordings from pairs of coupled olivary neurons revealed that the post-junctional responses to both spontaneous (Figure 3A) and evoked (Figure 3B) action potentials in one neuron were precisely correlated with depolarizing events in the coupled neuron. Both the spontaneous and the evoked events resembled the spontaneously recorded slow events depicted in Figure 1. These events had an amplitude of 1.2 ± 0.12 mV, a rise time of 3.7 ± 0.9 ms and a duration of 14.9 ± 4.0 ms, thus well within the range of spontaneously measured slow events. Paired recordings from 30 neurons showed that the amplitudes of the events varied from 0.12 to 1.40 mV (average of 0.61 ± 0.35 mV) whereas the average rise times and half durations were 2.61 ± 1.09 ms and 14.31 ± 6.72 ms, respectively, in line with the measured distribution of spontaneously occurring slow events (Figure 3—figure supplement 1C, for rise time and duration p=0.58 and p=0.15 respectively, paired t-test).

In order to identify the source of the spontaneously occurring slow events, we characterized and compared three types of subthreshold events: the spontaneous slow events; the events triggered by action potentials in pair recording and the chemical synaptic potentials triggered by ChR activation in Thy1 mice. The responses to minimal light intensity is shown in Figure 3—figure supplement 1B. The shapes of the evoked synaptic events differed significantly from those of the spontaneous slow events in the same neurons (p<0.002 for all comparisons (rise time, half duration and amplitudes), paired t-test, n = 17 cells), as well as from evoked slow events measured in pair recordings (Figure 3—figure supplement 1C, black circles; p<0.002 for all comparisons, paired t-test). This strongly suggests that the small and slow spontaneous events represent action potentials occurring in electrically coupled neurons. To further support this possibility, we measured the effect of excitatory synaptic blockers on the occurrence of the slow events. The chemical synaptic blockers drastically reduced the frequency of the slow events (from 2.27 ± 1.75 Hz to 0.068 ± 0.078 Hz) while amplitude, rise time and duration at half amplitude were not affected (p=0.8, 0.25 and 0.96 respectively; paired KS test; Figure 3—figure supplement 1E). In addition, evoked slow events could readily be seen in pair recordings with DNQX (Figure 3—figure supplement 1D, n = 10 cells). The decrease in the frequency of the slow events could suggest that a subpopulation of slow events represent chemical synaptic potentials. However, the spontaneous spiking activity of olivary neurons is triggered by the fast events (Figure 3—figure supplement 2), that are completely eliminated in the presence of chemical synaptic blockers (see above), causing a drastic reduction in spiking activity and their electrical posts-junctional presentation, the slow events.

We conclude that the slow events represent the post-junctional responses to action potentials in coupled cells and therefore we refer to them as ‘spikelets’.

The relatively broad range of spikelet parameters (Figure 1) can be attributed to a wide range of coupling strengths, different locations of the gap junctions along the dendritic structure or different durations and shapes of the pre-junctional action potential, which is a well-known feature of olivary action potentials (Llinás and Yarom, 1981a; Llinás and Yarom, 1981b). We first examined the effect of coupling strength by calculating the ratio of the amplitudes of the pre-junctional action potential to the post-junctional spikelet and compared it to the coupling coefficient measured by direct current injection (see Materials and methods). As shown in Figure 3C, there was a significant positive correlation (with a slope of 0.134; R2 = 0.614, p<0.0001; Pearson correlation). Next, we examined the effect of the shape of the pre-junctional action potential on the spikelet parameters. To that end, we partially blocked the voltage dependent potassium current by adding TEA (10 mM) to the bath solution. In the presence of TEA, a variety of action potential waveforms were elicited by current injection (Figure 3D). In particular, the initial upstroke of the action potential was unaffected, but there was a significant broadening of the repolarizing phase (Figure 3D, upper panel, blue) that often elicited a second calcium-dependent action potential (Figure 3D, upper panel, cyan). This variety of action potential waveforms was always associated with electrical post-junctional responses that could be clustered into two distinct groups (Figure 3D, lower panel). The prolongation of the action potential was, as expected, followed by a matching increase in the duration of the post-junctional responses (Figure 3D, lower panel, blue traces). The appearance of the second component was associated with a slow wave of depolarization in the post-junctional cell (cyan traces). This suggests that the wide range of spikelet parameters (Figure 1) can be accounted for by the variability in coupling strength and pre-junctional action potential waveforms.

Finally, we examined the occurrence of spikelets in neurons that exhibited subthreshold oscillatory activity. Since these oscillations occurred simultaneously in several neurons (Lefler et al., 2013), it was expected that spikelet occurrence will be correlated with the oscillatory activity. About 50% of the olivary neurons showed spontaneous subthreshold oscillations (Figure 3E). Careful examination of the peaks of the oscillations (Figure 3F) revealed that they were crowned with spikelets. To quantify this observation, we calculated the distribution of the inter-spikelet-interval (ISLI, Figure 3G, black bars), and found distinct groups appearing at intervals of 200 ms. We then calculated the autocorrelation function of the subthreshold oscillations (Figure 3G, yellow line) and found that it matched the ISLI perfectly. It is important to note that a similar fit was observed in 60% of the oscillating neurons (n = 18) whereas in non-oscillating neurons (n = 70) the ISLI exhibited a Poisson-like distribution (Figure 3H). The strong correlation between oscillatory behavior and the occurrence of spikelets further supports the conclusion that these events represent activity in adjacent electrically coupled neurons.

Estimating network connectivity from dual cell recordings of simultaneously occurring spikelets

Figure 4A depicts the spontaneous activity recorded simultaneously from two neurons. As described above (Figure 3) action potentials (diagonal bars in Figure 4A) occurred irregularly in either of the two neurons and were always associated with spikelets in the paired neuron (Figure 4B). The subthreshold activity was dominated by spikelets which appeared randomly in the two neurons. However, occasionally spikelets occurred simultaneously in both cells (marked in Figure 4A and shown at high resolution in Figure 4C) which we refer to as ‘common spikelets’. Each of the three examples shown in Figure 4C, which occurred without measurable time difference, have variable amplitudes. The first and the third spikelets had larger amplitudes in the red neuron (cell 2) whereas the middle spikelet had a larger amplitude in the black neuron (cell 1). Since action potentials in one neuron evoke very similar spikelets in the other (Figure 3A–B), the most likely explanation is that each of these common spikelets represents the action potential in an additional neuron that is coupled to both of the recorded neurons (see Discussion). On the population level, 18 out of 30 pairs had common spikelets (60%). Of these pairs, the occurrence of common spikelets varied from 0.02 to 1.1 Hz, which is 3.5–66% of the total number of measurable spikelets (Figure 4D).

Figure 4
Download asset Open asset
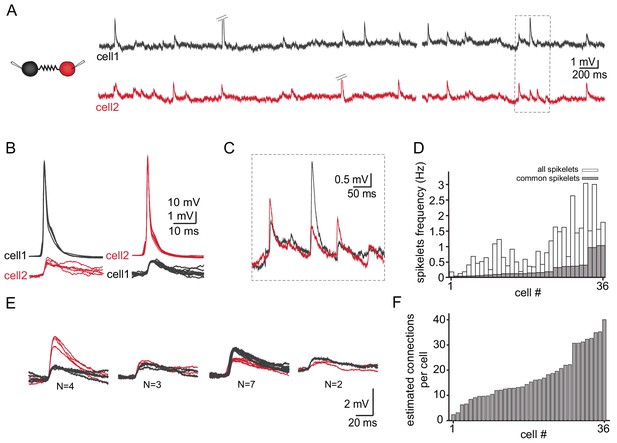
Common groups of spikelets during paired recording reveals the estimated number of neurons that are electrically coupled.

(A) Simultaneous recording from two electrically coupled neurons. Action potentials were truncated (doubled diagonal lines) and an example of the occurrence of common spikelets is marked (dashed rectangle). (B) Superimposed traces of spontaneous action potentials in either cell 1 (black neuron) or cell 2 (red neuron) and the corresponding spikelets in the other neuron. (C) Higher magnification of the rectangle marked in A, showing spikelets that occur simultaneously in both neurons. (D) Histogram of the frequency of spikelets in neurons recorded in pairs, showing all the spikelets (white bars) and all the common spikelets (gray bars; n = 18 pairs), sorted by increasing frequency of common spikelets. (E) Example of common spikelets from the pair presented in A-C. The spikelets could be divided into four groups, with N = 2–7 spikelets in each group. (F) Histogram of the estimated number of neurons that are electrically coupled to each of the pair-recorded neurons (n = 18 pairs).

Figure 4—source data 1

Trace for Figure 4.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig4-data1-v1.mat

The occurrence of common spikelets can be used to estimate the number of neurons that are electrically coupled to each neuron in the olivary network. In this example of a paired recording, four different groups were identified (see Materials and methods, Figure 4E), which indicates that at least four neurons were electrically coupled to both recorded neurons. Further analysis of these data provided an estimate of the total number of neurons connected to each of the two recorded neurons. In this example, a total of 16 common spikelets, organized in four groups, were recorded. The four groups thus represent four neurons that are coupled to the two recorded neurons. Each of these neurons fired on average four times during the recording period. Therefore, we can assume that each neuron in the network also fired on average four times during the recording period. In addition to the common spikelets, nine non-common spikelets were recorded in the black cell and 32 in the red one. These non-common spikelets thus represent spikes in ~2 additional neurons (9/4) connected to the black neuron and eight neurons (32/4) connected to the red neuron. The result of this numerical consideration is that the black neuron is connected to the red neuron, to four additional neurons that are connected to both recorded neurons and to estimated two additional neurons, totaling seven neurons. Similarly, the red neuron is estimated to be connected to 13 neurons. This analysis was performed on 18 dual recordings and the results, which are summarized in Figure 4F, indicate that a neuron can connect to as many as 40 other neurons (average of 19.2 ± 10.3). It should be noted that the use of a slice preparation undoubtedly contributed to the wide range of connected neurons and to some degree of underestimation (see Discussion).

We re-examined the approach to estimate the number of connections per neuron by reconstructing a realistic olivary network (Figure 5A, see Materials and methods). The firing rate of neurons in the network was set to 0.058 Hz ±0.04 Hz (as observed experimentally) and the number of common spikelets in pairs of neurons occurring within 15 min of simulation was measured. Recordings from a sample pair are shown Figure 5B and C. In this example, four groups of spikelets that appear 26, 16, 65 and 32 times were detected (Figure 5C). By applying the same calculation as performed in the experimental observations (Figure 4), we concluded that the red neuron was electrically connected to 24 neurons whereas the black neuron was connected to 26 neurons. In this model, the red and black neurons were actually connected to 17 and 20 neurons, respectively (pink circles in Figure 5D). We performed the same calculation in 20 randomly selected pairs of neurons and plotted the estimated versus the real number of connections per cell (Figure 5D). The results were distributed along the diagonal (with the average marked by + sign), demonstrating the validity of this approach in estimating the number of connections for each neuron. However, the accuracy of the estimation depends strongly on variability in firing rate and the recording duration. As shown in Figure 5E the difference between the estimated and real number of connections per neuron decreases as a function of simulation duration. Moreover, at high variability in firing rate (black curve), longer recording duration does not improve the error compared to low variability firing rate (light gray curve). However, the estimation of the mean number of connected cells (+ sign in Figure 5D) is less sensitive to simulation duration or to variability in firing rate (Figure 5F, see discussion). We conclude that this approach provides a reliable estimate of the mean number of connected cells.

Figure 5
Download asset Open asset
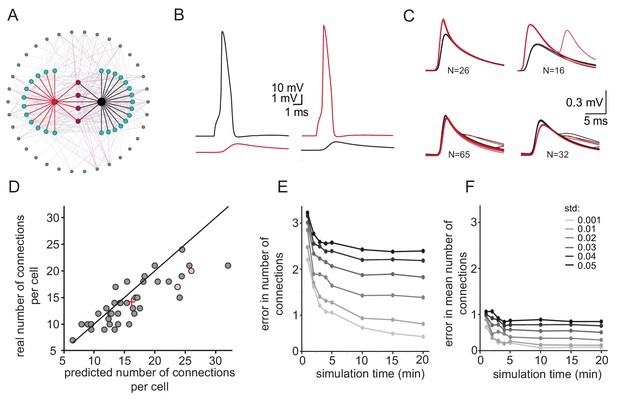
Simulations examining the method used for estimating the number of connections per cell.

(A) Schematics of the modeled network where the recorded pairs of neurons (black and red circles) are connected to four common neurons (purple) and to 12 and 15 additional neurons (cyan); 34 other neurons (gray) that are connected to either the cyan or the purple neurons are also shown. (B) Example action potential and their post junctional responses from the red and black neurons in A. (C) The four common groups of spikelets recorded in the black and red cells with N = 16–65 spikelets in each group. (D) Plot of the predicted number of connections per cell, estimated from the common groups of spikelets, against the real number of connections per cell. The line marks the diagonal, the + sign marks the mean and the pink circles represent the two cells in A. (E) Difference between the estimated and real number of connections per neurons as a function of simulation duration for six different firing rate variabilities (std; color-coded as in the legend). (F) The difference in estimating the mean number of connections in the network (+ sign in D) as a function of simulation duration for six different firing rate variabilities (std). The calculation was done only on neurons that had common neighbors (n = 278 pairs). Mean firing rate was 0.058 Hz.

Insights into the network architecture from the distribution of groups of common spikelets

Further insights into the organization of the network can be extracted from the distribution of the number of groups of common spikelets. Figure 6A depicts three examples of common groups of spikelets obtained from three different paired recordings, showing the reliability of the grouping procedure. The number of common groups (Figure 6B) varied from 0 to 7 with a markedly higher incidence at 2–4 groups. The distribution of the number of groups of common spikelets (Figure 6B) provides information on the organization of the network. This was examined by constructing artificial networks, each with different connectivity matrix, and calculating the expected distribution of common groups in the connectivity matrix. To that end, we first used experimental results showing that the probability to detect electrically coupled olivary neurons is distance dependent (dark green line in Figure 6D; Devor and Yarom, 2002a). After fitting these results with a Gaussian curve (Figure 6D, blue line) we constructed networks in which randomly selected neurons show the probability of connection as a function of inter-somatic distance fits the experimental distribution (Figure 6D,G; gray bars). Additionally, we checked the distribution of common neighbors (proxy for groups of common spikelets in Figure 6B) in the matrix (Figure 6E,H; gray bars) and compared it to the experimental distribution (Figure 6E, green line).

Figure 6 with 1 supplement see all
Download asset Open asset
Simulations examining the network connectivity that accounts for the experimental distribution of common groups of spikelets.

(A) Experimental example of common spikelets from three different pairs, that were divided to 1, 4 or 6 common groups (pair 1,2 and 3, respectively). (B) The distribution of the number of common groups in all experimentally recorded pairs. (C–E) The expected distribution of the common groups in a model where the probability of connection is distance- dependent. (C) Schematic illustration of a distance-dependent connectivity. The connection probability is color coded. (D) The probability of connection in the model (gray bars) and in the experiments (blue line) as a function of the inter-somatic distance. The blue curve represents a Gaussian fit to the data. The green curve represents the experimental results (Devor and Yarom, 2002a; see actual data in Figure 6—figure supplement 1). (E) Distribution of the common groups in the model (gray bars) and experiment (as in B; green line) for cells of up to 40 µm apart. (F–H) Same as C-E for a network that is organized in clusters of neurons with a high probability of connection within a cluster and a low probability between clusters (See Materials and methods). Each cluster consisted of about 40 neurons.

Figure 6—source data 1

Traces for Figure 6.

https://cdn.elifesciences.org/articles/43560/elife-43560-fig6-data1-v1.mat

We examined two possible connectivity patterns that might support this type of distribution (see Materials and methods; network connectivity matrices). The first is a network where the probability of a connection between two neurons depends solely on their inter-somatic distance (Figure 6C–E). The second assumes that the network is organized into clusters of neurons (Figure 6F–H), where the probability of connection within a cluster is larger than between clusters (both probabilities are distance-dependent).

As shown in Figure 6C–E, the simple distance-dependent network captured the distance-dependent probability of a connection (Figure 6D, p=0.99, for detailed statistical analysis see Materials and methods and Figure 6—figure supplement 1), but it failed to reproduce the distribution of common spikelet groups as found experimentally (Figure 6E, p<0.002, Fisher’s Exact). On the other hand, when the modeled network was organized in clusters, it replicated both the experimental distribution of common groups (Figure 6H, p=0.13) and the distance-dependent connection probability (Figure 6G, p=0.96). Note that in all modeled networks, each neuron was connected to about 11–21 neurons, which lay within the numbers estimated from the experimental observations (Figure 4F).

To further investigate the robustness of the result that the IO network is organized in clusters of coupled neurons, we searched for possible experimental or computational artifacts that may affect this conclusion. First, we examined the possibility that the experimental observation of the distribution of common groups is inaccurate. To that end, we tested the possibilities that we either failed to detect common groups or incorrectly identified groups of common spikelets.

Accordingly, we increased the number of pairs that did not show common groups to 18 (6 additional pairs) and removed one pair from each of the other groups (Figure 7A, green line). Alternatively, we reduced the number of pairs that did not show common groups by half (six pairs) and distributed them among the other pairs (Figure 7B, green line). As shown in Figure 7A and B, these variations did not change the main conclusion, namely the non-cluster organization cannot account for the distribution of the common groups (p<10−6 for Figure 7A and p=0.0025 for Figure 7B; see Materials and methods).

Figure 7
Download asset Open asset
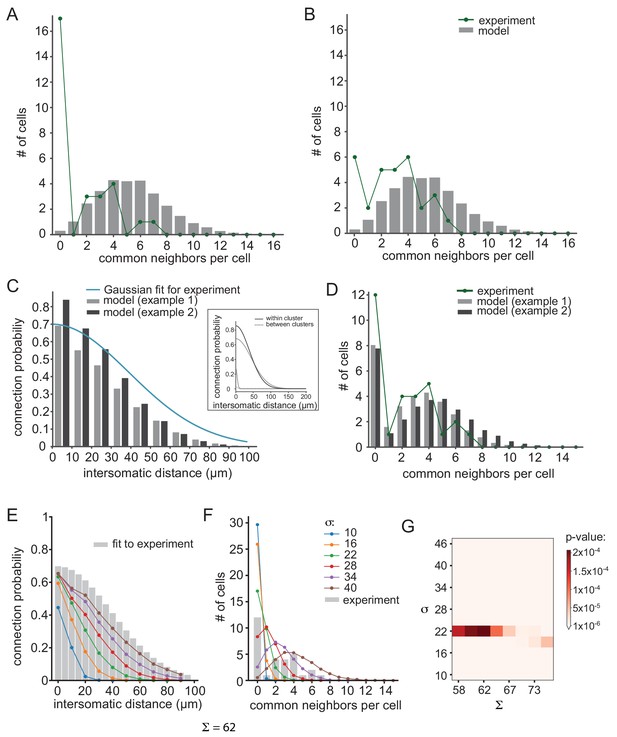
Further examination of possible network connectivity reveals the robustness of cluster organization as the best explanation for the experimental data.

(A) and (B) Examining the possibility that inaccurate detection of common groups led to the clustered organization. (A) Compensating for possible over estimation of common groups, by increasing the number of pairs that had zero common groups. (B) Compensating for possible underestimation of common groups, by reducing the number of pairs that has zero common group. Green lines are the corrected distribution of common group; bars are the expected distribution assuming distance-dependent connectivity (As in Figure 6C–E). (C–D) Two additional cluster models that can account for the connectivity probability and common neighbor distribution that were found experimentally (as in Figure 6F–H). The different connectivity profiles of the models are shown in the inset. (E–G) Color lines show the distance- dependent connection probability (E) and common neighbor distribution (F) for seven different distance- dependent models with Σ = 62 and different σ (see legend). All models did not fit the experimental common neighbor distribution (p<0.05). (G) Summary of the fit between the experimental common neighbor distribution and modeled common neighbor distribution, for different distance dependent models. The x axis represents the Σ that was used for each network and the y axis represent the σ that was used. All p values were below 0.05 (see color bar). The networks in E and F correspond to the column marked by Σ = 62.

Furthermore, we also examined other cluster connectivity profiles (see Materials and methods). Figure 7C and D demonstrate two additional examples of clustered organizations (gray and black bars) that differ in their maximal connectivity value (Σ) and the reduction of probability of connection as a function of distance both for within and between clusters (σ, see inset for connectivity profiles). Both models faithfully reproduced the distance-dependent probability of a connection (Figure 7C; p=0.7 and p=0.75 for gray and black, respectively) and the distribution of common groups (Figure 7D, p=0.9 and p=0.67 for gray and black, respectively). On the other hand, under non-clustered organization, changing the maximal connectivity value (Σ) or the reduction of probability of connection as a function of distance (σ, color coded) did not reproduce the observed distribution of common groups (Figure 7E–G). We scanned different σ, Σ and show that all networks produce a distribution of common neighbors that is significantly different than the experimental result (Figure 7G).

Thus, we show that the IO is not connected with a simple distance-dependent rule; instead it is more likely that it is organized into clusters of neurons with a higher probability of connection within clusters and a low connection probability between clusters.

Discussion

In this study, we measured subthreshold unitary activity from neurons of the inferior olive in slice preparation. The implementation of a variety of experimental approaches linked to computational simulation led to several important conclusions regarding the organization of the network of electrically coupled neurons in the inferior olive nucleus. We showed that there are two populations of unitary events that differ in their waveform and amplitude. The spikelets represent the occurrence of action potentials in a coupled neuron, while the fast events are likely to represent intrinsic regenerative responses at remote locations. It should be noted that in the scientific literature the word ‘spikelet’ refers to all non-synaptic subthreshold unitary events and thus creates a certain lack of consistency regarding their origin (see Introduction; Michalikova et al., 2019). The uniqueness of our experimental system lies in its ability to differentiate between two types of non-synaptic unitary events and thus to characterize them. We then used the spikelets recorded simultaneously from two neurons to gain insights into the size and organization of the electrically coupled network within the IO nucleus. Analysis of the experimental results showed that each olivary neuron is connected to ~20 other neurons and theoretical considerations indicated that the neurons are not connected in a simple distance-dependent manner, rather that the network is organized into clusters of neurons, where the probability of connection within a cluster is higher than the probability of connection between clusters.

The electrically coupled network in the olivary nucleus

It is well-established that the olivary nucleus forms an electrically coupled network. It has been suggested that this network operates as a synchronous rhythmic device, capable of generating precise temporal patterns (Jacobson et al., 2008). Both synchronicity and rhythmicity are generated by the delicate interplay between electrical coupling and ionic conductances. Thus, a single cell by itself cannot oscillate, whereas in a network formation the neurons generate subthreshold oscillations (Manor et al., 1997; Loewenstein et al., 2001; Chorev et al., 2007). In this work, we studied the relationship between spikelets and subthreshold oscillatory activity and found that in oscillating cells the occurrence of spikelets coincided with the depolarizing phase of the oscillation whereas in non-oscillating cells they seemed to be randomly distributed (Figure 3G,H). This result strongly supports our previous hypothesis that the occurrence of subthreshold oscillations is a network phenomenon. Therefore, when the recorded cell is oscillating, the entire network is synchronously oscillating, thus generating action potentials at the peak of the oscillation that appear in the recorded cell as spikelets. Theoretically, by calculating the number of spikelets at the peak of the oscillatory activity, one should be able to calculate the number of coupled neurons in the oscillating network. Although tempting, this is practically impossible because spikelets, given their small amplitude and noisy environment, cannot be classified into groups. Therefore, we used the common spikelets to estimate the number of coupled neurons.

Recording from two olivary neurons revealed spikelets that occurred simultaneously in both recorded neurons. Given that the average rate of spikelets is 0.56 ± 0.62 Hz, the probability that these common spikelets reflect random occurrence is extremely low. Furthermore, the repeated appearance of common spikelets with the same relationships (amplitude ratio and waveforms) further supports the non-random occurrence of these events. Thus, the accurate timing of common spikelets can only be attributed to a common source; that is a single pre-junctional neuron. The number of neurons that were coupled to the two recorded neurons, which varied from 1 to 7, should be correlated with the size of the network; more common spikelets are expected in larger interconnected networks.

Our simple method of calculating the size of a coupled network is based on data obtained during simultaneous recordings from two neurons and on the assumption that the neurons display a similar rate of spontaneous spiking activity. Our simulations show that the accuracy of this method is mainly affected by variability in the firing rate (Figure 5E,F). To minimize the error in estimating the firing rate of the neurons in the network, we used only the spontaneous rate of the common spikelets, and not the firing rates in the recorded neurons which are affected by the intracellular recordings. Under this assumption, we showed that neurons are connected to 3–40 other neurons. This is in line with other studies reporting 1–38 (Hoge et al., 2011) or 0–33 (Placantonakis et al., 2006) dye-coupled neurons. This broad variability can be attributed to the use of an in- vitro system, where differences in the number of cells and the integrity of the circuit are characteristic features. Alternatively, this large variability might reflect an innate feature of the IO nucleus where electrical coupling is under continuous modulation (Lefler et al., 2014; Mathy et al., 2014; Turecek et al., 2014).

In addition to calculating the number of connected cells, the distribution of common spikelets enabled us to study the connectivity profile within the nucleus. Our data showed that each two neurons had 1–7 common groups. However, there were a large number of paired recordings that failed to show common groups. Using a theoretical approach, we demonstrated that this distribution should not be expected if we assume that the probability of connection depends solely on the distance between the neurons. On the other hand, if the nucleus is organized into clusters where the probability of connection within the cluster is higher than between clusters, the observed distribution of common groups can be reproduced. Although the size of the clusters, as well as the probability of connection cannot be defined with the current data, this constitutes the first physiological study that supports the assumption of clustered organization of the nucleus deduced mainly from morphological studies.

This approach to analyze electrically coupled networks should not be restricted to the inferior olive network. Most of the studies on electrical coupling in central neurons used paired recordings, an essential procedure to demonstrate electrical coupling. In many of these recordings spontaneous spikelets are readily observed. In the work of Curti et al. (2012) on the Mesencephalic Trigeminal Nucleus, the occurrence of a spikelet in only one of the neurons is taken as indication for additionally connected cell. Similarly, the work of Long et al. (2004) on the Thalamic Reticular nucleus demonstrates spontaneously occurring spikelets of different sizes in both recorded neurons. Thus, to implement our approach all one needs is paired recordings of spontaneous activity of cells in electrically coupled network.

In summary, we presented a comprehensive study that implemented a wide range of research approaches to unravel the functional architecture of the inferior olivary network. We showed that new insights into the organization of the network can be gained by analyzing spontaneous subthreshold events, thus paving the way for a novel experimental and theoretical approach to the study of electrically coupled networks.

Materials and methods

Animals

All experimental procedures were approved by the Hebrew University’s Animal Care and Use Committee. Brain stem slices were prepared from the following strains of mice: C57BL/6, B6.Cg-Tg (Thy1-COP4/EYFP; Jackson Laboratory) and Gad2-tm2(cre)Zjh/J (Jackson Laboratory).

Slice preparation

Request a detailed protocol

Mice were anesthetized with an intraperitoneal injection of Pentobarbital (60 mg/Kg), and 300 µm coronal brainstem slices containing the inferior olive were dissected using a Campden 700smz slicer (Campden Instruments), in 35°C physiological solution containing 126 mM NaCl, 3 mM KCl, 1.3 mM MgSO4, 1.2 mM KH2PO4, 26 mM NaHCO3, 10 mM glucose, and 2.4 mM CaCl2, gassed with 95% O2 and 5% CO2. Slices were left in physiological solution at 35°C for 0.5–8 hr until transferred to the recording chamber.

Electrophysiological recordings and ChR stimulation

Request a detailed protocol

The recording chamber was perfused with 95% O2 and 5% CO2 physiological solution at 24–28°C. Slices were visualized using a 40X water-immersion objective in an Olympus BX61WIF microscope equipped with infrared differential interference contrast (DIC). In order to record from intact olivary networks, recordings were targeted to the deepest neurons possible in the slice. For pair recordings, two cells located up to 50 µm apart were selected. Whole-cell recordings were performed using 6–9 MΩ glass pipettes with intracellular solution containing 4 mM NaCl, 10−3mM CaCl2, 140 mM K-gluconate, 10−2 mM EGTA, 4 mM Mg-ATP, and 10 mM HEPES (pH 7.2). Signals were acquired at 10–20 KHz using a Multiclamp 700B (Molecular Devices) and LabView-based custom-made acquisition software (National Instruments and ZerLabs). For the ChR experiments in Thy1 mice, a custom-made digital mirror light stimulator with a LED light source (460 nm; Prizmatics) was used to activate the ChR at defined locations on the slice. In some experiments either TEA (10 mM), DNQX (20–40 µM) or DNQX (40–60 µM) and AP-5 (40–100 µM) were added to the recording solution.

Data analysis and statistics

Request a detailed protocol

Analysis was performed using MATLAB (R2014b and R2016a, MathWorks) for the experimental data and Python 2.7 for the simulation data. The 70 neurons that were selected for detailed analysis had a frequency of subthreshold events exceeding 0.02 Hz. The events were divided into two different groups according to their amplitude and rise time. The event rise time was calculated as 10–90% of the amplitude. The fast event groups were clustered using the K-means clustering method, using the MATLAB ‘evalclusters’ function. The effect of the DC current injection in Figure 2C–H was measured in 16 neurons for different values of current injection. For each neuron, the average value for each current injection was calculated (gray dots in Figure 2C–H) and fitted with a linear line (dashed gray lines). To calculate the average slope (black lines), we averaged the gray dots for each current injection (black dots) and fitted them with a linear line. Error bars represent STD. A one-sample t-test was used to compare the distribution of the slopes of the linear fits of each cell (dashed gray lines) to a distribution with a mean equal to zero. A paired t-test was used to test for differences in the effect on spikelets and fast events. The frequency values for spikelets and fast events (Figure 2G–H) were normalized for each cell to the highest value. The normalized fast events frequency (Figure 2H) was calculated from both fast events and the action potentials that were evoked from the fast events.

The coupling coefficient (CC, Figure 3C) was calculated as the ratio between the change in the steady-state voltage of the post-junctional cell and that of the pre-junctional cell in response to 250 ms current injection in the pre-junctional cell. The spike coupling coefficient was measured as the amplitude of the post-junctional spikelet divided by the amplitude of the pre-junctional action potential. A Pearson correlation was used to calculate the p-value of the linear regression in Figure 3C. To detect spikelets in oscillatory traces, the raw trace was subtracted with a low-pass filtered trace. The Inter-spikelet-interval (ISLI) in oscillating neurons (Figure 3E) was only calculated in neurons that had more than 150 spikelets during the session. The ISLI histogram was computed using 4 ms time bins, and the autocorrelation in oscillating neurons was calculated using a lag of 1 ms.

Common spikelets were defined as spikelets that were detected in a paired recording in both cells simultaneously. To that end, we searched for spikelets which peaks occurred in both cells within a time window of 8 msec. Groups of common spikelets in the two cells were clustered according to their amplitudes using k-means analysis. These clusters were then grouped according to the ratios between amplitudes in the two cells and verified manually. To estimate the number of connections per cell, the total number of spikelets (Tspikelets) was multiplied by the number of groups (Ngroups) and divided by the number of common spikelets (Cspikelets):

Estimatedconnectionspercell=Tspikelets ∗Ngroups  Cspikelets

If the two recorded cells were coupled (i.e., a spike in one cell gave rise to a spikelet in the other cell), +one was added to the estimation of connections for these two cells.

Neuron models

Request a detailed protocol

In a few experiments (using C57BL/6 mice), Neurobiotin (0.5%; Vector Laboratories) was added to the pipette solution to label the recorded neurons. Slices were then fixed in 4% paraformaldehyde overnight, washed in PBS and stained with 1 µg/ml Streptavidin AlexaFluor 488 (Life Technologies). Using the Neurolucida software (MBF Bioscience), three olivary neurons were reconstructed from fluorescence image stacks acquired using a Leica TCS SP5 confocal microscope (Leica Microsystems). To compensate for tissue shrinkage, the z-axis of the reconstruction was multiplied by a factor of 3. A compartmental model was generated from the morphological reconstruction using NEURON (Carnevale and Hines, 2006). The axial resistance (Ra) was set to 100 Ωcm, the specific membrane capacitance (Cm) to 1 µF/cm2 and the specific membrane resistivity (Rm) for the three reconstructed cells were 4300, 4500, 3800 Ωcm2 respectively. These values were chosen to yield an input resistance (Rin) that was within the experimental range (115 ± 43 MΩ).

Building the IO network connectivity matrices

Request a detailed protocol

We constructed a network of IO composed of 1134 neurons randomly distributed within a volume of 250 × 500×200 µm, which resulted in 0.045 neurons per 10 µm3. We then clustered the neurons by their location using k-means clustering, and varied the number of neurons in a cluster by choosing k to be 1134 divided by the number of neurons in a cluster. The probability of a connection between two neurons decays with distance according to a Gaussian profile:

Σ*e-x22*σ2100

where Σ is the maximal probability for connection (when the distance between the neurons is 0), x is the distance between neurons and σ sets the decay of connection probability with distance (see Figure 7C inset for examples). Note that the shape profile of neuron connectivity within a cluster could have a different Σ and σ than the connectivity profile of neurons belonging to different clusters. The common neighbor distribution (Figure 6F,I) was extracted on randomly selected pairs of neurons within a distance of 40 µm from the connectivity matrix. The network shown in Figure 6G and H had Σ and σ of 77 and 45 within a cluster and 15 and 20 between clusters, respectively. The networks shown in Figure 7C and D had Σ and σ within cluster of 68.1, 44.3 (gray model) and 85.6, 38.5 (black model), respectively. And Σ, σ between clusters of 2.4, 4.5 (gray model) and 27.3, 4 (black model), respectively. Number of neurons in a cluster was set to 40 in all cases.

Constructing the IO network model

Request a detailed protocol

To simulate a realistic network of IO neurons (Figure 5), we followed the steps described above but with a few modifications. The network volume was 125 × 250×100 µm, and populated with 180 neurons (0.057 neurons for 10 µm3). These neurons were cloned from the three 3D-reconstructed olivary neurons. Σ and σ within cluster were 77 and 45, respectively; and Σ, σ between clusters were 15 and 20, respectively (as in Figure 6G,H). The electrical connection between two neurons was mediated by two gap junctions (GJs). A GJ conductance (GJc) of 0.3 nS resulted in a coupling coefficient of 0.03 ± 0.019 as in the experimental range (0.039 ± 0.029). After adding GJc to the modeled cell, Rm was modified to maintain the experimental value of Rin (see details in Amsalem et al., 2016). The spikes in the networks were created by current injection to the soma (simulated spikes) following a Poisson process. We ran the network for 15 seconds with dt of 0.025 ms, we automatically detected the spikelets and clustered them as done experimently, but using bd-scan instead of k-means. Figure 5E, F represent the best-case scenario, assuming all spikelets were detected and clustered correctly.

Statistical comparison between the model prediction and the experimental observation

Request a detailed protocol

The experimental observations were compared with the models’ predictions on two levels. One is the probability to get the distribution of common group and the second is the probability of connection as a function of distance. To compare the distribution of common groups (Figures 6–7), we used the Monte Carlo Fisher’s Exact method (Noutahi, 2018) with 100,000 replicates (see example in Figure 6—figure supplement 1C).

To compare the distribution of probability for connection as a function of distance, for each network configuration we tested the connectivity of pairs sampled from the model and used two statistical methods to compare the experimental sample to the sample from the model. In the first method we constructed a contingency table from the model and the experimental data, and for each distance calculate the p-value using Fisher’s Exact (2 × 2, using Python SciPy), we then merged those 10 p-values with Fisher's combined probability test.

In a second method, for every distance we normalized the expected data and multiplied by the number of sampled in the experimental data for this distance, providing a vector of expected observation (see example in Figure 6—figure supplement 1A,B). We used Chi-square (using Python SciPy) to compare between these expected values to the observed values. (In order to get five samples per cell, we merged cells 60–70, 70–80, 80–90 and 90–100 in the connected column, and cells 80–90 with 90–100 in the non- connected column). Both statistical methods resulted with comparable p- values. The p- values presented in the main text are for the Fisher’s Exact method.

Data availability

All source data for this article is provided in the source data files associated with the figures.

References

  7. Book
    1. Carnevale NT
    2. Hines ML
    (2006)
    The NEURON Book
    Cambridge University Press.
    1. Noutahi E
    (2018) Fisher's exact test for MxN contingency table
    Fisher's exact test for MxN contingency table, http://doi.org/10.5281/zenodo.2587757.
    http://doi.org/10.5281/zenodo.2587757

Decision letter

  1. Ronald L Calabrese
    Senior and Reviewing Editor; Emory University, United States
  2. Alberto E Pereda
    Reviewer; Albert Einstein College of Medicine, United States
  3. Chris I De Zeeuw
    Reviewer; Erasmus Medical Center, Netherlands

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This paper provides novel insights on the properties and organization of neural networks in the inferior olive, and electrically coupled networks in the vertebrate CNS in general. In contrast to chemical synapses, networks formed by electrical coupling are more difficult to analyze because of their characteristic bidirectionality of transmission. Inferior olivary neurons are connected only by electrical coupling, thus providing an ideal structure to explore networks primarily organized by electrical coupling. The analysis presented makes the convincing argument that, rather than forming a single 'matrix' of electrically coupled cells, there exist clusters of functionally interconnected (electrically coupled) neurons. The authors arrive to this conclusion by disambiguating the nature of subthreshold responses and analyzing those representing coupling of action potentials, a step that allows them to estimate of the number of coupled cells with fair accuracy. These estimates were supported by computer simulations which provided novel insights into the organization of the network. The experiments are elegantly designed, and the paper is well illustrated. One of the important features of the work is that it presents a physiological framework for analyzing the functional architecture of other electrically coupled networks.

Decision letter after peer review:

Thank you for submitting your article "Using subthreshold events to characterize the functional architecture of electrically coupled networks" for consideration by eLife. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by Ronald Calabrese as the Senior and Reviewing Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Alberto Pereda (Reviewer #1); Chris I De Zeeuw (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

The authors have studied subthreshold membrane fluctuations of inferior olivary (IO) neurons in vitro. They observed two distinct types of events: fast, relatively large "Internal Regenerative Events (IREs)" that they identify as intrinsically generated regenerative events, and slower, smaller "spikelets" that they identify as electrical synapse-mediated events. Using various electrophysiological and computational lines of evidence they conclude that the IREs are likely initiated at axonal spines near the somata of IO cells (a significant novel finding), while spikelets are electrical synapse (gap junction)-mediated events generated by presynaptic action potentials. The authors also use spikelet data to estimate the size and pattern of electrically coupled neuronal clusters.

Essential revisions:

The experiments and modeling are well done, the analyses are interesting, and the conclusions of the study are potentially very important. There are several concerns about the main findings – the origins of the IRE and the network (neuronal cluster) analyses that must be addressed in revision. The detailed comments of the reviewers amplify these major required revisions described below; the focus in revision should be on these major points and not on minor differences in the reviewer comments.

1) All reviewers agree the synaptic pharmacology needs to be better both for the IRE and spikelet stories. The authors state they tested 19 cells in CNQX/APV, so perhaps all that's left is to do more detailed analysis and document it in the paper.

2) Are axonal spines really as common and beautiful in mouse cells as De Zeeuw showed them to be in the cat? The authors have already dye-filled mouse IO cells, but didn't show them in the paper. These spines should be documented in the paper (LM level) and perhaps these data are already available.

3) Can the authors provide more direct evidence that the IREs are coming from spines? Modeling is not enough, especially when we don't even know if axonal spines exist. Most people believe spikes initiate at axon initial segments because of high Na channel density there, and there are nice markers for initial segment-specific protein complexes (e.g. immuno for ankyrin-G, or Na channels themselves). Such a demonstration in axonal spines (LM level) by itself would be enough. Better electrophysiology (glutamate uncaging, axonal recording) would also be great, but probably too time-consuming for revision.

4) Regarding the functional significance of the IREs, the authors never mention whether those big subthreshold IREs trigger electrotonically propagated events (small spikelets?) in coupled cells. These are data the authors should already have from their paired recordings. In general, it's not at all clear how IREs, spikelets, spontaneous oscillations, and full spikes interact in coupled networks of IO neurons; the authors should present a more holistic view of how all these membrane events interact.

5) The other major and potentially interesting but problematic part of the paper is about spikelets, coupling, and clustering. The authors might be able to strengthen this without doing more experiments, if they can address some of the technical issues raised in the reviews (about clarity of description, noise and detection thresholds, alternative connection schemes in the model, statistical reliability of modeling curve fits, etc).

Reviewer #1:

There are several concerns:

– The paper has two sections, the analysis of the subthreshold responses and the use of spikelets to analyze network connectivity. While the first section reads very well I had problems with the transition to network analysis. I found the two sentences at the start of paragraph two of subsection “Estimating network architecture from dual cell recordings of simultaneously occurring spikelets” very confusing. I had to read them several times. There is little information on how common spikelet amplitude and ratio is used to generate the groups. Although I understand the notion, the details still unclear to me. The criteria and usefulness of these values for grouping spikelets should be explicit and not let the reader guessing.

– Coupling between inferior olivary neurons is heterogenous and one cell can be differentially coupled to its various neighbors. I am not sure how this would impact the analysis performed by the authors, in particular the ratio between common spikelets. Was coupling heterogeneity incorporated into computer simulations? The authors should address this issue.

– I suggest making the title specific to the inferior olive, perhaps ‘Using subthreshold events to characterize the functional architecture of the inferior olive’. While the number of coupled cells was not a surprise and consistent with previous reports using different methodology, the analysis performed by the authors provides further insights on the organization of the networks (favors the existence of compartments of functionally connected neurons) and this should be reflected in the title. In addition, although theoretically possible, it is unclear if the method could be used to analyze other, less known, networks. Are the authors suggesting the method could be applied other networks? If so, they should specifically discuss this point in the Discussion section.

Reviewer #2:

I have several suggestions to improve the manuscript:

– The spike-rates of the IO cells were approximated, and thus a possible source of bias. Though the authors do say they estimated the firing rates based on spontaneous slow event-rates, and not on the spiking rate of the recorded cells as these are affected by the intracellular solution, I wonder to what extent the estimates of the variability and frequency of the cells' firing rates result from the cell-attached recordings.

– With regard to the source of the fast spontaneous events, or "Internally Regenerative Events (IREs)", the authors find that these IREs do not depend on gap-junctions, but originate from spines in the axon hillock of the cell. I find this hypothesis quite plausible and attractive, but I wonder whether some additional electrophysiological experiments can be provided, either with glutamate uncaging or maybe glutamate or AMPA application with a secondary "puffing" pipette. This might confirm the effects of these "overruling" axonal spines on the IO neurons. More specifically, it would be nice to see an experiment with direct and/or solitary stimulation of the axonal spines.

– The authors suggest that the amplitudes of the IREs are predominantly determined by the neck length. However, I wonder why the observed amplitudes are not normally distributed but distributed in a sinusoid shape (see Figure 1B). I would assume that the spine neck lengths would be distributed normally. If the assumption is that the higher amplitudes are the result of summation, then I wonder why the sinusoid is so clean (because variable neck length would reduce the precision of the sinusoid shape, as the individual events that make up the summated event would be more variable as well). Additionally, as is mentioned in the text, De Zeeuw et al., 1990 showed that up to 8 spines emerge from the axon initial segment. Would the authors not expect a larger spread of amplitudes if that were the case?

– Given that the slow spikelets predominantly occur on top of the STOs, given that action potentials in one cell often lead to spikelets in electronically coupled cells, and given that IREs often induce action potentials, wouldn't the authors expect more spikelets outside of the normal STO-spikelet-window? Or do the authors assume that the afferents to the axonal spines are somehow also influenced by the STOs? Or do the effects of the IREs depend on the phase of the subthreshold oscillations? If that were the case, would the functionality of an emergent action-potential inducer that foregoes dendritic input not be somewhat hampered?

– There is a dependency between the underlying oscillations and the number of slow spikelets. However, spikelets would be harder to detect in steep rising phases of the oscillation. How did the authors deal with this potential confounder?

– The distribution of data about amplitudes and timing is probably not normal, so it might be better to report median and quartiles rather than mean and standard deviations throughout the article.

– I miss a plot of the distribution of STO amplitudes, particularly in the context of the claim that gap junctions are necessary for spontaneous oscillations. Our current understanding of the cell mechanisms generating the oscillations suggests that STO's may be generated in a few high amplitude cells, with other cells either reporting that oscillation, or indeed, engaging in them. Possibly in a network in which cells are connected by gap junctions a combination of these two phenomena exists. In fact Leznik and Llinas, 2004, showed that STO's are maintained within single cells following gap junction blocking, though the network synchrony is disrupted. So in my view, it is a combination in which the level of coupling will contribute to the level of STO's, while the coupling is not absolutely essential.

– The manuscript gives the impression that cells are either oscillating or not, while the literature has reported intermediate cells 'conditional oscillators'. This is an important point, since dynamical system's analysis shows that a non-oscillating cell can promptly be led to oscillate upon perturbations (Schweighofer et al., 1999).

– While it is likely that oscillations are potentiated by coupling, 'network oscillations' of a couple of mV's could simply be a read-out of high amplitude oscillators. Please discuss this point more extensively.

– It would have been nice to see simulation runs with two alternate connectivity scenarios. One with fewer connections, the other with more – the latter reflecting the possible scenario in the intact preparation.

Reviewer #3:

The experiments and modeling were well done, the analyses are interesting, and the conclusions of the study are potentially important. If small spike-like events actually originate from spine-like structures on the axon initial segment, it would be a novel and unique observation as far as I know. If electrical synapse-generated spikelets can be used to reliably estimate the size and patterns of gap junction-coupled neuron clusters, that would be an important contribution to IO neurobiology and perhaps more widely. As presented here, however, I don't think either conclusion is strongly supported by the evidence.

1) This study rests entirely on the properties of small, subthreshold events, so clear reporting of their characteristics is critical. A first-order question is whether any of these events represent chemical synaptic input. Are they EPSPs? Are they triggered by EPSPs? The answers here are vague. The authors report that the application of CNQX reduced the rate of "unitary unipolar events" from an average of 0.7 Hz to "below 0.02 Hz" (Results paragraph one), but no details are provided. This control rate was apparently taken from a large group of cells, not from the 19 cells to which the drug was applied. The authors should report the data properly, with measurements from the same neurons before and after CNQX. They should also report the characteristics of the subthreshold events remaining after CNQX, including amplitudes and kinetics, and compare them to events from the same cells in the absence of the drug. Later on, the authors say that fast events are "independent of chemical transmission", but they do not show any evidence for this. All of this bears on a key question: what, if anything, do EPSPs contribute to the subthreshold events and their properties?

2) Were all of the data in Figure 1 recorded in the absence of CNQX? If the answer is yes, and CNQX reduced the frequency of those subthreshold events by 97% (see previous comment), then shouldn't we expect a large fraction of the subthreshold events to be spontaneous EPSPs rather than spikelets?

3) The recording and analyses of subthreshold events are limited by detection thresholds and signal-to-noise ratios. Some of the events (spikelets and perhaps IREs) are presumably too small to see. This has implications for the inferences one can draw from the recordings, including the estimates of coupled-neuron cluster size. Noise levels are not reported here. The authors' modeling could provide estimates of the limits of their detection given signal-to-noise limitations, and perhaps support the reliability of their cluster estimates. The authors should discuss this issue.

4) As the authors say (twice), the origins of the IREs "are a mystery". The evidence that the small spikelets are the postsynaptic result of a presynaptic action potential passing through electrical synapses is highly compelling. The smoking gun comes from paired-cell recordings that were demonstrated by various labs years ago. However, the evidence that the larger, faster "IREs" originate in axonal spines adjacent to the soma is weak, inferential, and indirect.

The modeling results about IREs are suggestive, but I agree with the authors that "The locations and mechanism of generation of the IREs are not completely resolved". In fact, without some additional experimental evidence, I do not believe this part of the story is compelling. It certainly does not live up to the overstatement in the Abstract: "fast events represent a regenerative response in unique excitable spine-like structures in the axon hillock". First, it is not even clear whether axonal spines exist in mouse IO cells. If so, they should be illustrated. The authors refer to original data on axonal spines from De Zeeuw, but that work was done on cat neurons. Second, some more direct evidence for the location of IRE generation would help to make the conclusion convincing, e.g. direct recordings from axon initial segments or spines using electrodes or photoindicators, or molecular/structural demonstrations of high-density sodium channels at axonal spines.

5) The analysis of groups of "common spikelets" in paired recordings (Figure 7) as a way to infer the size of electrically coupled clusters of cells is interesting and clever. I wonder, however, about the limitations of the data and what they mean for the cluster size estimates. One example pair is illustrated, from which four groups of common spikelets were claimed (Figure 7E). The spikelet amplitudes are small and variable, of course, and the samples of common (and noncommon) spikelets in each cell were also small (as few as two in the example pair). The Materials and methods are vague about the statistical reliability of this form of cluster counting. For example, the two spikelet clusters on the right of Figure 7E don't look very different to me, especially since the samples are so small and the spikelet sizes/shapes are so variable. The spikelet size distributions in Figure 1 also imply large and continuous variance (rather than the peaky distributions shown for the IREs). Loose criteria for spikelet clustering would lead to overestimates of the size of electrically coupled clusters. The illustrated cell pair (Figure 7E) has some of the smallest numbers of estimated connections (Figure 7F). It seems the problem of defining distinct common spikelet clusters (and estimates of connections) must also increase as the number of clusters increases in a cell. This issue requires more rigorous justification and discussion.

The modeling results in Figure 8 test the analysis in Figure 7, to some extent, by varying the sampling period and the firing frequencies. However the modeled data look much less variable (in amplitude) than the real data (cf. Figure 8B with 7B and E, for example). I also infer from the descriptions that the model network did not include noise.

6) The modeling in Figure 8 does not provide convincing support for the authors' hypothesized clustering of gap junction connectivity, as compared to a simple distance-dependent model of connectivity. This seems to boil down to another eyeball comparison of estimates from the spikelet analyses of Figure 7 to the results of a model (Figure 8). Specifically, the authors conclude that the distance model "failed to reproduce the distribution of common groups as found experimentally (Figure 8F)", whereas the clustering model "replicated the distance-dependent connection probability (Figure 8H)". To my eye the fits in Figure 8F and H seem about equally good (or bad). Interestingly, the authors conclude that the fits to data measurements in Figure 8E and H are about equally good, but to my eye the fit in Figure 8H looks about as good (or bad) as that in Figure 8F and H. In other words, the modeling results seem to be very weak evidence for deciding between these cluster vs. distance-dependence scenarios.

In this regard, it would seem that experimental studies of tracer-coupling among IO cells (as in Devor and Yarom, 2004; Placantonakis et al., 2006; Hoge et al., 2011) in the same slices as those analyzed with the common spikelet method would be a more reliable way to determine whether electrical coupling is random/distance-dependent or is determined by clustering.

7) The authors discuss the occurrence of "common spikelets", but don't say much about IREs and electrical coupling. What happens in an electrically coupled cell when an IRE occurs in the paired cell? Are these events even detectable? The Discussion simply says, "an IRE in one neuron never coincided with a spikelet in the other neuron", but I don't believe the paper tells us what does coincide with an IRE.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for sending your article entitled "Using subthreshold events to characterize the functional architecture of the electrically coupled inferior olive network" for peer review at eLife. Your article is being evaluated by two peer reviewers, and the evaluation is being overseen by Ronald Calabrese as the Senior and Reviewing Editor.

The authors should be guided by the expert reviews. In particular, the authors must make their network modeling more complete (e.g., add noise) and clarify the pharmacology to make the paper strong. The clustering result and their computational method for evaluating it is potentially (pending revisions) very interesting.

Making a story about spiking axonal spines convincing appears beyond the reach of this paper, and the claims about them need to be significantly reduced or eliminated as explained in the expert reviews.

Reviewer #2:

The authors have addressed all my comments. It is a too bad that they did not provide EM pictures of the mouse axonal spines, but I find the LM sufficiently convincing.

Reviewer #3:

The authors have addressed some of the weaknesses in the original manuscript. I still think there are major shortcomings, however. The argument that IREs likely originate in axonal spines is unconvincing, in my opinion. The analysis and modeling of spikelets is a stronger story, but the modeling does not address the effects of noise in the cells. Also, the pharmacological results are still confusingly described. Specifically:

1) IRE origins and axonal spines. The authors' have slightly tempered their provocative conclusion that IREs are generated in axonal spines, although the Abstract still says: "We suggest that the fast events represent a regenerative response in unique excitable spine-like structures in the axon hillock." In my opinion the data supporting this suggestion are still exceedingly weak, for these reasons:

A) The authors' evidence for even the existence of axonal spines in mouse neurons is unconvincing. Only a single image of one mouse IO neuron was provided in the authors' response to reviews (Author response image 1). The image resolution is low, and each putative axonal spine seems to be represented by a small number of pixels. The blow-up image in Author response image 1B includes a dotted outline (hand-drawn?) that is an overly optimistic interpretation of the pixels, and the graphic in Author response image 1C is simply a cartoon version of Author response image 1B. I can appreciate that imaging these small structures is technically difficult, but without knowing if spines are common, how large they are, where they are placed, and how well they correlate with the IREs, the conclusion that IREs are generated by axonal spines is simply not convincing.

B) The authors did not provide any more morphological, molecular, or electrophysiological evidence that helps to connect the origin of IREs to axonal spines (as they replied: "…we are working on this issue but currently we cannot provide this information. We hope that the demonstration of their existence is sufficient for the current report.") But their manuscript goes far beyond simply demonstrating the existence or IREs. Speculations about exotic mechanisms should wait for supporting evidence.

C) The authors simulated several possible mechanisms of IRE generation. They first showed that IRE-like events can be generated by modeling "hot spots" of excitability in the dendrites, or alternatively by simulating spike failures at increasingly distal axonal nodes. Then they dismissed these possibilities by saying "it is difficult to envisage a biological mechanism that either specifically localizes channels in a restricted dendritic 'hot spot' or that simultaneously blocks two, three or more Nodes of Ranvier" (fourth paragraph, subsection “Modelling the Intrinsic Regenerative Events (IREs)”). Perhaps so, although two papers the authors cite show evidence for relatively high densities of sodium channels in dendritic spines (Araya et al., 2007; Bywalez et al., 2015). I find it just as difficult to envisage hot spots of ion channels in biologically unique axonal spines that have not been clearly demonstrated either in the olivary cells under study or, indeed, in any other class of vertebrate neuron.

D) The modeling of spike generation in putative axonal spines (Figure 5) explored a very limited and biologically unjustified parameter space. The authors included high densities of sodium and potassium channels (identical to those in the axon initial segment) in both the spine heads and in the axon hillock, while the excitability of the axonal nodes of Ranvier was actually eliminated (the excitable hillock and the inexcitable axon are mentioned only in the Materials and methods, and not in the main text or legend). The consensus in the field is that channel densities in the axon hillocks of vertebrate neurons are quite low, especially compared to the initial segment. Perhaps mouse olivary cells are not like other neurons, but in the absence of evidence we just don't know. What was the rationale for making the rest of the axon entirely inexcitable while modeling excitable spines? Only a few results of this modeling are illustrated in the manuscript; how robust are these results? What are the consequences of varying channel densities and types, distributions, spatial patterns, spine morphology and number, etc.?

2) Network modeling and the absence of noise. The most novel and interesting conclusion from the network modeling is that the IO cells may be organized into electrically coupled clusters of cells (the connection probability predictions largely agree with the widely variable range suggested by previous studies). The clustering conclusion rests entirely on fits of the "common spikelet" distributions in recorded cell pairs to predictions of the network model. The authors note that the accuracy of the modeled connection distributions depend strongly on the cells' firing frequencies and the length of the recording samples. Should it not also depend on noise? An important feature of the biological preparation that is absent from the model is any source of noise or variability (apart from the Poisson timing of the somatic currents triggering spikes), especially in the subthreshold membrane voltages. The authors' recordings implied that blocking fast glutamate receptors reduced spontaneous spiking rates dramatically, so one can infer that there is normally a considerable of chemical synaptic noise in addition to other potential sources. How does the absence of noise in the model affect the network predictions and the fits to spikelet data, and in particular the prediction that cells are clustered?

3) Pharmacology. The pharmacology (synaptic blocker) data are still confusingly described and not very helpful. From the Results, subsection “Spontaneous unitary events recorded in neurons of the inferior olive”: "However, application of synaptic blockers (see Materials and methods) completely eliminated the presence of the fast events (n=19 neurons; in 4 of these neurons where CNQX was added during recording the frequency changed from 0.017 ± 0.005 Hz to 0 Hz) whereas the frequency of spontaneous slow events decreased significantly (from 0.92 ± 0.73 Hz 163 to 0.26 ± 0.16 Hz, p=0.019, paired t-test, n=9 neurons)." My questions:

A) What were the blockers? This Results sentence says just CNQX, the legend to Figure 2—figure supplement 1 says APV plus either CNQX or DNQX, and the Materials and methods simply list all the drugs.

B) The sample sizes tested are still ambiguous. The phrase about fast events says n=19, but then talks about n=4 "where CNQX was added". Was the drug not added to the other 15 cells? The phrase about slow events then cites n=9. Were the same cells tested before and after addition of blockers? Are the 4 and 9 cells subsets of the 19, or different samples? Please clarify.

C) The authors say they did a "thorough analysis" of the effects of blockers on slow event waveforms, but they actually report data from only two example cells in Figure 2—figure supplement 1. These data showed rise-times and half-durations, but not amplitudes.

https://doi.org/10.7554/eLife.43560.sa1

Author response

Essential revisions:

The experiments and modeling are well done, the analyses are interesting, and the conclusions of the study are potentially very important. There are several concerns about the main findings – the origins of the IRE and the network (neuronal cluster) analyses that must be addressed in revision. The detailed comments of the reviewers amplify these major required revisions described below; the focus in revision should be on these major points and not on minor differences in the reviewer comments.

Thank you for your encouraging response. The reviewers did a thorough job that end with important comments that undoubtedly will lead to a significant improvement of the presentation and conclusion of this study. In the revised manuscript, we re-organized the description of the data, substantially increased the description of the statistical methods used for the pharmacological treatments and modeling approach and did our best to respond to all reviewers’ comments. However, this study is an attempt to investigate the structure of electrically coupled networks by analyzing subthreshold events that represent electrical coupling. Thus, a major issue is to identify these events. In our recordings from the inferior olive neurons we encountered electrically coupled spikelets, as well as other subthreshold events, the IREs, that had to be identified before excluding them from the analysis. We suggest that they represent regenerative responses in spines that are located at the axon initial segment. We do agree that this is “a significant novel finding” that require a thorough study. In fact, we started a new line of research where anatomical, physiological and imaging technique will be used to examine our suggestion on the origin of these events. Thus, currently we can provide only anecdotal observations of spines on the axon in the mouse. A through study of spike distribution in many neurons, as well as correlation between the number of spines and the number of IREs in a given neuron and the specific activation of these spines, all are absolutely needed, and cannot be provided at this stage. Nevertheless, we did our best to reply to the reviewers’ comments and we hope that it will meet your approval.

1) All reviewers agree the synaptic pharmacology needs to be better both for the IRE and spikelet stories. The authors state they tested 19 cells in CNQX/APV, so perhaps all that's left is to do more detailed analysis and document it in the paper.

In the revised manuscript, we provided a better and more comprehensive descriptionof the pharmacological experiments. We first compared the rate of occurrence of the spontaneous events demonstrating that although the rate of spikelets are drastically reduced (n= 9 cells), the IREs are completely absent (n=4 cells). As suggested, we added a thorough description of the synaptic blockers effect on spikelets’ shape, and on appearance of evoked spikelets (Figure 2—figure supplement 1; Figure 6—figure supplement 1) to show that the reduction in frequency is due to a reduction in excitability of the network, and not because some of the spikelets we record are of synaptic origin.

The IREs, which are intrinsic events, are not encountered in the presence of synaptic blockers, but are also not of synaptic origin, as presented in Figure 2 (Figure 3 in the original manuscript). Since most of the action potentials in IO neurons are triggered by IREs, in the presence of synaptic blockers, the frequency of action potentials is highly reduced, and thus the frequency of spikelets. However, the spikelets can still be evoked with synaptic blockers, when action potentials are evoked in a coupled cell (Figure 6—figure supplement 1).

We changed the order of appearance of Figures 2 and 3 of the original manuscript in order to explain and discuss these findings.

2) Are axonal spines really as common and beautiful in mouse cells as De Zeeuw showed them to be in the cat? The authors have already dye-filled mouse IO cells, but didn't show them in the paper. These spines should be documented in the paper (LM level) and perhaps these data are already available.

Author response image 1 is a figure showing axonal spines on a mouse olivary neuron using sparse viral-labeling procedure (A). The region where the axon branches off the soma is shown in high magnification (B), and schematic illustration of the axonal spines (C). This figure can be added as a supplementary figure if needed. At this stage, we cannot provide a more detailed description of the axonal spines, as identifying the axon in IO cells is not a simple task, due to extensive bifurcations of the dendrites and the tendency of axons to emerge from a dendrite.

Author response image 1
Download asset Open asset

3) Can the authors provide more direct evidence that the IREs are coming from spines? Modeling is not enough, especially when we don't even know if axonal spines exist. Most people believe spikes initiate at axon initial segments because of high Na channel density there, and there are nice markers for initial segment-specific protein complexes (e.g. immuno for ankyrin-G, or Na channels themselves). Such a demonstration in axonal spines (LM level) by itself would be enough. Better electrophysiology (glutamate uncaging, axonal recording) would also be great, but probably too time-consuming for revision.

As we stated above, we are working on this issue but currently we cannot provide this information. We hope that the demonstration of their existence is sufficient for the current report.

4) Regarding the functional significance of the IREs, the authors never mention whether those big subthreshold IREs trigger electrotonically propagated events (small spikelets?) in coupled cells. These are data the authors should already have from their paired recordings. In general, it's not at all clear how IREs, spikelets, spontaneous oscillations, and full spikes interact in coupled networks of IO neurons; the authors should present a more holistic view of how all these membrane events interact.

In the manuscript, we specifically reported that in pair recording we neverencountered a correlated signal with the IRE. In fact, this was our main drive to search for an alternative possibility. If the IREs were originating at dendritic level, they should have resulted in a much higher signal in the post junctional neuron. We added a clearer description of this issue in the Results section.

We added our holistic view on the interaction between these events in the Discussion.

5) The other major and potentially interesting but problematic part of the paper is about spikelets, coupling, and clustering. The authors might be able to strengthen this without doing more experiments, if they can address some of the technical issues raised in the reviews (about clarity of description, noise and detection thresholds, alternative connection schemes in the model, statistical reliability of modeling curve fits, etc).

We have addressed all technical issues, as suggested by the reviewers, listed in each specific point below.

Reviewer #1:

There are several concerns:

– The paper has two sections, the analysis of the subthreshold responses and the use of spikelets to analyze network connectivity. While the first section reads very well I had problems with the transition to network analysis. I found the two sentences at the start of paragraph two of subsection “Estimating network architecture from dual cell recordings of simultaneously occurring spikelets” very confusing. I had to read them several times. There is little information on how common spikelet amplitude and ratio is used to generate the groups. Although I understand the notion, the details still unclear to me. The criteria and usefulness of these values for grouping spikelets should be explicit and not let the reader guessing.

We rephrased these sentences in the Results section and in the Materials and methods sections.

– Coupling between inferior olivary neurons is heterogenous and one cell can be differentially coupled to its various neighbors. I am not sure how this would impact the analysis performed by the authors, in particular the ratio between common spikelets. Was coupling heterogeneity incorporated into computer simulations? The authors should address this issue.

We are not sure if the comment refers to heterogeneous strength of the coupling or to the heterogeneous number of neurons that are connected to each neuron. In the model, the number of neurons connected were heterogeneous (Figure 8C). The conductance of each gap-junction was identical, but the position on the dendritic tree and the cells’ morphology and membrane properties were different, thus creating heterogeneity in spikelets, as shown in Figure 8B and in figure in response to reviewer #3 comment 5.

– I suggest making the title specific to the inferior olive, perhaps ‘Using subthreshold events to characterize the functional architecture of the inferior olive’. While the number of coupled cells was not a surprise and consistent with previous reports using different methodology, the analysis performed by the authors provides further insights on the organization of the networks (favors the existence of compartments of functionally connected neurons) and this should be reflected in the title. In addition, although theoretically possible, it is unclear if the method could be used to analyze other, less known, networks. Are the authors suggesting the method could be applied other networks? If so, they should specifically discuss this point in the Discussion section.

We thank the reviewer for the title suggestion. We changed the title to be more specific to the inferior olive: 'Using subthreshold events to characterize the functional architecture of the electrically coupled inferior olive network’.

In addition, the relevance of our approach to other networks was added to the last section of Discussion section.

Reviewer #2:

I have several suggestions to improve the manuscript:

– The spike-rates of the IO cells were approximated, and thus a possible source of bias. Though the authors do say they estimated the firing rates based on spontaneous slow event-rates, and not on the spiking rate of the recorded cells as these are affected by the intracellular solution, I wonder to what extent the estimates of the variability and frequency of the cells' firing rates result from the cell-attached recordings.

The comment is not clear to us. To avoid artefacts of spiking activity due to the recording procedure, we estimated the firing rate from the frequency of the common spikelets that reflect the activity in single cells undisturbed by the recording. We did not use any cell-attached recordings in our experiments.

– With regard to the source of the fast spontaneous events, or "Internally Regenerative Events (IREs)", the authors find that these IREs do not depend on gap-junctions, but originate from spines in the axon hillock of the cell. I find this hypothesis quite plausible and attractive, but I wonder whether some additional electrophysiological experiments can be provided, either with glutamate uncaging or maybe glutamate or AMPA application with a secondary "puffing" pipette. This might confirm the effects of these "overruling" axonal spines on the IO neurons. More specifically, it would be nice to see an experiment with direct and/or solitary stimulation of the axonal spines.

Please see reply to editor point number 3.

– The authors suggest that the amplitudes of the IREs are predominantly determined by the neck length. However, I wonder why the observed amplitudes are not normally distributed but distributed in a sinusoid shape (see Figure 1B). I would assume that the spine neck lengths would be distributed normally. If the assumption is that the higher amplitudes are the result of summation, then I wonder why the sinusoid is so clean (because variable neck length would reduce the precision of the sinusoid shape, as the individual events that make up the summated event would be more variable as well). Additionally, as is mentioned in the text, De Zeeuw et al., 1990 showed that up to 8 spines emerge from the axon initial segment. Would the authors not expect a larger spread of amplitudes if that were the case?

Indeed, the quantal-like distribution is an interesting observation, however, this was not observed in all cells. Author response image 2 (A) represents a different example where the amplitudes are not equally distributed.

Author response image 2
Download asset Open asset

We do not assume that the higher amplitudes are a result of summation, as this entails that both spines are innervated by the same axon. We did observe very few IREs where a break in rise-time was clearly observed (arrow in B). We assume these are the result of summation of activity in two spines. However, these IREs were omitted from analysis.

We do not expect a larger spread of amplitudes, since according to De Zeeuw et al., 1990, up to 8 spines are detected, some of them are only receiving GABAergic innervation, which will not result in IREs.

– Given that the slow spikelets predominantly occur on top of the STOs, given that action potentials in one cell often lead to spikelets in electronically coupled cells, and given that IREs often induce action potentials, wouldn't the authors expect more spikelets outside of the normal STO-spikelet-window? Or do the authors assume that the afferents to the axonal spines are somehow also influenced by the STOs? Or do the effects of the IREs depend on the phase of the subthreshold oscillations? If that were the case, would the functionality of an emergent action-potential inducer that foregoes dendritic input not be somewhat hampered?

As demonstrated in Figure 2H (former Figure 3H), as opposed to spikelets, the frequency of IREs depend on membrane potential, thus an IRE is less likely to be evoked at the trough of the STO. Moreover, it is less likely that an IRE will evoke an action potential at the trough of oscillations. Thus, although it seems that “the afferents to the axonal spines are somehow also influenced by the STOs”, it is likely to be the results of the voltage sensitivity of these events.

– There is a dependency between the underlying oscillations and the number of slow spikelets. However, spikelets would be harder to detect in steep rising phases of the oscillation. How did the authors deal with this potential confounder?

Spikelets in oscillatory traces were detected after subtracting a low pass filtered trace from the raw trace. In this way, even small spikelets on the rising and falling edges could be easily detected. We added this discerption to the Materials and methods section “Data analysis and statistics”.

– The distribution of data about amplitudes and timing is probably not normal, so it might be better to report median and quartiles rather than mean and standard deviations throughout the article.

According to Shapiro-Wilk normality test, some of the distribution are normal or close to normal, and the median/mean ratio is in some cases >0.95 and in others >0.9. Calculating the median and quartiles gave the following results, which are not very different than the mean+std:

Fast events rise time 1.4 ± 0.4 ms (median is 1.333)

Duration 4.2 ± 1.3 ms (median 3.86)

Slow events rise time 2.5 ± 0.6 ms (median 2.4)

Duration 12.7 ± 3.9 ms (median 12.6)

As such, we prefer to keep the mean+std description as this is more readable. If still needed we are happy to replace all numbers.

– I miss a plot of the distribution of STO amplitudes, particularly in the context of the claim that gap junctions are necessary for spontaneous oscillations. Our current understanding of the cell mechanisms generating the oscillations suggests that STO's may be generated in a few high amplitude cells, with other cells either reporting that oscillation, or indeed, engaging in them. Possibly in a network in which cells are connected by gap junctions a combination of these two phenomena exists. In fact Leznik and Llinas, 2004, showed that STO's are maintained within single cells following gap junction blocking, though the network synchrony is disrupted. So, in my view, it is a combination in which the level of coupling will contribute to the level of STO's, while the coupling is not absolutely essential.

– The manuscript gives the impression that cells are either oscillating or not, while the literature has reported intermediate cells 'conditional oscillators'. This is an important point, since dynamical system's analysis shows that a non-oscillating cell can promptly be led to oscillate upon perturbations (Schweighofer et al., 1999).

– While it is likely that oscillations are potentiated by coupling, 'network oscillations' of a couple of mV's could simply be a read-out of high amplitude oscillators. Please discuss this point more extensively.

We are puzzled by these comments. Indeed, the mechanism of generation of STO in the olivary nucleus is debated, but it is not the issue of this study. In the analysis demonstrated in Figure 6 (former Figure 2), where only stable oscillating cells were used, we used the spikelets occurrence as an indication that in this electrically coupled network all the coupled neurons oscillate at a similar frequency, which is in agreement with the different views on the source of IO oscillations, and is not discussed further.

– It would have been nice to see simulation runs with two alternate connectivity scenarios. One with fewer connections, the other with more – the latter reflecting the possible scenario in the intact preparation.

We are not sure if we completely understand the comment. In the response to comment 6 of reviewer #3 we present more connectivity scenarios.

Reviewer #3:

The experiments and modeling were well done, the analyses are interesting, and the conclusions of the study are potentially important. If small spike-like events actually originate from spine-like structures on the axon initial segment, it would be a novel and unique observation as far as I know. If electrical synapse-generated spikelets can be used to reliably estimate the size and patterns of gap junction-coupled neuron clusters, that would be an important contribution to IO neurobiology and perhaps more widely. As presented here, however, I don't think either conclusion is strongly supported by the evidence.

1) This study rests entirely on the properties of small, subthreshold events, so clear reporting of their characteristics is critical. A first-order question is whether any of these events represent chemical synaptic input. Are they EPSPs? Are they triggered by EPSPs? The answers here are vague. The authors report that the application of CNQX reduced the rate of "unitary unipolar events" from an average of 0.7 Hz to "below 0.02 Hz" (Results paragraph one), but no details are provided. This control rate was apparently taken from a large group of cells, not from the 19 cells to which the drug was applied. The authors should report the data properly, with measurements from the same neurons before and after CNQX. They should also report the characteristics of the subthreshold events remaining after CNQX, including amplitudes and kinetics, and compare them to events from the same cells in the absence of the drug. Later on, the authors say that fast events are "independent of chemical transmission", but they do not show any evidence for this. All of this bears on a key question: what, if anything, do EPSPs contribute to the subthreshold events and their properties?

Please see elaborated response to the editor comment 1.

2) Were all of the data in Figure 1 recorded in the absence of CNQX? If the answer is yes, and CNQX reduced the frequency of those subthreshold events by 97% (see previous comment), then shouldn't we expect a large fraction of the subthreshold events to be spontaneous EPSPs rather than spikelets?

Yes, CNQX was not used in any of the neurons presented in Figure 1. Reduction in spikelets under CNQX is explained as reduction in firing in the network. We added a new supplementary figure (Figure 2—figure supplement 1) and discussed the issue further in the Result section.

3) The recording and analyses of subthreshold events are limited by detection thresholds and signal-to-noise ratios. Some of the events (spikelets and perhaps IREs) are presumably too small to see. This has implications for the inferences one can draw from the recordings, including the estimates of coupled-neuron cluster size. Noise levels are not reported here. The authors' modeling could provide estimates of the limits of their detection given signal-to-noise limitations, and perhaps support the reliability of their cluster estimates. The authors should discuss this issue.

We agree that the analysis is restricted by the signal to noise ratio. Indeed, we discussed that our results are likely to be an underestimation of the number of spikelets and common groups. However, this limitation could only significantly affect our conclusion that the connectivity is organized in clusters. In order to test whether this will hinder our ability to reject the distance dependent configuration we reduced by half (6 pairs) the number of pairs without common groups and distributed those 6 pairs in common groups uniformly (see Author response image 3). This modified data still rejects the distance-dependent model (A, p value<0.002) and support the cluster organization (B, p value>0.05). In addition, it should be noted that in the case of 12 pairs that did not have common groups, we carefully verified that spikelets in one cell never coincide with any voltage change in the other cell.

Author response image 3
Download asset Open asset

4) As the authors say (twice), the origins of the IREs "are a mystery". The evidence that the small spikelets are the postsynaptic result of a presynaptic action potential passing through electrical synapses is highly compelling. The smoking gun comes from paired-cell recordings that were demonstrated by various labs years ago. However, the evidence that the larger, faster "IREs" originate in axonal spines adjacent to the soma is weak, inferential, and indirect.

The modeling results about IREs are suggestive, but I agree with the authors that "The locations and mechanism of generation of the IREs are not completely resolved". In fact, without some additional experimental evidence, I do not believe this part of the story is compelling. It certainly does not live up to the overstatement in the Abstract: "fast events represent a regenerative response in unique excitable spine-like structures in the axon hillock". First, it is not even clear whether axonal spines exist in mouse IO cells. If so, they should be illustrated. The authors refer to original data on axonal spines from De Zeeuw, but that work was done on cat neurons. Second, some more direct evidence for the location of IRE generation would help to make the conclusion convincing, e.g. direct recordings from axon initial segments or spines using electrodes or photoindicators, or molecular/structural demonstrations of high-density sodium channels at axonal spines.

We completely agree that the source and mechanism of IRE is far from being convincing, and will need a thorough work which we are now pursuing. However, in order to decide whether to include or exclude the IREs from the organization analysis of the electrically coupled network, we had to give enough indications that they do not represent electrical coupling potentials. We added a preliminary observation on the existence of axonal spines in mouse IO cell, and amended the phrasing in the Abstract. See our elaborated response to editor comment #2.

5) The analysis of groups of "common spikelets" in paired recordings (Figure 7) as a way to infer the size of electrically coupled clusters of cells is interesting and clever. I wonder, however, about the limitations of the data and what they mean for the cluster size estimates. One example pair is illustrated, from which four groups of common spikelets were claimed (Figure 7E). The spikelet amplitudes are small and variable, of course, and the samples of common (and noncommon) spikelets in each cell were also small (as few as two in the example pair). The Materials and methods are vague about the statistical reliability of this form of cluster counting. For example, the two spikelet clusters on the right of Figure 7E don't look very different to me, especially since the samples are so small and the spikelet sizes/shapes are so variable. The spikelet size distributions in Figure 1 also imply large and continuous variance (rather than the peaky distributions shown for the IREs). Loose criteria for spikelet clustering would lead to overestimates of the size of electrically coupled clusters. The illustrated cell pair (Figure 7E) has some of the smallest numbers of estimated connections (Figure 7F). It seems the problem of defining distinct common spikelet clusters (and estimates of connections) must also increase as the number of clusters increases in a cell. This issue requires more rigorous justification and discussion.

We agree with the reviewer that incorrect spikelet clustering will hamper our estimation of connected cells, and for this reason we took every effort to devise an analysis that will correctly cluster the traces. It is true that, as shown in Figure 1, the distribution of spikelets’ amplitudes is large. However, when taking the 3 parameters: amplitude of common spikelet in the first cell; amplitude of common spikelet in the second cell; difference between the two amplitudes, one gets a very clear spikelet clusters.

In both the experimental and modelling parts we initially used the DBSCAN clustering algorithm to cluster the common spikelets according to their peak amplitudes and differance between amplitudes. However, while the algorithm works well for the model, it is less ideal for the noisy experimental traces although the number of groups detected by the algorithm was not substantially different than the manual curation. In Author response image 4 we compare the manual curation to the DBSCAN results in another example pair. Whereas the similarity of two modes of analysis are clearly seen, the algorithm predicted 7 groups whereas the manual analysis resulted in 6 groups. First, it is clear that the manual curation is more accurate. Second, as we demonstrate above (response to comment 3), a small change in the number of common groups did not affect the significance of our claim.

In the example shown in Figure 7, the two right clusters indeed have similar black traces, but the red traces could easily be grouped in two different clusters according to their amplitudes. We chose this example, since we believe it is an easy example to explain our methodological approach with.

We added a clearer description of the analysis in the Materials and methods section.

Author response image 4
Download asset Open asset

The modeling results in Figure 8 test the analysis in Figure 7, to some extent, by varying the sampling period and the firing frequencies. However the modeled data look much less variable (in amplitude) than the real data (cf. Figure 8B with 7B and E, for example). I also infer from the descriptions that the model network did not include noise.

Indeed, in the example given in Figure 8 there is little variance, however, this was not a common feature, as shown in another example in Author response image 5. The difference in spikelets’ amplitude was originated from the difference in GJ locations and the cells’ morphology and membrane properties. There was also noise originating from the difference in the mean firing rate of the cells, which effect we quantified in Figure 8—figure supplement 1. Noise was not added to the voltage traces.

Author response image 5
Download asset Open asset

6) The modeling in Figure 8 does not provide convincing support for the authors' hypothesized clustering of gap junction connectivity, as compared to a simple distance-dependent model of connectivity. This seems to boil down to another eyeball comparison of estimates from the spikelet analyses of Figure 7 to the results of a model (Figure 8). Specifically, the authors conclude that the distance model "failed to reproduce the distribution of common groups as found experimentally (Figure 8F)", whereas the clustering model "replicated the distance-dependent connection probability (Figure 8H)". To my eye the fits in Figure 8F and H seem about equally good (or bad). Interestingly, the authors conclude that the fits to data measurements in Figure 8E and H are about equally good, but to my eye the fit in Figure 8H looks about as good (or bad) as that in Figure 8F and H. In other words, the modeling results seem to be very weak evidence for deciding between these cluster vs. distance-dependence scenarios.

In this regard, it would seem that experimental studies of tracer-coupling among IO cells (as in Devor and Yarom, 2004; Placantonakis et al., 2006; Hoge et al., 2011) in the same slices as those analyzed with the common spikelet method would be a more reliable way to determine whether electrical coupling is random/distance-dependent or is determined by clustering.

Thank you for the comment. We conducted a full statistical analysis on this issue which is discussed in a new section in the Materials and methods and a supplementary figure (Figure 8 —figure supplement 2).

In short, we added a p-value for Figure 8F and 8I (<0.002 for 8F, and 0.907 and 0.125 for 8I black and gray, respectively). And also for Figure 8E and H (all > 0.05).

Furthermore, in the original manuscript we tested the common group distribution only for one distance dependent connectivity configuration. Here we validated that our results are not constrained only to that specific distant-dependent configuration, as also pointed by the two other reviewers. In Author response image 6 are connectivity analysis of networks with different distance dependent connectivity probability (left), in which the Σ and σ (see Materials and methods, connectivity matrices) are different, and the corresponding common neighbor distribution (right). For all those connectivity configurations, the p values for the common neighbor distribution were <0.05.

Author response image 6
Download asset Open asset

7) The authors discuss the occurrence of "common spikelets", but don't say much about IREs and electrical coupling. What happens in an electrically coupled cell when an IRE occurs in the paired cell? Are these events even detectable? The Discussion simply says, "an IRE in one neuron never coincided with a spikelet in the other neuron", but I don't believe the paper tells us what does coincide with an IRE.

We did not see any event or change in membrane potential in one cell while IRE was apparent in the other cell, nor we saw an IRE in one cell due to spike in the other cell. These evidences highly support the hypothesis that IREs are not evoked in the dendrites, as this will pass through gap-junction to coupled neurons. This was indeed our reason to search for other possibility to the origin of the IREs, after dismissing the direct-indirect spikelets possibility which is presented in Figure 4—figure supplement 1. This point was elaborated in the Result section and Discussion.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

The major change of the current submission is a complete removal of the axonal spines and focus on the organization of the network.

In the current version we also answered the reviewer’s comments by:

a) Performed a new set of pharmacological experiments, showing that the fast events are blocked by synaptic blockers whereas the spikelets are still present and therefore are likely to reflect electrical coupling. As mentioned by the reviewers, the fact that the frequency of spikelets is significantly reduced by the drugs may suggest that some of the slow subthreshold events might be a chemical synaptic event, a possibility that will question the use of spontaneous events to study the network organization. To resolve this issue, we first compared the spontaneous spikelets to the evoked ones (in pair recordings) and show their similarity. Second, we analyzed a new set of experiments of light-evoked chemical synapses in the Thy1 mouse, demonstrating that their waveform and amplitude are different from the spontaneous and evoked slow events. Thus, we conclude that most, if not all, of the spontaneous slow events are indeed due to electrical coupling.

In addition, we discuss the reduction in spikelets activity under drug conditions, arguing that spontaneous spiking activity is triggered by the fast events and that blocking the fast events result in a reduction in the frequency of spikelets.

b) We study the role of noise in detecting common groups of spikelets by assuming either failure or over detections. This is summarized in Figure 7. We also added simulation of the expected distribution of common groups under different assumptions. In all these simulations it is rather clear that a network where the probability of connections is only distance dependent cannot account for the experimentally observed distribution. Thus the main conclusion of this study, that the inferior olive nucleus is organized in clustered of connected cells, is fully supported by the experimental observations.

In our opinion, it is convincing that we offer a novel experimental and theoretical approach to the study of electrically-coupled network and hope it will meet your approval.

Reviewer #3:

The authors have addressed some of the weaknesses in the original manuscript. I still think there are major shortcomings, however. The argument that IREs likely originate in axonal spines is unconvincing, in my opinion. The analysis and modeling of spikelets is a stronger story, but the modeling does not address the effects of noise in the cells. Also, the pharmacological results are still confusingly described.

1) IRE origins and axonal spines. The authors' have slightly tempered their provocative conclusion that IREs are generated in axonal spines, although the Abstract still says: "We suggest that the fast events represent a regenerative response in unique excitable spine-like structures in the axon hillock." In my opinion the data supporting this suggestion are still exceedingly weak, for these reasons:

A) The authors' evidence for even the existence of axonal spines in mouse neurons is unconvincing. Only a single image of one mouse IO neuron was provided in the authors' response to reviews (Author response image 1). The image resolution is low, and each putative axonal spine seems to be represented by a small number of pixels. The blow-up image in Author response image 1B includes a dotted outline (hand-drawn?) that is an overly optimistic interpretation of the pixels, and the graphic in Author response image 1C is simply a cartoon version of Author response image 1B. I can appreciate that imaging these small structures is technically difficult, but without knowing if spines are common, how large they are, where they are placed, and how well they correlate with the IREs, the conclusion that IREs are generated by axonal spines is simply not convincing.

B) The authors did not provide any more morphological, molecular, or electrophysiological evidence that helps to connect the origin of IREs to axonal spines (as they replied: "…we are working on this issue but currently we cannot provide this information. We hope that the demonstration of their existence is sufficient for the current report.") But their manuscript goes far beyond simply demonstrating the existence or IREs. Speculations about exotic mechanisms should wait for supporting evidence.

C) The authors simulated several possible mechanisms of IRE generation. They first showed that IRE-like events can be generated by modeling "hot spots" of excitability in the dendrites, or alternatively by simulating spike failures at increasingly distal axonal nodes. Then they dismissed these possibilities by saying "it is difficult to envisage a biological mechanism that either specifically localizes channels in a restricted dendritic 'hot spot' or that simultaneously blocks two, three or more Nodes of Ranvier" (fourth paragraph, subsection “Modelling the Intrinsic Regenerative Events (IREs)”). Perhaps so, although two papers the authors cite show evidence for relatively high densities of sodium channels in dendritic spines (Araya et al., 2007; Bywalez et al., 2015). I find it just as difficult to envisage hot spots of ion channels in biologically unique axonal spines that have not been clearly demonstrated either in the olivary cells under study or, indeed, in any other class of vertebrate neuron.

D) The modeling of spike generation in putative axonal spines (Figure 5) explored a very limited and biologically unjustified parameter space. The authors included high densities of sodium and potassium channels (identical to those in the axon initial segment) in both the spine heads and in the axon hillock, while the excitability of the axonal nodes of Ranvier was actually eliminated (the excitable hillock and the inexcitable axon are mentioned only in the Materials and methods, and not in the main text or legend). The consensus in the field is that channel densities in the axon hillocks of vertebrate neurons are quite low, especially compared to the initial segment. Perhaps mouse olivary cells are not like other neurons, but in the absence of evidence we just don't know. What was the rationale for making the rest of the axon entirely inexcitable while modeling excitable spines? Only a few results of this modeling are illustrated in the manuscript; how robust are these results? What are the consequences of varying channel densities and types, distributions, spatial patterns, spine morphology and number, etc.?

As mentioned above this part has been removed.

2) Network modeling and the absence of noise. The most novel and interesting conclusion from the network modeling is that the IO cells may be organized into electrically coupled clusters of cells (the connection probability predictions largely agree with the widely variable range suggested by previous studies).

Thank you. We certainly agree with this description.

The clustering conclusion rests entirely on fits of the "common spikelet" distributions in recorded cell pairs to predictions of the network model. The authors note that the accuracy of the modeled connection distributions depend strongly on the cells' firing frequencies and the length of the recording samples. Should it not also depend on noise? An important feature of the biological preparation that is absent from the model is any source of noise or variability (apart from the Poisson timing of the somatic currents triggering spikes), especially in the subthreshold membrane voltages.

We study the role of noise in detecting common groups of spikelets by assuming either failure or over detections. This is summarized in the new Figure 7, showing that even if we assume a failure in detecting common group, or inaccuracy in the number of common groups detection, the clustered organization is still the only possible explanation. Furthermore, we examined several distance-dependent connectivity possibilities and none of them produce a distribution of common groups that fits the experimental results. Thus we can strongly conclude that the only explanation for the observed distribution is clustered organization.

The authors' recordings implied that blocking fast glutamate receptors reduced spontaneous spiking rates dramatically, so one can infer that there is normally a considerable of chemical synaptic noise in addition to other potential sources.

As mentioned above, the reduction in spikelets activity is highly correlated with reduction in the fast events which in the IO trigger spiking activity (Figure 3—figure supplement 2). Thus blocking the fast events will lead to a reduction in spiking activity followed by a reduction in spikelets. The synaptic potentials that trigger the fast events cannot be recorded at somatic location. Spontaneous synaptic events are rarely encountered. However, to examine the possible involvement of chemical synapses in the spontaneous activity we analyzed synaptic events that were triggered by ChR activation of excitatory axons projecting to IO neurons in Thy1 mice. Using minimal light duration we were able to activate putatively unitary events. We then compared the waveforms of the synaptic potentials to the waveforms of the slow events. As shown in Figure 3—figure supplement 1, the synaptic potentials’ waveform and amplitude are clearly different from the spontaneous slow event (n=17 cells). Furthermore, we demonstrate (Figure 2) that the spikelets are insensitive to membrane potential. This, which has been examined in large population of neurons, further supports our conclusion that most, if not all, of the slow events are a reflection of electrical coupling. One can argue that the insensitivity to membrane potential might be due to distal location of the synapse, however, the shape of the spikelets does not support such possibility.

3) Pharmacology. The pharmacology (synaptic blocker) data are still confusingly described and not very helpful. From the Results, subsection “Spontaneous unitary events recorded in neurons of the inferior olive”: "However, application of synaptic blockers (see Materials and methods) completely eliminated the presence of the fast events (n=19 neurons; in 4 of these neurons where CNQX was added during recording the frequency changed from 0.017 ± 0.005 Hz to 0 Hz) whereas the frequency of spontaneous slow events decreased significantly (from 0.92 ± 0.73 Hz 163 to 0.26 ± 0.16 Hz, p=0.019, paired t-test, n=9 neurons)." My questions:

A) What were the blockers? This Results sentence says just CNQX, the legend to Figure 2—figure supplement 1 says APV plus either CNQX or DNQX, and the Materials and methods simply list all the drugs.

B) The sample sizes tested are still ambiguous. The phrase about fast events says n=19, but then talks about n=4 "where CNQX was added". Was the drug not added to the other 15 cells? The phrase about slow events then cites n=9. Were the same cells tested before and after addition of blockers? Are the 4 and 9 cells subsets of the 19, or different samples? Please clarify.

C) The authors say they did a "thorough analysis" of the effects of blockers on slow event waveforms, but they actually report data from only two example cells in Figure 2—figure supplement 1. These data showed rise-times and half-durations, but not amplitudes.

We added a new cohort of data and simplified the description of the drug effect. As mentioned above, we show that the drug completely eliminated the fast events accompanied by significant reduction in spikelets activity. This has been added to the text, and to Figure 3—figure supplement 1, and we hope it is now clear.

https://doi.org/10.7554/eLife.43560.sa2

Article and author information

Author details

  1. Yaara Lefler

    1. Department of Neurobiology, Institute of Life Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    2. Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    Present address
    UCL Sainsbury Wellcome Centre for Neural Circuits and Behaviour, London, United Kingdom
    Contribution
    Data curation, Formal analysis, Investigation, Visualization, Methodology
    Contributed equally with
    Oren Amsalem
    For correspondence
    yaara.lefler@mail.huji.ac.il
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-8911-7034

  2. Oren Amsalem

    1. Department of Neurobiology, Institute of Life Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    2. Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    Contribution
    Data curation, Software, Formal analysis, Investigation, Visualization, Methodology
    Contributed equally with
    Yaara Lefler
    For correspondence
    oren.amsalem1@mail.huji.ac.il
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-8070-0378

  3. Nora Vrieler

    1. Department of Neurobiology, Institute of Life Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    2. Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    Contribution
    Data curation
    Competing interests
    No competing interests declared

  4. Idan Segev

    1. Department of Neurobiology, Institute of Life Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    2. Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    Contribution
    Supervision, Funding acquisition
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0001-7279-9630

  5. Yosef Yarom

    1. Department of Neurobiology, Institute of Life Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    2. Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
    Contribution
    Conceptualization, Supervision, Funding acquisition
    Competing interests
    No competing interests declared

Funding

Israel Science Foundation (#1496_2016)

  • Idan Segev
  • Yosef Yarom

Gatsby Charitable Foundation

  • Idan Segev

Human Brain Project (604102)

  • Idan Segev

Edmund and Lily Safra Center for Brain Sciences

  • Yaara Lefler

Einstein Foundation Berlin

  • Yosef Yarom

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This study was supported by the Israel Science Foundation (http://www.isf.org.il/) grant #1496_2016 and by the Einstein Foundation Berlin. IS and OA were supported by grant agreement no. 604102 ‘Human Brain Project’, a collaborative grant under the Blue Brain Project and a grant from the Gatsby Charitable Foundation. YL was supported by a postdoctoral fellowship from the Edmund and Lily Safra Center for Brain Sciences (ELSC). We wish to thank Prof. Israel Nelken for statistical advice.

Ethics

Animal experimentation: All experimental procedures were approved by the Hebrew University's Animal Care and Use Committee. The Hebrew University is an Association for Assessment and Accreditation of Laboratory Animal Care (AAALAC)-accredited institution #12005.

Senior and Reviewing Editor

  1. Ronald L Calabrese, Emory University, United States

Reviewers

  1. Alberto E Pereda, Albert Einstein College of Medicine, United States
  2. Chris I De Zeeuw, Erasmus Medical Center, Netherlands

Publication history

  1. Received: November 11, 2018
  2. Accepted: January 13, 2020
  3. Version of Record published: February 11, 2020 (version 1)

Copyright

© 2020, Lefler et al.

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 1,064
    Page views
  • 131
    Downloads
  • 7
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Yaara Lefler
  2. Oren Amsalem
  3. Nora Vrieler
  4. Idan Segev
  5. Yosef Yarom
(2020)
Using subthreshold events to characterize the functional architecture of the electrically coupled inferior olive network
eLife 9:e43560.
https://doi.org/10.7554/eLife.43560

Categories and tags

Research organism

Further reading

    1. Computational and Systems Biology
    2. Neuroscience

    Multilayer brain networks can identify the epileptogenic zone and seizure dynamics

    Hossein Shahabi, Dileep R Nair, Richard M Leahy
    Research Article Updated

    Seizure generation, propagation, and termination occur through spatiotemporal brain networks. In this paper, we demonstrate the significance of large-scale brain interactions in high-frequency (80–200Hz) for the identification of the epileptogenic zone (EZ) and seizure evolution. To incorporate the continuity of neural dynamics, here we have modeled brain connectivity constructed from stereoelectroencephalography (SEEG) data during seizures using multilayer networks. After introducing a new measure of brain connectivity for temporal networks, named multilayer eigenvector centrality (mlEVC), we applied a consensus hierarchical clustering on the developed model to identify the EZ as a cluster of nodes with distinctive brain connectivity in the ictal period. Our algorithm could successfully predict electrodes inside the resected volume as EZ for 88% of participants, who all were seizure-free for at least 12 months after surgery. Our findings illustrated significant and unique desynchronization between EZ and the rest of the brain in the early to mid-seizure. We showed that aging and the duration of epilepsy intensify this desynchronization, which can be the outcome of abnormal neuroplasticity. Additionally, we illustrated that seizures evolve with various network topologies, confirming the existence of different epileptogenic networks in each patient. Our findings suggest not only the importance of early intervention in epilepsy but possible factors that correlate with disease severity. Moreover, by analyzing the propagation patterns of different seizures, we demonstrate the necessity of collecting sufficient data for identifying epileptogenic networks.

    1. Neuroscience

    Model-based whole-brain perturbational landscape of neurodegenerative diseases

    Yonatan Sanz Perl, Sol Fittipaldi ... Enzo Tagliazucchi
    Research Article

    The treatment of neurodegenerative diseases is hindered by lack of interventions capable of steering multimodal whole-brain dynamics towards patterns indicative of preserved brain health. To address this problem, we combined deep learning with a model capable of reproducing whole-brain functional connectivity in patients diagnosed with Alzheimer’s disease (AD) and behavioral variant frontotemporal dementia (bvFTD). These models included disease-specific atrophy maps as priors to modulate local parameters, revealing increased stability of hippocampal and insular dynamics as signatures of brain atrophy in AD and bvFTD, respectively. Using variational autoencoders, we visualized different pathologies and their severity as the evolution of trajectories in a low-dimensional latent space. Finally, we perturbed the model to reveal key AD- and bvFTD-specific regions to induce transitions from pathological to healthy brain states. Overall, we obtained novel insights on disease progression and control by means of external stimulation, while identifying dynamical mechanisms that underlie functional alterations in neurodegeneration.

    1. Neuroscience

    Distinct roles of forward and backward alpha-band waves in spatial visual attention

    Andrea Alamia, Lucie Terral ... Rufin VanRullen
    Research Article Updated

    Previous research has associated alpha-band [8–12 Hz] oscillations with inhibitory functions: for instance, several studies showed that visual attention increases alpha-band power in the hemisphere ipsilateral to the attended location. However, other studies demonstrated that alpha oscillations positively correlate with visual perception, hinting at different processes underlying their dynamics. Here, using an approach based on traveling waves, we demonstrate that there are two functionally distinct alpha-band oscillations propagating in different directions. We analyzed EEG recordings from three datasets of human participants performing a covert visual attention task (one new dataset with N = 16, two previously published datasets with N = 16 and N = 31). Participants were instructed to detect a brief target by covertly attending to the screen’s left or right side. Our analysis reveals two distinct processes: allocating attention to one hemifield increases top-down alpha-band waves propagating from frontal to occipital regions ipsilateral to the attended location, both with and without visual stimulation. These top-down oscillatory waves correlate positively with alpha-band power in frontal and occipital regions. Yet, different alpha-band waves propagate from occipital to frontal regions and contralateral to the attended location. Crucially, these forward waves were present only during visual stimulation, suggesting a separate mechanism related to visual processing. Together, these results reveal two distinct processes reflected by different propagation directions, demonstrating the importance of considering oscillations as traveling waves when characterizing their functional role.