Structural state recognition facilitates tip tracking of EB1 at growing microtubule ends
- University of Minnesota, United States
- Vanderbilt University, United States
Abstract
The microtubule binding protein EB1 specifically targets the growing ends of microtubules in cells, where EB1 facilitates the interactions of cellular proteins with microtubule plus-ends. Microtubule end targeting of EB1 has been attributed to high-affinity binding of EB1 to GTP-tubulin that is present at growing microtubule ends. However, our 3D single-molecule diffusion simulations predicted a ~ 6000% increase in EB1 arrivals to open, tapered microtubule tip structures relative to closed lattice conformations. Using quantitative fluorescence, single-molecule, and electron microscopy experiments, we found that the binding of EB1 onto opened, structurally disrupted microtubules was dramatically increased relative to closed, intact microtubules, regardless of hydrolysis state. Correspondingly, in cells, the blunting of growing microtubule plus-ends by Vinblastine was correlated with reduced EB1 targeting. Together, our results suggest that microtubule structural recognition, based on a fundamental diffusion-limited binding model, facilitates the tip tracking of EB1 at growing microtubule ends.
https://doi.org/10.7554/eLife.48117.001Introduction
Microtubules are long, thin polymers that mechanically contribute to cell morphology, act as a track for molecular motor-based transport within the cell, and serve as a platform for binding of microtubule-associated proteins (Howard and Hyman, 2003; Mitchison and Kirschner, 1984; Ross et al., 2008). Microtubules are composed of αβ tubulin heterodimers stacked end-to-end into ‘protofilaments’. Typically, a microtubule is composed of 13 laterally associated protofilaments (Tilney et al., 1973). Each tubulin heterodimer contains an exchangeable nucleotide site on the β-tubulin subunit, and individual tubulin heterodimers polymerize onto the plus-end of the microtubule with the β-tubulin subunit bound to a GTP nucleotide. After integration into the microtubule, the β-tubulin-bound nucleotide then stochastically undergoes hydrolysis and converts via GDP-Pi to GDP. GDP-bound tubulin is less stable in the microtubule lattice than GTP-bound tubulin, but the microtubule remains intact and continues to grow at its plus-end due to the continued addition of GTP-bound tubulin, which forms a ‘GTP cap’ at the growing plus-end of the microtubule (Desai and Mitchison, 1997; Mitchison and Kirschner, 1984).
Recent literature suggests that microtubule structure may be more complex than previously considered, especially at the microtubule plus-end. A perfectly intact, closed microtubule lattice with ‘blunt’ ends is defined by a regular arrangement of tubulin dimers into a thirteen protofilament tube, with all equal-length protofilaments terminating at the microtubule ends. In contrast, microtubule plus-ends have been observed by cryo-electron microscopy to have open, sheet-like or tapered conformations, which diverge greatly from a closed tube conformation (Chrétien et al., 1995; Guesdon et al., 2016; Manka and Moores, 2018a). These findings have also been supported by quantitative analysis of fluorescence images (Coombes et al., 2013). This type of tapered, gently curved tip structure likely plays a role in the binding of Doublecortin and other proteins to microtubule plus-ends (Bechstedt and Brouhard, 2012; Bechstedt et al., 2014); reviewed in Brouhard and Rice (2014). Further, it has recently been reported that lattice damage and tubulin turnover can occur on the microtubule lattice itself, leading to irregularities along the length of a dynamic microtubule (Schaedel et al., 2015).
The microtubule tip tracking protein EB1 is a highly conserved protein that autonomously tracks the growing plus-ends of microtubules (Bieling et al., 2007; Dixit et al., 2009; Morrison et al., 1998). At the plus-end, EB1 recruits many other +TIP family proteins that have little to no native affinity for microtubules but that must localize to microtubule plus ends to perform their functions (Bieling et al., 2007; Dixit et al., 2009; Lansbergen and Akhmanova, 2006). High-affinity binding of EB1 to the GTP-cap at growing microtubule plus-ends may contribute to its plus-end localization (Maurer et al., 2011; Zanic et al., 2009). The increased affinity of EB1 for GTP tubulin relative to GDP tubulin has been demonstrated through the use of GTP analogs, most commonly GMPCPP and GTP-γ-S. In both cases, there was an increase in overall EB1 binding to the GTP-analog-bound microtubules as compared to GDP-microtubules (Maurer et al., 2011; Zanic et al., 2009). However, the mechanism for how EB1 rapidly and efficiently targets to growing microtubule plus-ends, thus allowing for robust tip tracking, remains unknown.
In this work, we perfomed 3D single-molecule diffusion simulations, which predicted a ~ 6000% increase in EB1 arrivals to open, tapered microtubule tip structures relative to closed lattice conformations. Using quantitative fluorescence, single-molecule, and electron microcopy experiments, we found that the binding of EB1 onto opened, structurally disrupted microtubules was dramatically increased relative to closed, intact microtubules, regardless of hydrolysis state. Further, we converted growing microtubule ends in LLC-Pk1 cells from a tapered to a blunt configuration, and observed a dose-dependent reduction in EB1 targeting. Together, our results suggest that microtubule structural recognition, based on a simple diffusion-limited binding model, facilitates EB1 tip tracking at growing microtubule plus-ends.
Results
At intermediate salt concentrations, EB1 preferentially binds to GMPCPP microtubule end structures
Previous in vitro studies have shown that while EB1 uniformly coats GTP-analog (GMPCPP) microtubules in the absence of added salt, the addition of KCl increasingly drives EB1 off of the GMPCPP lattice (Dixit et al., 2009; Maurer et al., 2011; Zanic et al., 2009). Thus, we used an intermediate KCl concentration to explore the localization of EB1-GFP on reconstituted microtubules under relatively weak EB1 binding conditions (Figure 1A, 30 mM KCl). We reasoned that under these conditions, any localized binding of EB1-GFP to GMPCPP microtubules could reveal an additional layer of regulation for EB1 binding, beyond exclusively tubulin subunit nucleotide state. Interestingly, we observed that, at 30 mM KCl, EB1 was often localized to GMPCPP microtubule ends (Figure 1B, green).
Figure 1 with 1 supplement see all
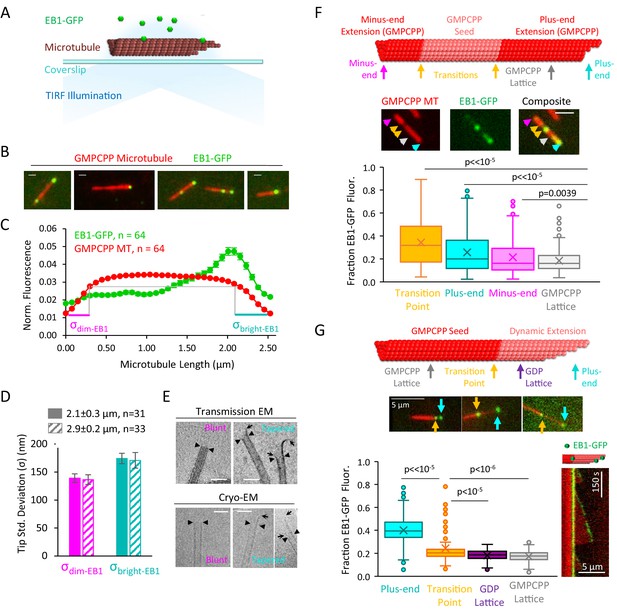
EB1-GFP recognizes structural disruptions and tapered ends on GMPCPP microtubules.
(A) Schematic of EB1-GFP TIRF experiment. (B) Representative images of EB1-GFP (green) on rhodamine-labeled GMPCPP microtubules (red), showing preferential end localization. Scale bars: 0.4 μm. (C) Super-averaged intensity profile of 64 microtubules of length 2.5 ± 0.48 μm (mean ± SD) with EB1-GFP. Individual microtubules within the averaged line scan were aligned with brighter EB1-GFP fluorescence on the right. Error bars show standard error at each point. (D) Bar graph with fitted tip standard deviations for microtubules of length 2.1 ± 0.3 μm (solid bars) and 2.9 ± 0.2 μm (hashed bars) (curve fits shown in Figure 1—figure supplement 1A). Low tip standard deviation corresponds to blunt microtubule ends (left), high tip standard deviation correspond to ends with more variable protofilament lengths (right). Error bars: SE calculated from 95% confidence intervals. (E) Electron microscopy images of blunt and tapered GMPCPP microtubules ends. Closed triangles indicate the most distal portion of the microtubule with a complete tubular lattice. Open arrows indicate the extrema of protruding protofilaments. Scale bars: 50 nm. (F) Top: Schematic of polarity-marked GMPCPP microtubule layout and reference positions for analysis. Center: Representative TIRF images of EB1-GFP on GMPCPP microtubules, colored arrows indicate the corresponding points used for analysis. Scale bars: 3 μm. Bottom: Box and whisker plot of the fraction of total EB1 fluorescence located at each position. The two transition points were averaged to provide a single value. Plus-ends, minus-ends, and transition points all showed significant differences as compared to lattice binding region (n = 309 microtubules). (G) Top: Schematic of bright GMPCPP seed with dim dynamic microtubule extension, with reference positions for analysis. Center: Representative TIRF images of EB1-GFP on GMPCPP microtubules, colored arrows indicate the corresponding points used for analysis. Scale bars: 5 μm. Bottom-left: Box and whisker plot of the fraction of total EB1 fluorescence located at each position. Plus-ends and transition points both showed significant differences as compared to lattice binding region (n = 134 microtubules). Bottom-right: Representative kymograph of EB1-GFP at transition point and plus-end during dynamic microtubule growth.
To detect whether there could be an underlying structure of the GMPCPP microtubule ends that would predispose them to EB1-GFP binding, we collected intensity line-scans of green EB1-GFP and red (rhodamine) GMPCPP microtubule fluorescence along the microtubules’ lengths to create average intensity profiles over all microtubules. The line-scans for 64 microtubules of similar length were rebinned to the mean microtubule length (see Gardner et al., 2008) and Materials and methods), and the ensemble average across all 64 microtubules was plotted for both the red and green channels (Figure 1C). Prior to averaging, the line-scans in both the red and green channels for each microtubule were oriented such that the microtubule end with the brighter intensity of green EB1-GFP fluorescence was on the right side, with the dimmer EB1-GFP intensity on the left side (Figure 1C, green, ensemble average over n = 64 microtubules) (Coombes et al., 2016).
Similar to our qualitative observations, an increase in EB1-GFP intensity was observed at the brighter EB1-GFP microtubule end as compared to the center region and the dimmer EB1-GFP end of the microtubule (Figure 1C). Strikingly, we noted that by aligning the brighter EB1-GFP intensity on the right side of the line scan, this resulted in a qualitative difference in the underlying microtubule intensity profile at the microtubule ends (Figure 1C, red, ensemble average over n = 64 microtubules). Here, the red microtubule fluorescence on the right (brighter EB1-GFP) side of the line-scan plot appeared to drop off more slowly to background as compared to the left side of the line-scan plot (Figure 1C, compare teal vs magenta line lengths).
To quantify this observation, we fit a Gaussian error-function to the red fluorescence intensity drop-off at each microtubule end, as previously described (Coombes et al., 2013; Demchouk et al., 2011). This fitting process allowed us to estimate a ‘tip standard deviation’, which is a measure of tip tapering that arises as a result of protofilament length variability at the microtubule ends. To ensure that the tip fitting was not biased by rebinning a large range of microtubule lengths into one standard length, we subsampled two groups of microtubules (length standard deviation ≤0.3 μm in each case). Importantly, regardless of microtubule length, we found that the microtubule end with a brighter EB1-GFP signal had a larger average tip standard deviation, and thus more tip tapering due to protofilament length variation, than the opposite, dimmer EB1-GFP signal end, of the microtubule (Figure 1D; 2.1 ± 0.3 μm group (mean ± SD): p=0.00017, Z-statistic = 3.79; 2.9 ± 0.2 μm group (mean ± SD): p=0.013, Z-statistic = 2.47; Fit curves in Figure 1—figure supplement 1A,B). We then used both Transmission Electron Microscopy (TEM) and Cryo-Electron Microscopy to verify that tapered and blunt ends were indeed present in the GMPCPP microtubule population (Figure 1E), similar to previous observations (Atherton et al., 2018).
We then asked whether the inclusion of specific structural disruption points on the GMPCPP microtubules would alter EB1-GFP localization. Thus, polarity-labeled GMPCPP microtubule seeds were generated by growing bright-red GMPCPP extensions from dim-red GMPCPP seeds (Figure 1F, top). These two-color microtubules allowed for identification of the microtubule plus-end as the end with the longer bright-red extension (Figure 1F, top, teal). However, importantly, the polarity-labeled seeds also generated transition points between the original GMPCPP seeds and the GMPCPP extensions, which likely caused lattice discontinuities, defects, and holes at each transition point (Figure 1F, top, yellow). Thus, we analyzed the brightness of EB1-GFP at five positions along the GMPCPP microtubules (Figure 1F, top): the minus end tip (magenta), the two transition points (yellow), the plus-end tip (cyan), and the GMPCPP lattice (gray; for consistency and to minimize overlap with other positions, the lattice position used was always halfway between the plus-end and the nearest transition point). At each of the five positions, we summed the total green EB1-GFP intensity over a 9-pixel box, centered at the defined position, and then reported the fraction of EB1-GFP intensity at each position (=box intensity/summed intensity over all five boxes). For the transition point intensity, we reported an average of the two transition point box intensities for each microtubule. We found that the average transition point (p<<10−5, t-test), plus-end (p<10−8, t-test), and minus end (p=0.0039, t-test) of the GMPCPP microtubules all showed a significantly higher fraction of EB1-GFP fluorescence than the GMPCPP lattice position (Figure 1G; n = 309 microtubules).
Finally, to determine whether specific structural disruption points on the microtubule lattice could lead to EB1 binding even in the presence of dynamic microtubules, dim-red dynamic (GTP) microtubules were grown from bright-red GMPCPP seeds (Figure 1G top) in the presence of 100 nM EB1-GFP and 55 mM KCl (Gell et al., 2010). We collected independent, individual microtubule images (Figure 1G middle), and analyzed the brightness of EB1-GFP within a 9-pixel box at four positions along the microtubules (Figure 1G, top and middle): the growing GTP-tubulin plus-end tip (cyan), the GDP lattice (purple), the transition point between the GMPCPP seed and the dynamic GDP microtubule extension (yellow), and the GMPCPP lattice (gray; note that for consistency and to minimize overlap with other positions, the GMPCPP and GDP lattice positions used were always halfway between the microtubule end and the nearest transition point). We found that, as would be expected, EB1-GFP intensity was ~2.3 fold (230%) higher at growing microtubule plus-ends as compared to the overall average intensity on the GDP lattice and GMPCPP seeds (Figure 1G bottom-left, cyan). However, consistent with our GMPCPP microtubule results, the EB1-GFP fluorescence at the GMPCPP/GDP transition point was 38% higher than the average intensity on the GDP lattice and GMPCPP seeds (Figure 1G bottom-left; p<10−5 vs GDP lattice, p<10−6 vs GMPCPP seeds, n = 134 microtubules). Further, in kymographs of dynamic microtubules, targeting of EB1-GFP to the GMPCPP/GDP transition occasionally persisted throughout entire microtubule growth and shortening events (Figure 1G bottom-right).
EB1 preferentially binds to disrupted-structure microtubules on GMPCPP, GTPγS, and GDP microtubule populations
Taken together, our GMPCPP and dynamic microtubule results suggested that EB1 may preferentially bind to regions of microtubules that have extended, tapered tip structures, or a discontinuous tubular lattice. To test this idea using microtubule populations with various tubulin-bound nucleotides, we used a previously published method to create pools of microtubules with common nucleotide states, but with varying degrees of lattice structural integrity (Reid et al., 2017). These protocols allowed for generation of ‘closed’ microtubules with relatively intact, closed lattice structures (Figure 2A, left), and ‘disrupted-structure’ microtubules with lattice structures that had increased frequencies of defects, gaps in the lattice, and open sheet conformations (Figure 2A, right, red subunits at structural disruptions). These ‘closed’ and ‘disrupted-structure’ populations were described for the three most commonly used in vitro microtubule nucleotides (GDP, GMPPCP, and GTPγS (Figure 2B)) (Reid et al., 2017), and so we used these populations as a tool to reveal potential differences in EB1 binding based on microtubule structure. Here, closed and disrupted-structure populations were made for GDP and GTPγS populations via taxol treatments, which created breaks, holes, and tapering in the microtubules, followed by differing storage conditions to alter the degree of overnight repair (Figure 2B) (see (Reid et al., 2017) and Materials and methods). In contrast, disrupted-structure GMPCPP microtubule populations were generated via Ca2+ treatment (Figure 2B, center) (see (Reid et al., 2017) and Materials and methods). Careful quantification that demonstrated a statistically significant structural disruption in the ‘disrupted-structure’ populations as compared to the respective closed microtubule population in each case was previously performed using both fluorescent tubulin repair assays, and electron microscopy (Reid et al., 2017). We note that while the preparation protocols for microtubules using the three different nucleotides were distinct, each of these protocols reflected commonly used methods for producing stabilized in vitro microtubules, and so no extreme or unusual conditions or preparation techniques were employed in preparing the microtubules.
Figure 2
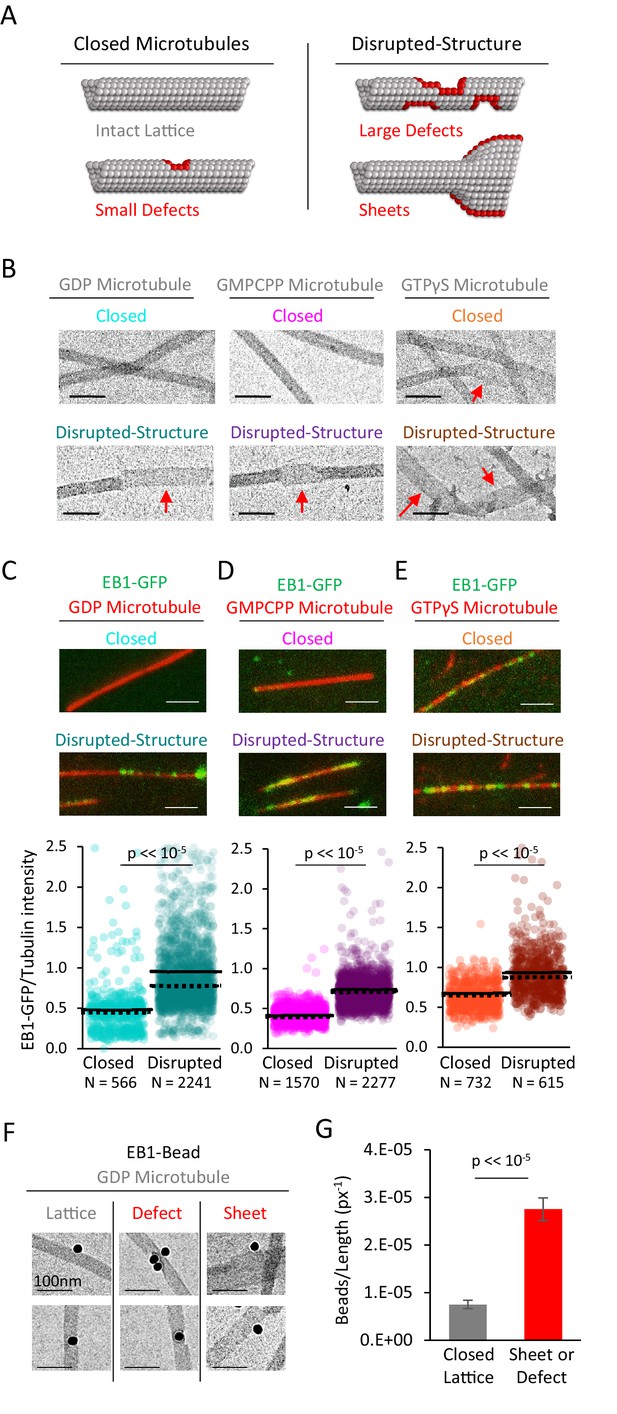
EB1-GFP shows preferential binding to disrupted-structure microtubules, regardless of nucleotide state.
(A) Illustration of the two categories of microtubules used in this analysis. Left: ‘Closed’ microtubules with predominantly intact, closed lattice structures. Right: ‘Disrupted-structure’ microtubules have larger and more frequent gaps, defects, and sheet-like regions. Stylized red tubulin used to highlight defects. (B) Electron microscopy images of closed and disrupted-structure microtubules for GDP microtubules (left), GMPCPP microtubules (center), and GTPγS microtubules (right). Red arrows indicate structural disruptions, scale bars 50 nm. (C–E) Top: EB1-GFP (green) on microtubules (red) for closed and disrupted-structure conditions (scale bars 2 μm). Bottom: Cloud plots of EB1-GFP/Tubulin intensity ratio for individual microtubules. Each semi-transparent circle is the data point from a single microtubule. Solid lines are the average EB1-GFP/Tubulin binding ratio for each population, dotted lines are the median EB1-GFP/Tubulin binding ratio for each population. (F) Electron microscopy of EB1 conjugated to gold beads on GDP microtubules. Example images of EB1-beads bound on the microtubule lattice (left), at a lattice defect (center), and on a sheet (right). (G) Frequency of EB1-beads bound to the microtubule lattice compared to EB1-beads bound at either a defect or on a sheet, normalized to observed microtubule length in each category. Non-normalized values yield a ~ 1.7 fold increase in binding to defects and edges relative to a closed lattice (n = 74 on lattice, n = 128 on defect or sheet). Error bars SEM.
Thus, closed and disrupted-structure microtubule populations were generated for each nucleotide type, and were separately introduced into imaging chambers. Time was allowed for the microtubules to adhere to the coverslip surface, and then a solution of EB1-GFP and imaging buffer was introduced into the chambers (see Materials and methods). After allowing time for EB1-GFP binding to reach steady-state (20–30 min), the microtubules with bound EB1-GFP were imaged using TIRF microscopy. We then reported the average EB1-GFP fluorescence intensity over green background for each microtubule, which was then normalized to the average Rhodamine-tubulin fluorescence intensity over red background for each microtubule, resulting in an ‘EB1-GFP/tubulin intensity ratio’ that was reported for each individual microtubule in the analysis (see Materials and methods).
For the taxol-stabilized GDP microtubules, we observed a marked increase in the EB1-GFP/tubulin intensity ratio for the disrupted-structure pool of microtubules as compared to the closed microtubules (Figure 2C, top). Upon quantification, the average EB1-GFP/tubulin intensity ratio in the disrupted-structure microtubule pool was ~98% higher than the average EB1-GFP/tubulin intensity ratio in the closed microtubule pool (Figure 2C, bottom; p<<10−5, t-test). GMPCPP microtubules from the disrupted-structure pool also showed an increase in the average EB1-GFP/tubulin intensity ratio (Figure 2D, top), which was ~75% higher than the average EB1-GFP/tubulin intensity ratio in the closed microtubules (Figure 2D, bottom; p<<10−5, t-test). Finally, the average EB1-GFP/tubulin intensity ratio was higher on disrupted-structure GTPγS microtubules as compared to closed GTPγS microtubules, with a quantitative increase of ~50% (Figure 2E; p<<10−5, t-test).
EB1 preferentially binds to disrupted-structure microtubules in electron microscopy experiments
To directly test whether EB1 preferentially binds to disrupted microtubule lattice structures on individual GDP microtubules, we used EB1 conjugated to gold beads, and examined the binding of these beads onto pre-stabilized microtubules using electron microscopy (Figure 2F). For each microtubule-bound bead, the microtubule-binding region was classified either as a complete lattice, or as a defect/sheet, and, further, the total available microtubule length for each classification was determined. Overall, we observed more EB1-gold beads that were bound to defects or sheets than to complete lattice regions (n = 74 on lattice, n = 128 on defect or sheet), regardless of total available length for each microtubule classification. However, when we normalized the frequency of bead location to the total available microtubule length for each classification, we found that the EB1-gold beads were nearly four-fold more likely to bind at defects or sheets than to a complete microtubule lattice (Figure 2G; p<2.3×10−54, Chi-squared test).
Single-molecule diffusion simulations predict a dramatic increase in EB1 on-rate to tapered microtubule structures
Taken together, our experimental results suggested that EB1 preferentially binds to regions of microtubules that have extended, tapered tip structures, or to a discontinuous tubular lattice. However, the mechanism for this preference remained unclear. Therefore, we developed a single-molecule diffusion-based computational simulation to explore a mechanistic explanation for our results.
For simplicity, we included three fundamental rules in the simulation: (1) EB1 molecules diffused in three dimensions with translational and rotational diffusion coefficients that depended on EB1 protein size (Figures 3A, 1; see Materials and methods) (Castle and Odde, 2013; Mirtich, 1998); (2) EB1 molecules could not pass through a microtubule, but rather would collide and then diffuse in another direction (Figures 3A,2); and (3) the conformation of EB1, and its binding pocket within the microtubule lattice, were representative of their published molecular structures (Figure 3A,3). To develop an approximation for the EB1 binding pocket within the microtubule, we used previously published Cryo-EM structural data as our guide (Figure 3B, left; source data from Zhang et al., 2015), and from this data, we created an approximation of the tubulin heterodimer shape (Figure 3B, center), with careful consideration for EB1’s binding pocket, located between four tubulin dimers. EB1’s microtubule binding domain shape was similarly modeled from previously published Cryo-EM structures (Zhang et al., 2015), and the modeled shape was then verified to fit into our modeled 4-tubulin binding pocket in the correct orientation (3B, right). We note that each EB1 molecule could bind only one unique tubulin interface, and in only one unique orientation.
Figure 3 with 1 supplement see all
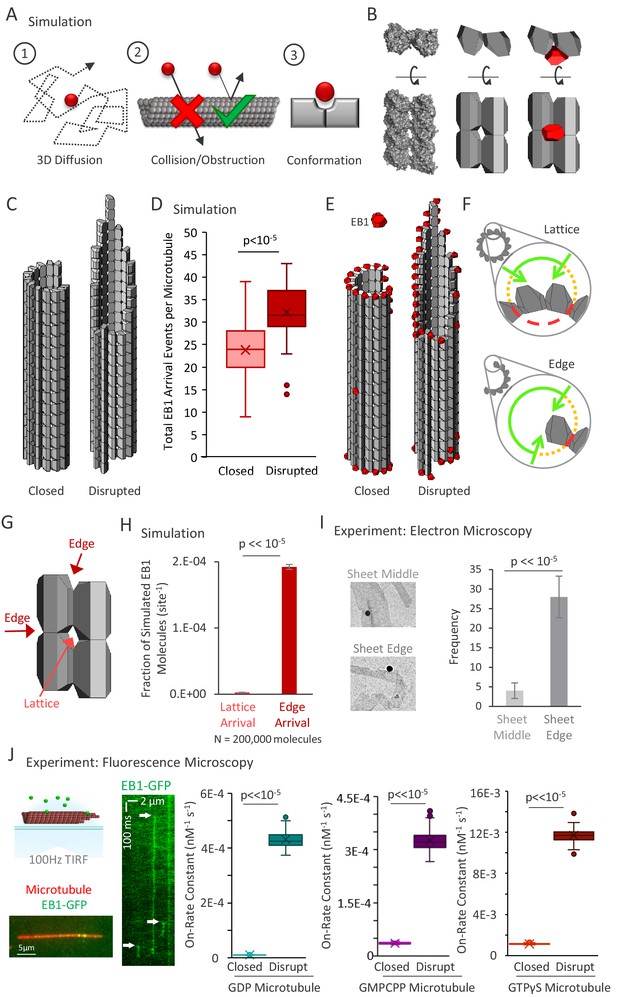
3D diffusion-based simulations of EB1 predict an increased arrival rate at protofilament edge sites relative to closed, full lattice sites.
(A) Simulation rules and parameters: (1) EB1 diffuses in three dimensions, (2) EB1 is obstructed by tubulin dimers and cannot pass through microtubules, (3) EB1 and tubulin dimer three-dimensional shapes reproduce EB1-tubulin binding interface. (B) Development of simulation shapes for EB1 and tubulin: Left: Cryo-EM reconstruction data (from PDB ID 3JAR) of tubulin dimers in a lattice: Left-top: Top-down view, with the lower portion being the outside of the microtubule. Left-bottom; Side view of four tubulin dimers, viewing the portion on the outside surface of the microtubule; Middle: Approximation of tubulin dimers for use in the simulation, derived from the cryo structure; Right: EB1 (red) also modeled as an approximation of cryo-structure data (not shown), with the binding interface correctly positioned at the pocket located between four adjacent tubulin dimers. (C) Two microtubule conditions used in the simulation analysis. Left: A closed, blunt-ended microtubule. Right: A ‘disrupted-structure’ microtubule with a tapered tip. Both the ‘closed’ and ‘disrupted structure’ configurations contain the same total number of tubulin dimers. (D) Results of 50 simulations of 4000 EB1 molecules each for each microtubule condition. Each data point in the box and whisker plot represents the total number of EB1 arrival events per microtubule for 4000 different simulated EB1 molecules. (E) Visualization of EB1 arrival events (red) on closed and ‘disrupted-structure’ microtubules from N = 10,000 simulated EB1 in each condition. (F) Illustration of the hypothesis that EB1’s pocket-located binding site leads to a high local steric hindrance for EB1 binding to a lattice conformation (top), and a lower steric hindrance for EB1 binding to an edge conformation (bottom). Green lines: portion of the local volume with high accessibility to binding site. Yellow dotted lines: reduced accessibility volume. Red dashed lines: volume with no direct accessibility. In an edge conformation (bottom), the high accessibility region (green) is much larger than in the lattice conformation (top). (G) Dark Red arrows: Binding sites with two adjacent tubulin dimers, such as at the ends of protofilaments, or at exposed edges of protofilaments with no neighbor, are termed ‘Edge’ sites. Light red arrow: Sites with four adjacent tubulin dimers are termed ‘Lattice’ sites. Sites with only one tubulin dimer and with three adjacent tubulin dimers were not included in this analysis. (H) Fraction of simulated EB1 molecules that arrived at lattice sites (light red) or at edge sites (dark red). Data used was from the closed microtubule arrangement (panel C,E, left)). Values were determined by dividing the total number of EB1 bound at any lattice or edge site by the total number of available lattice or edge sites, respectively. EB1 was ~70 fold more likely to bind a given edge site as compared to a given lattice site. (I) Left: example electron microscopy images of EB1 conjugated to gold beads on GDP microtubules. This image shows EB1-gold bound at a sheet edge, and one bound at a sheet middle (beads at ambiguous locations were conservatively classified as ‘middle’). Right: Count of total number of sheet bound beads observed over all images, divided into ‘Middle’ of sheet and ‘Edge’ of sheet. (J) Far Left Top; Experimental setup, rhodamine-labeled microtubules are affixed to a coverslip (red), EB1-GFP is introduced in solution (green), and the sample imaged at 100 frames per second using total internal reflection fluorescence (TIRF) microscopy. Far Left Bottom; Sample image of EB1-GFP on the microtubule. Left: Kymograph of EB1-GFP with length along the x-axis and time down the y-axis. White arrows indicate EB1-GFP binding events, which appear as vertical streaks. Example shows atypically long EB1 association events, for clarity. The lower limit of the vertical streaks are the dissociation event of EB1-GFP from the microtubule. Right: EB1-GFP on-rate constant for closed and disrupted-structure microtubules in each nucleotide population.
To run the simulation, a microtubule was fixed in space, and then individual EB1 molecules were allowed to diffuse, starting from random positions far away from the microtubule (see Materials and methods). Two arrangements of microtubules, each with 207 tubulin dimers (average protofilament length ~16 dimers), were simulated to mimic ‘closed’ and ‘disrupted-structure’ pools of microtubules. For the closed microtubules, a microtubule with a blunt end was defined (Figure 3C, left), and for the ‘disrupted-structure’ model, a microtubule with a tapered end was defined (Figure 3C, right). Starting from a random position away from the microtubule (see Materials and methods), each EB1 molecule was then allowed to randomly diffuse either until it exceeded 2 μm away from the microtubule, or until the center of its binding interface was oriented properly and within 1 nm of each of its corresponding binding interface centers at any microtubule binding location (defined as an ‘arrival event’). Once either of these conditions was achieved for a particular EB1 molecule, the simulation for that molecule was ended, and, for EB1 molecules with arrival events, their arrival position on the microtubule was recorded. We note that off-rates (or dwell times) were not determined as part of this simulation, as a binding event concluded the simulation for an individual microtubule.
First, we ran simulations to evaluate the arrival events of EB1 molecules onto the two microtubule configurations, regardless of EB1-tubulin binding configuration (e.g. 1–4 tubulin binding interfaces were allowed per EB1 molecule). We ran 50 simulations of 4000 EB1 molecules in each simulation for both the closed and the disrupted-structure microtubules, and calculated the total number of EB1 arrival events per microtubule in each simulation. We found that the mean number of successful arrival events of EB1 onto individual ‘disrupted-structure’ microtubules was ~33% higher than onto closed ‘blunt’ microtubules with the same number of tubulin subunits (Figure 3D; p<<10−5, Binomial test). Strikingly, by examining the simulated arrival locations of individual EB1 molecules, we found that the EB1 molecules had arrived at nearly all of the sites at the microtubule end or along laterally exposed protofilaments, while very few arrived within a complete, closed lattice, both for the closed and the ‘disrupted-structure’ microtubules (Figure 3E, random representative subset of 10,000 simulated EB1 molecules).
Based on this observation, we hypothesized that the unique location of EB1’s binding site in the ‘pocket’ between four tubulin dimers was responsible for the simulated ‘structural recognition’ of EB1 (Figure 3F, cutaway view – tubulin subunits above and below the section are not shown). Specifically, when a full lattice is present, the nature of the binding pocket between four tubulin dimers would restrict access of EB1 to its binding site, due to the high diffusional steric hindrance barrier generated by the nearby tubulin subunits, and the specific orientation that is required for EB1 to fit into this pocket and simultaneously bind at four locations (Figure 3F, top, short green arc shows restricted access). However, when there is a region of the microtubule with exposed protofilament edges, the steric hindrance barrier would be dramatically reduced, thus allowing for increased accessibility and ease of EB1 binding to the laterally exposed edges (Figure 3F, bottom, longer green arc shows increased access). This effect is likely even more dramatic than Figure 3F would suggest, since if this schematic were extrapolated to three dimensions, only a small wedge of a sphere would have high accessibility to an EB1 binding site for a closed lattice configuration. Importantly, a natural result of this model is that the on-rate of EB1 would be much higher at laterally (or longitudinally) exposed microtubule binding sites as compared to the binding pocket within a closed microtubule lattice.
To directly test the idea that the arrival rate of EB1 would be increased at laterally or longitudinally exposed microtubule binding sites, we ran simulations to compare the fraction of simulated EB1 arrival events onto closed-lattice microtubule-binding sites with four adjacent tubulin dimers (Figure 3G, light red arrow), to edge-located microtubule-binding sites, with only two adjacent tubulin dimers either horizontally or vertically (Figure 3G, dark red arrows). Thus, we specifically compared simulated EB1 arrivals to 2-tubulin vs 4-tubulin sites, excluding both1-tubulin sites that could potentially have a very high off-rate, and 3-tubulin sites. This allowed us to limit our analysis to the partial binding EB1 sites that have been previously observed using electron microscopy (Guesdon et al., 2016), and that we observed using electron microscopy in our new work (Figure 2F).
Strikingly, in this simulation, the fraction of EB1 arrivals was ~70 fold higher for 2-tubulin sites with lower steric hindrance, such as those at protofilament edges (Figure 3H, dark red), as compared to 4-tubulin sites on the closed microtubule lattice (Figure 3H, light red; p<<10−5, Chi-squared test). In order to compare these simulated arrival rates with the theoretical upper limit for our simulation, we modeled EB1 binding to a single, isolated tubulin heterodimer. In this instance, there would be no significant steric hindrance to binding, although arrival to the 1-tubulin site was still stereospecific, such that EB1 could not bind ‘upside down’. We found that the fraction of EB1 arrivals to these 1-tubulin sites was 309-fold higher than the fraction of arrivals to full lattice 4-tubulin sites, and 4.6-fold higher than the fraction of arrivals to 2-tubulin edge binding sites. This difference clearly demonstrates the large impact of steric hindrance for the pocket-located binding site of EB1 in the simulation, especially when fully enclosed within the lattice.
Electron microscopy experiments demonstrate binding of EB1-gold beads to microtubule sheet edges
To test this model experimentally, we further analyzed the binding of EB1-beads onto stabilized microtubule sheets from our electron microscopy experiments (Figure 3I, left). Qualitatively, we observed EB1-beads that bound to the stabilized microtubule sheets, both in the middle of the sheet, and on the edges of sheets (Figure 3I, left), as has been previously observed on the more transient microtubule sheets that are present at dynamic microtubule plus-ends (Guesdon et al., 2016). To quantify this observation, we counted the number of beads located at sheet edges as compared to the middle of sheets. Here, beads that were ambiguously located were conservatively classified as being at the middle of the sheet. We observed that, for sheet-like regions of microtubules, there were sevenfold more beads associated with sheet edges than with the middle of the sheet (Figure 3I, right; p<<10−5, Chi-squared test). This suggests that EB1 can indeed bind at edge sites on a microtubule, despite the reduced number of inter-site binding partners. Further, the ratio of edge sites to total binding sites within a sheet is estimated at 2:14 (edge sites to total binding sites), and so by normalizing to the number of available sites in each case, this yields an observed ~49 fold preference for edge sites over lattice sites. This fold preference is on the order of the ~70 fold increase in EB1 on-rates for edge sites as compared to lattice sites from the 3D diffusion simulation (Figure 3H). We note that there was a lower reported ratio of edge to middle position binding on dynamic microtubule sheets (1:18, Guesdon et al., 2016). However, for growing microtubules in the presence of free tubulin, the possibility that EB1 first binds to a sheet edge, and that this edge binding position is then converted to a sheet-middle position by subsequent addition of new tubulin subunits, cannot be ruled out. In contrast, for our stabilized microtubules with no free tubulin, binding in a sheet-middle position would require that EB1 binds directly to the sheet-middle position. Therefore, the mechanism for localization of EB1 to sheet-middle positions may be very different for stable microtubule experiments with no free tubulin, as compared to dynamic, growing microtubule experiments in the presence of free tubulin.
Rapid frame-rate fluorescence microscopy experiments demonstrate increased on-rate of EB1-GFP to disrupted-structure microtubule pools
Our 3D single-molecule diffusion simulations predicted a ~ 70 fold rise in the fraction of EB1 arrivals to 2-tubulin edge structures relative to a 4-tubulin-pocket closed lattice conformation, due to a high diffusional steric hindrance barrier that frustrates EB1 from binding in the pocket-like interface between four adjacent tubulin dimers in the lattice. Thus, the simulated arrival rate of EB1 to its binding site on the microtubule was dictated by the structural state of the microtubule itself. To experimentally test this model prediction, we collected rapid frame-rate (100 Hz) movies using TIRF microscopy, and then tracked the association and dissociation events of individual EB1-GFP molecules with microtubules (Figure 3J, left; white arrows in EB1-GFP kymograph indicate EB1 association events). Because it was not possible to directly distinguish between EB1-GFP that was bound to a protofilament edge vs EB1-GFP that was bound at a closed lattice site in our TIRF experiments, we used our closed and disrupted-structure microtubule preparation protocols (Figure 2) to measure the difference in EB1-GFP association and dissociation rates between closed microtubules, and microtubules that likely had an increased number of exposed edge binding sites (disrupted-structure microtubules). The EB1-GFP on-rate was calculated in each case by fitting a decaying exponential to the dwell time histogram for individual binding events (Figure 3—figure supplement 1A), which allowed us to calculate the expected total number of binding events, including those with a very short dwell time (Telley et al., 2009) (See Materials and methods).
We found that the association rate for EB1-GFP was ~45 fold higher for disrupted-structure microtubules as compared to closed microtubules for the GDP microtubule pools (Figure 3J, center, teal; p<<10−5; Z-test). This fold increase was similar to the normalized results for the electron microscopy EB1-bead studies (Figure 3I), suggesting that there was a substantial increase in edge-binding sites in the disrupted-structure pool as compared to the closed pool. For the GMPCPP microtubule pool, there was a ~ 12 fold increase in the EB1-GFP association rate constant in the disrupted-structure microtubule pool relative to the closed pool (Figure 3J, center, purple; p<10−64; Z-test), suggesting that the CaCl2 treatments used to disrupt microtubule structure may be less efficient at producing edge-binding sites than the protocol for the GDP microtubule pools, which relied on damage initiated by Taxol treatment. Finally, the EB1-GFP association rate constant was ~3.5 fold higher in the disrupted-structure microtubule pool as compared to the closed microtubules for the GTPγS microtubules (Figure 3J, right, brown; p=1.7×10−16; Z-test). This more moderate increase in the association rate constant may be due to a smaller difference in microtubule structure between the closed and disrupted-structure pools of GTPγS microtubules, as the closed microtubule pool itself was shown to exhibit structural disruption (Reid et al., 2017).
We then calculated EB1-GFP dwell times on the microtubule lattice from fits to our experimentally observed exponentially decaying dwell-time histograms (Figure 3—figure supplement 1A). We found that all pools of disrupted-structure microtubules had lower characteristic dwell-times than their respective closed pools (Figure 3—figure supplement 1B), suggesting that, while EB1 binding to protofilament edges may be rapid due to low steric hindrance, a twofold reduction in the number of EB1-tubulin bonds at the edge binding sites would lead to an increased EB1 off-rate. Consistent with this model, we found that EB1 dwell time distributions were best modeled as two exponential distributions (Figure 3—figure supplement 1C,D), one with a short dwell time (~20 ms), which could be associated with edge-bound EB1, and a second underlying distribution with a longer dwell time (~150 ms), which may correspond to lattice-bound EB1.
In experiments and simulations, a tubulin face-binding protein does not exhibit microtubule structure recognition
Taken together, our data suggests that the pocket localization of EB1’s binding site on the microtubule acts to limit access of EB1 to 4-tubulin lattice binding sites relative to 2-tubulin edge binding sites (Figure 4A, left vs right, lighter green arc shows large increase in accessibility). In contrast, this model predicts that a protein with a binding site on the face of a tubulin dimer would have similar binding site accessibility on both lattice and edge sites (Figure 4B, left vs right, lighter green arc shows small difference in accessibility). Thus, we predicted that a tubulin face binding protein would not show an increased number of arrival events to disrupted-structure microtubules.
Figure 4
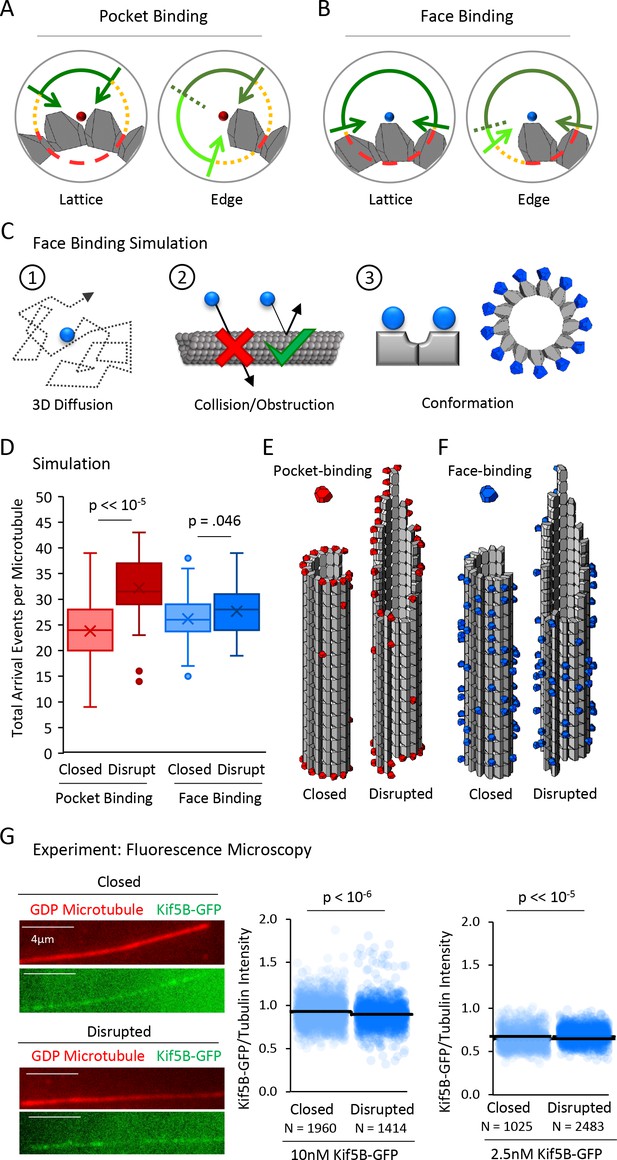
A tubulin face binding protein does not demonstrate microtubule structure recognition in experiment and simulation.
(A) Hypothesis schematic showing large increase in direct access to a pocket binding site (dark green + light green) upon change from lattice conformation (left) to an edge conformation (right) for a pocket-binding protein. (B) Face binding hypothesis model predicts only a small change in direct access to a face binding site upon change from lattice conformation (left) to an edge conformation (right). (C) Simulation rules and parameters for face binding are identical to a pocket binding simulation with respect to (1) 3D diffusion, and (2) obstruction of the binding molecule by tubulin molecules. (3) The only change in the simulation was in the location of the binding site (left), with the arrangement of simulated face-binding protein on a microtubule at right. (D) Total arrival events per microtubule for a simulated pocket binding protein (EB1, red) and face binding protein (blue), showing molecular arrival events on closed (light red/light blue) and ‘disrupted-structure’ (dark red/dark blue) microtubule conformations. Results of 50 simulations of 4,000 EB1 molecules each for each microtubule condition. Each data point in the box and whisker plots represents the total number of EB1 arrival events per microtubule for 4000 different simulated EB1 molecules. (E) Representative visualizations of arrival event location distribution of pocket binding protein such as EB1 (red) on closed and disrupted-structure microtubules. (F) Representative visualizations of arrival event location distribution of face binding protein (blue) on closed and disrupted-structure microtubules, illustrating the loss of preference for edge-located binding sites. (G) Left: Representative images of Kif5B-GFP (green), which is a tubulin face binding protein, on GDP microtubules (red) (scale bar 4 µm). Right: Cloud plots of Kif5B-GFP/Tubulin intensity ratio for individual microtubules. Each semi-transparent circle is the data point from a single microtubule. Solid lines are the average Kif5B-GFP/Tubulin intensity ratio for each population.
To ask whether our simulation supported this prediction, we first performed tubulin ‘face binding’ simulations that had identical rules to the EB1 diffusion simulations (Figure 4C, 1–2), but with the exception that the protein binding site was located on the outer face of a tubulin dimer (Figure 4C, 3), rather than inside the four-tubulin pocket between dimers. Thus, we used our previous tubulin dimer and EB1 conformations, but instead moved the protein binding location to the outer face of the tubulin heterodimer, instead of within the four-dimer pocket between tubulin dimers (Figures 4C, 3, right). We then asked how the total number of face-binding molecule arrival events per microtubule in the closed and disrupted-structure microtubule simulations would be altered by changing this rule.
In previous EB1 simulations, the mean number of EB1 arrival events per microtubule was increased for the disrupted-structure microtubules relative to the closed microtubules (Figure 4D, red; p=3.2×10−28, Binomial test; 4000 EB1 molecules per simulation, 50 simulations). In contrast, we found that when the protein binding site was located on the tubulin heterodimer’s outward face, the mean number of face-binding molecule arrival events for disrupted-structure microtubules was not substantially increased relative to the closed microtubules (Figure 4D, blue; p=0.046, Binomial test; 4000 face-binding molecules per simulation, 50 simulations), consistent with our hypothesis that the face-binding protein would not differentiate between edge and lattice binding sites. Similarly, the previous observation that simulated, pocket-binding EB1 molecules showed preferential arrivals to edge-proximal tubulin heterodimers (Figure 4E, red) was strikingly altered in the tubulin face-binding simulations: the face-binding protein arrival events were located non-specifically along the lattice, and with no enrichment on edge dimers (Figure 4F, blue; random representative subset of 10,000 simulated EB1 molecules). Thus, our simulations predicted that a tubulin face-binding protein would show similar rates of arrival to both closed and disrupted-structure microtubule populations, due to a similar steric hindrance to binding in both cases.
To experimentally test this prediction, we used a monomeric Kif5B-GFP kinesin construct in the presence of 10 mM AMPPNP, to allow for microtubule binding analysis of the monomeric kinesin (K339-GFP) (Case et al., 2000; Tomishige and Vale, 2000). The Kinesin-1 Kif5B protein has been shown to dock with a stoichiometry of one kinesin motor per tubulin heterodimer, and binds to the outer surface of the α and β tubulin monomers, rather than the lateral surfaces, in electron microscopy experiments (Hirose and Amos, 1999; Kikkawa et al., 2000; Kozielski et al., 1998; Löwe et al., 2001; Marx et al., 2006; Moores et al., 2002; Nogales et al., 1999; Rice et al., 1999; Sosa et al., 1997). Thus, we used the Kif5B-GFP construct to determine whether a tubulin face-binding protein would show differential binding to closed and disrupted-structure microtubule populations, as was observed for the EB1-GFP protein (Figure 2B).
We first used 10 nM Kif5B-GFP, and compared overall binding of the Kif5B-GFP to closed and disrupted-structure pools of GDP microtubules, similar to the procedure for our EB1-GFP experiments (Figure 2B). Qualitatively, and in contrast to the EB1-GFP experiments, the degree of binding between the closed and disrupted-structure pools of GDP microtubules appeared similar (Figure 4G, left). Quantification of the TIRF images demonstrated that the average Kif5B-GFP/tubulin intensity ratio for the disrupted-structure pool of GDP microtubules was not higher than in the closed microtubules (p=1; one-sided t-test), but rather appeared to be slightly lower than in the closed microtubules (p=2.7×10−7, 2-sided t-test), perhaps suggesting a slight suppression of Kif5B-GFP binding to microtubules with disrupted-structure structures. Similar results were observed using a lower concentration of Kif5B-GFP (2.5 nM, Figure 4G, right; p<10−15, two-sided t-test). These results suggest that the binding location of EB1 on microtubules may dictate its preferential binding to the disrupted-structure pool of microtubules relative to the closed microtubules, and that binding to the face of a tubulin dimer by Kif5B does not yield this preferential binding behavior.
EB1 tip tracking by microtubule structure recognition
We then asked how the rapid binding of EB1 onto protofilament edges could be integrated with current models for tip tracking behavior on growing microtubule ends. It has been previously shown that EB1-GFP is concentrated in a location on growing microtubule ends that is slightly behind the distal tip (Maurer et al., 2014). This EB1-GFP fluorescence distribution has been explained via a model in which EB1 first binds the microtubule with high affinity in a location that is penultimate to the microtubule tip, and then, over time, a conformational change occurs on the microtubule that lowers the affinity of EB1 for this binding site (Maurer et al., 2014). Because EB1 binds the microtubule with high affinity in a location that is penultimate to the microtubule tip, one hypothesis is that EB1 binds with high affinity to a GDP-Pi lattice, which would be localized behind the tip of the microtubule due to a delay in hydrolysis of newly added GTP-tubulin subunits at the microtubule tip (Zhang et al., 2015). In this model, the conversion of the microtubule lattice from a GDP-Pi state to a GDP state would then lower the affinity of EB1 for its binding site. Thus, we analyzed the overall binding of EB1-GFP to GDP-Pi microtubules as compared to GDP microtubules, to determine whether EB1-GFP binds with high affinity to GDP-Pi microtubules, and with a lower affinity to GDP microtubules.
It has been previously shown that the Kd of Pi for GDP is ~25 mM (Carlier et al., 1988; Raw et al., 1997). Furthermore, the depolymerization rate of GDP microtubules is substantially slowed in the presence of 50 mM of inorganic phosphate, indicating that Pi binds to GDP-tubulin under these conditions (Carlier et al., 1988). Therefore, under these conditions, we compared the binding of EB1-GFP to GDP and GDP+Pi microtubules to determine whether EB1 exhibits preferential binding to GDP+Pi microtubules (Figure 5A; see Materials and methods). Surprisingly, EB1-GFP binding appeared to be reduced on GDP+Pi microtubules relative to GDP microtubules, for both closed and disrupted-structure microtubules (Figure 5B). By quantifying EB1-GFP binding on each microtubule type using our previously described automated analysis tool (Reid et al., 2017), we found that there was a −53% reduction in binding of EB1-GFP to closed GDP+Pi microtubules relative to closed GDP microtubules (p<<10−5, t-test) (Figure 5C, experimental repeats Figure 5—figure supplement 1A).
Figure 5 with 1 supplement see all
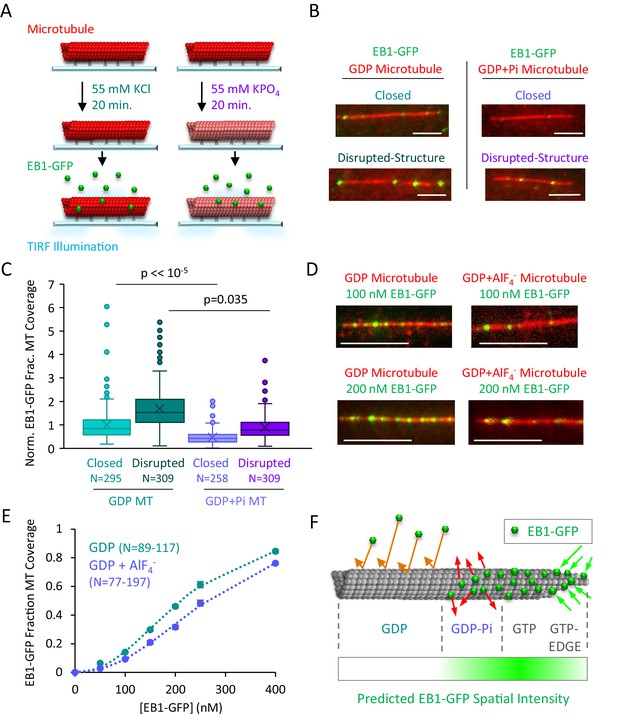
EB1-GFP binding is suppressed on GDP-Pi microtubules.
(A) Experiment to compare EB1-GFP binding to GDP and GDP+Pi microtubules (see Materials and methods). (B) Representative images of EB1-GFP binding to GDP and GDP+Pi microtubules (scale bar 5 µm). (C) Quantitative binding comparison, based on EB1-GFP fractional coverage area of microtubules. All values normalized to the average fractional coverage area in the closed GDP microtubule population. Sample sizes represent number of independent images analyzed. (D) Representative images of EB1-GDP binding to closed microtubules in the presence and absence of the phosphate analog AlF4- (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000) (scale bar 5 μm). (E) Quantitative analysis of EB1-GFP binding under conditions of increasing EB1 concentrations. As previously described, the EB1 binding data was best fit using a cooperative binding curve (Lopez and Valentine, 2016; Zhu et al., 2009), which demonstrated a ~ 2 fold lower affinity of EB1 for the GDP-Pi-Analog relative to the GDP microtubules. (F) Implementation of structural recognition into a two-state model for EB1 binding and microtubule tip structure maturation.
In the KPO4 experiments (Figure 5A–C), while the molarity of the salts in the experiments were matched (55 mM KPO4 vs 55 mM KCl), the ionic strengths of the reaction mixtures were mismatched, which could influence EB1 binding to the lattice. Therefore, we performed further experiments using an analog of phosphate, AlF4- (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000). Here, the molarity and ionic strengths of the salts included in both experiments were identical (52.5 mM KCl and 2 mM NaF for both experiments). However, 10 μM AlCl3 was included in the phosphate analog experiments, allowing the Al3+ and F- ions form the Pi analog AlF4-, which mimics a phosphate group, but with 1000-fold higher affinity (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000).
Similar to the KPO4 experiments, we observed reduced EB1 binding in the GDP+AlF4-experiments as compared to the GDP-alone experiments (Figure 5D). We then quantified EB1-GFP binding using our previously described automated analysis tool (Reid et al., 2017) under conditions of increasing EB1 concentrations (Figure 5E). As previously described, the EB1 binding data was best fit using a cooperative binding curve (Lopez and Valentine, 2016; Zhu et al., 2009), and so we fit the results in each case to a Hill equation, which demonstrated a ~ 2 fold lower affinity of EB1 for the GDP-Pi-Analog relative to the GDP microtubules (Figure 5E, see Materials and methods; Kd,GDP=1.9x105 nM, nGDP = 2.2; Kd,Analogue=4.2x105 nM, nAnalogue = 2.3).
These results could perhaps be explained by previous cryo-electron microscopy findings in which it was demonstrated that the GDP-Pi microtubule structural state is distinct from that of GDP microtubules (Manka and Moores, 2018b). Further, published cryo-EM structures of microtubules coassembled with EB3 show that EB1 may promote a compacted microtubule lattice with a lattice twist, once it is bound to the microtubule (Zhang et al., 2015). This structural transition could account for the ultimate destruction of the stable 4-tubulin binding site of EB1 as the lattice-bound tubulin subunits transition from GTP to GDP-Pi, and ultimately to a GDP conformations, perhaps promoted by the binding of EB1 to the microtubule. Thus, we conclude that EB1 does not likely directly bind to GDP-Pi microtubules, but, instead, that hydrolysis of GTP-tubulin to GDP-Pi -tubulin could initiate formation of a low-affinity EB1 binding site.
Our finding that EB1 binds with low affinity to GDP-Pi lattices is perhaps unexpected based on previous dynamic microtubule experiments in which it was observed that Mal3-GFP was bound to the entire dynamic microtubule lattice in the presence of GTP together with BeF3- (Maurer et al., 2011). Here, while BeF3- is thought to replace the dissociated phosphate on the GDP lattice, perhaps mimicking a GDP-Pi state, it may be that BeF3- instead acts to lock the dynamic microtubule lattice into a GTP-like state in the presence of excess GTP, which is required in a dynamic microtubule assay. However, GTP was absent in our GDP-Pi and GDP-Pi-Analog microtubule experiments, thus ensuring that phosphate was bound only to the GDP lattice.
Thus, our GDP+Pi data, combined with our protofilament edge binding data, led us to hypothesize that the process of EB1 binding at the growing microtubule end could be characterized by (1) rapid EB1 binding to edge sites at the distal end of the microtubule, followed by maturation into a tight EB1 binding configuration through the addition of new GTP-tubulin subunits at locations of edge-bound EB1, which would stabilize EB1 binding by completing its 4-tubulin pocket binding configuration (Figure 5D, right), and (2) subsequent destruction of the stable 4-GTP-tubulin pocket binding site by hydrolysis of GTP-tubulin into GDP-Pi (Figure 5D, center), and, ultimately, GDP-tubulin, which may be accelerated by the binding of EB1 into its 4-tubulin pocket binding configuration (Maurer et al., 2014; Zhang et al., 2015; Zhang et al., 2018).
We predict that rapid binding to protofilament edge sites at tapered microtubule ends would remain consistent with observations that the highest density of EB1-GFP is 80–160 nm behind the most distal end of the microtubule (Maurer et al., 2014). Here, although new edge sites are continuously generated as a result of tubulin subunit additions to growing microtubule plus-ends, the density of edge sites on an open, tapered microtubule sheet is, by definition, seven-fold lower than that of lattice sites on a closed microtubule tube (ratio of edge-binding-sites to total-binding-sites per tubulin layer for an open microtubule sheet is 2:14). Thus, even with rapid loading of EB1 onto edge sites at the most distal positions on the microtubule tip, the peak in EB1-GFP intensity for a plus-end EB1-GFP comet would be penultimate to the tapered tip, in the location where a high density of EB1 molecules are bound to the much higher density, four-GTP-tubulin pocket lattice binding sites, perhaps via addition of new, incoming GTP-tubulin subunits onto the location of previously edge-bound EB1 molecules. Consistent with this prediction, by generating simulated microscope images of microtubule tips with complete occupancy of EB1-GFP at distal tip edge sites and an exponentially decaying occupancy of EB1-GFP away from the distal tip on the closed microtubule lattice sites (Figure 5—figure supplement 1B), we observed that the highest density of EB1-GFP lagged behind the distal microtubule end (Figure 5—figure supplement 1C), as previously described (Maurer et al., 2014). Thus, in a model where EB1 is preferentially targeted to edge binding sites at tapered microtubule ends, the reduced density of edge binding sites relative to closed microtubule lattice binding sites could explain the penultimate location of EB1 at growing microtubule ends (Figure 5D).
Blunting of tapered microtubule tip structures correlates with suppressed EB1 binding in cells
An important prediction of a structural-recognition model, in which EB1 tip tracking is facilitated by tapered microtubule ends (Figure 5D), is that the pruning of extended, tapered tip structures at growing microtubule ends, leading to blunt ends with fewer protofilament-edge EB1-binding sites, would suppress EB1 tip tracking in cells. To test this idea, we treated LLC-Pk1 cells that expressed Tubulin-GFP (Rusan et al., 2001) with increasing, low-dose concentrations of the microtubule destabilizing drug Vinblastine, to determine whether we could alter the structure of the growing microtubule plus-ends. While Vinblastine does not alter the hydrolysis rate of GTP-tubulin (Castle et al., 2017), it interferes with tubulin assembly into protofilaments (Gigant et al., 2005), and could thus suppress the tapered multi-protofilament extensions that have been observed at rapidly growing microtubule plus-ends (Chrétien et al., 1995; Coombes et al., 2013; Guesdon et al., 2016).
We treated LLC-Pk1 cells with low concentrations of Vinblastine, which still allowed for robust growth of microtubules (Figure 6A). Then, we collected line scans of the drop-off in tubulin-GFP fluorescence at growing microtubule plus-ends, to assess whether microtubule tip structures were altered (Figure 6B). Qualitatively, it appeared that tubulin-GFP fluorescence at the tips of microtubules in the control cells dropped off more slowly to background as compared to the 10 nM Vinblastine-treated cells, in which the fluorescence dropped off more abruptly (Figure 6B, blue vs yellow). To quantify this observation, we fit a Gaussian error function to the fluorescence intensity drop-off at each microtubule end, as previously described (Coombes et al., 2013; Demchouk et al., 2011), which allowed us to estimate tip tapering that arises as a result of protofilament length variability at the microtubule ends. Consistent with our qualitative observations, we found that the microtubule tip standard deviation was significantly reduced with Vinblastine treatments as low as 1 nM (Figure 6C; Control vs 1 nM: p=0.004, Z = 2.89; Control vs 10 nM: p=6×10−5, Z = 4.01), indicating that treatment with the microtubule destabilizing drug Vinblastine acted to prune protofilament extensions at growing microtubule plus-ends, eliminating tapered tips with extensive protofilament-edge binding sites. Indeed, tip standard deviations in 10 nM Vinblastine approached the point spread function of the microscope, similar to the blunt ends of GMPCPP microtubules (Figure 6C (yellow) vs Figure 1D), suggesting that extended protofilaments and associated tip tapering at growing microtubule ends had been eliminated at higher Vinblastine concentrations.
Figure 6 with 1 supplement see all
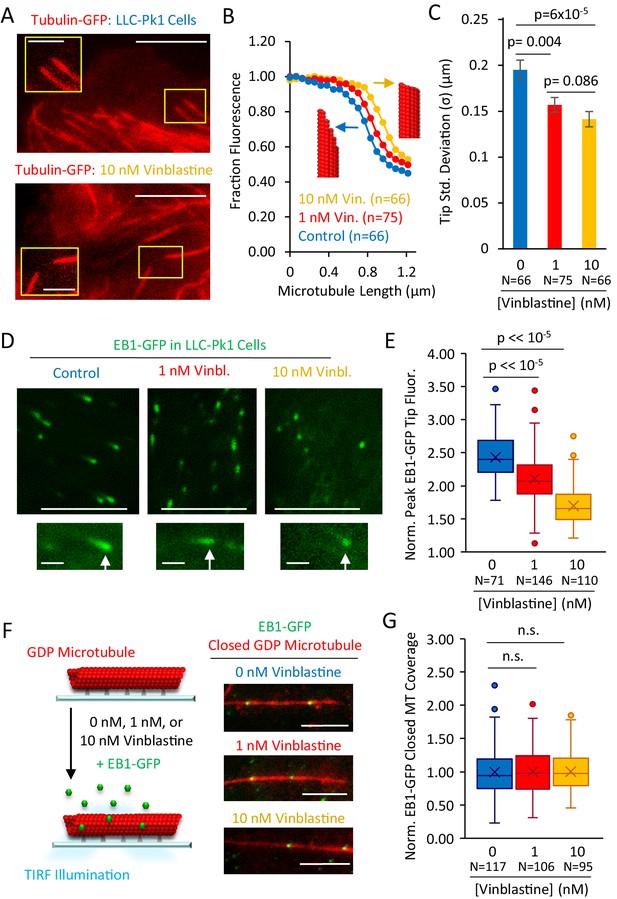
Structural recognition facilitates EB1 tip tracking at growing microtubule plus-ends in cells.
(A) Representative images of Tubulin-GFP expressed in LLC-Pk1 cells with inset detail of growing microtubule tips (control cells, top, 10 nM Vinblastine treated, bottom; see Materials and methods) (scale bar 5 µm, insets 2 µm). (B) Average linescans that show the dropoff in intensity of tubulin at the tips of microtubules in control and Vinblastine treated cells. A sharper drop-off (yellow) is suggestive of a blunt microtubule end, and a slower dropoff (blue), is suggestive of a more tapered microtubule end, as shown by the red microtubule cartoons. (C) Tip standard deviations as estimated by fitting to the graphs in panel F. (D) Representative images of EB1-GFP expressed in LLC-Pk1 cells (top) with inset EB1-GFP comets at growing microtubule tips (bottom) (control cells, left; 1 nM Vinblastine treated, center; 10 nM Vinblastine treated, right; see Materials and methods) (scale bar 5 µm, comet detail scale bar 1 µm). (E) Peak EB1-GFP fluorescence normalized to lattice EB1-GFP fluorescence. (F) Experiment (left) and representative images (right) of in-vitro experiment to quantify binding of EB1-GFP to closed GDP microtubules in the presence of increasing concentrations of Vinblastine (scale bar, 5 µm). (G) Quantitative binding of EB1-GFP to closed GDP microtubules, based on EB1-GFP binding area on microtubules. All values normalized to the average binding area in the 0 nM Vinblastine population. Sample sizes represent number of independent images analyzed (p=0.91, t-test 0 nM vs 1 nM Vin.; p=0.88, t-test 0 nM vs 10 nM Vin.).
We then asked whether blunting of the microtubule tip structure, leading to a reduced number of protofilament-edge binding sites, would be correlated with the efficiency of EB1 tip tracking. Thus, we used an LLC-Pk1 strain with EB1-GFP (Piehl and Cassimeris, 2003), and measured the peak intensity of EB1-GFP at growing microtubule ends, relative to lattice bound EB1-GFP (Figure 6D; see Materials and methods). Consistent with qualitative observations (Figure 6D, bottom, white arrows), we found that peak EB1-GFP intensity at microtubule ends was reduced with increasing Vinblastine concentrations (Figure 6E, p<<10−5, t-test), suggesting that, with flattened end structures, EB1-GFP could not efficiently target to growing microtubule plus-ends. To ensure that the reduced EB1 targeting was not a consequence of shorter EB1-GFP comet lengths in Vinblastine treatment, we then compared the peak intensity of EB1-GFP comets at similar EB1-GFP comet lengths between controls and in 1 nM Vinblastine (Control comet length: 0.60 ± 0.06 µm, n = 62; 1 nM Vinblastine comet length: 0.59 ± 0.07 µm, n = 90; (mean ± SD)). Here, while the EB1-GFP comet lengths were statistically indistinguishable in our samples (p=0.89, t-test), we nevertheless observed a significant decrease in peak comet intensity in the Vinblastine-treated cells relative to the same-comet-length control cells (p=4.5×10−6, t-test, Figure 6—figure supplement 1A).
Finally, to verify that the reduced peak EB1-GFP comet intensity in Vinblastine was not the result of an overall lower affinity of EB1 for microtubules in the presence of Vinblastine, we measured EB1-GFP binding to closed in vitro GDP microtubules in the presence of increasing Vinblastine concentrations (Figure 6F). Importantly, and in contrast to the reduced peak intensity of EB1-GFP comets on dynamic microtubules in cells, the binding of EB1-GFP to closed GDP microtubules was similar regardless of Vinblastine concentration (Figure 6G, no significant differences, t-test; experiment repeats, Figure 6—figure supplement 1B). We conclude that the efficiency of cellular EB1-GFP tip tracking is disrupted with Vinblastine treatment, perhaps due to the blunting of tapered tip structures at growing microtubule ends, which cuts the availability of high-accessibility EB1 protofilament-edge binding sites. However, we cannot exclude that other structural or chemical cellular responses to Vinblastine may be at play as well.
Discussion
Taken together, our results suggest a new model to explain EB1 tip tracking at growing microtubule plus-ends, in which EB1 recognizes and rapidly binds to the protofilament edges at open, tapered microtubule end structures. The subsequent addition of new GTP-tubulin subunits may then facilitate the maturation of EB1 into a high-affinity binding state on the closed GTP-tubulin lattice. Ultimately, tubulin hydrolysis into a GDP-Pi or GDP state destroys the EB1 binding site, catalyzing its release from the microtubule (Figure 5F).
We found that EB1 dwell time distributions on our disrupted structure microtubules were best modeled as two exponential distributions (Fig S2C,D), including one with a short dwell time (~20 ms), which could be associated with edge-bound EB1. In evaluating this dwell time relative to the kinetics of αβ-tubulin association, in 10 µM tubulin it has been estimated that a free tubulin subunit would arrive to the growing end of the microtubule as rapidly as every ~2 ms (Gardner et al., 2011), or as slowly as every ~10 ms (Mickolajczyk et al., 2019). Therefore, even the relatively short dwell times of edge-bounded EB1 molecules would be long enough to allow for multiple tubulin subunit arrivals while EB1 is bound to a protofilament edge. These kinetics suggest that if EB1 first binds to a protofilament edge, subsequent tubulin subunit arrivals could lock EB1 into its stable 4-tubulin pocket binding site. This pathway to establishing EB1 binding into its 4-tubulin pocket binding location would be efficient both for EB1, in which the steric hindrance for its direct binding into a 4-tubulin pocket was nearly insurmountable in our diffusion simulations, and for incoming tubulin subunits, which would be stabilized longitudinally and/or laterally by binding to EB1 in addition to other protofilament-bound GTP-tubulin subunits.
Overall, we propose that structural recognition by EB1 could promote rapid loading of EB1 at the open, tapered growing microtubule plus-end with its more easily accessible edge sites. Specifically, our results predict that the on-rate for EB1 binding to the closed microtubule lattice would be extremely low, due to very high steric hindrance and low accessibility. In contrast, we predict that the EB1 on-rate would be ~70 fold (~6000%) higher at tapered, growing microtubule plus-ends, due to the presence of easily accessible, low steric hindrance sites at exposed protofilament edges. This was the most surprising conclusion from our diffusion simulations: while we expected that tubulin edges would be more accessible to EB1 binding, the enormous magnitude of this preference was surprising to us. Importantly, the binding site geometries and diffusion coefficients used in the simulation were constrained by prior electron microscopy reconstructions and molecule size, and so the molecular diffusion simulations did not rely on any free parameters.
After binding to an edge-site, EB1 would likely undergo a higher off-rate as a result of the partial binding interface that is inherent to these edge-sites. However, our results show an increase in steady-state binding to disrupted microtubule structures, regardless of nucleotide state (Figure 2C–E), suggesting that the overall affinity of EB1 may be higher on disrupted structures, regardless of the likely increase in off-rates. This increase in affinity may be due to a stronger effect of disrupted microtubule structure in accelerating the EB1 on-rate, as compared to increasing the EB1 off-rates. For example, we observed a ~ 45 fold increase in EB1 on-rates to disrupted GDP microtubule structures relative to closed microtubule structures (Figure 3J), while the ‘short’ EB1 dwell times, which could be associated with edge-bound EB1 on GDP microtubules, were only ~8 fold faster than the lattice-bound ‘long’ dwell times (Figure 3—figure supplement 1D), resulting in a net affinity increase of ~5 fold.
The effect of microtubule structure on microtubule-associated protein binding preference is not likely restricted to EB1, as we find that this preference stems from the physical accessibility of microtubule binding sites, and thus may be pertinent to any polymer binding protein. We expect that the magnitude of this effect will be strongly impacted by the location of the protein binding site on the microtubule lattice, as suggested by the difference in our pocket vs face binding simulations. Here, any protein that has its binding site located in the dip between protofilaments or at the crease between stacked subunits could potentially display microtubule structural recognition. For example, the microtubule-associated protein Doublecortin (DCX) has a similar binding site to EB1. DCX has been reported to recognize microtubule curvature, a configuration that would require an incomplete lattice with exposed protofilament edges to allow for outward protofilament curvature (Bechstedt and Brouhard, 2012; Bechstedt et al., 2014; Fourniol et al., 2010). Similarly, microtubules grown in the presence of CLIP-170 have been associated with the growth of curved oligomers (Arnal et al., 2004), and it has been shown that microtubule lattice defects may be recognized by CLIP-170 to stimulate microtubule rescue (de Forges et al., 2016). Thus, recognition of microtubule curvature or lattice defects by microtubule-associated proteins could rely, at least in part, on an increased arrival rate to exposed protofilament edge sites. Further, a recent electron microscopy study reported that the tips of growing microtubules within mitotic spindles display a gentle outward curvature of individual protofilaments (McIntosh et al., 2018). This outward curvature could enhance a structural recognition mechanism by increasing the availability of exposed protofilament edge sites at growing microtubule ends, due to the increased separation between individual protofilaments. In contrast, proteins such as TPX2, which binds in part across the faces of α and β tubulin subunits (Zhang et al., 2017), and TOG1-domain containing proteins such as XMAP215 and Stu2, where the TOG1 domain binds predominantly on the β-tubulin face (Byrnes and Slep, 2017), may be less likely to display structural recognition.
As noted above, because outward protofilament curvature at growing microtubule ends is necessarily associated with exposed protofilament edges, we cannot exclude the possibility that EB1 may also preferentially bind to curved protofilaments (Guesdon et al., 2016). However, we find that decreased steric hindrance can increase the arrival rate of EB1 to protofilament edges by ~70 fold (~6000%, Figure 3), while no similar effect would apply to protofilament curvature. Further, we did not routinely observe outward protofilament curvature at holes and defects within the lattice (Figure 2B), suggesting that the increased affinity of EB1 to disrupted lattice structures (Figure 2C) was not a result of outwardly curved protofilaments that were present within the microtubule lattice.
Our simulations model only one microtubule binding domain of EB1, yet EB1 is typically a homodimer. We anticipate that EB1’s dimerization activity would not alter the observed microtubule structural preference in our simulations, but would likely increase the dwell time of edge-associated EB1, as once one domain binds to the more easily accessible protofilament edge sites, EB1’s second binding domain would be constrained to a small area, and therefore much more likely to bind, even within a 4-tubulin pocket, due to the high local availability of binding sites. Thus, the EB1 homodimer as a whole would become more stably bound to the microtubule. EB1 dwell time was not included in our current simulations, as the simulation for a particular molecule was ended upon arrival to the microtubule lattice, but future iterations of our simulation could model dwell time to test this idea.
In conclusion, we find that a high steric hindrance barrier impedes EB1 from binding directly into the pocket-like interface between four adjacent tubulin dimers in the lattice, and that this barrier is markedly reduced at tapered microtubule ends. Protofilament edge-binding greatly increases the arrival rate of EB1 to growing microtubule plus-ends, which facilitates EB1 tip tracking in cells. Finally, our results support a general principle in which microtubule-associated protein binding rates are influenced by the location and conformation of the protein binding interface.
Materials and methods
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Cell line (porcine, kidney) | LLC-Pk1 Express Tubulin-GFP | (Rusan et al., 2001) | RRID:CVCL_0391 | Gift from Dr. Pat Wadsworth |
| Cell line (porcine, kidney) | LLC-Pk1 Express EB1-GFP | (Piehl and Cassimeris, 2003) | RRID:CVCL_0391 | Gift from Dr. Lynne Cassimeris |
| Recombinant DNA reagent | pETEMM1-HIS6x-tev-EB1-GFP (plasmid) | (Zanic et al., 2009) | ||
| Recombinant DNA reagent | RP hk339-GFP (monomeric Kif5B-GFP-HIS6x plasmid) | (Tomishige and Vale, 2000) | Addgene plasmid #24431 | Gift from Dr. Ron Vale |
Tubulin purification and labelling
Request a detailed protocolTubulin was purified and labeled as per Gell et al. (2010).
EB1-GFP purification
Request a detailed protocolPlasmid pETEMM1-HIS6x-tev-EB1-GFP was transformed into Rosetta(DE3) pLysS E. coli, grown in 10 ml of LB+cam+kan at 37° overnight, and then subcultured into 1L of the same media, mixing at 37° for 2 hr to an A600 of 0.44. IPTG was then added to 2 mM and the culture was mixed at 18° for 14 hr. The culture was centrifuged 30 min. at 4°, 4400 xg. The cell pellet was resuspended into 12 ml of PBS/0.1% tween-20/5 mM B-mercaptoethanol/1 mg/ml lysozyme and protease inhibitors (1 mM AEBSF/10 μM pepstatin A/0.3 μM aprotinin/10 uM E-64), mixed at 4°, 2 hr., and then sonicated on ice at 80% power, 50% duty, 10 × 1 min. The lysate was centrifuged at 4°, 1 hr., 18000 xg. The supernatant was passed through 2 ml of Talon Metal Affinity Resin and the resin was sequentially washed with five column volumes Buffer A (50 mM sodium phosphate pH7.5/300 mM KCl/10% glycerol/5 mM B-mercaptoethanol). Next, the column was washed with 95% buffer A/5% bufferB (Buffer A/300 mM imidazole), followed by a wash with 90% A/10% B, and finally 85% Buffer A/15% Buffer B. All buffers had the protease inhibitors 1 mM AEBSF, 10 uM pepstatin A and 10 uM E-64). Protein was eluted with 1 ml fractions of 100% Buffer B + above protease inhibitors. Elution fractions were analyzed on coomassie and western blot. Relevant fractions were combined and dialyzed against Buffer A overnight at 4°, then 2 hr. at 18° in the presence of HIS6-taggedTEV protease (Expedeon TEV0010) at a 1:100 w/w protein ratio). Dialysate was then mixed with additional Talon resin to remove cleaved HIS6x tag.
Kif5B-GFP purification
Request a detailed protocolThe RP hk339-GFP construct (monomeric Kif5B-GFP-HIS6x), a gift from Ron Vale (Addgene plasmid #24431; Tomishige and Vale, 2000), was transformed into the E. coli Rosetta (DE3) pLysS. This strain was cultured in LB+amp+cam at 30° overnight to an A600 of 1.5, then subcultured into 1200 ml of the same media, mixed at 37°, 3 hr to an A600 of 0.47. IPTG was added to 0.2 mM final and growth continued at 16° for 19 hr. The culture was centrifuged at 2100 xg, 4° for 30 min, supernatant discarded and cells resuspended in lysis buffer (50 mM sodium phosphate pH 6.2/250 mM NaCl/20 mM imidazole/5 mM B-mercaptoethanol/1 mM MgCl2/0.5 mM ATP/0.5% triton X-100 plus protease inhibitors (1 mM AEBSF/10 uM pepstatin A/10 uM E-64/0.3 μM aprotinin/1 mM benzamidine). Lysozyme was added to 0.1 mg/ml with 150U DNAse I and mixed at 4°, 1 hr. The cell suspension was lysed by sonication on ice, 2 × 10 min. at 90% power, 50% duty and centrifuged at 4°, 14,000 xg for 40 min. The supernatant was pH’ed to 7.6 and mixed with 1 ml Talon Metal affinity resin (Clontech 635509) for 30 min at 4°. Resin was washed 5x with two column volumes of lysis buffer + 0.1x protease inhibitors and protein was eluted with sequential 1 ml volumes of lysis buffer containing 300 mM imidazole pH7 + 0.1x protease inhibitors. The elution fractions were analyzed by coomassie and western blot and the peak fractions used in experiments.
EB1 conjugation to gold beads
Request a detailed protocolUnlabeled EB1 was conjugated to 20 nm gold particles using the Innovacoat Gold Particle labeling Mini Kit (Innovacoat 229–0005) as per kit instructions. EB1 was buffer-exchanged into PBS by centrifuging and washing with a 0.5 ml Amicon Ultra centrifugation filter (30 kd cut off). 10 μl (5.5 μg) of EB1 was diluted with 2 μl of kit dilution buffer and 42 μl of kit reaction buffer. 45 μl of this mixture was added to the kit’s gold reagent and allowed to sit 25 min. 5 μl of the kit’s quencher buffer was added and incubated for 5 min. 1 ml of a 1:10 dilution of quencher buffer was added, mixed, and Centrifuged at 4° for 20 min. at 9000 xg. The supernatant was discarded and the gold pellet was suspended in Brb80 buffer.
Microtubule pool preparations
Request a detailed protocolMicrotubules for the bound nucleotides GDP, GMPCPP, and GTPγS of both closed and disrupted-structure were prepared as described in Reid et al. (2017).
Briefly, GDP microtubules were grown using a mixture of 33 μM tubulin, 1 mM GTP, 4 mM MgCl2, and 4% DMSO, and incubated for 30 min at 37°C. The solution was then diluted 100-fold into BRB80 solution with 10 μM Taxol and stored at either 37°C (for closed microtubules) or at 25°C (for disrupted-structure microtubules).
GMCPP microtubules were grown using a mixture of 3.9 μM tubulin and 1 mM GMPCPP in BRB80, which was incubated for 1 hr at 37°C. To generate disrupted-structure GMPCPP microtubules, closed GMPCPP microtubules were incubated in 40 μM CaCl2 for 40 min immediately before use in an experiment.
GTPγS microtubules were grown using a mixture of 12 μM tubulin, 50 mM KCl, 10 mM DTT, 0.1 mg/ml Casein, 4 mM GTPγS, and unlabeled GMPCPP ‘seed’ microtubules to serve as nucleation points. The mixture was incubated for 1 hr at 37°C, then diluted 3.5-fold and stored at 37°C overnight. The disrupted-structure GTPγS microtubules were prepared similarly, but with the following changes; the initial mixture contained higher tubulin concentration (25.5 μM instead of 12 μM), after incubation the mixture was diluted 26-fold instead of 3.5-fold, and was stored at 25°C overnight instead of at 37°C.
Construction and preparation of flow chambers for TIRF microscopy imaging
Request a detailed protocolImaging flow chambers were constructed as in Section VII of Gell et al. (2010), with the following modifications: two narrow strips of parafilm replaced double-sided scotch tape as chamber dividers: following placement of the smaller coverslip onto the parafilm strips, the chamber was heated to melt the parafilm and create a seal between the coverslips; typically only three strips of parafilm were used, resulting in two chambers per holder. Chambers were prepared with anti-rhodamine antibody followed by blocking with Pluronic F127, as described in Section VIII of Gell et al. (2010).
Microtubules were adhered to the chamber coverslip, and the chamber was flushed gently with warm BRB80. The flow chamber was heated to 35°C using an objective heater on the microtubule stage, and then 3–4 channel volumes of imaging buffer were flushed through the chamber.
Microtubules were imaged on a Nikon TiE microscope using 488 nm and 561 nm lasers sent through a Ti-TIRF-PAU for Total Internal Reflectance Flourescence (TIRF) illumination. An Andor iXon3 EM-CCD camera fitted with a 2.5X projection lens was used to capture images with high signal to noise and small pixel size (64 nm). Images were collected using TIRF with a Nikon CFI Apochromat 100 × 1.49 NA oil objective.
EB1-GFP binding to GMPCPP microtubules
Request a detailed protocolClosed GMPCPP microtubules, prepared as described above, were introduced into an imaging chamber and allowed 30 s-3min to bind the antibody on the coverslip. The imaging chamber was then flushed with 1X Imaging Buffer. 1X Imaging Buffer consisted of BRB80 supplemented with the following: Casien 80 μg/ml, D-Glucose 20 mM, Glucose oxidase 20 μg/ml, Catalase 10 μg/ml, DTT 10 mM, KCl 30 mM, and Tween-20 1%.
EB1-GFP solution (100 μL Imaging Buffer, 1.5 μL of 11 μM EB1-GFP (163 nM final EB1-GFP concentration) was then introduced into the imaging chamber and allowed 10–15 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm respectively).
EB1-GFP binding to microtubule pools
Request a detailed protocolGDP microtubules, either closed or disrupted-structure, were prepared as described above and introduced into an imaging chamber. Microtubules were allowed 30 s-3min to bind the antibody on the coverslip. The microtubule solution was then flushed out of the chamber with 1X imaging buffer (2X Imaging buffer = 110 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol). EB1-GFP solution (50 μL 2X imaging buffer, 45 uL BRB80, 5 μL of 5 μM EB1-GFP) was flowed into the imaging chamber and allowed 10–15 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm, respectively).
GMPCPP microtubules, either closed or disrupted-structure, were prepared as described and introduced into an imaging chamber. Microtubules were allowed 30 s-3min to bind the antibody on the coverslip. The microtubule solution was then flushed with low-salt imaging buffer (Low-salt 2X Imaging buffer = 25 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol). EB1-GFP solution (50 μL low-salt 2X imaging buffer, 45 uL BRB80, 5 μL of 5 μM EB1-GFP) was flowed into the imaging chamber and allowed 10–15 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm, respectively).
GTPγS microtubules, either closed or disrupted-structure, were prepared as described and introduced into an imaging chamber. Microtubules were allowed 30 s-3min to bind the antibody on the coverslip. The imaging chamber was then flushed with 1X imaging buffer (2X Imaging buffer = 110 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol). EB1-GFP solution (50 μL 2X imaging buffer, 45 μL BRB80, 5 μL of 5 μM EB1-GFP (250 nM final EB1-GFP concentration)) was flowed into the imaging chamber and allowed 10–15 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm, respectively).
EB1-GFP on-rate and dwell time movies
Request a detailed protocolMicrotubules were prepared as described above and introduced into an imaging chamber. Microtubules were allowed 30 s-3 min to bind the antibody on the coverslip. The imaging chamber was then flushed with 1X imaging buffer (2X Imaging buffer = 110 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol). EB1-GFP solution (25 μL 2X imaging buffer, 20 μL BRB80, 5 μL of 5 μM EB1-GFP) was flowed into the imaging chamber. Using a capture rate of 100 frames per second, 10 s of images were collected per microtubule in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm, respectively).
Kif5B-GFP global binding to microtubules
Request a detailed protocolGDP microtubules, either closed or disrupted-structure, were prepared as described above and then introduced into an imaging chamber. Microtubules were allowed 30 s-3min to bind the antibody on the coverslip. The microtubule solution was then flushed with 1X imaging buffer (2X Imaging buffer = 110 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol). Either 2.5 nM Kib5B-GFP solution (25 μL 2X imaging buffer, 14.5 uL BRB80, 5 μL of 25 μM Kif5, and 5 μL 100 mM AMPPNP) or 10 nM Kif5B-GFP solution (25 μL 2X imaging buffer, 14.5 uL BRB80, 5 μL of 100 μM Kif5, and 5 μL 100 mM AMPPNP) was flowed into the imaging chamber and allowed 10–15 min to bind, after which images were collected in both the microtubule (red) and Kif5 (green) channels (561 nm and 488 nm, respectively).
EB1-GFP binding to GDP and GDP+Pimicrotubules
Request a detailed protocolGDP microtubules, either closed or disrupted-structure (prepared as described above), were introduced into an imaging chamber, as described above. The imaging chamber with GDP microtubules was then flushed with either 1X GDP+Pi imaging buffer (2X GDP+Pi Imaging buffer = 110 mM KPO4, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol; all in Brb80) or 1X GDP imaging buffer (2X GDP imaging buffer = 110 mM KCl, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol; all in Brb80), and were allowed to sit for 20 min. Microtubules were flushed with 1X imaging buffer again, after which an EB1-GFP solution (20 μL 2X GDP+Pi or GDP imaging buffer, 13 μL BRB80, 4 μL of 2.5 μM EB1-GFP) was flowed into the imaging chamber. EB1-GFP was allowed 10 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm, respectively).
EB1-GFP binding to GDP and GDP-Pi analogue (AlF4-) microtubules
Request a detailed protocolStock solutions of 1 mM AlCl3 and 100 mM NaF were diluted into the imaging buffers to the concentrations shown. Together, the Al3+ and F- ions form the Pi analogue AlF4- that mimics the phosphate group with 1000-fold higher affinity (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000).
Closed GDP microtubules (prepared as described above), were introduced into an imaging chamber, as described above. The imaging chamber with GDP microtubules was then flushed with either 1X GDP-Pi-Analog imaging buffer (2X GDP-Pi-Analog Imaging buffer = 105 mM KCl, 4 mM NaF, 20 μM AlCl3, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol; all in Brb80) or 1X GDP imaging buffer (2X GDP imaging buffer = 105 mM KCl, 4 mM NaF, 40 μg/ml Glucose Oxidase, 20 μg/ml Catalase, 40 mM D-Glucose, 20 mM DTT, 160 μg/ml Casein, 2% Tween-20, and 20 μM Taxol; all in Brb80), and were allowed to sit for 20 min. Microtubules were flushed with 1X imaging buffer again, after which an EB1-GFP solution (2X GDP-Pi-Analog or GDP imaging buffer, BRB80, EB1-GFP) was flowed into the imaging chamber. EB1-GFP was allowed 10 min to bind, after which images were collected in both the microtubule (red) and EB1-GFP (green) channels (561 nm and 488 nm respectively).
Cell lines
Request a detailed protocolThe LLC-Pk1 cell line expressing EB1-GFP was a gift from Patricia Wadsworth, and the cell line expressing GFP-Tubulin was a gift from Lynne Cassimeris. The identity of the cell lines (non-human) were authenticated by microscopy observation and analysis. To test the LLC-Pk1 strains containing EB1-GFP and Tubulin-GFP for mycoplasma contamination, we used the Sigma-Aldrich LookOut Mycoplasma PCR Detection Kit (#MP0035) along with Sigma-Aldrich JumpStart Taq Polymerase (#D6558) as per the kit instructions. The test was negative for mycoplasma contamination for both strains.
Culture, imaging, and drug treatment of LLC-Pk1 cells
Request a detailed protocolThe LLC-Pk1 cell line expressing EB1-GFP, or expressing GFP-Tubulin, was grown in Optimem media (ThermoFisher #31985070), 10% fetal bovine sera + penicillin/streptomycin at 37° and 5% CO2. Cells were grown in 35-mm glass bottom dishes for visualization by microscopy.
For drug treatments, the Optimem media was replaced with CO2 independent imaging media and drug dissolved in DMSO, or only DMSO as a control, was added to the final concentration needed. Cells were incubated with the drug/DMSO for 30 min prior to imaging.
Analysis of EB1-GFP binding profile on GMPCPP microtubules
Request a detailed protocolMicrotubule and EB1-GFP fluorescence intensity were analyzed, and the microtubule aligned, as previously described (Coombes et al., 2016). Briefly, the single time point images of GMPCPP microtubules with EB1-GFP were cropped to separate each microtubule into a single image using ImageJ. Then, integrated and averaged line scans of each microtubule image were created using a MATLAB script. In each case, the microtubule was aligned with the brighter EB1-GFP (green) fluorescence end on the right, and then the red and green fluorescence were plotted as a function of microtubule length from the dimmer EB1-GFP signal end to the brighter EB1-GFP signal end. To do this, the green EB1-GFP fluorescence was integrated along the length of each microtubule ± 4 pixels above and below the microtubule centerline to account for point spread function and variability in properly finding the microtubule centerline. Then, the green fluorescence intensity was summed over the last 9 pixels on both ends of the microtubule. The lower summed value was considered the dimmer EB1-GFP end, while the higher summed value was deemed the brighter EB1-GFP end. To combine all individual microtubule data into an ensemble average plot, the microtubules were rebinned to a common length, represented by the mean length of all observed microtubules (Gardner et al., 2005). Scatter plots of the ensemble average values were created by importing the integrated line scan fluorescence data into Excel.
Microtubule tip structure analysis
Request a detailed protocolAverage tip standard deviation values were calculated by fitting an error function to the microtubule ends, as previously described (Demchouk et al., 2011).
EB1-GFP/tubulin intensity ratio analysis
Request a detailed protocolThe EB1-GFP/Tubulin intensity ratio was analyzed for every individual microtubule using a previously described MATLAB script (Coombes et al., 2016). Briefly, the ends of each microtubule image were manually clicked by a user. Then, the average green and red fluorescence intensity between the clicks, including +/- 4 pixels above and below the centerline (256 nm) established by the two clicks, was calculated. Background in the red and green channels was estimated by calculating the average green and red fluorescence between the two clicks, but in the pixels 8–22 above the centerline established by the two clicks, and in the pixels 8–22 below the centerline established by the two clicks. For each microtubule, the average EB1-GFP signal over background was calculated by dividing the average signal along the microtubule by the average background estimate. Similarly, the average red microtubule signal over background was calculated by dividing the average red microtubule signal by the average red background estimate. Finally, the intensity ratio of average green signal over background to average red signal over background was calculated and reported for each microtubule.
EB1-GFP binding coverage analysis
Request a detailed protocolTo compare relative binding of EB1-GFP on GDP and GDP-Pi microtubules, and in the presence of Vinblastine, the total length of green (EB1-GFP) occupancy was divided by the total length of the red microtubules on each image (defined as EB1-GFP ‘microtubule coverage’). This was accomplished by using previously described semi-automated MATLAB analysis code (Reid et al., 2017). Briefly, first, automatic processing of the red microtubule channel was used to determine the microtubule-positive regions, which then allowed for conversion of the red channel into a binary image with white microtubules and a black background. The green EB1-GFP channel was then also pre-processed to smooth high-frequency noise and to correct for TIRF illumination inhomogeneity. The green channel threshold was then manually adjusted to ensure visualization of all EB1-GFP binding areas on each microtubule. Measurements of the total EB1-GDP length were then automatically collected from the identified microtubule regions. For presentation, the EB1-GFP microtubule coverage values for each image and condition were normalized to a specific grand average control value.
Analysis of peak EB1-GFP binding to microtubules in LLC-Pk1 cells
Request a detailed protocolTo analyze the peak EB1-GFP binding to growing microtubule ends, individual comets were analyzed using MATLAB. EB1-GFP comet movies were first analyzed to ensure that only mature comets were selected for analysis. For each mature comet, MATLAB code was used which allowed two manual clicks on each comet: at the location of the highest intensity spot on each comet, and on the microtubule lattice just outside the end of the comet. In addition, the user clicked twice to measure the length of the comet. Then, the fluorescence intensity at the highest intensity spot on the comet was divided by the fluorescence intensity on the microtubule lattice outside of the comet, which we defined as the normalized peak EB1-GFP tip fluorescence.
Electron microscopy experiments
Request a detailed protocolTo collect electron microscopy images of GMPCPP microtubules, the microtubules were prepared as described above. One drop of the microtubule solution was placed on a 300-mesh carbon coated copper grid for a duration of 60 s, after which the grid was stained with 1% uranyl acetate for 60 s. The stain was the wicked away using filter paper, and the grid was left to dry and then stored until use. The samples were imaged using an FEI Technai Spirit BioTWIN transmission electron microscope. Cryo-EM was performed on the same electron microscope. Samples were prepared on a 300-mesh copper grid with a lacey-carbon support film. Grids were treated in a Pelco Glow Discharger before the addition of the GDP microtubule sample and freezing in vitreous ice using a FEI Vitrobot.
Electron microscopy imaging of EB1 conjugated to gold beads was performed by placing one drop of a solution containing disrupted-structure GDP microtubules (prepared as described above) with gold-bead-conjugated EB1 onto a 300-mesh carbon coated copper grid. The sample grid was treated identically to the procedure described above for TEM of GMPCPP microtubules.
Analysis of EB1-bead experiment
Request a detailed protocolImages of EB1 conjugated to gold beads were analyzed in two parts. First, each image was examined manually. Gold beads appearing in an image were tallied and classified according to their proximity to a microtubule and the appearance of the microtubule at the location of the bead. Only beads directly contacting a microtubule were tallied, and were classified into the following categories: Edges, for gold beads localized at the edges of sheet-like regions of a microtubule or at a microtubule end; Defect, for gold beads localized to regions of the microtubule with visible defects such as gaps or breaks; and Lattice, for gold beads localized to intact regions of the microtubule. Additionally, gold beads found on sheet-like regions were sub-classified based on their location on the sheet, as either Sheet-Edge or Sheet-Middle. To be classified as a Sheet-Edge, a bead was required to overlap with the sheet edge but have its center located beyond, not overlapping, the sheet. Secondly, using a previously described MATLAB script, the total perimeter of the all microtubules in the gathered images was traced and each segment was classified as being Lattice or Edge/Defect, based on how a bead would have been classified if it was located at the given segment of microtubule (Reid et al., 2017). The lengths for each classification were summed and used to normalize the counts.
EB1 3D diffusion and binding simulation: setup and assumptions
Request a detailed protocolApproximations for the shapes of a tubulin dimer and EB1 microtubule binding domain (PDB ID: 3JAR; Zhang et al., 2015) were created manually based off of Cryo-EM reconstruction data using 3D modeling software (Blender) and exported to an. obj object file format. EB1’s binding site coordinates were determined by calculating the center of the contacting faces for each of the four adjacent tubulin dimers, and the binding center was determined as the average position of the four binding interface coordinates.
The simulation was coded and run using MATLAB 2015a (Mathworks). The tubulin dimer subunits were arranged into the canonical microtubule arrangement, with either a blunt or tapered end, maintaining 207 tubulin dimers (average protofilament length ~16 dimers) for both conditions. EB1 was initialized at a random position on a sphere of radius 500 nm centered on the microtubule. We note that while the simulated microtubule shape was approximately cylindrical with a height of ~128 nm, the random initial localization of EB1 within a 500 nm radius of the microtubule did not bias the simulated EB1 molecules toward the microtubule ends, as demonstrated by our face-binding simulations (Figure 4F), in which no end bias was observed.
EB1 3D diffusion and binding simulation: dynamic calculation of time step size
Request a detailed protocolIn order to run the simulation efficiently, the time step for the simulation was dynamically adjusted based on the distance of EB1 from the microtubule, similar to Castle and Odde (2013). Briefly, the time step was large (~7×10−6 s) when the simulated EB1 molecule was far from the microtubule (≥100 nm), and small (~4×10−12 s) when the EB1 molecule was close to the microtubule (≤1 nm). Specifically, the scaled time step sizes were calculated based on the translational diffusion speed of the EB1 molecule, where the translational diffusion step size was governed by:
(1)
Where Δx = translational diffusion molecule step size, d = dimensions (=3), Dc = translational diffusion coefficient (see below), and Δt = time step size. This equation was then used to determine the scaled time step size, such that when the EB1 molecule was ≥100 nm from the microtubule (e.g., Disti ≥ 100), the time step size was then calculated from Equation 1 such that the molecule would be five steps away from the microtubule (e.g., Δxi ≡ Disti/5), and when EB1 was ≤1 nm from the microtubule, the time step size was then calculated from Equation 1 such that the molecule would be 20 steps away from the microtubule (e.g., Δxi ≡ Disti/20). The time step size was scaled linearly between those lengths, and so that a step closer to the microtubule reduced the time step size, until the EB1 molecule was 1 nm from a binding site, at which time a fixed time step was used that resulted in typical diffusion lengths of 0.5 angstroms per step. The distance used in these calculations (Disti) was the separation distance between the closest points on the microtubule and on EB1, not the center-to-center distance.
EB1 3D diffusion and binding simulation: EB1 3D diffusion
Request a detailed protocolEach EB1 molecule was allowed to diffuse both translationally and rotationally until the molecule was either further than 2000 nm from the simulation center, or else had the EB1-binding interface properly oriented and within 1 nm of the binding interface center of any microtubule binding location. EB1 diffusion was governed by the calculated translational and rotational diffusion coefficients as determined by Equations 2 and 3, respectively:
(2)
(3)
In the above equations, ρ is viscosity of water, and r is the radius of the EB1 molecule, approximated as the average radius of all its vertex points. Diffusion and rotation was assumed to be equal across all axes.
The translational distance that the EB1 molecule traveled in a time step was then calculated based on random sampling from a Gaussian distribution governed by:
(4)
(5)
(6)
where dx, dy, and dz were the translational displacement in x, y and z respectively, and rGauss was a normally distributed random number (mean: 0, standard deviation: 1).
Similarly, in the same time step, the angle of rotation for EB1 was also determined from normally distributed random number, and the rotational diffusion constant:
(7)
(8)
(9)
EB1 3D diffusion and binding simulation: EB1 collision with a microtubule
Request a detailed protocolEB1 was not permitted to pass through or intersect volumes with any tubulin dimers. The dynamic time steps prevent skipping from one side of a tubulin dimer to the other in one time step, thus avoiding collision, by maintaining appropriately small step sizes when near a tubulin dimer. Collisions and measurements of the nearest point distance between EB1 and any tubulin subunit were conducted using the Voronoi-Clip (vClip) algorithm (Mirtich, 1998).
Briefly, the closest point between the EB1 polyhedron and a tubulin dimer polyhedron were determined by randomly selecting initial candidate features (vertex, edge or face) for each object. Then, the neighboring features of the EB1 candidate were tested to find one that was closer to the Tubulin candidate feature. If a feature was found to be closer than the initial candidate, it became the new candidate. This was repeated for both the EB1 and Tubulin objects until no two candidates could be found that were closer together than the current pair. Then, if the distance between them was less than or equal to zero (with respect to the object’s outer surface), that indicated that they were intersecting and a collision had occurred, in which case the EB1 position was reverted to the previously recorded value, and the EB1 molecule permitted another attempt at diffusion without collision. If the distance between candidate features was greater than zero, no collision had occurred and the simulation proceeded to the next time step.
The vClip method is useful in reducing computational load, because the final candidate features can be stored from the last time step and used as the initial candidate features for the next test (Mirtich, 1998). Because the time steps are small, the saved candidate features are often the optimal candidate features (or adjacent to the optimal candidate features) for the new position (that has moved and rotated only slightly).
A second optimization technique was used to avoid testing against every tubulin dimer at every time step. Briefly, a much more rapid test for center to center distance was calculated for EB1 to detect ‘nearby’ tubulin dimers (determined by the sum of the maximum vertex radius for both EB1 and the tubulin dimer, and a buffer distance) as compared to the more expensive and accurate vClip test. ‘Nearby’ was determined by a ‘Sweep and Prune’ algorithm, specifically a hierarchical binary tree of tubulin dimer bounding-boxes that was used to very quickly determine if any tubulin dimers needed be considered ‘Nearby’.
EB1 3D diffusion and binding simulation: EB1 binding to a microtubule
Request a detailed protocolEB1 stopped diffusing, and the simulation was ended for that molecule, when its binding interface was oriented properly and within 1 nm of a binding interface on the microtubule. This ‘binding’ configuration was constrained by both distance and molecule orientation relative to its binding site on the microtubule: if the binding interface was oriented away from the microtubule, the separation distance could be as little as 0 nm, and the binding interface would still be >4 nm (EB1 diameter) away from the tubulin pocket binding interface. In this situation, the simulation would not stop, but the EB1 molecule would continue to diffuse and rotate until it entered into the proper binding position, or diffused out of the simulated volume.
Data availability
All data generated or analysed during this study are included in the manuscript and supporting files.
References
-
Characterization of the aluminum and beryllium fluoride species which activate transducin. Analysis of the binding and dissociation kineticsThe Journal of Biological Chemistry 267:6710–6718.
-
Microtubule architecture in vitro and in cells revealed by cryo-electron tomographyActa Crystallographica Section D Structural Biology 74:572–584.https://doi.org/10.1107/S2059798318001948
-
The contribution of αβ-tubulin curvature to microtubule dynamicsThe Journal of Cell Biology 207:323–334.https://doi.org/10.1083/jcb.201407095
-
TOG-tubulin binding specificity promotes microtubule dynamics and mitotic spindle formationThe Journal of Cell Biology 216:1641–1657.https://doi.org/10.1083/jcb.201610090
-
Mechanisms of kinetic stabilization by the drugs paclitaxel and vinblastineMolecular Biology of the Cell 28:1238–1257.https://doi.org/10.1091/mbc.e16-08-0567
-
Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable ratesThe Journal of Cell Biology 129:1311–1328.https://doi.org/10.1083/jcb.129.5.1311
-
Localized mechanical stress promotes microtubule rescueCurrent Biology 26:3399–3406.https://doi.org/10.1016/j.cub.2016.10.048
-
Microtubule tip tracking and tip structures at the nanometer scale using digital fluorescence microscopyCellular and Molecular Bioengineering 4:192–204.https://doi.org/10.1007/s12195-010-0155-6
-
Microtubule polymerization dynamicsAnnual Review of Cell and Developmental Biology 13:83–117.https://doi.org/10.1146/annurev.cellbio.13.1.83
-
Template-free 13-protofilament microtubule-MAP assembly visualized at 8 A resolutionThe Journal of Cell Biology 191:463–470.https://doi.org/10.1083/jcb.201007081
-
Tension-dependent regulation of Microtubule dynamics at Kinetochores can explain metaphase congression in yeastMolecular Biology of the Cell 16:3764–3775.https://doi.org/10.1091/mbc.e05-04-0275
-
EB1 interacts with outwardly curved and straight regions of the microtubule latticeNature Cell Biology 18:1102–1108.https://doi.org/10.1038/ncb3412
-
Three-dimensional structure of motor moleculesCellular and Molecular Life Sciences 56:184–199.https://doi.org/10.1007/s000180050421
-
Refined structure of alpha beta-tubulin at 3.5 A resolutionJournal of Molecular Biology 313:1045–1057.https://doi.org/10.1006/jmbi.2001.5077
-
Microtubule structure by cryo-EM: snapshots of dynamic instabilityEssays in Biochemistry 62:737–751.https://doi.org/10.1042/EBC20180031
-
The role of tubulin-tubulin lattice contacts in the mechanism of microtubule dynamic instabilityNature Structural & Molecular Biology 25:607–615.https://doi.org/10.1038/s41594-018-0087-8
-
Interaction of kinesin motors, microtubules, and MAPsJournal of Muscle Research and Cell Motility 27:125–137.https://doi.org/10.1007/s10974-005-9051-4
-
Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilamentsThe Journal of Cell Biology 217:2691–2708.https://doi.org/10.1083/jcb.201802138
-
V-Clip: fast and robust polyhedral collision detectionACM Transactions on Graphics 17:177–208.https://doi.org/10.1145/285857.285860
-
Organization and dynamics of growing microtubule plus ends during early mitosisMolecular Biology of the Cell 14:916–925.https://doi.org/10.1091/mbc.e02-09-0607
-
Cargo transport: molecular motors navigate a complex cytoskeletonCurrent Opinion in Cell Biology 20:41–47.https://doi.org/10.1016/j.ceb.2007.11.006
-
Cell cycle-dependent changes in Microtubule dynamics in living cells expressing green fluorescent protein-alpha tubulinMolecular Biology of the Cell 12:971–980.https://doi.org/10.1091/mbc.12.4.971
-
Microtubules self-repair in response to mechanical stressNature Materials 14:1156–1163.https://doi.org/10.1038/nmat4396
-
Microtubules: evidence for 13 protofilamentsThe Journal of Cell Biology 59:267–275.https://doi.org/10.1083/jcb.59.2.267
-
Controlling kinesin by reversible disulfide cross-linking. Identifying the motility-producing conformational changeThe Journal of Cell Biology 151:1081–1092.https://doi.org/10.1083/jcb.151.5.1081
-
Interactions between EB1 and microtubules: dramatic effect of affinity tags and evidence for cooperative behaviorThe Journal of Biological Chemistry 284:32651–32661.https://doi.org/10.1074/jbc.M109.013466
Decision letter
-
Andrew P CarterReviewing Editor; MRC Laboratory of Molecular Biology, United Kingdom
-
Anna AkhmanovaSenior Editor; Utrecht University, Netherlands
-
Manuel TheryReviewer; CEA, France
In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.
[Editors’ note: a previous version of this study was rejected after peer review, but the authors submitted for reconsideration. The first decision letter after peer review is shown below.]
Thank you for submitting your work entitled "Microtubule Structural State Recognition Can Explain the Rapid Flux of EB1 to Microtubule Ends" for consideration by eLife. Your article has been reviewed by a Reviewing Editor and a Senior Editor, a Reviewing Editor, and three reviewers. The following individuals involved in review of your submission have agreed to reveal their identity: Manuel Thery (Reviewer #1).
Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.
A major point of interest in the manuscript is the role of specific microtubule lattice structures (defects/edges) in the initial binding of EB1 to microtubules. One reviewer considered that this, and the implication that nucleotide state of tubulin is not the key feature for recognition, was intrinsically interesting. The other two reviewers felt that you were discussing a more nuanced scenario where partial/edge binding sites provide the first binding interaction for EB1 which is then locked in by arrival of new tubulins. These two reviewers were, however, not convinced that the data in the paper were sufficient to support this model over other possibilities.
We discussed the paper among the reviewers at some length and I am afraid the consensus was that it is not possible to ask for revisions at this stage. I include all the reviewers comments below so you can get an idea of whether you want to try a new submission to eLife or to modify the manuscript to submit elsewhere.
Reviewer #1:
In this manuscript the authors argue that EB1 recognizes specific microtubule lattice structures (presenting the lateral side of tubulin dimers) rather than the nucleotide state of the tubulin (i.e. GTP versus GDP). Thereby they contradict a long-standing belief in the field. As such this paper is ground breaking and deserves publication in a top quality journal such as eLife.
The main arguments allowing them to reach these conclusions are:
- EB1 binds more frequently to the plus tips of GMPCPP microtubules (ie microtubules made of GTP-like tubulin) than along the lattice. So the tubulin state is not sufficient to determine the affinity of EB1.
- EB1 binds the transition between microtubule seeds and the GMPCPP lattice even more than plus tip. So it is not the tip per se but some structural features that EB1 binds to.
- EB1 binds disrupted lattice more than intact lattice. They used EB1-beads and cryo EM to correlate lattice structure and EB1 localization.
- EB1 binds the edge of sheet-like microtubule structures rather than the central part of the sheet. Arguing again that it recognizes a structure more than the nucleotide state.
- key control experiment: Kif5b, which is supposed to recognize the outer rather than the lateral part of tubulins (is this really clear? Demonstrated previously?), does not bind disrupted lattice more than intact lattice.
My concerns are the following:
- differences between intact lattice and tips on GDP microtubules are significant but really small. Differences are huge when the lattice is so much damaged that is incompatible with actual microtubules (they would depolymerise immediately). Have these difference any physiological relevance?
- tricks to disrupt the lattice are quite strong and may have unexpected side-effects.
- On dynamic GDP/GTP microtubules there is a high concentration of EB1 at the growing tips. Does the nucleotide state also matters? Or only the structure? Does the normalization in Figure 2C (between normal and disrupted lattices) hide the fact that EB1 binds much more to GMPCPP and GTPgammaS microtubules than to GDP microtubule and thus that the tubulin state actually matters "more" than the lattice structure? It would be nice to show the non-normalized values and comment on this point.
- The fact that EB1 binds more to tapered end than to the lattice is known (Guesdon et al, 2016). The fact that EB1 binds to the side of tubulin dimers is known (Zhang et al, 2015). The fact that Kif5b binds the outer part of tubulin is known (at least it is assumed by the authors but I am not sure how this is actually demonstrated). So, it is no surprise that EB1 binding is structure-sensitive and that Kif5b is not. One could consider that all evidences were already present and thus contest the actual innovation of this work.
- I can't prevent myself from being frustrated that our work, which showed for the very first time some tubulin dynamics on supposedly damaged lattice regions is not cited here. I hope this is not intentional to claim for more novelty.
- The authors did not discuss the work of Pous and Perez, 2016 in which they showed that Clip170 binds to damaged microtubule lattice. We should also take into account that the observations in Pous and Perez paper somehow limit the novelty of this work.
Reviewer #2:
The submission from Reid et al., addresses an interesting question about how EB1 recognizes the growing microtubule end. Although there has been a lot of work on this question from multiple groups, I think it is fair to say that the science is not exactly settled. In their work, the authors use quantitative fluorescence microscopy along with computational simulations of association and methods developed by the Gardner lab to create microtubules with 'damaged' regions (disruptions in the lattice). The logic of the manuscript goes as follows. Tow experimental observations (i) that EB1 prefers to bind more tapered microtubule ends, which correlates with the plus end; EB1 also localizes preferentially at the transition between seed and new growth, which may contain lattice defects (Figure 1); and (ii) that EB1 prefers to bind microtubules containing disruptions (Figure 2); motivate the hypothesis that EB1 may prefer to associate with 'edge' sites. An implementation of this hypothesis into a computational simulation of association kinetics shows that edge association can lead to faster association (Figure 3), and control simulations using a 'face binder' (and a control experiment using kinesin) demonstrate that edge binding is not an obligatory outcome of this kind of modeling. This leads to a model (Figure 5) wherein EB1 arrives via a 'lock-in' mechanism that entails rapid (but weak/transient) associations with partial/edge-binding sites that can get 'locked in' to a higher affinity state by arrival of new ab-tubulins that complete the EB1 binding site.
I appreciate that the authors are looking at this question in a new way, and deploying new approaches to do it. The manuscript is well-written, and the figures are logical and clear and obviously prepared with care. However, there appear to be some inconsistencies in logic/interpretation that make me question whether all of the data add up in the way the authors say they do. Additionally, and independent of my concern about inconsistency, given that this is a pretty well-studied problem already, I don't think that in its present form the manuscript has done enough to convincingly rule out alternative mechanisms (e.g. that EB simply associates directly with 'cap' sites without going through a 'lock-in'), to justify the need for the alternative model presented, or to show it can quantitatively explain existing data from other groups (e.g. Maurer et al., 2014). In the end, while it may be that EB1 can rapidly and transiently associate with edge sites, I'm not yet convinced that is necessary for the mechanism of its end binding.
Connection between experiments and simulations.
The experiments showing association of EB1 with damaged lattices are interesting. But the molecular nature of those sites is not known. The authors pursue a model in which the defining characteristic of those sites is elevated edge content. But can they rule out that in those damaged sites tubulin adopts more 'sheet-like' conformations that mimic end taper and curvature (e.g. Guesdon)?
- They simulate association kinetics, but nearly all experiments measure binding in a way that probably reflects affinity
The simulations (for which the use of blunt and tapered microtubule segments is clever) simulate the rate of association in what I think is a reasonable way. Mostly they are clear about this, but in a few places the work 'binding' is used in a way that could be misleading. The authors reasonably state that these partial edge binding sites are likely to be low-affinity ones, but multiple supporting figure panels essentially reflect equilibrium binding, which should show the high-affinity sites, not the low-affinity ones the authors care about. This apparent contradiction needs to be clarified. I think the details of the 'lock-in' also need to be fleshed out in terms of the relative kinetics of EB1 dissociation from edge sites and ab-tubulin association to complete EB1 binding sites. Under what regimes can this work?
- Integration with current knowledge
Maurer et al., 2014 contains a minimal kinetic model that can describe quantitative observations about EB1 comets. The authors are essentially proposing a different model for how EB1 gets to its comet site. I think they need to explain better why an alternate model is needed, and maybe even show that theirs can actually do what Surrey's toy model did.
In subsection “Rapid frame-rate fluorescence microscopy experiments demonstrate increased on-rate of EB1-GFP to disrupted-structure microtubule pools”, the wording seems to indicate that Guesdon et al., also observed significant edge binding. But if I read Guesdon et al., correctly, only 2.1% of their observed binding was at an edge or on the inside of a sheet. This is a borderline minor point, but I think they authors need to be clearer about where prior data support their model, and about where their data appear to be in conflict with prior data.
Reviewer #3:
Reid et al. have studied how EB1-GFP binds to different microtubule structures using TIRF microscopy, electron microscopy, and computational modeling. They show that EB1-GFP binds to the ends of GMPCPP microtubules at intermediate salt concentrations and binds preferentially to "disrupted" microtubules that were prepared with Taxol. The idea is that these structures have incomplete EB binding sites, which is why EB prefers them. Their computational model is a Brownian dynamics simulation that measures the amount of time that EB diffuses become coming close to its binding site. They propose that EB binds with faster on-rates to incomplete binding sites located at the very end of the microtubule. They conclude with a model for EB end-recognition wherein the tapered, incomplete end of the lattice is the location where EB loads onto the microtubule.
It's important to state that this manuscript is squarely at odds with some ideas circulating in the field. A few labs (e.g, Surrey) have published data showing that the EB signal is displaced back from the very end of the microtubule, with polymerases like XMAP215 being found at the very end instead. There are a few hypotheses for why EB is displaced. One hypothesis is that EB prefers GDP-Pi lattices (Nogales). My favorite idea is that the end is tapered, which means that the binding sites for EB1 are incomplete, and thus EB doesn't bind there. I should say that a recent paper by Guesdon et al., used EM to show that EB can bind at the very end, but the fluorescence data is very hard to ignore, given the much larger number of observations relative to the EM. This manuscript argues that the "EB-free zone" is not EB free and is rather the zone that EB uses to load onto the lattice.
Overall, the manuscript does a poor job engaging with the debate. Also, in order to overturn an emerging consensus, the expectation re: data and analysis is high. Unfortunately, I'm not sure that the paper brings enough to the table. I will highlight some technical concerns that I have below. But I'm surprised to have a paper on EB binding that doesn't have any analysis of end-tracking of dynamic microtubules in it. There is no direct evidence that the tapered end is where the EB loads on, which could only come from clever experiments using dynamic microtubules. Combined with the problems highlighted below, I cannot support publication in eLife.
Figure 1
1) I would like to see some positive control data on their EB1-GFP. Does the protein form nice comets that match the literature in terms of size, etc.? Does the salt concentration they use affect end-tracking behavior? Are the EB1-GFP signals in Figure 1B and Figure 1F single molecules? They look like larger puncta. If they are not single molecules, are the larger signals forming by accumulation or are they aggregates? Quality control of this type would be very welcome.
2) I was surprised by the observation of extensive tapering on the ends of the GMPCPP microtubules in Figure 1C. Where does this tapering coming from? The degree of tapering observed by TIRF microscopy (on the order of 1.5 um) is much larger than the degree of tapering observed by EM, where the length of the taper is similar to the width of the MT (on the order of 25 nm). Why does the degree of tapering differ so much? Microtubule ends are sometimes ragged after they are broken during pipetting. But even for GMPCPP microtubules, these ragged ends shrink back to blunt ends within a few minutes. So my concern is that the tapering in Figure 1C is coming from the computational procedure wherein the microtubules were aligned and then rebinned to a common length. If the end of each microtubule is not at the same location within the bins, this will create a spreading out of the fluorescence signal, won't it? The methods did not provide enough information about the alignment and binning procedure for me to rule this out. The methods did make clear that the fitting of the data to the error function happened only after the alignment and rebinning. Individual microtubules were not fit to the error function, which means that the alignment procedure did not have sub-pixel accuracy. Why not fit each microtubule separately, calculate its σ, and then average all of the σ values together? In principle, this should return the same σ value as the current method. At the moment, I'm not convinced that individual MTs have tapered ends, primarily because I have not been shown data on individual MTs, and I don't understand where the tapering comes from.
Figure 2
3) Figure 2C has some of the strongest data in the paper--it's clear that EB1-GFP is binding preferentially to the "disrupted" microtubules. The analysis method for this data is to divide the EB1-GFP signal by the underlying tubulin signal, with the idea being that tubulin signal will be dimmer in "disrupted" areas. But how does the labeling ratio of the tubulin affect this analysis? Due to the Poisson statistics of labeling and label incorporation, there are always dimmer areas on labeled microtubules. If the label reduces the affinity of EB1-GFP for microtubules at all, you'll see increased EB1-GFP binding in dim areas, which is perhaps why there is an upward spread in the control data. In any case, how is the uneven fluorescence of the microtubules accounted for in their analysis?
Figure 3
4) I'm confused by their computational model. We know the EB binding site is the vertex of 4 tubulin dimers, but the model seems to allow binding to incomplete sites with fewer than 4 dimers. In Figure 3F, it appears that a single tubulin dimer can bind to an EB protein. In other words, the model does not distinguish between complete and incomplete binding sites. I don't understand how this is realistic. The model measures the distance between EB and its site and scores a hit when the distance is only 1 nm, regardless of whether the site is complete. But presumably the affinity of EB1 for its site will fall if the site is incomplete - there are contact surfaces missing. When you are down to a single tubulin, the affinity may be so low that the interaction is equivalent to a transient, non-specific interaction.
5) I don't know what a normalized on-rate is. What are the units? I'm used to seeing on-rates with units of events per unit concentration per unit time. What is the diffusion limit and how was it calculated? Is it the Smoluchowski limit?
[Editors’ note: what now follows is the decision letter after the authors submitted for further consideration.]
Thank you for submitting your article "Structural state recognition facilitates tip tracking of EB1 at growing microtubule ends in cells" for consideration by eLife. Your article has been reviewed by Anna Akhmanova as the Senior Editor, a Reviewing Editor, and two reviewers. The following individuals involved in review of your submission have agreed to reveal their identity: Manuel Thery (Reviewer #2).
The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.
Summary:
The authors have resubmitted their manuscript on the binding of EB1-GFP to microtubules and have included substantial new data.
The resubmission does a good job of clarifying the authors' arguments and of distinguishing between "arrival events" and "binding." Overall, after reading the revised manuscript, we came away thinking that the authors might be on to something. This data should be published so that the field can grapple with it and what it might mean.
That said, the reviewers and myself have concerns about some of the new data, in particular the binding experiments of EB1-GFP to different microtubule lattices. Also, in its current form the manuscript makes several bold claims that are not well supported and does not adequately discuss the structural biology that is relevant to the topic. These problems should be straightforward to fix.
Essential revisions:
1) GDP-Pi microtubules.
We were not convinced that you are measuring the change in affinity due to changes in the lattice by comparing GDP microtubules in the presence of KPO4 vs KCl. The ionic strength of these two salts is different and from your methods you appear to have no buffer (e.g. Tris, Hepes etc) in your imaging conditions. We would expect small changes in ionic strength or pH to have large effects on EB1 binding. We also note than many in the field use acetate rather the chloride ions.
We think you need to go all-in on these nucleotide experiments or remove them from the manuscript. All-in means:
- careful controls for the buffers (e.g. matched ionic strengths, pHs)
- use phosphate analogs (BeFx etc) so that binding can be done under similar buffer conditions
- titration of EB1 to determine affinities
Essentially, experiments to the standard of Maurer 2011 or similar.
2) Positive control data. In previous reviews we asked for positive control data on EB1-GFP. The manuscript now includes data showing that their EB1-GFP can track growing ends (previously not included), but true positive control data is still missing, e.g., the comet decay length as a function of microtubule growth rate.
3) Structural biology. There is no discussion of expansion, compaction, lattice twist, etc. The Zhang et al., 2015 paper is cited, but only to support their modeling of the EB binding site and, oddly, to support the claim than microtubules have 13 protofilaments (the correct one there is Tilney, 1973). The central idea of Zhang et al., 2015 is that EB recognizes a "compacted and twisted" state. There is also the Manka and Moores, 2018 paper that claimed to capture the GDP-Pi state. Also missing is the McIntosh et al., 2018 paper that provided tomograms of microtubule ends in cells and in vitro. We understand that a lot of this science is not settled and are personally confused about expansion and compaction (e.g., there are conflicting reports about kinesin's in this regard, and the yeast tubulins are oddly behaved). But unsettled debates shouldn't just be ignored.
4) Vinblastine data. The authors add vinblastine to cells and claim that it "blunts" the microtubule ends, which is why they see reduced EB binding. But vinblastine also induces outward curvature of protofilaments. If the protofilaments are separated from each other and outwardly curved, could that be the reason that EB has reduced affinity for them? See also the McIntosh data, in which the microtubules in cells are already relatively blunt. Could you realistically get the magnitude of signal reduction that you observe with only a small increase in relative bluntness? The vinblastine part of the paper took an overly-simplified view of the drug's mechanism of action and did not engage with the structural biology here either.
5) On a related note you include a statement in the abstract "Correspondingly, in cells, the conversion of growing microtubule ends from a tapered into a blunt configuration resulted in reduced EB1 targeting.". We feel this is really FAR too strong compared to the data you have – it is not even clear that there are tapered ends in cells at all (no, if you believe the McIntosh paper), so you need to revise this statement.
6) Putting the biochemistry all together. It seems that the authors have on-rate constants (directly measured + modeled), as well as off-rate constants (from lifetimes in their single molecule assays on various lattices), which yields K_D values. They also have equilibrium data on tips, closed lattices, disrupted lattices, etc., at specific EB concentrations. Do these numbers all line up?
7) Killer experiment. From reviewer #1
I don't know if it's fair to ask, but there is an obvious killer experiment. The author's argument is that EB1 has a higher on-rate to incomplete sites + a higher off-rate. But because the on-rate is proportionally higher than the off-rate, they get an increase in binding at equilibrium (Figure 2C). This argument implies that EB will flux more through the incomplete sites, even if the steady-state occupancy is higher. So, they should be able to test that directly with FRAP. E.g., take the disrupted vs. closed lattices, FRAP them, and observe faster recovery to a higher equilibrium fluorescence.
https://doi.org/10.7554/eLife.48117.014Author response
[Editors’ note: the author responses to the first round of peer review follow.]
Our decision has been reached after consultation between the reviewers. Based on these discussions and the individual reviews below, we regret to inform you that your work will not be considered further for publication in eLife.
A major point of interest in the manuscript is the role of specific microtubule lattice structures (defects/edges) in the initial binding of EB1 to microtubules. One reviewer considered that this, and the implication that nucleotide state of tubulin is not the key feature for recognition, was intrinsically interesting. The other two reviewers felt that you were discussing a more nuanced scenario where partial/edge binding sites provide the first binding interaction for EB1 which is then locked in by arrival of new tubulins. These two reviewers were, however, not convinced that the data in the paper were sufficient to support this model over other possibilities.
We discussed the paper among the reviewers at some length and I am afraid the consensus was that it is not possible to ask for revisions at this stage. I include all the reviewers comments below so you can get an idea of whether you want to try a new submission to eLife or to modify the manuscript to submit elsewhere.
Reviewer #1:
In this manuscript the authors argue that EB1 recognizes specific microtubule lattice structures (presenting the lateral side of tubulin dimers) rather than the nucleotide state of the tubulin (ie GTP versus GDP). Thereby they contradict a long-standing belief in the field. As such this paper is ground breaking and deserves publication in a top quality journal such as eLife.
The main arguments allowing them to reach these conclusions are:
- EB1 binds more frequently to the plus tips of GMPCPP microtubules (ie microtubules made of GTP-like tubulin) than along the lattice. So the tubulin state is not sufficient to determine the affinity of EB1.
- EB1 binds the transition between microtubule seeds and the GMPCPP lattice even more than plus tip. So it is not the tip per se but some structural features that EB1 binds to.
- EB1 binds disrupted lattice more than intact lattice. They used EB1-beads and cryo EM to correlate lattice structure and EB1 localization.
- EB1 binds the edge of sheet-like microtubule structures rather than the central part of the sheet. Arguing again that it recognizes a structure more than the nucleotide state.
- key control experiment: Kif5b, which is supposed to recognize the outer rather than the lateral part of tubulins (is this really clear? Demonstrated previously?), does not bind disrupted lattice more than intact lattice.
My concerns are the following:
- differences between intact lattice and tips on GDP microtubules are significant but really small. Differences are huge when the lattice is so much damaged that is incompatible with actual microtubules (they would depolymerise immediately). Have these difference any physiological relevance?
In the paper, we used lattice damage as a tool to explore potential differences in EB1 affinity for microtubules based on structure, and did not intend to imply that this level of damage would be typical of microtubules in cells. We have clarified this reasoning in the text, as follows: “These “control” and “disrupted‐structure” populations were described for the three most commonly used in‐vitro microtubule nucleotides: GDP, GMPCPP, and GTPγS. We used the “disrupted‐structure” populations with disruptions in lattice integrity as a tool to reveal potential differences in EB1 binding based on microtubule structure.”
Through our experiments and simulations, we find that the on‐rate of EB1 to edge sites is predicted to be ~70‐fold faster than to lattice sites, which could have a physiological impact at the tips of GTP microtubules, which have been previously shown to be enriched in edge sites.
- Tricks to disrupt the lattice are quite strong and may have unexpected side-effects.
While we do use “disrupted‐structure” microtubule populations to explore the effect of structure on EB1 affinity for the microtubule, the methods used to create these populations reflect commonly used methods to generate in‐vitro microtubules, and so we do not predict that unexpected side‐effects are likely. In addition, the methods used for the three different nucleotides are distinct, and so it is unlikely that similar side effects would occur in each case. We will clarify the text, as follows: “We note that, while the preparation protocols for microtubules using the three different nucleotides were distinct, all of these protocols reflect commonly used methods for producing stable in vitro microtubules.”
- On dynamic GDP/GTP microtubules there is a high concentration of EB1 at the growing tips. Does the nucleotide state also matters? Or only the structure? Does the normalization in Figure 2C (between normal and disrupted lattices) hide the fact that EB1 binds much more to GMPCPP and GTPgammaS microtubules than to GDP microtubule and thus that the tubulin state actually matters "more" than the lattice structure? It would be nice to show the non-normalized values and comment on this point.
We predict that, based on previously published work, EB1 likely has differential affinity to different GTP nucleotide states, and we did not intend to contradict or weigh in on this argument. Because the microtubules in Figure 2C are generated with distinct protocols for each nucleotide type, we believe that direct comparisons of EB1 binding to the “control” populations between nucleotide states would be an over‐interpretation of our data. Therefore, although normalization to the average binding intensity of each respective control seems appropriate for Figure 2C, we will provide the baseline average control binding intensity for each nucleotide in the main text, as follows: “The EB1‐GFP/tubulin ratios for each microtubule were normalized to the grand average EB1‐GFP/tubulin ratio for the control microtubule population in each case, to allow for direct comparisons between the disrupted‐structure data and their respective controls (average EB1‐GFP/tubulin binding values used for normalization were as follows: GMPCPP: 0.098 ± 0.0009; GDP: 0.100 ± 0.006; GTPγS: 0.68 ± 0.007 (mean ± SEM); see Materials and methods section).”
The fact that Kif5b binds the outer part of tubulin is known (at least it is assumed by the authors but I am not sure how this is actually demonstrated).
Electron microscopy work has been completed for the specific monomeric Kif5b construct used in our analysis to demonstrate binding to the outer face of a single tubulin subunit. The following text is included to clarify this point: “… we used a monomeric Kif5B‐GFP kinesin construct…to allow for microtubule binding analysis of the monomeric kinesin (K339‐GFP) (Case et al., 2000; Tomishige and Vale, 2000). The Kinesin‐1 Kif5B protein has been shown to dock with a stoichiometry of one kinesin motor per tubulin heterodimer, and binds to the outer surface of the α or β tubulin monomers, rather than the lateral surfaces, in electron microscopy experiments (Hirose and Amos, 1999; Hoenger et al., 1998; Kikkawa et al., 2000; Kozielski et al., 1998; Löwe et al., 2001; Marx et al., 2006; Moores et al., 2002; Nogales et al., 1999; Rice et al., 1999; Sosa et al., 1997)”
- The fact that EB1 binds more to tappered end than to the lattice is known (Guesdon et al., 2016). The fact that EB1 binds to the side of tubulin dimers is known (Zhang et al., 2015). The fact that Kif5b binds the outer part of tubulin is known (at least it is assumed by the authors but I am not sure how this is actually demonstrated). So, it is no surprise that EB1 binding is structure-sensitive and that Kif5b is not. One could consider that all evidences were already present and thus contest the actual innovation of this work.
We agree that evidence exists in the literature to support our argument that EB1 binding is structure sensitive, which we feel strengthens our conclusions.
- I can't prevent myself from being frustrated that our work, which showed for the very first time some tubulin dynamics on supposedly damaged lattice regions is not cited here. I hope this is not intentional to claim for more novelty.
We apologize for this inadvertent omission, and this work is now cited in the introduction, as follows: “… recent work has discovered that lattice damage and tubulin turnover can occur on the microtubule lattice, leading to irregularities along the lattice itself (Schaedel et al., (2015)).”
- The authors did not discuss the work of Pous and Perez, 2016 in which they showed that Clip170 binds to damaged microtubule lattice. We should also take into account that the observations in Pous and Perez paper somehow limit the novelty of this work.
We have added the following description of this work to the discussion: “…it has been shown that microtubule lattice defects resulting from microtubule‐microtubule contacts may be recognized by CLIP‐170 to stimulate microtubule rescue (DeForges, 2016).”
However, we feel that the primary novelty of our new work is in dissecting how the binding location of EB1 on the microtubule may lead to structural recognition based on a steric‐hindrance‐mediated onrate. This has now been clarified throughout the text and in the paper title.
Reviewer #2:
The submission from Reid et al., addresses an interesting question about how EB1 recognizes the growing microtubule end. Although there has been a lot of work on this question from multiple groups, I think it is fair to say that the science is not exactly settled. In their work, the authors use quantitative fluorescence microscopy along with computational simulations of association and methods developed by the Gardner lab to create microtubules with 'damaged' regions (disruptions in the lattice). The logic of the manuscript goes as follows. Tow experimental observations (i) that EB1 prefers to bind more tapered microtubule ends, which correlates with the plus end; EB1 also localizes preferentially at the transition between seed and new growth, which may contain lattice defects (Figure 1); and (ii) that EB1 prefers to bind microtubules containing disruptions (Figure 2); motivate the hypothesis that EB1 may prefer to associate with 'edge' sites. An implementation of this hypothesis into a computational simulation of association kinetics shows that edge association can lead to faster association (Figure 3), and control simulations using a 'face binder' (and a control experiment using kinesin) demonstrate that edge binding is not an obligatory outcome of this kind of modeling. This leads to a model (Figure 5) wherein EB1 arrives via a 'lock-in' mechanism that entails rapid (but weak/transient) associations with partial/edge-binding sites that can get 'locked in' to a higher affinity state by arrival of new ab-tubulins that complete the EB1 binding site.
I appreciate that the authors are looking at this question in a new way, and deploying new approaches to do it. The manuscript is well-written, and the figures are logical and clear and obviously prepared with care. However, there appear to be some inconsistencies in logic/interpretation that make me question whether all of the data add up in the way the authors say they do.
The proposed responses to these issues are addressed in detail below.
Additionally, and independent of my concern about inconsistency, given that this is a pretty well-studied problem already, I don't think that in its present form the manuscript has done enough to convincingly rule out alternative mechanisms (e.g. that EB simply associates directly with 'cap' sites without going through a 'lock-in'), to justify the need for the alternative model presented, or to show it can quantitatively explain existing data from other groups (e.g. Maurer et al., 2014).
Once we received the reviews for our manuscript, we realized that we did not properly convey our perspective regarding the contribution of our work to the discussion regarding EB1 tip tracking. In general, we did not intend to put forward a new model to overturn existing models for EB1 tip tracking. Essentially, we feel that the idea that the on‐rate of EB1 to microtubules may be sensitive to microtubule structure is interesting, and could potentially speed the arrival of EB1 to microtubule plusends. In providing the final (speculative) cartoon, our attempt was to integrate this general idea with current models for EB1 tip tracking. However, the final cartoon was perhaps overly suggestive that we were proposing an alternate model for tip tracking. Thus, we plan to drop the final cartoon, and to limit our discussion of “tip tracking” to a short paragraph in the Discussion section. Further, we will refocus the manuscript on our key result, which is that the on‐rate of EB1 to microtubules may be sensitive to the structure of the microtubule itself.
In the end, while it may be that EB1 can rapidly and transiently associate with edge sites, I'm not yet convinced that is necessary for the mechanism of its end binding.
We agree that data was not presented in the manuscript to suggest this mechanism is necessary for tip tracking of EB1. As noted above, we have refocused the manuscript on our key result regarding the onrates of EB1 to microtubules based on structure. To specifically address this concern, we will also add the following sentence to the discussion: “Overall, while we feel that this process will contribute to rapid binding of EB1 to the microtubule tip, starting at the open, tapered growing end with its more easily accessible edge sites, its specific contribution to the mechanism of tip tracking remains an open question.”
Essential revisions:
Connection between experiments and simulations.
The experiments showing association of EB1 with damaged lattices are interesting. But the molecular nature of those sites is not known. The authors pursue a model in which the defining characteristic of those sites is elevated edge content. But can they rule out that in those damaged sites tubulin adopts more 'sheet-like' conformations that mimic end taper and curvature (e.g. Guesdon)?
Based on our analysis, we predict that the damaged lattices mimic end‐taper and “sheet‐like” conformations, which would correspondingly increase the number of edge sites, and we did not observe excessive curvature in our electron microscopy analysis of the damaged lattices. However, we will add the following sentence to the discussion to address this concern “… we cannot exclude that curvature of microtubule sheets could potentially act to alter EB1 on‐rates.”
- They simulate association kinetics, but nearly all experiments measure binding in a way that probably reflects affinity
The simulations (for which the use of blunt and tapered microtubule segments is clever) simulate the rate of association in what I think is a reasonable way. Mostly they are clear about this, but in a few places the work 'binding' is used in a way that could be misleading.
We agree that the simulation itself does not measure affinity or steady‐state binding, and that the term “binding” in regards to the simulation could be misleading. We have now renamed simulated EB1 “binding” as simulated EB1 “arrival events” throughout the manuscript text and in the figures, to clarify that the simulation does not reflect steady‐state binding, but rather the locations where EB1 arrives (in proper binding orientation and position) most rapidly onto the microtubule.
The authors reasonably state that these partial edge binding sites are likely to be low-affinity ones, but multiple supporting figure panels essentially reflect equilibrium binding, which should show the high-affinity sites, not the low-affinity ones the authors care about. This apparent contradiction needs to be clarified.
This is a good point, and has caused us to think carefully about our results. We propose adding the following comment to the discussion: “After binding to an edge‐site, EB1 would likely undergo a higher off‐rate as a result of the partial binding interface that is inherent to these edge‐sites. However, our results show an increase in steady‐state binding to disrupted microtubule structures, regardless of nucleotide state (Figure 2C‐E), suggesting that the affinity of EB1 is higher on disrupted structures, regardless of the likely increase in off‐rates. This increase in affinity may be due to a stronger effect of disrupted microtubule structure in accelerating the EB1 on‐rate, as compared to increasing the EB1 offrates. For example, we observed a ~45‐fold increase in EB1 on‐rates to disrupted GDP microtubule structures relative to controls (Figure 3J), while the “short” EB1 dwell times, which could be associated with edge‐bound EB1 on GDP microtubules, were only ~8 fold faster than the lattice‐bound “long” dwell times (Figure S2D), resulting in a net affinity increase of ~5‐fold.”
I think the details of the 'lock-in' also need to be fleshed out in terms of the relative kinetics of EB1 dissociation from edge sites and ab-tubulin association to complete EB1 binding sites. Under what regimes can this work?
We agree that this is an interesting question, however, the “lock‐in” model was only speculative at this point, and further experimental work will be required to determine whether a “lock‐in” model contributes to EB1 tip tracking of growing microtubule plus‐ends. To focus the manuscript on our current data and key results, we have dropped the final cartoon (and associated text) that included this speculative idea.
- Integration with current knowledge
Maurer et al., 2014 contains a minimal kinetic model that can describe quantitative observations about EB1 comets. The authors are essentially proposing a different model for how EB1 gets to its comet site. I think they need to explain better why an alternate model is needed, and maybe even show that theirs can actually do what Surrey's toy model did.
As noted above, we did not intend to discard existing models for the general mechanism of EB1 tip tracking, but rather to describe how the arrival rates of EB1 to microtubules may be influenced by microtubule structure. We have refocused the manuscript on our key result regarding the on‐rates of EB1 to microtubules based on structure, which is supported both experimentally and in simulation. In addition, we have added the following comment to the discussion: “Overall, while we feel that this process will contribute to rapid binding of EB1 to the microtubule tip, starting at the open, tapered growing end with its more easily accessible edge sites, its specific contribution to the mechanism of tip tracking remains an open question.”
In subsection “Rapid frame-rate fluorescence microscopy experiments demonstrate increased on-rate of EB1-GFP to disrupted-structure microtubule pools”, the wording seems to indicate that Guesdon et al., also observed significant edge binding. But if I read Guesdon et al., correctly, only 2.1% of their observed binding was at an edge or on the inside of a sheet. This is a borderline minor point, but I think they authors need to be clearer about where prior data support their model, and about where their data appear to be in conflict with prior data.
There are important differences between the observed binding percentages between our new work and that of Guesdon et al., which are: (1) we have normalized the binding percentages to the number of available sites in each case. For example, the number of full lattice sites far exceeds the number of edge sites, and so by normalizing to the number of available sites in each case, our normalized binding frequencies would be substantially larger than the absolute binding frequencies as reported by Guesdon et al., and (2) the work of Guesdon et al., was performed on dynamic microtubules, rather than stabilized microtubules as in our work, and so while new edges would continually be generated during growth, the lifetime of individual edge sites would likely be much more transient than that of full lattice sites. Therefore, for a direct percent‐binding comparison to the stabilized microtubules in our work (in which the time availability of each site is equal), the percentages in Guesdon et a.,l would need to be normalized to account for the total time availability of each site. Thus, a direct comparison of binding percentages between our work and that of Guesdon et al., would require further analysis. However, we have clarified the wording regarding this reference, as follows: “Qualitatively, we observed EB1‐beads that bound to microtubule sheets, both in the middle of the sheet, and on the edges of sheets (Figure 3I, left), as has been previously observed on dynamic microtubules (Guesdon et al., 2016).
Reviewer #3:
Reid et al. have studied how EB1-GFP binds to different microtubule structures using TIRF microscopy, electron microscopy, and computational modeling. They show that EB1-GFP binds to the ends of GMPCPP microtubules at intermediate salt concentrations and binds preferentially to "disrupted" microtubules that were prepared with Taxol. The idea is that these structures have incomplete EB binding sites, which is why EB prefers them. Their computational model is a Brownian dynamics simulation that measures the amount of time that EB diffuses become coming close to its binding site. They propose that EB binds with faster on-rates to incomplete binding sites located at the very end of the microtubule. They conclude with a model for EB end-recognition wherein the tapered, incomplete end of the lattice is the location where EB loads onto the microtubule.
It's important to state that this manuscript is squarely at odds with some ideas circulating in the field. A few labs (e.g, Surrey) have published data showing that the EB signal is displaced back from the very end of the microtubule, with polymerases like XMAP215 being found at the very end instead. There are a few hypotheses for why EB is displaced. One hypothesis is that EB prefers GDP-Pi lattices (Nogales). My favorite idea is that the end is tapered, which means that the binding sites for EB1 are incomplete, and thus EB doesn't bind there. I should say that a recent paper by Guesdon et al., used EM to show that EB can bind at the very end, but the fluorescence data is very hard to ignore, given the much larger number of observations relative to the EM. This manuscript argues that the "EB-free zone" is not EB free and is rather the zone that EB uses to load onto the lattice.
While we have refocused the manuscript text to emphasize our primary conclusion regarding the ability of EB1 to detect microtubule structure, we do not feel that a higher on‐rate of EB1 onto edge sites at microtubule tips would necessarily be at odds with the previously described peak concentration of EB1 away from the very end of the microtubule, due to the difference in binding site density for edge sites as compared to full lattice sites. We have added the following explanation regarding this issue to the Discussion section:
“Overall, we propose that [structural recognition by EB1] will promote rapid loading of EB1 at the microtubule tip, starting at the open, tapered growing end with its more easily accessible edge sites. Although new edge sites are continuously generated as a result of tubulin subunit additions to growing microtubule plus‐ends, we note that the density of edge sites on an open, tapered microtubule lattice would be ~7‐fold lower than that of lattice sites for a closed microtubule tube (ratio 2:14 edge sites: total binding sites per tubulin layer), and so regardless of whether structural recognition facilitates rapid loading of EB1 onto edge sites at the microtubule tip, the peak in EB1‐GFP intensity for a plus‐end EB1GFP comet may be penultimate to the tapered tip (as previously described, Maurer et al., 2014), in a location where a high density of EB1 molecules are bound to the much higher density, four‐GTP‐tubulin pocket lattice binding sites, potentially via addition of new, incoming GTP‐tubulin subunits onto the location of previously edge‐bound EB1 molecules.”
Overall, the manuscript does a poor job engaging with the debate. Also, in order to overturn an emerging consensus, the expectation re: data and analysis is high. Unfortunately, I'm not sure that the paper brings enough to the table.
We have now clarified the Abstract, Results section, and Discussion section to focus on our primary result, which is that structural recognition substantially increases the on‐rate of EB1 to microtubules. While we feel that this is an exciting and important new concept, we do not present evidence to suggest that current EB1 tip tracking models, such as the increased affinity of EB1 to GTP‐tubulin as opposed to GDP‐tubulin, should be overturned or discarded. In addition, we did not intend to suggest that this mechanism could exclusively explain tip‐tracking of EB1, but rather that structural recognition could help to facilitate rapid arrivals of EB1 to the microtubule plus‐end. We apologize for this lack of clarity, and, in addition to dropping the final speculative cartoon, we have added the following sentence to clarify our thinking in this regard: “Overall, while we feel that this process will contribute to rapid binding of EB1 at the microtubule tip, starting at the open, tapered growing end with its more easily accessible edge sites, its specific contribution to the mechanism of tip tracking remains an open question.”
I will highlight some technical concerns that I have below. But I'm surprised to have a paper on EB binding that doesn't have any analysis of end-tracking of dynamic microtubules in it. There is no direct evidence that the tapered end is where the EB loads on, which could only come from clever experiments using dynamic microtubules. Combined with the problems highlighted below, I cannot support publication in eLife.
As noted above, we have refocused the manuscript to emphasize the primary result, which is that the nature of EB1’s binding site on the microtubule allows for microtubule structure recognition as a result of steric hindrance in binding to its four‐tubulin pocket binding site in the lattice. However, we agree that the inclusion of dynamic microtubule results would strengthen the manuscript. Therefore, we have completed dynamic microtubule experiments in which we compared average EB1‐GFP binding intensities at growing microtubule plus‐ends, on the GDP lattice, on the GMPCPP‐seed, and at the transition between the GDP‐lattice and the GMPCPP‐seed. We found that, as would be expected, EB1GFP intensity was ~2.3‐fold (230%) higher at growing microtubule plus‐ends as compared to the overall average intensity on the GDP lattice and GMPCPP seeds. However, consistent with our conclusion that EB1 may recognize microtubule structure, the EB1‐GFP fluorescence at the seed/GDP‐lattice transition point was 38% higher than the average intensity on the GDP lattice and GMPCPP seeds (p<10‐5 vs GDP lattice, p<10‐6vs GMPCPP seeds, n=134 microtubules). These results are consistent with our conclusion that EB1 may recognize microtubule structure, even in the presence of free tubulin in a dynamic microtubule assay. However, EB1‐GFP binding at growing microtubule plus‐ends remained substantially higher than transition point binding (p<10‐16), allowing us to reiterate that this finding may contribute to, but does not overturn, current models for EB1 tip tracking.
Figure 1
1) I would like to see some positive control data on their EB1-GFP. Does the protein form nice comets that match the literature in terms of size, etc? Does the salt concentration they use affect end-tracking behavior? Are the EB1-GFP signals in Figure 1B and Figure 1F single molecules? They look like larger puncta. If they are not single molecules, are the larger signals forming by accumulation or are they aggregates? Quality control of this type would be very welcome.
Dynamic microtubule experiments have been added at two different salt concentrations encompassing experimental work in the manuscript, both of which exhibited robust end tracking behavior, with no evidence of EB1 protein aggregates. The Figure 1 data was not intended as single‐molecule data, but we see no evidence of aggregation or aggregates in our new time‐lapse data. We have now also included images over a range of EB1‐GFP signal intensities in Figure 1, to demonstrate a robust result regardless of EB1‐GFP intensity.
2) I was surprised by the observation of extensive tapering on the ends of the GMPCPP microtubules in Figure 1C. Where does this tapering coming from? The degree of tapering observed by TIRF microscopy (on the order of 1.5 um) is much larger than the degree of tapering observed by EM, where the length of the taper is similar to the width of the MT (on the order of 25 nm). Why does the degree of tapering differ so much? Microtubule ends are sometimes ragged after they are broken during pipetting. But even for GMPCPP microtubules, these ragged ends shrink back to blunt ends within a few minutes. So my concern is that the tapering in Figure 1C is coming from the computational procedure wherein the microtubules were aligned and then rebinned to a common length. If the end of each microtubule is not at the same location within the bins, this will create a spreading out of the fluorescence signal, won't it? The methods did not provide enough information about the alignment and binning procedure for me to rule this out. The methods did make clear that the fitting of the data to the error function happened only after the alignment and rebinning. Individual microtubules were not fit to the error function, which means that the alignment procedure did not have sub-pixel accuracy. Why not fit each microtubule separately, calculate its σ, and then average all of the σ values together? In principle, this should return the same σ value as the current method. At the moment, I'm not convinced that individual MTs have tapered ends, primarily because I have not been shown data on individual MTs, and I don't understand where the tapering comes from.
We thank the reviewer for this observation – yes, the calculated tip standard deviations were large, and although the microtubule fluorescence binning procedure (which has now been more clearly described in the methods) equally redistributes microtubule fluorescence into a standard number of bins regardless of microtubule length, we were performing the analysis over a very large range of microtubule lengths, which artificially inflated the calculated tip standard deviation values. While fitting to individual microtubules was too noisy due to stochastic labeling, we addressed this issue by performing the analysis on small groups of similar length microtubules (maximum microtubule length standard deviation = 0.7 μm in each case). In addition, we verified that our calculated tip standard deviations were statistically indistinguishable even if a group of microtubules with a very small microtubule length standard deviation was used (maximum microtubule length standard deviation = 0.2 μm). While the result that tip standard deviations were larger on the microtubule ends with brighter EB1‐GFP signals remained unchanged with our new analysis, the calculated tip standard deviations are now substantially smaller, in line with our EM observations in Figure 1E.
Figure 2
3) Figure 2C has some of the strongest data in the paper--it's clear that EB1-GFP is binding preferentially to the "disrupted" microtubules. The analysis method for this data is to divide the EB1-GFP signal by the underlying tubulin signal, with the idea being that tubulin signal will be dimmer in "disrupted" areas. But how does the labeling ratio of the tubulin affect this analysis? Due to the Poisson statistics of labeling and label incorporation, there are always dimmer areas on labeled microtubules. If the label reduces the affinity of EB1-GFP for microtubules at all, you'll see increased EB1-GFP binding in dim areas, which is perhaps why there is an upward spread in the control data. In any case, how is the uneven fluorescence of the microtubules accounted for in their analysis?
We have now clarified the description of the data that makes up Figure 2 to note that we did not perform a spatial analysis of EB1 distribution along the length of each microtubules, as follows: “We…measured the average EB1‐GFP fluorescence intensity over background for each microtubule, which was normalized to the average Rhodamine‐tubulin fluorescence intensity over background for each microtubule…. The average EB1‐GFP/tubulin ratios for each microtubule were then normalized to the grand‐average EB1‐GFP/tubulin ratio for the control microtubule population in each case, to allow for comparisons between the disrupted‐structure data and the controls.” We also note that the degree of labeling was consistent between the controls and disrupted‐structure microtubules (microtubules were made from a common reaction mixture for each control/disrupted experiment), and so if the rhodamine label reduced the affinity of EB1‐GFP for microtubules, this effect would be similar in both cases.
Figure 3
4) I'm confused by their computational model. We know the EB binding site is the vertex of 4 tubulin dimers, but the model seems to allow binding to incomplete sites with fewer than 4 dimers. In Figure 3F, it appears that a single tubulin dimer can bind to an EB protein. In other words, the model does not distinguish between complete and incomplete binding sites. I don't understand how this is realistic.
As noted above, the simulation does not measure affinity or steady‐state binding rates, so the term “binding” could be misleading. We have now renamed simulated EB1 “binding” as EB1 “arrival events” throughout the manuscript text and in the figures, to clarify that the simulation does not reflect steadystate binding, but rather the locations in which EB1 arrives (in proper binding position and orientation) most rapidly onto the lattice. In Figure 3F, we explore the number of arrival events of EB1 to each microtubule type (control/disrupted) per every 4000 simulated EB1 molecules, regardless of the tubulin binding site configuration (1‐4 tubulin subunits). Thus, we have clarified the y‐axis in panel D – now called “total arrival events per microtubule”. The purpose of this analysis was to determine whether there would be a differential arrival rate of EB1 to different binding site configurations, regardless of the subsequent off‐rate or dwell time of EB1 at that particular site.
The model measures the distance between EB and its site and scores a hit when the distance is only 1 nm, regardless of whether the site is complete. But presumably the affinity of EB1 for its site will fall if the site is incomplete - there are contact surfaces missing. When you are down to a single tubulin, the affinity may be so low that the interaction is equivalent to a transient, non-specific interaction.
As noted above, we have clarified our wording to note that the computational model does not account for off‐rates and/or affinity of a particular site, but rather, the model specifically explores whether the on‐rate of EB1 to microtubules may be affected by microtubule structure. However, we note that in panels 3G and 3H, we present a specific comparison of simulated EB1 arrivals to 2‐tubulin vs 4‐tubulin sites, excluding 1‐tubulin sites that could potentially have a high off‐rate, and thus limiting our analysis to the partial binding sites that have been observed using electron microscopy in our work as well as in previous work (Guesdon et al.,). Here, we find that there is a ~70‐fold increase in the arrival rate (in proper orientation and position) to 2‐tubulin sites as compared to 4‐tubulin sites.
5) I don't know what a normalized on-rate is. What are the units? I'm used to seeing on-rates with units of events per unit concentration per unit time.
We agree that term “normalized on‐rate” in this graph was too vague. This term has now been dropped, and the units in panel 3H are now shown as “Fraction of Simulated EB1 Molecules”. In this simulation, the ultimate fate of each of the 200,000 simulated EB1 molecule was recorded (e.g., an EB1 molecule never arrives to a microtubule, an EB1 molecule arrives at 2‐tubulin site, an EB1 molecule arrives at a 4tubulin site, etc). Therefore, the numbers in panel 3H show a direct comparison of the fraction of simulated EB1 molecules that arrived at a 2‐tubulin (edge) site, as compared to the fraction that arrived at a 4‐tubulin (lattice pocket) site in the simulation. While these numbers reflect the relative on‐rates, they are not measured in terms of EB1 concentration or arrivals per unit time, and so the term “on‐rate” has been dropped.
What is the diffusion limit and how was it calculated? Is it the Smoluchowski limit?
The term “diffusion limit” has now also been altered, to avoid confusion. The intent with the “diffusion limit” value was to demonstrate that the 2‐tubulin (edge) site EB1 arrivals were still substantially (~4fold) less frequent than the 1‐tubulin site EB1 arrivals. The 1‐tubulin site arrivals are suggestive of a “diffusion limit” in that the steric hindrance to a 1‐tubulin site arrival would be negligible, however, as noted above, arrival to these sites was still stereospecific, such that EB1 could not bind “upside down”, even to a 1‐tubulin site. This comparison is now clarified in the text.
[Editors’ note: the author response to the re-review follow.]
Thank you for submitting your article "Structural state recognition facilitates tip tracking of EB1 at growing microtubule ends in cells" for consideration by eLife. Your article has been reviewed by Anna Akhmanova as the Senior Editor, a Reviewing Editor, and two reviewers. The following individuals involved in review of your submission have agreed to reveal their identity: Manuel Thery (Reviewer #2).
The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.
Summary:
The authors have resubmitted their manuscript on the binding of EB1-GFP to microtubules and have included substantial new data.
The resubmission does a good job of clarifying the authors' arguments and of distinguishing between "arrival events" and "binding." Overall, after reading the revised manuscript, we came away thinking that the authors might be on to something. This data should be published so that the field can grapple with it and what it might mean.
That said, the reviewers and myself have concerns about some of the new data, in particular the binding experiments of EB1-GFP to different microtubule lattices. Also, in its current form the manuscript makes several bold claims that are not well supported and does not adequately discuss the structural biology that is relevant to the topic. These problems should be straightforward to fix.
Essential revisions:
1) GDP-Pi microtubules.
We were not convinced that you are measuring the change in affinity due to changes in the lattice by comparing GDP microtubules in the presence of KPO4 vs KCl. The ionic strength of these two salts is different and from your methods you appear to have no buffer (e.g. Tris, Hepes etc) in your imaging conditions. We would expect small changes in ionic strength or pH to have large effects on EB1 binding. We also note than many in the field use acetate rather the chloride ions.
We think you need to go all-in on these nucleotide experiments or remove them from the manuscript. All-in means:
- careful controls for the buffers (e.g. matched ionic strengths, pHs)
- use phosphate analogs (BeFx etc) so that binding can be done under similar buffer conditions
- titration of EB1 to determine affinities
Essentially, experiments to the standard of Maurer 2011 or similar.
We thank the reviewers for noting this concern, which we had not previously considered. In order to perform experiments with matched ionic strengths, with have now added new data with a phosphate analog, which, as the reviewer notes, has now allowed us to perform detailed binding experiments at matching ionic strengths and salt molarities. The new figures and manuscript text have been copied below. We note that, because the results with the analog were very similar to our original results, we kept our original data in the manuscript, which had matching salt molarities, even though the ionic strengths were not matched in these experiments. However, we clearly note the concern regarding mismatched ionic strengths in the text, to motivate the use of the phosphate analog for the subsequent data set (manuscript text copied below). In addition, due to the environmental and safety hazards of using Beryllium in the lab, we have selected an alternative analogue, AlF4-, described alongside BeF3- in Carlier et al., 1988.
Subsection “EB1 tip tracking by microtubule structure recognition”, introduction to analogue experiments:
“In the KPO4 experiments (Figure 5A-C), while the molarity of the salts in the experiments were matched (55 mM KPO4 vs 55 mM KCl), the ionic strengths of the reaction mixtures were mismatched, which could influence EB1 binding to the lattice. Therefore, we performed further experiments using an analogue of phosphate, AlF4- (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000). Here, the molarity and ionic strengths of the salts included in both experiments were identical (52.5 mM KCl and 2 mM NaF for both experiments). However, 10 μM AlCl3 was included in the phosphate analogue experiments, allowing the Al3+ and F- ions form the π analogue AlF4-, which mimics a phosphate group, but with 1000-fold higher affinity (Antonny and Chabre, 1992; Carlier et al., 1988; Petsko, 2000).”
Subsection “EB1 tip tracking by microtubule structure recognition”, next paragraph, new results text:
“Similar to the KPO4 experiments, we observed reduced EB1 binding in the GDP+AlCl3 experiments as compared to the GDP-alone experiments (Figure 5D). We then quantified EB1-GFP binding using our previously described automated analysis tool (Reid et al., 2017) under conditions of increasing EB1 concentrations (Figure 5E). As previously described, the EB1 binding data was best fit using a cooperative binding curve (Lopez and Valentine, 2016; Zhu et al., 2009), and so we fit the results in each case to a Hill equation, which demonstrated a ~2-fold lower affinity of EB1 for the GDP-Pi-Analogue relative to the GDP microtubules (Figure 5E, see Materials and methods; Kd,GDP=1.9x105 nM, nGDP=2.2; Kd,Analogue=4.2x105.”
2) Positive control data. In previous reviews we asked for positive control data on EB1-GFP. The manuscript now includes data showing that their EB1-GFP can track growing ends (previously not included), but true positive control data is still missing, e.g., the comet decay length as a function of microtubule growth rate.
We have added positive control data, in the form of a comet length vs microtubule growth rate graph, as new Figure 1—figure supplement 1D, as follows:
3) Structural biology. There is no discussion of expansion, compaction, lattice twist, etc. The Zhang, 2015 paper is cited, but only to support their modeling of the EB binding site and, oddly, to support the claim than microtubules have 13 protofilaments (the correct one there is Tilney, 1973).
The reference regarding 13 protofilaments has now been corrected, although Zhang, 2015 is cited at multiple locations in the paper as we used the Cryo-EM structural data from this paper to model the EB1 binding site on the microtubule (Figure 3B, left; source data from Zhang et al., 2015).
The central idea of Zhang, 2015 is that EB recognizes a "compacted and twisted" state. There is also the Manka and Moores, 2018 paper that claimed to capture the GDP-Pi state. Also missing is the McIntosh, 2018 paper that provided tomograms of microtubule ends in cells and in vitro. We understand that a lot of this science is not settled and are personally confused about expansion and compaction (e.g., there are conflicting reports about kinesin's in this regard, and the yeast tubulins are oddly behaved). But unsettled debates shouldn't just be ignored.
We have attempted to address these issues regarding the underlying structural biology, as follows:
a) Reviewer: “The central idea of Zhang et al., 2015 is that EB recognizes a "compacted and twisted" state. There is also the Manka and Moores, 2018 paper that claimed to capture the GDP-Pi state.”
In the previous version of the paper, we mentioned the Manka and Moores, 2018 paper within the Results section as part of our GDP-Pi results. However, we have expanded our comments to include the Zhang et al., 2015 paper. Given that this structural biology connection seemed quite speculative on our part, we have kept our comments quite brief. Following is the manuscript text:
“…These results could perhaps be explained by previous cryo-electron microscopy findings in which it was demonstrated that the GDP-Pi microtubule structural state is distinct from that of GDP microtubules (Manka and Moores, 2018b). Further, published cryo-EM structures of microtubules co-assembled with EB3 show that EB1 may promote a compacted microtubule lattice with a unique twist, once it is bound to the microtubule (Zhang et al., 2015). This structural transition could account for the ultimate destruction of the stable 4-tubulin binding site of EB1 as the lattice-bound tubulin subunits transition from GTP to GDP-Pi conformations, perhaps promoted by the binding of EB1 to the microtubule. We conclude that EB1 does not likely directly bind to GDP-Pi microtubules, but, instead, that hydrolysis of GTP-tubulin to GDP-Pi -tubulin could initiate formation of a low-affinity EB1 binding site.”
b) Reviewer “Also missing is the McIntosh, 2018 paper that provided tomograms of microtubule ends in cells and in vitro.”
We thank the reviewers for noting this omission, and have added the following comment to the Discussion section:
“…a recent electron microscopy study reported that the tips of growing microtubules within mitotic spindles display a gentle outward curvature of individual protofilaments (McIntosh et al., 2018). This outward curvature could enhance a structural recognition mechanism by increasing the availability of exposed protofilament edge sites at growing microtubule ends, due to the increased separation between individual protofilaments.”
4) Vinblastine data. The authors add vinblastine to cells and claim that it "blunts" the microtubule ends, which is why they see reduced EB binding. But vinblastine also induces outward curvature of protofilaments. If the protofilaments are separated from each other and outwardly curved, could that be the reason that EB has reduced affinity for them? See also the McIntosh data, in which the microtubules in cells are already relatively blunt. Could you realistically get the magnitude of signal reduction that you observe with only a small increase in relative bluntness? The vinblastine part of the paper took an overly-simplified view of the drug's mechanism of action and did not engage with the structural biology here either.
In Figure 6(A-C), we quantitatively estimated the microtubule protofilament tip extension in our LLC-Pk1 cells, and found that tip protofilament extensions were decreased with increasing concentrations of Vinblastine (Figure 6A-C). Therefore, at least in interphase LLC-Pk1 cells, it may be that Vinblastine ultimately leads to blunting of the growing microtubule end, rather than stabilization of outwardly curved protofilaments. Further, based on our model, stabilization of separated, outwardly curved protofilaments would be predicted to increase the affinity of EB1 for the microtubule ends by increasing the density of exposed protofilament edge sites, rather than reduce the affinity.
Data from the McIntosh et al., 2018 paper was presented for kinetochore or interpolar microtubules in mitosis, which, due to the physical and regulatory constraints within the mitotic spindle, may not be representative of the rapidly growing interphase microtubules in the LLC-Pk1 cells that were used in our study. Regardless, extended, flared, protofilaments from 30-54 nm in length were observed in the McIntosh study, which, especially given the separation of protofilaments, we would predict may increase targeting of EB1 to growing microtubule plus-ends in untreated cells, based on our current results.
That said, we acknowledge that our cellular results are correlative, and that there could be other effects of the drug that could alter EB1 binding at the growing microtubule plus-ends. Thus, we agree that our conclusions should be softened accordingly. Thus, we have reviewed all text relating to the cell experiments in Figure 6, and updated text wording regarding the conclusions, as follows:
Subsection Title changed to:
“Blunting of tapered microtubule tip structures correlates with suppressed EB1 binding in cells”
Experiment motivation:
“We then asked whether blunting of the microtubule tip structure, leading to a reduced number of protofilament-edge binding sites, would be correlated with the efficiency of EB1 tip tracking.”
Results section conclusion:
“We conclude that the efficiency of cellular EB1-GFP tip tracking is disrupted with Vinblastine treatment, perhaps due to the blunting of tapered tip structures at growing microtubule ends, which cuts the availability of high-accessibility EB1 protofilament-edge binding sites. However, we cannot exclude that other structural or chemical cellular responses to Vinblastine may be at play as well.”
5) On a related note you include a statement in the abstract "Correspondingly, in cells, the conversion of growing microtubule ends from a tapered into a blunt configuration resulted in reduced EB1 targeting.". We feel this is really FAR too strong compared to the data you have – it is not even clear that there are tapered ends in cells at all (no, if you believe the McIntosh paper), so you need to revise this statement.
As noted above, we quantitatively estimated the tip taper in control cells and upon Vinblastine treatment of these cells (Figure 6A-C). Regardless, we agree that the Abstract statement was too strong. Thus, we have revised as follows:
“Correspondingly, in cells, the blunting of growing microtubule plus-ends by Vinblastine was correlated with reduced EB1 targeting.”
6) Putting the biochemistry all together. It seems that the authors have on-rate constants (directly measured + modeled), as well as off-rate constants (from lifetimes in their single molecule assays on various lattices), which yields K_D values. They also have equilibrium data on tips, closed lattices, disrupted lattices, etc., at specific EB concentrations. Do these numbers all line up?
We have added a new supplemental Figure 3F to predict the average ratio of EB1-GFP equilibrium binding to closed microtubule structures vs disrupted microtubule structures (Figure 2C), based on theoretical binding curves generated from the on and off rate constants measured in this study. In all cases, the predicted values are similar to the experimental equilibrium binding measurements in Figure 2C-E.
7) Killer experiment. From reviewer #1
I don't know if it's fair to ask, but there is an obvious killer experiment. The author's argument is that EB1 has a higher on-rate to incomplete sites + a higher off-rate. But because the on-rate is proportionally higher than the off-rate, they get an increase in binding at equilibrium (Figure 2C). This argument implies that EB will flux more through the incomplete sites, even if the steady-state occupancy is higher. So, they should be able to test that directly with FRAP. E.g., take the disrupted vs. closed lattices, FRAP them, and observe faster recovery to a higher equilibrium fluorescence.
Given that FRAP fluorescence recovery is controlled by the off-rate of molecules from the microtubule, we estimate that with a dwell time of ~20 ms, the FRAP recovery half-time would be ~15 ms. Thus, we attempted to use very rapid imaging and a fast, high-powered laser to perform this experiment, however, were not able to photobleach effectively. We concluded that while this is a very interesting experiment, it will require careful planning, and we are currently investigating a new FRAP laser for our laboratory. Therefore, we view this as a longer-term experiment, and will continue our efforts in this regard as future work.
https://doi.org/10.7554/eLife.48117.015Article and author information
Author details
Funding
National Institutes of Health (R01-GM103833)
- Melissa K Gardner
National Institutes of Health (R35-GM126974)
- Melissa K Gardner
National Science Foundation (1350741)
- Melissa K Gardner
The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
Acknowledgements
This work was supported by National Institutes of Health grant NIGMS R01-GM103833 and R35-GM126974 and National Science Foundation CAREER award 1350741 to MKG. MZ acknowledges the support of National Institutes of Health grant R35-GM119552, the Human Frontier Science Program and the Searle Scholars Program. The authors have no conflicts of interest to disclose. Parts of this work were carried out in the Characterization Facility, University of Minnesota, a member of the NSF-funded Materials Research Facilities Network (www.mrfn.org) via the MRSEC program. We thank Drs. Joe Howard and Ron Vale for gifting reagents used as part of this project. We thank Holly Goodson and the Gardner Laboratory for helpful discussions.
Senior Editor
- Anna Akhmanova, Utrecht University, Netherlands
Reviewing Editor
- Andrew P Carter, MRC Laboratory of Molecular Biology, United Kingdom
Reviewer
- Manuel Thery, CEA, France
Version history
- Received: May 1, 2019
- Accepted: August 23, 2019
- Accepted Manuscript published: September 3, 2019 (version 1)
- Version of Record published: September 12, 2019 (version 2)
Copyright
© 2019, Reid et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.
Metrics
-
- 3,288
- Page views
-
- 440
- Downloads
-
- 12
- Citations
Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Structural state recognition facilitates tip tracking of EB1 at growing microtubule ends
eLife 8:e48117.
https://doi.org/10.7554/eLife.48117
Further reading
-
- Biochemistry and Chemical Biology
- Cell Biology
The ATPase p97 (also known as VCP, Cdc48) has crucial functions in a variety of important cellular processes such as protein quality control, organellar homeostasis, and DNA damage repair, and its de-regulation is linked to neuromuscular diseases and cancer. p97 is tightly controlled by numerous regulatory cofactors, but the full range and function of the p97–cofactor network is unknown. Here, we identify the hitherto uncharacterized FAM104 proteins as a conserved family of p97 interactors. The two human family members VCP nuclear cofactor family member 1 and 2 (VCF1/2) bind p97 directly via a novel, alpha-helical motif and associate with p97-UFD1-NPL4 and p97-UBXN2B complexes in cells. VCF1/2 localize to the nucleus and promote the nuclear import of p97. Loss of VCF1/2 results in reduced nuclear p97 levels, slow growth, and hypersensitivity to chemical inhibition of p97 in the absence and presence of DNA damage, suggesting that FAM104 proteins are critical regulators of nuclear p97 functions.
-
- Cell Biology
- Neuroscience
The amyloid beta (Aβ) plaques found in Alzheimer’s disease (AD) patients’ brains contain collagens and are embedded extracellularly. Several collagens have been proposed to influence Aβ aggregate formation, yet their role in clearance is unknown. To investigate the potential role of collagens in forming and clearance of extracellular aggregates in vivo, we created a transgenic Caenorhabditis elegans strain that expresses and secretes human Aβ1-42. This secreted Aβ forms aggregates in two distinct places within the extracellular matrix. In a screen for extracellular human Aβ aggregation regulators, we identified different collagens to ameliorate or potentiate Aβ aggregation. We show that a disintegrin and metalloprotease a disintegrin and metalloprotease 2 (ADM-2), an ortholog of ADAM9, reduces the load of extracellular Aβ aggregates. ADM-2 is required and sufficient to remove the extracellular Aβ aggregates. Thus, we provide in vivo evidence of collagens essential for aggregate formation and metalloprotease participating in extracellular Aβ aggregate removal.
