1. Neuroscience

Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network

  1. Eric Hart  Is a corresponding author
  2. Alexander C Huk
  1. Center for Perceptual Systems, Department of Neuroscience, Department of Psychology, The University of Texas at Austin, United States
https://doi.org/10.7554/eLife.52460
Share this article
Cite this article
  1. Eric Hart
  2. Alexander C Huk
(2020)
Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network
eLife 9:e52460.
https://doi.org/10.7554/eLife.52460
  2. Download BibTeX
  3. Download .RIS

Abstract

During delayed oculomotor response tasks, neurons in the lateral intraparietal area (LIP) and the frontal eye fields (FEF) exhibit persistent activity that reflects the active maintenance of behaviorally relevant information. Despite many computational models of the mechanisms of persistent activity, there is a lack of circuit-level data from the primate to inform the theories. To fill this gap, we simultaneously recorded ensembles of neurons in both LIP and FEF while macaques performed a memory-guided saccade task. A population encoding model revealed strong and symmetric long-timescale recurrent excitation between LIP and FEF. Unexpectedly, LIP exhibited stronger local functional connectivity than FEF, and many neurons in LIP had longer network and intrinsic timescales. The differences in connectivity could be explained by the strength of recurrent dynamics in attractor networks. These findings reveal reciprocal multi-area circuit dynamics in the frontoparietal network during persistent activity and lay the groundwork for quantitative comparisons to theoretical models.

Introduction

Persistent neural activity is prevalent in many cortical and subcortical areas (Andersen et al., 1987; Bruce and Goldberg, 1985; Constantinidis and Steinmetz, 1996; Fuster and Alexander, 1971; Fuster and Jervey, 1981; Bolkan et al., 2017; Ferraina et al., 2002; Guo et al., 2017; Inagaki et al., 2019; Mays and Sparks, 1980; Schmitt et al., 2017), and has been studied extensively in the context of delayed oculomotor response tasks (Funahashi et al., 1989; Gnadt and Andersen, 1988; Hikosaka and Wurtz, 1983). In these tasks, a subject must remember the location of a visual stimulus and make a saccadic eye movement to that location after a delay. During this delay period, single neurons in many primate brain areas, such as the lateral intraparietal area (LIP) and frontal eye fields (FEF), continue to spike vigorously in absence of the stimulus, leading up to the behavioral response (Balan and Ferrera, 2003; Clark et al., 2012; Funahashi et al., 1989; Gnadt and Andersen, 1988). This neural activity bridges sensory inputs with subsequent motor outputs and is thought to reflect the active maintenance of information in working memory, a process that forms the basis of many complex adaptive behaviors (Baddeley, 2012).

Because persistent activity lasts far longer than the intrinsic cellular time constants of most neurons, theoretical models of persistent activity have focused on how a mix of circuit and cellular mechanisms might interact to transcend the timescale of individual neurons. Classically, these models rely on a core architecture that includes recurrent excitatory connectivity, balanced inhibition, and a subset of single neurons with long (but realistic) intrinsic time constants (Amit and Brunel, 1997; Compte, 2006; Compte et al., 2000; Tegnér et al., 2002; Wang, 1999; Wang, 2001). Although these models are remarkable for using biologically plausible elements to show how the brain could in theory exhibit persistent activity at an aggregate level, little is known about the detailed patterns of circuit-scale spiking activity in the primate brain areas that originally motivated these theories. Furthermore, population models have yet to reconcile the fact that real neurons with persistent activity are often highly dynamic, heterogeneous, and exhibit mixtures of sensory and motor response components (Meister et al., 2013; Premereur et al., 2011; Rigotti et al., 2013).

To fill these gaps, we conducted simultaneous recordings of neural ensembles in LIP and FEF during a memory-guided saccade task and characterized the trial-by-trial dynamics in this circuit with a multi-neuron generalized linear model (GLM). This task is often employed to evoke persistent responses in both LIP and FEF, and is routinely used to identify neurons with long timescale dynamics that are thought to play a role in sensory integration (Chafee and Goldman-Rakic, 1998; Gold and Shadlen, 2007). It also serves as the fundamental test case for modeling persistent activity in theoretical studies (Murray et al., 2017a; Murray et al., 2017b; Spaak et al., 2017). The population-level GLM allowed us to isolate the effects of each neuron’s spiking activity on the activity of other simultaneously recorded neurons, while statistically parceling out the effects of shared task variables (such as visual responses to the flashed target, and motor responses related to the impending saccade). This analysis revealed remarkably strong and slow recurrent excitation both within and between areas. Interneuronal coupling between LIP and FEF was highly reciprocal, without a clear asymmetry between feedforward and feedback connections. Furthermore, the spiking activity of most neurons was driven by spikes from other neurons more than the cell’s own recent spike history. In addition to slow recurrent excitation, inhibition with moderate timescales was also present, followed by more standard fast timescale excitation. The existence of corresponding inhibitory interactions lends support to the idea that inhibition may act as a stabilizing mechanism to curb runaway excitation.

Together, these results demonstrate the core aspects of theoretical models (i.e. slow recurrent excitation, balancing inhibition) while also providing quantitative estimates of the various timescales and magnitudes of these theorized components. However, we also found that there were stronger local functional interactions within LIP than FEF, and that many neurons in LIP had longer spike-history and coupling timescales. These aspects of our results run contrary to recent theoretical hypotheses about the relative roles of LIP and FEF (e.g. Murray et al., 2017b), but concur with previous findings that examine correlations between pairs of neurons locally in each area (Katsuki et al., 2014). By analyzing synthetic spike trains from a classic ‘bump’ attractor network used to model spatial working memory (Compte et al., 2000; Gerstner et al., 2014), we found that the differences in coupling between LIP and FEF could be explained by differences in the strength of recurrent connections in attractor networks. Interestingly, this analysis revealed that both areas could support persistent activity independently, but between-area interactions alone were insufficient to generate persistent activity (despite reflecting statistically-significant coupling). Thus, our results support and refine key components in models of persistent activity, and offer unexpected insights into how and where the brain implements circuit-based computations critical for linking sensation and action over time.

Results

Simultaneous recordings in LIP and FEF during memory-guided saccades

In order to test whether recurrent functional interactions in the frontoparietal network underlie persistent activity, we recorded ensembles of neurons (~5–20 cells per session) in areas LIP and FEF simultaneously (Figure 1a; 967 units, LIP: 407; FEF: 560; 7448 pairs). This allowed us to measure and compare the neuronal interactions both locally (within a cortical area) and over longer distances (between cortical areas). Macaques performed a classical memory-guided saccade task with two crucial refinements. First, the timing of all trial events including the delay period was variable (Figure 1b). Second, the location of the target was continuously jittered in space, thus the ensuing saccades also had variability in their timings and endpoints. This trial-by-trial spatiotemporal variability allowed us to fit a population encoding model (on ensembles of simultaneously-recorded neurons) at the level of single trials which, in turn, enabled us to disentangle the relative influences of various task events and network activity on the spiking activity of each recorded neuron. The saccade target was presented either within the constellation of receptive fields (‘in-RF’) of the neurons under study (in the hemifield contralateral relative to the recording sites), or diametrically opposed in the ipsilateral hemifield (‘out-RF’; Figure 1c). Figure 1 (d,e bottom) shows two example simultaneously recorded neurons with canonical responses. Each example neuron responded transiently to the visual target, and exhibited stimulus-selective persistent activity throughout the delay period. However, even in these example cells (selected to show robust and fairly constant persistent activity), substantial variability was present in their single-trial responses, reinforcing the value of an analysis scheme that can capture single-trial dynamics when assessing interactions between neurons (rasters Figure 1d,e top).

Figure 1
Download asset Open asset
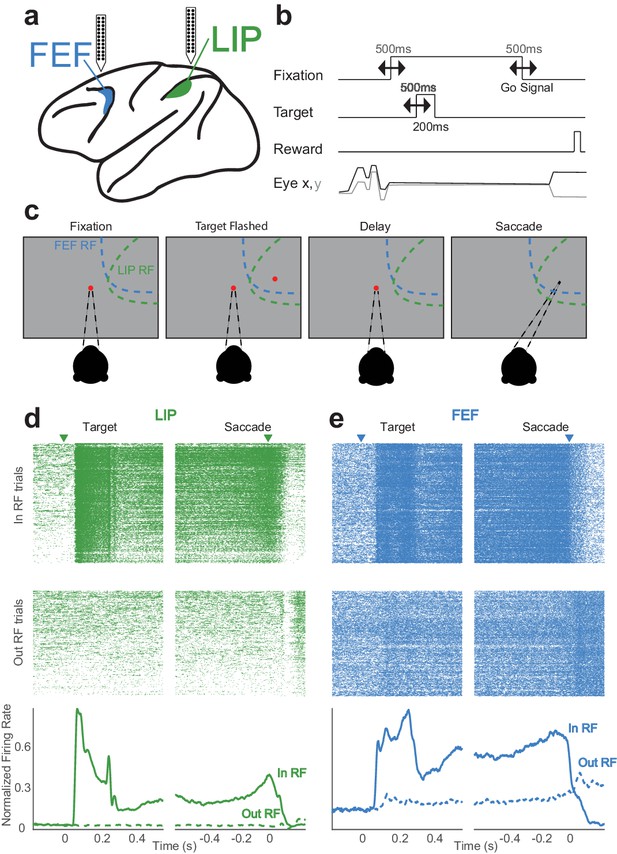
Memory-guided saccade task and simultaneously recorded neurons in LIP and FEF.

(a) Linear (stereotrode) probes (24–32 channels) were used to record in both LIP and FEF. (b) The timings of task events were varied continuously from trial to trial, making the delay (memory) period variable. (c) The monkey fixates and a target is flashed in the periphery (either ‘in’ or ‘out’ of the receptive fields); after a delay period (in which the monkey must maintain fixation) the fixation point is removed, indicating a ‘go-signal,’ and the monkey must make a saccade to where the target was. (d,e) Simultaneously recorded neurons in LIP (d) and FEF (e) with canonical responses. Each has a transient response to the visual target and a sustained response throughout the delay period (PSTH, bottom image). Even in these example neurons with strong persistent activity, there is significant variability during single trials (rasters, top image).

Persistent activity is traditionally observed (and quantified) in the average responses of neurons across many trials, but during natural behavior, the monkey must remember the stimulus and make decisions based solely on individual trials. To characterize and exploit the dynamics of single-trial responses across the circuit, we developed a population encoding model (i.e. a fully coupled generalized linear model [GLM]; Figure 2a). This regression-based statistical approach describes the time-varying spike rate of each neuron in terms of the external task events (i.e. the visual target being flashed and the saccadic response), the recent spike-history of that neuron, and the activity of other simultaneously recorded neurons. This approach allowed us to investigate the single-trial interactions between neurons while parceling out the influences of the visual stimulus (Figure 2b, first column), the motor response (Figure 2c), and each neuron’s autocorrelation (i.e. the ‘spike-history’; Figure 2d). We characterized the functional interactions between neurons with ‘coupling kernels,’ which describe the statistical dependencies between single-trial spike trains over time (Figure 2e). Critically, these coupling terms explain variance not explained by the other predictors, and are fit directionally (i.e. they capture the impact of one neuron’s spikes on the subsequent activity of another neuron). The population GLM goes beyond simple pairwise comparisons by fitting the model using spikes from all simultaneously recorded neurons. Thus, the ‘full’ population GLM characterizes the response of the fitted neuron with respect to the spiking activity of all the other neurons, providing a less ambiguous characterization than standard one-pair-at-a-time pairwise correlations (Stevenson et al., 2008). This model-based approach provides a disentangled estimate of spike-on-spike coupling across all recorded neurons, while simultaneously parsing out the shared drive due to the stimulus or motor response (i.e. it naturally ‘models out’ the signal correlation).

Figure 2 with 1 supplement see all
Download asset Open asset
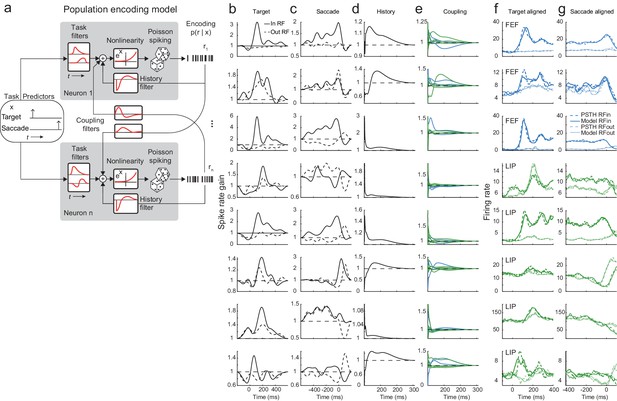
Population encoding model and analysis of example session.

(a) This generalized linear model (GLM)-based approach describes the time-varying spike rate of each neuron in terms of the external task events (i.e. the saccade target being flashed and the saccadic response), the recent spike-history of that neuron, and the activity of other simultaneously recorded neurons (within and across regions). The model is defined by three stages: 1) a linear stage that takes a weighted sum of the covariates and temporal filters, 2) an exponential point non-linearity that converts the linear output to a spike rate, and 3) conditionally Poisson spiking. (b–g) Each row corresponds to a neuron (1–3 in FEF, 4–8 LIP) and each column corresponds to the kernel of a particular predictor: (b) onset of the visual target; target in RF (solid line) and out RF (dashed line), (c) time of the saccade response, (d) recent spike-history and (e) coupling from other neurons (in LIP: green; in FEF: blue). Each kernel represents the time-varying gain on spiking for the fitted neuron due to the particular predictor while simultaneously accounting for the influence of the other predictors. (f,g) Each column displays the true PSTH (dashed lines) and predicted PSTH (solid lines) for each neuron (rows) for targets in (dark lines) and out (light lines) of the RF, aligned to the (f) target on and the (g) saccade. The predicted PSTHs were constructed from generating single-trial spike trains from the full population model for each neuron and averaging them.

The example session (Figure 2b–e) showcases the diversity of responses of eight simultaneously recorded neurons. The GLM captures all aspects of the apparent heterogeneity well: idiosyncrasies in temporal dynamics, variations in functional interactions, and cell-to-cell differences in stimulus dependence. As an initial standard validation, we simulated single-trial spike trains from the GLM fits and averaged these to calculate a predicted peristimulus time histogram (PSTH), which captured the average responses of each neuron quite well (Figure 2f,g). The GLM-derived measure of coupling reveals similar patterns as seen via traditional measures of correlations (Figure 2—figure supplement 1; Pillow et al., 2008) but offers the advantage that it can ‘explain away’ potentially misleading correlations by leveraging the simultaneous fits across the ensemble of neurons and thus provides a cleaner estimate of the true functional connectivity of the network (Stevenson et al., 2008). Although of course a perfect characterization would require measuring every single neuron in the network (Aertsen et al., 1989), these methods have been previously validated in physiological circuits with better-known connectivity (Gerhard et al., 2013; Pillow et al., 2008).

Strong coupling exists both within and between areas but is stronger within LIP

Strong coupling was observed throughout the frontoparietal network. We quantified the overall coupling strength for each pair of simultaneously recorded neurons by summing the weight of each coupling kernel, allowing the overall effect of coupling for each neuron pair to be excitatory or inhibitory (i.e. one neuron was more or less likely to spike given another neuron’s spike). Figure 3a (left column) summarizes the overall strengths of coupling for the four main classes of interneuronal interactions: both neurons within LIP (‘LIP-LIP’), both neurons within FEF (‘FEF-FEF’), from an LIP neuron to an FEF neuron (‘LIP-FEF’), and from an FEF neuron to an LIP neuron (‘FEF-LIP’). For all of these functional interactions, the observed coupling (colored bars in histograms) was far stronger than expected by a null distribution (gray bars, calculated by permuting the trial order of other neurons relative to the neuron being fitted, and then re-fitting the model; permuting the data in this way destroys the correlational structure between the neurons, but crucially preserves the spike times and model-based analysis of task events for all spike trains [Pillow et al., 2008]; Wilcoxon rank-sum test, LIP-LIP, p=6.45×10−79; FEF-FEF, p=6.78×10−165; LIP-FEF, p=1.69×10−86; FEF-LIP, p=8.52×10−84). A large fraction of the individual coupling kernels was substantially greater than the null distribution (>2 SD of mean of the null [~0]) for each area interaction (LIP-LIP = 60%; FEF-FEF = 54%; LIP-FEF = 60%; FEF-LIP = 58%).

Figure 3 with 2 supplements see all
Download asset Open asset
Exceptionally strong coupling both within and between areas.

(a) Distributions of raw coupling weights (colored histograms) defined by the sum of each kernel for each area interaction (LIP-LIP, FEF-FEF, LIP-FEF, FEF-LIP). Positive weights denote an excitatory interaction (the fitted neuron was more likely to spike given that another neuron just spiked) and negative weights indicate an inhibitory interaction (the fitted neuron was less likely to spike given that another neuron just spiked). A null distribution was constructed by shuffling the order of the trials for each neuron (gray histograms), effectively destroying the correlations between the ensemble of neurons but preserving the stimulus dependence and spike times. These distributions describe the probability of observing coupling due to chance alone (Wilcoxon rank-sum test, p=6.45×10−79; p=6.78×10−165; p=1.69×10−86; p=8.52×10−84). (b) Principal components analysis was performed on the coupling kernels split by each area interaction (as in (a)); the first three principal components (dark to light lines) accounted for around 90% of the variance (legend: variance explained for each PC). (c) Cumulative fraction of coupling weights for each interaction, corresponding to the distributions in (a). (d) Variance explained of the predicted PSTHs of the coupled model vs. the uncoupled model (median 76% variance explained under both models). Coupling was unnecessary to capture the average response of most neurons (the points fell near the unity line). (e) Predicted single-trial spike times (in units of bits-per-spike) of the coupled model vs. the uncoupled model. Coupling improved the predictions of the single-trial spike trains by 22% on average (25% for LIP; 19% for FEF; points fell above the unity line).

Interneuronal coupling often manifested as excitatory interactions (i.e. positive values), but many instances of stronger-than-chance suppressive interactions were also evident (i.e. negative values). The coupling components were strongest for the within-LIP interactions, although within-FEF interactions were also far greater than chance levels. Between-area coupling (LIP-FEF and FEF-LIP) was also strong and spanned approximately the same range of magnitudes as the within-FEF interactions. These quantitative comparisons of the distributions of coupling strength are graphically apparent in the cumulative distributions (Figure 3c). The results also held for a comparison of the absolute coupling magnitudes, as well as a comparison of the overall excitation and inhibition (Figure 3—figure supplement 1).

Beyond assessing the overall magnitudes of each interaction, we examined the time courses of the coupling kernels by performing principal components analysis (PCA) on all of the kernels within each of the four interaction types (LIP-LIP, FEF-FEF, LIP-FEF, and FEF-LIP), and plotted the first three PCs (which together accounted for ~90% of the variance). Across all interaction types, coupling was dominated by long timescale excitation, indicating that spikes from one neuron increased the gain on spiking of other neurons for up to ~200 ms (Figure 3b, first PC/darkest curves). A second, sharper, fast excitation component followed (Figure 3b, 2nd PC/medium shaded curves), and was more pronounced within both areas than between areas, consistent with this component reflecting local interneuronal interactions. Finally, a third component was primarily suppressive (Figure 3b, 3rd PC/lightest curves), with a timescale between the first (slow) and second (fast) excitatory components. The suppressive component was proportional to the fast excitation component in magnitude and lag. These three timescales and signs of interaction are ubiquitous in biophysical models of persistent activity, and are posited to reflect the relative contributions of NMDA, AMPA, and GABA receptors, respectively (Compte et al., 2000; Goldman-Rakic, 1995; Wang, 1999).

We verified the fits across all sessions (Figure 3d) by comparing predicted PSTHs generated from the GLM to the true PSTHs (as in Figure 2f,g); the predicted PSTHs did a good job of explaining the real PSTHs of most neurons regardless of whether the neurons were treated independently (in an ‘uncoupled’ model with only task and history kernels) or not (in the ‘full’ coupled model with task, history, and coupling kernels; median 76% variance explained under both models). Although interneuronal coupling terms did not improve predictions of the average response (i.e., the PSTH; Figure 3d), they were important for capturing the spike times in single-trial spike trains (Figure 3e; the coupled model provides 22% more information on average). This distinction has been noted previously (Pillow et al., 2008; Runyan et al., 2017) and means that the shared variability of the population carries information about a single neuron’s spike trains beyond that provided by the task components alone, and is unsurprising given that the PSTHs naturally obscure the single-trial dynamics by averaging them away. These findings emphasize the value of this analysis scheme because it allows us to examine the single-trial dynamics of the network during the timescales relevant for working memory.

In addition to comparing the observed coupling to null (permutation-fitted) distributions and an uncoupled model (with independent neurons by design), we also compared our results in the LIP-FEF network to similar coupling quantifications from other brain areas and tasks. Coupling between simultaneously-recorded neurons in visual area MT (recorded in the lab for other projects), although detectable, was considerably weaker than observed in these experiments (mean gain of max coupling filters, MT-MT = 1.08; LIP-LIP = 1.34; FEF-FEF = 1.16, LIP-FEF = 1.10; FEF-LIP = 1.12; Figure 3—figure supplement 2). Likewise, analysis of coupling between MT and LIP during a perceptual decision-making task was unable to detect interactions beyond that expected by chance (Yates et al., 2017).

Thus, conventional statistical tests, quantitative and qualitative comparisons to a null distribution, and comparisons of effect sizes measured in other contexts, all point to the existence of exceptionally strong recurrent interactions within the frontoparietal network. These were most pronounced within area LIP but were prevalent throughout this multi-area circuit. These interactions were primarily excitatory, but also contained substantial instances of suppression. Between-area coupling was roughly symmetrical in strength and timescale (Figure 3a,b), consistent with anatomy (Andersen et al., 1990; Ferraina et al., 2002; Selemon and Goldman-Rakic, 1988). Together, these results suggest a reciprocal inter-area network rather than a serial multi-stage system.

Interneuronal coupling outweighs spike-history dynamics, especially in LIP

In the prior section, we described how certain neurons impacted the probability of other neurons’ subsequent spiking. It is also reasonable to expect that a cell’s own spiking affects the probability of its subsequent firing. To characterize the relative impacts of (interneuronal) coupling and (‘intrinsic’) spike-history for each neuron, we defined predictive indices as the difference between the performance of the GLM with and without coupling, or with and without spike-history. For example, a coupling index of one would indicate that the neuron’s spike trains are completely predictable from the spiking activity of other neurons, and a value of zero would mean that spikes from other neurons add no predictive power over and above the task predictors and the neuron’s recent spike-history. The history index was constructed in an analogous fashion.

Figure 4 shows the relative effects of interneuronal coupling and spike-history for neurons in both areas. A greater number of neurons in FEF were predicted by their own spike-history than in LIP (Figure 4a), whereas the spike trains of LIP neurons were better predicted by spikes from other neurons than the analogous case in FEF (Figure 4b). These contrasting results may reflect fundamental differences in the functional connectivity and distributions of cell types in the underlying neural populations (Masse et al., 2017; Rosenbaum et al., 2017). However, overall, neurons in both areas were more influenced by interneuronal coupling than by their own spike-history (Figure 4c), pointing to the importance of circuit-level interactions driving spiking activity. This is especially striking given that the coupling is estimated while also accounting for the responses of all neurons to the task events, and thus reflects the interactions while statistically controlling for shared responses due to visual and motor drive. Neurons in both LIP and FEF tended to be driven by either the concurrent spiking activity of the population, or by their own spike-history, with few neurons impacted equally by both (Figure 4c).

Figure 4 with 1 supplement see all
Download asset Open asset
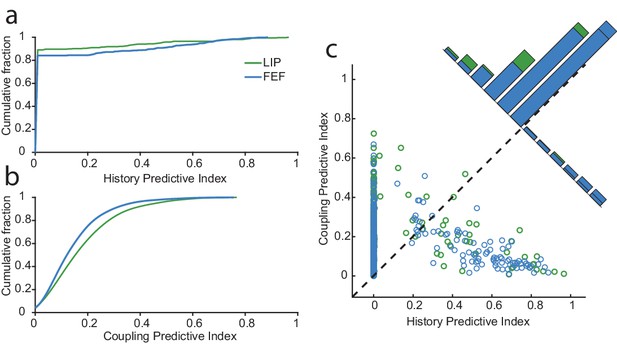
Network drive dominates circuit dynamics, especially in LIP.

For each neuron, we constructed predictive indices to further assess the influence of the spiking activity from other neurons (coupling) and itself (history). These indices are defined as the difference between the deviance explained by the model with or without history (a) or with or without coupling (b). (a) The cumulative fraction of history indices for neurons in each area. Overall, more neurons in FEF than LIP were impacted by their recent spike-history. (b) Same as in (a) but for coupling. Conversely, more neurons in LIP were influenced by the spiking activity of other neurons. (c) Comparison of the history and coupling indices. On the whole, spiking activity of neurons in both regions was more predicted by coupling than history (88.4% of neurons). For a large fraction of neurons, the history term was uninformative over and above the coupling and task terms (many neurons had a history index of zero). For a small subset of neurons (11%), predominantly in FEF, history had far more influence than coupling.

Across both areas, the ability to predict spikes for a large number of neurons was not improved by including a history term, meaning that their spike trains were predicted just as well by a model with only spikes from other neurons and the task components (Figure 4c). However, for a small subset of neurons (11%), the recent spike-history was far more predictive than coupling. Interestingly, these neurons were predominantly in FEF (nearly twice as many as in LIP; Figure 4c). Overall, these results imply that network dynamics play a more vital role than intrinsic dynamics for most neurons in both areas during persistent activity. Network contributions were especially strong in LIP, consistent with our prior observation that the magnitudes of the within-area coupling kernels were especially large in LIP (Figure 3a). We also wanted to assess whether neurons with strong persistent activity (determined in the traditional way, via inspection of their PSTH) were more driven by coupling or spike-history effects. Interestingly, there was no clear relationship to either (Figure 4—figure supplement 1). This emphasizes the earlier point that the average responses of single neurons may reveal little about the single-trial dynamics of the network (Latimer et al., 2015; Stokes and Spaak, 2016). The most ‘persistent’ responses evident in trial-averaged assays might be those that are more reliably driven by regular task events (i.e. the pre-motor build-up or the decaying visual response, or both), as opposed to reflecting a unique and persistent network contribution.

The interplay and balance of intrinsic versus network time constants is a major component of successful models of persistent activity (Cavanagh et al., 2018; Runyan et al., 2017). We therefore assessed the relative contributions of spike-history and interneuronal coupling timescales. The history kernels are of course an intriguing but imperfect extracellular lens into the intrinsic time constants of the neurons, estimated by modeling the effect of recent spikes on that neuron’s probability of spiking as a function of time and excluding the effects of task and coupling drive. Although the history kernel does not necessarily or directly describe intracellular or biophysical mechanisms, it does characterize the temporal response properties of the neuron due to ‘self-drive’ (e.g. long timescale autocorrelation, refractory periods, bursting dynamics etc.) as distinct from the effects of other (recorded) neurons and the task events that drive most (or all) neurons. We summarized the history kernels for each area with the first three principal components (Figure 5a,b). The dominant history component for both areas reflected a slow, gradually decaying time course. We estimated the spike-history time constants of each neuron by fitting an exponential curve to the history kernels (Figure 5c). Most neurons in both areas had short time constants, but the distributions had heavy right tails, with many neurons exhibiting longer timescales (100–300 ms). Overall, LIP had more neurons with long time constants than FEF (Figure 5c, inset), which may be surprising given the traditional notion that FEF lies higher up the cortical hierarchy of the visual system (which usually constitutes longer timescales; Honey et al., 2012; Murray et al., 2014). However, from the oculomotor point of view, the hierarchy is reversed, given that FEF receives direct input from subcortical areas involved in eye movements, and exhibits lower microstimulation thresholds for generating saccades (Ferraina et al., 2002; Kimmel and Moore, 2007).

Figure 5
Download asset Open asset
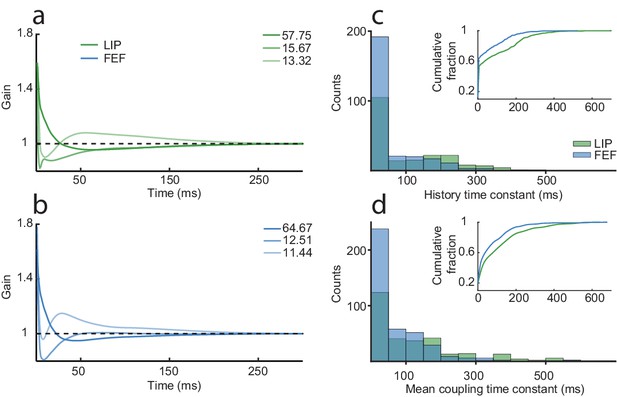
Spike-history and coupling time constants are similar but longer in LIP than FEF.

The first three principal components for the history kernels in LIP (a) and FEF (b), which capture the spike-history time constant of the neurons, while controlling for the task and coupling drive. The dominant component in both areas was a slow decay. An exponential curve was fit to the history kernel of each neuron to estimate a time constant (tau). (c) The distribution of spike-history time constants differed between areas (Wilcoxon rank-sum test, p=1.20×10−06; LIP mean = 99.6 ms; FEF mean = 68.2 ms). Most neurons had short time constants, but there was a ‘long tail’ of neurons with much longer time constants (100–300 ms). (d) Same as (c) but for the mean coupling kernel of each neuron. Coupling time constants were larger overall than history time constants and also differed between areas (Wilcoxon rank-sum test, p=6.43×10−07; LIP mean = 133.8 ms; FEF mean = 76.5 ms). Insets shows the cumulative distributions of the time constants; LIP had more neurons than FEF with long coupling and history time constants.

We estimated the time constant from the mean coupling kernel for each neuron in an analogous way, and found that coupling time constants were similar to the spike-history time constants on the whole (Figure 5d). These findings are consistent with the idea that persistent activity results from a combination of network and intrinsic dynamics, both with relatively slow time constants that can extend into the 200–300 millisecond-long range. We emphasize that the population GLM estimates both the coupling and spike-history kernels while simultaneously accounting for the effects of the task variables that presumably drive most, if not all, of the neurons. In simpler, traditional analyses (such as the autocorrelation from binned spike counts), the impact of visual and motor drive would overshadow and confound the measured network dynamics (Cohen and Kohn, 2011).

Interneuronal coupling is dynamic across behavioral epochs

The nature of neural population dynamics during working memory is currently a matter of debate (Cavanagh et al., 2018; Constantinidis et al., 2018; Lundqvist et al., 2018). Some models of working memory propose that the activity of the network should remain stable over time and others suggest that it can drift, or that the time-varying activity is critical to the computation (Barak and Tsodyks, 2014; Stokes, 2015). To examine how the dynamics of the network evolved over the course of the trial in the neural data, we compared coupling between several temporal epochs. As a baseline, we measured the coupling during the fixation period at the beginning of each trial and compared it to coupling during the delay period. In both cases, the visual input was identical (i.e. a fixation point and nothing else on the screen), but during the delay period the monkey had to remember the location of the target in order to perform the subsequent memory-guided saccade.

We found strong coupling across the circuit even during fixation, in accordance with earlier findings investigating local pairwise correlations (Katsuki et al., 2014). Rather than a profound global change in network interactions from fixation to delay, we observed a subtle yet systematic shift in increased excitatory coupling in all area interactions, with the most pronounced change occurring locally within LIP (Figure 6a; Wilcoxon rank-sum test, LIP-LIP, p=4.87×10−09; FEF-FEF, p=5.17×10−04; LIP-FEF, p=1.64×10−04; FEF-LIP, p=3.01×10−03). This highlights the potential role of nuanced changes in the dynamics of the network, rather than an indiscriminate increase in overall population activity. This is consistent with work showing that the distribution of firing rates of the population in PFC remains relatively constant between the fixation period and the delay period, despite changes in firing rates of individual neurons (Murray et al., 2017a).

Figure 6 with 2 supplements see all
Download asset Open asset
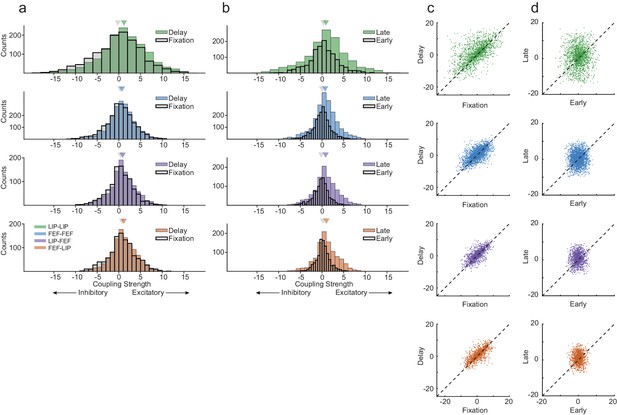
Interneuronal coupling is dynamic across behavioral epochs.

(a) The strength of coupling increased between the fixation period and delay period across all area interactions, especially within LIP (Wilcoxon rank-sum test, p=4.87×10−09; p=5.17×10−04; p=1.64×10−04; p=3.01×10−03). Strong coupling was observed even during fixation. (b) Coupling increased from early in the delay period to late in the delay across all area interactions (Wilcoxon rank-sum test, p=1.08×10−06; p=1.65×10−27; p=3.96×10−23; p=1.97×10−17). LIP exhibited increases in excitatory and inhibitory interneuronal interactions, whereas FEF and between area interactions were dominated by increases in excitatory connectivity. (c) Interneuronal coupling between the fixation and the delay period was systematic (Pearson’s r, R = 0.61; R = 0.66; R = 0.70; R = 0.72), (d) whereas the coupling strength between early and late in the delay showed no relationship (Pearson’s r, R = 0.04; R = 0.04; R = 0.06; R = 0.03).

One potential explanation for the differences in coupling between LIP and FEF (Figure 3) could be due to differences in receptive field overlap between pairs of neurons. However, the finding that differences in coupling exist even during fixation (Figure 6a) suggests true differences in the underlying functional organization of the areas rather than simply an artifact of sampling. To explore the relationship between spatial selectivity and coupling further, we analyzed the coupling between neurons as a function of their spatial tuning similarity based on the distance between the peaks of the their 1D tuning curves (Figure 6—figure supplement 1). We found that coupling was modestly stronger for pairs of neurons with more similar spatial tuning, which was most pronounced for neurons within LIP. Interestingly, this feature is predicted by classic bump attractor models of spatial working memory.

To assess the temporal stability of the network interactions across the delay period, we compared coupling early in the delay period to coupling late in the delay period. Coupling increased late in the delay period for all interactions (Figure 6b; Wilcoxon rank-sum test, LIP-LIP, p=1.08×10−06; FEF-FEF, p=1.65×10−27; LIP-FEF, p=3.96×10−23; FEF-LIP, p=1.97×10−17). LIP exhibited the smallest change overall, but a closer view of the distribution of within-LIP coupling kernels revealed a relatively symmetrical increase in excitatory and inhibitory weights. In contrast, within-FEF and between-area coupling reflected primarily excitatory shifts (Figure 6b).

Although the increase in coupling between the fixation period and delay period was subtle, it was systematic across all interactions within and between areas (Figure 6c). However, unlike the pair-by-pair relationship between fixation and delay coupling, there was little correlation between coupling early and late in the delay period (Figure 6d). Notably, within-LIP activity had the largest increase in excitatory coupling from the fixation period to the delay (Figure 6a), but the smallest change from early to late in the delay period (Figure 6b). This temporal pattern suggests that the network dynamics within LIP are engaged first and then the larger circuit becomes more strongly coupled as the delay period goes on.

We also examined the dynamics of single neurons’ spike-history across the temporal epochs. The strength of the spike-history kernels remained consistent between the fixation and delay periods as one might expect (Figure 6—figure supplement 2a,b), but interestingly many neurons in FEF had larger spike-history effects later rather than earlier in the delay period (Figure 6—figure supplement 2c,d), meaning that their autocorrelation increased over the delay. Crucially, remember that the impact of the history term is estimated while controlling for the drive of the saccadic response.

Coupling differences in LIP and FEF can be explained by the strength of recurrent connectivity in attractor networks

To further explore the implications of our results for mechanistic models of persistent activity, we fit the population GLM to spiking data from a classical ‘bump’ attractor network used to model spatial working memory (Figure 7a,b; Gerstner et al., 2014; Compte et al., 2000). Our main goal was to attempt to infer the recurrent connectivity of the attractor network using the GLM to provide a benchmark to relate the data to the mechanistic models (or perhaps vice versa). We parametrically varied the recurrent connection strength of the excitatory population in the attractor network while holding all other parameters constant (at their default values) to generate synthetic datasets from each of these network variants. We then sampled spike trains from a subset of the total network population, akin to a real experiment (20 neurons, 500 trials per session). To further mimic the real experiment, we varied the onset and location of the stimulus on a per trial basis, and the sample of neurons remained the same throughout each session. We fit the population GLM to the spike trains of the ensemble of neurons in each session in the exact same way we did for the real datasets.

Figure 7 with 2 supplements see all
Download asset Open asset
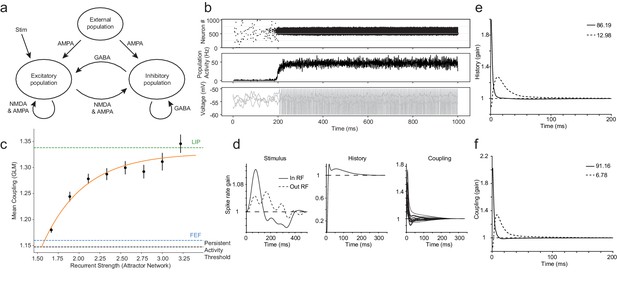
Coupling differences in LIP and FEF can be explained by the strength of recurrent connectivity in attractor networks.

Synthetic datasets were generated from a classic attractor network and fit with the GLM using the same procedure used with the real data. (a) Schematic of classic attractor network used to model spatial working memory (adapted from Gerstner et al., 2014). (b) Population activity of attractor network for an example session with high recurrent strength (2.3): a stimulus triggers selective persistent activity (top, middle row); voltage traces from three example neurons (bottom row). (c) A systematic relationship was revealed between the mean coupling (estimated from the fitted GLM) and the internal recurrent strength of the attractor network (error bars = SEM). The black dashed line indicates the level of coupling at the minimum recurrent strength necessary to generate persistent activity. The green and blue lines are LIP and FEF’s coupling determined from the data, respectively. (d) Stimulus, spike-history, and coupling kernels of an example neuron. PCA of history (e) and coupling (f) kernels for an example session revealed the ‘fast’ and ‘slow’ dynamics of the neurons specified in the network, which accounted for virtually all the variance explained (legend).

The coupling between neurons (determined by the GLM) systematically increased with greater recurrent connectivity in the attractor network, confirming that coupling can act as a valuable proxy for the strength of the recurrent weights of the population (Figure 7c). The black dashed line in Figure 7c indicates the level of coupling at the minimum recurrent strength necessary to generate persistent activity. The green and blue lines are LIP and FEF’s true coupling determined from the data, respectively. Given these simulations, LIP appears to exhibit strong attractor dynamics (i.e. near the point of saturation of recurrent functional connectivity), whereas FEF acts as a weak attractor, but one still independently capable of maintaining persistent activity (i.e. near the model’s theoretical minimum for exhibiting persistent firing, at least given the other parameter settings). The coupling we observed between LIP and FEF was statistically significant, but lay below the threshold to be able to generate persistent activity on their own (Figure 7—figure supplement 1). Data from area MT (from other experiments, described earlier) had even lower coupling (Figure 7—figure supplement 1), consistent with that area’s role in visual function and lack of strong persistent responses.

The stimulus, history, and coupling kernels fit to spike trains from the attractor network all resembled those recovered from the real data. The GLM captured the effects of the stimulus, both when it was in or out of the receptive fields of the sampled neurons (Figure 7d, panel 1). The history term recovered the ‘built-in’ hard refractory period of the neurons, as well as the longer autocorrelation (Figure 7d, panel 2). The coupling terms captured the strong and prevalent interneuronal correlations (Figure 7d, panel 3), although coupling tended to be faster in the attractor network than in the data, which may be an interesting difference worthy of consideration in modeling. The first two principal components (Figure 7e,f) of all the history kernels and coupling kernels (Figure 7—figure supplement 2) explained virtually all of the variance, and revealed the temporal profiles of the fast and slow excitatory components (AMPA and NMDA receptors, respectively), which are explicitly specified as part of the synaptic weights of the population in the attractor network. It is unsurprising that the coupling and history kernels are similar, given that the artificial neurons in the population are all identical and the profile of connection weights yokes the between-neuron connection strength and self-recurrent strength in the attractor network.

These findings from the GLM analysis of the attractor network serve not only to verify the inferences that came from the core analysis scheme as applied to real data, but also to help situate our results more broadly with respect to theoretical models. The GLM recovered reasonable stimulus, history, and coupling kernels from the artificial population, and captured the underlying strength of recurrent connections in the attractor network. Our initial comparisons also revealed that LIP and FEF both fell within the range of theoretically-predicted couplings required for persistent activity, although at intriguingly different positions within that range. There are, of course, numerous parameter tradeoffs that can be explored in this and other similar network models (Chaudhuri and Fiete, 2016; Zylberberg and Strowbridge, 2017). The analyses reported above are only the first steps to interrogating attractor networks in detail and linking the theories back to data, but they demonstrate the exciting feasibility and validity of using a population GLM to link theoretical spiking models with recordings of neuronal ensembles.

Discussion

The primate frontoparietal network is often put forth as a model system in which to study cognitive processes, yet little is known about the circuit-level spiking activity within and between regions in this network. We therefore characterized the interneuronal interactions in this circuit during oculomotor working memory using multi-area multi-site simultaneous recordings, and a population encoding framework that extended the generalized linear model to simultaneous fits of multiple neurons recorded at the same time in two cortical areas. This enabled us to isolate the contributions of network and intrinsic dynamics to persistent activity while simultaneously disambiguating the effects of task variables.

Historically, models of cortical persistent activity have focused on the challenges posed to generic architectures, identifying particular network interactions and cellular properties whose interplay might be capable of maintaining the sorts of persistent activity seen in the brain (for review: Wang, 2001). Such models have emphasized strong recurrent activity (to maintain spiking without additional input), broadly tuned inhibition (useful for damping the runaway dynamics), and a degree of (realistic) slow intrinsic time constants to stabilize the network (perhaps mediated by NMDA receptors). Using a population encoding model, we were able to identify several of these key features in the population activity, and to map these on to data from specific brain areas.

We found evidence of strong reciprocal interactions both between and within FEF and LIP. These circuit-level interactions comprised three main components. First, the slow timescale excitation we observed confirms the existence of strong reverberatory activity, the primary functional component used in models to generate persistent activity. Second, slow inhibitory interactions were present that could serve to perform the hypothesized tempering of reverberatory excitation, curbing potentially runaway attractor dynamics. Finally, we observed a fast excitation component, primarily within areas, which corresponds to more conventional local neuron-to-neuron interactions. The magnitude and time courses of all components serendipitously map on to three key biophysical features that are prevalent in theoretical models of persistent activity: NMDARs, GABARs, and AMPARs (Compte et al., 2000; Goldman-Rakic, 1995; Wang, 1999). Of course, our characterizations provide summaries of temporal scales at the level of spikes, and how these quantitatively relate to intracellular mechanisms invites further study. Recent work suggests a more complicated story at such lower biophysical levels (Rodermund et al., 2020). However, our validation of the GLM analysis with the attractor network lends credence to the estimates of the neurons’ temporal dynamics. The time constants of neuron-to-neuron interactions, as well as the history dynamics of individual cells, were on order of 100–250 ms, and are therefore consistent with the relatively long dynamics that are called for theoretically to maintain persistent activity over timescales of many 100 s of milliseconds to a few seconds.

Theories of persistent activity have only recently begun to tackle the multi-area circuit dynamics underlying working memory (e.g. Murray et al., 2017b). This distributed frontoparietal model attempts to explain working memory and perceptual decision making with two interconnected modules with differences in the recurrent structure of the local networks. The idea is that stronger attractor dynamics in PFC than PPC leads to more robust persistent activity during working memory, and categorically different computations during decision making (i.e. winner-take-all choice in PFC, and slow temporal integration in PPC). Work by Murray et al. (2017b) nicely lays out several potential scenarios for the local and long-range network structure that could support attractor dynamics in the frontoparietal circuit. Our GLM analysis of the attractor network provides the unique opportunity to speak directly to these architectures. Both LIP and FEF appear to be independently capable of stable attractor dynamics, whereas the between-area interactions fell below the threshold for independently generating persistent activity, despite significant coupling (this is the first option: row 1 of Figure 3c of their paper). However, unexpectedly, LIP had much stronger recurrent connectivity than FEF, which runs counter to the initial proposal for the specific differences in local structure in the two areas. Thus, our results suggest that the proposed underlying differences in network structure are unlikely responsible for the theoretical functional differences between LIP and FEF in this distributed frontoparietal model (or at least not in the expected way).

Although our results suggest that LIP has a stronger degree of locally-recurrent connectivity, the strong interactions both between and within these areas on single trials support the idea of a tightly linked network which might be better thought of as parts of a single functional unit. The observed timescales of recurrent excitation between neurons likely indicate evidence for attractor-like models of network dynamics, not only within LIP and FEF, but across the entire circuit, which could be effectively acting as a single distributed attractor with only quantitative differences across areal nodes. The superior colliculus and thalamus are also likely critical parts of this circuit (Ferraina et al., 2002). Recent work in rodents has suggested that the thalamus plays a central role in maintaining persistent activity (Bolkan et al., 2017; Guo et al., 2017; Inagaki et al., 2019; Schmitt et al., 2017), a proposition that needs to be tested in the primate, and which might further enrich our perspective on the full network (or networks) involved in even simple instances of persistent activity.

Taken together, our results provide direct empirical support for strong recurrent excitation and balancing inhibition in primate brain areas that exhibit persistent activity. These findings inform and constrain the structure of the connectivity, both qualitatively and quantitatively. An important next step will be to test a multi-area mechanistic model that incorporates attractor dynamics within and between areas using magnitudes and timescales informed by our data, and which takes into account the differences in architecture and network/intrinsic drive in each area. However, a crucial difference between the data and the model may lie in the fact that bump attractor networks fundamentally link the spatial connectivity of the network to the spatial selectivity profile of the neurons in the population, but relatively little is known about the fine-grained retinotopy (and microcircuit architecture) in area LIP (Arcaro et al., 2011). Augmenting the attractor network model by incorporating heterogenous tuning functions and/or extending the model to capture 2D receptive field profiles would be valuable next steps to better understand the nature of the functional architecture in these areas. It is possible that the heterogeneity and mixed selectivity prevalent in this circuit is a result of heavily interconnected networks that are continuously active (Fusi et al., 2016; Meister et al., 2013; Rigotti et al., 2013). These features may be critical for normal oculomotor behavior, in which the eyes move almost constantly, and sensory inputs must be continuously and flexibly mapped to motor actions.

Materials and methods

Stimulus presentation apparatus

Request a detailed protocol

Macaques were seated, head-fixed, in custom primate chairs facing a rear-projection screen (IRUS; Draper; 150 cm ×86 cm) at a distance of 57 cm, which covered the central 106◦×73◦ of visual angle. Images were projected onto the screen by a PROPixx projector (VPixx; resolution = 1920 × 1080 pixels, refresh rate = 120 Hz). Visual stimuli were generated using Matlab (MathWorks) and Psychtoolbox (Brainard, 1997; Kleiner et al., 2007). Neural data and task events were recorded with the OmniPlex system (Plexon) using a Datapixx I/O box (VPixx) for precise temporal registration. Electrical microstimulation was administered with a PlexStim device (Plexon). All hardware and software were integrated using the PLDAPS experimental framework (Eastman and Huk, 2012). Eye position was tracked using an Eyelink 1000 video eye tracker (SR Research), sampled at 1 kHz. Reward was delivered through a computer-controlled syringe pump (New Era).

Memory-guided saccade task

Request a detailed protocol

Macaques were trained to perform a classic visuospatial delayed-response task: memory-guided saccades. On a trial, the monkey fixates on a central point while a target is flashed (for 200 ms) at a random location in the periphery. After a delay period, in which he must maintain fixation, a ‘go signal’ is indicated by extinguishing the fixation point, and he must make a saccade to the remembered location of the target. There are two key differences in our specific version of this task: 1) the timing of the task events: the fixation point onset (1–1.5 s durations), target onset, and fixation off (go signal) are variable, making the delay period variable on a trial-by-trial basis (delays = 0.5 s - 2 s), and 2) the spatial location of the target is jittered continuously (eccentricities were drawn from a Gaussian distribution, mean = 10°, SD = 5°), rather than being presented at one of an array of fixed grid locations. The spatial jitter was applied to the position of the target in X and Y in the visual field (in degrees of visual angle), not radially from the center. The delay durations (as well as other task timings) were constructed from uniform distributions. This task served a dual purpose: to functionally map LIP and FEF, and as our primary way to investigate persistent activity during working memory.

Preparation and electrophysiology

Request a detailed protocol

We performed electrophysiological recordings in cortical areas LIP and FEF in two male rhesus macaques (9 y.o., 10.1 kg, and 5 y.o., 6.8 kg). Each monkey had two custom titanium chambers implanted over the regions of interest (ROIs) to allow for simultaneous recordings in both areas. Chambers were placed according to structural MRI scans and anatomical landmarks. An accurate 3D model of the skull (both digitally, and 3D-printed) was used to craft an individualized fit of the chamber to the skull for a more stable and sealed implant. All experimental protocols were approved by The University of Texas Institutional Animal Care and Use Committee and in accordance with National Institute of Health standards for care and use of laboratory animals.

Extracellular electrophysiological recordings were conducted with multisite linear electrode arrays (U-probes; Plexon; 24 or 32 channels) with stereotrode geometry (50 µm between adjacent sites; 100 µm between pairs). Probes were lowered daily into both chambers. ROIs were identified using electrode depths, sulci landmarks (using the physiological characteristics of white/gray matter), neuronal properties, and in the case of FEF, electrical microstimulation. Both LIP and FEF were functionally identified and mapped by observing spatially selective visual and saccadic activity, as well as delay-period persistent activity in the memory-guided saccade task (Gnadt and Andersen, 1988). In addition, FEF was mapped with a well-established microstimulation protocol (Kimmel and Moore, 2007; Moore and Fallah, 2001), in which conventional currents (~50µa, 200 Hz) tended to generate fixed vector saccades to regions of visual space.

Neural analysis

Request a detailed protocol

We collected a wide sample of units in LIP and FEF (967 units; LIP: 407; FEF: 560; Monkey A: 459; Monkey L: 508; 160 sessions; 7448 pairs; mean firing rates: FEF: 36 sp/s; LIP: 28 sp/s; p=1.16×10−5 Wilcoxon Rank-Sum test). Offline spike sorting was conducted in a semi-automatic fashion, first with KiloSort (Pachitariu et al., 2016), and then manually in Phy. Clusters were merged or split based on the units’ characteristics: waveforms, ISI distributions, temporal continuity, and principal components. Peri-stimulus time histograms (PSTHs) were constructed by aligning the spike times to the major task events (target onset or saccade), binning at 1 ms resolution, averaging across trials, and smoothing with a Gaussian filter (SD = 30 ms). MT data were collected during a different experiment under the same behavioral conditions in prior reports (Yates et al., 2017).

Encoding model

Request a detailed protocol

We built and compared several population encoding models, which were all variants of a generalized linear model (GLM). This statistical approach allowed us to characterize how a neuron’s spike trains (on single trials) depended on the task events (the visual stimulus and motor response), spikes from simultaneously recorded neurons, and the fitted neuron’s own recent spike-history. In this way, we could infer the functional connectivity of the network on a trial-by-trial basis. Each daily session (including all simultaneously recorded neurons) went into the GLM analysis. The data (and fits) were then summarized across all sessions.

Spike trains were discretized into 1 ms bins (Δ). Covariates were represented as delta functions at the time of the event and parameterized with temporal filters (nonlinearly time-scaled raised cosine functions) following previous conventions (Pillow et al., 2008; Park et al., 2014; Yates et al., 2017). The conditions inside and outside the receptive field were modeled together along with the rest of the parameters. The model does not include details about the specific saccade location or the stimulus spatial jitter. The number of parameters and data points depends on the number of simultaneously recorded neurons in each session (and the length of the trials which varies; time bins = 1 ms). For each neuron, the target and saccade kernels are each 8 parameters and 800 ms long, and the history and coupling filters are each 10 parameters and 250 ms long. There are n-1 coupling filters for each neuron, where n is the number of simultaneously recorded neurons during each session. These parameterizations are conventional and conform to previous uses of this method (Pillow et al., 2008; Park et al., 2014; Yates et al., 2017).

Each neuron was fit with a GLM using maximum a posteriori estimation (MAP) with a log-Gaussian prior, where the instantaneous spike rate (conditional intensity) of the fully coupled model at time t is given by

λt=exp(k∗xt+h∗rt−1+c∗st+b)

where k comprises the ni weights on the m task covariates x, and k*x is shorthand for

∑i=1m∑j=1nikijfj(xi(t−τ:t))

where f is the temporal basis functions described previously. h is the weights on the recent spike-history (which is notation for the neuron’s spikes leading up to but excluding the current time bin), c is the coupling weights on s simultaneously recorded spikes, and b is a constant term that captures the neuron’s baseline firing rate. We used an exponential as our choice of nonlinearity (inverse-link function) to map the linear predictors to Poisson spiking.

The log-likelihood of a Poisson GLM for a single neuron is

L(λ;r)=∑trtlog(Δλt)−Δλt

Only simultaneously recorded neurons within each session were included in the full (coupled) population encoding models. To prevent overfitting, we used ridge regression to penalize the weights on the regressors, which has the effect of shrinking the coefficients.

α=(‖k‖2+‖h‖2+‖c‖2)

For each neuron, we performed 5-fold cross-validation, in which the model was trained on 80% of the data and tested on the withheld 20%. The goodness-of-fit was computed by generating spike trains from the model, averaging them to get a predicted PSTH and calculating the variance explained of the real PSTH (R-squared).

To evaluate and compare the performance of the models, we calculated a likelihood test statistic by taking the difference of the log-likelihood for the full model and the log-likelihood of a homogeneous Poisson process model (with a constant rate), which acts as a null or ‘saturated’ model (Runyan et al., 2017),

LL=(L(λ;r)−L(λ¯;r))/∑trt

where λ¯ is the mean firing rate of the neuron (over the entire trial) and we divide by the sum of the spike counts. This formulation gives the prediction accuracy in units of bits per spike (Paninski et al., 2004; Pillow et al., 2008).

The models we considered varied in their inclusion of the coupling, history, and stimulus terms, as well as their parameterizations. We verified the fits by comparing the variance explained of the PSTHs and single-trial spike trains between the full model (with coupling, history, and task terms) and an ‘uncoupled’ model, which had no coupling terms (i.e. no connections between the neurons) but was otherwise the same. Unsurprisingly, adding coupling to the model (which captures the correlational structure of the single-trial spike trains) does not improve the fit of the predicted PSTHs (Figure 3d; points fell around the unity line; median 76% variance explained under both models) because PSTHs (by their very nature) ignore single-trial dynamics by averaging across trials. However, crucially, predictions of the single-trial spike trains universally benefit from the inclusion of the coupling terms (Figure 3e; points fell above the unity line; on average a log-likelihood improvement of 22% in units of bits per spike).

We also compared models that only included spikes from different temporal epochs of the trial to identify neural population dynamics that varied as a function of task demands. In the cases where two temporal epochs were compared, the window sizes and task parameters were matched. To summarize the coupling results within and between ROIs, we performed principal component analysis (PCA) on the coupling kernels sorted by each interaction. The first three principal components explained around 90% of the variance for each interaction. The same was true for the history kernels. To estimate the history and coupling time constants, we fit a double exponential curve to each kernel or the first principal component of the kernels for each ROI. History kernels exhibiting strong refractory periods rather than long timescale dynamics were poorly fit by an exponential decay and were excluded from this analysis (48%). To further characterize the impact of the coupling terms for each neuron, we constructed a predictive index defined by the difference between the deviance explained by the full model, and the deviance explained by the model without coupling (the ‘uncoupled’ model— only task and history predictors) divided by the deviance explained by the coupled model (Runyan et al., 2017; Agresti, 2002). A coupling index of one indicates that the neuron’s spike trains are completely predicted by the spiking activity of other neurons, and a value of zero indicates that spikes from other neurons add no predictive power over and above the task predictors and the neuron’s recent spike-history. We constructed the analogous index for the spike-history as well.

To further validate the coupling, we constructed null distributions by fitting the GLM to permuted data (following Pillow et al., 2008; see supplement). We permuted the order of the trials (i.e. trial identity) for each neuron (whose spike trains are used as predictors) relative to each fitted neuron, which eliminates the correlations between neurons but maintains the temporal dependencies of the task events and the spike times within each trial for the fitted neuron. In other words, the signal correlations are preserved while the noise correlations are disrupted. Crucially, the task events and spike times are never misaligned on single trials (on which the model is fit). This procedure is equivalent to treating each neuron independently in the model and obscuring the simultaneous nature of the recordings. The permutation analysis provides a clear null model against which to identify functional interactions within the GLM (i.e. beyond what is expected by chance) and is a principled validation of the coupling (Pillow et al., 2008; Yates et al., 2017; Runyan et al., 2017).

An additional concern might be that the differences in coupling between areas is driven by differences in receptive field overlap due to artifacts of sampling. The overall differences in coupling between LIP and FEF were also present during fixation when there is no visual stimulus in the receptive fields or memory of the stimulus being maintained (Figure 6a), meaning the coupling differences are likely due to differences in the underlying functional connectivity and not due to sampling artifacts regarding the receptive fields (which concurs with previous work: Katsuki et al., 2014). In addition, experiments were conducted using identical methods in both areas during simultaneous recordings and using a relatively indiscriminate sampling protocol (all neurons with isolatable waveforms were included regardless of selectivity). We also quantified the effect of coupling as a function of tuning similarity (using 1D circular Gaussian tuning curves), and found that coupling was modestly stronger for pairs of neurons with more similar spatial tuning across all interactions, and that relationship was most pronounced for neurons within LIP (Figure 6—figure supplement 1), a feature predicted by classic attractor network models. However, to fully address this question, the extent, shape, and response profile of the response fields would need to be mapped in greater spatial detail.

In addition, differences in coupling between the ROIs were unlikely due to overall differences in mean spike rates. The coupling kernels for each area were compared to the null (shuffled) distributions within each respective area. Under both conditions, the spike rates were identical but during the shuffled condition the correlation structure between neurons was broken, providing an independent estimate of coupling due to chance alone for each area regardless of mean spike rates. We have also demonstrated this in the GLM analysis of the simulated data from the attractor network (Figure 7—figure supplement 1), in which coupling tracked the internal recurrent strength of the attractor network independent of overall changes in mean firing rate. These results are further bolstered by the data– neurons in FEF actually had a significantly higher mean firing rate than LIP, whereas LIP had much stronger coupling than FEF.

Area MT’s coupling was estimated using the same GLM analysis, but the data was collected during a perceptual decision making task rather than a working memory task (details described in Yates et al., 2017). Coupling within MT was significantly lower than each other area interaction (Figure 3—figure supplement 2): LIP-LIP, FEF-FEF, LIP-FEF, FEF-LIP, (Wilcoxon rank-sum test): p=2.19×10−143; p=6.92×10−103; p=2.18×10−07; p=7.98×10−22. Magnitude of the effect size (Cohen’s D): LIP-LIP = 0.89 (large effect), FEF-FEF = 0.41 (medium effect), LIP-FEF = 0.16 (small effect), FEF-LIP = 0.24 (small effect).

Attractor network

Request a detailed protocol

To validate our analyses and situate our results more broadly we generated synthetic datasets from a spiking attractor network (Gerstner et al., 2014; https://neuronaldynamics.epfl.ch/) and fit them with the GLM. This attractor network was based on a classic model of spatial working memory (Compte et al., 2000). We parametrically varied the strength of the recurrent connections in the excitatory population while holding all other parameters constant. To replicate the real experiments, we varied the location and onset of the stimulus (i.e. the ‘visual target’) trial-by-trial (200 ms duration; onset jittered from 200 to 500 ms; 1 s trial duration), and sampled a small subset of neurons from the overall population (N = 20). 500 trials were simulated per session and this sample of neurons remained the same throughout the session. Parameters of the network were kept at their default values unless otherwise noted, as in the case of the recurrent strength of the excitatory population. Some of the main parameters of interest are noted (using their names from the simulation code): N_excitatory = 1024, N_inhibitory = 256, N_extern_poisson = 1000, poisson_firing_rate = 1.3 * hertz, weight_scaling_factor = 2.0, sigma_weight_profile = 20.0, Jpos_excit2excit = 1.6 (strength of the recurrent input), stimulus_center_deg = 120, stimulus_width_deg = 30, stimulus_strength = 0.06 * b2.namp. Note that the default NMDA time constant was 65 ms (Gerstner et al., 2014) rather than the 100 ms in the original model (Compte et al., 2000).

Data availability

Data files have been deposited to Data Dryad under https://doi.org/10.5061/dryad.gb5mkkwk7.

The following data sets were generated
    1. Hart E
    2. Huk AC
    (2019) Data Dryad
    ID 10.5061/dryad.gb5mkkwk7. Data from: Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network.
    https://doi.org/10.5061/dryad.gb5mkkwk7

References

Decision letter

  1. Emilio Salinas
    Reviewing Editor; Wake Forest School of Medicine, United States
  2. Timothy E Behrens
    Senior Editor; University of Oxford, United Kingdom
  3. Emilio Salinas
    Reviewer; Wake Forest School of Medicine, United States
  4. Albert Compte
    Reviewer; Institut d'Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS), Spain

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This study combines multi-neuron recordings from two cortical areas, FEF and LIP, with advanced fitting techniques (GLM modeling) to investigate the underlying neuronal dynamics that unfold during a classic memory-based visuomotor task. The approach is notable because it teases apart the contributions of task events, firing history, and functional coupling across neurons to the evoked spiking activity, doing so in a way that is interpretable. The observed neuronal interactions (magnitudes and timescales) are broadly consistent with those proposed by classic theoretical models of persistent activity and working memory, but the data also reveal intriguing differences and similarities between FEF and LIP that should serve to constrain and refine future models of the frontoparietal attentional network.

Decision letter after peer review:

Thank you for submitting your article "Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network" for consideration by eLife. Your article has been reviewed by three peer reviewers, including Emilio Salinas as the Reviewing Editor and Reviewer #1, and the evaluation has been overseen by Timothy Behrens as the Senior Editor. The following individual involved in review of your submission has agreed to reveal their identity: Albert Compte (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

This manuscript analyzes single-neuron activity in the FEF and area LIP during the classic memory-guided saccade task. The novelty here lies in the recording of multiple neurons (5-20 per session) from both areas simultaneously, and in the GLM analyses, which are able to tease apart how task events, firing history, and interneuronal coupling determine the spikes fired by each neuron. The results provide a statistical view of the recurrent interactions between and within these two areas that is of relevance to their functional characterization, and to models of recurrent circuits and working memory in general.

All reviewers agreed that this is fantastic data set and that the analysis is interesting and novel. The general concern was that the methods require more thorough validation in order to put the interpretations on a more solid footing. The suggested revisions will require additional analyses, but not additional experiments. The consensus was that they are important for supporting the conclusions (which could change as a result).

Essential revisions:

1) All reviewers identified potential problems with the analysis/interpretation of the results of the GLM procedure, as can be seen in the individual reviews below. However, as detailed by reviewer 2, many of these concerns could be addressed by testing the GLM methods against synthetic data from the very network models that the results seem to support. This would require substantial work, but is in principle straightforward. This sort of analysis, where the model is tested with designed data sets for which the correct answers are known, would substantially strengthen the credibility of the results and their interpretation.

Some important methodological concerns that could be at least partially addressed in this way are the following:

a) It is not entirely clear why the "exceptionally strong coupling" between neurons contributes in such a subtle way to the predictions of neural activity (i.e., they are not needed to accurately replicate the PSTHs).

b) Verifying the shuffling procedure (null hypothesis) for determining the significance of the coupling terms.

c) It is unclear whether the history-dependent kernels only capture intrinsic neuronal properties, as opposed to influences from other neurons that could be equivalent to history effects.

d) How do the results depend on receptive field overlap? In particular, it is possible that the differences between LIP and FEF are the consequence of different overlap patterns in the two areas.

2) The total coupling strength, which is the net result of adding the positive and negative (inhibitory) kernel weights, is used as a summary measure of coupling between neurons. As elaborated by reviewer 1, this is a potentially misleading quantity, as it does not consider the magnitudes of the excitatory and inhibitory components. The analyses should be run also with alternative measures that take this distinction into account.

3) Consideration of differences across neuronal classes; in particular, whether the results are distinctly different for neurons with significant delay period activity, as mentioned by reviewer 2.

4) There is insufficient validation of the model against traditional analysis techniques, such as cross-correlation analyses.

5) There is insufficient description of some of the analytical procedures (see specific comments below).

Reviewer #1:

This work addresses important problems in oculomotor physiology, is sound, clearly described, and contains many interesting nuggets about the FEF-LIP circuitry. Just to mention one of them, the three interaction kernels provide convincing measures of the time constants of these circuits, confirming long-help ideas based on theory and modeling. Other results, such as the stronger interactions across than within areas, are interesting precisely because they do go a bit against the grain.

I only have one substantial comment. Several analyses are based on the total coupling strength, which is the net result of adding the positive and negative (inhibitory) kernel weights. This leads to the conclusion that "coupling in LIP was greater than FEF, suggesting a greater degree of recurrent connectivity in LIP". But the total strength is a crude measure. If the subtraction of excitation and inhibition gives 1 = 20 – 19 net excitation in one area and 2 = 5 – 3 in the other, is it really fair to say that the coupling is stronger in the latter? Clearly not. Stronger nonlinearities are expected for highly balanced circuits in which both excitation and inhibition are stronger. This intuition is missing in the Discussion paragraphs four and five. In that case, identical excitation in both areas but stronger inhibition in FEF than LIP would be perfectly consistent with stronger winner-take-all dynamics in FEF and more tolerance to spatial ambiguity in LIP, in turn consistent with saccade selection in the former and divided attention in the latter.

My suggestion is to quantify the excitatory and inhibitory interactions separately. For instance, by computing the total excitatory coupling on one hand, and the total inhibitory coupling on the other. If both terms and the net result are stronger in LIP than FEF, then that would credibly verify the current conclusion ("greater coupling in LIP than FEF"). But I suspect (from Figure 3B) that the situation is a bit more nuanced. For instance, stronger inhibitory coupling in FEF would be consistent with stronger motor competition and/or narrower visual tuning. Likewise, one could argue that the relevant indicator of stronger or more reliable delay-period activity is not the net coupling (excitation minus inhibition) but the total absolute coupling (i.e., the total summed magnitude of the coupling weights). I think that, in general, consideration of these alternatives beyond the net coupling would provide a broader and more substantial view of the data, and a more nuanced basis for their functional interpretation, without any alterations to the GLM model.

Reviewer #2:

This manuscript provides evidence that recurrent mechanisms in LIP, FEF and between these two areas are engaged during persistent activity in a delayed response task. This is supported by fitting neuronal spiking data simultaneously recorded in these areas with a population encoding model. A GLM fitting procedure estimates parameters for visual and motor dependencies, neuronal history dependence, and coupling kernels between simultaneously recorded neurons. The coupling kernels are reported strong in comparison to history kernels, and contain time scales consistent with excitatory and inhibitory mechanisms typically included in attractor models of working memory.

The manuscript is a valuable and significant contribution to the research on the mechanisms of working memory. For this classic task, a population-level analysis of simultaneous recordings in two cortical areas has not yet been presented, and provides important insights into the relative importance of different mechanisms that have been proposed to support persistent activity: intrinsic mechanisms, local circuit recurrence, and recurrent interactions between areas. The methods applied are aimed at testing this with advanced statistical methods.

My major concerns regarding the conclusions drawn from these analyses are:

1) There is an inconsistency in the manuscript in that, on the one hand, interneuronal couplings do not improve PSTH predictions (Figure 3D) and yet various analyses (Figure 3A, Figure 4C) are interpreted as demonstrating "exceptionally strong coupling", "exceptionally strong recurrent interactions" or that "network dynamics play a more vital role than intrinsic dynamics". If recurrent interactions are removed from an attractor model persistent activity collapses, and PSTHs are profoundly affected. At face value, the findings thus do not seem to represent a direct support of these models. The fact that exceptionally strong couplings do not have an impact in the PSTH should be better explained.

2) I am concerned about the "null hypothesis" in Figure 3A: if trials are shuffled for each neuron before the fit, then neural activity is modeled with spiking data of other neurons obtained in trials with different delay duration, so not aligned to the stimulus and saccade predictors used in the model. Since these events are typically associated with an increase in firing rate, interneuronal couplings will be reduced in this model because of these misalignments. The reading of "strong recurrence" that now emanates from the comparison with this "null hypothesis" might instead result from this misalignment. Maybe a more direct assessment of how strong is the contribution of couplings to the network would be to evaluate what fraction they represent in the sum of all predictor terms in the model.

3) The manuscript emphasizes the role of recurrent interactions in generating persistent activity. However, not all neurons recorded in LIP and FEF show persistent activity in this task. In particular, Figure 2 shows that neurons with robust persistent activity show sustained history kernels, which supposedly affect just a minority of neurons in the database (Figure 4C). Some of the conclusions may change if one considers separately neurons with strong persistent activity from other neurons. For instance, if neurons with persistent activity mostly populate the right cloud of dots in Figure 4C the interpretation of this panel's results would be very different. Example neurons shown in Figure 1 could be explicitly identified in Figure 4C and other panels with individual neuron data. If the question is how persistent activity is generated, then it should be relevant to consider separately neurons with and without persistent activity.

4) The interpretations in the manuscript jump very easily between the statistical description contained in the fitted kernels and biophysical mechanisms, and this should be more carefully considered. Any "temporal integration above and beyond that explained by the external task elements" (Park et al., 2014) and the spike times of the few simultaneously recorded neurons in that session will be attributed to history kernels, which would therefore be inappropriate to attribute to intrinsic cellular mechanisms. In general, authors should be cautious with the possible confusion in using "intrinsic" to refer to the history kernel. The history kernel might include traces of other network dynamics not captured by the few neurons recorded simultaneously in the session.

Importantly, many of these concerns could be directly addressed by analyzing spike trains from a few neurons selected from attractor network simulations (many of which freely available) to verify if their GLM approach is able to extract the biophysically-based parameters of the model, as currently argued. My intuition is that model neurons without any specific intrinsic mechanism with long time course would show a long-lasting history dependence (self excitation) when modeled against the activity of just a handful of their close neighbors. The number of neurons used as predictors, or the similarity of their memory fields, could also conceivably have an impact in the decay time of history and coupling kernels, and thus contribute to possible differences between FEF and LIP in this analysis. These computational models are freely available (for instance https://neuronaldynamics-exercises.readthedocs.io/en/latest/) and the model data can be generated easily and analyzed with the authors' methods.

Reviewer #3:

The paper uses a novel analytical technique to infer functional connectivity among FEF and LIP cells during a memory guided saccade task. The analysis takes a GLM-based approach and fits spike trains of simultaneously recorded FEF and LIP cells as weighted combinations of kernels related to (1) target location, (2) saccade direction, (3) coupling filters modeling interactions among cells and (4) history filter modeling within-neuron autocorrelations. The main conclusions are that FEF and LIP neurons show strong coupling both within and across areas, and that LIP shows stronger coupling and longer intrinsic timescales than FEF.

While the approach is interesting and potentially useful, I am afraid it is not sufficiently justified in the present version of the manuscript. The level of detail provided is simply not sufficient to support the claims based on this novel analysis technique. I see two main problems with the manuscript as it is now:

1) There is insufficient control for potentially differential sampling of neurons in FEF and LIP: Could the apparent stronger coupling in LIP vs. FEF be due to different neural sampling in the two areas? For instance, if the RF of the recorded cells had more overlap in LIP relative to FEF, that may produce stronger apparent coupling in two different ways. Stronger coupling may arise if the model mis-attributes shared stimulus/saccade related activity to the coupling weights. The authors emphasize that their model identified coupling above and beyond any stimulus-related response, but they provide little evidence to substantiate this assertion. Stronger coupling may also arise if the model correctly attributes variance but the neurons are in fact more coupled by virtue of being more functionally similar. In that case, the areal differences are only artefacts of the neurons the authors happened to sample. We need much more thorough analyses of the similarity in RF profiles and temporal response profiles of the recorded cells to rule out a sampling confound.

2) There is insufficient validation of the model against traditional analysis techniques. The field has several traditional, established measures of neural coupling or connectivity, including noise correlations and joint PSTHs or autocorrelograms. The authors dismiss those analyses off hand with little justification except for saying that they do not adequately remove stimulus-evoked activity. But there are actually many ways for them to get around confounds with these methods. Comparing their model results to these traditional analyses is essential to validate their results.

3) There is insufficient description of the analytical procedures:

– How were the neurons combined across recording days? Clearly, the neurons that were simultaneously recorded each day could be fit using the described method. But the authors say that they simultaneously fit the entire data set – including neurons recorded on different days. How precisely did they set this up and how did this affect the results?

– What were the kernels that the authors used in the model fits? How were those kernels selected? What properties must the kernels have to make the model work? Are the conclusions robust over reasonable changes in kernel shape?

– Goodness of fit and model comparisons: The authors should provide a complete description of the type of models they compared.

– Individual monkey results: How many cells were recorded in each monkey? Did the critical results hold in both monkeys?

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for re-submitting your article "Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network" for consideration by eLife. Your article has been reviewed by two peer reviewers, including Emilio Salinas as the Reviewing Editor and Reviewer #1, and the evaluation has been overseen by Timothy Behrens as the Senior Editor.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

The authors have been very responsive to the comments made in the original reviews, and have thoroughly revised the manuscript. The methods are clearer and the conclusions and rationale for the model more robust. Importantly, the GLM approach has now been validated by applying it to simulated data, and the new results are largely consistent with the original intuition provided by the authors.

However, several implementation details that can potentially affect the results were still unclear and require more thorough explanation.

Essential revisions:

1) What exactly is the uncoupled model?

2) How exactly is the shuffling across trials performed?

3) More careful analyses of the activity during fixation and early delay.

4) Clarification of the dependence on overall firing rate (separate from the variations in connectivity).

These points are discussed at length by reviewer 2 below.

Reviewer #2:

The revised manuscript contains significant improvements over the previous version, notably the new computational model data that provides support to the methods applied. However, I still maintain some relevant concerns on the controls required to support the interpretations of their analyses as couplings between neurons. This concerns primarily the shuffle approach and the control of firing rate confounds as detailed below.

1) Related to previous Major concern 1.

I realize that part of the confusion here is that the “uncoupled model” is never fully described. I understood that this was the full fitted model, to which couplings were set to zero. From this model I would expect PSTHs to differ largely from measured PSTHs, if couplings are contributing significantly to the GLM. Instead, I gather from Pillow et al. (2008) that the uncoupled model is a reduced model refitted to the data, and then I understand that the fit may be good even if couplings for the full model are strong contributors to the fit. I urge the authors to explain clearly what their uncoupled model is. In fact, in the current revision this is further confused in the Materials and methods (“Unsurprisingly,…”), where the “uncoupled method” is commented in the middle of the description of the shuffle approach. These two separate controls should be clearly distinguished and specified so the reader understands their separate implications. Now this is very confusing.

2) Related to previous Major concern 2.

I am still not convinced about the shuffle approach on which the "extraordinarily strong coupling" result is based. If I understand it correctly, the structure of the data is as schematically depicted in Decision letter image 1, with simultaneous spike trains recorded (here 10 neurons in 10 lines per panel) for separate trials (here 8 trials in 8 panels), where in each trial the stimulus is presented in different locations (here different colors of the simulus and response shadings) and delay durations are also different from trial to trial. Neurons respond with spiking activity depending on whether the stimulus falls within their receptive field or not.

Decision letter image 1
Download asset Open asset

The GLM for the neuron on the gray background would then model spikes based on its specific stimulus and response events for each different trial, on its previous spikes in the corresponding trial, and on the previous spikes of all other neurons in the corresponding trials. Crucially the spikes for these other same-trial neurons are collected based on the same stimulus location, response and delay duration.If I understand correctly the shuffle condition applied in Figure 3, the GLM now models the gray-background neuron based on its specific stimulus and response events for each different trial and on its previous spikes in the corresponding trial, exactly as before, but now the spikes of other neurons are taken from randomly picked trials. This is represented in the schematic in Decision letter image 2 (notice the first lines of each panel are the same for both schematics). If this is the case, then now the spikes for these other shuffled neurons were not collected based on the same stimulus location, response and delay duration as the modeled neuron. As a result, the consistency of stimulus activation of neuron 9 and neuron 7 shown in Decision letter image 1 (they are both active or inactive in response to stimuli in all trials), and the consistency of the timing of response events, are broken with the shuffle in Decision letter image 2. This will lead to a radical change in the cross-correlations between these two neurons, even if these spike trains were totally independently generated.

Decision letter image 2
Download asset Open asset

I have run this simulation. Data for these spike trains were independently generated for each neuron (so with no coupling between them), only keeping the consistency of stimulus, response and delay within trials. As shown in the histograms in Decision letter image 3, the mean cross-correlations (as a proxy of the couplings obtained with the GLM) were radically affected by the shuffling procedure. This does not demonstrate any functional coupling between the neurons, but the fact that task events that elicited neural responses were misaligned by the shuffling procedure.

Decision letter image 3
Download asset Open asset

In my view, this effect could explain the extraordinary changes in shuffle histograms in Figure 3. To clarify this, the shuffle should be performed only between trials with equal stimulus location and delay duration, or else apply other commonly used resampling procedures to estimate cross- correlations (Fujisawa et al., 2008; Katsuki et al., 2014), such as within-trial jitter correction methods (Amarasingham et al., J Neurophysiol 2012).3) The section on “Interneuronal coupling is dynamic across behavioral epochs” is very confusing and is not really addressing the point that they are formulating. The fact that there are not very marked changes between couplings measured in the fixation and delay periods is taken as evidence of dynamical working memory without much justification. Later on the comparison of early and late delay periods yields stronger couplings as delay progresses. In my view, this attempt to contribute to the debate on dynamic delay activity, or even activity-silent working memory (Stokes et al., 2015) is overambitious and needs more specific analyses (consider for instance possible traces of the stimuli in the couplings after the response period, by comparing in and out conditions in the baseline period where there is no confound of firing rate for in/out conditions, e.g. Spaak et al., SfN 2017 #339.14; Barbosa et al., Biorxiv, 2019, doi:10.1101/763938). Further, in the interpretations of this paragraph it is disclosed that their measure of coupling is confounded by changes in firing rate (“This finding highlights the potential role of nuanced changes in the dynamics of the network rather than an overall increase in population activity”). This should be declared early on, as this confound may affect many of the interpretations. Any interpretations of difference in coupling strengths should be cautious in previously demonstrating no difference in firing rates, or else in applying more stringent rate-correcting methods such as jitter correction (Fujisawa et al., 2008). Currently, the manuscript does not parallel each of the coupling comparisons (FEF-LIP, fixation-delay, etc.) with corresponding comparisons of mean firing rates, or rate-correcting measures, to support these conclusions.

4) The computational model is a nice demonstration of their methods, in particular of the retrieval of the correct time scale of the interactions between neurons (the AMPA and NMDA current time courses). However, in terms of the strengths of the couplings, the model may also be confounded by changes in firing rate. It will be useful to plot the mean firing rate of model neurons as recurrent connectivity is increased. If this mean firing rate is increasing too, then some compensatory change may be introduced to maintain rates constant as recurrent connectivity increases in order to resolve this concern. The stimulus kernels derived from the model in Figure 7D, left panel, do not seem to correspond to the simulation results: stimuli in receptive fields should generate increase in rates, and stimuli outside the receptive field a suppression of rates.

5) Because of the possible rate confound that affects the coupling measure, the manuscript should provide a mean firing rate description of the various areas and task periods, for instance through average PSTHs.

https://doi.org/10.7554/eLife.52460.sa1

Author response

Summary:

This manuscript analyzes single-neuron activity in the FEF and area LIP during the classic memory-guided saccade task. The novelty here lies in the recording of multiple neurons (5-20 per session) from both areas simultaneously, and in the GLM analyses, which are able to tease apart how task events, firing history, and interneuronal coupling determine the spikes fired by each neuron. The results provide a statistical view of the recurrent interactions between and within these two areas that is of relevance to their functional characterization, and to models of recurrent circuits and working memory in general.

All reviewers agreed that this is fantastic data set and that the analysis is interesting and novel. The general concern was that the methods require more thorough validation in order to put the interpretations on a more solid footing. The suggested revisions will require additional analyses, but not additional experiments. The consensus was that they are important for supporting the conclusions (which could change as a result).

We thank the reviewers and editor for the thoughtful feedback, and were very happy that there is shared enthusiasm about the value of these experiments. We are grateful for the chance to both add and clarify validation assessments. These are very important both for making inferences about the data, and for linking those inferences to theories of persistent activity. We describe specifics below, but at a high level, we have addressed this issue in a number of ways.

First, we have clarified the value of the shuffling analyses that we used throughout the first submitted version. There was some misunderstanding on how this validation procedure works, which we have elaborated on in the specific responses, the methods, and in the manuscript. In short, we shuffle the order (i.e., trial numbers) of the trials for each neuron relative to other neurons – which eliminates the correlations between neurons but maintains the temporal dependencies of the task events and the spike times within each trial. This is equivalent to treating each neuron independently in the model and ignoring the simultaneous nature of the recordings. Unsurprisingly, adding coupling to the model (which captures the correlational structure of the single-trial spike trains) does not improve the fit of the predicted PSTHs because PSTHs (by their very nature) ignore single trial dynamics by averaging across trials (a point that we discuss in more detail in specific responses). The shuffling analysis provides a clear null model against which to identify functional interactions within the GLM (i.e., beyond what is expected by chance) and was used as a validation in the original coupled-GLM work (Pillow et al., 2008). It is therefore well-suited to provide the very validation of the coupling required by the reviewers (and ourselves).

Second, we have run the same GLM-based analyses on simulated datasets generated from a conventional attractor network (Figure 7). This is the closest we could come to the spirit of the request to do an analysis where the “correct answers are known” (beyond the null model). There is a wrinkle to this, which is that, in fact, although the synthetic network architecture is of course known, the resulting covariance structure is not known. To the best of our (and some of our more computationally-expert collaborators) knowledge, there is no general way to specify in advance the correlation structure of an attractor-style spiking network, which of course have a series of interacting nonlinearities that would make this exceedingly difficult. Regardless of this technical point, we think that direct comparison to the classical model is highly valuable. We had envisioned saving this for a second paper, as there are a plethora of potential analyses one could do to test the mechanistic models against our dataset. But we spent a lot of time on the core comparison and provide some interesting results at the end of the revised manuscript. Indeed, we were pleasantly surprised to see that the GLM did a really nice job of estimating the recurrent connectivity of the network and recovering the temporal dynamics built into the model neurons, which we take as an additional validation along the lines of the “known right answer” logic proposed by the reviews.

Third, we have also clarified the value of the simultaneous fitting (i.e., estimation of all neuron-to-neuron interactions within a recording session). In retrospect, we really goofed on making both the nature of the “simultaneous” fitting and its value clear in the first submission. The revised manuscript now clarifies how the simultaneous fitting is done (i.e., at the level of all neurons recorded within a session), and how this approach mitigates the usual interpretive ambiguities of standard pairwise correlation measures. Imagine that Cell A drives both Cell B and Cell C, without any additional drive between B and C. Standard pairwise correlations, estimated one pair at a time in series, would identify correlations not just between A and B and A and C, but also between B and C (the latter by virtue of their shared input from A, which is not considered in a pairwise correlation). But by estimating these impacts simultaneously, the fully-coupled GLM could capture the impacts of A on B and C, but can also “explain away” the correlation between B and C. This issue has been laid out nicely in Stevenson et al. (2008), which we now cite. We have also added comparisons to more traditional measures of correlations in the supplemental.

Essential revisions:

1) All reviewers identified potential problems with the analysis/interpretation of the results of the GLM procedure, as can be seen in the individual reviews below. However, as detailed by reviewer 2, many of these concerns could be addressed by testing the GLM methods against synthetic data from the very network models that the results seem to support. This would require substantial work, but is in principle straightforward. This sort of analysis, where the model is tested with designed data sets for which the correct answers are known, would substantially strengthen the credibility of the results and their interpretation.

We appreciate the push to directly compare data to theory. This was planned to be a detailed second paper, and we have several collaborations underway to that effect. Nevertheless, we have made, frankly, faster and more clear progress on this than we expected. We have generated synthetic datasets from an attractor network while parametrically varying the recurrent strength of the excitatory population (Figure 7). We sampled spike trains from these networks akin to the experiment and fit the GLM in the exact same way we did for the real data. We found that coupling (estimated from the GLM) is systematically related to the internal connectivity strength of the attractor network. This finding is not only an important validation but allows us to situate our LIP and FEF results relative not just to each other, but to theory. We now conclude the manuscript with these analyses.

Some important methodological concerns that could be at least partially addressed in this way are the following:

a) It is not entirely clear why the "exceptionally strong coupling" between neurons contributes in such a subtle way to the predictions of neural activity (i.e., they are not needed to accurately replicate the PSTHs).

We have clarified the dissociation between explaining the mean responses (PSTHs) and explaining the single-trial responses (which benefit from characterizations of correlated noise, both between and within neurons). This dissociation is commonly observed in such single-trial fitting schemes, such as the classic population GLM paper by Pillow et al., as well as in more recent work in LIP and MT (Park et al., 2014; Yates et al., 2017). It’s worth mentioning that the contribution of coupling to the predictions of neural activity are not “subtle” in the data. As explained, coupling has little effect on predicting the PSTHs because they collapse across trials and ignore correlations (Figure 3D), but coupling universally benefits the predictions for single-trial spike trains (Figure 3E). As noted in the manuscript and in our more detailed replies, to understand the network dynamics underlying persistent activity during behaviorally relevant timescales, we must focus on single trials rather than averages that obscure the single-trial dynamics (for more discussion see Stokes and Spaak, 2016; Latimer et al., 2015). That said, it is also important to note that the GLM does a very good job predicting the PSTH of most neurons regardless of coupling (variance explained in Figure 3D) which is also consistent with the work cited above. We have attempted to clarify and emphasize this point in the manuscript.

b) Verifying the shuffling procedure (null hypothesis) for determining the significance of the coupling terms.

This appears to reflect a major weakness in our description of our validation procedures. Either that, or we’re not exactly sure what additional verification of the shuffling procedure (already akin to a permutation test, which is a standard nonparametric validation) would be. So, we’ve tried to clarify the description of this and to emphasize the value of the shuffling at appropriate points. In our detailed reply to reviewer 2, we similarly state that there might have been a misunderstanding of the methods as originally described, as the reviewer appears to request an important validation that was provided in the original manuscript. Our utmost apologies, we have worked on the phrasing around that important part in the revised manuscript. We have also noted that this procedure was used to validate the coupling in the seminal coupled-GLM work (Pillow et al., 2008; see supplement) and many more recent uses of this analysis scheme (Runyan et al., 2017; Yates et al., 2017).

c) It is unclear whether the history-dependent kernels only capture intrinsic neuronal properties, as opposed to influences from other neurons that could be equivalent to history effects.

We have clarified this point in the revised manuscript. At a first pass, the simultaneous nature of the fit allows the model to parse out distinct effects of history and other neurons (in addition to task factors). This is another facet of the “explaining away” issue described above. However, at a deeper level, this “explaining away” is only as good as the data are complete, and so it is indeed possible that some of the history properties reflect the impacts of unobserved inputs as opposed to intrinsic cellular properties. We have now clarified this in the manuscript.

d) How do the results depend on receptive field overlap? In particular, it is possible that the differences between LIP and FEF are the consequence of different overlap patterns in the two areas.

We did not map the 2D spatial extent of the receptive fields in detail. For the two-area ensembles we recorded from, doing so would require another more complex (e.g., white noise) stimulus and additional data collection time. We would love to have such data but in the interest of statistical power and stability for the main experiment, we did coarser online mapping of the ensemble response fields. Therefore we cannot estimate the precise overlap of the receptive fields. Few studies have done this during working memory tasks, but it’s a very interesting question that we had considered previously, and our thinking was that the very large size and idiosyncratic shapes of RFs in these areas may dilute the potential for nuanced insights with the topic becoming the primary focus of an experiment.

Regardless, we did our best to explore this issue in our data. Classical experiments (and simulations) use a simplified 1D representation of the spatial selectivity: the angle (saccade direction) from fixation. We have added a supplemental figure showing the relationship between coupling and the similarity of the neurons’ spatial tuning using this type of tuning curve (Figure 6—figure supplement 1). However, critically, the differences in coupling between LIP and FEF are present even during the fixation period when there is no visual stimulus (or memory of the stimulus) driving the RFs of the neurons (Figure 6A). Therefore, this result is hard to explain simply by differences in selectivity for the stimuli. This result is in accordance with previous findings that relied on a similar analysis and logic (Katsuki et al., 2014). We have also elaborated on this topic in the Discussion.

2) The total coupling strength, which is the net result of adding the positive and negative (inhibitory) kernel weights, is used as a summary measure of coupling between neurons. As elaborated by reviewer 1, this is a potentially misleading quantity, as it does not consider the magnitudes of the excitatory and inhibitory components. The analyses should be run also with alternative measures that take this distinction into account.

Absolutely a fair point. We’d previously explored a range of metrics and now include alternatives. No major changes in the pattern or interpretation of the results present themselves. We do wish to point out that quantifying the coupling impact by calculating the sum of the kernel weights over time is indeed quite coarse, but it is not “misleading” because the magnitudes and excitatory and inhibitory components are considered in the sum. So this seems a pretty legitimate way to simply describe the time-averaged net impact. The major shortcoming of this approach is that it collapses over time, but that’s what the remaining analyses that use PCA serve to add.

3) Consideration of differences across neuronal classes; in particular, whether the results are distinctly different for neurons with significant delay period activity, as mentioned by reviewer 2.

We were interested in this as well, but unfortunately no clear patterns emerged. We have added a supplemental figure depicting what the reviewer suggests (Figure 4—figure supplement 1).

4) There is insufficient validation of the model against traditional analysis techniques, such as cross-correlation analyses.

We had performed these internally as an initial validation before feeling good about relying on the GLM fits, but we now add these in the revised manuscript and the supplement (Figure 2—figure supplement 1). However, from our perspective, these more traditional assessments of correlation suffer from a weakness that the population GLM was designed to fix (as described previously; Stevenson et al., 2008). Additionally, this GLM approach has been validated in physiological circuits/populations where the connectivity was better-known (Gerhard et al., 2013; Pillow et al., 2008). Bottom line, we were in a bit too “in our heads” in trusting the GLM, but we hope we’ve shared convergent evidence to build the reviewer’s trust in the technique now.

5) There is insufficient description of some of the analytical procedures (see specific comments below).

Agreed. Internally, we had relied on nearly-identical analysis schemes in Yates et al. (2017) and Park et al. (2014) and were likely too internally context-deep when we summarized the methods to others. We are big proponents of manuscripts standing on their own and have expanded the treatment of the analytic procedures both in the methods and at various interpretive points. These are indeed important clarifications, which are of relevance to some of the major/general issues described above. Thanks for pushing us to improve on this axis.

Reviewer #1:

This work addresses important problems in oculomotor physiology, is sound, clearly described, and contains many interesting nuggets about the FEF-LIP circuitry. Just to mention one of them, the three interaction kernels provide convincing measures of the time constants of these circuits, confirming long-help ideas based on theory and modeling. Other results, such as the stronger interactions across than within areas, are interesting precisely because the do go a bit against the grain.

I only have one substantial comment. Several analyses are based on the total coupling strength, which is the net result of adding the positive and negative (inhibitory) kernel weights. This leads to the conclusion that "coupling in LIP was greater than FEF, suggesting a greater degree of recurrent connectivity in LIP". But the total strength is a crude measure. If the subtraction of excitation and inhibition gives 1 = 20 – 19 net excitation in one area and 2 = 5 – 3 in the other, is it really fair to say that the coupling is stronger in the latter? Clearly not. Stronger nonlinearities are expected for highly balanced circuits in which both excitation and inhibition are stronger. This intuition is missing in the Discussion paragraphs four and five. In that case, identical excitation in both areas but stronger inhibition in FEF than LIP would be perfectly consistent with stronger winner-take-all dynamics in FEF and more tolerance to spatial ambiguity in LIP, in turn consistent with saccade selection in the former and divided attention in the latter.

My suggestion is to quantify the excitatory and inhibitory interactions separately. For instance, by computing the total excitatory coupling on one hand, and the total inhibitory coupling on the other. If both terms AND the net result are stronger in LIP than FEF, then that would credibly verify the current conclusion ("greater coupling in LIP than FEF"). But I suspect (from Figure 3B) that the situation is a bit more nuanced. For instance, stronger inhibitory coupling in FEF would be consistent with stronger motor competition and/or narrower visual tuning. Likewise, one could argue that the relevant indicator of stronger or more reliable delay-period activity is not the net coupling (excitation minus inhibition) but the total absolute coupling (i.e., the total summed magnitude of the coupling weights). I think that, in general, consideration of these alternatives beyond the net coupling would provide a broader and more substantial view of the data, and a more nuanced basis for their functional interpretation, without any alterations to the GLM model.

This is a valid concern; we struggled to find a good way to summarize the coupling with a single metric that was devoid of caveats. We have plotted the absolute coupling (Figure 3—figure supplement 1A), and the primary result holds. Considering the excitatory/inhibitory comparison, in the current analysis (just to clarify) the coupling strength is only summed for each individual kernel across time, not across kernels, providing a simple scalar measure of the net impact of one neuron’s spikes on another. Thus, the histograms in Figure 3 show the net relationship of each neuron pair, and show how many neuron pairs were (in general) excitatory and inhibitory for each area interaction (the tails of the distributions). It is true that this is a coarse metric and can obscure the changes in positive and negative weights over the time period of each kernel, but we were looking for a simple descriptive measure of the overall relationship of each neuron pair. If we were to sum all positive and negative weights for all time bins separately we lose the fundamental relationships between the kernels (and thus the pairs of neurons), which can be challenging to interpret. Nevertheless, we have included separate comparisons of the overall excitatory and inhibitory interactions as well (Figure 3—figure supplement 1B,C). Most importantly, this is one of the reasons we used PCA to summarize the temporal profile of the kernels in a more principled way.

Reviewer #2:

This manuscript provides evidence that recurrent mechanisms in LIP, FEF and between these two areas are engaged during persistent activity in a delayed response task. This is supported by fitting neuronal spiking data simultaneously recorded in these areas with a population encoding model. A GLM fitting procedure estimates parameters for visual and motor dependencies, neuronal history dependence, and coupling kernels between simultaneously recorded neurons. The coupling kernels are reported strong in comparison to history kernels, and contain time scales consistent with excitatory and inhibitory mechanisms typically included in attractor models of working memory.

The manuscript is a valuable and significant contribution to the research on the mechanisms of working memory. For this classic task, a population-level analysis of simultaneous recordings in two cortical areas has not yet been presented, and provides important insights into the relative importance of different mechanisms that have been proposed to support persistent activity: intrinsic mechanisms, local circuit recurrence, and recurrent interactions between areas. The methods applied are aimed at testing this with advanced statistical methods.

My major concerns regarding the conclusions drawn from these analyses are:

1) There is an inconsistency in the manuscript in that, on the one hand, interneuronal couplings do not improve PSTH predictions (Figure 3D) and yet various analyses (Figure 3A, Figure 4C) are interpreted as demonstrating "exceptionally strong coupling", "exceptionally strong recurrent interactions" or that "network dynamics play a more vital role than intrinsic dynamics". If recurrent interactions are removed from an attractor model persistent activity collapses, and PSTHs are profoundly affected. At face value, the findings thus do not seem to represent a direct support of these models. The fact that exceptionally strong couplings do not have an impact in the PSTH should be better explained.

This is an important issue and (as stated in the general reply above) one we have tried to clarify substantially. PSTHs only quantify the average responses of the neurons across trials. The memory of the target itself, and thus, the neural dynamics act on single trials, the behavioral relevant time periods. Our findings show that coupling (and thus the correlations between the neurons) is not necessary to capture the average responses, (i.e. considering the spike trains from each neuron as independent would give you the same result; Figure 3D). But, if you look at the predicted spike trains on individual trials (recalling that the model was fit on individual trials), you can see that there is useful information in the correlations between neurons that increase the accuracy of predictions of single trial responses (Figure 3E). Hence, the interesting result here is that the correlation structure matters for the population code on individual trials. It is not surprising that it does not matter for the average responses across trials because PSTHs obscure (i.e. average away) single-trial fluctuations by design. This distinction was also found in the retina in the seminal work applying the coupled-GLM approach to modeling population data (Pillow et al., 2008). This finding emphasizes that PSTHs may be a limited way of trying to understand the population code on the time scale that matters for working memory. We have attempted to clarify and elaborate these points in the revised manuscript.

2) I am concerned about the "null hypothesis" in Figure 3A: if trials are shuffled for each neuron before the fit, then neural activity is modeled with spiking data of other neurons obtained in trials with different delay duration, so not aligned to the stimulus and saccade predictors used in the model. Since these events are typically associated with an increase in firing rate, interneuronal couplings will be reduced in this model because of these misalignments. The reading of "strong recurrence" that now emanates from the comparison with this "null hypothesis" might instead result from this misalignment. Maybe a more direct assessment of how strong is the contribution of couplings to the network would be to evaluate what fraction they represent in the sum of all predictor terms in the model.

Thanks for raising this! We believe there is an essential clarification (but not a problem with the shuffling procedure). As noted in the manuscript, the timings of the trial events and spikes within each trial are always preserved in the GLM analysis. Only the order of the trials is shuffled (i.e., the trial “labels”), e.g. what might be considered trial 1 for neuron 1 is trial 23 for neuron 2 etc (but each neuron still gets the “right” event times for that spike train within each trial). Therefore, only the temporal relationship between neurons is disrupted. That is why this approach is an especially strong test of the presence of coupling, because only the correlations between the neurons are eliminated while the task dependence and autocorrelation are unaffected. This procedure was used to validate the presence of coupling in the seminal neural GLM paper (Pillow et al., 2008).

With that clarification, we hope it’s clear that the coupling predictive index (Figure 4) is in essence what the reviewer suggests. It describes the contribution of the coupling filters in terms of their deviance explained (a classic goodness-of-fit measure for GLMs) as a fraction of the deviance explained by all the predictors in the ‘“full” model (Materials and methods). Sorry, again, for not being sufficiently clear about this.

3) The manuscript emphasizes the role of recurrent interactions in generating persistent activity. However, not all neurons recorded in LIP and FEF show persistent activity in this task. In particular, Figure 2 shows that neurons with robust persistent activity show sustained history kernels, which supposedly affect just a minority of neurons in the database (Figure 4C). Some of the conclusions may change if one considers separately neurons with strong persistent activity from other neurons. For instance, if neurons with persistent activity mostly populate the right cloud of dots in Figure 4C the interpretation of this panel's results would be very different. Example neurons shown in Figure 1 could be explicitly identified in Figure 4C and other panels with individual neuron data. If the question is how persistent activity is generated, then it should be relevant to consider separately neurons with and without persistent activity.

These were our thoughts exactly. We conducted these analyses, but unfortunately there was no systematic relationship between traditionally determined persistent activity (from PSTHs) and the coupling or history terms. This is demonstrated in the supplement by an updated version of Figure 4C (Figure 4—figure supplement 1). We believe this finding reemphasizes the above point – that single-trial dynamics and the across-trial average responses may be very different, and the traditional ways of describing single-neuron activity may be too limited to capture the dynamics of the network during which working memory is actually active. Furthermore, we acquired large somewhat unbiased samples of neurons from the ROIs, and although we looked for neurons with traditionally-determined persistent activity to place our recording probes, we included all isolated units in our analyses. Our goal was to get a broad sample of the network. Therefore, unlike classical experiments, we do not cater the stimulus to a single neuron’s RF (this would be impossible, as we get many neurons with a variety of RFs). Hence, this difference in approach may have an effect on the traditional measures of persistent activity in the single neuron PSTHs. As approaches have moved to large scale simultaneous recordings, we must revisit how we go about analyzing and thinking about this kind of data. This topic has been expanded in the Discussion.

4) The interpretations in the manuscript jump very easily between the statistical description contained in the fitted kernels and biophysical mechanisms, and this should be more carefully considered. Any "temporal integration above and beyond that explained by the external task elements" (Park et al., 2014) and the spike times of the few simultaneously recorded neurons in that session will be attributed to history kernels, which would therefore be inappropriate to attribute to intrinsic cellular mechanisms. In general, authors should be cautious with the possible confusion in using "intrinsic" to refer to the history kernel. The history kernel might include traces of other network dynamics not captured by the few neurons recorded simultaneously in the session.

Importantly, many of these concerns could be directly addressed by analyzing spike trains from a few neurons selected from attractor network simulations (many of which freely available) to verify if their GLM approach is able to extract the biophysically-based parameters of the model, as currently argued. My intuition is that model neurons without any specific intrinsic mechanism with long time course would show a long-lasting history dependence (self excitation) when modeled against the activity of just a handful of their close neighbors. The number of neurons used as predictors, or the similarity of their memory fields, could also conceivably have an impact in the decay time of history and coupling kernels, and thus contribute to possible differences between FEF and LIP in this analysis. These computational models are freely available (for instance https://neuronaldynamics-exercises.readthedocs.io/en/latest/) and the model data can be generated easily and analyzed with the authors' methods.

Thanks a million! This is a good point and we are deeply grateful for the pointer to that model.

The reviewer has a valid concern regarding over-attributing the history effects to intrinsic biophysical mechanisms. It is true that the model cannot account for the influence of unobserved neurons (which no doubt play a substantial role), although to be fair, all electrophysiological recordings and analyses deal with this limitation. However, only the fitted neuron’s own spikes impact the history kernel, and although the model cannot account for the role of unobserved neurons driving that spiking, it is not true that simply any unexplained variance by the other predictors will show up in the history kernel (i.e., they would need to be well correlated with the cell’s spike train). All parameters are fit in the model simultaneously, and only the predictive power of the neuron’s own spikes can contribute to the history term. The history kernel does a good job of capturing the neuron’s autocorrelation while partialling out the effects of the other (observed) predictors, and hence gives a reasonable estimate of “self-drive,” but it’s true we cannot make any specific claims about the biophysical mechanisms, only statistical relationships. We have edited the main text to remove and clarify the usage of intrinsic in reference to the history kernels. It’s also worth mentioning that GLM approaches can extract accurate parameter estimates of intracellular mechanisms when modeling these explicitly (Latimer et al., 2014).

We thank the reviewer for suggesting this resource for the spiking attractor network models. We have used it for our additional analyses that conclude the manuscript (Figure 7). We highlight several important insights (above and in the manuscript), but of relevance here: the analysis of the model recovers the temporal dynamics of the neurons with known properties, so this is a useful validation.

Reviewer #3:

The paper uses a novel analytical technique to infer functional connectivity among FEF and LIP cells during a memory guided saccade task. The analysis takes a GLM-based approach and fits spike trains of simultaneously recorded FEF and LIP cells as weighted combinations of kernels related to (1) target location, (2) saccade direction, (3) coupling filters modeling interactions among cells and (4) history filter modeling within-neuron autocorrelations. The main conclusions are that FEF and LIP neurons show strong coupling both within and across areas, and that LIP shows stronger coupling and longer intrinsic timescales than FEF.

While the approach is interesting and potentially useful, I am afraid it is not sufficiently justified in the present version of the manuscript. The level of detail provided is simply not sufficient to support the claims based on this novel analysis technique. I see two main problems with the manuscript as it is now:

1) There is insufficient control for potentially differential sampling of neurons in FEF and LIP: Could the apparent stronger coupling in LIP vs. FEF be due to different neural sampling in the two areas? For instance, if the RF of the recorded cells had more overlap in LIP relative to FEF, that may produce stronger apparent coupling in two different ways. Stronger coupling may arise if the model mis-attributes shared stimulus/saccade related activity to the coupling weights. The authors emphasize that their model identified coupling above and beyond any stimulus-related response, but they provide little evidence to substantiate this assertion. Stronger coupling may also arise if the model correctly attributes variance but the neurons are in fact more coupled by virtue of being more functionally similar. In that case, the areal differences are only artefacts of the neurons the authors happened to sample. We need much more thorough analyses of the similarity in RF profiles and temporal response profiles of the recorded cells to rule out a sampling confound.

This is an important point. The differences in RF organization between these areas and the implications for network architecture is an interesting (and open) question, but unfortunately our dataset (as with most prior work) is not equipped to perfectly disentangle sampling noise from true areal differences. To really nail this issue, we would need to more precisely map the spatial extent and temporal profile of very many neurons with a dynamic (white noise) stimulus in addition to the current experiment (and/or to already know the full distribution of RFs in each area).

It’s worth mentioning that the 2D nature of the receptive fields (and the memory representation) is often simplified in classical experiments (and simulations) to 1D tuning curves representing the saccade direction angle from fixation. In this classical form of the analysis, the spatial structure and extent of the RFs are summarized rather coarsely. Despite this missing detail, we compared the coupling between neurons as a function of their spatial tuning similarity in an effort to address these questions (Figure 6—figure supplement 1). For all area interactions coupling was slightly stronger for pairs of neurons with more similar spatial tuning, and that relationship was most pronounced for neurons within LIP, a feature predicted by classic attractor network models. However, most importantly, the overall differences in coupling between LIP and FEF were also present during fixation when there is no visual stimulus in the receptive fields or memory being maintained (Figure 6A), meaning the coupling differences could not be simply due to differentially driving RFs with different degrees of overlap. This result points to differences in the functional connectivity.

Of course, differences in sampling can always be a potential problem in electrophysiology experiments, but we conducted the experiments using identical recording equipment, under identical conditions within the same sessions (which we suggest is the best we could do given current methods viable in these areas in the macaque). If we may muse a bit more beyond the pragmatic realities of currently available data, it’s intriguing to appreciate that functional differences in the organization of receptive fields may reflect differences in the underlying architecture; there is no strong reason to assume identical coverage of the visual fields with respect to receptive field sampling. Thus, differences in coupling due to receptive fields could be due to the underlying cortical organization and potentially interesting rather than just an artifact of sampling.

Regarding the concern that: “Stronger coupling may arise if the model mis-attributes shared stimulus/saccade related activity to the coupling weights. The authors emphasize that their model identified coupling above and beyond any stimulus-related response, but they provide little evidence to substantiate this assertion.” This is a separate issue, and as we have clarified in the revised paper (and in several of the replies above): All the parameters are fit simultaneously, so variance explained by one of the covariates can not be explained by another. In other words, the coupling kernels only explain variance not explained by the stimulus, saccade, and history kernels. So it’s not just catch all; it’s predicated on the likelihood of one neuron spiking given that another neuron spiked, given the likelihood of all other covariates in the model (effectively “partialling out” or “controlling for” their impact).

2) There is insufficient validation of the model against traditional analysis techniques. The field has several traditional, established measures of neural coupling or connectivity, including noise correlations and joint PSTHs or autocorrelograms. The authors dismiss those analyses off hand with little justification except for saying that they do not adequately remove stimulus-evoked activity. But there are actually many ways for them to get around confounds with these methods. Comparing their model results to these traditional analyses is essential to validate their results.

We are very happy to add in these analyses, as we’d actually file-drawered them after doing many such validations early in the project. We have added supplemental figures showing cross-correlograms and the relationship between correlations and coupling estimated from the GLM (Figure 2—figure supplement 1). These methods have also been validated previously with traditional correlations in physiological circuits with better-known connectivity (Gerhard et al., 2013; Pillow et al., 2008). In addition, previous work has shown the merits of GLM approaches over traditional measures of cross-correlations (see above replies for a treatment of this issue; for a previous review article on the topic, see Stevenson et al., 2008). We highlight (now, more clearly) that we jointly fit all simultaneously recorded neurons from each session, unlike correlation measures that only consider pairwise combinations in isolation. This approach allows us to “explain away” potentially misleading correlations and better estimate the connectivity of the network.

3) There is insufficient description of the analytical procedures:

– How were the neurons combined across recording days? Clearly, the neurons that were simultaneously recorded each day could be fit using the described method. But the authors say that they simultaneously fit the entire data set – including neurons recorded on different days. How precisely did they set this up and how did this affect the results?

We regret the lack of clarity and have updated the manuscript. Neurons were not combined across recording days. Each daily session (including all simultaneously recorded neurons) was fit with the model. The data (and fits) were then summarized across all sessions. These points are now clarified in the Materials and methods.

– What were the kernels that the authors used in the model fits? How were those kernels selected? What properties must the kernels have to make the model work? Are the conclusions robust over reasonable changes in kernel shape?

Kernels were constructed from smooth temporal basis functions (nonlinearly time-scaled raised cosine functions) as described in previous work (Pillow et al., 2008; Park et al., 2014; Yates et al., 2017). Kernel fitting procedures were consistent with these previous studies and fits have been shown to be insensitive to reasonable changes in the lengths and shapes of the kernels. (But still sorry for not putting these details into the initial submission!). These parameterizations are conventional in the literature and simply used to capture smooth temporal dependencies and reduce the dimensionality (i.e. as an alternative to specifying a parameter at every single time bin). The Materials and methods have been expanded to include more details about the kernels to accompany the references.

– Goodness of fit and model comparisons: The authors should provide a complete description of the type of models they compared.

Of course. The description of model comparisons has been elaborated in the Materials and methods.

Figure 3D shows the goodness-of-fit as the variance explained of each neuron for the coupled and uncoupled models. Figure 3E shows the accuracy of single-trial spike train predictions. Figure 4 shows the results of model comparisons for models with and without coupling (coupling predictive index), and with and without history (history predictive index). These are measures of the deviance explained of the GLMs (Agresti, 2002).

o Individual monkey results: How many cells were recorded in each monkey? Did the critical results hold in both monkeys?

The results held for both monkeys (number of neurons: Monkey A = 459, Monkey L = 508). Symbols indicating from which subject the data came has been added to the goodness-of-fit plots (Figure 3D,E). This has been updated in the manuscript.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Essential revisions:

The main concern communicated in the last set of reviews had to do with, not just a lack of clarity regarding the GLM validation via permutation, but a pair of regrettable misunderstandings. One to do with the shuffling, and one to do with the role of the uncoupled model. We do our best, in words and in code, to clarify these issues.

We now call the shuffling test a “permutation” process in the manuscript to hopefully avoid any misinterpretations that might be associated with “shuffling” in related contexts. That said, the permutation test is not the key statistical test – the comparison to the uncoupled model is (i.e., it supports principled validations of the GLM and model comparisons, the results of which suggest highly significant coupling contributions). The permutation/shuffling results are useful supplemental analyses because they provide reasonable estimates of null distributions in the same language and units as the main results (i.e. coupling strengths). Unsurprisingly, the shuffling analysis provides similar results to the uncoupled model, because they are simply different ways of making the neurons independent. In the uncoupled model, the neurons are truly independent (there are no connections between them) and in the shuffling case the correlation structure is disrupted which effectively makes the connections random. However, the shuffling analysis has the added benefit of providing a comparison using the full model (with all the same parameters). The field usually uses both, as we have.

We hope to have now sufficiently explained both to reviewers and to a potentially broad readership that the major criticism/concern put forth does not apply to our analysis (or to the large number of preceding papers that have used the same permutation process).

1) What exactly is the uncoupled model?

The uncoupled model does not include any coupling kernels – only task and history kernels (i.e. there are no connections between the neurons in the uncoupled model; each fitted neuron does not take into account spikes from other neurons, but it does still take its own spikes into account via its history kernel). This “dropping of terms” is akin to standard linear regression techniques (e.g., stepwise, nested tests, etc.), where terms might be added or removed and the resulting changes in quality of fit are assessed and interpreted.

The uncoupled model is therefore the standard principled statistical technique for validating the explanatory power of the coupling kernels. This is reflected in several ways in the paper: as the difference in the variance explained (goodness-of-fit) between the two models (in the PSTHs, Figure 3D and on single trials, Figure 3E), and also in the model comparisons (measured as the deviance explained between models with and without coupling and history terms; Figure 4; Materials and methods). All of these methods are used to quantify the explanatory power of adding coupling (or history) to the model over and above the other covariates. We have clarified the importance of the uncoupled model’s role in the manuscript.

2) How exactly is the shuffling across trials performed?

We very much regret that our ways of describing the shuffling procedure clearly weren’t working for some of the audience. In the last round of reviews, there was still a misunderstanding regarding how the shuffling procedure is performed – something we certainly need to get right. We deeply appreciate the reviewer’s willingness to dig in and build a simulation. Here we explain how the simulation helped us understand the disconnect here – for all readers, we wish to state clearly that the concern reflected in the simulations does not apply to our actual analysis scheme.

The shuffle-trained GLM includes all parameters of the full model (task, history, and coupling). The permutation procedure we use only disrupts the relationship between neurons (i.e., the coupling kernels) but leaves the dependence on the task (stimulus, saccade etc.) and history for all neurons intact (more on this below). The stimulus/trial event times and spike times are never misaligned for any spike train, and the time bins in which these events occur are never shuffled within trials (which seems to make our analysis different from what the reviewer so patiently and constructively coded up— the colored raster figure was key, thanks!). How is this done? It is difficult to conceive in the mindset of standard shuffling analyses, so let’s start fresh…

Consider Neuron A, which is the neuron being fitted in this run of the GLM. A standard fully-coupled GLM would then model neuron A’s response as a function of task events, its own spike history, and the impacts of Neurons B through Z (in the hypothetical case of 26 simultaneously-recorded neurons). The “impacts” of Neurons B through Z are simultaneously modeled with respect to the task events and history of the fitted neuron, so only the residual spikes of Neuron A are predicted by the spikes from the other neurons. The effective use of residuals to capture coupling is one of the most powerful aspects of a GLM, as it allows for the task terms to remove the signal drive, while still allowing for the unexplained activity to be used for other aspects of the fit (e.g., for the history and coupling terms). (We discuss more of these big picture issues later, but now get back to the permutation analysis implementation).

By relying on the GLM’s modeling of the task variables (which always use the correct timings while fitting each trial), the permutation can now be done. For each trial, we keep Neuron A’s original spike train (and its stimulus drive and autocorrelation is simultaneously partialed out), and we use the spike trains for Neurons B through Z from other independently/randomly selected trials (i.e., shuffled without replacement) as predictors. We do not then need to pretend that those spike trains came from the original trial – the goal is to solely eliminate the relationship between the neurons. The spike trains from other trials should not have any predictive power with respect to the fitted neuron’s spike train (Neuron A) beyond simple chance, allowing us to estimate a baseline level of coupling due to noise. The spike trains from Neuron’s B-Z are then analyzed with respect to the task events from the respective/corresponding trials when those neurons’ spike trains are fit.

This scheme effectively treats each neuron independently (analogous to removing the simultaneous nature of the recordings and is similar to the uncoupled model where the neurons are independent by design, i.e. there are no coupling kernels). But, again, the single-trial time courses of the spikes and task events for each neuron are unchanged. So, from the perspective of a fitted single neuron, nothing is different except its relationship to other neurons in the session; the fitted neuron’s autocorrelation and stimulus dependence is preserved. This can be seen in the PSTHs, which are unaffected by this shuffling procedure – and shouldn’t be because the model’s fitting of the task event terms is still totally proper. In summary, this model-based analysis is flexible enough to use trials with different timings (because it is fit on single trials) to allow the signal correlations to be maintained while the noise correlations are disrupted.

In practice, of course, no model is perfect. The possibility of mis-modeled aspects of the neurons’ responses is certainly possible, but because the task events are randomly-timed from trial to trial, this is solely likely to create coupling estimates around zero simply due to noise, as opposed to having any bias (which can be confirmed via simulation of neurons that are independent by design). Additionally (and critically), since the task events are jittered trial by trial, any “bleed through” effect of task dependence on the coupling terms from other trials actually makes the shuffled comparison a more conservative estimate, because this would artificially inflate the null distribution and hence make our estimate of the true coupling smaller.

Although the scheme is clearly not straightforward to explain, especially in the historical context of standard CCGs and shuffling controls, we hope that it is not just clear, but more directly addresses (i.e., models out) the potential for stimulus drive contamination, which many clever but imperfect traditional shuffling controls attempt to sidestep. But it’s nothing magic – the catch is that if you want to use a GLM, you need event timings to be randomized from trial to trial to decorrelate the predictors (and you can use all trials for the coupling analysis); if you want to use CCGs, you prefer to have multiple repetitions of trials that are as identical as possible. We favored the former technique because it allows for all simultaneously recorded neurons (B-Z) to go into the coupling for Neuron A at the same time, thus being able to “explain away” partial correlations in a way that standard pairwise correlation analyses cannot (the GLM also has other nice properties, because it provides descriptions of a cell’s own spike history and responses to various task events, all in the same fit and language). Finally, the permutation analysis is really just meant to be an intuitive way to visualize the magnitude of the observed coupling relative to a reasonable null model. The statistical comparison between the fully-coupled GLM and the uncoupled model (i.e., the GLM without the coupling terms) is the more straightforward test of whether coupling adds to the quality of fit and is also used when assessing the relative impacts of coupling and history via the model comparisons (between models with and without coupling and history).

We have clarified this in the body of the manuscript and in the Materials and methods. In addition, this is how such a model has been described in previous work, both originally and more recently (e.g., Pillow et al., 2008; Yates et al., 2017; Runyan et al., 2017). Runyan et al. shows a more recent example of this shuffling control for the GLM which was conducted (and explained) in the same way (Runyan et al., 2017).

In addition, we have attached some code and figures demonstrating how the shuffling/permutation procedure works with an example session looking using cross-correlations and have also shared a simplified version of the GLM fit to simulated data from the attractor network. Jonathan Pillow also has a series of detailed GLM tutorials using the same sort of approach on his website which may be beneficial: https://github.com/pillowlab/GLMspiketraintutorial.

Again, we really appreciate the reviewer putting the time into the code and figures. To revisit the clarification in the context of their generous analysis, in the reviewer’s example (in the non-shuffled figure), imagine shuffling only the rows (the neurons’ identities) within each panel (each trial) – the stimulus alignments (and spike times) over the time course of the trial would remain unchanged. If you do this for each trial, the relationship between neurons across trials is broken but the within trial time courses are preserved. This is not exactly what we did, but is similar conceptually to what we explained earlier. Instead, in our data structure, each panel would be a neuron, the number of rows would be trials, and the columns would still be time bins (i.e. conventional raster plots for each neuron). Now, if we shuffle the rows (the trials) for each other neuron (each panel) independently, nothing has changed for the fitted neuron whose response we are modelling, the single trial timings are the same, and the PSTH (which averages across rows in this scenario) is identical, but now the relationship to the other neurons is made random. Thus, the true timings of the covariates in the GLM (the stimulus on, the saccade, spike times etc.) on single trials are always used. Keep in mind that, because in our task (unlike traditional ones) the trial parameters are variable on every trial, the analyses must always be referenced to the values on individual trials (e.g. PSTHs are plotted aligned to the target or the saccade; spikes are counted in windows around those events on each trial), so single-trial timings must always be preserved. In addition, that means it’s impossible to construct some sort of conditioned-matched surrogate dataset with the shuffling analysis since every trial is unique.

In the reviewer’s code, it appears that a difference might arise because the randomization is done on every trial with replacement and thus there can be an effect of “double dipping,” but it’s hard to know for sure without being able to run the code (we tried; more on this below). To replicate our permutation procedure in spirit, one would want to do the permutation in the neuron loop, or make sure the trials are sampled without replacement. In essence, the reviewer has also highlighted why cross-correlations are fraught measures for estimating connectivity – by showing how illusory correlations can arise between independently simulated neurons. This reiterates one of the points of using the permutation procedure as a control, because one can actually estimate the amount of coupling due to chance alone (in effectively independent neurons) and use that to construct a reasonable null distribution.

3) More careful analyses of the activity during fixation and early delay.

Please see below for detailed replies – we have tried to clarify these issues in the manuscript, and remove any implications/interpretations for other models that were deemed overly ambitious.

4) Clarification of the dependence on overall firing rate (separate from the variations in connectivity).

We believe this issue also stems from the regrettable mutual disconnect regarding the GLM and the shuffling procedure. One of the benefits to using the GLM approach is to avoid confounds like this, and give a better estimate of interneuronal interactions (i.e, more pure, via “modeling out” the task events). Baseline firing rates are captured by an additive (constant) term in the GLM. Coupling can be thought of as lagged correlations in the residuals after controlling for the other covariates (i.e. visual/motor responses, auto-correlation, and baseline firing rate). Thus, estimates of coupling already partial out effects of baseline firing rate.

To further assuage any remaining wonder about whether the overall differences in firing rates between the areas could affect coupling, the shuffling control comes in handy again. The coupling kernels for each area were compared to null (shuffled) distributions within each respective area, hence the spike rates in the normal case and the shuffled control were identical (the number and time of spikes are unchanged), but during shuffling the relationship between the neurons is obliterated giving us an estimate of coupling simply due to noise. Therefore, we have an estimation of how much coupling exceeds what is expected by chance for each particular area while controlling for differences in spike rate. We have included an additional supplemental figure demonstrating that this holds in the GLM analysis of simulated data from the attractor network (Figure 7—figure supplement 1). Furthermore, we have now included data on the mean firing rates in LIP and FEF, and FEF actually has significantly higher mean firing rates than LIP whereas LIP had much stronger coupling. Thus, this provides empirical confirmation that coupling is unlikely driven by a confound in firing rates.

These points are discussed at length by reviewer 2 below.

Reviewer #2:

The revised manuscript contains significant improvements over the previous version, notably the new computational model data that provides support to the methods applied. However, I still maintain some relevant concerns on the controls required to support the interpretations of their analyses as couplings between neurons. This concerns primarily the shuffle approach and the control of firing rate confounds as detailed below.

1) Related to previous Major concern 1.

I realize that part of the confusion here is that the “uncoupled model” is never fully described. I understood that this was the full fitted model, to which couplings were set to zero. From this model I would expect PSTHs to differ largely from measured PSTHs, if couplings are contributing significantly to the GLM. Instead, I gather from (Pillow et al., 2008) that the uncoupled model is a reduced model refitted to the data, and then I understand that the fit may be good even if couplings for the full model are strong contributors to the fit. I urge the authors to explain clearly what their uncoupled model is. In fact, in the current revision this is further confused in the Materials and methods (“Unsurprisingly,…”), where the “uncoupled method” is commented in the middle of the description of the shuffle approach. These two separate controls should be clearly distinguished and specified so the reader understands their separate implications. Now this is very confusing.

We have revised the manuscript to make this more clear. Thank you for calling our attention to it. In addition, as mentioned previously, the inclusion or not of coupling parameters in the model or their disruption with shuffling has little (or no) effect on the PSTHs because these are averages across trials that by their very nature obscure the trial-by-trial correlations between neurons (Figure 3D).

2) related to previous Major concern 2.

I am still not convinced about the shuffle approach on which the "extraordinarily strong coupling" result is based. If I understand it correctly, the structure of the data is as schematically depicted in Decision letter image 1, with simultaneous spike trains recorded (here 10 neurons in 10 lines per panel) for separate trials (here 8 trials in 8 panels), where in each trial the stimulus is presented in different locations (here different colors of the simulus and response shadings) and delay durations are also different from trial to trial. Neurons respond with spiking activity depending on whether the stimulus falls within their receptive field or not.

The GLM for the neuron on the gray background would then model spikes based on its specific stimulus and response events for each different trial, on its previous spikes in the corresponding trial, and on the previous spikes of all other neurons in the corresponding trials. Crucially the spikes for these other same-trial neurons are collected based on the same stimulus location, response and delay duration.

If I understand correctly the shuffle condition applied in Figure 3, the GLM now models the gray-background neuron based on its specific stimulus and response events for each different trial and on its previous spikes in the corresponding trial, exactly as before, but now the spikes of other neurons are taken from randomly picked trials. This is represented in the schematic in Decision letter image 2 (notice the first lines of each panel are the same for both schematics). If this is the case, then now the spikes for these other shuffled neurons were not collected based on the same stimulus location, response and delay duration as the modeled neuron. As a result, the consistency of stimulus activation of neuron 9 and neuron 7 shown in Decision letter image 1 (they are both active or inactive in response to stimuli in all trials), and the consistency of the timing of response events, are broken with the shuffle in Decision letter image 2. This will lead to a radical change in the cross-correlations between these two neurons, even if these spike trains were totally independently generated.

<Decision letter image 2>

I have run this simulation. Data for these spike trains were independently generated for each neuron (so with no coupling between them), only keeping the consistency of stimulus, response and delay within trials. As shown in the histograms in Decision letter image 3, the mean cross- correlations (as a proxy of the couplings obtained with the GLM) were radically affected by the shuffling procedure. This does not demonstrate any functional coupling between the neurons, but the fact that task events that elicited neural responses were misaligned by the shuffling procedure.

In my view, this effect could explain the extraordinary changes in shuffle histograms in Figure 3. To clarify this, the shuffle should be performed only between trials with equal stimulus location and delay duration, or else apply other commonly used resampling procedures to estimate cross- correlations (Fujisawa et al., 2008; Katsuki et al., 2014), such as within-trial jitter correction methods (Amarasingham et al., J Neurophysiol, 2012).

Unfortunately, we were unable to run the attached simulation code. There were errors in some of the lines and the intention of the code at this point was a bit unclear to us, so after a few attempts we ended up reading the code and studying the figures – regardless, they were very helpful! We hope that the main issues have been explained to the reviewer’s satisfaction in the earlier reply. We have provided examples of how the shuffling procedure works using real data and simulations in an example session with cross-correlations and also with the GLM. This illustrates what we have discussed in the general reply above. The confusion comes from a simple misunderstanding of how we permute the data, and how the GLM preserves the task dependence, which we hope is now clear. We have also added additional supplementary figures showing the shuffling analysis of the simulated attractor network data and the possible firing rate confound (Figure 7—figure supplement 1A,B). See below for more details on the possible firing rate confound.

3) The section on “Interneuronal coupling is dynamic across behavioral epochs” is very confusing and is not really addressing the point that they are formulating. The fact that there are not very marked changes between couplings measured in the fixation and delay periods is taken as evidence of dynamical working memory without much justification. Later on the comparison of early and late delay periods yields stronger couplings as delay progresses. In my view, this attempt to contribute to the debate on dynamic delay activity, or even activity-silent working memory (Stokes et al., 2015) is overambitious and needs more specific analyses (consider for instance possible traces of the stimuli in the couplings after the response period, by comparing in and out conditions in the baseline period where there is no confound of firing rate for in/out conditions, e.g. Spaak et al. SfN 2017 #339.14; Barbosa et al., Biorxiv, 2019, doi:10.1101/763938). Further, in the interpretations of this paragraph it is disclosed that their measure of coupling is confounded by changes in firing rate (“This finding highlights the potential role of nuanced changes in the dynamics of the network rather than an overall increase in population activity”). This should be declared early on, as this confound may affect many of the interpretations. Any interpretations of difference in coupling strengths should be cautious in previously demonstrating no difference in firing rates, or else in applying more stringent rate-correcting methods such as jitter correction (Fujisawa et al., 2008). Currently, the manuscript does not parallel each of the coupling comparisons (FEF-LIP, fixation-delay, etc.) with corresponding comparisons of mean firing rates, or rate-correcting measures, to support these conclusions.

Good points. It was not our intention to weigh in definitively on the debates about dynamic or stable coding, or activity-silent working memory. We are simply reporting what we found from analyzing the network dynamics during different trial epochs, which (like several other aspects of these data) will be of interest to these debates, but are in this case just the first descriptive step. We have attempted to remove any interpretations or implications that could be viewed as overreaching, as we believe a complete treatment of these issues warrants a rather long follow-up study as well. We do note that dynamics in the population activity (which are commonly observed) do not necessarily mean a dynamic code for working memory (Murray et al., 2017), which is definitely not what we wished to imply. We have rewritten the text to be more responsible and constrained here.

We also hope that the earlier responses explain why the GLM coupling estimates are inherently “rate-corrected.” We also note that the GLM parcels out the effect of the stimulus – both “in RF” and “out of RF” covariates are fit simultaneously, thus, the model is the same in both conditions (in the different trial epochs), as are the stimulus and task parameters.

Regarding: “Further, in the interpretations of this paragraph it is disclosed that their measure of coupling is confounded by changes in firing rate (“This finding highlights the potential role of nuanced changes in the dynamics of the network rather than an overall increase in population activity”)”

We were puzzled why this statement in the conclusions might be taken as admission of a flaw regarding a firing rate confound in the GLM analysis. Any help would be appreciated here. We re-read it a few times ourselves, trying to figure out how to avoid this unintended interpretation, but in the context we think it is clear that statement is simply highlighting the connection to other work (Murray et al., 2017, see above) that calls attention to the possibility of a more complicated story in the dynamics rather than a simple overall increase in persistent activity. (We discuss the firing rate issue both above and below.)

4) The computational model is a nice demonstration of their methods, in particular of the retrieval of the correct time scale of the interactions between neurons (the AMPA and NMDA current time courses). However, in terms of the strengths of the couplings, the model may also be confounded by changes in firing rate. It will be useful to plot the mean firing rate of model neurons as recurrent connectivity is increased. If this mean firing rate is increasing too, then some compensatory change may be introduced to maintain rates constant as recurrent connectivity increases in order to resolve this concern. The stimulus kernels derived from the model in Figure 7D, left panel, do not seem to correspond to the simulation results: stimuli in receptive fields should generate increase in rates, and stimuli outside the receptive field a suppression of rates.

As discussed in the response to general questions above, the GLM analysis parcels out changes in firing rate, and we also have provided an additional supplementary figure addressing this concern using the simulated data from the attractor network (Figure 7—figure supplement 1). This figure shows that coupling estimated from the GLM provides an accurate inference of the recurrent connectivity of the network regardless of changes in the mean spike rates. This analysis is yet another sanity check showing that the shuffling procedure disrupts the estimate of coupling of the network without affecting the time course of the neurons (or their PSTHs) and maintains identical spike rates as the true condition.

Specifically regarding: “The stimulus kernels derived from the model in Figure 7D, left panel, do not seem to correspond to the simulation results: stimuli in receptive fields should generate increase in rates, and stimuli outside the receptive field a suppression of rates.”

Thanks for the careful look at this, we checked the analysis and simulation and believe everything is OK here. The large bump (in the “in RF” condition) captures the transient response to the stimulus, the rest of the time course is simply noise around zero (a gain of 1) in both conditions. We are only sampling from a small number of neurons, and if the stimulus is not presented in their RFs we should expect no changes in their responses in either direction (which is what you see in real data for such conditions). Even in the idealized scenario in the attractor model, a suppressive effect would depend on how far the stimulus is presented from the RFs of the neurons you are observing, the strength and width (in RF size) of the stimulus, and the strength and range of the inhibitory connections. Thus, there are many potential factors at play here.

5) Because of the possible rate confound that affects the coupling measure, the manuscript should provide a mean firing rate description of the various areas and task periods, for instance through average PSTHs.

We have discussed the possible firing rate confound in the other responses, and now we have included descriptions of the mean firing rates of both areas in the Materials and methods. Neurons in FEF actually had a significantly higher mean firing rate than LIP (FEF: 36 sp/s; LIP: 28 sp/s; P=1.16x10-5Wilcoxon Rank-Sum test) which provides further evidence that coupling was not artificially inflated by differences in firing rate given that LIP had much higher coupling the FEF.

https://doi.org/10.7554/eLife.52460.sa2

Article and author information

Author details

  1. Eric Hart

    Center for Perceptual Systems, Department of Neuroscience, Department of Psychology, The University of Texas at Austin, Austin, United States
    Contribution
    Conceptualization, Data curation, Software, Formal analysis, Validation, Investigation, Visualization, Methodology
    For correspondence
    ehart004@gmail.com
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0002-6042-8389

  2. Alexander C Huk

    Center for Perceptual Systems, Department of Neuroscience, Department of Psychology, The University of Texas at Austin, Austin, United States
    Contribution
    Conceptualization, Supervision, Funding acquisition, Project administration
    Competing interests
    No competing interests declared
    ORCID icon "This ORCID iD identifies the author of this article:" 0000-0003-1430-6935

Funding

National Science Foundation (IIS-173491)

  • Alexander C Huk

National Eye Institute (R01-EY017366)

  • Alexander C Huk

National Eye Institute (T32-EY021462)

  • Eric Hart

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank A Levi for sharing the MT data, C Badillo for technical support, and A Laudano, K Mitchell, and C Carter for animal support. We also thank E Salinas, A Compte, and an anonymous reviewer for their helpful comments, and W Gerstner, W M Kistler, R Naud, and L Paninksi for making the attractor network code available. This research was supported by a National Science Foundation grant (IIS-173491) to ACH and Il Memming Park (Stony Brook University) and a National Eye Institute grant (R01-EY017366) to ACH, and a National Eye Institute training grant (T32-EY021462).

Ethics

Animal experimentation: All experimental protocols were approved by The University of Texas Institutional Animal Care and Use Committee (AUP-20418-00063, AUP-2015-00068) and in accordance with National Institute of Health standards for care and use of laboratory animals.

Senior Editor

  1. Timothy E Behrens, University of Oxford, United Kingdom

Reviewing Editor

  1. Emilio Salinas, Wake Forest School of Medicine, United States

Reviewers

  1. Emilio Salinas, Wake Forest School of Medicine, United States
  2. Albert Compte, Institut d'Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS), Spain

Version history

  1. Received: October 4, 2019
  2. Accepted: April 23, 2020
  3. Version of Record published: May 7, 2020 (version 1)

Copyright

© 2020, Hart and Huk

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

  • 2,825
    Page views
  • 374
    Downloads
  • 28
    Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Eric Hart
  2. Alexander C Huk
(2020)
Recurrent circuit dynamics underlie persistent activity in the macaque frontoparietal network
eLife 9:e52460.
https://doi.org/10.7554/eLife.52460

Categories and tags

Research organism

Further reading

    1. Neuroscience

    Event-related modulation of alpha rhythm explains the auditory P300-evoked response in EEG

    Alina Studenova, Carina Forster ... Vadim Nikulin
    Research Article

    Evoked responses and oscillations represent two major electrophysiological phenomena in the human brain yet the link between them remains rather obscure. Here we show how most frequently studied EEG signals: the P300-evoked response and alpha oscillations (8–12 Hz) can be linked with the baseline-shift mechanism. This mechanism states that oscillations generate evoked responses if oscillations have a non-zero mean and their amplitude is modulated by the stimulus. Therefore, the following predictions should hold: (1) the temporal evolution of P300 and alpha amplitude is similar, (2) spatial localisations of the P300 and alpha amplitude modulation overlap, (3) oscillations are non-zero mean, (4) P300 and alpha amplitude correlate with cognitive scores in a similar fashion. To validate these predictions, we analysed the data set of elderly participants (N=2230, 60–82 years old), using (a) resting-state EEG recordings to quantify the mean of oscillations, (b) the event-related data, to extract parameters of P300 and alpha rhythm amplitude envelope. We showed that P300 is indeed linked to alpha rhythm, according to all four predictions. Our results provide an unifying view on the interdependency of evoked responses and neuronal oscillations and suggest that P300, at least partly, is generated by the modulation of alpha oscillations.

    1. Neuroscience

    Catecholaminergic neuromodulation and selective attention jointly shape perceptual decision-making

    Stijn A Nuiten, Jan Willem de Gee ... Simon van Gaal
    Research Article

    Perceptual decisions about sensory input are influenced by fluctuations in ongoing neural activity, most prominently driven by attention and neuromodulator systems. It is currently unknown if neuromodulator activity and attention differentially modulate perceptual decision-making and/or whether neuromodulatory systems in fact control attentional processes. To investigate the effects of two distinct neuromodulatory systems and spatial attention on perceptual decisions, we pharmacologically elevated cholinergic (through donepezil) and catecholaminergic (through atomoxetine) levels in humans performing a visuo-spatial attention task, while we measured electroencephalography (EEG). Both attention and catecholaminergic enhancement improved decision-making at the behavioral and algorithmic level, as reflected in increased perceptual sensitivity and the modulation of the drift rate parameter derived from drift diffusion modeling. Univariate analyses of EEG data time-locked to the attentional cue, the target stimulus, and the motor response further revealed that attention and catecholaminergic enhancement both modulated pre-stimulus cortical excitability, cue- and stimulus-evoked sensory activity, as well as parietal evidence accumulation signals. Interestingly, we observed both similar, unique, and interactive effects of attention and catecholaminergic neuromodulation on these behavioral, algorithmic, and neural markers of the decision-making process. Thereby, this study reveals an intricate relationship between attentional and catecholaminergic systems and advances our understanding about how these systems jointly shape various stages of perceptual decision-making.

    1. Neuroscience

    Two human brain systems micro-structurally associated with obesity

    Manfred G Kitzbichler, Daniel Martins ... Neil A Harrison
    Research Article Updated

    The relationship between obesity and human brain structure is incompletely understood. Using diffusion-weighted MRI from ∼30,000 UK Biobank participants, we test the hypothesis that obesity (waist-to-hip ratio, WHR) is associated with regional differences in two micro-structural MRI metrics: isotropic volume fraction (ISOVF), an index of free water, and intra-cellular volume fraction (ICVF), an index of neurite density. We observed significant associations with obesity in two coupled but distinct brain systems: a prefrontal/temporal/striatal system associated with ISOVF and a medial temporal/occipital/striatal system associated with ICVF. The ISOVF~WHR system colocated with expression of genes enriched for innate immune functions, decreased glial density, and high mu opioid (MOR) and other neurotransmitter receptor density. Conversely, the ICVF~WHR system co-located with expression of genes enriched for G-protein coupled receptors and decreased density of MOR and other receptors. To test whether these distinct brain phenotypes might differ in terms of their underlying shared genetics or relationship to maps of the inflammatory marker C-reactive Protein (CRP), we estimated the genetic correlations between WHR and ISOVF (rg = 0.026, P = 0.36) and ICVF (rg = 0.112, P < 9×10−4) as well as comparing correlations between WHR maps and equivalent CRP maps for ISOVF and ICVF (P<0.05). These correlational results are consistent with a two-way mechanistic model whereby genetically determined differences in neurite density in the medial temporal system may contribute to obesity, whereas water content in the prefrontal system could reflect a consequence of obesity mediated by innate immune system activation.