Figures and data in Learning steers the ontogeny of an efficient hunting sequence in zebrafish larvae | eLife

Figures
Videos
Additional files

12 figures, 1 video and 1 additional file

Figures

Figure 1

Download asset Open asset

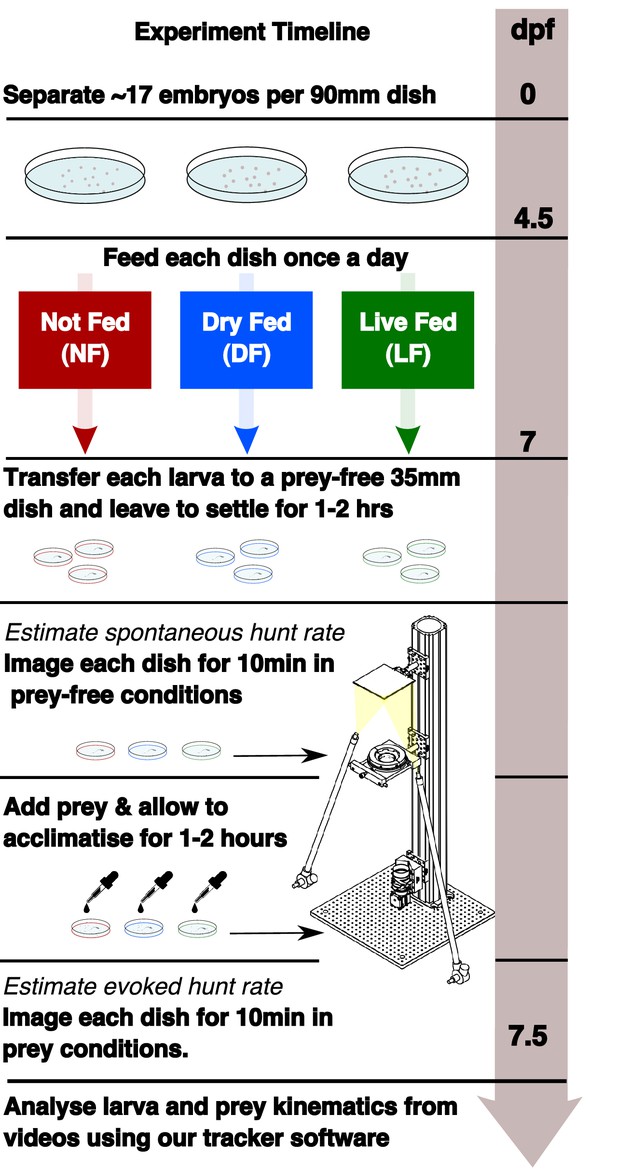
Experimental timeline showing the different feeding regimes during rearing and the recording of spontaneous and evoked hunt behavior.

Embryos are separated in three dishes, with differential feeding initiated at 4.5 dpf. Each group receives a feed once per day (see Materials and methods). Behavioral recording is performed at 7 dpf. Spontaneous eye-vergence events are measured by recording individual larvae for 10 min in the absence of prey. Live prey (≈30 Rotifers) are then added. Acclimatization in prey conditions for a period of ≈1–2 hr is followed by recording of larvae in the presence of live prey. Live prey is topped up to initial level prior to recording.

Figure 2 with 2 supplements

Download asset Open asset

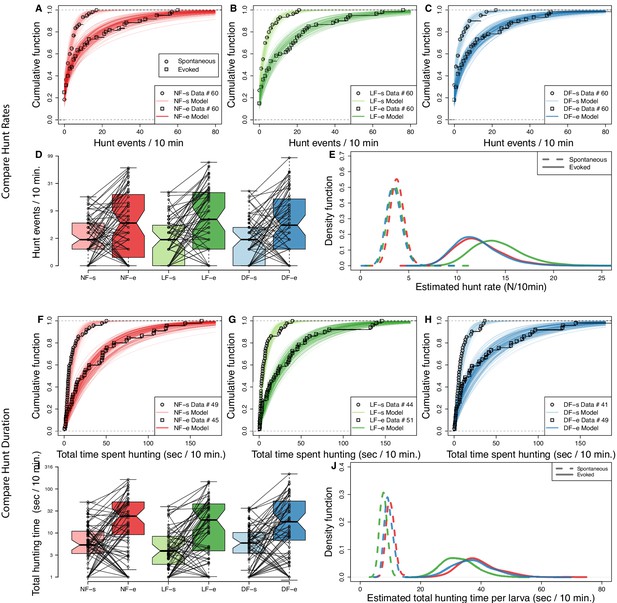
Experience increases hunt rate but decreases total time spent hunting.

Hunting effort of each group is characterized in terms of the distribution in number of hunt events and total hunting duration recorded from the 10 min behavioral recordings. The two test conditions, in the absence and in the presence of prey, are modeled separately to evaluate spontaneous (s) and evoked (e) hunt events, respectively. (A,B,C) Cumulative density function (CDF) of hunt event counts per larva (open squares) reveals that hunt-event frequency increases across groups once prey is added (NF, not-fed; DR, dry-fed; LF, live-fed). Lines indicate 200 cumulative density functions of negative binomial distributions, which have been inferred from hunt-frequency data. (D) Box plots showing number of hunt events per larvae indicate similar spontaneous and evoked counts in each feeding group. Connecting lines indicate that for most larvae the number of hunt events increases on addition of prey. (E) The distribution of estimated mean hunt-rate for each group, as inferred from the models’ parameters, confirms that hunt-rates increase from spontaneous (dotted lines) to evoked (solid lines) conditions. All groups (indicated by line color) show similar mean spontaneous hunt-rates ( $R_{s}$ ), with a somewhat higher rate observed in NF larvae ( $P [μ_{R_{s}}^{N F} > μ_{R_{s}}^{L F}] = 0.60$ , $P [μ_{R_{s}}^{N F} > μ_{R_{s}}^{D F}] = 0.66$ ). In the presence of prey, however, LF larvae are more likely to exhibit higher hunt-rates than NF and DF larvae ( $P [μ_{R_{e}}^{L F} > μ_{R_{e}}^{N F}] = 0.72, P [μ_{R_{e}}^{L F} > μ_{R_{e}}^{D F}] = 0.75$ ). Overall, the mean estimated group hunt-rate (events/10 min.) in spontaneous/evoked conditions were $μ_{R}^{L F} = 3.6 / 14.3$ , $μ_{R}^{N F} = 3.8 / 12.3$ , $μ_{R}^{D F} = 3.5 / 12.0$ . (F,G,H) Cumulative function plots showing the total time spent hunting under spontaneous and evoked conditions. Open squares show recorded data and lines indicate 200 cumulative density functions drawn from similar statistical model as in (A,B,C, see Materials and methods). All groups show an increase in total time spent hunting when prey is added. (I) Box plots showing the amount of time spent hunting increases from spontaneous to evoked test conditions for most larvae. (J) The estimated densities of mean hunt-duration of each group, as inferred from the model, clearly show that on average larvae spent more time hunting in evoked conditions (solid lines) than in spontaneous (dotted lines) conditions. Although DF and NF distributions look identical, the model reveals a noticeable shift towards shorter hunt durations ( $D$ ) for LF larvae on average in both evoked $(P [μ_{D_{e}}^{L F} < μ_{D_{e}}^{N F}] = 0.76, P [μ_{D_{e}}^{L F} < μ_{D_{e}}^{D F}] = 0.72)$ and spontaneous conditions $(P [μ_{D_{s}}^{L F} < μ_{D_{e}}^{N F}] = 0.90, P [μ_{D_{s}}^{L F} < μ_{D_{e}}^{D F}] = 0.84)$ .

Figure 2—figure supplement 1

Download asset Open asset

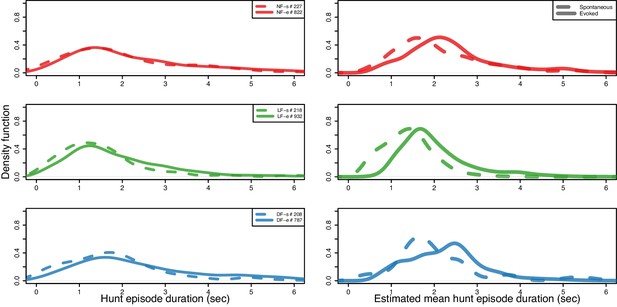
Hunt episode duration shorter in LF group in both spontaneous and evoked hunt events.

(Right) Comparing mean hunt episode durations by fitting a Gamma distribution model to pooled hunt-episode duration data for each group’s spontaneous (dashed) and evoked hunt evens (solid). Hunt episode duration shorter in LF group in both spontaneous $μ_{s}^{N F} = 2.1, μ_{s}^{D F} = 2.0$ , $μ_{s}^{L F} = 1.4$ , with probability $P [μ_{s}^{L F} < μ_{s}^{N F}] = 0.80$ , $P [μ_{s}^{L F} < μ_{s}^{D F}] = 0.75$ , and evoked hunt events $μ_{e}^{N F} = 2.5, μ_{e}^{D F} = 2.3$ , $μ_{e}^{L F} = 2.0$ , with probability $P [μ_{e}^{L F} < μ_{e}^{N F}] = 0.65$ , $P [μ_{e}^{L F} < μ_{e}^{D F}] = 0.69$ . An increase in mean episode duration between spontaneous (no prey) and evoked hunt events is mostly evident in LF and less so in NF hunt events, which are likely to show similar episode durations between conditions $(P [μ_{e}^{N F} > μ_{s}^{N F}] = 0.56)$ . (Left) Kernel density (BW = 0.25 s) estimation using recorded data from spontaneous and evoked hunting events. Distributions across conditions and groups show large overlap in episode duration. 95% of the spontaneous hunt-episode duration data are below 3.5 s. for LF, while this interval includes 78% of NF and 88% of DF. The NF group’s 95% percentile is at 5.02 s. indicating that there are some comparatively longer spontaneous events in this group.

Figure 2—figure supplement 2

Download asset Open asset

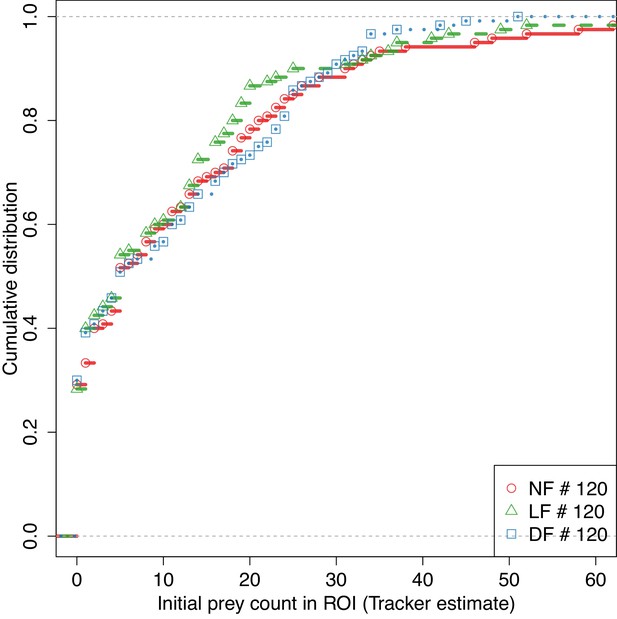
Evoked and spontaneous hunt-rates were tested in similar prey density conditions between groups.

CDF of number of detected prey at the beginning of each experiment in both spontaneous ( $n = 60$ per group) and evoked conditions ( $n = 60$ per group), shows that measuring evoked hunt-rates in the presence of prey was conducted across similar prey density conditions between groups (NS difference in prey-count between groups using pairwise two-sided t-test, Holm's correction).

Figure 3 with 1 supplement

Download asset Open asset

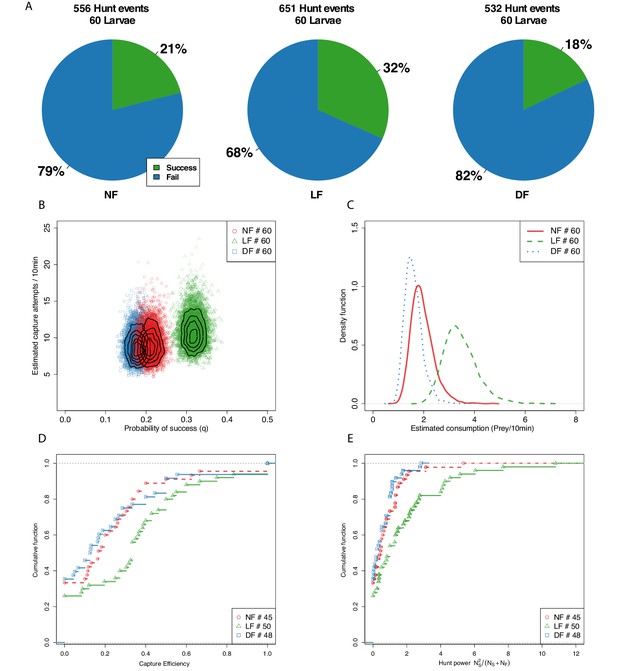
Capture efficiency is experience-dependent.

(A) Proportion of successful and unsuccessful hunt events in each feeding group based on manually labeled outcomes of hunt episodes. Ranking of proportion of successful hunt events: LF>NF>DF. (B) We model the joint distribution of probability of capture success and number of capture attempts (see Materials and methods). Each point represents a likely value for the estimated quantities, and contour lines indicate their distribution. The likely distribution of success probability (q) for the LF group has a distinctively higher mean ( $P [q^{L F} > q^{N F}] = 1$ , $P [q^{L F} > q^{D F}] = 1$ ) than the NF and DF groups, with $P [q^{N F} > q^{D F}] = 0.55$ confirming that nutrition alone does not explain improved capture success. The distributions for the three groups overlap considerably in terms of capture attempts, but consistent with hunt-rates in Figure 2E, the model predicts that mean capture attempts ( $μ_{C}$ ) between DF and NF are similar ( $P [μ_{C}^{N F} > μ_{C}^{D F}] = 0.55$ ), but higher for the LF group ( $P [μ_{C}^{L F} > μ_{C}^{N F}] = 0.74$ , $P [μ_{C}^{L F} > μ_{C}^{D F}] = 0.79$ ), with differences in mean rates being modest ( $μ_{C}^{L F} = 10.9$ , $μ_{C}^{N F} = 9.2$ , $μ_{C}^{D F} = 8.9$ ). (C) Combining estimated hunt and success rates we plot the probability density function (PDF) of likely consumption per group and find that the LF group’s consumption is almost double that of the NF and DF groups. (D) CDF of hunt efficiency in terms of fraction of capture successes against capture attempts, shows a general shift rightwards for LF, meaning fewer lower performing larvae as a result of experience. ≈50% of LF larvae have efficiency above 0.33, while that is 0.13 and 0.16 for the DF and NF groups, respectively. (E) We define a hunt power index (HPI), as the product of efficiency and number of captured prey, in order to account for the number of captured prey in the scoring of hunting ability (for larvae for which we recorded at least one prey capture attempt). A cumulative HPI distribution for each group reveals a difference in slope of LF. A subset of 20% of individuals in the LF group have an HPI higher than top performing DF, NF larvae.

Figure 3—figure supplement 1

Download asset Open asset

Hunting ability is not explained by larval size.

Kernel density estimation of a sampled distribution of Spearman’s correlation coefficients (BW=0.05), obtained by bootstraping 80% of data in each group, shows that larval length does not positively correlate with hunting success in naive larvae (p=1 one-sided t-test for NF and DF), but only in experienced (LF, $p < 2.2 \times 10^{- 16}$ one-sided t-test). The fact that a positive correlation only exists for LF suggests a causal relationship by which growth can be impacted by hunting ability, and not vice-versa.

Figure 4 with 2 supplements

Download asset Open asset

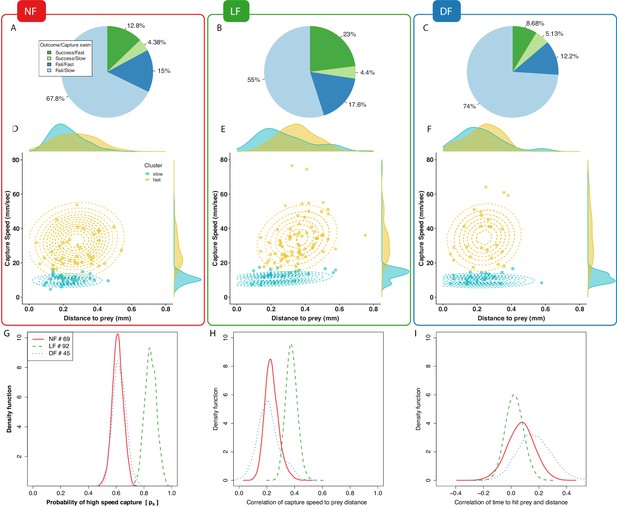
Experience-dependent adaptation of capture swims.

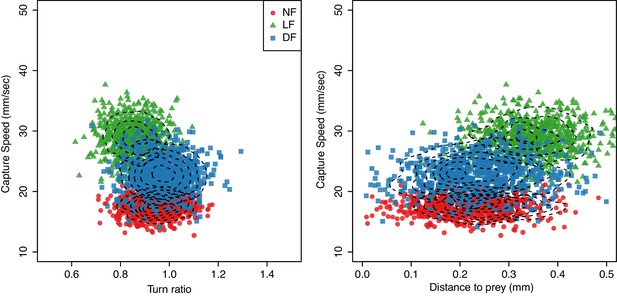
(A,B,C) Manual labeling of captures: Majority of successful hunting episodes used a fast capture swim and these are more frequently observed in LF group. (D,E,F) Clustering peak capture-swim speed and prey-distance data points of successful captures in fast/slow (yellow/cyan) using a mixture of two Gaussians model. Marginal density plots for prey-distance show most slower captures executed nearer to prey than fast captures, and that most fast-captures of LF are executed further than those DF,NF. (G) Fraction of points that are likely to be clustered as high-speed capture swims ( $p_{s}$ ) is higher in the LF group than in other groups ( $P [p_{s}^{L F} > p_{s}^{N F}] = 1$ , $P [p_{s}^{L F} > p_{s}^{D F}] = 1$ ), which is in agreement with our labeled results (A–C). (H) Capture data exhibit an increase of maximum swim-speed with prey-distance. Distribution of Pearson’s correlation ( $C_{s - d}$ ) by bootstrapping (80%) capture events pooled across larvae. The mean speed-distance correlation coefficient is positive in capture data across groups (in all groups $p < 10^{- 3}$ one sample t-test and two sample against shuffled data, see also Figure 7—figure supplement 4 for a group level statistical model that does not pool data across larvae). (I) The correlation between the time it takes to reach prey ( $t_{p r e y}$ ) and prey-distance in fast-capture swims is smaller in LF compared to NF. Distribution of Spearman’s correlation values estimated by bootstrapping (80% of pooled data across larvae) give mean correlations of time vs distance of ${\bar{C}}_{d - t}^{N F} = 0.07$ , ${\bar{C}}_{d - t}^{L F} = 0.02$ , ${\bar{C}}_{d - t}^{D F} = 0.168$ , with the LF group’s being the lowest ( ${\bar{C}}_{d - t}^{L F} < {\bar{C}}_{d - t}^{N F}$ two-sample t-test $p < 2.2 \times 10^{- 16}$ , $P [C_{d - t}^{L F} < C_{d - t}^{N F}] = 0.65$ , and ${\bar{C}}_{d - t}^{L F} < {\bar{C}}_{d - t}^{D F}$ t-test $p < 2.2 \times 10^{- 16}$ , $P [C_{d - t}^{N F} < C_{d - t}^{D F}] = 0.72$ ), and with the lowest probability of being positive $P [C_{d - t}^{N F} > 0] = 0.76$ , $P [C_{d - t}^{L F} > 0] = 0.64$ , $P [C_{d - t}^{D F} > 0] = 0.92$ . Scatter plots of $t_{p r e y}$ are shown on Appendix 4.

Figure 4—figure supplement 1

Download asset Open asset

The speed of fast-capture manoeuvres also depends on prey distance, and this correlation is strongest for LF data.

Bootstrapping the speed-distance correlation (Pearsons on 80% data) over the fast-cluster data points alone shows correlations, revealing that it is not simply the case that the choice of fast/slow strategy is regulated by distance, but rather that the speed of fast capture swims is graded depending on the distance as well.

Figure 4—figure supplement 2

Download asset Open asset

The relationship between prey-distance and the speed of the capture swim could be a reflection of larvae choosing their capture manoeuvre (fast/slow) depending on prey distance.

Here, we find evidence that this relationship also exists within fast capture-swims. This means fast-capture manoeuvres are not stereotyped but are adapted to prey distance, and this relationship develops further with experience. (A) Correlation of the fast-cluster shows maximum speed of fast capture-swims depends on the distance to prey ( $P [{\bar{ρ}}_{s - d}^{N F} > 0] = 0.83$ , $P [{\bar{ρ}}_{s - d}^{L F} > 0] = 0.99$ , $P [{\bar{ρ}}_{s - d}^{D F} > 0] = 0.75$ ) and it is strongest in LF data ( $P [{\bar{ρ}}_{s - d}^{L F} > {\bar{ρ}}_{s - d}^{N F}] = 0.84$ , $P [{\bar{ρ}}_{s - d}^{L F} > {\bar{ρ}}_{s - d}^{D F}] = 0.80$ ). (B) Bootstrapping the speed-distance correlation (Pearson’s coeff. on 80% data), only over the fast-cluster data points, confirms model finding in A, positive correlations exist in all groups (in all groups $p < 2.2 \times 10^{- 16}$ one side t-test, and two sided against shuffled data), with LF capture data showing stronger speed-distance correlations to controls ( $p < 2.2 \times 10^{- 16}$ two sample t-test).

Figure 5 with 2 supplements

Download asset Open asset

The angle of first turn-to-prey is experience-dependent.

(A) Hunting sequences begin with eye-vergence and a turn bout that re-orients larvae toward prey. We isolate the initial re-orientation toward prey as shown in an example hunting trajectory, which is drawn relative to the larva’s heading and mouth position (center), and color coded corresponding to eye-vergence. A large amplitude turn that re-orients it toward prey coincides with an increase in eye-vergence angle. Inset shows turning over time, with red highlighting the extracted first-turn behavior and light grey indicating post-capture turn. (B–D) Prey azimuth vs magnitude of re-orienting first-turn data points along with regression lines (dark), and 5–95% confidence intervals (light), according to a linear fit. Hunt events from the LF group show the highest deviation from dotted line, which indicate the slope of turn angles that would precisely align larvae with prey. (E) The inferred slope density from the linear statistical regression model reveals that the mean first-turn behavior (γ) of hunt events pooled from the LF group have a lower slope than NF ( $P [γ^{L F} < γ^{N F}] = 1$ ), and DF ( $P [γ^{L F} < γ^{D F}] = 1$ ), while DF shows the least undershooting ( $P [γ^{N F} < γ^{D F}] = 0.90$ ). The ranking in mean turn-ratios according to pooled data across individuals goes LF>NF>DF, but this can be biased toward more active individuals within each group, see Figure 7 where group behavior is estimated without this bias.

Figure 5—figure supplement 1

Download asset Open asset

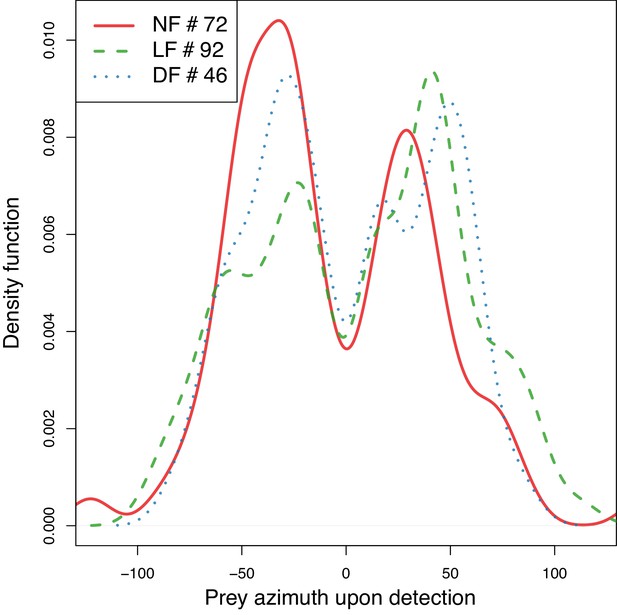
The distributions of prey azimuth at the onset of successful hunting episodes are similar between groups, and favor prey on the lateral visual field.

Prey azimuth at start of successful hunting event (azimuth of prey detection). Differences in undershooting are not due to differences over the angle at which prey are being detected. Estimated density of prey detection angle (BW = 10°) shows that the hunt data across groups have similar bimodal distributions of initial prey-detection azimuth, with peaks around 30°-50° on either side of the midsaggital axis.

Figure 5—figure supplement 2

Download asset Open asset

Turn-ratio histogram per group also show undershoot bias for LF.

Histogram of turn-ratio data confirms that hunt events from the LF group have a bias towards turn ratios below unity (undershooting).

Figure 6 with 1 supplement

Download asset Open asset

Experience associates undershooting to fast capture swims.

(A,B,C) Pooled data points across larvae on capture-speed and turn-ratio. The densities shown along the top margins suggest that fast captures (yellow, see Figure 4) are biased toward low turn-ratios (undershooting) in the LF group, while no such preference is seen in the NF and DF groups. (D) Distribution of bootstrapped (80%) Spearman’s correlation coefficient between turn-ratio and capture-speed; Hunt events from LF larvae show a relationship between low turn-ratio (undershoot on their first-turn to prey) with the speed of the final capture swim ( $p < 2.2 \times 10^{- 16}$ one-sided t-test, $P [C_{γ - S}^{L F} < 0] > 0.99$ ). This relationship is not innate but rather driven by experience because although DF and NF larvae may occasionally undershoot on their first-turn to prey, this turn is not systematically associated with a fast-capture swim. NF shows the opposite, a positive correlation ( $p < 2.2 \times 10^{- 16}$ one-sided t-test, $P [C_{γ - S}^{N F} < 0] = 0.35$ ), while DF also show evidence of combining undershoot with capture ( $p < 2.2 \times 10^{- 16}$ one-sided t-test, $P [C_{γ - S}^{D F} < 0] = 0.60$ ), but correlation is not as strong as in LF ( $p < 2.2 \times 10^{- 16}$ two sample one-sided t-test).

Figure 6—figure supplement 1

Download asset Open asset

Prey azimuth prior to capture manoeuver.

Differences in turn ratio do not alter the positioning of prey prior to successful captures (no statistical difference in mean prey-azimuth between groups ANOVA F=2.62, p > 0.01), across all groups the majority (>75%) of prey azimuths are within the range ±25^o. Although, these are similarly located within the anterior field zone of eye vergence across groups, the distance to prey is different between groups (see Figure 4).

Figure 7 with 5 supplements

Download asset Open asset

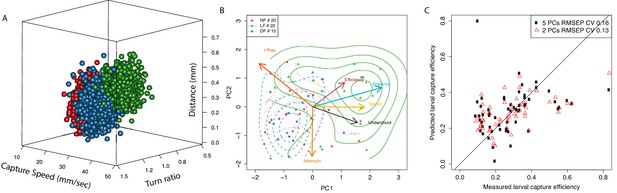
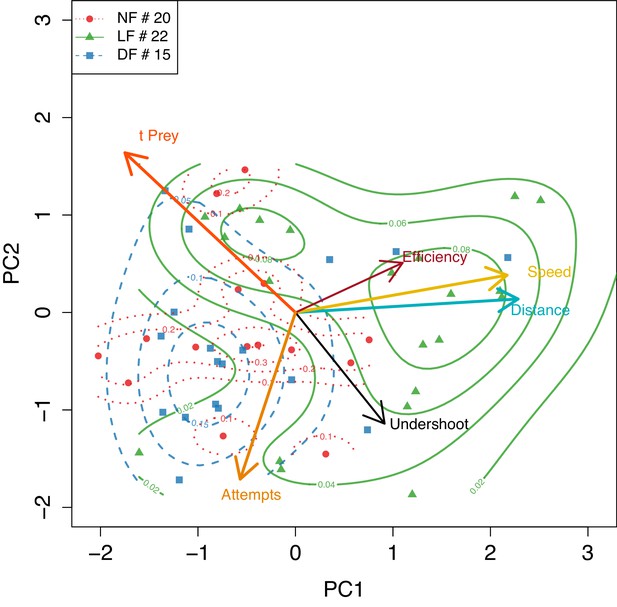
Typical behavior of experienced larvae is distinct and relates to their increased capture efficiency.

(A) Estimated distribution of mean hunting behavior based on capture speed, distance to prey and initial turn for each group according to a multivariate normal hierarchical model of group behavior. The LF group’s model has a mean capture distance ( $μ_{d}^{L F}$ ) in successful hunt episodes that is longer than control groups ( $P [μ_{d}^{L F} > μ_{d}^{N F}] = 0.87$ , $P [μ_{d}^{L F} > μ_{d}^{D F}] = 0.82$ ). Estimated group mean capture distances (mm) are $μ_{d}^{L F} = 0.35$ , $μ_{d}^{N F F} = 0.23$ , $μ_{d}^{D F} = 0.24$ . LF also has the highest mean capture-speed: $μ_{s}^{L F} = 28.2$ , $μ_{s}^{N F} = 17.5$ , $μ_{s}^{D F} = 23.3$ ( $P [μ_{s}^{L F} > μ_{s}^{N F}] > 0.99$ , $P [μ_{s}^{L F} > μ_{s}^{D F}] = 0.90$ ). The LF mean turn-ratio $μ_{γ}^{L F} = 0.85$ shows the group clearly undershoots ( $P [μ_{γ}^{L F} < 1] = 0.96$ ), as a result of experience as it stands distinct to controls ( $P [μ_{γ}^{L F} < μ_{γ}^{N F}] = 0.80$ , $P [μ_{γ}^{L F} < μ_{γ}^{D F}] = 0.70$ ), whose turn-ratios stand closer to unity $μ_{γ}^{N F} = 0.94$ , $μ_{γ}^{D F} = 0.92$ . (B) PCA in larval hunting behavioral space showing the axes for hunting behavior and the position of individual larva across groups as seen from the first 2 PCs. Larvae are positioned in this PCA space based on their mean hunt behavior (capture speed, turn-ratio, capture distance) as estimated by the model, their mean capture efficiency (min. five capture attempts), along with their number of capture attempts and the mean time to hit prey ( $t_{Prey}$ ). Distributions per group (contour lines) confirm separation of the LF group from controls and shift toward region pointed to by the efficiency axis (red). Members of the LF group are shown to be more efficient hunters, they undershoot on their first turn to prey (black), and execute fast capture swims (yellow) from a relatively longer distance to prey (cyan), thus suggesting a relationship of these behaviors with hunting efficiency (red). (C) Linear regression model shows that two principal components of a larva’s mean behavior, as in B, can be used to predict its capture efficiency.

Figure 7—figure supplement 1

Download asset Open asset

Detailed sections of 3D parameter distributions shown on panel A.

Detailed 2D views of Figure 7A that compare the parameter distributions between models of group hunt behavior. The LF group has a distinct behavioral signature compared to controls verifying that experience modifies larval behavior. Also, larval behavior is more consistent within the LF group compared to the wider distributions of uncertainty over DF and NF behavior.

Figure 7—figure supplement 2

Download asset Open asset

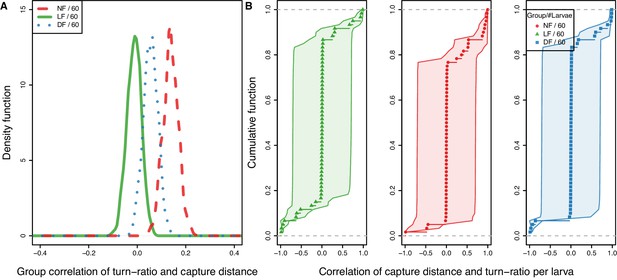
Model-estimated group correlation of capture speed and turn-ratio show LF more likely to combine undershoot with a fast capture swims.

(A) Distribution of group mean correlation coefficient ${\bar{ρ}}_{s - t}$ between capture-speed and turn-ratio ( ${\bar{ρ}}_{s - t}^{L F}$ ) confirm that capture speed and undershoot are combined with experience, as they are correlated in LF $P [{\bar{ρ}}_{s - t}^{L F} < 0] > 0.98$ but instead the opposite tendency, to overshoot ( ${\bar{ρ}}_{s - t} > 0$ ) is associated with fast capture swims in control group larvae ( $P [{\bar{ρ}}_{s - t}^{N F} > 0] > 0.98$ , $P [{\bar{ρ}}_{s - t}^{D F} > 0] > 0.99$ ). Estimated group means: ${\bar{ρ}}_{s - t}^{N F} = 0.06$ , ${\bar{ρ}}_{s - t}^{L F} = - 0.06$ , ${\bar{ρ}}_{s - t}^{D F} = 0.08$ . (B) CDF of larval mean correlation along with 1 SD uncertainty (shaded); larvae lacking capture data appear with mean value $ρ_{s - t} = 0$ and wide confidence intervals. We estimate the probability that a larva combines undershooting with higher capture speeds by setting threshold at $ρ_{s - t} < - 0.1$ , and in the LF group the probability observing larvae that combine these strategies is ( $P [ρ_{s - d}^{L F} < - 0.1] = 0.53$ ), and this is higher than control groups ( $P [ρ_{s - d}^{N F} < - 0.1] = 0.40$ , $P [ρ_{s - d}^{D F} < - 0.1] = 0.35$ ).

Figure 7—figure supplement 3

Download asset Open asset

Model-estimated group correlation between capture distance and turn-ratio show LF more likely to undershoot with a longer range capture swims.

First turn-to-prey and capture-distance reveal a unique relationship between undershooting and increased capture distance for the LF group. (A) Distribution of group mean correlation coefficient ${\bar{ρ}}_{d - t}$ between capture-speed and turn-ratio with ${\bar{ρ}}_{d - t}^{N F} = 0.13$ , ${\bar{ρ}}_{d - t}^{L F} = - 0.01$ , ${\bar{ρ}}_{d - t}^{D F} = 0.05$ , with the LF correlation being distinct to controls ( $P [{\bar{ρ}}_{d - t}^{N F} > {\bar{ρ}}_{d - t}^{L F}] > 0.99$ , $P [{\bar{ρ}}_{d - t}^{D F} > {\bar{ρ}}_{d - t}^{L F}] = 0.94$ ). (B) CDF of mean correlation among larva in a group along 1 SD uncertainty (shaded); larvae lacking capture data appear with mean value $\bar{ρ_{d - t}} = 0$ and wide confidence intervals. We estimate the probability that a larva combines undershoot with longer capture distance by setting threshold at $ρ_{s - t} < - 0.1$ , and find that undershoot-distance correlation is more common in LF group larvae with $P [ρ_{d - t}^{L F} < - 0.1] = 0.48$ , than DF $P [ρ_{d - t}^{D F} < - 0.1] = 0.37$ and NF $P [ρ_{d - t}^{N F} < - 0.1] = 0.29$ .

Figure 7—figure supplement 4

Download asset Open asset

Model-estimated correlation of capture speed and prey distance shows fed groups (LF/DF) more likely to modulate capture speed with distance.

Estimates of mean correlation coefficient ( $ρ_{s - d}$ ) in capture speed and prey distance derived from statistical model, at the group level (A) and for each larva (B). This correlation reflects the tendency to choose between a fast (strike), or a slow (approach) capture strategy depending on distance from prey, but also the more subtle tendency of making finer adjustments to the speed of fast capture swims depending on prey distance. (A) Distribution of estimated mean correlation coefficient for each group ${\bar{ρ}}_{s - d}$ between capture speed and prey-distance (estimated group averages : ${\bar{ρ}}_{s - d}^{N F} = 0.04$ , ${\bar{ρ}}_{s - d}^{L F} = 0.11$ , ${\bar{ρ}}_{s - d}^{D F} = 0.14$ ). At the group level, mean capture speed-distance ${\bar{ρ}}_{s - d}$ is positive across groups ( $P [{\bar{ρ}}_{s - d}^{N F} > 0] > 0.90$ , $P [{\bar{ρ}}_{s - d}^{L F} > 0] > 0.99$ , $P [{\bar{ρ}}_{s - d}^{D F} > 0] > 0.99$ ), with LF’s correlation being stronger to NF ( $P [{\bar{ρ}}_{s - d}^{L F} > {\bar{ρ}}_{s - d}^{N F}] > 0.95$ ), but weaker than DF’s ( $P [{\bar{ρ}}_{s - d}^{D F} > {\bar{ρ}}_{s - d}^{L F}] > 0.78$ ). (B) CDF of mean correlation per larva along 1 SD uncertainty (shaded); larvae lacking capture data appear with mean value $ρ_{s - d} = 0$ and wide confidence intervals. For comparison, we may estimate the probability that we observe a larva that increases capture speed with prey-distance in each group by calculating probability of observing $ρ_{s - d} > 0.1$ : $P [ρ_{s - d}^{N F} > 0.1] = 0.53$ , $P [ρ_{s - d}^{L F} > 0.1] = 0.62$ , $P [ρ_{s - d}^{D F} > 0.1] = 0.71$ . We find that mean group behavior is not representative of individual larvae as there is heterogeneity in all groups. Nevertheless, group behavioral estimates represent the balance in the observed behavioral variability between the larvae of each group. Here, the evidence that DF exhibit the highest mean correlation as a group is accompanied with a higher probability of observing a larva with a correlation between capture-speed and distance. It appears that NF contains a balanced mixture of larvae with opposing capture speed adjustment strategies, while in DF/LF groups, larvae with positive speed-distance correlations are more prominent.

Figure 7—figure supplement 5

Download asset Open asset

PCA applied to mean larva behavior calculated empirically showing agreement with model based in B.

PCA applied to mean larva behavior, using the subset of larva that have more than five successful hunt events, only here mean behavior is calculated empirically, but nevertheless segregation of groups shows qualitative agreement with the model based estimates in Figure 7B .

Appendix 1—figure 1

Download asset Open asset

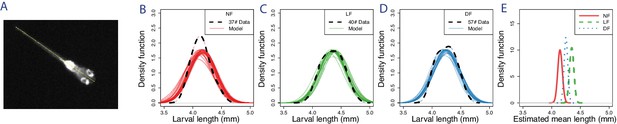
Analysis of larval length shows small statistical differences in mean length, with larvae on live-prey being the longest.

(A) Larval length is measured in pixels from mouth point to edge of tail on video frames when the larva is not in hunting mode and in straight posture. As the tail-fin is not visible or measured, our measurements are equivalent to the established developmental measures of standard-length (SL) (Parichy et al., 2009), which we convert from pixels to mm using an estimate of the mm/px calibration of our setup. (B–D) Distribution of body lengths in the different feeding regimes. Dotted black lines indicate kernel density smoothed distributions of measured larva lengths (Gaussian kernel BW = 0.1) and solid lines show 30 samples of likely body length distributions based on a Gaussian model fit, whose parameters (μ,σ) were estimated from the data using Bayesian inference. (E) The estimated probability densities of mean body length based on Gaussian model fitting. The estimated mean SL of each feeding group (NF = 4.15 mm, LF = 4.37 mm, DF = 4.21 mm) are distinct, ( $P [L F > N F] > 0.99$ ), ( $P [L F > D F] > 0.98$ ) and ( $P [D F > N F] > 0.97$ ), with LF having the largest mean length, being larger to NF by $μ_{L F - N F} \approx 0.2 m m$ and $μ_{L F - D F} \approx 0.1 m m$ .

Appendix 2—figure 1

Download asset Open asset

Behavior imaging system.

Behavior is recorded from below a 35 mm petridish arena, with the camera connected to custom software such that after triggering a default recording event at the start experiment, subsequent recordings events are triggered when the larva is within a circular region of interest (ROI). An a long-pass filter is fitted on the camera lens, and a custom IR light-ring illuminates the arena uniformly. Diffused light is used to illuminate the arena, that obtained via lab-bench light-source pointing upwards onto a frosted glass that sits above the arena. The event ROI is set such that Behavior is recorded only when larval is sufficiently away from the edge of the petridish. The recording session timeout is 10 min, beyond which time new recording events are not triggered. The maximum duration of recording events is limited to two mins. If the larva is still in the ROI after those 2 min, and the maximum experimental period (10 min) timeout has not been exceeded, then a new recording event is initiated.

Appendix 3—figure 1

Download asset Open asset

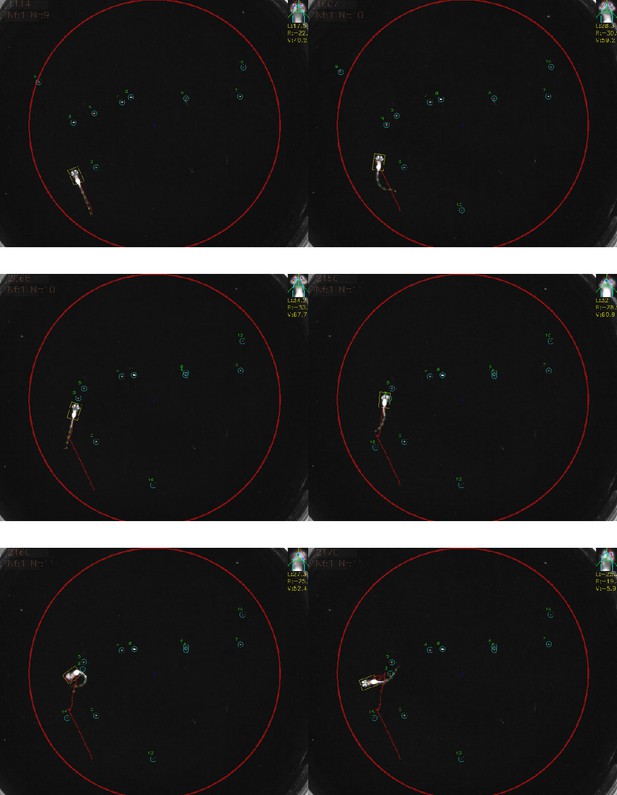
Example frames from a hunting sequence being tracked via our software showing initial detection of prey, turn to prey, approach and capture.

The eye vergence angle is detected and shown at the top right of the screen.

Appendix 4—figure 1

Download asset Open asset

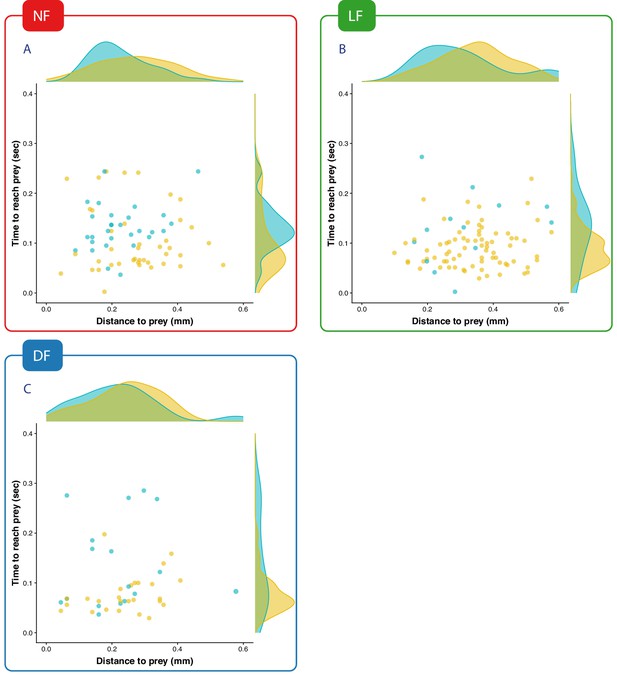
The time it takes to reach prey for successful fast capture swims does not strongly depend on the distance from which these are executed.

Points are coloured according to the classification in capture speed as in Figure 4 Yellow: fast-capture swims, cyan:slow capture swims. In all groups the time to reach prey is longer for the capture swims that were clustered as slow, while for fast-captures swims the timing is more compactly distributed below 0.15 s. Maintaining such timing would require adjusting capture speed with prey-distance. It appears that LF (B) can regularly do this even for prey distances beyond 0.4 mm, where successful hunt episodes from NF, DF (A,C) are rare. The overall distributions of time-to-reach prey match the ranges of maximum gape-timing reported in Mearns et al., 2020, and therefore support the hypothesis that time of maximum gape is synchronized to the time the larva reaches/hits prey during a capture swim.

Appendix 5—figure 1

Download asset Open asset

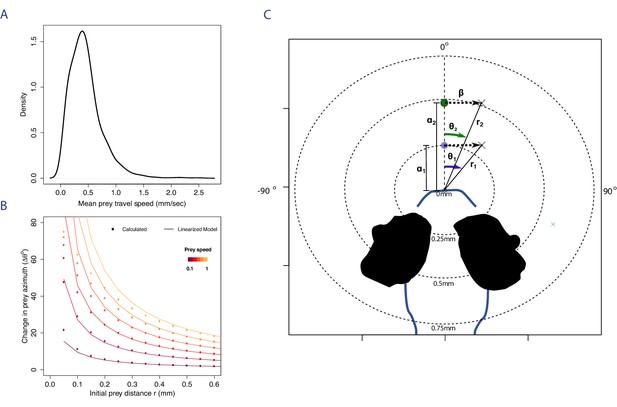
The aiming accuracy prior to a capture swim is strongly dependent on capture distance for the observed prey speeds.

(A) The distribution of mean prey travel speeds is estimated by measuring the total displacements per second from a random sample of videos each containing approximately $n \approx 15 - 30$ freely swimming Rotifers. By analysing tracks of prey motion we estimated mean travel speeds by excluding track regions where prey is not moving (prey displacement is <0.05 mm/sec), and obtained the distribution of mean speeds using kernel density methods (BW = 0.1). This is a skewed distribution, with overall mean prey speed estimated at 0.46 (mm/sec) SE: 0.007, and maximum of 2.5 mm/sec. (B) To maintain prey azimuth within the range of observed in successful captures (ie., ±25°), assuming prey is moving at average speed (≈ 0.5 mm/sec), then capture distance needs to be >0.2 mm. This is shown by calculating the changes in θ (dots) between prey moving from initially in front of the larva at a distance $α = r$ , with $β_{0} = 0$ (ie. $θ = 0$ ) to different positions $β_{1}$ during a typical interbout interval of 200 ms. The lines show how our linear approximation model, which uses the derivatives evaluated at position $β_{o}$ , r, capture the growth of $Δ θ$ with increasing prey displacement ( $Δ β$ ) and decreasing distance r. (C) Diagram showing how for prey moving at a fixed speed β the angular velocity of prey azimuth increases with distance from the larva. Thus, corrections to aiming prior to executing a capture swim become harder when the prey is closer, as they increase with $r^{- 2}$ (see text).

Videos

Appendix 3—video 1

Download asset

posterframe for video — Re-tracking a successful capture event within a custom ROI: slow playback speed x1/16.

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/55119/elife-55119-transrepform-v2.docx
Download elife-55119-transrepform-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Konstantinos Lagogiannis
Giovanni Diana
Martin P Meyer

(2020)

Learning steers the ontogeny of an efficient hunting sequence in zebrafish larvae

eLife 9:e55119.

https://doi.org/10.7554/eLife.55119

Sign up for email alerts

Privacy notice