The role of cochlear place coding in the perception of frequency modulation

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

Natural sounds convey information via frequency and amplitude modulations (FM and AM). Humans are acutely sensitive to the slow rates of FM that are crucial for speech and music. This sensitivity has long been thought to rely on precise stimulus-driven auditory-nerve spike timing (time code), whereas a coarser code, based on variations in the cochlear place of stimulation (place code), represents faster FM rates. We tested this theory in listeners with normal and impaired hearing, spanning a wide range of place-coding fidelity. Contrary to predictions, sensitivity to both slow and fast FM correlated with place-coding fidelity. We also used incoherent AM on two carriers to simulate place coding of FM and observed poorer sensitivity at high carrier frequencies and fast rates, two properties of FM detection previously ascribed to the limits of time coding. The results suggest a unitary place-based neural code for FM across all rates and carrier frequencies.

Introduction

Modulations in frequency (FM) and amplitude (AM) carry critical information in biologically relevant sounds, such as speech, music, and animal vocalizations (Attias and Schreiner, 1997; Nelken et al., 1999). In humans, AM is crucial for understanding speech in quiet (Shannon et al., 1995; Smith et al., 2002), while FM is particularly important for perceiving melodies, recognizing talkers, determining speech prosody and emotion, and may aid in the perception of speech presented in competing background sounds (Zeng et al., 2005; Strelcyk and Dau, 2009; Sheft et al., 2012; Johannesen et al., 2016; Lopez-Poveda et al., 2017; Parthasarathy et al., 2019). The perception of FM at both slow and fast modulation rates is often degraded in older people and those with hearing loss (Lacher-Fougère and Demany, 1998; Moore and Skrodzka, 2002; He et al., 2007; Strelcyk and Dau, 2009; Grose and Mamo, 2012; Paraouty et al., 2016; Wallaert et al., 2016; Paraouty and Lorenzi, 2017; Whiteford et al., 2017). This deficit likely contributes to the communication difficulties experienced by such listeners in noisy real-world environments, which may in turn help explain why age-related hearing loss has been associated with decreased social engagement, greater rates of cognitive decline, and increased risk of dementia (Lin et al., 2011; Lin et al., 2013; Lin and Albert, 2014; Deal et al., 2017; Thomson et al., 2017). Current assistive listening devices, such as hearing aids and cochlear implants, have been generally unsuccessful in restoring FM sensitivity (Chen and Zeng, 2004; Ives et al., 2013). This lack of success may be related to a gap in our scientific understanding regarding how FM is extracted by the brain from the information available in the auditory periphery.

The coding of AM begins in the auditory nerve with periodic increases and decreases in the instantaneous firing rate of auditory nerve fibers that mirror the fluctuations in the temporal envelope of the stimulus (Schreiner and Langner, 1988; Joris et al., 2004). As early as the inferior colliculus and extending to the auditory cortex, rapid AM rates are transformed to a code that is no longer time-locked to the stimulus envelope and instead relies on overall firing rate, with different neurons displaying lowpass, highpass, or bandpass responses to different AM rates (Schreiner and Langner, 1988; Nelson and Carney, 2007; Wang et al., 2008). The coding of FM is less straightforward. For a pure tone with FM, the temporal envelope of the stimulus is flat; however, the changes in frequency lead to dynamic shifts in the tone’s tonotopic representation along the basilar membrane, resulting in a transformation of FM into AM at the level of the auditory nerve (Zwicker, 1956; Khanna and Teich, 1989; Moore and Sek, 1995; Saberi and Hafter, 1995; Sek and Moore, 1995).

Although this FM-to-AM conversion provides a unified and neurally efficient code for both AM and FM (Saberi and Hafter, 1995), it falls short of explaining human behavioral trends in FM sensitivity. Specifically, at low carrier frequencies (f_c <~4–5 kHz) and slow modulation rates (f_m <~10 Hz) FM sensitivity is considerably greater than at higher carrier frequencies or fast modulation rates in a way that is not predicted by a simple FM-to-AM conversion mechanism (Demany and Semal, 1989; Moore and Sek, 1995; Moore and Sek, 1996; Sek and Moore, 1995; He et al., 2007; Whiteford and Oxenham, 2015; Whiteford et al., 2017). This discrepancy is important, because it is FM at low frequencies and slow modulation rates that is most critical for human communication, including speech and music, as well as many animal vocalizations (Attias and Schreiner, 1997; Nelken et al., 1999). The enhanced sensitivity to slow FM at low carrier frequencies has been explained in terms of an additional neural code based on stimulus-driven spike timing in the auditory nerve that is phase-locked to the temporal fine structure of the stimulus (Rose et al., 1967; Moore and Sek, 1995; Parthasarathy et al., 2019). Although a code based on time intervals between phase-locked neural spikes can potentially provide greater accuracy (Siebert, 1970; Heinz et al., 2001), be maintained to some extent in the auditory brainstem (Paraouty et al., 2018), and be used for spatial localization (Moiseff and Konishi, 1981; Grothe et al., 2010), it is not known whether or how this timing information is extracted by higher stages of the auditory system to encode periodicity (pitch) and FM.

If the detection of FM at fast rates depends on an FM-to-AM conversion, whereas the detection of FM at slow rates does not, then fast-rate FM detection thresholds should depend on the sharpness of cochlear tuning (Figure 1), whereas slow-rate FM detection thresholds should not. Previous studies using normal-hearing listeners have not demonstrated such a relationship for either slow or fast FM rates (Whiteford and Oxenham, 2015; Whiteford et al., 2017). However, this failure to find a correlation may be due to a lack of variability in cochlear filtering within the normal-hearing population. Johannesen et al., 2016 found only a modest correlation between slow-rate FM (f_c = 1500 Hz; f_m = 2 Hz) and cochlear mechanical gain loss, but FM thresholds were measured in the presence of superimposed AM, which could have increased the between-subject variability in the measurements (e.g., King et al., 2019). Furthermore, FM sensitivity was not measured at a faster rate, where only place cues are thought to be utilized. People with cochlear hearing loss often have poorer frequency selectivity (Glasberg and Moore, 1986; Moore et al., 1999), due to a broadening of cochlear tuning (Robertson and Manley, 1974; Liberman et al., 1986; Moore, 2007). By contrast, damage to the cochlea is not thought to lead to a degradation of auditory-nerve phase locking to temporal fine structure for sounds presented in quiet (Henry and Heinz, 2012; Henry et al., 2019), so we would not expect to find a strong relationship between slow-rate FM detection thresholds and hearing-loss-induced changes in cochlear tuning if slow-rate FM relies primarily on a time code.

Figure 1

Download asset Open asset

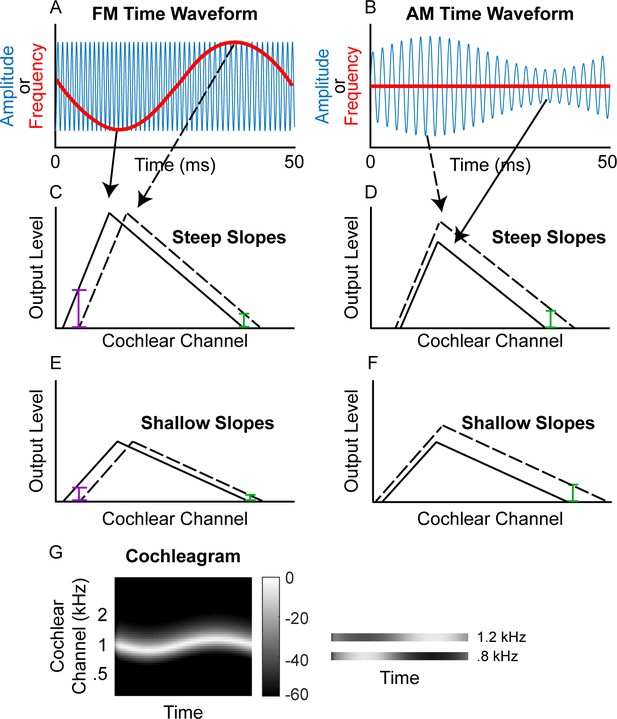
Schematic of (A) FM and (B) AM time waveforms (*f_c* = 1 kHz; *f_m* = 20 Hz) and the resulting changes in basilar-membrane excitation for steep (C and D) and shallow (E and F) slopes.

In A and B, the blue time waveforms represent amplitude over time, while the superimposed red waveforms are the same stimuli plotted in terms of instantaneous frequency over time. Panels C and E demonstrate that a place code for FM would result in a greater change in output level on the low-frequency side of the excitation pattern (purple bars) relative to the high-frequency side (green bars) and that shallower filter slopes result in poorer FM coding (larger colored bars in C than in E) but not poorer AM coding (same size colored bars in D and F). (G) Schematic cochleagram of an FM tone, showing how the output from two separate cochlear channels (right) with center frequencies on either side of the carrier frequency is AM that is out of phase.

Experiment 1 measured FM and AM detection thresholds at slow (f_m = 1 Hz) and fast (f_m = 20 Hz) modulation rates in a large sample of listeners with hearing thresholds at the carrier frequency (f_c = 1 kHz) ranging from normal (~0 dB sound pressure level, SPL) to severely impaired (~70 dB SPL), consistent with sensorineural hearing loss (SNHL). The fidelity of cochlear frequency tuning was assessed using a psychophysical method to estimate the slopes of the forward masking pattern around 1 kHz (e.g., Kidd and Feth, 1981). The results revealed a relationship between the estimated sharpness of cochlear tuning and sensitivity to FM at both fast and slow modulation rates, suggesting that place coding fidelity directly affects FM sensitivity. This relationship remained significant even after controlling for potentially confounding factors such as degree of hearing loss, sensitivity to AM, and age.

Experiment 2 provided a direct test of earlier assumptions that had led to the conclusion that phase-locked timing information is necessary to code slow FM. We simulated important aspects of the cochlear response to FM without the presence of auditory-nerve timing cues by presenting two tones, spaced far enough away from each other in frequency to avoid peripheral interactions, and applying out-of-phase AM to them. This resulted in a simulation of the out-of-phase AM produced by a single FM tone. Sensitivity to the out-of-phase AM mirrored that seen in traditional psychophysical studies of FM detection, with sensitivity highest at low frequencies and slow rates, despite the lack of any usable timing cues based on temporal fine structure. Taken together, our results suggest that a time-interval code is not necessary to represent slow-rate FM and instead imply a unitary neural code for FM across all rates and frequencies.

Results

Experiment 1

Relationship between hearing loss and frequency selectivity

The fidelity of place coding at the test frequency (1 kHz) was measured using pure-tone forward-masking patterns. The 56 participants had to detect a brief tone pip that followed a masker tone presented at 1 kHz. The level of the tone pip was adapted to track its detection threshold. Without the presence of a masker, the threshold level of the tone pip reflects the absolute threshold (Figure 2—figure supplement 1, unfilled circles). In the presence of a pure-tone forward masker, the level of the tone pip depends on the tone pip’s frequency proximity to the masker and on an individual’s frequency selectivity, as determined by their cochlear tuning (Shera et al., 2002; Sumner et al., 2018). For each participant, the steepness of the low- and high-frequency slopes of the masking function was estimated via linear regression of the thresholds (in dB SPL) for the four tone-pip frequencies below (800, 860, 920, and 980 Hz) and above (1020, 1080, 1140, and 1200 Hz) the masker frequency. Within-subject test-retest reliability of the estimated slope functions was high (bootstrapped simulated test-retest correlations of r = 0.98 and r = 0.953 for the low and high slopes, respectively; see Materials and methods). The range of measured masking function slopes in the present study spanned 152 dB/octave for the low slope (−24 to 128 dB/octave; $\bar{x}$ =49.4) and 120 dB/octave for the high slope (−92.7 to 28.3 dB/octave; Figure 2, y-axis; $\bar{x}$ =−23.3), which was greater than the typical range in just normal-hearing listeners at 500 Hz (e.g., 128 dB/octave range for the low slope and 89 dB/octave range for the high slope in Whiteford et al., 2017).

Figure 2 with 1 supplement see all

Download asset Open asset

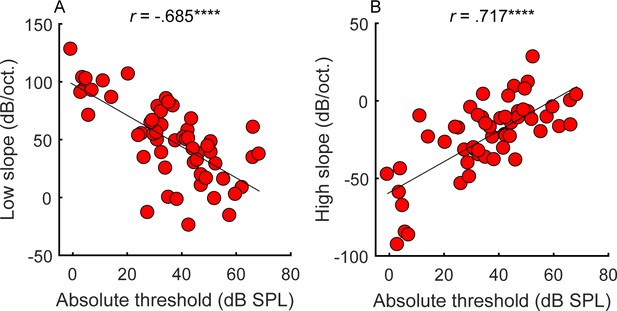
Correlations between average absolute thresholds at 1 kHz in the tested ear (x-axis) and the steepness of the (A) low and (B) high side of the cochlear filter slopes (n = 55).

Participants with greater hearing loss at 1 kHz tended to have shallower filter slopes. Correlations marked with an * are significant after Holm’s correction (****p<0.0001).

Figure 2—source data 1 Figure 2 data. Rows are individual subjects.: https://cdn.elifesciences.org/articles/58468/elife-58468-fig2-data1-v2.xlsx
Download elife-58468-fig2-data1-v2.xlsx

Consistent with expectations (Glasberg and Moore, 1986), the amount of hearing loss at the tone-pip frequency correlated with the slopes of the masking functions (Figure 2; low slope: r = −0.685, p<0.0001, CI = [−0.804, −0.513]; high slope: r = 0.717, p<0.0001, CI = [.559, .826]), supporting the idea that hearing loss is associated with poorer frequency tuning. However, frequency tuning is believed to be governed solely by basilar membrane mechanics and outer hair cell function (Ruggero and Rich, 1991; Sumner et al., 2018), whereas overall hearing loss may include contributions from other factors, such as conductive loss or the function of the inner hair cells and the auditory nerve. These additional factors may explain why filter slopes account for only approximately half the variance observed in absolute thresholds.

Relationship between FM and AM detection

When compared to earlier results from normal-hearing listeners varying in age (Whiteford et al., 2017), the range of FM detection thresholds was much wider in the present study, whereas the range of AM detection thresholds was comparable (Figure 2 from Whiteford et al., 2017 with the current Figure 3). This result confirms that hearing loss affects the detection of FM more than AM (Lacher-Fougère and Demany, 1998). Test-retest reliability for the estimation of AM and FM detection thresholds was very high (average correlations using a bootstrapping procedure: slow FM, r = 0.973, p<0.0001, CI = [.954, .984]; fast FM, r = 0.97, p<0.0001, CI = [.949, .983]; slow AM, r = 0.925, p<0.0001, CI = [.874, .956]; fast AM, r = 0.956, p<0.0001, CI = [.925, .974]). If slow FM utilizes a time-interval code, then across-listener variability in slow FM detection should partly reflect variability in time coding. This means that across-listener correlations in tasks thought to use a shared code (fast FM, slow AM, and fast AM) should be greater than in tasks thought to use different codes (slow FM with any other task). Inconsistent with this prediction, slow and fast FM detection thresholds were strongly correlated (r = 0.826, p<0.0001, CI = [.718, .895]; Figure 3, panel A). Significant correlations were also observed between detection thresholds for slow and fast AM (r = 0.638, p<0.0001, CI = [.449, .773]; Figure 3, panel B) fast FM and fast AM (r = 0.317, p=0.028, CI = [.056, .537]; Figure 3, panel C) and fast FM and slow AM (r = 0.366, p=0.012, CI = [.112, .575]; not shown), all measures thought to rely on a place code. The correlation between slow FM and slow AM was not significant (r = 0.199, p=0.145, CI = [−0.07, .441]; Figure 3, panel D) nor was the correlation between slow FM and fast AM (r = 0.021, p=0.438, CI = [−0.246, .285]; not shown). The lack of a significant correlation between slow FM and AM could reflect the use of an additional time code in slow FM. However, because the correlation between slow FM and slow AM was not significantly different from the correlation between fast FM and fast AM (Z = −0.906, p=0.365, two-tailed), these differences in magnitudes should be interpreted with caution. Overall, the patterns of FM and AM correlations do not strongly support one hypothesis over another.

Figure 3

Download asset Open asset

Individual thresholds for slow (*f_m* = 1 Hz) and fast (*f_m* = 20 Hz) FM and AM detection (n = 55).

Black, white, and gray circles represent slow, fast, and mixed modulation rates, respectively. FM and AM thresholds are plotted in percent peak-to-peak frequency change (2∆f(%)) and 20log(m), where ∆f is the frequency excursion from the carrier and m is the modulation depth (ranging from 0 to 1). For all tasks, lower values represent better thresholds. Shown in the different panels are the relationships between thresholds in slow and fast FM (A), slow and fast AM (B), fast AM and FM (C), and slow AM and FM (D). Correlations marked with an * are significant after Holm’s correction (****p<0.0001, ***p<0.001, **p<0.01, and *p<0.05).

Figure 3—source data 1 Figure 3 data. Rows are individual subjects. Slow = 1 Hz modulation rate; Fast = 20 Hz modulation rate.: https://cdn.elifesciences.org/articles/58468/elife-58468-fig3-data1-v2.xlsx
Download elife-58468-fig3-data1-v2.xlsx

Relationship between frequency selectivity and FM detection thresholds

The unitary neural coding theory of FM and AM predicts that steeper masking functions (implying sharper cochlear tuning) should be related to better FM detection thresholds (Zwicker, 1956). Furthermore, this relationship should hold even after controlling for central aspects of processing known to relate to FM detection, such as aging and sensitivity to AM at the same rate (Whiteford and Oxenham, 2015; Whiteford et al., 2017), as well as overall hearing loss for the tested ear, which could affect time coding independently of place coding (e.g., Ewert et al., 2020). The current consensus is that place theory applies to fast but not slow FM detection (Moore and Sek, 1995; Moore and Sek, 1996; Lacher-Fougère and Demany, 1998; Strelcyk and Dau, 2009). Our results contradict this consensus by showing that both slow and fast FM detection thresholds were strongly and similarly related to the masking function slopes (Figure 4). Notably, a few participants had masking function slopes of zero, or even in the opposite direction (i.e., negative low slopes and/or positive high slopes), presumably due to measurement noise. Imputing these ‘opposite’ slope values with 0 or removing these participants did not affect the statistical outcomes of the analysis. Age and sensitivity to AM could confound effects of cochlear filtering because they are both correlated with FM detection in listeners with normal hearing (Whiteford and Oxenham, 2015; Paraouty et al., 2016; Whiteford et al., 2017). Audibility is not thought to affect FM for levels that are 25 dB or more above absolute threshold (Zurek and Formby, 1981), but average absolute thresholds for the carrier frequency in the tested ear were included in the partial correlation analysis as a precaution, since a few listeners with the most hearing loss had stimuli presented at or near 20 dB sensation level (SL), and because hearing loss has been postulated to affect time coding, independent of place coding (Ewert et al., 2020). Partial correlations between FM detection and masking function slopes were conducted, controlling for age, absolute thresholds at 1 kHz, and AM detection thresholds at the corresponding rate, in an attempt to isolate the role of place coding in FM detection. The correlations between the residuals (Figure 5) demonstrate a significant relationship between the low slopes of the masking function and FM detection thresholds at both rates (slow FM: r_p = −0.364, p=0.016, CI = [−0.58, −0.101]; fast FM: r_p = −0.377, p=0.015, CI = [−0.589, −0.116]) but no relation between the high slope and FM (slow FM: r_p = −0.064, p=0.555, CI = [−0.331, .213]; fast FM: r_p = −0.084, p=0.555, CI = [−0.349, .194]). Because the low slope of the masking function (reflecting the upper slopes of the cochlear filters) is generally steeper than the high slope (e.g., Figure 2—figure supplement 1), it provides more information about frequency change than the high slope (Figure 1, leftmost column), and is therefore predicted to dominate FM performance (Zwicker, 1956). The correlations between the low slope and FM thresholds were significantly stronger than the correlations between the high slope and FM thresholds for both slow and fast FM before correcting for multiple comparisons (slow FM: Z = −1.83, p=0.034; fast FM: Z = −1.81, p=0.035) but not after (slow FM: p=0.065; fast FM: p=0.065), providing modest but mixed evidence that the low side of the excitation patterns matters most for FM-to-AM conversion. Sensitivity to AM detection was not related to either the low slopes (slow AM: r = 0.058, p>0.499, CI = [−0.211, .318]; fast AM: r = 0.277, p=0.076, CI = [.013, .505]) or the high slopes (slow AM: r = 0.007, p>0.499, CI = [−0.259, .272]; fast AM: r = −0.281, p=0.076, CI = [−0.508, −0.017]) of the masking functions. Importantly, the correlations between FM detection thresholds and the low slopes were significantly stronger than the correlations between AM and the low slopes (slow: Z = −4.42, p<0.0001; fast: Z = −4.89, p<0.0001), demonstrating that the relation between masking function slopes and modulation detection is specific to FM, as predicted by the place-coding theory (Figure 1). The results therefore provide strong support for the hypothesis that place coding is utilized for FM detection at both slow and fast rates.

Figure 4 with 2 supplements see all

Download asset Open asset

Correlations between the low slope (A and C) and high slope (B and D) and slow (*f_m* = 1 Hz; black) and fast (*f_m* = 20 Hz; white) FM detection (n = 55).

Correlations marked with an * are significant after Holm’s correction (****p<0.0001, ***p<0.001, **p<0.01, and *p<0.05).

Figure 4—source data 1 Figure 4 data. Rows are individual subjects. Slow = 1 Hz modulation rate; Fast = 20 Hz modulation rate.: https://cdn.elifesciences.org/articles/58468/elife-58468-fig4-data1-v2.xlsx
Download elife-58468-fig4-data1-v2.xlsx

Figure 5 with 2 supplements see all

Download asset Open asset

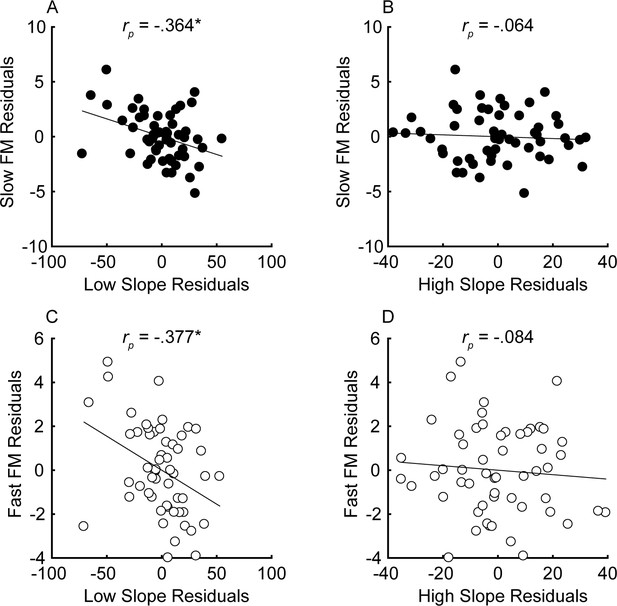
Partial correlations between the steepness of the masking function slopes (x-axis) and FM detection (y-axis) for slow (**A and B**) and fast FM (**C and D**) after variance due to audibility, sensitivity to AM, and age has been partialled out for n = 55 participants.

Units of the x and y axes are arbitrary because they correspond to the residual variance for slow (*f_m* = 1 Hz; black) and fast FM detection (*f_m* = 20 Hz; white). Correlations marked with an * are significant after Holm’s correction (****p<0.0001, ***p<0.001, **p<0.01, and *p<0.05).

Figure 5—source data 1 Figure 5 data. Rows are individual subjects. Slow = 1 Hz modulation rate; Fast = 20 Hz modulation rate.: https://cdn.elifesciences.org/articles/58468/elife-58468-fig5-data1-v2.xlsx
Download elife-58468-fig5-data1-v2.xlsx

Quantifying contributions from absolute thresholds, age, and sensitivity to AM

Multiple linear regression was conducted to determine how much variance each factor contributes to FM sensitivity. Unlike correlations, which are bi-directional, multiple linear regression is a conservative, directional approach to examining the amount of variance accounted for by each variable. Because many of the variables are correlated, the order the variables are entered into the model will affect the percentage of variance explained by each variable. The Variance Inflation Factors ranged from 1.1 to 3.69 for the slow FM model and 1.06–3.62 for the fast FM model, well below the common cutoff of 10, indicating that the independent variables are not too highly collinear with one another (Marquardt, 1970). We took the most conservative approach by entering the low and high slopes last, after all the other variables. Factors known or believed to contribute to FM sensitivity (1 kHz absolute thresholds in the measured ear, age, sensitivity to AM at the corresponding rate, low slope, and high slope, entered in this order) were entered into the model, fitted using the Ordinary Least Squares method. The full models, with all variables entered, explained 59.5% (p<0.0001) and 52.1% (p<0.0001) of the variance in slow and fast FM, respectively. When sequentially entering each variable, absolute thresholds accounted for 45.2% (p=0.022) and 21.7% (p=0.11, n.s.) of the variance for slow and fast FM, respectively (note that all of the p values here correspond to the significance of the variable in the full model). Because age is known to impair FM detection (He et al., 2007; Strelcyk and Dau, 2009; Grose and Mamo, 2012; Paraouty et al., 2016; Wallaert et al., 2016; Paraouty and Lorenzi, 2017; Whiteford et al., 2017), age was entered into the model second, accounting for an additional 4.03% (slow FM: p=0.074, n.s.) and 3.78% (fast FM: p=0.16, n.s.) of the variance, while AM thresholds, entered third accounted for 4.03% (slow FM: p=0.039) and 18.7% (fast FM: p<0.0001). The low slope (slow FM: 6.2%, p=0.009; fast FM: 7.91%, p=0.008) but not the high slope (slow FM: .03%, p=0.864; fast FM: .01%, p=0.938) significantly contributed to the variance in sensitivity to FM at both rates, consistent with the partial correlation analysis (Figure 5). Note that entering the slopes first, instead of last, into the regression means that the variance explained is the same as the squared correlations plotted in panels A and C of Figure 5 (e.g., slow FM and low slope: 39.3%; fast FM and low slope: 22.1% variance explained), but the total variance explained in the full models is unaffected. Entering just the low slope and AM at the corresponding rate into the MLRs, which would be consistent with Zwicker's (1956) place model, accounts for 44.9% and 43.7% of the variance for slow and fast FM, respectively, with significant contributions from both the low slope (slow FM: p<0.0001; fast FM: p<0.0001) and AM (slow FM: p=0.026; fast FM: p<0.0001). Overall, the results are consistent with a role of a place code in FM detection at both slow and fast rates.

Experiment 2: Simulating FM through AM incoherence

The results from experiment 1 suggest that the fidelity of place coding relates to FM sensitivity, but they do not preclude the possibility that a time code is used that is dependent on frequency selectivity (e.g., Shamma and Klein, 2000). The strongest arguments in support of a time-interval code for slow-rate FM are (1) that FM sensitivity is higher (better) at slow rates than at fast rates (in contrast to AM sensitivity), possibly reflecting ‘sluggishness’ in the ability to evaluate phase-locked timing information, and (2) that sensitivity to slow-rate FM degrades at high carrier frequencies (Sek and Moore, 1995), where phase-locked timing information in the auditory nerve also degrades (Johnson, 1980; Palmer and Russell, 1986; Verschooten et al., 2019), whereas sensitivity to AM does not (Kohlrausch et al., 2000). Experiment 2 was designed to test whether these two properties of FM in normal-hearing listeners could also be explained via a place-coding mechanism. If FM is coded via an FM-to-AM place-based mechanism, then sensitivity to out-of-phase fluctuations in amplitude at nearby cochlear locations (as also produced by FM; see Figure 6, panels A and B) should be greater at slow than at fast fluctuation rates. We applied AM to two separate carriers, with the modulation either in phase (coherent) or out of phase (incoherent) between the two carriers, at fast and slow modulation rates, and with the carriers presented at frequencies that ranged from within to outside the putative range of human auditory-nerve phase locking (Verschooten et al., 2018). The wide spectral separation of the two carriers (2/3 and 4/3 octaves), their low sound level (45 dB SPL), as well as the narrowband noise added in the spectral gap between them, ruled out any peripheral interactions (including combination tones) between the carriers. We tested whether young normal-hearing listeners’ ability to discriminate incoherent from coherent AM, as well as their ability to detect incoherent AM, varied in the same way that FM detection thresholds varied with modulation rate and carrier frequency, as would be predicted by the place-coding theory of FM perception.

Figure 6

Download asset Open asset

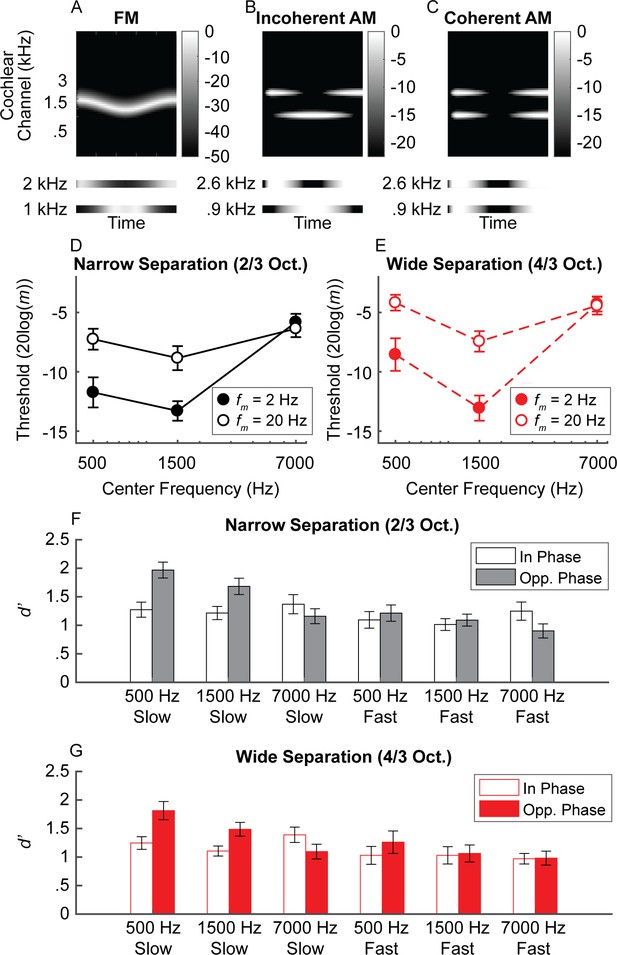
Experiment 2 schematic cochleagram and results.

(A) Schematic cochleagram of an FM tone. The magnitude responses for two off-frequency filters (bottom) are 180-degrees out of phase for any given snapshot in time. (**B and C**) The schematic cochleagrams of two-component AM dyads with envelopes that are in opposite phase (incoherent) versus in phase (coherent). Incoherent envelopes lead to rate-place fluctuations similar to that observed in FM. (**D and E**) Average sensitivity for discriminating incoherent AM at slow (filled circles) and fast (open circles) rates in the narrow (black) and wide (red) frequency separation conditions. Sensitivity for simulated FM is best at lower center frequencies and slow rates, with slightly higher thresholds at very low center frequencies, similar to traditional FM sensitivity (Sek and Moore, 1995). (**F and G**) Sensitivity for detecting in-phase (open bars) and opposite-phase (filled bars) AM for two-component dyads. Sensitivity for opposite-phase AM (i.e., simulated FM) is only boosted for low center frequencies at slow rates, meaning a unified neural place code can account for limits in human FM sensitivity. N = 20 in all measures. Error bars represent ±1 standard error of the mean.

Figure 6—source data 1 Figure 6 data. Rows are individual subjects. Nrw = 2/3 octave frequency separation; Wide = 4/3 octave frequency separation; Slow = 2 Hz modulation rate; Fast = 20 Hz modulation rate; In = in phase; Out = out of phase. The number in each column label (e.g., 500) corresponds to the center frequency.: https://cdn.elifesciences.org/articles/58468/elife-58468-fig6-data1-v2.xlsx
Download elife-58468-fig6-data1-v2.xlsx

AM incoherence discrimination

Participants heard a sequence of three AM dyads. The task was to pick the dyad with components that had temporal envelopes 180° out of phase (Figure 6D–E). Carrier frequencies were presented either 2/3 (narrow frequency separation) or 4/3 (wide frequency separation) octaves apart, thereby simulating the effects of FM on the cochlear place representation, but without the presence of any informative fine timing cues produced by peripheral interactions between the two carriers. As predicted, sensitivity to incoherent AM mirrors trends seen in traditional FM sensitivity (center frequency × rate interaction: F_1.51,28.7 = 16.6, p<0.0001; Figure 6; Supplementary file 1A), with better performance at the slow than the fast rate for low (500 Hz: p=0.012; 1500 Hz: p=0.0002) but not high center frequencies (7000 Hz: p=0.648). The effect of rate on center frequency was not influenced by frequency separation (F_2,38 = .841, p=0.439), although there was an interaction between frequency separation and center frequency (F_2,38 = 11.6, p=0.0001). Performance was generally elevated in the wide condition, but more so at the 500 Hz and 7000 Hz center frequencies than at 1500 Hz (p ≤ .012 for all three narrow versus wide comparisons at each center frequency). The pattern of sensitivity to AM incoherence suggests that effects of carrier frequency and rate on modulation sensitivity are not unique to the phase-locked neural response to temporal fine structure.

Complex AM detection

Detecting the presence of incoherent AM (simulated FM) is closer to the demands of FM detection than a discrimination task. A unitary place code for FM predicts that sensitivity to simulated FM via incoherent AM should be best in low-frequency regions (<4–5 kHz) and at slow modulation rates (<10 Hz). To test this hypothesis, we assessed our normal-hearing listeners’ sensitivity for AM dyads that were either in phase (traditional AM) or in opposite phase (incoherent AM, simulating FM), with the modulation depth of each component set to 4 dB below each individual’s AM detection threshold. Sensitivity was assessed for the same center frequencies, rates, and frequency separations as in the discrimination experiment. As predicted, the results revealed a significant three-way interaction between phase, center frequency, and rate (Figure 6F–G; Supplementary file 1B; phase × center frequency × rate: F_(2,38) = 7.58, p=0.002). Sensitivity was greater for the opposite-phase conditions than for the in-phase conditions, but only when the center frequencies were low and the rate was slow (slow 500 Hz: p=0.0003; fast 500 Hz: p=0.132; slow 1500 Hz: p=0.01; fast 1500 Hz: p=0.501). At the highest center frequency, the slow-rate benefit for the opposite-phase condition was eliminated (slow 7000 Hz: p=0.132; fast 7000 Hz: p=0.132). This finding was not dependent on the amount of separation between the two carrier frequencies, as there was no significant main effect of frequency separation and no significant interactions. In summary, our detection tasks involving incoherent AM revealed the same pattern of results that are found in FM detection: performance was best at low carrier frequencies and slow modulation rates and was degraded at high modulation rates and/or high carrier frequencies.

Discussion

A unitary code for FM

Our finding that cochlear place coding is equally important for both slow- and fast-rate FM detection was unexpected. Humans’ acute sensitivity to slow changes in frequency at carriers important for speech and music has been thought to result from precise neural synchronization to the temporal fine structure of the waveform or the combination of place and temporal fine structure cues (Demany and Semal, 1989; Moore and Sek, 1995; Moore and Sek, 1996; Sek and Moore, 1995; Lacher-Fougère and Demany, 1998; Buss et al., 2004; Strelcyk and Dau, 2009; Johannesen et al., 2016; Paraouty et al., 2018). Multiple linear regression analyses showed that the combined effect of audibility, age, sensitivity to AM, and masking function slopes accounted for about 60% and 52% of the total variance in slow and fast FM detection thresholds, respectively. This is a high proportion of the variance, particularly considering the approximate and indirect nature of the behavioral measure used to estimate cochlear tuning.

The clear role for place coding in slow FM detection is contrary to the widely accepted view that time coding is used to detect FM at the slow rates found in speech and music. Instead, our results provide evidence for a unitary code for two crucial features of natural sounds, AM and FM, that extends across the entire range of naturally encountered fluctuation rates. Experiment 2 directly addresses the arguments that have been used in the past to support the use of a time-interval code or a dual place-time code for slow-rate FM and demonstrates that enhanced slow-rate FM sensitivity can be accounted for by limitations in humans’ sensitivity to across-frequency variations in AM coherence, without recourse to the properties of auditory-nerve phase locking. This finding likely extends to simple frequency discrimination, which is believed to rely on the same mechanism as slow FM (Sek and Moore, 1995). A unitary code for FM and AM at all rates also helps explain the generally high-multicollinearity between FM and AM sensitivity observed here (Figure 3) and in several previous studies with normal-hearing listeners (Whiteford and Oxenham, 2015; Otsuka et al., 2016; Paraouty and Lorenzi, 2017; Whiteford et al., 2017), although the effect size of the correlation between slow-rate FM and AM was smaller than observed in previous studies. It may also help explain why attempts to improve speech and music perception by reintroducing fine timing cues via electrical pulses in cochlear implants have not been successful (Zeng et al., 2005; Schatzer et al., 2010).

Implications for the perception and neural coding of complex tones

This study used pure tones, which are not frequently encountered in the natural environment. However, combinations of pure tones form harmonic complex tones, such as musical instrument sounds, voiced speech, and many animal vocalizations. It is known that humans perceive the pitch of harmonic complex tones in ways that are fundamentally different from other commonly studied species, such as the chinchilla (Shofner and Chaney, 2013), ferret (Walker et al., 2019), or songbird (Bregman et al., 2016). Recent work (Shofner and Chaney, 2013; Walker et al., 2019) has suggested that part of this difference can be explained by the substantially sharper cochlear tuning found in humans than in smaller mammals (Shera et al., 2002; Shera et al., 2010; Sumner et al., 2018; Verschooten et al., 2018). Specifically, sharper human cochlear tuning is believed to explain why humans (Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003) and some other primates (Song et al., 2016) rely primarily on low-numbered spectrally resolved harmonics to extract pitch, whereas smaller mammals, such as ferrets and chinchillas, seem to rely primarily on the cues in the temporal envelope, which are provided by spectrally unresolved harmonics (Shofner and Chaney, 2013; Walker et al., 2019).

Results from the present study suggest that resolved harmonics, which are most important for human pitch perception, may be represented by their place of stimulation rather than by the temporal fine structure information encoded via the stimulus-driven spike timing (phase locking). This conclusion is consistent with other studies showing that pitch perception is possible even with spectrally resolved harmonics that are usually assumed to be too high in frequency to elicit phase locking (Oxenham et al., 2011; Lau et al., 2017; Carcagno et al., 2019) and with studies showing that steep filter slopes are required to represent harmonics from filtered noise in noise-vocoder simulations (Mehta and Oxenham, 2017). It is also supported by recent data from the inferior colliculus of the rabbit, showing that place coding of low-numbered harmonics from high F0s in the midbrain is robust over a relatively wide range of sound levels (Su and Delgutte, 2020), a finding that should generalize to low F0s in humans, given our superior frequency selectivity.

Alternative interpretations

One alternative interpretation of our results from experiment 1 is that hearing loss leads to a degradation in both spectral resolution and neural phase locking to temporal fine structure, and that it is the degradation in the phase locking, not cochlear filtering, that drives the relationship between spectral resolution and FM coding observed here. There are several reasons why this interpretation is unlikely. First, physiological studies with non-human animals have generally found little or no effect of SNHL on phase locking in the auditory nerve (Harrison and Evans, 1979; Miller et al., 1997; Henry and Heinz, 2012; Henry et al., 2019), with the exception of one study (Woolf et al., 1981). Support from human studies is based on indirect evidence from behavioral results showing poorer performance in hearing-impaired listeners in tasks thought to use time coding (Lorenzi et al., 2006; Moore et al., 2006; Moore et al., 2012; Hopkins and Moore, 2007; Hopkins and Moore, 2011; Moore, 2014; Füllgrabe and Moore, 2017). However, all of these, with the exception of binaural tasks, could be affected by poorer cochlear tuning (Oxenham et al., 2009). Binaural tasks, involving the discrimination of interaural time differences (ITDs) in the temporal fine structure of stimuli, are likely to rely on phase-locked coding. These studies have not always found a clear relationship between ITD sensitivity and hearing loss, once effects of age and audibility are accounted for (e.g., Smoski and Trahiotis, 1986; Hopkins and Moore, 2011), although a recent meta-analysis suggests a small effect of hearing loss on ITDs once controlling for age (Füllgrabe and Moore, 2018).

A second reason why it is unlikely for the role of place coding in FM to be a byproduct of degraded time coding with SNHL is that the relationship between place coding fidelity and FM sensitivity remained significant even after the effects of age, AM sensitivity, and hearing loss at 1 kHz were accounted for via partial correlation. Controlling for hearing loss should ensure that possible confounding changes in temporal fine structure coding with poorer frequency tuning are factored out, whereas controlling for aging and sensitivity to AM accounts for central aspects of processing that may affect FM thresholds, including task demands (i.e., the ability to perform a two-interval modulation detection task) and processing efficiency (Whiteford and Oxenham, 2015; Whiteford et al., 2017). The results therefore suggest that degradations of time coding with hearing loss or central aspects of aging do not fully account for the observed effects.

Another alternative interpretation is that a dual code, based on combined place and timing cues, accounts for slow FM sensitivity, rather than a unitary code. A dual code could potentially explain the high collinearity often observed between measures of FM and AM sensitivity (Whiteford and Oxenham, 2015; Otsuka et al., 2016; Paraouty and Lorenzi, 2017; Whiteford et al., 2017), as well as the observation from experiment one that slow-rate FM sensitivity may not be as strongly correlated to AM sensitivity as fast-rate FM (although these differences in correlation strength were not statistically significant). In addition, it has been found that AM can interfere with the detection of FM, particularly at fast rates and high carrier frequencies, perhaps pointing to the possibility of a dual code (Moore and Sek, 1996; Ernst and Moore, 2010; King et al., 2019). However, just as experiment 2 showed that timing cues are not necessary to explain enhanced slow-rate, low-carrier FM sensitivity, it may be that coherent AM across two carriers also interferes with the detection of incoherent AM in the same way that it interferes with FM detection. This prediction remains to be tested.

Explaining superior FM perception at low rates and low carrier frequencies within a unitary framework

A pure cochlear place-based model for FM proposes that FM is transduced to AM via cochlear filtering (Zwicker, 1956). As the frequency sweeps across the tonotopic axis, this is reflected via periodic amplitude fluctuations in the responses of cochlear filters. Experiment 2 demonstrated that a place-only model can account for the different rate- and frequency-dependent trends in FM and AM sensitivity observed in many previous studies (Viemeister, 1979; Sheft and Yost, 1990; Moore and Sek, 1995; Moore and Sek, 1996; Sek and Moore, 1995; Lacher-Fougère and Demany, 1998; Moore and Skrodzka, 2002; Whiteford and Oxenham, 2015; Whiteford et al., 2017; Whiteford and Oxenham, 2017), based on limitations in sensitivity to AM incoherence at high carrier frequencies and/or high modulation rates. Previous studies examining sensitivity to AM incoherence had either only tested fast rates (Green et al., 1990) or lower center frequencies (Moore and Sęk, 2019). Moore and Sęk, 2019 noted that the very large AM depths needed to discriminate AM incoherence, also observed here, are larger than one might expect if such a task were reflective of the same mechanism used in FM coding. However, the carriers used in AM-incoherence experiments must be spaced far enough apart to avoid peripheral interactions (in our case 2/3 or 4/3 octaves), meaning that the separation is much greater than for the two sides of excitation produced by a single carrier in an FM experiment. This in itself could explain why overall sensitivity is poorer in the AM simulations than in true FM detection and discrimination experiments.

Our combined findings suggest the auditory system’s ability to compare changes in the output between nearby cochlear filters is more efficient at slow than at fast rates, but only at low center frequencies. This interpretation is partly supported by a computational modeling study showing that frequency and intensity can be represented by a single code, if inter-neuronal noise correlations (Cohen and Kohn, 2011) are taken into account (Micheyl et al., 2013). Such correlations would require relatively long time windows to play a functional role, and so would only provide a benefit at low modulation rates, where the duration of the necessary time window does not exceed one period of the modulation. It is not currently known why such effects are dependent on the carrier frequency, but it may be that auditory cortical representations of the highest frequencies (>6 kHz) may be less extensive, due to their relative unimportance for everyday auditory stimuli, such as speech and music, which in turn could produce poorer sensitivity in fine discrimination tasks, analogous to the effects of visual crowding observed in the visual periphery (e.g., Whitney and Levi, 2011).

Materials and methods

Experiment 1

Participants

All tasks in experiment one were completed by 56 participants (19 male, 37 female; average age of 66.5 years, range: 19.4–78.5 years) with no reported history of cognitive impairment. All participants underwent audiometric screening, involving air- and bone-conduction audiometric threshold measurements at octave frequencies between 250 and 8000 Hz. Nine participants had clinically normal hearing at the test frequency of 1 kHz (audiometric thresholds ≤ 20 dB hearing level, HL) in both ears. The other 47 participants had varying degrees of SNHL, with audiometric thresholds at 1 kHz poorer than 20 dB HL in at least one ear and air-bone gaps < 10 dB to preclude a conductive hearing loss. Psychoacoustic measurements of absolute threshold for a 500 ms 1 kHz tone resulted in thresholds ranging from −0.7 to 68.5 dB SPL. Ears with thresholds of 70 dB SPL or more at 1 kHz were not included in the study. Participants with symmetric hearing (n = 37; difference in absolute thresholds at 1 kHz ≤10 dB) completed all experimental tasks using the ear with the higher threshold at 1 kHz. Six participants had SNHL at 1 kHz in both ears, but loss in the poorer ear exceeded the study criterion; for these subjects, tasks were completed in the better ear only. One additional participant was only assessed in their better ear because loss in the poorer ear was near the study criterion (68.6 dB SPL at 1 kHz), and the subject indicated the sound level was uncomfortable. An additional three participants had one normal ear and one ear with SNHL at 1 kHz, and only measurements from the impaired ear were used in analyses. The final nine participants had asymmetric SNHL in both ears, defined as a difference in absolute thresholds > 10 dB at 1 kHz. For eight of these subjects, the experimental tasks were completed for both ears separately. One participant with asymmetric hearing only completed tasks in their poorer ear due to time constraints (Table 1). However, only performance in the poorer ear was used in the analyses for all nine of these listeners (see Figures 4–5 – Figure 4—figure supplement 1 and Figure 5—figure supplement 1 for both ears included from all asymmetric listeners). Participants provided informed consent and were compensated with hourly payment or course credit for their time. The Institutional Review Board of the University of Minnesota approved all experimental protocols.

Table 1

Summary of participants.

Measured ear	# of Participants	Notes
Worse ear	38	Subjects with symmetric 1 kHz thresholds (asymmetry <= 10 dB; n = 37) or who could only be assessed in their worse ear due to time constraints (n = 1).
Better ear	7	Subjects with 1 kHz thresholds in the worse ear that exceeded the study criterion (n = 6) or indicated the SL in their worse ear was uncomfortable (n = 1).
Both ears (worse ear used in analyses)	11	1 kHz asymmetry > 10 dB; n = 3 had normal hearing in their better ear, and n = 8 had SNHL in both ears.

Share this article

Cite this article

Schematic of (A) FM and (B) AM time waveforms (fc = 1 kHz; fm = 20 Hz) and the resulting changes in basilar-membrane excitation for steep (C and D) and shallow (E and F) slopes.

Correlations between average absolute thresholds at 1 kHz in the tested ear (x-axis) and the steepness of the (A) low and (B) high side of the cochlear filter slopes (n = 55).

Figure 2—source data 1

Individual thresholds for slow (fm = 1 Hz) and fast (fm = 20 Hz) FM and AM detection (n = 55).

Figure 3—source data 1

Correlations between the low slope (A and C) and high slope (B and D) and slow (fm = 1 Hz; black) and fast (fm = 20 Hz; white) FM detection (n = 55).

Figure 4—source data 1

Partial correlations between the steepness of the masking function slopes (x-axis) and FM detection (y-axis) for slow (A and B) and fast FM (C and D) after variance due to audibility, sensitivity to AM, and age has been partialled out for n = 55 participants.

Figure 5—source data 1

Experiment 2 schematic cochleagram and results.

Figure 6—source data 1

Summary of participants.

Author details

Kelly L Whiteford

Contribution

For correspondence

Competing interests

Heather A Kreft

Contribution

Competing interests

Andrew J Oxenham

Contribution

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading

Schematic of (A) FM and (B) AM time waveforms (f_c = 1 kHz; f_m = 20 Hz) and the resulting changes in basilar-membrane excitation for steep (C and D) and shallow (E and F) slopes.

Individual thresholds for slow (f_m = 1 Hz) and fast (f_m = 20 Hz) FM and AM detection (n = 55).

Correlations between the low slope (A and C) and high slope (B and D) and slow (f_m = 1 Hz; black) and fast (f_m = 20 Hz; white) FM detection (n = 55).