Shadow enhancers can suppress input transcription factor noise through distinct regulatory logic

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: September 10, 2020 (This version)
Accepted Manuscript published: August 17, 2020 (Go to version)
Accepted: August 14, 2020
Received: May 27, 2020

1. Of interest
Avoiding false discoveries in single-cell RNA-seq by revisiting the first Alzheimer’s disease dataset

Alan E Murphy, Nurun Fancy, Nathan Skene

Research Article Dec 4, 2023
Further reading

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Shadow enhancers, groups of seemingly redundant enhancers, are found in a wide range of organisms and are critical for robust developmental patterning. However, their mechanism of action is unknown. We hypothesized that shadow enhancers drive consistent expression levels by buffering upstream noise through a separation of transcription factor (TF) inputs at the individual enhancers. By measuring the transcriptional dynamics of several Kruppel shadow enhancer configurations in live Drosophila embryos, we showed that individual member enhancers act largely independently. We found that TF fluctuations are an appreciable source of noise that the shadow enhancer pair can better buffer than duplicated enhancers. The shadow enhancer pair is also uniquely able to maintain low levels of expression noise across a wide range of temperatures. A stochastic model demonstrated the separation of TF inputs is sufficient to explain these findings. Our results suggest the widespread use of shadow enhancers is partially due to their noise suppressing ability.

eLife digest

In all higher organisms, life begins with a single cell. During the early stages of development, this single cell grows and divides multiple times to develop into the many different kinds of cells that make up an organism. This is a highly regulated process during which cells receive instructions telling them what kind of cell to become.

These instructions are relayed via genes, and a particular combination of activated genes determines the cell’s fate. Specific pieces of DNA, known as enhancers, act as switches that control when and where genes are active, while so-called shadow enhancers are found in groups and work together to turn on the same gene in a similar way.

Shadow enhancers are often active during the early stages of life to direct the formation of specialized cells in different parts of the body. But so far, it has been unclear why it is beneficial to the divide the role of activating genes across several shadow enhancers rather than a single one.

Here, Waymack et al. examined shadow enhancers around a gene called Kruppel in embryos of the fruit fly Drosophila melanogaster. Manipulating the shadow enhancers showed that they help to make gene activity more resistant to changes. Factors such as fluctuations in temperature have different effects on each shadow enhancer. Having several shadow enhancers working together ensures that, whatever happens, the right genes still get activated. For genes like Kruppel, which are key for healthy development, the ability to withstand unexpected changes is a valuable evolutionary benefit.

The study of Waymack et al. reveals why shadow enhancers are involved in the regulation of many genes, which may help to better understand developmental defects. Many conditions caused by such defects are influenced by both genetics and the environment. Genetic illnesses can vary in severity, which may be related to the roles of shadow enhancers. As such, studying shadow enhancers could lead to new approaches for treating genetic diseases.

Introduction

The first evidence that transcription occurred in bursts, as opposed to as a smooth, continuous process, was observed in Drosophila embryos. Electron micrographs showed that even highly transcribed genes had regions of chromatin lacking associated transcripts in between regions densely associated with nascent transcripts (McKnight and Miller, 1979). As visualization techniques have improved, it is increasingly clear that transcriptional bursting is the predominant mode of expression across organisms from bacteria to mammals (Chubb et al., 2006; Dar et al., 2012; Sanchez and Golding, 2013; Zenklusen et al., 2008; Bothma et al., 2014). These bursts of transcriptional activity, separated by periods of relative silence, have important implications for cellular function, as mRNA numbers and fluctuations largely dictate these quantities at the protein level (Csárdi et al., 2015; Hansen et al., 2018). Such fluctuations in regulatory proteins, like TFs and signaling molecules, can propagate down a gene regulatory network, significantly altering the expression levels or noise of downstream target genes (Blake et al., 2003).

Given the inevitable fluctuations in regulatory proteins like TFs, it is unclear how organisms establish and maintain the precise levels of gene expression seen during development, where expression patterns can be reproducible down to half-nuclear distances in Drosophila embryos (Dubuis et al., 2013; Gregor et al., 2007). Many mechanisms that buffer against expression noise, either inherent or stemming from genetic or environmental variation, have been observed (Lagha et al., 2012; Stapel et al., 2017; Raj et al., 2010). For example, organisms use temporal and spatial averaging mechanisms and redundancy in genetic circuits to achieve the precision required for proper development (Stapel et al., 2017; Raj et al., 2010; Erdmann et al., 2009; Lagha et al., 2012). Here, we propose that shadow enhancers may be another mechanism by which developmental systems manage noise (Barolo, 2012).

Shadow enhancers are groups of two or more enhancers that control the same target gene and drive overlapping spatiotemporal expression patterns (Hong et al., 2008; Barolo, 2012). Shadow enhancers are found in a wide range of organisms, from insects to plants to mammals, particularly in association with developmental genes (Cannavò et al., 2016; Osterwalder et al., 2018; Garnett et al., 2012; Bomblies et al., 1999). While seemingly redundant, the individual enhancers of a shadow enhancer group have been shown to be critical for proper gene expression in the face of both environmental and genetic perturbations (Frankel et al., 2010; Osterwalder et al., 2018; Perry et al., 2010). Such perturbations may exacerbate fluctuations in upstream regulators (Cheung and Ma, 2015; Chen et al., 2015). Although shadow enhancers are shown to be pervasive in developmental systems and necessary for robust gene expression, their precise mechanism of action is still unknown. One proposed mechanism is that having multiple enhancers controlling the same promoter reduces the effective ‘failure rate’ of the promoter and ensures a critical threshold of gene expression is reached (Lam et al., 2015; Perry et al., 2011). An alternative, but not mutually exclusive, possibility is that shadow enhancers ensure robust expression by buffering noise in upstream regulators. Several studies suggest that individual enhancers of a shadow enhancer group tend to be controlled by different sets of TFs, which we call a ‘separation of inputs’ (Wunderlich et al., 2015; Cannavò et al., 2016; Ghiasvand et al., 2011). We hypothesize that this separation of inputs allows shadow enhancers to buffer against fluctuations in upstream TF levels to drive more consistent expression levels.

The Drosophila gap gene Kruppel (Kr) provides a useful system in which to probe the mechanisms of action of shadow enhancers. During early embryogenesis, Kr expression is critical for thorax formation, and like the other gap genes in the Drosophila embryo, has quite low noise (Preiss et al., 1985; Dubuis et al., 2013). During this time, Kr is controlled by the activity of two enhancers, proximal and distal (Perry et al., 2011), that drive overlapping expression in the center of the embryo (Figure 1—figure supplement 1). We call the two individual enhancers together the shadow enhancer pair. Previous experiments have shown that each enhancer is activated by different TFs (Figure 1A; Wunderlich et al., 2015). Here, we focus on differences in activation, as the key repressors of Kr, Knirps and Giant, are likely to regulate both enhancers. By measuring live mRNA dynamics, we can use the Kr system in Drosophila embryos to assess whether and how shadow enhancers act to buffer noise and to identify the sources of noise in the developing embryo.

Figure 1 with 3 supplements see all

Download asset Open asset

Dual allele imaging shows the individual *Kruppel* enhancers drive largely independent transcriptional dynamics.

(A) Schematic of the endogenous *Kruppel* locus with distal (blue) and proximal (orange) shadow enhancers driving Kr (teal) expression in the central region of the embryo. Known transcriptional activators of the two enhancers are shown. (B) Schematics of single enhancer reporter constructs driving expression of MS2 sequence and a *yellow* reporter. When transcribed, the MS2 sequence forms stem loops that are bound by GFP-tagged MCP expressed in the embryos. Proximal embryos have expression on each allele controlled by the 1.5 kb proximal enhancer at its endogenous spacing from the Kr promoter, while distal embryos have expression on each allele controlled by the 1.1 kb distal enhancer at the same spacing from the Kr promoter. Shadow heterozygote embryos have expression on one allele controlled by the proximal enhancer and expression on the other allele controlled by the distal enhancer. (C). Still frame from live imaging experiment where nuclei are red circles and active sites of transcription are green spots. MCP-GFP is visible as spots above background at sites of nascent transcription (Garcia et al., 2013). (D) The fluorescence of each allele in individual nuclei can be tracked across time as a measure of transcriptional activity. The graph shows a representative trace of transcriptional activity of the two alleles in a single nucleus across the time of nc14. These traces are used to calculate the Pearson correlation coefficient between the transcriptional activity of the two alleles in a nucleus across the time of nc14. Correlation values are grouped by position of the nucleus in the embryo and averaged across all imaged nuclei in all embryos of each construct. (E) Graph of average correlation between the two alleles in each nucleus as a function of egg length. 0% egg length corresponds to the anterior end. Error bars indicate 95% confidence intervals. The shadow heterozygotes have much lower allele correlation than either homozygote, demonstrating that the individual shadow enhancers drive nearly independent transcriptional activity and that upstream fluctuations in regulators are a significant driver of transcriptional bursts. The total number of nuclei used in calculations for each construct by anterior-posterior (AP) bin are given in Supplementary file 1.

To test our hypothesis, we measured live mRNA dynamics driven by either single Kr enhancer, duplicated enhancers, or the shadow enhancer pair and compared the dynamics and noise associated with each. We showed that the individual Kr enhancers can act largely independently in the same nucleus, while identical enhancers display correlated activity. We constructed a simple mathematical model to describe this system and found that TF fluctuations are necessary to reproduce the correlated activity of identical enhancers in the same nucleus. The shadow enhancer pair drives lower noise than either duplicated enhancer, and using the model, we found that this is a natural consequence of the separation of TF inputs. Additional experiments, including simultaneous measurements of TF levels and expression and a decomposition of noise sources, further demonstrate that the shadow enhancer pair is less sensitive to fluctuations in TF levels than is a single enhancer. Additionally, the shadow enhancer pair is uniquely able to maintain low levels of expression noise across a wide range of temperatures. We suggest that this noise suppression ability is one of the key features that explains the prevalence of shadow enhancers in developmental systems.

Results

Individual enhancers in the shadow enhancer pair act nearly independently within a nucleus

To test our hypothesis that the separation of inputs between Kruppel’s (Kr) shadow enhancers provides them with noise-buffering capabilities, we needed to first test the ability of each enhancer to act independently. In previous work, we found that the individual enhancers in the shadow enhancer pair are controlled by different activating TFs (Wunderlich et al., 2015). These experiments established that the enhancers responded differently to perturbations in key TFs, indicating that each enhancer uses a distinct regulatory logic. The proximal enhancer is activated by Hunchback (Hb) and Stat92E, and the distal enhancer is activated by Bicoid (Bcd) and Zelda (Zld) (Figure 1A). Given this separation of inputs, the shadow enhancer pair could provide a form of noise buffering if variability in gene expression is driven primarily by fluctuations in upstream factors. Conversely, variability in upstream regulators may be low enough in the developing embryo that these fluctuations are not the primary driver of downstream expression noise. If this were the case, the separation of inputs is unlikely to be a key requirement of shadow enhancer function.

To investigate these possibilities, we measured and compared the correlation of allele activity in homozygous or heterozygous embryos that carry two reporter genes. Proximal homozygotes contained the proximal enhancer driving a reporter, inserted in the same location on both homologous chromosomes, and distal homozygotes similarly had the distal enhancer driving reporter expression on both homologous chromosomes (Figure 1B). We also made heterozygous embryos, called shadow heterozygotes, which had one proximal and one distal reporter, again in the same location on both homologous chromosomes. To measure live mRNA dynamics and correlations in allele activity, we used the MS2-MCP reporter system (Figure 1C,D). This system allows the visualization of mRNAs that contain the MS2 RNA sequence, which is bound by an MCP-GFP fusion protein (Bertrand et al., 1998). In the developing embryo, only the site of nascent transcription is visible, as single transcripts are too dim, allowing us to measure the rate of transcription (Garcia et al., 2013; Lucas et al., 2013). In blastoderm-stage embryos with two MS2 reporter genes, we can observe two distinct foci of fluorescence corresponding to the two alleles (Figure 1D; Videos 1, 2, 3, 4, 5, 6), in line with previous results that suggest there are low levels of transvection at this stage (Lim et al., 2018; Fukaya and Levine, 2017). To confirm our ability to distinguish the two alleles, we imaged transcription in embryos hemizygous for our reporter constructs, which only show one spot of fluorescence per nucleus. Our counts of active transcription sites in homozygous embryos correspond well to the expected value calculated from hemizygous embryos (Figure 1—figure supplement 1). Therefore, we are able to measure the correlation of allele activity, although we cannot identify which spot corresponds to which reporter.

Video 1

Download asset

posterframe for video — Transcriptional dynamics of distal enhancer reporter homozygotes.

Movie showing maximum projection of transcription driven by the distal enhancer reporter in homozygous embryos from 15 min into nc14 through 35 min into nc14. Anterior is to the left and dorsal side is up. Elapsed time of movie is shown in upper right corner. Imaging region is centered at approximately 37% egg length.

Video 2

Download asset

Video 3

Download asset

Video 4

Download asset

Video 5

Download asset

Video 6

Download asset

We predicted that if variability in gene expression is driven by fluctuations in input TFs, we would observe lower correlations of allele activity in shadow heterozygotes than in either the proximal or distal homozygotes. However, if global factors affecting both enhancers dominate, there would be no difference in allele activity correlations. During the ~1 hr of nuclear cycle 14 (nc14) we found that allele activity is more than twice as correlated in both proximal and distal homozygotes than in shadow heterozygote embryos at 47–57% egg length, which encompasses the central region of Kr expression during this time period (Figure 1). The difference in our ability to measure allele correlation in the more anterior and posterior regions of the embryo stems from the slightly different expression patterns driven by the proximal and distal enhancers (Figure 1—figure supplements 1,2). The lower allele correlation in shadow heterozygote embryos indicates not only that the individual member enhancers of the shadow enhancer pair can act largely independently in the same nucleus, but that differential TF inputs are likely the primary determinants of transcriptional bursts in this system. Notably, heterozygotes still show marginal allele correlation, indicating that some correlation is induced by either shared input TFs or factors that affect transcription globally. The independence of individual Kr enhancers allows for the possibility that shadow enhancers can act to buffer noise by providing distinct inputs to the same gene expression output.

Transcription factor fluctuations are required for the observed differences in the correlations of enhancer activity

To explore the conditions needed for the two Kr enhancers to act nearly independently within the same nucleus, we generated a simple model of enhancer-driven dynamics. We considered an enhancer E_i that interacts with a transcription factor T_i, which together bind to the promoter to form the active promoter-enhancer complex C_i (Figure 2A). When the promoter is bound by the enhancer, it drives the production of mRNA. Since the MS2 system only allows us to observe mRNA at the site of transcription, we modeled the diffusion of mRNA away from the transcription site as decay. The transcription factor T_i is produced in bursts of n_i molecules at a time, and it degrades linearly. For simplicity, the transcription factor T_i is an abstraction of the multiple activating TFs that interact with the enhancer, and T_i corresponds to a different set of TFs for the proximal and distal enhancer. This nonlinear model generalizes the linear model by Bothma et al., 2015 by explicitly taking into account the presence of TFs.

Figure 2 with 4 supplements see all

Download asset Open asset

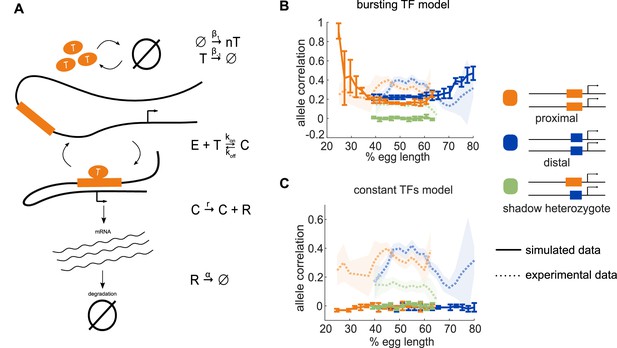
Model of enhancer-driven dynamics demonstrates TF fluctuations are required for correlated reporter activity.

To investigate the factors required for the observed correlated behavior of identical enhancers and largely independent behavior of the individual enhancers, we developed a simple stochastic model of enhancer-driven transcription. (A) Schematic of model of transcription driven by a single enhancer (the *bursting TFs* model). For each enhancer, we assume there is a single activating TF, T_i, that appears in bursts of size n_i molecules at a rate β₁, which varies by the position in the embryo. TFs degrade linearly at rate β_-1. When present, T_i can bind the enhancer, E_i, to form a transcriptionally active complex, C_i, at a rate *k_on* and dissociates at rate *k_off*. This complex then produces mRNA at an experimentally determined rate r that degrades at an experimentally determined rate, α. (B) The bursting TFs model is able to recapitulate the experimentally observed pattern of allele correlation. We plot the correlation between the two alleles in a nucleus as a function of egg length. Simulated data is created using the lowest energy parameter set for each enhancer. The data shown is the average of five simulated embryos that have 80 transcriptional spots per AP bin. In B and C, simulated data are shown by solid lines, experimental data are shown by dotted lines. (C) The constant TFs model fails to recapitulate the experimentally observed pattern of allele correlation. Without TF fluctuations, both heterozygous and homozygous embryos display independent allele activity. Error bars and shaded regions in B and C represent 95% confidence intervals.

We estimated some model parameters directly from experimental data and others by fitting using simulated annealing. The mRNA degradation parameter α and production parameter r were measured directly from fluorescence data without any input from the model (see Materials and methods for details). The remaining parameters were first estimated using mathematical analysis, then fine-tuned using simulated annealing. We found separate parameter sets for the proximal and distal enhancers that, when used to simulate transcription, fit the experimentally measured characteristics of the transcriptional traces, including transcription burst size, frequency, and duration, as well as the total mRNA produced (Figure 2—figure supplement 1).

We hypothesized that a model that lacks fluctuations in the input TFs could not recapitulate the high correlation of transcriptional activity in homozygotes versus the low correlation in heterozygotes. To test this hypothesis, we generated another model of TF production. We call our original model described above bursting TFs. The other model is one in which TF numbers are constant over time, which we call constant TFs and is equivalent to the model in Bothma et al., 2015. If the difference in transcription correlation between homozygotes and heterozygotes is due to fluctuating numbers of TFs, we expected that the bursting TFs model will recapitulate this behavior, while the constant TFs model will not. However, if the constant TFs model is also able to recapitulate the observed difference in correlations, then the correlations are likely a consequence of the identical enhancers simply being regulated by the same set of TFs.

For each model, we used the 10 best parameter sets to simulate transcriptional activity in homozygote and heterozygote embryos and analyzed the resulting allele correlations. We found that the bursting TFs model always produced results in which both homozygote allele correlations are significantly higher than the heterozygote, which qualitatively mirrors the experimental observations (Figure 2B). None of the best fitting parameter sets for the constant TF model were able to produce the experimentally-observed behavior and always resulted in near zero correlations for both the homozygote and heterozygote embryos (Figure 2C). Notably, using the bursting TFs model, all the simulated allele correlations were lower than the experimentally observed values, for example the simulated heterozygote allele correlation was near zero, while the experimental value was 0.14 at the embryo’s midpoint. We hypothesized that this discrepancy was because the model assumes complete independence of the proximal and distal enhancer input TFs, while in reality, there may be some degree of shared inputs, either of known TFs or a general component of the transcriptional machinery. To test this hypothesis, we generated a model that added a common TF to the bursting TFs model and attempted to fit the model parameters. Some of the best parameter sets recapitulated the nonzero correlation of the heterozygote embryos, indicating that a shared factor may play a role in this system; however, this behavior was inconsistent from one parameter set to the next (Figure 2—figure supplement 2). Therefore, we concluded that the simpler bursting TFs model, which consistently recapitulated the key features of the allele correlation data, was more suitable for subsequent analysis.

In conclusion, in our minimalist model of enhancer-driven transcription, the presence of TF fluctuations is required for the observed differences in allele correlation. These results also demonstrate the advantage of using a single generic TF for each enhancer. By abstracting away TF interactions, we reduced the complexity and number of parameters in the model, which allowed us to explore the relationship between TF production and allele correlation.

The shadow pair’s activity is less sensitive to fluctuations in Bicoid levels than is the activity of a single enhancer

Both the experimental measurements of allele correlation and the computational model suggest that input TF fluctuations are an appreciable source of noise for enhancer activity. Further, previous experimental work (Wunderlich et al., 2015) and the low correlation of transcriptional activity in heterozygotes (Figure 1E) indicates that each individual Kr enhancer receives different TF input signals. This suggests that the shadow enhancer pair will be less sensitive to an input TF fluctuation than a single enhancer, because the shadow enhancer pair’s activity is dependent on a broader range of TF inputs. To directly observe the relationship between input TF levels and enhancer output, we simultaneously tracked Bcd levels and enhancer activity in individual nuclei (Figure 3; Supp. Videos 7–8). We measured this relationship for both the distal enhancer, which is activated by Bcd, and the shadow enhancer pair, and predicted that the distal enhancer’s transcription dynamics are more strongly influenced by fluctuations in Bcd levels.

Figure 3

Download asset Open asset

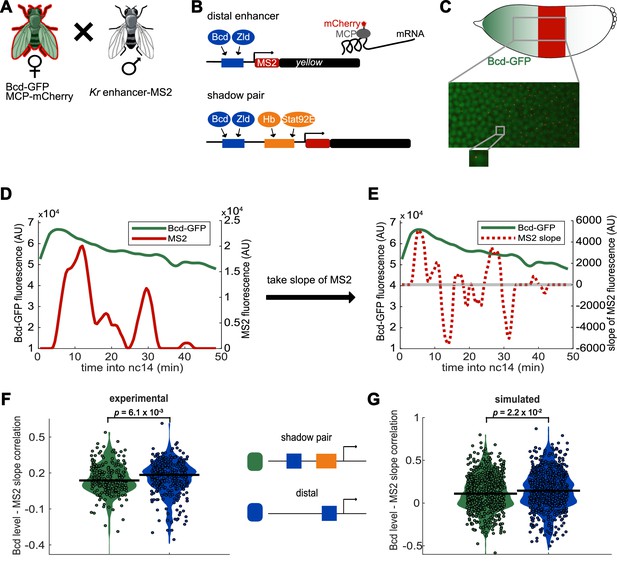
Activity of Kr shadow pair is less correlated with Bcd levels than is activity of single distal enhancer.

To assess whether fluctuations in enhancer activity across time are associated with fluctuations in TF levels, we simultaneously measured Bcd levels and enhancer-driven transcription in individual nuclei. (A) To track Bcd levels and enhancer activity in the same nuclei, we crossed flies expressing a Kr enhancer-MS2 transgene to flies expressing Bcd-GFP and MCP-mCherry. In the resulting embryos, Bcd levels can be measured by GFP fluorescence and enhancer reporter activity can be measured by mCherry fluorescence. (B) Schematic of the enhancer reporters used for simultaneous tracking of TF levels and enhancer activity. As in Figure 1, the transcribed MS2 sequence forms stem loops that are bound by MCP, which is here tagged with mCherry. (C) Bcd-GFP expression forms a gradient from the anterior to posterior of the embryo, whereas the Kr enhancer reporters drive expression in the center region of the embryo. The magnified section of the embryo shows a still frame from live imaging indicating nuclei (green) and active transcription spots (red). (D) Bcd levels and enhancer activity can be simultaneously tracked in individual nuclei. Graph shows a representative trace of Bcd-GFP levels (in green) and distal enhancer transcriptional activity (in red) in a nucleus across the time of nc14. (E) Activator TF levels regulate enhancer activity, so to assess the sensitivity of our enhancer constructs to input TF fluctuations, we compare the levels of nuclear Bcd-GFP to the slope of MS2 fluorescence across the time of nc14. Positive slope values indicate an increase in enhancer activity, while negative values indicate a decrease in enhancer activity. The graph shows nuclear Bcd-GFP levels (as in D), in solid green line, and MS2 slope values (of the MS2 trace shown in D), in dashed red line, across the time of nc14. Horizontal grey line indicates a slope value of 0. (F) Changes in the shadow pair’s activity are significantly less correlated with Bcd-GFP levels than are changes in the distal enhancer’s activity. Shown are violin plots of the distribution of correlation values between Bcd-GFP levels and MS2 slopes in individual nuclei for either the shadow pair or distal enhancer. Circles correspond to the correlation values of individual nuclei and the horizontal lines indicate the median. This correlation is significantly higher for the distal enhancer than it is for the shadow pair (median r values are 0.18 and 0.14, respectively. p-value=6.1×10⁻³ from Kruskal-Wallis pairwise comparison.) The total number of nuclei used in calculations for each construct by AP bin are given in Supplementary file 2. (G) Our enhancer model recapitulates the lower correlation between Bcd-GFP levels and enhancer activity seen with the shadow pair than with the distal enhancer. Graph is as in F, but showing the distribution of correlation values in simulated nuclei, using 100 nuclei per AP bin. Median r values for simulation are 0.14 for the distal enhancer and 0.11 for the shadow pair. p-value=2.2×10⁻² from Kruskal-Wallis pairwise comparison of correlations.

Video 7

Download asset

Video 8

Download asset

To allow for tracking of both Bcd levels and enhancer activity, we crossed female flies that express eGFP-tagged Bcd in the place of endogenous Bcd (called Bcd-GFP from here on; Gregor et al., 2007) and MCP-mCherry with male flies homozygous for either the shadow pair or distal enhancer reporter. As the Bcd-GFP transgene was inserted in a Bcd null background, the resulting embryos should receive roughly WT levels of Bcd. The females flies were heterozygous for the maternally deposited Bcd-GFP, and therefore, we estimate that roughly half of the Bcd proteins were labeled. Given the previous work demonstrating the normal function and expression levels of tagged Bcd, we expect the Bcd-GFP levels to be a representative sample of total Bcd (Gregor et al., 2007).

Higher activator TF levels increase enhancer activity. We therefore measured the correlation of nuclear Bcd-GFP levels to the slope of MS2 signal. When the enhancer is active, MS2 signal has a positive slope, when the enhancer is inactive, slope is negative. If the shadow enhancer pair is less sensitive than the distal enhancer to fluctuations in Bcd levels, we would predict higher correlation between Bcd-GFP levels and the activity of the distal enhancer than that of the shadow enhancer pair. We find that the transcription dynamics driven by the distal enhancer are indeed significantly more correlated to nuclear Bcd-GFP levels (median r = 0.18) than the dynamics driven by the shadow pair (median r = 0.14; Figure 3F; p-value=6.1×10⁻³), although both correlations are modest (see Discussion). The lower correlation indicates that transcription driven by the shadow pair is less sensitive to Bcd level fluctuations than is the distal enhancer. Our modeling recapitulates this finding, showing that the separated TF inputs of the shadow pair are sufficient to explain the observed decreased sensitivity to TF fluctuations (median r = 0.14 for the distal enhancer; 0.11 for the shadow pair; p-value=2.2×10⁻²; Figure 3G). These findings indicate that the shadow enhancer pair is better able to buffer fluctuations in a single activating TF than a single enhancer, likely due to the shadow enhancer pair’s separation of TF inputs.

The shadow enhancer pair drives less noisy expression than enhancer duplications

We wanted to further test whether the shadow enhancer pair drives less noisy gene expression output than a simple enhancer duplication. We compared the noise in expression driven by the shadow enhancer pair to that driven by two copies of either the distal or proximal enhancer (Figure 4). If the shadow enhancer pair drives lower noise, this suggests that having two independently acting enhancers is a critical feature of shadow enhancers’ ability to reduce variability and mediate robustness. Alternatively, if duplicated enhancers drive similar levels of expression noise, this suggests that enhancer independence is not critical for shadow enhancer function and that shadow enhancers mediate robustness through a different mechanism, such as ensuring a critical threshold of expression is met (Lam et al., 2015; Perry et al., 2011).

Figure 4 with 1 supplement see all

Download asset Open asset

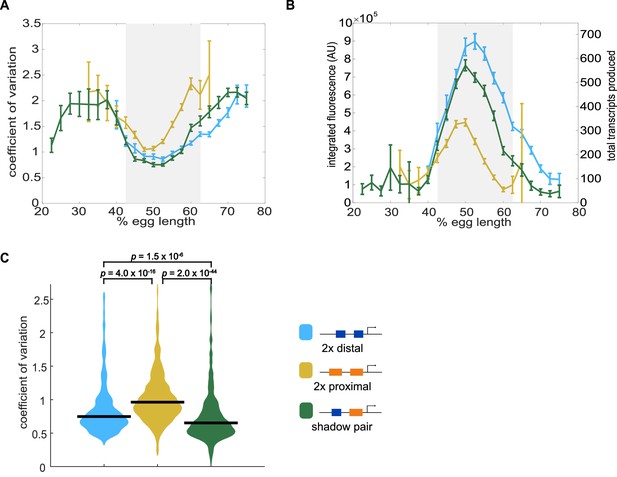
Shadow enhancer pair produces lower expression noise than duplicated enhancers.

To investigate whether the shadow enhancer pair drives less noisy expression, we calculate the coefficient of variation (CV) associated with the shadow enhancer pair or either duplicated enhancer across time of nc14. (A) The shadow enhancer pair displays lower temporal expression noise than either duplicated enhancer. Graph is mean coefficient of variation of fluorescence traces across time as a function of embryo position. The grey rectangle in A and B highlights the region of endogenous Kr expression (boundaries where 33% maximal expression occurs). (B) The shadow enhancer pair shows the lowest expression noise, but not the highest expression levels, indicating that the lower noise is not simply a function of higher expression. Graph is average total expression during nc14 as a function of embryo position. Error bars in A and B represent 95% confidence intervals. Total number of transcriptional spots used for graphs are given in Supplementary file 3 by construct and AP bin. (C) Violin plot of distribution of CV values at AP bin of peak expression for each enhancer construct (corresponding to 50% egg length for shadow pair and duplicated proximal, 52.5% egg length for duplicated distal), horizontal bar indicates median. Y-axis limited to 99th percentile of the construct with highest expression noise (duplicated proximal). The shadow pair drives significantly lower expression noise than either duplicated enhancer (p-value=1.5×10⁻⁶ for duplicated distal and shadow pair. p-value=2.0×10⁻⁴⁴ for duplicated proximal and shadow pair). p-Values were calculated using Kruskal Wallis pairwise comparison with Bonferroni multiple comparison correction.

We tracked transcriptional activity in embryos expressing MS2 under the control of the shadow enhancer pair, a duplicated proximal enhancer, or a duplicated distal enhancer (Figure 4). To measure noise associated with each enhancer, we used these traces to calculate the coefficient of variation (CV) of transcriptional activity across nc14. CV is the standard deviation divided by the mean and provides a unitless measure of noise to allow comparisons among our enhancer constructs. We then grouped these CV values by the embryo position of the transcriptional spots and found the average CV at each position for each enhancer construct. All the enhancer constructs display the lowest expression noise at the embryo position of their peak expression (Figure 4A), in agreement with previous findings of an inverse relationship between mean expression and noise levels (Dar et al., 2016; Figure 4—figure supplement 1). The shadow enhancer pair’s expression noise is ~30% or 15% lower, respectively, than that of the duplicated proximal or distal enhancers in their positions of maximum expression (Figure 4C).

If the primary function of shadow enhancers is only to ensure a critical threshold of expression is reached, we would not expect to also see the lower expression noise associated with the shadow enhancer pair compared to either duplicated enhancer. Furthermore, this decreased expression noise is not simply a consequence of higher expression levels, as the shadow enhancer pair produces less mRNA than the duplicated distal enhancer during nc14 (Figure 4B). The lower expression noise associated with the shadow enhancer pair suggests that it is less susceptible to fluctuations in upstream TFs than multiple identical enhancers.

Modeling indicates the separation of input TFs is sufficient to explain the low noise driven by the shadow enhancer pair

To explore which factors drive the difference in CVs between the duplicated and shadow enhancer constructs, we extended our model to have a single promoter controlled by two enhancers (Figure 5A). To do so, we assumed that either or both enhancers can be looped to the promoter and drive mRNA production. The rate of mRNA production when both enhancers are looped is the sum of the rates driven by the individual enhancers. We assumed that some parameters, for example the TF production rates and mRNA decay rate, are the same as the single enhancer case. We allowed the parameters describing the promoter-enhancer looping dynamics (the k_on and k_off values) to differ, depending on the enhancer’s position in the construct relative to the promoter and whether another enhancer is present. To fit the k_on and k_off values, we used the medians of the 10 best single enhancer parameter sets as a starting point and performed simulated annealing to refine them.

Figure 5 with 1 supplement see all

Download asset Open asset

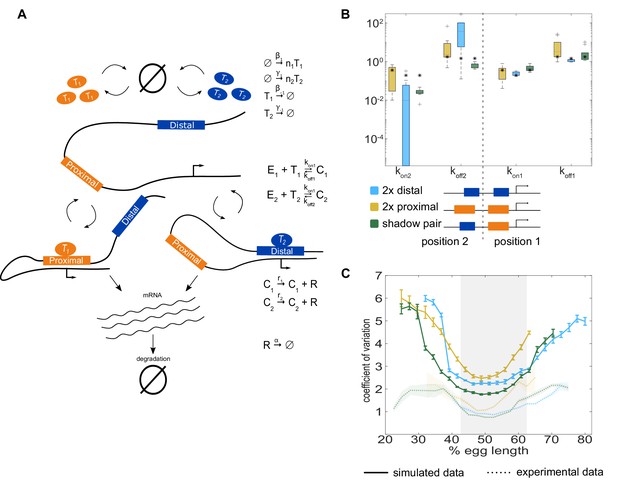
The two enhancer model recapitulates low expression noise associated with the shadow enhancer pair.

To assess whether the separation of input TFs mediates the lower expression noise driven by the shadow enhancer pair, we expanded our model to incorporate two enhancers driving transcription. (A) Schematic of the two enhancer model. We assume that when two enhancers control a single promoter, either or both can loop to the promoter and drive transcription. We defined model parameters as in Figure 2, and only allowed the *k_on* and *k_off* values to vary from the single enhancer model. (B) To understand the effect of adding a second enhancer, we examined how the *k_on* and *k_off* values vary from those in the single enhancer model. We plotted the distribution of the values for *k_on* and *k_off* for each enhancer in the three different constructs measured. The distribution shows the values derived from the 10 best-fitting parameter sets, and the black star in each column indicates the *k_on* or *k_off* value from the corresponding single enhancer model. In general, the *k_off* values increased relative to the single enhancer model, and the *k_on* values decreased, indicating that the presence of a second enhancer inhibits the activity of the first. (C) Graph of average coefficient of variation of simulated (solid lines) or experimental (dotted lines) transcriptional traces as a function of egg length. The model is able to recapitulate the lower expression noise seen with the shadow enhancer pair with no additional fitting, indicating that the separation of TF inputs to the two enhancers is sufficient to explain this observation. Error bars of simulated data and shaded region of experimental data indicate 95% confidence intervals.

This approach allowed us to examine how the model parameters that describe promoter-enhancer looping dynamics change when two enhancers are controlling the same promoter. We compared the k_off and k_on values for each enhancer in the two enhancer constructs to their values from the single enhancer model. We generally found that k_off values increased and k_on values decreased (Figure 5B). The effect is most pronounced in the duplicated distal enhancer, with large changes to the k_off and k_on values for the enhancer in the position far from the promoter (position 2). Given that our model assumes that enhancers act additively and only allows for changes in the k_off and k_on values, these observed effects may indicate that either the presence of a second enhancer interferes with promoter-enhancer looping or that the promoter can be saturated. Our model cannot distinguish between these two possibilities, but these observations are consistent with our (Figure 5—figure supplement 1) and previous results indicating that the Kr enhancers can act sub-additively (Scholes et al., 2019). Additionally, the dramatic changes in k_off and k_on values in the duplicated distal enhancer are consistent with a previous assertion that enhancer sub-additivity is most pronounced in cases of strong enhancers (Bothma et al., 2015).

We used these models to simulate transcription and predict the resulting CVs from the duplicated enhancer and shadow pair constructs. In line with experimental data, we found the model predicts that the shadow pair construct drives lower noise than the duplicated distal or duplicated proximal enhancer constructs in the middle of the embryo (Figure 5C). This is particularly notable, as we did not explicitly fit our model to reproduce the experimentally observed CVs. There is only one fundamental difference between the shadow pair and duplicated enhancer models, namely the use of separate TF inputs for the shadow pair. Therefore, in our simplified model, we can conclude that the separation of input TFs is sufficient to explain the lower noise driven by the shadow enhancer pair construct.

The shadow enhancer pair buffers against intrinsic and extrinsic sources of noise

To further understand the sources of noise the shadow enhancer pair is able to buffer, we compared the extrinsic and intrinsic noise associated with the shadow enhancer pair to that associated with either single or duplicated enhancers. To do so, we measured the transcriptional dynamics of embryos with two identical reporters in each nucleus and calculated noise sources using the approach of Elowitz et al., 2002. Intrinsic noise corresponds to sources of noise, such as TF binding and unbinding, that affect each allele separately. It is quantified by the degree to which the activities of the two reporters in a single nucleus differ. Extrinsic noise corresponds to global sources of noise, such as TF levels, that affect both alleles simultaneously. It is measured by the degree to which the activities of the two reporters change together. Intrinsic and extrinsic noise are defined such that, when squared, their sum is equal to total noise², which corresponds to the CV² of the two identical alleles in each nucleus in our system (see Materials and methods). Because our data do not meet one key assumption needed to measure extrinsic and intrinsic noise with the two-reporter approach (see Discussion; Figure 6—figure supplement 1), we use the terms inter-allele noise and covariance in place of intrinsic and extrinsic noise.

Based on our separation of inputs hypothesis and CV data, we expected the total noise associated with the shadow enhancer pair to be lower than that associated with the duplicated enhancers. We predicted that the shadow enhancer pair will mediate lower total expression noise through lower covariance, as the two member enhancers are regulated by different TFs. Given the complexity of predicting inter-allele noise from first principles (Materials and methods; Figure 6—figure supplement 2), we predicted that constructs with two enhancers will have lower inter-allele noise than single enhancer constructs but did not have a strong prediction regarding the relative inter-allele noise among the different two-enhancer constructs. Comparisons of noise between the single and duplicated enhancer constructs would further allow us to discern whether reductions in noise are generally associated with two-enhancer constructs or whether this is a particular feature of the shadow enhancer pair.

Neither the duplicated proximal nor distal enhancers drive significantly lower total noise than the corresponding single enhancers, indicating that the addition of an identical enhancer is not sufficient to reduce expression noise in this system (Figure 6A). The shadow enhancer pair drives lower total expression noise than either single or duplicated enhancer, consistent with the temporal CV data in Figure 4. The median total expression noise associated with the duplicated distal and duplicated proximal enhancers is 1.4 or 2.4 times higher, respectively, than that associated with the shadow enhancer pair (Figure 6A). Note that for measurements of noise, our distal construct places the enhancer at the endogenous spacing from the promoter, as we wanted to control for positional effects on expression and noise (Scholes et al., 2019; Figure 6—figure supplement 3).

Figure 6 with 3 supplements see all

Download asset Open asset

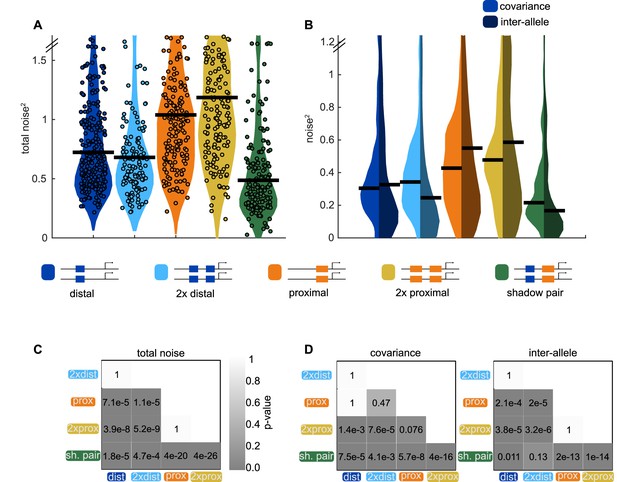
Shadow enhancer pair achieves lower total noise by buffering global and allele-specific sources of noise.

To determine how the shadow enhancer pair produces lower expression noise, we calculated the total noise associated with each enhancer construct and decomposed this into the contributions of covariance and inter-allele noise. Covariance is a measure of how the activities of the two alleles in a nucleus change together and is indicative of global sources of noise. Inter-allele noise is a measure of how the activities of the two alleles differ and is indicative of allele-specific sources of noise. (A) The shadow enhancer pair has lower total noise than single or duplicated enhancers. Circles are total noise values for individual nuclei in AP bin of peak expression for the given enhancer construct. Horizontal line represents the median. The y-axis is limited to 75th percentile of the proximal enhancer, which has the largest noise values. The shadow enhancer pair has significantly lower total noise than all other constructs. (B) The shadow enhancer pair displays significantly lower covariance than either single or duplicated enhancer and significantly lower inter-allele noise than both single enhancers and the duplicated proximal enhancer. The left half of each violin plot shows the distribution of covariance values of nuclei in the AP bin of peak expression, while the right half shows the distribution of inter-allele noise values. Horizontal lines represent median. The y-axis is again limited to the 75th percentile of enhancer with the largest noise values, which is duplicated proximal. The lower covariance and inter-allele noise associated with the shadow enhancer pair indicates it is better able to buffer both global and allele-specific sources of noise. (C) p-Value table of Kruskal-Wallis pairwise comparison of the total noise values of each enhancer construct. p-Value gradient legend applies to C and D. (D) p-Value table of Kruskal-Wallis pairwise comparison of covariance (on left) and inter-allele noise (on right) values for each enhancer construct. Bonferroni multiple comparison corrections were used for p-values in C and D. Total number of nuclei used in noise calculations are given in Supplementary file 1.

In line with our expectations, the shadow enhancer pair has significantly lower covariance levels than either single or duplicated enhancer (Figure 6B). The shadow enhancer pair also has lower inter-allele noise than all of the other constructs, though these differences are only marginally significant (p=0.13) when compared to the duplicated distal enhancer. Covariance makes a larger contribution to the total noise for the duplicated distal enhancer and the shadow enhancer pair, while inter-allele noise is the larger source of noise for the single distal enhancer and the single or duplicated proximal enhancers (Figure 6B).

The lower total noise and covariance of the shadow enhancer pair support our hypothesis that, by separating regulation of the member enhancers, the shadow enhancer pair can buffer against upstream fluctuations. The lower inter-allele noise associated with the shadow enhancer pair warrants further investigation. A simple theoretical approach predicts that two enhancer constructs will have lower inter-allele noise (Figure 6—figure supplement 2). Given that this is not universally observed in our data, this suggests that there is still much to discover about how inter-allele noise changes as additional enhancers control a gene’s transcription.

The shadow enhancer pair drives low noise at several temperatures

We showed the Kr shadow enhancer pair drives expression with lower total noise than either single or duplicated enhancer, yet previous studies have generally found individual member enhancers of a shadow enhancer set are dispensable under ideal conditions (Frankel et al., 2010; Perry et al., 2011; Osterwalder et al., 2018). However, in the face of environmental or genetic stress, the full shadow enhancer group is necessary for proper development (Frankel et al., 2010; Osterwalder et al., 2018; Perry et al., 2011). We therefore decided to investigate whether temperature stress causes significant increases in expression noise and whether the shadow enhancer pair or duplicated enhancers can buffer these potential increases in noise.

Similar to our findings at ambient temperature (26.5°C), the shadow enhancer pair drives lower total noise than all other tested enhancer constructs at 32°C (Figure 7B). At 32°C, the duplicated distal and duplicated proximal enhancers display 35% or 52%, respectively, higher total noise than the shadow enhancer pair. At 17°C, the shadow enhancer pair has approximately 46% lower total noise than either the single or duplicated proximal enhancer, 21% lower total noise than the single distal enhancer, and is not significantly different than the duplicated distal enhancer (Figure 7A). As seen by the variety of shapes in the temperature response curves (Figure 7C), temperature perturbations have enhancer-specific effects, suggesting input TFs may differ in their response to temperature change. The low noise driven by the shadow enhancer pair across conditions is consistent with previous studies showing shadow enhancers are required for robust gene expression at elevated and lowered temperatures (Frankel et al., 2010; Perry et al., 2010).

Figure 7

Download asset Open asset

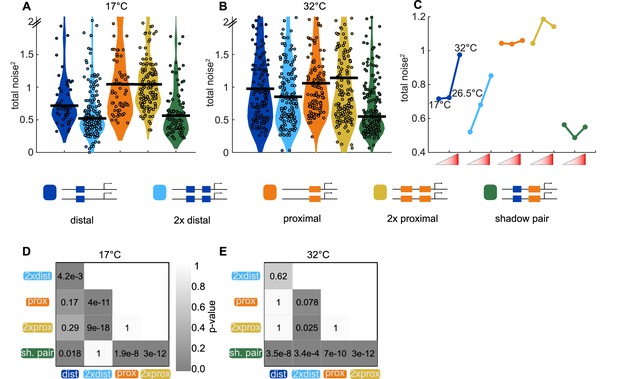
Shadow enhancer pair maintains lower total noise across temperature perturbations.

To test the ability of each enhancer construct to buffer temperature perturbations, we measured the total expression noise associated with each for embryos imaged at 17°C or 32°C. (A) The shadow enhancer pair displays significantly lower total noise than the single or duplicated proximal enhancer and the single distal enhancer at 17°C. Circles are total noise values for individual nuclei in AP bin of peak expression for the given enhancer construct and horizontal bars represent medians. The y-axis is limited to 75th percentile of construct with highest total noise at 17°C (single proximal). (B) The shadow enhancer pair has significantly lower total noise than all other constructs at 32°C. The y-axis is limited to 75th percentile of the enhancer construct with highest total noise at 32°C (duplicated proximal). (C) Temperature changes have different effects on the total noise associated with the different enhancers. The median total noise value at the AP bin of peak expression at the three measured temperatures is shown for each enhancer construct. Within each enhancer, the median total noise values are shown left to right for 17°C, 26.5°C, and 32°C. (D) p-Value table of Kruskal-Wallis pairwise comparison of the total noise values of each enhancer construct at 17°C. p-value gradient legend applies to D and E. (E) p-Value table of Kruskal-Wallis pairwise comparison of the total noise values of each enhancer construct at 32°C. Bonferroni multiple comparison corrections were used for p-values in D and E.

Discussion

Fluctuations in the levels of transcripts and proteins are an unavoidable challenge to precise developmental patterning (Raser and O'Shea, 2005; Arias and Hayward, 2006; Hansen et al., 2018). Given that shadow enhancers are common and necessary for robust gene expression (Osterwalder et al., 2018; Frankel et al., 2010; Perry et al., 2010), we proposed that shadow enhancers may function to buffer the effects of fluctuations in the levels of key developmental TFs. To address this, we have, for the first time, extensively characterized the noise associated with shadow enhancers critical for patterning the early Drosophila embryo. By either tracking biallelic transcription or simultaneously measuring input TF levels and transcription, we tested the hypothesis that shadow enhancers buffer noise through a separation of TF inputs to the individual member enhancers. Our results show that TF fluctuations play a significant role in transcriptional noise and that a shadow enhancer pair is better able to buffer both extrinsic and intrinsic sources of noise than duplicated enhancers. Using a simple mathematical model, we found that fluctuations in TF levels are required to reproduce the observed correlations between reporter activity and that the low noise driven by the shadow enhancer pair may be a natural consequence of the separation of TF inputs to the member enhancers. Lastly, we showed that a shadow enhancer pair is uniquely able to buffer expression noise across a wide range of temperatures. Together, these results support the hypothesis that shadow enhancers buffer input TF noise to drive robust gene expression patterns during development.

Temporal fluctuations in transcription factor levels drive expression noise in the embryo

When measured in fixed embryos, the TFs used in Drosophila embryonic development show remarkably precise expression patterns, displaying errors smaller than the width of a single nucleus (Dubuis et al., 2013; Gregor et al., 2007; Little et al., 2013; He et al., 2008). It therefore was unclear whether fluctuations in these regulators play a significant role in transcriptional noise in the developing embryo. By measuring the temporal dynamics of the individual Kr enhancers, each of which is controlled by different transcriptional activators, we show that TF fluctuations do significantly contribute to the noise in transcriptional output of a single enhancer. Within a nucleus, expression controlled by the two different Kr enhancers is far less correlated than expression driven by two copies of the same enhancer, indicating that TF inputs, as opposed to more global factors, are the primary regulators of transcriptional bursting in this system. Our current findings leave open the possibility that additional mechanisms, such as differences in 3D nuclear organization between different reporters, may also contribute to the differences in noise that we see.

We also showed that activity driven by the Kr shadow enhancer pair is less sensitive to levels of a single TF than is activity driven by an individual Kr enhancer. While prior work has shown that changes in TF levels precede changes in target transcription (Bothma et al., 2018), the sensitivity of individual enhancers to changes in TF levels had not been previously quantified. The correlation between Bcd levels and activity of the distal enhancer is modest, and we expect that this reflects both the influence of additional TF inputs and nuclear heterogeneity that causes the local Bcd levels available to the enhancer to differ from total nuclear levels (Mir et al., 2018). We suspect that the correlation between the activity of the distal enhancer and Bcd levels in the microenvironment surrounding the enhancer is higher than what we were able to measure here. New and emerging technologies will likely allow for live measurements of multiple TF inputs at higher spatial resolution, enabling further insights into the dynamics of expression regulation.

The finding that the Kr shadow enhancer pair is less sensitive to TF levels helps reconcile our finding that the individual Kr enhancers are influenced by fluctuations in input TFs with previous studies showing that endogenous Kr expression patterns are rather reproducible (Little et al., 2013). Previous work has cited the role of spatial and temporal averaging, which buffers noisy nascent transcriptional dynamics to generate more precise expression levels. Shadow enhancers operate upstream of this averaging, driving less noisy nascent transcription than either single enhancers or enhancer duplications.

A stochastic model underscores importance of transcription factor fluctuations

We developed a stochastic mathematical model of Kr enhancer dynamics and mRNA production that recapitulates our main experimental results. This model is based on that by Bothma et al., 2015, but it is expanded to include the dynamics of a TF that regulates each enhancer. We placed a strong emphasis on the simplicity of this model, for example by using a single abstract TF for each enhancer. This choice both avoids a combinatorial explosion of parameters and makes the model results and parameters easier to interpret. One of the most notable features of the model is that it recreates the differences in noise between shadow and duplicated enhancer constructs without any additional fitting, indicating that these differences in the model system are a direct result of the separation of input TFs to the proximal and distal enhancers.

Future versions of this model can include refinements. For example, in the current model, we do not include the influence of repressive TFs or consider the multiple modes of action used by activating TFs. Future experiments and models can also be designed to identify the mechanism of enhancer non-additivity: changes in promoter-enhancer looping, saturation of the promoter, or other mechanisms.

Noise source decomposition suggests competition between reporters

In our investigation of sources of noise, we decomposed total noise into extrinsic and intrinsic components as in Elowitz et al., 2002. In that study, the authors showed that the activity of one reporter did not inhibit expression of the other reporter, and therefore their calculations assumed no negative covariance between the reporters’ expression output. In our system, we found a small amount of negative covariance between the activity of two alleles in the same nucleus (Figure 6—figure supplement 1). For this reason, we called our measurements covariance and inter-allele noise. The negative covariance we observed indicates that activity at one allele can sometimes interfere with activity at the other allele, suggesting competition for limited amounts of a factor necessary for reporter visualization. The two possible limiting factors are MCP-GFP or an endogenous factor required for transcription. If MCP-GFP were limiting, we would expect to see the highest levels of negative covariance at the center of the embryo, where the highest number of transcripts are produced and bound by MCP-GFP. Since the fraction of nuclei with negative covariance is highest at the edges of the expression domain (Figure 6—figure supplement 1), the limiting resource is likely not MCP-GFP, but instead a spatially-patterned endogenous factor, like a TF.

Currently, the field largely assumes that adding reporters does not appreciably affect expression of other genes. However, sequestering TFs within repetitive regions of DNA can impact gene expression (Liu et al., 2007; Janssen et al., 2000), and a few case studies show that reporters can affect endogenous gene expression (Laboulaye et al., 2018; Thompson and Gasson, 2001). If TF competition is responsible for the observed negative covariance between reporters, a closer examination of the effects of transgenic reporters on the endogenous system is warranted. In addition, TF competition may be a feature, not a bug, of developmental gene expression control, as modeling has indicated that molecular competition can decrease expression noise and correlate expression of multiple targets (Wei et al., 2019).

Additional functions of shadow enhancers and outlook

There are likely several features of shadow enhancers selected by evolution outside of their noise-suppression capabilities. Preger-Ben Noon, et al. showed that all shadow enhancers of shavenbaby, a developmental TF gene in Drosophila, drive expression patterns in tissues and times outside of their previously characterized domains in the larval cuticle (Preger-Ben Noon et al., 2018). This suggests that shadow enhancers, while seemingly redundant at one developmental stage, may play separate, non-redundant roles in other stages or tissues. Additionally, a recent study investigating shadow enhancer pairs associated with genes involved in Drosophila embryonic development found that CRISPR deletions of the individual enhancers result in different phenotypes, suggesting each plays a slightly different role in regulating gene expression (Dunipace et al., 2019). In several other cases, both members of a shadow enhancer pair are required for the precise expression pattern generated by the endogenous locus (El-Sherif and Levine, 2016; Perry et al., 2012; Dunipace et al., 2011; Perry et al., 2011; Yan et al., 2017). These sharpened expression patterns achieved by a shadow enhancer pair may reflect enhancer dominance or other forms of enhancer-enhancer interaction and are likely another important function of shadow enhancers (El-Sherif and Levine, 2016).

In the case of Kr, the endogenous expression pattern is best recapitulated by the shadow enhancer pair, with the individual enhancers driving slightly more anterior or posterior patterns of expression (Figure 1—figure supplement 1; El-Sherif and Levine, 2016). Additionally, the early embryonic Kr enhancers drive observable levels of expression in additional tissues and time points, but these expression patterns overlap those driven by additional, generally stronger, enhancers, suggesting that the primary role of the proximal and distal enhancers is in early embryonic patterning (Hoch et al., 1990). Therefore, while we cannot rule out the possibility that the proximal and distal enhancers perform separate functions at later stages, it seems that their primary function, and evolutionary substrate, is controlling Kr expression pattern and noise levels during early embryonic development.

Here, we have investigated the details of shadow enhancer function for a particular system, and we expect that some key observations may generalize to many sets of shadow enhancers. Shadow enhancers seem to be a general feature of developmental systems (Cannavò et al., 2016; Osterwalder et al., 2018), but the diversity among them has yet to be specifically addressed. While we worked with a pair of shadow enhancers with clearly separated TF activators, shadow enhancers can come in much larger groups and with varying degrees of TF input separation between the individual enhancers (Cannavò et al., 2016; Osterwalder et al., 2018). To discern how expression dynamics and noise driven by shadow enhancers depend on their degree of TF input separation, we are investigating these characteristics in additional sets of shadow enhancers with varying degrees of differential TF regulation. Our current results combined with data gathered from additional shadow enhancers will inform fuller models of how developmental systems ensure precision and robustness.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Genetic reagent (Drosophila melanogaster)	ChrII attP site; PBac{y[+]-attP-3B}VK00002	Bloomington Drosophila Stock Center	BDSC:9723 FLYB: FBti0076425	Fly line injected for transgenic reporters
Genetic reagent (D. melanogaster)	Kr proximal enhancer	This paper		Fly line with MS2 expression driven by Kr proximal enhancer inserted on chromosome II
Genetic reagent (D. melanogaster)	Kr distal enhancer	This paper		Fly line with MS2 expression driven by Kr distal enhancer inserted on chromosome II
Genetic reagent (D. melanogaster)	shadow enhancer pair	This paper		Fly line with MS2 expression driven by Kr shadow enhancer pair inserted on chromosome II
Genetic reagent (D. melanogaster)	duplicated distal enhancer	This paper		Fly line with MS2 expression driven by two copies of Kr distal enhancer inserted on chromosome II
Genetic reagent (D. melanogaster)	duplicated proximal enhancer	This paper		Fly line with MS2 expression driven by two copies of Kr proximal enhancer inserted on chromosome II
Genetic reagent (D. melanogaster)	endogenous distal enhancer	This paper		Fly line with MS2 expression driven by Kr distal enhancer at endogenous spacing from promoter, inserted on chromosome II
Genetic reagent (D. melanogaster)	Bcd-GFP; Bcd-eGFP	Gregor et al., 2007, Cell		Fly line with mutated endogenous Bcd (bcd^E1) rescued with GFP-tagged Bcd transgene on X chromosome
Genetic reagent (D. melanogaster)	MCP-GFP	Garcia et al., 2013, Current Biology		Fly line expressing MCP-GFP on chromosome III and His-RFP on chromosome II
Genetic reagent (D. melanogaster)	MCP-mCherry	Hernan Garcia Lab		Fly line expressing MCP-mCherry as transgene on Chromosome II
Genetic reagent (D. melanogaster)	hunchback P2 enhancer	Garcia et al., 2013, Current Biology		Fly line with MS2 expression driven by hb P2 enhancer on chromosome II
Software, algorithm	mRNADynamics	Garcia et al., 2013, Current Biology		MATLAB pipeline for tracking and analysing MS2 transcriptional spots

Generation of transgenic reporter fly lines

Request a detailed protocol

The single, duplicated, or shadow enhancers were each cloned into the pBphi vector, upstream of the Kruppel promoter, 24 MS2 repeats, and a yellow reporter gene as in Fukaya et al., 2016. We defined the proximal enhancer as chromosome 2R:25224832–25226417, the distal enhancer as chromosome 2R:25222618–25223777, and the promoter as chromosome 2R:25226611–25226951, using the Drosophila melanogaster dm6 release coordinates. The precise sequences for each reporter construct are given in Supplementary file 4. For the allele correlation experiments, each enhancer was cloned 192 bp upstream of the Kr promoter, separated by the endogenous sequence found between the proximal enhancer and the promoter. For transcriptional noise experiments, the distal enhancer was placed at its endogenous spacing, 2835 bp upstream of the promoter, and the proximal enhancer sequence was replaced by a region of the lambda genome that is predicted to have few relevant TF-binding sites. In the shadow enhancer pair or duplicated enhancer constructs, the two enhancers were separated by the sequence separating the proximal and distal enhancers in the endogenous locus.

Using phiC31-mediated integration, each reporter construct was integrated into the same site on the second chromosomes by injection into yw; PBac{y[+]-attP-3B}VK00002 (BDRC stock #9723) embryos by BestGene Inc (Chino Hills, CA). To produce embryos with biallelic expression of the MS2 reporter, female flies expressing RFP-tagged histones and GFP-tagged MCP (yw; His-RFP/Cyo; MCP-GFP/TM3.Sb) were crossed with males containing one of the enhancer-MS2 reporter constructs. Virgin female F1 offspring were then mated with males of the same parental genotype, except in the case of shadow heterozygous flies, which were mated with males containing the other single enhancer-MS2 reporter.

Sample preparation and image acquisition

Request a detailed protocol

Live embryos were collected prior to nc14, dechorionated, mounted on a permeable membrane, immersed in Halocarbon 27 oil, and put under a glass coverslip as in Garcia et al., 2013. Individual embryos were then imaged on a Nikon A1R point scanning confocal microscope using a 60X/1.4 N.A. oil immersion objective and laser settings of 40uW for 488 nm and 35uW for 561 nm. To track transcription, 21 slice Z-stacks, at 0.5 um steps, were taken throughout the length of nc14 at roughly 30 s intervals. To identify the Z-stack’s position in the embryo, the whole embryo was imaged after the end of nc14 at 20x using the same laser power settings. Later in the analysis, each transcriptional spot’s location is described as falling into one of 42 anterior-posterior (AP) bins, with the first bin at the anterior of the embryo. Unless otherwise indicated, embryos were imaged at ambient temperature, which was on average 26.5°C. To image at other temperatures, embryos were either heated or cooled using the Bioscience Tools (Highland, CA) heating-cooling stage and accompanying water-cooling unit.

Burst calling and calculation of transcription parameters

Request a detailed protocol

Tracking of nuclei and transcriptional spots was done using the image analysis Matlab pipeline described in Garcia et al., 2013. For every spot of transcription imaged, background fluorescence at each time point is estimated as the offset of fitting the 2D maximum projection of the Z-stack image centered around the transcriptional spot to a gaussian curve, using Matlab lsqnonlin. This background estimate is subtracted from the raw spot fluorescence intensity. The resulting fluorescence traces across the time of nc14 are then subject to smoothing by the LOWESS method with a span of 10%. The smoothed traces were used to measure transcriptional parameters and noise. Traces consisting of fewer than three time frames were removed from calculations. To calculate transcription parameters, we used the smoothed traces to determine if the promoter was active or inactive at each time point. A promoter was called active if the slope of its trace (change in fluorescence) between one point and the next was greater than or equal to the instantaneous fluorescence value calculated for one mRNA molecule (F_RNAP, described below). Once called active, the promoter is considered active until the slope of the fluorescence trace becomes less than or equal to the negative instantaneous fluorescence value of one mRNA molecule, at which point it is called inactive until another active point is reached. The instantaneous fluorescence of a single mRNA was chosen as the threshold because we reasoned that an increase in fluorescence greater than or equal to that of a single transcript is indicative of an actively producing promoter, while a decrease in fluorescence greater than that associated with a single transcript indicates transcripts are primarily dissociating from, not being produced from, this locus. Visual inspection of fluorescence traces agreed well with the burst calling produced by this method (Figure 2—figure supplement 3).

Using these traces and promoter states, we measured burst size, frequency and duration. Burst size is defined as the integrated area under the curve of each transcriptional burst, from one ‘ON’ frame to the next ‘ON’ frame, with the value of 0 set to the floor of the background-subtracted florescence trace (Figure 2—figure supplement 3 panel C). Duration is defined as the amount of time occurring between the frame a promoter is determined active and the frame it is next determined inactive (Figure 2—figure supplement 3 panel F). Frequency is defined as the number of bursts occurring in the period of time from the first time the promoter is called active until 50 min into nc14 or the movie ends, whichever is first (Figure 2—figure supplement 3 panel E). The time of first activity was used for frequency calculations because the different enhancer constructs showed different characteristic times to first transcriptional burst during nc14. For these, and all other measurements, we control for the embryo position of the transcription trace by first individually analyzing the trace and then using all the traces in each AP bin (anterior-posterior; the embryo is divided into 41 bins each containing 2.5% of the embryo’s length) to calculate summary statistics of the transcriptional dynamics and noise values at that AP position.

All Matlab codes used for burst calling, noise measurements, and other image processing are available at the Wunderlich Lab GitHub (Waymack, 2020; copy archived at https://github.com/elifesciences-publications/KrShadowEnhancerCode).

Simultaneous tracking of Bcd-GFP and enhancer activity

Request a detailed protocol

To compare the sensitivity of the activity of the shadow pair and distal enhancer to Bcd levels, we tracked the fluorescence of Bcd-GFP and MCP-mCherry in individual nuclei across the time of nc14. To obtain embryos for simultaneous tracking, we crossed female flies heterozygous for Bcd-GFP and MCP-mcherry with male flies homozygous for either the shadow pair or distal enhancer reporter. Bcd-GFP and MCP-mCherry are maternally deposited and thereby allow us to measure levels of Bcd and enhancer activity in individual nuclei of the resulting embryos. Embryo collection and preparation was performed as described above. The same microscope, objective, and Z-step profile were used as described above, but laser settings were switched to 40uW for 561 nm and 35uW for 488 nm. Analysis of transcriptional activity was performed as described above. Time traces of Bcd-GFP levels in individual nuclei were subjected to background correction by subtracting the average fluorescence of the regions of the image not containing a nucleus at each time point from the raw Bcd-GFP fluorescence. The resulting Bcd-GFP time traces were then subjected to smoothing by the MATLAB smooth function, using the LOWESS method with a span of 10%. To measure the sensitivity of enhancer activity to Bcd levels, we correlated the slope of MS2 traces to the corresponding Bcd-GFP levels in the same nucleus. Slope was calculated between the MS2 values at consecutive time points and compared to the Bcd-GFP value at the earlier of the two time points. This process was done for all time points through 50 min into nc14.

Conversion of integrated fluorescence to mRNA molecules

Request a detailed protocol

To put our results in physiologically relevant units, we calibrated our fluorescence measurements in terms of mRNA molecules. As in Lammers et al., 2018, for our microscope, we determined a calibration factor, α, between our MS2 signal integrated over nc13, F_MS2, and the number of mRNAs generated by a single allele from the same reporter construct in the same time interval, N_FISH, using the hunchback P2 enhancer reporter construct (Garcia et al., 2013). Using this conversion factor, we can calculate the integrated fluorescence of a single mRNA (F₁) as well as the instantaneous fluorescence of an mRNA molecule (F_RNAP). With our microscope, F_RNAP is 379 AU/RNAP and F₁ is 1338 AU/RNAP∙min. With these values, we are able to convert both integrated and instantaneous fluorescence into total mRNAs produced and number of nascent mRNAs present at a single time point, by dividing by F₁ and F_RNAP, respectively.

Calculation of noise metrics

Request a detailed protocol

To calculate the temporal CV each transcriptional spot i, we used the formula:

C V (i) = \frac{s t a n d a r d d e v i a t i o n (m_{i} (t))}{m e a n (m_{i} (t))}

where m_i(t) is the fluorescence of spot i at time t.

We also decomposed the total noise experienced in each nucleus to inter-allele noise and co-variance, analogous to the approach of Elowitz et al., 2002.

Inter-allele noise is calculated one nucleus at a time. It is the mean square difference between the fluorescence of the two alleles in a single nucleus:

η_{I A}^{2} = \frac{⟨ {(m_{1} (t) - m_{2} (t))}^{2} ⟩}{2 ⟨ m_{1} (t) ⟩ ⟨ m_{2} (t) ⟩}

where m₁(t) is the fluorescence of one allele in the nucleus at time t, and m₂(t) is the fluorescence of the other allele in the same nucleus and the angled brackets indicate the mean across the time of nc14.

Covariance is the covariance of the activity of the two alleles in the same nucleus across the time of nc14:

η_{C V}^{2} = \frac{⟨ m_{1} (t) m_{2} (t) ⟩ - ⟨ m_{1} (t) ⟩ ⟨ m_{2} (t) ⟩}{⟨ m_{1} (t) ⟩ ⟨ m_{2} (t) ⟩}

The inter-allele and covariance values are defined such that they sum to give the total transcriptional noise displayed by the two alleles in a single nucleus.

η_{t o t}^{2} = \frac{⟨ {m_{1} (t)}^{2} {{+ m}_{2} (t)}^{2} ⟩ - 2 ⟨ m_{1} (t) ⟩ ⟨ m_{2} (t) ⟩}{2 ⟨ m_{1} (t) ⟩ ⟨ m_{2} (t) ⟩}

This total noise value is equal to the coefficient of variation of the expression of the two alleles in a single nucleus across the time of nc14.

Statistical methods

Request a detailed protocol

To determine any significant differences in total noise, covariance, or inter-allele noise values between the different enhancer constructs, we performed Kruskal-Wallis tests with the Bonferroni multiple comparison correction.

Description of the single enhancer model and associated parameters

Request a detailed protocol

We constructed a model of enhancer-driven transcription based on the following chemical reaction network:

T + E ⇌_{k_{o f f}}^{k_{o n}} C \overset{r}{\to} C + R

\begin{array}{ll} \emptyset \overset{β_{1}}{\to} n T \\ T \overset{β_{- 1}}{\to} \emptyset \\ R \overset{α}{\to} \emptyset \end{array}

where E is an enhancer that interacts with a transcription factor T, which together bind to the promoter at a rate k_on to form the active promoter-enhancer complex C. When the promoter is in this active form, it leads to the production of mRNA denoted by R, which degrades by diffusion from the gene locus at a rate α. Transcription is interrupted whenever the complex C disassociates spontaneously at a rate k_off. In the bursting TFs model, the transcription factor T appears at a rate β₁ and degrades at a rate β₋₁. To recapitulate Kruppel expression patterns, the value of β₁ was assumed to be given by

f (x) = c \frac{1}{\sqrt{2 π σ^{2}}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}},

where x is the percentage along the length of the egg and c is a scaling constant. Since Kruppel activity peaks near the center of the egg, we chose µ = 50, while c and σ were fitted along with the other parameters. Lastly, n was assumed to be fixed across the length of the egg.

We also generated a constant TF model, which is an adaptation of the model in Bothma et al., 2015. This model implicitly assumes that TF numbers are constant and, therefore, are incorporated into the value of k_on as described by the reactions

E ⇌_{k_{o f f}}^{T k_{o n}} C \overset{r}{\to} C + R

R \overset{α}{\to} \emptyset

In this case, the value for T was fitted for each bin in a similar way to β₁, that is the constant number of TFs was assumed to be described by Equation (1) (values were rounded to the nearest integer).

To simulate the transcriptional traces, we implemented a stochastic approach. Individual chemical events such as enhancer-promoter looping take place at random times and are influenced by transcription factor numbers. Individual trajectories of chemical species over time were calculated using the Gillespie algorithm (Gillespie, 1976), and these trajectories are comparable to the experimentally measured transcriptional traces. Since the enhancer is either bound or not bound to the promoter, we imposed the constraint that C + E = 1 when simulating model dynamics.

Estimation of model parameters from experimental data

Request a detailed protocol

To yield a starting estimate for the k_on and k_off parameters, we defined the start and end of a burst as the time when the reactions $E \to C$ and $C \to E$ occur, respectively. The length of the ith burst was defined as the range of [b_i,p_i] where b_i corresponds to the time of the i^th instance of the reaction $E \to C$ and p_i to the time of the i^th instance of the reaction $C \to E$ . The time between the i^th burst and the i + 1^th burst is [p_i,b_i₊₁]. The Gillespie algorithm dictates that the time spent in any given state is determined by an exponentially distributed random variable with a rate parameter equal to the product of two parts: the sum of rate constants of the outgoing reactions, and the number of possible reactions. If the enhancer is either bound or unbound, we have that C = 1 or E = 1, respectively. Therefore, by letting t_b be the average time between bursts and t_d be the average duration of a burst, we can write

t_{b} = \underset{M \to \infty}{l i m} \frac{1}{M} \sum_{j = 1}^{M} (\frac{1}{N - 1} \sum_{i = 1}^{N - 1} (b_{{i + 1}_{j}} - p_{i_{j}})) = \frac{1}{k_{o n} E T} \approx \frac{1}{k_{o n}}

and

t_{d} = \underset{M \to \infty}{l i m} \frac{1}{M} \sum_{j = 1}^{M} (\frac{1}{N} \sum_{i = 1}^{N} (p_{i_{j}} - b_{i_{j}})) = \frac{1}{k_{o f f} C} = \frac{1}{k_{o f f}}

where N is the number of bursts for spot j, b_ij and p_ij denote the beginning and end of burst i in spot j respectively, and M denotes the total number of spots in the egg. The right-hand sides are given by the expected value of the exponential distribution and the assumption that, on average, T is close to 1. While this may not be the case for T, the assumption provides a convenient upper bound for the average time between bursts, which is likely not to have a much smaller value for a lower bound. (A low enough value of t_b would imply nearly constant fluorescence intensity instead of bursts.) Finally, the average duration of a burst t_d can be calculated directly from the data and used to obtain k_off by calculating 1/t_d. Similarly, the average time between bursts t_b is readily available from the data giving us k_on ≈ 1/t_b.

We were able to directly estimate mRNA production and degradation rates from the experimental data. To estimate α, we focused on periods of mRNA decay; that is periods where no active transcription is taking place and are thus described by

R^{'} = - α R,

which in turn can be solved to be

R = c e^{- t α},

where c is a constant of integration. Taking the derivative of Equation 2 yields

R^{'} (t) = - α c e^{- t α},

which corresponds to the slope of the decaying burst. We define the interval of decay of the i^th burst as [p_i,b_i₊₁]. For some point t₀ ∈ (p_i,b_i₊₁), let $R_{0} = R (t_{0}) = c e^{- t_{0} α}$ . Solving this expression for c gives that $c = R_{0} e^{t_{0} α}$ . Substituting for c in Equation 3 evaluated at t₀ results in $R^{'} (t_{0}) = - α R_{0} e^{t_{0} α} e^{- t_{0} α} = - α R_{0}$ . Then, it follows that

α = - \frac{R^{'} (t_{0})}{R_{0}} .

In other words, the rate of decay of mRNA fluorescence can be calculated from any trace by taking the ratio of the slope during burst decay and its intensity at a given time t₀ ∈ (p_i,b_i₊₁).

Adjacent measurements of fluorescence intensity from the single enhancer systems were used to approximate the slope at each point in the traces. Then, Equation 4 was applied to each point. A histogram of all calculated values was generated (Figure 2—figure supplement 4). In this figure, there was a clear peak, which provided us with an estimate of α ≈ 1.95.

The estimation of r was done for periods of active transcription, which are also accompanied by simultaneous mRNA decay. By noting that C = 1 during mRNA transcription, we can approximate these periods as the zeroth order process

\emptyset ⇌_{α}^{r} R

The differential equation associated with this system is given by

R^{'} = r - α R,

and has steady state R^∗=r/α. Equation 5 can be solved explicitly for R by choosing

R (t) = \frac{r}{α} + c e^{- t α},

where c is a constant of integration. For two adjacent measurements at times t₁ and t₂ we can write their respective measured amounts of mRNA as

R_{1} = \frac{r}{α} + c_{1} e^{- t_{1} α},

and

R_{2} = \frac{r}{α} + c_{2} e^{- t_{2} α},

Solving for c₁ and c₂ gives

\begin{array}{ll} c_{1} = (R_{1} - \frac{r}{α}) e^{t_{1} α} \\ c_{2} = (R_{2} - \frac{r}{α}) e^{t_{2} α} . \end{array}

The short-term fluctuations of mRNA from R₁ to R₂ between two adjacent discrete time points in the stochastic system can be approximated by Equations 6 and 7. This implies that

(R_{1} - \frac{r}{α}) e^{t_{1} α} = (R_{2} - \frac{r}{α}) e^{t_{2} α},

which in turn gives

r = α \frac{R_{1} - R_{2} e^{α Δ t}}{1 - e^{α Δ t}} .

Therefore, the estimation of r can be computed given two adjacent measurements of fluorescence and the time between them. Finally, we used a similar approach as done with α to calculate values of r from fluorescence data. However, unlike α, r was calculated for each bin to account for differences in transcriptional efficiency across the length of the embryo.

Parameter fitting with simulated annealing

Request a detailed protocol

Simulations and parameter fitting were done with MATLAB. Optimization in fitting was done by minimizing the sum of squared errors (SSE) between the normalized vectors of burst properties and allele correlations of the experimental and simulated data. In particular, a vector y of experimental data was created by concatenating the following vectors: burst size, integrated fluorescence, frequency, duration, and allele correlation across the length of the embryo. The vector y was subsequently normalized by dividing each burst property by the largest element in their respective vectors (except correlation which by definition is unitless between −1 and 1). A vector x was created in an analogous fashion to y but using simulated instead of experimental data. However, x was normalized using the same elements that were used to normalize y. Then, the discrepancy between the experimental and simulated data was measured by:

S S E = \sum_{i = 1}^{n} {(y_{i} - x_{i})}^{2}

We used a high-performance computing cluster to compute 200 independent runs of parameter fitting with simulated annealing for each model variant. The algorithm requires an initial guess of the parameter set P₀, an initial temperature Γ₀, a final temperature Γ’, the number of iterations per temperature N, and a cooling factor µ. Then, each iteration is as follows:

If the current iteration i is such that i > N, then update the current temperature Γ_k = µ^kΓ₀ to µ^k⁺¹Γ₀ and set i = 0. Otherwise, set i to i + 1.
Check if Γ_k < Γ’. If so, return the current parameter set P_j and terminate.
Choose a parameter randomly from P_j and multiply it by a value sampled from a normal distribution with a mean equal to 1. The standard deviation of such distribution should be continuously updated to be Γ_k. The result of this step is the newly generated parameter set P_j₊₁.
Calculate ∆E as the difference in SSE between the data generated by P_j and that generated by P_j₊₁. Update P_j to P_j₊₁ if ∆E < 0 or with probability p<e^∆^E/^Γk where p is a uniformly distributed random number.
Repeat all steps until termination.

To generate our results, we chose Γ₀ = 1, Γ’ = Γ₀/10, N = 30, and µ = 0.8. We observed an improvement in the quality of the fittings by using analysis-derived parameter values as initial guesses instead of values given through random sampling. The sampled space ranged from 10⁻³ to 10³ for all parameters, except n, which was sampled from 10⁰ to 10², and σ, which was randomly chosen to be an integer between 1 and 20. Equal numbers of parameter values were sampled at each order of magnitude. The analysis in the section above was used to estimate the parameters in P₀. Parameters that were not estimated in the previous section were given the following initial guesses: n = 10, β₋₁ = 1, σ = 6, and c = 40. Initial guesses for c and σ were based on the experimental observation that there is little transcription outside of 20–80% egg length. Based on this observation, simulations were limited to this egg length range, as well. For the constant TFs model, both analysis-derived and random initial parameter values were used to maximize the likelihood of finding any parameter set capable of recapitulating the observed allele correlation.

Generation of simulated experimental data

Request a detailed protocol

Parameter sets resulting from fitting were sorted in ascending order based on their sum of squared errors, and the 10 lowest error parameter sets are what we called the 10 best parameter sets. For all figures, we simulated 80 spots per bin and simulated each bin five times to generate error bars. Data for the distal enhancer at the proximal location was used to reproduce simulated allele correlations in all cases.

Gillespie simulations update the counts of each chemical species at random time intervals. However, for ease of parameter fitting and to better recapitulate the experiments, we generated data in two distinct timescales: one consisting of 30 second intervals after which mRNA counts were recorded, and another consisting of random time intervals generated by the algorithm after which chemical counts were updated. The former one was used for all parameter fitting rounds and generation of figures.

Description of two enhancer model, parameter estimation, and fitting

Request a detailed protocol

To explore two enhancer systems, we expanded our previous model to include an additional enhancer. First, we considered duplicated enhancer systems, which consist of either two proximal or two distal enhancers. Enhancers were denoted by E₁ and E₂, which correspond to two identical enhancers that exist in different locations relative to the promoter. They are activated by the same transcription factors as described by the reactions

\begin{array}{ll} T + E_{1} ⇌_{k_{o f f_{1}}}^{k_{o n_{1}}} C_{1} \overset{r_{1}}{\to} C_{1} + R \\ T + E_{2} ⇌_{k_{o f f_{2}}}^{k_{o n_{2}}} C_{2} \overset{r_{2}}{\to} C_{2} + R \end{array}

\begin{array}{ll} \emptyset \overset{β_{1}}{\to} n T \\ T \overset{β_{- 1}}{\to} \emptyset \\ R \overset{α}{\to} \emptyset \end{array}

Without loss of generality, we used E₁ to denote the enhancer at the proximal location and E₂ to denote the enhancer at the distal location. This model describes independent enhancer dynamics; that is the behavior of one enhancer does not affect the behavior of the other, and, as such, both enhancers can be simultaneously looped to the promoter. Consequently, to account for potential enhancer interference or competition for the promoter, we assumed distinct k_on and k_off values for each enhancer in the duplicated enhancer constructs. We also used distinct values of r for each distal enhancer in the duplicated distal construct since fluorescence data was available for this enhancer at the proximal and endogenous location. For proximal enhancers, we assume r₁ = r₂.

To describe the dynamics of the shadow enhancer pair, we denoted the activators for E₁ (the proximal enhancer) and E₂ (the distal enhancer) by T₁ and T₂, respectively:

\begin{array}{ll} T_{1} + E_{1} ⇌_{k_{o f f_{1}}}^{k_{o n_{1}}} C_{1} \overset{r_{1}}{\to} C_{1} + R \\ T_{2} + E_{2} ⇌_{k_{o f f_{2}}}^{k_{o n_{2}}} C_{2} \overset{r_{2}}{\to} C_{2} + R \end{array}

\begin{array}{ll} \emptyset \overset{β_{1}}{\to} n_{1} T_{1} \\ \emptyset \overset{γ_{1}}{\to} n_{2} T_{2} \\ T_{1} \overset{β_{- 1}}{\to} \emptyset \\ T_{2} \overset{γ_{- 1}}{\to} \emptyset \\ R \overset{α}{\to} \emptyset \end{array}

The production rate of T₂, γ₁, was calculated in the same way as production rate of T₁, β₁, but differed in the values of c and σ. The two enhancer models were also used to calculate allele correlation between homozygotes and heterozygotes because a distinction between the mRNA produced by C₁ and C₂ was made. This approach works because, for example when considering the homozygote embryos, each single enhancer resides in the same nucleus and is therefore affected by the same fluctuating TF numbers. In the duplicated enhancer model, each enhancer E₁ or E₂ is affected by the same fluctuations in the number of transcription factor T. An analogous logic applies to the heterozygotes.

To fit the two enhancer models to experimental data, we retained several parameters from the single enhancer models. Parameters r and α were directly calculated from the data, and, as such, did not vary across models. We assume that parameters concerning transcription factors (β₁, β₋₁, γ₁, γ₋₁, n₁, and n₂) are not affected by the presence of an additional enhancer. Therefore, in our model, only k_on and k_off are free to change. To fit the values of k_on1, k_on2, k_off1, and k_off2, we set the other model parameters to the median values of the 10 best parameter sets in the respective single enhancer model. We then used a similar simulating annealing approach to fit the k_on and k_off values. We used the resulting values to simulate transcriptional traces and to calculate the predicted CV values shown in Figure 5.

Theoretical modeling of inter-allele noise

Request a detailed protocol

To make a prediction about the expected change in inter-allele noise between single and two enhancer reporter constructs, we used the theory put forth in Sánchez and Kondev, 2008; Sanchez et al., 2011. This formalism can be used to calculate the expected mean and variance of the transcriptional output of a promoter, given the possible states of the promoter, transition rates between states, and the rate of transcription resulting from each state. In these papers, the authors apply their formalism to different promoter architectures. Here, we generate a simpler model, in which we abstract away the individual transcription factor (TF) binding configurations, which would be numerous and poorly parametrized, and simply define states by whether an enhancer is looped to the promoter and activating transcription. Since these models do not account for fluctuations that would contribute to extrinsic noise, for example fluctuations in TF or RNA polymerase levels, they can predict the dependence of intrinsic noise on enhancer arrangement.

To apply this model to our system, we used these parameters: γ, degradation rate of mRNA; p, production rate of mRNA; k, on rate for enhancer-promoter looping; l, off rate for enhancer-promoter looping. We generated five models that represent different configurations of either one or two enhancers controlling a single promoter. Key assumptions are that the parameters describing this system are independent of both the position of the enhancer relative to the promoter and the presence of a second enhancer controlling the same promoter. In Model 1, there is a single enhancer controlling one promoter. There are two states, when the enhancer and promoter are not looped (mRNA production rate of 0), and when the enhancer and promoter are looped (mRNA production rate of p). In Model 2 (OR model), there are two enhancers controlling one promoter, transcription is activated if either enhancer is looped, and both enhancers can’t be bound at the same time. In Model 3 (additive model), there are two enhancers controlling one promoter, transcription is activated if either enhancer is looped, and, if both enhancers are bound, transcription occurs at twice the rate of single enhancer looping states. In Model 4 (synergistic model), there are two enhancers controlling one promoter, transcription is activated if either enhancer is looped, and, if both enhancers are bound, transcription occurs at three times the rate of single enhancer looping states. In Model 5 (XOR model), there are two enhancers controlling one promoter, transcription is activated if either enhancer is looped, and, if both enhancers are bound, no transcription occurs. Results of these models are shown in Figure 6—figure supplement 2.

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files. Code for analyzing the transcriptional traces and for creating the computational models is available on GitHub: https://github.com/WunderlichLab/KrShadowEnhancerCode (copy archived at https://github.com/elifesciences-publications/KrShadowEnhancerCode).

References

1. Arias AM
2. Hayward P
(2006) Filtering transcriptional noise during development: concepts and mechanisms
Nature Reviews Genetics 7:34–44.
https://doi.org/10.1038/nrg1750
- PubMed
- Google Scholar
1. Barolo S
(2012) Shadow enhancers: frequently asked questions about distributed cis-regulatory information and enhancer redundancy
BioEssays 34:135–141.
https://doi.org/10.1002/bies.201100121
- PubMed
- Google Scholar
1. Bertrand E
2. Chartrand P
3. Schaefer M
4. Shenoy SM
5. Singer RH
6. Long RM
(1998) Localization of ASH1 mRNA particles in living yeast
Molecular Cell 2:437–445.
https://doi.org/10.1016/S1097-2765(00)80143-4
- Google Scholar
1. Blake WJ
2. KAErn M
3. Cantor CR
4. Collins JJ
(2003) Noise in eukaryotic gene expression
Nature 422:633–637.
https://doi.org/10.1038/nature01546
- PubMed
- Google Scholar
(1999) Redundant Enhancers Mediate Transcriptional Repression of AGAMOUS by APETALA2
Developmental Biology 216:260–264.
https://doi.org/10.1006/dbio.1999.9504
- Google Scholar
1. Bothma JP
2. Garcia HG
3. Esposito E
4. Schlissel G
5. Gregor T
6. Levine M
(2014) Dynamic regulation of eve stripe 2 expression reveals transcriptional bursts in living Drosophila embryos
PNAS 111:10598–10603.
https://doi.org/10.1073/pnas.1410022111
- PubMed
- Google Scholar
1. Bothma JP
2. Garcia HG
3. Ng S
4. Perry MW
5. Gregor T
6. Levine M
(2015) Enhancer additivity and non-additivity are determined by enhancer strength in the Drosophila embryo
eLife 4:e07956.
https://doi.org/10.7554/eLife.07956
- Google Scholar
(2018) LlamaTags: a versatile tool to image transcription factor dynamics in live embryos
Cell 173:1810–1822.
https://doi.org/10.1016/j.cell.2018.03.069
- PubMed
- Google Scholar
1. Cannavò E
2. Khoueiry P
3. Garfield DA
4. Geeleher P
5. Zichner T
6. Gustafson EH
7. Ciglar L
8. Korbel JO
9. Furlong EE
(2016) Shadow enhancers are pervasive features of developmental regulatory networks
Current Biology 26:38–51.
https://doi.org/10.1016/j.cub.2015.11.034
- PubMed
- Google Scholar
(2015) Temperature stress mediates decanalization and dominance of gene expression in Drosophila melanogaster
PLOS Genetics 11:e1004883.
https://doi.org/10.1371/journal.pgen.1004883
- PubMed
- Google Scholar
1. Cheung D
2. Ma J
(2015) Probing the impact of temperature on molecular events in a developmental system
Scientific Reports 5:13124.
https://doi.org/10.1038/srep13124
- PubMed
- Google Scholar
1. Chubb JR
2. Trcek T
3. Shenoy SM
4. Singer RH
(2006) Transcriptional pulsing of a developmental gene
Current Biology 16:1018–1025.
https://doi.org/10.1016/j.cub.2006.03.092
- PubMed
- Google Scholar
1. Csárdi G
2. Franks A
3. Choi DS
4. Airoldi EM
5. Drummond DA
(2015) Accounting for experimental noise reveals that mRNA levels, amplified by post-transcriptional processes, largely determine steady-state protein levels in yeast
PLOS Genetics 11:e1005206.
https://doi.org/10.1371/journal.pgen.1005206
- PubMed
- Google Scholar
1. Dar RD
2. Razooky BS
3. Singh A
4. Trimeloni TV
5. McCollum JM
6. Cox CD
7. Simpson ML
8. Weinberger LS
(2012) Transcriptional burst frequency and burst size are equally modulated across the human genome
PNAS 109:17454–17459.
https://doi.org/10.1073/pnas.1213530109
- PubMed
- Google Scholar
1. Dar RD
2. Shaffer SM
3. Singh A
4. Razooky BS
5. Simpson ML
6. Raj A
7. Weinberger LS
(2016) Transcriptional bursting explains the Noise-Versus-Mean relationship in mRNA and protein levels
PLOS ONE 11:e0158298.
https://doi.org/10.1371/journal.pone.0158298
- PubMed
- Google Scholar
(2013) Accurate measurements of dynamics and reproducibility in small genetic networks
Molecular Systems Biology 9:639.
https://doi.org/10.1038/msb.2012.72
- PubMed
- Google Scholar
(2011) Complex interactions between cis-regulatory modules in native conformation are critical for Drosophila snail expression
Development 138:4566.
https://doi.org/10.1242/dev.074377
- Google Scholar
(2019) Coacting enhancers can have complementary functions within gene regulatory networks and promote canalization
PLOS Genetics 15:e1008525.
https://doi.org/10.1371/journal.pgen.1008525
- PubMed
- Google Scholar
1. El-Sherif E
2. Levine M
(2016) Shadow enhancers mediate dynamic shifts of gap gene expression in the Drosophila Embryo
Current Biology 26:1164–1169.
https://doi.org/10.1016/j.cub.2016.02.054
- PubMed
- Google Scholar
(2002) Stochastic gene expression in a single cell
Science 297:1183–1186.
https://doi.org/10.1126/science.1070919
- PubMed
- Google Scholar
(2009) Role of spatial averaging in the precision of gene expression patterns
Physical Review Letters 103:258101.
https://doi.org/10.1103/PhysRevLett.103.258101
- PubMed
- Google Scholar
1. Frankel N
2. Davis GK
3. Vargas D
4. Wang S
5. Payre F
6. Stern DL
(2010) Phenotypic robustness conferred by apparently redundant transcriptional enhancers
Nature 466:490–493.
https://doi.org/10.1038/nature09158
- PubMed
- Google Scholar
1. Fukaya T
2. Lim B
3. Levine M
(2016) Enhancer control of transcriptional bursting
Cell 166:358–368.
https://doi.org/10.1016/j.cell.2016.05.025
- PubMed
- Google Scholar
1. Fukaya T
2. Levine M
(2017) Transvection
Current Biology 27:R1047–R1049.
https://doi.org/10.1016/j.cub.2017.08.001
- PubMed
- Google Scholar
1. Garcia HG
2. Tikhonov M
3. Lin A
4. Gregor T
(2013) Quantitative imaging of transcription in living Drosophila embryos links polymerase activity to patterning
Current Biology 23:2140–2145.
https://doi.org/10.1016/j.cub.2013.08.054
- PubMed
- Google Scholar
(2012) BMP, wnt and FGF signals are integrated through evolutionarily conserved enhancers to achieve robust expression of Pax3 and zic genes at the zebrafish neural plate border
Development 139:4220–4231.
https://doi.org/10.1242/dev.081497
- PubMed
- Google Scholar
(2011) Deletion of a remote enhancer near ATOH7 disrupts retinal neurogenesis, causing NCRNA disease
Nature Neuroscience 14:578–586.
https://doi.org/10.1038/nn.2798
- PubMed
- Google Scholar
1. Gillespie DT
(1976) A general method for numerically simulating the stochastic time evolution of coupled chemical reactions
Journal of Computational Physics 22:403–434.
https://doi.org/10.1016/0021-9991(76)90041-3
- Google Scholar
(2007) Probing the limits to positional information
Cell 130:153–164.
https://doi.org/10.1016/j.cell.2007.05.025
- PubMed
- Google Scholar
(2018) Cytoplasmic amplification of transcriptional noise generates substantial Cell-to-Cell variability
Cell Systems 7:384–397.
https://doi.org/10.1016/j.cels.2018.08.002
- PubMed
- Google Scholar
1. He F
2. Wen Y
3. Deng J
4. Lin X
5. Lu LJ
6. Jiao R
7. Ma J
(2008) Probing intrinsic properties of a robust morphogen gradient in Drosophila
Developmental Cell 15:558–567.
https://doi.org/10.1016/j.devcel.2008.09.004
- PubMed
- Google Scholar
(1990) cis-acting control elements for krüppel expression in the Drosophila embryo
The EMBO Journal 9:2587–2595.
https://doi.org/10.1002/j.1460-2075.1990.tb07440.x
- PubMed
- Google Scholar
(2008) Shadow enhancers as a source of evolutionary novelty
Science 321:1314.
https://doi.org/10.1126/science.1160631
- PubMed
- Google Scholar
1. Jaeger J
2. Blagov M
3. Kosman D
4. Kozlov KN
5. Manu
6. Myasnikova E
7. Surkova S
8. Vanario-Alonso CE
9. Samsonova M
10. Sharp DH
11. Reinitz J
(2004) Dynamical analysis of regulatory interactions in the gap gene system of Drosophila melanogaster
Genetics 167:1721–1737.
https://doi.org/10.1534/genetics.104.027334
- PubMed
- Google Scholar
(2000) Specific gain- and loss-of-function phenotypes induced by satellite-specific DNA-binding drugs fed to Drosophila melanogaster
Molecular Cell 6:1013–1024.
https://doi.org/10.1016/S1097-2765(00)00100-3
- PubMed
- Google Scholar
1. Laboulaye MA
2. Duan X
3. Qiao M
4. Whitney IE
5. Sanes JR
(2018) Mapping transgene insertion sites reveals complex interactions between mouse transgenes and neighboring endogenous genes
Frontiers in Molecular Neuroscience 11:385.
https://doi.org/10.3389/fnmol.2018.00385
- PubMed
- Google Scholar
(2012) Mechanisms of transcriptional precision in animal development
Trends in Genetics 28:409–416.
https://doi.org/10.1016/j.tig.2012.03.006
- PubMed
- Google Scholar
1. Lam DD
2. de Souza FS
3. Nasif S
4. Yamashita M
5. López-Leal R
6. Otero-Corchon V
7. Meece K
8. Sampath H
9. Mercer AJ
10. Wardlaw SL
11. Rubinstein M
12. Low MJ
(2015) Partially redundant enhancers cooperatively maintain mammalian pomc expression above a critical functional threshold
PLOS Genetics 11:e1004935.
https://doi.org/10.1371/journal.pgen.1004935
- PubMed
- Google Scholar
Preprint
(2018) Binary transcriptional control of pattern formation in development
bioRxiv.
https://doi.org/10.1101/335919
- Google Scholar
1. Lim B
2. Heist T
3. Levine M
4. Fukaya T
(2018) Visualization of transvection in living Drosophila Embryos
Molecular Cell 70:287–296.
https://doi.org/10.1016/j.molcel.2018.02.029
- PubMed
- Google Scholar
(2013) Precise developmental gene expression arises from globally stochastic transcriptional activity
Cell 154:789–800.
https://doi.org/10.1016/j.cell.2013.07.025
- PubMed
- Google Scholar
1. Liu X
2. Wu B
3. Szary J
4. Kofoed EM
5. Schaufele F
(2007) Functional sequestration of transcription factor activity by repetitive DNA
Journal of Biological Chemistry 282:20868–20876.
https://doi.org/10.1074/jbc.M702547200
- PubMed
- Google Scholar
(2013) Live imaging of bicoid-dependent transcription in Drosophila embryos
Current Biology 23:2135–2139.
https://doi.org/10.1016/j.cub.2013.08.053
- PubMed
- Google Scholar
1. McKnight SL
2. Miller OL
(1979) Post-replicative nonribosomal transcription units in D. melanogaster embryos
Cell 17:551–563.
https://doi.org/10.1016/0092-8674(79)90263-0
- PubMed
- Google Scholar
1. Mir M
2. Stadler MR
3. Ortiz SA
4. Hannon CE
5. Harrison MM
6. Darzacq X
7. Eisen MB
(2018) Dynamic multifactor hubs interact transiently with sites of active transcription in Drosophila embryos
eLife 7:e40497.
https://doi.org/10.7554/eLife.40497
- PubMed
- Google Scholar
1. Osterwalder M
2. Barozzi I
3. Tissières V
4. Fukuda-Yuzawa Y
5. Mannion BJ
6. Afzal SY
7. Lee EA
8. Zhu Y
9. Plajzer-Frick I
10. Pickle CS
11. Kato M
12. Garvin TH
13. Pham QT
14. Harrington AN
15. Akiyama JA
16. Afzal V
17. Lopez-Rios J
18. Dickel DE
19. Visel A
20. Pennacchio LA
(2018) Enhancer redundancy provides phenotypic robustness in mammalian development
Nature 554:239–243.
https://doi.org/10.1038/nature25461
- PubMed
- Google Scholar
(2010) Shadow enhancers foster robustness of Drosophila gastrulation
Current Biology 20:1562–1567.
https://doi.org/10.1016/j.cub.2010.07.043
- PubMed
- Google Scholar
(2011) Multiple enhancers ensure precision of gap gene-expression patterns in the Drosophila embryo
PNAS 108:13570–13575.
https://doi.org/10.1073/pnas.1109873108
- PubMed
- Google Scholar
1. Perry MW
2. Bothma JP
3. Luu RD
4. Levine M
(2012) Precision of hunchback expression in the Drosophila embryo
Current Biology 22:2247–2252.
https://doi.org/10.1016/j.cub.2012.09.051
- PubMed
- Google Scholar
(2018) Comprehensive analysis of a cis-Regulatory region reveals pleiotropy in enhancer function
Cell Reports 22:3021–3031.
https://doi.org/10.1016/j.celrep.2018.02.073
- PubMed
- Google Scholar
(1985) Molecular genetics of krüppel, a gene required for segmentation of the Drosophila embryo
Nature 313:27–32.
https://doi.org/10.1038/313027a0
- PubMed
- Google Scholar
(2010) Variability in gene expression underlies incomplete penetrance
Nature 463:913–918.
https://doi.org/10.1038/nature08781
- PubMed
- Google Scholar
1. Raser JM
2. O'Shea EK
(2005) Noise in gene expression: origins, consequences, and control
Science 309:2010–2013.
https://doi.org/10.1126/science.1105891
- PubMed
- Google Scholar
1. Sanchez A
2. Garcia HG
3. Jones D
4. Phillips R
5. Kondev J
(2011) Effect of promoter architecture on the cell-to-cell variability in gene expression
PLOS Computational Biology 7:e1001100.
https://doi.org/10.1371/journal.pcbi.1001100
- PubMed
- Google Scholar
1. Sanchez A
2. Golding I
(2013) Genetic determinants and cellular constraints in noisy gene expression
Science 342:1188–1193.
https://doi.org/10.1126/science.1242975
- PubMed
- Google Scholar
1. Sánchez A
2. Kondev J
(2008) Transcriptional control of noise in gene expression
PNAS 105:5081–5086.
https://doi.org/10.1073/pnas.0707904105
- PubMed
- Google Scholar
(2019) Signal integration by shadow enhancers and enhancer duplications varies across the Drosophila Embryo
Cell Reports 26:2407–2418.
https://doi.org/10.1016/j.celrep.2019.01.115
- PubMed
- Google Scholar
(2017) Uniform gene expression in embryos is achieved by temporal averaging of transcription noise
Genes & Development 31:1635–1640.
https://doi.org/10.1101/gad.302935.117
- PubMed
- Google Scholar
1. Thompson A
2. Gasson MJ
(2001) Location effects of a reporter gene on expression levels and on native protein synthesis in Lactococcus lactis and Saccharomyces cerevisiae
Applied and Environmental Microbiology 67:3434–3439.
https://doi.org/10.1128/AEM.67.8.3434-3439.2001
- PubMed
- Google Scholar
Software
1. Waymack R
(2020) KrShadowEnhancerCode, version 11d5630
GitHub.

https://github.com/WunderlichLab/KrShadowEnhancerCode
1. Wei L
2. Yuan Y
3. Hu T
4. Li S
5. Cheng T
6. Lei J
7. Xie Z
8. Zhang MQ
9. Wang X
(2019) Regulation by competition: a hidden layer of gene regulatory network
Quantitative Biology 7:110–121.
https://doi.org/10.1007/s40484-018-0162-5
- Google Scholar
(2015) Krüppel expression levels are maintained through compensatory evolution of shadow enhancers
Cell Reports 12:1740–1747.
https://doi.org/10.1016/j.celrep.2015.08.021
- PubMed
- Google Scholar
1. Yan J
2. Anderson C
3. Viets K
4. Tran S
5. Goldberg G
6. Small S
7. Johnston RJ
(2017) Regulatory logic driving stable levels of defective proventriculus expression during terminal photoreceptor specification in flies
Development 144:844–855.
https://doi.org/10.1242/dev.144030
- PubMed
- Google Scholar
(2008) Single-RNA counting reveals alternative modes of gene expression in yeast
Nature Structural & Molecular Biology 15:1263–1271.
https://doi.org/10.1038/nsmb.1514
- PubMed
- Google Scholar

Decision letter

Patricia J Wittkopp

Senior and Reviewing Editor; University of Michigan, United States
Justin Crocker

Reviewer; European Molecular Biology Laboratory, Germany

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This study uses creative approaches to examine sources of gene expression noise and the relationships among shadow enhancers in Drosophila embryos. A novel live imaging strategy is used to track expression of allele-specific expression that, combined with careful genetic analysis and manipulation of transcription factor levels, shows how the distinct regulation of different shadow enhancers reduces expression noise compared to identical copies of enhancers. Consequently, this work advances our understanding of how enhancers with largely overlapping functions interact and how variation in transcription factors relates to gene expression noise.

Decision letter after peer review:

Thank you for choosing to send your work, "Shadow enhancers suppress input transcription factor noise through distinct regulatory logic", for consideration at eLife.

All three reviewers found the premise of this work exciting and novel, with intriguing functional data. They also all appreciated the modeling work. However, they were also in unanimous agreement that additional experimental work is needed to elevate the impact of this work on the field to the level expected for publication in this particular journal. Because this work is expected to take longer than the typical 2 month revision timeline for eLife, I am rejecting this work, but encouraging resubmission of a version that addresses the issues raised. As one reviewer wrote during our discussion " It was frustrating to see great data, ideas, and analyses that were not critically tested." The reviewers' full comments are below.

The post-review discussion highlighted the following points as most critical:

1) Addressing the technical concerns raised in the reviews and clarifying methods. As one reviewer wrote "it's extremely hard to judge the quality of the current results (even in the Materials and methods)".

2) At a minimum, use smFISH to confirm the live imaging results/model predictions. Better would be to more directly measure fluctuations of input TFs (e.g., HaloTags or LlamaTags).

3) Functional data testing arguments emerging from the model. Specifically, analyzing enhancers with specific TF binding sites mutated/deleted and examining the impact of manipulating TFs were suggested as ways to further test the credibility of the conclusions presented.

Please note that we aim to publish articles with a single round of revision that would typically be accomplished within two months. This means that work that has potential, but in our judgment would need extensive additional work, will not be considered for in-depth review. We do not intend any criticism of the quality of the data or the rigor of the science. We wish you good luck with your work and we hope you will consider eLife for future submissions.

Reviewer #1:

In this manuscript, Waymack et al. investigate the control of transcriptional dynamics of the gap gene Kruppel in the Drosophila embryo via two independent shadow enhancers. I like the main experiment in Figure 1 and I think the results are clear. Measuring expression from two identical alleles shows higher correlation than when two different enhancers are used, suggesting A) the factors that provide input into each enhancer may be different, and B) that variations in local concentrations of upstream activators and repressors play a role in transcriptional activation/dynamics. All in one shot.

Presumably properties of the traces from each locus in the heterozygote could be used to predict whether expression from a particular site of transcription was driven by the proximal or distal enhancer. It might have been nice to use two different reporters (MS2 vs. PP7) to label the two alleles independently and unambiguously, but this would have required additional constructs and controls and I think the results should be basically the same. This is an elegant experiment using existing tools.

They go on to examine the amount of noise created by input transcription factor fluctuations using a largely modeling-based approach. This is one of the central claims of the paper, though the coefficient of variation is only very slightly improved. Though I'm not able to fully evaluate the model, the idea does make sense; if noise in activator A is independent from noise in activator B, under certain regimes one input and therefore output will remain accurate despite a certain amount of variability. It is nice to formalize this in a model and find it to be true at least some of the time. Importantly, results in Figure 3 begin to test their initial model and they find that identical pairs of enhancers together in the same construct do not buffer noise as well as a heterologous shadow enhancer pair. Doubling the number of enhancers does not reduce noise if the enhancers rely on the same inputs.

What I would have liked to see is additional experimental tests. 1) It would be great to know whether the upstream inputs do indeed differ, and if changing their contributions would modify the system in a predictable way based on the models. 2) It would be great to measure an upstream input directly and determine whether its fluctuations correlate with the observed output.

For 1): A main conclusion is that each enhancer has different inputs, which is suggested by the observed correlation between identical alleles but which breaks down comparing across alleles. Each enhancer is likely to share some inputs while others may vary; they are after all quite similar spatial patterns. These potential inputs are discussed only minimally and the authors do not attempt to test what they might be. Zld, Bcd, Hb, and Stat – all their predicted inputs – have nicely characterized binding sites. I would have liked to see a small number of constructs in which potential input factor binding sites have been mutagenized or added. This may reduce (or increase) expression levels or patterns, but the remaining pattern could be evaluated for dynamics and correlation. Zld binding sites, for instance, can often be removed without removing the pattern but with changes to expression dynamics. Or, Zld sites could be added to an enhancer missing them to make the enhancer pair more similar.

For 2): New methods are available to visualize protein live and compare it directly to RNA output. Since a major claim of the paper depends on variability of upstream input it would be fantastic to measure an input relative to output and see if that also fits the predictions about variability and noise, and to measure output using either identical or different enhancers. It is possible that fluctuations in local chromatin state, for example, or local changes in topology create noise and not TF concentrations. Measuring TFs directly would allow for direct attribution (or not!). This may be beyond the current scope, but this would have been a way to add impact and reinforce the central claims of the manuscript.

Overall the manuscript is a bit light on experimental data and does not attempt to validate their models or predictions other than fitting the original data, then testing pairs of the same enhancers. Seeing similar effects for a second gene would help, but 1) and/or 2) above would be even better. That said, I like the direction of the work and the data from Figure 1. Given the reluctance of eLife to recommend additional experiments and that reviewers should evaluate the work as it stands, I do like the manuscript, and I think the conclusions drawn are reasonably well supported by the data provided. I think stronger arguments could be made with additional experimental data. I am generally positive but a little on the fence on my recommendation and look forward to seeing what other reviewers think.

Reviewer #2:

In this manuscript, the authors interrogate the role of shadow enhancers. They use two apparently redundant enhancers of the Kr gene as a paradigm. They generated MS2<yellow transgenic reporters, driven either by the proximal or distal Kr enhancer, or a combination of both (referred to as shadow het or pair). The authors use an elegant approach to study the impact of fluctuations in TF inputs in single nuclei, by tracking biallelic transcription within a developmental pattern. By combining quantitative imaging with mathematical modeling, they show that a major function of the Kr shadow enhancers is to buffer transcriptional noise. This buffering is attributed to the natural variation in input regulators that is created by the presence of two separated enhancers.

To my knowledge, such in depth characterization of bi-allelic cross-correlation in transcriptional output has never been performed in vivo, and as such the results are novel and exciting. In particular, the question of noise buffering in an in vivo developmental context is fundamental and quantified in depth in this manuscript. However, I do have some concerns about the quantification methodology, in particular because the precise description underlying how this quantification was developed and the nature of its underlying assumptions is lacking. Moreover, given that noise buffering is among the key findings of the paper, I think that the authors should demonstrate it using an orthogonal approach. If the authors can address the major questions raised, I would recommend this work for publication.

General comments:

– Is there a particular reason to justify the usage of different transgenic lines for the allelic correlation aspect (Figure 1-2) and the noise quantification? It would be less confusing to quantify these two metrics using the same genetic paradigm.

In all figures:

• Dotted lines are too dim

• Error bars for experimental data should be added

• Numerical statistics (number of nuclei, number of videos) in each figure legend should be added instead of putting the information separately in Table 2.

To help understanding the similarities and distinctions of the two enhancers, the authors should provide a quantitative description of each enhancer alone, and the shadow heterozygote, in terms of

a) % of activation across A/P axis, with ideally still images at different time points in nc14 (and videos in supplemental data). This will clarify the mono- versus bi-allelic activation at the border of the pattern. This may help understand why measurements of the allelic correlation in the anterior most part of the embryo (20%-40% egg length) is only shown for “proximal”. Similarly, can the authors explain why the allelic correlation is measured at the posterior part only for “distal”? If this is due to the documented “shift” in Kr pattern (Jaeger 2004, El Sherif et al., 2016), the authors should comment on it.

b) Intensity profiles over time, at different positions of egg length (as in Scholes et al., 2019), and intensity per nucleus across the embryo length (similar to Bothma et al., 2014).

c) In the main text, the authors should be more explicit with the differential inputs: from the schematic in Figure 1, the distal enhancer seems to be regulated by the pioneer factor Zelda, while the proximal is not. Knowing that Zelda acts as a quantitative timer (Dufourt et al., 2018, Yamada et al., 2019), to what extent is noise buffering due to priming by a pioneer factor? Would the shadow pair still show low transcriptional noise in embryos depleted of maternal Zelda?

Allelic correlation:

To quantitatively compare the effect of each enhancer and the combined trans-heterozygote, they measure the correlation in allelic activity. This is the major result of Figure 1 and yet the authors don't explain clearly how they measure it. An explicative panel and a few sentences in the main text should help.

Moreover, they do not mention the presence of sister chromatids: if they observe transcription from duplicated sister chromatids, how does that affect the quantification analysis? Do they assume that replication occurs independently in both alleles? If so they should explicitly mention this.

Image analysis:

Does the procedure include an estimation of background intensities (free MCP-GFP), which varies substantially from embryo to embryo and within embryos? This is not mentioned in the Materials and methods.

Spot detection:

For each trace, how is the zero determined? This should be mentioned in the text.

Is spot detection performed in 2D (max projected Z-stacks) or in 3D?

Bursting:

The description of the burst calling algorithm is absent. If burst calling is arbitraty/manually determined, this should be clearly stated. This point is not critical for the results of this manuscript. However, authors should pay attention in clearly stating the assumptions for inferring promoter switching rates: indeed with a temporal resolution of 30 seconds, and without single molecule sensitivity, defining what is a clear “OFF” state (versus low activity below the threshold of detection) is difficult. Moreover in the Figure 5—figure supplement 1, can the author show raw traces instead of smoothened ones such as those depicted? The figure legend of this figure should be corrected: red circles should be the “on” promoters and not the black ones.

When comparing their model to the experimental data in Figure 1—figure supplement 2, error bars are present for the simulated data but absent from the experimental data. This should be corrected.

Calibration:

The authors mention Lammers et al. as the procedure they follow, but this paper is not referenced (and to my knowledge only deposited on Biorxiv, and thus has not been peer-reviewed). However Lammers at al. state clearly that their calibration procedure with the hb-MS2 transgene “should generalize to all measurements taken using the same microscope”.

Given that the authors use heterozygous MCP-GFP females (while Garcia et al., Lammers et al. use homozygous) and that imaging settings/laser power etc varies dramatically from one lab to another, I am concerned about this calibration, although I agree that this factor may not dramatically alter the results of the manuscript.

However, to have another independent assay and avoid increasing uncertainty with multiple obscure calibration steps, I recommend performing single molecule FISH experiments on their transgenes. It would then be relatively straightforward to convert integrated MCP-GFP traces to absolute mRNA counts. If the authors end up with a similar calibration factor, this orthogonal method will strengthen their conclusion. Moreover, single molecule experiments could be used to examine the effect of the two Kr enhancers on the variability of mRNA production (see below).

Quantification of noise:

The formula of the CV is wrong and is the opposite of what is described in the main text.

Figure 3: can the author explain how they found a 15% difference in CV for the shadow pair compared to the 2x distal transgene. Was this calculated at a particular %egg length?

Can the author discuss why the shadow pair does not demonstrate any minimal noise beyond 60% egg length? A similar trend is observed with the simulated data (Figure 4C).

These results suggest that the shadow enhancer pair buffers noise, but only under certain circumstances and only by a 15% difference. Thus, the authors should dampen their conclusions to better reflect the data presented.

A major finding of this manuscript is noise buffering is accomplished at least in part by the presence of shadow enhancers. Yet transcriptional noise is measured with only one approach, live imaging, from which image analysis part is critical and not well-described here. Therefore, the authors should confirm the observed differences in transcriptional noise with an orthogonal approach such as single molecule FISH, as performed in Little et al., 2013 or Boettiger, 2013. By assessing the production of each “pseudo-cell” in nc14 or alternatively within a “column” of nuclei at a given position of the A/P axis, the authors could then assess how variable is the production of mRNA in each of the genotypes. These experiments would also permit to discuss the effect of spatial and temporal averaging as mentioned by the authors.

Reviewer #3:

In their manuscript, "Shadow enhancers suppress input transcription factor noise through distinct regulatory logic," Waymack and colleagues explore how shadow enhancers drive consistent expression levels by buffering upstream noise through a separation of transcription factor inputs at individual enhancers. By measuring the transcriptional dynamics of several Kruppel shadow enhancer configurations in live Drosophila embryos, show that enhancers act largely independently. The authors suggest that TF fluctuations are an appreciable source of noise that the shadow enhancer pair can better buffer than duplicated enhancers. The authors demonstrate that shadow enhancer pairs are uniquely able to maintain low levels of expression noise across a wide range of temperatures. Finally, a stochastic model supports their conclusion that the separation of TF inputs is enough to explain these findings.

Overall, this was a great paper and is exploring an important question in the field. It is well controlled with thoughtful experiments and modeling.

That said, I have some suggestions that could help the authors solidify their conclusions. Namely, one of the main conclusions is that TF fluctuations are the main source of noise that is suppressed by enhancers with different inputs. The authors go on to explore how shadow enhancers suppress noise across a wide range of temperatures. However, this does not test the effects of TF fluctuations and how they impact transcription directly. It would be great if they could test this though perturbations at either binding sites in the enhancers, or better still, through transient increases or decreases in the varying TF inputs. This could be done, for example, by noisy promoters driving the TFs in early embryos (HS::Hb or another variant), or by playing with copy number, etc. The authors could also image the distribution of the factors around the sites of transcription (Tsai et al., 2017, 2019). Again, this would explore how TF fluctuations impact shadow enhancers in a more direct way.

[Editors’ note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Shadow enhancers can suppress input transcription factor noise through distinct regulatory logic" for consideration by eLife. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by Patricia Wittkopp as the Senior and Reviewing Editor. The following individual involved in review of your submission has agreed to reveal their identity: Justin Crocker (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

We would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). Specifically, we are asking editors to accept without delay manuscripts, like yours, that they judge can stand as eLife papers without additional data, even if they feel that they would make the manuscript stronger. Thus the revisions requested below only address clarity and presentation.

Summary:

This study uses creative approaches to examine sources of gene expression noise. As reviewers wrote: The quantification of noise in a multicellular organism with live imaging is very elegant and has, to my knowledge, never been performed by this bi-allelic approach in Drosophila embryos. The Kr system with its set of two types of enhancers is very well adapted to the question. GFP-tagged Bcd was also used to measure Bicoid fluctuations and enhancer activity (shadow pair or distal enhancer) in the same nucleus, which showed that changes in the activity of the shadow pair were less correlated with Bcd levels than changes in the activity of the distal enhancer.

Overall, the reviewers were very pleased with the revisions and new data added directly visualizing transcription factor input alongside mRNA response. They were also all enthusiastic about this work being suitable for eLife. One reviewer, however, had some reservations about Bcd experiment and thus strength of one element of the conclusions. I've included this reviewer’s concerns (which were supported by the other two reviewers during the discussion phase) below. I anticipate that these concerns can be addressed with only text revisions to moderate the strength of conclusions drawn in one part of the manuscript and to add missing information about the copy number of Bcd-GFP

Revisions:

I think the data presented in the manuscript strongly support the first part of the title : “Shadow enhancers can suppress input TF noise”. However, more experimental data are needed to support the conclusion that noise buffering is achieved via “distinct regulatory logic”.

I appreciate the efforts of the authors to quantify Bicoid fluctuations while assessing transcriptional output dictated by the distal enhancer or the shadow pair (new Figure 3). However, I think that these data should be interpreted with caution.

First, the quantification are performed in a 3Xbicoid background (unless the authors introduced Bcd-GFP in a Bcdnull background, but this is not mentioned). Thus, the statement that half the Bcd proteins were labeled would not be strictly rigourous. If indeed there are 3 copies of Bcd, the shape of the Bcd gradient might be affected. Moreover, I would expect that fluctuations in this TF activator would be higher if Bcd was solely produced by the transgene Bcd-GFP. If there are indeed only two copies of Bcd, this should be clarified in text.

Second and most importantly, knowing that Bcd nuclear distribution is not homogeneous (as alluded to in the Discussion) (Mir, 2017, Mir et al., 2018), Bcd concentration should have been measured at the Transcription Site, as performed in Tsai, 2017 or Yamada, 2018, not across the entire nucleus.

Additionally, the difference in the correlation of Bcd-MS2 between the two transgenes (shadow pair vs distal) presented in Figure 3F is relatively modest. This panel would benefit from the control proximal alone.

I understand that with the current pandemic, it is quite difficult to perform experiments. However, to claim that noise buffering is achieved via distinct responses to TF fluctuations, the paper would need more data (such as smFISH, imaging new transgenes with TF mutations, and perturbing TF concentrations with heterozygous mutants in trans).

Having said that, I believe that a re-written manuscript with less emphasis on the cause of noise buffering would be a of great value that clearly deserve publication in eLife. I would build the manuscript around the solid finding that shadow enhancers buffer noise and perhaps end the paper with the possible explanation of noise buffering (actual Figure 3 results revised, see comments above). This may also help to clarify the manuscript, as the text itself is highly complex and could be well-served by simplifying the structure to highlight a single key advance per sentence.

https://doi.org/10.7554/eLife.59351.sa1

Author response

[Editors’ note: the authors resubmitted a revised version of the paper for consideration. What follows is the authors’ response to the first round of review.]

The post-review discussion highlighted the following points as most critical:

1) Addressing the technical concerns raised in the reviews and clarifying methods. As one reviewer wrote "it's extremely hard to judge the quality of the current results (even in the Materials and methods)".

2) At a minimum, use smFISH to confirm the live imaging results/model predictions. Better would be to more directly measure fluctuations of input TFs (e.g., HaloTags or LlamaTags).

3) Functional data testing arguments emerging from the model. Specifically, analyzing enhancers with specific TF binding sites mutated/deleted and examining the impact of manipulating TFs were suggested as ways to further test the credibility of the conclusions presented.

We are so pleased that the reviewers found this work exciting and novel, and we are happy to share a revised manuscript, in which we have attempted to address all the reviewer comments.

With regards to the three critical points below:

1) We have added all the requested details about our experimental methods to the manuscript and thank the reviewers for pointing out this shortcoming.

2) To address the request for additional experimental data, we simultaneously imaged Bicoid levels and enhancer transcriptional activity to more directly measure the relationship between transcription factor fluctuations and the resulting transcription. These results are summarized in a new Figure 3 and subsection “The shadow pair’s activity is less sensitive to fluctuations in Bicoid levels than is the activity of a

single enhancer” of the main text. Using eGFP-tagged Bcd, we simultaneously measured Bcd fluctuations and enhancer activity (shadow enhancer pair or distal enhancer) in the same nucleus across the time of nc14. Bcd primarily activates the distal but not the proximal enhancer, and therefore, we hypothesized that the shadow enhancer pair activity would be less influenced by Bcd levels than the distal enhancer. Experimentally, we find that the activity of the shadow pair is significantly less correlated with Bcd levels than the activity of the distal enhancer (Figure 3E). We agree that this experiment was an important addition to the paper and allowed for an exciting finding!

3) We have designed and ordered flies that contain enhancer mutations to test our computational model. However, due to the coronavirus pandemic, the results from these flies have been severely delayed. Our institution has not yet opened for non-essential research activity, so a timeline for these results is unclear. Instead, to address the concerns about further model testing, we have added two modeling components to the study:

a) We noted that the modeling results of single enhancer allele correlations presented in Figure 2 matched our experimental results qualitatively, but not quantitatively. Specifically, the model predicted that heterozygotes carrying a copy each of the proximal and distal reporter would have no correlation in transcriptional activity, while the experiments resulted in a modest, positive correlation in these heterozygotes. We hypothesized that the discrepancy between model and experiment might be due to a shared transcription factor. By modifying the model to include a shared transcription factor, our model can recapitulate the nonzero correlation in the heterozygotes, suggesting that a shared factor may play a role in this system (now included in Figure 2—figure supplement 2).

b) With the addition of experimental measurements of transcription factor levels, we realized we had the opportunity to use our model to generate predictions of the correlations between transcription factor levels and enhancer activity, to match our experimental measurements. We found that, without any modifications, our model yielded predicted correlations that closely match the experimental data (now included in Figure 3G).

In addition to these changes, we have also included a point-by-point response to all the reviewers’ comments. We hope that these additions and revisions have satisfied all the reviewers’ questions and concerns.

Reviewer #1:

[…] For 1): A main conclusion is that each enhancer has different inputs, which is suggested by the observed correlation between identical alleles but which breaks down comparing across alleles. Each enhancer is likely to share some inputs while others may vary; they are after all quite similar spatial patterns. These potential inputs are discussed only minimally and the authors do not attempt to test what they might be. Zld, Bcd, Hb, and Stat – all their predicted inputs – have nicely characterized binding sites. I would have liked to see a small number of constructs in which potential input factor binding sites have been mutagenized or added. This may reduce (or increase) expression levels or patterns, but the remaining pattern could be evaluated for dynamics and correlation. Zld binding sites, for instance, can often be removed without removing the pattern but with changes to expression dynamics. Or, Zld sites could be added to an enhancer missing them to make the enhancer pair more similar.

We thank the reviewer for pointing out that we did not sufficiently explain the experimental evidence for differences in TF regulation between the two Kr enhancers. To clarify this in the text we have added the following:

“In previous work, we found that the individual enhancers in the shadow enhancer pair are controlled by different activating TFs (Wunderlich et al., 2015). Our experiments showed that the proximal enhancer is activated by Hunchback (Hb) and Stat92E, and the distal enhancer is activated by Bicoid (Bcd) and Zelda (Zld) (Figure 1A).”

In our 2015 study, we showed the differential TF regulation of the Kr enhancers through a combination computationally predicted binding sites and experimental techniques. RNAi knockdown of Stat92E results in decreased expression of the proximal enhancer with no change in expression driven by the distal enhancer, while Bcd knockdown results in decreased expression of the distal enhancer with weaker (likely indirect) effects on expression of the proximal enhancer. RNAi was not possible for Hb and Zelda at that time, so we used alternative approaches. Ventral mis-expression of Hb results in expanded expression of the proximal enhancer, but reduced expression of the distal enhancer. To assess the regulation by Zelda of the different enhancers, we measured expression in stage 4, pre-blastoderm, embryos. We show that the distal, but not proximal, enhancer is active at this stage, consistent with the distal, but not proximal, enhancer being activated by Zelda. Additionally, the Zelda ChIP-seq binding profiles also show higher binding at the distal enhancer than the proximal enhancer.

For 2): New methods are available to visualize protein live and compare it directly to RNA output. Since a major claim of the paper depends on variability of upstream input it would be fantastic to measure an input relative to output and see if that also fits the predictions about variability and noise, and to measure output using either identical or different enhancers. It is possible that fluctuations in local chromatin state, for example, or local changes in topology create noise and not TF concentrations. Measuring TFs directly would allow for direct attribution (or not!). This may be beyond the current scope, but this would have been a way to add impact and reinforce the central claims of the manuscript.

We thank the reviewer for this valuable suggestion and describe our new experiment simultaneously measuring TF levels and enhancer activity in the answer to point #2 at the top of this response.

Reviewer #2:

[…] General comments:

– Is there a particular reason to justify the usage of different transgenic lines for the allelic correlation aspect (Figure 1-2) and the noise quantification? It would be less confusing to quantify these two metrics using the same genetic paradigm.

Our use of the single enhancers for allele correlation but duplicated enhancers for noise measurements stems from wanting to investigate slightly different things in these experiments. In Figures 1-2, we are measuring allele correlation to test whether TF fluctuations are a significant source of noise in this system and whether individual Kr enhancers, with different TF inputs, can independently respond to these fluctuations. For this reason, we did not use our duplicated enhancer constructs in this experiment as they are a further departure from the endogenous system. When measuring the temporal CV (noise) associated with the different enhancers in Figures 4-5, we compared the shadow enhancer pair to either duplicated enhancer to understand if the shadow pair conferred additional benefits beyond those gained by simply having two enhancers. We hypothesized that a shadow enhancer pair with different TF inputs, as opposed to a simple enhancer duplication, had been selected in part to drive more stable gene expression and so we wanted to compare expression noise associated with the shadow enhancer pair to that of either duplicated enhancer.

In all figures:

• Dotted lines are too dim

We have made all dotted lines thicker to improve visibility

• Error bars for experimental data should be added

To aid in comparisons of our experimental and simulated data, we have added shaded error bars to the experimental data in Figures 2 and 5. Additionally, we include error bars for all experimental data that we do not otherwise show the distribution of. This is seen in Figure 1E, Figure 4A/B, Figure 1—figure supplement 1, Figure 1—figure supplement 3, Figure 5—figure supplement 1, and Figure 6—figure supplement 2.

• Numerical statistics (number of nuclei, number of videos) in each figure legend should be added instead of putting the information separately in Table 2.

We put these statistics in a separate table based on the eLife submission guidelines to avoid overly long and complicated figure legends, but in our figure legends, we have indicated where these statistics can be found.

To help understanding the similarities and distinctions of the two enhancers, the authors should provide a quantitative description of each enhancer alone, and the shadow heterozygote, in terms of

a) % of activation across A/P axis, with ideally still images at different time points in nc14 (and videos in supplemental data). This will clarify the mono- versus bi-allelic activation at the border of the pattern. This may help understand why measurements of the allelic correlation in the anterior most part of the embryo (20%-40% egg length) is only shown for “proximal”. Similarly, can the authors explain why the allelic correlation is measured at the posterior part only for “distal”? If this is due to the documented “shift” in Kr pattern (Jaeger, 2004, El Sherif et al., 2016), the authors should comment on it.

We agree clarification was needed to explain the different spatial patterns of allele correlation for the two enhancers. In the text we have added: “The difference in our ability to measure allele correlation in the more anterior and posterior regions of the embryo stems from the slightly different expression patterns driven by the proximal and distal enhancers (Figure 1—figure supplement 1; Figure 1—figure supplement 3).” Figure 1—figure supplement 1 has been added to show the fraction of nuclei transcribing at different times in nc14 as a function of embryo position. This illustrates our observation that the proximal enhancer alone drives slightly more anterior expression, while the distal enhancer drives slightly more posterior expression. These differences are particularly noticeable at later points in nc14 (see 30 and 40 minutes into nc14 Figure 1—figure supplement 1), due to the shift in the overall Kruppel expression pattern.

b) Intensity profiles over time, at different positions of egg length (as in Scholes et al. 2019), and intensity per nucleus across the embryo length (similar to Bothma et al., 2014).

We have added Figure 1—figure supplement 3 to show the average expression profile of each enhancer construct at different embryo positions as a function of time into nc14. In

Figure 2—figure supplement 1, we also provide graphs of total mRNA produced by each enhancer as a function of embryo position (Figure 2—figure supplement 1A and B).

c) In the main text, the authors should be more explicit with the differential inputs: from the schematic in Figure 1, the distal enhancer seems to be regulated by the pioneer factor Zelda, while the proximal is not. Knowing that Zelda acts as a quantitative timer (Dufourt et al., 2018, Yamada et al., 2019), to what extent is noise buffering due to priming by a pioneer factor? Would the shadow pair still show low transcriptional noise in embryos depleted of maternal Zelda?

We thank the reviewer for pointing out that we did not sufficiently explain the differences in TF regulation between the two Kr enhancers in the main text. To clarify this, we have added the following:

The reviewer is right that Zelda acts as a developmental timer, and we can see this in the different activity patterns of the two Kr enhancers. Our previous work found that expression from the distal enhancer is observed at earlier developmental stages (stage 4) than the proximal enhancer. Additionally, we find in our current data that the distal enhancer becomes active 5-10 minutes earlier in nc14 than the proximal enhancer (Figure 1—figure supplement 3).

We would expect that the reviewer’s hypothesis would bear out. Any severe depletion of a key maternal factor like Zelda will drive higher noise and abnormal or possibly fatal developmental patterning. However, because the activity of the proximal enhancer is relatively independent of Zelda levels, we would predict the shadow enhancer pair could better tolerate physiological fluctuations in Zelda than a Kruppel locus lacking the proximal enhancer.

Allelic correlation:

To quantitatively compare the effect of each enhancer and the combined trans-heterozygote, they measure the correlation in allelic activity. This is the major result of Figure 1 and yet the authors don't explain clearly how they measure it. An explicative panel and a few sentences in the main text should help.

We agree that this is an important point that should be clarified for the reader. To better explain how allele correlation was calculated, we have added more detail in the Figure 1D legend “Graph shows a representative trace of transcriptional activity of the two alleles in a single nucleus across the time of nc14. These traces are used to calculate the correlation of allele activity in each nucleus. The Pearson correlation coefficient is calculated between the transcriptional activity of the two alleles in a nucleus across the time of nc14. Correlation values are grouped by position of the nucleus in the embryo and averaged across all imaged nuclei in all embryos of each construct.”

Moreover, they do not mention the presence of sister chromatids: if they observe transcription from duplicated sister chromatids, how does that affect the quantification analysis? Do they assume that replication occurs independently in both alleles? If so they should explicitly mention this.

While we can occasionally distinguish sister chromatids, the majority of the time the two copies are visualized as one spot due to cohesion between them. In the rare instances where the two sister chromatids are distinguishable, the spot tracking algorithm saves only the brightest of the two spots per nucleus. As the reviewer is suggesting, this means we are generally measuring the total fluorescence of both sister chromatids after replication, which we assume happens with similar timing in all of our constructs, which are inserted into the same chromosomal position. In the context of shadow enhancers’ role in buffering transcriptional noise, since our measurement of noise (CV) normalizes for expression levels, we do not expect this to significantly affect our results. We were further convinced that this was a reasonable approach by the findings of (Lammers et al., 2020), which showed that a model of transcriptional bursting that took into account the activity of both sister chromatids produces the same results as a model that did not distinguish the two sister chromatids.

Image analysis:

Does the procedure include an estimation of background intensities (free MCP-GFP), which varies substantially from embryo to embryo and within embryos? This is not mentioned in the Materials and methods.

We appreciate this point from the reviewer and have clarified how we perform background correction for our imaging. We have added “For every spot of transcription imaged, background fluorescence at each time point is estimated as the offset of fitting the 2D maximum projection of the Z-stack image centered around the transcriptional spot to a gaussian curve, using Matlab lsqnonlin. This background estimate is subtracted from the raw spot fluorescence intensity.”

Spot detection:

For each trace, how is the zero determined? This should be mentioned in the text.

Is spot detection performed in 2D (max projected Z-stacks) or in 3D?

We use the background corrected fluorescence traces, as described above, to perform all analysis. In our measurements of burst size, the value of zero is set to the floor of the fluorescence trace, above which we integrate the area under the curve of the transcriptional trace. To clarify this in the text we have added: “Burst size is defined as the integrated area under the curve of each transcriptional burst, from one “ON” frame to the next “ON” frame, with the value of 0 set to the floor of the background-subtracted florescence trace (Figure 6—figure supplement 3C).”

Spot detection is performed in 2D on maximum projection Z-stacks. We have added this clarification in our description of background correction in subsection “Burst calling and calculation of transcription parameters”.

Bursting:

The description of the burst calling algorithm is absent. If burst calling is arbitraty/manually determined, this should be clearly stated. This point is not critical for the results of this manuscript. However, authors should pay attention in clearly stating the assumptions for inferring promoter switching rates: indeed with a temporal resolution of 30 seconds, and without single molecule sensitivity, defining what is a clear “OFF” state (versus low activity below the threshold of detection) is difficult. Moreover in the Figure 5—figure supplement 1, can the author show raw traces instead of smoothened ones such as those depicted? The figure legend of this figure should be corrected: red circles should be the “on” promoters and not the black ones.

When comparing their model to the experimental data in Figure 1—figure supplement 2, error bars are present for the simulated data but absent from the experimental data. This should be corrected.

We agree our assumptions in burst calling should be clearly stated. In subsection “Burst calling and calculation of transcription parameters” we describe how we call a promoter as “ON” or “OFF”, which correspond to the beginning and end of a burst respectively. “To calculate transcription parameters, we used the smoothed traces to determine if the promoter was active or inactive at each time point. A promoter was called active if the slope of its trace (change in fluorescence) between one point and the next was greater than or equal to the instantaneous fluorescence value calculated for one mRNA molecule (F_RNAP, described below). Once called active, the promoter is considered active until the slope of the fluorescence trace becomes less than or equal to the negative instantaneous fluorescence value of one mRNA molecule, at which point it is called inactive until another active point is reached. The instantaneous fluorescence of a single mRNA was chosen as the threshold because we reasoned that an increase in fluorescence greater than or equal to that of a single transcript is indicative of an actively producing promoter, while a decrease in fluorescence greater than that associated with a single transcript indicates transcripts are primarily dissociating from, not being produced from, this locus.”

In Figure 6—figure supplement 3, we have added a panel showing how a raw fluorescent trace is smoothed to the resulting curves. We show the burst properties on the smoothed traces because we calculate these parameters using the smoothed traces. In these figures the black open circles are indicating the time points in the trace where the promoter was switched to “ON”, while the red filled circles indicate the time points in the trace where the promoter was switched to “OFF”. As the reviewer points out, this was unclear in our original figure legend so we have adjusted it to read: “Black open circles indicate time points where the promoter is switched to being called “on”, red filled circles indicate time points where the promoter is switched to being called “off””.

When comparing their model to the experimental data in Figure 1—figure supplement 2, error bars are present for the simulated data but absent from the experimental data. This should be corrected.

We have corrected this.

Calibration:

The authors mention Lammers et al. as the procedure they follow, but this paper is not referenced (and to my knowledge only deposited on Biorxiv, and thus has not been peer-reviewed). However Lammers at al. state clearly that their calibration procedure with the hb-MS2 transgene “should generalize to all measurements taken using the same microscope”.

Given that the authors use heterozygous MCP-GFP females (while Garcia et al., Lammers et al. use homozygous) and that imaging settings/laser power etc varies dramatically from one lab to another, I am concerned about this calibration, although I agree that this factor may not dramatically alter the results of the manuscript.

However, to have another independent assay and avoid increasing uncertainty with multiple obscure calibration steps, I recommend performing single molecule FISH experiments on their transgenes. It would then be relatively straightforward to convert integrated MCP-GFP traces to absolute mRNA counts. If the authors end up with a similar calibration factor, this orthogonal method will strengthen their conclusion. Moreover, single molecule experiments could be used to examine the effect of the two Kr enhancers on the variability of mRNA production (see below).

Thank you for this question. We did indeed carry out a calibration using the same protocol as Lammers, et al. (which is now published), but specifically using measurements taken with our own microscope, using our standard imaging parameters. We measure the F_MS2 value for our microscope, which is the average integrated fluorescence of one transcriptional spot driven by the hb P2 enhancer construct during the time of nuclear cycle 13 (nc13). As in the published protocol, we relate this value to N_FISH, the published value of the mean number of transcripts produced by a single locus of this enhancer during the same time period of nc13 (measured by FISH), with the equation α = N_FISH/F_MS2. The calculated calibration factor, α, is then specific for our microscope and imaging parameters and enables us to estimate the instantaneous and integrated fluorescence of single mRNA molecules as described in subsection “Conversion of integrated fluorescence to mRNA molecules”. As the reviewer notes, this conversion is not crucial for our study as none of our conclusions rest on knowing the number of transcripts produced by any of the enhancer constructs. We simply chose to include estimates of enhancer activity in terms of number of transcripts produced to display our results in more biologically-relevant units.

Quantification of noise:

The formula of the CV is wrong and is the opposite of what is described in the main text.

Thank you for catching this mistake, we have corrected the formula to read “CV(i) = standard deviation(mⁱ(t))/mean(mⁱ(t))”

Figure 3: can the author explain how they found a 15% difference in CV for the shadow pair compared to the 2x distal transgene. Was this calculated at a particular %egg length?

Yes, this comparison was performed with the CV value of the shadow pair and 2x distal at the AP positions of their peak expression. We have clarified this: “The shadow enhancer pair’s expression noise is almost 30% or 15% lower, respectively, than that of the duplicated proximal or distal enhancers in their positions of maximum expression.”

Can the author discuss why the shadow pair does not demonstrate any minimal noise beyond 60% egg length? A similar trend is observed with the simulated data (Figure 4C).

This is likely due to the low levels of expression driven by the shadow pair at this region in the embryo as the shadow pair’s expression pattern sharply drops off after ~55% egg length (Figure 4B). We have added a supplemental figure (Figure 1—figure supplement 1) showing the fraction of active nuclei as a function of embryo position at different times during nc14 to help clarify this point.

These results suggest that the shadow enhancer pair buffers noise, but only under certain circumstances and only by a 15% difference. Thus, the authors should dampen their conclusions to better reflect the data presented.

We agree on wanting to most accurately describe our findings and have edited the text to read “Therefore, we can conclude that the separation of input TFs is sufficient to explain the lower noise driven by the shadow enhancer construct.”

A major finding of this manuscript is noise buffering is accomplished at least in part by the presence of shadow enhancers. Yet transcriptional noise is measured with only one approach, live imaging, from which image analysis part is critical and not well-described here. Therefore, the authors should confirm the observed differences in transcriptional noise with an orthogonal approach such as single molecule FISH, as performed in Little et al., 2013 or Boettiger, 2013. By assessing the production of each “pseudo-cell” in nc14 or alternatively within a “column” of nuclei at a given position of the A/P axis, the authors could then assess how variable is the production of mRNA in each of the genotypes. These experiments would also permit to discuss the effect of spatial and temporal averaging as mentioned by the authors.

We appreciate the reviewers request for additional approaches to measure transcriptional noise. From the editor’s summary of the reviewer comments, the consensus was that we needed to either perform smFISH or simultaneous TF-MS2 tracking to further address the role of shadow enhancers and transcriptional noise. We opted to perform simultaneous TF-MS2 tracking to assess the relationship of TF levels and enhancer activity. We describe this experiment and the results in subsection “The shadow pair’s activity is less sensitive to fluctuations in Bicoid levels than is the activity of a single enhancer” of the modified manuscript and in the answer to point #2 at the top of this response letter. We appreciate the reviewers’ requests for these additional experiments as they enabled the finding that the activity of the Kr shadow enhancer pair is less sensitive to fluctuations in Bcd levels than is that of the single distal enhancer (new Figure 3).

Reviewer #3:

[…] That said, I have some suggestions that could help the authors solidify their conclusions. Namely, one of the main conclusions is that TF fluctuations are the main source of noise that is suppressed by enhancers with different inputs. The authors go on to explore how shadow enhancers suppress noise across a wide range of temperatures. However, this does not test the effects of TF fluctuations and how they impact transcription directly. It would be great if they could test this though perturbations at either binding sites in the enhancers, or better still, through transient increases or decreases in the varying TF inputs. This could be done, for example, by noisy promoters driving the TFs in early embryos (HS::Hb or another variant), or by playing with copy number, etc. The authors could also image the distribution of the factors around the sites of transcription (Tsai et al., 2017, 2019). Again, this would explore how TF fluctuations impact shadow enhancers in a more direct way.

We appreciate these comments from the reviewer and have added additional experimental data addressing the question of the relationship between TF fluctuations and resulting transcription. These results are summarized in a new Figure 3 and subsection “The shadow pair’s activity is less sensitive to fluctuations in Bicoid levels than is the activity of a single enhancer” of the main text, as well as the answer to point #2 at the beginning of this response letter. Using GFP-tagged Bcd, we simultaneously measured TF (Bcd) fluctuations and enhancer activity (shadow pair or distal enhancer) in the same nucleus across the time of nc14. We find that changes in the activity of the shadow pair are significantly less correlated with Bcd levels than are changes in the activity of the distal enhancer (Figure 3E). We agree that this experiment was an important addition to the paper and allowed for an exciting finding!

[Editors’ note: what follows is the authors’ response to the second round of review.]

Revisions:

I think the data presented in the manuscript strongly support the first part of the title : “Shadow enhancers can suppress input TF noise”. However, more experimental data are needed to support the conclusion that noise buffering is achieved via “distinct regulatory logic”.

I appreciate the efforts of the authors to quantify Bicoid fluctuations while assessing transcriptional output dictated by the distal enhancer or the shadow pair (new Figure 3). However, I think that these data should be interpreted with caution.

We thank the reviewer for this comment. However, we would like to leave the title as is. There are three pieces of evidence that show that the two Kruppel enhancers use distinct regulatory logic:

1) The first, and strongest piece of evidence, which we build upon here, comes from our previous work (Wunderlich et al., 2015). In this work, we demonstrated that the individual enhancers respond differently to depletion or over-expression of three key transcription factors (Bicoid, Hunchback, and Stat92E). We have clarified the experimental basis for this claim, where we write:

“These experiments established that the enhancers responded differently to perturbations in key TFs, indicating that each enhancer uses a distinct regulatory logic.”

2) The second piece of evidence is the difference in correlations between homozygous and heterozygous embryos shown in Figure 1. We have tried hard to think of alternative explanations as to why homozygote reporter embryos would have higher correlations than heterozygote embryos, and, while we introduce a possible alternative in the manuscript, we still feel distinct regulatory logic is the most likely explanation.

3) Lastly, some of the reviewer’s concerns seem to stem from the assumption that the embryos we imaged with tagged Bcd were 3X Bcd. However, the embryos were actually 2X Bcd, which we have clarified in the text.

Therefore, we want to keep the existing title as it best conveys our main message. However, we have dampened our conclusions regarding our Bcd fluctuation experiments and added discussion of other possible mechanisms, as addressed below.

First, the quantification are performed in a 3Xbicoid background (unless the authors introduced Bcd-GFP in a Bcdnull background, but this is not mentioned). Thus, the statement that half the Bcd proteins were labeled would not be strictly rigourous. If indeed there are 3 copies of Bcd, the shape of the Bcd gradient might be affected. Moreover, I would expect that fluctuations in this TF activator would be higher if Bcd was solely produced by the transgene Bcd-GFP. If there are indeed only two copies of Bcd, this should be clarified in text.

We appreciate this concern from the reviewers and realize that we did not make clear that the embryos in our experiments have 2X levels of Bcd. The tagged Bcd-GFP was placed in a Bcd-null background (Gregor et al., 2007), and we have added the following to clarify this:

“To allow for tracking of both Bcd levels and enhancer activity, we crossed female flies that express eGFP-tagged Bcd in the place of endogenous Bcd (called Bcd-GFP from here on; Gregor et al., 2007) and MCP-mCherry with male flies homozygous for either the shadow pair or distal enhancer reporter. As the Bcd-GFP transgene was inserted in a Bcd null background, the resulting embryos should receive roughly WT levels of Bcd.”

Second and most importantly, knowing that Bcd nuclear distribution is not homogeneous (as alluded to in the Discussion) (Mir 2017, Mir 2018), Bcd concentration should have been measured at the Transcription Site, as performed in Tsai, 2017 or Yamada, 2018, not across the entire nucleus.

We agree with the reviewers that looking at local Bcd levels around the transcriptional sites would be the best method of quantification, but, due to the pandemic, we cannot access a microscope with this level of spatial resolution. While total nuclear levels of Bcd do not completely capture the levels of Bcd available to an individual transcription site, it does provide an upper limit to the amount of Bcd available to a transcription site as well as a rough lower limit to the degree of Bcd fluctuations. Since local levels of Bcd will likely fluctuate much more than total nuclear levels, we suspect that differences in enhancer activity correlation between the Kr distal enhancer versus the shadow enhancer pair with local Bcd levels would be larger than what we observe with total nuclear Bcd levels. We emphasize this distinction between total nuclear Bcd levels and local levels available to an enhancer in the Discussion:

“The correlation between Bcd levels and activity of the distal enhancer is modest, and we expect that this reflects both the influence of additional TF inputs and nuclear heterogeneity that causes the local Bcd levels available to the enhancer to differ from total nuclear levels (Mir et al., 2018). We suspect that the correlation between the activity of the distal enhancer and Bcd levels in the microenvironment surrounding the enhancer is higher than what we were able to measure here.”

Additionally, the difference in the correlation of Bcd-MS2 between the two transgenes (shadow pair vs distal) presented in Figure 3F is relatively modest. This panel would benefit from the control proximal alone.

I understand that with the current pandemic, it is quite difficult to perform experiments. However, to claim that noise buffering is achieved via distinct responses to TF fluctuations, the paper would need more data (such as smFISH, imaging new transgenes with TF mutations, and perturbing TF concentrations with heterozygous mutants in trans).

Having said that, I believe that a re-written manuscript with less emphasis on the cause of noise buffering would be a of great value that clearly deserve publication in eLife. I would build the manuscript around the solid finding that shadow enhancers buffer noise and perhaps end the paper with the possible explanation of noise buffering (actual Figure 3 results revised, see comments above).

We agree that measuring the correlation between Bcd levels and activity of the proximal enhancer would be informative and also appreciate the reviewers’ empathy regarding the current situation and the difficulty of performing additional experiments. Regarding our claim of distinct responses to TF fluctuations between the two enhancers, in our previous work, we have conclusively shown that the two enhancers respond differently to TF inputs (Wunderlich et al., 2015). In our current work, our allele correlation experiments (Figure 1) strongly suggest that the low correlation seen between the two enhancers in heterozygous embryos, compared to the significantly higher correlation between identical enhancers in homozygous embryos, is a result of the different TF regulation of the two enhancers. Given that these reporters are in the same trans environment, in the same genomic location and genetic background, the only difference between our homozygous and heterozygous embryos is the DNA sequence of the two reporters. Therefore, TF fluctuations are the most likely cause of the different activities of the two enhancers in a single nucleus. We do appreciate that further experiments could be done to test if other mechanism are at play. To address this and temper our conclusions as requested, we have made the following changes to the text:

Subsection “The shadow pair’s activity is less sensitive to fluctuations in Bicoid levels than is the activity of a single enhancer” – alteration of the sentence: “These findings indicate that the shadow enhancer pair is better able to buffer fluctuations in a single activating TF than is single enhancer, likely due to the shadow enhancer pairs’ separation of TF inputs.”

Subsection “Modeling indicates the separation of input TFs is sufficient to explain the low noise driven by the shadow enhancer pair” – alteration of the sentence: “Therefore, in our simplified model, we can conclude that the separation of input TFs is sufficient to explain the lower noise driven by the shadow enhancer pair construct.”

Discussion paragraph one – alteration of the sentence: “Together, these results support the hypothesis that shadow enhancers buffer input TF noise to drive robust gene expression patterns during development.”

Discussion paragraph two – addition of the following: “Our current findings leave open the possibility that additional mechanisms, such as differences in 3D nuclear organization between different reporters, may also contribute to the differences in noise that we see.”

Subsection “A stochastic model underscores importance of transcription factor fluctuations” – alteration of the sentence: “indicating that these differences in the model system are a direct result of the separation of input TFs to the proximal and distal enhancers.”

This may also help to clarify the manuscript, as the text itself is highly complex and could be well-served by simplifying the structure to highlight a single key advance per sentence.

We have revised the manuscript to simplify several complex sentences.

https://doi.org/10.7554/eLife.59351.sa2

Article and author information

Author details

Rachel Waymack

Department of Developmental and Cell Biology, University of California, Irvine, Irvine, United States

Contribution
Conceptualization, Software, Formal analysis, Funding acquisition, Investigation, Visualization, Methodology, Writing - original draft, Writing - review and editing

Competing interests
No competing interests declared
Alvaro Fletcher

Mathematical, Computational, and Systems Biology Graduate Program, University of California, Irvine, Irvine, United States

Contribution
Conceptualization, Software, Formal analysis, Funding acquisition, Investigation, Visualization, Methodology, Writing - review and editing

Competing interests
No competing interests declared
German Enciso
1. Department of Developmental and Cell Biology, University of California, Irvine, Irvine, United States
2. Department of Mathematics, University of California, Irvine, Irvine, United States
Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Writing - review and editing

Competing interests
No competing interests declared
Zeba Wunderlich

Department of Developmental and Cell Biology, University of California, Irvine, Irvine, United States

Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Investigation, Writing - original draft, Writing - review and editing

For correspondence
zeba@uci.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-4491-5715

Funding

Eunice Kennedy Shriver National Institute of Child Health and Human Development (R00-HD073191)

Zeba Wunderlich

Eunice Kennedy Shriver National Institute of Child Health and Human Development (R01-HD095246)

Zeba Wunderlich

Hellman Foundation

Zeba Wunderlich

National Institute of Biomedical Imaging and Bioengineering (T32-EB009418)

Alvaro Fletcher

ARCS Foundation

Rachel Waymack

National Science Foundation (DMS1763272)

German Enciso

Simons Foundation (594598)

German Enciso

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors thank Hernan Garcia for providing advice on MS2 imaging, the MCP-GFP fly line, and a plasmid containing the MS2 reporter construct, Nick Lammers for assistance in the calibration of MS2 signal to mRNA counts, Clarissa Scholes for assistance in image processing, Lily Li for assistance in data analysis and comments on the text, Ceazar Nave for feedback on the text and figures, and Thomas Schilling and Rahul Warrior for useful suggestions for the project. We thank the reviewers and editor for their helpful suggestions during the review process.

Senior and Reviewing Editor

Patricia J Wittkopp, University of Michigan, United States

Reviewer

Justin Crocker, European Molecular Biology Laboratory, Germany

Version history

Received: May 27, 2020
Accepted: August 14, 2020
Accepted Manuscript published: August 17, 2020 (version 1)
Version of Record published: September 10, 2020 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

3,418

Page views
448

Downloads
23

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Rachel Waymack
Alvaro Fletcher
German Enciso
Zeba Wunderlich

(2020)

Shadow enhancers can suppress input transcription factor noise through distinct regulatory logic

eLife 9:e59351.

https://doi.org/10.7554/eLife.59351

Categories and tags

Research organism

D. melanogaster

Share this article

Cite this article

Dual allele imaging shows the individual Kruppel enhancers drive largely independent transcriptional dynamics.

Transcriptional dynamics of distal enhancer reporter homozygotes.

Transcriptional dynamics of proximal enhancer reporter homozygotes.

Transcriptional dynamics of shadow heterozygote embryos.

Transcriptional dynamics of duplicated distal reporter homozygotes.

Transcriptional dynamics of duplicated proximal reporter homozygotes.

Transcriptional dynamics of shadow enhancer pair homozygotes.

Model of enhancer-driven dynamics demonstrates TF fluctuations are required for correlated reporter activity.

Activity of Kr shadow pair is less correlated with Bcd levels than is activity of single distal enhancer.

Simultaneous tracking of Bcd-GFP and distal enhancer activity.

Simultaneous tracking of Bcd-GFP and shadow pair activity.

Shadow enhancer pair produces lower expression noise than duplicated enhancers.

The two enhancer model recapitulates low expression noise associated with the shadow enhancer pair.

Shadow enhancer pair achieves lower total noise by buffering global and allele-specific sources of noise.

Shadow enhancer pair maintains lower total noise across temperature perturbations.

Author details

Rachel Waymack

Contribution

Competing interests

Alvaro Fletcher

Contribution

Competing interests

German Enciso

Contribution

Competing interests

Zeba Wunderlich

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading