Condensation tendency and planar isotropic actin gradient induce radial alignment in confined monolayers

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: September 28, 2021 (This version)
Accepted Manuscript published: September 20, 2021 (Go to version)
Accepted: September 9, 2021
Received: June 24, 2020
Preprint posted: June 24, 2020 (Go to version)

1. Of interest
A mechanosensing mechanism controls plasma membrane shape homeostasis at the nanoscale

Xarxa Quiroga, Nikhil Walani ... Pere Roca-Cusachs

Research Article Sep 25, 2023
Further reading

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

A monolayer of highly motile cells can establish long-range orientational order, which can be explained by hydrodynamic theory of active gels and fluids. However, it is less clear how cell shape changes and rearrangement are governed when the monolayer is in mechanical equilibrium states when cell motility diminishes. In this work, we report that rat embryonic fibroblasts (REF), when confined in circular mesoscale patterns on rigid substrates, can transition from the spindle shapes to more compact morphologies. Cells align radially only at the pattern boundary when they are in the mechanical equilibrium. This radial alignment disappears when cell contractility or cell-cell adhesion is reduced. Unlike monolayers of spindle-like cells such as NIH-3T3 fibroblasts with minimal intercellular interactions or epithelial cells like Madin-Darby canine kidney (MDCK) with strong cortical actin network, confined REF monolayers present an actin gradient with isotropic meshwork, suggesting the existence of a stiffness gradient. In addition, the REF cells tend to condense on soft substrates, a collective cell behavior we refer to as the ‘condensation tendency’. This condensation tendency, together with geometrical confinement, induces tensile prestretch (i.e. an isotropic stretch that causes tissue to contract when released) to the confined monolayer. By developing a Voronoi-cell model, we demonstrate that the combined global tissue prestretch and cell stiffness differential between the inner and boundary cells can sufficiently define the cell radial alignment at the pattern boundary.

Introduction

The collective migration and rearrangement of cells play a critical role in various biological processes such as morphogenesis (Friedl et al., 2004), wound healing (Gurtner et al., 2008), and cancer metastasis (Trepat et al., 2012). For epithelial cells which have well-defined cell-cell junctions and cortical actin network, biomechanics of the monolayer has been characterized in detail (Trepat and Sahai, 2018; Tambe et al., 2011; Trepat and Fredberg, 2011; Rodríguez-Franco et al., 2017). Further, polygonal-cell-based models, such as Vertex models and Voronoi models have been developed to understand how cell-cell adhesion, contractility, and self-propulsion determine cell topography (Farhadifar et al., 2007), single-cell motility (Bi et al., 2016), and collective migration (Tetley et al., 2019). Recently, theories of active nematic liquid crystals have been applied to cell monolayers to understand the cell organization in various cell types such as NIH-3T3 fibroblasts (Duclos et al., 2017), neural progenitor cells (Kawaguchi et al., 2017), and myoblast cells (Blanch-Mercader et al., 2021a; Blanch-Mercader et al., 2021b). A general observation obtained in these cell systems is that cells align their shapes with one another, and eventually form half-integer (Duclos et al., 2017; Kawaguchi et al., 2017; Saw et al., 2017) and single-integer (Blanch-Mercader et al., 2021a; Blanch-Mercader et al., 2021b; Guillamat et al., 2020) topological defects. In these works, individual cells are treated as elongated and self-propelled particles, and the long-range alignment of these cells is well described by the hydrodynamic theory of active gels and fluids. It has been revealed that cells located at topological defects experience large compressive stress which leads to the apoptotic exclusion of cells, differentiation, and establishment of out-of-plane tissue architecture (Saw et al., 2017; Guillamat et al., 2020).

Distinct from spindle-like fibroblasts with minimal intercellular interactions or epithelial cells with cortically distributed actin cytoskeleton, various mesenchymal cells such as neural crest cells (Achilleos and Trainor, 2012), mesenchymal stem cells (Aomatsu et al., 2014), and chondrocytes (Tavella et al., 1994), express a significant level of intercellular adhesion molecules like N-cadherin and have isotropic actin network. It is unclear how the mechanical interactions among these cells contribute to their collective behaviors and biological functions.

In this work, we use a rat embryonic fibroblast (REF) cell line (REF-52) as a model system for the aforementioned mesenchymal cells to study their collective behaviors under mechanical equilibrium states when cell motility reduces significantly. Unlike 3T3 fibroblasts, REF cells express a significant level of cell adhesion molecules, such as N-cadherin and β-catenin (Mary et al., 2002), and have isotropic actin meshwork in contrast to cortically distributed actin in epithelial cells. We demonstrate that REF cells can robustly form radial alignment and show significant area expansion at pattern boundaries when confined in circular mesoscale patterns on a rigid substrate. When cultured on soft substrates, the REF monolayer retracts, and cells aggregate to the pattern centers, a collective cell behavior we term as ‘condensation tendency’ because this is a reminiscence of the mesenchymal condensation phenomenon, a prevalent morphogenetic transition in development that involves the aggregation of mesenchymal cells (Mammoto et al., 2011; Klumpers et al., 2014; Lim et al., 2015). Notably, such condensation tendency is similar to the recently discovered ‘active dewetting’ process in a monolayer of MDA-MB-231 cells with inducible E-cadherin, where cell contractility and intercellular adhesion drive the retraction of the tissue monolayer (Pérez-González et al., 2019). New to the active dewetting process, we show that when confined in circular mesoscale patterns on rigid substrates, the boundary REF cells can robustly develop radial alignment in mechanical equilibrium. By developing a Voronoi cell model (Bi et al., 2016; Olaranont, 2019), we discover that such condensation tendency, together with an autonomously established tissue-scale actin gradient, are sufficient to explain the observed radial alignment in confined circular geometries. The distinct behavior of REF-like cells may play a functional role in the collective migration and mesenchymal condensation, which are conventionally considered driven by chemotaxis (Takebe et al., 2015; Szabó and Mayor, 2018).

Results

REF 2c cells align radially on circular mesoscale patterns

We first sought to investigate whether various types of cells with different intra- and intercellular forces and cell shapes have similar self-organization behavior under confinement. We found that when REF 2c cells, a subclone of the REF52 cell line, were placed on circular micro-contact printed patterns (diameter = 344 µm), the boundary cells radially aligned over a period of 48 hr after cell seeding (Figure 1A). Video tracking of individual inner and boundary cells showed that the radial alignment of boundary cells was not caused by oriented cell migration toward or away from the center (Figure 1—figure supplement 1A, Figure 1—video 1), as most boundary cells stayed on the periphery of the pattern. Moreover, both the innermost and boundary cells migrated longer and faster between 24 and 36 hr than 36 and 48 hr (Figure 1—figure supplement 1B–C). This reduced cell migration coincided with the formation of radial alignment of cells on the pattern boundary. In contrast, 3T3 fibroblasts maintained circumferential alignment on the boundary at both 24 and 48 hr (Figure 1A), consistent with previous reports. To quantify the cell alignment, we traced the cell outlines and measured the cell angle deviation, defined as the angle between the long axis of an ellipse-fitted cell and the line that connects the pattern center and the centroid of the cell; cell elongation, defined as the ratio of the major axis to the minor axis of the ellipse-fitted cells; and projected cell area using an ellipse-fitting-based method (Figure 1—figure supplement 2). We found that at 48 hr, the REF 2c cells were more compact compared to 24 hr, and much more compact than 3T3 cells, as indicated by the smaller elongation parameter (Figure 1C, Figure 1—figure supplement 3). Further, for REF 2c cells, the boundary cells were significantly more aligned with the radial direction than the inner cells at 48 hr, although these cells showed circumferential alignment similar to 3T3 cells at 24 hr (Figure 1B). Boundary cells were also significantly more elongated and had a significantly larger cell area than inner cells (Figure 1C,D). The boundary 3T3 cells were significantly more circumferentially aligned and elongated than the inner cells but did not have any significant differences in cell area (Figure 1B–D). Confocal fluorescence images of REF 2c cells stained with a cell membrane permeable dye CellTracker-Green suggested that the average tissue thickness increased slightly due to the cell radial alignment, while the boundary cells had a wedge-shape with a drastically reduced cell thickness on the pattern boundary side (Figure 1—figure supplement 4). The change in tissue thickness suggests cell volume conservation as the whole pattern condensed slightly while boundary cell area increased.

Figure 1 with 6 supplements see all

Download asset Open asset

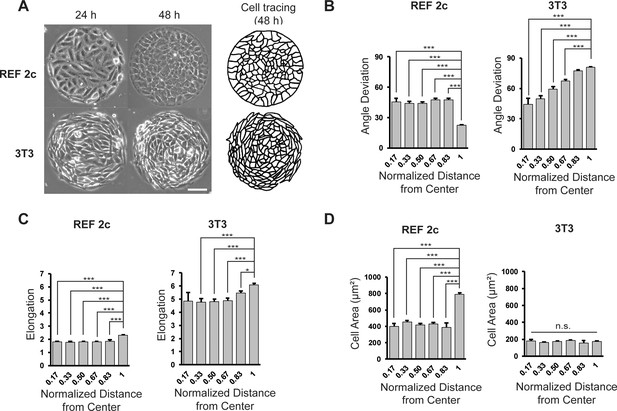
REF 2c cells align radially on circular mesoscale patterns.

(A) Phase images showing REF 2c and 3T3 cells cultured on patterns for 24 and 48 hr. Scale bar: 100 µm. Cell tracing showed the cell boundaries at 48 hr. (B) REF 2c and 3T3 cell angle deviation at 48 hr as a function of normalized distance from the center of the pattern. n = 16 patterns. (C) REF 2c and 3T3 cell elongation at 48 hr as a function of the normalized distance from the center of the pattern. n = 16 patterns. (D) REF 2c and 3T3 cell area at 48 hr as a function of normalized distance from the center of the pattern. Cell area is defined as the area of the ellipse-fitted cells. n = 16 patterns. Data are represented as mean ± s.e.m. *, p < 0.05; ***, p < 0.001; *n.s.*, p > 0.05.

As cells were patterned on PDMS substrates (Young’s modulus E = 2.5 MPa), which are significantly stiffer than physiological extracellular matrices, we next tested whether a similar phenomenon could be observed on substrates with physiologically relevant stiffness. Here we applied a well-established PDMS micropost array (PMA) system with identical surface geometry and different post heights to tune substrate rigidity (Figure 1—figure supplement 5; Sun et al., 2014). We found that on soft PMA substrates (E = 5 kPa, post height = 8.4 µm), REF 2c cells became polarized at 48 hr and condensed towards the center of patterns, resulting in reduced total cell area on each pattern. On stiff PMA substrates (E = 1 MPa, post height = 0.7 µm), however, the total cell area on each pattern did not change between 4 and 48 hr, and only cells on the boundary became radially aligned, which is consistent with the results on flat PDMS substrates. To accurately quantify the cell shape and angle deviation changes, we used rigid (E > 1 MPa) PDMS substrates for the rest of the experiments.

Cell contractility and cell-cell adhesion are required for radial alignment

As all previous works demonstrated circumferential alignment of non-epithelial cells on circular patterns, we asked what factors contribute to the radial alignment of REF 2c cells. We isolated and expanded several subclones of the REF cell line, and identified one subclone, named REF 11b, which did not radially align at 48 hr on circular patterns (Figure 2A). RNA-seq data revealed that while most genes have similar expression levels in REF 11b and REF 2c subclones, a small subset of genes were expressed significantly differently (Figure 2—figure supplement 1). As some of these genes are associated with cell-substrate adhesion and contraction (e.g. INTEGRIN α7 and α8, MYL9, and COL16A1), we then measured the cell contractility of these two subclones. Traction force measurements for single cells of REF 2c and 11b showed that for both total force and force per area, REF 11b cells were significantly less contractile than REF 2c cells (Figure 2B). To verify that the cell contractility was required for radial alignment, we treated patterned REF 2c cells with Blebbistatin (to inhibit myosin ATPase activity) and Y27632 (to inhibit Rho kinase activity), drugs known to reduce cell contractility (Beningo et al., 2006), at 24 hr, and then imaged the patterned cells at 48 hr (Figure 2C). The boundary cells of the Blebbistatin and Y27632-treated groups were not significantly more radially aligned than the inner cells, compared to the vehicle control group with DMSO (Figure 2C). These results suggest that cell contractility is required for radial alignment formation.

Figure 2 with 4 supplements see all

Download asset Open asset

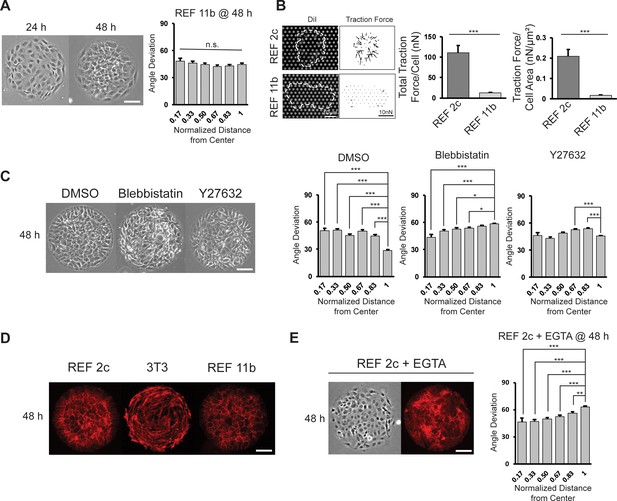
Effect of cell contractility and cell-cell adhesion on cell alignment.

(A) Phase images of REF 11b at 24 hr and 48 hr after cell seeding. Average cell angle deviation is quantified with respect to distance from the center of the pattern. n = 16 patterns. Scale bar: 100 μm. (B) Representative images showing single REF cells cultured on PMA substrates and vector map of deduced traction forces. Plots show the total traction force per cell and traction force per cell area of individual REF 2c and 11b cells. n = 15 cells per subclone. (C) Phase images of REF 2c treated with DMSO, Blebbistatin, and Y27632 at 48 hr. Average cell angle deviation is quantified with respect to distance from the center of the pattern. n = 16 patterns per group. Scale bar: 100 μm. (D) Immunofluorescence images showing the expression of β-catenin in REF 2c, 3T3, and REF 11b cells at 48 hr. Scale bar: 100 μm. (E) Phase and fluorescence images showing cell orientation and β-catenin expression in EGTA treated REF 2c cells at 48 hr. Average cell angle deviation is quantified with respect to distance from the center of the pattern. Scale bar: 100 μm. Data are represented as mean ± s.e.m. *, p < 0.05; **, p < 0.01; ***, p < 0.001; *n.s.*, p > 0.05.

As 3T3 cells have a similar level of contractility compared with REF 2c cells (Ghibaudo et al., 2008), we rationalized that other factors must also contribute to the radial alignment. Staining with β-catenin suggested that there were cadherin-mediated cell-cell interactions among REF 2c and REF 11b cells while overlapping and empty spaces could be found among 3T3 cells without clear cell-cell junctions (Figure 2D, Figure 2—figure supplement 2). These observations suggested that such cell-cell adhesion may be required for the establishment of radial alignment. To confirm this, we treated REF 2c cells with EGTA, which reduced cadherin-based cell-cell adhesion without significantly affecting cell adhesion to substrates (Pérez-González et al., 2019; Ohgushi et al., 2010; Rothen-Rutishauser et al., 2002; Al-Kilani et al., 2011; Koutsouki et al., 2005; Charrasse et al., 2002), at 24 hr and then examined the cell alignment at 48 hr. We found that when treated with EGTA, the boundary cells were significantly more circumferentially aligned than the inner cells (Figure 2E). To confirm that EGTA treatment did not significantly affect cell substrates interactions, we measured the contractility of single cells using the PMAs. As shown in Figure 2—figure supplement 3, EGTA treatment did not change the total traction force per cell or per cell area, suggesting calmodulin-mediated contractility does not predominate this system. Together, we identify that cell contractility and cell-cell adhesion are two essential factors required for the establishment of radial alignment of patterned cells. Importantly, REF 2c cells form aggregates on soft substrates and show similar tendency on rigid substrates (reflected by the radial alignment). We define this collective cell behavior as ‘condensation tendency’, which requires both cell contractility and cell-cell adhesion.

Cell proliferation is not required for the formation of cell radial alignment

It is notable that cell proliferation between 24 and 48 hr after cell seeding may lead to the remodeling and dissipation of elastic energy. To test this, we treated REF 2c cells with aphidicolin (1 µg/ml), an inhibitor of DNA replication (Ikegami et al., 1978). We found that with aphidicolin treatment, the cell number did not increase significantly from 24 to 48 hr (Figure 2—figure supplement 4A,B). In this condition, we still observed the radial alignment of boundary cells, which is quantitatively comparable with untreated controls (Figure 2—figure supplement 4C). Thus, we believe that the cell proliferation mediated remodeling is unimportant for the formation of cell radial alignment.

A graded isotropic actin meshwork was established in patterned REF cells

The REF 2c tissue is reminiscent of the epithelial cell monolayers with coherent intercellular junctions. However, previous studies showed that no alignment was found when epithelial cells were confined on similar circular patterns (Doxzen et al., 2013). A critical difference between epithelial cells and fibroblasts is that the actomyosin network mainly distributes on the cell-cell boundaries in epithelial cell monolayer with apical-basal polarity while fibroblast cells have continuous actin meshwork. Thus, we investigate the spatial organization of actin filaments and the concentration of phosphorylated myosin light chain in confined REF monolayers. Surprisingly, we found a decrease in actin intensity occurred near the boundary of patterns for REF 2c cells, in the same location as the transition between isotropically oriented inner cells and radially aligned boundary cells. (Figure 3). To evaluate the statistical significance of this intensity gradient, we divided the pattern into six segments with the same width, and quantified actin intensity and actin intensity per cell as a function of distance to pattern center (Figure 3—figure supplement 1A). Our Analysis of Variance (ANOVA) results clearly demonstrated that the actin intensity in the outmost layer was significantly lower than that of the inner cells. To exclude the possibility that such actin intensity gradient is simply a result of cell density difference, we also quantified the total actin intensity and actin intensity per cell in inner cells and the outmost boundary cells. Consistently, a significant difference was found between inner and boundary cells, suggesting this actin intensity gradient was not simply a result of cell density differences (Figure 3—figure supplement 1B,C). In contrast, for REF 11b, there was a continued decrease in intensity from the center of the pattern to the outermost edge (Figure 3). This is in sharp contrast to the actin distribution of 3T3 cells, in which no actin gradient was identified (Figure 3). Notably, the sharp drop in the intensity profiles near the very end of the intensity plot for actin was an artifact as the outermost cells did not fully cover the pattern boundary. We further analyzed the correlation between actin gradient in individual patterns and corresponding angle deviation of boundary cells (Figure 3—figure supplement 2). Our results showed that increasing steepness of the actin gradient negatively correlates with boundary cell angle deviation (r = − 0.533), suggesting actin gradient may contribute to the boundary cell radial alignment.

Figure 3 with 4 supplements see all

Download asset Open asset

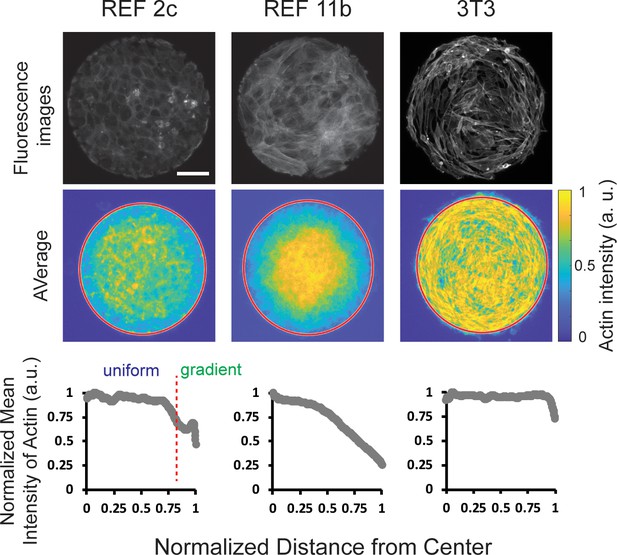
Tissue-scale actin intensity gradients were observed in patterned REF cells but not in 3T3 cells.

Top: fluorescence images showing the actin staining of REF 2c, REF 11b, and 3T3 cells. Scale bar: 100 μm. Middle: colorimetric maps showing the average actin intensity profiles obtained by overlapping actin staining images. n = 20 patterns per group. Bottom: normalized mean intensity of these overlapping images plotted as a function of the normalized distance from the center of the pattern.

A Voronoi-cell model demonstrated that the condensation tendency with actin gradient is sufficient for establishing cell radial alignment at the pattern boundary

We next asked what are the deterministic factors that dictate the polar alignment of REF 2c cells. On one hand, the experimental data suggest that the condensation tendency is essential for the polar alignment (Figure 2). In addition, the data shows that the alignment is associated with the elongation of the boundary cells (Figure 1), which suggests that these boundary cells are stretched more along the radial direction than along the circumferential direction. On the other hand, the actin gradient decreasing towards the boundary (Figure 3) suggests that there is a stiffness differential between the inner and boundary cells, given it is well-documented that actin intensity is proportional to the local cell stiffness (Tavares et al., 2017; Rotsch and Radmacher, 2000; Nawaz et al., 2012; Gavara and Chadwick, 2016). To examine the possibility that increased actin intensity is associated with increased contractility, we examined the distribution of contractility levels in confined REF 2c cells by immunostaining phosphorylated myosin (p-myosin). It was found that unlike actin distributions, the p-myosin distribution was almost uniform across the whole pattern, with only a small increase near the pattern boundary (Figure 3—figure supplement 3). Thus, we hypothesize that the radial alignment and elongation at the boundary in mechanical equilibrium is due to the condensation tendency and the cell stiffness differential between the inner and boundary cells.

We developed a Voronoi-cell model (Bi et al., 2016; Olaranont, 2019) to test our hypothesis (see Materials and methods). Given the actin orientation being neither radially nor circumferentially aligned (see Figure 3—figure supplement 4 and Materials and methods), we assume that the stiffness of the cells is isotropic. Similarly, we introduce an isotropic prestretch parameter 0 < $g$ ≤1 to describe the global condensation tendency in the patterned fibroblasts, which is a factor of the intrinsic cell area. The more $g$ deviates from 1, the larger the condensation tendency. As suggested by the direction of actin gradient (Figure 3), we introduce the stiffness differential between the boundary and the inner cells as $0 < ρ \leq 1$ . Noticeably, although the mechanical interaction between the cell monolayer and the substrate has been experimentally measured previously (Tambe et al., 2011), it is challenging in our case because to accurately measure the traction forces using PMA substrates, the effective Young’s modulus of the substrates needs to be less than 5 kPa, on which REF cells form aggregates due to the condensation tendency we described previously. Thus, we consider the mechanical equilibrium as a result of cell-cell mechanical interactions and the confinement at the tissue boundary (see Materials and methods for numerical implementation).

Our simulations show the radial alignment emerges when both condensation tendency $g$ and stiffness differential $ρ$ deviate from 1 (Figure 4A, Figure 4—figure supplement 1). Our shape analysis shows that in the radial-alignment case, the boundary cells are larger in size and more elongated (Figure 4B), consistent with the experiments (see Figure 1C,D, REF 2c cells). The results also explain the cell morphology observed in REF 11b cells, where no radial alignment is observed without contractility (see Figure 4B and Figure 4—figure supplement 1A, top rows). In addition, we show that when the value of $g$ is smaller in the boundary cells than that in the inner cells, and without stiffness differential ( $ρ = 1$ ), boundary cells have smaller areas but do not align in the radial direction (Figure 4—figure supplement 2). This suggests that the slight elevation of p-myosin in the boundary cells (Figure 3—figure supplement 3) is not the cause of the radial alignment.

Figure 4 with 9 supplements see all

Download asset Open asset

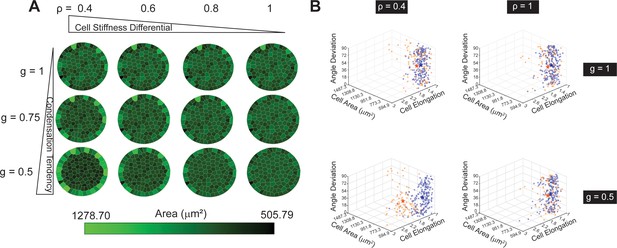
Condensation tendency and cell stiffness differential explain the radial-alignment boundary.

(A) Voronoi cell modeling results from varying condensation tendency parameter $g$ and cell stiffness differential parameter $ρ$ . Smaller $g$ and $ρ$ contribute to larger cell area along the boundary. (B) 3D Scatter plots of three cell-morphological parameters: angle deviation, cell area, and cell elongation. The three parameters on inner (orange) and boundary cells (blue) become significantly different when both $ρ$ and $g$ are small (e.g. $ρ = 0.4$ and $g = 0.5$ ; the stars represent the mean values among each cell group). n = 5 patterns.

The stress and strain analysis on individual cells from simulations show that the boundary cells and the inner cells are under different mechanical cues (Figure 4—figure supplement 3). Compared to the inner cells, the boundary cells are under more significant and anisotropic strains but more minor tensile stresses, on average. The differences in mechanical cues, especially the anisotropic stretch of the boundary cells might induce the actin cytoskeleton reorganization in cells. Thus, the observed radial alignment may also be due to the adaption of cell shapes to mechanical cues. To evaluate this possibility, we stained a focal adhesion protein, vinculin (Goldmann, 2016; Figure 4—figure supplement 4), and a canonical mechanosensor, YAP (Dupont et al., 2011) at 48 hr when radial alignment is prominent (Figure 4—figure supplement 5). If mechanotransduction is involved, we expect to see higher intensities of vinculin (Sigaut et al., 2018) and/or nuclear YAP (Elosegui-Artola et al., 2017) in the boundary cells. However, we found that the distribution of vinculin was uniform across the pattern area, except for reduced vinculin intensity near the pattern boundary. The overall vinculin intensity per cell in the outmost layer of cells was still comparable with inner cells. We also found that most of the REF 2c cells expressed nuclear YAP, which is independent of confinement and cell alignment status (24 hr vs. 48 hr). These results suggest local activation of these mechanotransduction pathways in boundary cells is unlikely the cause for cell radial alignment, although we cannot rule out the involvement of other mechanotransduction pathways, such as those mediated by mechanosensitive ion channels and certain G protein coupled-receptors (Martino et al., 2018; Holle and Engler, 2011; Marullo et al., 2020).

In summary, we have shown that condensation tendency with stiffness differential near the pattern boundary is sufficient to replicate the radial alignment and increased elongation and area of the boundary cells compared to inner cells in the REF 2c in vitro.

Actin gradient and condensation tendency maintain under the change of tissue topology

Our results demonstrated that the emergence of a cell stiffness gradient along the radial direction is critical for cell alignment. We next investigated whether such gradient maintains at the outer boundary under the change of the topology. To do so, we designed two ring patterns with different inner diameters (200 µm and 300 µm) and the same outer diameter (400 µm). We found that surprisingly, both REF 2c and 11b cultured on ring patterns robustly showed an actin intensity gradient from the center to the boundary, regardless of the change of topology and the radius of the inner boundary. In contrast, 3T3 cells did not have an actin gradient for any ring patterns (Figure 4—figure supplement 6). Similar to the circular patterns, we calculated the actin fiber angle deviation and the structure parameter k_H for REF 2c cells (Figure 4—figure supplement 7). Compared to the full circle pattern, the distribution of the structure parameter k_H in ring patterns reveals that the actin fibers are mostly aligned along the tangential direction at the inner boundary and the tangential alignment decreases along the radius, suggesting a complex interaction between the actin network and the inner boundary. For the thicker ring pattern, the actin network almost becomes isotropic ( $k_{H} ~ 0.65$ ) at the outer boundary. We then sought to investigate whether changing tissue topology to ring shapes change the REF 2c cell alignment. We found that for both thick and thin ring patterns, the outermost boundary REF 2c cells radially aligned, but not REF 11b cells or 3T3 cells, which are quantified using angle deviation (Figure 4—figure supplement 8). The cell area increased significantly near the exterior pattern boundary for REF 2c (Figure 4—figure supplement 9). Interestingly, the innermost boundary cells aligned circumferentially along the inner boundary.

Discussion

There is a growing interest in understanding the physical principles of the autonomous collective behavior of cells. Epithelial cells are often modeled as polygon arrays, and the mechanical states are described by the active stress between neighboring cells (Farhadifar et al., 2007; Bi et al., 2016; Tetley et al., 2019). On the other hand, actin-rich mesenchymal cells are often modeled as self-propelled particles, and they are believed to self-assemble as active nematics (Duclos et al., 2014; Doostmohammadi et al., 2018). Our results revealed a new class of behavior of the actin-rich cells with significant intercellular adhesion, represented by REF cells. We showed that these cells could form compact morphology and displays a condensation tendency, resulting in a change of cell size and cell elongation at the tissue boundary on rigid substrates. Unlike skeletal muscle cells, such condensation tendency is not originated from the anisotropy of actin bundles, as the actin network in REF monolayer is found to be isotropic (Figure 3—figure supplement 4). Our theoretical analysis suggests that such condensation tendency of the tissue, together with an autonomously established stiffness gradient in the monolayer, are sufficient to form the radial cell alignment tissue boundary in the confined planar geometries. Disrupting the cell-cell adhesion using EGTA also abolished the radial cell alignment of REF 2c cells (Figure 2E).

In this work, we describe the cell monolayer mechanics associated with cell contractility and differential cell stiffness by developing a cell-based model. Vertex models (Farhadifar et al., 2007; Tetley et al., 2019) and Voronoi cell models Bi et al., 2016; Olaranont, 2019 have been well-established for epithelial-like cells with strong cell-cell adhesion (Farhadifar et al., 2007), because of the cortical distribution of actin cytoskeleton. In previous cell-based modeling, vertex models (Farhadifar et al., 2007; Tetley et al., 2019) and Voronoi cell models (Bi et al., 2016; Olaranont, 2019) often describe the epithelial cell contractility along the intercellular junctions due to the cortical distribution of actin cytoskeleton with strong cell-cell adhesion. In our case of REF monolayer where the actin network does not spread coincidentally with the intercellular junctions, we modify the Voronoi-cell model to describe the condensation tendency as a prestretch on individual cell area, which has not been considered in the previous vertex or Voronoi cell models. We have shown that condensation tendency and a stiffness differential between the inner and boundary cells are sufficient to establish the radial-cell-alignment tissue boundary.

The cell system we described here is different from epithelial cells, which also have strong intercellular adhesion and contractility as individual cells. Epithelial cells, when confined in circular patterns, form nematic symmetry that is similar to 3T3 cells (Saw et al., 2017; Doxzen et al., 2013). However, when they are confined in ring-shape patterns, chiral spiral defects can be found (Wan et al., 2011). The different cell alignment between epithelial cells and REF cells is likely due to the distribution of actin network. It is well-known that actin is mainly distributed in the cell-cell junctions for epithelial cells (Fanning et al., 2012), while actin stress fibers can be found in REF cells even when they form a compact monolayer. Notably, neuroepithelial cells derived from pluripotent stem cells could form rosettes-like structures in vitro, with tight and adherence junctions presented at the side facing the internal lumen (Knight et al., 2018; Elkabetz et al., 2008). However, the formation of neural rosettes may require a completely different mechanism as neuroepithelial cells are planar polarized (Davey et al., 2016), and the junctional proteins distributed homogenously for REF cells. Recently, Roux, Kruse, and colleagues reported that C2C12 myoblasts could self-organize into spiral patterns when confined using similar circular confinement (Blanch-Mercader et al., 2021a; Blanch-Mercader et al., 2021b; Guillamat et al., 2020). When cell proliferation is allowed, the system continues to evolve to aster pattern with boundary cells elongated and radially aligned (Blanch-Mercader et al., 2021b) and eventually out-of-plane mounds in pattern center (Guillamat et al., 2020). Using hydrodynamic descriptions, they attributed the formation of such patterns to both directional traction forces and nematic active stresses (Blanch-Mercader et al., 2021a; Blanch-Mercader et al., 2021b). Computational and experimental works also confirmed that the tissue is contractile and generates compressive forces to cells in the pattern center. While our observation of radial cell alignment on pattern boundary is reminiscent of the aster patterns observed in those works, an important difference is that the cell proliferation is not required for the radial alignment to appear (Figure 2—figure supplement 4). Further, the radial alignment in C2C12 cells seems to be an intermediate state between the spiral tissue flow to mound growth, while the REF radial alignment is an equilibrium state where the cell velocity is nearly zero (Figure 1—figure supplement 1). While cell proliferation is a critical driving factor in aster pattern formation in the C2C12 system, in our REF system, the stiffness differential is indispensable for the radial alignment formation. Together, the REF cells represented a unique class of cell systems that are different from typical spindle-like 3T3 cells, epithelial cells, and C2C12 myoblasts. Future studies will be needed to investigate whether other cells that may fall into this category, such as neural crest cells, chondrocytes, and epithelial cells undergoing epithelial-mesenchymal transition, also behave similarly on patterned substrates. Interestingly, neural crest cells migrate as a cohesive group mediated by self-secreted C3a (Carmona-Fontaine et al., 2011), and chondrocytes form mesenchymal condensation mediated by EGF signals (Qin and Beier, 2019). The condensation tendency of these cells may be relevant to their biological functions by facilitating their orientation towards the signal center.

In multiple developmental and physiological processes, previous focuses have been on the differential growth and contractility as a stress-and-strain driver (Ambrosi et al., 2019; Streichan et al., 2018), while there is a lack of elucidation of the role on differential stiffness (except in Drosophila gastulation [Polyakov et al., 2014; Rauzi et al., 2015]). In 2D tissues, it is difficult to disentangle differential contractility and stiffness as the two mechanical properties are both connected to the actomyosin activities. A positive correlation between the actin and myosin spatial distributions has been widely reported previously (Martin et al., 2009; Banerjee et al., 2017). However, in the REF microtissue, we have found that the myosin gradient is not evident and does not coincide with that of the actin gradient. While it is well-documented that myosin is associated with higher contractile force (Murrell et al., 2015) and actin is associated with higher stiffness (Tavares et al., 2017; Rotsch and Radmacher, 2000; Nawaz et al., 2012; Gavara and Chadwick, 2016), in theory, we disentangled their roles in regulating the cell morphology at the REF tissue boundary. We reason that differential stiffness with uniform contractility is sufficient to explain the radial-cell-alignment tissue boundary. Indeed, the actin mesh architecture may also affect the contractile machinery, such as through the concentration of the crosslinking proteins (Kasza and Zallen, 2011). Thus, we cannot exclude the possibility of a contractility differential associated with the observed actomyosin intensity field. Notably, in a very recent work, the authors associated actin intensity differential with contractility differential during mesoderm invagination in the early Drosophila melanogaster embryo (Denk-Lobnig et al., 2021). However, this possibility requires further analysis on how myosin motors and actin network molecules interact to generate macroscopic network contraction. Future work will investigate how tissue-level actin gradient and orientation field and tissue flow interact in response to geometric and mechanical cues. In particular, a Maxwell-type viscoelastic continuum model will be needed to couple the actin dynamics with active tissue mechanics to explain the onset of tissue flow and the maintenance of the tissue mechanical equilibrium (Wei and Wu, 2021). This new framework will account for the energy dissipation due to cell-cell junction and cytoskeletal rearrangement during the tissue flow before equilibrium.

In summary, this work reports a unique behavior of REF cells that develop radial-alignment boundary when confined in circular and ring mesoscale patterns. The formation of such radial alignment is not a result of directed cell migration and requires a condensation tendency and an emergent cell stiffness differential. Future work must be done to understand the molecular mechanisms of this novel collective cell behavior and its contribution to relevant biological functions.

Materials and methods

Cell culture

Request a detailed protocol

Original Rat Embryo Fibroblast cell line (REF-52; RRID:CVCL_6848) stably expressing yellow fluorescent protein (YFP) - paxillin fusion protein is a gift from Dr. Jianping Fu. REF 11b and 2c subclones were generated by single-cell clone selection. Cells were maintained in high-glucose Dulbecco’s modified Eagle’s medium (DMEM, no glutamine; Invitrogen) supplemented with 10% fetal bovine serum (FBS; Invitrogen), 4 mM L-glutamine (Invitrogen), 100 units/mL penicillin (Invitrogen), and 100 μg/mL streptomycin (Invitrogen). NIH/3T3 cells (a gift from Dr. Mingxu You; RRID:CVCL_0594) were cultured in DMEM medium (with glutamine, Invitrogen) supplemented with 10% calf serum as suggested by ATCC, 100 units/mL penicillin (Invitrogen), and 100 μg/mL streptomycin (Invitrogen). Although not recommended, culturing 3T3 cells using media containing FBS did not significantly change experimental outcomes. Both 3T3 and REF cells were subcultured at about 80% confluency following standard cell culture procedures. All cells were cultured at 37°C and 5% CO₂. NIH-3T3 cells were authenticated using the STR profiling service provided by ATCC. All the cell lines have been tested for mycoplasma contamination using PCR-based methods and negative testing results were obtained.

RNA sequencing and data analysis

Request a detailed protocol

Total RNA was extracted from REF subclones 2c and 11b using the Aurum Total RNA Mini Kit (Bio-rad) following the manufacturer's instructions. RNA quality was assessed using 6000 Nano Agilent 2100 Bioanalyzer (Agilent Technologies, Santa Clara, CA). The concentration of the libraries was measured using Qubit 3.0 fluorometer (Life Technologies, Carlsbad, CA). cDNA libraries were single-end sequenced in 76 cycles using a NextSeq 500 Kit v2 (FC-404–2005, Illumina, San-Diego, CA). High-throughput sequencing was performed using NextSeq500 sequencing system (Illumina, San-Diego, CA) in the Genomic Resource Laboratory of the University of Massachusetts, Amherst. All sequencing data were uploaded to the GEO public repository (https://www.ncbi.nlm.nih.gov/geo/) and were assigned series GSE148155. Validation of sequence quality was performed using the BaseSpace cloud computing service supported by Illumina (BaseSpace Sequence Hub, https://basespace.illumina.com/home/index). RNA-seq reads were aligned to the rat reference genome (Rattus norvegicus UCSC rn5) using TopHat Alignment. Then, the differential gene expression analyses were performed by Cufflinks Assembly and DE using previous alignment results produced by the TopHat app as input. Shortlists of significantly differentially expressed genes were identified by applying thresholds of 2-fold differential expression and false discovery rate q ≤ 0.05.

Cell migration assay

Request a detailed protocol

To track the migration of patterned REF 2c cells, brightfield live-cell imaging was performed at 37°C, 5% CO₂ using an automated digital microscope with a 10× objective with a gas controller (Cytation three microplate reader, BioTek Instruments Inc, Winooski, VT, USA). Images were collected every 10 min for 24 hr. Acquired brightfield images were merged and corrected for frame drift. To analyze cell migration, individual cell positions were manually tracked using CellTracker software (Piccinini et al., 2016) implemented in MATLAB (MATLAB R2020a, MathWorks). The average speed for each cell was calculated as the total migration length of each cell divided by the total time. Mann–Whitney test was used to compare the migration length and average speed of the cells since the data were not normally distributed (Shapiro-Wilk test). Statistical differences were defined as where *, p < 0.05; **, p <0.01; ***, p <0.001.

Microcontact printing

Request a detailed protocol

Soft lithography was used to generate patterned polydimethylsiloxane (PDMS) stamps from negative SU8 molds that were fabricated using photolithography. These PDMS stamps were used to generate patterned cell colonies using microcontact printing, as described previously (Zhu et al., 2019). Briefly, to generate patterned cell colonies on flat PDMS surfaces, round glass coverslips (diameter = 25 mm, Fisher Scientific) were spin-coated (Spin Coater; Laurell Technologies) with a thin layer of PDMS prepolymer comprising of PDMS base monomer and curing agent (10:1 w/w; Sylgard 184, Dow-Corning). PDMS coating layer was then thermally cured at 110°C for at least 24 hr. In parallel, PDMS stamps were incubated with a fibronectin solution (50 µg·ml⁻¹, in deionized water) for 1 hr at room temperature before being blown dry with a stream of nitrogen. Excess fibronectin was then washed away by distilled water and the stamps were dried under nitrogen. Fibronectin-coated PDMS stamps were then placed on top of ultraviolet ozone-treated PDMS (7 min, UV-ozone cleaner; Jetlight) on coverslips with a conformal contact. The stamps were pressed gently to facilitate the transfer of fibronectin to PDMS-coated coverslips. After removing stamps, coverslips were disinfected by submerging in 70% ethanol. Protein adsorption to PDMS surfaces without printed fibronectin was prevented by incubating coverslips in 0.2% Pluronic F127 solution (P2443-250G, Sigma) for 30 min at room temperature. Coverslips were rinsed with PBS before placed into tissue culture plates for cell seeding. For patterned cell colonies, PDMS stamps containing circular patterns with a diameter of 344 µm, and ring patterns with an outer diameter of 400 µm and inner diameter of either 200 µm (thick ring) or 300 µm (thin ring) were used.

Immunocytochemistry

Request a detailed protocol

Four percent paraformaldehyde (Electron Microscopy Sciences) was used for cell fixation before permeabilization with 0.1% Triton X-100 (Fisher Scientific). Cells were blocked in 10% donkey serum for 1 hr at room temperature. Primary antibodies used were anti-β-catenin from rabbit (51067–2-AP, Proteintech), anti-α-tubulin from mouse (66031–1-Ig, Proteintech), anti-p-myosin from rabbit (3671T, Cell Signalling), anti-vinculin from mouse (V9131, Sigma), and anti-YAP from mouse (sc-101199, Santa Cruz). For immunolabeling, donkey-anti goat Alexa Fluor 488, donkey-anti rabbit Alexa Fluor 555, and donkey-anti mouse Alexa Fluor 647 were used. For actin filaments visualization, Alexa Fluor 488 conjugated phalloidin (Invitrogen) was used. Samples were counterstained with 4,6-diamidino-2- phenylindole (DAPI; Invitrogen) to visualize the cell nucleus.

Small-molecule drugs treatment assays

Request a detailed protocol

Blebbistatin (10 µM, Cayman Chemical, cat.no.13013), Y27632 (10 µM, Cayman Chemical, cat.no.10005583), and Aphidicolin (1 µg/ml, Cayman Chemical, cat.no.14007) were dissolved in DMSO. Ethylene Glycol Tetraacetic Acid, (EGTA, 2 mM, Santa Cruz Biotechnology, cat.no. sc-3593A) was prepared in distilled water. Cells were treated with these drugs for 24 hr at 37°C.

Traction force measurement

Request a detailed protocol

The protocol for generating microposts and measuring traction force has been published previously (Xie et al., 2017). For single cell traction force measurement, REF cells were incubated for 48 hr on DiI stained micropost arrays, then live-cell imaged. Microposts with a diameter of 2 µm and a height of 8.4 µm (effective modulus E_eff ₌5 kPa) were used. Custom MATLAB script was written to quantify post deflection using Equation 1:

F = (\frac{3 E I}{L^{3}}) x,

where F is the force applied to the tip of the post, E is the elastic modulus of PDMS, I is the area moment of inertia, L is the post height, and x is the deflection of the post tip (MathWorks; https://www.mathworks.com/).

Image analysis

Request a detailed protocol

Phase contrast and fluorescence images of patterned cell colonies were recorded using an inverted epifluorescence microscope (Leica DMi8; Leica Microsystems) equipped with a monochrome charge-coupled device (CCD) camera. Since the cell colonies were circle-like in shape and the approximate radii of the circles were known, the centers of the colonies could be found using the circle Hough transformation which is the MATLAB function imfindcircles. The distance vector between the center of each cell colony and the center of the image frame shifted each pixel of the image. Using the shifted images, the stacked images could be generated by adding the values at the same position of the pixels. The fluorescence intensity of each pixel in stacked images was normalized by the maximum intensity identified in each image. To plot average intensity as a function of distance from the pattern centroid, the stacked intensity maps were divided into 310, 186, and 91 concentric zones for the circle, thick ring, and thin ring, respectively, with single pixel width. The average pixel intensity in each concentric zone was calculated and plotted against the normalized distance of the concentric zone from the pattern centroid.

Fiber angle deviation

Request a detailed protocol

The vector module of the Orientation J plug-in (Rezakhaniha et al., 2012) was used with Fiji (Schneider et al., 2012) to quantify the angle deviation of actin and α-tubulin stained fibers in REF cell images. Five images were analyzed for each group (circle, thick ring, thin ring). The mean fiber angle deviation was plotted versus the normalized distance from the center of the pattern. A step size of 172/31 ≈ 5.55 µm for the circle, 100/18 ≈ 5.56 µm for the thick ring, and 50/9 ≈ 5.56 µm for the thin ring patterns were used to generate approximately the same number of points respective to the size of the pattern. The schematic of (α), fiber angle deviation from the radius, was drawn in Figure 3—figure supplement 4.

Structure tensor

Request a detailed protocol

The structure parameter, k_H, was calculated from histograms developed from the variation of fiber angle deviation at each concentric distance from the center or innermost edge of the patterns (Figure 3—figure supplement 4 and Figure 4—figure supplement 7). We used a 2D structure tensor $H$ to quantify the averaged fiber orientation of the fibers at each point along the radius (Wu and Ben Amar, 2015):

H = \frac{1}{π} \int_{- π / 2}^{π / 2} ρ (α) E_{α} \otimes E_{α} d α = k_{H} I + (1 - 2 k_{H}) E_{R} \otimes E_{R}

where $α$ is the angle between the outward radial direction $E_{R}$ and actin fiber direction $E_{α}$ (See Figure 3—figure supplement 4) and $ρ (α)$ is the normalized orientation density function satisfying $ρ (α) = ρ (- α)$ and $\frac{1}{π} \int_{- π / 2}^{π / 2} ρ (α) d α = 1 .$ As $I$ is the 2 × 2 identity matrix and $E_{R} \otimes E_{R} = [\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}]$ , the structure tensor H can be represented by the structure parameter

k_{H} = \frac{1}{π} \int_{- π / 2}^{π / 2} ρ (α) {(\sin α)}^{2} d α .

By definition, 0 ≤ k_H ≤ 1, and the ﬁber distribution is more aligned with the radial (circumferential) direction as k_H decreases (increases). k_H = 0.5 indicates that the actin ﬁber distribution is not aligned with either direction. From the actin intensity field, our quantification shows that $k_{H}$ is approximately 0.4 ~ 0.6 along the radius, suggesting an isotropic distribution of the fiber orientation (Figure 3—figure supplement 4D). The scripts for structure tensor calculation are available through Github, copy archived at swh:1:rev:0a5972451e8e747ea755cba6613ef0d81c8aabfd (St Pierre and Wu, 2021).

Voronoi cell mathematical model

Cell-tissue configurations

Request a detailed protocol

We begin with a 2D domain and generate polygonal cells from the 2D Voronoi tessellation to represent the cell configurations. The graph of Voronoi cell tessellation is dual to the Delaunay triangulations. In particular, the relation between a trio of adjacent Voronoi cell centers (<r_i, r_j, r_k>) and its corresponding vertex (ω_<i,j,k>) is given by the following equations (Bi et al., 2016, Olaranont, 2019):

{\vec{ω}}_{< i, j, k >} = a {\vec{r}}_{i} + b {\vec{r}}_{j} + c {\vec{r}}_{k}

where

a = {‖ {\vec{r}}_{j} - {\vec{r}}_{k} ‖}^{2} ({\vec{r}}_{i} - {\vec{r}}_{j}) \cdot ({\vec{r}}_{i} - {\vec{r}}_{k}) / D,

b = {‖ {\vec{r}}_{i} - {\vec{r}}_{k} ‖}^{2} ({\vec{r}}_{j} - {\vec{r}}_{i}) \cdot ({\vec{r}}_{j} - {\vec{r}}_{k}) / D,

c = {‖ {\vec{r}}_{i} - {\vec{r}}_{j} ‖}^{2} ({\vec{r}}_{k} - {\vec{r}}_{i}) \cdot ({\vec{r}}_{k} - {\vec{r}}_{j}) / D,

D = 2 {‖ ({\vec{r}}_{i} - {\vec{r}}_{j}) \times ({\vec{r}}_{j} - {\vec{r}}_{k}) ‖}^{2} .

Cell prestretch and differential stiffness

Request a detailed protocol

To describe the monolayer mechanics, we define a total energy that is generally a function of the areas of cells $A^{α}$ and lengths of junctions $l_{β}^{α}$ :

E_{t o t a l} = \sum_{α} E^{α}; E^{α} = \frac{1}{2} K^{α} {(g A}_{0}^{α}) (\frac{A^{α}}{g A_{0}^{α}} - 1)^{2} + \sum_{β \in Γ} λ l_{β}^{α},

where $α$ indicates each cell, $β$ indexes junctions of cell $α$ , and $Γ$ is the set of junctions of cell $α$ with tension. For modeling epithelial cells, the tension is considered on each intercellular junction to represent the net mechanical effect of actomyosin contraction and intercellular adhesion at the apical surface of the tissue. We apply tension to the intercellular junctions, and on the junctions located at the boundaries of the micropattern to ensure the circularity of the microtissue (see Geometric confinement below). To model the condensation tendency, we introduce the prestretch $0 < g \leq 1$ which decreases the intrinsic cell size $A_{0}^{α}$ of each cell. To describe the stiffness gradient between the boundary cells and interior cells (Figure 4A, the stiffness of boundary cells is smaller than or equal to that of the interior cells), we introduce the stiffness differential parameter $0 < ρ \leq 1$ , which is the ratio of the stiffness $K^{α}$ between boundary and interior cells. To describe the contractility gradient between the boundary cells and interior cells (Figure 4—figure supplement 2), the contractility of boundary cells is larger than or equal to that of the interior cells, meaning the prestretch of the boundary cells is smaller than or equal to that of the interior cells, we introduce the contractility differential parameter $0 < ρ_{g} \leq 1$ , which is the ratio of the prestretch between boundary and interior cells.

Mechanical equilibrium among cells

Request a detailed protocol

$E_{t o t a l}$ is a function of the coordinates of vertices via its dependence on lengths of junctions and areas of cells. In particular, the length of each junction is $l_{β}^{α} = ‖ {\vec{ω}}_{β, 1} - {\vec{ω}}_{β, 2} ‖$ where 1 and 2 indicate the adjacent vertices of $β$ junction, and the area of each cell is $A^{α} = \frac{1}{2} \sum_{m = 0}^{z^{α} - 1} ‖ {\vec{ω}}_{m}^{α} \times {\vec{ω}}_{m + 1}^{α} ‖$ , where $z^{α}$ is the number of vertices of cell $α$ (Notice that ${\vec{ω}}_{z^{α}}^{α} = {\vec{ω}}_{0}^{α}$ ). In addition, the coordinates of vertices depend on the coordinates of a trio of neighboring Voronoi cell centers through Equations (4) and (5). By the chain rule, we can solve the cell configurations by minimizing the energy $E_{t o t a l}$ following the dynamics of cell centers:

\frac{d r_{x}^{α}}{d t} = F_{x}^{α} \equiv - \frac{\partial E_{t o t a l}}{\partial r_{x}^{α}} = - (\sum_{m} \frac{\partial E^{α}}{\partial ω_{m x}^{a}} \frac{\partial ω_{m x}^{a}}{\partial r_{x}^{α}} + \sum_{m} \frac{\partial E^{α}}{\partial ω_{m y}^{α}} \frac{\partial ω_{m y}^{a}}{\partial r_{x}^{α}}),

\frac{d r_{y}^{α}}{d t} = F_{y}^{α} \equiv - \frac{\partial E_{t o t a l}}{\partial r_{y}^{α}} = - (\sum_{m} \frac{\partial E^{α}}{\partial ω_{m x}^{a}} \frac{\partial ω_{m x}^{a}}{\partial r_{y}^{a}} + \sum_{m} \frac{\partial E^{α}}{\partial ω_{m y}^{a}} \frac{\partial ω_{m y}^{a}}{\partial r_{y}^{a}})

where $m$ is the index of the vertices of cell $α$ . The subscripts x and y indicate the component x or y of the vector we are considering.

Geometric confinement at the boundary

Request a detailed protocol

We define a full circle or annulus inside the squared domain to initialize the micropattern, by calibrating the size ratio between individual cell and the micropattern according to the in vitro setup. Initially, there are 625 cells in the squared domain. From the experiments, the number of cells in the circular pattern is approximately 121 cells. Therefore, to simulate the results, the circular domain is demarcated by thresholding the distance of cells from the origin which covers around 120–124 cells depending on the random initial configuration. To round up the circular border, we minimize the following energy:

E_{i n i t i a l} = \sum_{α} E^{α} + \frac{1}{2} k_{b} A_{0} (\frac{A}{A_{0}} - 1)^{2};

E^{α} = \frac{1}{2} K^{α} A_{0}^{α} (\frac{A^{α}}{A_{0}^{α}} - 1)^{2} + \sum_{β \in Γ} λ l_{β}^{α} + \sum_{β \in Γ_{o u t}} λ_{o u t} l_{β}^{α}

with $K^{α} = 1, {λ = 15, λ}_{o u t} = 20,$ and $k_{b} = 0.1 .$ The tension term $\sum_{β \in Γ_{o u t}} λ_{o u t} l_{β}^{α}$ is included to ensure the circularity of the boundary, and the term $\frac{1}{2} k_{b} A_{0} (\frac{A}{A_{0}} - 1)^{2}$ is included to ensure that the total area $A$ of the micropattern is close to the initial tissue area $A_{0}$ . Once $E_{i n i t i a l}$ reached a local minimum, the centroids of the boundary cells and cells outside of the circular domain were fixed. When the prestretch, stiffness differential and tension on the intercellular junctions are considered in Equation (6), all the non-boundary cell centers move and reach equilibrium following Equation (7).

Cell geometry analysis

Request a detailed protocol

For the cell elongation parameter and angle deviation (Figure 4B), we first compute the shape tensor $S_{α} = \frac{1}{Z_{α}} \sum_{i = 1}^{Z_{α}} {\vec{z}}_{α}^{i} \otimes {\vec{z}}_{α}^{i}$ where ${\vec{z}}_{α}^{i}$ is the vector from the cell centroid to vertex i (Nestor-Bergmann et al., 2018). The shape tensor comes with two positive eigenvalues $λ_{a}$ and $λ_{b}$ and their corresponding eigenvectors.

The cell elongation parameter is computed by $m a x (λ_{a} {, λ}_{b}) / m i n (λ_{a} {, λ}_{b})$ . The angle deviation is quantified between the eigenvector of $m a x (λ_{a} {, λ}_{b})$ and the local radial vector.

Stress and strain analysis

Request a detailed protocol

We compute the average stress and strain on each Voronoi-cell by the following procedure. The average stress on the cell $α$ is calculated as

σ^{α} = \frac{1}{A^{α}} \iint_{\partial Ω^{α} \cup Ω^{α}}^{} σ d A = \frac{1}{A^{α}} \sum_{β = 1}^{Z^{α}} \frac{Λ_{β}^{α}}{2} {\hat{t}}_{β}^{α} \otimes {\hat{t}}_{β}^{α} l_{β}^{α} + K (\frac{A^{α}}{g^{α} A_{0}^{α}} - 1) I

where ${\hat{t}}_{β}^{α}$ denotes the unit vector along the junction $β$ . $Z_{α}$ denotes the total number of junctions (or vertices) of the cell (Batchelor, 1970). The radial and circumferential stresses (Figure 4—figure supplement 3) are computed by $\hat{r} \cdot σ^{α} \hat{r}$ and $\hat{θ} \cdot σ^{α} \hat{θ}$ , respectively, where $\hat{r}$ is the local unit radial vector and $\hat{θ}$ is the local unit tangential vector.

For the strain, we rescale the two eigenvalues of the shape tensor $S_{α}$ by $\sqrt{A^{α} / π λ_{a} λ_{b}}$ such that the rescaled $λ_{a}$ and $λ_{b}$ represent the two principal axes of the ellipses with cell area $A^{α}$ . By assuming the stress-free cell configuration as a circle with area ${g A}_{0}^{α}$ , we compute the two principal cell strains of the cell as $λ_{a} / \sqrt{{g A}_{0}^{α} / π}$ and $λ_{b} / \sqrt{{g A}_{0}^{α} / π}$ (Figure 4—figure supplement 3).

The scripts for the Voronoi cell model are available through Github, copy archived at swh:1:rev:c943c5d773d4748b9fbc96c9c846279e04173d12 (Olaranont and St Pierre, 2021).

Statistical analysis

Request a detailed protocol

Student’s t-test was used when there were two groups. One-way ANOVA and post-hoc Tukey’s test were used for three or more groups. Mann–Whitney test was used for data that was found not normally distributed. Data are represented as mean ± s.e.m. The n values are determined using G*Power, using the standard deviation and effect size from pilot experiments, with a type I error rate α = 0.05 and power of 80%. In all cases, the actual n values are significantly larger than the desired n value. All the experiments were repeated at least three times independently (biological replicates), and in each experiment, at least two technical replicates (replicates within each experiment) were used. Samples were randomly allocated into experimental groups in the drug treatment experiments, while masking was not used during group allocation, data collection, and/or data analysis.

Customized MATLAB scripts

Request a detailed protocol

The MATLAB scripts used in the modeling and quantification of this work were made available to the research community.

The Voronoi cell model: https://github.com/nolarano/2D_Voronoi_Cell_Radial_Alignment.

The scripts for determining the fiber angle deviation structure tensor: https://github.com/nolarano/AngleDev_StructureTensor.git.

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files. All sequencing data were uploaded to the GEO public repository (https://www.ncbi.nlm.nih.gov/geo/) and were assigned series (GSE148155).

The following data sets were generated

1. Xie T
2. Pierre SR
3. Sun Y
(2020) NCBI Gene Expression Omnibus
ID GSE148155. Cell contractility and an actin gradient drive polar alignment of fibroblasts in constrained geometries.

https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE148155

References

1. Achilleos A
2. Trainor PA
(2012) Neural crest stem cells: discovery, properties and potential for therapy
Cell Research 22:288–304.
https://doi.org/10.1038/cr.2012.11
- PubMed
- Google Scholar
(2011) Negative feedback from integrins to cadherins: a micromechanical study
Biophysical Journal 101:336–344.
https://doi.org/10.1016/j.bpj.2011.06.009
- PubMed
- Google Scholar
1. Ambrosi D
2. Ben Amar M
3. Cyron CJ
4. DeSimone A
5. Goriely A
6. Humphrey JD
7. Kuhl E
(2019) Growth and remodelling of living tissues: perspectives, challenges and opportunities
Journal of the Royal Society Interface 16:20190233.
https://doi.org/10.1098/rsif.2019.0233
- PubMed
- Google Scholar
1. Aomatsu E
2. Chosa N
3. Nishihira S
4. Sugiyama Y
5. Miura H
6. Ishisaki A
(2014) Cell-cell adhesion through N-cadherin enhances VCAM-1 expression via PDGFRβ in a ligand-independent manner in mesenchymal stem cells
International Journal of Molecular Medicine 33:565–572.
https://doi.org/10.3892/ijmm.2013.1607
- PubMed
- Google Scholar
1. Banerjee DS
2. Munjal A
3. Lecuit T
4. Rao M
(2017) Actomyosin pulsation and flows in an active elastomer with turnover and network remodeling
Nature Communications 8:1121.
https://doi.org/10.1038/s41467-017-01130-1
- PubMed
- Google Scholar
1. Batchelor GK
(1970) The stress system in a suspension of force-free particles
Journal of Fluid Mechanics 41:545–570.
https://doi.org/10.1017/S0022112070000745
- Google Scholar
1. Beningo KA
2. Hamao K
3. Dembo M
4. Wang YL
5. Hosoya H
(2006) Traction forces of fibroblasts are regulated by the Rho-dependent kinase but not by the myosin light chain kinase
Archives of Biochemistry and Biophysics 456:224–231.
https://doi.org/10.1016/j.abb.2006.09.025
- PubMed
- Google Scholar
1. Bi D
2. Yang X
3. Marchetti MC
4. Manning ML
(2016) Motility-driven glass and jamming transitions in biological tissues
Physical Review X 6:021011.
https://doi.org/10.1103/PhysRevX.6.021011
- PubMed
- Google Scholar
(2021a) Integer topological defects of cell monolayers: Mechanics and flows
Physical Rreview. E 103:012405.
https://doi.org/10.1103/PhysRevE.103.012405
- PubMed
- Google Scholar
(2021b) Quantifying Material Properties of Cell Monolayers by Analyzing Integer Topological Defects
Physical Review Letters 126:028101.
https://doi.org/10.1103/PhysRevLett.126.028101
- PubMed
- Google Scholar
1. Carmona-Fontaine C
2. Theveneau E
3. Tzekou A
4. Tada M
5. Woods M
6. Page KM
7. Parsons M
8. Lambris JD
9. Mayor R
(2011) Complement fragment C3a controls mutual cell attraction during collective cell migration
Developmental Cell 21:1026–1037.
https://doi.org/10.1016/j.devcel.2011.10.012
- PubMed
- Google Scholar
(2002) N-cadherin-dependent cell-cell contact regulates rho GTPases and beta-catenin localization in mouse C2C12 myoblasts
Journal of Cell Biology 158:953–965.
https://doi.org/10.1083/jcb.200202034
- PubMed
- Google Scholar
(2016) PCP signaling between migrating neurons and their Planar-Polarized neuroepithelial environment controls filopodial dynamics and directional migration
PLOS Genetics 12:e1005934.
https://doi.org/10.1371/journal.pgen.1005934
- PubMed
- Google Scholar
1. Denk-Lobnig M
2. Totz JF
3. Heer NC
4. Dunkel J
5. Martin AC
(2021) Combinatorial patterns of graded RhoA activation and uniform F-actin depletion promote tissue curvature
Development 148:dev199232.
https://doi.org/10.1242/dev.199232
- PubMed
- Google Scholar
(2018) Active nematics
Nature Communications 9:3246.
https://doi.org/10.1038/s41467-018-05666-8
- PubMed
- Google Scholar
1. Doxzen K
2. Vedula SR
3. Leong MC
4. Hirata H
5. Gov NS
6. Kabla AJ
7. Ladoux B
8. Lim CT
(2013) Guidance of collective cell migration by substrate geometry
Integrative Biology 5:1026–1035.
https://doi.org/10.1039/c3ib40054a
- PubMed
- Google Scholar
(2014) Perfect nematic order in confined monolayers of spindle-shaped cells
Soft Matter 10:2346–2353.
https://doi.org/10.1039/c3sm52323c
- PubMed
- Google Scholar
(2017) Topological defects in confined populations of spindle-shaped cells
Nature Physics 13:58–62.
https://doi.org/10.1038/nphys3876
- Google Scholar
1. Dupont S
2. Morsut L
3. Aragona M
4. Enzo E
5. Giulitti S
6. Cordenonsi M
7. Zanconato F
8. Le Digabel J
9. Forcato M
10. Bicciato S
11. Elvassore N
12. Piccolo S
(2011) Role of YAP/TAZ in mechanotransduction
Nature 474:179–183.
https://doi.org/10.1038/nature10137
- PubMed
- Google Scholar
(2008) Human ES cell-derived neural rosettes reveal a functionally distinct early neural stem cell stage
Genes & Development 22:152–165.
https://doi.org/10.1101/gad.1616208
- PubMed
- Google Scholar
(2017) Force Triggers YAP Nuclear Entry by Regulating Transport across Nuclear Pores
Cell 171:1397–1410.
https://doi.org/10.1016/j.cell.2017.10.008
- PubMed
- Google Scholar
(2012) Zonula occludens-1 and -2 regulate apical cell structure and the zonula adherens cytoskeleton in polarized epithelia
Molecular Biology of the Cell 23:577–590.
https://doi.org/10.1091/mbc.E11-09-0791
- PubMed
- Google Scholar
(2007) The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing
Current Biology 17:2095–2104.
https://doi.org/10.1016/j.cub.2007.11.049
- PubMed
- Google Scholar
(2004) Collective cell migration in Morphogenesis and Cancer
The International Journal of Developmental Biology 48:441–449.
https://doi.org/10.1387/ijdb.041821pf
- PubMed
- Google Scholar
1. Gavara N
2. Chadwick RS
(2016) Relationship between cell stiffness and stress fiber amount, assessed by simultaneous atomic force microscopy and live-cell fluorescence imaging
Biomechanics and Modeling in Mechanobiology 15:511–523.
https://doi.org/10.1007/s10237-015-0706-9
- PubMed
- Google Scholar
1. Ghibaudo M
2. Saez A
3. Trichet L
4. Xayaphoummine A
5. Browaeys J
6. Silberzan P
7. Buguin A
8. Ladoux B
(2008) Traction forces and rigidity sensing regulate cell functions
Soft Matter 4:1836–1843.
https://doi.org/10.1039/b804103b
- Google Scholar
1. Goldmann WH
(2016) Role of vinculin in cellular mechanotransduction
Cell Biology International 40:241–256.
https://doi.org/10.1002/cbin.10563
- PubMed
- Google Scholar
Preprint
(2020) Integer topological defects organize stresses driving tissue morphogenesis
bioRxiv.
https://doi.org/10.1101/2020.06.02.129262
- Google Scholar
(2008) Wound repair and regeneration
Nature 453:314–321.
https://doi.org/10.1038/nature07039
- PubMed
- Google Scholar
1. Holle AW
2. Engler AJ
(2011) More than a feeling: discovering, understanding, and influencing mechanosensing pathways
Current Opinion in Biotechnology 22:648–654.
https://doi.org/10.1016/j.copbio.2011.04.007
- PubMed
- Google Scholar
1. Ikegami S
2. Taguchi T
3. Ohashi M
4. Oguro M
5. Nagano H
6. Mano Y
(1978) Aphidicolin prevents mitotic cell division by interfering with the activity of DNA polymerase-alpha
Nature 275:458–460.
https://doi.org/10.1038/275458a0
- PubMed
- Google Scholar
1. Kasza KE
2. Zallen JA
(2011) Dynamics and regulation of contractile actin-myosin networks in morphogenesis
Current Opinion in Cell Biology 23:30–38.
https://doi.org/10.1016/j.ceb.2010.10.014
- PubMed
- Google Scholar
(2017) Topological defects control collective dynamics in neural progenitor cell cultures
Nature 545:327–331.
https://doi.org/10.1038/nature22321
- PubMed
- Google Scholar
1. Klumpers DD
2. Mao AS
3. Smit TH
4. Mooney DJ
(2014) Linear patterning of mesenchymal condensations is modulated by geometric constraints
Journal of the Royal Society, Interface 11:20140215.
https://doi.org/10.1098/rsif.2014.0215
- PubMed
- Google Scholar
1. Knight GT
2. Lundin BF
3. Iyer N
4. Ashton LM
5. Sethares WA
6. Willett RM
7. Ashton RS
(2018) Engineering induction of singular neural rosette emergence within hPSC-derived tissues
eLife 7:e37549.
https://doi.org/10.7554/eLife.37549
- PubMed
- Google Scholar
(2005) N-cadherin-dependent cell-cell contacts promote human saphenous vein smooth muscle cell survival
Arteriosclerosis, Thrombosis, and Vascular Biology 25:982–988.
https://doi.org/10.1161/01.ATV.0000163183.27658.4b
- PubMed
- Google Scholar
1. Lim J
2. Tu X
3. Choi K
4. Akiyama H
5. Mishina Y
6. Long F
(2015) BMP-Smad4 signaling is required for precartilaginous mesenchymal condensation independent of Sox9 in the mouse
Developmental Biology 400:132–138.
https://doi.org/10.1016/j.ydbio.2015.01.022
- PubMed
- Google Scholar
1. Mammoto T
2. Mammoto A
3. Torisawa YS
4. Tat T
5. Gibbs A
6. Derda R
7. Mannix R
8. de Bruijn M
9. Yung CW
10. Huh D
11. Ingber DE
12. Y-s T
13. Yung Chong W
14. Ingber Donald E
(2011) Mechanochemical control of mesenchymal condensation and embryonic tooth organ formation
Developmental Cell 21:758–769.
https://doi.org/10.1016/j.devcel.2011.07.006
- PubMed
- Google Scholar
(2009) Pulsed contractions of an actin-myosin network drive apical constriction
Nature 457:495–499.
https://doi.org/10.1038/nature07522
- PubMed
- Google Scholar
(2018) Cellular mechanotransduction: from tension to function
Frontiers in Physiology 9:824.
https://doi.org/10.3389/fphys.2018.00824
- PubMed
- Google Scholar
1. Marullo S
2. Doly S
3. Saha K
4. Enslen H
5. Scott MGH
6. Coureuil M
(2020) Mechanical GPCR Activation by Traction Forces Exerted on Receptor N-Glycans
ACS Pharmacology & Translational Science 3:171–178.
https://doi.org/10.1021/acsptsci.9b00106
- PubMed
- Google Scholar
(2002) Biogenesis of N-cadherin-dependent cell-cell contacts in living fibroblasts is a microtubule-dependent kinesin-driven mechanism
Molecular Biology of the Cell 13:285–301.
https://doi.org/10.1091/mbc.01-07-0337
- PubMed
- Google Scholar
1. Murrell M
2. Oakes PW
3. Lenz M
4. Gardel ML
(2015) Forcing cells into shape: the mechanics of actomyosin contractility
Nature Reviews. Molecular Cell Biology 16:486–498.
https://doi.org/10.1038/nrm4012
- PubMed
- Google Scholar
1. Nawaz S
2. Sánchez P
3. Bodensiek K
4. Li S
5. Simons M
6. Schaap IA
(2012) Cell visco-elasticity measured with AFM and optical trapping at sub-micrometer deformations
PLOS ONE 7:e45297.
https://doi.org/10.1371/journal.pone.0045297
- PubMed
- Google Scholar
(2018) Relating cell shape and mechanical stress in a spatially disordered epithelium using a vertex-based model
Mathematical Medicine and Biology 35:1–27.
https://doi.org/10.1093/imammb/dqx008
- PubMed
- Google Scholar
1. Ohgushi M
2. Matsumura M
3. Eiraku M
4. Murakami K
5. Aramaki T
6. Nishiyama A
7. Muguruma K
8. Nakano T
9. Suga H
10. Ueno M
11. Ishizaki T
12. Suemori H
13. Narumiya S
14. Niwa H
15. Sasai Y
(2010) Molecular pathway and cell state responsible for dissociation-induced apoptosis in human pluripotent stem cells
Cell Stem Cell 7:225–239.
https://doi.org/10.1016/j.stem.2010.06.018
- PubMed
- Google Scholar
Book
1. Olaranont N
(2019)
2-D Epithelial Tissues, Cell Mechanics, and Voronoi Tessellation

Worcester Polytechnic Institute.
- Google Scholar
Software
1. Olaranont N
2. St Pierre S
(2021) 2D_Voronoi_Cell_Radial_Alignment, version Github. swh:1:rev:c943c5d773d4748b9fbc96c9c846279e04173d12
Software Heritage.

https://archive.softwareheritage.org/swh:1:dir:58060b71988c1aae54007f16f298092e20f6de9e;origin=https://github.com/nolarano/2D_Voronoi_Cell_Radial_Alignment;visit=swh:1:snp:9c134d4abe5a5b5b11f70dff543e399d48ad80e5;anchor=swh:1:rev:c943c5d773d4748b9fbc96c9c846279e04173d12
(2019) Active wetting of epithelial tissues
Nature Physics 15:79–88.
https://doi.org/10.1038/s41567-018-0279-5
- PubMed
- Google Scholar
(2016) CellTracker (not only) for dummies
Bioinformatics 32:955–957.
https://doi.org/10.1093/bioinformatics/btv686
- PubMed
- Google Scholar
1. Polyakov O
2. He B
3. Swan M
4. Shaevitz JW
5. Kaschube M
6. Wieschaus E
(2014) Passive mechanical forces control cell-shape change during Drosophila ventral furrow formation
Biophysical Journal 107:998–1010.
https://doi.org/10.1016/j.bpj.2014.07.013
- PubMed
- Google Scholar
1. Qin L
2. Beier F
(2019) EGFR Signaling: Friend or Foe for Cartilage?
JBMR Plus 3:e10177.
https://doi.org/10.1002/jbm4.10177
- PubMed
- Google Scholar
1. Rauzi M
2. Krzic U
3. Saunders TE
4. Krajnc M
5. Ziherl P
6. Hufnagel L
7. Leptin M
(2015) Embryo-scale tissue mechanics during Drosophila gastrulation movements
Nature Communications 6:8677.
https://doi.org/10.1038/ncomms9677
- PubMed
- Google Scholar
(2012) Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy
Biomechanics and Modeling in Mechanobiology 11:461–473.
https://doi.org/10.1007/s10237-011-0325-z
- PubMed
- Google Scholar
(2017) Long-lived force patterns and deformation waves at repulsive epithelial boundaries
Nature Materials 16:1029–1037.
https://doi.org/10.1038/nmat4972
- PubMed
- Google Scholar
(2002) Dynamics of tight and adherens junctions under EGTA treatment
The Journal of Membrane Biology 188:151–162.
https://doi.org/10.1007/s00232-001-0182-2
- PubMed
- Google Scholar
1. Rotsch C
2. Radmacher M
(2000) Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study
Biophysical Journal 78:520–535.
https://doi.org/10.1016/S0006-3495(00)76614-8
- PubMed
- Google Scholar
1. Saw TB
2. Doostmohammadi A
3. Nier V
4. Kocgozlu L
5. Thampi S
6. Toyama Y
7. Marcq P
8. Lim CT
9. Yeomans JM
10. Ladoux B
(2017) Topological defects in epithelia govern cell death and extrusion
Nature 544:212–216.
https://doi.org/10.1038/nature21718
- PubMed
- Google Scholar
(2012) NIH Image to ImageJ: 25 years of image analysis
Nature Methods 9:671–675.
https://doi.org/10.1038/nmeth.2089
- PubMed
- Google Scholar
(2018) Live cell imaging reveals focal adhesions mechanoresponses in mammary epithelial cells under sustained equibiaxial stress
Scientific Reports 8:9788.
https://doi.org/10.1038/s41598-018-27948-3
- PubMed
- Google Scholar
Software
1. St Pierre S
2. Wu M
(2021) AngleDev_StructureTensor, version swh:1:rev:0a5972451e8e747ea755cba6613ef0d81c8aabfd
Software Heritage.

https://archive.softwareheritage.org/swh:1:dir:586748532f984f0c458cdafde11b725f20f2ac59;origin=https://github.com/nolarano/AngleDev_StructureTensor;visit=swh:1:snp:51fdc32ba769240dda72c49a15e1e1ea9042a66a;anchor=swh:1:rev:0a5972451e8e747ea755cba6613ef0d81c8aabfd
(2018) Global morphogenetic flow is accurately predicted by the spatial distribution of myosin motors
eLife 7:e27454.
https://doi.org/10.7554/eLife.27454
- PubMed
- Google Scholar
1. Sun Y
2. Yong KM
3. Villa-Diaz LG
4. Zhang X
5. Chen W
6. Philson R
7. Weng S
8. Xu H
9. Krebsbach PH
10. Fu J
(2014) Hippo/YAP-mediated rigidity-dependent motor neuron differentiation of human pluripotent stem cells
Nature Materials 13:599–604.
https://doi.org/10.1038/nmat3945
- PubMed
- Google Scholar
1. Szabó A
2. Mayor R
(2018) Mechanisms of Neural Crest Migration
Annual Review of Genetics 52:43–63.
https://doi.org/10.1146/annurev-genet-120417-031559
- PubMed
- Google Scholar
1. Takebe T
2. Enomura M
3. Yoshizawa E
4. Kimura M
5. Koike H
6. Ueno Y
7. Matsuzaki T
8. Yamazaki T
9. Toyohara T
10. Osafune K
11. Nakauchi H
12. Yoshikawa HY
13. Taniguchi H
(2015) Vascularized and Complex Organ Buds from Diverse Tissues via Mesenchymal Cell-Driven Condensation
Cell Stem Cell 16:556–565.
https://doi.org/10.1016/j.stem.2015.03.004
- PubMed
- Google Scholar
1. Tambe DT
2. Hardin CC
3. Angelini TE
4. Rajendran K
5. Park CY
6. Serra-Picamal X
7. Zhou EH
8. Zaman MH
9. Butler JP
10. Weitz DA
11. Fredberg JJ
12. Trepat X
(2011) Collective cell guidance by cooperative intercellular forces
Nature Materials 10:469–475.
https://doi.org/10.1038/nmat3025
- PubMed
- Google Scholar
1. Tavares S
2. Vieira AF
3. Taubenberger AV
4. Araújo M
5. Martins NP
6. Brás-Pereira C
7. Polónia A
8. Herbig M
9. Barreto C
10. Otto O
11. Cardoso J
12. Pereira-Leal JB
13. Guck J
14. Paredes J
15. Janody F
(2017) Actin stress fiber organization promotes cell stiffening and proliferation of pre-invasive breast cancer cells
Nature Communications 8:15237.
https://doi.org/10.1038/ncomms15237
- PubMed
- Google Scholar
(1994) N-CAM and N-cadherin expression during in vitro chondrogenesis
Experimental Cell Research 215:354–362.
https://doi.org/10.1006/excr.1994.1352
- PubMed
- Google Scholar
1. Tetley RJ
2. Staddon MF
3. Heller D
4. Hoppe A
5. Banerjee S
6. Mao Y
(2019) Tissue Fluidity Promotes Epithelial Wound Healing
Nature Physics 15:1195–1203.
https://doi.org/10.1038/s41567-019-0618-1
- PubMed
- Google Scholar
(2012) Cell migration
Comprehensive Physiology 2:2369–2392.
https://doi.org/10.1002/cphy.c110012
- PubMed
- Google Scholar
1. Trepat X
2. Fredberg JJ
(2011) Plithotaxis and emergent dynamics in collective cellular migration
Trends in Cell Biology 21:638–646.
https://doi.org/10.1016/j.tcb.2011.06.006
- PubMed
- Google Scholar
1. Trepat X
2. Sahai E
(2018) Mesoscale physical principles of collective cell organization
Nature Physics 14:671–682.
https://doi.org/10.1038/s41567-018-0194-9
- Google Scholar
1. Wan LQ
2. Ronaldson K
3. Park M
4. Taylor G
5. Zhang Y
6. Gimble JM
7. Vunjak-Novakovic G
(2011) Micropatterned mammalian cells exhibit phenotype-specific left-right asymmetry
PNAS 108:12295–12300.
https://doi.org/10.1073/pnas.1103834108
- PubMed
- Google Scholar
Preprint
1. Wei C
2. Wu M
(2021) Nonlinear modeling reveals multi-timescale and higher-order effects in active tissue mechanics
arXiv.

https://arxiv.org/abs/2103.09427
- Google Scholar
1. Wu M
2. Ben Amar M
(2015) Modelling fibers in growing disks of soft tissues
Mathematics and Mechanics of Solids 20:663–679.
https://doi.org/10.1177/1081286514550571
- Google Scholar
Book
1. Xie T
2. Hawkins J
3. Sun Y
(2017) Traction Force Measurement Using Deformable Microposts
In: Rittié L, editors. Fibrosis: Methods and Protocols. New York: Humana Press. pp. 235–244.
https://doi.org/10.1007/978-1-4939-7113-8_16
- Google Scholar
1. Zhu P
2. Tseng NH
3. Xie T
4. Li N
5. Fitts-Sprague I
6. Peyton SR
7. Sun Y
(2019) Biomechanical Microenvironment Regulates Fusogenicity of Breast Cancer Cells
ACS Biomaterials Science & Engineering 5:3817–3827.
https://doi.org/10.1021/acsbiomaterials.8b00861
- PubMed
- Google Scholar

Decision letter

Aleksandra M Walczak

Senior and Reviewing Editor; École Normale Supérieure, France

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

The manuscript combines an impressive array of experimental and modeling approaches to study cell morphological changes due to stiffness heterogeneities and contractility. The article is an interesting, well-written contribution to the field, with the discussion and conclusion well supported by the experimental data.

Decision letter after peer review:

Thank you for submitting your article "Condensation tendency of connected contractile tissue with planar isotropic actin network" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by a Reviewing Editor and Aleksandra Walczak as the Senior Editor.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

As the editors have judged that your manuscript is of interest, but as described below that additional experiments are required before it is published, we would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). First, because many researchers have temporarily lost access to the labs, we will give authors as much time as they need to submit revised manuscripts. We are also offering, if you choose, to post the manuscript to bioRxiv (if it is not already there) along with this decision letter and a formal designation that the manuscript is "in revision at eLife". Please let us know if you would like to pursue this option. (If your work is more suitable for medRxiv, you will need to post the preprint yourself, as the mechanisms for us to do so are still in development.)

This article reports the radial alignment of rat embryonic fibroblasts at the periphery of circular confinement patterns. It combines a large array of experimental and modeling approaches to study the origin of this phenomenon and find that contractility, adhesion and stiffness gradient are necessary to obtain this alignment.

Summary:

The authors study the effect of confinement on the alignment of REF cells confined within circular micropatterned islands. They observed that the cells are aligned perpendicularly to the boundary after 48h, contrary to other elongated cells such as NIH-3T3. After testing several subclones of that cell line, they identified cell contractility and cell-cell adhesion affect the organization of the cells in the circular patterns. They confirmed this finding using drugs that affect contractility and disrupt cell adhesion. Then they compared their results to a continuum model and to a Voronoi model.

Enthusiasm for the work is diminished by the limited experimental support for key assumptions of the conceptual and math models (e.g. existence of stiffness gradient, assumption of uniform contractility, use of calcium chelator to show importance of adhesion). Further, integration of model and experiment could be improved, and some of the narrower assumptions of the models (e.g. omitting cell proliferation, remodeling of cell-cell contacts, and cell-substrate interactions, assuming uniform contractility) need better justification. Also, a clear correlate to specific events in development, physiology, or disease would highlight the broader impact of the work beyond a very specific event in a carefully engineered system. Finally, 3 similar papers came out on arxiv from the Roux group. They should be discussed in the manuscript and cited.

Essential revisions:

1. Several assumptions underlying the models need substantiation.

a) The assumption of a purely elastic process: Figure 1A show a dramatic increase in the number of REF2c cells from 24 to 48 hours, suggesting that cells are proliferating. This, together with continuous remodeling of cell-cell contacts, would result in deformations that dissipate elastic energy. Neither modeling approach accounts for this. It would be important for authors incorporate these behaviors, or to provide evidence that cell proliferation and remodeling are unimportant, and similar between the three cell populations being compared.

b) The assumption that contractility is uniform: Work cited (Tambe et al) shows on the contrary that collective cell behaviors exhibit highly heterogeneous active stresses. Experimentally, there are a few potential ways to clarify this point. The authors could use the stiffer (1 MPa) micro post cultures, which recreate radial alignment seen on micropatterned PDMS islands, and compute force variations from post deflection. Alternatively, the authors could perform short time lapse experiments to measure deformations following treatment with blebbistatin or Y27632. Yet another option would be to perform staining for contractile proteins such as phospho-myosin light chain, GTP-bound RhoA, or others, to confirm they are uniformly distributed despite the heterogeneity of F-actin (although such experiments might not reveal uniform contractility when F-actin is nonuniform). Finally, if no experimental support is possible, then authors could turn to model simulations to test whether spatial heterogeneities in contractility alter the overall behavior of the system. In addition to either modeling or experimental support for the assumption that contractility is uniform, authors should provide examples from the literature on related systems that support this assumption.

c) The importance of a stiffness gradient in the cell population, which is one of the key aspects of this work: evidence for the existence of such a gradient is provided only by staining for F-actin, which is insufficient. While F-actin is indeed a key cytoskeletal component in defining the stiffness of cells, the link between intensity of staining and stiffness needs to be proven. Only a single reference is provided, which focused on one specific cancer cell line and the role of stress fibers in stiffening the cell. Moreover, given that F-actin interacts with nonmuscle myosin to form the key contractile machinery of most cell types, heterogeneity in F-actin likely implies heterogeneity in contractility as well. There are also concerns with the measurement of F-actin abundance, including need for statistics on the spatial distribution, and to normalize per cell to reflect variations in F-actin as opposed to simply variations in cell density, which are also present (Figure 1A). Finally, the F-actin gradient is only shown and quantified when intensities are summed over many samples. It would be important to demonstrate a significant gradient within individual samples, and how it varies across samples.

2. The importance of cell-cell adhesion is another crux of the story, pointing to differences underlying the various polarization phenotypes. However, the only experimental support for this is via treatment with a calcium chelator, EGTA. Only one reference is provided for this method (#35, Chen et al), yet Chen et al. appear not to have used EGTA at all, and instead disrupted E-Cadherin using neutralizing antibodies. This is a much more specific and direct approach that the authors of the present study should consider in place of EGTA. In the absence of this or similarly targeted approaches (RNAi, etc), author should include control experiments that demonstrate this rather broad perturbation does not alter contractility or cell-substrate interactions. This could be done at least in part, by using the traction force measurement system the authors have devised. It is particularly important to do so given the importance of calcium for cytoskeletal contraction via calmodulin. A second experiment authors could supplement this with is pharmacologic inhibition of calcium-depdendent contractility, with the hope/expectation that calmodulin-mediated contractility does not predominate this system. Even with these experiments, however, the authors need to provide support from published work that this method of disrupting cell-cell adhesion is well established.

3. The relationship between the in vitro system used by the authors and in vivo phenomena is weak. This is particularly true for the continuum model, where it is nontrivial to relate strain and stress to cell shape changes, given that cell shape is not simply an affine elastic deformation owing to stresses acting on it, but instead a response to stresses integrated with cell autonomous behaviors. There is a large body of literature on the alignment of cells relative to the direction of applied static or dynamic stretch. This mechano-responsivity that dictates cell shape is not considered in the present study. Even without considering these complicating cell behaviors, it is not clear how the magnitude of stress or strain relate to the change in cell shape. In addition, authors would ideally make use of the models to pinpoint what underlies the distinct polarization phenotypes between REF2c, REF11, and 3T3 cell types. The in vitro system should be used to measure directly the cell generated forces.

4. Some terms are either not properly defined or misused and the writing is sometimes unclear. What is the "condensation" process the authors are referring to and how this is related to the boundary alignment of the REF cells. It is the first word in the title of the manuscript, still it appears for the first time in the text only on page 18, where it is poorly defined. Please, read the work of Trepat et al. on active dewetting published in 2018. What do the authors mean by "tendency" (sometimes there is condensation, sometime there isn't?). A different wording to explain their results might be better. Furthermore, terms like nematic, or symmetry are misused.

5. There is a lot of data, analysis and model, but their presentation is not well organized, such that serious rewriting and re-organizing seems in order. The authors chose to show all the analysis they could do in the figures, and therefore there is no clear take-home message. Are all those plots necessary? What is the main result? We suggest to focus on the essential findings. Also, plot the 2 cells types in the same graph instead of showing one graph/cell type.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Condensation tendency and planar isotropic actin gradient induce radial alignment in confined monolayers" for consideration by eLife. Your article has been reviewed by 3 peer reviewers, and the evaluation has been overseen by Aleksandra Walczak as the Senior and Reviewing Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed their reviews with one another, and the Reviewing Editor has drafted this to help you prepare a revised submission.

Essential revisions:

Please answer the Reviewers comments. They are mainly discussion points (you do not need to do new experiments), but please do so carefully.

Reviewer #1:

The authors were extremely responsive to reviewer critiques, including text changes, new experiments, and modeling simulation. There are some key places where concerns remain, and these should be addressed via text changes, explicitly describing limitations in the Discussion. Specifically:

1) The modeling of cell responses as purely elastic in the continuum model remains problematic. While new data indicates that cell alignment does not require proliferation, authors do not address the extent to which energy is dissipated via remodeling of cell-cell junctions. This is accounted for in the Voronoi model, as author's point out, but it's absence from the continuum model is a strong limitation that should be noted.

2) Most critically, there remains only indirect support for two key assumptions of the work. One that there is a stiffness gradient, inferred from actin staining, and the other that contractility is uniform and/or unimportant. Given that contraction is produced by interaction of myosin and actin, homogeneous myosin and graded actin can still produce heterogeneous contractile forces. The authors have performed some simulations to test a role for contractility but this is within a modeling framework built on the interpretation of authors, so to some extent you get out what you put in. It would have been ideal to see inhibitor experiments that block myosin activity along with model predictions of the resulting phenotype. I'm the absence of this, some concession on these assumptions needs to be articulated in the Discussion.

Reviewer #2:

This submission is a revised manuscript on the radial alignment of REF cells at the periphery of circular confinement patterns. The revisions are significant, and address the comments raised by the reviewers with a number of new experiments and analyses. I recommend publication in eLife.

Reviewer #3:

I'd like to thank the authors for their corrections. I think the manuscript has improved in clarity significantly. Still, some of the main comments remain unaddressed.

I am summarizing below the main concerns from the last round of reviews and whether they were addressed or not.

1. Justification of the model assumptions:

– Existence of stiffness gradient: ok (thanks to more citations);

– Calcium chelation: ok (thanks to more citations);

– No cell proliferation: ok (thanks to new experiments);

– Uniform contractility: NOT ok (not enough evidence, details below).

2. Integration of model and experiment: No changes.

3. Connection to development, physiology, or disease: No changes.

4. Discussion of the Roux papers: not ok.

I am now giving more details on some of the main points that were not adequately addressed:

1. Uniform contractility: The authors performed new immunostaining and new simulations. They showed that the density of myosin motors was uniform on most of the tissue, with a slight increase on the boundary cells. they then performed simulations to show that this slight increase of contractility at the edge does not lead to radial alignment. However, this is not enough experimental evidence to conclude that contractility is uniform. indeed, uniform myosin + non-uniform Factin does not necessarily mean uniform contractility as both proteins are required for contraction.

The authors show in simulations that an increase of contractility at the edge leads to smaller boundary cells. What would happen if contractility follows the actin gradient? Could that be enough to reproduce the radial alignment of the cells, even in the absence of cell contractility differential or condensation?

2. Integration of model and experiments. there is no quantitative comparison between theory and experiments. The simulation results are summarized in the new panel Figure 4B. Instead, why not showing the same radial profiles as for the experiments? It will make the comparison between experiments and theory easier.

It would be neat to see how sensitive the cell alignment is to rho, g and their gradients.

Along those lines, can the authors comment on how steep the stiffness gradient has to be in order to re-align the cells radially? Can this be quantitatively compared to the actin gradients measured in Figure S3-1? Not all the patches seem to display the gradient (see images in the 3rd column). Can the authors show if the steepness of the actin gradient correlates with the radial alignment of the cells or their size for each pattern instead of showing that the average gradient value and the average alignment are correlated?

3. Discussion of the 3 papers from Aurelien Roux's lab: The papers are cited in the bulk of the introduction, but not properly discussed. It seems to me that the transition from parallel to perpendicular anchoring is particularly important to mention in this manuscript. The authors claim in their response that they discussed the papers in the discussion. I could not find this section (none of the 3 papers are cited in the Discussion section). I think comparing and contrasting the results of those papers with this manuscript would greatly improve our understanding of how contractility and circular confinement impact the organization of dense layers of elongated cells.

https://doi.org/10.7554/eLife.60381.sa1

Author response

Summary:

The authors study the effect of confinement on the alignment of REF cells confined within circular micropatterned islands. They observed that the cells are aligned perpendicularly to the boundary after 48h, contrary to other elongated cells such as NIH-3T3. After testing several subclones of that cell line, they identified cell contractility and cell-cell adhesion affect the organization of the cells in the circular patterns. They confirmed this finding using drugs that affect contractility and disrupt cell adhesion. Then they compared their results to a continuum model and to a Voronoi model.

Enthusiasm for the work is diminished by the limited experimental support for key assumptions of the conceptual and math models (e.g. existence of stiffness gradient, assumption of uniform contractility, use of calcium chelator to show importance of adhesion). Further, integration of model and experiment could be improved, and some of the narrower assumptions of the models (e.g. omitting cell proliferation, remodeling of cell-cell contacts, and cell-substrate interactions, assuming uniform contractility) need better justification. Also, a clear correlate to specific events in development, physiology, or disease would highlight the broader impact of the work beyond a very specific event in a carefully engineered system. Finally, 3 similar papers came out on arxiv from the Roux group. They should be discussed in the manuscript and cited.

As the reviewers will see below, we have done more experiments and quantifications to support the existence of the stiffness gradient, the assumption of uniform contractility, and the importance of coherent cell-cell adhesions. Our model focuses on the mechanical equilibrium when the dynamics of cell-cell contact exchange and cell proliferation have ceased. Additionally, we have further shown the radial alignment is not caused directly by proliferation and mechanotransduction. We believe the new experiments and simulations have pinned our major conclusion that in the connected contractile REF tissue, the radial-alignment boundary is due to the combination of the condensation tendency, which describes the collective cell behavior that cells condense on soft substrates, and cell stiffness differential.

In multiple developmental and physiological processes, previous focuses have been on the differential growth/contractility as a tissue flow-and-deformation driver^{1, 2} while there is relatively little evidence (except in Drosophila development^{3, 4}) that the differential stiffness also plays an important role. In 2D tissues, it is difficult to disentangle differential contractility and stiffness as the two mechanical properties are both connected to the actomyosin activities. Using engineered systems, we have disentangled both experimentally and theoretically their roles in regulating the cell morphology at the REF tissue boundary and we reason it is the differential stiffness rather than the differential contractility that contributes to the radial-alignment boundary. While engineered patterns help the quantitative study of the cell behaviors, we believe the condensation tendency and the emerging stiffness gradient are intrinsic tissue properties that contribute to tissue morphogenesis. For example, when epithelial cells undergo epithelial-mesenchymal transition, the actin stress fiber distribution starts to change while maintaining functional cell-cell junctions. It is possible that local condensations can be observed in this process. Also, neural crest cells and chondrocytes migrate collectively and form aggregates during craniofacial and tooth development, respectively. It is also possible that these mesenchymal condensation processes are also regulated by cell-stiffness differential and condensation tendency, in addition to chemoattractant as previously thought. We have highlighted these potential broader impacts in the discussion of the revised manuscript.

We appreciate the reviewers for pointing out the important recent works by Roux group. We have cited and discussed these 3 papers in the introduction and discussion^5-7.

Essential revisions:

1. Several assumptions underlying the models need substantiation.

a) The assumption of a purely elastic process: Figure 1A show a dramatic increase in the number of REF2c cells from 24 to 48 hours, suggesting that cells are proliferating. This, together with continuous remodeling of cell-cell contacts, would result in deformations that dissipate elastic energy. Neither modeling approach accounts for this. It would be important for authors incorporate these behaviors, or to provide evidence that cell proliferation and remodeling are unimportant, and similar between the three cell populations being compared.

We agree that the cell proliferation from 24 to 48 hrs may lead to deformations that dissipate elastic energy. To evaluate whether cell proliferation changes the cell alignment results, we treated REF2c cells with aphidicolin, an inhibitor of DNA replication. We found that with aphidicolin treatment, the cell proliferation was significantly inhibited, as reflected by a non-significant cell number increase. In this condition, we still observed the radial alignment of boundary cells, which is quantitatively comparable with untreated controls. Thus, we believe that the cell proliferation mediated remodeling is unimportant for the formation of cell radial alignment (Figure 4—figure supplement 1).

We have developed a Voronoi model to explain the cell radial alignment in the mechanical equilibrium, with stiffness differential between the inner and boundary cells and cell contractility. This equilibrium is due to the minimization of the tissue elastic energy. During the relaxation of the tissue energy, cell centroids move along the direction that decreases (dissipates) the total energy, where cell-cell contact may change.

b) The assumption that contractility is uniform: Work cited (Tambe et al) shows on the contrary that collective cell behaviors exhibit highly heterogeneous active stresses. Experimentally, there are a few potential ways to clarify this point. The authors could use the stiffer (1 MPa) micro post cultures, which recreate radial alignment seen on micropatterned PDMS islands, and compute force variations from post deflection. Alternatively, the authors could perform short time lapse experiments to measure deformations following treatment with blebbistatin or Y27632. Yet another option would be to perform staining for contractile proteins such as phospho-myosin light chain, GTP-bound RhoA, or others, to confirm they are uniformly distributed despite the heterogeneity of F-actin (although such experiments might not reveal uniform contractility when F-actin is nonuniform). Finally, if no experimental support is possible, then authors could turn to model simulations to test whether spatial heterogeneities in contractility alter the overall behavior of the system. In addition to either modeling or experimental support for the assumption that contractility is uniform, authors should provide examples from the literature on related systems that support this assumption.

We thank the reviewers for this insightful comment. We combined experiments and simulations to investigate whether the contractility was uniform within the pattern and the importance of the uniformity of the contractility to our model. To evaluate the total contractility, it is not accurate to only measure traction forces due to strong cell-cell adhesions. In addition, as shown in Figure 1—figure supplement 5, the traction force measurement is challenging using soft PDMS micropost arrays (8.4 µm) due to the condensation of the cell colony. It is not possible to use stiffer micropost arrays to measure traction force, as the deflections are too small to be measured accurately⁸. Thus, as suggested by the reviewers, we performed staining for phosphorylated-myosin (p-myosin) light chain to investigate the distribution of p-myosin (see Figure 3—figure supplement 3). We found that although F-actin gradients existed within the patterns, the p-myosin distribution was more uniform, with only a slight increase near the pattern boundary, which was more significant when normalized by cell area, as the boundary cells were larger than inner cells. This is opposite to the increasing F-actin intensity towards the pattern center.

We further performed simulations in the Voronoi cell model and have found that the contractility gradient suggested by the image data of phosphorylated-myosin distribution could not result in the radial alignment of boundary cells (Figure 4, figure supplement 2). Rather, only smaller cell areas at the border were found, which contradicts the experimental observation in REF2c tissues. Combining both old and new simulation results, we further confirm that the actin gradient is responsible for the radial alignment of boundary cells.

c) The importance of a stiffness gradient in the cell population, which is one of the key aspects of this work: evidence for the existence of such a gradient is provided only by staining for F-actin, which is insufficient. While F-actin is indeed a key cytoskeletal component in defining the stiffness of cells, the link between intensity of staining and stiffness needs to be proven. Only a single reference is provided, which focused on one specific cancer cell line and the role of stress fibers in stiffening the cell. Moreover, given that F-actin interacts with nonmuscle myosin to form the key contractile machinery of most cell types, heterogeneity in F-actin likely implies heterogeneity in contractility as well. There are also concerns with the measurement of F-actin abundance, including need for statistics on the spatial distribution, and to normalize per cell to reflect variations in F-actin as opposed to simply variations in cell density, which are also present (Figure 1A).

Finally, the F-actin gradient is only shown and quantified when intensities are summed over many samples. It would be important to demonstrate a significant gradient within individual samples, and how it varies across samples.

We provided more references to support the connection between F-actin intensity and cell stiffness^9-11. The heterogeneity in contractility has been addressed in our response to comment 1b above. As suggested, we further performed statistical analysis by dividing the pattern into 6 regions and compared average actin intensity within each zone. As shown in Figure 3, figure supplement 2A, a significant decrease was found in the outmost layer. To exclude the possibility that this drop in actin intensity is due to decreased cell density in the pattern boundary, we compared both average actin intensity (Figure 3, figure supplement 2B) and average actin intensity per cell (Figure 3, figure supplement 2B) between inner cells and boundary cells (cells in the outmost layer). The statistical analysis results supported that a significant decrease in actin intensity could still be found after normalizing to cell density.

As suggested by the reviewers, we now include three representative fluorescence images and actin intensity profiles showing the actin gradient within individual patterns (Figure 3, figure supplement 1). These images further confirmed such actin intensity gradient could be found within each individual pattern.

2. The importance of cell-cell adhesion is another crux of the story, pointing to differences underlying the various polarization phenotypes. However, the only experimental support for this is via treatment with a calcium chelator, EGTA. Only one reference is provided for this method (#35, Chen et al), yet Chen et al. appear not to have used EGTA at all, and instead disrupted E-Cadherin using neutralizing antibodies. This is a much more specific and direct approach that the authors of the present study should consider in place of EGTA. In the absence of this or similarly targeted approaches (RNAi, etc), author should include control experiments that demonstrate this rather broad perturbation does not alter contractility or cell-substrate interactions. This could be done at least in part, by using the traction force measurement system the authors have devised. It is particularly important to do so given the importance of calcium for cytoskeletal contraction via calmodulin. A second experiment authors could supplement this with is pharmacologic inhibition of calcium-dependent contractility, with the hope/expectation that calmodulin-mediated contractility does not predominate this system. Even with these experiments, however, the authors need to provide support from published work that this method of disrupting cell-cell adhesion is well established.

We apologize for this wrong reference and replaced it with the correct one¹². In Figure 4D-F of this paper, Ohgushi et al. used EGTA to “disrupts the cadherin-mediated cell attachment and caused hESC to detach from one another but not from the plate bottom”. It is challenging to design targeted inhibition experiments, because unlike epithelial cells in most previous studies, it is unclear what types of cadherin the REF2c cells express, and thus we chose to use a calcium chelator to universally inhibit all cadherin-mediated cell-cell adhesion.

To further confirm that EGTA treatment mainly regulates cell-cell interactions but not cell-substrate interactions, we measured the contractility of cells using the PDMS micropost arrays as suggested by the reviewers. We found that the EGTA treatment did not significantly change cell contractility (see Figure 2—figure supplement 3), suggesting calmodulin-mediated contractility does not predominate this system. As suggested by the reviewers, we also provided more references to support the use of EGTA to disrupt cell-cell adhesions. For example, in the paper mentioned several times by reviewers (Pérez-González et al., 2019), EGTA was used to disrupt cell-cell adhesion¹³. Others have also reported using EGTA to disrupt E-cadherin dependent cell-cell adhesions in MDCK cells¹⁴ and S180 cells¹⁵, and N-cadherin dependent cell-cell adhesions in vascular smooth muscle cell¹⁶ and C2C12 myoblasts¹⁷. We believe those works are sufficient to support that EGTA has been widely used to disrupt cell-cell adhesions.

3. The relationship between the in vitro system used by the authors and in vivo phenomena is weak. This is particularly true for the continuum model, where it is nontrivial to relate strain and stress to cell shape changes, given that cell shape is not simply an affine elastic deformation owing to stresses acting on it, but instead a response to stresses integrated with cell autonomous behaviors. There is a large body of literature on the alignment of cells relative to the direction of applied static or dynamic stretch. This mechano-responsivity that dictates cell shape is not considered in the present study. Even without considering these complicating cell behaviors, it is not clear how the magnitude of stress or strain relate to the change in cell shape. In addition, authors would ideally make use of the models to pinpoint what underlies the distinct polarization phenotypes between REF2c, REF11, and 3T3 cell types. The in vitro system should be used to measure directly the cell generated forces.

We thank the reviewers for bringing up this important issue. It is well-documented that various types of cells respond to mechanical stretching by aligning perpendicular to the stretching directions. As pointed out by the reviewers, complex mechanotransduction pathways, including focal adhesion mediated signaling^18-20 and YAP-TEAD signaling^21-23. In our case, we believe the cell shape changes are modeled as the direct responses to material properties changes of cells due to actin remodeling. This does not exclude the possibility that cells actively respond to mechanical forces and remodel the actin cytoskeleton. To further examine the activation of mechanotransduction signals in our system, we stained focal adhesion proteins vinculin (Figure 4—figure supplement 4) and canonical mechanosensor YAP at 48 hr when radial alignment is prominent (Figure 4—figure supplement 5). If mechanotransduction is involved, we expect to see a higher intensity of vinculin and/or nuclear YAP in the boundary cells. However, we found that the distribution of vinculin was mostly uniform across the pattern area, except for reduced signals near the pattern boundary. Notably, the overall vinculin intensity per cell in the outmost layer of cells was still comparable with inner cells. We also found that most of the REF2c cells expressed nuclear YAP, which is independent of confinement and cell alignment status (24 hr vs. 48 hr). These results suggest local activation of these mechanotransduction pathways in boundary cells is unlikely the cause for its radial alignment.

As suggested by the reviewers, we further used our model to reveal the quantitative relationship between the magnitude of stress or strain and the change in cell shape and orientation. We agree with the reviewers that it is non-trivial to connect cell shape with cell strain in both the Voronoi model and the continuum model, since the reference stress-free shape of the cell is not known. Nevertheless, due to the isotropic orientation of actin, we assume that the reference stress-free configuration of the cell is isotropic and the reference cell size (area) is determined by the level of contractility (see Stress and Strain Analysis in the Materials and methods). Then we can estimate the cell stress and strain under different levels of stiffness gradient and contractility, and their connection with cell shape and orientation. (Figure 4 and Figure 4—figure supplement 3, orange dots: boundary cells; blue dots: inner cells). REF2c is represented by contractile cells with stiffness gradient (e.g., g = 0.5 and $ρ = 0.4$ ) and REF11b is represented by non-contractile cells with stiffness gradient (e.g., g = 1 and $ρ = 0.4$ ). We think that the 3T3 cell pattern cannot be simulated by our modeling approaches where the REF tissue is clearly a continuum. Since there is no clear junction between 3T3 cells (see β-catenin in Figure 2—figure supplement 2), the dominant mechanical interaction can be very different between 3T3 and REF cells.

We agree with the reviewers that a direct measurement of traction force distribution is critical. However, as we have shown in Figure 1—figure supplement 5, a strong tendency of condensation of PDMS micropost arrays with an effective modulus of 5 kPa was observed, making it challenging to measure the traction forces, as the post deflection will be too small to be measured accurately if using shorter, and thus stiffer, PDMS microposts⁸.

4. Some terms are either not properly defined or misused and the writing is sometimes unclear. What is the "condensation" process the authors are referring to and how this is related to the boundary alignment of the REF cells. It is the first word in the title of the manuscript, still it appears for the first time in the text only on page 18, where it is poorly defined. Please, read the work of Trepat et al. on active dewetting published in 2018. What do the authora mean by "tendency" (sometimes there is condensation, sometime there isn't?). A different wording to explain their results might be better. Furthermore, terms like nematic, or symmetry are misused.

We thank the reviewers to point this term out and refer our work to Pérez-González et al., 2019. In our system, we observed this radial alignment of boundary cells when REF2c cells were confined on rigid substrates, driven by an actin gradient concentrated in the pattern center. As shown in Figure 1—figure supplement 5, we observed a clear increase of cell density in the pattern center on PDMS micropost arrays substrates with lower stiffness. This is also a reminiscence of the mesenchymal condensation phenomenon, which is a prevalent morphogenetic transition that involves the aggregation of mesenchymal cells^24-26. We used the term “tendency” to describe the fact that when cells were cultured on flat PDMS substrates, they reached an equilibrium state without significant cell motions, so the cells do not actually “condense” to the center (while they indeed condensed on soft substrates). We would like to describe this emergent collective behavior of REF2c cells and differentiate it from conventional mesenchymal condensation.

It is notable that our observation, to some extent, is indeed similar to the dewetting process in the epithelial tissue in Pérez-González et al., 2019. While Pérez-González et al., 2019 aimed to explain the out-of-equilibrium process by describing the tissue as active viscous fluid, we are trying to explain the cell alignment in mechanical equilibrium when the tissue is confined in a stiffer substrate, which is not observed in the epithelial tissue. Moreover, the active viscous fluid theory developed in Pérez-González et al., 2019, where active forces drive the tissue flow cannot explain a final tissue pattern in static equilibrium, but rather the initial onset of tissue retraction. In the revised manuscript, we have provided a detailed explanation of the condensation tendency at the beginning of the manuscript, and referred to Pérez-González et al., 2019, and discuss the similarity in the strong contractility plus cell-cell junction and difference in equilibrium state and out-of-equilibrium process.

5. There is a lot of data, analysis and model, but their presentation is not well organized, such that serious rewriting and re-organizing seems in order. The authors chose to show all the analysis they could do in the figures, and therefore there is no clear take-home message. Are all those plots necessary? What is the main result? We suggest to focus on the essential findings. Also, plot the 2 cells types in the same graph instead of showing one graph/cell type.

We have reorganized the figures and the manuscript to focus on essential findings in the main figures and moving supporting results to the supplementary information. Specifically, we removed the continuum model results (original Figure 4) and simulation results for the ring patterns (Original Figure 6). We also moved the ring pattern experimental results (original Figure 7) to supplementary figures. In the Voronoi cell model (original Figure 5), we moved original bar plots showing statistical analysis (original Figure 5C-D) to supplementary figures and added scatter plots showing angle deviation, elongation, and cell area, and generate new scatter plots to show the changes of cell shape in relation to stress and strains (see the new Figure 4). We believe these substantial changes help us to focus on the essential findings. In all the figures, we presented results from various cell types in parallel.

References:

1. Ambrosi D, Ben Amar M, Cyron CJ, DeSimone A, Goriely A, Humphrey JD, Kuhl E. Growth and remodelling of living tissues: perspectives, challenges and opportunities. J R Soc Interface. 2019;16(157).

2. Streichan SJ, Lefebvre MF, Noll N, Wieschaus EF, Shraiman BI. Global morphogenetic flow is accurately predicted by the spatial distribution of myosin motors. eLife. 2018;7:e27454.

3. Polyakov O, He B, Swan M, Shaevitz JW, Kaschube M, Wieschaus E. Passive mechanical forces control cell-shape change during Drosophila ventral furrow formation. Biophys J. 2014;107(4):998-1010.

4. Rauzi M, Krzic U, Saunders TE, Krajnc M, Ziherl P, Hufnagel L, Leptin M. Embryo-scale tissue mechanics during Drosophila gastrulation movements. Nat Commun. 2015;6:8677.

5. Blanch-Mercader C, Guillamat P, Roux A, Kruse K. Integer topological defects of cell monolayers: Mechanics and flows. Phys Rev E. 2021;103(1-1):012405.

6. Blanch-Mercader C, Guillamat P, Roux A, Kruse K. Quantifying Material Properties of Cell Monolayers by Analyzing Integer Topological Defects. Phys Rev Lett. 2021;126(2):028101.

7. Guillamat P, Blanch-Mercader C, Kruse K, Roux A. Integer topological defects organize stresses driving tissue morphogenesis. bioRxiv. 2020:2020.06.02.129262.

8. Fu JP, Wang YK, Yang MT, Desai RA, Yu XA, Liu ZJ, Chen CS. Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat Meth. 2010;7(9):733-6.

9. Rotsch C, Radmacher M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys J. 2000;78(1):520-35.

10. Nawaz S, Sánchez P, Bodensiek K, Li S, Simons M, Schaap IAT. Cell Visco-Elasticity Measured with AFM and Optical Trapping at Sub-Micrometer Deformations. PLOS ONE. 2012;7(9):e45297.

11. Gavara N, Chadwick RS. Relationship between cell stiffness and stress fiber amount, assessed by simultaneous atomic force microscopy and live-cell fluorescence imaging. Biomech Model Mechanobiol. 2016;15(3):511-23.

12. Ohgushi M, Matsumura M, Eiraku M, Murakami K, Aramaki T, Nishiyama A, Muguruma K, Nakano T, Suga H, Ueno M, Ishizaki T, Suemori H, Narumiya S, Niwa H, Sasai Y. Molecular Pathway and Cell State Responsible for Dissociation-Induced Apoptosis in Human Pluripotent Stem Cells. Cell Stem Cell. 2010;7(2):225-39.

13. Perez-Gonzalez C, Alert R, Blanch-Mercader C, Gomez-Gonzalez M, Kolodziej T, Bazellieres E, Casademunt J, Trepat X. Active wetting of epithelial tissues. Nat Phys. 2019;15(1):79-88.

14. Rothen-Rutishauser B, Riesen FK, Braun A, Gunthert M, Wunderli-Allenspach H. Dynamics of tight and adherens junctions under EGTA treatment. J Membr Biol. 2002;188(2):151-62.

15. Al-Kilani A, de Freitas O, Dufour S, Gallet F. Negative feedback from integrins to cadherins: a micromechanical study. Biophys J. 2011;101(2):336-44.

16. Koutsouki E, Beeching Cressida A, Slater Sadie C, Blaschuk Orest W, Sala-Newby Graciela B, George Sarah J. N-Cadherin–Dependent Cell–Cell Contacts Promote Human Saphenous Vein Smooth Muscle Cell Survival. Arteriosclerosis, Thrombosis, and Vascular Biology. 2005;25(5):982-8.

17. Charrasse S, Meriane M, Comunale F, Blangy A, Gauthier-Rouvière Cc. N-cadherin–dependent cell–cell contact regulates Rho GTPases and β-catenin localization in mouse C2C12 myoblasts. Journal of Cell Biology. 2002;158(5):953-65.

18. Greiner AM, Chen H, Spatz JP, Kemkemer R. Cyclic tensile strain controls cell shape and directs actin stress fiber formation and focal adhesion alignment in spreading cells. PLoS One. 2013;8(10):e77328.

19. Greiner AM, Biela SA, Chen H, Spatz JP, Kemkemer R. Temporal responses of human endothelial and smooth muscle cells exposed to uniaxial cyclic tensile strain. Exp Biol Med (Maywood). 2015;240(10):1298-309.

20. Qian J, Liu H, Lin Y, Chen W, Gao H. A mechanochemical model of cell reorientation on substrates under cyclic stretch. PLoS One. 2013;8(6):e65864.

21. Ugolini GS, Rasponi M, Pavesi A, Santoro R, Kamm R, Fiore GB, Pesce M, Soncini M. On-chip assessment of human primary cardiac fibroblasts proliferative responses to uniaxial cyclic mechanical strain. Biotechnol Bioeng. 2016;113(4):859-69.

22. Aragona M, Sifrim A, Malfait M, Song Y, Van Herck J, Dekoninck S, Gargouri S, Lapouge G, Swedlund B, Dubois C, Baatsen P, Vints K, Han S, Tissir F, Voet T, Simons BD, Blanpain C. Mechanisms of stretch-mediated skin expansion at single-cell resolution. Nature. 2020;584(7820):268-73.

23. Panciera T, Azzolin L, Cordenonsi M, Piccolo S. Mechanobiology of YAP and TAZ in physiology and disease. Nat Rev Mol Cell Biol. 2017;18(12):758-70.

24. Mammoto T, Mammoto A, Torisawa Y-s, Tat T, Gibbs A, Derda R, Mannix R, de Bruijn M, Yung Chong W, Huh D, Ingber Donald E. Mechanochemical Control of Mesenchymal Condensation and Embryonic Tooth Organ Formation. Developmental Cell. 2011;21(4):758-69.

25. Klumpers DD, Mao AS, Smit TH, Mooney DJ. Linear patterning of mesenchymal condensations is modulated by geometric constraints. J R Soc Interface. 2014;11(95):20140215.

26. Lim J, Tu X, Choi K, Akiyama H, Mishina Y, Long F. BMP–Smad4 signaling is required for precartilaginous mesenchymal condensation independent of Sox9 in the mouse. Developmental Biology. 2015;400(1):132-8.

27. Kranenburg O, Poland M, Gebbink M, Oomen L, Moolenaar WH. Dissociation of LPA-induced cytoskeletal contraction from stress fiber formation by differential localization of RhoA. J Cell Sci. 1997;110 ( Pt 19):2417-27.

28. Toews ML, Ustinova EE, Schultz HD. Lysophosphatidic acid enhances contractility of isolated airway smooth muscle. J Appl Physiol (1985). 1997;83(4):1216-22.

29. Kole TP, Tseng Y, Huang L, Katz JL, Wirtz D. Rho kinase regulates the intracellular micromechanical response of adherent cells to rho activation. Mol Biol Cell. 2004;15(7):3475-84.

30. Duclos G, Erlenkamper C, Joanny JF, Silberzan P. Topological defects in confined populations of spindle-shaped cells. Nat Phys. 2017;13(1):58-62.

31. Takebe T, Enomura M, Yoshizawa E, Kimura M, Koike H, Ueno Y, Matsuzaki T, Yamazaki T, Toyohara T, Osafune K, Nakauchi H, Yoshikawa HY, Taniguchi H. Vascularized and Complex Organ Buds from Diverse Tissues via Mesenchymal Cell-Driven Condensation. Cell Stem Cell. 2015;16(5):556-65.

32. Szabo A, Mayor R. Mechanisms of Neural Crest Migration. Annu Rev Genet. 2018;52:43-63.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Essential revisions:

Please answer the Reviewers comments. They are mainly discussion points (you do not need to do new experiments), but please do so carefully.

Reviewer #1:

The authors were extremely responsive to reviewer critiques, including text changes, new experiments, and modeling simulation. There are some key places where concerns remain, and these should be addressed via text changes, explicitly describing limitations in the Discussion. Specifically:

1) The modeling of cell responses as purely elastic in the continuum model remains problematic. While new data indicates that cell alignment does not require proliferation, authors do not address the extent to which energy is dissipated via remodeling of cell cell junctions. This is accounted for in the Voronoi model, as author's point out, but it's absence from the continuum model is a strong limitation that should be noted.

As suggested by the reviewers, we have completely deleted the theoretical results related to the continuum pure elastic model in the last revision. In the Discussion section, we have now mentioned that we are currently developing a continuum model to explain the tissue flow before the mechanical equilibrium. This continuum model is a Maxwell-type viscoelastic model, in which the energy dissipation due to the cell-cell junction and cytoskeletal remodeling will be accounted for at the tissue scale. The added discussion reads as follows:

“In particular, a Maxwell-type viscoelastic continuum model will be needed to couple the actin dynamics with active tissue mechanics to explain the onset of tissue flow and the maintenance of the tissue mechanical equilibrium (1). This new framework will account for the energy dissipation due to cell-cell junction and cytoskeletal rearrangement during the tissue flow before equilibrium.”

2) Most critically, there remains only indirect support for two key assumptions of the work. One that there is a stiffness gradient, inferred from actin staining, and the other that contractility is uniform and/or unimportant. Given that contraction is produced by interaction of myosin and actin, homogeneous myosin and graded actin can still produce heterogeneous contractile forces. The authors have performed some simulations to test a role for contractility but this is within a modeling framework built on the interpretation of authors, so to some extent you get out what you put in. It would have been ideal to see inhibitor experiments that block myosin activity along with model predictions of the resulting phenotype. I'm the absence of this, some concession on these assumptions needs to be articulated in the Discussion.

While a positive correlation between the myosin level and contractility is well-documented, as the reviewer suggested, it is not impossible that the increasing actin density can be associated with a higher level of contractility because the actomyosin contractility depends on both the myosin and the architecture of the mesh (2). While we have not found results supporting actin mesh density alone can increase the contractility in the literature, it is still possible because the macroscopic network contraction also depends on the concentration of actin cross-linking proteins. We have modified our discussion on the role of stiffness versus contractility in forming the radial elongation and elaborated more details concerning both possibilities in the discussion, which reads as follows:

“A positive correlation between the actin and myosin spatial distributions has been widely reported previously (3, 4). […] However, this possibility requires further analysis on how myosin motors and actin network molecules interact to generate macroscopic network contraction.”

We indeed have already demonstrated that inhibiting myosin activities (through Blebbistatin and ROCK inhibitors, shown in Figure 2C) led to disruption of radial alignment and attributed this finding to the change of condensation tendency. However, it is challenging to pharmaceutical control myosin gradient within the patterns and thus cannot be used to study the role of myosin gradient. Future works are needed to locally regulate myosin activities.

Reviewer #3:

I'd like to thank the authors for their corrections. I think the manuscript has improved in clarity significantly. Still, some of the main comments remain unaddressed.

I am summarizing below the main concerns from the last round of reviews and whether they were addressed or not.

1. Justification of the model assumptions:

– Existence of stiffness gradient: ok (thanks to more citations);

– Calcium chelation: ok (thanks to more citations);

– No cell proliferation: ok (thanks to new experiments);

– Uniform contractility: not ok (not enough evidence, details below).

2. Integration of model and experiment: No changes.

3. Connection to development, physiology, or disease: No changes.

4. Discussion of the Roux papers: not ok.

I am now giving more details on some of the main points that were not adequately addressed:

1. Uniform contractility: The authors performed new immunostaining and new simulations. They showed that the density of myosin motors was uniform on most of the tissue, with a slight increase on the boundary cells. they then performed simulations to show that this slight increase of contractility at the edge does not lead to radial alignment. However, this is not enough experimental evidence to conclude that contractility is uniform. indeed, uniform myosin + non-uniform Factin does not necessarily mean uniform contractility as both proteins are required for contraction.

The authors show in simulations that an increase of contractility at the edge leads to smaller boundary cells. What would happen if contractility follows the actin gradient? Could that be enough to reproduce the radial alignment of the cells, even in the absence of cell contractility differential or condensation?

We thank this reviewer for this insightful comment, which is in line with comment #2 of Reviewer #1. Please see also see our response to that comment.

As pointed out by both reviewers, it is not impossible that the actin gradient also affects the contractility because the actomyosin-based contractility depends on both the myosin at work and the architecture of the actin mesh. In our model, we did not emphasize that uniform contractility is necessary, and we did not exclude the possibility of a contractility gradient associated with the actin. However, since multiple studies are supporting that the stiffness gradient is aligned with the actin gradient, we reason the stiffness differential due to the actin gradient together with the contractility (either graded or not) and intercellular adhesion are sufficient for the radial alignment. We have added more details in the discussion to concern the possibility of a contractility gradient associated with the actin gradient.

2. Integration of model and experiments. there is no quantitative comparison between theory and experiments. The simulation results are summarized in the new panel Figure 4B. Instead, why not showing the same radial profiles as for the experiments? It will make the comparison between experiments and theory easier.

Our model is essential to demonstrate the independent role of condensation tendency and stiffness differential in forming the boundary radial alignment. While we agree that a direct comparison between modeling and experimental results will be interesting, it is difficult to have a fair comparison, mainly because it is difficult to calibrate the prestretch (g) in the model in experiments. Therefore, we believe the qualitative comparison between the model and experimental results is suitable in our case.

It would be neat to see how sensitive the cell alignment is to rho, g and their gradients.

These sensitivity studies have already been shown in Figure. 4.

Along those lines, can the authors comment on how steep the stiffness gradient has to be in order to re-align the cells radially? Can this be quantitatively compared to the actin gradients measured in Figure S3-1? Not all the patches seem to display the gradient (see images in the 3rd column). Can the authors show if the steepness of the actin gradient correlates with the radial alignment of the cells or their size for each pattern instead of showing that the average gradient value and the average alignment are correlated?

We thank the reviewer for this suggestion. As the radial alignment of boundary cells is mainly characterized by cell angle deviation, elongation, and cell area, there is not a clear threshold for such alignment. Instead, as suggested by this reviewer, the best way is to investigate the correlation between actin gradient and radial alignment. In that regard, we analyzed a total of 16 colonies. The colonies shown in Figure 3—figure supplement 1A are two typical colonies with different steepness of actin gradient. We found that the bottom one with a steeper actin gradient did show radial alignment more clearly (Figure 3—figure supplement 2A). To quantify this correlation, we generated a scatterplot and performed linear regression analysis and correlation analysis (Figure 3—figure supplement 2B). The results show that angle deviations of boundary cells are negatively correlated with actin gradient with a Pearson correlation coefficient of − 0.533 and a P value of 0.0335, indicating a high probability of correlation (smaller angle deviation means better radial alignment). Thus, these results further support that actin gradient is essential for the establishment of boundary cell radial alignment.

3. Discussion of the 3 papers from Aurelien Roux's lab: The papers are cited in the bulk of the introduction, but not properly discussed. It seems to me that the transition from parallel to perpendicular anchoring is particularly important to mention in this manuscript. The authors claim in their response that they discussed the papers in the discussion. I could not find this section (none of the 3 papers are cited in the Discussion section). I think comparing and contrasting the results of those papers with this manuscript would greatly improve our understanding of how contractility and circular confinement impact the organization of dense layers of elongated cells.

We agree with this reviewer that a detailed discussion of the three recent papers from Roux’s group is important. The significant difference between our work and their works is that we have found an equilibrium with the radial elongation pattern while their multicellular system evolves from spiral to radial cell alignment and from radial alignment to out-of-plane tissue growth as cell proliferation continues. We have added a thorough discussion in the revision to compare and contrast the results from our manuscript to the three papers from Aurelien Roux’s lab, which reads as follows:

“Recently, Roux, Kruse, and colleagues reported that C2C12 myoblasts could self-organize into spiral patterns when confined using similar circular confinement (10-12). […] While cell proliferation is a critical driving factor in aster pattern formation in the C2C12 system, in our REF system, the stiffness differential is indispensable for the radial alignment formation.”

References:

1. Chaozhen Wei MW. Nonlinear modeling reveals multi-timescale and higher-order effects in active tissue mechanics. arXiv:210309427. 2021.

2. Kasza KE, Zallen JA. Dynamics and regulation of contractile actin-myosin networks in morphogenesis. Curr Opin Cell Biol. 2011;23(1):30-8.

3. Martin AC, Kaschube M, Wieschaus EF. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457(7228):495-9.

4. Banerjee DS, Munjal A, Lecuit T, Rao M. Actomyosin pulsation and flows in an active elastomer with turnover and network remodeling. Nat Commun. 2017;8(1):1121.

5. Murrell M, Oakes PW, Lenz M, Gardel ML. Forcing cells into shape: the mechanics of actomyosin contractility. Nat Rev Mol Cell Biol. 2015;16(8):486-98.

6. Tavares S, Vieira AF, Taubenberger AV, Araujo M, Martins NP, Bras-Pereira C, et al. Actin stress fiber organization promotes cell stiffening and proliferation of pre-invasive breast cancer cells. Nat Commun. 2017;8:15237.

7. Rotsch C, Radmacher M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys J. 2000;78(1):520-35.

8. Nawaz S, Sánchez P, Bodensiek K, Li S, Simons M, Schaap IAT. Cell Visco-Elasticity Measured with AFM and Optical Trapping at Sub-Micrometer Deformations. PLOS ONE. 2012;7(9):e45297.

9. Gavara N, Chadwick RS. Relationship between cell stiffness and stress fiber amount, assessed by simultaneous atomic force microscopy and live-cell fluorescence imaging. Biomech Model Mechanobiol. 2016;15(3):511-23.

10. Blanch-Mercader C, Guillamat P, Roux A, Kruse K. Integer topological defects of cell monolayers: Mechanics and flows. Phys Rev E. 2021;103(1-1):012405.

11. Guillamat P, Blanch-Mercader C, Kruse K, Roux A. Integer topological defects organize stresses driving tissue morphogenesis. bioRxiv. 2020:2020.06.02.129262.

12. Blanch-Mercader C, Guillamat P, Roux A, Kruse K. Quantifying Material Properties of Cell Monolayers by Analyzing Integer Topological Defects. Phys Rev Lett. 2021;126(2):028101.

13. Martino F, Perestrelo AR, Vinarský V, Pagliari S, Forte G. Cellular Mechanotransduction: From Tension to Function. Frontiers in Physiology. 2018;9(824).

14. Holle AW, Engler AJ. More than a feeling: discovering, understanding, and influencing mechanosensing pathways. Curr Opin Biotech. 2011;22(5):648-54.

15. Marullo S, Doly S, Saha K, Enslen H, Scott MGH, Coureuil M. Mechanical GPCR Activation by Traction Forces Exerted on Receptor N-Glycans. ACS Pharmacology and Translational Science. 2020;3(2):171-8.

https://doi.org/10.7554/eLife.60381.sa2

Article and author information

Author details

Tianfa Xie

Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, United States

Contribution
Conceptualization, Formal analysis, Investigation, Writing - original draft

Contributed equally with
Sarah R St Pierre and Nonthakorn Olaranont

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-1332-4373
Sarah R St Pierre

Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, United States

Contribution
Software, Formal analysis, Investigation, Methodology, Writing - original draft

Contributed equally with
Tianfa Xie and Nonthakorn Olaranont

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9774-8709
Nonthakorn Olaranont

Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, United States

Contribution
Software, Formal analysis, Investigation, Methodology, Writing - review and editing

Contributed equally with
Tianfa Xie and Sarah R St Pierre

Competing interests
No competing interests declared
Lauren E Brown

Department of Biomedical Engineering, University of Massachusetts, Amherst, United States

Contribution
Formal analysis, Writing - review and editing

Competing interests
No competing interests declared
Min Wu

Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, United States

Contribution
Conceptualization, Software, Formal analysis, Supervision, Funding acquisition, Investigation, Writing - original draft, Project administration

For correspondence
mwu2@wpi.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-4728-6475
Yubing Sun
1. Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, United States
2. Department of Biomedical Engineering, University of Massachusetts, Amherst, United States
3. Department of Chemical Engineering, University of Massachusetts, Amherst, United States
Contribution
Conceptualization, Formal analysis, Supervision, Funding acquisition, Writing - original draft, Project administration

For correspondence
ybsun@umass.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6831-3383

Funding

National Science Foundation (CMMI 1662835)

Yubing Sun

National Science Foundation (CMMI 1846866)

Yubing Sun

National Science Foundation (DMS 2012330)

Min Wu

University of Massachusetts Amherst

Yubing Sun

Worcester Polytechnic Institute

Min Wu

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

This work is supported in part by the National Science Foundation (CMMI 1662835 and CMMI 1846866 to Y.S., and DMS 2012330 to M.W), the Department of Mechanical and Industrial Engineering at the University of Massachusetts Amherst, and Department of Mathematical Sciences at Worcester Polytechnic Institute. The Conte Nanotechnology Cleanroom Lab is acknowledged for support in microfabrication. The authors acknowledge the University of Massachusetts Amherst Light Microscopy Core for confocal microscopy and Genomics Resource Laboratory for genomics services. M.W thanks Sam Walcott for insightful discussions.

Senior and Reviewing Editor

Aleksandra M Walczak, École Normale Supérieure, France

Version history

Preprint posted: June 24, 2020 (view preprint)
Received: June 24, 2020
Accepted: September 9, 2021
Accepted Manuscript published: September 20, 2021 (version 1)
Version of Record published: September 28, 2021 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.