Hydrodynamics of sponge pumps and evolution of the sponge body plan

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: December 22, 2020 (This version)
Accepted Manuscript published: November 30, 2020 (Go to version)
Accepted: November 27, 2020
Received: July 13, 2020

1. Of interest
Hierarchical morphogenesis of swallowtail butterfly wing scale nanostructures

Kwi Shan Seah, Vinodkumar Saranathan

Research Article Sep 28, 2023
Further reading

Abstract
Introduction
Results and discussion
Materials and methods
Appendix 1
Appendix 2
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Sponges are suspension feeders that filter vast amounts of water. Pumping is carried out by flagellated chambers that are connected to an inhalant and exhalant canal system. In ‘leucon’ sponges with relatively high-pressure resistance due to a complex and narrow canal system, pumping and filtering are only possible owing to the presence of a gasket-like structure (forming a canopy above the collar filters). Here, we combine numerical and experimental work and demonstrate how sponges that lack such sealing elements are able to efficiently pump and force the flagella-driven flow through their collar filter, thanks to the formation of a ‘hydrodynamic gasket’ above the collar. Our findings link the architecture of flagellated chambers to that of the canal system, and lend support to the current view that the sponge aquiferous system evolved from an open-type filtration system, and that the first metazoans were filter feeders.

Introduction

Many aquatic suspension feeders use cilia and flagella to generate feeding flows from which they capture prey particles. Unlike ciliary arrays that drive fluid tangential to their attachment surface (Brooks and Wallingford, 2014; Narematsu et al., 2015; Gilpin et al., 2020), flagellated collar-cells (choanocytes) in sponges must pump water perpendicular to and through a perforated surface, working against a pressure resistance. Several choanocytes are closely packed inside chambers that are connected to inhalant and exhalant canal systems. The canal architecture and its associated pressure resistance impacts the operating condition of choanocyte chambers, and dictates morphological adaptation in such pumping units. Most sponges possess an elaborate aquiferous system (leucon) (Reiswig, 1975a), but some Calcarea, a small class of the Porifera, have a less elaborate aquiferous system (ascon and syconoid) (Manuel, 2006) Figure 1.

Figure 1

Download asset Open asset

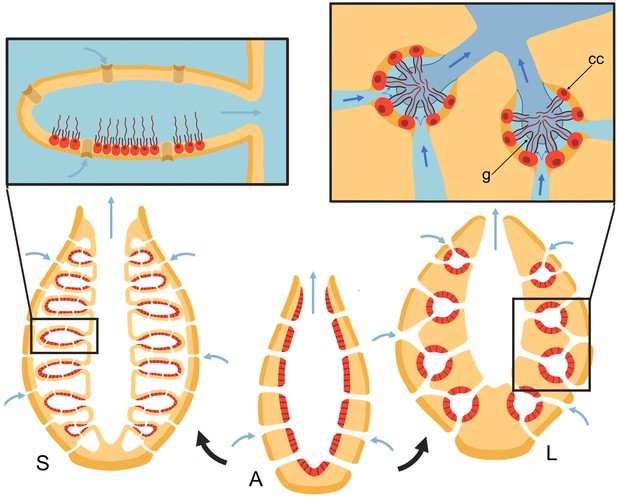
Schematic of sponge body types in ascon (A), sycon (S), and leucon (L) with evolutionary view of grades of morphological complexity in calcareous sponges (black arrows).

Insets show zoom-in water path (blue arrows) into the chambers in sycons and leucons, where in the latter, water is forced to go through collar filters (black) of choanocytes (red, cc) due to the presence of a physical gasket (g).

Asconoid forms are organized as a single tube in which the choanocytes form a single layer on the inner surface of the tube wall. Syconoid forms, in turn, possess many ascon-shaped cylindrical chambers branching off a central cavity (atrium). Water enters through short canals or directly through openings (ostia) into the chambers and leaves through a single outlet (apopyle) to the atrium and from there out of the osculum. In leuconoid forms, the holes in the surface of the body are connected to a complex canal system with a multitude of small chamber pump units.

Although these are often depicted as a progressive gain in complexity in the evolution of leuconoid from ascon and sycon forms, phylogenetic analyses indicate that in Calcarea both leucon and sycon type sponges most likely arose independently from ascon forms (Manuel, 2006), and some evidence points to the opposite process in which ascon and sycon forms may have derived from a rigid leucon body architecture (Dohrmann et al., 2006). It is unknown what gave rise to the leuconoid forms of the other three sponge classes. One of the greatest modern puzzles is whether Porifera or Ctenophora branched first in the evolution of multicellular animals (Whelan et al., 2015; Telford et al., 2016; Feuda et al., 2017). Therefore, understanding how the sponge filtration system came about would go a long way to helping resolve whether sponges evolved from a colonial unicellular ancestor (Porifera first hypothesis) or from a tissue-grade metazoan (as in some interpretations of the Ctenophora first hypothesis).

Both choanocytes and choanoflagellates, a group of free-living unicellular and colonial flagellates, share ancestory to animals, and possess similar collar-flagellated cells, to generate adequate feeding currents. In both cells, presence of a flagellar vane, a sheet-like structure along the length of the flagellum, has been observed (Afzelius, 1961; Fjerdingstad, 1961; Mehl and Reiswig, 1991; Weissenfels, 1992; Leadbeater, 2006; Mah et al., 2014). Vanes differ from mastigonemes, which are extracellular nanometer-thick fibers that protrude perpendicular to the flagellum (Bouck, 1971; Fenchel, 1982), both morphologically and functionally. Mastigonemes appear to exist and remain in the beat plane and are thought to reverse the thrust generation by the flagellum (Holwill and Peters, 1974). Vanes, however, are horizontal fibers of glycocalyx that extend perpendicularly from the flagellar axis and appear to augment the thrust generation (Nielsen et al., 2017).

Choanocytes in sponges, in addition to driving the flow through the collar, must also overcome the pressure resistance arising from the canal system. The narrow canals in leuconoid body plans add significant pressure resistance to the pump, between 2 and 50 Pa for different sponge species (Larsen and Riisgåd, 1994; Leys et al., 2011; Ludeman et al., 2017). Our recent study (Asadzadeh et al., 2019a) demonstrated that directional flow and efficient filtration at such hydrodynamic conditions is only possible because the pumping unit is sealed against back flow, by three extracellular elements, namely, a tight mesh on the distal part of the collar, a vane on the flagellum, and finally a gasket-like structure called Sollas’ membrane (Dendy, 1888; Sollas, 1889), that connects the microvilli (collar elements) at their tips (Figure 1). These features divide the chamber into two regions of low and high pressure, and force the inflow through the collar slits at its base. In contrast, calcareous sponges have fewer canals and thus have less pressure resistance, and appear to lack the gasket and tight mesh that covers the collar (Dendy, 1888; Eerkes-Medrano and Leys, 2006).

Here, we ask how sponges with apparent absence of a gasket, and therefore an open aquiferous system, can nevertheless effectively pump and filter water for prey, and what the trade-offs and limitations in such pumping systems are. We combine modeling with experiments to study the pumping and feeding in calcareous sponges using Sycon coactum as a model organism. Because of the geometric complexity, rather than attempting to use singularities to model the low Reynolds flow, as done for example for flows near a hole in a plane wall (Davis et al., 1981), or flagella-driven flows (Roper et al., 2013), we use computational fluid dynamic (CFD) simulations to investigate the functionality of the pumping elements in the absence of a gasket. Specifically, we study the role of each pumping element in pumping sufficient water through the ostia and into the chamber and examine the mechanism that forces the inhalant flow to pass through the collar filter. The modeled pumping rates are compared to measured exhalant flow rates and the predicted retention efficiency of calcareous sponges is contrasted with actual retention efficiencies measured for different prey types. The limitations and trade-offs between the pumping rate and retention efficiency shed light on what may have been the first poriferan filtration system.

Morphology of the flagellated chamber

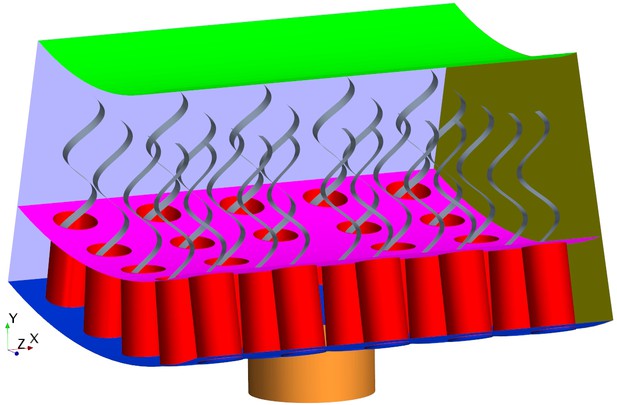
Each flagellated chamber in Sycon coactum contains thousands of choanocytes that pump water through hundreds of ostia (Leys and Eerkes-Medrano, 2006) Appendix 1—figure 1. To reduce the computational costs, we consider a cylindrical axisymmetric and axially periodic chamber. The computational domain is thereby reduced to a wedge section into the cylindrical chamber that includes a central ostium surrounded by 24 choanocytes (Figure 2). The boundary conditions (BCs) are periodic along the long axis of the chamber (due to the periodic occurrence of ostia) and laterally symmetric on the left and right sides of the section modeled (if one is facing the long axis), due to cylindrical symmetry of the tubular chamber. Once fluid leaves the computational domain vertically into the inner cylindrical core of the choanocyte chamber, it is directed axially toward the open end of the chamber (apopyle). Pressure variation inside the core of the chamber is negligible (Appendix 1—figure 2), hence a uniform pressure boundary is applied on the top surface of the computational domain.

Figure 2

Download asset Open asset

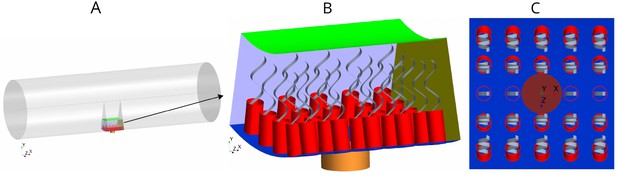
Morphology of the modeled flagellated chamber in calcareous sponges.

(A) The computational domain is a wedged section into the cylindrical, ascon-like flagellated chamber (85 µm in diameter). (B) A side view magnification of the modeled section. The water is pumped into the domain through a central tubular ostium, its inlet (brown, shown in C) is subjected to a uniform pressure and its surface (orange) to no-slip boundary conditions. The domain includes 24 porous collars (red) with 24 flagella (gray) attached to the inner surface of the chamber (blue) and subjected to no-slip boundary conditions. Two sides of the domain that are perpendicular to the x axis (olive, for clarity only one side shown) are subject to periodic boundary conditions, and the other two sides that are parallel to both the x and y axis (light blue, one side shown) are subjected to symmetric boundary conditions. The water leaves the domain from the top (green, subjected to a uniform pressure boundary conditions) into the chamber core. (C) Top view showing arrangements of the inlet and nearby collars.

The collars are modeled as a porous structure (Equation 6) with a porosity that corresponds to that of a network of parallel and equally spaced cylinders (Keller, 1964) representing the microvilli of 0.1 µm in diameter. Although recent observations (Appendix 1—figure 2) have shown some mesh structures appearing locally between collars, chambers in S. coactum appear to lack a solid gasket. Hence we do not include a physical gasket in the CFD model. However, to study the effect of the gasket, we also consider cases where a physical gasket is included in the model. (Appendix 2—figure 1). Each flagellum is modeled as a thin sheet of width W (resembling the vane, Appendix 1—figure 2) that beats in a plane and is subject to a no-slip and no-penetration boundary condition with a prescribed motion given in Equation 3.

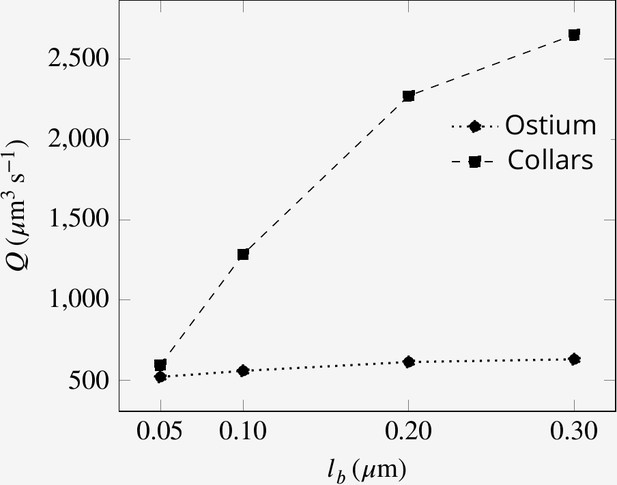
We initially consider mean measured values for the dimension of the chamber elements: spacing between flagella of 5 µm, collars of diameter $D_{c o l} = 2.5 μ m$ , and length $L_{c o l} = 4.8 μ m$ with spacing between microvilli of $l = 0.05 μ m$ , and an ostium of diameter $D_{o s t} = 7.0 μ m$ and length $L_{o s t} = 3.0 μ m$ . Flagella have a wavelength of $λ = 5.0 μ m$ , an amplitude of $a = 1.0 μ m$ (with length scale $δ = 1.0 μ m$ , see Equation 3) and vane width of 0.7 µm, all beating in phase at a frequency of 30 Hz (base case). In subsequent experimental simulations, these dimensions are varied along with the dimensions of other elements involved in the pumping system (e.g. length of the collar, length and diameter of the ostium, porosity of the collar etc.).

Results and discussion

Pumping mechanism

To facilitate efficient feeding, particles carried in the inhalant flow should reach the collars where the prey particles are filtered (Reiswig, 1971; Reiswig, 1975b; Weissenfels, 1976; Imsiecke, 1993). To investigate how the flow is forced through the collar rather than bypassing it in the absence of a gasket, we examine the average velocity field in two perpendicular planes in the middle of the computational domain (Figure 3AB). The velocity fields reveal a large backflow in the middle of the domain above the ostium where the spacing between the flagella is large. The pressure drop after the ostium provides a suction drawing the water from the higher pressure region above the flagella to the spacing between the flagella. This flow meets the inhalant flow from the ostium nearly at the same height as that of the collar, resulting in a stagnation zone that acts as a ‘hydrodynamic gasket’ that forces the inhalant flow toward the collars. Videos 1 and 2 demonstrate how formation of the hydrodynamic gasket ensures an efficient encounter of particles with the collar and prevents particles from bypassing the collars in the absence of a physical gasket.

Figure 3

Download asset Open asset

Simulated flow field inside the chamber.

The averaged velocity field is plotted along the xy-plane (A) and yz-plane (B). Colors represent water velocity magnitude according to the color bar at the side; flow direction is indicated by white arrows; the flagella are indicated by black lines and the collars by gray lines. Due to the symmetry with respect to the yz-plane only one half of each of the planes is shown. A zone of stagnant water is formed by the backflow in the relatively large spacing between the flagella and above the ostium (**H–G**). This backflow serves as an effective ‘hydrodynamic gasket’ that forces the inflow through the collars. (C) Pumping rate (Q) through the ostium and filtration rate through the collars (Q) for different width (W) of the flagellar vane. The larger symbols correspond to the case where the vane width is 1.4 µm on the unconfined part of flagellum and 0.7 µm on the confined part.

Video 1

Download asset

posterframe for video — Side view of passive particles entering into the chamber through the ostium and carried by the flow.

Particle color denotes its velocity according to the color scale at the bottom. Particles that arrive at the collar are removed from the simulation.

Video 2

Download asset

The flow passing through the collar (filtration rate) is several times higher than the flow through the ostium (pumping rate) (Figure 3C), suggesting that a large proportion of the water is re-filtered inside the chamber. Increasing the vane width increases both the pumping and filtration rate, but the vane width has a larger effect on the latter (Figure 3C), likely due to the confinement and hydrodynamic interaction between the individual flagellum and its associated collar (Nielsen et al., 2017; Asadzadeh et al., 2019b). For instance, increasing the vane width from 0.3 to 0.7 µm increases the pumping rate by 53%, while the filtration rate is more than doubled.

To elucidate the mechanism responsible for pumping water through the ostia and to differentiate it from the mechanism that drives the water through the collars, we consider two hypothetical cases: (1) with flagella that beat only above the collars (Figure 4A) and (2) with short flagella confined to the collar height (Figure 4B). Flagella that are only present outside and above the collars are as efficient as complete flagella in pumping water into the chamber but are not able to drive water through the collar Figure 4C. In contrast, short flagella that are confined inside the collars are almost as efficient as complete flagella in driving water through the collars but are not able to pump new water through the ostium into the chamber. These results demonstrate two separate contributions from the confined and unconfined part of the flagellum of calcareous sponges. This pumping mechanism is distinctly different from that of demosponges and glass sponges, both of which possess a tissue or mucus gasket, in which the confined part of the flagellum with vanes that span the full diameter of the fine-meshed collars (Mah et al., 2014) is the pumping unit (Asadzadeh et al., 2019a).

Figure 4

Download asset Open asset

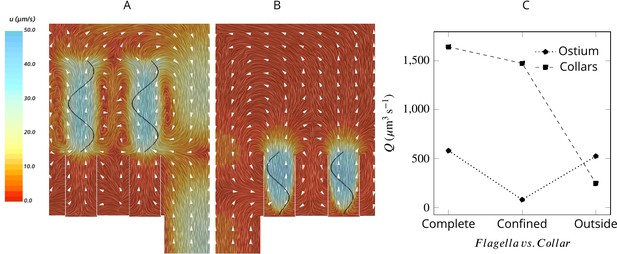
Averaged velocity field for two hypothetical cases: (A) only the unconfined part of the flagella exists, and (B) only the confined part of the flagella exists.

A comparison of the pumping and filtration rates provided in (C) demonstrate that unconfined flagella contribute substantially to the pumping rate into the chamber, but not through the collars. On the other hand, the confined region of the flagella draws in the flow through the collars and have a minor effect on the pumping rate.

Pump characteristic curve

To analyze the functionality of the pump at different hydrodynamic conditions, we consider the pump characteristic curve. In so doing, one should differentiate the basic pumping unit (pressure-generating unit) from the pressure-resistive parts of the system (the canal system). The basic pumping units are the simplest subdivision of the choanocyte chamber exposed to the same pressure difference resulting from the canal system. Hence, these units all work in parallel. For sponges lacking a physical gasket, the unit is one hole (ostium of zero length) with several neighboring choanocytes (Figure 2B). Presence of a physical gasket, however, leads to two zones of high and low pressure inside the spherical choanocyte chambers (Weissenfels, 1992; Asadzadeh et al., 2019a), effectively exposing each individual choanocyte to the same pressure difference. Therefore, in sponges with a physical gasket, the basic pumping unit is only one choanocyte, irrespective of its proximity to the nearest ostium (Asadzadeh et al., 2019a).

Basic pumping units are characterized by a maximum pumping rate $Q_{𝑚𝑎𝑥}$ (at zero pressure load), and a maximum pressure $P_{𝑚𝑎𝑥}$ (at zero net flow). Due to the linearity of the governing equations at low Reynolds numbers, the pump characteristic of the unit is linear, hence:

\hat{P} = 1 - \hat{Q}

where $\hat{P} = P_{} / P_{𝑚𝑎𝑥}$ and $\hat{Q} = Q_{} / Q_{𝑚𝑎𝑥}$ are normalized pressure and pumping rate, respectively. Assuming Poiseuille flow in the canal system, and a tubular ostium of length $L_{𝑜𝑠𝑡}$ and diameter $D_{𝑜𝑠𝑡}$ , the pressure resistance (of the system) is given by White, 2011:

\hat{P} = \frac{R_{o s t}}{C_{p u m p}} \hat{Q}

where $R_{o s t} = \frac{128}{π} (μ L_{𝑜𝑠𝑡} / D_{𝑜𝑠𝑡}^{4})$ is the canal resistance, µ the dynamic water viscosity, and $C_{p u m p} = P_{m a x} / Q_{m a x}$ is a characteristic of the pumping unit. Figure 5 depicts the dimensionless pump (Equation 1) and system (Equation 2) characteristic curves for different sponge pumps. Intersection of the two characteristics defines the operating condition of the pumping unit. Employing typical dimensions of the ostium and $C_{p u m p}$ of the syconoid pumping unit (e.g. $C_{p u m p} = 0.058 / 1114 = 50 μ Pa . s μ m^{- 3}$ for the pumping unit in Figure 2B) results in $R_{o s t} / C_{p u m p} ≃ 1$ , indicating $Q ≃ 0.5 Q_{m a x}$ at the operating condition. The higher the resistance from the canal system, the higher the slope of the system curve, hence the lower the pumping rate. As shown in Figure 5, the functionality of the syconoid pumping unit would be impaired if connected to a complex and narrow canal system with two orders of magnitude higher pressure resistance (e.g. $R_{o s t} / C_{p u m p} = 100$ ). For such hydrodynamic conditions, a modification of the pumping unit to that of the leucon type employing a physical gasket is inevitable. Thanks to the sealing elements, $C_{p u m p, g a s k e t}$ in such pumps are much higher (typically 3 orders of magnitudes) than syconoid ones (Asadzadeh et al., 2019a), resulting in a much lower slope of the system curve ( $R_{o s t} / C_{p u m p, g a s k e t} ≃ 0.1$ ) yielding $Q ≃ Q_{m a x}$ at the operating condition. Note that the actual characteristic curve in the leucon pump is non-linear, which has been ascribed to the bending of the vane at the relatively higher working pressure (Asadzadeh et al., 2019a).

Figure 5

Download asset Open asset

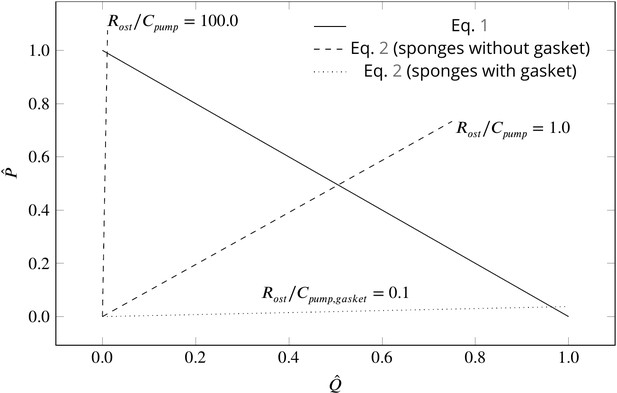
Dimensionless pump (solid line) and system (dashed and dotted lines) characteristics for different pumping units and canal systems in sponges.

At their operating condition (intersection of the pump and system lines), pumping units lacking a physical gasket deliver half of their maximum pumping capacity ( $R_{o s t} / C_{p u m p} = 1.0$ ). Functionality of such pumps would be impaired if connected to highly resistive canal system ( $R_{o s t} / C_{p u m p} = 100$ ). At such hydrodynamic conditions, a modification of the pump to that of leucon type having a physical gasket ( $C_{p u m p, g a s k e t} ≫ C_{p u m p}$ ) lowers the slope of the system curve ( $R_{o s t} / C_{p u m p, g a s k e t} ≃ 0.1$ ), resulting in an efficient pumping at their operating condition.

Although sponges with a complex canal system appear to have a 'gasket-present’ pumping unit, a ’gasket-absent’ unit can still function efficiently if connected to a complex, yet open and less resistive canal system, or inefficiently if connected to an open canal system, but with highly resistive ostia. Therefore, there could well be sponges characterized as leuconoid types yet missing a physical gasket, or as syconoid types but with a physical gasket. The appearance, structure, and nature of the gasket would also depend on the hydrodynamics dictated by the canal system. Therefore, further research, using better preservation and imaging techniques, is required to elucidate the exact nature of the sealant element, and to investigate the role that hydrodynamics is playing in forming the seal in different sponges.

Hydrodynamic trade offs in the morphology of sponges

The open architecture of the syconoid pump dictates a delicate trade-off between the pumping rate and the retention efficiency. Although a wider and shorter ostium provides less resistance to flow hence higher pumping rate, the reduced pressure loss comes with a cost of a weaker backflow in the core of the region and thus a weaker hydrodynamic gasket located further into the chamber and above the collar tips. Under such circumstances, a larger fraction of the flow bypasses the collars and the retention efficiency drops. Lower retention efficiency of the calcareous sponge Pericharax heteroraphis as compared to different species of demposponges has been previously ascribed to its wider ostia and large chambers (Wilkinson, 1978). In contrast, a narrow and long ostium with higher resistance to flow results in a reduced pumping rate but an increased retention efficiency as the hydrodynamic gasket is located below the tip of the collars and the stronger backflow is more efficient in preventing flow from bypassing the collar filter (Appendix 1—figure 4).

The dependency of the pumping rate into the chamber on the length of the collar suggests another trade-off: choanocytes with shorter collars and a longer unconfined part of the flagellum can pump more water into the chamber, but this comes at the cost of more flow bypassing the collar, and vice versa. As a result, regions of the chamber having shorter collars will be less efficient in filtering the inhalant flow. This effect may explain the presence of pseudopodial extensions extending from the cell surface in these regions (Leys and Eerkes-Medrano, 2006). The pseudopodia, which are on average twice as long as the collars, have been observed to reach beyond the collar and seem to be involved in particle capture (Leys and Eerkes-Medrano, 2006), potentially compensating for the decreased filtration efficiency of the collars.

On individual collars, the spacing between adjacent microvilli appears wider at the base but becomes smaller toward the tip of the collar where the microvilli tips are occasionally fused together (Leys and Eerkes-Medrano, 2006). To study the effect of non-uniform porosity along the collars on the performance of the sponge pump, we consider cases where the spacing between microvilli decreases from the base to the tip of the collar. We find that more widely spaced (higher porosity) microvilli on collars enhance the filtration rate with a minimal effect on the pumping rate into the chamber (compare the plots in Appendix 1—figure 5). This result further highlights the fact that the pumping rate into the chamber is nearly independent of the confined part of the flagellum, while the filtration rate is greatly affected by the local collar-flagella parameters.

Flagella kinematics

Thus far, we have considered a synchronous beat and constant amplitude. We now consider different scenarios, that is, phase shift among the flagella, flagella beating in different planes (Appendix 1—figure 6), different frequencies, and different wavelength (Appendix 1—figure 7 and 8). The results show that beat synchronization among choanocytes is not necessary for the functionality of the pump. Despite improved efficiency of pumping in ciliary arrays by synchronization (Niedermayer et al., 2008; Golestanian et al., 2011; Elgeti and Gompper, 2013), asynchronized flagella in sponges continue to pump efficiently into the chamber (discussed in details in the SI). Lack of synchronization has been reported both within colonies of the choanoflagellate Salpingoeca rosetta (Roper et al., 2013; Kirkegaard et al., 2016), and in choanocyte chambers of the freshwater sponge Spongilla lacustris (Mah et al., 2014).

The amplitude of the flagella waveform is limited inside the collars, but it can increase outside, a behavior observed in choanocytes of the S. lacustris (Mah et al., 2014). To study the effect of increased amplitude, we modify the beat form in Equation 3 by setting $a = 5 μ m$ and $δ = 22 μ m$ , which results in the increased amplitude of the waveform to a maximum of 2 µm at the tip of the flagella. This modulation in the beat form improves pumping rate by 51% (to $Q_{𝑜𝑠𝑡} = 874 μ m^{3} s^{- 1}$ ) while keeping the stagnation area at the same height relative to the base (Figure 3A), but it is only 37% more energetically demanding, suggesting that such a modification is beneficial to the sponge.

To compare the CFD predictions with observations, we estimate the volume flow rate per ostium in Sycon coactum by dividing the experimentally measured exhalant flux rate by the estimated total number of ostia. This results in an estimated flow rate of $Q_{𝑜𝑠𝑡, 𝑒𝑥𝑝} = 1151 μ m^{3} s^{- 1}$ per ostium, and $Q_{𝑐ℎ, 𝑒𝑥𝑝} = 48 μ m^{3} s^{- 1}$ per choanocyte (given 24 choanocytes). CFD results show that ascon and sycon type sponges with typical values and dimensions of the morphological elements, are able to pump more than $Q_{𝑜𝑠𝑡} \sim 1000 μ m^{3} s^{- 1}$ through an ostium without any requirement for a physical gasket (e.g. for the case with increased amplitude and a vane width of 1.4 µm on the unconfined part of the flagellum, $Q_{𝑜𝑠𝑡} = 1295 μ m^{3} s^{- 1}$ ). Furthermore, both experimental and CFD estimates of flow rate per choanocyte ( $Q_{𝑐ℎ, 𝑒𝑥𝑝}$ ) are comparable to published estimates for leucon sponges that range from 17 to $236 μ m^{3} s^{- 1}$ for different species of demosponges and glass sponges (Larsen and Riisgåd, 1994; Leys et al., 2011; Ludeman et al., 2017), suggesting similar pumping capacity despite different pumping mechanism.

Effect of a gasket

To study the effect of a physical gasket on the flow and pumping rate, we model this structure as an impermeable baffle and incorporate it into the computational domain (Appendix 2—figure 1). The inclusion of a physical gasket improves the pumping rate by 21% if the collar is long (4.8 µm), but it does not alter the pattern of the averaged flow much (Figure 6AB). However, with shorter collars, a physical gasket decreases the pumping rate, and the more so the shorter the collar (Figure 6C). This phenomenon may explain the shorter collars in calcareous sponges compared to those in demosponges (Leys and Eerkes-Medrano, 2006) .

Figure 6

Download asset Open asset

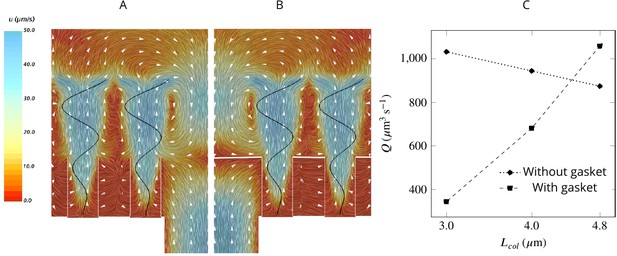
A comparison of mean velocity fields and the performance of (A) a hydrodynamic, and (B) a physical gasket (both with an increased amplitude of the flagella beat waveform and collar length of 4.8 µm).

(C) The volume flow rate through the ostium for different collar lengths. Inclusion of the physical gasket does not significantly affect the flow pattern inside the chamber. In sponges with relatively short collars (calcareous sponges), choanocytes pump more through the ostium the shorter the collar but increasing less through the collars (C).

Retention efficiency

Simulations of passive prey particles (Videos 1 and 2) show that the prey retention efficiency is potentially 100%. However, these simulations assume that all particles encountering the filter are retained. In reality, however, the retention efficiency can vary for different prey types, especially in the absence of a gasket sealing off the collar filter area from the rest of the chamber. We studied experimentally the retention efficiency in Sycon coactum of three different prey types: small micro-algae (Euk < 20 µm), and non-photosynthetic bacteria with high (HNA) and low (LNA) nucleic acid content. While Euk and HNA were retained with near 100% efficiency, the efficiency of retention for the LNA prey particles was considerably lower (60 ± 6%) (Figure 7). LNA is largely associated with SAR11, the smallest and most abundant bacterial clade in the ocean (Mary et al., 2006). These bacteria may slip through the mucus filter of tunicates (Dadon-Pilosof et al., 2017; Dadon‐Pilosof et al., 2019) and evade filtration in many sponges (Ribes et al., 2012).

Figure 7

Download asset Open asset

Retention efficiency (%) of different prey types counted by flow cytometry in the water inhaled and exhaled by *Sycon coactum*.

Euk are small nano and pico eukaryotic algae; HNA and LNA are non-photosynthetic bacteria with high and low nucleic acid content, respectively. Centre lines in each box show medians; box limits indicate the 25th and 75th percentiles; whiskers represent local minima and maxima, that is, they extend to data points that are less than 1.5 × IQR away from the 25th and 75th percentiles (*IQR* is the interquartile range), outliers are represented by dots.

Figure 7—source data 1 Sycon feeding and filtration.: https://cdn.elifesciences.org/articles/61012/elife-61012-fig7-data1-v2.zip
Download elife-61012-fig7-data1-v2.zip

Evolutionary implications

Our modeling and experimental analyses indicate that the morphology of different sponge body plans results in different hydrodynamics with associated trade-offs in the sponge pump in terms of volume filtered and retention efficiency. Although the presence of sealing elements is crucial for the functionality of the high-pressure leucon sponge pump, the open architecture of the ascon and sycon type pumps is as efficient at particle capture without these structures. Taken in this light, our findings have implications for interpreting the first poriferan body plans. Neoproterozoic oceans were food and oxygen poor, with smaller bodied animals (Sperling and Stockey, 2018). In a Neoproterozoic ocean, competition with colonial flagellates could have favored a filter-feeder that captured larger particles without clogging, as is the case in ascon and sycon forms. With the Cambrian explosion came additional food sources providing the energy to enable specialization of the pump and filter to capture food in a range of habitats. Our findings demonstrate that the presence of sealing elements around the sponge collar is directly related to the hydrodynamics of operating conditions associated with the body architecture, and comes with delicate trade-offs between the sponge pumping rate and retention of particles. These analyses support the view (Manuel et al., 2003; Cavalier-Smith, 2017; Nielsen, 2019) that the sponge aquiferous system evolved from an open-type ascon-like filtration system, and the idea that the first metazoans were filter feeders.

Materials and methods

Numerical simulations

Request a detailed protocol

We use computational fluid dynamics (CFD) to solve the governing Navier-Stokes equations of the flow inside the computational domain (Figure 2). A finite volume method is used to discretize and solve the equations on a discrete representation of the computational domain consisting of polyhedral cells by applying the commercial CFD code STAR-CCM+ (14.04.013-R8). We use mesh morphing along with the overset method to move the computational mesh (Appendix 2, Section 2). The morphing motion redistributes mesh vertices in response to the movement of the flagellum. Video 3 shows the moving mesh (viewed in the xy-plane), inside the computational domain. To ensure that the solutions are independent of the computational mesh sizes, the simulations (for the base case) have been repeated using four coarser and one finer meshes (Appendix 2—figure 5). To demonstrate the independence of the CFD results from the global boundary conditions (BC) of the flagellate chambers (i.e. the chamber being closed at one end and open at the other end (apopyle), one simulation was conducted in an extended slice of a cylindrical domain including five ostia, closed (no-slip BC) at one end and open (uniform pressure BC) at the other end (Appendix 2—figures 3 and 4)).

Video 3

Download asset

Measurement of the pumping rate and retention efficiency in live sponges

Request a detailed protocol

Ten specimens of Sycon coactum were retrieved by scuba divers and transported at controlled temperatures to the laboratory at the Bamfield Marine Sciences Center, Bamfield, BC, Canada. Specimens were cleaned of macro-epibionts and left in large tanks with a flow-through system until the experiments were performed.

The volume flow rate through the oscula was calculated as the product of the ex-current jet speed and osculum area assuming a plug flow profile across the oscula (Dye Speed, DS, methods see Morganti et al., 2017 and references therein). Briefly, the excurrent jet speed was measured by releasing small amounts of filtered (0.2 µm) seawater mixed with sodium fluorescein dye next to the sponge ostia and videotaping the dye front in the excurrent jet along with a known scale. This procedure was repeated 5–10 times per sponge, and the DS was measured by recording the time it took the dye front to travel a short distance (10–20 mm). The osculum area was measured from photographs of each osculum using ImageJ (Schindelin et al., 2012).

To measure the retention efficiency of the sponges, we used a direct comparison of prey cell concentration in the water inhaled and exhaled by the sponge as described by Yahel et al., 2006. For the In-Ex method experiments, samples were processed in pairs (inhaled and exhaled samples). All samples were spiked with 1.0 µm Polysciences Inc Fluoresbrite yellow-green beads (Cat # 17154) from a stock solution that had been pre-calibrated with Becton Dickinson Trucount Control beads (Cat # 340335). Instrument flow rate was determined using bead counts. For the current analysis, we excluded the picocyanobacteria as their numbers were low, and identification was uncertain. Retention efficiency (%) was calculated as: $100 (C_{i n} - C_{e x}) / C_{i n}$ , where $C_{𝑖𝑛}$ and $C_{𝑒𝑥}$ are the cell concentration in the inhaled and exhaled water, respectively.

Appendix 1

The calcareous sponge Sycon coactum

The general anatomy of S. coactum is illustrated in Appendix 1—figure 1. The sponge forms a single tube, 8 cm long, with a wall thickness of ∼1 mm and an inner diameter of 8 mm. A 1 mm² piece of the wall was estimated to contain 36 chambers. Each chamber, in turn, was estimated to posses ∼283 ostia, each surrounded by 20–25 choanocytes. An excurrent jet velocity of 7.5 mms⁻¹ was measured by dye visualization of the jet from an osculum with a diameter of 2 mm (Appendix 1—video 1).

Appendix 1—figure 1

Download asset Open asset

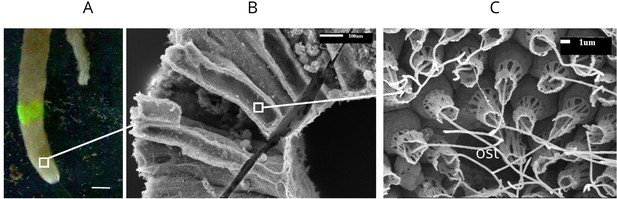
Calcareous sponge *Sycon coactum*.

(A) In natural habitat (scale bar: 1 cm). (B) A fracture across the body of the sponge showing relatively large cylindrically shaped chambers. (C) An ostium (ost) with the surrounding choanocytes in the chamber. Note that although flagella here appear as smooth, they do have a vane as shown in Appendix 1—figure 2.

Appendix 1—figure 2

Download asset Open asset

Observation of vane in the calcareous sponge *Sycon coactum* (scale bar: 2 µm).

The flagellar vane appears as two symmetrical wing-like projection (short arrows). Some mesh structure (long arrow) appears locally between collars, attached not to the collar tips, but rather lying further down the collar and attaching to the glycocalyx mesh that occurs between collar microvilli; it possibly functions to guide flow to the collar microvilli filters.

Appendix 1—video 1

Download asset

Flagella beat model

The waveform of each individual flagellum is modeled as:

d (Y, t) = a (1 - e^{- (Y - Y_{b}) / δ}) \sin (\frac{2 π}{λ} [(Y - Y_{b}) - V t])

where d is the local lateral displacement of the each flagellum, a is the amplitude modulation of the waveform, $δ$ is the characteristic length scale of the amplitude, Y is the coordinate along the centerline axis of the flagellum, Y_b is the coordinate of the flagellum at its base on the cell surface, $V = λ f$ is the wave speed, where f is the frequency, and $λ$ the wavelength, and t is time. Note that in the model of Equation 3, the flagellum would be extensible and its length varies slightly during the beat cycle (ca. 2%), resulting in marginally wrong velocities on the flagellum. However, implementing Equation 3 in the numerical scheme is computationally cheaper than preserving the arclength. Re-running the simulation for the base case while the arclength is preserved shows that the flow field in the domain (Appendix 1—figure 3) is insignificantly affected with less than 4% difference in the pumping rate.

Appendix 1—figure 3

Download asset Open asset

Snapshots of velolicty field for cases where the flagellum is extensible (A) and inextensible (B).

For the flagellate pumps, the Reynolds number ( $Re = ρ V L / μ$ ), the ratio of inertia to viscous forces, is small (2.9 × 10⁻³), employing water density $ρ = 1022 kg m^{- 3}$ and dynamic viscosity $μ = 0.001 Pa s$ , flagella length of $L = 15.5 μ m$ , flagella wave speed of $V = λ f = 150 μ m s^{- 1}$ . As a result, the unsteady inertia terms in the governing equations can be neglected and flow is quasi-steady and symmetrical in respect to the flagellum beat. Therefore, to obtain the average velocity and pressure field, the simulation was conducted only for half of a beat cycles. For the particle filtration, however, the simulation is conducted for a 145 beat cycles in order to track the particles inside the domain.

The mechanical power expenditure by the flagellum is given by:

𝒫 = \iint_{S_{f l}} u \cdot (σ \cdot n) d S

where $σ = - p 𝐈 + μ (\nabla 𝐮 + {(\nabla 𝐮)}^{T})$ denotes the stress tensor, $𝐧$ is the unit normal vector on the surface S pointing into the fluid, and $S_{𝑓𝑙}$ is the surface area of the flagella.

Simulations of particle filtration

Appendix 1—figure 4

Download asset Open asset

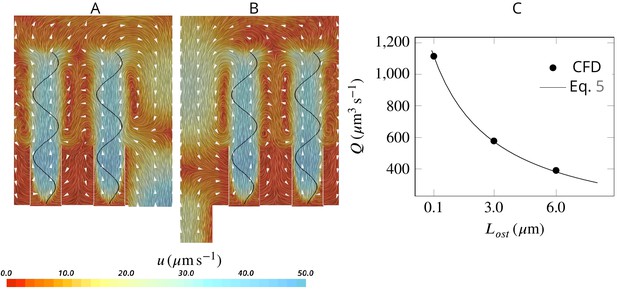
Effect of ostia length and diameter on the pumping rate and the backflow in the core of the region, and thus the position of the stagnation area.

A very short and wide ostium (A) increases the pumping rate, but at the cost of a high level of flow bypassing the collar. A longer and narrower ostium (B), as observed in sponges, reduces the pumping rate but lowers the height of the stagnation area. (C) Validity of Equation 5 vs CFD results for three different length of the ostium.

Videos 1 and 2 illustrate passive particles entering into the chamber through the ostium and carried by the flow. Particle color denotes its velocity according to the color scale at the bottom. Particles that arrive at the collar are removed from the simulation. Note that while most of the particles are carried almost directly toward the collars, some are carried upward, above the collars, and toward the tip of the flagella, but almost all the particles are eventually returned by the back eddies and are captured. Simulation duration is 145 beat cycles. Side view (Video 1). Top view (Video 2).

Effect of ostium length and diameter on the pumping

Assuming a fully developed flow in a tubular ostium of length $L_{𝑜𝑠𝑡}$ and diameter $D_{𝑜𝑠𝑡}$ , the pressure resistance is given by White, 2011: $P_{𝑜𝑠𝑡} = \frac{128}{π} (μ L_{𝑜𝑠𝑡} / D_{𝑜𝑠𝑡}^{4}) Q_{𝑝𝑢𝑚𝑝}$ , where μ is the dynamic water viscosity (here $μ = 0.001 Pa s$ , corresponding to seawater at 20°C with salinity of 30 PSU). Note that pressure resistance due to the apopyle is 2 orders of magnitude smaller than that of the ostium (hence negligible), given the averaged dimensions of the apopyle $D_{𝑎𝑝𝑜𝑝} = 56 μ m$ , $L_{𝑎𝑝𝑜𝑝} = 17 μ m$ and of the ostium $D_{𝑜𝑠𝑡} = 5 μ m$ , $L_{𝑜𝑠𝑡} = 5 μ m$ , and 283 ostia per apopyle. Due to the linearity of the governing equations at low Reynolds numbers, the pump characteristic of the unit is linear, hence: $Q_{𝑝𝑢𝑚𝑝} = Q_{𝑚𝑎𝑥} - Q_{𝑚𝑎𝑥} (P_{𝑜𝑠𝑡} / P_{𝑚𝑎𝑥})$ , where $Q_{𝑚𝑎𝑥}$ and $P_{𝑚𝑎𝑥}$ are the maximum flow rate (at zero length ostia) and pressure delivered by the pump, respectively. Combining these two equations, the pumping rate of the unit as a function of the ostium dimension is:

Q_{p u m p} (L_{o s t}, D_{o s t}) = \frac{Q_{m a x}}{1 + 128 μ L_{o s t} Q_{m a x} / (π D_{o s t}^{4} P_{m a x})}

Having $Q_{m a x}$ and $P_{m a x}$ , Equation 5 accurately predicts the pumping rate for a given length of the ostium as tested against CFD results Appendix 1—figure 4C.

Porosity of the collar filter

We model the porosity of a collar filter composed of several microvilli of radius $b$ as

v_{n} = κ \frac{b}{μ} P_{c}

where $v_{n}$ is the velocity normal to the filter subject to pressure drop, $P_{c}$ , κ is the dimensionless porosity of a network of parallel and equidistantly spaced cylinders (Keller, 1964), and μ is the viscosity of the water.

For the case of non-uniform porosity along the length of the collars (Appendix 1—figure 5), the dimensionless porosity κ of the collar is modeled as $κ = \frac{1}{2} κ_{b} (1 + \cos (π y_{c} / L_{c}))$ , where κ_b is the dimensionless porosity at the base corresponding to the maximum spacing ( $l_{b}$ ) between adjacent microvilli, $y_{c}$ the position along the collar with respect to the base, and $L_{c}$ the length of the collar.

Appendix 1—figure 5

Download asset Open asset

Effect of collar elements spacing ( $l_{b}$ ) on pumping rate ( $Q$ ) and volume flow rate ( $Q$ ) through the collars for different porosity levels of the collars.

$l_{b}$ is the maximum spacing between adjacent microvilli and the porosity is decreases to zero at the tip of the collars (see text).

Asynchronization among flagella

Choanocytes are closely packed in the chambers with spacing between neighboring flagella of ∼5–10 µm. At such relatively short distances, synchronization of flagella beat might be expected (Brumley et al., 2014), although lack of synchronization has been reported both within a colony of the choanoflagellate Salpingoeca rosetta (Kirkegaard et al., 2016; Roper et al., 2013), and in choanocyte chambers of the sponge Spongilla lacustris (Mah et al., 2014). To investigate the potential effect of synchronized and asynchronized flagella beat on the mechanical energy produced by the flagella, we consider three different scenarios where: (1) neighboring flagella beat slightly out of phase (phase shift angle between neighboring flagella of $ϕ_{f} = 4 π / 25$ ), (2) neighboring flagella are completely out of phase ( $ϕ_{f} = π$ ), and (3) neighboring flagella beat in different (perpendicular) planes.

The snapshots of flow fields (Appendix 1—figure 6AB) are highly affected by the position of the neighboring flagella with respect to each other, especially near and between the flagella. However, the pumping rate and flow through the collar filter - lower and upper data, respectively, in C - are insignificantly affected by asyncronization among flagella (Appendix 1—figure 6C).

Appendix 1—figure 6

Download asset Open asset

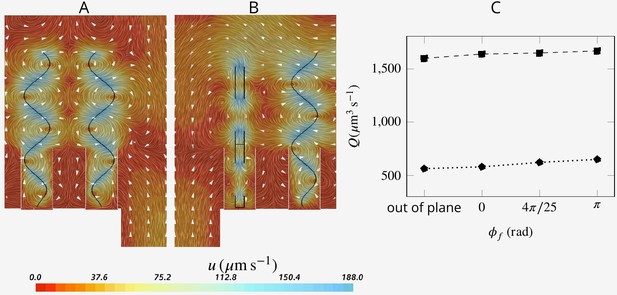
Snapshot of velocity fields when neighboring flagella beat completely out of phase (A, $ϕ_{f} = 0$ ) and in perpendicular planes (B).

Although snapshots of velocity differ for different scenarios, the pumping rate and flow through the collar filter are insignificantly affected by asyncronization among flagella (C).

Multi-cilia and ciliary arrays beat in phase (Wan, 2018) or slightly out of phase that is, metachronal waves (Niedermayer et al., 2008; Golestanian et al., 2011; Elgeti and Gompper, 2013) to produce strong flows tangential to the surfaces to which they are attached. When the cilia beating is completely out of phase, the tangential forces of neighboring cilia cancel each other and no flow is created. In contrast, the array of flagella that lines the inner walls of sponge chambers produces a flow that is moving perpendicular to the attachment surface (and through it). In addition, some flagella are located in proximity to the water sources (ostium) while others are more distanced. To investigate the relationships between flagella location, their synchronization, and the mechanical power produced we compare the base case in which all flagella are beating in phase to two cases where the beat of the flagella next to the ostium (eight proximal flagella) is not synchronized to that of the 16 distal flagella. In the first case, the proximal flagella are beating faster ( $f_{p} = 60 Hz$ ) than the distal flagella ( $f_{d} = 30$ ) and in the second case, the proximal flagella beat slower ( $f_{d} = 30 Hz$ ) and the distal flagella beat faster ( $f_{d} = 60 Hz$ Appendix 1—figure 7AB). Results show that pumping rate is not impaired by such asynchronous flagella beat. Moreover, pumping rate of the first case (where proximal flagella pump faster (Appendix 1—figure 7A)) is 22% higher than that of the second case where the distal flagella beat faster ( $Q_{1} = 984 μ m^{3} s^{- 1}$ vs $Q_{2} = 808 μ m^{3} s^{- 1}$ ) despite the smaller number of the proximal flagella. The improved pumping rate in the first case is ascribed to higher capability of the proximal flagella in pumping due to their proximity to the ostium (for the case of synchronized flagella beat they contribute 64% of the total pumping, despite being only a third of the flagella in the array). Additionally, faster proximal flagella leads to 33% less mechanical power expenditure ( $𝒫_{1} = 97.3 fW$ vs $𝒫_{2} = 144.9 fW$ , where $𝒫_{i}$ is the averaged total power expenditure by all 24 flagella over the beat cycle for the $i$ -th case). Considering that pumping rate increases linearly with the beat frequency, whereas the power expenditure increases as the square of the beat frequency ( $P \propto f^{2}$ , $Q \propto f$ ), employing faster beating of the fewer proximal flagella can be a suitable compromise between the power expenditure and pumping rate.

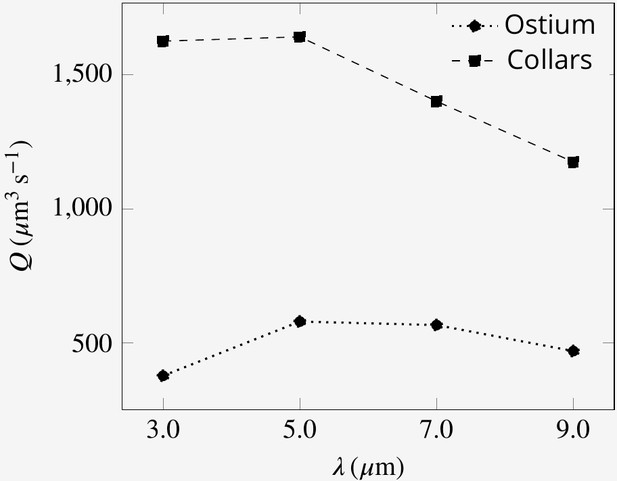
The presence of both proximal and distal flagella, and their collective imparted upward momentum is essential for efficient pumping of the inflow through the collars. Without the presence of the distal flagella, the system continues to pump, but the operation of the hydrodynamic gasket is impaired and water flow through the collars is dramatically reduced. The vacant space created by the absence of distal flagella, shifts the location of the back flow from above ostium toward the vacant space. Consequently, a significant part of the inflow bypasses the collars and leaves the domain without being filtered (Appendix 1—figure 7C). Considering the minor effect of synchronous flagella beat in reducing the power expenditure, the required imparted momentum of the distal flagella can potentially also be achieved with flagella having a different waveform, for example different wavelength, as long as the averaged upward flow velocity due the presence of the flagella is able to maintain the hydrodynamic gasket in place (Appendix 1—figure 7D). We find that the volume flow rate is affected by the wavelength, with an optimum wavelength of 5 µm (Appendix 1—figure 8).

Appendix 1—figure 7

Download asset Open asset

Hydrodynamic interaction between the flagella.

A And B show average velocity fields for the cases with doubled beat frequency on the proximal compared to the distal flagella ( $f_{p} = 60$ and $f_{d} = 30 Hz$ ), and vice versa (A and B, respectively). Asynchronization between the proximal and distal flagella does not impair pumping. It does, however, affect the pumping rate, but the effect is due to the unequal contribution of the proximal and distal flagella on the pumping. (C) The presence of the distal flagella and thus their imparted momentum is important for creating the recirculation in the core of the region, without which the location of recirculation is shifted. The momentum may be imparted by flagella with different wavelength. (D) Averaged velocity field for wavelength $λ = 9 μ m$ .

Appendix 1—figure 8

Download asset Open asset

Pumping rate and volume flow rate through the collars for flagella with different wavelength.

Appendix 2

Inclusion of gasket into the model

We model the gasket as an impermeable plate that forms a canopy at the tip of the collars as depicted in Appendix 2—figure 1.

Appendix 2—figure 1

Download asset Open asset

The simulation unit with presence of the gasket (pink).

Moving computational mesh

We use mesh morphing along with the overset method to move the computational mesh corresponding to the motion of the flagella. With the overset method, rather than moving the entire mesh, it deforms the mesh only around the flagella, so-called the overset region, which significantly reduces the computational cost. A background stationary mesh including the collars is also generated which is superimposed by the overlapping overset mesh. The two mesh regions are implicitly coupled, the field data are interpolated back and forth between the two meshes (i.e. the overset and background meshes) to generate a smooth solution at each iteration.

Visualization of the flow field in the inner core of the chamber

Once fluid leaves the computational domain vertically into the core of choanocyte chamber, it is accumulated and directed axially toward one end of the chamber (apopyle) where it is open. To illustrate this, we model the flow in the cylindrical core of the chamber Figure 2A in the main text. The flow enters the cylinder from the lateral surface and one end (velocity inlet boundary of 1 µms⁻¹, in the range of the mean velocity of flow leaving the wedge geometry of Figure 2), and exit from the other end (uniform pressure boundary). Figure 2 shows the velocity and pressure fields in a cross-section oriented axially in the center of the domain. Lateral flow and shear close to sides (hence right above flagella tip) is relatively weak, and we assume that the flagella action is not strongly affected.

Appendix 2—figure 2

Download asset Open asset

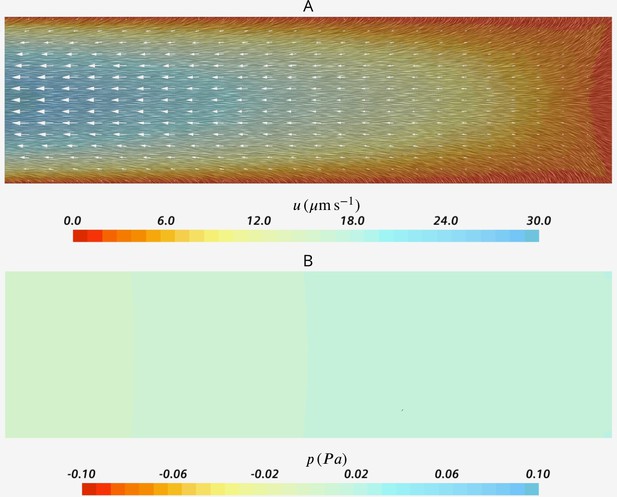
Velocity (A) and pressure (B) fields in the cross section of the inner core cylinder.

The modeled cylinder is 200 µm long (=8 wedge-unit long), with diameter $D_{c o r e} = D_{c h a m b e r} - 2 * h_{w e d g e} = 55 μ m$ , where $D_{c h a m b e r}$ is the diameter of chamber and $h_{w e d g e}$ the height of the wedge geometry of Figure 2.

Independence of solution from the global boundary conditions

Appendix 2—figure 4A shows snapshots of the velocity field in three middle units (separated by the white dashed lines) of the domain. The velocity field is virtually periodic in all these units indicating the minor effect of the domain ends on each single units, independent of their location with respect to the ends. Appendix 2—figure 4B shows the snapshots of the pressure field in the middle unit. Despite high variation inside the ostium and between the flagella, the pressure is nearly uniform above the flagella.

Appendix 2—figure 3

Download asset Open asset

The simulation domain in an extended slice of the cylindrical chamber including five pumping units, that is, 5 ostia and 120 collar-flagella, closed (no-slip BC) at one end but open (uniform pressure BC) at the other end (green).

Appendix 2—figure 4

Download asset Open asset

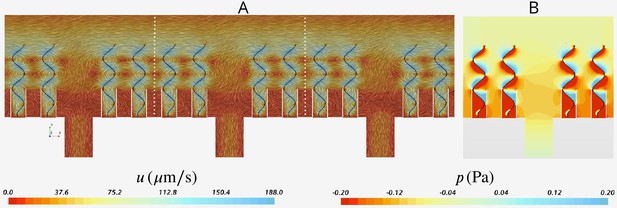
Snapshot of velocity and pressure fields for the simulation domain including five units depicted in Appendix 2—figure 3B.

(A) Velocity field in the three middle units (separated by white dash lines) shows the periodicity of the flow fields in these units independent of their location with respect to the outlet to the left (apopyle). (B) Pressure field in one single unit illustrating uniformity of the pressure above the flagella. Accordingly, the computational domain is reduced to one single unit using periodic and uniform pressure boundary conditions as shown in Figure 2.

Mesh convergence study

In order for the solution to be independent of the mesh sizes, the CFD simulations are conducted at different mesh size. Because the problem is quasi-steady, the mesh convergence study has been performed at one arbitrary time step. Appendix 2—figure 5 shows the independence of the solution from the mesh sizes for the base case.

Appendix 2—figure 5

Download asset Open asset

Mesh size independence of volume flow rate through the collars Q_c and the power expenditure by the flagella $𝒫$ at an arbitrary time step.

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files.

References

1. Afzelius BA
(1961) Flimmer-flagellum of the sponge
Nature 191:1318–1319.
https://doi.org/10.1038/1911318b0
- Google Scholar
(2019a) Hydrodynamics of the Leucon sponge pump
Journal of the Royal Society Interface 16:20180630.
https://doi.org/10.1098/rsif.2018.0630
- PubMed
- Google Scholar
(2019b) Hydrodynamic functionality of the Lorica in choanoflagellates
Journal of the Royal Society Interface 16:20180478.
https://doi.org/10.1098/rsif.2018.0478
- PubMed
- Google Scholar
1. Bouck GB
(1971) The structure, origin, isolation, and composition of the tubular mastigonemes of the ochromas flagellum
Journal of Cell Biology 50:362–384.
https://doi.org/10.1083/jcb.50.2.362
- PubMed
- Google Scholar
1. Brooks ER
2. Wallingford JB
(2014) Multiciliated cells
Current Biology 24:R973–R982.
https://doi.org/10.1016/j.cub.2014.08.047
- PubMed
- Google Scholar
(2014) Flagellar synchronization through direct hydrodynamic interactions
eLife 3:e02750.
https://doi.org/10.7554/eLife.02750
- PubMed
- Google Scholar
1. Cavalier-Smith T
(2017) Origin of animal multicellularity: precursors, causes, consequences-the choanoflagellate/sponge transition, neurogenesis and the cambrian explosion
Philosophical Transactions of the Royal Society B: Biological Sciences 372:20150476.
https://doi.org/10.1098/rstb.2015.0476
- PubMed
- Google Scholar
1. Dadon-Pilosof A
2. Conley KR
3. Jacobi Y
4. Haber M
5. Lombard F
6. Sutherland KR
7. Steindler L
8. Tikochinski Y
9. Richter M
10. Glöckner FO
11. Suzuki MT
12. West NJ
13. Genin A
14. Yahel G
(2017) Surface properties of SAR11 Bacteria facilitate grazing avoidance
Nature Microbiology 2:1608–1615.
https://doi.org/10.1038/s41564-017-0030-5
- PubMed
- Google Scholar
(2019) Prey taxonomy rather than size determines salp diets
Limnology and Oceanography 64:1996–2010.
https://doi.org/10.1002/lno.11165
- Google Scholar
(1981) Axisymmetric stokes flows due to a rotlet or stokeslet near a hole in a plane wall: filtration flows
Journal of Fluid Mechanics 103:183–205.
https://doi.org/10.1017/S0022112081001298
- Google Scholar
1. Dendy A
(1888)
Studies on the comparative anatomy of sponges. II. On the anatomy and histology of stelospongus flabelliformis, Carter, with notes on the development

Quarterly Journal of Microscopical Science 29:325–358.
- Google Scholar
(2006) Non-monophyly of most supraspecific taxa of calcareous sponges (Porifera, calcarea) revealed by increased taxon sampling and partitioned bayesian analysis of ribosomal DNA
Molecular Phylogenetics and Evolution 40:830–843.
https://doi.org/10.1016/j.ympev.2006.04.016
- PubMed
- Google Scholar
1. Eerkes-Medrano DI
2. Leys SP
(2006) Ultrastructure and embryonic development of a syconoid calcareous sponge
Invertebrate Biology 125:177–194.
https://doi.org/10.1111/j.1744-7410.2006.00051.x
- Google Scholar
1. Elgeti J
2. Gompper G
(2013) Emergence of metachronal waves in cilia arrays
PNAS 110:4470–4475.
https://doi.org/10.1073/pnas.1218869110
- PubMed
- Google Scholar
1. Fenchel T
(1982) Ecology of heterotrophic microflagellates. I. some important forms and their functional morphology
Marine Ecology Progress Series 8:211–223.
https://doi.org/10.3354/meps008211
- Google Scholar
1. Feuda R
2. Dohrmann M
3. Pett W
4. Philippe H
5. Rota-Stabelli O
6. Lartillot N
7. Wörheide G
8. Pisani D
(2017) Improved modeling of compositional heterogeneity supports sponges as sister to all other animals
Current Biology 27:3864–3870.
https://doi.org/10.1016/j.cub.2017.11.008
- PubMed
- Google Scholar
1. Fjerdingstad EJ
(1961) The ultrastructure of choanocyte collars in Spongilla lacustris (L.)
Zeitschrift für Zellforschung und Mikroskopische Anatomie 53:645–657.
https://doi.org/10.1007/BF00339512
- Google Scholar
(2020) The multiscale physics of cilia and flagella
Nature Reviews Physics 2:74–88.
https://doi.org/10.1038/s42254-019-0129-0
- Google Scholar
(2011) Hydrodynamic synchronization at low Reynolds number
Soft Matter 7:3074–3082.
https://doi.org/10.1039/c0sm01121e
- Google Scholar
1. Holwill ME
2. Peters PD
(1974) Dynamics of the hispid flagellum of Ochromonas danica. The role of mastigonemes
The Journal of Cell Biology 62:322.
https://doi.org/10.1083/jcb.62.2.322
- PubMed
- Google Scholar
1. Imsiecke G
(1993) Ingestion, digestion, and egestion in Spongilla lacustris (Porifera, Spongillidae) after pulse feeding with Chlamydomonas reinhardtii (Volvocales)
Zoomorphology 113:233–244.
https://doi.org/10.1007/BF00403314
- Google Scholar
1. Keller JB
(1964) Viscous flow through a grating or lattice of cylinders
Journal of Fluid Mechanics 18:94–96.
https://doi.org/10.1017/S0022112064000064
- Google Scholar
(2016) Motility of colonial choanoflagellates and the statistics of aggregate random walkers
Physical Review Letters 116:038102.
https://doi.org/10.1103/PhysRevLett.116.038102
- PubMed
- Google Scholar
1. Larsen PS
2. Riisgåd HU
(1994) The sponge pump
Journal of Theoretical Biology 168:53–63.
https://doi.org/10.1006/jtbi.1994.1087
- Google Scholar
1. Leadbeater BSC
(2006)
The mystery of the flagellar vane in choanoflagellates

Nova Hedwigia. Beiheft 130:213.
- Google Scholar
(2011) The sponge pump: the role of current induced flow in the design of the sponge body plan
PLOS ONE 6:e27787.
https://doi.org/10.1371/journal.pone.0027787
- PubMed
- Google Scholar
1. Leys SP
2. Eerkes-Medrano DI
(2006) Feeding in a calcareous sponge: particle uptake by pseudopodia
The Biological Bulletin 211:157–171.
https://doi.org/10.2307/4134590
- PubMed
- Google Scholar
(2017) The energetic cost of filtration by demosponges and their behavioural response to ambient currents
The Journal of Experimental Biology 220:995–1007.
https://doi.org/10.1242/jeb.146076
- PubMed
- Google Scholar
(2014) Choanoflagellate and choanocyte collar-flagellar systems and the assumption of homology
Evolution & Development 16:25–37.
https://doi.org/10.1111/ede.12060
- PubMed
- Google Scholar
(2003) Phylogeny and evolution of calcareous sponges: monophyly of calcinea and calcaronea, high level of morphological homoplasy, and the primitive nature of axial symmetry
Systematic Biology 52:311–333.
https://doi.org/10.1080/10635150390196966
- PubMed
- Google Scholar
1. Manuel M
(2006) Phylogeny and evolution of calcareous sponges
Canadian Journal of Zoology 84:225–241.
https://doi.org/10.1139/z06-005
- Google Scholar
1. Mary I
2. Heywood JL
3. Fuchs BM
4. Amann R
5. Tarran GA
6. Burkill PH
7. Zubkov MV
(2006) SAR11 dominance among metabolically active low nucleic acid bacterioplankton in surface waters along an Atlantic meridional transect
Aquatic Microbial Ecology 45:107–113.
https://doi.org/10.3354/ame045107
- Google Scholar
1. Mehl D
2. Reiswig HM
(1991) The presence of flagellar vanes in choanomeres of porifera and their possible phylogenetic implications
Journal of Zoological Systematics and Evolutionary Research 29:312–319.
https://doi.org/10.1111/j.1439-0469.1991.tb00676.x
- Google Scholar
1. Morganti T
2. Coma R
3. Yahel G
4. Ribes M
(2017) Trophic niche separation that facilitates co-existence of high and low microbial abundance sponges is revealed by in situ study of carbon and nitrogen fluxes
Limnology and Oceanography 62:1963–1983.
https://doi.org/10.1002/lno.10546
- Google Scholar
1. Narematsu N
2. Quek R
3. Chiam KH
4. Iwadate Y
(2015) Ciliary metachronal wave propagation on the compliant surface of Paramecium cells
Cytoskeleton 72:633–646.
https://doi.org/10.1002/cm.21266
- PubMed
- Google Scholar
(2008) Synchronization, phase locking, and metachronal wave formation in ciliary chains
Chaos: An Interdisciplinary Journal of Nonlinear Science 18:037128.
https://doi.org/10.1063/1.2956984
- PubMed
- Google Scholar
(2017) Hydrodynamics of microbial filter feeding
PNAS 114:9373–9378.
https://doi.org/10.1073/pnas.1708873114
- PubMed
- Google Scholar
1. Nielsen C
(2019) Early animal evolution: a morphologist's view
Royal Society Open Science 6:190638.
https://doi.org/10.1098/rsos.190638
- PubMed
- Google Scholar
1. Reiswig HM
(1971) Particle feeding in natural populations of three marine demosponges
The Biological Bulletin 141:568–591.
https://doi.org/10.2307/1540270
- Google Scholar
1. Reiswig HM
(1975a) The aquiferous systems of three marine demospongiae
Journal of Morphology 145:493–502.
https://doi.org/10.1002/jmor.1051450407
- PubMed
- Google Scholar
1. Reiswig HM
(1975b) Bacteria as food for temperate-water marine sponges
Canadian Journal of Zoology 53:582–589.
https://doi.org/10.1139/z75-072
- Google Scholar
1. Ribes M
2. Jiménez E
3. Yahel G
4. López-Sendino P
5. Diez B
6. Massana R
7. Sharp JH
8. Coma R
(2012) Functional convergence of microbes associated with temperate marine sponges
Environmental Microbiology 14:1224–1239.
https://doi.org/10.1111/j.1462-2920.2012.02701.x
- PubMed
- Google Scholar
1. Roper M
2. Dayel MJ
3. Pepper RE
4. Koehl MA
(2013) Cooperatively generated stresslet flows supply fresh fluid to multicellular choanoflagellate colonies
Physical Review Letters 110:228104.
https://doi.org/10.1103/PhysRevLett.110.228104
- PubMed
- Google Scholar
1. Schindelin J
2. Arganda-Carreras I
3. Frise E
4. Kaynig V
5. Longair M
6. Pietzsch T
7. Preibisch S
8. Rueden C
9. Saalfeld S
10. Schmid B
11. Tinevez JY
12. White DJ
13. Hartenstein V
14. Eliceiri K
15. Tomancak P
16. Cardona A
(2012) Fiji: an open-source platform for biological-image analysis
Nature Methods 9:676–682.
https://doi.org/10.1038/nmeth.2019
- PubMed
- Google Scholar
1. Sollas I
(1889)
Sponges

Encyclopaedia Britannica 22:426–445.
- Google Scholar
1. Sperling EA
2. Stockey RG
(2018) The temporal and environmental context of early animal evolution: considering all the ingredients of an "Explosion"
Integrative and Comparative Biology 58:605–622.
https://doi.org/10.1093/icb/icy088
- PubMed
- Google Scholar
(2016) Evolution: a sisterly dispute
Nature 529:286–287.
https://doi.org/10.1038/529286a
- PubMed
- Google Scholar
1. Wan KY
(2018) Coordination of eukaryotic cilia and flagella
Essays in Biochemistry 62:829–838.
https://doi.org/10.1042/EBC20180029
- PubMed
- Google Scholar
1. Weissenfels N
(1976) Bau und funktion des Süsswasserschwamms Ephydatia fluviatilis L. (Porifera). III. Nahrungsaufnahme, Verdauung Und Defäkation
The Biological Bulletin 85:73–88.
https://doi.org/10.1007/BF01342232
- Google Scholar
1. Weissenfels N
(1992) The filtration apparatus for food collection in freshwater sponges (Porifera, Spongillidae)
Zoomorphology 112:51–55.
https://doi.org/10.1007/BF01632994
- Google Scholar
(2015) Error, signal, and the placement of ctenophora sister to all other animals
PNAS 112:5773–5778.
https://doi.org/10.1073/pnas.1503453112
- PubMed
- Google Scholar
Book
1. White FM
(2011)
Fluid Mechanics (7 edn)

McGraw Hill, Inc.
- Google Scholar
1. Wilkinson CR
(1978) Microbial associations in sponges. I. Ecology, physiology and microbial populations of coral reef sponges
Marine Biology 49:161–167.
https://doi.org/10.1007/BF00387115
- Google Scholar
(2006) Size independent selective filtration of ultraplankton by hexactinellid glass sponges
Aquatic Microbial Ecology 45:181–194.
https://doi.org/10.3354/ame045181
- Google Scholar

Decision letter

Raymond E Goldstein

Reviewing Editor; University of Cambridge, United Kingdom
Aleksandra M Walczak

Senior Editor; École Normale Supérieure, France

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

The fluid dynamics of filter feeding in sponges is a complex problem on many length scales, from the flagella of filter-feeding cells within small chambers to the large scale flow past the entire sponge. Asadzadeh et al. address a significant puzzle in the physiology of sponges lacking the "gasket" which, in other species, diverts flow toward the filtration devices on the feeding cells. Through a combination of experimental work and numerical computations the authors demonstrate the existence of an unusual flow pattern that accomplishes this diversion, and suggest implications for our understanding of the evolution of the first metazoans.

Decision letter after peer review:

Thank you for submitting your article "Hydodynamics of sponge pumps and evolution of the sponge body plan" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Aleksandra Walczak as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

As the editors have judged that your manuscript is of interest, but as described below that substantial revisions are required before it is published, we would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). First, because many researchers have temporarily lost access to the labs, we will give authors as much time as they need to submit revised manuscripts. We are also offering, if you choose, to post the manuscript to bioRxiv (if it is not already there) along with this decision letter and a formal designation that the manuscript is "in revision at eLife". Please let us know if you would like to pursue this option. (If your work is more suitable for medRxiv, you will need to post the preprint yourself, as the mechanisms for us to do so are still in development.)

Summary:

The authors present a numerical and experimental investigation of the pumping mechanism in filter feeding sponges. The feeding is performed by choanocytes, which comprise a pumping flagellum and a feeding collar that protrude from the wall of the feeding chambers, which has periodically arranged holes through which unfiltered fluid can enter when pulled by the flagellar action.

In this study, the mechanism is examined for the case of sponges that do not possess a "gasket" (canopy-structure) over these feeding collars. The key question that the authors examine is, then, "how is the flow forced through the collars (allowing particle capture), when there is no gasket to stop it simply going straight to the centre of the chamber"?

The answer given is that just as flow is pulled through the holes, a reverse flow (which arises from the condition that flow in the chamber is, at least locally, divergence free), forms above the hole, which creates a stagnation point that pushes the incoming fluid laterally out through the feeding collars.

Essential revisions:

1) On the whole we found this to be a solid paper that addresses an important question by means of computational studies. Having said that, we are disappointed at the lack of physical interpretation given to the setup of the system and the results. In essence, the papers reads like an experimental study of the system with essentially no interpretation of the magnitudes of any of the physical quantities calculated, particularly in light of the fact that sponge hydrodynamics is not a commonly studied subject for the readers of eLife. The authors need to do a serious job of re-presentation of the results to establish the physical significance of various pressures (are these arising from Bernoulli-like pressure differences across the sponge body due to the external flow?), flow rates (say, by comparing them to Poiseuille flow), powers (comparing to the flagellar input power), etc. There is very little in the way of dimensional analysis to make the results intuitively clear. As such, the very many numerical values of physical quantities have no context.

2) From a fluid dynamics perspective, the fundamental result is fairly easy to see, and is simply a manifestation of local mass conservation (though of course retrodiction is of course much easier than prediction). The presentation would be greatly aided by a very simple schematic of the streamlines from two forces above a wall, either side of a hole, below a no-penetration (not no slip) boundary. We would have liked to have seen a reduced model of this kind involving stokeslets over a wall with a gap, which the authors should consider looking at, but this is not is a necessity for publication.

3) The description of the "flagellar vane" is a bit arcane. We are familiar with standard flagellae, and flagellae with mastigonemes, but have not come across this sort of ultrastructure before (is this a uniquely choanoflagellate/sponge structure). Reading other papers helped, but the manuscript needs a clearer description of these 3 types of flagellae, particularly when the image in Appendix 1—figure 1C seems to have ordinary flagellae.

4) An image of gasket-type vs. non gasket type would have helped our understanding of the motivation for the study earlier on. In general, we found that it was only possible to understand what was actually going on by the end of the paper, so it would be good to go through the Introduction once more to make sure it is as clear as possible to the more general reader.

5) The flagellum model (Equation 1) is not arclength preserving. Reading a previous paper it seems that the total change in arclength is only a few percent over a beat, however the velocities on the flagellum will also be subtly wrong, as material points will not be exhibiting the characteristic figure of eight motion. We have convinced ourselves that this doesn't affect the results too significantly (any error would be smaller than the error associated with taking very difficult experimental measurements), so we will not insist on a rerunning of the results, but it would not have been hard to make the waveform arclength preserving.

6) We are confused by the wedge geometry of Figure 2. If fluid leaves the computational domain "vertically" then how is there any net transport of fluid along the long axis of the ascon? Would not the flagella be strongly perturbed by the lateral flow?

7) No detail is given at all as to how the flagella beating is modelled in the CFD code. Are there regularized Stokeslets? Is slender body hydrodynamics used? Please clarify.

8) We strongly suggest the authors avoid the rainbow colourmap wherever possible, as it is not perceptually uniform (see https://peterkovesi.com/projects/colourmaps/) and is also generally bad for people who are colour blind.

9) The authors end up documenting a large number of individual differences between ascon and leucon sponges, but only study them in isolation – and only a subset of them. Compared to leucons, ascons have: (1) no physical gasket (2) shorter collars and (3) one large incurrent pore for 24 choanocytes (per choanocyte chamber), instead of many small pores (one per choanocyte.) Only the third difference is usually considered part of the definition of leuconoid vs. asconoid type, but the paper focuses almost entirely on the first and second differences. We recommend that the authors comment on the third parameter as well – if only by drawing a comparison with their earlier, published model.

10) Regarding the total difference of overall efficiency between the leuconoid and asconoid organizations, the discussion is a bit unclear. The authors state that "Our results indicate that reduced resistance in the ascon and sycon-type aquiferous systems comes with reduced volume filtered for high retention efficiency." But the paper performs no explicit comparison of filtered volumes between sycon and leucons until the very end, and even then it concludes that these are actually not really different: "Furthermore, both experimental and CFD estimates of flow rate per choanocyte [in sycons] are comparable to published estimates for leucon sponges that range from 17 to 236 µm3 s^-1 for different species of demosponges and glass sponges (Larsen and Riisgård, 1994; Leys et al., 2011; Ludeman et al., 2017), suggesting similar pumping capacity despite different pumping mechanism." This contradicts the statement of the Introduction – even though the highest pumping capacity reported for a leuconoid sponge (236 µm3 s^-1 per choanocyte) is higher than the one reported for syconoid sponges (48 µm3 s^-1 per choanocyte) suggesting that the leucon organization has at least higher potential.

We think the authors should settle on one of their two interpretations, or alternatively state that both are valid alternatives. In particular, if leucons do not have higher filtration capacity, what advantage do they have over ascons and sycons (which additionally do not risk clogging, as the authors mention)? What is the specific niche of leuconoid sponges?

11) Figure 2 shows that all flagella within the chamber beat in the same plane (with all vanes parallel to each other), parallel to the long axis. Are there reasons to think this reflects biological reality or is it a simplification of the model?

12) Subsection “Pumping mechanism”: the vane width considered is in the 0.3-0.7 µm range. How was this range of values decided? Is it close to real vanes of calcareous sponges? Why does it stay so far below the collar diameter (2.5 µm)?

13) Some calcareous sponges have a leuconoid organization, yet lack a physical gasket. Can the authors comment on how they think these sponges work?

https://doi.org/10.7554/eLife.61012.sa1

Author response

Essential revisions:

1) On the whole we found this to be a solid paper that addresses an important question by means of computational studies. Having said that, we are disappointed at the lack of physical interpretation given to the setup of the system and the results. In essence, the papers reads like an experimental study of the system with essentially no interpretation of the magnitudes of any of the physical quantities calculated, particularly in light of the fact that sponge hydrodynamics is not a commonly studied subject for the readers of eLife. The authors need to do a serious job of re-presentation of the results to establish the physical significance of various pressures (are these arising from Bernoulli-like pressure differences across the sponge body due to the external flow?), flow rates (say, by comparing them to Poiseuille flow), powers (comparing to the flagellar input power), etc. There is very little in the way of dimensional analysis to make the results intuitively clear. As such, the very many numerical values of physical quantities have no context.

We agree that there is a lack of physical interpretation of the system and the results. A major obstacle in the way of such interpretation is the fact that, the flow regime is highly viscous (low Reynolds number regime), and most of the energy is dissipated inside the chamber. For example, in the current case, less than 1% of the flagella power input is converted to pressure delivered to overcome the flow through the tubular ostium, the rest is dissipated due to large velocity gradients associated with recirculation and pressure loss through collars. As a partial remedy, we considered the pump curve characteristics and provide a plot of pressure vs. flow rate for the pumping unit and the canal system.

Beside revealing and highlighting the hydrodynamic gasket that ensures an efficient prey retention, another goal of the current manuscript is to investigate (by employing typical dimensions of a model organism) whether ascons and sycons would be able to pump and filter enough water, if they truly lack a physical gasket, and if so, what are the determining factors and trade-offs.

An entire new subsection (“Pump curve characteristic”) has been written, in an attempt to give physical interpretation of the pumping system both in ascons/sycons, and leucons.

2) From a fluid dynamics perspective, the fundamental result is fairly easy to see, and is simply a manifestation of local mass conservation (though of course retrodiction is of course much easier than prediction). The presentation would be greatly aided by a very simple schematic of the streamlines from two forces above a wall, either side of a hole, below a no-penetration (not no slip) boundary. We would have liked to have seen a reduced model of this kind involving stokeslets over a wall with a gap, which the authors should consider looking at, but this is not is a necessity for publication.

We agree with reviewers that simple models would greatly aid the presentation, and we tried our best to make the CFD model as simple as possible, to the point that the key flow structures, both qualitatively and quantitatively, are preserved. However, as now explained in the new subsection “Pump characteristic curve”, we believe the CFD unit in Figure 2 is an integrated basic pumping unit of the asconoid and syconoid sponges, and further simplification would not explain the phenomena. For example, as suggested, we considered and modeled two stokeslets above a wall (at the height of h_s = 4.7µm, corresponding to the length of collar filters), either side of a hole (at horizontal distances of x_i = ±iµm), below a no-penetration boundary (at the height of h_np = 42.5µm, corresponding to the radius of the choanocyte chamber). Author response image 1 shows the streamlines for two cases (x₅ and x₁₀, corresponding to the horizontal location of flagella with respect to the hole). In the first case (Author response image 1A), there will be no recirculation created above the hole. A weak circulation region is formed above the hole once the stokeslets are positioned far away from the hole (case x₁₀, Author response image 1B); this recirculation shows elements of the hydrodynamic gasket: with downflow to a stagnation point (about 1-2µm above the inlet) and radially directed outflow (the remaining flow may be ignored). It is noted that the pumping through the hole drops dramatically (Author response image 1C) as the stokeslets are positioned away from the hole.

The real problem is more complex due to many forces distributed along the beating flagella (Figure 2); As shown, e.g., in Appendix 1—figure 7C, the presence of both proximal and distal flagella, and their collective imparted upward momentum is essential for efficient pumping of the inflow through the collars. Additionally, the flow field is markedly dependent on the presence of porous structure (collar filter) around force generating flagella (e.g. Figure 4).

Author response image 1

Download asset Open asset

Streamlines and pumping rate of two stokeslet above a wall (at the height of *h_s* = 4.7µm), either side of a hole, below a no-penetration boundary.

Note that due to the symmetry, the results are shown only in half of the plane. A weak recirculation region is formed above the hole as the horizontal distances *x_i* increases (x₅ = ±5µm (A) to x₁₀ = ±10µm (B)), but it’s formation comes at the cost of a dramatically reduced pumping rate into the hole (C).

3) The description of the "flagellar vane" is a bit arcane. We are familiar with standard flagellae, and flagellae with mastigonemes, but have not come across this sort of ultrastructure before (is this a uniquely choanoflagellate/sponge structure). Reading other papers helped, but the manuscript needs a clearer description of these 3 types of flagellae, particularly when the image in Appendix 1—figure 1C seems to have ordinary flagellae.

Flagella vanes are believed to be present in all sponges, and have been well illustrated in both demosponges and Hexactinellids.

A new paragraph has been added in the Introduction clarifying the differences between mastigonemes and vanes. Also a recently taken image is now been added in the appendix (Appendix 1—figure 2) visualizing the vane in calcareous sponge S. coactum for the first time.

4) An image of gasket-type vs. non gasket type would have helped our understanding of the motivation for the study earlier on. In general, we found that it was only possible to understand what was actually going on by the end of the paper, so it would be good to go through the Introduction once more to make sure it is as clear as possible to the more general reader.

We agree and now explain the concept of gasket in the Introduction.

5) The flagellum model (Equation 1) is not arclength preserving. Reading a previous paper it seems that the total change in arclength is only a few percent over a beat, however the velocities on the flagellum will also be subtly wrong, as material points will not be exhibiting the characteristic figure of eight motion.

We have convinced ourselves that this doesn't affect the results too significantly (any error would be smaller than the error associated with taking very difficult experimental measurements), so we will not insist on a rerunning of the results, but it would not have been hard to make the waveform arclength preserving.

We agree, indeed, in our model, the flagellum would be extensible and its length varies slightly during the beat cycle (ca. 2%), resulting in marginally wrong velocities on the flagellum. However, implementing Equation 1 in the numerical scheme is computationally cheaper than preserving the arclength. This is because the latter requires importing a table of motion data and interpolating the velocities of each point on the flagellum at each time step. To exemplify the insignificant error involved, we reran the simulation results for the base case with an inextensible flagellum that preserves the arc length. Appendix 1—figure 3 shows two snapshots of velocity field for an extensible vs. inextensible flagellum. Although the velocity of the flagellum slightly differ, the flow field in the domain is insignificantly affected with less than 4% difference in the pumping rate.

It has also been argued [3] that the extensible and inextensible sheets have the same swimming velocity (hence the same generated force) to leading order in ak, where a is the amplitude of the beat, and k the wavenumber.

6) We are confused by the wedge geometry of Figure 2. If fluid leaves the computational domain "vertically" then how is there any net transport of fluid along the long axis of the ascon? Would not the flagella be strongly perturbed by the lateral flow?

Once fluid leaves the computational domain vertically into the core of the choanocyte chamber, it is directed axially toward one open end of the chamber (apopyle). To illustrate this, we model the flow in the cylindrical core of the chamber, closed at the right end and open through the apopyle at the other end. The flow enters the cylinder from the lateral surface and one end (velocity inlet boundary of 1µms⁻¹, which is in the range of the mean velocity of flow leaving the wedge geometry of Figure 2), and exit from the other end (uniform pressure boundary). Appendix 2—figure 2 shows the velocity and pressure fields in a cross section oriented axially in the center of the domain. Lateral flow and shear close to sides (hence right above flagella tip) is relatively weak, and we assume that the flagella action is not strongly affected.

Furthermore, considering an extended computational domain including 5 pumping units (Appendix 2—figure 3), we illustrate that the boundary conditions applied on the wedge geometry is independent of the global boundary conditions of the entire chamber, hence from the directional axial flow in the core region (Appendix 2—figure 4 and Appendix 2—figure 2B).

Appendix 2—figure 2 is referred to in the subsection “Morphology of the flagellated chamber”.

7) No detail is given at all as to how the flagella beating is modelled in the CFD code. Are there regularized Stokeslets? Is slender body hydrodynamics used? Please clarify.

The numerical method is the finite volume discretization and solution of the Navier-Stokes equations does not involve singularities, as described in the Materials and methods. But we agree that more clarification is needed, specifically on how the flagella and corresponding computational cell motion is modeled.

More explanation has been added in the subsection “Morphology of the flagellated chamber” and in the Materials and methods.

8) We strongly suggest the authors avoid the rainbow colourmap wherever possible, as it is not perceptually uniform (see https://peterkovesi.com/projects/colourmaps/) and is also generally bad for people who are colour blind.

We thank the reviewers for this important comment. We have changed all the colour maps from the rainbow to the Kelvin temperature.

9) The authors end up documenting a large number of individual differences between ascon and leucon sponges, but only study them in isolation – and only a subset of them. Compared to leucons, ascons have: (1) no physical gasket (2) shorter collars and (3) one large incurrent pore for 24 choanocytes (per choanocyte chamber), instead of many small pores (one per choanocyte.) Only the third difference is usually considered part of the definition of leuconoid vs. asconoid type, but the paper focuses almost entirely on the first and second differences. We recommend that the authors comment on the third parameter as well – if only by drawing a comparison with their earlier, published model.

We agree with the reviewers that more clarification is needed regarding the difference between the two basic pumping units. To the best of our knowledge, even in leucons there are several (less than 10) choancytes per incurrent pore. The difference, though, is that, in leucons, the basic pumping units differ from those of ascons or sycons. The basic pumping units, are the simplest subdivision of choanocyte chamber exposed to the same pressure difference resulting from the canal system. Hence, these units all work in parallel. For sponges lacking a physical gasket, the unit is one ostium with several neighbouring choanocytes (Figure 2B). Presence of a physical gasket (leucons), however, leads to two zones of high and low pressure inside the chambers [5, 2], effectively exposing each individual choanocyte to the same pressure difference. Therefore, in leucons, the basic pumping unit is a further reduced subdivision of chamber including only one choanocyte, irrespective of the location of the choanocyte with respect to the ostium [2].

These differences are now clarified and highlighted in the new added subsection “Pump characteristic curve”.

10) Regarding the total difference of overall efficiency between the leuconoid and asconoid organizations, the discussion is a bit unclear. The authors state that "Our results indicate that reduced resistance in the ascon and sycon-type aquiferous systems comes with reduced volume filtered for high retention efficiency." But the paper performs no explicit comparison of filtered volumes between sycon and leucons until the very end, and even then it concludes that these are actually not really different: "Furthermore, both experimental and CFD estimates of flow rate per choanocyte [in sycons] are comparable to published estimates for leucon sponges that range from 17 to 236 µm3 s^-1 for different species of demosponges and glass sponges (Larsen and Riisgård, 1994; Leys et al., 2011; Ludeman et al., 2017), suggesting similar pumping capacity despite different pumping mechanism." This contradicts the statement of the Introduction – even though the highest pumping capacity reported for a leuconoid sponge (236 µm3 s^-1 per choanocyte) is higher than the one reported for syconoid sponges (48 µm3 s^-1 per choanocyte) suggesting that the leucon organization has at least higher potential.

We think the authors should settle on one of their two interpretations, or alternatively state that both are valid alternatives. In particular, if leucons do not have higher filtration capacity, what advantage do they have over ascons and sycons (which additionally do not risk clogging, as the authors mention)? What is the specific niche of leuconoid sponges?

The latter statement referred to the pumping capacity of the choanocyte, but the first statement in the Introduction, to the pumping capacity of the whole sponge in ascons and sycons, which has fewer choanocytes (compared to leucons) due to the architecture of the chambers. Still, we agree that our comments on the filtration capacity do not seem coherent. The statement in the Introduction was removed to avoid any inconsistency in the interpretation.

The architecture of leuconid sponges allows the sponge to grow larger and have greater surface area. However, we think that the large surface area does take a lot of energy to maintain and so generally leucons thrive in food rich environments.

11) Figure 2 shows that all flagella within the chamber beat in the same plane (with all vanes parallel to each other), parallel to the long axis. Are there reasons to think this reflects biological reality or is it a simplification of the model?

Indeed, this is a simplification of the model. In the manuscript, we have illustrated that asynchronization among flagella does not matter, but this was done only for cases where all flagella beat in the same plane. Following the reviewers comments, we have also examined whether the pumping and average flow structure would be significantly affected, even if some flagella beat in a different plane. We considered the same computational domain as in Figure 2, where now every 2nd column of flagella beat in a perpendicular plane (Author response image 2). The results show less than 3% difference in the pumping rate into the chamber as a result of not all flagella beating in the same plane.

Author response image 2

Download asset Open asset

Computational geometry where some flagella beat in a perpendicular plane.

The results for the new simulation case have been added to the subsection “Asynchronization among flagella”, and referred to in the main text.

12) Subsection “Pumping mechanism”: the vane width considered is in the 0.3-0.7 µm range. How was this range of values decided? Is it close to real vanes of calcareous sponges? Why does it stay so far below the collar diameter (2.5 µm)?

A base width of 0.7 µm has been chosen based on an image showing the remnant of vane in calcareous ascon Leucosolenia eleanor (Author response image 3). However, to the best of our knowledge, at the time of conducting the simulations, there was no data on the actual dimension of vane in calcareous sponges, despite their presence being reported [1, 4]. We initially present the result for a range of different vane width 0.3-0.7 µm. However, we also consider cases where the vane width is 1.4 µm on the unconfined part of flagellum, but 0.7 µm on the confined part. Width of 0.7 µm is technically the maximum width (on the confined part of the flagellum) which allows the flagellum motion without becoming in contact with the collar. Although some leucons have vanes that span the collar which leads to a high pressure ’positive displacement pump’ thanks to their physical gasket, vanes spanning the collar in sycons would not be important because of the different pumping mechanism (Figure 4).

Furthermore, a recently taken image has now been added as Appendix 1—figure 2 visualizing the vane in S. coactum indicating a vane width of ∼ 1µm.

Author response image 3

Download asset Open asset

SEM image of calcareous ascon *Leucosolenia eleanor* showing flagellum with remnants of about ∼ 0.7µm wide vanes extending over the full flagellum length.

The range has been increased to 0.3-1.4 µm, and Figure 3 has been updated, and as mentioned above, a new image visualising the vane has been added in Appendix 1.

13) Some calcareous sponges have a leuconoid organization, yet lack a physical gasket. Can the authors comment on how they think these sponges work?

Although sponges with a complex canal system appear to have a ’gasket-present’ pumping unit, a ’gasket-absent’ unit can still function efficiently if connected to a complex, yet open and less resistive canal system, or inefficiently if connected to an open canal system, but with highly resistive ostia. Therefore, there could well be sponges characterized as leuconoid types yet missing a physical gasket, or as syconoid types but with a physical gasket. The appearance, structure and nature of the gasket would also depend on the hydrodynamics dictated by the canal system. Therefore, further research, using better preservation and imaging techniques, is required to elucidate the exact nature of the sealant element, and to investigate the role that hydrodynamics is playing in forming the seal in different sponges. Recent observations of sycon coactum (Appendix 1—figure 2) have shown some mesh structures that could have a similar (gasket) effect of guiding flow to filters.

The above explanation has been added at the end of the subsection “Pump curve characteristic”.

References:

1) Bjorn A. Afzelius. Flimmer-flagellum of the sponge. Nature, 191(4795):1318, 1961.

2) Sayed Saeed Asadzadeh, Poul S. Larsen, Hans Ulrik Riisgard, and Jens H. Walther. Hydrodynamics of the leucon sponge pump. J. Roy. Soc. Inter, 16(150):20180630, 2019.

3) Eric Lauga and Thomas R. Powers. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys., 72(9):096601, 2009.

4) TL Simpson. The cell biology of sponges. Springer, Berlin Heidelberg, New York, 1984.

5) Norbert Weissenfels. The filtration apparatus for food collection in freshwater sponges (Porifera, Spongillidae). Zoomorphology, 112(1):51–55, 1992.

https://doi.org/10.7554/eLife.61012.sa2

Article and author information

Author details

Seyed Saeed Asadzadeh

National Institute of Aquatic Resources and Centre for Ocean Life, Technical University of Denmark, Lyngby, Denmark

Contribution
Conceptualization, Software, Validation, Methodology, Writing - original draft

For correspondence
sesasa@aqua.dtu.dk

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-6360-8924
Thomas Kiørboe

National Institute of Aquatic Resources and Centre for Ocean Life, Technical University of Denmark, Lyngby, Denmark

Contribution
Conceptualization, Resources, Supervision, Funding acquisition, Methodology, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3265-336X
Poul Scheel Larsen

Department of Mechanical Engineering, Technical University of Denmark, Lyngby, Denmark

Contribution
Conceptualization, Formal analysis, Visualization, Methodology, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-7155-5965
Sally P Leys

Department of Biological Sciences, University of Alberta, CW 405 Biological Sciences Building, Edmonton, Canada

Contribution
Conceptualization, Resources, Data curation, Formal analysis, Investigation, Methodology, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-9268-2181
Gitai Yahel

The Faculty of Marine Science, Ruppin Academic Center, Michmoret, Israel

Contribution
Resources, Data curation, Formal analysis, Investigation, Visualization, Methodology, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2306-355X
Jens H Walther
1. Department of Mechanical Engineering, Technical University of Denmark, Lyngby, Denmark
2. Computational Science and Engineering Laboratory, Swiss Federal Institute of Technology Zürich, Zürich, Switzerland
Contribution
Conceptualization, Resources, Software, Formal analysis, Supervision, Funding acquisition, Methodology, Writing - review and editing

Competing interests
No competing interests declared

Funding

Villum Fonden (9278)

Seyed Saeed Asadzadeh
Poul Scheel Larsen
Jens H Walther

NSERC (2016-05446)

Sally P Leys

Villum Fonden

Seyed Saeed Asadzadeh

Danish Council for Independent Research Natural Sciences (7014-00033B)

Thomas Kiørboe

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We acknowledge support from the Danish Council for independent Research (7014-00033B) to TK, from the Villum Foundation for JHW. through research grant no. 9278 and from NSERC Discovery Grant 2016–05446 to SPL. The Centre for Ocean Life is supported by the Villum Foundation.

Senior Editor

Aleksandra M Walczak, École Normale Supérieure, France

Reviewing Editor

Raymond E Goldstein, University of Cambridge, United Kingdom

Version history

Received: July 13, 2020
Accepted: November 27, 2020
Accepted Manuscript published: November 30, 2020 (version 1)
Version of Record published: December 22, 2020 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

3,071

Page views
300

Downloads
7

Citations

Article citation count generated by polling the highest count across the following sources: Crossref, PubMed Central, Scopus.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Seyed Saeed Asadzadeh
Thomas Kiørboe
Poul Scheel Larsen
Sally P Leys
Gitai Yahel
Jens H Walther

(2020)

Hydrodynamics of sponge pumps and evolution of the sponge body plan

eLife 9:e61012.

https://doi.org/10.7554/eLife.61012

Share this article

Cite this article

Schematic of sponge body types in ascon (A), sycon (S), and leucon (L) with evolutionary view of grades of morphological complexity in calcareous sponges (black arrows).

Morphology of the modeled flagellated chamber in calcareous sponges.

Simulated flow field inside the chamber.

Side view of passive particles entering into the chamber through the ostium and carried by the flow.

Top view of passive particles entering into the chamber through the ostium and carried by the flow.

Averaged velocity field for two hypothetical cases: (A) only the unconfined part of the flagella exists, and (B) only the confined part of the flagella exists.

Dimensionless pump (solid line) and system (dashed and dotted lines) characteristics for different pumping units and canal systems in sponges.

A comparison of mean velocity fields and the performance of (A) a hydrodynamic, and (B) a physical gasket (both with an increased amplitude of the flagella beat waveform and collar length of 4.8 µm).

Retention efficiency (%) of different prey types counted by flow cytometry in the water inhaled and exhaled by Sycon coactum.

Figure 7—source data 1

The moving mesh (viewed in the xy-plane) inside the computational domain.

Calcareous sponge Sycon coactum.

Observation of vane in the calcareous sponge Sycon coactum (scale bar: 2 µm).

Dye visualization of the jet from an osculum with a diameter of 2 mm.

Snapshots of velolicty field for cases where the flagellum is extensible (A) and inextensible (B).

Effect of ostia length and diameter on the pumping rate and the backflow in the core of the region, and thus the position of the stagnation area.

Effect of collar elements spacing (lb) on pumping rate (Q) and volume flow rate (Q) through the collars for different porosity levels of the collars.

Snapshot of velocity fields when neighboring flagella beat completely out of phase (A, ϕf=0) and in perpendicular planes (B).

Hydrodynamic interaction between the flagella.

Pumping rate and volume flow rate through the collars for flagella with different wavelength.

The simulation unit with presence of the gasket (pink).

Velocity (A) and pressure (B) fields in the cross section of the inner core cylinder.

The simulation domain in an extended slice of the cylindrical chamber including five pumping units, that is, 5 ostia and 120 collar-flagella, closed (no-slip BC) at one end but open (uniform pressure BC) at the other end (green).

Snapshot of velocity and pressure fields for the simulation domain including five units depicted in Appendix 2—figure 3B.

Mesh size independence of volume flow rate through the collars Qc and the power expenditure by the flagella 𝒫 at an arbitrary time step.

Streamlines and pumping rate of two stokeslet above a wall (at the height of hs = 4.7µm), either side of a hole, below a no-penetration boundary.

Computational geometry where some flagella beat in a perpendicular plane.

SEM image of calcareous ascon Leucosolenia eleanor showing flagellum with remnants of about ∼ 0.7µm wide vanes extending over the full flagellum length.

Author details

Seyed Saeed Asadzadeh

Contribution

For correspondence

Competing interests

Thomas Kiørboe

Contribution

Competing interests

Poul Scheel Larsen

Contribution

Competing interests

Sally P Leys

Contribution

Competing interests

Gitai Yahel

Contribution

Competing interests

Jens H Walther

Contribution

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading

Effect of collar elements spacing ( $l_{b}$ ) on pumping rate ( $Q$ ) and volume flow rate ( $Q$ ) through the collars for different porosity levels of the collars.

Snapshot of velocity fields when neighboring flagella beat completely out of phase (A, $ϕ_{f} = 0$ ) and in perpendicular planes (B).

Mesh size independence of volume flow rate through the collars Q_c and the power expenditure by the flagella $𝒫$ at an arbitrary time step.

Streamlines and pumping rate of two stokeslet above a wall (at the height of h_s = 4.7µm), either side of a hole, below a no-penetration boundary.