A new model of decision processing in instrumental learning tasks

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

Learning and decision-making are interactive processes, yet cognitive modeling of error-driven learning and decision-making have largely evolved separately. Recently, evidence accumulation models (EAMs) of decision-making and reinforcement learning (RL) models of error-driven learning have been combined into joint RL-EAMs that can in principle address these interactions. However, we show that the most commonly used combination, based on the diffusion decision model (DDM) for binary choice, consistently fails to capture crucial aspects of response times observed during reinforcement learning. We propose a new RL-EAM based on an advantage racing diffusion (ARD) framework for choices among two or more options that not only addresses this problem but captures stimulus difficulty, speed-accuracy trade-off, and stimulus-response-mapping reversal effects. The RL-ARD avoids fundamental limitations imposed by the DDM on addressing effects of absolute values of choices, as well as extensions beyond binary choice, and provides a computationally tractable basis for wider applications.

Introduction

Learning and decision-making are mutually influential cognitive processes. Learning processes refine the internal preferences and representations that inform decisions, and the outcomes of decisions underpin feedback-driven learning (Bogacz and Larsen, 2011). Although this relation between learning and decision-making has been acknowledged (Bogacz and Larsen, 2011; Dayan and Daw, 2008), the study of cognitive processes underlying feedback-driven learning on the one hand, and of perceptual and value-based decision-making on the other, have progressed as largely separate scientific fields. In the study of error-driven learning (O'Doherty et al., 2017; Sutton and Barto, 2018), the decision process is typically simplified to soft-max, a descriptive model that offers no process-level understanding of how decisions arise from representations, and ignores choice response times (RTs). In contrast, evidence-accumulation models (EAMs; Donkin and Brown, 2018; Forstmann et al., 2016; Ratcliff et al., 2016) provide a detailed process account of decision-making but are typically applied to tasks that minimize the influence of learning, and residual variability caused by learning is treated as noise.

Recent advances have emphasized how both modeling traditions can be combined in joint models of reinforcement learning (RL) and evidence-accumulation decision-making processes, providing mutual benefits for both fields (Fontanesi et al., 2019a; Fontanesi et al., 2019b; Luzardo et al., 2017; McDougle and Collins, 2020; Miletić et al., 2020; Millner et al., 2018; Pedersen et al., 2017; Pedersen and Frank, 2020; Sewell et al., 2019; Sewell and Stallman, 2020; Shahar et al., 2019; Turner, 2019). Combined models generally propose that value-based decision-making and learning interact as follows: For each decision, a subject gradually accumulates evidence for each choice option by sampling from a running average of the subjective value (or expected reward) associated with each choice option (known as Q-values). Once a threshold level of evidence is reached, they commit to the decision and initiate a corresponding motor process. The response triggers feedback, which is used to update the internal representation of subjective values. The next time the subject encounters the same choice options this updated internal representation changes evidence accumulation.

The RL-EAM framework has many benefits (Miletić et al., 2020). It allows for studying a rich set of behavioral data simultaneously, including entire RT distributions and trial-by-trial dependencies in choices and RTs. It posits a theory of evidence accumulation that assumes a memory representation of rewards is the source of evidence, and it formalizes how these memory representations change due to learning. It complements earlier work connecting theories of reinforcement learning and decision-making (Bogacz and Larsen, 2011; Dayan and Daw, 2008) and their potential neural implementation in basal ganglia circuits (Bogacz and Larsen, 2011), by presenting a measurement model that can be fit to, and makes predictions about, behavioral data. Adding to benefits in terms of theory building, the RL-EAM framework also has potential to improve parameter recovery properties compared to standard RL models (Shahar et al., 2019), and allows for the estimation of single-trial parameters of the decision model, which can be crucial in the analysis of neuroimaging data.

An important challenge of this framework is the number of modeling options in both the fields of reinforcement learning and decision-making. Even considering only model-free (as opposed to model-based, see Daw and Dayan, 2014) reinforcement learning, there exists a variety of learning rules (e.g. Palminteri et al., 2015; Rescorla and Wagner, 1972; Rummery and Niranjan, 1994; Sutton, 1988), as well as the possibility of multiple learning rates for positive and negative prediction errors (Christakou et al., 2013; Daw et al., 2002; Frank et al., 2009; Gershman, 2015; Frank et al., 2007; Niv et al., 2012), and many additional concepts, such as eligibility traces to allow for updating of previously visited states (Barto et al., 1981; Bogacz et al., 2007). Similarly, in the decision-making literature, there exists a wide range of evidence-accumulation models, including most prominently the diffusion decision model (DDM; Ratcliff, 1978; Ratcliff et al., 2016) and race models such as the linear ballistic accumulator model (LBA; Brown and Heathcote, 2008) and racing diffusion (RD) models (Boucher et al., 2007; Hawkins and Heathcote, 2020; Leite and Ratcliff, 2010; Logan et al., 2014; Purcell et al., 2010; Ratcliff et al., 2011; Tillman et al., 2020).

The existence of this wide variety of modeling options is a double-edged sword. On the one hand, it highlights the success of the general principles underlying both modeling traditions (i.e. learning from prediction errors and accumulate-to-threshold decisions) in explaining behavior, and it allows for studying specific learning/decision-making phenomena. On the other hand, it constitutes a bewildering combinatorial explosion of potential RL-EAMs; here, we provide empirical grounds to navigate this problem with respect to EAMs.

The DDM is the dominant EAM as currently used in reinforcement learning (Fontanesi et al., 2019a; Fontanesi et al., 2019b; Millner et al., 2018; Pedersen et al., 2017; Pedersen and Frank, 2020; Sewell et al., 2019; Sewell and Stallman, 2020; Shahar et al., 2019), but this choice is without experimental justification. Furthermore, the DDM has several theoretical drawbacks, such as its inability to explain multi-alternative decision-making and its strong commitment to the accumulation of the evidence difference, which leads to difficulties in explaining behavioral effects of absolute stimulus and reward magnitudes without additional mechanisms (Fontanesi et al., 2019a; Ratcliff et al., 2018; Teodorescu et al., 2016). Here, we compare the performance of different decision-making models in explaining choice behavior in a variety of instrumental learning tasks. Models that fail to capture crucial aspects of performance run the risk of producing misleading psychological inferences. For EAMs, the full RT distribution (i.e. its level of variability and skew) have proven to be crucial. Hence, it is important to assess which RL-EAMs are able to capture not only learning-related changes in choice probabilities and mean RT, but also the general shape of the entire RT distribution and how it changes with learning. Further, in order to be held forth as a general modeling framework, it is important to capture how all these measures interact with key phenomena in the decision-making and learning literature.

We compare the RL-DDM with two RL-EAMs based on a racing accumulator architecture (Figure 1). All the RL-EAMs assume evidence accumulation is driven by Q-values, which change based on error-driven learning as governed by the classical delta update rule. Rather than a two-sided DDM process (Figure 1A), the alternative models adopt a neurally plausible RD architecture (Ratcliff et al., 2007), which conceptualize decision-making as a statistically independent race between single-sided diffusive accumulators, each collecting evidence for a different choice option. The first accumulator to reach its threshold triggers motor processes that execute the corresponding decision. The alternative models differ in how the mean values of evidence are constituted. The first model, the RL-RD (Figure 1B), postulates accumulators are driven by the expected reward for their choice, plus a stimulus-independent baseline (c.f. an urgency signal; Miletić and van Maanen, 2019). The second model, the RL-ARD (advantage racing diffusion), uses the recently proposed advantage framework (van Ravenzwaaij et al., 2020), assuming that each accumulator is driven by weighted combination of three terms: the difference (‘advantage’) in mean reward expectancy of one choice option over the other, the sum of the mean reward expectancies, and the urgency signal. In perceptual choice, the advantage term consistently dominates the sum term by an order of magnitude (van Ravenzwaaij et al., 2020), but the sum term is necessary to explain the effects of absolute stimulus magnitude. We also fit a limited version of this model, RL-lARD, with the weight of the sum term set to zero to test whether accounting for the influence of the sum is necessary even when reward magnitude is not manipulated, as was the case in our first experiments. The importance of sum and advantage terms is also quantified by their weights as estimated in full RL-ARD model fits.

Figure 1

Download asset Open asset

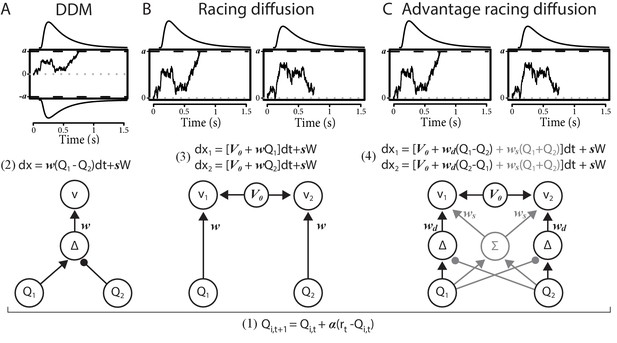
Comparison of the decision-making models.

Bottom graphs visualize how Q-values are linked to accumulation rates. Top panel illustrates the evidence-accumulation process of the DDM (panel A) and racing diffusion (RD) models (panels B and C). Note that in the race models there is no lower bound. Equations 2–4 formally link Q-values to evidence-accumulation rates. In the RL-DDM, the difference $(Δ)$ in Q-values is accumulated, weighted by free parameter $w$ , plus additive within-trial white noise W with standard deviation $s$ . In the RL-RD, the (weighted) Q-values for both choice options are independently accumulated. An evidence-independent baseline urgency term, $V_{0}$ (equal for all accumulators), further drives evidence accumulation. In the RL-ARD models, the advantages $(Δ)$ in Q-values are accumulated as well, plus the evidence-independent baseline term $V_{0}$ . The gray icons indicate the influence of the Q-value *sum* $(Σ)$ on evidence accumulation, which is not included in the limited variant of the RL-ARD. In all panels, bold-italic faced characters indicate parameters. Q1 and Q₂ are Q-values for both choice options, which are updated according to a delta learning rule (Equation 1 at the bottom of the graph), with learning rate $α$ .

For all models, we first test how well they account for RT distributions (central tendency, variability, and skewness of RTs), accuracies, and learning-related changes in RT distributions and accuracies in a typical instrumental learning task (Frank et al., 2004). In this experiment, we also manipulated difficulty, that is, the magnitude of the difference in average reward between pairs of options. In two further experiments, we test the ability of the RL-EAMs to capture key behavioral phenomena in the decision-making and reinforcement-learning literatures, respectively, speed-accuracy trade-off (SAT), and reversals in reward contingencies, again in binary choice. In a final experiment, we show that the RL-ARD extends beyond binary choice, successfully explaining accuracy and full RT distributions from a three-alternative instrumental learning task that manipulates reward magnitude.

Results

In the first experiment, participants made decisions between four sets of two abstract choice stimuli, each associated with a fixed reward probability (Figure 2A). On each trial, one choice option always had a higher expected reward than the other; we refer to this choice as the ‘correct’ choice. After each choice, participants received feedback in the form of points. Reward probabilities, and therefore choice difficulty, differed between the four sets (Figure 2B). In total, data from 55 subjects were included in the analysis, each performing 208 trials (see Materials and methods).

Figure 2

Download asset Open asset

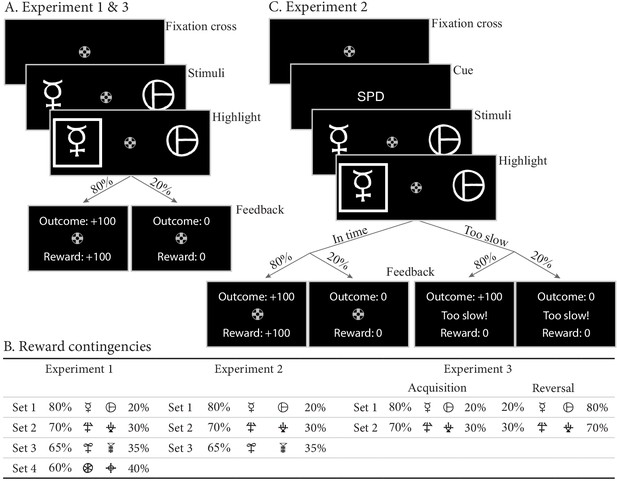
Paradigms for experiments 1–3.

(A) Example trial for experiments 1 and 3. Each trial starts with a fixation cross, followed by the presentation of the stimulus (until choice is made or 2.5 s elapses), a brief highlight of the chosen option, and probabilistic feedback. Reward probabilities are summarized in (B). Percentages indicate the probabilities of receiving +100 points for a choice (with 0 otherwise). The actual symbols used differed between experiments and participants. In experiment 3, the acquisition phase lasted 61–68 trials (uniformly sampled each block), after which the reward contingencies for each stimulus set reversed. (C) Example trial for experiment 2, which added a cue prior to each trial (‘SPD’ or ‘ACC’), and had feedback contingent on both the choice and choice timing. In the SPD condition, RTs under 600 ms were considered in time, and too slow otherwise. In the ACC condition, choices were in time as long as they were made in the stimulus window of 1.5 s. Positive feedback ‘Outcome: +100’ and ‘Reward: +100’ were shown in green letters, negative feedback (‘Outcome: 0’, ‘Reward: 0’, and ‘Too slow!”) were shown in red letters.

Throughout, we summarize RT distributions by calculating the 10th, 50th (median), and 90th percentiles separately for correct and error responses. The median summarizes central tendency, the difference between 10th and 90th percentiles summarizes variability and the larger difference between the 90th and 50th percentiles than between the 50th and 10th percentiles summarizes the positive skew that is always observed in RT distributions. To visualize the effect of learning, we divided all trials in 10 bins (approximately 20 trials each), and calculated accuracy and the RT percentiles per bin. Note that model fitting was not based on these data summaries. Instead, we used hierarchical Bayesian methods to fit models to the data from every trial and participant simultaneously. We compared model fits informally using posterior predictive distributions—calculating the same summary statistics on data generated from the fitted model as we did for the empirical data—and formally using the Bayesian Predictive Information Criterion (BPIC; Ando, 2007). The former method allows us to assess the absolute quality of fit (Palminteri et al., 2017) and detect misfits; the latter provides a model-selection criterion that trades off quality of fit with model complexity (lower BPICs are preferred), ensuring that a better fit is not only due to greater model flexibility.

We first examine results aggregated over difficulty conditions. The posterior predictives of all four RL-EAMs are shown in Figure 3, with the top row showing accuracies, and the middle and bottom rows correct and error RT distributions (parameter estimates for all models can be found in Table 1). The RL-DDM generally explains the learning-related increase in accuracy well, and if only the central tendency were relevant it might be considered to provide an adequate account of RT, although correct median RT is systematically under-estimated. However, RT variability and skew are severely over-estimated. The RL-RD largely overcomes the RT distribution misfit, but it overestimates RTs in the first trial bins, and while capturing an increase in accuracy over trials, it is systematically underestimated. The RL-ARD models provide the best explanation of all key aspects of the data: except for a slight underestimation of accuracy in early trial bins (largely shared with the RL-DDM), they capture accuracy well, and like the RL-RD, they capture the RT distributions well, but without overpredicting the RTs in the early trials. The two RL-ARD models do not differ greatly in fit, except that the limited version slightly underestimates the decrease in RT with learning.

Figure 3 with 4 supplements see all

Download asset Open asset

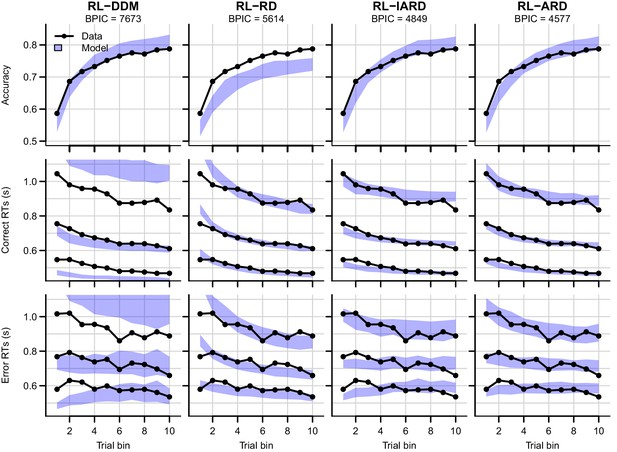
Comparison of posterior predictive distributions of the four RL-EAMs.

Data (black) and posterior predictive distribution (blue) of the RL-DDM (left column), RL-RD, RL-lARD, and RL-ARD (right column). Top row depicts accuracy over trial bins. Middle and bottom row show 10th, 50th, and 90th RT percentiles for the correct (middle row) and error (bottom row) response over trial bins. Shaded areas correspond to the 95% credible interval of the posterior predictive distributions. All data are collapsed across participants and difficulty conditions.

Table 1

Posterior parameter estimates (across-subject mean and SD of the median of the posterior distributions) for all models and experiments.

For models including $s_{t 0}$ , the non-decision time is assumed to be uniformly distributed with bounds $[t 0, t 0 + s_{t 0}]$ .

Experiment 1
RL-DDM	$α$	$a$	$t 0$	$w$					BPIC
	0.14 (0.11)	1.48 (0.19)	0.30 (0.06)	3.21 (1.11)					7673
RL-RD	$α$	$a$	$t 0$	$V_{0}$	$w$
	0.12 (0.08)	2.16 (0.27)	0.10 (0.04)	1.92 (0.42)	3.09 (1.32)				5613
RL-lARD	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$
	0.13 (0.12)	2.05 (0.24)	0.12 (0.05)	2.48 (0.43)	2.36 (0.95)				4849
RL-ARD	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$
	0.13 (0.11)	2.14 (0.26)	0.11 (0.04)	2.46 (0.59)	2.25 (0.78)	0.36 (0.79)			4577
RL-DDM A1	$α$	$a$	$t 0$	$w$	$v_{m a x}$
	0.14 (0.12)	1.49 (0.20)	0.30 (0.06)	3.01 (0.66)	2.81 (0.72)				7717
RL-DDM A2	$α$	$a$	$t 0$	$w$	$s_{z}$	$s_{v}$
	0.14 (0.11)	1.48 (0.19)	0.30 (0.06)	3.21 (1.12)	1.79e⁻³ (0.4e⁻³)	1.8e⁻³ (0.4e-³)			7637
RL-DDM A3	$α$	$a$	$t 0$	$w$	$s_{z}$	$s_{v}$	$s_{t 0}$
	0.13 (0.12)	1.13 (0.19)	0.27 (0.06)	5.31 (2.04)	0.00 (0.00)	0.31 (0.13)	0.37 (0.13)		4844
RL-DDM A4	$α$	$a$	$t 0$	$w$	$v_{m a x}$	$s_{v}$	$s_{z}$	$s_{t 0}$
	0.13 (0.12)	1.15 (0.17)	0.27 (0.06)	2.02 (0)	5.16 (1.18)	0.55 (0.24)	1.57e⁻³ (0)	0.36 (0.13)	4884
RL-ALBA	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$	A
	0.13 (0.11)	3.53 (0.53)	0.03 (0.00)	3.03 (0.57)	2.03 (0.59)	0.33 (0.78)	1.73 (0.43)		4836
Experiment 2
RL-DDM 1	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$w$
	0.13 (0.06)	1.11 (0.18)/1.42 (0.23)	0.26 (0.06)	3.28 (0.66)					979
RL-DDM 2	$α$	$a$	$t 0$	$w_{s p d}$ / $w_{a c c}$
	0.13 (0.05)	3.01 (0.63)	0.26 (0.06)	3.46 (0.79)/3.01 (0.63)					1518
RL-DDM 3	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$w_{s p d}$ / $w_{a c c}$
	0.13 (0.06)	1.10 (0.18)/1.44 (0.23)	0.26 (0.06)	3.11 (0.68)/3.48 (0.72)					999
RL-ARD 1	$α$	$a_{s p d} / a_{a c c}$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$
	0.12 (0.05)	1.45 (0.35)/1.82 (0.35)	0.15 (0.07)	2.59 (0.50)	2.24 (0.53)	0.47 (0.34)			−1044
RL-ARD 2	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$	$m_{v, s p d}$
	0.12 (0.05)	1.83 (0.36)	0.12 (0.07)	2.52 (0.53)	1.83 (0.56)	0.32 (0.26)	1.31 (0.20)		−827
RL-ARD 3	$α$	$a$	$t 0$	$V_{0, s p d}$ / $V_{0, a c c}$	$w_{d}$	$w_{s}$
	0.12 (0.05)	1.83 (0.35)	0.12 (0.07)	3.37 (0.84)/3.37 (0.54)	2.11 (0.52)	0.39 (0.30)			−934
RL-ARD 4	$α$	$a_{s p d} / a_{a c c}$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$	$m_{v, s p d}$
	0.12 (0.05)	1.04 (0.14)/1.82 (0.35)	0.15 (0.07)	2.59 (0.52)	2.21 (0.51)	0.44 (0.38)	1.04 (0.14)		−1055
RL-ARD 5	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$V_{0, s p d}$ / $V_{0, a c c}$	$w_{d}$	$w_{s}$
	0.12 (0.05)	1.59 (0.40)/1.83 (0.32)	0.14 (0.06)	2.92 (0.65)/2.52 (0.50)	2.21 (0.50)	0.43 (0.33)			−1071
RL-ARD 6	$α$	$a$	$t 0$	$V_{0, s p d}$ / $V_{0, a c c}$	$w_{d}$	$w_{s}$	$m_{v, s p d}$
	0.12 (0.05)	1.86 (0.35)	0.12 (0.07)	4.13 (0.98)/2.40 (0.54)	2.28 (0.53)	0.44 (0.33)	0.84 (0.03)		−897
RL-ARD 7	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$V_{0, s p d}$ / $V_{0, a c c}$	$w_{d}$	$w_{s}$	$m_{v, s p d}$
	0.12 (0.05)	1.61 (0.40)/1.87 (0.32)	0.14 (0.06)	3.66 (0.74)/2.52 (0.50)	2.41 (0.53)	0.48 (0.38)	0.82 (0.08)		−1060
RL-DDM A3 1	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$w$	$s_{z}$	$s_{v}$	$s_{t 0}$
	0.12 (0.05)	0.81 (0.16)/1.14 (0.17)	0.23 (0.06)	4.46 (0.79)	0.10 (0.01)	0.18 (0.05)	0.26 (0.09)		−862
RL-DDM A3 2	$α$	$a$	$t 0$	$w_{s p d}$ / $w_{a c c}$	$s_{z}$	$s_{v}$	$s_{t 0}$
	0.12 (0.05)	1.03 (0.14)	0.24 (0.06)	18.4 (23.34)/4.44 (0.84)	0.26 (0.07)	0.61 (0.50)	0.28 (0.10)		−325
RL-DDM A3 3	$α$	$a_{s p d}$ / $a_{a c c}$	$t 0$	$w_{s p d}$ / $w_{a c c}$	$s_{z}$	$s_{v}$	$s_{t 0}$
	0.12 (0.05)	0.81 (0.16)/1.14 (0.17)	0.23 (0.06)	4.45 (0.83)/4.45 (0.83)	0.07 (0.00)	0.17 (0.04)	0.26 (0.09)		−849

Experiment 3
Soft-max	$α$	$β$
	0.40 (0.14)	2.82 (1.1)							23,727
RL-DDM	$α$	$a$	$t 0$
	0.38 (0.14)	1.37 (0.24)	0.24 (0.07)						15,599
RL-ARD	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$
	0.35 (0.15)	1.48 (0.34)	0.13 (0.08)	1.86 (0.51)	1.52 (0.63)	0.23 (0.25)			11,548
RL-DDM A3	$α$	$a$	$t 0$	$w$	$s_{z}$	$s_{v}$	$s_{t 0}$
	0.38 (0.14)	1.15 (0.22)	0.22 (0.07)	2.72 (1.16)	0.21 (0.09)	0.28 (0.15)	0.27 (0.17)		11,659
Experiment 4
RL-ARD (Win-All)	$α$	$a$	$t 0$	$V_{0}$	$w_{d}$	$w_{s}$
	0.10 (0.04)	1.6 (0.33)	0.07 (0.05)	1.14 (0.22)	1.6 (0.36)	0.15 (0.26)			36,512

Figure 4 shows the data and RL-ARD model fit separated by difficulty (see Figure 4—figure supplement 1 for equivalent RL-DDM fits, which again fail to capture RT distributions). The RL-ARD model displays the same excellent fit as to data aggregated over difficulty, except that it underestimates accuracy in early trials in the easiest condition (Figure 4, bottom right panel). Further inspections of the data revealed that 17 participants (31%) reached perfect accuracy in the first bin in this condition. Likely, they guessed correctly on the first occurrence of the easiest choice pair, repeated their choice, and received too little negative feedback in the next repetitions to change their choice strategy. Figure 4—figure supplement 2 shows that, with these 17 participants removed, the overestimation is largely mitigated. The delta rule assumes learning from feedback, and so cannot explain such high early accuracies. Working memory processes could have aided performance in the easiest condition, since the total number of stimuli pairs was limited and feedback was quite reliable, making it relatively easy to remember correct-choice options (Collins and Frank, 2018; Collins and Frank, 2012; McDougle and Collins, 2020).

Figure 4 with 4 supplements see all

Download asset Open asset

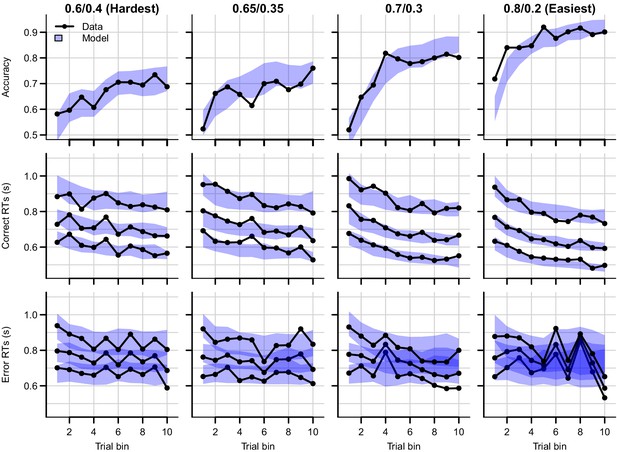
Data (black) and posterior predictive distribution of the RL-ARD (blue), separately for each difficulty condition.

Column titles indicate the reward probabilities, with 0.6/0.4 being the most difficult, and 0.8/0.2 the easiest condition. Top row depicts accuracy over trial bins. Middle and bottom rows show 10th, 50th, and 90th RT percentiles for the correct (middle row) and error (bottom row) response over trial bins. Shaded areas correspond to the 95% credible interval of the posterior predictive distributions. All data and fits are collapsed across participants.

Reward magnitude and Q-value evolution

Q-values represent the participants’ internal beliefs about how rewarding each choice option is. The RL-lARD and RL-DDM assume drift rates are driven only by the difference in Q-values (Figure 5), and both underestimate the learning-related decrease in RTs. Similar RL-DDM underestimation has been detected before (Pedersen et al., 2017), with the proposed remedy being a decrease in the decision bound with time (but with no account of RT distributions). The RL-ARD explains the additional speed-up through the increasing sum of Q-values over trials (Figure 5C), which in turn increases drift rates (Figure 5D). In line with observations in perceptual decision-making (van Ravenzwaaij et al., 2020), the effect of the expected reward magnitude on drift rate is smaller (on average, $w_{s} = 0.36$ ) than that of the Q-value difference ( $w_{d} = 2.25$ ) and the urgency signal ( $V_{0} = 2.45$ ). Earlier work using an RL-DDM (Fontanesi et al., 2019a) showed that higher reward magnitudes decrease RTs in reinforcement learning paradigms. There, the reward magnitude effect on RT was accounted for by allowing the threshold to change as a function of magnitude. However, this requires participants to rapidly adjust their threshold based on the identity of the stimuli, something that is usually not considered possible in EAMs (Donkin et al., 2011; Ratcliff, 1978). The RL-ARD avoids this problem, with magnitude effects entirely mediated by drift rates, and our results show that the expected reward magnitudes influence RTs due to learning even in the absence of a reward magnitude manipulation. Because the sum affects each accumulator equally, it changes RT with little effect on accuracy.

Figure 5

Download asset Open asset

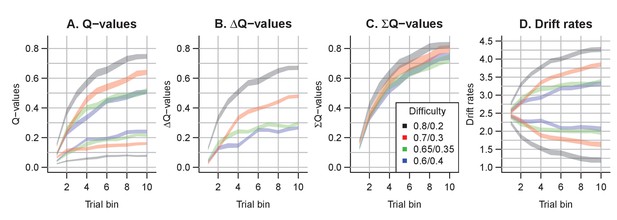
The evolution of Q-values and their effect on drift rates in the RL-ARD.

A depicts raw Q-values, separate for each difficulty condition (colors). B and C depict the Q-value differences and the Q-value sums over time. The drift rates (D) are a weighted sum of the Q-value differences and Q-value sums, plus an intercept.

Speed-accuracy trade-off

Speed-accuracy trade-off (SAT) refers to the ability to strategically trade-off decision speed for decision accuracy (Bogacz et al., 2010; Pachella and Pew, 1968; Ratcliff and Rouder, 1998). As participants can voluntarily trade speed for accuracy, RT and accuracy are not independent variables, so analysis methods considering only one of these variables while ignoring the other can be misleading. EAMs simultaneously consider RTs and accuracy and allow for estimation of SAT settings. The classical explanation in the DDM framework (Ratcliff and Rouder, 1998) holds that participants adjust their SAT by changing the decision threshold: increasing thresholds require a participant to accumulate more evidence, leading to slower but more accurate responses.

Empirical work draws a more complex picture. Several papers suggest that in addition to thresholds, drift rates (Arnold et al., 2015; Heathcote and Love, 2012; Ho et al., 2012; Rae et al., 2014; Sewell and Stallman, 2020) and sometimes even non-decision times (Arnold et al., 2015; Voss et al., 2004) can be affected. Increases in drift rates in a race model could indicate an urgency signal, implemented by drift gain modulation, with qualitatively similar effects to collapsing thresholds over the course of a decision (Cisek et al., 2009; Hawkins et al., 2015; Miletić, 2016; Miletić and van Maanen, 2019; Murphy et al., 2016; Thura and Cisek, 2016; Trueblood et al., 2021; van Maanen et al., 2019). In cognitively demanding tasks, it has been shown that two distinct components of evidence accumulation (quality and quantity of evidence) are affected by SAT manipulations, with quantity of evidence being analogous to an urgency signal (Boag et al., 2019b; Boag et al., 2019a). Recent evidence suggests that different SAT manipulations can affect different psychological processes: cue-based manipulations that instruct participants to be fast or accurate lead to overall threshold adjustments, whereas deadline-based manipulations can lead to a collapse of thresholds (Katsimpokis et al., 2020).

Here, we apply an SAT manipulation to an instrumental learning task (Figure 2C). The paradigm differs from experiment one by the inclusion of a cue-based instruction to either stress response speed (‘SPD’) or response accuracy (‘ACC’) prior to each choice (randomly interleaved). Furthermore, on speed trials, participants had to respond within 0.6 s to receive a reward. Feedback was determined based on both the choice’s probabilistic outcome (‘+100’ or ‘+0’) and the RT: On trials where participants responded too late, they were additionally informed of the reward associated with their choice, had they been in time, so that they always received the feedback required to learn from their choices. After exclusions (see Materials and methods), data from 19 participants (324 trials each) were included in the analyses.

We used two mixed effects models to confirm the effect of the manipulation. A linear model predicting RT confirmed an interaction between trial bin and cue (b = 0.014, SE = 1.53*10^-3, 95% CI [0.011, 0.017], p < 10^-16), a main effect of cue (b = -0.189, SE = 9.5*10^-3, 95% CI [-0.207, -0.170], p < 10^-16) and a main effect of trial bin (b = -0.015, SE = 1.08*10^-3, 95% CI [-0.018, -0.013], p < 10^-16). Thus, RTs decreased with trial bin, were faster for the speed condition, but the effect of the cue was smaller for later trial bins. A logistic mixed effects model of choice accuracy showed a main effect of the cue (b = -0.39, SE = 0.13, 95% CI [-0.65, -0.13], p = 0.003) and trial bin (b = 0.42, SE = 0.06, 95% CI [0.30, 0.53], p = 3.1*10^-12), but not for an interaction (b = 0.115, SE = 0.08, 95% CI [-0.05, 0.28], p = 0.165). Hence, participants were more often correct in the accuracy condition, and their accuracy increased over trial bins, but there was no evidence for a difference in the increase (on a logit scale) between SAT conditions.

Next, we compared the RL-DDM and RL-ARD. In light of the multiple psychological mechanisms potentially affected by the SAT manipulation, we allowed different combinations of threshold, drift rate, and for the RL-ARD urgency, to vary with the SAT manipulation. We fit three RL-DDM models, varying either threshold, the Q-value weighting on the drift rates parameter (Sewell and Stallman, 2020), or both. For the RL-ARD, we fit all seven possible models with different combinations of the threshold, urgency, and drift rate parameters free to vary between SAT conditions.

Formal model comparison (see Table 1 for all BPIC values) indicates that the RL-ARD model combining response caution and urgency effects provides the best explanation of the data, in line with earlier research in non-learning contexts (Katsimpokis et al., 2020; Miletić and van Maanen, 2019; Rae et al., 2014; Thura and Cisek, 2016). The advantage for the RL-ARD was substantial; the best RL-DDM (with only a threshold effect) performed worse than the worst RL-ARD model. The data and posterior predictive distributions of the best RL-DDM model and the winning RL-ARD model are shown in Figure 6. As in experiment 1, the RL-DDM failed to capture the shape of RT distributions, although it fit the SAT effect on accuracy and median RTs. The RL-ARD model provides a much better account of the RT distributions, including the differences between SAT conditions. In Figure 6—figure supplement 1, we show that adding non-decision time variability to the RL-DDM mitigates some of the misfit of the RT distributions, although it still consistently under-predicted the 10th percentile in the accuracy condition. Further, this model was still substantially outperformed by the RL-ARD in formal model selection (ΔBPIC = 209), and non-decision time variability was estimated as much greater than what is found in non-learning contexts, raising the question of its psychological plausibility.

Figure 6 with 5 supplements see all

Download asset Open asset

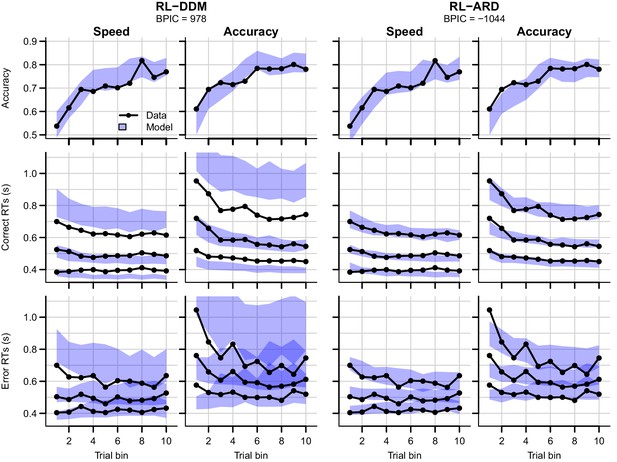
Data (black) and posterior predictive distributions (blue) of the best-fitting RL-DDM (left columns) and the winning RL-ARD model (right columns), separate for the speed and accuracy emphasis conditions.

Top row depicts accuracy over trial bins. Middle and bottom row show 10th, 50th, and 90th RT percentiles for the correct (middle row) and error (bottom row) response over trial bins. Shaded areas in the middle and right column correspond to the 95% credible interval of the posterior predictive distribution.

Both RL-DDM and RL-ARD models tended to underestimate RTs and choice accuracy in the early trial bins in the accuracy emphasis condition. As in experiment 1, working memory may have contributed to the accurate but slow responses in the first trial bin for the accuracy condition (Collins and Frank, 2018; Collins and Frank, 2012; McDougle and Collins, 2020).

Reversal learning

Next, we tested whether the RL-ARD can capture changes in accuracy and RTs caused by a perturbation in the learning process due to reversals in reward contingencies. In the reversal learning paradigm (Behrens et al., 2007; Costa et al., 2015; Izquierdo et al., 2017) participants first learn a contingency between choice options and probabilistic rewards (the acquisition phase) that is then suddenly reversed without any warning (the reversal phase). If the link between Q-values and decision mechanisms as proposed by the RL-ARD underlies decisions, the model should be able to account for the behavioral consequences (RT distributions and decisions) of Q-value changes induced by the reversal.

Our reversal learning task had the same general structure as experiment 1 (Figure 1), except for the presence of reversals. Forty-seven participants completed four blocks of 128 trials each. Within each block, two pairs of stimuli were randomly interleaved. Between trials 61 and 68 (uniformly sampled) in each block, the reward probability switched between stimuli, such that stimuli that were correct during acquisition were incorrect after reversal (and vice versa). Participants were not informed of the reversals prior to the experiment, but many reported noticing them.

Data and the posterior predictive distributions of the RL-DDM and the RL-ARD models are shown in Figure 7. Both models captured the change in choice proportions after the reversal reasonably well, although they underestimate the speed of change. In Figure 7—figure supplement 1, we show that the same is true for a standard soft-max model, suggesting that the learning rule is the cause of this problem. Recent evidence indicates that, instead of only estimating expected values of both choice options by error-driven learning, participants may additionally learn the task structure, estimate the probability of a reversal occurring and adjust choice behavior accordingly. Such a model-based learning strategy could increase the speed with which choice behavior changes after a reversal (Costa et al., 2015; Izquierdo et al., 2017; Jang et al., 2015), but as yet a learning rule that implements this strategy has not been developed.

Figure 7 with 5 supplements see all

Download asset Open asset

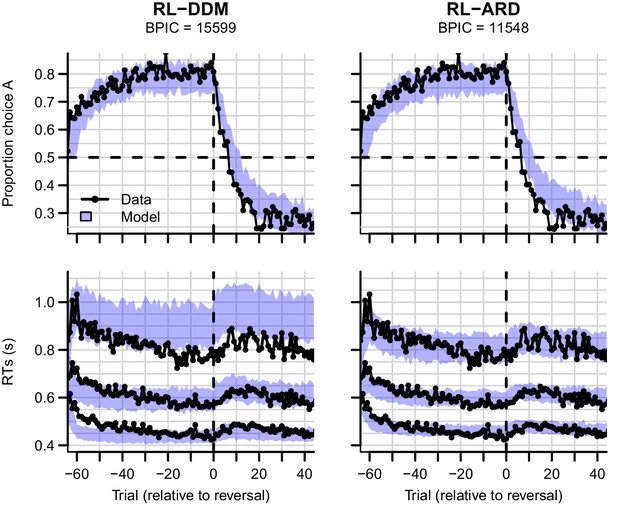
Experiment three data (black) and posterior predictive distributions (blue) for the RL-DDM (left) and RL-ARD (right).

Top row: choice proportions over trials, with choice option A defined as the high-probability choice before the reversal in reward contingencies. Bottom row: 10th, 50th, and 90th RT percentiles. The data are ordered relative to the trial at which the reversal first occurred (trial 0, with negative trial numbers indicated trials prior to the reversal). Shaded areas correspond to the 95% credible interval of the posterior predictive distributions.

The change in RT around the reversal was less marked than the change in choice probability. Once again, the RL-DDM overestimates variability and skew. Both models fit the effects of learning and reversal similarly, but the fastest responses for the RL-DDM decrease much too quickly during initial learning and the reduction in speed for the slowest responses due to the reversal is strongly overestimated. The RL-ARD provides a much better account of the shape of the RT distributions, and furthermore captures the increase in entire RT distributions (instead of only the median) after the reversal point. Formal model comparison also very strongly favors the RL-ARD over the RL-DDM ( $Δ B P I C = 4051$ ). Figure 7—figure supplement 2 provides model comparisons to RL-DDMs with between-trial variability parameters, which lead to the same conclusion.

A notable aspect of the data is that choice behavior stabilizes approximately 20 trials after the reversal, whereas RTs remain high compared to just prior to the reversal point for up to ~40 trials. The RL-ARD explains this behavior through relatively high Q-values for the choice option that was correct during the acquisition (but not reversal) phase (i.e. choice A). Figure 8 depicts the evolution of Q-values, Q-value differences and sums, and drift rates in the RL-ARD model. The Q-values for both choice options increase until the reversal (Figure 8A), with a much faster increase for Q_A. At the reversal Q_A decreases and Q_B increases, but as Q_A decreases faster than Q_B increases there is a temporary decrease in Q-value sums (Figure 8C). After approximately 10 trials post-reversal, Q_B is higher than for Q_A, which flips the sign of the Q-value differences (Figure 8B). However, Q_A after the reversal remains higher than the Q_B before the reversal, which causes the (absolute) Q-value differences to be lower after the reversal than before. As a consequence, the drift rates for B after the reversal remain lower than the drift rates for A before the reversal, which increases RT. Clearly, it is important to take account of the sum of inputs to accumulators as well as the difference between them in order to provide an accurate account of the effects of learning.

Figure 8

Download asset Open asset

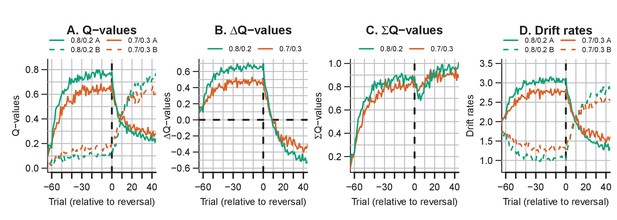
The evolution of Q-values and their effect on drift rates in the RL-ARD in experiment 3, aggregated across participants.

Left panel depicts raw Q-values, separate for each difficulty condition (colors). The second and third panel depict the Q-value differences and the Q-value sums over time. The drift rates (right panel) are a weighted sum of the Q-value differences and Q-value sums, plus an intercept. Choice A (solid lines) refers to the option that had the high probability of reward during the acquisition phase, and choice B (dashed lines) to the option that had the high probability of reward after the reversal.

Multi-alternative choice

Finally, we again drew on the advantage framework (van Ravenzwaaij et al., 2020) to extend the RL-ARD to multi-alternative choice tasks, a domain where the RL-DDM cannot be applied. As in the two-choice case, the multi-alternative RL-ARD assumes one accumulator per pairwise difference between choice options. With three choice options (e.g. 1, 2, 3), there are six (directional) pairwise differences (1-2, 1-3, 2-1, 2-3, 3-1, 3-2), and therefore six accumulators (see Figure 9). All accumulators are assumed to race toward a common threshold, with their drift rates determined by the advantage framework’s combination of an urgency, an advantage, and a sum term. Since each response is associated with two accumulators (e.g. for option 1, one accumulating the advantage 1–2, and the other accumulating the advantage 1–3), a stopping rule is required to determine when a commitment to a response is made and evidence accumulation stops. Following Van Ravenzwaaij et al., we used the Win-All stopping rule, which proposes that the first response option for which both accumulators have reached their thresholds wins. RT is the first passage time of the slowest of these two winning accumulators, plus non-decision time.

Figure 9

Download asset Open asset

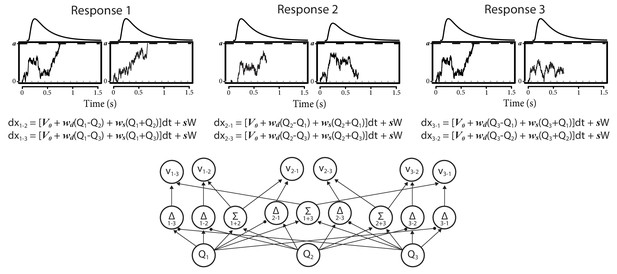
Architecture of the three-alternative RL-ARD.

In three-choice settings, there are three Q-values. The multi-alternative RL-ARD has one accumulator per directional pairwise difference, hence there are six accumulators. The bottom graph visualizes the connections between Q-values and drift rates ( $V_{0}$ is left out to improve readability). The equations formalize the within-trial dynamics of each accumulator. Top panels illustrate one example trial, in which both accumulators corresponding to response option 1 reached their thresholds. In this example trial, the model chose option 1, with the RT determined by the slowest of the winning accumulators (here, the leftmost accumulator). Decision-related parameters $V_{0}, w_{d}, w_{s}, a, t 0$ are all identical across the six accumulators.

To test how well the Win-All RL-ARD can explain empirical data, we performed a fourth experiment in which participants were required to repeatedly make decisions between three choice options (Figure 10). Within each of the four blocks, there were four randomly interleaved stimulus triplets that differed in difficulty (defined as the difference in reward probability between target stimulus and distractors) and reward magnitude (defined as the average reward probability): 0.8/0.25/0.25 (easy, high magnitude), 0.7/0.3/0.3 (hard, high magnitude), 0.7/0.15/0.15 (easy, low magnitude), and 0.6/0.2/0.2 (hard, low magnitude). This enabled us to simultaneously test whether the RL-ARD can account for a manipulation of difficulty and mean reward magnitude. Furthermore, we predicted that the requirement to learn 12 individual stimuli (per block) would interfere with the participants’ ability to rely on working memory (Collins and Frank, 2012), and therefore expected that the RL-ARD would provide a better account of accuracy in the early trial bins compared to experiments 1 and 2. After exclusions (see Materials and methods), data from 34 participants (432 trials each) were included in the analyses.

Figure 10

Download asset Open asset

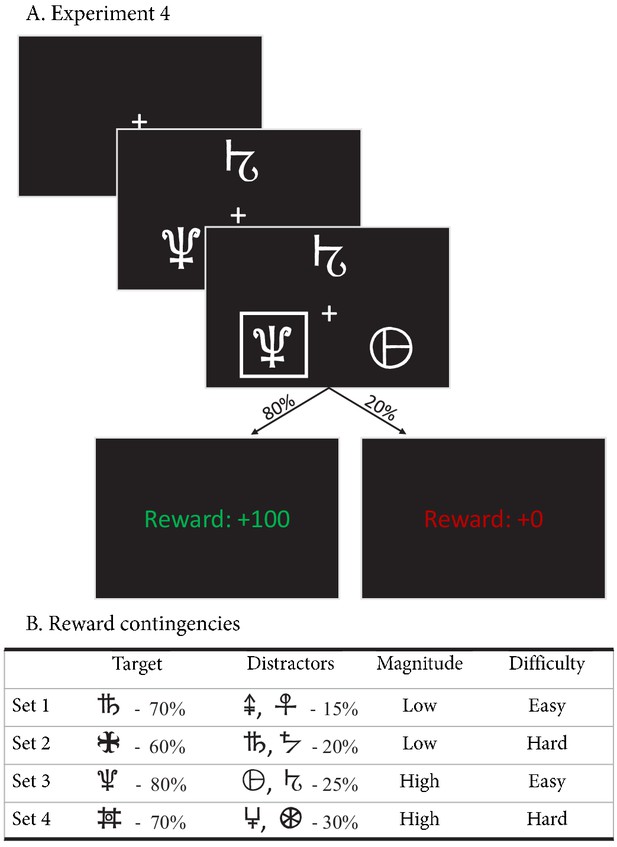
Experimental paradigm of experiment 4.

(A) Example trial of experiment 4. Each trial started with a fixation cross, followed by the stimulus (three choice options; until the subject made a choice, up to 3 s), a brief highlight of the choice, and the choice’s reward was shown. (B) Reward contingencies for the target stimulus and two distractors per condition. Percentages indicate the probability of receiving +100 points (+0 otherwise). Presented symbols are examples, the actual symbols differed per block and participant (counterbalanced to prevent potential item effects from confounding the learning process).

Data and posterior predictive distributions of the RL-ARD are shown in Figure 11. The top row represents accuracy, the middle row the RT quantiles corresponding to the correct (target) choice option, and the bottom row the RT quantiles of the incorrect choices (collapsed across the two distractor response options). Compared to experiments 1–3, the task was substantially more difficult, as evidenced by the relatively low accuracies. The RL-ARD model was able to account for all patterns in the data, including the increase in accuracy and decrease in RTs due to learning, the shape of the full RT distributions, as well as the difficulty and magnitude effects. Furthermore, there was a decrease in variance in the error RTs due to learning (the 10th quantile RTs even mildly increased), which was also captured by the model. Note finally that, contrary to experiments 1 and 2, the model did not underestimate the accuracy in early bins in the easy conditions, which suggests that the influence of working memory was, as predicted, more limited than in earlier experiments. A parameter recovery study (Figure 11—figure supplement 1) demonstrated that the model’s parameters could be recovered accurately.

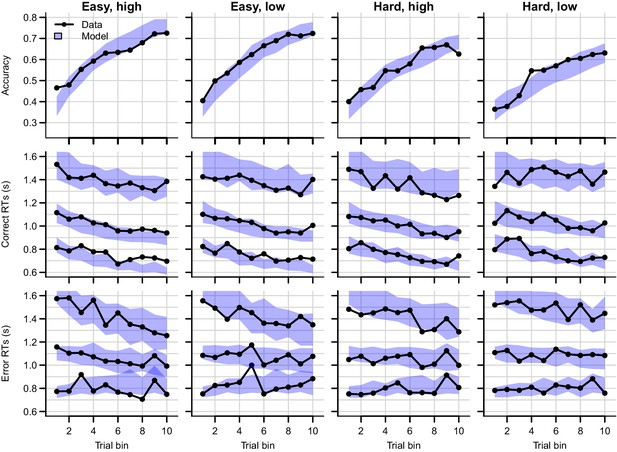
Figure 11 with 3 supplements see all

Download asset Open asset

Data (black) and posterior predictive distribution of the RL-ARD (blue), separately for each difficulty condition.

Column titles indicate the magnitude and difficulty condition. Top row depicts accuracy over trial bins. Middle and bottom rows show 10th, 50th, and 90th RT percentiles for the correct (middle row) and error (bottom row) response over trial bins. The error responses are collapsed across distractors. Shaded areas correspond to the 95% credible interval of the posterior predictive distributions. All data and fits are collapsed across participants.

Notably, Figure 11 suggests that the effects of the magnitude manipulation were larger in the hard than in the easy condition. As in previous experiments, we inspected the Q-value evolution (Figure 12) to understand how this interaction arose. As expected, the high magnitude condition led to higher Q-values (Figure 12A) than the low magnitude condition, increasing the Q-value sums (Figure 12C). However, there was a second effect of the increased magnitude: even though the true reward probability differences were equal between magnitude conditions, the Q-value differences for the response accumulators ( ${Δ Q}_{T - D}$ ; Figure 12B) were larger in the high compared to the low magnitude condition, particularly for harder choices. As a consequence, both the Q-value sum (weighted by median $w_{s} = 0.15$ ), and the smaller changes in the Q-value difference (weighted by median $w_{d} = 1.6$ ), increased the drift rates for the response accumulators ( $v_{T - D}$ ; Figure 12D), which led to higher accuracy and faster responses.

Figure 12

Download asset Open asset

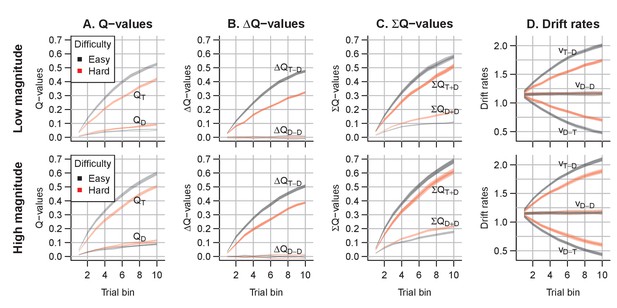
Q-value evolution in experiment 4.

Top row corresponds to the low magnitude condition, bottom to the high magnitude condition. Colors indicate choice difficulty. (A) Q-values for target ( $Q_{T}$ ) and distractor stimuli ( $Q_{D}$ ). (B) Difference in Q-values, for target – distractor ( $Δ Q_{T - D}$ ) and between the two distractors ( $Δ Q_{D - D}$ ). The Q-value difference $Δ Q_{D - T}$ is omitted from the graph to aid readability (but $Δ Q_{D - T} = - Δ Q_{T - D}$ ). (C) Sum of Q-values. (D) Resulting drift rates for target response accumulators ( $v_{T - D}$ ), and accumulators for the distractor choice options ( $v_{D - T}, v_{D - D})$ . Note that within each condition, there is a single Q-value trace per choice option, but since there are two distractors, there are two overlapping traces for $Δ Q_{T - D}$ , $Σ Q_{T + D}$ , and for all drift rates.

Discussion

We compared combinations of different evidence-accumulations models with a simple delta reinforcement learning rule (RL-EAMs). The comparison tested the ability of the RL-EAMs to provide a comprehensive account of behavior in learning contexts, not only in terms of the choices made but also the full distribution of the times to make them (RT). We examined a standard instrumental learning paradigm (Frank et al., 2004) that manipulated the difference in rewards between binary options (i.e. decision difficulty). We also examined two elaborations of that paradigm testing key phenomena from the decision-making and learning literatures, speed-accuracy trade-offs (SAT), and reward reversals, respectively. Our benchmark was the dual threshold Diffusion Decision Model (DDM; Ratcliff, 1978), which has been used in almost all previous RL-EAM research, but has not been compared to other RL-EAMs, and has not been thoroughly evaluated on its ability to account for RT distributions in learning tasks. Our comparison used several different racing diffusion (RD) models, where decisions depend on the winner of a race between single barrier diffusion processes.

The RL-DDM provided a markedly inferior account to the other models, consistently overestimating RT variability and skew. As these aspects of behavior are considered critical in evaluating models in decision-making literature (Forstmann et al., 2016; Ratcliff and McKoon, 2008; Voss et al., 2013), our results question whether the RL-DDM provides an adequate model of instrumental learning. Furthermore, the DDM carries with it two important theoretical limitations. First, it can only address binary choice. This is unfortunate given that perhaps the most widely used clinical application of reinforcement learning, the Iowa gambling task (Bechara et al., 1994), requires choices among four options. Second, the input to the DDM combines the evidence for each choice (i.e., ‘Q’ values determined by the learning rule) into a single difference, and so requires extra mechanisms to account for known effects of overall reward magnitude (Fontanesi et al., 2019a). Although there are potential ways that the RL-DDM might be modified to account for magnitude effects, such as increasing between-trial drift rate variability in proportion to the mean rate (Ratcliff et al., 2018), its inability to extend beyond binary choice remains an enduring impediment.

The best alternative model that we tested, the RL-ARD (advantage racing diffusion), which is based on the recently proposed advantage accumulation framework (van Ravenzwaaij et al., 2020), remedied all of these problems. The input to each accumulator is the weighted sum of three components: stimulus independent ‘urgency’, the difference between evidence for the choice corresponding to the accumulator and the alternative (the advantage), and the sum of the two evidence values. The urgency component had a large effect in all fits and played a key role in explaining the effect of speed-accuracy trade-offs. Although an urgency mechanism such as collapsing bounds (Boehm et al., 2016; Bowman et al., 2012; Hawkins et al., 2015; Milosavljevic et al., 2010) or gain modulation (Boehm et al., 2016; Churchland et al., 2008; Ditterich, 2006; Hawkins et al., 2015) could potentially improve the fits of the RL-DDM, fitting DDMs with such mechanisms is computationally very expensive, usually requiring the researcher to use simulation-based approximations (e.g. Turner and Sederberg, 2014). This expense becomes infeasible in the case of RL-EAMs since these models assume different drift rates per trial, requiring the simulation of an entire dataset per trial in the empirical data (for each iteration of the MCMC sampling process). Furthermore, the origin of the concept of urgency lies in studies using racing accumulator models (Ditterich, 2006; Mazurek et al., 2003; Reddi and Carpenter, 2000), which was only later incorporated in the DDM (Milosavljevic et al., 2010); the implementation in the RL-ARD remains conceptually close to the early proposals.

The advantage component of the RL-ARD, which is similar to the input to the DDM, was strongly supported over a model in which each accumulator only receives evidence favoring its own choice. The sum component provides a simple and theoretically transparent way to deal with reward magnitude effects in instrumental learning. Despite having the weakest effect among the three components, the sum was clearly necessary to provide an accurate fit to our data. It also played an important role in explaining the effect of reward reversals.

In all our models, we assumed a linear function to link Q-value differences to drift rates. This may not be adequate in all settings. For example, Fontanesi et al., 2019a showed (within an RL-DDM) that a non-linear linking function provided a better fit to their data. This could be caused by a non-linear mapping between objective values and subjective values; the account of perceptual choice using the advantage framework (van Ravenzwaaij et al., 2020) relied on a logarithmic mapping between (objective) luminance and (subjective) brightness magnitudes. Prospect Theory (e.g. Tversky and Kahneman, 1992) also assumes that increasingly large objective values relative to a reference point lead to increasingly small increases in subjective value. Such non-linear effects only become evident for sufficiently large differences over an appropriate range. Although in our experiments the RL-ARD was able to explain the data well using a simple linear function, future applications may need to explicitly incorporate a non-linear value function.

Finally, we showed that the RL-ARD can be extended to multi-alternative choice. In a three-alternative instrumental learning experiment, it accurately predicted the learning curves and full RT distributions for four conditions that differed in difficulty and reward magnitude. Furthermore, examination of Q-value evolution clarified how the reward magnitude manipulation led to the observed behavioral effects. Notably, the number of choice options only changes the architecture of the RL-ARD while the number of parameters remains constant, and all accumulators in the model remain driven by the same three components: an urgency signal, an advantage, and a sum component. As a consequence, parametric complexity does not increase with number of choices and the model remained fully recoverable despite the relatively low number of trials.

It is perhaps surprising that the RL-DDM consistently overestimated RT variability and skewness given that the DDM typically provides much better fits to data from perceptual decision-making tasks without learning. The inclusion of between-trial variability in non-decision times partially mitigated the misfit but required an implausibly high non-decision time variability, and model comparisons still favored the RL-ARD. Previous work on the RL-DDM did not investigate this issue. In many RL-DDM papers, RT distributions are either not visualized at all, or are plotted using (defective) probability density functions on top of a histogram of RT data, making it hard to detect misfit, particularly with respect to skew due to the slow tail of the distribution. One exception is Pedersen and Frank, 2020, whose quantile-based plots show the same pattern that we found here of over-estimated variability and skewness for more difficult choice conditions, despite including between-trial variability in non-decision times. In a non-learning context, it has been shown that the DDM overestimates skewness in high-risk preferential choice data (Dutilh and Rieskamp, 2016). Together these results suggest that decision processes in value-based decision in general, and instrumental learning tasks in particular, may be fundamentally different from a two-sided diffusion process, and instead better captured by a race model such as the RL-ARD.

In the current work, we chose to use racing diffusion processes over the more often used LBA models for reasons of parsimony: error-driven learning introduces between-trial variability in accumulation rates, which are explicitly modeled in the RL-EAM framework. As the LBA includes between-trial variability in drift rates as a free parameter, multiple parameters can account for the same variance. Nonetheless, exploratory fits (see Figure 4—figure supplement 3) confirmed our expectation that an RL-ALBA (Advantage LBA) model fit the data of experiment one well, although formal model comparisons preferred the RL-ARD. Future work might consider completely replacing one or more sources of between trial variability in the LBA with structured fluctuations due to learning and adaption mechanisms.

The parametrization of the ARD model used in the current paper followed the ALBA model proposed by van Ravenzwaaij et al., 2020. This parametrization interprets the influence on drift rates in terms of advantages and magnitudes. However, as both the weights on Q-value differences and sums ( $w_{d}$ and $w_{s}$ ) are freely estimated parameters, the equations that define the drift rates can be rearranged as follows:

\begin{array}{ll} d x_{1} = [V_{0} + w_{e} Q_{1} - w_{i} Q_{2}] d t + s W \\ d x_{2} = [V_{0} + w_{e} Q_{2} - w_{i} Q_{1}] d t + s W \end{array}

where $w_{e} = w_{d} + w_{s}$ in the parametrization of Equation 4, and $w_{i} = w_{d} - w_{s}$ . This re-parametrization shows that each drift rate is determined by an excitatory influence $w_{e}$ of the Q-value associated with the accumulator, and an inhibitory influence $w_{i}$ of the Q-value associated with the other accumulator. Turner, 2019 proposed that inhibition plays an important role in learning tasks. Although the locus of inhibition is different in the two models, there are clear parallels that bear further investigation.

A limitation of the current work is that we collapsed across blocks in analyzing the data of experiments 2, 3, and 4. However, in more detailed explorations (see Figure 6—figure supplement 3) there were indications of second-order changes across blocks. In experiment 2, participants were faster in the first trial bin of the second and third block compared to the first block, suggesting additional practice or adaptation effects at the beginning of the experiment. In experiment 3, participants slowed down, and learned the reversal faster, after the first block. This suggests they learned about the presence of reversals in the first block and applied a different strategy in the later blocks. Although it is known that participants increase their learning rates in volatile environments (Behrens et al., 2007), this by itself does not explain a decrease in response speed. Potentially, if participants understood the task structure after the first block, model-based strategies, such as estimating the probability of a reversal having occurred, also slowed down responses. In experiment 4, participants were slower (but equally accurate) in the first block compared to the later blocks, suggesting again additional practice or adaptation effects. Future experiments should investigate the nature of these additional adaptation effects.

Although the account of data provided by the RL-ARD model was generally quite accurate, some elements of misfit suggest the need for further model development. RT and accuracy were underestimated in the initial trials of the easiest condition in experiment 1, in the accuracy emphasis condition in experiment 2, and prior to reversals in experiment 3. Furthermore, the RL-ARD model underestimated the speed with which choice probability changed after reversal of stimulus-response mappings. These misfits point to a limited ability to capture the learning-related changes in behavior. This is to some degree unsurprising, since we used a very simple model of error-driven learning. Future work might explore more sophisticated mechanisms, such as multiple learning rates (Daw et al., 2002; Fontanesi et al., 2019a; Gershman, 2015; Pedersen et al., 2017) or different learning rules (Fontanesi et al., 2019b; Fontanesi et al., 2019a). Furthermore, there is clearly a role for working memory in some reinforcement learning tasks (Collins and Frank, 2018; Collins and Frank, 2012), likely explaining the accurate but slow responses we observed in the early trial bins for easy conditions in experiments 1–3. The multi-alternative choice experiment, with 12 individual stimuli per block, hampered participants’ ability to employ working memory strategies, so even early-trial performance was explained by purely error-driven learning.

In summary, we believe that the ARD decision mechanism provides a firm basis for further explorations of the mutual benefits that arise from the combination of reinforcement learning and evidence-accumulation models, providing constraint that is based on a more comprehensive account of data than has been possible in the past. As it stands, the RL-ARD’s parameter recovery properties are good even with relatively low trial numbers, making it a suitable measurement model for simultaneously studying learning and decision-making processes, and inter-individual differences therein. Further, the advantage framework extends to multiple choice while maintaining analytical tractability and addressing key empirical phenomena in that domain, such as Hick’s Law and response-competition effects (van Ravenzwaaij et al., 2020), enabling future applications to clinical settings, such as in the Iowa gambling task (Bechara et al., 1994).

Materials and methods

Experiment 1

Participants

61 participants (mean age 21 years old [SD 2.33], 47 women, 56 right handed) were recruited from the subject pool of the department of Psychology, University of Amsterdam, and participated for course credits. All participants had normal or corrected-to-normal vision and gave written informed consent prior to the experiment onset. They did not participate in the other experiments. The study was approved by the local ethics committee.

Share this article

Cite this article

Comparison of the decision-making models.

Paradigms for experiments 1–3.

Comparison of posterior predictive distributions of the four RL-EAMs.

Posterior parameter estimates (across-subject mean and SD of the median of the posterior distributions) for all models and experiments.

Data (black) and posterior predictive distribution of the RL-ARD (blue), separately for each difficulty condition.

The evolution of Q-values and their effect on drift rates in the RL-ARD.

Data (black) and posterior predictive distributions (blue) of the best-fitting RL-DDM (left columns) and the winning RL-ARD model (right columns), separate for the speed and accuracy emphasis conditions.

Experiment three data (black) and posterior predictive distributions (blue) for the RL-DDM (left) and RL-ARD (right).

The evolution of Q-values and their effect on drift rates in the RL-ARD in experiment 3, aggregated across participants.

Architecture of the three-alternative RL-ARD.

Experimental paradigm of experiment 4.

Data (black) and posterior predictive distribution of the RL-ARD (blue), separately for each difficulty condition.

Q-value evolution in experiment 4.

Author details

Steven Miletić

Contribution

For correspondence

Competing interests

Russell J Boag

Contribution

Competing interests

Anne C Trutti

Contribution

Competing interests

Niek Stevenson

Contribution

Competing interests

Birte U Forstmann

Contribution

Competing interests

Andrew Heathcote

Contribution

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Research organism

Further reading